Exact Treatment of the Ground States of Three Two-Dimensional Contact Interactions in a Uniform Magnetic Field

Abstract

The Green function for an electron confined to a plane in the presence of a uniform perpendicular magnetic field is derived and is decorated by several modified Dirac delta functions (MDF). In each case the ground state energy is examined as a function of the field strength, the spacing and the coupling constant of the MDFs. The results suggest that the magnetic field is ionising and the strength of the MDFs must attain a field-dependent critical value in order that a bound state be formed. This offers a new perspective on the question of whether a static magnetic field can be ionising.

1. Introduction

The aim of this note is to propose an exactly solvable quantum-mechanical model based on contact interactions in accordance with the subject of this issue of $Symmetry$. To this end, we consider a particle in the presence of three static attractive modified two-dimensional Dirac delta functions (MDF) in a uniform magnetic field perpendicular to the plane formed by the MDFs. We examine the behaviour of the ground-state energy of the particle with respect to the strength of the MDF (assumed to be the same for all) and their configuration.

We consider the contact interactions introduced by Horing et al. [1,2] who have examined various energy levels of a a pair of dissimilar MDF subject to uniform magnetic fields. They call their contact potentials “quantum dots”, although this term generally refers to the more realistic Fock–Darwin parabolic model [3,4]. To avoid confusion we will not use their term. Furthermore, their analysis is based on truncating a slowly convergent series representation of the exact Green function used here. For completeness, we shall also investigate the one and two MDF models.

To introduce the modified contact interaction, the zero field case is treated next for a single “MDF”( the two “MDF” case is examined in the Appendix A) More detailed information can be found in [5].

The Schroedinger equation for the Hamiltonian $p^2/2m-\lambda \delta (\overrightarrow{r})$ in momentum space has the solution

$$\widehat{\psi }\left(p\right)=\frac{2m\lambda }{{\hslash }^2}\psi \left(0\right){[p^2+{\kappa }^2]}^{-1},\kappa =\sqrt{-2mE}/\hslash >0$$

(1)

Thus,

$$\psi \left(r\right)=\frac{2m\lambda }{{\hslash }^2}\psi \left(0\right)\int \frac{d\overrightarrow{k}}{{\left(2\pi \right)}^2}\frac{e^{i\overrightarrow{k}·\overrightarrow{r}}}{k^2+{\kappa }^2}=\frac{m\lambda }{\pi {\hslash }^2}\psi \left(0\right)K_0\left(\kappa r\right)$$

(2)

Now, to determine $\kappa$ one should set $r=0$ and cancel $\psi \left(0\right)$ to obtain a transcendental equation for $\kappa$, but this leads to $\psi \left(r\right)=0\mathrm{or}\infty$. To obtain sensible results we replace 0 by the cut-off a giving the transcendental equation

$$1=\frac{m\lambda }{\pi {\hslash }^2}{K}_0\left(\kappa a\right)$$

(3)

Setting $a=5\sqrt{2}$, say, for a MDF radius of roughly 6 Bohr units, gives the bound state energies shown in Figure 1.

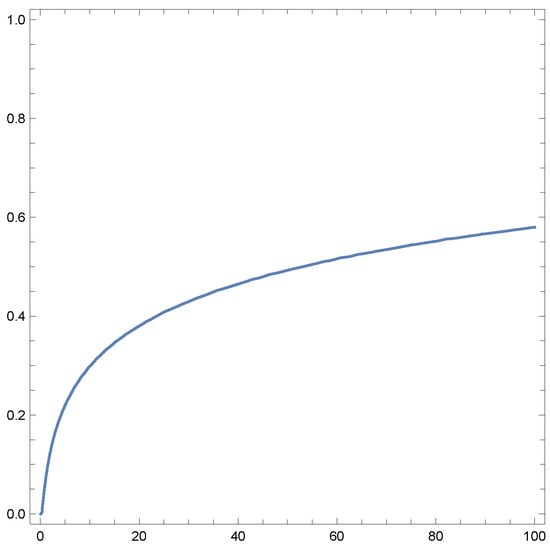
Figure 1. Single MDF: $\kappa$ vs. $\lambda$ for $B=0$, (atomic units).

Similarly, the zero field $\kappa$ vs $\lambda$ relation for two MDFs, given by (A5) (see Appendix A) is shown in Figure 2 for $a=2\sqrt{2}$ and separation distance $d=9$.

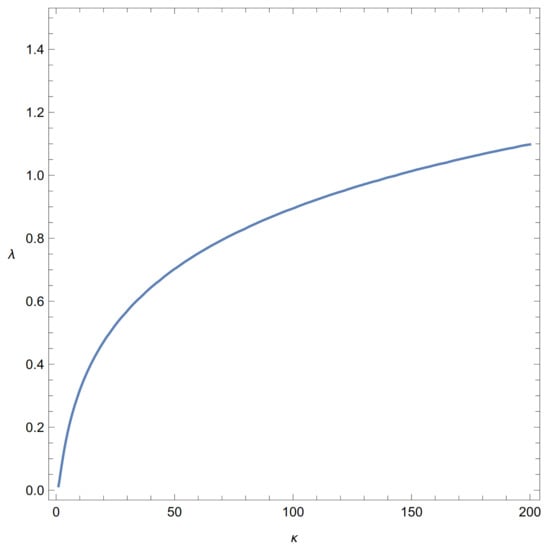
Figure 2. Two MDFs: $\kappa$ vs. $\lambda$ for $B=0$, $a=2\sqrt{2}$, $d=9$ (atomic units).

In the next section we work out a convenient form of the Green function for a charged particle in a plane subject only to a uniform perpendicular magnetic field $\overrightarrow{B}=\nabla \times \overrightarrow{A}$. In Section 3 this is applied to obtain the ground state equation for such a system decorated by N identical “fuzzy” delta functions, which is then solved for $N=1,2,3$ such quantum MDFs in various configurations. The note ends with a brief discussion of the results.

2. Green Function

The Green function for an electron, in two- and three-dimensions, in a uniform magnetic field $\overrightarrow{B}=B\widehat{z}=\nabla \times \overrightarrow{A}$ is closely related to the solution of the Sturm–Liouville problem for the Harmonic Oscillator solved in the 1850s and summarised briefly by Titchmarsh [6] in 1946. The result has been re-derived many times by a variety of techniques; a representative sample of these is contained in references [7,8,9,10,11,12]. We, next, present a brief derivation of the two-dimensional case g, ($\overrightarrow{r}=(x,y)$), in a form convenient for quantising fields in the z-direction.

For an electron system with energy levels $\left\{\alpha \right\}$ the resolvent operator is ($\hslash =2m=1$)

$$G=\sum _{\alpha }\frac{|\alpha ⟩⟨\alpha |}{w-\alpha }$$

(4)

Translation by the arbitrary vector $\overrightarrow{v}$ corresponds to the operator $T_v=e^{i\overrightarrow{v}·\overrightarrow{P}}$ where, in a magnetic field $\overrightarrow{B}=\nabla \times \overrightarrow{A}$, $\overrightarrow{P}=\overrightarrow{p}+e\overrightarrow{A}$ (in the symmetric gauge $\overrightarrow{A}=\frac{1}{2}\overrightarrow{B}\times \overrightarrow{r}$). Thus

$$T_{v}F\left(\overrightarrow{r}\right)=e^{\frac{1}{2}i\overrightarrow{v}·(\overrightarrow{B}\times \overrightarrow{r})}F(\overrightarrow{r}+\overrightarrow{v}).$$

(5)

Since $T_{\overrightarrow{v}}$ commutes with the Hamiltonian for a free particle, the Green function obeys

$$G(\overrightarrow{r},{\overrightarrow{r}}^{\prime };w)=$$

$$⟨\overrightarrow{r}\left|G\right|{\overrightarrow{r}}^{\prime }⟩=\sum _{\alpha }\frac{⟨\overrightarrow{r}|T_v|\alpha ⟩⟨|\alpha |T_v|{\overrightarrow{r}}^{\prime }⟩}{w-\alpha }=e^{i\overrightarrow{B}·\overrightarrow{V}\times (\overrightarrow{r}-\overrightarrow{r^{\prime }})}⟨\overrightarrow{r}+\overrightarrow{v}\left|G\right|{\overrightarrow{r}}^{\prime }+\overrightarrow{v}⟩$$

(6)

Next, choose $\overrightarrow{v}=-{\overrightarrow{r}}^{\prime }$ so in a magnetic field (with $\overrightarrow{\rho }=\overrightarrow{r}-{\overrightarrow{r}}^{\prime }$),

$$⟨\overrightarrow{r}\left|G\right|{\overrightarrow{r}}^{\prime }⟩=e^{\frac{1}{2}i\overrightarrow{B}·\overrightarrow{r}\times {\overrightarrow{r}}^{\prime }}⟨\overrightarrow{\rho }\left|G\right|0⟩$$

(7)

Suppose we change $\overrightarrow{A}\to \overrightarrow{A}+\nabla \varphi$. Then, in the new gauge the Green function becomes

$$⟨\overrightarrow{r}|e^{ie\varphi \left(\overrightarrow{r}\right)}G{e}^{-ie\varphi \left({\overrightarrow{r}}^{\prime }\right)}|{\overrightarrow{r}}^{\prime }⟩=e^{i[\varphi \left(\overrightarrow{r}\right)-\varphi \left({\overrightarrow{r}}^{\prime }\right])}⟨\overrightarrow{r}\left|G\right|{\overrightarrow{r}}^{\prime }⟩=e^{i\frac{1}{2}\overrightarrow{B}·(\overrightarrow{r}\times {\overrightarrow{r}}^{\prime })}{e}^{i[\varphi \left(\overrightarrow{r}\right)-\varphi \left({\overrightarrow{r}}^{\prime }\right)]}⟨\overrightarrow{\rho }\left|G\right|0⟩$$

(8)

i.e.,

$$G(\overrightarrow{r},{\overrightarrow{r}}^{\prime };E)=C(\overrightarrow{r},{\overrightarrow{r}}^{\prime })g({\overrightarrow{\rho }}^{\prime };E)$$

(9)

where the so-called Peierls factor C is unimodular and g is gauge invariant. Since C cancels out in what follows, we omit it and use the symmetric gauge. The cyclotron frequency ${\omega }_0=2eB/c$ serves as a field strength parameter.

We start with the well-known Green equation

$$\left\{-{\nabla }^2-ieB(y{\partial }_x-x{\partial }_y)+\frac{1}{4}{e}^2{B}^2(x^2+y^2)-E\right\}G(\overrightarrow{r},{\overrightarrow{r}}^{\prime };E)=-\delta (\overrightarrow{r}-{\overrightarrow{r}}^{\prime }),$$

(10)

where, in the causal variant, E has a positive infinitesimal imaginary part, and after introducing $\xi =\frac{1}{2}{\omega }_0{(\overrightarrow{r}-{\overrightarrow{r}}^{\prime })}^2$, find the inhomogeneous confluent hypergeometric equation $(\omega =E/{\omega }_0)$

$$\left\{\xi {\partial }_{\xi }^2+{\partial }_{\xi }-\frac{1}{4}\xi +\omega \right\}g(\xi ;\omega )=\frac{1}{4\pi }\delta \left(\xi \right).$$

(11)

whose homogeneous solution is

$$[A_1{}_1{F}_1(1/2-\omega ;1;\xi )+A_{2}U(1/2-\omega ;1;\xi )]e^{-\xi /2}.$$

(12)

The method of undetermined coefficients next yields,

$$g(\xi ;\omega )=-\frac{1}{4\sqrt{\xi }}\frac{sec\left(\pi \omega \right)}{\Gamma \left(\omega +\frac{1}{2}\right)}{W}_{\omega ,0}\left(\xi \right),$$

(13)

where the identity

$$U\left(\frac{1}{2}-w,1,s\right)=\frac{e^{s/2}{W}_{w,0}\left(s\right)}{\sqrt{s}}$$

(14)

has been incorporated and $W_{\kappa ,\mu }\left(z\right)$ is Whittaker’s confluent hypergeometric function [13].

3. Calculation

As introduced in Section 1, a point quantum MDF can be modelled by the contact potential $V\left(\overrightarrow{r}\right)=-\lambda \delta \left(\overrightarrow{r}\right)$, but to avoid divergences and to simulate a real dot we introduces a minimum radius ${\xi }_0=2a^2/\omega$ by imposing $g(0;\omega )=g({\xi }_0;\omega )$. As representative MDF radii of about 3.7 Bohr units, we have set $a=2\sqrt{2}$ and for an attractive quantum MDF, $\lambda >0$.

The Green function for N MDFs in a magnetic field can be worked out exactly [14], but is quite complicated. Fortunately, we only require its denominators $D_N$ whose smallest real roots correspond to the ground state energies. (For $N=1,2,3$, the complete expressions have been given in [2,14]). The eigenvalue equations are, for a single MDF

$$\alpha \left(a\right)=\beta$$

(15)

where

$$\beta =\frac{a\sqrt{8{\omega }_0}}{\lambda }$$

$$\alpha \left(c\right)=\frac{sec\left(\pi \omega \right)}{\Gamma (\omega +\frac{1}{2})}{W}_{\omega ,0}(\frac{1}{2}{\omega }_0{c}^2)$$

(16)

The solutions are shown in Figure 3

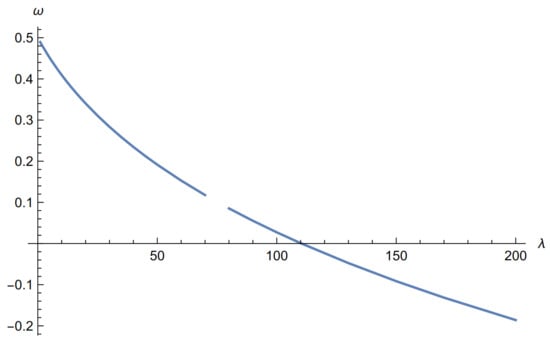
Figure 3. Single MDF: $\omega$ vs. $\lambda$ for ${\omega }_0=1$, $a=2\sqrt{2}$.

For two MDFs a Distance d Apart

The ground state is the lower root of the two equations

$$\alpha \left(a\right)\pm \frac{a}{d}\alpha \left(d\right)=\beta .$$

(17)

The ground state energy is shown in Figure 4 and Figure 5 for two MDFs separated by $9a_0$ in a weak field (${\omega }_0=1$) and in Figure 6 for ${\omega }_0=3$, $d=9$. Figure 7 also shows below.

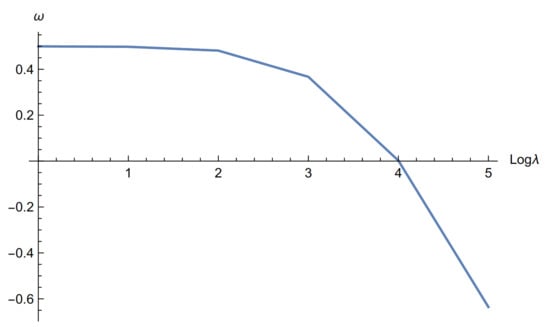
Figure 4. Single MDF: $\omega$ vs. $Log\left(\lambda \right)$ for ${\omega }_0=3$, $a=2\sqrt{2}$.

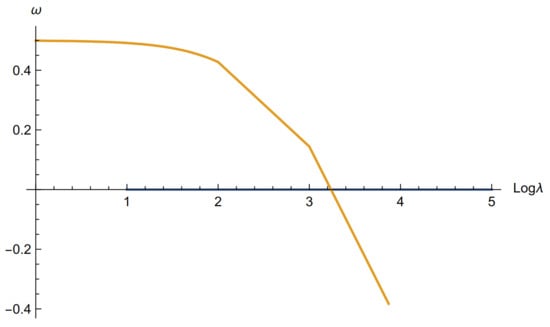
Figure 5. Two MDFs: $\omega$ vs. $\lambda$ for ${\omega }_0=1$, $a=5\sqrt{2}$, $d=9$ Bohr units.

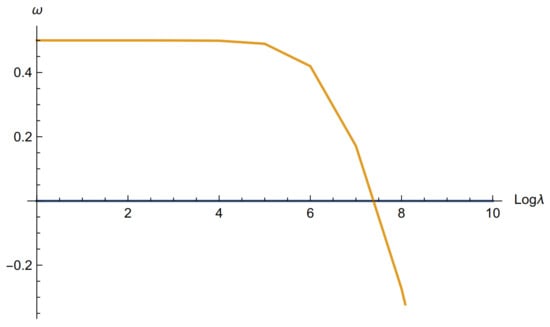
Figure 6. Two MDFs: $\omega$ vs. $\lambda$ for ${\omega }_0=3$, $a=5\sqrt{2}$,$d=9$ Bohr units.

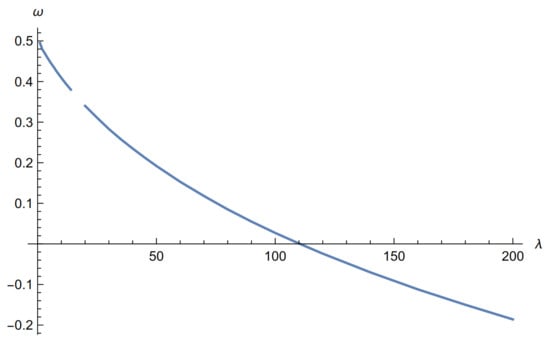
Figure 7. Triangle: $\omega$ vs. $\lambda$ for ${\omega }_0=1$, $a=2\sqrt{2}$, $d=9$.

In the case of an equilateral triangle of side d the eigenvalue equation can be written

$$3A(\lambda ,\omega )\{1-A(\lambda ,\omega )[1-{\rho }^2\left(\omega \right)]+\frac{1}{3}{A}^2(\lambda ,\omega )[1-{\rho }^3\left(\omega \right)]\}=1,$$

(18)

with

$$A(\lambda ,\omega )=\frac{\lambda }{a\sqrt{8{\omega }_0}}\frac{sec\left(\pi \omega \right)}{\Gamma (\omega +1/2)}{W}_{\omega ,0}({\omega }_0{a}^2/2)$$

(19)

$$\rho \left(\omega \right)=\frac{a{W}_{\omega ,0}({\omega }_0{d}^2/2)}{d{W}_{\omega ,0}({\omega }_0{a}^2/2)}$$

(20)

Finally, for three MDFs in a Row with Separation d one has the eigenvalue equation

$$3A(\lambda ,\omega )\{1-A(\lambda ,\omega [1-\frac{2}{3}{\rho }^2\left(\omega \right)]-\frac{1}{3}{A}^2(\lambda ,\omega )[1+{\rho }^2\left(\omega \right)\sigma \left(\omega \right)]\}=1,$$

(21)

where

$$\sigma \left(\omega \right)=\frac{a{W}_{\omega ,0}\left(2d^2{\omega }_0\right)}{d{W}_{\omega ,0}(a^2{\omega }_0/2)}.$$

(22)

4. Conclusions

The first striking result of this calculation is the loss of the bound state unless the magnitude of the coupling constant $\lambda$ exceeds a critical value, which is zero if the field strength is zero. This magnetic ionisation effect. is a feature of the $\lambda$-dependence of the ground state for all the configurations. The second is to note from Figure 8 and Figure 9 that for a row of MDFs the effect of Landau quantisation is evident, but not in the triangular case. Additionally, it is hard to account for the suppression of the ground state energy for very small $\lambda$ seen in Figure 9. It will be interesting to see if these features are preserved for a more realistic Quantum Dot model, such as the Fock–Darwin harmonic system. Figure 10 and Figure 11, below, show the value of $\lambda$ below which the bound state of a single MDF is ionised vs the cyclotron frequency. The dependence of the field on ${\lambda }_c$ is logarithmic. The values for all the configurations considered are identical.

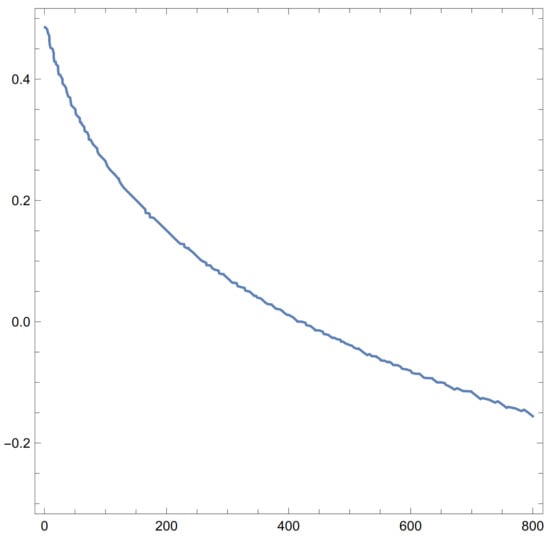
Figure 8. Triangle: $\omega$ vs. $\lambda$ for ${\omega }_0=3$, $a=2\sqrt{2}$, $d=9$.

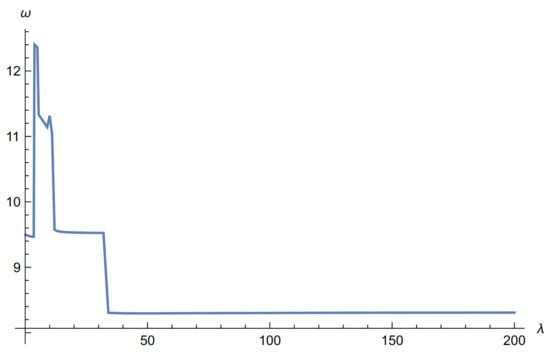
Figure 9. Three in row: $\omega$ vs. $\lambda$ for ${\omega }_0=1$$a=2\sqrt{2}$, $d=9$.

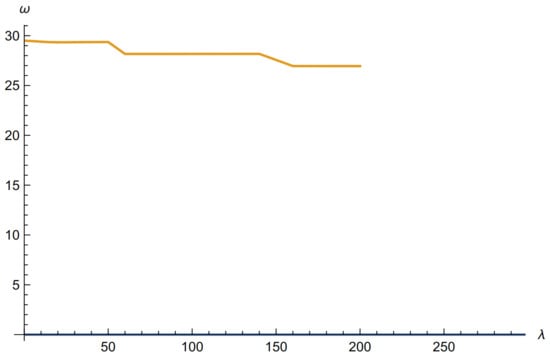
Figure 10. Three in row: $\omega$ vs. $\lambda$ for ${\omega }_0=3$$a=2\sqrt{2}$, $d=9$.

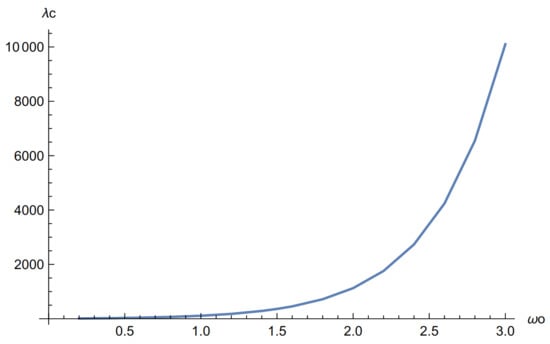
Figure 11. ${\lambda }_c$ vs. ${\omega }_0$ for all configurations.

The only previous study that has been made for two “MDFs” is [6] where the coupling constants, expressed in terms of well-depth, are allowed to be different. The authors of [6] have examined a number of excited states as well, but the results are insufficiently systematic to allow comparison with this work or to observe regularities. In addition, they use an approximate Green function obtained by truncating a slowly convergent series, which has been summed exactly in this work.