Abstract
In the present work, a neotype chaotic product trigonometric map (PTM) system is proposed. We demonstrate the chaotic characteristics of a PTM system by using a series of complexity criteria, such as bifurcation diagrams, Lyapunov exponents, approximate entropy, permutation entropy, time-series diagrams, cobweb graphs, and NIST tests. It is proved that the PTM system has a wider chaotic parameter interval and more complex chaotic performance than the existing sine map system. In addition, a novel PTM based symmetric image encryption scheme is proposed, in which the key is related to the hash value of the image. The algorithm realizes the encryption strategy of one-graph-one-key, which can resist plaintext attack. A two-dimensional coordinate traversal matrix for image scrambling and a one-dimensional integer traversal sequence for image pixel value transformation encryption are generated by the pseudo-random integer generator (PRING). Security analysis and various simulation test results show that the proposed image encryption scheme has good cryptographic performance and high time efficiency.
1. Introduction
Chaos is a common objective phenomenon in nature. It is also an important research branch of nonlinear science. The inherent characteristics of chaos are its high sensitivity to initial conditions and system parameters, unpredictability, pseudo-randomness, etc., which makes it penetrate into various scientific fields. In recent years, the application of chaos theory has attracted extensive attention. Applications of chaos can be seen everywhere, especially in multimedia data encryption in the case of confidential communication.
With the increasing frequency of network communication, information security has become an urgent problems that needs to be solved urgently, especially when dealing with information shared through the Internet or other publicly accessed communication channels. An important type of secret information that needs to be transmitted confidentially is picture data, because in many cases, pictures contain sensitive information that needs to be prevented from leakage, such as pictures related to national defence and personal privacy information [1,2]. Encryption plays an important role in the process of information security. Traditional encryption algorithms mainly include advanced encryption standard (AES) and data encryption standard (DES) [3]. Digital images are characterized by the high correlation between adjacent pixels and are also less sensitive to changes because small changes in pixel values do not translate in drastic changes in picture quality compared with text data [4]. As a result, conventional encryption methods (such as AES and DES) are not suitable for image encryption because of their significant time cost and computational resource consumption. In order to solve the above problems, many image safety measures have been proposed in recent years [5,6,7,8,9]. The safety measures based on chaos has the characteristics of fast encryption speed, high complexity, high security and reasonable computing power overhead. It is considered to be the best in practical applications.
Following C. E. Shannon [10], image encryption mainly has two key steps: confusion and diffusion. Diffusion means the relationship between plaintext and encrypted image. If a slight change in the original image can cause a complete change in the encrypted image, the encryption method is considered to be more effective. Confusion means the relationship between the secret key and the ciphertext image. Especially in this case, if changing one bit of the key produces different encrypted images, it is considered that the encryption method is more effective.
The traits of chaos also determine its role in the confidential communication occasion. From the expression of the mathematical model, chaotic systems can be divided into continuous time chaotic systems and discrete-time chaotic maps. Among them, the typical models of continuous time chaotic systems are Lorenz system, Chen system, among others. Typical discrete chaotic system models include the Arnold map, logistic map, sine map, Henon map and other models. According to another classification method of chaotic system model, a chaotic system can be divided into an integer form system and a fractional form system. In fact, a fractional system is a more general system model. Recently, some typical fractional chaotic maps have been proposed, such as Hénon–Lozi type map [11], which exhibits a rich complex dynamic behavior. In [12], a hyperchaotic fractional Grassi–Miller map is proposed and the hardware implementation of the hyperchaotic fractional map is carried out. In [13], a new fractional order chaotic map is proposed and explored. Regarding the application of chaos in image encryption, many works can be found in the literature. Some typical research works are listed below. Liu et al. [14] proposed a high-speed and safe image encryption scheme based on a new simple one-dimensional (1D) chaotic map. Although the key space of one-dimensional chaotic system is small, the structure of the 1D chaotic system is simple. When applied to image encryption, 1D chaotic maps have the advantages of faster speed and easier hardware implementation. The combination of good chaotic system and complex encryption algorithm can be better used for image encryption, which is undoubtedly the research hotspot of chaotic encryption. A discrete compound chaotic system based on sine trigonometric function and tent map is proposed in [9]. For large parameter space, it has good statistical characteristics. Li et al. [15] used piecewise linear chaotic mapping and trigonometric function to define generalized chaotic mapping. Yu et al. [16] studies the nonlinear dynamic system composed of cosine function with a large chaotic interval and strong chaotic characteristics. Trigonometric function itself has some unique characteristics, such as periodicity and boundedness, and their reciprocal is still a trigonometric function. The problem of chaotic system is solved, and encryption is also an important part of it. In [17], the authors proposed an image encryption algorithm by using bisection method and a 1D piecewise chaotic map. Gopalakrishnan et al. [18] used hyperchaotic system to generate a pseudo-random sequence, and used scrambling and diffusion encryption to encrypt the image. Zahmoul et al. [19] proposed a new 1D chaotic map, called Beta chaotic map, based on Beta function and used it in image encryption. Alawida et al. [20] proposed a new hybrid chaotic system combines two 1D chaotic maps and used it in a new image cryptosystem. Nepomuceno et al. [21] proposed a new image encryption algorithm based on the pseudo-orbits of a 1D chaotic map. Mansouri et al. [22] proposed an 1D sine powered chaotic map and sued it in image encryption. To expand the key space, Huang et al. [23] proposed an efficient symmetric image encryption by using a new 2D chaotic map. Askar et al. [24] utilized a 2D economic chaotic map and logistic map to design an image encryption algorithm. Khan et al. [25] proposed a new type of encryption method based on keys derived from DNA and plaintext image. Lu et al. [26] proposed an picture encryption scheme combining an S-Box and logistic–sine system.
Inspired by the works mentioned above, we construct a new one-dimensional chaotic system composed of product trigonometric function, which is more chaotic than the famous sine map system. The chaotic sequence generated by the system is used to encrypt the image, and the encryption effect is better. As far as we know, few articles used a triangular chaotic system for image encryption. Therefore, an image encryption research method based on product triangular chaotic mapping system is proposed in this paper. In order to improve the security and time efficiency of the encryption system, the proposed scheme uses equivalent encryption key associated with images, which can effectively resist chosen-plaintext attacks [27,28]. The encryption scheme combines scrambling and diffusion. The main contributions of the present work are as follows:
- (1)
- A new product trigonometric chaotic system is constructed. By means of various measures, the chaotic dynamic behavior of the system is analyzed in detail, and the good chaotic characteristics of the system are verified.
- (2)
- A novel symmetric image encryption scheme based on the novel product trigonometric chaotic system is proposed. The system consists of an efficient scrambling process and a secure diffusion operation. The secret keys are generated from the plaintext image by using SHA-256 to resist the chosen-plaintext attacks. Such that any slight change in the plaintext image will affect the whole ciphertext image.
- (3)
- The proposed scheme has been compared with some other recently proposed image encryption schemes. It is verified that the present work outperforms other previously published image encryption schemes and shows better cryptographic performance, while using less computational resources.
The rest of this paper is organized as follows: Section 2 introduces the mathematical model of PTM system and analyzes its chaotic dynamic characteristics. Section 3 describes the proposed image encryption and decryption algorithm. In Section 4, the security analysis and experimental evaluation of the proposed image encryption scheme are carried out. Section 5 summarizes the work and gives the conclusion of this paper.
2. The New Chaotic Product Trigonometric Map
2.1. The Sine Map System
In the field of chaos research, there is a well-known triangular chaotic system, that is, the sine map (SM) system, and its mathematical model is expressed by formula (1).
In Equation (1), xn denotes the state variable of the map at the n-th point of discrete time (n = 1, 2, …) and x1 denotes the initial state value. u denotes the system parameter. The chaotic dynamic behavior of the sine map is similar to that of the logistic map, and its chaotic interval is relatively narrow. Figure 1a,b are the bifurcation diagram and Lyapunov exponent graph of sine map to the system parameter u, respectively, and the range of chaotic parameter is u ∈ [3.4610, 4]. The width of the parameter interval of chaotic behavior is Δu = 0.5390, but there are still some narrow periodic windows in this interval.
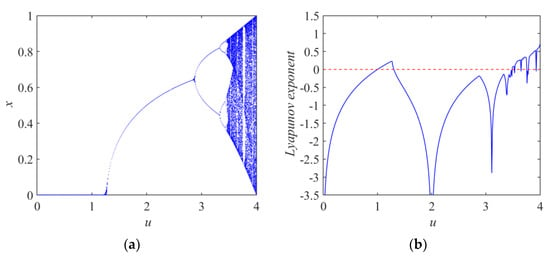
Figure 1.
Bifurcation diagram and Lyapunov exponent of sine map system. (a) Bifurcation of system state versus parameter u; (b) the graph of Lyapunov exponent versus parameter u.
2.2. The Proposed Chaotic Product Trigonometric Map
In this paper, a product trigonometric map (PTM) chaotic system was proposed. The PTM system can be expressed by mathematical model as Equation (2).
where are state variables of the system and u and k are two control parameters of the system. In this paper, we fixed k = 1.3.
2.2.1. Bifurcation and Lyapunov Exponent Diagram of PTM System
Considering the fixed k = 1.3, Figure 2a,b are the bifurcation diagram and Lyapunov exponent graph of the PTM system to the system parameter u, respectively. It can be observed that its chaotic parameter interval is u ∈ [2.5410, 5.180]. The width of the parameter interval of the chaotic behavior is Δu = 2.6390, which is far larger than the value 0.5390 of the sine map system, though there are also still some narrow periodic windows in this interval. Figure 2c,d are the bifurcation and Lyapunov exponent diagrams of the PTM system to the system parameter k, respectively. One can see that the chaotic range for k with fixed u = 5 is k ∈ (0, 2.558).
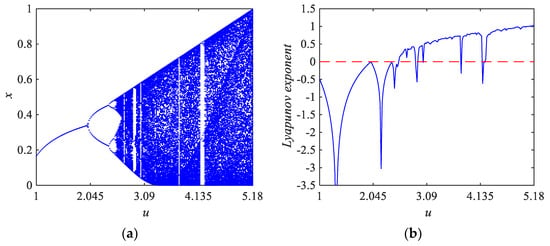
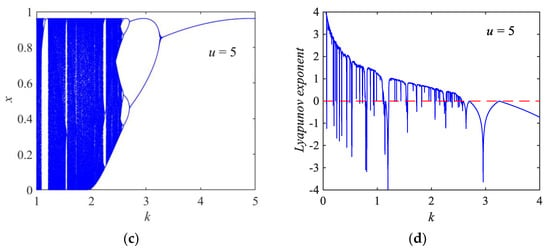
Figure 2.
Bifurcation diagram and Lyapunov exponent of the PTM chaotic system. (a) Bifurcation of system state versus parameter u; (b) Lyapunov exponent curve with parameter u. (c) Bifurcation scene with parameter k; (d) the graph of Lyapunov exponent versus parameter k.
2.2.2. Approximate Entropy and Permutation Entropy of PTM System
Approximate entropy (ApEn) and permutation entropy (PeEn) describe the complexity of time series from different angles, so it should be more convincing to detect the complexity of time series by two description methods.
Approximate entropy tests the probability of the new style generated in the sequences with the embedding dimension growth, which is a common technical indicator to describe the complexity and randomness of time series. If the approximate entropy of a time series is zero, it denotes that the time series is periodic. If the approximate entropy of a time series is greater than zero, it denotes that the time series is aperiodic. The larger the approximate entropy, the more complex the corresponding time series and the stronger the randomness. Figure 3a displays the approximate entropy of the sequences generated by PTM and SM systems with the system parameter u changes from 3.46 to 4. The results of Figure 3a show that the PTM system has an approximate entropy larger than zero in the whole parameter range u ∈ [3.46, 4], and its approximate entropy is greater than those of SM system in the whole parameter range. It is proved that the sequences generated by the PTM system are more complex than those of SM system.
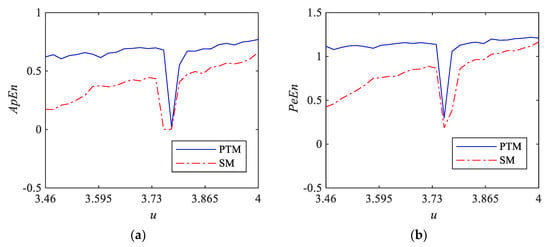
Figure 3.
Comparison of ApEn and PeEn of sequences generated by two systems. (a) The approximate entropy (ApEn) and (b) permutation entropy (PeEn).
Permutation entropy is another indicator to describe the complexity of time series, which uses Shannon’s entropy to measure the probabilities of different order types of consecutive values in the sequences. If the permutation entropy of a time series is zero, it means that the time series is periodic; if the permutation entropy of a time series is greater than zero, it means that the time series is aperiodic. The larger the permutation entropy, the more complex the corresponding time series. Figure 3b displays the permutation entropy of sequences generated by PTM and SM systems with the system parameter u changes from 3.46 to 4. From Figure 3b, one can see that the PTM system has a permutation entropy greater than zero in the whole parameter range u ∈ [3.46, 4], and the permutation entropy is greater than those of SM systems in the whole parameter range. The above results once again prove that PTM system is more complex than SM system.
2.2.3. The Time-Series and Cobweb Graph of PTM System
The time-series graph shows the behavior of the system state variable changing with time. Moreover, it shows the sensitivity of time series to the initial conditions. Figure 4a shows the trajectories of two time series with an initial state value difference of 10−12. The results of Figure 4a show that the evolution of system state values is very sensitive to the initial values, and the slight difference of the initial values causes a great separation between two adjacent orbits.

Figure 4.
Time-sequences and cobweb chart of PTM system. (a) Two time-series with two initial values have slight differences (x0 = 0.23 and y0 = 0.23 + 10−12); (b) the cobweb graph.
The cobweb diagram provides a powerful technical way to observe the motion behavior of the dynamic system. From its cobweb diagram, people can intuitively find out whether the motion behavior of the dynamic system is periodic orbit or chaotic orbit. Figure 4b displays the cobweb diagram generated by iterating the PTM system repeatedly. The system parameter is u = 5.18 and the initial state value is x0 = 0.11. From Figure 4b, one can see that the system traverses unlimited non-repetitive chaotic orbits, which proves the existence of a chaotic behavior of system (2) more intuitively.
2.2.4. The NIST Test of PTM System
NIST is a standard test software package to evaluate the stochastic performance of time series. NIST contains 15 test indicators, and multiple sequences are required. Each packet length of the sequence needs to reach 1,000,000 bits. It mainly uses two performance indicators: p-value and pass rate to measure the random performance of time series. Usually, 1000 binary sequences should be tested, and the default value of significant level is α = 0.01. If there are M sequences that have p-values greater than 0.01, then the pass rate is M/1000. The confidence interval used to test the pass rate is defined as: . When α = 0.01 and m = 1000, the confidence interval is 1 − 0.01 ± 3 = 0.99 ± 0.0094393 = [0.980561, 0.9994393], which means that the minimum pass rate must be above 980/1000.
In [29], the authors proposed a pseudo-random bit generator (PRBG) and measured its randomness NIST. This paper proposes a new PRBG based on the PTM system. In the experimental test for our pseudo-random bit generator, we iterated the PTM system with the initial value x0 = 0.2345 and the system parameter u = 3.9999 to generate a chaotic real number sequence with a length of 109, then convert it into a binary pseudo-random sequence with a length of 109 bits, and divide the sequence into 1000 groups, with each group having a length of 106 bits for NIST test. Here, the algorithm for converting a chaotic real number x into an 8-bit binary number uIntx is shown in Algorithm 1. Specifically, given a chaotic real number x, we transformed the real value of x to a 64-bit binary string, following the IEEE 754 double precision floating point number standard. Then, the binary digital numbers from 33-th to 40-th in each binary string were sampled as the output of Algorithm 1. Thus, each of the chaotic outputs generates an 8-bit binary numbers.
| Algorithm 1: Convert a chaotic real number x into an 8-bit binary number uIntx. |
| Input: A real number x |
| Output: A byte digital uIntx |
| 1: Convert the x to a 64-bit binary string b1b2…b64 following the IEEE 754 standard; |
| 2: Intercept 8 digits of the binary x to form unsigned integer: uIntx ← b33b34…b40; |
| 3: Output the unsigned integer uIntx in binary format. |
The results of NIST test with all 15 statistical tests are listed in Table 1. Among them, the cumulative sums and serial test contain 2 sub-tests, so there are actually 17 tests in total. The results show that all p-value > 0.01, and the least pass rate of every statistical test is 985/1000, which is larger than 0.980561.

Table 1.
NIST statistical test results for 1000 sequences of size 1 million bits.
3. Image Encryption and Decryption Algorithm
In order to comprehensively optimize the security and efficiency of the algorithm, this method realizes image replacement and diffusion encryption based on chaos. Additionally, the equivalent key is associated with the image content.
3.1. The Encryption Algorithm
Our proposed encryption scheme can be divided into three main stages. In the first stage, SHA-2 256 hash algorithm was used to obtain the hash of plaintext image, and the encryption key was generated from it. In this paper, SHA-2 256 was chosen instead of SHA-1 or SHA-3, which is a compromise between security and computational complexity. The hash string was quartered, and the value of each part was mapped to a decimal greater than 0 and less than 1, and this decimal was taken as the initial state value of the chaotic PTM system. Then, the initial state values and the control parameter u of the PTM were used to generate pseudorandom numbers. In the second phase, row and column permutation was performed on the pixels of the picture by using pseudorandom numbers generated by the chaotic PTM system. In the third stage, a diffusion operation was applied to the permutated image and the final encrypted image was obtained. Figure 5 shows the flow block diagram of the proposed encryption procedure.
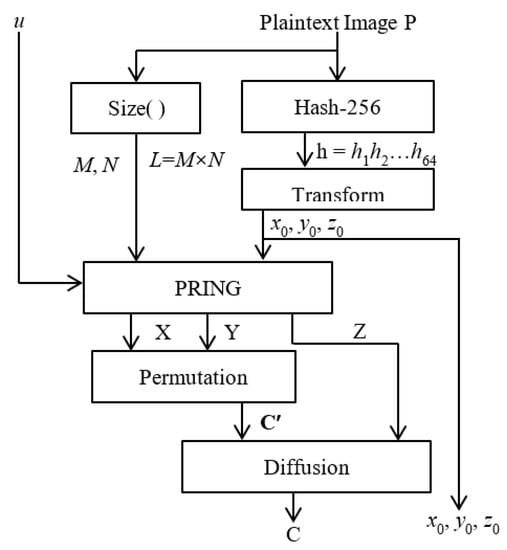
Figure 5.
The block diagram of the proposed encryption algorithm.
The detailed steps of this algorithm for image encryption are described in detail as follows. Each 2D matrix data can also be expressed as a 1D array by scanning it in row-by-row or column-by-column scan order. So, the 2D and 1D forms can be mutually converted. Hence, the 2D and 1D expression forms were not distinguished strictly in this paper.
Step 1: Read the plaintext image to be encrypted, and the data matrix of plaintext image is represented by P. Obtain the image size, that is, the number of pixel rows M and the number of columns N of the image. So, P = {p(i, j)}, i = 1, 2, …, M; j = 1, 2, …, N. p(i, j) represents the pixel value of the i-th row and the j-th column. Additionally, input the parameter u for the chaotic map (2).
Step 2: Apply SHA-256 on the plaintext image P to produce a hash value in hexadecimal digit string for the plaintext image. The string is composed of 64 hexadecimal digital symbols, and its shape is as follows: .
Step 3: Mapping the hash digit string into three decimal values as:
where ASCII(hi) represents the ASCII value of the character hi.
Step 4: Use the keys of {x0, y0, z0} produced in Step 3 as the initial value together with the parameter u for the chaotic map to output three pseudo-random integer number sequences X = {x(i)}, Y = {y(j)}, and Z = {z(l)}, respectively, by the pseudo-random integer number generator (PRING). Where, i = 1, 2, …, M; j = 1, 2, …, N; l = 1, 2, …, L = M × N. x(i) ∈ {1, 2, …, M} and x(i) ≠ x(i’) if i ≠ i’. y(j) ∈ {1, 2, …, N} and y(j) ≠ y(j’) if j ≠ j’. z(l) ∈ {1, 2, …, L} and z(l) ≠ z(l’) if l ≠ l’. Algorithm 2 explains the detailed steps of the pseudo-random integer number generator (PRING).
| Algorithm 2: Generating a pseudo random integer number sequence. |
| Input: x0, u, k, integer M |
| Output: A pseudorandom integer number sequence X with length of M |
| 1: Initialize: flag ← zeros(1, M); X ← zeros(1, M); x ← x0; |
| 2: Circularly generate M mutually different integers: 1, 2, …, M. |
| for i ← 1: M do |
| x ← u/4*sin(2π/k*x)*cos(π/k*x); |
| j ← mod(floor(x*10^12), M)+1; |
| while (flag(j) = 1) do |
| x ← u/4*sin(2π/k*x)*cos(π/k*x); |
| j ← mod(floor(x*10^12), M)+1; |
| end while |
| X(i) ← j; flag(j) ← 1; |
| end for i |
| 3: Output X = {X(i)} |
Step 5: Carry out row and column permutation on the picture by using pseudorandom number sequences X and Y to obtain the permutated image C’ = {c’(i, j)}, i = 1, 2, …, M; j = 1, 2, …, N. The permutation operations are as follows:
c’(i, j) = p(x(i), y(j)), i = 1, 2, …, M; j = 1, 2, …, N.
Step 6: Perform diffusion operation by using pseudorandom number sequence Z to obtain the final cipher-text image C = {c(i, j)}, i = 1, 2, …, M; j = 1, 2, …, N. The diffusion operations are as follows:
c(1) = bitxor(mod(z(1) + c’(1), 256), 255),
c(l) = bitxor(mod(z(l) + c’(l), 256), c(l − 1)), l = 2, 3, …, L.
Step 7: Output the final encrypted image matrix C.
Some comments about the PRINT: since the X sequence consists of M numbers in the set {1, 2, …, M}, each element x(i) in X is different from each other, the Y sequence consists of N numbers in the set {1, 2, …, N}, and each element y(j) in Y is also different from each other. The set composed of element pairs {(x(i), y(j))} is equivalent to a two-dimensional coordinate ergodic matrix, so the ergodic matrix can effectively realize the image scrambling operation. Similarly, the Z sequence is composed of L numbers in the set {1, 2, …, L} (L = M × N), and each element z(l) in Z is also different from each other. Therefore, the Z sequence is used for image pixel value replacement encryption, which can provide a different key for pixels in different positions.
3.2. The Decryption Algorithm
The decryption steps of the proposed scheme are elaborated as follows:
Step 1: Read the encrypted image C along with the hash value and the parameter u. Obtain the image size to get the values of M, N and L.
Step 2: Calculate {x0, y0, z0} by using Equation (3a–c).
Step 3: Use {x0, y0, z0} as initial values and parameter u for the PTM system (2) to produce pseudo-random number sequences X, Y, and Z.
Step 4: Perform inverse diffusion operation by using the pseudorandom number sequence Z to obtain the permutated image C’ = {c’(i, j)}, i = 1, 2, …, M; j = 1, 2, …, N. The inverse diffusion operations are as follows:
c’(i) = mod(bitxor(c(i), c(i − 1)) − z(i), 256), l = L, L − 1, L − 2, …, 2,
c’(1) = mod(bitxor(c(1), 255) − z(1), 256),
Step 5: Perform chaotic row and column permutation in reverse order using pseudo-random number sequences X and Y to obtain the deciphered image P = {p(i, j)}; the operation is expressed as follows:
p(x(i), y(j)) = c’(i, j), i = 1, 2, …, M; j = 1, 2, …, N.
Step 6: Output the decrypted image matrix P.
4. Security Analysis and Simulation Results
To check the validity of the proposed image encryption algorithm, we carried out simulation experiments with several standard test images, such as lena, cameraman, mandrill, peppers and boat that were obtained from the CVG-UGR image database (https://ccia.ugr.es/cvg/dbimagenes/ (accessed on 3 February 2022)), and other test images that were obtained from the miscellaneous volume of USC-SIPI image database. The USC-SIPI image database is available and maintained by the University of Southern California Signal and Image Processing Institute (http://sipi.usc.edu/database/ (accessed on 3 February 2022)). The secret key parameters of the cryptosystem were (x0, y0, z0, u). The simulation was carried out on the Matlab R2021b platform running on a computer with Intel Core i7-9700 @ 3.00GHz processor, 16 GB memory and Windows 10 operating system. In our simulation tests, the secret key parameters {x0, y0, z0} were generated with the plaintext image to be encrypted, and u was set as 5.167.
4.1. Encryption Effect
Figure 6 shows the four standard test images and their encrypted ones by the proposed algorithm. One can see that the encrypted images are not related to the original ones, and can no longer be understood.


Figure 6.
The standard test images and their encrypted ones. (a) The plaintext image cameraman. (b) The plaintext image peppers. (c) The plaintext all-white image. (d) The plaintext all-black image. (e) The encrypted image cameraman. (f) The encrypted image peppers. (g) The encrypted all-white image. (h) The encrypted all-black image.
4.2. Key Space Analysis
Since the original keys of {x0, y0, z0} were generated with the 256 bit plaintext image hash value, the parameter u was a double precision real number, which had 15 significant digits after the decimal point, and the total key space was 2256 × 1015 > 2305. At present, a cryptosystem is secure when the secret key space is larger than or equal to 2100. Hence, the secret key space of the proposed scheme was large enough to meet the safety requirements.
4.3. Histogram Analysis
The histogram of an image can vividly show the number distribution of pixels of various gray levels in an image. In order to resist various statistical analysis attacks, the histogram of an encrypted image should be uniformly distributed. Figure 7 shows the histogram of some histograms of several standard test images and their cipher-text images. We can see that every encrypted image has a uniformly distributed histogram and is significantly different from that of the plain image.
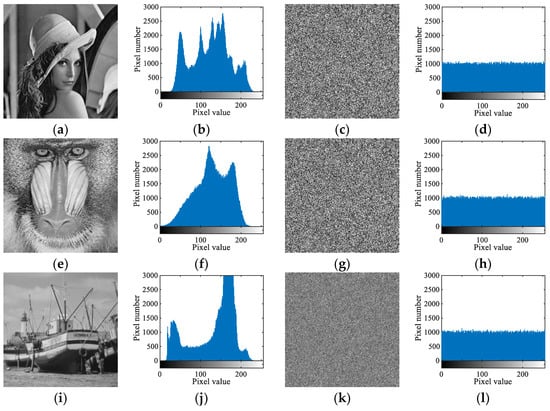
Figure 7.
Plaintext/encrypted images and their histograms. (a) Plaintext image lena. (b) Histogram of (a). (c) Encrypted image lena. (d) Histogram of (c). (e) Plaintext image mandrill. (f) Histogram of (e). (g) Encrypted image mandrill. (h) Histogram of (g). (i) Plaintext image boat. (j) Histogram of (i). (k) Encrypted image boat. (l) Histogram of (k).
Moreover, we adopted the chi-square test to further prove the uniformity of the histogram of the cipher-text image. The chi-square can be computed as follows:
where I represents the total gray level of the image; Oi represents the observed occurrence frequency of the i-th level gray; and Ei represents the expected ideal occurrence frequency of the i-th level gray. For a significance level α = 0.05, the critical value for 8-bit gray scale image (I = 256) is equal to χ2(255, 0.05) = 293.2478. The encrypted images should have a value lower than the critical value 293.2478. We applied the test on some images and their encrypted images, and the experimental results are listed in Table 2.

Table 2.
χ2 values of plaintext images and encrypted images by different algorithms.
From Table 2, one can see that all the experimental results are lower than the critical value, which indicates that the encrypted images have a uniform distribution. Compared with the results in [17], our proposed algorithm has lower values than those of the [17]. In conclusion, the encrypted image obtained by our scheme is more evenly distributed in terms of pixels, proving that the encrypted images can resist attacks based on the frequency distribution.
4.4. Information Entropy
Information entropy is a classical statistical test measure of uncertainty in information theory [10], which can be used to estimate the randomness of a dynamic system. Its calculation formula is shown in formula (9):
where S is a random variable and P(Si) is the probability of assurance of instance Si. For an 8-bit gray image, each pixel value is a random variable, and there are 256 possible values. If the probability of occurrence of each value is equal, then H(S) = 8. Generally speaking, the entropy of the actual image is always less than the ideal value of 8. Therefore, the closer the entropy is to 8, the better the image encryption effect. Table 3 lists the information results of this paper, and lists some comparative results. Therefore, the image encrypted by this method has a very ideal entropy value, and the multi-value is higher than other methods, which indicates that it has better cryptographic performance than the others.

Table 3.
Information entropy of encrypted images for several different algorithms.
4.5. Correlation Coefficients between Consecutive Pixels
This indicator measures the correlation degree of adjacent pixels in the image. A good encryption algorithm should make this correlation very small, that is, the absolute value of correlation coefficient should be close to 0. To assess local associations, this paper analyzed the correlation by calculating the correlation coefficients of the encrypted images in three adjacent directions. The method that the absolute value of correlation coefficient is closer to 0 was considered to be better. The calculation method of the correlation coefficient is shown in formulas (10)–(13):
Among them, (xi, yi) represent a pair of gray values of two adjacent pixels in the image and represents the number of total pairs of randomly selected pixels from the image. Some test images were tested, and the experimental results are listed in Table 4, which also lists some comparison results. Compared with the data reported in the literature, this algorithm achieved satisfactory results.

Table 4.
Correlation coefficients of the cipher images encrypted by different algorithms.
The correlation between adjacent pixels can also be intuitively displayed by the pixel value distribution graph. Figure 8 shows the distributions of adjacent pixels in the plaintext image Peppers and encrypted Peppers. From Figure 8, one can see that the adjacent points of the original image Peppers are distributed in a straight line or close to the straight line. After being encrypted, the adjacent points of the cipher-text image are evenly distributed, which effectively resists statistical attacks.
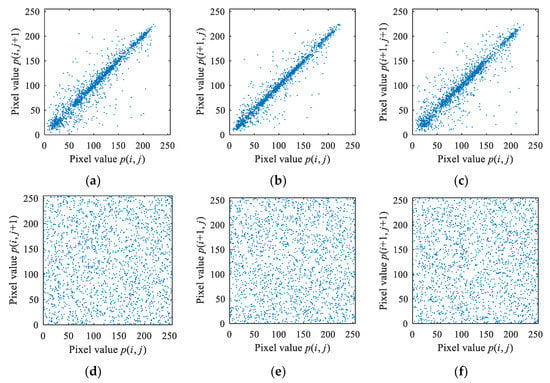
Figure 8.
Horizontal, vertical, and diagonal correlation point diagrams of plaintext image Peppers and encrypted image Peppers. (a) Original Peppers horizontal; (b) Original Peppers vertical; (c) Original Peppers diagonal; (d) Encrypted Peppers horizontal; (e) Encrypted Peppers vertical; adn (f) Encrypted Peppers diagonal.
4.6. Resistance to Differential Attacks
Differential cryptanalysis is based on finding the differences between different plaintext images and corresponding encrypted images. If the corresponding ciphertext images of two plaintext images with very small differences are very different, the stronger the ability of the algorithm to resist this attack. This ability is often described by two indicators, namely, the rate of change of the number of pixels (NPCR) and the unified average change intensity (UACI). Their calculation formulas are as follows:
where M and N are the row number and column number of the image. C is the one cipher image and C′ is another cipher image after changing a pixel value in plaintext image. C(i, j) is the pixel of cipher image C at the position (i, j) and C′(i, j) is the pixel of cipher image C′ at the position (i, j). The ideal values are NPCR = 99.6094% and UACI = 33.4635%. The larger the value of NPCR and UACI, the greater the difference between cipher-texts, and the better the algorithm is. In our experimental tests, NPCR and UACI are calculated by using Equations (14) to (16) for the Lena image five times. The average values of NPCR and UACI for the proposed method and other methods are shown in Table 5. The results show that the proposed method has satisfactory ability to resist differential cryptanalysis.

Table 5.
Values of NPCR and UACI in several different encryption schemes.
4.7. Time Performance Analysis
In the tests, the 256 × 256 size gray scale images were adopted as experimental images. The decryption speed of the methods introduced in this paper is listed in Table 6, and the results of the methods in the centralized literature are listed. The comparison shows that this proposed method has faster encryption speed than other methods.

Table 6.
Comparison of encryption and decryption time for a 256 × 256 size image (second).
5. Conclusions
This paper proposes a new chaotic product trigonometric map (PTM) system and a symmetric image encryption algorithm based on the PTM system. Firstly, we proposed a new PTM system, and demonstrated the chaotic characteristics of a PTM system by using a series of chaotic performance criteria, and proves that the new PTM system shows larger chaotic parameter interval and more complex chaotic behavior than the existing sine map system, which makes PTM system have better application value in image encryption. Furthermore, this PTM system is applied to image encryption. A scrambling-diffusion structure image encryption algorithm is proposed, in which the key is related to the hash value of the image. The algorithm realizes the encryption strategy of one-graph-one-key, which can resist plaintext attack. The pseudo-random integer generation algorithm designed can generate a two-dimensional coordinate traversal matrix for image scrambling. Additionally, a one-dimensional integer traversal sequence is generated for image pixel value transformation encryption. Image scrambling algorithm based on two-dimensional coordinate traversal matrix can quickly achieve good scrambling effect. Cipher-text feedback mechanism is introduced in the process of pixel value transformation encryption, which can improve cipher-text diffusion performance. Security analysis and various simulation test results show that the proposed image encryption scheme has good cryptographic performance and little time cost, showing its good application potential in real-time secure communication applications.
Author Contributions
Conceptualization, C.Z. and Q.L.; methodology, L.Y.; software, C.Z.; validation, C.Z., Q.L., and L.Y.; formal analysis, C.Z.; investigation, Q.L.; resources, Q.L.; data curation, Q.L.; writing—original draft preparation, Q.L.; writing—review and editing, C.Z. and L.Y.; visualization, C.Z.; supervision, C.Z.; project administration, Q.L. and L.Y.; funding acquisition, Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Open Research Fund of Key Laboratory of Network Crime Investigation of Hunan Provincial Colleges under Grant 2020WLFZZC002, in part by the Science and Technology Innovation Leading Plan for High-tech Industry of Hunan Province (Science and Technology Tackling) Project under Grant 2020GK2029, in part by the Scientific Research Excellent Youth Project of Hunan Education Department under Grant 21B0849, and in part by the National Natural Science Foundation of China under Grant 62071496.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable.
Acknowledgments
The authors are thankful to the reviewers for their comments and suggestions to improve the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ahmad, J.; Masood, F.; Shah, S.A.; Jamal, S.S.; Hussain, I. A Novel Secure Occupancy Monitoring Scheme Based on Multi-Chaos Mapping. Symmetry 2020, 12, 350. [Google Scholar] [CrossRef] [Green Version]
- Masood, F.; Boulila, W.; Ahmad, J.; Arshad; Sankar, S.; Rubaiee, S.; Buchanan, W.J. A Novel Privacy Approach of Digital Aerial Images Based on Mersenne Twister Method with DNA Genetic Encoding and Chaos. Remote Sens. 2020, 12, 1893. [Google Scholar] [CrossRef]
- Buell, D. Modern Symmetric Ciphers—DES and AES. In Fundamentals of Cryptography; Morgan Kaufmann: Burlington, MA, USA, 2021; pp. 123–147. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Khan, J.S.; Ahmad, J. Chaos based efficient selective image encryption. Multidimens. Syst. Signal Process. 2019, 30, 943–961. [Google Scholar] [CrossRef]
- Lu, Q.; Yu, L.; Zhu, C. A New Conservative Hyperchaotic System-Based Image Symmetric Encryption Scheme with DNA Coding. Symmetry 2021, 13, 2317. [Google Scholar] [CrossRef]
- Zhu, S.; Deng, X.; Zhang, W.; Zhu, C. A New One-Dimensional Compound Chaotic System and Its Application in High-Speed Image Encryption. Appl. Sci. 2021, 11, 11206. [Google Scholar] [CrossRef]
- Masood, F.; Ahmad, J.; Shah, S.A.; Jamal, S.S.; Hussain, I. A Novel Hybrid Secure Image Encryption Based on Julia Set of Fractals and 3D Lorenz Chaotic Map. Entropy 2020, 22, 274. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Wang, G.; Zhu, C. A Secure and Fast Image Encryption Scheme based on Double Chaotic S-Boxes. Entropy 2019, 21, 790. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Wang, X.; Pham, V.-T.; Boulaaras, S.; Momani, S. Bifurcation and chaos in the fractional form of Hénon-Lozi type map. Eur. Phys. J. Spec. Top. 2020, 229, 2261–2273. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Oussaeif, T.-E.; Pham, V.-T.; Grassi, G.; Dibi, Z. Hyperchaotic fractional Grassi–Miller map and its hardware implementation. Integration 2021, 80, 13–19. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Boulaaras, S.; Pham, V.-T.; Azar, A.T. A fractional map with hidden attractors: Chaos and control. Eur. Phys. J. Spec. Top. 2020, 229, 1083–1093. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. A new simple one-dimensional chaotic map and its application for image encryption. Multimed. Tools Appl. 2018, 77, 21445–21462. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Liu, X. A fast and efficient hash function based on generalized chaotic mapping with variable parameters. Neural Comput. Appl. 2016, 28, 1405–1415. [Google Scholar] [CrossRef]
- Yu, W.; Yu, T. Analysis of chaotic characteristics of trigonometric function system. Mod. Phys. Lett. B 2020, 34, 2050210. [Google Scholar] [CrossRef]
- Elghandour, A.N.; Salah, A.M.; Elmasry, Y.A.; Karawia, A.A. An Image Encryption Algorithm Based on Bisection Method and One-Dimensional Piecewise Chaotic Map. IEEE Access 2021, 9, 43411–43421. [Google Scholar] [CrossRef]
- Gopalakrishnan, T.; Ramakrishnan, S. Image Encryption Using Hyper-chaotic Map for Permutation and Diffusion by Multiple Hyper-chaotic Maps. Wirel. Pers. Commun. 2019, 109, 437–454. [Google Scholar] [CrossRef]
- Zahmoul, R.; Ejbali, R.; Zaied, M. Image encryption based on new Beta chaotic maps. Opt. Lasers Eng. 2017, 96, 39–49. [Google Scholar] [CrossRef]
- Alawida, M.; Samsudin, A.; Teh, J.S.; Alkhawaldeh, R.S. A new hybrid digital chaotic system with applications in image encryption. Signal Process. 2019, 160, 45–58. [Google Scholar] [CrossRef]
- Nepomuceno, E.G.; Nardo, L.G.; Arias-Garcia, J.; Butusov, D.N.; Tutueva, A. Image encryption based on the pseudo-orbits from 1D chaotic map. Chaos 2019, 29, 061101. [Google Scholar] [CrossRef]
- Mansouri, A.; Wang, X. A novel one-dimensional sine powered chaotic map and its application in a new image encryption scheme. Inf. Sci. 2020, 520, 46–62. [Google Scholar] [CrossRef]
- Huang, H.; Yang, S.; Ye, R. Efficient symmetric image encryption by using a novel 2D chaotic system. IET Image Process. 2020, 14, 1157–1163. [Google Scholar] [CrossRef]
- Askar, S.; Karawia, A.; Al-Khedhairi, A.; Al-Ammar, F. An Algorithm of Image Encryption Using Logistic and Two-Dimensional Chaotic Economic Maps. Entropy 2019, 21, 44. [Google Scholar] [CrossRef] [Green Version]
- Khan, J.S.; Boulila, W.; Ahmad, J.; Rubaiee, S.; Rehman, A.U.; Alroobaea, R.; Buchanan, W.J. DNA and Plaintext Dependent Chaotic Visual Selective Image Encryption. IEEE Access 2020, 8, 159732–159744. [Google Scholar] [CrossRef]
- Lu, Q.; Zhu, C.; Deng, X. An Efficient Image Encryption Scheme Based on the LSS Chaotic Map and Single S-Box. IEEE Access 2020, 8, 25664–25678. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, C. Security Analysis and Improvement of an Image Encryption Cryptosystem Based on Bit Plane Extraction and Multi Chaos. Entropy 2021, 23, 505. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, C. An efficient chosen-plaintext attack on an image fusion encryption algorithm based on DNA operation and hyperchaos. Entropy 2021, 23, 804. [Google Scholar] [CrossRef]
- Stoyanov, B.; Kordov, K. Image Encryption Using Chebyshev Map and Rotation Equation. Entropy 2015, 17, 2117–2139. [Google Scholar] [CrossRef]
- Yan, X.; Wang, X.; Xian, Y. Chaotic image encryption algorithm based on arithmetic sequence scrambling model and DNA encoding operation. Multimed. Tools Appl. 2021, 80, 10949–10983. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).