Product of Hessians and Discriminant of Critical Points of Level Function Attached to Sphere Arrangement

Abstract

We state the product formulae of the values of the levels of functions at critical points involved in asymptotic behaviors of hypergeometric integrals associated with symmetric arrangements of three-dimensional spheres. We show, in an explicit way, how the product of the Hessian, regarding the level functions at all critical points, is related to the behavior of its critical points. We also state two conjectures concerning the same problem associated with general hypersphere arrangements.

1. Introduction

For a given ${\alpha }_{j0}\in \mathbb{R}$ and ${\alpha }_j=({\alpha }_{j1},\dots ,{\alpha }_{jn})\in {\mathbb{R}}^n$$(j=1,2,\dots ,n+1)$, let $f_j$ be real quadratic polynomials in $\mathbb{R}\left[x\right]=\mathbb{R}[x_1,\dots ,x_n]$ specified by

$$f_j\left(x\right):=(x,x)+2({\alpha }_j,x)+{\alpha }_{j0}=|x+{\alpha }_j{|}^2-{\left|{\alpha }_j\right|}^2+{\alpha }_{j0},$$

where $(x,y):={\sum }_{\nu =1}^n{x}_{\nu }{y}_{\nu }$ and ${\left|x\right|}^2:=(x,x)$ for $x=(x_1,\dots ,x_n)$, $y=(y_1,\dots ,y_n)\in {\mathbb{R}}^n$. Let $O_j$ be the point $-{\alpha }_j\in {\mathbb{R}}^n$, which is the center of the hypersphere $\{x\in {\mathbb{R}}^n|f_j\left(x\right)=0\}$. The radius $r_i>0$ of $S_i$ and the distance ${\rho }_{jk}>0$ between $O_j$ and $O_k$ are given by

$$r_j^2=-{\alpha }_{j0}+|{\alpha }_j{|}^2\mathrm{and}{\rho }_{jk}^2={|{\alpha }_j-{\alpha }_k|}^2,$$

respectively. In this paper we assume that the points $O_1,\dots ,O_{n+1}\in {\mathbb{R}}^n$ make an n-simplex, so that without loss of generality, we may assume the following:

$${\alpha }_{j\nu }=0(1\le j\le n+1,n-j+1<\nu \le n)\mathrm{and}{\alpha }_{j,n-j+1}>0(1\le j\le n),$$

(1)

i.e.,

$$\begin{array}{cc}\hfill O_1& =-{\alpha }_1=-({\alpha }_{11},{\alpha }_{12},\dots ,{\alpha }_{1,n-2},{\alpha }_{1,n-1},{\alpha }_{1n}),{\alpha }_{1n}>0,\hfill \\ \hfill O_2& =-{\alpha }_2=-({\alpha }_{21},{\alpha }_{22},\dots ,{\alpha }_{2,n-2},{\alpha }_{2,n-1},0),{\alpha }_{2,n-1}>0,\hfill \\ \hfill O_3& =-{\alpha }_3=-({\alpha }_{31},{\alpha }_{32},\dots ,{\alpha }_{3,n-2},0,0),{\alpha }_{3,n-2}>0,\hfill \\ \hfill & ⋮⋮\hfill \\ \hfill O_n& =-{\alpha }_n=-({\alpha }_{n1},0,\dots ,0,0,0),{\alpha }_{n1}>0,\hfill \\ \hfill O_{n+1}& =-{\alpha }_{n+1}=(0,0,\dots ,0,0,0).\hfill \end{array}$$

Here, we consider the $n-1$ dimensional hyperspheres $f_j\left(x\right)=0$ in ${\mathbb{C}}^n$, i.e., we define $S_j$ as

$$S_j=\{x\in {\mathbb{C}}^n|f_j\left(x\right)=0\}.$$

For $\lambda =({\lambda }_1,\dots ,{\lambda }_{n+1})\in {\mathbb{R}}^{n+1}$ let $\mathsf{\Phi }\left(x\right)=\mathsf{\Phi }(x_1,\dots ,x_n)$ be a multiplicative meromorphic function on ${\mathbb{C}}^n$ specified by

$$\mathsf{\Phi }\left(x\right):=\prod _{j=1}^{n+1}{f}_j{\left(x\right)}^{{\lambda }_j}.$$

We set $X:={\mathbb{C}}^n-{\bigcup }_{j=1}^{n+1}{S}_j$. For $0\le r\le n$, we denote by ${\mathsf{\Omega }}^r={\mathsf{\Omega }}^r(X,★{\bigcup }_{j=1}^{n+1}{S}_j)$ the space of rational r-forms on X whose singularities all lie in the set ${\bigcup }_{j=1}^{n+1}{S}_j$. For the complex

$${\mathsf{\Omega }}^{·}:0\to {\mathsf{\Omega }}^0\stackrel{\nabla }{⟶}{\mathsf{\Omega }}^1\stackrel{\nabla }{⟶}{\mathsf{\Omega }}^2\stackrel{\nabla }{⟶}\cdots \stackrel{\nabla }{⟶}{\mathsf{\Omega }}^n\stackrel{\nabla }{⟶}0,$$

where $\nabla :{\mathsf{\Omega }}^r\to {\mathsf{\Omega }}^{r+1}$ is the covariant derivation given by

$$\nabla \psi :=d\psi +dlog\mathsf{\Phi }\wedge \psi (\psi \in {\mathsf{\Omega }}^r),$$

the rth twisted de Rham cohomology $H_{\nabla }^r(X,{\mathsf{\Omega }}^{·})$ is defined by

$$H_{\nabla }^r(X,{\mathsf{\Omega }}^{·}):=\mathrm{Ker}(\nabla :{\mathsf{\Omega }}^r\to {\mathsf{\Omega }}^{r+1})/\mathrm{Im}(\nabla :{\mathsf{\Omega }}^{r-1}\to {\mathsf{\Omega }}^r).$$

See [1,2] for more details. For $\phi \left(x\right)d{x}_1\wedge \cdots \wedge d{x}_n\in {\mathsf{\Omega }}^n$ as a representative in $H_{\nabla }^n(X,{\mathsf{\Omega }}^{·})$, the hypergeometric integral associated with $\mathsf{\Phi }\left(x\right)$ over an n-twisted cycle $\mathfrak{z}$ is defined as

$${\mathcal{J}}_{\lambda }(\phi ;\mathfrak{z}):={\int }_{\mathfrak{z}}\mathsf{\Phi }\left(x\right)\phi \left(x\right)d{x}_1\wedge \cdots \wedge d{x}_n={\int }_{\mathfrak{z}}\phi \left(x\right)\prod _{j=1}^{n+1}{f}_j{\left(x\right)}^{{\lambda }_j}d{x}_1\wedge \cdots \wedge d{x}_n.$$

For an arbitrary integer N, we put $\lambda =N\mu +{\lambda }^{\prime }$, where $\mu =({\mu }_1,\dots ,{\mu }_{n+1})\in {\mathbb{Z}}^{n+1}$ and ${\lambda }^{\prime }=({\lambda }_1^{\prime },\dots ,{\lambda }_{n+1}^{\prime })\in {\mathbb{R}}^{n+1}$ are fixed. When $\phi \left(x\right)$ is independent of N, we are interested in the asymptotic behavior of the following integral as $N\to \infty$ in the direction $\mu$:

$${\mathcal{J}}_{N\mu +{\lambda }^{\prime }}(\phi ;\mathfrak{z})={\int }_{\mathfrak{z}}{e}^{NF\left(x\right)}\phi \left(x\right)\prod _{j=1}^{n+1}{f}_j{\left(x\right)}^{{\lambda }_j^{\prime }}d{x}_1\wedge \cdots \wedge d{x}_n,$$

where

$$F\left(x\right)=\sum _{j=1}^{n+1}{\mu }_{j}log{f}_j\left(x\right).$$

For the real valued level function $\mathfrak{Re}F$ corresponding to $|e^{NF\left(x\right)}|=e^{N\mathfrak{Re}F\left(x\right)}$, the singularity of the gradient flow of $\mathbf{v}=\mathrm{grad}\mathfrak{Re}F$ in X coincides with the set of its critical points given by

$$\mathcal{C}:=\{x\in X|dF\left(x\right)=\sum _{j=1}^{n+1}{\mu }_{j}dlog{f}_j\left(x\right)=0\}.$$

(2)

By definition $dF$ is explicitly written as

$$dF=\sum _{j=1}^{n+1}{\mu }_{j}dlog{f}_j=\sum _{\nu =1}^n\left(\sum _{j=1}^{n+1}\frac{{\mu }_j}{f_j}\frac{\partial f_j}{\partial x_{\nu }}\right)d{x}_{\nu }=\sum _{\nu =1}^n\left(\sum _{j=1}^{n+1}{\mu }_j\frac{2(x_{\nu }+{\alpha }_{j\nu })}{f_j}\right)d{x}_{\nu }.$$

In this paper, we assume that the direction $\mu$ of the asymptotic behavior is specifically fixed as

$$\mu =\mathbf{1}=(1,1,\dots ,1)\in {\mathbb{Z}}^{n+1}.$$

Then, the set $\mathcal{C}$ of critical points given by (2) is rewritten as

$$\mathcal{C}=\{x\in X|G_1\left(x\right)=G_2\left(x\right)=\cdots =G_n\left(x\right)=0\},$$

(3)

where

$$G_{\nu }\left(x\right):=\frac{1}{2}\frac{\partial F}{\partial x_{\nu }}=\sum _{j=1}^{n+1}\frac{x_{\nu }+{\alpha }_{j\nu }}{f_j\left(x\right)}(\nu =1,2,\dots ,n).$$

The functions $G_{\nu }\left(x\right)$ $(\nu =1,2,\dots ,n)$ play an important role in describing the asymptotic behavior of $J_{N\mathbf{1}+{\lambda }^{\prime }}\left(\phi \right)$ for large N (see Theorems 4.9 and 4.10 in [1]). The Hessian of F is defined by $\mathrm{Hess}\left(F\right):=det{\left(\frac{{\partial }^{2}F}{\partial x_i\partial x_j}\right)}_{1\le i,j\le n},$ and is expressed as the Jacobian of $G_{\nu }\left(x\right)$ $(\nu =1,2,\dots ,n)$, i.e.,

$$\frac{1}{2^n}\mathrm{Hess}\left(F\right)=\frac{\partial (G_1,G_2,\dots ,G_n)}{\partial (x_1,x_2,\dots ,x_n)}.$$

(4)

According to the method of steepest decent (saddle-point method), if an n-twisted cycle $\mathfrak{z}$ includes the critical point (saddle point) $\mathbf{c}\in \mathcal{C}$ which gives the maximal value of $\mathfrak{Re}F$ on $\mathfrak{z}$, then the asymptotic behavior of ${\mathcal{J}}_{N\mathbf{1}+{\lambda }^{\prime }}(\phi ;\mathfrak{z})$$(N\to \infty )$ is expressed as

$${\mathcal{J}}_{N\mathbf{1}+{\lambda }^{\prime }}(\phi ;\mathfrak{z})\sim \mathsf{\Phi }\left(\mathbf{c}\right)\phi \left(\mathbf{c}\right)\sqrt{\frac{{\pi }^n}{{(-N)}^n{\mathrm{Hess}\left(F\right)|}_{x=\mathbf{c}}}}(N\to \infty ).$$

(5)

If $S_j$$(1\le j\le n+1)$ are located as general position in ${\mathbb{C}}^n$, for generic exponents $\lambda =({\lambda }_1,\dots ,{\lambda }_{n+1})\in {\mathbb{R}}^{n+1}$ the dimension of the nth cohomology $H_{\nabla }^n(X,{\mathsf{\Omega }}^{·})={\mathsf{\Omega }}^n/\nabla {\mathsf{\Omega }}^{n-1}$ as a $\mathbb{C}$-linear space is known to be $\kappa =2^{n+1}-1$, i.e., ${dim}_{\mathbb{C}}{H}_{\nabla }^n(X,{\mathsf{\Omega }}^{·})=\kappa$ (see [3,4] for hypergeometric integrals associated with hypersphere arrangements). The basis of $H_{\nabla }^n(X,{\mathsf{\Omega }}^{·})$ can generally be chosen as an NBC (non-broken circuit) basis for a commutative algebra associated with hypersphere arrangement (see [5]). The number $\kappa$ also coincides with the absolute value of the Euler number of X. It also equals the number of the critical points of the function F specified by (3) provided that they are non-degenerate and different from each other. We denote by ${\mathbf{c}}_j$$(1\le j\le \kappa )$ all of the critical points (real or imaginary) in X, i.e., $\mathcal{C}=\left\{{\mathbf{c}}_j\right|1\le j\le \kappa \}.$ For a rational function $\phi$ on X, we denote by $\mathcal{N}\left(\phi \right)$ the product of the critical values at all points in $\mathcal{C}$, i.e.,

$$\mathcal{N}\left(\phi \right):=\prod _{j=1}^{\kappa }\phi \left({\mathbf{c}}_j\right),$$

which is called the norm of $\phi$. Here, we state our first claim as follows.

Conjecture 1.

Suppose that $S_j$$(1\le j\le n+1)$ are located as general position in ${\mathbb{C}}^n$. Then,

$$\mathcal{N}\left(\mathrm{Hess}\right(F\left)\right)\ne 0$$

if and only if every critical point in $\mathcal{C}$ is different from each other.

Remark 1.

When Conjecture 1 holds true, if the n-dimensional stable Lagrangian cycles ${\mathfrak{z}}_j$ include ${\mathbf{c}}_j\in \mathcal{C}$ as their limiting points, respectively, then by (5) the pairing

$${\left({\mathcal{J}}_{N\mathbf{1}+{\lambda }^{\prime }}({\phi }_i;{\mathfrak{z}}_j)\right)}_{i,j=1}^{\kappa },$$

where ${\phi }_i\left(x\right)d{x}_1\wedge \cdots \wedge d{x}_n\in {\mathsf{\Omega }}^n$ are representatives in $H_{\nabla }^n(X,{\mathsf{\Omega }}^{·})$, satisfies the following asymptotic behavior

$$det{\left({\mathcal{J}}_{N\mathbf{1}+{\lambda }^{\prime }}({\phi }_i;{\mathfrak{z}}_j)\right)}_{i,j=1}^{\kappa }\sim \frac{{\prod }_{j=1}^{\kappa }\mathsf{\Phi }\left({\mathbf{c}}_j\right){\pi }^{n/2}}{\sqrt{{(-N)}^n\mathcal{N}\left(\mathrm{Hess}\left(F\right)\right)}}det{\left({\phi }_i\left({\mathbf{c}}_j\right)\right)}_{i,j=1}^{\kappa }(N\to \infty ),$$

which gives a criterion for $\mathbb{C}$-linear independence of the set $\left\{{\mathcal{J}}_{\lambda }({\phi }_i;\mathfrak{z})\right|1\le i\le \kappa \}$. This is a rough explanation as to why we consider Conjecture 1.

In this paper, one of our aims is to confirm Conjecture 1 when $n=3$ for a special pyramid $▵O_1{O}_2{O}_3{O}_4$. The result is stated in Theorem 4. For this purpose, we need to compute $\mathcal{N}\left(f_j\right)$ and $\mathcal{N}({\sum }_{j=1}^{n+1}{f}_j^{-1})$. In order to state the explicit expressions of $\mathcal{N}\left(f_j\right)$ and $\mathcal{N}\left({\sum }_{j=1}^{n+1}{f}_j^{-1}\right)$ we introduce the Cayley–Menger determinants as follows.

Consider the $(n+3)\times (n+3)$ symmetric matrix $B={\left(b_{ij}\right)}_{i,j=0,★,1,2,‥,n+1}$, whose entries are given by $b_{00}=0$, $b_{★★}=0$, $b_{0★}=b_{0j}=1$$(1\le j\le n+1)$, $b_{1★}=r_j^2$$(1\le j\le n+1)$, $b_{ij}={\rho }_{ij}^2$$(1\le i,j\le n+1)$, i.e.,

$$B=\left(\begin{array}{cccccccc}0& 1& 1& 1& 1& 1& \cdots & 1\\ 1& 0& r_1^2& r_2^2& r_3^2& r_4^2& \cdots & r_{n+1}^2\\ 1& r_1^2& 0& {\rho }_{12}^2& {\rho }_{13}^2& {\rho }_{14}^2& \cdots & {\rho }_{1,n+1}^2\\ 1& r_2^2& {\rho }_{21}^2& 0& {\rho }_{23}^2& {\rho }_{24}^2& \cdots & {\rho }_{2,n+1}^2\\ 1& r_3^2& {\rho }_{31}^2& {\rho }_{32}^2& 0& {\rho }_{34}^2& \cdots & {\rho }_{3,n+1}^2\\ 1& r_4^2& {\rho }_{41}^2& {\rho }_{42}^2& {\rho }_{43}^2& 0& \ddots & ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & \ddots & {\rho }_{n,n+1}^2\\ 1& r_{n+1}^2& {\rho }_{n+1,1}^2& {\rho }_{n+1,2}^2& {\rho }_{n+1,3}^2& \cdots & {\rho }_{n+1,n}^2& 0\end{array}\right).$$

The Cayley–Menger determinants are defined as the minors of the matrix of B. See [4].

Definition 1.

Denote by ${\rho }_{★j}={\rho }_{j★}$ the radius $r_j$ for $j\in \{1,2,\dots ,n+1\}$ or 0 for $j=★$. The determinant

$$B\left(\begin{array}{cc}0& J\\ 0& K\end{array}\right)=B\left(\begin{array}{c}0j_1\cdots j_p\hfill \\ 0k_1\cdots k_p\hfill \end{array}\right):=\left|\begin{array}{cccc}0& 1& \dots & 1\\ 1& {\rho }_{j_1{k}_1}^2& \cdots & {\rho }_{j_1{k}_p}^2\\ ⋮& ⋮& \ddots & ⋮\\ 1& {\rho }_{j_p{k}_1}^2& \dots & {\rho }_{j_p{k}_p}^2\end{array}\right|$$

is called the Cayley–Menger determinant, where $J=\{j_1,\dots ,j_p\}$ and $K=\{k_1,\dots ,k_p\}$ denote two subsets of the indices in $\{★,1,\dots ,n+1\}$. We simply write $B\left(0J\right)$ instead of $B\left(\begin{array}{cc}0& J\\ 0& J\end{array}\right)$. Notice that $B\left(0j\right)=-1$, $B(0★j)=2r_j^2>0$, $B\left(0jk\right)=2{\rho }_{jk}^2>0$ and

$$\begin{array}{cc}\hfill & B(0★jk)=-({\rho }_{jk}+r_j-r_k)({\rho }_{jk}-r_j+r_k)(-{\rho }_{jk}+r_j+r_k)({\rho }_{jk}+r_j+r_k),\hfill \\ \hfill & B\left(0jkl\right)=-({\rho }_{jk}+{\rho }_{jl}-{\rho }_{kl})({\rho }_{jk}-{\rho }_{jl}+{\rho }_{kl})(-{\rho }_{jk}+{\rho }_{jl}+{\rho }_{kl})({\rho }_{jk}+{\rho }_{jl}+{\rho }_{kl}).\hfill \end{array}$$

Using the Cayley–Menger determinants, the latter assumption of (1) is rewritten as

$$\prod _{k=1}^{n-j+1}{\alpha }_{n+1-k,k}=\sqrt{\frac{{(-1)}^{n-j}B(0jj+1\cdots n+1)}{2^{n-j+1}}}>0$$

for $j=1,2,\dots ,n$.

Throughout this paper, we suppose the condition

$$\left({\mathcal{H}}_0\right):B\left(0J\right)\ne 0\mathrm{and}B(0★J)\ne 0$$

for $J=\{j_1<j_2<\cdots <j_p\}\subset \{1,2,\dots ,n+1\}.$ The condition $\left({\mathcal{H}}_0\right)$ gives the moduli space of arrangement of n dimensional real hyperspheres in general position in ${\mathbb{C}}^n$.

Denote $D_j$ the n dimensional real open ball with boundary $\mathfrak{Re}{S}_j$ in ${\mathbb{R}}^n$, where $\mathfrak{Re}{S}_j=\{x\in {\mathbb{R}}^n|f_j\left(x\right)=0\}.$ One sees that

$${(-1)}^{\left|J\right|}B\left(0J\right)>0\mathrm{for\; all\; non-empty}J\subset \{1,2,\dots ,n+1\},$$

where $\left|J\right|$ is the cardinality of J. In general every real critical point lies in ${\bigcup }_{j=1}^{n+1}{D}_j$ or the real simplex $▵O_1\dots O_{n+1}$. If further

$${(-1)}^{\left|J\right|}B(0★J)<0\mathrm{for\; all\; non-empty}J\subset \{1,2,\dots ,n+1\},$$

then every intersection $\left({\bigcap }_{j\in J}{D}_j\right)\cap \left({\bigcap }_{k\in J^c}{\overline{D}}_k^c\right)$ is not empty, where ${\overline{D}}_k^c$ means the complement of the closure ${\overline{D}}_k$. There exists a unique critical point of $\mathfrak{Re}F$ (and so of F) there.

We now state the other claim of ours for the explicit forms of $\mathcal{N}\left(f_j\right)$ and $\mathcal{N}\left({\sum }_{j=1}^{n+1}{f}_j^{-1}\right)$ using the Cayley–Menger determinants.

Conjecture 2.

For $j=1,\dots ,n+1$ let $I_{\widehat{j}}$ be the set $\{1,2,\dots ,n+1\}-\left\{j\right\}$. Under the condition $\left({\mathcal{H}}_0\right)$, the norms $\mathcal{N}\left(f_j\right)$ and $\mathcal{N}\left({\sum }_{j=1}^{n+1}{f}_j^{-1}\right)$ are expressed as

$$\begin{array}{cc}\hfill & \mathcal{N}\left(f_j\right)=\frac{B(0★j)}{2{(n+1)}^{2^n}}\prod _{p=1}^n\prod _{\begin{array}{c}K\subset I_{\widehat{j}}\\ \left|K\right|=p\end{array}}\frac{B(0★jK)}{B\left(0K\right)}(1\le j\le n+1),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \mathcal{N}\left(\sum _{j=1}^{n+1}\frac{1}{f_j}\right)=2{(n+1)}^{2^{n+1}-1}\prod _{p=1}^{n+1}\prod _{\begin{array}{c}K\subset I_{\widehat{j}}\\ \left|K\right|=p\end{array}}\frac{B\left(0K\right)}{B(0★K)}.\hfill \end{array}$$

(7)

Remark 2.

We call φ theunit relative to the set of all critical points $\mathcal{C}$ if $\mathcal{N}\left(\phi \right)$ does not vanish under the condition $\left({\mathcal{H}}_0\right)$. In this sense $f_j$ and $\sum f_j^{-1}$ are all units if Conjecture 2 holds for them.

Remark 3.

If $n=2$, (6) of Conjecture 2 implies

$$\begin{array}{cc}\hfill \mathcal{N}\left(f_1\right)& =\frac{2r_1^2}{2·3^4}B(0★12)B(0★13)\frac{B(0★123)}{2{\rho }_{23}^2},\hfill \\ \hfill \mathcal{N}\left(f_2\right)& =\frac{2r_2^2}{2·3^4}B(0★12)B(0★23)\frac{B(0★123)}{2{\rho }_{13}^2},\hfill \\ \hfill \mathcal{N}\left(f_3\right)& =\frac{2r_3^2}{2·3^4}B(0★13)B(0★23)\frac{B(0★123)}{2{\rho }_{12}^2},\hfill \end{array}$$

which have been confirmed under the situation $r_1=r_2=r_3$. See Theorems 5.19 in [6]. Moreover, using these formulae, consequently $\mathcal{N}\left(\mathrm{Hess}\right(F\left)\right)$ is also obtained explicitly when $▵O_1{O}_2{O}_3$ is an arbitrary isosceles triangle under $r_1=r_2=r_3$. Thus, Conjecture 1 is confirmed when $n=2$, $r_1=r_2=r_3$ and ${\rho }_{12}={\rho }_{13}$. See also Corollary 7.16 in [6] for details.

Remark 4.

If $n=3$, (6) and (7) of Conjecture 2 are written as

$$\begin{array}{cc}\hfill \mathcal{N}\left(f_1\right)& =\frac{2r_1^2}{2·4^8}\frac{B(0★12)}{-1}\frac{B(0★13)}{-1}\frac{B(0★14)}{-1}\hfill \\ \hfill & \times \frac{B(0★123)}{2{\rho }_{23}^2}\frac{B(0★124)}{2{\rho }_{24}^2}\frac{B(0★134)}{2{\rho }_{34}^2}\frac{B(0★1234)}{B\left(0234\right)},\hfill \\ \hfill \mathcal{N}\left(\sum _{j=1}^4\frac{1}{f_j}\right)& =\frac{2·4^{15}}{2^4{\left(r_1{r}_2{r}_3{r}_4\right)}^2}\frac{B\left(01234\right)}{B(0★1234)}\prod _{1\le i<j<k\le 4}\frac{B\left(0ijk\right)}{B(0★ijk)}\prod _{1\le j<k\le 4}\frac{2{\rho }_{jk}^2}{B(0★jk)}.\hfill \end{array}$$

In Section 5, we shall prove Conjecture 2 in a special pyramid case ($n=3$) when the base triangle $▵O_1{O}_2{O}_3$ is regular and each edge length ${\rho }_{j4}(1\le j\le 3)$ and each radius $r_j(1\le j\le 4)$ are all equal respectively (see Corollary 2).

This paper is organized as follows. In Section 2 we confirm that Conjecture 2 holds for the very special case, where $▵O_1\dots O_{n+1}$ is the regular simplex and all hyperspheres $S_j$ have the same radius. The result is stated as Theorem 1. From Section 3 to Section 7, we discuss three-dimensional case. In Section 3, we introduce a special coordinate system (denoted by $t=(t_1,t_2,t_3)\in \tilde{X}\subset {\mathbb{C}}^3$) attached to a tetrahedron, i.e., the fundamental three-dimensional simplex $▵O_1{O}_2{O}_3{O}_4$, and by means of the projective map $\iota :\tilde{X}\to X;t\mapsto x$ we transfer the terms relative to $\mathcal{C}$ to those of $\tilde{\mathcal{C}}={\iota }^{-1}\mathcal{C}=\{t\in \tilde{X}|{\tilde{g}}_1={\tilde{g}}_2={\tilde{g}}_3=0\}$, where ${\tilde{g}}_j$ are polynomials in t of degree 3 given by (48). In particular, we call $t_1$ the basic parameter, and a rational curve $t_2={\omega }_2\left(t_1\right),t_3={\omega }_3\left(t_1\right)$ passing through specified points in $\tilde{\mathcal{C}}$, which we call the interpolation curve of those points in $\tilde{\mathcal{C}}$, plays an important role in this paper. In Section 4, we restrict ourselves to a special symmetric case when $▵O_1{O}_2{O}_3{O}_4$ is a pyramid with an axis of symmetry whose base triangle $▵O_1{O}_2{O}_3$ is regular and all spheres have the same radius. The critical points are classified into typical four parts ${\tilde{\mathcal{C}}}_j$$(1\le j\le 4)$. In Section 5, under the assumption ${\rho }_{12}\ne {\rho }_{14}$, for each ${\tilde{\mathcal{C}}}_j$ the interpolation curve $\omega \left(t_1\right)=(t_1,{\omega }_2\left(t_1\right),{\omega }_3\left(t_1\right))\in \tilde{X}$ is still significant, and we calculate the norms of several linear functions on $\tilde{X}$ solving the defining equation ${\psi }_j\left(t_1\right)=0$ of ${\tilde{\mathcal{C}}}_j$, where ${\psi }_j\left(t_1\right)$ is the characteristic function of ${\tilde{\mathcal{C}}}_j$ defined by ${\psi }_j\left(t_1\right):={\tilde{g}}_1\left(\omega \left(t_1\right)\right)$. Using these norms, we evaluate $\mathcal{N}\left(f_j\right)$ and $\mathcal{N}({\sum }_{j=1}^4{f}_j^{-1})$ and, thus, prove Conjecture 2 for our symmetric special case. See Corollary 2. In Section 6, we consider the other case, ${\rho }_{12}={\rho }_{14}$, i.e., the case where $▵O_1{O}_2{O}_3{O}_4$ is the regular tetrahedron. The results in this section compensate for those in Section 5. In Section 7, under the same constraint as Section 5, we shall show the explicit formula for the norm $\mathcal{N}\left(\mathrm{Hess}\right(F\left)\right)$ of the Hessian of the level function F relative to the critical points $\mathcal{C}$. The formula is expressed in terms of the discriminant associated with $\mathcal{C}$ (or equivalently $\tilde{\mathcal{C}}$), see the invariants ${\mathsf{\Delta }}_2$, ${\mathsf{\Delta }}_3$ and ${\mathsf{\Delta }}_4$ in Theorem 4. Consequently, we also prove Corollary 8, which is Conjecture 1 for our symmetric special case. The method of proving Theorem 4 and Corollary 8 can be regarded as a generalization of the Routh–Hurwitz scheme to a case of several variables. This scheme is stated in terms of Hankel matrices and a system of resultants related to a pair of polynomials in a single variable (see Chapter XV in [7] or Chapter X in [8], for example).

We note in passing that there is an analogy between the notions “differente”, “discriminant” in the theory of algebraic numbers, and the ones “Hessian”, “norm of Hessian” in our present situation, respectively (see [9,10,11,12,13] for general definition of “discriminant” of algebraic numbers, algebraic functions, or more generally commutative algebra).

In [14], there is an interesting argument on zero points of coquaternionic polynomials using characteristic polynomials, which enable to linearize the problem by Euclidean algorithm. Moreover, our argument goes along the similar line in a more complicated situation.

2. Configuration of Critical Points in the Case of Regular Simplex

In this section, we consider the very special case when $▵O_1\dots O_{n+1}$ is a regular simplex and all hyperspheres $S_j$ have the same radius:

$${\rho }_{jk}^2={\rho }^2(1\le j<k\le n+1),r_j^2=r^2(1\le j\le n+1).$$

(8)

In this case, all of the critical points can be explicitly described. The total number of critical points is equal to $2^{n+1}-1.$

Denote by $I=\{1,2,\dots ,n+1\}.$ For the set $J=\{j_1,\dots ,j_p\}\subset I$, let $W_J$ be the central point of each $\left(\right|J|-1)$-dimensional face $▵O_J:=▵O_{j_1}\dots O_{j_p}$ defined by

$$W_J:=\frac{1}{\left|J\right|}\sum _{j\in J}{O}_j,$$

where $\left|J\right|$ denotes the size of J. In particular, we see that $W_j=O_j$$(1\le j\le n+1)$ and we simply denote by W the center $W_I$ of $▵O_1\dots O_{n+1}$. For $J\subset I$ we denote by $J^c$ the complement $I-J$. For $\varnothing ⊊J⊊I$ let $\mathfrak{l}(W_J,W_{J^c})$ be the straight line passing through two points $W_J$ and $W_{J^c}$, which is parameterized by

$$\mathfrak{l}(W_J,W_{J^c}):x=(1-\tau )W_J+\tau W_{J^c}(-\infty <\tau <\infty ).$$

(9)

An arbitrary line $\mathfrak{l}(W_J,W_{J^c})$ passes through the center $W=W_N$ of $▵O_1\dots O_{n+1}$, so that

$$\left\{W\right\}=\bigcap _{\varnothing ⊊J⊊I}\mathfrak{l}(W_J,W_{J^c}).$$

Symmetry argument shows that every linear p-dimensional real affine subspace ${\mathfrak{p}}_{J,J^c}$ spanned by the real p-simplex $▵O_{j_1}\dots O_{j_p}{W}_{J^c}$ is preserved by the vector field $\mathrm{grad}\mathfrak{Re}F$. In particular the real straight line $\mathfrak{l}(W_J,W_{J^c})$ is a trajectory of $\mathrm{grad}\mathfrak{Re}F$.

We now consider the critical points on $\mathfrak{l}(W_J,W_{J^c})$ for $\varnothing ⊊J⊊I$.

Lemma 1.

Suppose that $\left|J\right|=p$$(1\le p\le n)$. Then $f_j$ on $\mathfrak{l}(W_J,W_{J^c})$ as a function of τ is expressed as

$$\begin{array}{cc}\hfill f_j\left(x\right)& =f_j((1-\tau )W_J+\tau W_{J^c})\hfill \\ \hfill & =\left\{\begin{array}{ccc}{\displaystyle \left(\frac{n+1}{p(n+1-p)}{\tau }^2+\frac{p-1}{p}\right)\frac{{\rho }^2}{2}-r^2}& \mathrm{if}& j\in J,\hfill \\ {\displaystyle \left(\frac{n+1}{p(n+1-p)}{(\tau -1)}^2+\frac{n-p}{n+1-p}\right)\frac{{\rho }^2}{2}-r^2}& \mathrm{if}& j\in J^c.\hfill \end{array}\right.\hfill \end{array}$$

(10)

Proof. 

Without loss of generality we may assume that $J=\{1,2,\dots ,p\}$ and $J^c=\{p+1,\dots ,n+1\}$$(1\le p\le n)$. From (9), for $x\in \mathfrak{l}(W_J,W_{J^c})$ we have

$$x+{\alpha }_j=(1-\tau )W_J+\tau W_{J^c}+{\alpha }_j=(1-\tau )\sum _{k=1}^p\frac{{\alpha }_j-{\alpha }_k}{p}+\tau \sum _{l=p+1}^{n+1}\frac{{\alpha }_j-{\alpha }_l}{n+1-p},$$

so that we have

$$\begin{array}{cc}\hfill |x+{\alpha }_j{|}^2& =\frac{{(1-\tau )}^2}{p^2}|\sum _{k=1}^p({\alpha }_j-{\alpha }_k){|}^2+\frac{{\tau }^2}{{(n+1-p)}^2}|\sum _{l=p+1}^{n+1}({\alpha }_j-{\alpha }_k){|}^2\hfill \\ & +\frac{(1-\tau )\tau }{p(n+1-p)}\sum _{k=1}^p\sum _{l=p+1}^{n+1}2({\alpha }_j-{\alpha }_k,{\alpha }_j-{\alpha }_l)\hfill \\ & =\frac{{(1-\tau )}^2}{p^2}\left\{\sum _{k=1}^p{|{\alpha }_j-{\alpha }_k|}^2+\sum _{1\le k<l\le p}2({\alpha }_j-{\alpha }_k,{\alpha }_j-{\alpha }_l)\right\}\hfill \\ \hfill & +\frac{{\tau }^2}{{(n+1-p)}^2}\left\{\sum _{l=p+1}^{n+1}{|{\alpha }_j-{\alpha }_l|}^2+\sum _{p+1\le k<l\le n+1}2({\alpha }_j-{\alpha }_k,{\alpha }_j-{\alpha }_l)\right\}\hfill \end{array}$$

$$\begin{array}{c}\hfill +\frac{(1-\tau )\tau }{p(n+1-p)}\sum _{k=1}^p\sum _{l=p+1}^{n+1}2({\alpha }_j-{\alpha }_k,{\alpha }_j-{\alpha }_l).\end{array}$$

(11)

Since $▵O_1\dots O_{n+1}$ is regular, we have

$$\begin{array}{cc}\hfill |{\alpha }_j-{\alpha }_k{|}^2& ={\rho }^2(j\ne k),\hfill \\ \hfill 2({\alpha }_j-{\alpha }_k,{\alpha }_j-{\alpha }_l)& =2{\rho }^{2}cos(\pi /3)={\rho }^2(j\ne k,j\ne l,k\ne l).\hfill \end{array}$$

Therefore, if $1\le j\le p$, then (11) implies that

$$\begin{array}{cc}\hfill |x+{\alpha }_j{|}^2& =\frac{{(1-\tau )}^2}{p^2}\left\{(p-1){\rho }^2+\frac{(p-1)(p-2)}{2}{\rho }^2\right\}+\frac{{\tau }^2}{{(n+1-p)}^2}\{(n+1-p){\rho }^2\hfill \\ & +\frac{(n+1-p)(n-p)}{2}{\rho }^2\}+\frac{(1-\tau )\tau }{p(n+1-p)}(p-1)(n+1-p){\rho }^2\hfill \\ & =\left\{\frac{{(1-\tau )}^2}{2}\frac{p-1}{p}+\frac{{\tau }^2}{2}\frac{n+2-p}{n+1-p}+(1-\tau )\tau \frac{p-1}{p}\right\}{\rho }^2\hfill \\ & =\left(\frac{n+1}{p(n+1-p)}{\tau }^2+\frac{p-1}{p}\right)\frac{{\rho }^2}{2},\hfill \end{array}$$

so that $f_j\left(x\right)={|x+{\alpha }_j|}^2-r^2$ coincides with (10). In the same way as above, if $p+1\le j\le n+1$, then we see that (11) implies (10). □

By Lemma 1 F on $\mathfrak{l}(W_J,W_{J^c})$ is expressed as

$$F=\sum _{j=1}^{n+1}log{f}_j=\sum _{j\in J}log{f}_j+\sum _{k\in J^c}log{f}_k=plog{f}_j+(n+1-p)log{f}_k(j\in J,k\in J^c),$$

so that $dF$ on $\mathfrak{l}(W_J,W_{J^c})$ is written as

$$\begin{array}{cc}\hfill & dF=pdlog{f}_j+(n+1-p)dlog{f}_k=\left(p{f}_k\frac{d{f}_j}{d\tau }+(n+1-p)f_j\frac{d{f}_k}{d\tau }\right)\frac{d\tau }{f_j{f}_k}\hfill \\ \hfill & =\frac{{(n+1)}^3{\rho }^4}{2{(n+1-p)}^2{p}^2}\left(\tau -\frac{n+1-p}{n+1}\right)\left\{{\tau }^2-\frac{2p}{n+1}\tau +\frac{n+1-p}{n+1}\left(p-1-2p\frac{r^2}{{\rho }^2}\right)\right\}\frac{d\tau }{f_j{f}_k}.\hfill \end{array}$$

The critical points on $\mathfrak{l}(W_J,W_{J^c})$ correspond to the solutions $\tau$ of the equation $dF=0$, which is equivalent to

$$\left(\tau -\frac{n+1-p}{n+1}\right)\left\{{\tau }^2-\frac{2p}{n+1}\tau +\frac{n+1-p}{n+1}\left(p-1-2p\frac{r^2}{{\rho }^2}\right)\right\}=0.$$

(12)

The point $x=(1-\tau )W_J+\tau W_{J^c}$ on $\mathfrak{l}(W_J,W_{J^c})$ for $\tau =\frac{n+1-p}{n+1}$ coincides with W. The other two points on $\mathfrak{l}(W_J,W_{J^c})$ differ from W and satisfy the quadratic equation

$${\tau }^2-\frac{2p}{n+1}\tau +\frac{n+1-p}{n+1}\left(p-1-2p\frac{r^2}{{\rho }^2}\right)=0.$$

(13)

The discriminant of this quadratic equation is given by ${\mathfrak{D}}_p/{(n+1)}^2$, where

$${\mathfrak{D}}_p=p^2-(n+1-p)(n+1)\left(p-1-2p\frac{r^2}{{\rho }^2}\right),$$

(14)

which satisfies

$${\mathfrak{D}}_p={\mathfrak{D}}_{n+1-p}.$$

Denote by ${\tau }_1,{\tau }_2$ the two solutions of (13) such that ${\tau }_1<{\tau }_2$ if ${\mathfrak{D}}_p>0$. We denote by $Q_J$ and $Q_{J^c}$ the corresponding two points in $\mathfrak{l}(W_J,W_{J^c})$ to ${\tau }_1$ and ${\tau }_2$, respectively. In addition to W all these points in $\mathfrak{l}(W_J,W_{J^c})$$(\varnothing ⊊J⊊I)$ give all the critical points of F in X. One can prove the following proposition.

Proposition 1.

The number of critical points is equal to $2^{n+1}-1$. All the critical points of F lie on one of the straight lines $\mathfrak{l}(W_J,W_{J^c})$$(\varnothing ⊊J⊊I)$. Suppose that r satisfies

$$\left\{\begin{array}{cc}{\displaystyle \frac{n-2}{2(n+1)}{\rho }^2<r^2}& if n is odd,\hfill \\ {\displaystyle \frac{n^3-4n-4}{2n(n+1)(n+2)}{\rho }^2<r^2<\frac{n-2}{2(n+1)}{\rho }^{2}or\frac{n-2}{2(n+1)}{\rho }^2<r^2}& if n is even.\hfill \end{array}\right.$$

(15)

Then, all of these, W, $Q_J$$(\varnothing ⊊J⊊I)$, are real and distinct from each other.

Proof. 

For the situation where all critical points W, $Q_J$$(\varnothing ⊊J⊊I)$ are real and distinct from each other, we need the condition that each solution of (12) is real and is not a double point. This condition is equivalent to: (a) The discriminants ${\mathfrak{D}}_p$$(1\le p\le n)$ of the Equation (13) are greater than 0; and (b) The left-hand side of (13) at $\tau =\frac{n+1-p}{n+1}$ does not vanish. We discuss (b) first. The condition for (b) is written as

$${\left(\frac{n+1-p}{n+1}\right)}^2-\frac{2p}{n+1}\left(\frac{n+1-p}{n+1}\right)+\frac{n+1-p}{n+1}\left(p-1-2p\frac{r^2}{{\rho }^2}\right)\ne 0,$$

which is equivalent to

$$p\frac{n+1-p}{n+1}\left(\frac{n-2}{2(n+1)}-\frac{r^2}{{\rho }^2}\right)\ne 0,i.e.,\frac{r^2}{{\rho }^2}\ne \frac{n-2}{2(n+1)}.$$

(16)

Next, we consider the condition (a). Since the discriminant ${\mathfrak{D}}_p$ of (13) is rewritten as

$${\mathfrak{D}}_p=2p(n+1-p)(n+1)\left(\frac{r^2}{{\rho }^2}-\frac{n+2}{2(n+1)}+\frac{n+1}{2p(n+1-p)}\right),$$

if n is odd, then we need

$$\begin{array}{cc}\hfill & min\left\{\frac{r^2}{{\rho }^2}-\frac{n+2}{2(n+1)}+\frac{n+1}{2p(n+1-p)}|p=1,2,\dots ,n\right\}\hfill \\ \hfill & =\frac{r^2}{{\rho }^2}-\frac{n+2}{2(n+1)}+\frac{n+1}{2p(n+1-p)}{|}_{p=\frac{n+1}{2}}=\frac{r^2}{{\rho }^2}-\frac{n-2}{2(n+1)}>0,\hfill \end{array}$$

(17)

while if n is even, then we need

$$\begin{array}{cc}\hfill & min\left\{\frac{r^2}{{\rho }^2}-\frac{n+2}{2(n+1)}+\frac{n+1}{2p(n+1-p)}|p=1,2,\dots ,n\right\}\hfill \\ \hfill & =\frac{r^2}{{\rho }^2}-\frac{n+2}{2(n+1)}+\frac{n+1}{2p(n+1-p)}{|}_{p=\frac{n}{2}}=\frac{r^2}{{\rho }^2}-\frac{n^3-4n-4}{2n(n+1)(n+2)}>0.\hfill \end{array}$$

(18)

Therefore, (16)–(18) imply that conditions (a) and (b) are satisfied if (15) holds for r. This completes the proof. □

Before we prove Conjecture 2 under the condition (8), we show the following identities:

Lemma 2.

Suppose that J is fixed as $p=\left|J\right|$$(1\le p\le n)$. Then we have

$$f_j\left(W\right)=\frac{n{\rho }^2}{2(n+1)}-r^2(1\le j\le n+1).$$

(19)

If $j\in J$, $k\in J^c$, then $f_j\left(Q_J\right)$, $f_k\left(Q_J\right)$, $f_j\left(Q_{J^c}\right)$ and $f_k\left(Q_{J^c}\right)$ are expressed as

$$f_j\left(Q_J\right)=\frac{{\rho }^2}{n+1-p}\tau \left(Q_J\right),f_k\left(Q_J\right)=\frac{{\rho }^2}{p}(1-\tau \left(Q_J\right)),$$

(20)

$$f_j\left(Q_{J^c}\right)=\frac{{\rho }^2}{n+1-p}\tau \left(Q_{J^c}\right),f_k\left(Q_{J^c}\right)=\frac{{\rho }^2}{p}(1-\tau \left(Q_{J^c}\right)),$$

(21)

where

$$\tau \left(Q_J\right)=\frac{p-\sqrt{{\mathfrak{D}}_p}}{n+1},\tau \left(Q_{J^c}\right)=\frac{p+\sqrt{{\mathfrak{D}}_p}}{n+1},$$

(22)

$$1-\tau \left(Q_J\right)=\frac{n+1-p+\sqrt{{\mathfrak{D}}_p}}{n+1},1-\tau \left(Q_{J^c}\right)=\frac{n+1-p-\sqrt{{\mathfrak{D}}_p}}{n+1}.$$

(23)

Moreover, if $j\in J$, then we have

$$f_j\left(Q_J\right)f_j\left(Q_{J^c}\right)=\frac{{\rho }^2\left((p-1){\rho }^2-2p{r}^2\right)}{(n+1)(n+1-p)}.$$

(24)

Proof. 

From Lemma 1 and (12) we obtain (19)–(21), where ${\tau }_1=\tau \left(Q_J\right)$ and ${\tau }_2=\tau \left(Q_{J^c}\right)$ are the solutions of the quadratic Equation (13) satisfying ${\tau }_1<{\tau }_2$. We simply have (22) and (23) by the explicit forms of ${\tau }_1$ and ${\tau }_2$. We also have

$$f_j\left(Q_J\right)f_j\left(Q_{J^c}\right)=\frac{{\rho }^4}{{(n+1-p)}^2}\tau \left(Q_J\right)\tau \left(Q_{J^c}\right)=\frac{{\rho }^4}{{(n+1-p)}^2}\frac{n+1-p}{n+1}\left(p-1-2p\frac{r^2}{{\rho }^2}\right),$$

which coincides with (24). □

Using Lemma 2 we see that Conjecture 2 holds true under the condition (8).

Theorem 1.

Under the condition (8) the norms $\mathcal{N}\left(f_j\right)$ and $\mathcal{N}\left({\sum }_{j=1}^{n+1}{f}_j^{-1}\right)$ are expressed as

$$\begin{array}{cc}\hfill & \mathcal{N}\left(f_j\right)=\frac{B(0★1)}{2{(n+1)}^{2^n}}\prod _{p=2}^{n+1}{\left(\frac{B(0★12\dots p)}{B(023\dots p)}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n}{p-1}\right)}(1\le j\le n+1),\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & \mathcal{N}\left(\sum _{j=1}^{n+1}\frac{1}{f_j}\right)=2{(n+1)}^{2^{n+1}-1}\prod _{p=1}^{n+1}{\left(\frac{B(012\dots p)}{B(0★12\dots p)}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n+1}{p}\right)}.\hfill \end{array}$$

(26)

Proof. 

We prove (25) first. Without loss of generality we may assume $j=1$ for the proof of (25). By definition $\mathcal{N}\left(f_1\right)$ is expressed as

$$\begin{array}{cc}\hfill \mathcal{N}\left(f_1\right)& =f_1\left(W\right)\prod _{\varnothing ⊊J⊊I}{f}_1\left(Q_J\right)=f_1\left(W\right)\prod _{\begin{array}{c}\varnothing ⊊J⊊I\\ 1\in J\end{array}}{f}_1\left(Q_J\right)\prod _{\begin{array}{c}\varnothing ⊊J⊊I\\ 1\notin J\end{array}}{f}_1\left(Q_J\right)\hfill \\ \hfill & =f_1\left(W\right)\prod _{\begin{array}{c}\varnothing ⊊J⊊I\\ 1\in J\end{array}}{f}_1\left(Q_J\right)f_1\left(Q_{J^c}\right)=f_1\left(W\right)\prod _{p=1}^n\prod _{\begin{array}{c}\varnothing ⊊J⊊I\\ 1\in J,\left|J\right|=p\end{array}}{f}_1\left(Q_J\right)f_1\left(Q_{J^c}\right).\hfill \end{array}$$

(27)

Applying (19) and (24) in Lemma 2 to (27), $\mathcal{N}\left(f_1\right)$ is calculated as

$$\begin{array}{cc}\hfill \mathcal{N}\left(f_1\right)& =\left(\frac{n{\rho }^2}{2(n+1)}-r^2\right)\prod _{p=1}^n\prod _{\begin{array}{c}\varnothing ⊊J⊊I\\ 1\in J,\left|J\right|=p\end{array}}\frac{{\rho }^2\left((p-1){\rho }^2-2p{r}^2\right)}{(n+1)(n+1-p)}\hfill \\ \hfill & =\frac{n{\rho }^2-2(n+1)r^2}{2(n+1)}\prod _{p=1}^n{\left(\frac{{\rho }^2\left((p-1){\rho }^2-2p{r}^2\right)}{(n+1)(n+1-p)}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n}{p-1}\right)}\hfill \\ \hfill & =-\frac{2(n+1)r^2-n{\rho }^2}{2(n+1)}\prod _{p=1}^n{\left(\frac{-1}{n+1}\frac{{\rho }^2\left(2p{r}^2-(p-1){\rho }^2\right)}{n+1-p}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n}{p-1}\right)}\hfill \\ \hfill & =\frac{2r^2}{2}{\left(\frac{-1}{n+1}\right)}^{1+{\sum }_{p=1}^n\left(\genfrac{}{}{0.0pt}{}{n}{p-1}\right)}\prod _{p=2}^{n+1}{\left(\frac{{\rho }^2\left(2p{r}^2-(p-1){\rho }^2\right)}{p-1}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n}{p-1}\right)}\hfill \\ \hfill & =\frac{2r^2}{2{(n+1)}^{2^n}}\prod _{p=2}^{n+1}{\left(\frac{{\rho }^2\left(2p{r}^2-(p-1){\rho }^2\right)}{p-1}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n}{p-1}\right)}.\hfill \end{array}$$

(28)

On the other hand, by definition, we obtain

$$B(0★1)=2r^2,B(0★12\dots p)={(-1)}^{p-1}{\rho }^{2(p-1)}\{2p{r}^2-(p-1){\rho }^2\}$$

(29)

and

$$B(012\dots p)={(-1)}^p{\rho }^{2(p-1)}p,$$

(30)

so that

$$B(023\dots p)=B(012\dots p-1)={(-1)}^{p-1}{\rho }^{2(p-2)}(p-1).$$

(31)

Therefore, (29) and (31) imply that (28) coincides with (25).

Next, we prove (26). By definition $\mathcal{N}\left({\sum }_{j=1}^{n+1}{f}_j^{-1}\right)$ is expressed as

$$\begin{array}{cc}\hfill \mathcal{N}(\sum _{j=1}^{n+1}\frac{1}{f_j})& =(\sum _{j=1}^{n+1}\frac{1}{f_j\left(W\right)})\prod _{\varnothing ⊊J⊊I}(\sum _{j=1}^{n+1}\frac{1}{f_j\left(Q_J\right)})=(\sum _{j=1}^{n+1}\frac{1}{f_j\left(W\right)})\prod _{p=1}^n\prod _{\begin{array}{c}\varnothing ⊊J⊊I\\ \left|J\right|=p\end{array}}(\sum _{j=1}^{n+1}\frac{1}{f_j\left(Q_J\right)})\hfill \\ \hfill & =(\sum _{j=1}^{n+1}\frac{1}{f_j\left(W\right)})\prod _{p=1}^n\prod _{\begin{array}{c}\varnothing ⊊J⊊I\\ \left|J\right|=p\end{array}}(\sum _{j\in J}\frac{1}{f_j\left(Q_J\right)}+\sum _{k\in J^c}\frac{1}{f_k\left(Q_J\right)}).\hfill \end{array}$$

(32)

Applying (19)–(21) in Lemma 2 to (32), we have

$$\begin{array}{cc}\hfill \mathcal{N}(\sum _{j=1}^{n+1}\frac{1}{f_j})& =(\sum _{j=1}^{n+1}\frac{1}{f_j\left(W\right)})\prod _{p=1}^n\prod _{\begin{array}{c}\varnothing ⊊J⊊I\\ \left|J\right|=p\end{array}}(\sum _{j\in J}\frac{n+1-p}{{\rho }^2\tau \left(Q_J\right)}+\sum _{k\in J^c}\frac{p}{{\rho }^2(1-\tau \left(Q_J\right))})\hfill \\ \hfill & =\frac{2{(n+1)}^2}{n{\rho }^2-2(n+1)r^2}\prod _{p=1}^n\prod _{\begin{array}{c}\varnothing ⊊J⊊I\\ \left|J\right|=p\end{array}}(\frac{p(n+1-p)}{{\rho }^2\tau \left(Q_J\right)}+\frac{(n+1-p)p}{{\rho }^2(1-\tau \left(Q_J\right))})\hfill \\ \hfill & =\frac{2{(n+1)}^2}{n{\rho }^2-2(n+1)r^2}\prod _{p=1}^n\prod _{\begin{array}{c}\varnothing ⊊J⊊I\\ \left|J\right|=p\end{array}}\frac{p(n+1-p)}{{\rho }^2\tau \left(Q_J\right)(1-\tau \left(Q_J\right))}.\hfill \end{array}$$

(33)

Using (22), (23) and ${\mathfrak{D}}_p={\mathfrak{D}}_{n+1-p}$ for (33) we obtain

$$\begin{array}{cc}\hfill \mathcal{N}(\sum _{j=1}^{n+1}\frac{1}{f_j})& =\frac{2{(n+1)}^2}{n{\rho }^2-2(n+1)r^2}\prod _{p=1}^n{\left(\frac{{(n+1)}^{2}p(n+1-p)}{{\rho }^2(p-\sqrt{{\mathfrak{D}}_p})(n+1-p+\sqrt{{\mathfrak{D}}_{n+1-p}})}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n+1}{p}\right)}\hfill \\ \hfill & =\frac{2{(n+1)}^2}{n{\rho }^2-2(n+1)r^2}\prod _{p=1}^n{\left(\frac{{(n+1)}^{2}p(n+1-p)}{{\rho }^2(p-\sqrt{{\mathfrak{D}}_p})(p+\sqrt{{\mathfrak{D}}_p})}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n+1}{p}\right)}\hfill \\ \hfill & =\frac{2{(n+1)}^2}{n{\rho }^2-2(n+1)r^2}\prod _{p=1}^n{\left(\frac{{(n+1)}^{2}p(n+1-p)}{{\rho }^2(p^2-{\mathfrak{D}}_p)}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n+1}{p}\right)}.\hfill \end{array}$$

(34)

Since we have ${\rho }^2(p^2-{\mathfrak{D}}_p)=(n+1)(n+1-p)({\rho }^2(p-1)-2p{r}^2)$ from (14), (34) is written as

$$\begin{array}{cc}\hfill \mathcal{N}(\sum _{j=1}^{n+1}\frac{1}{f_j})& =\frac{2{(n+1)}^2}{n{\rho }^2-2(n+1)r^2}\prod _{p=1}^n{\left(\frac{{(n+1)}^{2}p(n+1-p)}{(n+1)(n+1-p)({\rho }^2(p-1)-2p{r}^2)}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n+1}{p}\right)}\hfill \\ \hfill & =\frac{2{(n+1)}^2}{n{\rho }^2-2(n+1)r^2}\prod _{p=1}^n{\left(\frac{(n+1)p}{{\rho }^2(p-1)-2p{r}^2}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n+1}{p}\right)}\hfill \\ \hfill & =2{(n+1)}^{{\sum }_{p=1}^{n+1}\left(\genfrac{}{}{0.0pt}{}{n+1}{p}\right)}\prod _{p=1}^{n+1}{\left(\frac{p}{{\rho }^2(p-1)-2p{r}^2}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n+1}{p}\right)}\hfill \\ \hfill & =2{(n+1)}^{2^{n+1}-1}\prod _{p=1}^{n+1}{\left(\frac{p}{{\rho }^2(p-1)-2p{r}^2}\right)}^{\left(\genfrac{}{}{0.0pt}{}{n+1}{p}\right)}.\hfill \end{array}$$

(35)

Hence, (29) and (30) imply that (35) coincides with (26). □

3. Special Coordinates (Three-Dimensional Case)

In this section, for a general three-dimensional case, we define the special coordinate system (denoted by $t_1,t_2,t_3$) attached to the fundamental three-dimensional simplex $▵O_1{O}_2{O}_3{O}_4$.

Each plane ${\mathfrak{p}}_{jkl}$ containing the three vertices $O_j,O_k,O_l$ is described by the equation

$${\mathfrak{p}}_{jkl}:L_{jkl}=0,$$

where the linear functions $L_{jkl}$ on X are given by

$$\begin{array}{cc}\hfill L_{123}\left(x\right)& :=-det(x+{\alpha }_1,x+{\alpha }_2,x+{\alpha }_3),\hfill \\ \hfill L_{124}\left(x\right)& :=det(x+{\alpha }_1,x+{\alpha }_2,x+{\alpha }_4),\hfill \\ \hfill L_{134}\left(x\right)& :=-det(x+{\alpha }_1,x+{\alpha }_3,x+{\alpha }_4),\hfill \\ \hfill L_{234}\left(x\right)& :=det(x+{\alpha }_2,x+{\alpha }_3,x+{\alpha }_4)\hfill \end{array}$$

(36)

for ${\alpha }_j=({\alpha }_{j1},{\alpha }_{j2},{\alpha }_{j3})\in {\mathbb{R}}^3$. Under our setting (1) the functions $L_{jkl}$ are explicitly expanded as

$$\begin{array}{cc}\hfill L_{123}& ={\alpha }_{13}{\alpha }_{22}(x_1+{\alpha }_{31})-{\alpha }_{13}({\alpha }_{21}-{\alpha }_{31})x_2+\{-({\alpha }_{11}-{\alpha }_{31}){\alpha }_{22}+{\alpha }_{12}({\alpha }_{21}-{\alpha }_{31})\}{x}_3,\hfill \\ \hfill L_{124}& =-{\alpha }_{13}{\alpha }_{22}{x}_1+{\alpha }_{21}{\alpha }_{13}{x}_2+({\alpha }_{11}{\alpha }_{22}-{\alpha }_{12}{\alpha }_{21})x_3,\hfill \\ \hfill L_{134}& =-{\alpha }_{13}{\alpha }_{31}{x}_2+{\alpha }_{31}{\alpha }_{12}{x}_3,\hfill \\ \hfill L_{234}& =-{\alpha }_{31}{\alpha }_{22}{x}_3,\hfill \end{array}$$

so that

$$L_{123}+L_{124}+L_{134}+L_{234}={\alpha }_{31}{\alpha }_{22}{\alpha }_{13}.$$

(37)

Hence, the simplex $▵O_1{O}_2{O}_3{O}_4$ can be defined by $L_{jkl}\ge 0$$(1\le j\le k\le 4)$. Remark that

$${\alpha }_{31}=\sqrt{\frac{B\left(034\right)}{2}}>0,{\alpha }_{31}{\alpha }_{22}=\sqrt{-\frac{B\left(0234\right)}{4}}>0,{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}=\sqrt{\frac{B\left(01234\right)}{8}}>0.$$

(38)

Definition 2.

Two rational functions ${\phi }_1,{\phi }_2$ on X are said to be congruent with respect to $\mathcal{C}$ and is denoted by

$${\phi }_1\equiv {\phi }_{2}modAnn\left(\mathcal{C}\right)$$

if ${\phi }_1,{\phi }_2$ have definite values at every point of $\mathcal{C}$ and

$${\phi }_1\left(x\right)={\phi }_2\left(x\right)$$

at each critical point x in $\mathcal{C}$ ($Ann\left(\mathcal{C}\right)$ means the annihilator of $\mathcal{C}$).

Lemma 3.

Let $g_1,g_2,g_3$ be polynomials in x of degree 3 specified by

$$g_1:=L_{123}{f}_4-L_{234}{f}_1,g_2:=L_{123}{f}_4-L_{134}{f}_2,g_3:=L_{123}{f}_4-L_{124}{f}_3.$$

(39)

Then, we have

$$g_j=-f_j{f}_4{M}_j,$$

(40)

where the functions $M_j$ are given by

$$M_j=\pm \left|\begin{array}{ccc}{x}_1+{\alpha }_{k1}& x_1+{\alpha }_{l1}& G_1\\ x_2+{\alpha }_{k2}& x_2+{\alpha }_{l2}& G_2\\ x_3+{\alpha }_{k3}& x_3+{\alpha }_{l3}& G_3\end{array}\right|.$$

Here, $\{j,k,l\}$ is a permutation of $\{1,2,3\}$ and ± denotes its sign. Moreover, we have the congruences

$$\frac{f_4}{f_1}\equiv \frac{L_{234}}{L_{123}},\frac{f_4}{f_2}\equiv \frac{L_{134}}{L_{123}},\frac{f_4}{f_3}\equiv \frac{L_{124}}{L_{123}}modAnn\left(\mathcal{C}\right).$$

(41)

Proof. 

Without loss of generality we prove (40) for $j=1$. Since $G_{\nu }$$(1\le \nu \le 3)$ are given as $G_{\nu }={\sum }_{j=1}^4(x_{\nu }+{\alpha }_{j\nu })/f_j$, using (36) $M_1$ is written as

$$\begin{array}{cc}\hfill M_1& =\sum _{j=1}^{4}det(x+{\alpha }_2,x+{\alpha }_3,x+{\alpha }_j)/f_j\hfill \\ \hfill & =det(x+{\alpha }_2,x+{\alpha }_3,x+{\alpha }_1)/f_1+det(x+{\alpha }_2,x+{\alpha }_3,x+{\alpha }_4)/f_4\hfill \\ \hfill & =-\frac{L_{123}}{f_1}+\frac{L_{234}}{f_4},\hfill \end{array}$$

which is equivalent to (40) for $j=1$. From (40), we obtain

$$\frac{f_4}{f_1}=\frac{L_{234}}{L_{123}}-\frac{f_4}{L_{123}}{M}_1,\frac{f_4}{f_2}=\frac{L_{134}}{L_{123}}-\frac{f_4}{L_{123}}{M}_2,\frac{f_4}{f_3}=\frac{L_{124}}{L_{123}}-\frac{f_4}{L_{123}}{M}_3.$$

This implies (41). □

According to Lemma 3, we can characterize the set of critical points $\mathcal{C}$ in X by the polynomials $g_j$ as follows.

Lemma 4.

Under the condition $\left({\mathcal{H}}_0\right)$, the system

$$G_1=G_2=G_3=0$$

on X is equivalent to the system

$$g_1=g_2=g_3=0$$

on X.

Lemma 5.

The following identity holds as function of $x=(x_1,x_2,x_3)$:

$$d{g}_1\wedge d{g}_2\wedge d{g}_3\equiv -L_{123}^2{f}_1{f}_2{f}_3{f}_4^{3}d{G}_1\wedge d{G}_2\wedge d{G}_{3}modAnn\left(\mathcal{C}\right).$$

(42)

Proof. 

By taking the derivatives of both sides of (40) in Lemma 3 one obtains

$$\frac{\partial g_j}{\partial x_{\nu }}\equiv -f_j{f}_4\left(a_{jj}^{*}\frac{\partial G_j}{\partial x_{\nu }}+a_{kj}^{*}\frac{\partial G_k}{\partial x_{\nu }}+a_{lj}^{*}\frac{\partial G_l}{\partial x_{\nu }}\right)modAnn\left(\mathcal{C}\right)$$

for the triple $\{j,k,l\}$, which is an even permutation of $\{1,2,3\}$, where $a_{pq}^{*}$ denotes the cofactor of the $(p,q)$-component of the $3\times 3$ matrix $A=(x+{\alpha }_1,x+{\alpha }_2,x+{\alpha }_3)$. Thus, we have

$$\left(\begin{array}{ccc}\frac{\partial g_1}{\partial x_1}& \frac{\partial g_1}{\partial x_2}& \frac{\partial g_1}{\partial x_3}\\ \frac{\partial g_2}{\partial x_1}& \frac{\partial g_2}{\partial x_2}& \frac{\partial g_2}{\partial x_3}\\ \frac{\partial g_3}{\partial x_1}& \frac{\partial g_3}{\partial x_2}& \frac{\partial g_3}{\partial x_3}\end{array}\right)\equiv -f_4\left(\begin{array}{ccc}{f}_1{a}_{11}^{*}& f_1{a}_{21}^{*}& f_1{a}_{31}^{*}\\ f_2{a}_{12}^{*}& f_2{a}_{22}^{*}& f_2{a}_{32}^{*}\\ f_3{a}_{13}^{*}& f_3{a}_{23}^{*}& f_3{a}_{33}^{*}\end{array}\right)\left(\begin{array}{ccc}\frac{\partial G_1}{\partial x_1}& \frac{\partial G_1}{\partial x_2}& \frac{\partial G_1}{\partial x_3}\\ \frac{\partial G_2}{\partial x_1}& \frac{\partial G_2}{\partial x_2}& \frac{\partial G_2}{\partial x_3}\\ \frac{\partial G_3}{\partial x_1}& \frac{\partial G_3}{\partial x_2}& \frac{\partial G_3}{\partial x_3}\end{array}\right)modAnn\left(\mathcal{C}\right).$$

Hence, we obtain

$$\frac{\partial (g_1,g_2,g_3)}{\partial (x_1,x_2,x_3)}\equiv -f_1{f}_2{f}_3{f}_4^3(det{A}^{*})\frac{\partial (G_1,G_2,G_3)}{\partial (x_1,x_2,x_3)}modAnn\left(\mathcal{C}\right),$$

(43)

where $A^{*}$ is the cofactor matrix of A given by

$$A^{*}=\left(\begin{array}{ccc}{a}_{11}^{*}& a_{21}^{*}& a_{31}^{*}\\ a_{12}^{*}& a_{22}^{*}& a_{32}^{*}\\ a_{13}^{*}& a_{23}^{*}& a_{33}^{*}\end{array}\right),A=\left(\begin{array}{ccc}{x}_1+{\alpha }_{11}& x_1+{\alpha }_{21}& x_1+{\alpha }_{31}\\ x_2+{\alpha }_{12}& x_2+{\alpha }_{22}& x_2+{\alpha }_{32}\\ x_3+{\alpha }_{13}& x_2+{\alpha }_{23}& x_3+{\alpha }_{33}\end{array}\right).$$

Since $A^{*}$ satisfies $A^{*}A=(detA)I$, where I is the identity matrix, (36) implies

$$det{A}^{*}={(detA)}^2={(-L_{123})}^2=L_{123}^2.$$

Therefore, we see that (43) is equivalent to (42). □

We now introduce special coordinates $t=(t_1,t_2,t_3)$ instead of $x=(x_1,x_2,x_3)$, given by

$$t_1:=\frac{L_{234}}{L_{123}},t_2:=\frac{L_{134}}{L_{123}},t_3:=\frac{L_{124}}{L_{123}}\mathrm{and}{t}_{\infty }:=\frac{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{L_{123}}.$$

(44)

The identity (37) implies

$$t_{\infty }=1+t_1+t_2+t_3.$$

Conversely, for given $t=(t_1,t_2,t_3)$ solving the system (44) with respect to $x=(x_1,x_2,x_3)$, we obtain

$$x_1=-\frac{{\alpha }_{11}{t}_1+{\alpha }_{21}{t}_2+{\alpha }_{31}{t}_3}{t_{\infty }},x_2=-\frac{{\alpha }_{12}{t}_1+{\alpha }_{22}{t}_2}{t_{\infty }},x_3=-\frac{{\alpha }_{13}{t}_1}{t_{\infty }}.$$

(45)

Therefore, (45) defines the projective map $\iota :\{t\in {\mathbb{C}}^3|1+t_1+t_2+t_3\ne 0\}\to {\mathbb{C}}^3$, i.e.,

$$t\mapsto x=\iota \left(t\right):=-\frac{t_1}{t_{\infty }}{\alpha }_1-\frac{t_2}{t_{\infty }}{\alpha }_2-\frac{t_3}{t_{\infty }}{\alpha }_3\in {\mathbb{C}}^3.$$

By definition, we notice that

Lemma 6.

$$d{x}_1\wedge d{x}_2\wedge d{x}_3=\frac{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{t_{\infty }^4}d{t}_1\wedge d{t}_2\wedge d{t}_3.$$

(46)

Proof. 

Differentiating both sides of $t_{\infty }{x}_j=-({\alpha }_{1j}{t}_1+{\alpha }_{2j}{t}_2+{\alpha }_{3j}{t}_3)$ with respect to $t_k$, we have $t_{\infty }\partial x_j/\partial t_k=-(x_j+{\alpha }_{kj})$, so that

$$\frac{\partial (x_1,x_2,x_3)}{\partial (t_1,t_2,t_3)}=\frac{-1}{t_{\infty }^3}det{\left(x_j+{\alpha }_{kj}\right)}_{j,k=1,2,3}=\frac{L_{123}}{t_{\infty }^3}=\frac{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{t_{\infty }^4},$$

which is equivalent to (46). □

Under the condition $\left({\mathcal{H}}_0\right)$, for the sets $\mathcal{C}$ and $X\subset {\mathbb{C}}^3$, we put $\tilde{\mathcal{C}}={\iota }^{-1}\mathcal{C}$ and $\tilde{X}:={\iota }^{-1}X$, respectively.

Definition 3.

Two rational functions ${\phi }_1,{\phi }_2$ on $\tilde{X}$ are said to be congruent with respect to $\tilde{\mathcal{C}}$ and written by

$${\phi }_1\equiv {\phi }_{2}modAnn\left(\tilde{\mathcal{C}}\right)$$

if their restriction to $\tilde{\mathcal{C}}$ are equal, i.e., if ${\phi }_1,{\phi }_2$ have definite values at every point of $\tilde{\mathcal{C}}$ and ${\phi }_1\left(t\right)={\phi }_2\left(t\right)$ at each critical point t in $\tilde{\mathcal{C}}$ ($Ann(\tilde{\mathcal{C}})$ means the annihilator of $\tilde{\mathcal{C}}$).

Remark 5.

From (41) of Lemma 3, (44) implies the congruences

$$t_1\equiv \frac{f_4}{f_1},t_2\equiv \frac{f_4}{f_2},t_3\equiv \frac{f_4}{f_3}modAnn\left(\tilde{\mathcal{C}}\right).$$

(47)

Through the projective map $\iota :\tilde{X}\to X$ we can characterize the set of critical points $\tilde{\mathcal{C}}$ in $\tilde{X}$ as follows:

Lemma 7.

Under the condition $\left({\mathcal{H}}_0\right)$, the system

$$g_1=g_2=g_3=0$$

on X is equivalent to the system

$${\tilde{g}}_1={\tilde{g}}_2={\tilde{g}}_3=0$$

on $\tilde{X}$, where ${\tilde{g}}_j$ are polynomials in t of degree 3 given by

$${\tilde{g}}_j\left(t\right):=\frac{t_{\infty }^3}{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{g}_j\left(x\right)=\frac{t_{\infty }^3}{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{g}_j\left(\iota \left(t\right)\right).$$

(48)

Moreover we have

$$d{g}_1\wedge d{g}_2\wedge d{g}_3\equiv \frac{{\alpha }_{31}^3{\alpha }_{22}^3{\alpha }_{13}^3}{t_{\infty }^9}d{\tilde{g}}_1\wedge d{\tilde{g}}_2\wedge d{\tilde{g}}_{3}modAnn\left(\tilde{\mathcal{C}}\right).$$

(49)

Proof. 

By definition the equivalence between $g_1=g_2=g_3=0$ and ${\tilde{g}}_1={\tilde{g}}_2={\tilde{g}}_3=0$ is obvious. The identity (49) is straightforward from (48). Here, we just confirm that ${\tilde{g}}_j\left(t\right)$ are polynomials in t of degree 3. By the definition (39) of $g_j$, we have

$${\tilde{g}}_1\left(t\right)=\frac{t_{\infty }^3}{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}(L_{123}{f}_4-L_{234}{f}_1)=\frac{t_{\infty }^3{L}_{123}}{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}(f_4-\frac{L_{234}}{L_{123}}{f}_1)=t_{\infty }^2(f_4-t_1{f}_1).$$

In the same way, we have the expression

$${\tilde{g}}_j\left(t\right)=t_{\infty }^2(f_4-t_j{f}_j)(j=1,2,3).$$

(50)

For $1\le j\le 4$, we have

$$\begin{array}{cc}\hfill t_{\infty }^2{f}_j& =t_{\infty }^2\left((x,x)+2({\alpha }_j,x)+{\alpha }_{j0}\right)=(t_{\infty }x,t_{\infty }x)+2t_{\infty }({\alpha }_j,t_{\infty }x)+{\alpha }_{j0}{t}_{\infty }^2\hfill \\ \hfill & =|\sum _{k=1}^3{t}_k{\alpha }_k{|}^2-2(1+\sum _{k=1}^3{t}_k)({\alpha }_j,\sum _{l=1}^3{t}_l{\alpha }_l)+{\alpha }_{j0}(1+\sum _{k=1}^3{t}_k{)}^2\hfill \\ \hfill & =\sum _{k=1}^3{|{\alpha }_k|}^2{t}_k^2+2\sum _{1\le k<l\le 3}({\alpha }_k,{\alpha }_l)t_k{t}_l-2(1+\sum _{k=1}^3{t}_k)\sum _{l=1}^3({\alpha }_j,{\alpha }_l)t_l+{\alpha }_{j0}(1+\sum _{k=1}^3{t}_k{)}^2,\hfill \end{array}$$

(51)

which are polynomials in t of degree 2. From (50), we see that ${\tilde{g}}_j$ are polynomials in t of degree 3. □

Before we show the explicit forms of the polynomials ${\tilde{g}}_j$, we prove two lemmas.

Lemma 8.

The following identities hold:

$$t_{\infty }(f_j-f_4)=\sum _{k=1}^{3}B\left(\begin{array}{ccc}0& ★& k\\ 0& j& 4\end{array}\right)t_k+B\left(\begin{array}{ccc}0& ★& 4\\ 0& j& 4\end{array}\right)(1\le j\le 3).$$

(52)

Proof. 

By definition, we have

$$\begin{array}{cc}\hfill B\left(\begin{array}{ccc}0& ★& k\\ 0& j& 4\end{array}\right)& =({\rho }_{kj}^2-r_j^2)-({\rho }_{k4}^2-r_4^2)\hfill \\ \hfill & =|{\alpha }_k-{\alpha }_j{|}^2-\left(\right|{\alpha }_j{|}^2-{\alpha }_{j0})-|{\alpha }_k-{\alpha }_4{|}^2+\left(\right|{\alpha }_4{|}^2-{\alpha }_{40})\hfill \\ \hfill & =2({\alpha }_k,{\alpha }_4-{\alpha }_j)+{\alpha }_{j0}-{\alpha }_{40}.\hfill \end{array}$$

(53)

On the other hand, by the definition of $f_j$ we have

$$\begin{array}{cc}\hfill t_{\infty }(f_j-f_4)& =t_{\infty }\{2(x,{\alpha }_j)-2(x,{\alpha }_4)+{\alpha }_{j0}-{\alpha }_{40}\}\hfill \\ \hfill & =2(-t_{\infty }x,{\alpha }_4-{\alpha }_j)+t_{\infty }({\alpha }_{j0}-{\alpha }_{40}).\hfill \end{array}$$

Applying the relations $-t_{\infty }x=t_1{\alpha }_1+t_2{\alpha }_2+t_3{\alpha }_3$ and $t_{\infty }=1+t_1+t_2+t_3$ to the above identity, we have

$$t_{\infty }(f_j-f_4)=\sum _{k=1}^3\{2({\alpha }_k,{\alpha }_4-{\alpha }_j)+({\alpha }_{j0}-{\alpha }_{40})\}{t}_k+({\alpha }_{j0}-{\alpha }_{40}).$$

(54)

Under ${\alpha }_4=0$, i.e., ${\rho }_{j4}^2={\left|{\alpha }_j\right|}^2$, (53) implies $B\left(\begin{array}{ccc}0& ★& 4\\ 0& j& 4\end{array}\right)={\alpha }_{j0}-{\alpha }_{40}$. Therefore, we obtain (52) from (53) and (54). □

Lemma 9.

$$t_{\infty }^2{f}_4=\sum _{j=1}^3({\rho }_{j4}^2-r_4^2)t_j^2+\sum _{1\le j<k\le 3}\left\{B\left(\begin{array}{ccc}0& j& 4\\ 0& k& 4\end{array}\right)-2r_4^2\right\}{t}_j{t}_k-2r_4^2(t_1+t_2+t_3)-r_4^2.$$

(55)

Proof. 

From (51), we have

$$\begin{array}{cc}\hfill t_{\infty }^2{f}_4& =\sum _{k=1}^3{\left|{\alpha }_k\right|}^2{t}_k^2+2\sum _{1\le k<l\le 3}({\alpha }_k,{\alpha }_l)t_k{t}_l+{\alpha }_{40}{(1+t_1+t_2+t_3)}^2\hfill \\ \hfill & =\sum _{j=1}^3{\rho }_{j4}^2{t}_j^2+\sum _{1\le j<k\le 3}B\left(\begin{array}{ccc}0& j& 4\\ 0& k& 4\end{array}\right)t_j{t}_k-r_4^2{(1+t_1+t_2+t_3)}^2,\hfill \end{array}$$

which coincides with (55). □

Proposition 2.

The polynomials ${\tilde{g}}_j$ in t of degree 3 given in (48) are expressed as

$$\begin{array}{cc}\hfill {\tilde{g}}_j& =r_j^2{t}_j^3+(r_j^2-{\rho }_{jk}^2)t_k^2{t}_j+(r_j^2-{\rho }_{jl}^2)t_l^2{t}_j+2r_j^2{t}_j^2(t_k+t_l)-\left\{B\left(\begin{array}{ccc}0& k& j\\ 0& l& j\end{array}\right)-2r_j^2\right\}{t}_j{t}_k{t}_l\hfill \\ \hfill & +({\rho }_{j4}^2-r_4^2+2r_j^2)t_j^2+({\rho }_{k4}^2-r_4^2)t_k^2+({\rho }_{l4}^2-r_4^2)t_l^2\hfill \\ \hfill & -2B\left(\begin{array}{ccc}0& ★& k\\ 0& j& 4\end{array}\right)t_j{t}_k-2B\left(\begin{array}{ccc}0& ★& l\\ 0& j& 4\end{array}\right)t_j{t}_l+\left\{B\left(\begin{array}{ccc}0& k& 4\\ 0& l& 4\end{array}\right)-2r_4^2\right\}{t}_k{t}_l\hfill \\ \hfill & +(r_j^2-2r_4^2-{\rho }_{j4}^2)t_j-2r_4^2(t_k+t_l)-r_4^2.\hfill \end{array}$$

Proof. 

From (50), for $1\le j\le 3$, we have

$$\begin{array}{cc}\hfill {\tilde{g}}_j& =(1-t_j)t_{\infty }^2{f}_4-t_j{t}_{\infty }^2(f_j-f_4)\hfill \\ \hfill & =(1-t_j)t_{\infty }^2{f}_4-t_j(1+t_1+t_2+t_3)t_{\infty }(f_j-f_4).\hfill \end{array}$$

Since the explicit forms of $t_{\infty }^2{f}_4$ and $t_{\infty }(f_j-f_4)$ have already been given in (55) and (52), respectively, we eventually obtain the result of Proposition 2. In particular, the identity

$$B\left(\begin{array}{ccc}0& k& j\\ 0& l& j\end{array}\right)-2r_j^2=B\left(\begin{array}{ccc}0& k& 4\\ 0& j& 4\end{array}\right)-2r_4^2+B\left(\begin{array}{ccc}0& ★& k\\ 0& j& 4\end{array}\right)+B\left(\begin{array}{ccc}0& ★& l\\ 0& j& 4\end{array}\right)$$

was applied to the coefficient of $t_j{t}_k{t}_l$. □

Lemma 10.

For $1\le j<k\le 3$ let ${\tilde{g}}_{jk}$ be functions specified by

$${\tilde{g}}_{jk}:=\frac{(1-t_k){\tilde{g}}_j-(1-t_j){\tilde{g}}_k}{t_{\infty }}.$$

(56)

Then, ${\tilde{g}}_{jk}$ are polynomials in t of degree 3, which are explicitly written as follows:

$$\begin{array}{cc}\hfill {\tilde{g}}_{jk}& =-t_j^2{t}_{k}B\left(\begin{array}{ccc}0& ★& j\\ 0& k& j\end{array}\right)+t_j{t}_k^{2}B\left(\begin{array}{ccc}0& ★& k\\ 0& j& k\end{array}\right)+t_j{t}_k{t}_{l}B\left(\begin{array}{ccc}0& l& ★\\ 0& k& j\end{array}\right)\hfill \\ \hfill & +t_j^{2}B\left(\begin{array}{ccc}0& ★& j\\ 0& 4& j\end{array}\right)-t_k^{2}B\left(\begin{array}{ccc}0& ★& k\\ 0& 4& k\end{array}\right)+t_j\left\{-B\left(\begin{array}{ccc}0& ★& 4\\ 0& j& 4\end{array}\right)-B\left(\begin{array}{ccc}0& ★& l\\ 0& j& 4\end{array}\right)t_l\right\}\hfill \\ \hfill & +t_k\left\{B\left(\begin{array}{ccc}0& ★& 4\\ 0& k& 4\end{array}\right)+B\left(\begin{array}{ccc}0& ★& l\\ 0& k& 4\end{array}\right)t_l\right\}\hfill \end{array}$$

such that $\{j,k,l\}$ is the uniquely determined permutation of $\{1,2,3\}.$

Proof. 

By the definition (50) of ${\tilde{g}}_j$, (56) implies

$${\tilde{g}}_{jk}=-t_j(1-t_k)t_{\infty }(f_j-f_4)+t_k(1-t_j)t_{\infty }(f_k-f_4).$$

Since the explicit form of $t_{\infty }(f_j-f_4)$ has already been given in (52) in Lemma 8, we obtain the result of Lemma 10. □

Remark 6.

As a consequence of Lemma 10, we have

$$(1-t_1){\tilde{g}}_{23}-(1-t_2){\tilde{g}}_{13}+(1-t_3){\tilde{g}}_{12}=0,$$

so that we immediately have

$$d{\tilde{g}}_{12}\wedge d{\tilde{g}}_{13}\wedge d{\tilde{g}}_{23}\equiv 0modAnn\left(\tilde{\mathcal{C}}\right).$$

The following is a key lemma to characterize the set $\tilde{\mathcal{C}}$ of critical points.

Lemma 11.

Suppose $t_1\ne 1$. Under the condition $\left({\mathcal{H}}_0\right)$ the system

$${\tilde{g}}_1={\tilde{g}}_2={\tilde{g}}_3=0$$

in $\tilde{X}$ is equivalent to the system

$${\tilde{g}}_1={\tilde{g}}_{12}={\tilde{g}}_{13}=0$$

(57)

in $\tilde{X}$. Moreover we have

$$d{\tilde{g}}_1\wedge d{\tilde{g}}_2\wedge d{\tilde{g}}_3\equiv \frac{t_{\infty }^2}{{(1-t_1)}^2}d{\tilde{g}}_1\wedge d{\tilde{g}}_{12}\wedge d{\tilde{g}}_{13}modAnn\left(\tilde{\mathcal{C}}\right).$$

(58)

Proof. 

By definition the equivalence between ${\tilde{g}}_1={\tilde{g}}_2={\tilde{g}}_3=0$ and ${\tilde{g}}_1={\tilde{g}}_{12}={\tilde{g}}_{13}=0$ is obvious under $t_1\ne 1$. From (56) we have

$$t_{\infty }d{\tilde{g}}_{1j}\equiv (1-t_j)d{\tilde{g}}_1-(1-t_1)d{\tilde{g}}_{j}modAnn\left(\tilde{\mathcal{C}}\right),$$

which implies (58). □

Then the following congruence identity holds true:

Lemma 12.

Regarding $G_j=G_j\left(x\right)$ as functions on $\tilde{X}$ through the map ι, i.e., $G_j=G_j\left(\iota \left(t\right)\right)$, we have

$$d{G}_1\wedge d{G}_2\wedge d{G}_3\equiv -\frac{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{f_1{f}_2{f}_3{f}_4^3}\frac{d{\tilde{g}}_1\wedge d{\tilde{g}}_2\wedge d{\tilde{g}}_3}{t_{\infty }^7}modAnn\left(\tilde{\mathcal{C}}\right).$$

(59)

If $t\in \tilde{\mathcal{C}}$ satisfies $t_1\ne 1$, then

$$d{G}_1\wedge d{G}_2\wedge d{G}_3\equiv -\frac{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{f_1{f}_2{f}_3{f}_4^3}\frac{d{\tilde{g}}_1\wedge d{\tilde{g}}_{12}\wedge d{\tilde{g}}_{13}}{t_{\infty }^5{(1-t_1)}^2}modAnn\left(\tilde{\mathcal{C}}\right).$$

(60)

Proof. 

From Lemma 5 and (49) in Lemma 7 we have (59) using the definition (44) of $t_{\infty }$. Furthermore, from (58) we see that (59) implies (60). □

Lemma 13.

For an arbitrary critical point $t\in \tilde{\mathcal{C}}$, the Hessian at $x=\iota \left(t\right)$ is expressed as

$$\frac{1}{2^3}\mathrm{Hess}\left(F\right){|}_{x=\iota \left(t\right)}=-\frac{1}{f_1{f}_2{f}_3{f}_4^3{t}_{\infty }^3}\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_2,{\tilde{g}}_3)}{\partial (t_1,t_2,t_3)}.$$

(61)

In particular, if $t\in \tilde{\mathcal{C}}$ satisfies $t_1\ne 1$, then

$$\frac{1}{2^3}\mathrm{Hess}\left(F\right){|}_{x=\iota \left(t\right)}=-\frac{1}{f_1{f}_2{f}_3{f}_4^3{t}_{\infty }{(1-t_1)}^2}\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}.$$

(62)

Proof. 

From (4), we have

$$\frac{1}{2^3}\mathrm{Hess}\left(F\right)=\frac{\partial (G_1,G_2,G_3)}{\partial (x_1,x_2,x_3)}.$$

According to (46) in Lemma 6 and (59), for $t\in \tilde{\mathcal{C}}$ we have

$$\begin{array}{cc}\hfill & \frac{\partial (G_1,G_2,G_3)}{\partial (x_1,x_2,x_3)}{|}_{x=\iota \left(t\right)}=\frac{\partial (G_1,G_2,G_3)}{\partial (t_1,t_2,t_3)}{\displaystyle /}\frac{\partial (x_1,x_2,x_3)}{\partial (t_1,t_2,t_3)}\hfill \\ & =-\frac{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{f_1{f}_2{f}_3{f}_4^3{t}_{\infty }^7}{\left(\frac{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{t_{\infty }^4}\right)}^{-1}\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_2,{\tilde{g}}_3)}{\partial (t_1,t_2,t_3)},\hfill \end{array}$$

which coincides with (61). On the other hand, if $t_1\ne 1$, then from (60) we obtain

$$\begin{array}{cc}\hfill & \frac{\partial (G_1,G_2,G_3)}{\partial (x_1,x_2,x_3)}{|}_{x=\iota \left(t\right)}=\frac{\partial (G_1,G_2,G_3)}{\partial (t_1,t_2,t_3)}{\displaystyle /}\frac{\partial (x_1,x_2,x_3)}{\partial (t_1,t_2,t_3)}\hfill \\ \hfill & =-\frac{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{f_1{f}_2{f}_3{f}_4^3{t}_{\infty }^5{(1-t_1)}^2}{\left(\frac{{\alpha }_{31}{\alpha }_{22}{\alpha }_{13}}{t_{\infty }^4}\right)}^{-1}\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)},\hfill \end{array}$$

which coincides with the right-hand side of (62). □

We denote by ${\mathbf{c}}_j$$(1\le j\le \kappa )$ all the critical points in X, i.e., $\mathcal{C}=\{{\mathbf{c}}_j\in X|1\le j\le \kappa \}$. For a rational function $\phi \left(x\right)$ on X we denote by $\mathcal{N}\left(\phi \right)$ the product of the critical values at all points in $\mathcal{C}$, i.e., $\mathcal{N}\left(\phi \right):={\prod }_{j=1}^{\kappa }\phi \left({\mathbf{c}}_j\right),$ which is called the norm of $\phi$ on X. We also denote by ${\tilde{\mathbf{c}}}_j$ the critical points in $\tilde{X}$ specified by ${\tilde{\mathbf{c}}}_j={\iota }^{-1}\left({\mathbf{c}}_j\right)$, i.e., $\tilde{\mathcal{C}}={\iota }^{-1}\mathcal{C}=\{{\tilde{\mathbf{c}}}_j\in \tilde{X}|1\le j\le \kappa \},$ where $\iota :\tilde{X}\to X$ is the projective map given by (45). For a rational function $\phi \left(t\right)$ on $\tilde{X}$ we also denote by $\mathcal{N}\left(\phi \right)$ the product of the critical values at all points in $\tilde{\mathcal{C}}$, i.e.,

$$\mathcal{N}\left(\phi \right):=\prod _{j=1}^{\kappa }\phi \left({\tilde{\mathbf{c}}}_j\right),$$

(63)

which is called the norm of $\phi$ on $\tilde{X}$.

Our aim is to study the norm $\mathcal{N}\left(\mathrm{Hess}\right(F\left)\right)$ on X, and the following proposition gives the formula for $\mathcal{N}\left(\mathrm{Hess}\right(F\left)\right)$ on X to be written by norms of several functions on $\tilde{X}$.

Proposition 3.

If an arbitrary $t\in \tilde{\mathcal{C}}$ satisfies $t_1\ne 1$, then

$$\begin{array}{cc}\hfill & \mathcal{N}(\mathrm{Hess}\left(F\right)/2^3)\hfill \\ \hfill & =-\frac{1}{\mathcal{N}\left(f_1\right)\mathcal{N}\left(f_2\right)\mathcal{N}\left(f_3\right){\left\{\mathcal{N}\left(f_4\right)\right\}}^3\mathcal{N}\left(t_{\infty }\right){\left\{\mathcal{N}(1-t_1)\right\}}^2}\mathcal{N}\left(\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\right).\hfill \end{array}$$

(64)

Proof. 

From (62) in Lemma 13 we have

$$\prod _{j=1}^{\kappa }\frac{\mathrm{Hess}\left(F\right)}{2^3}{|}_{x={\mathbf{c}}_j}=\prod _{j=1}^{\kappa }\left\{\frac{-1}{f_1{f}_2{f}_3{f}_4^3{t}_{\infty }{(1-t_1)}^2}\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\right\}{|}_{t={\tilde{\mathbf{c}}}_j},$$

which coincides with the right-hand side of (64). □

In order to calculate the part $\mathcal{N}\left(\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})/\partial (t_1,t_2,t_3)\right)$ in the right-hand side of (64) in Proposition 3 we will use the following lemma later.

Lemma 14.

Suppose that there exists rational curve $\omega :\mathbb{C}\to \tilde{X}$ in $\tilde{X}$ given by

$$\omega :t_1⟼(t_1,t_2={\omega }_2\left(t_1\right),t_3={\omega }_3\left(t_1\right))\in \tilde{X}$$

satisfies the equations

$${\tilde{g}}_{12}(t_1,{\omega }_2\left(t_1\right),{\omega }_3\left(t_1\right))=0and{\tilde{g}}_{13}(t_1,{\omega }_2\left(t_1\right),{\omega }_3\left(t_1\right))=0.$$

(65)

Suppose also that the curve ω interpolates some critical point in $\tilde{\mathcal{C}}$, i.e., there exists $\tau \in \mathbb{C}$ such that

$${\tilde{g}}_1(\tau ,{\omega }_2\left(\tau \right),{\omega }_3\left(\tau \right))=0.$$

Let ψ be function on $\mathbb{C}$ specified by

$$\psi \left(t_1\right):={\tilde{g}}_1(t_1,{\omega }_2\left(t_1\right),{\omega }_3\left(t_1\right)).$$

(66)

The following identity as a function on the curve ω in $\tilde{X}$ (i.e., as a function of $t_1$) holds.

$$\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}={\psi }^{\prime }\left(t_1\right)\times \frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)},$$

(67)

where ${\psi }^{\prime }\left(t_1\right)$ denotes the derivative $d\psi /d{t}_1$. In particular, for the point $\tau \in \mathbb{C}$ such that $T=(\tau ,{\omega }_2\left(\tau \right),{\omega }_3\left(\tau \right))\in \tilde{\mathcal{C}}$ it follows that

$$\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}{|}_{t=T}={\psi }^{\prime }\left(\tau \right)\times \frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{t=T}.$$

(68)

Proof. 

Applying chain rule to (65) and (66), we have

$$\left(\begin{array}{ccc}-{\psi }^{\prime }+\frac{\partial {\tilde{g}}_1}{\partial t_1}& \frac{\partial {\tilde{g}}_1}{\partial t_2}& \frac{\partial {\tilde{g}}_1}{\partial t_3}\\ \frac{\partial {\tilde{g}}_{12}}{\partial t_1}& \frac{\partial {\tilde{g}}_{12}}{\partial t_2}& \frac{\partial {\tilde{g}}_{12}}{\partial t_3}\\ \frac{\partial {\tilde{g}}_{13}}{\partial t_1}& \frac{\partial {\tilde{g}}_{13}}{\partial t_2}& \frac{\partial {\tilde{g}}_{13}}{\partial t_3}\end{array}\right)\left(\begin{array}{c}1\\ {\omega }_2^{\prime }\\ {\omega }_3^{\prime }\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right),$$

so that

$$0=\left|\begin{array}{ccc}-{\psi }^{\prime }+\frac{\partial {\tilde{g}}_1}{\partial t_1}& \frac{\partial {\tilde{g}}_1}{\partial t_2}& \frac{\partial {\tilde{g}}_1}{\partial t_3}\\ \frac{\partial {\tilde{g}}_{12}}{\partial t_1}& \frac{\partial {\tilde{g}}_{12}}{\partial t_2}& \frac{\partial {\tilde{g}}_{12}}{\partial t_3}\\ \frac{\partial {\tilde{g}}_{13}}{\partial t_1}& \frac{\partial {\tilde{g}}_{13}}{\partial t_2}& \frac{\partial {\tilde{g}}_{13}}{\partial t_3}\end{array}\right|=\left|\begin{array}{ccc}\frac{\partial {\tilde{g}}_1}{\partial t_1}& \frac{\partial {\tilde{g}}_1}{\partial t_2}& \frac{\partial {\tilde{g}}_1}{\partial t_3}\\ \frac{\partial {\tilde{g}}_{12}}{\partial t_1}& \frac{\partial {\tilde{g}}_{12}}{\partial t_2}& \frac{\partial {\tilde{g}}_{12}}{\partial t_3}\\ \frac{\partial {\tilde{g}}_{13}}{\partial t_1}& \frac{\partial {\tilde{g}}_{13}}{\partial t_2}& \frac{\partial {\tilde{g}}_{13}}{\partial t_3}\end{array}\right|-\left|\begin{array}{ccc}{\psi }^{\prime }& \frac{\partial {\tilde{g}}_1}{\partial t_2}& \frac{\partial {\tilde{g}}_1}{\partial t_3}\\ 0& \frac{\partial {\tilde{g}}_1}{\partial t_2}& \frac{\partial {\tilde{g}}_1}{\partial t_3}\\ 0& \frac{\partial {\tilde{g}}_1}{\partial t_2}& \frac{\partial {\tilde{g}}_1}{\partial t_3}\end{array}\right|,$$

which is equivalent to (67), and (68) is a special case of (67) when $t_1=\tau$. □

In the next section we consider a special symmetric case when ${\rho }_{12}^2={\rho }_{23}^2={\rho }_{13}^2$ and ${\rho }_{14}^2={\rho }_{24}^2={\rho }_{34}^2$, $r_j^2$ being the same. We shall present $\psi \left(t_1\right),\frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}$ and the norms of $f_j$ explicitly by taking the basic parameter $t_1$.

We shall also consider the cases when we take the basic parameter $t_{\infty }$ and s in place of $t_1$, where

$$t_{\infty }=1+t_1+t_2+t_3,s:=\frac{{\rho }_{13}^2-{\rho }_{14}^2}{{\rho }_{34}^2}{t}_1+\frac{{\rho }_{23}^2-{\rho }_{24}^2}{{\rho }_{34}^2}{t}_2-t_3.$$

(69)

From (52) of Lemma 8, for $t_{\infty }$ and s, we see that

$$f_3-f_4={\rho }_{34}^2\frac{s+1}{t_{\infty }}+\frac{(r_4^2-r_1^2)t_1+(r_4^2-r_2^2)t_2+(r_4^2-r_3^2)(t_3+1)}{t_{\infty }},$$

(70)

and we also see from (47) that

$$\sum _{j=1}^4\frac{1}{f_j}\equiv \frac{t_{\infty }}{f_4}modAnn\left(\tilde{\mathcal{C}}\right).$$

(71)

The relations (70) and (71) will be used in Section 5 to evaluate the norms of $f_3-f_4$ and ${\sum }_{j=1}^4{f}_j^{-1}$.

4. A Special Symmetric Case of $\mathbf{▵}{\mathit{O}}_{\mathbf{1}}{\mathit{O}}_{\mathbf{2}}{\mathit{O}}_{\mathbf{3}}{\mathit{O}}_{\mathbf{4}}$

In this section, we restrict ourselves to a special symmetric case when $▵O_1{O}_2{O}_3{O}_4$ is a pyramid with axis of symmetry whose base triangle $▵O_1{O}_2{O}_3$ is regular and all spheres have the same radius, i.e., throughout this section we assume

$$\left({\mathcal{H}}_1\right):{\rho }_{12}^2={\rho }_{13}^2={\rho }_{23}^2,{\rho }_{14}^2={\rho }_{24}^2={\rho }_{34}^2,r_j^2=r^2(1\le j\le 4).$$

We first see the fundamental invariants, i.e., the explicit forms of the Cayley–Menger determinants.

Lemma 15.

$$\begin{array}{cc}\hfill & B\left(012\right)=B\left(013\right)=B\left(023\right)=2{\rho }_{12}^2>0,B\left(014\right)=B\left(024\right)=B\left(034\right)=2{\rho }_{14}^2>0,\hfill \\ \hfill & B\left(0123\right)=-3{\rho }_{12}^4<0,B\left(0124\right)={\rho }_{12}^2({\rho }_{12}^2-4{\rho }_{14}^2)<0,\hfill \\ \hfill & B\left(01234\right)=-2{\rho }_{12}^4({\rho }_{12}^2-3{\rho }_{14}^2)>0.\hfill \end{array}$$

Lemma 16.

$$\begin{array}{cc}\hfill & B(0★j)=2r^2(1\le j\le 4),B(0★jk)={\rho }_{12}^2({\rho }_{12}^2-4r^2)(1\le j<k\le 3),\hfill \\ \hfill & B(0★j4)={\rho }_{14}^2({\rho }_{14}^2-4r^2)(1\le j\le 3),\hfill \\ \hfill & B(0★123)=2{\rho }_{12}^4(3r^2-{\rho }_{12}^2),B(0★124)=2{\rho }_{12}^2(4r^2{\rho }_{14}^2-r^2{\rho }_{12}^2-{\rho }_{14}^4),\hfill \\ \hfill & B(0★1234)={\rho }_{12}^4(3{\rho }_{14}^4+4r^2{\rho }_{12}^2-12r^2{\rho }_{14}^2)=\frac{3}{2}{\rho }_{12}^{2}B\left(124\right)-2r^{2}B\left(01234\right).\hfill \end{array}$$

Remark 7.

$B(0★jk)<0$, $B(0★jkl)>0$, $B(0★1234)<0$ for sufficiently large $r\gg 0.$

Lemma 17.

Under the condition $\left({\mathcal{H}}_1\right)$ the polynomials ${\tilde{g}}_j$$(1\le j\le 3)$ and ${\tilde{g}}_{jk}$$(1\le j<k\le 3)$ defined in (48) and (56) are written as

$$\begin{array}{cc}\hfill {\tilde{g}}_j\left(t\right)& =r^2{t}_j^3+(r^2-{\rho }_{12}^2)(t_k^2+t_l^2)t_j+2r^2{t}_j^2(t_k+t_l)-({\rho }_{12}^2-2r^2)t_j{t}_k{t}_l\hfill \\ & +({\rho }_{14}^2+r^2)(t_j^2+t_k^2+t_l^2)-2({\rho }_{12}^2-{\rho }_{14}^2)t_j(t_k+t_l)\hfill \\ & +(2{\rho }_{14}^2-{\rho }_{12}^2-2r^2)t_k{t}_l-({\rho }_{14}^2+r^2)t_j-2r^2(t_k+t_l)-r^2,\hfill \end{array}$$

(72)

$${\tilde{g}}_{jk}\left(t\right)=(t_k-t_j){\widehat{g}}_{jk}\left(t\right),{\widehat{g}}_{jk}\left(t\right):={\rho }_{12}^2{t}_j{t}_k+({\rho }_{12}^2-{\rho }_{14}^2)t_l-{\rho }_{14}^2(t_j+t_k-1),$$

(73)

respectively, where $\{j,k,l\}$ is a permutation of $\{1,2,3\}$.

Proof. 

Under the condition $\left({\mathcal{H}}_1\right)$, the following symbols become as

$$\begin{array}{cc}\hfill B\left(\begin{array}{ccc}0& k& j\\ 0& l& j\end{array}\right)& ={\rho }_{kj}^2+{\rho }_{lj}^2-{\rho }_{kj}^2={\rho }_{12}^2,\hfill \\ \hfill B\left(\begin{array}{ccc}0& k& 4\\ 0& j& 4\end{array}\right)& ={\rho }_{k4}^2+{\rho }_{l4}^2-{\rho }_{kj}^2=2{\rho }_{14}^2-{\rho }_{12}^2,\hfill \\ \hfill B\left(\begin{array}{ccc}0& ★& k\\ 0& j& 4\end{array}\right)& ={\rho }_{kj}^2-r_j^2-{\rho }_{k4}^2+r_4^2={\rho }_{12}^2-{\rho }_{14}^2={\mathsf{\Delta }}_0,\hfill \end{array}$$

where $\{j,k,l\}$ is a permutation of $\{1,2,3\}$. Applying them to Proposition 2 and Lemma 10 in Section 3, we obtain (72) and (73). □

Notice that ${\tilde{g}}_{jk}$ are independent of $r^2$ under the condition $\left({\mathcal{H}}_1\right)$. For the succeeding arguments we write ${\tilde{g}}_1$ as polynomial in $t_2$ and $t_3$ explicitly as follows.

$$\begin{array}{cc}\hfill & {\tilde{g}}_1(t_1,t_2,t_3)\hfill \\ \hfill & =\left[(r^2-{\rho }_{12}^2)t_1+{\rho }_{14}^2-r^2\right](t_2^2+t_3^2)+\left[(2r^2-{\rho }_{12}^2)t_1+2{\rho }_{14}^2-{\rho }_{12}^2-2r^2\right]t_2{t}_3\hfill \\ \hfill & +2\left[r^2{t}_1^2-({\rho }_{12}^2-{\rho }_{14}^2)t_1-r^2\right](t_2+t_3)+(t_1-1)(r^2{t}_1^2+(2r^2+{\rho }_{14}^2)t_1+r^2).\hfill \end{array}$$

(74)

By definition, we have the identity

$${\widehat{g}}_{12}\left(t\right)-{\widehat{g}}_{13}\left(t\right)={\rho }_{12}^2(t_1-1)(t_2-t_3).$$

(75)

We state a property of the set $\tilde{\mathcal{C}}=\{t\in \tilde{X}|{\tilde{g}}_1={\tilde{g}}_2={\tilde{g}}_3=0\}$ as follows.

Lemma 18.

There exists no point $t=(t_1,t_2,t_3)$ in $\tilde{\mathcal{C}}\subset \tilde{X}$ such that $t_1\ne t_2,t_2\ne t_3,t_1\ne t_3$.

Proof. 

Assume that $t=(t_1,t_2,t_3)\in \tilde{\mathcal{C}}$ satisfies $t_1\ne t_2,t_2\ne t_3,t_1\ne t_3$. If $t_1\ne 1$, then from Lemma 11 we see that $t\in \tilde{\mathcal{C}}$ satisfies the system ${\tilde{g}}_1={\tilde{g}}_{12}={\tilde{g}}_{13}=0$. Seeing (73) and $t_1\ne t_2$, $t_1\ne t_3$ we have $0={\widehat{g}}_{12}-{\widehat{g}}_{13}={\rho }_{12}^2(t_1-1)(t_2-t_3)$, which contradicts the assumption. If $t_1=1$, then we have $t_2\ne t_1=1$, so that again from Lemma 11 we see that $t\in \tilde{\mathcal{C}}$ satisfies the system ${\tilde{g}}_2={\tilde{g}}_{12}={\tilde{g}}_{23}=0$. In the same way as above we have a contradiction again. □

As a consequence of Lemma 18, the set $\tilde{\mathcal{C}}$ is partitioned into the following:

$${\tilde{\mathcal{C}}}_1:t_1=t_2=t_3,{\tilde{\mathcal{C}}}_2:t_1=t_2\ne t_3,{\tilde{\mathcal{C}}}_3:t_1=t_3\ne t_2,{\tilde{\mathcal{C}}}_4:t_2=t_3\ne t_1.$$

(76)

Denote ${\mathcal{C}}_j=\iota {\tilde{\mathcal{C}}}_j\subset X$, such that $\mathcal{C}$ is the disjoint union of ${\mathcal{C}}_j$ and that $\tilde{\mathcal{C}}$ is the disjoint union of ${\tilde{\mathcal{C}}}_j$:

$$\mathcal{C}=\underset{j=1}{\overset{4}{⨆}}{\mathcal{C}}_j,\tilde{\mathcal{C}}=\underset{j=1}{\overset{4}{⨆}}{\tilde{\mathcal{C}}}_j.$$

Remark 8.

The number of the critical points is $2^{3+1}-1=15$, i.e., $|\tilde{\mathcal{C}}|=15$. As we will see below, it is confirmed that $|{\tilde{\mathcal{C}}}_1|=3$ and $|{\tilde{\mathcal{C}}}_2|=|{\tilde{\mathcal{C}}}_3|=|{\tilde{\mathcal{C}}}_4|=4$.

For the set $\widetilde{{\mathcal{C}}_1}$, we immediately have the following:

Lemma 19.

For $(1,1,1)\in \tilde{X}$ the polynomials ${\tilde{g}}_j$$(j=1,2,3)$ are evaluated as

$${\tilde{g}}_1(1,1,1)={\tilde{g}}_2(1,1,1)={\tilde{g}}_3(1,1,1)=-8{\mathsf{\Delta }}_0,$$

where ${\mathsf{\Delta }}_0:={\rho }_{12}^2-{\rho }_{14}^2.$ In other words, the following equivalence holds:

$${\mathsf{\Delta }}_0=0⟺(1,1,1)\in \widetilde{{\mathcal{C}}_1}.$$

Our approach to study the structure of $\tilde{\mathcal{C}}$ depends on whether we impose the condition ${\mathsf{\Delta }}_0=0$ or not. In the following section, we first consider the case ${\mathsf{\Delta }}_0\ne 0$, while we devote Section 6 to the case ${\mathsf{\Delta }}_0=0$, i.e., the case where $▵O_1{O}_2{O}_3{O}_4$ is the regular tetrahedron.

5. Critical Points under $\left({\mathcal{H}}_{\mathbf{0}}\right)$, $\left({\mathcal{H}}_{\mathbf{1}}\right)$ and ${\mathbf{\rho }}_{\mathbf{12}}\ne {\mathbf{\rho }}_{\mathbf{14}}$

Throughout this section, in addition to the imposed conditions $\left({\mathcal{H}}_0\right)$ and $\left({\mathcal{H}}_1\right)$, we suppose further

$${\mathsf{\Delta }}_0:={\rho }_{12}^2-{\rho }_{14}^2\ne 0.$$

(77)

In this setting, the special parameter s introduced in (69) is given by

$$s:=\delta (t_1+t_2)-t_3,\mathrm{where}\delta =\frac{{\rho }_{12}^2-{\rho }_{14}^2}{{\rho }_{14}^2},$$

(78)

and (70) is reduced to

$$f_3-f_4={\rho }_{14}^2(s+1)/t_{\infty },$$

(79)

where $t_{\infty }=1+t_1+t_2+t_3$. Thus, $\mathcal{N}(s+1)$ will be used indirectly for calculation of $\mathcal{N}(f_3-f_4)$ later.

Lemma 20.

Under the conditions $\left({\mathcal{H}}_0\right)$, $\left({\mathcal{H}}_1\right)$ and ${\mathsf{\Delta }}_0\ne 0$, there exists no point $t=(t_1,t_2,t_3)$ in $\tilde{\mathcal{C}}\subset \tilde{X}$ such that $t_1=1$ if and only if ${\mathsf{\Delta }}_1\ne 0$, where

$${\mathsf{\Delta }}_1:=4r^2-3{\rho }_{12}^2-{\rho }_{14}^2.$$

(80)

Moreover, ${\mathsf{\Delta }}_1=0$ if and only if $\{(t_1,t_2,t_3)\in \tilde{\mathcal{C}}|t_1=1\}=\{(1,1,-1),(1,-1,1)\}$.

Proof. 

If $(1,t_2,t_3)\in \tilde{\mathcal{C}}$ then $(1,t_2,t_3)$ satisfies the condition (76) and the equation

$${\tilde{g}}_1(1,t_2,t_3)=-{\mathsf{\Delta }}_0(t_2+t_3)(t_2+t_3+2)=0.$$

(81)

Then, under the assumption ${\mathsf{\Delta }}_0\ne 0$, we need six possibilities for $(1,t_2,t_3)\in \tilde{\mathcal{C}}$, i.e.,

$$(1,t_2,t_3)=(1,1,-3),(1,1,-1),(1,-3,1),(1,-1,1),(1,-1,-1),(1,0,0).$$

Under the condition $\left({\mathcal{H}}_0\right)$, for these points we have

$$\begin{array}{cc}\hfill & {\tilde{g}}_1(1,1,-3)={\tilde{g}}_2(1,1,-3)=0,{\tilde{g}}_3(1,1,-3)=4(5{\rho }_{12}^2+{\rho }_{14}^2)>0,\hfill \\ \hfill & {\tilde{g}}_1(1,1,-1)={\tilde{g}}_2(1,1,-1)=0,{\tilde{g}}_3(1,1,-1)=-2{\mathsf{\Delta }}_1,\hfill \\ \hfill & {\tilde{g}}_1(1,-3,1)={\tilde{g}}_3(1,-3,1)=0,{\tilde{g}}_2(1,-3,1)=4(5{\rho }_{12}^2+{\rho }_{14}^2)>0,\hfill \\ \hfill & {\tilde{g}}_1(1,-1,1)={\tilde{g}}_3(1,-1,1)=0,{\tilde{g}}_2(1,-1,1)=-2{\mathsf{\Delta }}_1,\hfill \\ \hfill & {\tilde{g}}_1(1,-1,-1)=0,{\tilde{g}}_2(1,-1,-1)={\tilde{g}}_3(1,-1,-1)=2({\rho }_{12}^2+{\rho }_{14}^2)>0,\hfill \\ \hfill & {\tilde{g}}_1(1,0,0)=0,{\tilde{g}}_2(1,0,0)={\tilde{g}}_3(1,0,0)={\rho }_{14}^2-4r^2=\frac{2B(0★14)}{B\left(014\right)}\ne 0,\hfill \end{array}$$

so that we see

$$(1,1,-3),(1,-3,1),(1,-1,-1),(1,0,0)\notin \tilde{\mathcal{C}},$$

(82)

and therefore obtain

$$\begin{array}{cc}\hfill & {\mathsf{\Delta }}_1\ne 0⟺\{(t_1,t_2,t_3)\in \tilde{\mathcal{C}}|t_1=1\}=\varnothing ,\hfill \\ \hfill & {\mathsf{\Delta }}_1=0⟺\{(t_1,t_2,t_3)\in \tilde{\mathcal{C}}|t_1=1\}=\{(1,1,-1),(1,-1,1)\}.\hfill \end{array}$$

This completes the proof. □

Lemma 11 states the equivalence between the systems ${\tilde{g}}_1={\tilde{g}}_2={\tilde{g}}_3=0$ and ${\tilde{g}}_1={\tilde{g}}_{12}={\tilde{g}}_{13}=0$ under $t_1\ne 1$. If ${\mathsf{\Delta }}_1\ne 0$, then we can omit the condition $t_1\ne 1$ for this equivalence, because Lemma 20 says that each point $t\in \tilde{\mathcal{C}}=\{t\in \tilde{X}|{\tilde{g}}_1={\tilde{g}}_2={\tilde{g}}_3=0\}$ satisfies $t_1\ne 1$. Namely, $\tilde{\mathcal{C}}$ coincides with $\{t\in \tilde{X}|{\tilde{g}}_1={\tilde{g}}_{12}={\tilde{g}}_{13}=0\}$ if ${\mathsf{\Delta }}_1\ne 0$. On the other hand, if ${\mathsf{\Delta }}_1=0$, then Lemma 20 implies that $\tilde{\mathcal{C}}$ is expressed as

$$\tilde{\mathcal{C}}=\{(1,1,-1),(1,-1,1)\}\cup \{t\in \tilde{X}|{\tilde{g}}_1={\tilde{g}}_{12}={\tilde{g}}_{13}=0,t_1\ne 1\}.$$

However we eventually realize that this distinction is unnecessary whether ${\mathsf{\Delta }}_1=0$ or not (see explanation in Remark 10 after Lemma 21). Hereafter, we analyze the set $\tilde{\mathcal{C}}$ regarded as that of solutions of the system ${\tilde{g}}_1={\tilde{g}}_{12}={\tilde{g}}_{13}=0$ without constraint $t_1\ne 1$, i.e.,

$$\tilde{\mathcal{C}}=\{t\in \tilde{X}|{\tilde{g}}_1={\tilde{g}}_{12}={\tilde{g}}_{13}=0\}.$$

The aim of succeeding four subsections is to evaluate the norms $\mathcal{N}\left(t_j\right)$, $\mathcal{N}(1-t_j)$, $\mathcal{N}\left(t_{\infty }\right)$ and $\mathcal{N}(s+1)$ for each ${\tilde{\mathcal{C}}}_j$ $(j=1,2,3,4)$ given in (76). We denote ${\mathcal{N}}_j\left(\phi \right)$ the partial product of $\phi \left(t\right)$ $(t\in {\tilde{\mathcal{C}}}_j)$, i.e.,

$${\mathcal{N}}_j\left(\phi \right):=\prod _{t\in {\tilde{\mathcal{C}}}_j}\phi \left(t\right).$$

5.1. The Set ${\tilde{\mathcal{C}}}_1:t_1=t_2=t_3$

In this subsection, we assume that $t_1=t_2=t_3$ for the critical points. When $t_2=t_1$ and $t_3=t_1$, from (73) ${\tilde{g}}_{12}={\tilde{g}}_{13}=0$ is automatically satisfied. Then, the solutions of the equation ${\tilde{g}}_1(t_1,t_1,t_1)=0$ correspond to the critical points in ${\tilde{\mathcal{C}}}_1$. We define the characteristic polynomial ${\psi }_1\left(t_1\right)$ of the set ${\tilde{\mathcal{C}}}_1$ by

$${\psi }_1\left(t_1\right):={\tilde{g}}_1(t_1,t_1,t_1)=3(3r^2-{\rho }_{12}^2)t_1^3+(9{\rho }_{14}^2-5{\rho }_{12}^2-3r^2)t_1^2-(5r^2+{\rho }_{14}^2)t_1-r^2,$$

(83)

which gives ${\tilde{\mathcal{C}}}_1=\{(t_1,t_1,t_1)\in \tilde{X}|{\psi }_1(t_1)=0\}$. We denote the roots of the equation ${\psi }_1\left(t_1\right)=0$ by ${\zeta }_1,{\zeta }_2,{\zeta }_3$, then the points corresponding to ${\zeta }_j$ give the set of critical points ${\tilde{\mathcal{C}}}_1$ in the straight line $t_1=t_2=t_3.$ Let ${\overline{\psi }}_1$ be monic polynomial in $t_1$ specified by

$${\overline{\psi }}_1\left(t_1\right):=\prod _{j=1}^3(t_1-{\zeta }_j)=\frac{{\psi }_1\left(t_1\right)}{h_1},$$

(84)

where $h_1=3(3r^2-{\rho }_{12}^2)$ is the coefficient of highest degree of ${\psi }_1$. Then we obtain the following.

Proposition 4.

$$\begin{array}{cc}\hfill & {\mathcal{N}}_1\left(t_j\right)=\frac{r^2}{3(3r^2-{\rho }_{12}^2)}=\frac{2r^2{\rho }_{12}^4}{3B(0★123)}(j=1,2,3),\hfill \\ \hfill & {\mathcal{N}}_1(1-t_j)=-\frac{8{\mathsf{\Delta }}_0}{3(3r^2-{\rho }_{12}^2)}=-\frac{16{\mathsf{\Delta }}_0{\rho }_{12}^4}{3B(0★123)}(j=1,2,3),\hfill \\ \hfill & {\mathcal{N}}_1\left(t_{\infty }\right)=4\frac{{\rho }_{12}^2-3{\rho }_{14}^2}{3r^2-{\rho }_{12}^2}=-4\frac{B\left(01234\right)}{B(0★123)},\hfill \\ \hfill & {\mathcal{N}}_1(s+1)=\frac{2{\mathsf{\Delta }}_0({\rho }_{12}^2-3{\rho }_{14}^2)(3{\rho }_{14}^2+4r^2{\rho }_{12}^2-12r^2{\rho }_{14}^2)}{3{\rho }_{14}^6(3r^2-{\rho }_{12}^2)}=\frac{2{\mathsf{\Delta }}_{0}B\left(01234\right)B(0★1234)}{{\rho }_{14}^{6}B\left(0123\right)B(0★123)}.\hfill \end{array}$$

Proof. 

Since $t_1=t_2=t_3$, for $1\le j\le 3$ we have ${\mathcal{N}}_1\left(t_j\right)={\mathcal{N}}_1\left(t_1\right)$ and ${\mathcal{N}}_1(1-t_j)={\mathcal{N}}_1(1-t_1)$, which are evaluated as special values of ${\psi }_1\left(t\right)$, as follows:

$$\begin{array}{cc}\hfill {\mathcal{N}}_1\left(t_1\right)& ={\zeta }_1{\zeta }_2{\zeta }_3=-{\overline{\psi }}_1\left(0\right)=-\frac{{\psi }_1\left(0\right)}{h_1}=\frac{r^2}{3(3r^2-{\rho }_{12}^2)},\hfill \\ \hfill {\mathcal{N}}_1(1-t_1)& =\prod _{j=1}^3(1-{\zeta }_j)={\overline{\psi }}_1\left(1\right)=\frac{{\psi }_1\left(1\right)}{h_1}=-\frac{8{\mathsf{\Delta }}_0}{3(3r^2-{\rho }_{12}^2)}.\hfill \end{array}$$

In general, for arbitrary ${\gamma }_1$, ${\gamma }_2$ we can calculate the norm of ${\gamma }_1{t}_1-{\gamma }_2$ by

$${\mathcal{N}}_1({\gamma }_1{t}_1-{\gamma }_2)=\prod _{j=1}^3({\gamma }_1{\zeta }_j-{\gamma }_2)=-{\gamma }_1^3\prod _{j=1}^3\left(\frac{{\gamma }_2}{{\gamma }_1}-{\zeta }_j\right)=-\frac{{\gamma }_1^3}{h_1}{\psi }_1\left(\frac{{\gamma }_2}{{\gamma }_1}\right).$$

We can evaluate ${\psi }_1({\gamma }_2/{\gamma }_1)$ by a direct calculation from (83). Using this formula, we obtain

$$\begin{array}{cc}\hfill {\mathcal{N}}_1\left(t_{\infty }\right)& ={\mathcal{N}}_1(3t_1+1)=-\frac{27}{h_1}{\psi }_1\left(-\frac{1}{3}\right)=4\frac{{\rho }_{12}^2-3{\rho }_{14}^2}{3r^2-{\rho }_{12}^2},\hfill \\ \hfill {\mathcal{N}}_1(s+1)& ={\mathcal{N}}_1((2\delta -1)t_1+1)=-\frac{{(2\delta -1)}^3}{h_1}{\psi }_1\left(\frac{-1}{2\delta -1}\right)\hfill \\ & =\frac{{(3{\rho }_{14}^2-2{\rho }_{12}^2)}^3}{h_1{\rho }_{14}^6}{\psi }_1\left(\frac{{\rho }_{14}^2}{3{\rho }_{14}^2-2{\rho }_{12}^2}\right),\hfill \end{array}$$

which coincides with the result for ${\mathcal{N}}_1(s+1)$ in Proposition 4. □

5.2. The Set ${\tilde{\mathcal{C}}}_2:t_1=t_2\ne t_3$

We assume that $t_1=t_2\ne t_3$ for the critical points. From (73) $t_1=t_2$ implies that ${\tilde{g}}_{12}=0$ is automatically satisfied. When $t_1\ne t_3$, according to (73) it is necessary for ${\tilde{g}}_{13}=0$ that

$${\widehat{g}}_{13}(t_1,t_1,t_3)={\rho }_{12}^2{t}_1{t}_3+({\rho }_{12}^2-{\rho }_{14}^2)t_1-{\rho }_{14}^2(t_1+t_3-1)=0$$

is satisfied. Solving this equation, with respect to $t_3$, we have

$$t_3={\omega }_3\left(t_1\right):=\frac{(2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2}.$$

(85)

Hence, for the basic parameter $t_1$ the rational curve $(t_1,t_1,{\omega }_3\left(t_1\right))\in \tilde{X}$ interpolates the set of all critical points in ${\tilde{\mathcal{C}}}_2.$

Lemma 21.

Let ${\psi }_2$ be function specified by ${\psi }_2\left(t_1\right):={\tilde{g}}_1(t_1,t_1,{\omega }_3\left(t_1\right))$. Then ${\psi }_2$ has the factor $t_1-1$, namely it is written as

$${\psi }_2\left(t_1\right)=\frac{(t_1-1){\widehat{\psi }}_2\left(t_1\right)}{{\left({\rho }_{12}^2{t}_1-{\rho }_{14}^2\right)}^2},$$

(86)

where ${\widehat{\psi }}_2\left(t_1\right)$ is a polynomial in $t_1$ of degree 4. Moreover the explicit form of ${\widehat{\psi }}_2\left(t_1\right)$ is

$$\begin{array}{cc}\hfill {\widehat{\psi }}_2\left(t_1\right)& ={\rho }_{12}^4(4r^2-{\rho }_{12}^2)t_1^4+2{\rho }_{12}^4(2{\rho }_{14}^2-{\rho }_{12}^2)t_1^3+{\rho }_{12}^2{\rho }_{14}^2(-8r^2+{\rho }_{12}^2-3{\rho }_{14}^2)t_1^2\hfill \\ \hfill & +2{\rho }_{12}^2{\rho }_{14}^4{t}_1+{\rho }_{14}^4(4r^2-{\rho }_{14}^2).\hfill \end{array}$$

(87)

Proof. 

Since ${\omega }_3\left(t_1\right)$ is a ratio of two polynomials in $t_1$ of degree 1 as (85), and ${\tilde{g}}_1(t_1,t_1,t_3)$ is a polynomial in $t_3$ of degree 2 and in $t_1$ of degree 3, ${\psi }_2\left(t_1\right)={\tilde{g}}_1(t_1,t_1,{\omega }_3\left(t_1\right))$ can be written as ${\psi }_2\left(t_1\right)=(\mathrm{polynomial} \mathrm{in} t_1 \mathrm{of} \mathrm{degree} 5)/{\left({\rho }_{12}^2{t}_1-{\rho }_{14}^2\right)}^2$. In particular, from (81) we have ${\psi }_2\left(1\right)={\tilde{g}}_1(1,1,{\omega }_3\left(1\right))={\tilde{g}}_1(1,1,-1)=0$, so that ${\psi }_2\left(t_1\right)$ is divisible by $t_1-1$. Therefore, we obtain the expression (86). The explicit form (87) is obtained by direct calculation. □

Remark 9.

From Lemma 20, we see that $(1,1,{\omega }_3\left(1\right))=(1,1,-1)\notin \tilde{\mathcal{C}}$ if ${\mathsf{\Delta }}_1\ne 0$. This means that the root $t_1=1$ of the equation ${\psi }_2\left(t_1\right)=0$ does not correspond to any point in ${\tilde{\mathcal{C}}}_2$.

Since ${\widehat{\psi }}_2\left(t_1\right)$ is evaluated at $t_1={\rho }_{14}^2/{\rho }_{12}^2$ as ${\widehat{\psi }}_2({\rho }_{14}^2/{\rho }_{12}^2)=4r^2{\rho }_{14}^4{\mathsf{\Delta }}_0^2/{\rho }_{12}^4\ne 0$, we have the expression

$${\tilde{\mathcal{C}}}_2=\{(t_1,t_1,{\omega }_3(t_1))\in \tilde{X}|{\widehat{\psi }}_2(t_1)=0\},$$

where ${\omega }_3\left(t_1\right)$ is given by (85), and we call ${\widehat{\psi }}_2\left(t_1\right)$ the characteristic polynomial of ${\tilde{\mathcal{C}}}_2$.

Remark 10.

When ${\mathsf{\Delta }}_1=0$, i.e., $r^2=(3{\rho }_{12}^2+{\rho }_{14}^2)/4$, the characteristic polynomial ${\widehat{\psi }}_2\left(t_1\right)$ is expressed as ${\widehat{\psi }}_2\left(t_1\right)={\rho }_{12}^2{r}^2(t_1-1)\left({\rho }_{12}^2(2{\rho }_{12}^2+{\rho }_{14}^2)t_1^3+5{\rho }_{12}^2{\rho }_{14}^2{t}_1^2-5{\rho }_{14}^4{t}_1-3{\rho }_{14}^4\right),$ which has the factor $(t_1-1)$, so that $t_1=1$ is the double root of ${\psi }_2\left(t_1\right)=0$. The polynomial ${\widehat{\psi }}_2\left(t_1\right)$ was originally defined from the system ${\tilde{g}}_1={\tilde{g}}_{12}={\tilde{g}}_{13}=0$ for $t_1\ne 1$ under ${\mathsf{\Delta }}_1\ne 0$. In this sense $t_1=1$ is meaningless as a solution of ${\widehat{\psi }}_2\left(t_1\right)=0$, which corresponds to a point in ${\tilde{\mathcal{C}}}_2$. However, the point $(1,1,{\omega }_3\left(1\right))=(1,1,-1)$ formally corresponding to $t_1=1$ is indeed an element of $\in \tilde{\mathcal{C}}$ when ${\mathsf{\Delta }}_1=0$ (the fact $(1,1,-1)\in {\tilde{\mathcal{C}}}_2$ if ${\mathsf{\Delta }}_1=0$ was also confirmed in Lemma 20). This makes sense even when $t_1=1$, and eventually the imposed condition for $t_1$ or ${\mathsf{\Delta }}_1$ can be removed.

We denote the roots of the equation ${\widehat{\psi }}_2\left(t_1\right)=0$ by ${\zeta }_1,{\zeta }_2,{\zeta }_3,{\zeta }_4$, then the points corresponding to ${\zeta }_j$ give the set of critical points ${\tilde{\mathcal{C}}}_2$. Let ${\overline{\psi }}_2$ be monic polynomial in $t_1$ specified by

$${\overline{\psi }}_2\left(t_1\right):=\prod _{j=1}^4(t_1-{\zeta }_j)=\frac{{\widehat{\psi }}_2\left(t_1\right)}{h_2},$$

where $h_2:={\rho }_{12}^4(4r^2-{\rho }_{12}^2)$ is the coefficient of highest degree of ${\widehat{\psi }}_2$. Then we obtain the following:

Proposition 5.

$$\begin{array}{cc}\hfill & {\mathcal{N}}_2\left(t_1\right)={\mathcal{N}}_2\left(t_2\right)=\frac{{\rho }_{14}^4(4r^2-{\rho }_{14}^2)}{{\rho }_{12}^4(4r^2-{\rho }_{12}^2)}=-\frac{{\rho }_{14}^{2}B(0★14)}{{\rho }_{12}^{2}B(0★12)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\mathcal{N}}_2(1-t_1)={\mathcal{N}}_2(1-t_2)=\frac{{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_1}{{\rho }_{12}^4(4r^2-{\rho }_{12}^2)}=-\frac{{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_1}{{\rho }_{12}^{2}B(0★12)},\hfill \end{array}$$

(88)

$$\begin{array}{cc}\hfill & {\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)=\frac{4r^2{\rho }_{14}^4{\mathsf{\Delta }}_0^2}{4r^2-{\rho }_{12}^2}=-\frac{4r^2{\rho }_{12}^2{\rho }_{14}^4{\mathsf{\Delta }}_0^2}{B(0★12)},\hfill \\ \hfill & {\mathcal{N}}_2((2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2)\hfill \\ \hfill & =\frac{4{\rho }_{14}^4{\mathsf{\Delta }}_0^2({\rho }_{12}^2-4{\rho }_{14}^2)({\rho }_{14}^4+r^2{\rho }_{12}^2-4r^2{\rho }_{14}^2)}{{\rho }_{12}^4(4r^2-{\rho }_{12}^2)}=\frac{2{\rho }_{14}^4{\mathsf{\Delta }}_0^{2}B\left(0124\right)B(0★124)}{{\rho }_{12}^{6}B(0★12)},\hfill \end{array}$$

(89)

$$\begin{array}{cc}\hfill & {\mathcal{N}}_2({\rho }_{12}^2{t}_1^2-{\rho }_{14}^2)=-\frac{4{\rho }_{14}^6{\mathsf{\Delta }}_0^2({\rho }_{12}^2-4{\rho }_{14}^2)}{{(4r^2-{\rho }_{12}^2)}^2}=-\frac{4{\rho }_{12}^2{\rho }_{14}^6{\mathsf{\Delta }}_0^{2}B\left(0124\right)}{{\left\{B(0★12)\right\}}^2},\hfill \end{array}$$

(90)

where ${\mathsf{\Delta }}_1$ is given in (80).

Proof. 

Since $t_1=t_2$, we have ${\mathcal{N}}_2\left(t_1\right)={\mathcal{N}}_2\left(t_2\right)$ and ${\mathcal{N}}_2(1-t_1)={\mathcal{N}}_2(1-t_2)$. Indeed one can apply the formula

$${\mathcal{N}}_2({\gamma }_1{t}_1-{\gamma }_2)=\prod _{j=1}^4({\gamma }_1{\zeta }_j-{\gamma }_2)={\gamma }_1^4\prod _{j=1}^4\left(\frac{{\gamma }_2}{{\gamma }_1}-{\zeta }_j\right)={\gamma }_1^4{\overline{\psi }}_2\left(\frac{{\gamma }_2}{{\gamma }_1}\right)=\frac{{\gamma }_1^4}{h_2}{\widehat{\psi }}_2\left(\frac{{\gamma }_2}{{\gamma }_1}\right)$$

(91)

to every case except (90). ${\widehat{\psi }}_2({\gamma }_2/{\gamma }_1)$ can be evaluated by a direct calculation from (87).

For an arbitrary quadratic polynomial $c_2{t}_1^2+c_1{t}_1+c_0=c_2(t_1-\alpha )(t_1-\beta )$, there exist polynomials $P\left(t_1\right)$ and $q_1{t}_1+q_0$ such that

$${\widehat{\psi }}_2\left(t_1\right)=(c_2{t}_1^2+c_1{t}_1+c_0)P\left(t_1\right)+q_1{t}_1+q_0.$$

Then the norm of $c_2{t}_1^2+c_1{t}_1+c_0$ is calculated by reciprocity law as

$$\begin{array}{cc}\hfill & {\mathcal{N}}_2(c_2{t}_1^2+c_1{t}_1+c_0)=c_2^4\prod _{j=1}^4({\zeta }_j-\alpha )({\zeta }_j-\beta )=c_2^4{\overline{\psi }}_2\left(\alpha \right){\overline{\psi }}_2\left(\beta \right)\hfill \\ \hfill & =\frac{c_2^4}{h_2^2}{\widehat{\psi }}_2\left(\alpha \right){\widehat{\psi }}_2\left(\beta \right)=\frac{c_2^4}{h_2^2}(q_1\alpha +q_0)(q_1\beta +q_0)=\frac{c_2^4}{h_2^2}(q_1^2\alpha \beta +q_0{q}_1(\alpha +\beta )+q_0^2)\hfill \\ \hfill & =\frac{c_2^4}{h_2^2}(q_1^2\frac{c_0}{c_2}-q_0{q}_1\frac{c_1}{c_2}+q_0^2)=\frac{c_2^3}{h_2^2}(q_1^2{c}_0-q_0{q}_1{c}_1+q_0^2{c}_2).\hfill \end{array}$$

(92)

For $c_2={\rho }_{12}^2$, $c_1=0$, $c_0=-{\rho }_{14}^2$, by Euclidean division we have

$${\widehat{\psi }}_2\left(t_1\right)=({\rho }_{12}^2{t}_1^2-{\rho }_{14}^2)P\left(t_1\right)+q_1{t}_1+q_0,$$

where

$$P\left(t_1\right)={\rho }_{12}^2(4r^2-{\rho }_{12}^2)t_1^2+2{\rho }_{12}^2(2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2(4r^2-{\rho }_{14}^2)$$

and $q_1=2{\rho }_{12}^2{\rho }_{14}^2(3{\rho }_{14}^2-{\rho }_{12}^2)$, $q_0=-4{\rho }_{14}^6$. Then, using (92) we obtain

$$\begin{array}{cc}\hfill {\mathcal{N}}_2({\rho }_{12}^2{t}_1^2-{\rho }_{14}^2)& =\frac{{\rho }_{12}^6}{{\rho }_{12}^8{(4r^2-{\rho }_{12}^2)}^2}\{-4{\rho }_{12}^4{\rho }_{14}^6{(3{\rho }_{14}^2-{\rho }_{12}^2)}^2+16{\rho }_{14}^{12}{\rho }_{12}^2\},\hfill \end{array}$$

which is factorized simply and coincides with (90). □

Corollary 1.

$$\begin{array}{cc}\hfill & {\mathcal{N}}_2\left(t_3\right)=\frac{({\rho }_{12}^2-4{\rho }_{14}^2)({\rho }_{14}^4+r^2{\rho }_{12}^2-4r^2{\rho }_{14}^2)}{r^2{\rho }_{12}^4}=-\frac{B\left(0124\right)B(0★124)}{2r^2{\rho }_{12}^8},\hfill \\ \hfill & {\mathcal{N}}_2(1-t_3)=\frac{4{\mathsf{\Delta }}_0^2(4r^2-{\rho }_{14}^2)}{r^2{\rho }_{12}^4}=-4\frac{{\mathsf{\Delta }}_0^{2}B(0★14)}{r^2{\rho }_{12}^4{\rho }_{14}^2},\hfill \\ \hfill & {\mathcal{N}}_2(s+1)=4\frac{{\mathsf{\Delta }}_0^2{(4r^2-{\rho }_{14}^2)}^2}{r^2{\rho }_{14}^4(4r^2-{\rho }_{12}^2)}=-4\frac{{\mathsf{\Delta }}_0^2{\rho }_{12}^2{\left\{B(0★14)\right\}}^2}{r^2{\rho }_{14}^{8}B(0★12)},\hfill \\ \hfill & {\mathcal{N}}_2\left(t_{\infty }\right)=-16\frac{{\rho }_{14}^2({\rho }_{12}^2-4{\rho }_{14}^2)}{r^2(4r^2-{\rho }_{12}^2)}=16\frac{{\rho }_{14}^{2}B\left(0124\right)}{r^{2}B(0★12)}.\hfill \end{array}$$

Proof. 

Since parameters $t_3$, $1-t_3$, $s+1$ and $t_{\infty }$ are written as

$$\begin{array}{cc}\hfill t_3=\frac{(2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2},& 1-t_3=\frac{2{\mathsf{\Delta }}_0{t}_1}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2},\hfill \\ \hfill s+1=2\delta t_1-t_3+1=\frac{2{\rho }_{12}^2{\mathsf{\Delta }}_0{t}_1^2}{{\rho }_{14}^2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)},& t_{\infty }=1+2t_1+t_3=\frac{2({\rho }_{12}^2{t}_1^2-{\rho }_{14}^2)}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2},\hfill \end{array}$$

we obtain

$$\begin{array}{cc}\hfill {\mathcal{N}}_2\left(t_3\right)=\frac{{\mathcal{N}}_2((2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2)}{{\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)},& {\mathcal{N}}_2(1-t_3)=\frac{2^4{\mathsf{\Delta }}_0^4{\mathcal{N}}_2\left(t_1\right)}{{\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)},\hfill \\ \hfill {\mathcal{N}}_2(s+1)=\frac{2^4{\rho }_{12}^8{\mathsf{\Delta }}_0^4{\mathcal{N}}_2{\left(t_1\right)}^2}{{\rho }_{14}^8{\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)},& {\mathcal{N}}_2\left(t_{\infty }\right)=\frac{2^4{\mathcal{N}}_2({\rho }_{12}^2{t}_1^2-{\rho }_{14}^2)}{{\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)},\hfill \end{array}$$

respectively. They are all combinations of factors evaluated in Proposition 5. We therefore obtain the results. □

5.3. The Set ${\tilde{\mathcal{C}}}_3:t_1=t_3\ne t_2$

The case ${\tilde{\mathcal{C}}}_3:t_1=t_3\ne t_2$ for the admissible parameter $t_1$ is evaluated from that of ${\tilde{\mathcal{C}}}_2:t_1=t_2\ne t_3$ in previous subsection by the use of the transposition ${\sigma }_{23}$ of the coordinates $t_2$ and $t_3$. In fact, one may take as in (86) and (87), i.e.,

$${\psi }_3\left(t_1\right):={\psi }_2\left(t_1\right),{\widehat{\psi }}_3\left(t_1\right):={\widehat{\psi }}_2\left(t_1\right),$$

(93)

and for the basic parameter $t_1$, the rational curve $(t_1,{\omega }_2\left(t_1\right),t_1)\in \tilde{X}$ interpolates the set of all critical points in ${\tilde{\mathcal{C}}}_3$, where

$$t_2={\omega }_2\left(t_1\right)=\frac{(2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2},t_3=t_1,$$

(94)

so that we have the expression

$${\tilde{\mathcal{C}}}_3=\{(t_1,{\omega }_2(t_1),t_1)\in \tilde{X}|{\widehat{\psi }}_2(t_1)=0\}.$$

Then the same assertion as the preceding proposition holds true.

Proposition 6.

The points in ${\tilde{\mathcal{C}}}_3$ consist of the four points corresponding to the solutions ${\zeta }_j$ to the equation ${\widehat{\psi }}_3\left(t_1\right)=0$ with $t_2={\omega }_2\left(t_1\right),t_3=t_1$, and we have

$$\begin{array}{cc}\hfill & {\mathcal{N}}_3\left(t_1\right)={\mathcal{N}}_2\left(t_1\right),{\mathcal{N}}_3(1-t_1)={\mathcal{N}}_2(1-t_1),\hfill \\ \hfill & {\mathcal{N}}_3({\rho }_{12}^2{t}_1-{\rho }_{14}^2)={\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2),\hfill \\ \hfill & {\mathcal{N}}_3((2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2)={\mathcal{N}}_2((2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2),\hfill \\ \hfill & {\mathcal{N}}_3\left(t_{\infty }\right)={\mathcal{N}}_2\left(t_{\infty }\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\mathcal{N}}_3\left(t_2\right)={\mathcal{N}}_2\left(t_3\right),{\mathcal{N}}_3(1-t_2)={\mathcal{N}}_2(1-t_3),\hfill \\ & {\mathcal{N}}_3\left(t_3\right)={\mathcal{N}}_2\left(t_2\right),{\mathcal{N}}_3(1-t_3)={\mathcal{N}}_2(1-t_2).\hfill \end{array}$$

(95)

These are explicitly given in Proposition 5 and Corollary 1.

Proof. 

Indeed $t_1,t_{\infty }$ leave invariant under the transposition ${\sigma }_{23}$. Therefore, ${\mathcal{N}}_j\left(t_1\right)$, ${\mathcal{N}}_j(1-t_1)$, ${\mathcal{N}}_j({\rho }_{12}^2{t}_1-{\rho }_{14}^2),$ ${\mathcal{N}}_j\{(2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2\}$ and ${\mathcal{N}}_j\left(t_{\infty }\right)$ are all invariant under the transposition ${\sigma }_{23}$. The symmetry with respect to ${\sigma }_{23}$ also implies (95). □

Proposition 7.

For the special parameter s, we have

$${\mathcal{N}}_3(s+1)=\frac{{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_1({\rho }_{12}^2-4{\rho }_{14}^2)({\rho }_{14}^4+r^2{\rho }_{12}^2-4r^2{\rho }_{14}^2)}{r^2{\rho }_{14}^8(4r^2-{\rho }_{12}^2)}=\frac{{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_{1}B\left(0124\right)B(0★124)}{2r^2{\rho }_{14}^8{\rho }_{12}^{2}B(0★12)}.$$

(96)

Proof. 

From (94) the special parameter $s+1$ is calculated as

$$\begin{array}{cc}\hfill s+1& =\delta (t_1+t_2)-t_3+1=\frac{{\rho }_{12}^2-{\rho }_{14}^2}{{\rho }_{14}^2}\left(t_1+\frac{(2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2}\right)-t_1+1\hfill \\ \hfill & =\frac{{\rho }_{12}^2}{{\rho }_{14}^2}(1-t_1)\frac{(2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2}=\frac{{\rho }_{12}^2}{{\rho }_{14}^2}(1-t_1)t_2,\hfill \end{array}$$

so that, using (95) we have

$${\mathcal{N}}_3(s+1)=\frac{{\rho }_{12}^8}{{\rho }_{14}^8}{\mathcal{N}}_3(1-t_1){\mathcal{N}}_3\left(t_2\right)=\frac{{\rho }_{12}^8}{{\rho }_{14}^8}{\mathcal{N}}_2(1-t_1){\mathcal{N}}_2\left(t_3\right).$$

Since ${\mathcal{N}}_2(1-t_1)$ and ${\mathcal{N}}_2\left(t_3\right)$ are given in Proposition 5 and Corollary 1, respectively, we obtain

$${\mathcal{N}}_3(s+1)=\frac{{\rho }_{12}^8}{{\rho }_{14}^8}\times \frac{{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_1}{{\rho }_{12}^4(4r^2-{\rho }_{12}^2)}\times \frac{({\rho }_{12}^2-4{\rho }_{14}^2)({\rho }_{14}^4+r^2{\rho }_{12}^2-4r^2{\rho }_{14}^2)}{r^2{\rho }_{12}^4},$$

which coincides with (96). □

5.4. The Set ${\tilde{\mathcal{C}}}_4:t_2=t_3\ne t_1$

We assume that $t_2=t_3\ne t_1$ for the critical points. Since $t_1\ne t_2$ and $t_2=t_3$, from (73) it is necessary for ${\tilde{g}}_{12}={\tilde{g}}_{13}=0$ that

$${\widehat{g}}_{12}(t_1,t_2,t_2)={\widehat{g}}_{13}(t_1,t_2,t_2)={\rho }_{12}^2{t}_1{t}_2+({\rho }_{12}^2-{\rho }_{14}^2)t_2-{\rho }_{14}^2(t_1+t_2-1)=0.$$

is satisfied. Solving this equation with respect to $t_2$ we have

$$t_2={\omega }_2\left(t_1\right):=\frac{V\left(t_1\right)}{U\left(t_1\right)},$$

where

$$U\left(t_1\right):={\rho }_{12}^2{t}_1+{\rho }_{12}^2-2{\rho }_{14}^2,V\left(t_1\right):={\rho }_{14}^2(t_1-1).$$

(97)

We may take the interpolating curve $(t_1,{\omega }_2\left(t_1\right),{\omega }_3\left(t_1\right))\in \tilde{X}$ of the set ${\tilde{\mathcal{C}}}_4$ satisfying

$${\tilde{g}}_1(t_1,{\omega }_2\left(t_1\right),{\omega }_3\left(t_1\right))=0,$$

where

$$t_2={\omega }_2\left(t_1\right)=\frac{V}{U},t_3={\omega }_3\left(t_1\right):=\frac{V}{U}.$$

Furthermore

Lemma 22.

Let ${\psi }_4$ be function specified by ${\displaystyle {\psi }_4\left(t_1\right):={\tilde{g}}_1(t_1,\frac{V}{U},\frac{V}{U})}$. Then ${\psi }_4$ has the factor $t_1-1$, namely it is written as

$${\psi }_4\left(t_1\right)=\frac{(t_1-1){\widehat{\psi }}_4\left(t_1\right)}{U^2},$$

(98)

where ${\widehat{\psi }}_4\left(t_1\right)$ is a polynomial in $t_1$ of degree 4. Moreover the explicit form of ${\widehat{\psi }}_4\left(t_1\right)$ is

$$\begin{array}{cc}\hfill {\widehat{\psi }}_4\left(t_1\right)& =\left(r^2{t}_1^2+({\rho }_{14}^2+2r^2)t_1+r^2\right)U^2+4{\rho }_{14}^2\left(r^2{t}_1^2-({\rho }_{12}^2-{\rho }_{14}^2)t_1-r^2\right)U\hfill \\ \hfill & +{\rho }_{14}^4(t_1-1)\left((4r^2-3{\rho }_{12}^2)t_1+4{\rho }_{14}^2-{\rho }_{12}^2-4r^2\right)\hfill \end{array}$$

(99)

$$\begin{array}{cc}\hfill & ={\rho }_{12}^4{r}^2{t}_1^4+{\rho }_{12}^4({\rho }_{14}^2+4r^2)t_1^3+{\rho }_{12}^2(6{\rho }_{12}^2{r}^2-8{\rho }_{14}^2{r}^2-2{\rho }_{12}^2{\rho }_{14}^2-3{\rho }_{14}^4)t_1^2\hfill \\ \hfill & +{\rho }_{12}^2(4{\rho }_{12}^2{r}^2-16{\rho }_{14}^2{r}^2-3{\rho }_{12}^2{\rho }_{14}^2+10{\rho }_{14}^4)t_1\hfill \\ \hfill & +({\rho }_{12}^2-4{\rho }_{14}^2)({\rho }_{14}^4+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2)\hfill \end{array}$$

(100)

Proof. 

By the definition (74) of ${\tilde{g}}_1$, we have

$$\begin{array}{cc}\hfill & U^2{\psi }_4\left(t_1\right)=U^2{\tilde{g}}_1(t_1,\frac{V}{U},\frac{V}{U})\hfill \\ \hfill & =\left[2\left((r^2-{\rho }_{12}^2)t_1+{\rho }_{14}^2-r^2\right)+\left((2r^2-{\rho }_{12}^2)t_1+2{\rho }_{14}^2-{\rho }_{12}^2-2r^2\right)\right]V^2\hfill \\ \hfill & +4\left[r^2{t}_1^2-({\rho }_{12}^2-{\rho }_{14}^2)t_1-r^2\right]UV+(t_1-1)\left[r^2{t}_1^2+({\rho }_{14}^2+2r^2)t_1+r^2\right]U^2,\hfill \\ \hfill & =(t_1-1)[{\rho }_{14}^4(t_1-1)\left((4r^2-3{\rho }_{12}^2)t_1+4{\rho }_{14}^2-{\rho }_{12}^2-4r^2\right)\hfill \\ \hfill & +4{\rho }_{14}^2\left(r^2{t}_1^2-({\rho }_{12}^2-{\rho }_{14}^2)t_1-r^2\right)U+\left(r^2{t}_1^2+({\rho }_{14}^2+2r^2)t_1+r^2\right)U^2],\hfill \end{array}$$

which is a polynomial in $t_1$ of degree 5. Thus, we obtain

$$U^2{\psi }_4\left(t_1\right)=(t_1-1){\widehat{\psi }}_4\left(t_1\right),$$

where ${\widehat{\psi }}_4\left(t_1\right)$ is a polynomial in $t_1$ of degree 4 explicitly given by (99). We therefore obtain (98). The explicit form (100) is obtained by direct calculation from (99). □

Remark 11.

From (82), we see that $(1,{\omega }_2\left(1\right),{\omega }_3\left(1\right))=(1,0,0)\notin \tilde{\mathcal{C}}$. This means that the root $t_1=1$ of the equation ${\psi }_4\left(t_1\right)=0$ does not correspond to any point in ${\tilde{\mathcal{C}}}_4$.

Since ${\widehat{\psi }}_4\left(t_1\right)$ is evaluated at $t_1=(-{\rho }_{12}^2+2{\rho }_{14}^2)/{\rho }_{12}^2$ as

$${\widehat{\psi }}_4\left(\frac{-{\rho }_{12}^2+2{\rho }_{14}^2}{{\rho }_{12}^2}\right)=\frac{4{\rho }_{14}^4(4r^2-{\rho }_{12}^2){\mathsf{\Delta }}_0^2}{{\rho }_{12}^4}=-\frac{4{\rho }_{14}^{4}B(0★12)}{{\rho }_{12}^6}{\mathsf{\Delta }}_0^2\ne 0,$$

(101)

we have the expression

$${\tilde{\mathcal{C}}}_4=\{(t_1,\frac{V}{U},\frac{V}{U})\in \tilde{X}|{\widehat{\psi }}_4(t_1)=0\},$$

where $U\left(t_1\right)$, $V\left(t_1\right)$ are given by (97), and we call ${\widehat{\psi }}_4\left(t_1\right)$ the characteristic polynomial of ${\tilde{\mathcal{C}}}_4$. We denote the roots of the equation ${\widehat{\psi }}_4\left(t_1\right)=0$ by ${\zeta }_1,{\zeta }_2,{\zeta }_3,{\zeta }_4$, then the points corresponding to ${\zeta }_j$ give the set of critical points ${\tilde{\mathcal{C}}}_4$. Let ${\overline{\psi }}_4$ be monic polynomial in $t_1$ specified by

$${\overline{\psi }}_4\left(t_1\right):=\prod _{j=1}^4(t_1-{\zeta }_j)=\frac{{\widehat{\psi }}_4\left(t_1\right)}{h_4},$$

where $h_4:={\rho }_{12}^4{r}^2$ is the coefficient of highest degree of ${\widehat{\psi }}_4$. Due to Lemma 22 we obtain the following.

Lemma 23.

${\widehat{\psi }}_4\left(t_1\right)$ is a polynomial in $t_1$ of degree 4 with the leading term

$${\widehat{\psi }}_4\left(t_1\right)\approx h_4{t}_1^4\left(\right|t_1|\to \infty ),$$

and the leading coefficient is given by $h_4={\rho }_{12}^4{r}^2$. Furthermore we have

$$\begin{array}{cc}\hfill {\widehat{\psi }}_4\left(0\right)& =({\rho }_{12}^2-4{\rho }_{14}^2)({\rho }_{14}^4+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2),\hfill \\ \hfill {\widehat{\psi }}_4\left(1\right)& =4(4r^2-{\rho }_{14}^2){\mathsf{\Delta }}_0^2,\hfill \\ \hfill {\widehat{\psi }}_4(-1)& =4{\rho }_{14}^4{\mathsf{\Delta }}_1,\hfill \end{array}$$

and ${\widehat{\psi }}_4((-{\rho }_{12}^2+2{\rho }_{14}^2)/{\rho }_{12}^2)$ is provided as (101).

Proof. 

The results are calculated directly using (99) or (100). □

From the symmetry between ${\tilde{\mathcal{C}}}_4$ and ${\tilde{\mathcal{C}}}_2$, we immediately have the following:

Proposition 8.

$$\begin{array}{cc}\hfill & {\mathcal{N}}_4\left(t_1\right)={\mathcal{N}}_2\left(t_3\right),{\mathcal{N}}_4(1-t_1)={\mathcal{N}}_2(1-t_3)\hfill \\ \hfill & {\mathcal{N}}_4\left(t_2\right)={\mathcal{N}}_4\left(t_3\right)={\mathcal{N}}_2\left(t_1\right),{\mathcal{N}}_4(1-t_2)={\mathcal{N}}_4(1-t_3)={\mathcal{N}}_2(1-t_1)\hfill \\ \hfill & {\mathcal{N}}_4\left(t_{\infty }\right)={\mathcal{N}}_2\left(t_{\infty }\right).\hfill \end{array}$$

These are explicitly given in Proposition 5 and Corollary 1.

Since $s=\delta (t_1+t_2)-t_3$, from the symmetry between ${\tilde{\mathcal{C}}}_4$ and ${\tilde{\mathcal{C}}}_3$, we also immediately have the following:

Proposition 9.

${\mathcal{N}}_4(s+1)={\mathcal{N}}_3(s+1)$. The explicit form is given in Proposition 7.

Remark 12.

As a consequence of Lemma 23, we can explain another way to have the explicit forms of ${\mathcal{N}}_4\left(t_j\right)$$(j=1,2,3,\infty )$, ${\mathcal{N}}_4(1-t_j)$$(j=1,2,3)$ and ${\mathcal{N}}_4(s+1)$ using special values of ${\widehat{\psi }}_4\left(t_1\right)$ as follows. The basic idea is to use the following formula for arbitrary ${\gamma }_1$, ${\gamma }_2$:

$${\mathcal{N}}_4({\gamma }_1{t}_1-{\gamma }_2)=\frac{{\gamma }_1^4}{h_4}{\widehat{\psi }}_4\left(\frac{{\gamma }_2}{{\gamma }_1}\right),$$

which is explained in (91). Then, using Lemma 23, we obtain

$$\begin{array}{cc}\hfill {\mathcal{N}}_4\left(t_1\right)& =\frac{{\widehat{\psi }}_4\left(0\right)}{h_4},{\mathcal{N}}_4(1-t_1)=\frac{{\widehat{\psi }}_4\left(1\right)}{h_4},{\mathcal{N}}_4(t_1+1)=\frac{{\widehat{\psi }}_4(-1)}{h_4},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{N}}_4\left(U\right)& ={\mathcal{N}}_4({\rho }_{12}^2{t}_1+{\rho }_{12}^2-2{\rho }_{14}^2)=\frac{{\rho }_{12}^8}{h_4}{\widehat{\psi }}_4\left(\frac{-{\rho }_{12}^2+2{\rho }_{14}^2}{{\rho }_{12}^2}\right)\hfill \\ \hfill & =\frac{4{\rho }_{12}^4{\rho }_{14}^4(4r^2-{\rho }_{12}^2){\mathsf{\Delta }}_0^2}{h_4}\hfill \end{array}$$

(102)

$$\begin{array}{cc}\hfill {\mathcal{N}}_4\left(V\right)& ={\mathcal{N}}_4\left({\rho }_{14}^2\right(t_1-1\left)\right)=\frac{{\rho }_{14}^8}{h_4}{\widehat{\psi }}_4(1)\hfill \end{array}$$

For our setting $t_2=t_3=V/U$, we have $1-t_2=1-t_3={\mathsf{\Delta }}_0(t_1+1)/U$, so that

$$\begin{array}{cc}\hfill {\mathcal{N}}_4\left(t_2\right)& ={\mathcal{N}}_4\left(t_3\right)=\frac{{\mathcal{N}}_4\left(V\right)}{{\mathcal{N}}_4\left(U\right)},{\mathcal{N}}_4(1-t_2)={\mathcal{N}}_4(1-t_3)={\mathsf{\Delta }}_0^4\frac{{\mathcal{N}}_4(t_1+1)}{{\mathcal{N}}_4\left(U\right)}\hfill \end{array}$$

are simply calculated. Since $s+1$ is written as

$$s+1=\delta (t_1+t_2)-t_3+1=\delta \left(t_1+\frac{V}{U}\right)-\frac{V}{U}+1=\frac{{\rho }_{12}^2{\mathsf{\Delta }}_0}{{\rho }_{14}^2}\frac{t_1(t_1+1)}{U},$$

we have

$${\mathcal{N}}_4(s+1)=\frac{{\rho }_{12}^8{\mathsf{\Delta }}_0^4}{{\rho }_{14}^8}\frac{{\mathcal{N}}_4\left(t_1\right){\mathcal{N}}_4(t_1+1)}{{\mathcal{N}}_4\left(U\right)},$$

which is also simply calculated. Lastly, we evaluate ${\mathcal{N}}_4\left(t_{\infty }\right)$. The parameter $t_{\infty }$ is written as

$$t_{\infty }=1+t_1+t_2+t_3=1+t_1+2\frac{V}{U}=\frac{{\rho }_{12}^2{t}_1^2+2{\rho }_{12}^2{t}_1+{\rho }_{12}^2-4{\rho }_{14}^2}{U},$$

so that we have

$${\mathcal{N}}_4\left(t_{\infty }\right)=\frac{{\mathcal{N}}_4({\rho }_{12}^2{t}_1^2+2{\rho }_{12}^2{t}_1+{\rho }_{12}^2-4{\rho }_{14}^2)}{{\mathcal{N}}_4\left(U\right)}.$$

To evaluate the above numerator we use another method. By Euclidean division, we have

$${\widehat{\psi }}_4\left(t_1\right)=(c_2{t}_1^2+c_1{t}_1+c_0)P\left(t_1\right)+q_1{t}_1+q_0,$$

where, for setting $c_2{t}_1^2+c_1{t}_1+c_0={\rho }_{12}^2{t}_1^2+2{\rho }_{12}^2{t}_1+{\rho }_{12}^2-4{\rho }_{14}^2$, there exist

$$P\left(t_1\right)={\rho }_{12}^2{r}^2{t}_1^2+{\rho }_{12}^2({\rho }_{14}^2+2r^2)t_1+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2-3{\rho }_{14}^4-4{\rho }_{12}^2{\rho }_{14}^2$$

and $q_1=4{\rho }_{12}^2{\rho }_{14}^2({\rho }_{12}^2+5{\rho }_{14}^2)$, $q_0=4{\rho }_{14}^2({\rho }_{12}^2-4{\rho }_{14}^2)({\rho }_{12}^2+{\rho }_{14}^2).$ Using (92) we finally obtain

$${\mathcal{N}}_4({\rho }_{12}^2{t}_1^2+2{\rho }_{12}^2{t}_1+{\rho }_{12}^2-4{\rho }_{14}^2)=\frac{c_2^3}{h_4^2}(q_1^2{c}_0-q_0{q}_1{c}_1+q_0^2{c}_2)=\frac{64{\rho }_{14}^6(4{\rho }_{14}^2-{\rho }_{12}^2){\mathsf{\Delta }}_0^2}{r^4}.$$

5.5. Conclusions of This Section

In this subsection, we give a proof of Conjecture 2 under the conditions $\left({\mathcal{H}}_0\right)$, $\left({\mathcal{H}}_1\right)$ and ${\mathsf{\Delta }}_0\ne 0$. As we saw in (63), for a rational function $\phi$ on $\tilde{X}$, the norm of $\phi$ is defined by the product of the values over the set of all critical points $\tilde{\mathcal{C}}$, i.e.,

$$\mathcal{N}\left(\phi \right):=\prod _{Q\in \tilde{\mathcal{C}}}\phi \left(Q\right)=\prod _{j=1}^4{\mathcal{N}}_j\left(\phi \right).$$

Summing up Propositions 4–9 and Corollary 1, we have

Theorem 2.

$$\begin{array}{cc}\hfill & \mathcal{N}\left(t_j\right)=-\frac{{\rho }_{14}^8({\rho }_{12}^2-4{\rho }_{14}^2){({\rho }_{14}^2-4r^2)}^2({\rho }_{14}^4+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2)}{3{\rho }_{12}^{12}({\rho }_{12}^2-3r^2){({\rho }_{12}^2-4r^2)}^2}\hfill \\ \hfill & =\frac{B\left(0124\right)B(0★124){\left\{B(0★14)B\left(014\right)\right\}}^2}{B\left(0123\right)B(0★123){\left\{B(0★12)B\left(012\right)\right\}}^2}(j=1,2,3),\hfill \end{array}$$

(103)

$$\begin{array}{cc}\hfill & \mathcal{N}(1-t_j)=-\frac{32}{3}\frac{{\mathsf{\Delta }}_0^7{\mathsf{\Delta }}_1^2({\rho }_{14}^2-4r^2)}{r^2{\rho }_{12}^{12}({\rho }_{12}^2-3r^2){({\rho }_{12}^2-4r^2)}^2}\hfill \\ \hfill & =\frac{2^{10}}{3}\frac{{\mathsf{\Delta }}_0^7{\mathsf{\Delta }}_1^{2}B(0★14)}{B(0★1)B\left(014\right)B(0★123){\left\{B(0★12)B\left(012\right)\right\}}^2}(j=1,2,3),\hfill \end{array}$$

(104)

$$\begin{array}{cc}\hfill & \mathcal{N}\left(t_{\infty }\right)=-\frac{4^7{\rho }_{14}^6({\rho }_{12}^2-3{\rho }_{14}^2){({\rho }_{12}^2-4{\rho }_{14}^2)}^3}{r^6({\rho }_{12}^2-3r^2){({\rho }_{12}^2-4r^2)}^3}=-\frac{4^{7}B\left(01234\right){\left\{B\left(014\right)B\left(0124\right)\right\}}^3}{B(0★123){\left\{B(0★1)B(0★12)\right\}}^3},\hfill \end{array}$$

(105)

$$\begin{array}{cc}\hfill & \mathcal{N}(s+1)=\frac{8}{3}\frac{{\mathsf{\Delta }}_0^7{\mathsf{\Delta }}_1^2({\rho }_{12}^2-3{\rho }_{14}^2){({\rho }_{12}^2-4{\rho }_{14}^2)}^2{({\rho }_{14}^2-4r^2)}^2}{r^6{\rho }_{14}^{26}({\rho }_{12}^2-3r^2){({\rho }_{12}^2-4r^2)}^3}\hfill \\ \hfill & \times (3{\rho }_{14}^4+4{\rho }_{12}^2{r}^2-12{\rho }_{14}^2{r}^2){({\rho }_{14}^4+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2)}^2\hfill \\ \hfill & =\frac{2^7}{3}\frac{{\mathsf{\Delta }}_0^7{\mathsf{\Delta }}_1^2}{{\rho }_{14}^{30}}\frac{B\left(01234\right)B(0★1234){\left\{B(0★14)B(0★124)B\left(0124\right)\right\}}^2}{B(0★123){\left\{B(0★1)B(0★12)B\left(012\right)\right\}}^3}.\hfill \end{array}$$

(106)

Corollary 2.

$$\begin{array}{cc}\hfill & \mathcal{N}\left(f_j\right)=\frac{r^2{\rho }_{12}^{12}({\rho }_{12}^2-3r^2){({\rho }_{12}^2-4r^2)}^2({\rho }_{14}^2-4r^2)}{2^{16}{\rho }_{14}^2({\rho }_{12}^2-4{\rho }_{14}^2)}\hfill \\ \hfill & \times (3{\rho }_{14}^4+4{\rho }_{12}^2{r}^2-12{\rho }_{14}^2{r}^2){({\rho }_{14}^4+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2)}^2\hfill \\ \hfill & =-\frac{B(0★1)}{2·4^8}\frac{B(0★1234)B(0★123)B(0★14){\left\{B(0★124)B(0★12)\right\}}^2}{B\left(0124\right)B\left(012\right){\left\{B\left(014\right)\right\}}^2}\hfill \\ \hfill & (j=1,2,3),\hfill \end{array}$$

(107)

$$\begin{array}{cc}\hfill & \mathcal{N}\left(f_4\right)=-\frac{r^2{\rho }_{14}^6}{3·4^8}{({\rho }_{14}^2-4r^2)}^3(3{\rho }_{14}^4+4{\rho }_{12}^2{r}^2-12{\rho }_{14}^2{r}^2){({\rho }_{14}^4+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2)}^3\hfill \\ \hfill & =-\frac{B(0★1)}{2·4^8}\frac{B(0★1234){\left\{B(0★124)B(0★14)\right\}}^3}{B\left(0123\right){\left\{B\left(012\right)\right\}}^3},\hfill \end{array}$$

(108)

$$\begin{array}{cc}\hfill & \mathcal{N}(f_j-f_4)=-\frac{{\mathsf{\Delta }}_0^7{\mathsf{\Delta }}_1^2{({\rho }_{14}^2-4r^2)}^2(3{\rho }_{14}^4+4{\rho }_{12}^2{r}^2-12{\rho }_{14}^2{r}^2){({\rho }_{14}^4+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2)}^2}{3·2^{11}{\rho }_{14}^2({\rho }_{12}^2-4{\rho }_{14}^2)}\hfill \\ \hfill & =-\frac{{\mathsf{\Delta }}_0^7{\mathsf{\Delta }}_1^2}{3·2^7}\frac{B(0★1234)\{B(0★14)B(0★124){\}}^2}{B\left(0124\right){\left\{B\left(012\right)B\left(014\right)\right\}}^3}(j=1,2,3),\hfill \end{array}$$

(109)

$$\begin{array}{cc}\hfill & \mathcal{N}(f_j-f_k)=0(1\le j,k\le 3),\hfill \end{array}$$

(110)

$$\begin{array}{cc}\hfill & \mathcal{N}\left(\sum _{j=1}^4\frac{1}{f_j}\right)=\frac{3·4^{15}({\rho }_{12}^2-3{\rho }_{14}^2){({\rho }_{12}^2-4{\rho }_{14}^2)}^3}{({\rho }_{12}^2-3r^2){({\rho }_{12}^2-4r^2)}^3{({\rho }_{14}^2-4r^2)}^3}\hfill \\ \hfill & \times \frac{1}{(3{\rho }_{14}^4+4{\rho }_{12}^2{r}^2-12{\rho }_{14}^2{r}^2){({\rho }_{14}^4+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2)}^3}\hfill \\ \hfill & =\frac{2·4^{15}B\left(01234\right)B\left(0123\right){\left\{B\left(0124\right)B\left(012\right)B\left(014\right)\right\}}^3}{\{B(0★1){\}}^{4}B(0★1234)B(0★123)\{B(0★124)B(0★12)B(0★14){\}}^3},\hfill \end{array}$$

(111)

$$\begin{array}{cc}\hfill & \mathcal{N}\left(L_{123}\right)=\frac{{\left\{\frac{B\left(01234\right)}{8}\right\}}^{\frac{15}{2}}}{\mathcal{N}\left(t_{\infty }\right)},\mathcal{N}\left(L_{jk4}\right)=\mathcal{N}\left(t_l\right)\mathcal{N}\left(L_{123}\right),\hfill \end{array}$$

(112)

where $\{j,k,l\}$ denotes a permutation of $\{1,2,3\}$.

Proof. 

From (47) we have $f_j-f_4\equiv f_4(1-t_j)/t_{j}modAnn\left(\tilde{\mathcal{C}}\right)$$(j=1,2,3),$ so that we have $\mathcal{N}(f_j-f_4)=\mathcal{N}\left(f_4\right)\mathcal{N}(1-t_j)/\mathcal{N}\left(t_j\right)$ for $j=1,2,3$. Using (103) and (104) in Theorem 2, we see that $\mathcal{N}(f_1-f_4)=\mathcal{N}(f_2-f_4)=\mathcal{N}(f_3-f_4).$ On the other hand, from (79) we have $\mathcal{N}(f_3-f_4)={\rho }_{14}^{30}\mathcal{N}(s+1)/\mathcal{N}\left(t_{\infty }\right)$, which coincides with the right-hand side of (109) by using (105) and (106) in Theorem 2. We therefore obtain (109). From (47) we also have $\mathcal{N}\left(f_j\right)=\mathcal{N}\left(f_4\right)/\mathcal{N}\left(t_j\right)$ for $j=1,2,3$, so that we have $\mathcal{N}\left(f_1\right)=\mathcal{N}\left(f_2\right)=\mathcal{N}\left(f_3\right).$ On the other hand, using (47) again we have $f_3-f_4\equiv (1-t_3)f_{3}modAnn\left(\tilde{\mathcal{C}}\right)$, so that we obtain $\mathcal{N}\left(f_3\right)=\mathcal{N}(f_3-f_4)/\mathcal{N}(1-t_3)$, which is evaluated as the right-hand side of (107) by using (104) in Theorem 2 and (109). We therefore obtain (107). Moreover, from (47) we also obtain $\mathcal{N}\left(f_4\right)=\mathcal{N}\left(t_1\right)\mathcal{N}\left(f_1\right)$, which is evaluated as (108) by using (103) in Theorem 2 and (107). From (76), we have $t_j-t_k\equiv 0modAnn\left(\tilde{\mathcal{C}}\right)$ for $j,k\in \{1,2,3\}$, so that we have $\mathcal{N}(t_j-t_k)=0,$ which implies

$$\mathcal{N}(f_j-f_k)=\mathcal{N}\left(f_j{f}_k\right)\mathcal{N}(f_k^{-1}-f_j^{-1})=\frac{\mathcal{N}\left(f_j\right)\mathcal{N}\left(f_k\right)}{\mathcal{N}\left(f_4\right)}\mathcal{N}(t_k-t_j)=0\mathrm{for}j,k\in \{1,2,3\}.$$

We therefore obtain (110). From (71) we obtain $\mathcal{N}\left({\sum }_{j=1}^4{f}_j^{-1}\right)=\mathcal{N}\left(t_{\infty }\right)/\mathcal{N}\left(f_4\right)$, which coincides with (111) by using (105) in Theorem 2 and (108). Lastly (112) follows from the definition (44) of $L_{jkl}$ and (38). □

As we mentioned as Remark 2 of Conjecture 2 in the introduction, we have the following:

Theorem 3.

Under the conditions $\left({\mathcal{H}}_0\right)$, $\left({\mathcal{H}}_1\right)$, and ${\mathsf{\Delta }}_0\ne 0$,

$$f_1,f_2,f_3,f_4,\sum _{j=1}^4\frac{1}{f_j},L_{123},L_{124},L_{134},L_{234}$$

are all units.

Proof. 

From the product expressions for $\mathcal{N}\left(f_j\right)$, $\mathcal{N}\left({\sum }_{j=1}^4{f}_j^{-1}\right)$ and $\mathcal{N}\left(L_{jkl}\right)$ in Corollary 2 we see that there appears no factor of their numerators which vanishes. □

6. Regular Tetrahedron Case $({\mathbf{\rho }}_{\mathbf{12}}={\mathbf{\rho }}_{\mathbf{14}})$

In this section, we impose the conditions $\left({\mathcal{H}}_0\right)$ and $\left({\mathcal{H}}_1\right)$ with ${\mathsf{\Delta }}_0={\rho }_{12}^2-{\rho }_{14}^2=0$, which means $▵O_1{O}_2{O}_3{O}_4$ is a regular tetrahedron and all spheres $S_j$ have the same radius, i.e., ${\rho }_{jk}^2={\rho }^2$$(1\le j<k\le 4)$ and $r_j^2=r^2$$(1\le j\le 4)$. Under this setting, we present the explicit formulae for $\mathcal{N}\left(f_j\right)$, $\mathcal{N}\left({\sum }_{j=1}^4{f}_j^{-1}\right)$ and $\mathcal{N}\left(\mathrm{Hess}\right(F\left)\right)$ using the admissible parameters $t_1,t_2,t_3$, and show that Conjectures 1 and 2 stated in the introduction hold true.

The polynomials ${\tilde{g}}_j$$(1\le j\le 3)$ and ${\tilde{g}}_{jk}$$(1\le j<k\le 3)$ defined in (72) and (73) are simplified as

$$\begin{array}{cc}\hfill {\tilde{g}}_j\left(t\right)& =(t_j-1)[r^2{(t_j+1)}^2+{\rho }^2{t}_j+2r^2(t_j+1)(t_k+t_l)\hfill \\ & +(r^2-{\rho }^2)(t_k^2+t_l^2)+(2r^2-{\rho }^2)t_k{t}_l],\hfill \end{array}$$

(113)

$${\tilde{g}}_{jk}\left(t\right)=(t_k-t_j){\widehat{g}}_{jk}\left(t\right),{\widehat{g}}_{jk}\left(t\right):={\rho }^2(t_j-1)(t_k-1),$$

(114)

respectively, where $\{j,k,l\}$ is a permutation of $\{1,2,3\}$. Let $\tilde{\mathcal{C}}={\iota }^{-1}\mathcal{C}$ be the set of critical points characterized by $\tilde{\mathcal{C}}=\{t\in \tilde{X}|{\tilde{g}}_1(t)={\tilde{g}}_2(t)={\tilde{g}}_3(t)=0\}$. By Lemma 11 if $t_1\ne 1$ for $t\in \tilde{\mathcal{C}}$, then the system ${\tilde{g}}_1\left(t\right)={\tilde{g}}_2\left(t\right)={\tilde{g}}_3\left(t\right)=0$ is equivalent to

$${\tilde{g}}_1\left(t\right)={\tilde{g}}_{12}\left(t\right)={\tilde{g}}_{13}\left(t\right)=0.$$

We may use the same notation for the points corresponding to these points in $\tilde{X}$. As a result, the set of 15 critical points are tabulated as $W,Q_j,Q_{jk},Q_{jkl}$. One can also classify these points by the property (76). The set $\tilde{\mathcal{C}}$ is partitioned into four parts, i.e., $\tilde{\mathcal{C}}={⨆}_{j=1}^4{\tilde{\mathcal{C}}}_j$.

6.1. The Set ${\tilde{\mathcal{C}}}_1:t_1=t_2=t_3$

The point $(t_1,t_2,t_3)=(1,1,1)\in \tilde{X}$ satisfies the system ${\tilde{g}}_1\left(t\right)={\tilde{g}}_2\left(t\right)={\tilde{g}}_3\left(t\right)=0$, and this point corresponds to the point W. Since ${\tilde{g}}_1(t_1,t_1,t_1)=(t_1-1)\left[3(3r^2-{\rho }^2)t_1^2+(6r^2+{\rho }^2)t_1+r^2\right]$, if $t_1\ne 1$, then the two solutions of the quadratic equation

$$3(3r^2-{\rho }^2)t_1^2+(6r^2+{\rho }^2)t_1+r^2=0,$$

correspond to the points $Q_{123}$, $Q_4$. We obtain ${\mathcal{C}}_1=\{W,Q_{123},Q_4\}$.

6.2. The Set ${\tilde{\mathcal{C}}}_2:t_1=t_2\ne t_3$

If $t_3=1$ for $t\in {\tilde{\mathcal{C}}}_2$, then $t_1\ne 1$. Thus, $t\in {\tilde{\mathcal{C}}}_2$ satisfies ${\tilde{g}}_{12}(t_1,t_1,1)={\tilde{g}}_{13}(t_1,t_1,1)=0$ automatically. Since ${\tilde{g}}_1(t_1,t_1,1)=(t_1-1)[(4r^2-{\rho }^2)t_1^2+8r^2{t}_1+(4r^2-{\rho }^2)]$, the two solutions of the quadratic equation

$$(4r^2-{\rho }^2)t_1^2+8r^2{t}_1+(4r^2-{\rho }^2)=0$$

(115)

correspond to $Q_{12},Q_{34}$. On the other hand, if $t_3\ne 1$ for $t\in {\tilde{\mathcal{C}}}_2$, then $t\in {\tilde{\mathcal{C}}}_2$ satisfies the system

$${\tilde{g}}_3(t_1,t_1,t_3)={\tilde{g}}_{31}(t_1,t_1,t_3)={\tilde{g}}_{32}(t_1,t_1,t_3)=0.$$

Since ${\tilde{g}}_{31}(t_1,t_1,t_3)={\tilde{g}}_{32}(t_1,t_1,t_3)={\rho }^2(t_1-1)(t_3-1)(t_3-t_1)$, we need $t_1=1$ for $t\in {\tilde{\mathcal{C}}}_2$. Then we also need ${\tilde{g}}_3(1,1,t_3)=(t_3-1)\left[r^2{t}_3^2+(6r^2+{\rho }^2)t_3+3(3r^2-{\rho }^2)\right]=0$. Thus, the two solutions of the quadratic equation

$$r^2{t}_3^2+(6r^2+{\rho }^2)t_3+3(3r^2-{\rho }^2)=0$$

correspond to $Q_3$, $Q_{124}$. We obtain ${\mathcal{C}}_2=\{Q_{12},Q_{34},Q_3,Q_{124}\}$.

6.3. The Set ${\tilde{\mathcal{C}}}_3:t_1=t_3\ne t_2$

This occurs from ${\tilde{\mathcal{C}}}_2$ by exchange of $t_2,t_3$. The cases $t_2=1$ or $t_2\ne 1$ correspond to $Q_{13},Q_{24}$ or $Q_2,Q_{134}$, respectively. We obtain ${\mathcal{C}}_3=\{Q_{13},Q_{24},Q_2,Q_{134}\}$.

6.4. The Set ${\tilde{\mathcal{C}}}_4:t_2=t_3\ne t_1$

If $t_1=1$ for $t\in {\tilde{\mathcal{C}}}_4$, then $t_2\ne 1$. Thus, $t\in {\tilde{\mathcal{C}}}_4$ satisfies ${\tilde{g}}_{21}(1,t_2,t_2)={\tilde{g}}_{23}(1,t_2,t_2)=0$ automatically. Since ${\tilde{g}}_2(1,t_2,t_2)=(t_2-1)[(4r^2-{\rho }^2)t_2^2+8r^2{t}_2+(4r^2-{\rho }^2)]$, the two solutions of the quadratic equation

$$(4r^2-{\rho }^2)t_2^2+8r^2{t}_2+(4r^2-{\rho }^2)=0$$

correspond to $Q_{14},Q_{23}$. On the other hand, if $t_1\ne 1$ for $t\in {\tilde{\mathcal{C}}}_4$, then $t\in {\tilde{\mathcal{C}}}_4$ satisfies the system

$${\tilde{g}}_1(t_1,t_2,t_2)={\tilde{g}}_{12}(t_1,t_2,t_2)={\tilde{g}}_{13}(t_1,t_2,t_2)=0.$$

Since ${\tilde{g}}_{12}(t_1,t_2,t_2)={\tilde{g}}_{13}(t_1,t_2,t_2)={\rho }^2(t_1-1)(t_2-1)(t_2-t_1)$, we need $t_2=1$ for $t\in {\tilde{\mathcal{C}}}_4$. Then we also need ${\tilde{g}}_1(t_1,1,1)=(t_1-1)\left[r^2{t}_1^2+(6r^2+{\rho }^2)t_1+3(3r^2-{\rho }^2)\right]=0$. Thus, the two solutions of the quadratic equation

$$r^2{t}_1^2+(6r^2+{\rho }^2)t_1+3(3r^2-{\rho }^2)=0$$

(116)

correspond to $Q_1,Q_{234}$. We obtain ${\mathcal{C}}_4=\{Q_{14},Q_{23},Q_1,Q_{234}\}$.

6.5. Conclusions of This Section

We have the following two lemmas by a direct calculation:

Lemma 24.

$$\begin{array}{cc}\hfill & f_j\left(W\right)=\frac{3{\rho }^2-8r^2}{8}\mathrm{for}j\in \{1,2,3,4\},\hfill \\ \hfill & f_j\left(Q_j\right)=\frac{\rho (\rho -\sqrt{24r^2+{\rho }^2})}{12}\mathrm{for}j\in \{1,2,3,4\},\hfill \\ \hfill & f_k\left(Q_j\right)=\frac{\rho (3\rho +\sqrt{24r^2+{\rho }^2})}{4}\mathrm{for}k\ne j,\hfill \\ \hfill & f_j\left(Q_{jkl}\right)=\frac{\rho (3\rho -\sqrt{24r^2+{\rho }^2})}{4}\mathrm{for}\{j,k,l\}\subset \{1,2,3,4\},\hfill \\ \hfill & f_m\left(Q_{jkl}\right)=\frac{\rho (\rho +\sqrt{24r^2+{\rho }^2})}{12}\mathrm{for}m\notin \{j,k,l\}\subset \{1,2,3,4\},\hfill \\ \hfill & f_j\left(Q_{jk}\right)=\frac{\rho (\rho -\sqrt{8r^2-{\rho }^2})}{4}\mathrm{for}\{j,k\}\subset \{1,2,3,4\},\hfill \\ \hfill & f_l\left(Q_{jk}\right)=\frac{\rho (\rho +\sqrt{8r^2-{\rho }^2)}}{4}\mathrm{for}l\notin \{j,k\}.\hfill \end{array}$$

As a consequence

Corollary 3.

$$\begin{array}{cc}\hfill & \mathcal{N}\left(f_j\right)=\mathcal{N}\left(f_1\right)=-\frac{1}{3·4^8}{r}^2{\rho }^{14}(3{\rho }^2-8r^2){({\rho }^2-3r^2)}^3{({\rho }^2-4r^2)}^3\hfill \\ \hfill & =-\frac{2}{4^9}\frac{B(0★1){\left\{B(0★12)B(0★123)\right\}}^{3}B(0★1234)}{{\left\{B\left(012\right)\right\}}^{3}B\left(0123\right)}(1\le j\le 4),\hfill \end{array}$$

(117)

$$\begin{array}{cc}\hfill & \mathcal{N}\left(\sum _{j=1}^4\frac{1}{f_j}\right)=\frac{2·3^4·4^{15}}{r^8(3{\rho }^2-8r^2){({\rho }^2-3r^2)}^4{({\rho }^2-4r^2)}^6}\hfill \\ \hfill & =2·4^{15}\frac{B\left(01234\right){\left\{B\left(0123\right)\right\}}^4{\left\{B\left(012\right)\right\}}^6}{B(0★1234){\left\{B(0★123)\right\}}^4{\left\{B(0★12)\right\}}^6{\left\{B(0★1)\right\}}^4}.\hfill \end{array}$$

(118)

Proof. 

The above formulae are obtained by definition and from Lemma 24 in view of the following identities: $B(0★j)=2r^2$, $B(0★jk)={\rho }^2({\rho }^2-4r^2)$, $B(0★jkl)=2{\rho }^4(3r^2-{\rho }^2)$, $B(0★1234)={\rho }^6(3{\rho }^2-8r^2)$, $B\left(0jk\right)=2{\rho }^2$, $B\left(0jkl\right)=-3{\rho }^4$, $B\left(01234\right)=4{\rho }^6$. □

Lemma 25.

$$\begin{array}{cc}\hfill & \mathrm{Hess}\left(F\right){|}_{x=W}=4^9\frac{{({\rho }^2-8r^2)}^3}{{(3{\rho }^2-8r^2)}^6},\hfill \end{array}$$

(119)

$$\begin{array}{cc}\hfill & \mathrm{Hess}\left(F\right){|}_{x=Q_j}\times \mathrm{Hess}\left(F\right){|}_{x=Q_{klm}}=4^7\frac{({\rho }^2+24r^2){({\rho }^2-8r^2)}^3}{r^6{\rho }^4{({\rho }^2-3r^2)}^5},\hfill \end{array}$$

(120)

$$\begin{array}{cc}\hfill & \mathrm{Hess}\left(F\right){|}_{x=Q_{jk}}\times \mathrm{Hess}\left(F\right){|}_{x=Q_{lm}}=4^{13}\frac{{({\rho }^2-8r^2)}^4}{{\rho }^4{({\rho }^2-4r^2)}^8}\hfill \end{array}$$

(121)

for $\{j,k,l,m\}$ a permutation of $\{1,2,3,4\}$.

Proof. 

We prove (119) first. By the definition (113) of ${\tilde{g}}_j$ we have

$$\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_2,{\tilde{g}}_3)}{\partial (t_1,t_2,t_3)}{|}_{t_1=t_2=t_3=1}=\left|\begin{array}{ccc}2(8r^2-{\rho }^2)& & \\ & 2(8r^2-{\rho }^2)& \\ & & 2(8r^2-{\rho }^2)\end{array}\right|=8{(8r^2-{\rho }^2)}^3.$$

(122)

By definition, we also have

$$t_{\infty }{|}_{t_1=t_2=t_3=1}=(1+t_1+t_2+t_3){|}_{t_1=t_2=t_3=1}=4.$$

(123)

From Lemma 24, we obtain

$$f_1{f}_2{f}_3{f}_4^3{|}_{x=W}={(3{\rho }^2-8r^2)}^6/8^6.$$

(124)

Applying (122)–(124) to the formula (61), we therefore obtain (119).

Next, we show (120). Without loss of generality, we prove the case $\mathrm{Hess}\left(F\right){|}_{x=Q_1}\times \mathrm{Hess}\left(F\right){|}_{x=Q_{234}}$ only. We denote by ${\tau }_1,{\tau }_2$ the solutions of (116). Then $Q_1$ and $Q_{234}$ are written as $Q_1=\iota ({\tau }_1,1,1)$ and $Q_{234}=\iota ({\tau }_2,1,1)$, respectively. From (62) of Lemma 13 we have

$$\begin{array}{cc}\hfill & \mathrm{Hess}\left(F\right){|}_{x=Q_1}\times \mathrm{Hess}\left(F\right){|}_{x=Q_{234}}\hfill \\ \hfill & =2^6\prod _{j=1}^2\left(\frac{1}{f_1{f}_2{f}_3{f}_4^3{t}_{\infty }{(1-t_1)}^2}\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\right){|}_{\begin{array}{c}{t}_1={\tau }_j\\ \begin{array}{c}{t}_2=1\\ t_3=1\end{array}\end{array}}.\hfill \end{array}$$

(125)

We now calculate the right-hand side of (125) precisely. From Lemma 24 we have

$$\begin{array}{cc}\hfill & \left(f_1{f}_2{f}_3{f}_4^3\right){|}_{x=Q_1}\times \left(f_1{f}_2{f}_3{f}_4^3\right){|}_{x=Q_{234}}\hfill \\ & =-\frac{{\rho }^2{r}^2}{6}{\left(\frac{{\rho }^2({\rho }^2-3r^2)}{2}\right)}^5=-\frac{r^2{\rho }^{12}{({\rho }^2-3r^2)}^5}{2^{6}3}.\hfill \end{array}$$

(126)

From (68) in Lemma 14 we see that

$$\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}{|}_{\begin{array}{c}{t}_2=1\\ t_3=1\end{array}}=\frac{d\psi }{d{t}_1}\frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_2=1\\ t_3=1\end{array}},$$

where $\psi \left(t_1\right)={\tilde{g}}_1(t_1,1,1)=(t_1-1)\left[r^2{t}_1^2+(6r^2+{\rho }^2)t_1+3(3r^2-{\rho }^2)\right]$. This implies that for the solution $\tau$ of (116), we have

$$\begin{array}{cc}\hfill \frac{d\psi }{d{t}_1}{|}_{t_1=\tau }& =(\tau -1)(2r^2\tau +(6r^2+{\rho }^2))=2r^2{\tau }^2+(4r^2+{\rho }^2)\tau -(6r^2+{\rho }^2)\hfill \\ \hfill & =2[-(6r^2+{\rho }^2)\tau -3(3r^2-{\rho }^2)]+(4r^2+{\rho }^2)\tau -(6r^2+{\rho }^2)\hfill \\ \hfill & =-(8r^2+{\rho }^2)\tau -(24r^2-5{\rho }^2),\hfill \end{array}$$

so that we obtain

$$\begin{array}{cc}\hfill & \frac{d\psi }{d{t}_1}{|}_{t_1={\tau }_1}\times \frac{d\psi }{d{t}_1}{|}_{t_1={\tau }_2}={(8r^2+{\rho }^2)}^2{\tau }_1{\tau }_2+(8r^2+{\rho }^2)(24r^2-5{\rho }^2)({\tau }_1+{\tau }_2)+{(24r^2-5{\rho }^2)}^2\hfill \\ \hfill & ={(8r^2+{\rho }^2)}^2\frac{3(3r^2-{\rho }^2)}{r^2}-(8r^2+{\rho }^2)(24r^2-5{\rho }^2)\frac{6r^2+{\rho }^2}{r^2}+{(24r^2-5{\rho }^2)}^2\hfill \\ \hfill & =2{\rho }^2({\rho }^2-8r^2)({\rho }^2+24r^2)/r^2.\hfill \end{array}$$

(127)

Since we can calculate

$$\frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_2=1\\ t_3=1\end{array}}=\left|\begin{array}{cc}-{\rho }^2{(t_1-1)}^2& 0\\ 0& -{\rho }^2{(t_1-1)}^2\end{array}\right|={\rho }^4{(t_1-1)}^4,$$

we have

$$\frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_1={\tau }_1\\ \begin{array}{c}{t}_2=1\\ t_3=1\end{array}\end{array}}\times \frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_1={\tau }_2\\ \begin{array}{c}{t}_2=1\\ t_3=1\end{array}\end{array}}={\rho }^8{({\tau }_1-1)}^4{({\tau }_2-1)}^4.$$

(128)

Moreover, by definition we have

$$t_{\infty }{|}_{\begin{array}{c}{t}_2=1\\ t_3=1\end{array}}=(1+t_1+t_2+t_3){|}_{\begin{array}{c}{t}_2=1\\ t_3=1\end{array}}=t_1+3.$$

(129)

Applying (126)–(129) to the Equation (125) we therefore obtain

$$\mathrm{Hess}\left(F\right){|}_{x=Q_1}\times \mathrm{Hess}\left(F\right){|}_{x=Q_{234}}=-2^{13}\frac{3({\rho }^2-8r^2)({\rho }^2+24r^2)}{r^4{\rho }^2{({\rho }^2-3r^2)}^5}\frac{{({\tau }_1-1)}^2{({\tau }_2-1)}^2}{({\tau }_1+3)({\tau }_2+3)},$$

which coincides with (120) by calculating $({\tau }_1-1)({\tau }_2-1)$ and $({\tau }_1+3)({\tau }_2+3)$ as follows:

$$({\tau }_1-1)({\tau }_2-1)={\tau }_1{\tau }_2-({\tau }_1+{\tau }_2)+1=\frac{3(3r^2-{\rho }^2)}{r^2}+\frac{6r^2+{\rho }^2}{r^2}+1=\frac{2(8r^2-{\rho }^2)}{r^2},$$

$$({\tau }_1+3)({\tau }_2+3)={\tau }_1{\tau }_2+3({\tau }_1+{\tau }_2)+9=\frac{3(3r^2-{\rho }^2)}{r^2}-3\frac{6r^2+{\rho }^2}{r^2}+9=-\frac{6{\rho }^2}{r^2}.$$

Finally, we show (121). Without loss of generality, we prove the case $\mathrm{Hess}\left(F\right){|}_{x=Q_{12}}\times \mathrm{Hess}\left(F\right){|}_{x=Q_{34}}$ only. We denote by ${\sigma }_1,{\sigma }_2$ the solutions of (115). Then $Q_{12}$ and $Q_{34}$ are written as $Q_{12}=\iota ({\sigma }_1,{\sigma }_1,1)$ and $Q_{34}=\iota ({\sigma }_2,{\sigma }_2,1)$, respectively. From (62) of Lemma 13, we have

$$\begin{array}{cc}\hfill & \mathrm{Hess}\left(F\right){|}_{x=Q_{12}}\times \mathrm{Hess}\left(F\right){|}_{x=Q_{34}}\hfill \\ & =2^6\prod _{j=1}^2\left(\frac{1}{f_1{f}_2{f}_3{f}_4^3{t}_{\infty }{(1-t_1)}^2}\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\right){|}_{\begin{array}{c}{t}_1={\sigma }_j\\ \begin{array}{c}{t}_2={\sigma }_j\\ t_3=1\end{array}\end{array}}.\hfill \end{array}$$

(130)

We now calculate the right-hand side of (130) precisely. From Lemma 24, we have

$$\left(f_1{f}_2{f}_3{f}_4^3\right){|}_{x=Q_{12}}\times \left(f_1{f}_2{f}_3{f}_4^3\right){|}_{x=Q_{34}}={\left(\frac{{\rho }^2({\rho }^2-4r^2)}{8}\right)}^6=\frac{{\rho }^{12}{({\rho }^2-4r^2)}^6}{2^{18}}.$$

(131)

From (68) in Lemma 14, we see that

$$\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}{|}_{\begin{array}{c}{t}_2=t_1\\ t_3=1\end{array}}=\frac{d\psi }{d{t}_1}\frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_2=t_1\\ t_3=1\end{array}},$$

where $\psi \left(t_1\right)={\tilde{g}}_1(t_1,t_1,1)=(t_1-1)\left[(4r^2-{\rho }^2)t_1^2+8r^2{t}_1+(4r^2-{\rho }^2)\right]$. This implies that for the solution $\sigma$ of (115), we have

$$\begin{array}{cc}\hfill \frac{d\psi }{d{t}_1}{|}_{t_1=\sigma }& =(\sigma -1)(2(4r^2-{\rho }^2)\sigma +8r^2)=2[(4r^2-{\rho }^2){\sigma }^2+{\rho }^2\sigma -4{\rho }^2]\hfill \\ \hfill & =2[-(8r^2\sigma +4r^2-{\rho }^2)+{\rho }^2\sigma -4{\rho }^2]=2({\rho }^2-8r^2)(\sigma +1),\hfill \end{array}$$

so that we obtain

$$\frac{d\psi }{d{t}_1}{|}_{t_1={\sigma }_1}\times \frac{d\psi }{d{t}_1}{|}_{t_1={\sigma }_2}=2^2{({\rho }^2-8r^2)}^2({\sigma }_1+1)({\sigma }_2+1).$$

(132)

Since we can calculate

$$\frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_2=t_1\\ t_3=1\end{array}}=\left|\begin{array}{cc}{\rho }^2{(t_1-1)}^2& 0\\ 0& {\rho }^2{(t_1-1)}^2\end{array}\right|={\rho }^4{(t_1-1)}^4,$$

we have

$$\frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_1={\sigma }_1\\ \begin{array}{c}{t}_2={\sigma }_1\\ t_3=1\end{array}\end{array}}\times \frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_1={\sigma }_2\\ \begin{array}{c}{t}_2={\sigma }_2\\ t_3=1\end{array}\end{array}}={\rho }^8{({\sigma }_1-1)}^4{({\sigma }_2-1)}^4.$$

(133)

Moreover, by definition, we have

$$t_{\infty }{|}_{\begin{array}{c}{t}_2=t_1\\ t_3=1\end{array}}=(1+t_1+t_2+t_3){|}_{\begin{array}{c}{t}_2=t_1\\ t_3=1\end{array}}=2(t_1+1),$$

so that

$$t_{\infty }{|}_{\begin{array}{c}{t}_1={\sigma }_1\\ \begin{array}{c}{t}_2={\sigma }_1\\ t_3=1\end{array}\end{array}}\times t_{\infty }{|}_{\begin{array}{c}{t}_1={\sigma }_2\\ \begin{array}{c}{t}_2={\sigma }_2\\ t_3=1\end{array}\end{array}}=4({\sigma }_1+1)({\sigma }_2+1).$$

(134)

Applying (131)–(134) to the Equation (130) we therefore obtain

$$\mathrm{Hess}\left(F\right){|}_{x=Q_{12}}\times \mathrm{Hess}\left(F\right){|}_{x=Q_{34}}=2^{24}\frac{{({\rho }^2-8r^2)}^2}{{\rho }^4{({\rho }^2-4r^2)}^6}{({\sigma }_1-1)}^2{({\sigma }_2-1)}^2,$$

which coincides with (121) by calculating $({\sigma }_1-1)({\sigma }_2-1)$ as follows:

$$({\sigma }_1-1)({\sigma }_2-1)={\sigma }_1{\sigma }_2-({\sigma }_1+{\sigma }_2)+1=1+\frac{8r^2}{4r^2-{\rho }^2}+1=\frac{2(8r^2-{\rho }^2)}{4r^2-{\rho }^2}.$$

This completes the proof. □

From Lemma 25, we obtain:

Proposition 10.

$$\mathcal{N}\left(\mathrm{Hess}\left(F\right)\right)=4^{76}\frac{{({\rho }^2+24r^2)}^4{({\rho }^2-8r^2)}^{27}}{r^{24}{\rho }^{28}{(3{\rho }^2-8r^2)}^6{({\rho }^2-3r^2)}^{20}{({\rho }^2-4r^2)}^{24}}.$$

(135)

If $\mathcal{N}\left(\mathrm{Hess}F\right)=0$ then $8r^2={\rho }^2$ and vice versa. This case occurs when all critical points $Q_{jk}(j<k)$ and $Q_{jkl}(j<k<l)$ coincides with W the center of gravity.

Remark 13.

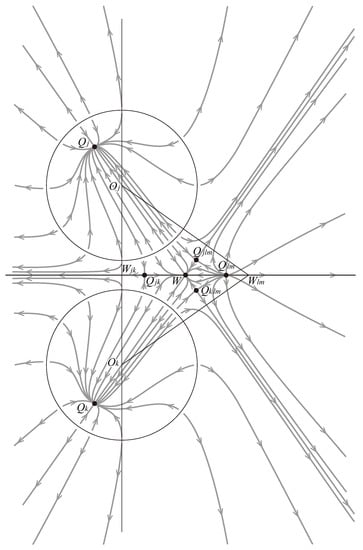
If $r^2>\frac{1}{8}{\rho }^2$, then all 15 critical points ${\mathbf{c}}_{\nu }$ are real and distinct from each other. If $r^2>\frac{3}{8}{\rho }^2$, then $D_1\cap D_2\cap D_3\cap D_4\ne \varnothing$. If $\frac{3}{8}{\rho }^2>r^2>\frac{1}{3}{\rho }^2$, then $D_j\cap D_k\cap D_l\cap {\overline{D}}_m^c\ne \varnothing$. If $\frac{1}{3}{\rho }^2>r^2>\frac{1}{4}{\rho }^2$, then $D_j\cap D_k\cap {\overline{D}}_l^c\cap {\overline{D}}_m^c\ne \varnothing$.

Let $\{j,k,l,m\}$ be an arbitrary permutation of $\{1,2,3,4\}$. Then $\mathrm{grad}\mathfrak{Re}F$ preserves every affine plane ${\mathfrak{p}}_{jk,lm}$ and the lines $\mathfrak{l}(W_j,W_{klm}),\mathfrak{l}(W_{jk},W_{lm})$ are trajectories of $\mathrm{grad}\mathfrak{Re}F$.

If $\frac{1}{4}{\rho }^2>r^2>\frac{1}{8}{\rho }^2$, then $D_j\cap D_k=\varnothing .$ The four points $Q_j$ lie one by one in the inside of each $\mathfrak{Re}{S}_j$. The remaining 11 points lie in the common part of the inside of the pyramid $\mathsf{\Delta }{O}_1{O}_2{O}_3{O}_4$ and the outside of all ${\overline{D}}_k$. The values of $\mathfrak{Re}F$ at $\mathfrak{Re}{S}_j,Q_{jk},Q_{jkl},W$ satisfy the ordering

$$\mathfrak{Re}F{|}_{\mathfrak{Re}{S}_j}=-\infty <\mathfrak{Re}F{|}_{Q_{jk}}<\mathfrak{Re}F{|}_{Q_{jkl}}<\mathfrak{Re}F{|}_W.$$

There exist the unique trajectories (separatrices) of the real vector field $\mathrm{grad}\mathfrak{Re}F$ starting from some point of $\mathfrak{Re}{S}_j$ and tending to $Q_j$, starting from $Q_j$ and tending to $Q_{jk}$, starting from $Q_{jkl}$ and tending to W respectively.

We assume that $\rho =2$. Take the axis $y_1$ and the ordinate $y_2$ to be the lines $\mathfrak{l}(W_{jk},W_{lm})$ and $\mathfrak{l}(O_j,O_k)$ such that $W_{jk}$ is the origin in the plane ${\mathfrak{p}}_{jk,lm}$. The restriction of $f_j$ to the plane is represented by

$$f_j=y_1^2+{(y_2+1)}^2-r^2,f_k=y_1^2+{(y_2-1)}^2-r^2,f_l=f_m={(y_1-\sqrt{2})}^2+y_2^2+1-r^2,$$

and the vector field $\mathrm{grad}\mathfrak{Re}F$ on ${\mathfrak{p}}_{jk.lm}$ is defined by the differential equation

$$\frac{d{y}_2}{d{y}_1}=\frac{v_2}{v_1},$$

where

$$v_1=\frac{2y_1}{f_j}+\frac{2y_1}{f_k}+\frac{4(y_1-\sqrt{2})}{f_l},v_2=\frac{2(y_2+1)}{f_j}+\frac{2(y_2-1)}{f_k}+\frac{4y_2}{f_l}.$$

Then every trajectory in ${\mathfrak{p}}_{jk,lm}$ tending to the infinity has an asymptotic expansion

$$y_2\approx C_{-1}(y_1-\frac{1}{\sqrt{2}})+\frac{C_2}{y_1^2}+\frac{C_3}{y_1^3}+\cdots \left(\right|y_1|\to \infty )$$

or

$$y_1\approx C_{-1}^{\prime }{y}_2+\frac{1}{\sqrt{2}}+\frac{C_2^{\prime }}{y_2^2}+\frac{C_3^{\prime }}{y_2^3}+\cdots \left(\right|y_2|\to \infty ).$$

where $C_{-1}$ or $C_{-1}^{\prime }$ denotes an arbitrary real constant and the remaining $C_{\nu },C_{\nu }^{\prime }(\nu \ge 2)$ are uniquely determined in a successive way. The phase portrait of $\mathrm{grad}\mathfrak{Re}F$ in ${\mathfrak{p}}_{jk,lm}$ is given as in the Figure 1.

Figure 1. Phase portrait of $\mathrm{grad}\mathfrak{Re}F$ in ${\mathfrak{p}}_{jk,lm}$.

The real vector field $\mathrm{grad}\mathfrak{Re}F$ preserves the two dimensional real plane ${\mathfrak{p}}_{jk,lm}$, which contains the critical points $Q_j$, $Q_k$, $Q_{jk}$, $Q_{lm}$, $Q_{jlm}$ and $Q_{klm}$. The three straight lines $\overline{Q_{j}W}$, $\overline{Q_{k}W}$ and $\overline{W_{jk}{W}_{lm}}$ are trajectories themselves. Every trajectory starts from each point of the circles $\mathfrak{Re}{S}_j\cap {\mathfrak{p}}_{jk,lm}$ and $\mathfrak{Re}{S}_k\cap {\mathfrak{p}}_{jk,lm}$ in a perpendicular manner to the circles, or from the point $Q_{lm}$ (unstable node). The points $Q_{jk}$, $Q_{jlm}$ and $Q_{klm}$ are saddle points. Every trajectory finally tends to one of the points $Q_j$, $Q_k$ and W (stable nodes), or to the infinity.

7. Product of Hessians

In this section, we evaluate the norm of the Hessian of F under the same constraints as Section 5, i.e., we still impose the conditions $\left({\mathcal{H}}_0\right)$, $\left({\mathcal{H}}_1\right)$ and ${\mathsf{\Delta }}_0\ne 0$. From (64) of Proposition 3 the Hessian of F satisfies that

$$\mathcal{N}\left(\frac{1}{2^3}\mathrm{Hess}\left(F\right)\right)=-\frac{1}{\mathcal{N}\left(f_1\right)\mathcal{N}\left(f_2\right)\mathcal{N}\left(f_3\right)\mathcal{N}{\left(f_4\right)}^3\mathcal{N}\left(t_{\infty }\right)\mathcal{N}{(1-t_1)}^2}\mathcal{N}\left(\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\right).$$

Since we have already evaluated $\mathcal{N}\left(t_j\right)$ $(j=1,2,3,\infty )$, $\mathcal{N}(1-t_j)$ $(j=1,2,3)$ and $\mathcal{N}\left(f_j\right)$ $(j=1,2,3,4)$ in Section 5, our aim in this section is to study the remaining part

$$\mathcal{N}\left(\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\right).$$

Since the set $\tilde{\mathcal{C}}$ is separated into four parts, which are specified in (76), i.e., $\tilde{\mathcal{C}}={⨆}_{j=1}^4{\tilde{\mathcal{C}}}_j$, we have

$$\mathcal{N}\left(\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\right)=\prod _{j=1}^4{\mathcal{N}}_j\left(\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\right).$$

Furthermore, from Lemma 14, it follows that

$${\mathcal{N}}_j\left(\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\right)={\mathcal{N}}_j\left(\frac{d{\psi }_j}{d{t}_1}\right){\mathcal{N}}_j\left(\frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}\right),$$

(136)

where ${\psi }_j\left(t_1\right)={\tilde{g}}_1\left(\omega \left(t_1\right)\right)$ are the characteristic functions defined by the interpolation curve $\omega :\mathbb{C}\to \tilde{X}$ associated with ${\tilde{\mathcal{C}}}_j$, respectively (see Section 5 for further detail on the functions ${\psi }_j\left(t_1\right)$). In the sequel, we shall abbreviate

$$Z=\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)},Z_0=\frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}$$

respectively.

Definition 4.

Let ${\widehat{\psi }}_j\left(t_1\right)$ $(1\le j\le 4)$ be the characteristic polynomials of ${\tilde{\mathcal{C}}}_j$ defined in Section 4 (see (83), (87), (93) and (100) for explicit forms of ${\widehat{\psi }}_1\left(t_1\right)={\psi }_1\left(t_1\right)$, ${\widehat{\psi }}_2\left(t_1\right)$, ${\widehat{\psi }}_3\left(t_1\right)$ and ${\widehat{\psi }}_4\left(t_1\right)$, respectively). For the polynomial ${\widehat{\psi }}_j\left(t_1\right)$ of degree m, let $\left\{{\zeta }_k\right|1\le k\le m\}$ be the set of roots of the equation ${\widehat{\psi }}_j\left(t_1\right)=0$.

$${\overline{\psi }}_j\left(t_1\right):=\prod _{k=1}^m(t_1-{\zeta }_k)=\frac{{\widehat{\psi }}_j\left(t_1\right)}{h_j},$$

where $h_j$ are the coefficients of the leading terms of ${\widehat{\psi }}_j\left(t_1\right)$. We define the discriminant of the polynomial ${\overline{\psi }}_j\left(t_1\right)$ associated with each ${\tilde{\mathcal{C}}}_j$ as follows:

$${\mathrm{Discri}}_j:=\prod _{1\le k<l\le m}{({\zeta }_k-{\zeta }_l)}^2.$$

(137)

By definition, we can immediately confirm that

$${\mathrm{Discri}}_j={(-1)}^{\left(\genfrac{}{}{0.0pt}{}{m}{2}\right)}{\mathcal{N}}_j\left({\overline{\psi }}_j^{\prime }\left(t_1\right)\right)={(-1)}^{\left(\genfrac{}{}{0.0pt}{}{m}{2}\right)}{h}_j^{-m}{\mathcal{N}}_j\left({\widehat{\psi }}_j^{\prime }\left(t_1\right)\right),$$

(138)

i.e., ${\mathrm{Discri}}_1=-h_1^{-3}{\mathcal{N}}_1\left({\psi }_1^{\prime }\left(t_1\right)\right)$ and ${\mathrm{Discri}}_j=h_j^{-4}{\mathcal{N}}_j\left({\widehat{\psi }}_j^{\prime }\left(t_1\right)\right)$$(j=2,3,4)$.

7.1. ${\mathcal{N}}_1\left(Z\right)$

In this subsection, we consider ${\mathcal{N}}_1\left(Z\right)$ for the set ${\tilde{\mathcal{C}}}_1$. As we saw in Section 5.1, an arbitrary critical point $t=(t_1,t_2,t_3)\in {\tilde{\mathcal{C}}}_1$ is characterized as a point on the interpolation curve $\omega :\mathbb{C}\to \tilde{X}$ defined by $\omega \left(t_1\right)=(t_1,{\omega }_2\left(t_1\right)$, ${\omega }_3\left(t_1\right))\in \tilde{X}$, where

$$t_2={\omega }_2\left(t_1\right):=t_1,t_3={\omega }_3\left(t_1\right):=t_1,$$

and $t=\omega \left(t_1\right)\in \tilde{X}$ satisfies the equation ${\tilde{g}}_1\left(\omega \left(t_1\right)\right)=0$. Since ${\tilde{g}}_{12}$ and ${\tilde{g}}_{13}$ are expressed as (73), ${\tilde{g}}_{12}={\tilde{g}}_{13}=0$ is automatically satisfied. The characteristic function ${\psi }_1$ relative to the parameter $t_1$ is defined by

$${\psi }_1\left(t_1\right)={\tilde{g}}_1(t_1,t_1,t_1)=a_0{t}_1^3+a_2{t}_1^2+a_3{t}_1+a_3=h_1{\overline{\psi }}_1\left(t_1\right),$$

where

$$h_1=a_0=3(3r^2-{\rho }_{12}^2),a_2=-3r^2+9{\rho }_{14}^2-5{\rho }_{12}^2,a_3=-(5r^2+{\rho }_{14}^2),a_4=-r^2.$$

(139)

Lemma 26.

Let ${\widehat{g}}_{12}$ and ${\widehat{g}}_{13}$ be polynomials in t given by (73). Then we have

$$Z_0\equiv {\widehat{g}}_{12}{\widehat{g}}_{13}modAnn\left({\tilde{\mathcal{C}}}_1\right),$$

(140)

namely

$${\mathcal{N}}_1\left(Z_0\right)={\mathcal{N}}_1\left({\widehat{g}}_{12}\right){\mathcal{N}}_1\left({\widehat{g}}_{13}\right).$$

(141)

Proof. 

Since ${\tilde{g}}_{12}=(t_2-t_1){\widehat{g}}_{12}$ and ${\tilde{g}}_{13}=(t_3-t_1){\widehat{g}}_{13}$, the point on the interpolation line $t_1=t_2=t_3$ satisfies

$$\begin{array}{cc}\hfill \frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_2=t_1\\ t_3=t_1\end{array}}& =det\left(\begin{array}{cc}{\widehat{g}}_{12}+(t_2-t_1)\frac{\partial {\widehat{g}}_{12}}{\partial t_2}& (t_2-t_1)\frac{\partial {\widehat{g}}_{12}}{\partial t_3}\\ (t_3-t_1)\frac{\partial {\widehat{g}}_{13}}{\partial t_2}& {\widehat{g}}_{13}+(t_3-t_1)\frac{\partial {\widehat{g}}_{13}}{\partial t_3}\end{array}\right){|}_{\begin{array}{c}{t}_2=t_1\\ t_3=t_1\end{array}}\hfill \\ & ={\widehat{g}}_{12}(t_1,t_1,t_1){\widehat{g}}_{13}(t_1,t_1,t_1),\hfill \end{array}$$

which implies (140). □

By definition, the polynomial ${\widehat{g}}_{12}(t_1,t_1,t_1)$ coincides with ${\widehat{g}}_{13}(t_1,t_1,t_1)$, and they are written as

$${\widehat{g}}_{12}(t_1,t_1,t_1)={\widehat{g}}_{13}(t_1,t_1,t_1)={\rho }_{12}^2{t}_1^2+({\rho }_{12}^2-3{\rho }_{14}^2)t_1+{\rho }_{14}^2.$$

Lemma 27.

$${\mathcal{N}}_1\left({\widehat{g}}_{12}(t_1,t_1,t_1)\right)={\mathcal{N}}_1\left({\widehat{g}}_{13}(t_1,t_1,t_1)\right)=\frac{2{\mathsf{\Delta }}_0{\mathsf{\Delta }}_2}{h_1^2}=\frac{2{\mathsf{\Delta }}_0{\mathsf{\Delta }}_2}{9{(3r^2-{\rho }_{12}^2)}^2},$$

(142)

where ${\mathsf{\Delta }}_2$ denotes

$${\mathsf{\Delta }}_2:=4r^4{({\rho }_{12}^2-9{\rho }_{14}^2)}^2+r^2({\rho }_{12}^2-9{\rho }_{14}^2)({\rho }_{12}^4-2{\rho }_{12}^2{\rho }_{14}^2+9{\rho }_{14}^4)+4{\rho }_{12}^4{\rho }_{14}^4.$$

(143)

Proof. 

For an arbitrary quadratic polynomial $c_2{t}_1^2+c_1{t}_1+c_0=c_2(t_1-\alpha )(t_1-\beta )$, there exist unique polynomials $P\left(t_1\right)$ and $q_1{t}_1+q_0$, such that ${\widehat{\psi }}_1\left(t_1\right)=(c_2{t}_1^2+c_1{t}_1+c_0)P\left(t_1\right)+q_1{t}_1+q_0.$ Then the norm of $c_2{t}_1^2+c_1{t}_1+c_0$ is calculated by reciprocity law as

$$\begin{array}{cc}\hfill & {\mathcal{N}}_1(c_2{t}_1^2+c_1{t}_1+c_0)=c_2^3\prod _{j=1}^3({\zeta }_j-\alpha )({\zeta }_j-\beta )=c_2^3{\overline{\psi }}_1\left(\alpha \right){\overline{\psi }}_1\left(\beta \right)\hfill \\ \hfill & =\frac{c_2^3}{h_1^2}{\widehat{\psi }}_1\left(\alpha \right){\widehat{\psi }}_1\left(\beta \right)=\frac{c_2^3}{h_1^2}(q_1\alpha +q_0)(q_1\beta +q_0)=\frac{c_2^3}{h_1^2}(q_1^2\alpha \beta +q_0{q}_1(\alpha +\beta )+q_0^2)\hfill \\ \hfill & =\frac{c_2^3}{h_1^2}(q_1^2\frac{c_0}{c_2}-q_0{q}_1\frac{c_1}{c_2}+q_0^2)=\frac{c_2^2}{h_1^2}(q_1^2{c}_0-q_0{q}_1{c}_1+q_0^2{c}_2).\hfill \end{array}$$

(144)

By Euclidean division, we have

$${\widehat{\psi }}_1\left(t_1\right)=(c_2{t}_1^2+c_1{t}_1+c_0)P\left(t_1\right)+q_1{t}_1+q_0,$$

where, for setting ${\widehat{g}}_{12}(t_1,t_1,t_1)=c_2{t}_1^2+c_1{t}_1+c_0={\rho }_{12}^2{t}_1^2+({\rho }_{12}^2-3{\rho }_{14}^2)t_1+{\rho }_{14}^2$, there exist

$$\begin{array}{cc}\hfill P\left(t_1\right)& =3{\rho }_{12}^{-2}(3r^2-{\rho }_{12}^2)t_1+{\rho }_{12}^{-4}(27{\rho }_{14}^2{r}^2-12{\rho }_{12}^2{r}^2-2{\rho }_{12}^4),\hfill \\ \hfill q_1& ={\rho }_{12}^{-4}(2{\rho }_{12}^6-4{\rho }_{14}^2{\rho }_{12}^4+7{\rho }_{12}^4{r}^2-72{\rho }_{12}^2{\rho }_{14}^2{r}^2+81{\rho }_{14}^4{r}^2),\hfill \\ \hfill q_0& ={\rho }_{12}^{-4}(2{\rho }_{12}^4{\rho }_{14}^2-{\rho }_{12}^4{r}^2+12{\rho }_{12}^2{\rho }_{14}^2{r}^2-27{\rho }_{14}^4{r}^2).\hfill \end{array}$$

Using (144), we obtain

$${\mathcal{N}}_1\left({\widehat{g}}_{12}(t_1,t_1,t_1)\right)=c_2^2(q_1^2{c}_0-q_0{q}_1{c}_1+q_0^2{c}_2)h_1^{-2}=2{\mathsf{\Delta }}_0{\mathsf{\Delta }}_2{h}_1^{-2},$$

which coincides with (142). □

Lemma 28.

The explicit form of ${\mathrm{Discri}}_1$ is given by

$${\mathrm{Discri}}_1=-\frac{({\rho }_{12}^2-3{\rho }_{14}^2){\mathsf{\Delta }}_3}{h_1^4},$$

(145)

where ${\mathsf{\Delta }}_3$ denotes

$$\begin{array}{cc}\hfill {\mathsf{\Delta }}_3& :=3072r^6-64(13{\rho }_{12}^2-3{\rho }_{14}^2)r^4+4(125{\rho }_{12}^4-430{\rho }_{12}^2{\rho }_{14}^2+309{\rho }_{14}^4)r^2\hfill \\ \hfill & -(25{\rho }_{12}^2-27{\rho }_{14}^2){\rho }_{14}^4.\hfill \end{array}$$

(146)

The explicit form of ${\mathcal{N}}_1\left({\psi }_1^{\prime }\right)$ is also expressed as

$${\mathcal{N}}_1\left({\psi }_1^{\prime }\right)=-h_1^3{\mathrm{Discri}}_1=\frac{({\rho }_{12}^2-3{\rho }_{14}^2){\mathsf{\Delta }}_3}{h_1}=\frac{({\rho }_{12}^2-3{\rho }_{14}^2){\mathsf{\Delta }}_3}{3(3r^2-{\rho }_{12}^2)}.$$

(147)

Proof. 

The resultant of ${\psi }_1$ and ${\psi }_1^{\prime }$ gives the discriminant of ${\psi }_1\left(t_1\right)$, i.e.,

$$R({\psi }_1,{\psi }_1^{\prime }):=\left|\begin{array}{ccccc}{a}_0& a_1& a_2& a_3& \\ & a_0& a_1& a_2& a_3\\ 3a_0& 2a_1& a_2& & \\ & 3a_0& 2a_1& a_2& \\ & & 3a_0& 2a_1& a_2\end{array}\right|=-a_0^5\prod _{1\le j<k\le 3}{({\zeta }_j-{\zeta }_k)}^2=-h_1^5{\mathrm{Discri}}_1,$$

where $a_0$, $a_1$, $a_2$, $a_3$ are given in (139). From direct calculation of the above determinant, we obtain

$$R({\psi }_1,{\psi }_1^{\prime })=3(3r^2-{\rho }_{12}^2)({\rho }_{12}^2-3{\rho }_{14}^2){\mathsf{\Delta }}_3=({\rho }_{12}^2-3{\rho }_{14}^2)h_1{\mathsf{\Delta }}_3,$$

which implies (145). Using (138) we obtain (147) from (145). □

Due to (145) we immediately have the following:

Corollary 4.

There exists no double point in ${\tilde{\mathcal{C}}}_1$ if and only if ${\mathsf{\Delta }}_3\ne 0$.

We conclude the following from (136) and Lemmas 26–28.

Proposition 11.

$${\mathcal{N}}_1\left(Z_0\right)=\frac{4{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_2^2}{h_1^4}=\frac{4{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_2^2}{3^4{(3r^2-{\rho }_{12}^2)}^4},$$

(148)

$${\mathcal{N}}_1\left(Z\right)=-\frac{4{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_2^2{\mathrm{Discri}}_1}{h_1}=\frac{4({\rho }_{12}^2-3{\rho }_{14}^2){\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_2^2{\mathsf{\Delta }}_3}{h_1^5}.$$

(149)

Proof. 

Applying (142) to (141) we have (148). Using (148) and (147), (136) implies (149). □

7.2. ${\mathcal{N}}_2\left(Z\right)$

As we saw in Section 5.2, an arbitrary critical point $t=(t_1,t_2,t_3)\in {\tilde{\mathcal{C}}}_2$ is characterized as a point on the interpolation curve $\omega :\mathbb{C}\to \tilde{X}$ defined by $\omega \left(t_1\right)=(t_1,{\omega }_2\left(t_1\right),{\omega }_3\left(t_1\right))\in \tilde{X},$ where

$$t_2={\omega }_2\left(t_1\right):=t_1,t_3={\omega }_3\left(t_1\right):=\frac{(2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2},$$

(150)

and $t=\omega \left(t_1\right)\in \tilde{X}$ satisfies the equation ${\tilde{g}}_1\left(\omega \left(t_1\right)\right)=0$. Since ${\tilde{g}}_{12}$ are expressed as (73), ${\tilde{g}}_{12}=0$ is automatically satisfied when $t_2=t_1$. The relation $t_3={\omega }_3\left(t_1\right)$ in (150) is determined by solving the equation ${\widehat{g}}_{13}(t_1,t_1,t_3)=0$, where

$${\widehat{g}}_{13}(t_1,t_1,t_3)={\rho }_{12}^2{t}_1{t}_3+{\mathsf{\Delta }}_0{t}_1-{\rho }_{14}^2(t_1+t_3-1).$$

In this setting,

$${\widehat{g}}_{12}(t_1,t_1,{\omega }_3\left(t_1\right))={\rho }_{12}^2{t}_1^2+{\mathsf{\Delta }}_0{t}_3-{\rho }_{14}^2(2t_1-1).$$

From (75), ${\widehat{g}}_{12}$ is also expressed as

$${\widehat{g}}_{12}(t_1,t_1,{\omega }_3\left(t_1\right))={\widehat{g}}_{12}(t_1,t_1,{\omega }_3\left(t_1\right))-{\widehat{g}}_{13}(t_1,t_1,{\omega }_3\left(t_1\right))={\rho }_{12}^2(t_1-1)(t_1-t_3).$$

The characteristic function ${\psi }_2$ relative to $t_1$ is defined by ${\psi }_2\left(t_1\right)={\tilde{g}}_1(t_1,t_1,{\omega }_3\left(t_1\right))$, and from Lemma 21 ${\psi }_2\left(t_1\right)$ is expressed as

$${\psi }_2\left(t_1\right)=\frac{(t_1-1){\widehat{\psi }}_2\left(t_1\right)}{{\left({\rho }_{12}^2{t}_1-{\rho }_{14}^2\right)}^2}.$$

(151)

Here, ${\widehat{\psi }}_2\left(t_1\right)$ is a polynomial in $t_1$ of degree 4 given by

$${\widehat{\psi }}_2\left(t_1\right)=a_0{t}_1^4+a_2{t}_1^3+a_3{t}_2+a_3{t}_1+a_4=h_2{\overline{\psi }}_2\left(t_1\right),$$

where

$$\begin{array}{cc}\hfill & h_2=a_0={\rho }_{12}^4(4r^2-{\rho }_{12}^2),a_1=2{\rho }_{12}^4(2{\rho }_{14}^2-{\rho }_{12}^2),\hfill \\ \hfill & a_2={\rho }_{12}^2{\rho }_{14}^2(-8r^2+{\rho }_{12}^2-3{\rho }_{14}^2),a_3=2{\rho }_{12}^2{\rho }_{14}^4,a_4={\rho }_{14}^4(4r^2-{\rho }_{14}^2).\hfill \end{array}$$

(152)

Lemma 29.

$$Z_0\equiv {\rho }_{12}^2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)(1-t_1){(t_1-t_3)}^{2}modAnn\left({\tilde{\mathcal{C}}}_2\right),$$

(153)

namely

$${\mathcal{N}}_2\left(Z_0\right)={\rho }_{12}^8{\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2){\mathcal{N}}_2(1-t_1){\left\{{\mathcal{N}}_2(t_1-t_3)\right\}}^2.$$

(154)

Proof. 

Since ${\tilde{g}}_{12}=(t_2-t_1){\widehat{g}}_{12}$ and ${\tilde{g}}_{13}=(t_3-t_1){\widehat{g}}_{13}$, the point on the interpolation curve $t_2=t_1,t_3={\omega }_3\left(t_1\right)$ satisfies

$$\begin{array}{cc}\hfill \frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_2=t_1\\ t_3={\omega }_3\left(t_1\right)\end{array}}& =det\left(\begin{array}{cc}{\widehat{g}}_{12}+(t_2-t_1)\frac{\partial {\widehat{g}}_{12}}{\partial t_2}& (t_2-t_1)\frac{\partial {\widehat{g}}_{12}}{\partial t_3}\\ (t_3-t_1)\frac{\partial {\widehat{g}}_{13}}{\partial t_2}& {\widehat{g}}_{13}+(t_3-t_1)\frac{\partial {\widehat{g}}_{13}}{\partial t_3}\end{array}\right){|}_{\begin{array}{c}{t}_2=t_1\\ t_3={\omega }_3\left(t_1\right)\end{array}}\hfill \\ & ={\widehat{g}}_{12}(t_1,t_1,t_3)\left[(t_3-t_1)\frac{\partial {\widehat{g}}_{13}}{\partial t_3}\right]=({\rho }_{12}^2{t}_1-{\rho }_{14}^2){\rho }_{12}^2(1-t_1){(t_1-t_3)}^2,\hfill \end{array}$$

which implies (153). □

Lemma 30.

$${\mathcal{N}}_2(t_1-t_3)={\mathcal{N}}_2(t_2-t_3)=\frac{{\mathsf{\Delta }}_2}{r^2{h}_2}=\frac{{\mathsf{\Delta }}_2}{r^2{\rho }_{12}^4(4r^2-{\rho }_{12}^2)},$$

(155)

where ${\mathsf{\Delta }}_2$ is given by (143).

Proof. 

Since $t_1-t_3$ on the curve $\omega$ is written as

$$t_1-t_3=t_1-{\omega }_3\left(t_1\right)=t_1-\frac{(2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2}=\frac{{\widehat{g}}_{12}(t_1,t_1,t_1)}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2},$$

where ${\widehat{g}}_{12}(t_1,t_1,t_1)={\rho }_{12}^2{t}_1^2+({\rho }_{12}^2-3{\rho }_{14}^2)t_1+{\rho }_{14}^2$, we have

$${\mathcal{N}}_2(t_1-t_3)=\frac{{\mathcal{N}}_2\left({\widehat{g}}_{12}(t_1,t_1,t_1)\right)}{{\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)}.$$

(156)

By Euclidean division, we have

$${\widehat{\psi }}_2\left(t_1\right)=(c_2{t}_1^2+c_1{t}_1+c_0)P\left(t_1\right)+q_1{t}_1+q_0,$$

where, for setting ${\widehat{g}}_{12}(t_1,t_1,t_1)=c_2{t}_1^2+c_1{t}_1+c_0={\rho }_{12}^2{t}_1^2+({\rho }_{12}^2-3{\rho }_{14}^2)t_1+{\rho }_{14}^2$, there exist

$$\begin{array}{cc}\hfill P\left(t_1\right)& ={\rho }_{12}^2(4r^2-{\rho }_{12}^2)t_1^2+(12{\rho }_{14}^2{r}^2-4{\rho }_{12}^2{r}^2+{\rho }_{12}^2{\rho }_{14}^2-{\rho }_{12}^4)t_1\hfill \\ \hfill & +{\rho }_{12}^{-2}(36{\rho }_{14}^4{r}^2-36{\rho }_{12}^2{\rho }_{14}^2{r}^2+4{\rho }_{12}^4{r}^2-2{\rho }_{12}^4{\rho }_{14}^2-{\rho }_{12}^6),\hfill \\ \hfill q_1& =-{\rho }_{12}^{-2}{\mathsf{\Delta }}_0(108{\rho }_{14}^4{r}^2-408{\rho }_{12}^2{\rho }_{12}^2{r}^2+4{\rho }_{12}^4{r}^2-5{\rho }_{12}^2{\rho }_{14}^2+{\rho }_{12}^2),\hfill \\ \hfill q_0& ={\rho }_{12}^{-2}{\mathsf{\Delta }}_0{\rho }_{14}^2(36{\rho }_{14}^2{r}^2-4{\rho }_{12}^2{r}^2+{\rho }_{12}^2{\rho }_{14}^2-{\rho }_{12}^4).\hfill \end{array}$$

Using (92), we obtain

$${\mathcal{N}}_2\left({\widehat{g}}_{12}(t_1,t_1,t_1)\right)=c_2^3(q_1^2{c}_0-q_0{q}_1{c}_1+q_0^2{c}_2)h_2^{-2}=4{\rho }_{12}^4{\rho }_{14}^4{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_2{h}_2^{-2}.$$

Since ${\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)=4r^2{\rho }_{12}^4{\rho }_{14}^4{\mathsf{\Delta }}_0^2{h}_2^{-1}$ is presented in Proposition 5, using (156), we therefore obtain ${\mathcal{N}}_2(t_1-t_3)={\mathsf{\Delta }}_2{r}^{-2}{h}_2^{-1}$, which coincides with (155). □

Corollary 5.

$${\mathcal{N}}_2(t_1-t_3)=\frac{9{(3r^2-{\rho }_{12}^2)}^2}{2r^2{\rho }_{12}^4{\mathsf{\Delta }}_0(4r^2-{\rho }_{12}^2)}{\mathcal{N}}_1\left({\widehat{g}}_{12}\right).$$

Proof. 

See (142) in Lemma 27. □

Proposition 12.

${\mathsf{\Delta }}_2=0$ if and only if ${\tilde{\mathcal{C}}}_j\cap {\tilde{\mathcal{C}}}_k\ne \varnothing$ $(1\le j<k\le 4)$.

Proof. 

By definition, the curve $\omega \left(t_1\right)=(t_1,t_1$, ${\omega }_3\left(t_1\right))\in \tilde{X}$ defined by (150) cross the line $t_1=t_2=t_3$, when ${\omega }_3\left(t_1\right)=t_1$, i.e., the parameter $t_1$ satisfies

$${\widehat{g}}_{13}(t_1,t_1,t_1)={\rho }_{12}^2{t}_1^2+({\rho }_{12}^2-3{\rho }_{14}^2)t_1+{\rho }_{14}^2=0,$$

(157)

which is equivalent to ${\widehat{g}}_{12}(t_1,t_1,t_1)=0,$ since ${\widehat{g}}_{12}(t_1,t_1,t_1)={\widehat{g}}_{13}(t_1,t_1,t_1)$. This means that ${\tilde{\mathcal{C}}}_2\cap {\tilde{\mathcal{C}}}_1\ne \varnothing$ if and only if there exists a solution $t_1=\zeta$ of the equation ${\widehat{\psi }}_2\left(t_1\right)=0$ satisfying (157), also means that ${\tilde{\mathcal{C}}}_2\cap {\tilde{\mathcal{C}}}_1\ne \varnothing$ if and only if there exists a solution $t_1=\zeta$ of ${\psi }_1\left(t_1\right)=0$ satisfying (157). Hence, by definition, ${\mathcal{N}}_2(t_1-t_3)=0$ holds if and only if there exists a solution $t_1=\zeta$ of the equation ${\widehat{\psi }}_2\left(t_1\right)=0$, such that $\zeta -{\omega }_3\left(\zeta \right)=0$, which is equivalent to ${\tilde{\mathcal{C}}}_1\cap {\tilde{\mathcal{C}}}_2\ne \varnothing$. The evaluation (155) in Lemma 30 implies the following:

$${\mathsf{\Delta }}_2=0⟺{\mathcal{N}}_2(t_1-t_3)=0⟺{\tilde{\mathcal{C}}}_1\cap {\tilde{\mathcal{C}}}_2\ne \varnothing .$$

(158)

Due to the symmetry of ${\tilde{\mathcal{C}}}_2$, ${\tilde{\mathcal{C}}}_3$ and ${\tilde{\mathcal{C}}}_4$,

$${\tilde{\mathcal{C}}}_1\cap {\tilde{\mathcal{C}}}_2\ne \varnothing ,{\tilde{\mathcal{C}}}_1\cap {\tilde{\mathcal{C}}}_3\ne \varnothing \mathrm{and}{\tilde{\mathcal{C}}}_1\cap {\tilde{\mathcal{C}}}_4\ne \varnothing$$

occur at the same time. Hence, we see that ${\mathsf{\Delta }}_2=0$ if and only if ${\tilde{\mathcal{C}}}_1\cap {\tilde{\mathcal{C}}}_j\ne \varnothing$ $(j=2,3,4)$. Moreover, since ${\mathcal{N}}_2(t_2-t_3)={\mathcal{N}}_2(t_1-t_3)$, (158) implies that ${\mathsf{\Delta }}_2=0$ if and only if ${\mathcal{N}}_2(t_2-t_3)=0$, which means ${\tilde{\mathcal{C}}}_2\cap {\tilde{\mathcal{C}}}_3\ne \varnothing$. Due to the symmetry of ${\tilde{\mathcal{C}}}_2$, ${\tilde{\mathcal{C}}}_3$, and ${\tilde{\mathcal{C}}}_4$,

$${\tilde{\mathcal{C}}}_2\cap {\tilde{\mathcal{C}}}_3\ne \varnothing ,{\tilde{\mathcal{C}}}_2\cap {\tilde{\mathcal{C}}}_4\ne \varnothing \mathrm{and}{\tilde{\mathcal{C}}}_3\cap {\tilde{\mathcal{C}}}_4\ne \varnothing$$

occur at the same time. As a result, we therefore obtain Proposition 12. □

Lemma 31.

The explicit form of ${\mathrm{Discri}}_2$ is given by

$${\mathrm{Discri}}_2=\frac{16{\rho }_{12}^{12}{\rho }_{14}^8{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4}{h_2^6}=\frac{16{\rho }_{14}^8{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4}{{\rho }_{12}^{12}{(4r^2-{\rho }_{12}^2)}^6},$$

(159)

where ${\mathsf{\Delta }}_4$ is the polynomial in $r^2$, ${\rho }_{12}^2$, ${\rho }_{14}^2$ of degree 12 given by

$$\begin{array}{cc}\hfill {\mathsf{\Delta }}_4& :=16384{\rho }_{14}^2(4{\rho }_{14}^2-{\rho }_{12}^2)r^8+2048{\rho }_{14}^2(3{\rho }_{12}^4-12{\rho }_{12}^2{\rho }_{14}^2+{\rho }_{14}^4)r^6\hfill \\ \hfill & -48(9{\rho }_{12}^8-56{\rho }_{12}^6{\rho }_{14}^2+122{\rho }_{12}^4{\rho }_{14}^4-177{\rho }_{12}^2{\rho }_{14}^6+69{\rho }_{14}^8)r^4\hfill \\ \hfill & +4{\mathsf{\Delta }}_0{\rho }_{14}^2(35{\rho }_{12}^6-141{\rho }_{12}^4{\rho }_{14}^2+9{\rho }_{12}^2{\rho }_{14}^4+81{\rho }_{14}^6)r^2\hfill \\ \hfill & +{\rho }_{12}^2{\rho }_{14}^4(9{\rho }_{12}^6-49{\rho }_{12}^4{\rho }_{14}^2+63{\rho }_{12}^2{\rho }_{14}^4-27{\rho }_{14}^6).\hfill \end{array}$$

(160)

The explicit form of ${\mathcal{N}}_2\left({\widehat{\psi }}_2^{\prime }\right)$ is also expressed as

$${\mathcal{N}}_2\left({\widehat{\psi }}_2^{\prime }\right)=h_2^4{\mathrm{Discri}}_2=\frac{16{\rho }_{12}^{12}{\rho }_{14}^8{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4}{h_2^2}=\frac{16{\rho }_{12}^4{\rho }_{14}^8{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4}{{(4r^2-{\rho }_{12}^2)}^2}.$$

(161)

Proof. 

The resultant of ${\widehat{\psi }}_2$ and ${\widehat{\psi }}_2^{\prime }$ gives the discriminant of ${\widehat{\psi }}_2\left(t_1\right)$, i.e.,

$$R({\widehat{\psi }}_2,{\widehat{\psi }}_2^{\prime }):=\left|\begin{array}{ccccccc}{a}_0& a_1& a_2& a_3& a_4& & \\ & a_0& a_1& a_2& a_3& a_4& \\ & & a_0& a_1& a_2& a_3& a_4\\ 4a_0& 3a_1& 2a_2& a_3& & & \\ & 4a_0& 3a_1& 2a_2& a_3& & \\ & & 4a_0& 3a_1& 2a_2& a_3& \\ & & & 4a_0& 3a_1& 2a_2& a_3\end{array}\right|=a_0^7\prod _{j<k}{({\zeta }_j-{\zeta }_k)}^2=h_2^7{\mathrm{Discri}}_2,$$

where $a_0$, $a_1$, $a_2$, $a_3$, $a_4$ are given in (152). From direct calculation of the above determinant, we obtain

$$R({\widehat{\psi }}_2,{\widehat{\psi }}_2^{\prime })=16{\rho }_{12}^{16}{\rho }_{14}^8(4r^2-{\rho }_{12}^2){\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4=16{\rho }_{12}^{12}{\rho }_{14}^8{h}_2{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4,$$

which implies (159). Using (138) we therefore obtain (161) from (159). □

Due to (159) we immediately have the following:

Corollary 6.

There exists no double point in ${\tilde{\mathcal{C}}}_2$ if and only if ${\mathsf{\Delta }}_4\ne 0$.

We conclude the following from Lemmas 30 and 31:

Proposition 13.

$${\mathcal{N}}_2\left(Z_0\right)=\frac{4{\rho }_{14}^4{\mathsf{\Delta }}_0^4{\mathsf{\Delta }}_1{\mathsf{\Delta }}_2^2}{r^2{\rho }_{12}^4{(4r^2-{\rho }_{12}^2)}^4},$$

(162)

$${\mathcal{N}}_2\left(Z\right)=\frac{{\rho }_{12}^4{h}_2}{4r^6{\rho }_{14}^4}{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_1^2{\mathsf{\Delta }}_2^2{\mathrm{Discri}}_2=4\frac{{\rho }_{12}^{16}{\rho }_{14}^4}{r^6{h}_2^5}{\mathsf{\Delta }}_0^4{\mathsf{\Delta }}_1^2{\mathsf{\Delta }}_2^2{\mathsf{\Delta }}_4.$$

(163)

Proof. 

Applying (88), (89) in Proposition 5 and (155) in Lemma 30 to (154) we have (162). Differentiating both sides of (151) with respect to $t_1$ we have

$${\psi }_2^{\prime }\left(t_1\right)\equiv \frac{(t_1-1){\widehat{\psi }}_2^{\prime }\left(t_1\right)}{{({\rho }_{12}^2{t}_1-{\rho }_{14}^2)}^2}modAnn\left({\tilde{\mathcal{C}}}_2\right),$$

so that

$${\mathcal{N}}_2\left({\psi }_2^{\prime }\right)=\frac{{\mathcal{N}}_2(t_1-1)}{{\left\{{\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)\right\}}^2}{\mathcal{N}}_2\left({\widehat{\psi }}_2^{\prime }\right).$$

(164)

Using (164) and (154) in Lemma 29, (136) implies

$${\mathcal{N}}_2\left(Z\right)={\mathcal{N}}_2\left(Z_0\right){\mathcal{N}}_2\left({\psi }_2^{\prime }\right)=\frac{{\rho }_{12}^8{\left\{{\mathcal{N}}_2(1-t_1){\mathcal{N}}_2(t_1-t_3)\right\}}^2}{{\mathcal{N}}_2({\rho }_{12}^2{t}_1-{\rho }_{14}^2)}{\mathcal{N}}_2\left({\widehat{\psi }}_2^{\prime }\right).$$

(165)

According to Proposition 5, Lemma 30 and (161) in Lemma 31, the right-hand side of (165) coincides with (163). □

7.3. ${\mathcal{N}}_3\left(Z\right)$

An arbitrary critical point $t=(t_1,t_2,t_3)\in {\tilde{\mathcal{C}}}_3$ is characterized as a point on the interpolation curve $\omega :\mathbb{C}\to \tilde{X}$ defined by $\omega \left(t_1\right)=(t_1,{\omega }_2\left(t_1\right),{\omega }_3\left(t_1\right))\in \tilde{X}$, where

$$t_2={\omega }_2\left(t_1\right):=\frac{(2{\rho }_{14}^2-{\rho }_{12}^2)t_1-{\rho }_{14}^2}{{\rho }_{12}^2{t}_1-{\rho }_{14}^2},t_3={\omega }_3\left(t_1\right):=t_1,$$

and $t=\omega \left(t_1\right)\in \tilde{X}$ satisfies the equation ${\tilde{g}}_1\left(\omega \left(t_1\right)\right)=0$. This situation is represented by the transposition ${\sigma }_{23}$ of the coordinates $t_2$ and $t_3$ from that of ${\tilde{\mathcal{C}}}_2$. Thus, the characteristic function of ${\tilde{\mathcal{C}}}_3$ is the same as ${\tilde{\mathcal{C}}}_2$, i.e., ${\psi }_3\left(t_1\right)={\tilde{g}}_1(t_1,{\omega }_2\left(t_1\right),{\omega }_3\left(t_1\right))={\psi }_2\left(t_1\right)$. Hence, our conclusion is:

Proposition 14.

${\mathcal{N}}_3\left(Z_0\right)={\mathcal{N}}_2\left(Z_0\right)$, ${\mathcal{N}}_3\left(Z\right)={\mathcal{N}}_2\left(Z\right)$. The explicit forms are given in Proposition 13.

7.4. ${\mathcal{N}}_4\left(Z\right)$

As we saw in Section 5.4, an arbitrary critical point $t=(t_1,t_2,t_3)\in {\tilde{\mathcal{C}}}_4$ is characterized as a point on the interpolation curve $\omega :\mathbb{C}\to \tilde{X}$ defined by $\omega \left(t_1\right)=(t_1,{\omega }_2\left(t_1\right)$, ${\omega }_3\left(t_1\right))\in \tilde{X}$, where

$$t_2={\omega }_2\left(t_1\right):=\frac{V\left(t_1\right)}{U\left(t_1\right)},t_3={\omega }_3\left(t_1\right):=\frac{V\left(t_1\right)}{U\left(t_1\right)},$$

(166)

$$U\left(t_1\right):={\rho }_{12}^2{t}_1+{\rho }_{12}^2-2{\rho }_{14}^2,V\left(t_1\right):={\rho }_{14}^2(t_1-1),$$

and $t=\omega \left(t_1\right)\in \tilde{X}$ satisfies the equation ${\tilde{g}}_1\left(\omega \left(t_1\right)\right)=0$. The relation $t_2=t_3=V\left(t_1\right)/U\left(t_1\right)$ in (166) is determined by solving the equation ${\widehat{g}}_{12}(t_1,t_2,t_2)=0$, where

$${\widehat{g}}_{12}(t_1,t_2,t_2)={\widehat{g}}_{13}(t_1,t_2,t_2)={\rho }_{12}^2{t}_1{t}_2+{\mathsf{\Delta }}_0{t}_2-{\rho }_{14}^2(t_1+t_2-1)=t_{2}U\left(t_1\right)-V\left(t_1\right).$$

The characteristic function ${\psi }_4$ relative to $t_1$ is defined by ${\psi }_4\left(t_1\right)={\tilde{g}}_1(t_1,{\omega }_2\left(t_1\right),{\omega }_3\left(t_1\right))$, and from Lemma 22 ${\psi }_4\left(t_1\right)$ is expressed as

$${\psi }_4\left(t_1\right)=\frac{(t_1-1){\widehat{\psi }}_4\left(t_1\right)}{U^2}.$$

(167)

Here ${\widehat{\psi }}_4\left(t_1\right)$ is a polynomial in $t_1$ of degree 4 given by

$${\widehat{\psi }}_4\left(t_1\right)=a_0{t}_1^4+a_2{t}_1^3+a_3{t}_2+a_3{t}_1+a_4=h_4{\overline{\psi }}_4\left(t_1\right),$$

where

$$\begin{array}{cc}\hfill & h_4=a_0={\rho }_{12}^4{r}^2,a_1={\rho }_{12}^4({\rho }_{14}^2+4r^2),\hfill \\ \hfill & a_2={\rho }_{12}^2(6{\rho }_{12}^2{r}^2-8{\rho }_{14}^2{r}^2-2{\rho }_{12}^2{\rho }_{14}^2-3{\rho }_{14}^4),\hfill \\ \hfill & a_3={\rho }_{12}^2(4{\rho }_{12}^2{r}^2-16{\rho }_{14}^2{r}^2-3{\rho }_{12}^2{\rho }_{14}^2+10{\rho }_{14}^4),\hfill \\ \hfill & a_4=({\rho }_{12}^2-4{\rho }_{14}^2)({\rho }_{14}^4+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2).\hfill \end{array}$$

(168)

Lemma 32.

$$Z_0\equiv {\rho }_{12}^2(t_1-1){(t_1-t_2)}^{2}U\left(t_1\right)\equiv \frac{{\rho }_{12}^2}{{\rho }_{14}^2}{(t_1-t_2)}^{2}U\left(t_1\right)V\left(t_1\right)modAnn\left({\tilde{\mathcal{C}}}_4\right),$$

(169)

namely

$${\mathcal{N}}_4\left(Z_0\right)={\rho }_{12}^8{\mathcal{N}}_4(1-t_1){\left\{{\mathcal{N}}_4(t_1-t_2)\right\}}^2{\mathcal{N}}_4\left(U\right)=\frac{{\rho }_{12}^8}{{\rho }_{14}^8}{\left\{{\mathcal{N}}_4(t_1-t_2)\right\}}^2{\mathcal{N}}_4\left(U\right){\mathcal{N}}_4\left(V\right).$$

(170)

Proof. 

Since ${\tilde{g}}_{12}=(t_2-t_1){\widehat{g}}_{12}$ and ${\tilde{g}}_{13}={\tilde{g}}_{12}$, the point on the interpolation curve $t_2=t_3=V\left(t_1\right)/U\left(t_1\right)$ satisfies

$$\begin{array}{cc}\hfill & \frac{\partial ({\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_2,t_3)}{|}_{\begin{array}{c}{t}_2=V/U\\ t_3=V/U\end{array}}=det\left(\begin{array}{cc}{\widehat{g}}_{12}+(t_2-t_1)\frac{\partial {\widehat{g}}_{12}}{\partial t_2}& (t_2-t_1)\frac{\partial {\widehat{g}}_{12}}{\partial t_3}\\ (t_3-t_1)\frac{\partial {\widehat{g}}_{13}}{\partial t_2}& {\widehat{g}}_{13}+(t_3-t_1)\frac{\partial {\widehat{g}}_{13}}{\partial t_3}\end{array}\right){|}_{\begin{array}{c}{t}_2=V/U\\ t_3=V/U\end{array}}\hfill \\ & ={\left\{(t_2-t_1)\frac{\partial {\widehat{g}}_{12}}{\partial t_2}\right\}}^2-{\left\{(t_2-t_1)\frac{\partial {\widehat{g}}_{13}}{\partial t_2}\right\}}^2={(t_2-t_1)}^2\{{({\rho }_{12}^2{t}_1-{\rho }_{14}^2)}^2-{\mathsf{\Delta }}_0^2\}\hfill \\ & ={(t_2-t_1)}^2{\rho }_{12}^2(t_1-1)({\rho }_{12}^2{t}_1+{\rho }_{12}^2-2{\rho }_{14}^2),\hfill \end{array}$$

which implies (169). □

From the symmetry between ${\tilde{\mathcal{C}}}_4$ and ${\tilde{\mathcal{C}}}_2$, we immediately have ${\mathcal{N}}_4(t_1-t_2)={\mathcal{N}}_2(t_3-t_1)$, which has already been evaluated as (155) in Lemma 30. Hence, we have the following:

Lemma 33.

$${\mathcal{N}}_4(t_1-t_2)={\mathcal{N}}_4(t_1-t_3)=\frac{{\mathsf{\Delta }}_2}{r^2{\rho }_{12}^4(4r^2-{\rho }_{12}^2)}.$$

(171)

Lemma 34.

The explicit form of ${\mathrm{Discri}}_4$ is given by

$${\mathrm{Discri}}_4=\frac{16{\rho }_{12}^{12}{\rho }_{14}^8{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4}{h_4^6}=\frac{16{\rho }_{14}^8{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4}{r^{12}{\rho }_{12}^{12}},$$

(172)

where ${\mathsf{\Delta }}_4$ is the polynomial in $r^2$, ${\rho }_{12}^2$, ${\rho }_{14}^2$ of degree 12 given by (160). ${\mathcal{N}}_4\left({\widehat{\psi }}_4^{\prime }\right)$ is also given as

$${\mathcal{N}}_4\left({\widehat{\psi }}_4^{\prime }\right)=h_4^4{\mathrm{Discri}}_4=\frac{16{\rho }_{12}^{12}{\rho }_{14}^8{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4}{h_4^2}=\frac{16{\rho }_{12}^4{\rho }_{14}^8{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4}{r^4}.$$

(173)

Proof. 

The resultant of ${\widehat{\psi }}_4$ and ${\widehat{\psi }}_4^{\prime }$ gives the discriminant of ${\widehat{\psi }}_4\left(t_1\right)$, i.e.,

$$R({\widehat{\psi }}_4,{\widehat{\psi }}_4^{\prime }):=\left|\begin{array}{ccccccc}{a}_0& a_1& a_2& a_3& a_4& & \\ & a_0& a_1& a_2& a_3& a_4& \\ & & a_0& a_1& a_2& a_3& a_4\\ 4a_0& 3a_1& 2a_2& a_3& & & \\ & 4a_0& 3a_1& 2a_2& a_3& & \\ & & 4a_0& 3a_1& 2a_2& a_3& \\ & & & 4a_0& 3a_1& 2a_2& a_3\end{array}\right|=a_0^7\prod _{j<k}{({\zeta }_j-{\zeta }_k)}^2=h_4^7{\mathrm{Discri}}_4,$$

where $a_0$, $a_1$, $a_2$, $a_3$, $a_4$ are given in (168). From direct calculation of the above determinant, we obtain

$$R({\widehat{\psi }}_4,{\widehat{\psi }}_4^{\prime })=16{\rho }_{12}^{16}{\rho }_{14}^8{r}^2{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4=16{\rho }_{12}^{12}{\rho }_{14}^8{h}_4{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_4,$$

which implies (172). Using (138) we therefore obtain (173) from (172). □

Due to (172) we immediately have the following:

Corollary 7.

There exists no double point in ${\tilde{\mathcal{C}}}_4$ if and only if ${\mathsf{\Delta }}_4\ne 0$.

We conclude the following from Lemmas 33 and 34:

Proposition 15.

$${\mathcal{N}}_4\left(Z_0\right)=16\frac{{\rho }_{14}^4(4r^2-{\rho }_{14}^2){\mathsf{\Delta }}_0^4{\mathsf{\Delta }}_2^2}{r^8{\rho }_{12}^4(4r^2-{\rho }_{12}^2)},$$

(174)

$${\mathcal{N}}_4\left(Z\right)=4\frac{{\rho }_{12}^4{(4r^2-{\rho }_{14}^2)}^2}{{\rho }_{14}^4{(4r^2-{\rho }_{12}^2)}^3}{\mathsf{\Delta }}_0^2{\mathsf{\Delta }}_2^2{h}_4{\mathrm{Discri}}_4=64\frac{{\rho }_{12}^{16}{\rho }_{14}^4{(4r^2-{\rho }_{14}^2)}^2}{{(4r^2-{\rho }_{12}^2)}^3}\frac{{\mathsf{\Delta }}_0^4{\mathsf{\Delta }}_2^2{\mathsf{\Delta }}_4}{h_4^5}.$$

(175)

Proof. 

Applying (102) and (171) to (170) in Lemma 32 we have (174). Differentiating both sides of (167), with respect to $t_1$, we have

$${\psi }_4^{\prime }\left(t_1\right)\equiv \frac{(t_1-1){\widehat{\psi }}_4^{\prime }\left(t_1\right)}{U^2}modAnn\left({\tilde{\mathcal{C}}}_4\right),$$

so that

$${\mathcal{N}}_4\left({\psi }_4^{\prime }\right)=\frac{{\mathcal{N}}_4(t_1-1)}{{\left\{{\mathcal{N}}_4\left(U\right)\right\}}^2}{\mathcal{N}}_4\left({\widehat{\psi }}_4^{\prime }\right).$$

(176)

Using (136), (176) and (170) in Lemma 32, (173) in Lemma 34 and Proposition 5, we obtain

$$\begin{array}{cc}\hfill {\mathcal{N}}_4\left(Z\right)& ={\mathcal{N}}_4\left(Z_0\right){\mathcal{N}}_4\left({\psi }_4^{\prime }\right)=\frac{{\rho }_{12}^8{\mathcal{N}}_4\left(V\right)}{{\rho }_{14}^8{\mathcal{N}}_4\left(U\right)}{\mathcal{N}}_4(1-t_1){\left\{{\mathcal{N}}_4(t_1-t_2)\right\}}^2{\mathcal{N}}_4\left({\widehat{\psi }}_4^{\prime }\right)\hfill \\ & =\frac{{\rho }_{12}^8}{{\rho }_{14}^8}{\mathcal{N}}_4\left(t_2\right){\mathcal{N}}_4(1-t_1){\left\{{\mathcal{N}}_4(t_1-t_2)\right\}}^2{\mathcal{N}}_4\left({\widehat{\psi }}_4^{\prime }\right)\hfill \\ & =\frac{{\rho }_{12}^8}{{\rho }_{14}^8}{\mathcal{N}}_2\left(t_1\right){\mathcal{N}}_2(1-t_3){\left\{{\mathcal{N}}_2(t_1-t_3)\right\}}^2{h}_4^4{\mathrm{Discri}}_4\hfill \\ & =\frac{{\rho }_{12}^8}{{\rho }_{14}^8}\times \frac{{\rho }_{14}^4(4r^2-{\rho }_{14}^2)}{{\rho }_{12}^4(4r^2-{\rho }_{12}^2)}\times \frac{4{\mathsf{\Delta }}_0^2(4r^2-{\rho }_{14}^2)}{r^2{\rho }_{12}^4}\times {\left[\frac{{\mathsf{\Delta }}_2}{r^2{\rho }_{12}^4(4r^2-{\rho }_{12}^2)}\right]}^2{h}_4^4{\mathrm{Discri}}_4,\hfill \end{array}$$

which coincides with (175). □

7.5. Conclusions of This Section

In this subsection, we give a proof of Conjecture 1 under the conditions $\left({\mathcal{H}}_0\right)$ and $\left({\mathcal{H}}_1\right)$. And we try to prove Conjecture 1 without the constraint $\left({\mathcal{H}}_1\right)$ in Appendix A.

Theorem 4.

Under the conditions $\left({\mathcal{H}}_0\right)$ and $\left({\mathcal{H}}_1\right)$ the norm of the Hessian of F relative to $\mathcal{C}$ is expressed as

$$\begin{array}{cc}\hfill \mathcal{N}\left(\mathrm{Hess}\right(F\left)\right)& =2^{129}\frac{{\mathsf{\Delta }}_2^8{\mathsf{\Delta }}_3{\mathsf{\Delta }}_4^3}{r^{24}{\rho }_{12}^{24}{\rho }_{14}^6{({\rho }_{12}^2-4r^2)}^{12}{({\rho }_{14}^2-4r^2)}^{12}{(3r^2-{\rho }_{12}^2)}^5}\hfill \\ \hfill & \times \frac{1}{{({\rho }_{14}^4+{\rho }_{12}^2{r}^2-4{\rho }_{14}^2{r}^2)}^{15}{(3{\rho }_{14}^4+4{\rho }_{12}^2{r}^2-12{\rho }_{14}^2{r}^2)}^6},\hfill \end{array}$$

(177)

where ${\mathsf{\Delta }}_2$, ${\mathsf{\Delta }}_3$ and ${\mathsf{\Delta }}_4$ are the polynomials in $r^2$, ${\rho }_{12}^2$, ${\rho }_{14}^2$ given by (143), (146), and (160), respectively. The right-hand side is written in terms of the Cayley–Menger determinants as

$$\frac{2^{161}{\rho }_{12}^{74}{\rho }_{14}^{18}}{{\left\{B(0★1)\right\}}^{12}}\frac{{\mathsf{\Delta }}_2^8{\mathsf{\Delta }}_3{\mathsf{\Delta }}_4^3}{{\left\{B(0★12)B(0★14)\right\}}^{12}{\left\{B(0★123)\right\}}^5{\left\{B(0★124)\right\}}^{15}{\left\{B(0★1234)\right\}}^6}.$$

Proof. 

From Propositions 11, 13, 14, and 15, we obtain

$$\mathcal{N}\left(Z\right)=\prod _{j=1}^4{\mathcal{N}}_j\left(Z\right)=\frac{2^{12}}{3^5}\frac{{\rho }_{14}^{12}({\rho }_{12}^2-3{\rho }_{14}^2){(4r^2-{\rho }_{14}^2)}^2{\mathsf{\Delta }}_0^{14}{\mathsf{\Delta }}_1^4{\mathsf{\Delta }}_2^8{\mathsf{\Delta }}_3{\mathsf{\Delta }}_4^3}{r^{22}{\rho }_{12}^{12}{(3r^2-{\rho }_{12}^2)}^5{(4r^2-{\rho }_{12}^2)}^{13}}.$$

(178)

Since we already had

$$\mathcal{N}\left(\mathrm{Hess}\left(F\right)\right)=2^{45}\frac{-\mathcal{N}\left(Z\right)}{\mathcal{N}\left(f_1\right)\mathcal{N}\left(f_2\right)\mathcal{N}\left(f_3\right){\left\{\mathcal{N}\left(f_4\right)\right\}}^3\mathcal{N}\left(t_{\infty }\right){\left\{\mathcal{N}(1-t_1)\right\}}^2}$$

(179)

by Proposition 3, using (178) and the results for $\mathcal{N}\left(f_j\right)$, $\mathcal{N}\left(t_{\infty }\right)$ and $\mathcal{N}(1-t_1)$ stated in Theorem 2 or Corollary 2, we therefore see that (179) coincides with (177). □

Remark 14.

While Theorem 4 was proved under ${\mathsf{\Delta }}_0\ne 0$ in the above proof, the formula (177) is also valid for ${\mathsf{\Delta }}_0=0$. When ${\mathsf{\Delta }}_0=0$, i.e., ${\rho }_{12}^2={\rho }_{14}^2$ the invariants ${\mathsf{\Delta }}_2$, ${\mathsf{\Delta }}_3$ and ${\mathsf{\Delta }}_4$ degenerate to

$${\mathsf{\Delta }}_2=4{\rho }^4{({\rho }^2-8r^2)}^2,{\mathsf{\Delta }}_3=2{({\rho }^2-8r^2)}^2({\rho }^2+24r^2)and{\mathsf{\Delta }}_4=-4{\rho }^4{({\rho }^2-8r^2)}^3({\rho }^2+24r^2),$$

respectively, so that we can confirm that the right-hand side of (177) degenerates to (135) in Proposition 10, which is the result proved independently under ${\mathsf{\Delta }}_0=0$.

Remark 15.

The factors ${\mathsf{\Delta }}_0$ and ${\mathsf{\Delta }}_1$ do not appear in the expression (177) of $\mathcal{N}\left(\mathrm{Hess}\right(F\left)\right)$, while $\mathcal{N}\left(Z\right)$ in (178) is divisible by ${\mathsf{\Delta }}_0^{14}{\mathsf{\Delta }}_1^4$. Since $\mathcal{N}(1-t_1)$ given in Theorem 2 is also divisible by ${\mathsf{\Delta }}_0^7{\mathsf{\Delta }}_1^2$, the factor ${\mathsf{\Delta }}_0^{14}{\mathsf{\Delta }}_1^4$ in the numerator and that in denominator of (179) are cancelled. For the right-hand side of the formula (177) as a meromorphic function of $r^2$, we see that the point $r^2=(3{\rho }_{12}^2+{\rho }_{14}^2)/4$ for ${\mathsf{\Delta }}_1=0$ is a removable singularity.

Corollary 8.

Under the conditions $\left({\mathcal{H}}_0\right)$ and $\left({\mathcal{H}}_1\right)$

$$\mathcal{N}\left(\mathrm{Hess}\right(F\left)\right)\ne 0$$

if and only if every critical point in $\mathcal{C}$ is different from each other.

Proof. 

By (177) in Theorem 4 we have $\mathcal{N}\left(\mathrm{Hess}\right(F\left)\right)\ne 0$ if and only if ${\mathsf{\Delta }}_2^8{\mathsf{\Delta }}_3{\mathsf{\Delta }}_4^3\ne 0$. According to Proposition 12, Corollaries 4, 6 and 7, we see that ${\mathsf{\Delta }}_2{\mathsf{\Delta }}_3{\mathsf{\Delta }}_4\ne 0$ if and only if every critical point in $\tilde{\mathcal{C}}={\bigsqcup }_{j=1}^4{\tilde{\mathcal{C}}}_j$ is different from each other. □

8. Conclusions

We discussed the norm of the Hessian of the level function F at critical points $\mathcal{C}$ involved in asymptotic behaviors of hypergeometric integrals associated with a symmetric arrangement of three-dimensional spheres. We also provided two conjectures (Conjectures 1 and 2) relevant to this topic. We provide a proof in a special symmetric case where $▵O_1{O}_2{O}_3{O}_4$ is a pyramid with the axis of symmetry, whose base triangle $▵O_1{O}_2{O}_3$ is regular and all spheres have the same radius.

Appendix A.1. Step 1

We fix the admissible parameter $t_1$. Then ${\tilde{g}}_1$ given in Proposition 2 is polynomial in $t_2,t_3$ whose coefficients are explicitly written using the parameter $t_1$ as follows:

$${\tilde{g}}_1={\beta }_{1,22}{t}_2^2+2{\beta }_{1,23}{t}_2{t}_3+{\beta }_{1,33}{t}_3^2+2{\beta }_{1,2}{t}_2+2{\beta }_{1,3}{t}_3+{\beta }_{1,\varnothing },$$

(A1)

where the coefficients ${\beta }_{1,*}$ are polynomials in $t_1$ of, at most, second degree:

$$\begin{array}{ccc}& & {\beta }_{1,22}=(r_1^2-{\rho }_{12}^2)t_1+{\rho }_{24}^2-r_4^2,\hfill \\ & & {\beta }_{1,33}=(r_1^2-{\rho }_{13}^2)t_1+{\rho }_{34}^2-r_4^2,\hfill \\ & & 2{\beta }_{1,23}=\left\{2r_1^2-B\left(\begin{array}{ccc}0& 2& 1\\ 0& 3& 1\end{array}\right)\right\}{t}_1-2r_4^2+B\left(\begin{array}{ccc}0& 2& 4\\ 0& 3& 4\end{array}\right),\hfill \\ & & 2{\beta }_{1,2}=2\left\{r_1^2{t}_1^2+B\left(\begin{array}{ccc}0& ★& 2\\ 0& 4& 1\end{array}\right)t_1-r_4^2\right\},\hfill \\ & & 2{\beta }_{1,3}=2\left\{r_1^2{t}_1^2+B\left(\begin{array}{ccc}0& ★& 3\\ 0& 4& 1\end{array}\right)t_1-r_4^2\right\},\hfill \\ & & {\beta }_{1,\varnothing }=r_1^2{t}_1^3+({\rho }_{14}^2-r_4^2+2r_1^2)t_1^2+(-{\rho }_{14}^2+r_1^2-2r_4^2)t_1-r_4^2.\hfill \end{array}$$

Moreover, ${\tilde{g}}_{12}$ and ${\tilde{g}}_{13}$ given in Lemma 10 are also polynomials in $t_2,t_3$, whose coefficients are explicitly written using the parameter $t_1$ as follows:

$${\tilde{g}}_{1j}={\beta }_{1j,jj}{t}_j^2+2{\beta }_{1j,jk}{t}_j{t}_k+{\beta }_{1j,kk}{t}_k^2+2{\beta }_{1j,j}{t}_j+2{\beta }_{1j,k}{t}_k+{\beta }_{1j,\varnothing }(j=2,3),$$

(A2)

where $\{j,k\}$ is a permutation of $\{2,3\}$ and the coefficients ${\beta }_{1j,*}$ are polynomials in $t_1$ of at most second degree:

$$\begin{array}{ccc}& & {\beta }_{1j,jj}=t_{1}B\left(\begin{array}{ccc}0& ★& j\\ 0& 1& j\end{array}\right)-B\left(\begin{array}{ccc}0& ★& j\\ 0& 4& j\end{array}\right),{\beta }_{1j,kk}=0,\hfill \\ & & 2{\beta }_{1j,jk}=t_{1}B\left(\begin{array}{ccc}0& k& ★\\ 0& j& 1\end{array}\right)+B\left(\begin{array}{ccc}0& ★& k\\ 0& j& 4\end{array}\right),\hfill \\ & & 2{\beta }_{1j,j}=-t_1^{2}B\left(\begin{array}{ccc}0& ★& 1\\ 0& j& 1\end{array}\right)+B\left(\begin{array}{ccc}0& ★& 4\\ 0& j& 4\end{array}\right),\hfill \\ & & 2{\beta }_{1j,k}=-t_{1}B\left(\begin{array}{ccc}0& ★& k\\ 0& 1& 4\end{array}\right),\hfill \\ & & {\beta }_{1j,\varnothing }=t_1^{2}B\left(\begin{array}{ccc}0& ★& 1\\ 0& 4& 1\end{array}\right)-t_{1}B\left(\begin{array}{ccc}0& ★& 4\\ 0& 1& 4\end{array}\right)(j=2,3).\hfill \end{array}$$

Appendix A.2. Step 2

We modify ${\tilde{g}}_1$ as

$${\tilde{g}}_1^{\prime }:={\tilde{g}}_1-\frac{{\beta }_{1,22}}{{\beta }_{12,22}}{\tilde{g}}_{12}-\frac{{\beta }_{1,33}}{{\beta }_{13,33}}{\tilde{g}}_{13},$$

which can be represented as

$${\tilde{g}}_1^{\prime }=2{\beta }_{1,23}^{\prime }{t}_2{t}_3+2{\beta }_{1,2}^{\prime }{t}_2+2{\beta }_{1,3}^{\prime }{t}_3+{\beta }_{1,\varnothing }^{\prime },$$

where

$$\begin{array}{ccc}& & 2{\beta }_{1,23}^{\prime }=2{\beta }_{1,23}-\frac{{\beta }_{1,22}}{{\beta }_{12,22}}2{\beta }_{12,23}-\frac{{\beta }_{1,33}}{{\beta }_{13,33}}2{\beta }_{13,23},\hfill \\ & & 2{\beta }_{1,2}^{\prime }=2{\beta }_{1,2}-\frac{{\beta }_{1,22}}{{\beta }_{12,22}}2{\beta }_{12,2}-\frac{{\beta }_{1,33}}{{\beta }_{13,33}}2{\beta }_{13,2},\hfill \\ & & 2{\beta }_{1,3}^{\prime }=2{\beta }_{1,3}-\frac{{\beta }_{1,33}}{{\beta }_{13,33}}2{\beta }_{13,3}-\frac{{\beta }_{1,22}}{{\beta }_{12,22}}2{\beta }_{12,3},\hfill \\ & & {\beta }_{1,\varnothing }^{\prime }={\beta }_{1,\varnothing }-\frac{{\beta }_{1,22}}{{\beta }_{12,22}}{\beta }_{12,\varnothing }-\frac{{\beta }_{1,33}}{{\beta }_{13,33}}{\beta }_{13,\varnothing }.\hfill \end{array}$$

We also modify ${\tilde{g}}_{1j}$ as

$$\begin{array}{ccc}& & {\tilde{g}}_{12}^{\prime }:={\tilde{g}}_{12}-\frac{{\beta }_{12,23}}{{\beta }_{1,23}^{\prime }}{\tilde{g}}_1^{\prime }={\beta }_{12,22}^{\prime }{t}_2^2+2{\beta }_{12,2}^{\prime }{t}_2+2{\beta }_{12,3}^{\prime }{t}_3+{\beta }_{12,\varnothing }^{\prime },\hfill \\ & & {\tilde{g}}_{13}^{\prime }:={\tilde{g}}_{13}-\frac{{\beta }_{13,23}}{{\beta }_{1,23}^{\prime }}{\tilde{g}}_1^{\prime }={\beta }_{13,33}^{\prime }{t}_3^2+2{\beta }_{13,2}^{\prime }{t}_2+2{\beta }_{13,3}^{\prime }{t}_3+{\beta }_{13,\varnothing }^{\prime },\hfill \end{array}$$

where

$$\begin{array}{ccc}& & {\beta }_{12,22}^{\prime }={\beta }_{12,22},{\beta }_{13,33}^{\prime }={\beta }_{13,33},\hfill \\ & & 2{\beta }_{12,2}^{\prime }=-\frac{{\beta }_{12,23}}{{\beta }_{1,23}^{\prime }}2{\beta }_{1,2}^{\prime }+2{\beta }_{12,2},2{\beta }_{13,3}^{\prime }=-\frac{{\beta }_{13,23}}{{\beta }_{1,23}^{\prime }}2{\beta }_{1,3}^{\prime }+2{\beta }_{13,3},\hfill \\ & & 2{\beta }_{12,3}^{\prime }=-\frac{{\beta }_{12,23}}{{\beta }_{1,23}^{\prime }}2{\beta }_{1,3}^{\prime }+2{\beta }_{12,3},2{\beta }_{13,2}^{\prime }=-\frac{{\beta }_{13,23}}{{\beta }_{1,23}^{\prime }}2{\beta }_{1,2}^{\prime }+2{\beta }_{13,2},\hfill \\ & & {\beta }_{12,\varnothing }^{\prime }=-\frac{{\beta }_{12,23}}{{\beta }_{1,23}^{\prime }}{\beta }_{1,\varnothing }^{\prime }+{\beta }_{12,\varnothing },{\beta }_{13,\varnothing }^{\prime }=-\frac{{\beta }_{13,23}}{{\beta }_{1,23}^{\prime }}{\beta }_{1,\varnothing }^{\prime }+{\beta }_{13,\varnothing }.\hfill \end{array}$$

Remark that $2{\beta }_{1j,jk}^{\prime }=0$ for $j=2,3$ and $j\ne k$. According to Lemma 11, we may conclude

Lemma A1.

Suppose that ${\beta }_{12,22}{\beta }_{13,33}\ne 0.$ Then under the condition $\left({\mathcal{H}}_0\right)$ the system (57) holds if and only if

$${\tilde{g}}_1^{\prime }={\tilde{g}}_{12}^{\prime }={\tilde{g}}_{13}^{\prime }=0.$$

(A3)

In this case, the identity

$$d{\tilde{g}}_1^{\prime }\wedge d{\tilde{g}}_{12}^{\prime }\wedge d{\tilde{g}}_{13}^{\prime }\equiv d{\tilde{g}}_1\wedge d{\tilde{g}}_{12}\wedge d{\tilde{g}}_{13}modAnn\left(\tilde{\mathcal{C}}\right)$$

holds, i.e.,

$$\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\equiv \frac{\partial ({\tilde{g}}_1^{\prime },{\tilde{g}}_{12}^{\prime },{\tilde{g}}_{13}^{\prime })}{\partial (t_1,t_2,t_3)}modAnn\left(\tilde{\mathcal{C}}\right).$$

Appendix A.3. Step 3

In this subsection, we want to express

$$\frac{\partial ({\tilde{g}}_1^{\prime },{\tilde{g}}_{12}^{\prime },{\tilde{g}}_{13}^{\prime })}{\partial (t_1,t_2,t_3)}$$

explicitly in terms of the resultant of ${\tilde{g}}_1^{\prime }$, ${\tilde{g}}_{12}^{\prime }$ and ${\tilde{g}}_{13}^{\prime }$. We assume that the monomials in $t_2,t_3$, of at most fourth degree, are arranged in the following order:

$$t_2^4\succ t_2^3{t}_3\succ t_2^2{t}_3^2\succ t_2{t}_3^3\succ t_3^4\succ t_2^3\succ t_3^3\succ t_2^2{t}_3\succ t_2{t}_3^2\succ t_2^2\succ t_3^2\succ t_2{t}_3\succ t_2\succ t_3\succ 1.$$

(A4)

Three fundamental linear relations among ${\tilde{g}}_1^{\prime },{\tilde{g}}_{12}^{\prime },{\tilde{g}}_{13}^{\prime }$ over the coefficients of quadratic polynomials are given as follows:

$$\begin{array}{cc}\hfill & ({\beta }_{12,22}^{\prime }{t}_2^2+2{\beta }_{12,2}^{\prime }{t}_2+2{\beta }_{12,3}^{\prime }{t}_3+{\beta }_{12,\varnothing }^{\prime }){\tilde{g}}_{13}^{\prime }-({\beta }_{13,33}^{\prime }{t}_3^2+2{\beta }_{13,2}^{\prime }{t}_2+2{\beta }_{13,3}^{\prime }{t}_3+{\beta }_{13,\varnothing }^{\prime }){\tilde{g}}_{12}^{\prime }=0,\hfill \\ \hfill & ({\beta }_{12,22}^{\prime }{t}_2^2+2{\beta }_{12,2}^{\prime }{t}_2+2{\beta }_{12,3}^{\prime }{t}_3+{\beta }_{12,\varnothing }^{\prime }){\tilde{g}}_1^{\prime }-(2{\beta }_{1,23}^{\prime }{t}_2{t}_3+2{\beta }_{1,2}^{\prime }{t}_2+2{\beta }_{1,3}^{\prime }{t}_3+{\beta }_{1,\varnothing }^{\prime }){\tilde{g}}_{12}^{\prime }=0,\hfill \\ \hfill & ({\beta }_{13,33}^{\prime }{t}_3^2+2{\beta }_{13,2}^{\prime }{t}_2+2{\beta }_{13,3}^{\prime }{t}_3+{\beta }_{13,\varnothing }^{\prime }){\tilde{g}}_1^{\prime }-(2{\beta }_{1,23}^{\prime }{t}_2{t}_3+2{\beta }_{1,2}^{\prime }{t}_2+2{\beta }_{1,3}^{\prime }{t}_3+{\beta }_{1,\varnothing }^{\prime }){\tilde{g}}_{13}^{\prime }=0.\hfill \end{array}$$

As a result $t_2^2{\tilde{g}}_{13}^{\prime }$ is a linear combination of

$$t_3^2{\tilde{g}}_{12}^{\prime },t_2{\tilde{g}}_{12}^{\prime },t_3{\tilde{g}}_{12}^{\prime },{\tilde{g}}_{12}^{\prime },t_2{\tilde{g}}_{13}^{\prime },t_3{\tilde{g}}_{13}^{\prime },{\tilde{g}}_{13}^{\prime },$$

and $t_2^2{\tilde{g}}_1^{\prime }$ is a linear combination of

$$t_2{\tilde{g}}_1^{\prime },t_3{\tilde{g}}_1^{\prime },{\tilde{g}}_1^{\prime },t_2{t}_3{\tilde{g}}_{12}^{\prime },t_2{\tilde{g}}_{12}^{\prime },t_3{\tilde{g}}_{12}^{\prime },{\tilde{g}}_{12}^{\prime }.$$

Moreover, $t_3^2{\tilde{g}}_1^{\prime }$ is also a linear combination of

$$t_2{\tilde{g}}_1^{\prime },t_3{\tilde{g}}_1^{\prime },{\tilde{g}}_1^{\prime },t_2{t}_3{\tilde{g}}_{13}^{\prime },t_2{\tilde{g}}_{13}^{\prime },t_3{\tilde{g}}_{13}^{\prime },{\tilde{g}}_{13}^{\prime }.$$

One can see:

Lemma A2.

The system of (ordered) 15 polynomials (denoted by $\mathcal{X}$)

$$\begin{array}{cc}\hfill & {\mathbf{x}}_1=t_2^2{\tilde{g}}_{12}^{\prime }\succ {\mathbf{x}}_2=t_2{t}_3{\tilde{g}}_{12}^{\prime }\succ {\mathbf{x}}_3=t_3^2{\tilde{g}}_{12}^{\prime }\succ {\mathbf{x}}_4=t_2{t}_3{\tilde{g}}_{13}^{\prime }\succ {\mathbf{x}}_5=t_3^2{\tilde{g}}_{13}^{\prime }\hfill \\ \hfill & \succ {\mathbf{x}}_6=t_2{\tilde{g}}_{12}^{\prime }\succ {\mathbf{x}}_7=t_3{\tilde{g}}_{13}^{\prime }\succ {\mathbf{x}}_8=t_3{\tilde{g}}_{12}^{\prime }\succ {\mathbf{x}}_9=t_2{\tilde{g}}_{13}^{\prime },\succ {\mathbf{x}}_{10}={\tilde{g}}_{12}^{\prime }\hfill \\ \hfill & \succ {\mathbf{x}}_{11}={\tilde{g}}_{13}^{\prime }\succ {\mathbf{x}}_{12}={\tilde{g}}_1^{\prime }\succ {\mathbf{x}}_{13}=t_2{\tilde{g}}_1^{\prime }\succ {\mathbf{x}}_{14}=t_3{\tilde{g}}_1^{\prime }\succ {\mathbf{x}}_{15}=t_2{t}_3{\tilde{g}}_1^{\prime }\hfill \end{array}$$

are linearly independent and span the linear space of polynomials at most fourth degree.

Definition A1.

The Macaulay’s diagram $\mathcal{X}$$15\times 15$ associated with the ordered basis ${\mathbf{x}}_j$ with respect to the monomials in the ordering (A4) is defined by the following equation:

$$\mathcal{X}:{}^T({\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_{15})=\mathcal{X}{}^T(t_2^4,t_2^3{t}_3,\dots ,t_2,t_3,1),$$

where $\mathcal{X}$ is the $15\times 15$ matrix given by

$$\mathcal{X}=\left(\begin{array}{ccccccccccccccc}{\beta }_{12,22}^{\prime }& & & & & 2{\beta }_{12,2}^{\prime }& & 2{\beta }_{12,3}^{\prime }& & {\beta }_{12,\varnothing }& & & & & \\ & {\beta }_{12,22}^{\prime }& & & & & & 2{\beta }_{12,2}^{\prime }& 2{\beta }_{12,3}^{\prime }& & & {\beta }_{12,\varnothing }^{\prime }& & \\ & & {\beta }_{12,22}^{\prime }& & & & 2{\beta }_{12,3}^{\prime }& & 2{\beta }_{12,2}^{\prime }& & {\beta }_{12,\varnothing }^{\prime }& & & & \\ & & & {\beta }_{13,33}^{\prime }& & & & 2{\beta }_{13,2}^{\prime }& 2{\beta }_{13,3}^{\prime }& & & {\beta }_{13,\varnothing }^{\prime }& & & \\ & & & & {\beta }_{13,33}^{\prime }& & 2{\beta }_{13,3}^{\prime }& & 2{\beta }_{13,2}^{\prime }& & {\beta }_{13,\varnothing }^{\prime }& & & & \\ & & & & & {\beta }_{12,22}^{\prime }& & & & 2{\beta }_{12,2}^{\prime }& & 2{\beta }_{12,3}^{\prime }& {\beta }_{12,\varnothing }^{\prime }& & \\ & & & & & & {\beta }_{13,33}^{\prime }& & & & 2{\beta }_{13,3}^{\prime }& 2{\beta }_{13,2}^{\prime }& & {\beta }_{13,\varnothing }^{\prime }& \\ & & & & & & & {\beta }_{12,22}^{\prime }& & & 2{\beta }_{12,3}^{\prime }& 2{\beta }_{12,2}^{\prime }& & {\beta }_{12,\varnothing }^{\prime }& \\ & & & & & & & & {\beta }_{13,33}^{\prime }& 2{\beta }_{13,2}^{\prime }& & 2{\beta }_{13,3}^{\prime }& {\beta }_{13,\varnothing }^{\prime }& & \\ & & & & & & & & & {\beta }_{12,22}^{\prime }& & & 2{\beta }_{12,2}^{\prime }& 2{\beta }_{12,3}^{\prime }& {\beta }_{12,\varnothing }^{\prime }\\ & & & & & & & & & & {\beta }_{13,33}^{\prime }& & 2{\beta }_{13,2}^{\prime }& 2{\beta }_{13,3}^{\prime }& {\beta }_{13,\varnothing }^{\prime }\\ & & & & & & & & & & & 2{\beta }_{1,23}^{\prime }& 2{\beta }_{1,2}^{\prime }& 2{\beta }_{1,3}^{\prime }& {\beta }_{1,\varnothing }^{\prime }\\ & & & & & & & 2{\beta }_{1,23}^{\prime }& & 2{\beta }_{1,2}^{\prime }& & 2{\beta }_{1,3}^{\prime }& {\beta }_{1,\varnothing }^{\prime }& & \\ & & & & & & & & 2{\beta }_{1,23}^{\prime }& & 2{\beta }_{1,3}^{\prime }& 2{\beta }_{1,2}^{\prime }& & {\beta }_{1,\varnothing }^{\prime }& \\ & & 2{\beta }_{1,23}^{\prime }& & & & & 2{\beta }_{1,2}^{\prime }& 2{\beta }_{1,3}^{\prime }& & & {\beta }_{1,\varnothing }^{\prime }& \end{array}\right).$$

The resultant of ${\tilde{g}}_{12}^{\prime },{\tilde{g}}_{13}^{\prime },{\tilde{g}}_1^{\prime }$, which we denote by $R({\tilde{g}}_{12}^{\prime },{\tilde{g}}_{13}^{\prime },{\tilde{g}}_1^{\prime })$ is related to $det\mathcal{X}$ as follows:

$$det\mathcal{X}={\left({\beta }_{12,22}^{\prime }\right)}^2\left({\beta }_{13,33}^{\prime }\right)R({\tilde{g}}_{12}^{\prime },{\tilde{g}}_{13}^{\prime },{\tilde{g}}_1^{\prime }),$$

(A5)

where

$$R({\tilde{g}}_{12}^{\prime },{\tilde{g}}_{13}^{\prime },{\tilde{g}}_1^{\prime })={\left({\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }\right)}^3{\left({\beta }_{1.\varnothing }^{\prime }\right)}^2\{{\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }{\left({\beta }_{1,\varnothing }^{\prime }\right)}^2-4{\left({\beta }_{1,23}^{\prime }\right)}^2{\beta }_{12,\varnothing }^{\prime }{\beta }_{13,\varnothing }^{\prime }\}+\cdots .$$

See [15] and W. Gröbner: Moderne Algebraische Geometrie [16] (pp. 70–71). Using (A1) and (A2), we first define

$$\begin{array}{cc}\hfill {\tilde{g}}_{12}^{″}& :=t_2{\tilde{g}}_1^{\prime }-\frac{2{\beta }_{1,23}^{\prime }}{{\beta }_{12,22}^{\prime }}{t}_3{\tilde{g}}_{12}^{\prime }={\xi }_{11}{t}_2^2+{\xi }_{12}{t}_3^2+{\xi }_{13}{t}_2{t}_3+{\xi }_{14}{t}_2+{\xi }_{15}{t}_3+{\xi }_{16},\hfill \\ \hfill {\tilde{g}}_{13}^{″}& :=t_3{\tilde{g}}_1^{\prime }-\frac{2{\beta }_{1,23}^{\prime }}{{\beta }_{13,33}^{\prime }}{t}_2{\tilde{g}}_{13}^{\prime }={\xi }_{21}{t}_2^2+{\xi }_{22}{t}_3^2+{\xi }_{23}{t}_2{t}_3+{\xi }_{24}{t}_2+{\xi }_{25}{t}_3+{\xi }_{26},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & {\xi }_{11}=2{\beta }_{1,2}^{\prime },{\xi }_{12}=-\frac{4{\beta }_{12,3}^{\prime }{\beta }_{1,23}^{\prime }}{{\beta }_{12,22}^{\prime }},{\xi }_{13}=2{\beta }_{1,3}^{\prime }-\frac{4{\beta }_{12,2}^{\prime }{\beta }_{1,23}^{\prime }}{{\beta }_{12,22}^{\prime }},\hfill \\ \hfill & {\xi }_{14}={\beta }_{1,\varnothing }^{\prime },{\xi }_{15}=-\frac{2{\beta }_{12,\varnothing }^{\prime }{\beta }_{1,23}^{\prime }}{{\beta }_{12,22}^{\prime }},{\xi }_{16}=0,\hfill \\ \hfill & {\xi }_{21}-\frac{4{\beta }_{13,2}^{\prime }{\beta }_{1,23}^{\prime }}{{\beta }_{13,33}^{\prime }},{\xi }_{22}=2{\beta }_{1,3}^{\prime },{\xi }_{23}=2{\beta }_{1,2}^{\prime }-\frac{4{\beta }_{13,3}^{\prime }{\beta }_{1,23}^{\prime }}{{\beta }_{13,33}^{\prime }},\hfill \\ \hfill & {\xi }_{24}={\beta }_{1,\varnothing }^{\prime },{\xi }_{25}=-\frac{2{\beta }_{13,\varnothing }^{\prime }{\beta }_{1,23}^{\prime }}{{\beta }_{13,33}^{\prime }},{\xi }_{26}=0.\hfill \end{array}$$

Then we have

$${}^T({\tilde{g}}_{12}^{″},{\tilde{g}}_{13}^{″},{\tilde{g}}_1^{\prime },{\tilde{g}}_{12}^{\prime },{\tilde{g}}_{13}^{\prime })=\Xi {}^T(t_2^2,t_3^2,t_2{t}_3,t_2,t_3,1),$$

where the $5\times 6$ matrix $\Xi$ is given by

$$\Xi :=\left(\begin{array}{cccccc}{\xi }_{11}& {\xi }_{12}& {\xi }_{13}& {\xi }_{14}& {\xi }_{15}& {\xi }_{16}\\ {\xi }_{21}& {\xi }_{22}& {\xi }_{23}& {\xi }_{24}& {\xi }_{25}& {\xi }_{26}\\ 0& 0& {\xi }_{33}& {\xi }_{34}& {\xi }_{35}& {\xi }_{36}\\ {\xi }_{41}& 0& 0& {\xi }_{44}& {\xi }_{45}& {\xi }_{46}\\ 0& {\xi }_{52}& 0& {\xi }_{54}& {\xi }_{55}& {\xi }_{56}\end{array}\right).$$

(A6)

Here, the entries ${\xi }_{ij}$ of the matrix $\Xi$ can be expressed as

$$\begin{array}{cc}\hfill & {\xi }_{33}=2{\beta }_{1,23}^{\prime },{\xi }_{34}=2{\beta }_{1,2}^{\prime },{\xi }_{35}=2{\beta }_{1,3}^{\prime },{\xi }_{36}={\beta }_{1,\varnothing }^{\prime },\hfill \\ \hfill & {\xi }_{41}={\beta }_{12,22}^{\prime },{\xi }_{44}=2{\beta }_{12,2}^{\prime },{\xi }_{45}=2{\beta }_{12,3}^{\prime },{\xi }_{46}={\beta }_{12,\varnothing }^{\prime },\hfill \\ \hfill & {\xi }_{52}={\beta }_{13,33}^{\prime },{\xi }_{54}=2{\beta }_{13,2}^{\prime },{\xi }_{55}=2{\beta }_{13,3}^{\prime },{\xi }_{56}={\beta }_{13,\varnothing }^{\prime }.\hfill \end{array}$$

Define further

$$\begin{array}{cc}\hfill {\tilde{g}}_{12}^{‴}& :={\tilde{g}}_{12}^{″}-\frac{{\xi }_{13}}{{\xi }_{33}}{\tilde{g}}_1^{\prime }-\frac{{\xi }_{11}}{{\xi }_{41}}{\tilde{g}}_{12}^{\prime }-\frac{{\xi }_{12}}{{\xi }_{52}}{\tilde{g}}_{13}^{\prime }={\xi }_{14}^{\prime }{t}_2+{\xi }_{15}^{\prime }{t}_3+{\xi }_{16}^{\prime },\hfill \end{array}$$

(A7)

$$\begin{array}{cc}\hfill {\tilde{g}}_{13}^{‴}& :={\tilde{g}}_{13}^{″}-\frac{{\xi }_{23}}{{\xi }_{33}}{\tilde{g}}_1^{\prime }-\frac{{\xi }_{21}}{{\xi }_{41}}{\tilde{g}}_{12}^{\prime }-\frac{{\xi }_{22}}{{\xi }_{52}}{\tilde{g}}_{13}^{\prime }={\xi }_{24}^{\prime }{t}_2+{\xi }_{25}^{\prime }{t}_3+{\xi }_{26}^{\prime },\hfill \end{array}$$

(A8)

where ${\xi }_{jk}^{\prime }$ can be expressed more concretely

$$\begin{array}{cc}\hfill & {\xi }_{14}^{\prime }={\beta }_{1,\varnothing }^{\prime }-2\frac{{\beta }_{1,2}^{\prime }{\beta }_{1,3}^{\prime }}{{\beta }_{1,23}^{\prime }}+8\frac{{\beta }_{1,23}^{\prime }{\beta }_{12,3}^{\prime }{\beta }_{13,2}^{\prime }}{{\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }},\hfill \\ \hfill & {\xi }_{15}^{\prime }=-\frac{4{\beta }_{1,2}^{\prime }{\beta }_{12,3}^{\prime }+2{\beta }_{1,23}^{\prime }{\beta }_{12,\varnothing }^{\prime }}{{\beta }_{12,22}^{\prime }}+8\frac{{\beta }_{1,23}^{\prime }{\beta }_{12,3}^{\prime }{\beta }_{13,3}^{\prime }}{{\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }}-2\frac{{\beta }_{1,3}^{\prime }({\beta }_{1,3}^{\prime }{\beta }_{12,22}^{\prime }-2{\beta }_{1,23}^{\prime }{\beta }_{12,2}^{\prime })}{{\beta }_{1,23}^{\prime }{\beta }_{12,22}^{\prime }},\hfill \\ \hfill & {\xi }_{16}^{\prime }=-\frac{{\beta }_{1,3}^{\prime }{\beta }_{1,\varnothing }^{\prime }}{{\beta }_{1,23}^{\prime }}+2\frac{-{\beta }_{1,2}^{\prime }{\beta }_{12,\varnothing }^{\prime }+{\beta }_{1,\varnothing }^{\prime }{\beta }_{12,2}^{\prime }}{{\beta }_{12,22}^{\prime }}+4\frac{{\beta }_{1,23}^{\prime }{\beta }_{12,3}^{\prime }{\beta }_{13,\varnothing }^{\prime }}{{\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }},\hfill \end{array}$$

(A9)

and likewise ${\xi }_{24}^{\prime }={\sigma }_{23}\left({\xi }_{15}^{\prime }\right),$ ${\xi }_{25}^{\prime }={\sigma }_{23}\left({\xi }_{14}^{\prime }\right)={\xi }_{14}^{\prime },$ ${\xi }_{26}^{\prime }={\sigma }_{23}\left({\xi }_{16}^{\prime }\right)$, where ${\sigma }_{23}$ denotes the transposition between the subscript $\{2,3\}$. The polynomials ${\tilde{g}}_{12}^{‴}$ and ${\tilde{g}}_{13}^{‴}$ are linear in $t_2,t_3$. Using the matrix ${\Xi }^{\prime }:={\left({\xi }_{jk}^{\prime }\right)}_{1\le j\le 2,1\le k\le 3}$ we have

$$\left(\begin{array}{c}{\tilde{g}}_{12}^{‴}\\ {\tilde{g}}_{13}^{‴}\end{array}\right)={\Xi }^{\prime }\left(\begin{array}{c}{t}_2\\ t_3\\ 1\end{array}\right).$$

Lemma A3.

Under the condition

$$\left({\mathcal{H}}_2\right):{\beta }_{12,22}^{\prime }\ne 0,{\beta }_{13,33}^{\prime }\ne 0,{\xi }_{14}^{\prime }\ne 0,$$

the system (A3) are equivalent to

$${\tilde{g}}_1^{\prime }={\tilde{g}}_{12}^{‴}={\tilde{g}}_{13}^{‴}=0.$$

(A10)

Proof. 

It is obvious from (A7) and (A8) that (A3) implies (A10). Conversely suppose that (A10) holds true. Then from (A7) and (A8) we have

$$0=\left(\frac{2{\beta }_{1,23}^{\prime }}{{\beta }_{12,22}^{\prime }}{t}_3+\frac{{\xi }_{11}}{{\xi }_{41}}\right){\tilde{g}}_{12}^{\prime }+\frac{{\xi }_{12}}{{\xi }_{52}}{\tilde{g}}_{13}^{\prime },0=\frac{{\xi }_{21}}{{\xi }_{41}}{\tilde{g}}_{12}^{\prime }+\left(\frac{2{\beta }_{1,23}^{\prime }}{{\beta }_{13,33}^{\prime }}{t}_2+\frac{{\xi }_{22}}{{\xi }_{52}}\right){\tilde{g}}_{13}^{\prime }.$$

Since $t_2,t_3$ satisfies ${\tilde{g}}_1^{\prime }=0$, the determinant

$$\left|\begin{array}{cc}\frac{2{\beta }_{1,23}^{\prime }}{{\beta }_{12,22}^{\prime }}{t}_3+\frac{{\xi }_{11}}{{\xi }_{41}}& \frac{{\xi }_{12}}{{\xi }_{52}}\\ \frac{{\xi }_{21}}{{\xi }_{41}}& \frac{2{\beta }_{1,23}^{\prime }}{{\beta }_{13,33}^{\prime }}{t}_2+\frac{{\xi }_{22}}{{\xi }_{52}}\end{array}\right|\equiv -\frac{2{\beta }_{1,23}^{\prime }{\xi }_{14}^{\prime }}{{\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }}$$

(A11)

does not vanish by hypothesis. Hence, we obtain ${\tilde{g}}_{12}^{\prime }={\tilde{g}}_{13}^{\prime }=0.$ □

One can also express $t_3{\tilde{g}}_{12}^{‴}$ and $t_3{\tilde{g}}_{13}^{‴}$ as linear combination of the basis $\mathcal{X}$:

Lemma A4.

$$\begin{array}{cc}\hfill t_3{\tilde{g}}_{12}^{‴}& =t_3({\xi }_{14}^{\prime }{t}_2+{\xi }_{15}^{\prime }{t}_3+{\xi }_{16}^{\prime })\hfill \\ \hfill & =t_2{t}_3{\tilde{g}}_1^{\prime }-\frac{2{\beta }_{1,23}^{\prime }}{{\beta }_{12,22}^{\prime }}{t}_3^2{\tilde{g}}_{12}^{\prime }-\frac{{\xi }_{13}}{{\xi }_{33}}{t}_3{\tilde{g}}_1^{\prime }-\frac{{\xi }_{11}}{{\xi }_{41}}{t}_3{\tilde{g}}_{12}^{\prime }-\frac{{\xi }_{12}}{{\xi }_{52}}{t}_3{\tilde{g}}_{13}^{\prime },\hfill \\ \hfill t_3{\tilde{g}}_{13}^{‴}& =t_3({\xi }_{24}^{\prime }{t}_2+{\xi }_{25}^{\prime }{t}_3+{\xi }_{26}^{\prime })\hfill \\ \hfill & =t_3^2{\tilde{g}}_1^{\prime }-\frac{2{\beta }_{1,23}^{\prime }}{{\beta }_{13,33}^{\prime }}{t}_2{t}_3{\tilde{g}}_{13}^{\prime }-\frac{{\xi }_{23}}{{\xi }_{33}}{t}_3{\tilde{g}}_1^{\prime }-\frac{{\xi }_{21}}{{\xi }_{41}}{t}_3{\tilde{g}}_{12}^{\prime }-\frac{{\xi }_{22}}{{\xi }_{52}}{t}_3{\tilde{g}}_{13}^{\prime }\hfill \\ \hfill & =-\left\{\frac{2{\beta }_{13,2}^{\prime }}{{\beta }_{13,33}^{\prime }}{t}_2+\left(\frac{2{\beta }_{13,3}^{\prime }}{{\beta }_{13,33}^{\prime }}+\frac{{\xi }_{23}}{{\xi }_{33}}\right)t_3+\frac{{\beta }_{13,\varnothing }^{\prime }}{{\beta }_{13,33}^{\prime }}\right\}{\tilde{g}}_1^{\prime }-\frac{{\xi }_{21}}{{\xi }_{41}}{t}_3{\tilde{g}}_{12}^{\prime }\hfill \\ \hfill & +\frac{2{\beta }_{1,2}^{\prime }{t}_2+(2{\beta }_{1,3}^{\prime }-{\xi }_{22})t_3+{\beta }_{1,\varnothing }^{\prime }}{{\beta }_{13,33}^{\prime }}{\tilde{g}}_{13}^{\prime }.\hfill \end{array}$$

Definition A2.

Macaulay’s diagram Y $5\times 5$ corresponding to ${\tilde{g}}_1^{\prime },{\tilde{g}}_{12}^{‴},{\tilde{g}}_{13}^{‴},t_3{\tilde{g}}_{12}^{‴},t_3{\tilde{g}}_{13}^{‴},$ is defined by

$$\left(\begin{array}{c}{\tilde{g}}_1^{\prime }\\ {\tilde{g}}_{12}^{‴}\\ {\tilde{g}}_{13}^{‴}\\ t_3{\tilde{g}}_{12}^{‴}\\ t_3{\tilde{g}}_{13}^{‴}\end{array}\right)=Y\left(\begin{array}{c}{t}_3^2\\ t_2{t}_3\\ t_2\\ t_3\\ 1\end{array}\right),\mathrm{where}Y=\left(\begin{array}{ccccc}0& {\xi }_{33}& {\xi }_{34}& {\xi }_{35}& {\xi }_{36}\\ 0& 0& {\xi }_{14}^{\prime }& {\xi }_{15}^{\prime }& {\xi }_{16}^{\prime }\\ 0& 0& {\xi }_{24}^{\prime }& {\xi }_{25}^{\prime }& {\xi }_{26}^{\prime }\\ {\xi }_{15}^{\prime }& {\xi }_{14}^{\prime }& 0& {\xi }_{16}^{\prime }& 0\\ {\xi }_{25}^{\prime }& {\xi }_{24}^{\prime }& 0& {\xi }_{26}^{\prime }& 0\end{array}\right).$$

Let $U_1$ be function specified by

$$U_1:=\frac{\partial ({\tilde{g}}_{12}^{‴},{\tilde{g}}_{13}^{‴})}{\partial (t_2,t_3)}=\left|\begin{array}{cc}{\xi }_{14}^{\prime }& {\xi }_{15}^{\prime }\\ {\xi }_{24}^{\prime }& {\xi }_{25}^{\prime }\end{array}\right|=\frac{\Xi \left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 1& 2& 3& 4& 5\end{array}\right)}{{\xi }_{33}{\xi }_{41}{\xi }_{52}},$$

where the minor determinants of order l for the matrix $\Xi =\left({\xi }_{jk}\right)$ given in (A6) are defined as

$$\Xi \left(\begin{array}{cccc}{j}_1& j_2& \cdots & j_l\\ k_1& k_2& \cdots & k_l\end{array}\right):=det{\left({\xi }_{j_p{k}_q}\right)}_{p,q=1,2,\dots ,l}$$

for $1\le j_1<j_2<\cdots <j_l\le 5$ and $1\le k_1<k_2<\cdots <k_l\le 6$.

Lemma A5.

Suppose that $U_1$ never vanishes at any point of $\tilde{\mathcal{C}}$. Then the equations

$${\tilde{g}}_{12}^{‴}={\tilde{g}}_{13}^{‴}=0$$

concerning $t_2,t_3$ can be uniquely solved by

$$({\omega }_2,{\omega }_3):t_2=\frac{U_2}{U_1},t_3=\frac{U_3}{U_1},$$

which defines a rational curve interpolating $\tilde{\mathcal{C}}$, where

$$\begin{array}{cc}\hfill & U_2=\left|\begin{array}{cc}{\xi }_{15}^{\prime }& {\xi }_{16}^{\prime }\\ {\xi }_{25}^{\prime }& {\xi }_{26}^{\prime }\end{array}\right|=\frac{\Xi \left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 1& 2& 3& 5& 6\end{array}\right)}{{\xi }_{33}{\xi }_{41}{\xi }_{52}},\hfill \\ \hfill & U_3=-\left|\begin{array}{cc}{\xi }_{14}^{\prime }& {\xi }_{16}^{\prime }\\ {\xi }_{24}^{\prime }& {\xi }_{26}^{\prime }\end{array}\right|=-\frac{\Xi \left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 1& 2& 3& 4& 6\end{array}\right)}{{\xi }_{33}{\xi }_{41}{\xi }_{52}}.\hfill \end{array}$$

The associated characteristic function $\psi =\psi \left(t_1\right)$ given by

$$\psi :={\tilde{g}}_1^{\prime }\left(t_1,\frac{U_2}{U_1},\frac{U_3}{U_1}\right)U_1^2$$

equals

$$\psi =-detY={\xi }_{33}{U}_2{U}_3+{\xi }_{34}{U}_2{U}_1+{\xi }_{35}{U}_3{U}_1+{\xi }_{36}{U}_1^2.$$

(A12)

Furthermore Lemma A3 shows that if $U_1$ is finite and $U_1\ne 0$ at all points of $\tilde{\mathcal{C}}$ then (A3) holds if and only if $\psi \left(t_1\right)=0$.

Lemma A6.

The system of (ordered) polynomials (denoted by $\mathcal{Y}$) is obtained from $\mathcal{X}$ after exchanging $\{{\mathbf{x}}_3,{\mathbf{x}}_{11},{\mathbf{x}}_{13},{\mathbf{x}}_{14}\}$ for $\{{\mathbf{y}}_{12},{\mathbf{y}}_{13},{\mathbf{y}}_{14},{\mathbf{y}}_{15}\}$

$$\begin{array}{cc}\hfill \mathcal{Y}& :=\left(\mathcal{X}-\{{\mathbf{x}}_3,{\mathbf{x}}_{11},{\mathbf{x}}_{13},{\mathbf{x}}_{14}\}\right)\cup \{{\mathbf{y}}_{12},{\mathbf{y}}_{13},{\mathbf{y}}_{14},{\mathbf{y}}_{15}\}=\left\{{\mathbf{y}}_1,{\mathbf{y}}_2,\dots ,{\mathbf{y}}_{15}\right\},\hfill \end{array}$$

where

$${\mathbf{y}}_{12}:={\tilde{g}}_{12}^{‴},{\mathbf{y}}_{13}:={\tilde{g}}_{13}^{‴},{\mathbf{y}}_{14}:=t_3{\tilde{g}}_{12}^{‴},{\mathbf{y}}_{15}:=t_3{\tilde{g}}_{13}^{‴}$$

and ${\mathbf{y}}_j$ are connected with ${\mathbf{x}}_k$ by the matrix $\mathcal{T}$:

$$\mathcal{T}:\left\{\begin{array}{c}{\mathbf{y}}_j={\mathbf{x}}_j(1\le j\le 2),\hfill \\ {\mathbf{y}}_j={\mathbf{x}}_{j+1}(3\le j\le 9),\hfill \\ {\mathbf{y}}_{10}={\mathbf{x}}_{15},\hfill \\ {\mathbf{y}}_{11}={\mathbf{x}}_{12}\hfill \\ {\mathbf{y}}_{12}\equiv c_2{\mathbf{x}}_{11}+{\mathbf{x}}_{13}mod({\mathbf{x}}_8,{\mathbf{x}}_{10},{\mathbf{x}}_{12}),\hfill \\ {\mathbf{y}}_{13}\equiv c_3{\mathbf{x}}_{11}+{\mathbf{x}}_{14}mod({\mathbf{x}}_9,{\mathbf{x}}_{10},{\mathbf{x}}_{12}),\hfill \\ {\mathbf{y}}_{14}\equiv c_1{\mathbf{x}}_3+{\mathbf{x}}_{15}mod({\mathbf{x}}_7,{\mathbf{x}}_8,{\mathbf{x}}_{14}),\hfill \\ {\mathbf{y}}_{15}\equiv c_4{\mathbf{x}}_{11}+c_5{\mathbf{x}}_{13}+c_6{\mathbf{x}}_{14}mod({\mathbf{x}}_7,{\mathbf{x}}_8,{\mathbf{x}}_9,{\mathbf{x}}_{12})\hfill \end{array}\right.$$

such that

$$c_1=-\frac{2{\beta }_{1,23}^{\prime }}{{\beta }_{12,22}^{\prime }},c_2=-\frac{{\xi }_{12}}{{\xi }_{52}},c_3=-\frac{{\xi }_{22}}{{\xi }_{52}},c_4=\frac{{\beta }_{1,\varnothing }^{\prime }}{{\beta }_{13,33}^{\prime }},c_5=-\frac{2{\beta }_{13,2}^{\prime }}{{\beta }_{13,33}^{\prime }},c_6=\frac{2{\beta }_{13,3}^{\prime }}{{\beta }_{13,33}^{\prime }}+\frac{{\xi }_{23}}{{\xi }_{33}},$$

and

$$det\mathcal{T}=c_1(c_4-c_2{c}_5-c_3{c}_6)=-\frac{2{\beta }_{1,23}^{\prime }{\xi }_{14}^{\prime }}{{\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }}.$$

(A13)

In other words,

$$\mathcal{Y}=\mathcal{T}\mathcal{X}$$

and hence

$$det\mathcal{Y}=det\mathcal{T}det\mathcal{X}.$$

(A14)

The ordered system ${\left({\mathbf{y}}_j\right)}_{1\le j\le 15}$ are linearly independent and span the linear space of polynomials at most fourth degree.

On the other hand

Lemma A7.

Macaulay’s diagram associated with the system $\mathcal{Y}$

$$\mathcal{Y}:={}^T({\mathbf{y}}_1,{\mathbf{y}}_2,\dots ,{\mathbf{y}}_{15})$$

is given as follows (each sum is expressed in the ordering (A4)):

$$\begin{array}{ccc}& & {\mathbf{y}}_1=t_2^2{\tilde{g}}_{12}^{\prime }={\beta }_{12.22}^{\prime }{t}_2^4+\cdots \left(lower order terms\right),\hfill \\ & & {\mathbf{y}}_2=t_2{t}_3{\tilde{g}}_{12}^{\prime }={\beta }_{12,22}^{\prime }{t}_2^3{t}_3+\cdots ,\hfill \\ & & {\mathbf{y}}_3=t_2{t}_3{\tilde{g}}_{13}^{\prime }={\beta }_{13,33}^{\prime }{t}_2{t}_3^3+\cdots ,\hfill \\ & & {\mathbf{y}}_4=t_3^2{\tilde{g}}_{13}^{\prime }={\beta }_{13,33}^{\prime }{t}_3^4+\cdots ,\hfill \\ & & {\mathbf{y}}_5=t_2{\tilde{g}}_{12}^{\prime }={\beta }_{12,22}^{\prime }{t}_2^3+\cdots ,\hfill \\ & & {\mathbf{y}}_6=t_3{\tilde{g}}_{13}^{\prime }={\beta }_{13,33}^{\prime }{t}_3^3+\cdots ,\hfill \\ & & {\mathbf{y}}_7=t_3{\tilde{g}}_{12}^{\prime }={\beta }_{12,22}^{\prime }{t}_2^2{t}_3+\cdots ,\hfill \\ & & {\mathbf{y}}_8=t_2{\tilde{g}}_{13}^{\prime }={\beta }_{13,33}^{\prime }{t}_2{t}_3^2+\cdots ,\hfill \\ & & {\mathbf{y}}_9={\tilde{g}}_{12}^{\prime }={\beta }_{12,22}^{\prime }{t}_2^2+\cdots ,\hfill \\ & & {\mathbf{y}}_{10}=t_2{t}_3{\tilde{g}}_1^{\prime }=2{\beta }_{1,23}^{\prime }{t}_2^2{t}_3^2+2{\beta }_{1,2}^{\prime }{t}_2^2{t}_3+2{\beta }_{1,3}^{\prime }{t}_2{t}_3^2+{\beta }_{1,\varnothing }^{\prime }{t}_2{t}_3,\hfill \\ & & {\mathbf{y}}_{11}={\tilde{g}}_1^{\prime }=2{\beta }_{1,23}^{\prime }{t}_2{t}_3+2{\beta }_{1,2}^{\prime }{t}_2+2{\beta }_{1,3}^{\prime }{t}_3+{\beta }_{1,\varnothing }^{\prime },\hfill \\ & & {\mathbf{y}}_{12}={\tilde{g}}_{12}^{‴}={\xi }_{14}^{\prime }{t}_2+{\xi }_{15}^{\prime }{t}_3+{\xi }_{16}^{\prime },\hfill \\ & & {\mathbf{y}}_{13}={\tilde{g}}_{13}^{‴}={\xi }_{24}^{\prime }{t}_2+{\xi }_{25}^{\prime }{t}_3+{\xi }_{26}^{\prime },\hfill \\ & & {\mathbf{y}}_{14}=t_3{\tilde{g}}_{12}^{‴}={\xi }_{15}^{\prime }{t}_3^2+{\xi }_{14}^{\prime }{t}_2{t}_3+{\xi }_{16}^{\prime }{t}_3,\hfill \\ & & {\mathbf{y}}_{15}=t_3{\tilde{g}}_{13}^{‴}={\xi }_{25}^{\prime }{t}_3^2+{\xi }_{24}^{\prime }{t}_2{t}_3+{\xi }_{26}^{\prime }{t}_3.\hfill \end{array}$$

so that

$$det\mathcal{Y}=2{\beta }_{1,23}^{\prime }{\left({\beta }_{12,22}^{\prime }\right)}^5{\left({\beta }_{13,33}^{\prime }\right)}^{4}detY.$$

(A15)

Hence, (A5), (A13), (A14) and (A15) imply the following identity:

Proposition A1.

ψ is related with the resultant $R({\tilde{g}}_{12}^{\prime },{\tilde{g}}_{13}^{\prime },{\tilde{g}}_1^{\prime })$ as follows:

$$\psi =-\frac{{\xi }_{14}^{\prime }}{{\left({\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }\right)}^4}R({\tilde{g}}_{12}^{\prime },{\tilde{g}}_{13}^{\prime },{\tilde{g}}_1^{\prime }),$$

where ${\xi }_{14}^{\prime }$ is given by (A9).

The determinant identity (A11) in the proof of Lemma A3 shows

Lemma A8.

$$d{\tilde{g}}_1^{\prime }\wedge d{\tilde{g}}_{12}^{‴}\wedge d{\tilde{g}}_{13}^{‴}\equiv -\frac{2{\beta }_{1,23}^{\prime }{\xi }_{14}^{\prime }}{{\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }}d{\tilde{g}}_1^{\prime }\wedge d{\tilde{g}}_{12}^{\prime }\wedge d{\tilde{g}}_{13}^{\prime }modAnn\left(\tilde{\mathcal{C}}\right).$$

(A16)

Proof. 

Indeed in view of (A7)–(A9)

$$\begin{array}{ccc}& & \mathrm{The} \mathrm{left}\text{-}\mathrm{hand} \mathrm{side} of \left(\mathsf{A}16\right)\hfill \\ & & \equiv \frac{1}{{\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }}\left|\begin{array}{cc}2{\beta }_{1,23}^{\prime }{t}_3+{\xi }_{11}& {\xi }_{12}\\ {\xi }_{21}& 2{\beta }_{1,23}^{\prime }{t}_2+{\xi }_{22}\end{array}\right|d{\tilde{g}}_1^{\prime }\wedge d{\tilde{g}}_{12}^{\prime }\wedge d{\tilde{g}}_{13}^{\prime }\hfill \\ & & \equiv -\frac{2{\beta }_{1,23}^{\prime }{\xi }_{14}^{\prime }}{{\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }}d{\tilde{g}}_1^{\prime }\wedge d{\tilde{g}}_{12}^{\prime }\wedge d{\tilde{g}}_{13}^{\prime }modAnn\left(\tilde{\mathcal{C}}\right)\hfill \end{array}$$

since ${\tilde{g}}_1^{\prime }\equiv 0$. □

We now assume that

$${\displaystyle \left({\mathcal{H}}_3\right):U_1=\frac{\partial ({\tilde{g}}_{12}^{‴},{\tilde{g}}_{13}^{‴})}{\partial (t_2,t_3)}\mathrm{does} \mathrm{not} \mathrm{have} \mathrm{any} \mathrm{zero} \mathrm{or} \mathrm{pole} \mathrm{at} \tilde{\mathcal{C}}.}$$

Then, we finally obtain the following fundamental equality:

Proposition A2.

Suppose that the conditions $\left({\mathcal{H}}_0\right)$, $\left({\mathcal{H}}_2\right)$ and $\left({\mathcal{H}}_3\right)$ are satisfied. Then,

$$t=(t_1,\frac{U_2}{U_1},\frac{U_3}{U_1})\in \tilde{\mathcal{C}}ifandonlyif\psi \left(t_1\right)=0,$$

and

$$\frac{\partial ({\tilde{g}}_1,{\tilde{g}}_{12},{\tilde{g}}_{13})}{\partial (t_1,t_2,t_3)}\equiv -\frac{{\beta }_{12,22}^{\prime }{\beta }_{13,33}^{\prime }}{2{\beta }_{1,23}^{\prime }{\xi }_{14}^{\prime }}\frac{\partial ({\tilde{g}}_1^{\prime },{\tilde{g}}_{12}^{‴},{\tilde{g}}_{13}^{‴})}{\partial (t_1,t_2,t_3)}modAnn\left(\tilde{\mathcal{C}}\right),$$

(A17)

where

$$\frac{\partial ({\tilde{g}}_1^{\prime },{\tilde{g}}_{12}^{‴},{\tilde{g}}_{13}^{‴})}{\partial (t_1,t_2,t_3)}\equiv \frac{1}{U_1}\frac{d\psi }{d{t}_1}modAnn\left(\tilde{\mathcal{C}}\right).$$

(A18)

Proof. 

Equation (A17) is a direct consequence of Lemmas A1 and A8. On the other hand, by a direct calculation, we have the identity

$$\frac{\partial ({\tilde{g}}_1^{\prime },{\tilde{g}}_{12}^{‴},{\tilde{g}}_{13}^{‴})}{\partial (t_1,t_2,t_3)}\equiv \frac{1}{U_1^2}\frac{d\psi }{d{t}_1}·\frac{\partial ({\tilde{g}}_{12}^{‴},{\tilde{g}}_{13}^{‴})}{\partial (t_2,t_3)}modAnn\left(\tilde{\mathcal{C}}\right).$$

This means (A18) in view of (A12). □