Applications of Energy-Based Evaluation Method of Element Importance to Grid Structures

Abstract

It is necessary to perform the robustness design for the progressive collapse resistance of grid structures. However, there is a lack of a comprehensive index to evaluate the member importance. An evaluation method on element importances is proposed based on the element strain energy and element removal technology. The element importance coefficients can be calculated based on the change of strain energy vectors after the removal of analyzed elements using ANSYS. The influence of the loading pattern, boundary condition, and geometric parameters of square pyramid grid structures are investigated. Moreover, the other three types of spatial grids are introduced to explore the difference in element importance distributions. The considerable difference in element importance coefficient distribution for different grid structures shows that it is essential to establish a general program for rapid model robustness analysis. This principle in this work can be easily integrated into the existing design and analysis platform to make up for this shortcoming.

1. Introduction

Over recent decades, with the sudden increase of accidents and terrorist activities, some progressive collapse accidents have occurred, causing serious casualties, property losses, and social impacts [1,2,3,4]. The safety of the structure has drawn paramount attention. The study of structural progressive collapse resistance has become a hot topic in research worldwide [5,6,7,8,9,10,11].

However, most of these research outputs are focused on frame structures, and there are fewer studies on the progressive collapse of space structures. A 3D finite element model of a double-layer space structure grid was built to investigate structural behavior, and several collapse scenarios were examined following the alternative path method defined in GSA [12]. The anti-progressive collapse mechanism of long-span single-layer spatial grid structures was investigated by constructing a model of substructures with eight full-scale test specimens [13]. A method, including kinked steel pipe reinforcement and extra member reinforcement, was proposed to improve the resistance of a single-layer spatial grid structure [14]. A review of the main advances made in the 21st century in the field of robustness and progressive collapse of building structures was carried out by Adam et al. [15]. This review pointed out that some areas still required deeper study, such as the evaluation of structures and decision making after a failure.

Understanding the behavior of structural elements is the basis for studying structural robustness. The structural robustness here refers to the performance of the structure against the impact of sudden events and the progressive collapse. It is easier to explain the safety of the structure under the impact load with small probability, but serious consequences [16]. The importance index of the element can reflect not only the impact of individual element damage caused by sudden incidents on the overall structural performance, but also one of the key points of the analysis of load path analysis. The element importance is not only related to the properties of the structure itself, but also to the external loads that the structure is subjected to. Wu et al. [17,18,19] proposed the theory of the structural vulnerability assessment. Then, an assessment method based on the sensitivity analysis was established by Pandey [16]. The main approach is to calculate the sensitivity coefficient of the structure based on the change of the structure under the initial damage caused by the sudden event. It is found that the structural redundancy is inversely proportional to the sensitivity of the element. Beeby and Institution [20] proposed permissible energy per unit volume based on structural energy. By specifying the lower limit of the allowable damage energy per unit volume limit, the structure ensures a certain deformation capacity of the structure, and no overall collapse occurs in an emergency. Gharaibeh et al. [21] established the system reliability theory on the influence of elements on reliability. The reliability theory is relatively complete and is used in various structural systems to simplify calculations by a large number of data statistics and assumptions of various factors such as load, material, and strength. Izzuddin et al. [22] proposed a simplified approach for the progressive collapse assessment of multi-story building structures, considering sudden column loss as a design scenario, offering, for the first time, a quantitative framework for the consideration of such important issues as ductility, redundancy, and energy absorption. It was found that the determinant of the stiffness matrix of the structure is closely related to the safety of the structure, and the importance coefficient of the element can be defined from the material stiffness matrix of the structure [23]. Based on previous research about the robustness, new theories or methods to element importance have been proposed successfully using new judgment indicators, where most are for frame structures, and a few are for grid structures [24,25,26,27,28,29].

It can be found from the literature that there is a lack of a rapid evaluation method for the robustness of grid structures, which is essential in the conceptual analysis stage after the preliminary design of the grid structures. In this paper, structural strain energy is selected as an index to determine the element importance, which can reflect the influence of geometry, topology and external loads simultaneously. Moreover, element removal technology is introduced to achieve rapid parametric evaluation. The square pyramid space grid is chosen to illustrate the proposed method in Section 3. Then, the distribution of important elements under different load patterns, support conditions, and spatial geometric parameters are studied in Section 4. Three types of spatial grids, diagonal square pyramid grids, bi-orthogonal lattice grids, and bi-orthogonal-diagonal lattice grids, are also chosen to study the influence of the topology on the element importance in Section 5. Section 6 draws the conclusion.

2. Evaluation Method of Element Importance

The accident that results in the progressive collapse of the grid structure is mostly attributable to the structural response to the initial element failure. Therefore, the initial failure is assumed to be one element removed. As the number of elements of the grid structures is large, it is computationally expensive to consider all members to be removed. As a result, a method for determining element importance should be proposed.

2.1. Hypothesis

In structural conceptual design or early design, the approach for evaluating element importance is applied. In this paper, the following hypothesis is assumed.

• Only linear elasticity and geometric nonlinearity are introduced in the analysis, while material damage and structural stability are not taken into account.
• The topological relationship will be modified by the conceptual removal method in the numerical simulation for the initial damage. The additional load and dynamic effects induced by falling and explosion are not included.
• In the event of an accident, the structure is rarely damaged by earthquake and wind loads simultaneously. As a result, only the vertical nodal load is taken into the evaluation.
• The external loads at the nodes are not affected by the failure of elements in the grid structures.

2.2. Element Importance Coefficient

Based on the sensitivity analysis theory [16], the importance coefficient of element i, α_i, is defined as

$${\alpha }_i=\left|1-\frac{{\Vert {\mathit{V}}_{\epsilon }{}_o\Vert }_1}{{\Vert {\mathit{V}}_{\epsilon }{}_{di}\Vert }_1}\right|$$

(1)

where V_εo and V_εdi are the element strain energy vectors of the undamaged structure and damaged structures after removing element i, respectively. The element strain energy can be defined as follows.

$$V_{\epsilon }=\frac{N^{2}l}{2EA}=\frac{EA{\left(\Delta l\right)}^2}{2l}=\frac{1}{2}\sigma \epsilon v=\frac{{\sigma }^{2}v}{2E}=\frac{E{\epsilon }^{2}v}{2}$$

(2)

where N, l and Δl are the axial force, the original length and the length variation of the element, respectively. A and ν are the corresponding section area and volume. Besides, E, ε and σ are the elastic modulus, strain and stress, respectively.

The range of the element importance coefficient α_i is set to be [0, 1]. When α_i is equal to be 0, there is almost no change in the strain energy after removing element i, indicating that the contribution of element i to the load transfer path is very small. A smaller coefficient α_i indicates there are more redundant constraints. It means that after the element is removed, there are more alternative force transmission paths to redistribute the external load to other parts of the structure. On the contrary, a greater importance coefficient α_i represents that the element is a minor subject to redundant constraints. It suggests that fewer force paths can be replaced in the remaining structure, and the load undertaken by the element is difficult to redistribute to other parts of the structure. When the coefficient α_i is close to 1, the deformation of the remaining structure becomes significant. It indicates there is higher stored strain energy.

2.3. Flow Chart of the Method

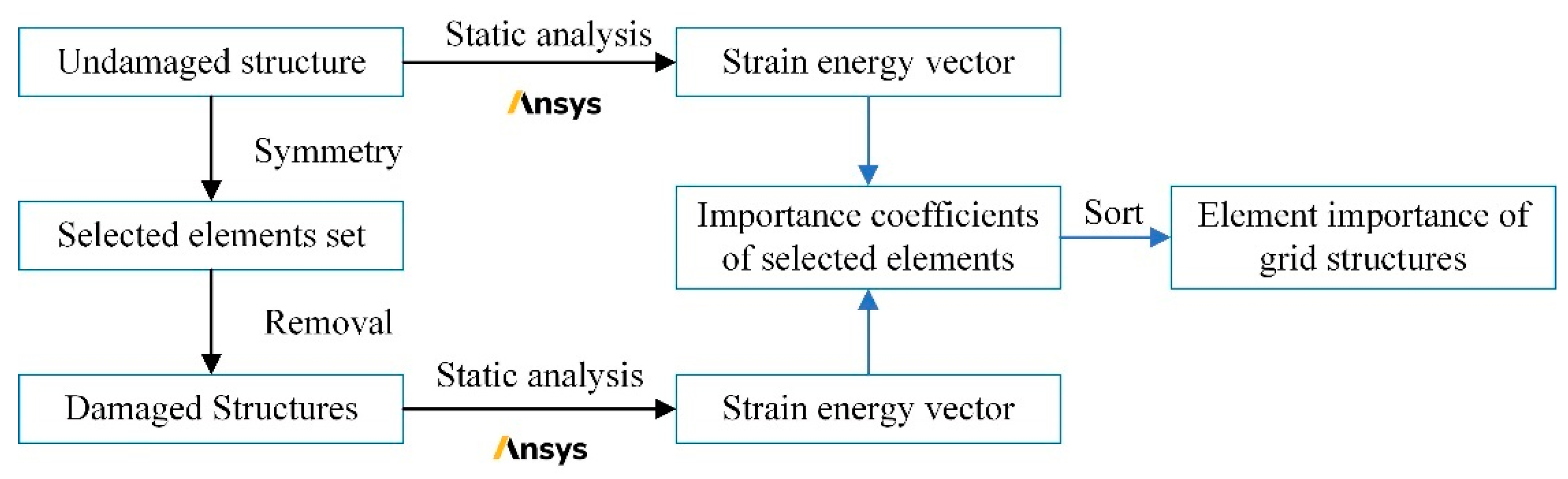
The steps of the evaluation method of element importance based on the strain energy are shown in Figure 1. Firstly, the linear elastic static analysis of the undamaged grid structure is carried out to get the element strain energy vector. Secondly, the elements that need to be evaluated are chosen based on the symmetry of the grid structure. Then, each selected element is removed in turn, and the linear elastic static analysis is performed on the corresponding remaining structure to calculate the strain energy. After that, the important coefficient for each element is obtained based on the method given in this paper. The element importance coefficient can be used to determine the initial loss for the progressive collapse analysis of the grid structures. Moreover, elements with higher importance coefficients could be strengthened to increase the robustness of the structures.

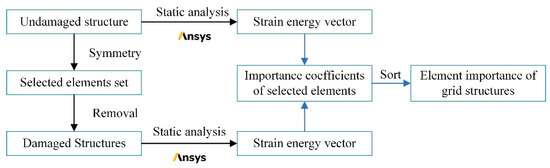
Figure 1. Flow diagram of the evaluation method.

Software ANSYS is chosen for the numerical simulation, and it is easier to establish parametric models of the grid structure using APDL descriptive language. Birth-death element technology is adopted to simulate the removal of the element.

3. Element Importance of Square Pyramid Space Grid Structures

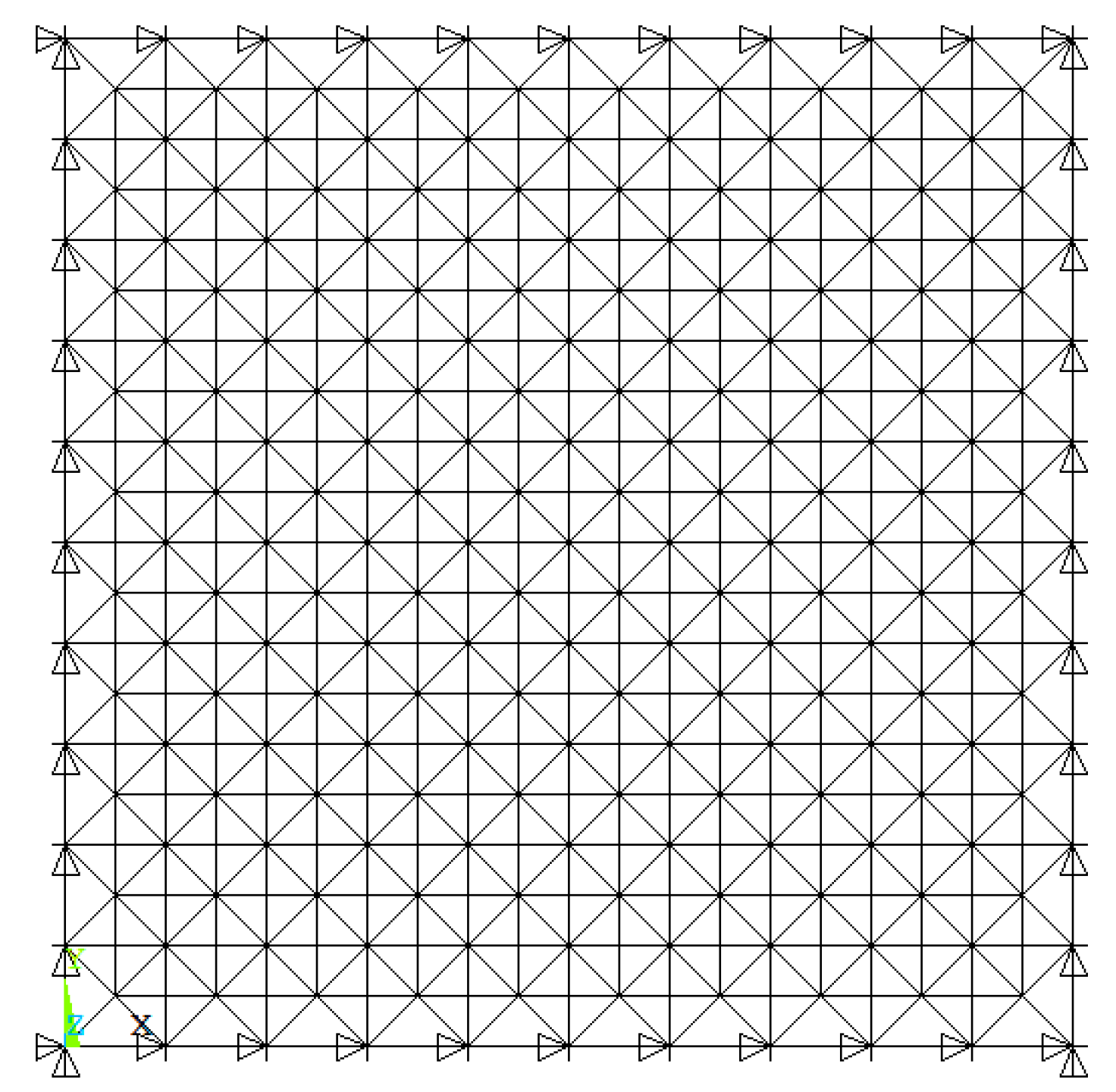
The element importance of a square pyramid space grid structure, depicted in Figure 2, is studied in this section. The planar dimension of the analyzed grid is 40 m × 40 m, with the grid number in both directions of 10 and the grid length of 4 m. The height of the grid structure and the upper chord and lower chord members are steel tubes with Φ159 mm × 8 mm (diameter × thickness), while the diagonal web members are steel tubes with Φ 114 mm × 4 mm (diameter × thickness). Q235 steel is used for the tubes with a Young’s modulus of 2.1 × 10⁵ MPa and Poisson’s ratio of 0.3. The nodal loads applied at the upper nodes include the dead load of 1 kN/m² and the live load of 0.5 kN/m² in the vertical direction. The upper surrounding nodes are fixed in the simulation.

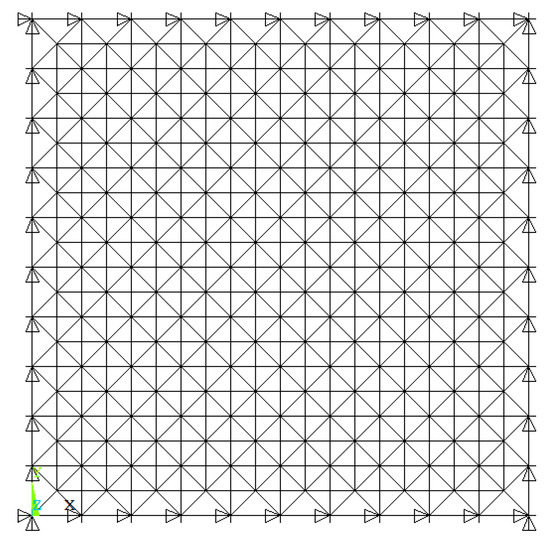
Figure 2. Square pyramid space grid structure.

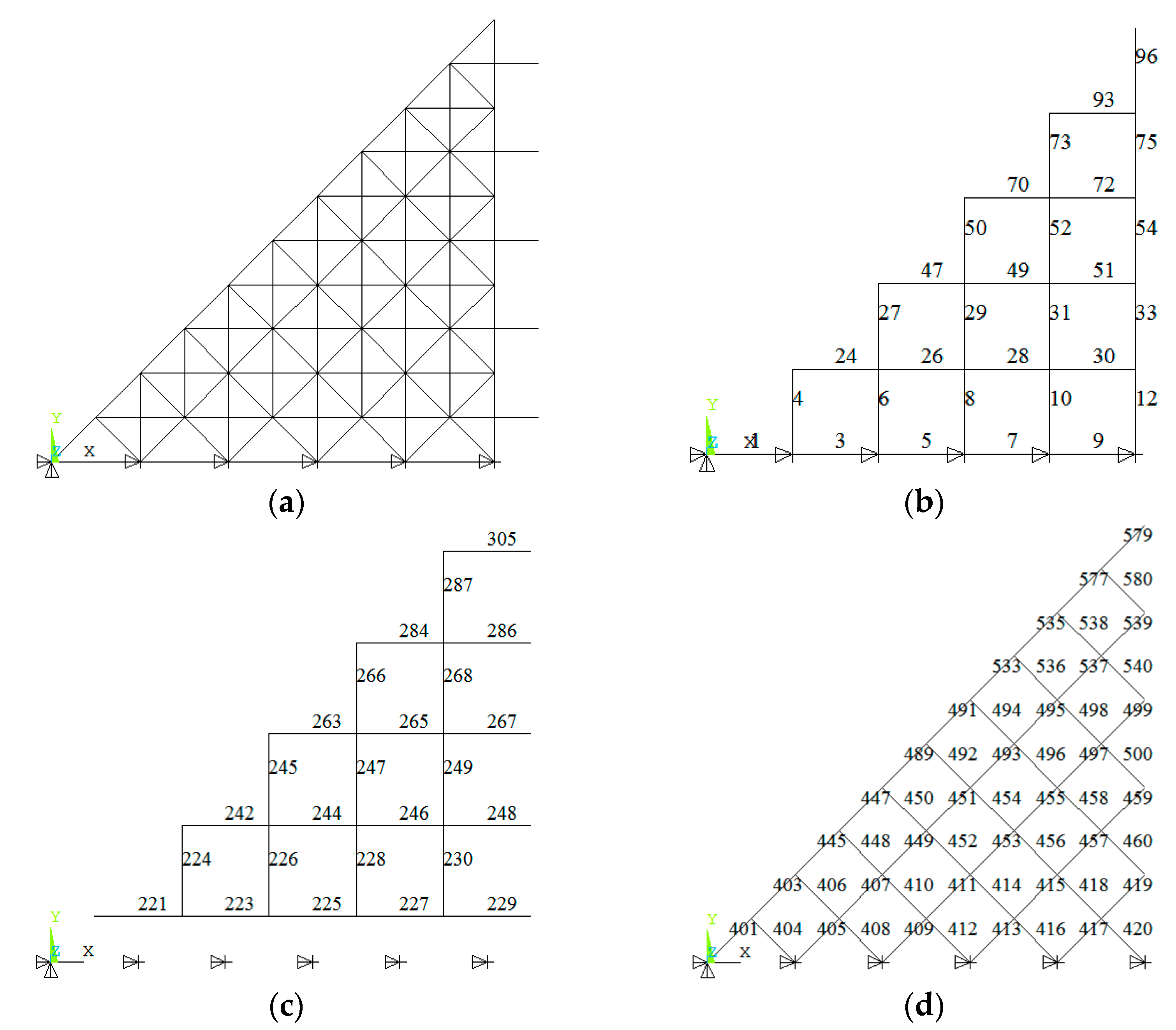
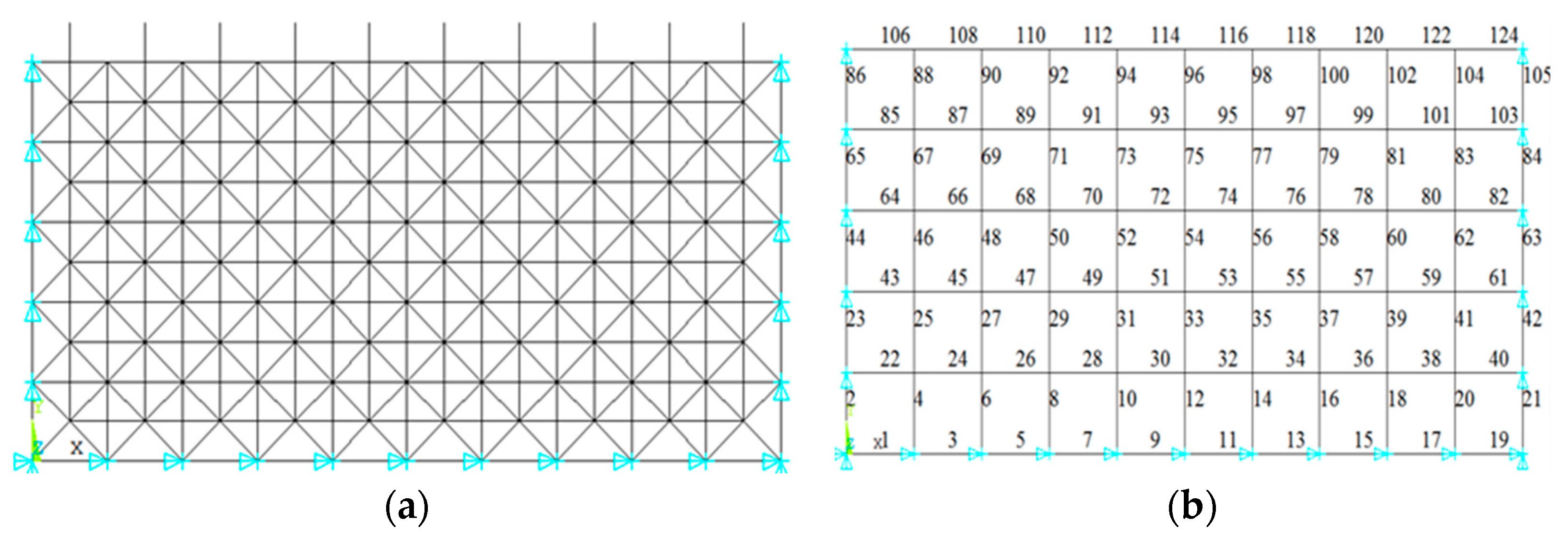
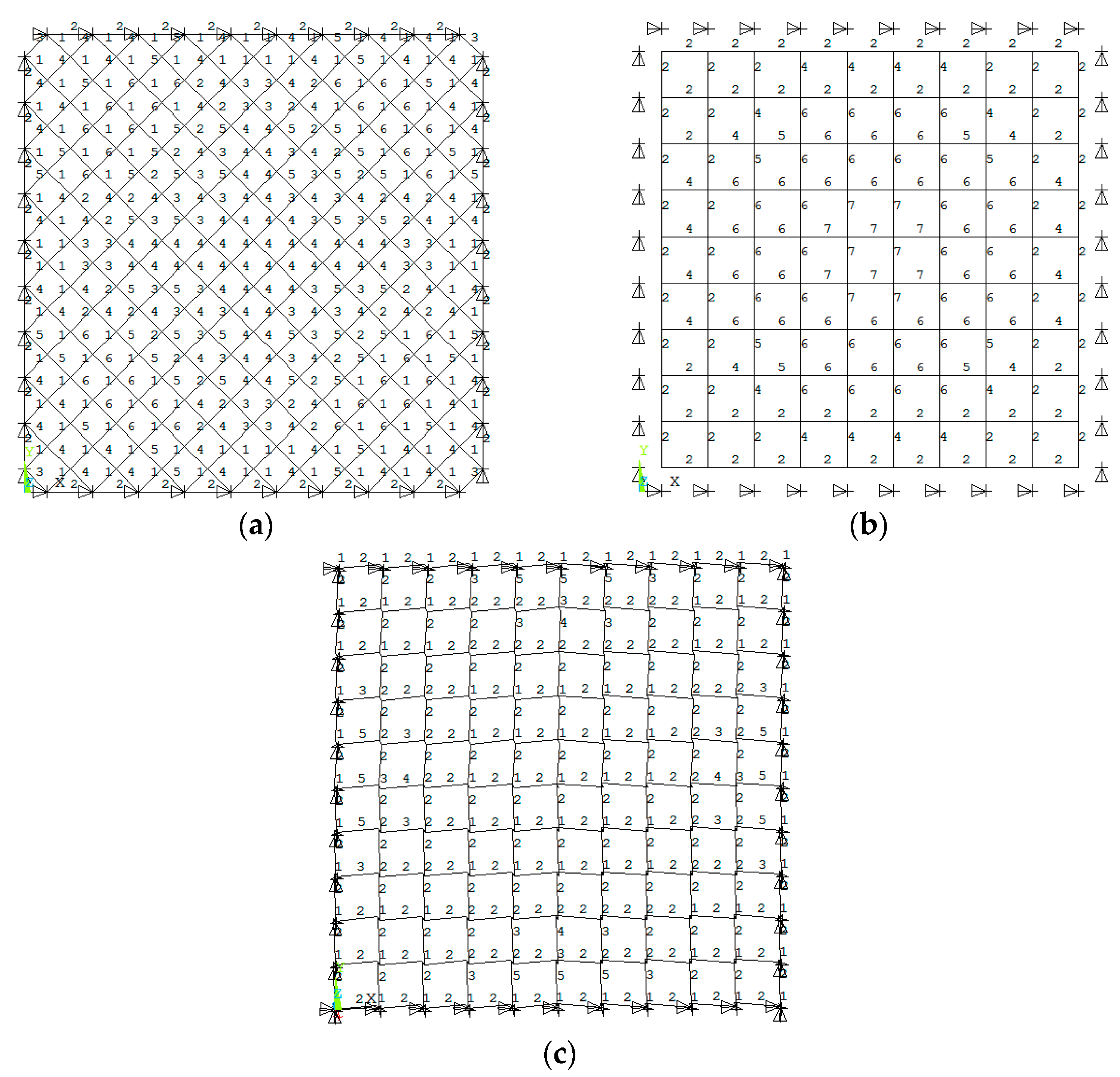
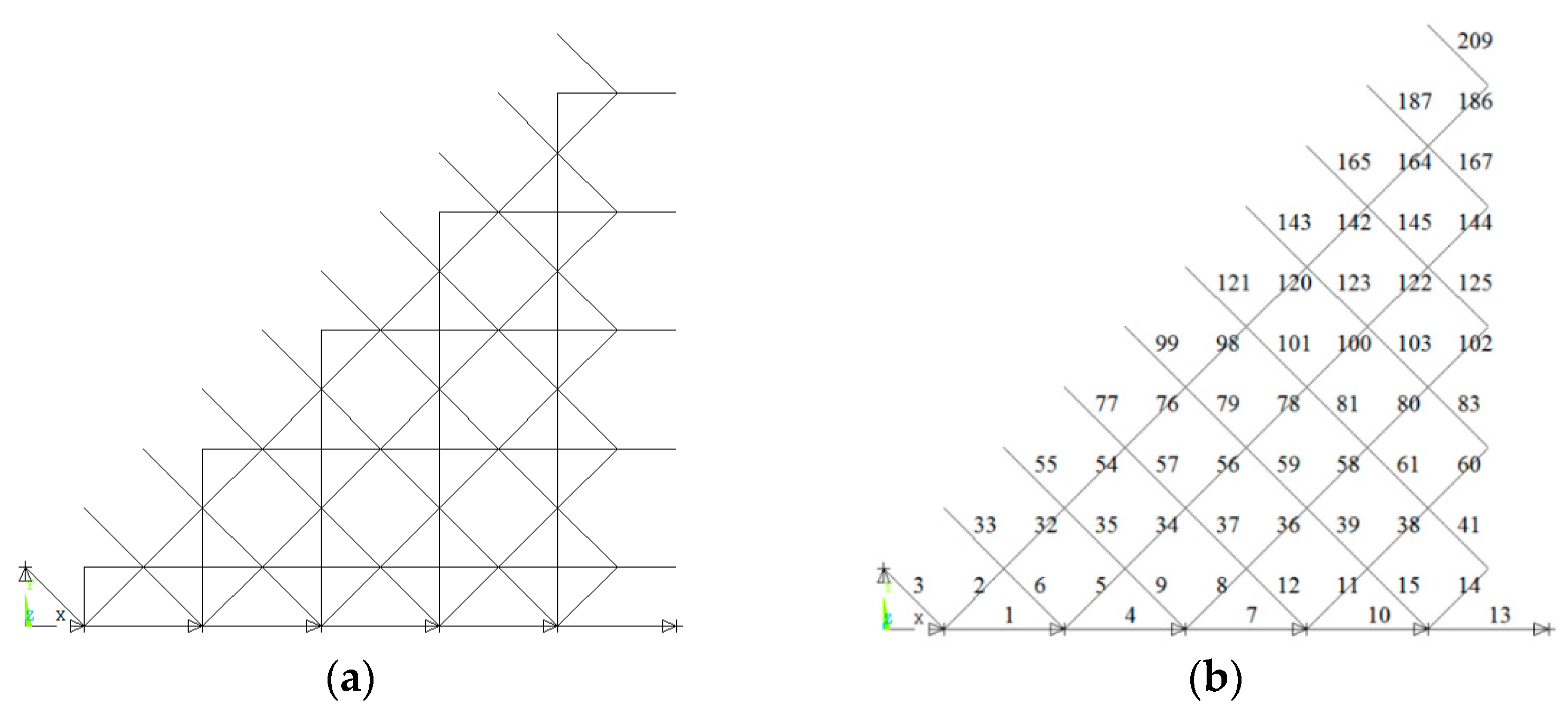
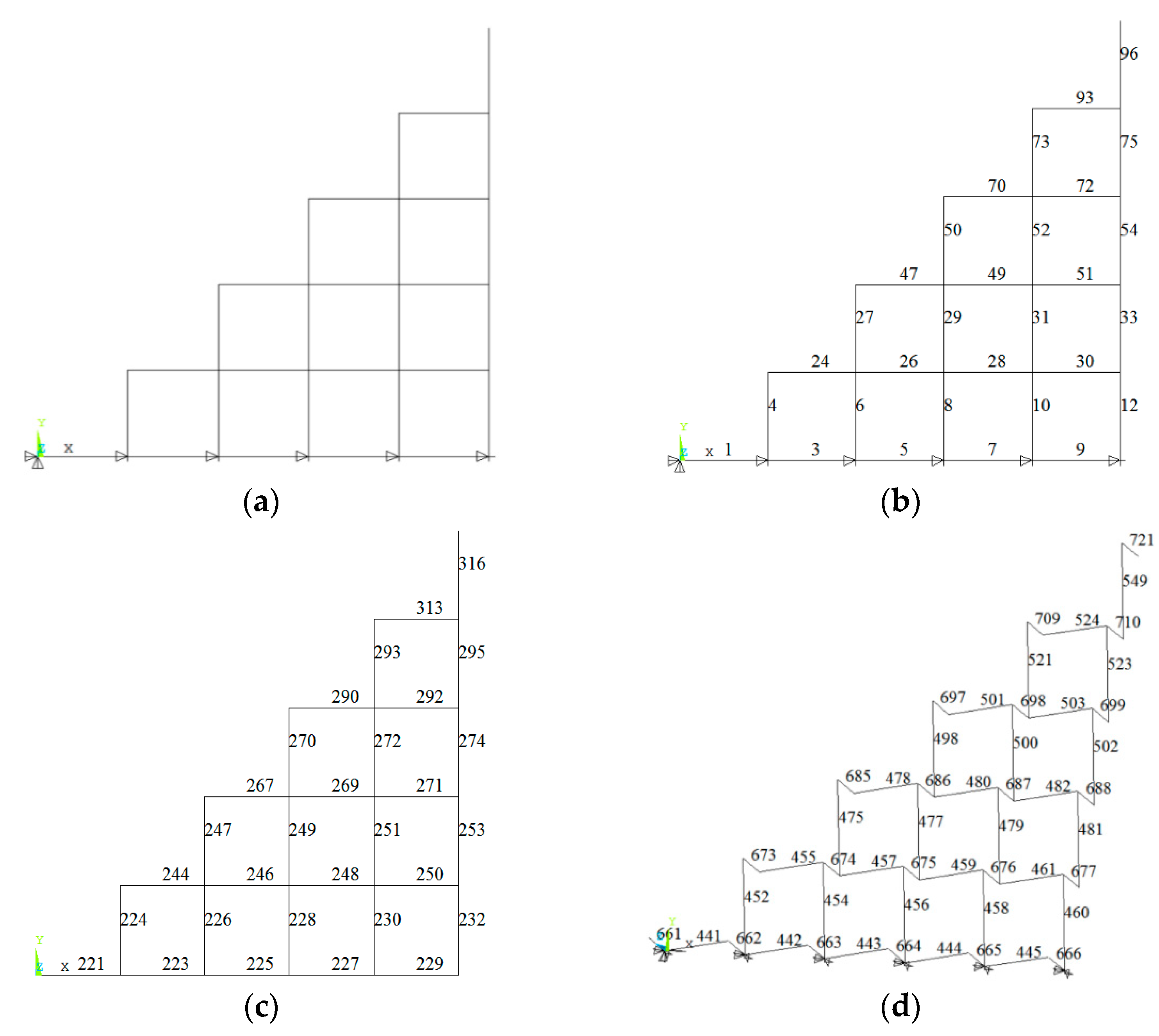
Given the loads and supports, the square pyramid grid structure is axisymmetric and centrally symmetric. Therefore, only an eighth of the structure was used to investigate the element importance, as shown in Figure 3a. The number of top chords, lower chords and diagonal web members are given in Figure 3b–d.

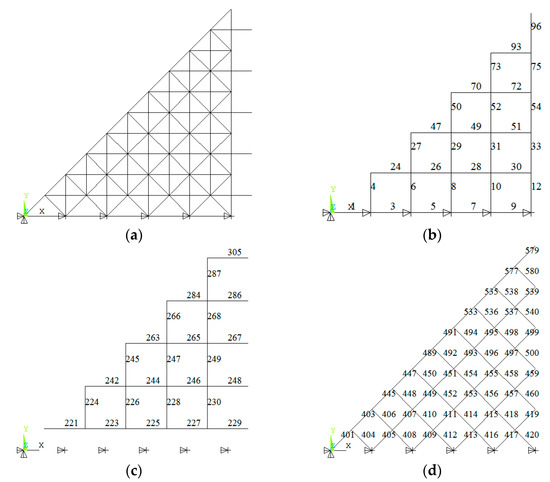
Figure 3. The eighth of structure system and the number of elements. (a) Eighth structure system; (b) number of top chords; (c) number of lower chords; (d) number of diagonal web members.

The results of the element importance of the square pyramid spatial grid structure are described in Table 1. It can be seen that the element importance coefficient is relatively small, ranging from 0 to 0.03256. It indicates that the square pyramid spatial grid structure has good robustness, and it can transfer external loads through many alternative paths. The influence of the loss of one element is slight. The importance coefficient of the lower chord 305 is the largest, and the second-largest is in chord 287. They are located at the center of the lower chord plane. The top chords with high importance coefficients are chords 96 and 93, located at the center, while the important diagonal web members are chords 418 and 419, close to the supports. It denotes that the lower and top chords are more important than the diagonal web members. The lower or top chords farther away from the support are more important. It is similar for the diagonal web members closer to the support.

Table 1. The importance coefficient of the elements for square pyramid spatial grid structures.

Element Number	αi	Element Number	αi	Element Number	αi
27	0.00437	228	0.00649	407	0.00113
29	0.00779	230	0.00766	409	0.00104
31	0.01024	245	0.00905	410	0.00106
33	0.01112	246	0.00615	411	0.00160
47	0.00720	247	0.01391	413	0.00145
49	0.00929	248	0.00647	414	0.00180
50	0.01339	249	0.01672	415	0.00204
51	0.01036	263	0.01308	416	0.00126
52	0.01802	265	0.01569	417	0.00162
54	0.01972	266	0.02062	418	0.00223
70	0.01762	267	0.01658	419	0.00229
72	0.01982	268	0.02510	420	0.00155
73	0.02406	284	0.02501	449	0.00106
75	0.02645	286	0.02652	453	0.00120
93	0.02722	287	0.03066	455	0.00101
96	0.02999	305	0.03256	457	0.00117

4. Influence of Load Pattern and Geometry

4.1. Effects of Load Patterns

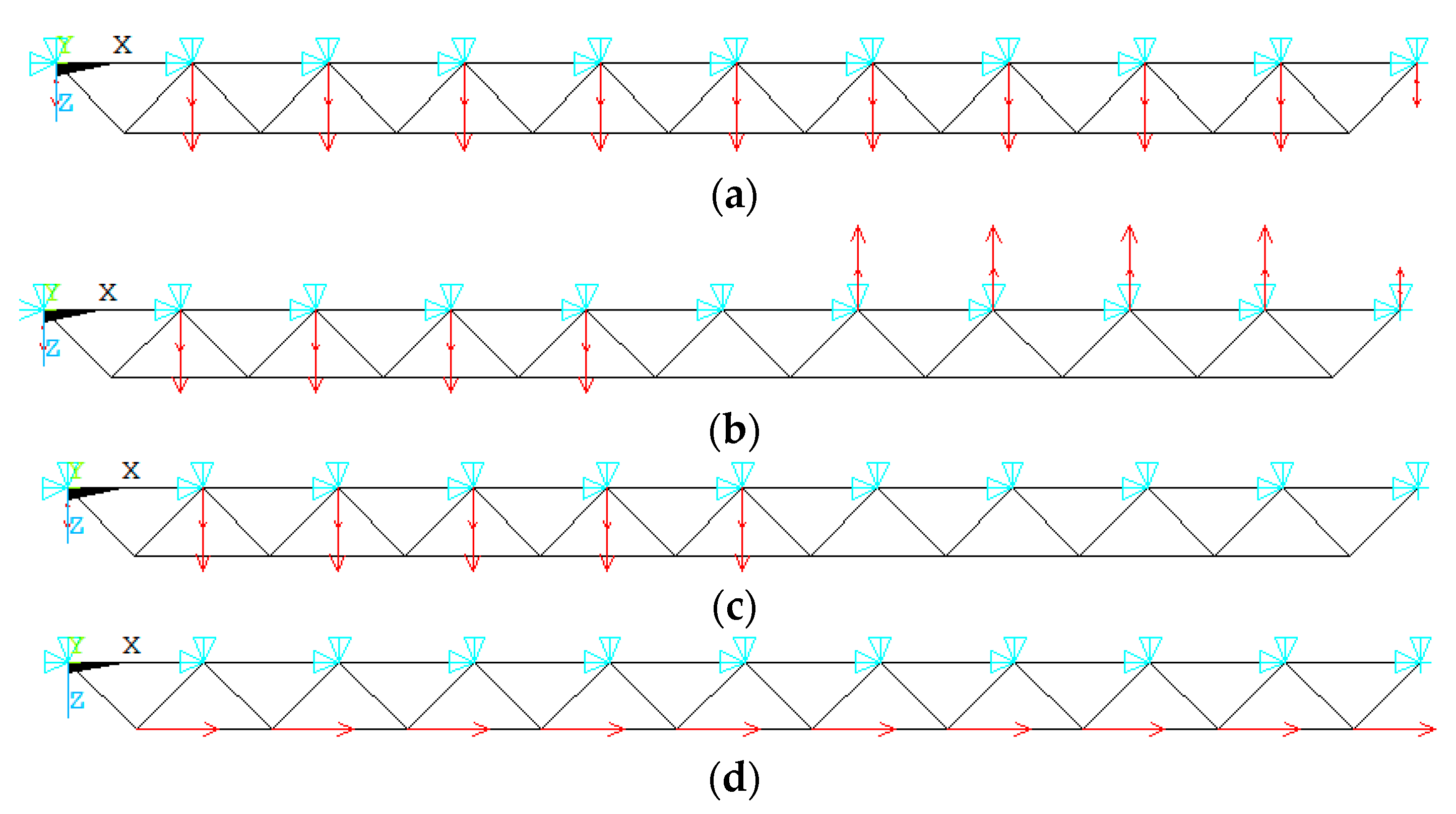
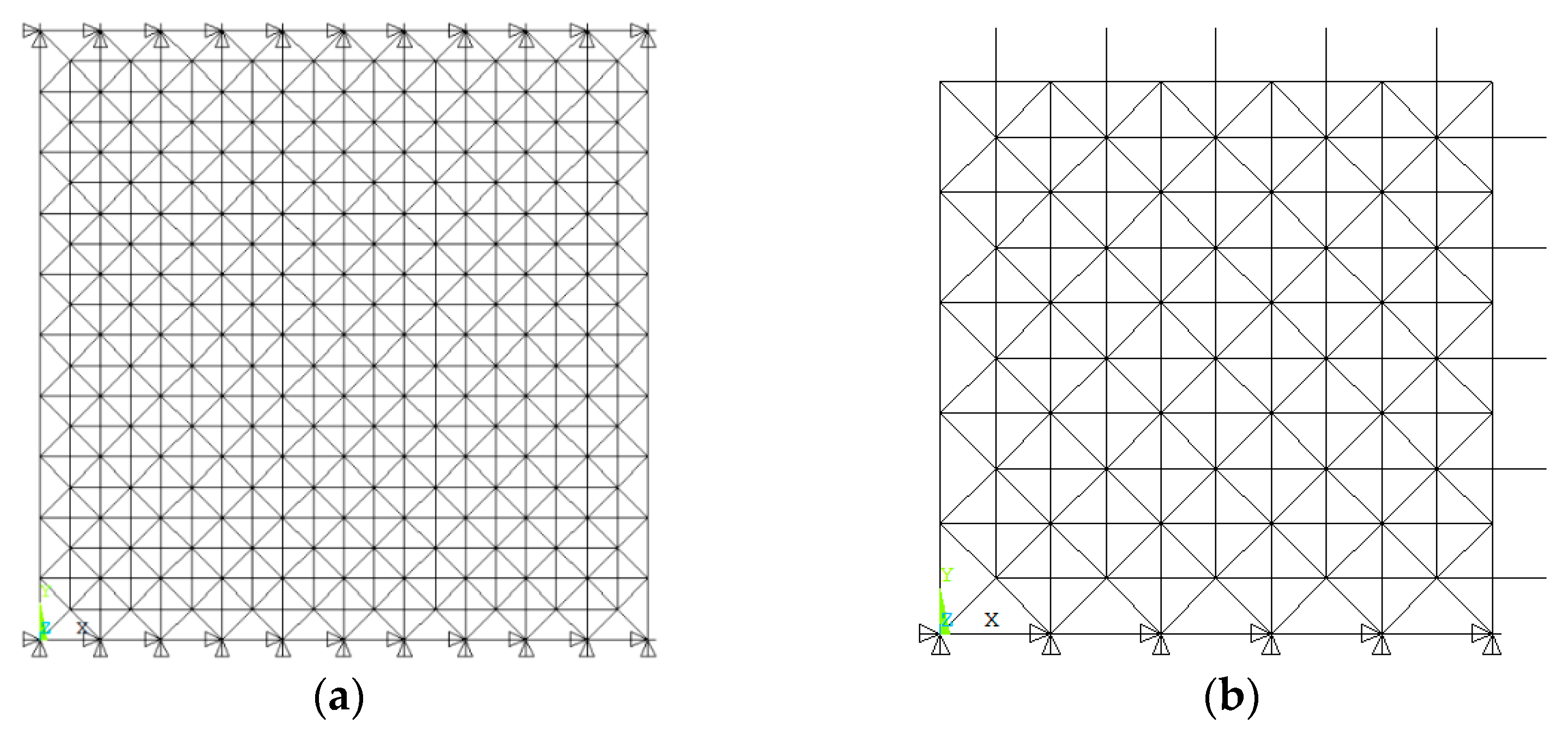
Four loading patterns, shown in Figure 4, are introduced to investigate the influence on the element importance of the square pyramid spatial grid structure. The loading pattern is defined as follows: (a) vertical symmetric load with the nodal load of 24.0 kN, (b) vertical anti-symmetric load with the nodal load of 24.0 kN, (c) half-span vertical load with the nodal load of 24.0 kN, and (d) horizontal load with the nodal load of 5.0 kN. The element importance distribution of the structure with the vertical symmetric load has been reported in Table 1. The symmetry criteria of the square pyramid space grid structures alter depending on the external load pattern. As a result, semi-structure is selected to consider all load patterns, as illustrated in Figure 5, and the element numbers are also provided.

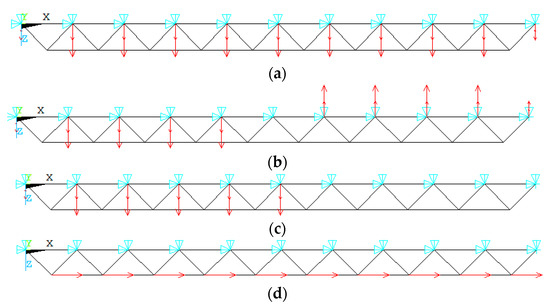
Figure 4. Four loading patterns. (a) Vertical symmetric load; (b) vertical anti-symmetric load; (c) half-span vertical load; (d) horizontal distributed load.

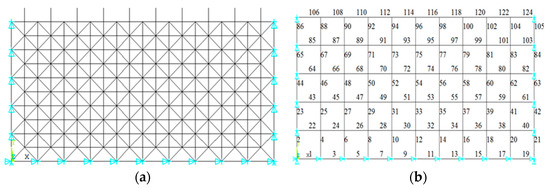
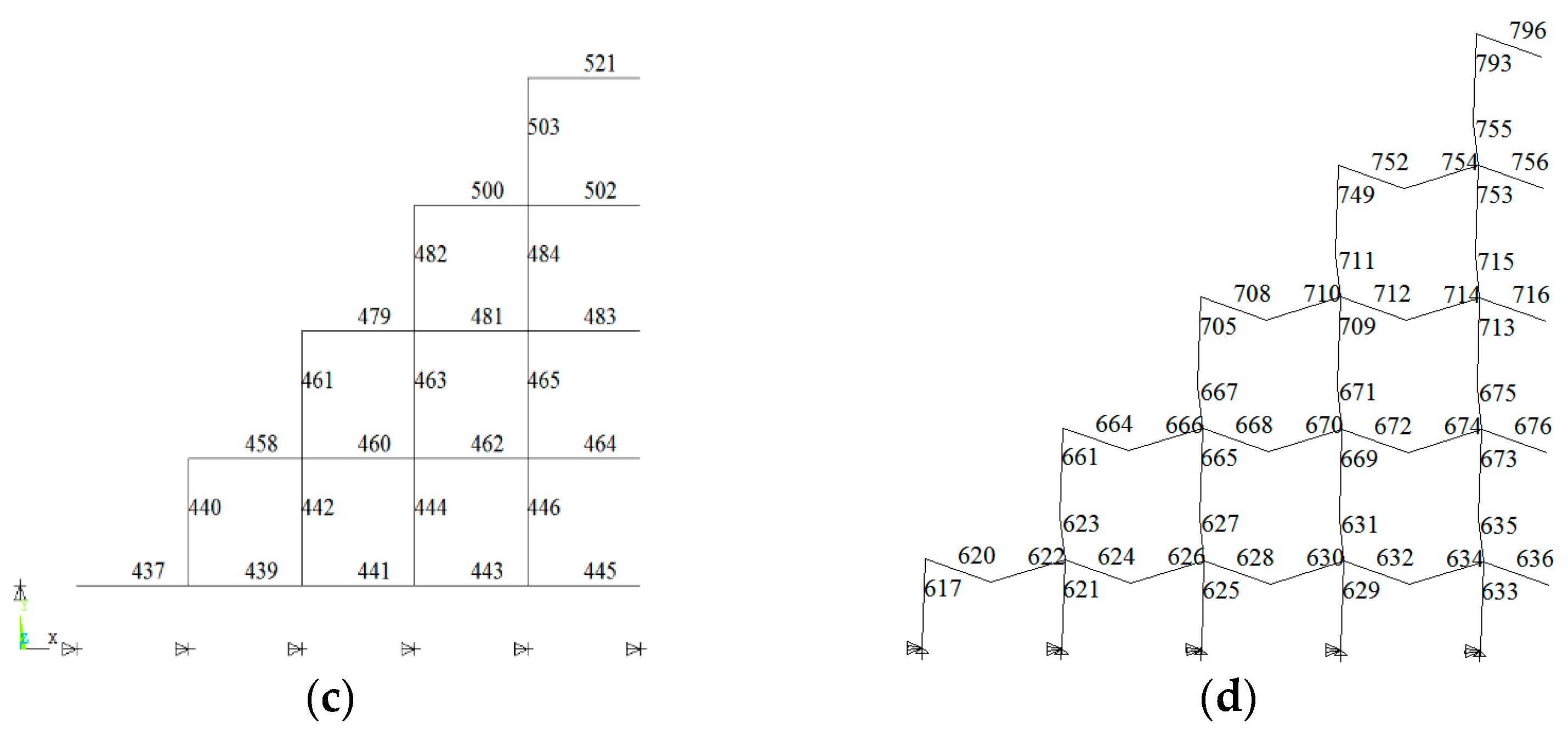
Figure 5. Semi-structure and its element number. (a) Semi-structure system; (b) number of the top chords; (c) number of the lower chords; (d) number of the diagonal web members.

The importance coefficients of some selected elements of the square pyramid spatial grid structure under different load distributions are given in Table 2, Table 3 and Table 4. It can be found that the element importance coefficients are changed with the different load patterns. When the structure is subjected to the vertical anti-symmetric load and the half-span vertical load, the corresponding largest element importance coefficient 0.0638 and 0.0406 are higher than the value of the element under the vertical symmetric load. However, the order of importance of the elements is only changed slightly. The importance of the lower and upper chords is generally higher than those of the web members, and the lower chord is somewhat more important than the upper chord. However, for the horizontal load, the importance of the web member is generally higher than the upper and the lower chord. The important upper chord members are located near the center along the loading direction, and the important lower chord members are located at the center of the bottom chord plane. Besides, the important members of the web member are located near the periphery of the web member plane.

Table 2. Element importance coefficient α_i under the vertical anti-symmetric load.

Element Number	αi	Element Number	αi	Element Number	αi
47	0.0275	261	0.0380	483	0.0075
66	0.0352	263	0.0390	522	0.0069
68	0.0465	278	0.0307	523	0.0093
70	0.0377	280	0.0532	524	0.0089
87	0.0439	282	0.0553	561	0.0072
89	0.0587	284	0.0338	562	0.0075
91	0.0481	297	0.0347	563	0.0103
108	0.0468	299	0.0608	564	0.0103
110	0.0628	301	0.0638	584	0.0066
112	0.0516	303	0.0394	544	0.0066

Table 3. Element importance coefficient α_i under the half-span vertical load.

Element Number	αi	Element Number	αi	Element Number	αi
70	0.0267	116	0.0243	306	0.0314
72	0.0240	282	0.0329	308	0.0286
73	0.0247	284	0.0337	418	0.0030
75	0.0249	285	0.0263	422	0.0032
89	0.0307	286	0.0268	483	0.0031
91	0.0358	287	0.0297	522	0.0026
93	0.0325	289	0.0268	523	0.0039
94	0.0275	299	0.0292	524	0.0034
96	0.0281	301	0.0393	561	0.0030
110	0.0333	303	0.0406	562	0.0030
112	0.0391	304	0.0276	563	0.0043
114	0.0356	305	0.0327	564	0.0042

Table 4. Element importance coefficient α_i under the horizontal distributed load.

Element Number	αi	Element Number	αi	Element Number	αi
54	0.0010	404	0.0194	416	0.0164
73	0.0012	405	0.0215	417	0.0219
75	0.0014	406	0.0205	418	0.0214
93	0.0014	407	0.0169	420	0.0161
96	0.0016	408	0.0182	445	0.0221
268	0.0012	409	0.0217	448	0.0183
284	0.0012	410	0.0208	449	0.0210
286	0.0013	411	0.0159	452	0.0168
287	0.0015	412	0.0170	453	0.0208
305	0.0016	413	0.0218	456	0.0160
401	0.0181	414	0.0212	457	0.0208
403	0.0189	415	0.0155	460	0.0156

4.2. Influence of the Support Conditions

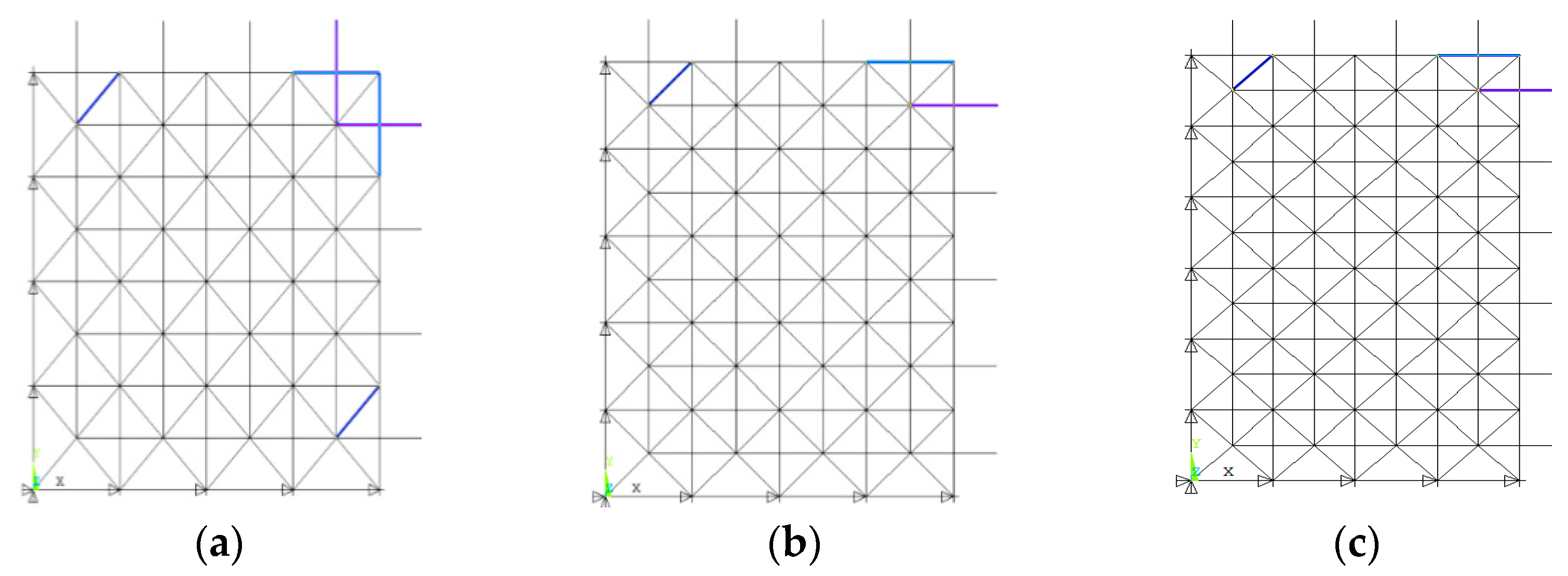
The influence of the support conditions is also studied in this section. As shown in Figure 6, only the nodes in the two opposite edges are fixed. Then, a quarter-size model is chosen according to the symmetry with the same element number in Figure 5. The calculated element importance coefficients are given in Table 5.

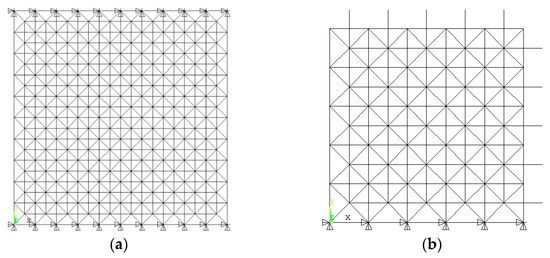
Figure 6. Square pyramid spatial trusses with opposite boundary fixed supports. (a) The boundary condition; (b) a quarter model.

Table 5. Element importance coefficient under different support conditions.

Element Number	Two Edges	Four Edges	Element Number	Two Edges	Four Edges	Element Number	Two Edges	Four Edges
2	0.0053	0	96	0.0029	0.0300	298	0.0913	0.0004
4	0.0087	0.0004	106	0.0068	0.0031	300	0.0548	0.0065
6	0.0093	0.0013	241	0.0475	0.0002	302	0.0519	0.0166
8	0.0093	0.0022	260	0.0697	0.0003	304	0.0509	0.0265
10	0.0093	0.0029	262	0.0402	0.0052	306	0.0506	0.0326
12	0.0093	0.0031	279	0.0856	0.0004	402	0.0064	0
64	0.0033	0.0022	281	0.0509	0.0061	406	0.0031	0.0003
85	0.0058	0.0029	283	0.0481	0.0157	407	0.0030	0.0011
92	0.0029	0.0198	285	0.0473	0.0250	441	0.0041	0.0005
94	0.0029	0.0272	287	0.0470	0.0307	442	0.0048	0.0004

It can be found that the influence of boundary conditions on the element importance is significant. The element importance coefficient of the grid structure with the opposite two edges fixed is higher than that with the surrounding four edges fixed. Under this opposite two edge fixed, the upper chords 6, 8, 10, 12 have the highest importance coefficient, and the lower chord 298 also has a higher importance coefficient. Among the web members, chord 402 has the highest importance coefficient, and the chords 441 and 442 are relatively higher. The important elements of the upper chords, lower chords and web members are located on the side of the fixed support, on the side of free support and in the corner of the plane, respectively. The change of support conditions reduces the importance of the middle members of the upper and lower chords while increasing the importance of the edge members. The important web members are also concentrated in the peripheral corners of the structure.

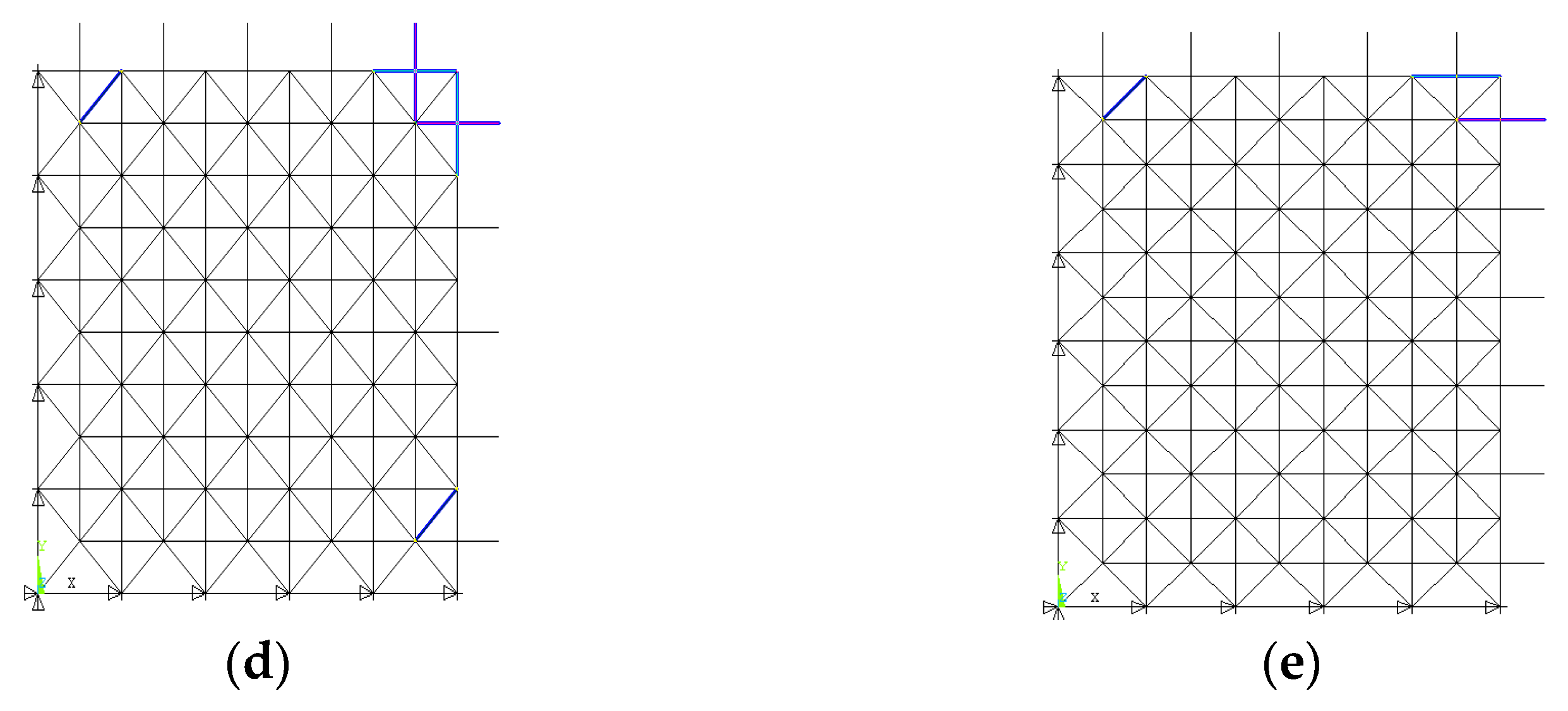
4.3. Influence of the Span

The influence of the span of the grid on the element importance is presented in this subsection. The size of the basic pyramid unit is 4 m × 4 m. The number of the basic unit is changed to form five different grid structures with the numbers of the basic grid of 8 × 8, 8 × 10, 8 × 12, 10 × 10, and 10 × 12, respectively. The vertical symmetric load, shown in Figure 4a, is used. A quarter model is chosen similarly, according to the symmetry. The importance coefficients of the most important upper chord, lower chord, and web member are given in Table 6, and the corresponding locations are shown in Figure 7. It can be found that the locations of the element with the highest importance coefficients in different grid structures are not affected by the structural span. If the plane projection of the grid structure is square, the most important chords are at the center, while the most important web members are adjacent to the boundary. If the plane projection of the truss is rectangular, the most important chords are parallel to the short span around the center part, while the most important web members are also just beside the boundary of the long span.

Table 6. Importance coefficients of the most important elements under different spans.

Number of Basic Pyramid Grids	8 × 8	8 × 10	8 × 12	10 × 10	10 × 12
Upper chord	0.0446	0.0520	0.0511	0.0300	0.0346
Lower chord	0.0472	0.0554	0.0546	0.0326	0.0377
Web member	0.0052	0.0050	0.0046	0.0023	0.0023

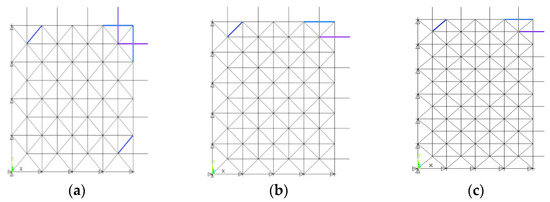
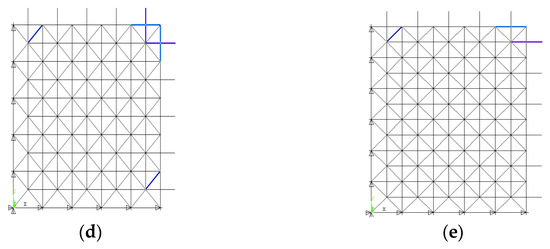
Figure 7. Locations of the important elements under different truss span. (a) 8 × 8; (b) 8 × 10; (c) 8 × 12; (d) 10 × 10; (e) 10 × 12.

4.4. Influence of Sizes of the Basic Pyramid Grid

In this subsection, the span of grid structures is kept as 40 m × 40 m. The sizes of the basic pyramid grid are changed with the numbers of the basic unit, which are assumed as 10 × 16, 10 × 12, 10 × 10, and 10 × 8, respectively. The importance coefficients of the most important elements are given in Table 7. Similarly, the locations of the important element in different grid structures are not affected by the size of the basic pyramid grid. When the number of basic units increases from 10 × 8 to 10 × 16, the size of the basic units becomes smaller, which leads to more numbers of elements. The importance coefficient of the most important element is reduced.

Table 7. Importance coefficient of the most important elements under different sizes of basic grids.

Number of Basic Pyramid Grids	10 × 16	10 × 12	10 × 10	10 × 8
Upper chord	0.0228	0.0270	0.0300	0.0361
Lower chord	0.0234	0.0286	0.0326	0.0394
Web member	0.0014	0.0018	0.0023	0.0035

For the square pyramid space grid structure, the element importance coefficients of lower chord members are higher than those of upper chord members, and the web members have the lowest importance. Moreover, the important upper and lower chord members are located at the center, while the important web members are located near the edge. The distribution will be independent of the geometry, while it will be changed for different load patterns and support conditions.

5. Effects of the Spatial Grid Topology

The grid structures with three different topologies are studied in this section, including diagonal square pyramid grids, bi-orthogonal lattice grids, and bi-orthogonal-diagonal lattice grids. The dimension, load level and support conditions are the same as those of square pyramid space grid structures. Similarly, the eighth model is selected to investigate the element importance for these three grid structures.

5.1. Diagonal Square Pyramid Grids

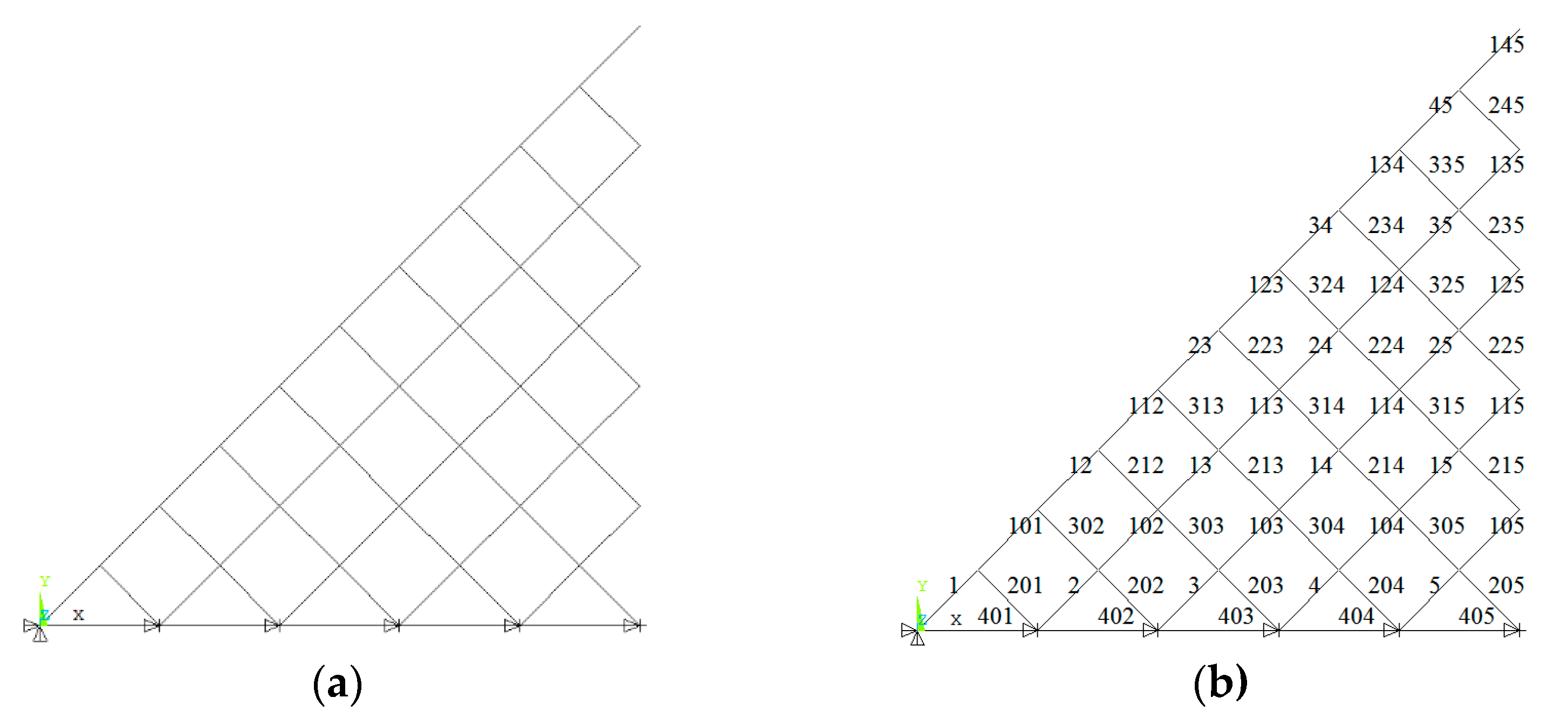
A diagonally square pyramid space grid structure, shown in Figure 8, is chosen as a case with cross-section numbers. The details of the cross-section of elements are given in Table 8. The corresponding cross-section are Φ60 × 4 (diameter × thickness), Φ76 × 4, Φ89 × 4, Φ114 × 4, Φ140 × 4, Φ159 × 6 and Φ159 × 8. The eighth model is shown in Figure 9.

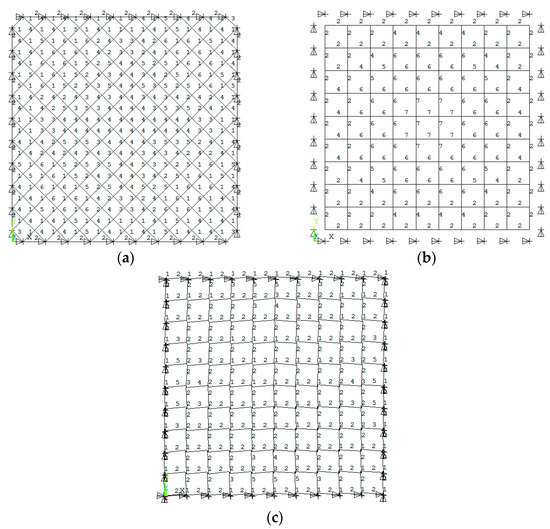
Figure 8. A diagonally square pyramid space grid structure. (a) Upper chords; (b) lower chords; (c) web members.

Table 8. Details of the cross-section of elements.

Number	1	2	3	4	5	6	7
Cross-section	Φ60 × 4	Φ76 × 4	Φ89 × 4	Φ114 × 4	Φ140 × 4	Φ159 × 6	Φ159 × 8

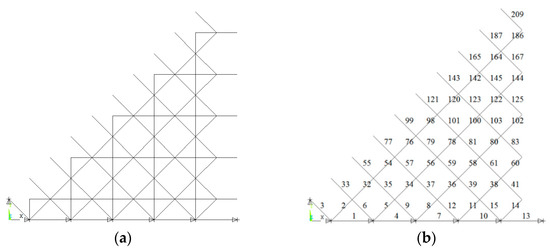
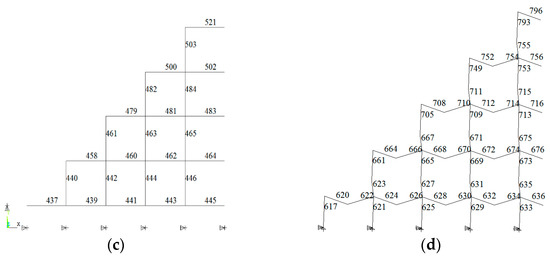
Figure 9. The eighth model of the diagonal square pyramid grids. (a) Eighth model; (b) number of the top chords; (c) number of the lower chords; (d) number of the diagonal web members.

Element importance coefficients of the diagonal square pyramid grids are given in Table 9. It can be found that the lower chord 521 has the largest element importance coefficient. It is at the center of the grid. The lower chords, 484, 500, 502, 503, which are located at the central part, are also very important. For the upper chord, the importance coefficient of chord 99 is the highest. Chord 635 is the most important element in diagonal web members. The web members, which are parallel to chord 635, such as chords 627, 629, 631, 669, 673, are relatively important. The important web members are close to the boundary.

Table 9. The element importance coefficient ${\alpha }_i$ for the diagonal square pyramid grids.

Element Number	${\mathit{\alpha }}_{\mathit{i}}$	Element Number	${\mathit{\alpha }}_{\mathit{i}}$	Element Number	${\mathit{\alpha }}_{\mathit{i}}$
9	0.0106	145	0.0119	502	0.0559
12	0.0145	165	0.0105	503	0.0673
37	0.0135	442	0.0180	521	0.0686
55	0.0126	444	0.0407	627	0.0184
57	0.0257	446	0.0414	629	0.0228
59	0.0242	461	0.0241	631	0.0363
77	0.0244	463	0.0489	633	0.0226
79	0.0261	465	0.0527	635	0.0385
99	0.0347	479	0.0280	661	0.0010
101	0.0192	481	0.0296	669	0.0250
103	0.0128	482	0.0542	671	0.0129
121	0.0148	483	0.0304	673	0.0275
123	0.0102	484	0.0621	675	0.0174
143	0.0142	500	0.0558	713	0.0101

5.2. Bi-Orthogonal Lattice Grids

As shown in Figure 10, a bi-orthogonal lattice grid structure is investigated with cross-section numbers. The corresponding cross-section are Φ60 × 4 (diameter × thickness), Φ76 × 4, Φ89 × 4, Φ114 × 4, Φ140 × 4, Φ159 × 6, Φ159 × 8, and Φ180 × 8, as given in Table 10.

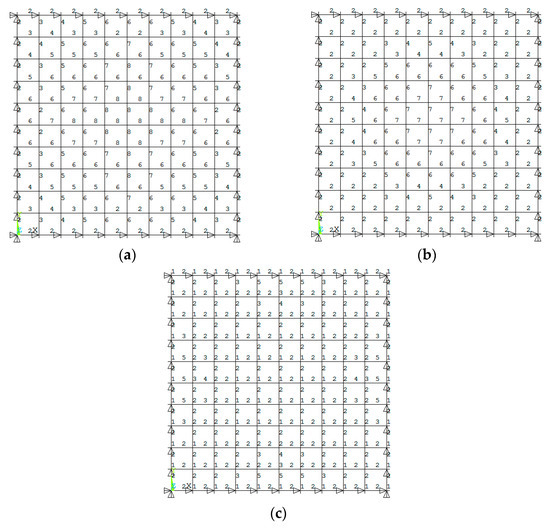
Figure 10. A bi-orthogonal lattice grid structure. (a) Upper chords; (b) lower chords; (c) web members.

Table 10. Details of the cross-section of elements.

Number	1	2	3	4	5	6	7	8
Cross-section	Φ60 × 4	Φ76 × 4	Φ89 × 4	Φ114 × 4	Φ140 × 4	Φ159 × 6	Φ159 × 8	Φ180 × 8

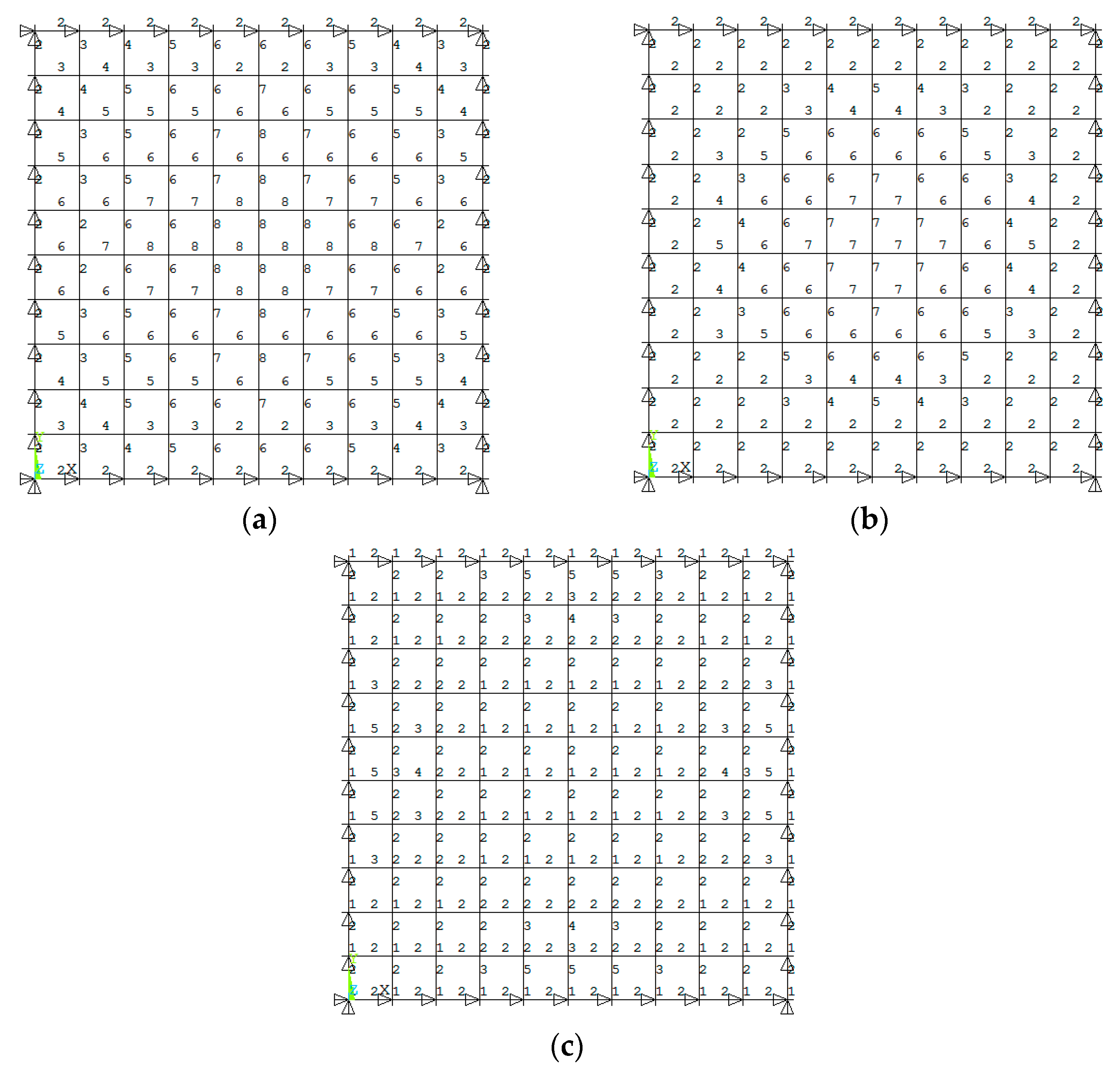
The corresponding eighth model is shown in Figure 11 with element numbers of upper chords, lower chords and web members. Element importance coefficients of the bi-orthogonal lattice grids are given in Table 11. It can be found that the web chord 721 has the largest element importance coefficient. It is at the center of the grid. The important elements of the web members are located in the vicinity of the periphery of the web surface except for the central vertical web member 721. The important elements of the upper chord are located near the line connecting chord 96 and chord 12 and are distributed in a stripe shape. The important elements of the lower chord are located at the center of the lower chord plane, presenting a blocky distribution. Compared with the diagonal square pyramid, the importance of each part is significantly increased.

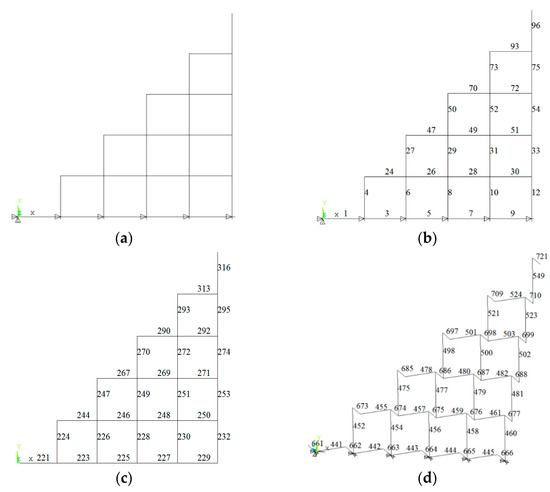
Figure 11. Bi-orthogonal lattice grid. (a) The eighth of the model; (b) the number of the top chords; (c) the number of the lower chords; (d) the number of the diagonal web members.

Table 11. Importance coefficient ${\alpha }_i$ of bars under vertical uniform load.

Upper Chord Number	${\mathit{\alpha }}_{\mathit{i}}$	Lower Chord Number	${\mathit{\alpha }}_{\mathit{i}}$	Web Member Number	${\mathit{\alpha }}_{\mathit{i}}$
8	0.0146	73	0.0693	295	0.0667
10	0.0259	75	0.0855	313	0.0610
12	0.0313	93	0.0703	316	0.0754
29	0.0276	96	0.0863	458	0.0257
31	0.0464	251	0.0247	460	0.0311
33	0.0552	253	0.0298	481	0.0183
47	0.0108	270	0.0244	675	0.0174
50	0.0347	272	0.0412	676	0.0293
52	0.0616	274	0.0493	677	0.0327
54	0.0774	290	0.0294	687	0.0199
70	0.0379	292	0.0331	688	0.0203
72	0.0360	293	0.0528	721	0.2497

5.3. Bi-Orthogonal-Diagonal Lattice Grids

A bi-orthogonal-diagonal lattice grid structure is studied, as shown in Figure 12. The numbers of the cross-section and its details are given in Figure 12 and Table 12, respectively. The corresponding cross-sections are Φ60 × 4 (diameter × thickness), Φ76 × 4, Φ89 × 4, Φ114 × 4, Φ140 × 4 and Φ159 × 6. Its eighth model is chosen to study the element importance, as shown in Figure 13. Element importance coefficients of the bi-orthogonal-diagonal lattice grids are given in Table 13. It can be found that web member 855 has the largest importance coefficient. The vertical chord in the web member is more important. Except for the central vertical web member 855, the other vertical webs are located near the periphery of the plane. The important member of the upper chord member is located close to the line connecting chord 212 and chord 203, parallel to chord 212, and distributed in a stripe shape. The important elements of the lower chord are located in the central area. The importance of vertical web members cannot be ignored.

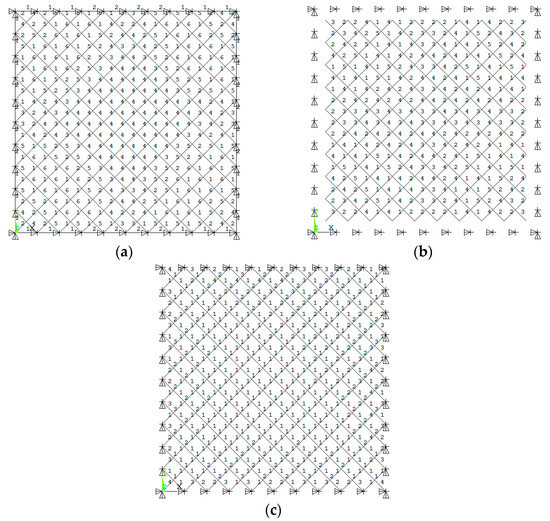
Figure 12. A bi-orthogonal-diagonal lattice grid structure. (a) Upper chords; (b) lower chords; (c) web members.

Table 12. Details of the cross-section of elements.

Number	1	2	3	4	5	6
Cross-section	Φ60 × 4	Φ76 × 4	Φ89 × 4	Φ114 × 4	Φ140 × 4	Φ159 × 6

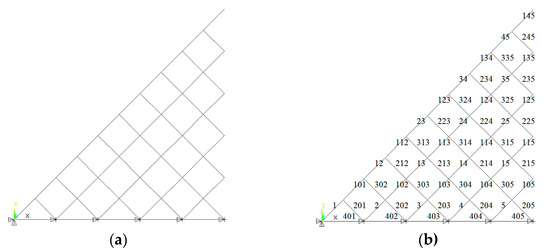
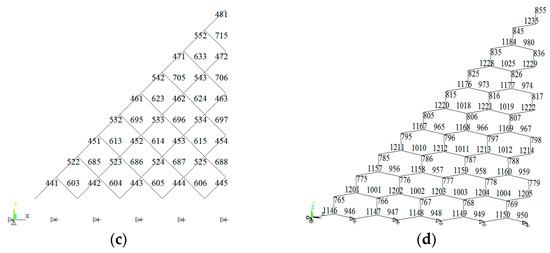
Figure 13. Bi-orthogonal-diagonal lattice Grid. (a) The eighth model; (b) number of the top chords; (c) number of the lower chords; (d) number of the diagonal web members.

Table 13. Importance coefficient ${\alpha }_i$ of bars under vertical uniform load.

Upper Chord Number	${\mathit{\alpha }}_{\mathit{i}}$	Lower Chord Number	${\mathit{\alpha }}_{\mathit{i}}$	Web Member Number	${\mathit{\alpha }}_{\mathit{i}}$
1	0.0109	314	0.0169	685	0.0130
201	0.0175	315	0.0103	686	0.0118
202	0.0204	324	0.0143	695	0.0165
203	0.0152	463	0.0123	696	0.0145
212	0.0253	472	0.0165	697	0.0114
213	0.0205	481	0.0148	705	0.0176
214	0.0134	543	0.0127	706	0.0162
223	0.0187	552	0.0131	715	0.0190
224	0.0129	613	0.0155	767	0.0149
234	0.0104	614	0.0136	768	0.0187
302	0.0237	615	0.0105	769	0.0202
303	0.0223	623	0.0170	778	0.0101
304	0.0155	624	0.0153	779	0.0104
313	0.0229	633	0.0186	855	0.0345

For the different types of grid structures, there are inconsistent distribution characteristics for the element importance coefficients. The main important lower and upper chord members are concentrated in the center, while the important web members are located near the edge. When the upper chord is arranged in parallel with the support side, the important elements of the upper chords are located in the mid-span and parallel to the support side. When the lower chords are arranged in parallel with the side of the support, the important lower chords are distributed in a block shape in the mid-span. When the upper and lower chords are placed at an angle of 45° to the side of the support, the important members are close to the supports and parallel to the diagonal of the structure. The different distribution of important members also reveals that the rapid model evaluation on element importances is essential in the conceptual analysis stage, reflecting the influence of geometric topology on the structural safety status.

6. Conclusions

This paper proposes a rapid model evaluation method on element importances of grid structures based on the element strain energy and element removal technology. The effects of the loading pattern, the boundary condition, and geometric parameters of square pyramid grid structures are investigated. Moreover, three types of spatial grids, diagonal square pyramid grids, bi-orthogonal lattice grids, and bi-orthogonal-diagonal lattice grids, are chosen to examine the influence of the topology on the element importance. The main conclusions are as follows.

(1)

For square pyramid grid structures, the results show that the lower and top chords are more important than the diagonal web members. The importance coefficients of the elements are different under different load patterns, and the order of importance of the elements is also changed when subjected to horizontal loads.

(2)

The change of the support condition reduces the importance of the upper and lower chords in the center area for square pyramid grid structures. The effects of the structural span and the size of the basic pyramid grid can be ignored for the location of the most important members.

(3)

There are different distribution characteristics for the element importance coefficients for grid structures with different topologies. The location of important elements for the upper chords, the lower chords and the web members are dependent on the relationship between the arrangement of these members and support sides.

Based on the proposed method in this paper, the rapid model and element evaluation can be performed in the conceptual analysis stage. It is an efficient way for the robustness design after the preliminary design of general grid structures. At last, it is easy to be integrated into the existing platform due to its simplicity and efficiency.