Abstract
A modified real-space-Pfaffian method is applied to characterize the topological superconducting transition of a one-dimensional p-wave superconductor with quasiperiodic potentials. We found that the Majorana zero-energy mode exists in the topological non-trivial phase, and its spatial distribution is localized at ends of the system, whereas in the topological trivial phase, there is no Majorana zero mode. Furthermore, we numerically found that due to the competition between the localized quasi-disorder and the extended p-wave pairing, there are mobility edges in the energy spectra. Our theoretical work enriches the research on the quasiperiodic p-wave superconducting models.
1. Introduction
The Majorana fermion is a kind of particular particle, whose antiparticle is itself [1,2,3]. During the last decade, the signatures of its presence have been found in many condensed matter systems, such as the semiconductor nanowires with strong spin–orbital couplings [4,5,6,7,8], ultracold atoms [9,10,11,12], magnetic atom chains [13,14,15,16], and the heterojunctions of normal superconductors and topological insulators [17,18,19,20,21,22,23,24]. Because of its application prospect in topological quantum computation [25,26], the Majorana fermion has attracted extensive research interest [27,28,29,30,31,32,33].
The Majorana fermion has been theoretically proven to exist in topological superconductors with p-wave pairings, which appears in Majorana zero mode (MZM) and is located at both ends of the system, protected by the topology [34]. As we all know, disorder gives rise to the localization phenomenon [35], which results in the destruction of the topological non-trivial phases in topological superconductors [36,37,38,39,40,41,42,43]. Cai et al. [44] discussed the influence of the quasi-disorder, namely the quasiperiodic disorder on the MZM. They found that, with the increase of the disorder potential, the system undergoes a transition from the topological non-trivial phase to the Anderson localized phase, that is the MZM keeps robust only to the weak disorder. Moreover, such a transition can be characterized by the quench dynamics [45] and the Kibble–Zurek mechanism [46]. Wang et al. [47] investigated in detail the delocalization properties of the topological phase where the MZM exists and revealed a new critical region.
We know that the presence and absence of the above-mentioned MZM can also be characterized by the Pfaffian [34]. With the Pfaffian method, we are capable of obtaining the topological phase diagram of the superconducting models, of either the homogeneous potential [34], the integer-periodic potential [48], or even the quasiperiodic potential [44]. We notice that the localized quasi-disorder will lead to a wider topological phase boundary compared to the extended superconducting pairings in the p-wave superconducting models [34,44]. However, there remain open questions on how the MZM responds to the competition between the extended p-wave pairing and the localized quasi-disorder and whether a mobility edge exists in a p-wave pairing system. Recently, a slowly varying incommensurate potential has been shown to induce a mobility edge in a topological superconducting model [49]. Nevertheless, beyond a slowly varying configuration, it is of practical interest to propose a more realistic and experimentally accessible potential, such as the quasi-periodic potential, which has been realized in cold atom experiments [50,51]. In addition, the superconducting pairings are within the reach of cold atomic systems by employing atomic internal states and the laser-assisted state-sensitive tunnelings [52,53,54,55] and Zeeman field modulated spin–orbital-coupled Fermi atomic gas [9,56]. Previous theoretical research has revealed that the homogeneous potential makes wave functions extended, while the quasi-disorder brings about the Anderson localization [44,47,57]. However, whether there exist mobility edges when both two types of potentials coexist is still elusive. In this paper, we considered a special case in which the potential consists of a homogeneous part and a quasi-disordered one in a p-wave superconducting model and made an attempt to reveal the topological properties and mobility edges to which this potential leads.
The rest of this paper is organized as follows. In Section 2, we introduce the Hamiltonian of a p-wave superconducting model with a generalized potential. In Section 3, we first introduce the modified real-space-Pfaffian method, and then, we discuss the topological properties and the mobility edges of the system. We give a brief summary in Section 4.
2. Model and Hamiltonian
Real quantum systems are more or less affected by disorder. In this paper, we studied a one-dimensional p-wave superconductor with quasiperiodic disordered on-site potentials, which is described by the following tight-binding Hamiltonian:
where denotes the fermion annihilation (creation) operator and L is the size of the system with n being the site index. The nearest-neighbor tunneling strength t and the nearest-superconducting pairing parameter are real constants. is set as the unit of energy. The quasiperiodic on-site potential is:
where V is the potential strength, is the modulation parameter, and is the incommensurate modulation frequency. When , the model goes back to the Kitaev model [34], where is the phase transition point, namely the topological boundary of the topological non-trivial phase () and the topological trivial one (). The potential can be understood as the superposition of a homogeneous potential and incommensurate potentials with different frequencies:
where is the constraint condition. The parameter b controls the number of summation terms. When b is small, can be truncated to the summation with finite terms. As discussed before, the homogeneous potential manifests the topological boundary of the p-wave superconductor located at , whereas Cai et al. [44] and Wang et al. [47] showed that the considered quasi-periodicity broadens the topological boundary. For our model, it is unknown how the fate of the topological boundary changes when both two types of potentials coexist. In addition, we know that the homogeneous potentials keep the wave functions extended, while the incommensurate potentials lead to the Anderson localization [44,47,57]. Whether there exist mobility edges is still elusive when both types of potentials coexist. In the next section, we investigate these two aspects.
In the particle–hole picture, the Hamiltonian is diagonalized. In order to obtain the full-energy spectrum, we shall introduce the Bogoliubov–de Gennes (BdG) transformation:
where j ranges from one to L and the components and are real numbers. Thus, the Hamiltonian in Equation (1) is diagonalized as:
where is the eigenenergy, which can be determined by the following BdG equations:
Furthermore, we represent the wave function as the following form:
then according to the BdG equations, we have the following BdG matrix:
where and ; C is a null matrix when considering the open boundary condition (OBC) and for the periodic boundary condition [47]. Intuitively, is a matrix. By using the Schmidt orthogonal decomposition method to diagonalize the BdG matrix, we can acquire the full-energy spectrum and the associated wave functions directly. These strategies are favorable for studying the topological properties, such as the MZM and energy gap, as well as the mobility edges. These investigations are presented in the following section.
3. Results
The topological property of the system is directly characterized by a topological invariant. According to Kitaev’s work, the Hamiltonian in Equation (1) can be expanded in terms of Majorana operators as:
where is real antisymmetric matrix, satisfying:
and is the Majorana operator with , which is defined as:
Accordingly, under the PBC, the represented Hamiltonian is:
For an antisymmetric matrix, its Pfaffian is defined as:
where denotes a series of permutations on these elements with being the sign of permutation. With the Pfaffian of the system, then the topological invariant M can be defined as [34,44]:
Although we know that we can calculate the Pfaffian to obtain the topological invariant of the p-wave superconducting system, for the quasiperiodic case, it is difficult to deal with the perturbation group operation directly. Therefore, we present a modified real-space-Pfaffian method to conveniently calculate the topological invariant. This method requires us to make a Schur decomposition [58] on the real anti-symmetric matrix h:
where U is a unitary matrix and D is an anti-symmetric tridiagonal matrix. Thus, the Pfaffian of h is redefined as:
is the determinant of the unitary matrix U. In practice, we can use Equations (14) and (16) to obtain the topological phase diagram, for the reason that and are numerically available (see the details in Appendix A).
We calculate the Pfaffian by the modified real-space-Pfaffian method and naturally obtain the topological phase diagram of the system, which is presented in Figure 1. The diagram shows that corresponds to the topological non-trivial phase, whereas corresponds to the topological trivial phase and the blue dashed line denotes the numerically obtained phase boundary. We know that when , our model goes back to the Kitaev model, whose transition is located at [34]. We notice that when b is taken at a small value, the phase transition is almost the same as that of the Kitaev model. This implies that the MZM is robust against the disordered perturbations. When b increases, the phase boundary bends in the direction of the decreasing V. This phenomenon is the direct result of the enhanced disorder effect, which compresses the topological non-trivial region. That is to say that we can not only realize the topological phase transition by adjusting the potential strength V, but also manipulate the phase transition by controlling the strength of the disorder, which is determined by the the parameter b in our system.
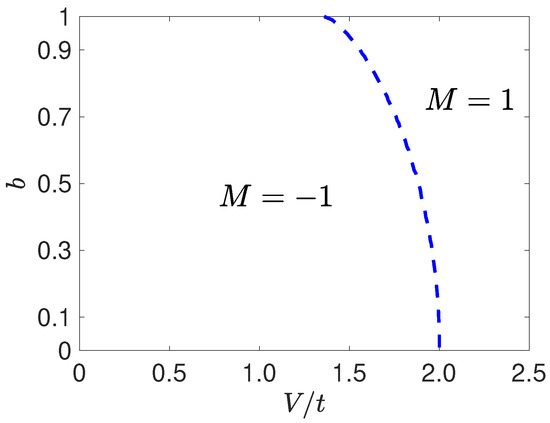
Figure 1.
(Color online) b- topological phase diagram for systems with , . corresponds to the topological non-trivial phase, and corresponds to the topological trivial phase. The blue dashed line denotes the phase boundary.
In topological systems, the topological phase transition is accompanied by the gap closing and reopening. Figure 2 plots the energy gap as a function of the potential strength V with various b. The is defined as the difference of the -th energy level and the L-th energy level under the periodic boundary condition, i.e. . It is readily seen that when the topological phase transition happens, the gap undergoes closing and reopening. Different from the quasiperiodic case [44,47], there appears a wider gap when the system is in the topological trivial phase. This phenomenon occurs because the uniform potential energy has more impact on the energy gap than that of quasi-periodic disordered perturbations [34,44]. Moreover, when b is small, the gap closing point is almost at . As b increases, the gap closing point moves towards the direction of the decreasing V. This feature is in accord with the topological boundary in Figure 1.
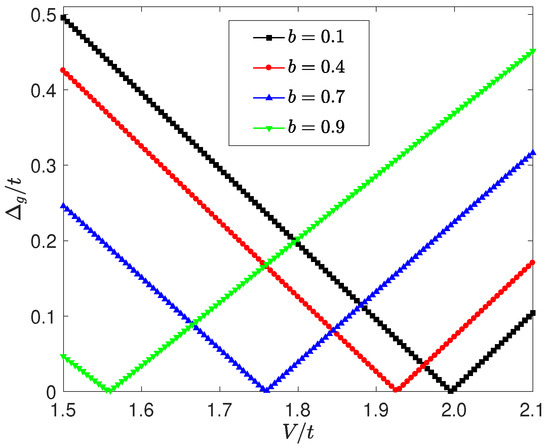
Figure 2.
(Color online) The energy gap versus V with various b. Other involved parameters are , , and .
The topological non-trivial phase implies the presence of the MZMs. Figure 3a shows the excitation energy spectrum as a function of the potential strength V under the open boundary condition. The spectrum reflects that the MZMs are only located in the topological non-trivial phase. To see the distributions of zero energy states, we rewrite the BdG operators as:
where and .
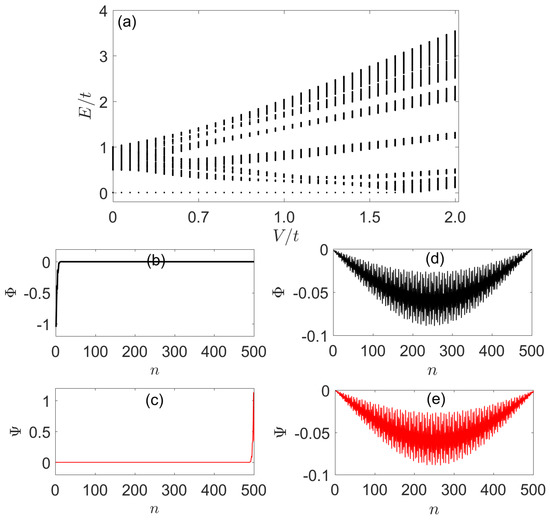
Figure 3.
(Color online) (a) Excitation energy spectrum of the system under the open boundary condition. (b–e) are respectively the spatial distributions of and for the lowest excitation state with (). Other involved parameters are , , , and .
Figure 3b,c respectively plots the spatial distributions and for the lowest excitation state with . Figure 3d,e is the distributions for the lowest excitation state with . When , we know that the system is in the topological non-trivial phase, so the lowest excitation state is the Majorana zero energy state. As the figures show, the distributions of the corresponding and are located at the ends of the system, reflecting the bulk boundary correspondence. The contrary consequence is that when , the system is in the topological trivial phase and the corresponding and distribute in the bulk of the system. This is interpreted as the system being in the topological trivial phase, and the lowest excitation state is no longer the Majorana edge state, but the bulk state.
We note that in the topological trivial phase, the spatial distributions of and for the lowest excitation state are no longer localized in the bulk, but expand throughout the whole system, presenting an extended state. We are aware that such a phenomenon in this quasiperiodic superconducting system has relevance for the mobility edge instead of the Anderson localization [44,47]. The localization–delocalization property can be characterized by the inverse participation ratio (IPR). For a given normalized wave function, the associated IPR is defined as [59,60]:
It is well known that for an extended wave function, the IPR scales as , and it approaches one for a localized wave function. We considered as an example to verify the above surmise and made an attempt to qualitatively analyze the influence of the superconducting pairing parameter on the mobility edge. By taking four different , we plot the excitation spectra and IPR as a function of V under the PBC, which are shown in Figure 4a–d, respectively. According to the numerical results, the distinction between the extended states and the localized states can be readily seen from the IPR (the color bar shows this). The transition boundary in energy is just the mobility edge. When is small, the low-energy excitation states are extended states, while those states with higher energy are localized. When becomes larger, the mobility edge moves towards the high-energy region. Moreover, we notice that when the quasiperiodic potential strength V is small, all the excitation states are extended. Moreover, the extended region becomes larger when increases. In other words, the superconducting pairing is robust against the weak disorder and makes the system more extended. From Figure 4a, we also notice that when , the IPR of the lowest excitation state approaches zero, signaling the extended state. The result answers why the and in Figure 3d,e distribute throughout the whole system.
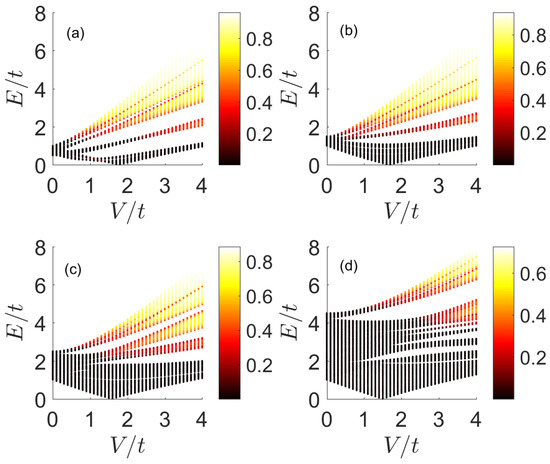
Figure 4.
(Color online) The excitation spectrum and IPR as a function of V with in (a), in (b), in (c), and in (d). Other involved parameters are , , and .
4. Summary
Herein, a quasiperiodic p-wave superconducting model with the coexistence of the homogeneous potential and quasiperiodic potential was investigated. A modified real-space-Pfaffian method was applied to calculate the topological invariants of this system. We demonstrated that the topological phases are protected by the gap. However, compared to the purely quasiperiodic case, the gap in the topological nontrivial is wider. We argued that this phenomenon occurs because the homogeneous potential has more impact on the gap. Besides, we uncovered that there are mobility edges in the p-wave superconducting model. We argued that the mobility edge originates from the competition between the extended p-wave pairing and the localized quasi-disorder. Furthermore, we discussed the influence of the superconducting pairing parameter on the mobility edge. From the analysis, we arrived at the qualitative fact that superconducting pairings tend to make the system extended and stronger pairings move the mobility edge towards the high-energy region. In general, our theoretical work, i.e., the modified real-space Pfaffian method, overcomes the technical problem of using the Pfaffian method to solve the topological invariants of a general p-wave superconductor and makes up for the limitation of the original Pfaffian. Moreover, the uncovered mobility edges promote a further understanding of the quasiperiodic p-wave superconductors.
Author Contributions
Data curation, S.C.; formal analysis, S.C.; investigation, S.C.; methodology, S.C.; validation, S.C.; visualization, S.C.; writing—original draft preparation, S.C.; writing—review and editing, Y.Z.; conceptualization, X.G.; formal analysis, X.G.; project administration, X.G.; resources, X.G.; supervision, X.G.; writing—review and editing, X.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the NSFC under Grant No. 11835011 and Grant No. 12174346.
Acknowledgments
Gao Xianlong and Shujie Cheng acknowledge the support from the NSFC under Grant No. 11835011 and Grant No. 12174346.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Modified Real-Space-Pfaffian Method
As mentioned in the main text, we can perform a Schur decomposition [58] on a general anti-symmetric matrix h, i.e., . After this operation, we obtain a anti-symmetric tridiagonal matrix D, which has the following configuration:
According to the original definition of the Pfaffian (Equation (13)), we can easily obtain the Pfaffian of the matrix D, which is given as:
Therefore, to obtain the Pfaffian of a general anti-symmetric matrix h, a standard strategy is that we first calculate the unitary matrix U and the target matrix D by the Schur decomposition, then obtain the Pfaffian of D by Equation (A2), and finally, obtain the Pfaffian of h by Equation (16). We name the Pfaffian method after the Schur decomposition as the modified real-space-Pfaffian method. In the following, we show how this method is effectively applied to obtain the topological phase diagram of p-wave superconducting models.
Test on the Kitaev model () [34]: We considered , , , and in all our tests. and were two chosen parameters. We know that the topological boundary is located at . Therefore, corresponds to the topological non-trivial phase and gives ; corresponds to the topological non-trivial phase and gives ; taking and other parameters into h and performing the Schur decomposition, we have and . According to Equation (16), we obtain the topological invariant . Next, we take and other parameters into h. After performing the Schur decomposition, we have and . According to Equation (16), we obtain . If leaving the V changing while other parameters invariable, by means of this method, we can obtain the topological phase diagram of the Kitaev model, as shown in Figure A1.
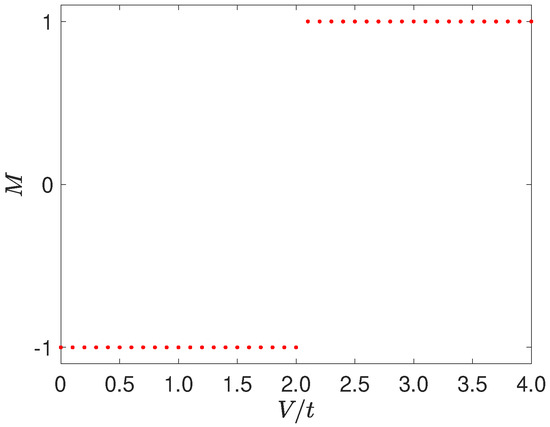
Figure A1.
(Color online) M- topological phase diagram of the Kitaev model.
Test on the quasiperiodicp-wave superconducting model [44,47]: This model requires , and its topological boundary is located at . Without loss of generality, we take ; thus, the topological boundary is . and are two chosen parameters, corresponding to the topological non-trivial phase () and topological trivial phase (), respectively. We first tested the case with . After performing the Schur decomposition, we obtain and . Therefore, the topological invariant is . Next, we take and other parameters into h. After performing the Schur decomposition, we obtain and , so the topological invariant is . If we change the V continuously and keep other parameters invariable, then we can obtain the topological phase diagram, as shown in Figure A2.
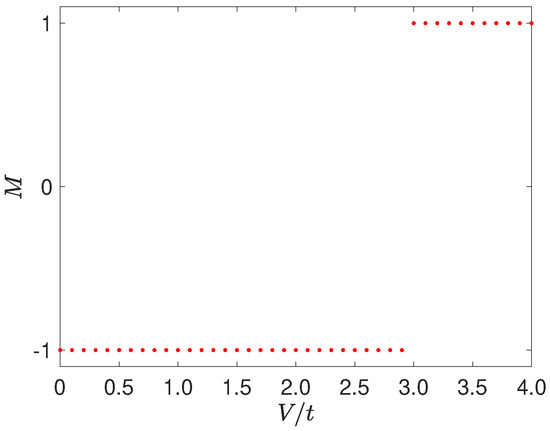
Figure A2.
(Color online) M- topological phase diagram of the quasiperiodic p-wave superconducting model.
Test on our model (see Equation (1)): The potential is presented in Equation (2). We considered in our test. According to the topological phase diagram in Figure 1, we know the numerical topological boundary is located at about . and are two chosen parameters, corresponding to the topological non-trivial phase and topological trivial phase, respectively. We first tested the case with . After performing the Schur decomposition, we have and . Therefore, the topological invariant is . Next, we tested the case with . In the same way, we performed the Schur decomposition, then we obtain and . Therefore, in this case, the topological invariant is . If we change V continuously and leave other parameters invariable, then we can obtain the topological phase diagram, as shown in Figure A3.
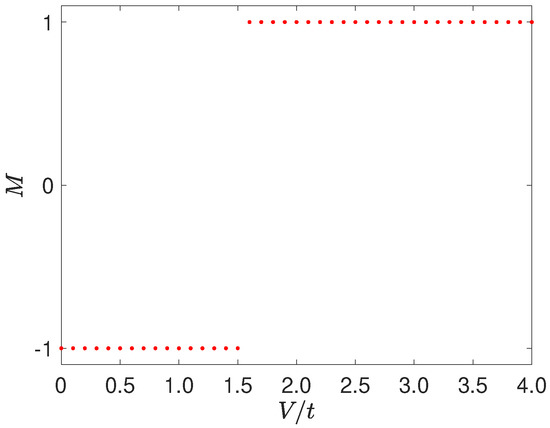
Figure A3.
(Color online) M- topological phase diagram of our model.
From the above tests, it is readily seen that this modified real-space-Pfaffian method is very convenient and accurate to numerically obtain the topological phase diagram of the p-wave superconducting model.
References
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.Q. Topological Insulators; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–221. [Google Scholar] [CrossRef] [Green Version]
- Aguado, R. Majorana quasiparticles in condensed matter. Riv. Nuovo Cim. 2017, 40, 523. [Google Scholar] [CrossRef]
- Mourik, V.; Zuo, K.; Frolov, S.M.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices. Science 2012, 336, 1003. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, S.M.; Higginbotham, A.P.; Madsen, M.; Kuemmeth, F.; Jesperson, T.S.; Nygard, J.; Krogstrup, P.; Marcus, C.M. Exponential protection of zero modes in Majorana islands. Nature 2016, 531, 206. [Google Scholar] [CrossRef] [Green Version]
- Deng, M.T.; Vaitiekenas, S.; Hansen, E.B.; Danon, J.; Leijnse, M.; Flensberg, K.; Nygard, J.; Krogstrup, P.; Marcus, C.M. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 2016, 354, 1557. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Yu, P.; Stenger, J.; Hocevar, M.; Car, D.; Plissard, S.R.; Bakkers, E.P.A.M.; Stanescu, T.D.; Frolov, S.M. Experimental phase diagram of zero-bias conductance peaks in superconductor/semiconductor nanowire devices. Sci. Adv. 2017, 3, e1701476. [Google Scholar] [CrossRef] [Green Version]
- Klinovaja, J.; Stano, P.; Loss, D. Transition from Fractional to Majorana Fermions in Rashba Nanowires. Phys. Rev. Lett. 2012, 109, 236801. [Google Scholar] [CrossRef]
- Liu, X.J.; Jiang, L.; Pu, H.; Hu, H. Probing Majorana fermions in spin-orbit-coupled atomic Fermi gases. Phys. Rev. A 2012, 85, 021603. [Google Scholar] [CrossRef] [Green Version]
- Qu, C.; Zheng, Z.; Gong, M.; Xu, Y.; Mao, L.; Zou, X.; Guo, G.; Zhang, C. Topological superfluids with finite-momentum pairing and Majorana fermions. Nat. Commun. 2013, 4, 2710. [Google Scholar] [CrossRef] [Green Version]
- Chen, C. Inhomogeneous Topological Superfluidity in One-Dimensional Spin-Orbit-Coupled Fermi Gases. Phys. Rev. Lett. 2013, 111, 235302. [Google Scholar] [CrossRef] [Green Version]
- Ruhman, J.; Berg, E.; Altman, E. Topological States in a One-Dimensional Fermi Gas with Attractive Interaction. Phys. Rev. Lett. 2015, 114, 100401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nadj-Perge, S.; Drozdov, I.K.; Bernevig, B.A.; Yazdani, A. Proposal for realizing Majorana fermions in chains of magnetic atoms on a superconductor. Phys. Rev. B 2013, 88, 020407. [Google Scholar] [CrossRef] [Green Version]
- Nadj-Perge, S.; Drozdov, I.K.; Li, J.; Chen, H.; Jeon, S.; Seo, J.; MacDonald, A.H.; Bernevig, B.A.; Yazdani, A. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 2014, 346, 602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dumitrescu, E.; Roberts, B.; Tewari, S.; Sau, J.D.; Sarma, S.D. Majorana fermions in chiral topological ferromagnetic nanowires. Phys. Rev. B 2015, 91, 094505. [Google Scholar] [CrossRef] [Green Version]
- Jeon, S.; Xie, Y.L.; Wang, Z.J.; Bernevig, B.A.; Yazdani, A. Distinguishing a Majorana zero mode using spin-resolved measurements. Science 2017, 358, 772. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cook, A.; Franz, M. Majorana fermions in a topological-insulator nanowire proximity-coupled to an s-wave superconductor. Phys. Rev. B 2011, 84, 201105. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, Y.; Sato, M.; Nagaosa, N. Symmetry and Topology in Superconductors –Odd-Frequency Pairing and Edge States. J. Phys. Soc. Jpn. 2012, 81, 011013. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.H.; Zhang, K.W.; Hu, L.H.; Li, C.; Wang, G.Y.; Ma, H.Y.; Xu, Z.A.; Gao, C.L.; Guan, D.D.; Li, Y.Y.; et al. Majorana Zero Mode Detected with Spin Selective Andreev Reflection in the Vortex of a Topological Superconductor. Phys. Rev. Lett. 2016, 116, 257003. [Google Scholar] [CrossRef] [Green Version]
- Hell, M.; Leijnse, M.; Flensberg, K. Two-Dimensional Platform for Networks of Majorana Bound States. Phys. Rev. Lett. 2017, 118, 107701. [Google Scholar] [CrossRef] [Green Version]
- Pientka, F.; Keselman, A.; Berg, E.; Yacoby, A.; Stern, A.; Halperin, B.I. Topological Superconductivity in a Planar Josephson Junction. Phys. Rev. X 2017, 7, 021032. [Google Scholar] [CrossRef] [Green Version]
- Fornieri, A.; Whiticar, A.M.; Setiawan, F.; Marín, E.P.; Asbjórn, C.C.D.; Keselman, A.; Gronin, S.; Thomas, C.; Wang, T.; Kallaher, R.; et al. Evidence of topological superconductivity in planar Josephson junctions. Nature 2019, 569, 89. [Google Scholar] [CrossRef] [PubMed]
- Takagi, D.; Tamura, S.; Tanaka, Y. Odd-frequency pairing and proximity effect in Kitaev chain systems including a topological critical point. Phys. Rev. B 2020, 101, 024509. [Google Scholar] [CrossRef] [Green Version]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Sarma, S.D. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083. [Google Scholar] [CrossRef] [Green Version]
- Aguado, R.; Kouwenhoven, L.P. Majorana qubits for topological quantum computing. Phys. Today 2020, 73, 44. [Google Scholar] [CrossRef]
- Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 2012, 75, 076501. [Google Scholar] [CrossRef] [Green Version]
- Beenakker, C.W.J. Search for Majorana Fermions in Superconductors. Ann. Rev. Condens. Matter Phys. 2013, 4, 113. [Google Scholar] [CrossRef] [Green Version]
- Elliott, S.R.; Franz, M. Colloquium: Majorana fermions in nuclear, particle, and solid-state physics. Rev. Mod. Phys. 2015, 87, 137. [Google Scholar] [CrossRef] [Green Version]
- Ando, Y.; Fu, L. Topological Crystalline Insulators and Topological Superconductors: From Concepts to Materials. Annu. Rev. Condens. Matter Phys. 2015, 6, 361. [Google Scholar] [CrossRef]
- Sato, M.; Ando, Y. Topological superconductors: A review. Rep. Prog. Phys. 2017, 80, 076501. [Google Scholar] [CrossRef] [Green Version]
- Becerra, V.F.; Sardella, E.; Peeters, F.M.; Milošević, M.V. Vortical versus skyrmionic states in mesoscopic p-wave superconductors. Phys. Rev. B 2016, 93, 014518. [Google Scholar] [CrossRef] [Green Version]
- Aguirre, C.; Blas, H.; Barba-Ortega, J. Mesoscale vortex pinning landscapes in a two component superconductor. Phys. C 2018, 554, 8. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Phys. Usp. 2001, 44, 131. [Google Scholar] [CrossRef]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492. [Google Scholar] [CrossRef]
- Brouwer, P.W.; Furusaki, A.; Gruzberg, I.A.; Mudry, C. Localization and Delocalization in Dirty Superconducting Wires. Phys. Rev. Lett. 2000, 85, 1064. [Google Scholar] [CrossRef] [Green Version]
- Motrunich, O.; Damle, K.; Huse, D.A. Griffiths effects and quantum critical points in dirty superconductors without spin-rotation invariance: One-dimensional examples. Phys. Rev. B 2001, 63, 224204. [Google Scholar] [CrossRef] [Green Version]
- Gruzberg, I.A.; Read, N.; Vishveshwara, S. Localization in disordered superconducting wires with broken spin-rotation symmetry. Phys. Rev. B 2005, 71, 245124. [Google Scholar] [CrossRef] [Green Version]
- Brouwer, P.W.; Duckheim, M.; Romita, A.; Oppen, F.V. Probability Distribution of Majorana End-State Energies in Disordered Wires. Phys. Rev. Lett. 2011, 107, 196804. [Google Scholar] [CrossRef] [Green Version]
- Lobos, A.; Lutchyn, R.; Sarma, S.D. Interplay of Disorder and Interaction in Majorana Quantum Wires. Phys. Rev. Lett. 2012, 109, 146403. [Google Scholar] [CrossRef] [Green Version]
- DeGottardi, W.; Sen, D.; Vishveshwara, S. Majorana Fermions in Superconducting 1D Systems Having Periodic, Quasiperiodic, and Disordered Potentials. Phys. Rev. Lett. 2013, 110, 146404. [Google Scholar] [CrossRef] [Green Version]
- DeGottardi, W.; Thakurathi, M.; Vishveshwara, S.; Sen, D. Majorana fermions in superconducting wires: Effects of long-range hopping, broken time-reversal symmetry, and potential landscapes. Phys. Rev. B 2013, 88, 165111. [Google Scholar] [CrossRef] [Green Version]
- Yahyavi, M.; Hetényi, B.; Tanatar, B. Generalized Aubry-André-Harper model with modulated hopping and p-wave pairing. Phys. Rev. B 2019, 100, 064202. [Google Scholar] [CrossRef] [Green Version]
- Cai, X.; Lang, L.J.; Chen, S.; Wang, Y. Topological Superconductor to Anderson Localization Transition in One-Dimensional Incommensurate Lattices. Phys. Rev. Lett. 2013, 110, 176403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeng, Q.B.; Shu, S.; Lü, R. Quench dynamics in the Aubry–André–Harper model with p-wave superconductivity. New. J. Phys. 2018, 20, 053012. [Google Scholar] [CrossRef]
- Tong, X.; Meng, Y.; Jiang, X.; Lee, C.; de Moraes Neto, G.D.; Xianlong, G. Dynamics of a quantum phase transition in the Aubry-André-Harper model with p-wave superconductivity. Phys. Rev. B 2021, 103, 104202. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.J.; Gao, X.; Hu, H. Phase diagram of a non-Abelian Aubry-André-Harper model with p-wave superfluidity. Phys. Rev. B 2016, 93, 104504. [Google Scholar] [CrossRef]
- Lang, L.J.; Chen, S. Majorana fermions in density-modulated p-wave superconducting wires. Phys. Rev. B 2012, 126, 205135. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Yan, H.Y.; Guo, H. Fate of topological states and mobility edges in one-dimensional slowly varying incommensurate potentials. Phys. Rev. B 2017, 96, 174207. [Google Scholar] [CrossRef] [Green Version]
- Roati, G.; Errico, C.D.; Fallani, L.; Fattori, M.; Fort, C.; Zaccanti, M.; Modugno, G.; Modugno, M.; Inguscio, M. Anderson localization of a non-interacting Bose–Einstein condensate. Nature 2008, 453, 895. [Google Scholar] [CrossRef] [Green Version]
- Alex, A.F.; Padavić, K.; Meier, E.J.; Hegde, S.; Ganeshan, S.; Pixley, J.H.; Vishveshwara, S.; Gadway, B. Interactions and Mobility Edges: Observing the Generalized Aubry-André Model. Phys. Rev. Lett. 2021, 126, 040603. [Google Scholar] [CrossRef]
- Osterloh, K.; Baig, M.; Santos, L.; Zoller, P.; Lewenstein, M. Cold Atoms in Non-Abelian Gauge Potentials: From the Hofstadter “Moth” to Lattice Gauge Theory. Phys. Rev. Lett. 2005, 95, 010403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldman, N.; Kubasiak, A.; Gaspard, P.; Lewenstein, M. Ultracold atomic gases in non-Abelian gauge potentials: The case of constant Wilson loop. Phys. Rev. A 2009, 79, 023624. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.; Kitagawa, T.; Alicea, J.; Akhmerov, A.R.; Pekker, D.; Refael, G.; Cirac, J.I.; Demler, E.; Lukin, M.D.; Zoller, P. Majorana Fermions in Equilibrium and in Driven Cold-Atom Quantum Wires. Phys. Rev. Lett. 2011, 106, 220402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldman, N.; Juzeliūnas, G.; Öhberg, P.; Spielman, I.B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 2014, 77, 126401. [Google Scholar] [CrossRef]
- Liu, X.J.; Hu, H. Topological superfluid in one-dimensional spin-orbit-coupled atomic Fermi gases. Phys. Rev. A 2012, 85, 033622. [Google Scholar] [CrossRef]
- Aubry, S.; André, G. Analyticity Breaking and Anderson Localization in Incommensurate Lattices. Ann. Isr. Phys. Soc. 1980, 3, 18. Available online: https://www.researchgate.net/publication/265502988_Analyticity_breaking_and_Anderson_localization_in_incommensurate_lattices (accessed on 23 January 2022).
- Paige, C.; Loan, C.V. A Schur decomposition for Hamiltonian matrices. Linear Algeb. Its Appl. 1981, 41, 11. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Cheng, S.; Guo, H.; Gao, X. Fate of Majorana zero modes, exact location of critical states, and unconventional real-complex transition in non-Hermitian quasiperiodic lattices. Phys. Rev. B 2021, 103, 104203. [Google Scholar] [CrossRef]
- Cheng, S.; Xianlong, G. Majorana zero modes, unconventional real–complex transition, and mobility edges in a one-dimensional non-Hermitian quasi-periodic lattice. Chin. Phys. B 2022, 31, 017401. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).