Capturing a Change in the Covariance Structure of a Multivariate Process

Abstract

This research is inspired from monitoring the process covariance structure of q attributes where samples are independent, having been collected from a multivariate normal distribution with known mean vector and unknown covariance matrix. The focus is on two matrix random variables, constructed from different Wishart ratios, that describe the process for the two consecutive time periods before and immediately after the change in the covariance structure took place. The product moments of these constructed random variables are highlighted and set the scene for a proposed measure to enable the practitioner to calculate the run-length probability to detect a shift immediately after a change in the covariance matrix occurs. Our results open a new approach and provides insight for detecting the change in the parameter structure as soon as possible once the underlying process, described by a multivariate normal process, encounters a permanent/sustained upward or downward shift.

1. Introduction

1.1. Problem Description and Approach

Ref.  [1] investigated the problem of monitoring an attribute from the start of production, whether or not prior information is available, and presented Q-charts assuming that the observations from each sample are independent and identically distributed normal random variables. The run-length is a measure to gain insight into the performance of a control chart. Ref. [2] proposed an accurate, analytic approximation, while the approach of [3] was embedded in a nonstationary, discrete-time Markov chain to compute the run-length distribution. Ref. [4] considered independent samples observed from a normal distribution and monitors the variance of the sequential process when it encounters an unknown sustained shift. Only a permanent upward or downward step shift in the variance was considered. The focus of [5,6] were to develop exact expressions for the probabilities of run-lengths, and as a result the joint distribution of the charting statistics is needed. The statistical property that is of interest is the moments of the random variables (charting statistics) to illustrate the behaviour of this distribution. The property is of relevance since, once the process is out-of-control, the charting statistics are no longer independent. The correlation structure is then of particular interest. We refer to the papers of [4,5,6] that provide an overview of the practical problem which is the genesis of the following random variables:

$$Q_0=\frac{\lambda T_0}{Z}\mathrm{and}{Q}_j=\frac{\lambda T_j}{Z+\lambda {\displaystyle \sum _{k=0}^{j-1}}{T}_k},j=1,2,\dots ,p\mathrm{with}\lambda >0$$

(1)

(see expression (6) p. 1049 of [5]) where Z and $T_j,$ $j=0,1,\dots ,p$ are central chi-squared random variables and $\lambda$ indicates the shift parameter when the process variance parameter has changed from ${\sigma }^2$ to ${\sigma }_1^2=\lambda {\sigma }^2$.

The direct focus of this paper is, however, on a multivariate process. Suppose the covariance structure of q attributes of the items of a single process are monitored simultaneously where the samples are independently observed, and at each point in time $\left(i\right)$ a sample of size $n_i$ is collected. Assume that these samples are collected from a multivariate normal distribution with known mean vector (${\underline{\mu }}_0$) and unknown covariance matrix ($\Sigma :q\times q$) which we’ll denote as $MVN\left({\underline{\mu }}_0,\Sigma \right)$. Let ${\mathbf{Y}}^{\left(i\right)}:n_i\times q$ denote the matrix of observations for time period $i,$ where ${\underline{Y}}_1^{\left(i\right)},{\underline{Y}}_2^{\left(i\right)},\dots ,{\underline{Y}}_q^{\left(i\right)}$ denote the column vectors (i.e., the $n_i$ observations of each attribute) and ${\underline{Y}}_{\left(1\right)}^{\left(i\right)},{\underline{Y}}_{\left(2\right)}^{\left(i\right)},\dots ,{\underline{Y}}_{\left(n_i\right)}^{\left(i\right)}$ denote the row vectors (i.e., observations of each sample) of ${\mathbf{Y}}^{\left(i\right)}$, i.e.,

$${\mathbf{Y}}^{\left(i\right)}:n_i\times q=\left(\begin{array}{cccc}\hfill Y_{11}^{\left(i\right)}& Y_{12}^{\left(i\right)}& \cdots \hfill & Y_{1q}^{\left(i\right)}\\ \hfill Y_{21}^{\left(i\right)}& Y_{22}^{\left(i\right)}& \cdots \hfill & Y_{2q}^{\left(i\right)}\\ \hfill ⋮& ⋮& \hfill & ⋮\\ \hfill Y_{n_{i}1}^{\left(i\right)}& Y_{n_{i}2}^{\left(i\right)}& \cdots \hfill & Y_{n_{i}q}^{\left(i\right)}\end{array}\right).$$

Assume further that the observations within each sample are independent, therefore the row vectors ${\underline{Y}}_{\left(1\right)}^{\left(i\right)},{\underline{Y}}_{\left(2\right)}^{\left(i\right)},\dots ,{\underline{Y}}_{\left(n_i\right)}^{\left(i\right)}$ represent independent observations from a $MVN\left({\underline{\mu }}_0,\Sigma \right)$ distribution. The sample covariance matrix at time i is denoted by ${\mathbf{S}}_i:q\times q$, where it is known that ${\mathbf{S}}_i$ follows a Wishart distribution (see [7]). Since we assume that $\Sigma$ is unknown, the first sample is used to obtain an initial point estimate of $\Sigma ,$ i.e., the sample covariance matrix ${\mathbf{S}}_1$. At sample number two, ${\mathbf{S}}_2$ is compared to ${\mathbf{S}}_1$ to investigate whether the covariance structure is still the same. If so, a pooled sample covariance matrix is calculated (based on the observations in samples 1 and 2) which will be compared to ${\mathbf{S}}_3$ at time period three. This sequential updating and testing procedure continues until the process is observed (or rather, declared) to be out-of-control.

The scenario under consideration in this paper is described in Figure 1, and, without loss of generality it is assumed that the mean vector is the null vector. Suppose that between samples $\kappa -1$ and $\kappa$ the covariance structure changes as shown in Figure 1, i.e., from $\Sigma$ to $\lambda \Sigma$ where $\lambda >0$ and $\lambda \ne 1$, where the location of the shift between these samples is unknown. In this paper the two matrix random variables, ${\mathbf{U}}_0$ and ${\mathbf{U}}_1,$ that correspond to the two successive time periods immediately after the change in the covariance structure occurred (i.e., sample $\kappa$ and sample $\kappa +1)$ will be the focus. Formally this can be described as

$$\begin{array}{ccc}\hfill {\mathbf{U}}_0& =& {\mathbf{X}}^{-\frac{1}{2}}\lambda {\mathbf{W}}_0{\mathbf{X}}^{-\frac{1}{2}}\hfill \\ \hfill {\mathbf{U}}_1& =& {\left(\mathbf{X}+\lambda {\mathbf{W}}_0\right)}^{-\frac{1}{2}}\lambda {\mathbf{W}}_1{\left(\mathbf{X}+\lambda {\mathbf{W}}_0\right)}^{-\frac{1}{2}}\hfill \end{array}$$

(2)

where ${\mathbf{C}}^{\frac{1}{2}}$ denotes the unique positive definite square root of a matrix $\mathbf{C}$. In this case $\mathbf{X}$ has a Wishart distribution with parameters $v_1$ and $\Sigma ,$ denoted $W_q\left(v_1,\Sigma \right),$ ${\mathbf{W}}_0$ is $W_q\left(v_2,\Sigma \right)$ distributed and ${\mathbf{W}}_1$ has a $W_q\left(v_3,\Sigma \right)$ distribution with $\mathbf{X}$, ${\mathbf{W}}_0$ and ${\mathbf{W}}_1$ independent $\left(v_i\ge q,i=1,2,3\right)$. In terms of the statistical process control (SPC) literature the parameters are interpretable as $v_1={\sum }_{i=1}^{\kappa -1}{n}_i,$$v_2=n_{\kappa }$ and $v_3=n_{\kappa +1}$.

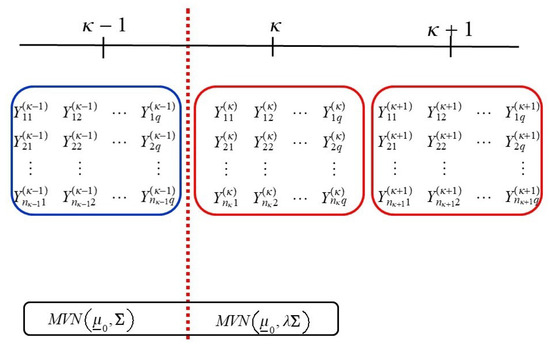
Figure 1. Schematic description of the multivariate process.

If $q=1$ in Equation (2), then the random variables simplify to the case for two successive time periods $\left(Q_0\mathrm{and}{Q}_1\right)$ in Equation (1), and so Equation (2) can be represented as

$$\begin{array}{ccc}\hfill {\mathbf{U}}_0& =& {\mathbf{X}}^{-\frac{1}{2}}{\mathbf{W}}_0{\mathbf{X}}^{-\frac{1}{2}}\hfill \\ \hfill {\mathbf{U}}_1& =& {\left(\mathbf{X}+{\mathbf{W}}_0\right)}^{-\frac{1}{2}}{\mathbf{W}}_1{\left(\mathbf{X}+{\mathbf{W}}_0\right)}^{-\frac{1}{2}}\hfill \end{array}$$

(3)

where $\mathbf{X}\sim W_q\left(v_1,\Sigma \right),$${\mathbf{W}}_0\sim W_q\left(v_2,\lambda \Sigma \right)$ and ${\mathbf{W}}_1\sim W_q\left(v_3,\lambda \Sigma \right)$. Refs. [8,9] previously described constructions of this nature. The advantage of this approach lies in the mathematical and statistical formulation of observing a change in the covariance matrix in such a sequential process, and to present this matrix-based framework and results for further future study within SPC.

1.2. Outline of Paper

In Section 2, the distribution of the matrix random variables (3) is unknown and will be investigated; and expressions for the marginal distributions and moments $E\left[|{\mathbf{U}}_i{|}^{h_j}|\right]$ are given for $i=0,1,j=1,2$, which are used to obtain exact expressions for the pdfs of $|{\mathbf{U}}_0|$ and $|{\mathbf{U}}_1|$ (relying on mathematical tools reviewed in Section 1.3. The cumulative distribution function (cdf) of $\left|{\mathbf{U}}_0\right|$ and $\left|{\mathbf{U}}_1\right|$ are given and used as part of the numerical example within an SPC environment in Section 3. In particular, a measure is proposed to determine the probability that a control chart will signal immediately after a change in the covariance matrix. The expressions are given in computable terms of Meijer’s G-function, and also theoretical terms involving zonal polynomials and hypergeometric functions with matrix argument which are often encountered in the literature (see [7,10,11,12,13,14,15]). Finally, Section 4 contains discussions and conclusions.

1.3. Mathematical Toolbox

Some essential mathematical tools and definitions for this paper are listed below.

• (Ref. [16]) The multivariate gamma function, denoted ${\mathrm{\Gamma }}_q\left(\alpha \right),$ is defined as

  $$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_q\left(\alpha \right)& =& {\int }_{\mathbf{S}>\mathbf{0}}etr\left(-\mathbf{S}\right){\left|\mathbf{S}\right|}^{\alpha -\frac{1}{2}\left(q+1\right)}d\mathbf{S}\hfill \\ & =& {\pi }^{\frac{1}{4}q\left(q-1\right)}\prod _{i=1}^q\mathrm{\Gamma }\left[\alpha -\frac{1}{2}\left(i-1\right)\right]\hfill \end{array}$$

  (4)

  where $\Re \left(\alpha \right)>\frac{1}{2}\left(q-1\right)$, and the integral is over the space of $q\times q$ positive definite matrices. For $q=1$ it simplifies to the gamma function. The generalised gamma function of weight $\tau$ is defined as

  $$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_q\left(\alpha ,\tau \right)& =& {\pi }^{\frac{1}{4}q\left(q-1\right)}\prod _{j=1}^q\mathrm{\Gamma }\left[\alpha +t_j-\frac{1}{2}\left(j-1\right)\right]\hfill \\ & =& {\left(\alpha \right)}_{\tau }{\mathrm{\Gamma }}_q\left(\alpha \right)\hfill \end{array}$$

  (5)

  where the integral is over the space of $q\times q$ positive definite matrices, ${\left(\alpha \right)}_{\tau }$ is the generalised hypergeometric coefficient, $\Re \left(\alpha \right)\ge \frac{1}{2}\left(q-1\right)-t_q,\tau =\left(t_1,\dots ,t_q\right)$, $t_1\ge \cdots \ge t_q\ge 0$, $t_1+\cdots +t_q=t$ and ${\mathrm{\Gamma }}_q\left(\alpha ,0\right)={\mathrm{\Gamma }}_q\left(\alpha \right)$. Finally then, the following Laplace transform is used subsequently and given by (see also [12]):

  $${\int }_{\mathbf{S}>\mathbf{0}}etr\left(-\mathbf{SX}\right){\left|\mathbf{S}\right|}^{\alpha -\frac{1}{2}\left(q+1\right)}d\mathbf{S}={\mathrm{\Gamma }}_q\left(\alpha \right){\left|\mathbf{S}\right|}^{-\alpha }.$$

  (6)
• (Ref. [16]) The multivariate beta function, denoted by ${\beta }_q\left(\alpha ,b\right)$, is defined as

  $${\beta }_q\left(\alpha ,\beta \right)={\int }_{\mathbf{0}<\mathbf{S}<{\mathbf{I}}_q}{\left|\mathbf{S}\right|}^{\alpha -\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{I}}_q-\mathbf{S}\right|}^{\beta -\frac{1}{2}\left(q+1\right)}d\mathbf{S}=\frac{{\mathrm{\Gamma }}_q\left(\alpha \right){\mathrm{\Gamma }}_q\left(\beta \right)}{{\mathrm{\Gamma }}_q\left(\alpha +\beta \right)}$$

  (7)

  where $\Re \left(\alpha \right)>\frac{1}{2}\left(q-1\right)$, $\Re \left(\beta \right)>\frac{1}{2}\left(q-1\right)$ and ${\mathrm{\Gamma }}_q\left(·\right)$ is the multivariate gamma function. For $q=1$ it simplifies to the usual beta function.
• (Ref. [15]) Meijer’s G-function with the parameters ${\alpha }_1,\dots ,{\alpha }_r$ and ${\beta }_1,\dots ,{\beta }_s$ is defined as

  $$G_{r,s}^{m,n}\left({x|}_{{\beta }_1,\dots ,{\beta }_s}^{{\alpha }_1,\dots ,{\alpha }_r}\right)=\frac{1}{2\pi i}{\int }_{L}g\left(h\right)x^{-h}dh$$

  (8)

  where $i=\sqrt{-1},$L is a suitable contour,$x\ne 0,$ and

  $$g\left(h\right)=\frac{{\prod }_{j=1}^m\mathrm{\Gamma }\left({\beta }_j+h\right){\prod }_{j=1}^n\mathrm{\Gamma }\left(1-{\alpha }_j-h\right)}{{\prod }_{j=m+1}^s\mathrm{\Gamma }\left(1-{\beta }_j-h\right){\prod }_{j=n+1}^r\mathrm{\Gamma }\left({\alpha }_j+h\right)}$$

  where $m,$n, r and s are integers with $0\le n\le r$ and $0\le m\le s.$
• (Refs. [15,17,18]) The hypergeometric function of matrix argument is defined by

  $${}_r{F}_s\left({\alpha }_1,\dots ,{\alpha }_r;{\beta }_1,\dots ,{\beta }_s;\mathbf{S}\right)=\sum _{t=0}^{\infty }\sum _{\tau }\frac{{\left({\alpha }_1\right)}_{\tau }\cdots {\left({\alpha }_r\right)}_{\tau }}{{\left({\beta }_1\right)}_{\tau }\cdots {\left({\beta }_s\right)}_{\tau }}\frac{1}{t!}{C}_{\tau }\left(\mathbf{S}\right),$$

  (9)

  where ${\alpha }_i$, $i=1,\dots ,r;$${\beta }_j,$$j=1,\dots ,s$ are arbitrary numbers, $\mathbf{S}$$\left(q\times q\right)$ is a real symmetric matrix, ${\sum }_{\tau }$ denotes summation over all partitions $\tau$, $C_{\tau }\left(\mathbf{S}\right)$ is the zonal polynomial of $\mathbf{S}$, ${\left(\alpha \right)}_{\tau }$ is the generalised hypergeometric coefficient.
• Two special cases of Equation (9) are of interest:

  1.

  If $\mathbf{X}:\left(q\times q\right)$ is a symmetric matrix where $∥\mathbf{X}∥<1,$ then

  $${}_1{F}_0\left(\alpha ;\mathbf{X}\right)=\frac{1}{{\mathrm{\Gamma }}_q\left(\alpha \right)}{\int }_{\mathbf{S}>\mathbf{0}}etr\left[-\mathbf{S}\left({\mathbf{I}}_q-\mathbf{X}\right)\right]{\left|\mathbf{S}\right|}^{\alpha -\frac{1}{2}\left(q+1\right)}d\mathbf{S}={\left|{\mathbf{I}}_q-\mathbf{X}\right|}^{-\alpha },$$

  (10)

  where $\Re \left(\alpha \right)>\frac{1}{2}\left(q-1\right).$

  2.

  If $\mathbf{X}:\left(q\times q\right)$ is a symmetric matrix where $∥\mathbf{X}∥<1,$ then

  $$\begin{array}{ccc}& & {}_2{F}_1\left(\alpha ,\beta ;c;\mathbf{X}\right)\hfill \\ & & =\frac{{\mathrm{\Gamma }}_q\left(c\right)}{{\mathrm{\Gamma }}_q\left(\alpha \right){\mathrm{\Gamma }}_q\left(c-\alpha \right)}{\int }_{\mathbf{0}<\mathbf{S}<{\mathbf{I}}_q}{\left|\mathbf{S}\right|}^{\alpha -\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{I}}_q-\mathbf{S}\right|}^{c-\alpha -\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{I}}_q-\mathbf{XS}\right|}^{-\beta }d\mathbf{S}\hfill \\ \hfill \end{array}$$

  (11)

  where $\Re \left(c\right)>\frac{1}{2}\left(q-1\right)$ and $\Re \left(c-\alpha \right)>\frac{1}{2}\left(q-1\right).$ This is known as the Gauss hypergeometric function of matrix argument.

• (Ref. [4]) Two particular results are of interest here.

  1.

  If $\mathbf{S}:\left(q\times q\right)$$>\mathbf{0},$ $\mathbf{B}:\left(q\times q\right)>\mathbf{0},\mathbf{B}$ free of elements of $\mathbf{S}$, then

  $$\begin{array}{ccc}& & {\int }_{\mathbf{S}>\mathbf{0}}{\left|\mathbf{S}\right|}^{\alpha -\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{I}}_q+\mathbf{S}\right|}^{-\beta }{\left|{\mathbf{I}}_q+\mathbf{BS}\right|}^{-c}d\mathbf{S}\hfill \\ & =& {\beta }_q\left(\alpha ,\beta +c-\alpha \right){\left|\mathbf{B}\right|}^{-c}{}_2{F}_1\left(\beta +c-\alpha ,c;\beta +c;{\mathbf{I}}_q-{\mathbf{B}}^{-1}\right)\hfill \end{array}$$

  (12)

  where $∥{\mathbf{I}}_q-{\mathbf{B}}^{-1}∥<1,$ $\Re \left(\beta +c-\alpha \right)>\frac{1}{2}\left(q-1\right)$, and $\Re \left(\alpha \right)>\frac{1}{2}\left(q-1\right)$.

  2.

  The confluent hypergeometric function $\mathrm{\Psi }(·)$ of symmetric matrix $\mathbf{R}:\left(q\times q\right)$ is defined by

  $$\mathrm{\Psi }\left(\alpha ,c,\mathbf{R}\right)=\frac{1}{{\mathrm{\Gamma }}_q\left(\alpha \right)}{\int }_{\mathbf{S}>\mathbf{0}}etr\left(-\mathbf{RS}\right){\left|\mathbf{S}\right|}^{\alpha -\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{I}}_q+\mathbf{S}\right|}^{c-\alpha -\frac{1}{2}\left(q+1\right)}d\mathbf{S}$$

  (13)

  where $\mathbf{R}>\mathbf{0}$ and $\Re \left(\alpha \right)>\frac{1}{2}\left(q-1\right).$ Then

  $$\begin{array}{ccc}& & {\int }_{\mathbf{Y}>\mathbf{0}}{\left|\mathbf{Y}\right|}^{\beta -\frac{1}{2}\left(q+1\right)}etr\left(-\mathbf{XY}\right)\mathrm{\Psi }\left(\alpha ,c,\mathbf{Y}\right)d\mathbf{Y}\hfill \\ & =& \frac{{\mathrm{\Gamma }}_q\left(\beta \right){\mathrm{\Gamma }}_q\left(\beta -c+\frac{1}{2}\left(q+1\right)\right)}{{\mathrm{\Gamma }}_q\left(\alpha +\beta -c+\frac{1}{2}\left(q+1\right)\right)}\hfill \\ & & {\times }_2{F}_1\left(\beta -c+\frac{1}{2}\left(q+1\right),\beta ;\alpha +\beta -c+\frac{1}{2}\left(q+1\right);{\mathbf{I}}_q-\mathbf{X}\right)\hfill \end{array}$$

  (14)

  where $∥{\mathbf{I}}_q-\mathbf{X}∥<1$ and $\Re \left(\alpha \right)>\frac{1}{2}\left(q-1\right),$ $\Re \left(\beta -c\right)>-1.$ Furthermore, let $\mathbf{B}>\mathbf{0}$. It can then be shown that

  $$\begin{array}{ccc}& & {\int }_{\mathbf{Y}>\mathbf{0}}{\left|\mathbf{Y}\right|}^{\beta -\frac{1}{2}\left(q+1\right)}etr\left(-\mathbf{XY}\right)\mathrm{\Psi }\left(\alpha ,c,{\mathbf{B}}^{\frac{1}{2}}{\mathbf{YB}}^{\frac{1}{2}}\right)d\mathbf{Y}\hfill \\ & =& {\left|\mathbf{B}\right|}^{-\beta }\frac{{\mathrm{\Gamma }}_q\left(\beta \right){\mathrm{\Gamma }}_q\left(\beta -c+\frac{1}{2}\left(q+1\right)\right)}{{\mathrm{\Gamma }}_q\left(\alpha +\beta -c+\frac{1}{2}\left(q+1\right)\right)}\hfill \\ & & {\times }_2{F}_1\left(\beta -c+\frac{1}{2}\left(q+1\right),\beta ;\left(\alpha +\beta -c+\frac{1}{2}\left(q+1\right)\right);{\mathbf{I}}_q-{\mathbf{B}}^{-\frac{1}{2}}{\mathbf{XB}}^{-\frac{1}{2}}\right)\hfill \end{array}$$

  (15)

  where $∥{\mathbf{I}}_q-{\mathbf{B}}^{-\frac{1}{2}}{\mathbf{XB}}^{-\frac{1}{2}}∥<1$ and $\Re \left(\alpha \right)>\frac{1}{2}\left(q-1\right),$ $\Re \left(\beta -c\right)>-1$.

2. Methodology

In this section the focus is to derive the joint distribution of ${\mathbf{U}}_0$ and ${\mathbf{U}}_1$ that capture the change in the covariance structure as depicted in Figure 1. From this joint distribution, the distributions of $\left|{\mathbf{U}}_0\right|$ and $\left|{\mathbf{U}}_1\right|$ are investigated to pave the way for the calculation of run-length probabilities in this matrix setting. The joint distribution of ${\mathbf{U}}_0$ and ${\mathbf{U}}_1$ is referred to as a generalised bimatrix variate beta type II distribution (functional symmetry is assumed as the symmetrization technique of [19] is inappropriate for this scenario). Without loss of generality, we assume that $\Sigma ={\mathbf{I}}_q$.

Theorem 1.

Suppose that $\mathbf{X}\sim W_q\left(v_1,\Sigma \right)$ is independent of ${\mathbf{W}}_0\sim W_q\left(v_2,\lambda \Sigma \right)$ and ${\mathbf{W}}_1\sim W_q\left(v_3,\lambda \Sigma \right)$. Let $C^{-1}=2^{\frac{1}{2}q\left(v_1+v_2+v_3\right)}{\sum }_{i=1}^3{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_i\right){\lambda }^{\frac{1}{2}q\left(v_2+v_3\right)}$. Then, the pdf of:

1. 

Equation (3) is given by

$$\begin{array}{ccc}& & f({\mathbf{U}}_0,{\mathbf{U}}_1)\hfill \\ & =& C{\left|{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_2-\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{I}}_q+{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_3}\hfill \\ & & \times {\left|{\mathbf{U}}_1\right|}^{\frac{1}{2}{v}_3-\frac{1}{2}\left(q+1\right)}{\int }_{\mathbf{U}>\mathbf{0}}{\left|\mathbf{U}\right|}^{\frac{1}{2}\left(v_1+v_2+v_3\right)-\frac{1}{2}\left(q+1\right)}\hfill \\ & & \times etr\left(-\frac{1}{2}\mathbf{U}\left({\mathbf{I}}_q+\frac{1}{\lambda }{\mathbf{U}}_0\right)\right)etr\left(-\frac{1}{2\lambda }{\mathbf{U}}^{\frac{1}{2}}\left({\mathbf{I}}_q+{\mathbf{U}}_0\right){\mathbf{U}}^{\frac{1}{2}}{\mathbf{U}}_1\right)\mathbf{dU},\hfill \end{array}$$

(16)

2. 

${\mathbf{U}}_0$ is given by

$$f\left({\mathbf{U}}_0\right)=\frac{{\mathrm{\Gamma }}_q\left(\frac{1}{2}\left(v_1+v_2\right)\right)}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_1\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_2\right)}{\lambda }^{\frac{1}{2}q{v}_1}{\left|{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_2-\frac{1}{2}\left(q+1\right)}{\left|\lambda {\mathbf{I}}_q+{\mathbf{U}}_0\right|}^{-\frac{1}{2}\left(v_1+v_2\right)},$$

(17)

3. 

${\mathbf{U}}_1$ is given by

$$\begin{array}{ccc}& & f\left({\mathbf{U}}_1\right)\hfill \\ & =& \frac{{\mathrm{\Gamma }}_q\left(\frac{1}{2}\left(v_1+v_2+v_3\right)\right)}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}\left(v_1+v_2\right)\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_3\right)}{\lambda }^{\frac{1}{2}q{v}_1}{\left|{\mathbf{U}}_1\right|}^{\frac{1}{2}{v}_3-\frac{1}{2}\left(q+1\right)}{\left|\lambda {\mathbf{I}}_q+{\mathbf{U}}_1\right|}^{-\frac{1}{2}\left(v_1+v_2+v_3\right)}\hfill \\ & & \times {}_2{F}_1\left(\frac{1}{2}{v}_2,\frac{1}{2}\left(v_1+v_2+v_3\right);\frac{1}{2}\left(v_1+v_2\right);{\mathbf{I}}_q-{\left({\mathbf{I}}_q+{\mathbf{U}}_1\right)}^{\frac{1}{2}}{\left(\lambda {\mathbf{I}}_q+{\mathbf{U}}_1\right)}^{-1}{\left({\mathbf{I}}_q+{\mathbf{U}}_1\right)}^{\frac{1}{2}}\right)\hfill \end{array}$$

(18)

where ${\mathbf{U}}_i>\mathbf{0},i=0,1$ with $\Re \left(v_i\right)>q-1,$ $i=1,2,3$, and 

$$∥{\mathbf{I}}_q-{\left({\mathbf{I}}_q+{\mathbf{U}}_1\right)}^{\frac{1}{2}}{\left(\lambda {\mathbf{I}}_q+{\mathbf{U}}_1\right)}^{-1}{\left({\mathbf{I}}_q+{\mathbf{U}}_1\right)}^{\frac{1}{2}}∥<1.$$

Proof. 

1.

The joint pdf of $\mathbf{X},{\mathbf{W}}_0,{\mathbf{W}}_1$ is given by

$$\begin{array}{ccc}\hfill f\left(\mathbf{X},{\mathbf{W}}_0,{\mathbf{W}}_1\right)& =& C{\left|\mathbf{X}\right|}^{\frac{1}{2}\left(v_1-q-1\right)}{\left|{\mathbf{W}}_0\right|}^{\frac{1}{2}\left(v_2-q-1\right)}{\left|{\mathbf{W}}_1\right|}^{\frac{1}{2}\left(v_3-q-1\right)}\hfill \\ & & \times etr\left(-\frac{1}{2}\mathbf{X}\right)etr\left(-\frac{1}{2}{\lambda }^{-1}{\mathbf{W}}_0\right)etr\left(-\frac{1}{2}{\lambda }^{-1}{\mathbf{W}}_1\right).\hfill \end{array}$$

(19)

Making the transformation

$$\mathbf{U}=\mathbf{X},{\mathbf{U}}_0={\mathbf{X}}^{-\frac{1}{2}}{\mathbf{W}}_0{\mathbf{X}}^{-\frac{1}{2}},{\mathbf{U}}_1={\left(\mathbf{X}+{\mathbf{W}}_0\right)}^{-\frac{1}{2}}{\mathbf{W}}_1{\left(\mathbf{X}+{\mathbf{W}}_0\right)}^{-\frac{1}{2}},$$

leaves

$$\mathbf{X}=\mathbf{U},{\mathbf{W}}_0={\mathbf{U}}^{\frac{1}{2}}{\mathbf{U}}_0{\mathbf{U}}^{\frac{1}{2}},{\mathbf{W}}_1={\left(\mathbf{U}+{\mathbf{U}}^{\frac{1}{2}}{\mathbf{U}}_0{\mathbf{U}}^{\frac{1}{2}}\right)}^{\frac{1}{2}}{\mathbf{U}}_1{\left(\mathbf{U}+{\mathbf{U}}^{\frac{1}{2}}{\mathbf{U}}_0{\mathbf{U}}^{\frac{1}{2}}\right)}^{\frac{1}{2}}.$$

From [16] p. 12, the Jacobian of the transformation is given by

$$\begin{array}{ccc}\hfill J\left(\mathbf{X},{\mathbf{W}}_0,{\mathbf{W}}_1\to \mathbf{U},{\mathbf{U}}_0,{\mathbf{U}}_1\right)& =& J\left(\mathbf{X}\to \mathbf{U}\right)J\left({\mathbf{W}}_0\to {\mathbf{U}}_0\right)J\left({\mathbf{W}}_1\to {\mathbf{U}}_1\right)\hfill \\ & =& {\left|\mathbf{U}\right|}^{q+1}{\left|{\mathbf{I}}_q+{\mathbf{U}}_0\right|}^{\frac{1}{2}\left(q+1\right)}.\hfill \end{array}$$

(20)

Therefore, substituting in Equation (19) gives the joint pdf of $\left(\mathbf{U},{\mathbf{U}}_0,{\mathbf{U}}_1\right)$ as

$$\begin{array}{ccc}& & f\left(\mathbf{U},{\mathbf{U}}_0,{\mathbf{U}}_1\right)\hfill \\ & =& C^{-1}{\left|\mathbf{U}\right|}^{\frac{1}{2}\left(v_1+v_2+v_3\right)-\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_2-\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{I}}_q+{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_3}{\left|{\mathbf{U}}_1\right|}^{\frac{1}{2}{v}_3-\frac{1}{2}\left(q+1\right)}\hfill \\ & & \times etr\left(-\frac{1}{2}\mathbf{U}\right)etr\left(-\frac{1}{2}{\lambda }^{-1}{\mathbf{UU}}_0\right)etr\left(-\frac{1}{2}{\lambda }^{-1}{\mathbf{U}}^{\frac{1}{2}}\left({\mathbf{I}}_q+{\mathbf{U}}_0\right){\mathbf{U}}^{\frac{1}{2}}{\mathbf{U}}_1\right)\hfill \end{array}$$

(21)

which leaves the final result.

2.

The marginal pdf of ${\mathbf{U}}_0$ is obtained by integrating $f({\mathbf{U}}_0,{\mathbf{U}}_1)$ (see Equation (16)) with respect to ${\mathbf{U}}_1$ using Equation (6):

$$\begin{array}{ccc}& & f\left({\mathbf{U}}_0\right)\hfill \\ & =& C{\left|{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_2-\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{I}}_q+{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_3}\hfill \\ & & \times {\int }_{\mathbf{U}>\mathbf{0}}{\left|\mathbf{U}\right|}^{\frac{1}{2}\left(v_1+v_2+v_3\right)-\frac{1}{2}\left(q+1\right)}etr\left(\frac{1}{2}\mathbf{U}\left({\mathbf{I}}_q+{\lambda }^{-1}{\mathbf{U}}_0\right)\right)\hfill \\ & & \times {\int }_{{\mathbf{U}}_1>\mathbf{0}}{\left|{\mathbf{U}}_1\right|}^{\frac{1}{2}{v}_3-\frac{1}{2}\left(q+1\right)}etr\left(-\frac{1}{2}{\lambda }^{-1}{\mathbf{U}}^{\frac{1}{2}}\left({\mathbf{I}}_{\mathbf{q}}+{\mathbf{U}}_0\right){\mathbf{U}}^{\frac{1}{2}}{\mathbf{U}}_1\right)d{\mathbf{U}}_{1}d\mathbf{U}\hfill \\ & =& C{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_3\right){\left(2\lambda \right)}^{\frac{1}{2}{v}_{3}q}{\left|{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_2-\frac{1}{2}\left(q+1\right)}\hfill \\ & & \times {\int }_{\mathbf{U}>\mathbf{0}}{\left|\mathbf{U}\right|}^{\frac{1}{2}\left(v_1+v_2\right)-\frac{1}{2}\left(q+1\right)}etr\left(-\frac{1}{2}\mathbf{U}\left({\mathbf{I}}_q+{\lambda }^{-1}{\mathbf{U}}_0\right)\right)d\mathbf{U}\hfill \end{array}$$

from where the result follows immediately.

3.

From Equations (16) and (13) and (14) it follows that

$$\begin{array}{ccc}\hfill & & f\left({\mathbf{U}}_1\right)\hfill \\ \hfill & =& C{\left|{\mathbf{U}}_1\right|}^{\frac{1}{2}{v}_3-\frac{1}{2}\left(q+1\right)}{\int }_{\mathbf{U}>\mathbf{0}}{\left|\mathbf{U}\right|}^{\frac{1}{2}\left(v_1+v_2+v_3\right)-\frac{1}{2}\left(q+1\right)}etr\left(-\frac{1}{2}\left({\mathbf{I}}_q+{\lambda }^{-1}{\mathbf{U}}_1\right)\mathbf{U}\right)\hfill \\ \hfill & & {\int }_{{\mathbf{U}}_0>\mathbf{0}}{\left|{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_2-\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{I}}_q+{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_3}etr\left(-\frac{1}{2}{\lambda }^{-1}\left(\mathbf{U}+{\mathbf{U}}^{\frac{1}{2}}{\mathbf{U}}_1{\mathbf{U}}^{\frac{1}{2}}\right){\mathbf{U}}_0\right)d{\mathbf{U}}_{0}d\mathbf{U}\hfill \\ \hfill & =& C{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_2\right){\left|{\mathbf{U}}_1\right|}^{\frac{1}{2}{v}_3-\frac{1}{2}\left(q+1\right)}{\int }_{\mathbf{U}>\mathbf{0}}{\left|\mathbf{U}\right|}^{\frac{1}{2}\left(v_1+v_2+v_3\right)-\frac{1}{2}\left(q+1\right)}etr\left(-\frac{1}{2}\left({\mathbf{I}}_q+{\lambda }^{-1}{\mathbf{U}}_1\right)\mathbf{U}\right)\hfill \\ \hfill & & \times \mathrm{\Psi }\left(\frac{1}{2}{v}_2,\frac{1}{2}{v}_2+\frac{1}{2}{v}_3+\frac{1}{2}\left(q+1\right),\frac{1}{2}{\lambda }^{-1}{\left({\mathbf{I}}_q+{\mathbf{U}}_1\right)}^{\frac{1}{2}}\mathbf{U}{\left(\mathbf{I}+{\mathbf{U}}_1\right)}^{\frac{1}{2}}\right)d\mathbf{U}\hfill \end{array}$$

(22)

from where the result follows. □

Remark 1.

Substituting $\lambda =1$ (i.e., there is no change in the covariance structure and therefore the process remains in-control) in Equation (17) gives the well-known matrix variate beta type II distribution with parameters ($\frac{1}{2}{v}_1,\frac{1}{2}{v}_2$) with pdf

$$\frac{{\mathrm{\Gamma }}_q\left(\frac{1}{2}\left(v_1+v_2\right)\right)}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_1\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_2\right)}{\left|{\mathbf{U}}_0\right|}^{\frac{1}{2}{v}_2-\frac{1}{2}\left(q+1\right)}{\left|{\mathbf{I}}_q+{\mathbf{U}}_0\right|}^{-\frac{1}{2}\left(v_1+v_2\right)}$$

where ${\mathbf{U}}_0>\mathbf{0}$.

The hth moments of $\left|{\mathbf{U}}_0\right|$ and $\left|{\mathbf{U}}_1\right|$ are given in the following corollary. The moments are used to determine the distribution of $\left|{\mathbf{U}}_0\right|$ and $\left|{\mathbf{U}}_1\right|$, and exact expressions for the pdfs and cdfs of $\left|{\mathbf{U}}_0\right|$ and $\left|{\mathbf{U}}_1\right|$ are subsequently derived.

Corollary 1.

Suppose that $\mathbf{X}\sim W_q\left(v_1,\Sigma \right)$ is independent of ${\mathbf{W}}_0\sim W_q\left(v_2,\lambda \Sigma \right)$ and ${\mathbf{W}}_1\sim W_q\left(v_3,\lambda \Sigma \right).$ If the joint pdf of Equation (3) is given by Equation (16), then

1. 

The product moment $E\left({\left|{\mathbf{U}}_0\right|}^{h_1}\right)$ is given by

$$E\left({\left|{\mathbf{U}}_0\right|}^{h_1}\right)=\frac{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_1-h_1\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_2+h_1\right)}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_1\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_2\right)}{\lambda }^{q{h}_1}$$

(23)

where $\Re \left(\frac{1}{2}{v}_1-h_1\right)>\frac{1}{2}\left(q-1\right),$ $\Re \left(\frac{1}{2}{v}_2+h_1\right)>\frac{1}{2}\left(q-1\right)$.

2. 

The product moment $E\left({\left|{\mathbf{U}}_1\right|}^{h_2}\right)$ is given by

$$\begin{array}{ccc}\hfill E\left({\left|{\mathbf{U}}_1\right|}^{h_2}\right)& =& \frac{{\mathrm{\Gamma }}_q\left(\frac{1}{2}\left(v_1+v_2\right)-h_2\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_3+h_2\right){\lambda }^{\frac{1}{2}{v}_{1}q}}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_3\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}\left(v_1+v_2\right)\right)}\hfill \\ & & {\times }_2{F}_1\left(\frac{1}{2}{v}_1,\frac{1}{2}\left(v_1+v_2\right)-h_2;\frac{1}{2}\left(v_1+v_2\right);\left(1-\lambda \right){\mathbf{I}}_q\right)\hfill \end{array}$$

(24)

where$∥\left(1-\lambda \right){\mathbf{I}}_q∥<1,$$\Re \left(\frac{1}{2}\left(v_1+v_2\right)-h_2\right)>\frac{1}{2}\left(q-1\right),$$\Re \left(\frac{1}{2}{v}_3+h_2\right)>\frac{1}{2}\left(q-1\right).$

Theorem 2.

Suppose that $\mathbf{X}\sim W_q\left(v_1,\Sigma \right)$ is independent of ${\mathbf{W}}_0\sim W_q\left(v_2,\lambda \Sigma \right)$ and ${\mathbf{W}}_1\sim W_q\left(v_3,\lambda \Sigma \right).$ If the joint pdf of Equation (3) is given by Equation (16) with marginal pdfs given in Equations (17) and (18) respectively, then

1. 

the pdf of $\left|{\mathbf{U}}_0\right|$ is given by

$$f\left(\left|{\mathbf{U}}_0\right|\right)=\frac{{\pi }^{\frac{q\left(q-1\right)}{2}}}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_1\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_2\right)}{\lambda }^{-q}{G}_{q,q}^{q,q}\left({\lambda }^{-q}\left|{\mathbf{U}}_0\right|{|}_{b_1,\dots ,b_q}^{a_1,\dots ,a_q}\right),\left|{\mathbf{U}}_0\right|>0$$

(25)

2. 

with cumulative distribution function (CDF)

$$\begin{array}{ccc}\hfill F_{\left|{\mathbf{U}}_0\right|}\left(c\right)& =& Pr\left(\left|{\mathbf{U}}_0\right|\le c\right)\hfill \\ & =& \frac{{\pi }^{\frac{q\left(q-1\right)}{2}}}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_1\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_2\right)}{G}_{q+1,q+1}^{q,q+1}\left({\lambda }^{-q}{c|}_{b_1+1,\dots ,b_q+1,0}^{1,a_1+1,\dots ,a_q+1}\right),c>0,\hfill \end{array}$$

(26)

where $G\left(·\right)$ denotes Meijer’s G-function Equation (8) and$a_j=-\frac{1}{2}{v}_1+\frac{1}{2}\left(j-1\right)$ and $b_j=\frac{1}{2}{v}_2-\frac{1}{2}\left(j+1\right)$ for $j=1,2,\dots ,q.$

3. 

The pdf of $\left|{\mathbf{U}}_1\right|$ is given by

$$\begin{array}{ccc}& & f\left(\left|{\mathbf{U}}_1\right|\right)\hfill \\ & =& \frac{{\lambda }^{\frac{1}{2}{v}_{1}q}{\pi }^{\frac{q\left(q-1\right)}{2}}}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_1\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_3\right)}\hfill \\ & & \times \sum _{t=0}^{\infty }\sum _{\tau }\frac{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_1,\tau \right)}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}\left(v_1+v_2\right),\tau \right)t!}{\left(1-\lambda \right)}^t{C}_{\tau }\left({\mathbf{I}}_q\right)G_{q,q}^{q,q}\left(\left|{\mathbf{U}}_1\right|{|}_{b_1,\dots ,b_q}^{a_1,\dots ,a_q}\right),\hfill \end{array}$$

(27)

such that $\left|{\mathbf{U}}_1\right|>0$ and where $C_{\tau }\left(·\right)$ is the corresponding zonal polynomial, with the values of the parameters such that $f\left(\left|{\mathbf{U}}_1\right|\right)$ is a valid pdf,

4. 

with CDF

$$\begin{array}{ccc}& & F_{\left|{\mathbf{U}}_1\right|}\left(c\right)\hfill \\ & =& Pr\left(\left|{\mathbf{U}}_1\right|\le c\right)\hfill \\ & =& \frac{{\lambda }^{\frac{1}{2}{v}_{1}q}{\pi }^{\frac{q\left(q-1\right)}{2}}}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_1\right){\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_3\right)}\hfill \\ & & \times \sum _{t=0}^{\infty }\sum _{\tau }\frac{{\mathrm{\Gamma }}_q\left(\frac{1}{2}{v}_1,\tau \right)}{{\mathrm{\Gamma }}_q\left(\frac{1}{2}\left(v_1+v_2\right),\tau \right)t!}{\left(1-\lambda \right)}^t{C}_{\tau }\left({\mathbf{I}}_q\right)G_{q+1,q+1}^{q,q+1}\left({c|}_{b_1+1,\dots ,b_q+1,0}^{1,a_1+1,\dots ,a_q+1}\right)\hfill \end{array}$$

(28)

such that $c>0$, where $a_j=-\frac{1}{2}\left(v_1+v_2\right)-t_j+\frac{1}{2}\left(j-1\right)$ and $b_j=\frac{1}{2}{v}_3-\frac{1}{2}\left(j+1\right)$ for $j=1,\dots ,q,$ with the values of the parameters such that $F_{\left|{\mathbf{U}}_1\right|}\left(c\right)$ is a valid CDF and ${\mathrm{\Gamma }}_q\left(·,·\right)$ denotes the generalised gamma function (see Equation (5)). The proof can be found in the Appendix A.

As a theoretical validation of the results, consider the case when $q=1$ in (25) and (27). Using [15] p. 130 yields the marginal pdf of $U_0$:

$$\begin{array}{ccc}\hfill f\left(u_0\right)& =& \frac{1}{\mathrm{\Gamma }\left(\frac{1}{2}{v}_1\right)\mathrm{\Gamma }\left(\frac{1}{2}{v}_2\right)}{\lambda }^{-1}{G}_{1,1}^{1,1}\left({\lambda }^{-1}{u}_0{|}_{\frac{1}{2}{v}_2-1}^{-\frac{1}{2}{v}_1}\right)\hfill \\ & =& \frac{\mathrm{\Gamma }\left(\frac{1}{2}\left(v_1+v_2\right)\right)}{\mathrm{\Gamma }\left(\frac{1}{2}{v}_1\right)\mathrm{\Gamma }\left(\frac{1}{2}{v}_2\right)}{\lambda }^{\frac{1}{2}{v}_1}{u}_0^{\frac{1}{2}{v}_2-1}{\left(\lambda +u_0\right)}^{-\frac{1}{2}\left(v_1+v_2\right)}\hfill \end{array}$$

where $u_0>0$ and the marginal pdf of $U_1$:

$$\begin{array}{ccc}& & f\left(u_1\right)\hfill \\ & =& \frac{{\lambda }^{\frac{1}{2}{v}_1}}{\mathrm{\Gamma }\left(\frac{1}{2}{v}_1\right)\mathrm{\Gamma }\left(\frac{1}{2}{v}_3\right)}\sum _{t=0}^{\infty }\frac{{\mathrm{\Gamma }}_1\left(\frac{1}{2}{v}_1,t\right)}{{\mathrm{\Gamma }}_1\left(\frac{1}{2}\left(v_1+v_2\right),t\right)t!}{\left(1-\lambda \right)}^t{C}_t\left({\mathbf{I}}_1\right)G_{1,1}^{1,1}\left(u_1{|}_{\frac{1}{2}{v}_3-1}^{-\frac{1}{2}\left(v_1+v_2\right)-t}\right)\hfill \\ & =& \frac{{\lambda }^{\frac{1}{2}{v}_1}}{\mathrm{\Gamma }\left(\frac{1}{2}{v}_1\right)\mathrm{\Gamma }\left(\frac{1}{2}{v}_3\right)}\sum _{t=0}^{\infty }\frac{{\left(\frac{1}{2}{v}_1\right)}_t\mathrm{\Gamma }\left(\frac{1}{2}{v}_1\right)}{{\left(\frac{1}{2}\left(v_1+v_2\right)\right)}_t\mathrm{\Gamma }\left(\frac{1}{2}\left(v_1+v_2\right)\right)t!}{\left(1-\lambda \right)}^t\hfill \\ & & \times \frac{\mathrm{\Gamma }\left(\frac{1}{2}\left(v_1+v_2+v_3\right)+t\right)u_1^{\frac{1}{2}{v}_3-1}}{{\left(1+u_1\right)}^{\frac{1}{2}\left(v_1+v_2+v_3\right)+t}}\hfill \\ & =& \frac{\mathrm{\Gamma }\left(\frac{1}{2}\left(v_1+v_2+v_3\right)\right){\lambda }^{\frac{1}{2}{v}_1}}{\mathrm{\Gamma }\left(\frac{1}{2}{v}_3\right)\mathrm{\Gamma }\left(\frac{1}{2}\left(v_1+v_2\right)\right)}{u}_1^{\frac{1}{2}{v}_3-1}{\left(1+u_1\right)}^{-\frac{1}{2}\left(v_1+v_2+v_3\right)}\hfill \\ & & {\times }_2{F}_1\left(\frac{1}{2}{v}_1,\frac{1}{2}\left(v_1+v_2+v_3\right);\frac{1}{2}\left(v_1+v_2\right);\frac{1-\lambda }{1+u_1}\right)\hfill \end{array}$$

where $u_1>0,\left|\frac{1-\lambda }{1+u_1}\right|<1$. It is valuable to note the special case of both of these preceeding results (when $q=1$) in the case when $\lambda =1$, i.e., no shift occurs. In both cases for $U_0$ and $U_1$, these marginal pdfs reflect beta type II distributions.

Remark 2.

Ref. [20] discussed the two kinds of Wilks’ statistic. If ${\mathbf{U}}_0={\mathbf{X}}^{-\frac{1}{2}}{\mathbf{W}}_0{\mathbf{X}}^{-\frac{1}{2}}$ with $\mathbf{X}$ and ${\mathbf{W}}_0$ Wishart matrices $(W_q\left(v_i,\Sigma \right)$, $i=1,2),$ then ${\mathbf{U}}_0$ has the matrix variate beta type II distribution. They derived the exact expression for the pdf of Wilks’ statistic type II: $\left|{\mathbf{U}}_0\right|$, the latter expressed as the product of q univariate betas of the second kind, which in turn, can be expressed as Meijer G-functions. Thus, Equations (25) and (27) can be considered as Wilks’ type II statistics.

3. Numerical Example

This section focusses on the calculation of run-length probabilities for this multivariate sequential process. In particular, some percentage points are calculated as an illustration for the probability to detect the shift instantly (i.e., a run-length of one). In this way, the calculation of run-length probabilities may be feasible and meaningful within the matrix environment.

The discrete random variable that defines the run-length is called the run-length random variable and often denoted by N with its distribution called the run-length distribution. Let $A_j$ be the event that a univariate random variable $U_j,$$j=0,1,\dots ,p,$ plots inside its respective control limits, i.e.,

$$A_j=LC{L}_{\kappa +j}<U_j<UC{L}_{\kappa +j}$$

(29)

where $LCL$ and $UCL$ denotes the lower and upper control limits respectively. The probability of detecting a shift immediately, in other words, the probability of a run-length of one is then

$$Pr(N=1)=Pr\left(A_0^C\right)=1-Pr\left(A_0\right)=1-Pr\left(LC{L}_{\kappa }<U_0<UC{L}_{\kappa }\right).$$

(30)

This probability is the probability that the charting statistic will plot on or outside the control limits upon collecting the first sample after the change in the variance (see Equation (30)). In the matrix environment $\left|{\mathbf{U}}_0\right|$ is of interest as a test statistic for testing the null hypothesis at time $\kappa$ that the covariance matrix structure did not change (practically, the process is in-control). Therefore, if the statistic $\left|{\mathbf{U}}_0\right|$ exceeds a critical value (say $c_0)$ it presents evidence that the covariance matrix structure changed and that the process is declared out-of-control. This proposed method deviates from the univariate case where a two sided hypothesis is considered (see Equation (30)). Thus, once the covariance matrix structure changes, the probability to detect this change immediately, in other words, the probability of a run-length of one is

$$Pr(N=1)\equiv P\left[\left|{\mathbf{U}}_0\right|\ge c_0\right].$$

(31)

Take note that $c_0$ indicates an upper critical value and not a control limit as before (see Equation (30)). If $q=1$ then $c_0$ is comparable to the UCL of a one-sided hypothesis in the univariate case.

In this example, percentage points are calculated for a run-length of one for the scenario as illustrated in Figure 1 where the covariance matrix changes with a scale factor from $\Sigma$ to $\lambda \Sigma .$ Two cases with $q=1$ and 2 (i.e., a univariate and bimatrix process) is considered. From Equation (31) $Pr(N=1)=1-F_{\left|{\mathbf{U}}_0\right|}\left(c_0\right),$ where $F_{\left|{\mathbf{U}}_0\right|}(·)$ is the CDF of $\left|{\mathbf{U}}_0\right|$ given in Equation (26)).

In particular, for $q=1$ see that

$$F_{\left|{\mathbf{U}}_0\right|}\left(c_0\right)=\frac{1}{\mathrm{\Gamma }\left(\frac{1}{2}{v}_1\right)\mathrm{\Gamma }\left(\frac{1}{2}{v}_2\right)}{G}_{2,2}^{1,2}\left({\lambda }^{-1}{c}_0{|}_{\frac{1}{2}{v}_2,0}^{1,-\frac{1}{2}{v}_1+1}\right),$$

(32)

and for $q=2$

$$\begin{array}{ccc}& & F_{\left|{\mathbf{U}}_0\right|}\left(c_0\right)\hfill \\ & =& \frac{1}{\mathrm{\Gamma }\left(\frac{1}{2}{v}_1\right)\mathrm{\Gamma }\left(\frac{1}{2}{v}_1-\frac{1}{2}\right)\mathrm{\Gamma }\left(\frac{1}{2}{v}_2\right)\mathrm{\Gamma }\left(\frac{1}{2}{v}_2-\frac{1}{2}\right)}{G}_{3,3}^{2,3}\left({\lambda }^{-2}{c}_0{|}_{\frac{1}{2}{v}_2,\frac{1}{2}{v}_2-\frac{1}{2},0}^{1,-\frac{1}{2}{v}_1+1,-\frac{1}{2}{v}_1+\frac{3}{2}}\right).\hfill \end{array}$$

The percentage points $c_0$ of $\left|{\mathbf{U}}_0\right|$ are obtained numerically by solving the equation

$$F_{\left|{\mathbf{U}}_0\right|}\left(c_0\right)=\underset{0}{\overset{c_0}{\int }}f\left(\left|{\mathbf{U}}_0\right|\right)d\left|{\mathbf{U}}_0\right|=1-\gamma$$

(33)

where $\gamma$ is a pre-specified probability of detecting a change in the covariance structure when the process is out-of-control. Solving for this value numerically involves the computation of Meijer’s G-function which is available in the R software as meijerG; in our case, we used MeijerG in the software Mathematica.

Table 1 provides the numerical values of $c_0$ for different values of $\lambda$ and $\gamma$ for the case if $q=1$ (univariate) and $q=2$ (bimatrix). In this example, samples of four equal sizes are collected at each point in time, i.e., $v_2=n=4$. It is assumed that the covariance matrix changes with a scale factor $\lambda ,$ between samples $\kappa -1$ and $\kappa$ where $\kappa =3,$ therefore $v_1=\left(\kappa -1\right)\times n=8.$

Table 1. Percentage points $c_0$ of $\left|{\mathbf{U}}_0\right|$.

$\mathit{\lambda }$	q	$\mathit{\gamma }=0.01$	$\mathit{\gamma }=0.025$	$\mathit{\gamma }=0.05$	$\mathit{\gamma }=0.1$
2	1	7.00608	5.05263	3.83785	2.80643
1	1	3.50304	2.52632	1.91893	1.40321
0.5	1	1.75152	1.26316	0.95946	0.70161
2	2	7.29343	4.50351	2.97902	1.80558
1	2	3.64671	2.25176	1.48951	0.91746
0.5	2	1.82336	1.12588	0.74475	0.46006

Remark 3.

The upper percentage points $c_0$ in the simple case when $q=1$ can be related to the control limits (see (30)). In the above example a one-sided test was considered, i.e., the chart would signal that the process is out-of-control if $\left|{\mathbf{U}}_0\right|\ge c_0.$ It is well-known that the type I error in hypothesis testing is $P(reject$$H_0$|$H_0$$true$). In the SPC context this is similar as the false alarm rate (FAR). The FAR is defined as the probability for a single charting statistic to plot on or outside the control limits when the process is in-control. The probability that $U_0$ plots on or outside the control limits given that the process variance did not encounter a shift, i.e., $\lambda =1$. Therefore

$$\begin{array}{ccc}\hfill FAR& =& 1-Pr\left(\left.LC{L}_{\kappa }<U_0<UC{L}_{\kappa }\right|\lambda =1\right)\hfill \\ & =& 1-{\int }_{LC{L}_{\kappa }}^{UC{L}_{\kappa }}f\left(u_0\right)d{u}_0(\mathrm{see}\mathrm{Equation}(17\left)\right)\hfill \\ & =& 0.0027.\hfill \end{array}$$

In the SPC environment it is desirable to have a FAR of $0.0027$. Substituting $\gamma =\frac{0.0027}{2}=0.00135$ in Equation (33) with $q=1$ and $\lambda =1$, gives $c_0=6.58684.$ This value corresponds to the UCL in the case of $q=1$ when, i.e.,

$$UC{L}_{\kappa =3}=\frac{F_{n_{\kappa },{\sum }_{i=1}^{\kappa -1}{n}_i}^{-1}\left[\mathrm{\Phi }\left(3\right)\right]}{\frac{{\sum }_{i=1}^{\kappa -1}{n}_i}{n_{\kappa }}}=\frac{F_{4,8}^{-1}\left[\mathrm{\Phi }\left(3\right)\right]}{\frac{8}{4}}=6.58684.$$

where $F_{v_1,v_2}^{-1}(.)$ and $\mathrm{\Phi }\left(.\right)$ denotes the inverse CDF of the $F_{v_1,v_2}(.)$ distribution and the CDF of the standard normal distribution respectively. See also [5,6] in this regard.

4. Discussion and Conclusions

In this paper, we introduced a generalised bimatrix variate beta type II distribution which originated from “ratios” of Wishart random variates, emanating from monitoring the process covariance structure of q attributes where samples are independent, having been collected from a multivariate normal distribution with known mean and unknown covariance matrix. In particular, the (i) pdfs of the marginal distributions and (ii) the pdfs of the determinants of the components of the generalised bimatrix variate beta type II distribution were derived. This paves the way for the proposed measure to capture the change in a multivariate process momentarily. An illustrative example was included where some percentage points were calculated to address the run-length concept in the matrix environment. In a similar way as described in this paper, the two matrix random variables ${\mathbf{U}}_0$ and ${\mathbf{U}}_1$ can be used to test if the covariance structure has changed significantly between time periods $\kappa -1$ and $\kappa$ as well as $\kappa$ and $\kappa +1$.

In a similar way the run-length of two implies that even though the covariance matrix changed, this change is not detected using the control chart at time $\kappa ,$ but that the chart only signals that the process is out-of-control at time $\kappa +1.$ Therefore

$$\begin{array}{cc}\hfill Pr(N=2)& \equiv Pr\left[\left|{\mathbf{U}}_0\right|<c_0,\left|{\mathbf{U}}_1\right|\ge c_1\right]\hfill \\ & \hfill =Pr\left[\left|{\mathbf{U}}_0\right|<c_0\right]-Pr\left[\left|{\mathbf{U}}_0\right|<c_0,\left|{\mathbf{U}}_1\right|<c_1\right].\end{array}$$

(34)

From Equation (34) it is evident that the joint pdf of $\left(\left|{\mathbf{U}}_0\right|,\left|{\mathbf{U}}_1\right|\right)$ is needed to calculate the probability of a run-length of two, but a closed form expression is not mathematically tractable. Another possibility is to assume independence of the statistics $\left|{\mathbf{U}}_0\right|$ and $\left|{\mathbf{U}}_1\right|$, then the approximate run-length probability is

$$Pr(N=2)\approx Pr\left[\left|{\mathbf{U}}_0\right|<c_0\right]-Pr\left[\left|{\mathbf{U}}_0\right|<c_0\right]Pr\left[\left|{\mathbf{U}}_1\right|<c_1\right].$$

Even in the case of the above approximation one still encounters computational challenges, see the pdf of $\left|{\mathbf{U}}_1\right|$ given in Equation (27).

Furthermore, as a two-sample statistic for testing the hypothesis at time $\kappa$ that the two independent samples (i.e., all observations from time $i=1$ to $\kappa -1$ vs. the observations in sample $\kappa$) are from the same $q$-variate multivariate normal distributions with the same unknown covariance matrix $\Sigma$, the statistic $|{\mathbf{U}}_0|$ may be of interest as a test statistic. Subsequently $|{\mathbf{U}}_1|$ can be used at time $\kappa +1$. Thus, $|{\mathbf{U}}_0|$ and $|{\mathbf{U}}_1|$ may be used as charting statistics for the multivariate process. In this scenario, $|{\mathbf{U}}_0|$ is in fact a test statistic to check whether $\lambda =1$ (i.e., the covariance matrices are the same) versus $\lambda \ne 1$ (i.e., the covariance matrix change with the scale factor $\lambda$). For $\lambda =1,$ $|{\mathbf{U}}_0|$ is the Wilks’ statistic type II ([20]).

Recent trends indicate a continued interest in modelling and theoretical capturing of shifts within covariance matrices within multivariate settings similar to the one under consideration in this paper. Ref. [21] develops a distribution-free control chart for this purpose, and [22,23] also refreshes the literature of methods for statistical surveillance of covariance structures with particularly developed control charts. The contribution of [24] is also a valuable contribution in literature based on machine learning approaches for the monitoring of the covariance matrix in multivariate SPC, and forms a basis for the departure of potential future studies. The case where there is a change in the mean vector in this sequential process may be considered as future work. As a future development, the practitioner may be interested in more than two successive time periods immediately after the change in the covariance structure occurred, which will lead to new matrix variate Dirichlet type II distributions.