Abstract
In this paper, we use an SIRD model to analyze the evolution of the COVID-19 pandemic in Spain, caused by a new virus called SARS-CoV-2 from the coronavirus family. This model is governed by a nonlinear system of differential equations that allows us to detect trends in the pandemic and make reliable predictions of the evolution of the infection in the short term. This work shows this evolution of the infection in various changing stages throughout the period of maximum alert in Spain. It also shows a quick adaptation of the parameters that define the disease in several stages. In addition, the model confirms the effectiveness of quarantine to avoid the exponential expansion of the pandemic and reduce the number of deaths. The analysis shows good short-term predictions using the SIRD model, which are useful to influence the evolution of the epidemic and thus carry out actions that help reduce its harmful effects.
1. Introduction
The detection of a new coronavirus (SARS-CoV-2) in December 2019 by the Municipal Health Commission in Wuhan (China) and its subsequent expansion throughout the world caused the World Health Organization (WHO) to declare a global pandemic of this infection on 11 March 2020. Its disease pattern has been named COVID-19. As of 2 May 2020, this disease has presented 3,272,202 confirmed cases and 230,104 deaths globally—with 25,264 in Spain [1].
In this work, we perform an analysis of the evolution of the epidemic in Spain using an SIRD model, which will be detailed below. The use of SIRD-type models to study epidemics has been very popular for decades [2,3,4,5,6,7]. They were proposed in 1927 [8] by two Scottish scientists: William O. Kermack, a biochemist, and Anderson G. McKendrick, a physicist and epidemiologist. For this reason, they are also known as Kermack–McKendrick models. These models show how an infection evolves when a certain number of sick people are detected within a healthy population. They are governed by systems of differential equations, which means that the solutions they provide are highly accurate from a mathematical point of view, but small variations in their parameters can cause significant changes in the solution.
Another drawback is that accurate knowledge of the evolution of the epidemic requires data that are only known at the end of it. Therefore, at the moment when the epidemic is taking place, it is difficult to predict its evolution in the long term. However, the simplicity of the model allows us to make quick parameter adjustments and carry out instant simulations and measure trends in the evolution of the epidemic in the short term.
In this paper, our aim is to analyze what has happened during the development of the epidemic and demonstrate how the SIRD model has great adaptability to predict the behavior of the COVID-19 pandemic in Spain during the course of the epidemic. Our analysis seeks to detect trends that allow short-term decisions to be made.
Fortunately, in today’s society, the COVID-19 pandemic is not expected to be as devastating as the Spanish Flu Pandemic at the beginning of the last century, which took place between 1918 and 1920 [9,10,11]. That terrible pandemic resulted in more than 40 million victims worldwide and Spain was one of the most badly-affected countries, with 8 million people infected and 300,000 deaths. The healthcare and technological resources, as well as the research potential that exists today, are far superior to those of the early twentieth century; it is therefore not likely to cause as many victims as in 1918 (in proportion to the population). At that time, the entire population was exposed to the risk of infection and there were not as many means of treatment as nowadays. Therefore, it is obvious that in this case, the isolation measures (quarantine) taken can alter the number of people exposed to the virus. This is one of the most effective actions to prevent contagion [12,13,14,15] and, consequently, deaths [16]. In Spain, several royal decrees have been published to ensure quarantine [17,18,19].
In addition to the works already considered about SIRD models, interested readers can find a wide variety of models for the study of the COVID-19 pandemic in the scientific literature published in the last months: using Bayesian and stochastic techniques [20,21,22], including mobility [23], confinement and quarantine [15,24], fractional models [25], and logistic models [26], among others.
2. Model Description
The simplest SIRD model considers three types of people:
- (S)
- Susceptible—the people who could become infected.
- (I)
- Infected—the people who are infected at that moment.
- (R)
- Recovered—the people who have had the disease and are now healthy.
In the case of the COVID-19 pandemic, many deaths have taken place [1,12,27], so we introduce a new variable. In this regard, we consider the variable that represents deaths:
- (D)
- Deceased—the people who have died of the disease.
If we assume that the population affected by the epidemic is satisfying the model, which we will call SIRD, it is governed by the following system of differential equations:
This model depends on three parameters: (recovery rate per unit of time), (infected rate per unit of time), and (death rate per unit of time).
Figure 1 shows the usual way in which the variables and D evolve. No ranges appear, because they depend on each particular epidemic.
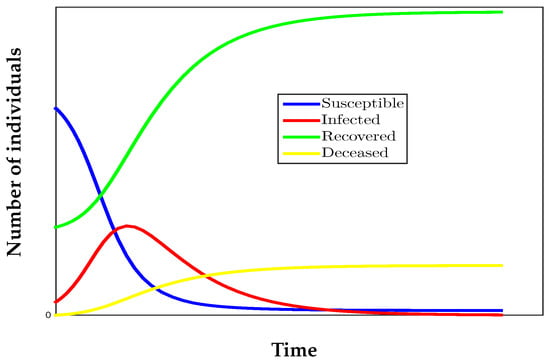
Figure 1.
Typical behavior of an epidemic’s evolution over time.
On the other hand, the recovery rate may change during the course of the epidemic, influenced by new medical treatments, which are becoming increasingly effective as research progresses. In addition, the value of can also change when the healthcare system is on the verge of collapse and the mildly ill are discharged to complete their recovery at home. Actually, such patients are not fully recovered, but the official data do not count them as infected. Considering the presented reasons, during the evolution of the epidemic, the predictions that can be made will only be reliable in the short term. However, this does not mean that they are not useful, since knowledge of these predictions can help to make decisions to minimize harmful effects during the course of the epidemic.
2.1. Equations Governing the Model
The SIRD epidemiological model that we are going to use to describe the evolution of the COVID-19 pandemic in Spain is a nonlinear ordinary differential equation system, presented in the previous section. It is governed by Equations (1)–(4), the formulation of which is described below.
Usually, the parameter infected rate per unit of time, is considered the product of two quantities: where p is the probability that contact with an infected person results in an infection and m is the number of contacts made by an infected person. So, is the number of people who have been infected by an infected person. Therefore, is the number of susceptible people who have been infected by all the infected people. Now, substituting the value of for we obtain Equation (1):
On the other hand, Equations (3) and (4) are deduced from the definitions of and
Finally, from the two previous expressions, Equation (2) is deduced:
Obviously, when we face an unknown epidemic, the constants to be determined to ensure adequate action are the parameters and For this reason, estimating them is a fundamental task that we will address in the following sections.
As discussed in the previous section, social isolation measures have been the most effective measures to control the spread of the epidemic and reduce the number of deaths [16]. In this way, the value of another important parameter has also been reduced. We refer to the number of infected people who have been infected by an infected person (we will call this the reproduction number). In mathematical terms:
If this parameter is greater than 1, then the expansion of the epidemic is exponential and therefore uncontrollable. However, when it is less than 1, the number of new infections decreases over time and the epidemic tends to subside. The reader can find more details of this parameter in [28,29]. For this reason, social isolation is effective, since, for a given epidemic with a given parameter the only way to decrease is to decrease the number of people at risk of being infected, that is,
2.2. Estimation of Parameters and
Suppose that the infection has become stable. Therefore, the class of infected people will no longer increase, so the differential equation that governs this class is
This equation has the following solution:
In this way, the proportion of individuals who remain infected at time or in other words, the probability that an individual remains infected at time is given by the quotient
Thus, the fraction of individuals who have left the infected class at time will be
where takes the form of the distribution function of a random variable which is defined as the time it takes an individual to leave the infected class. In our case, this happens when an infected person has overcome the disease or has died.
Calculating the density function of the variable we obtain
Under these conditions, we can calculate the average time it takes for a sick person to leave the infected class.
According to the available data [30,31], it takes an average of 14 days for an ill person to recover, while deaths occur on average 42 days after onset of the illness. If the fraction of deaths in relation to discharges of the sick in Spain as of 14 April 2020 [1] is then . From Equation (5), we have and in the case of the COVID-19 pandemic in Spain.
2.3. Estimation of Parameter
In order to estimate the value of we consider that and are known. Thus, system (1)–(4) is reduced to
Operating, we obtain
Therefore,
where C is the integration constant. Thus, the solutions of the system are given implicitly by
To continue with our estimate of , we need to make some assumptions: and Now, substituting in (6) to remove we obtain
Finally,
Obviously, when the epidemic is evolving and has not yet ended, is unknown and it will be necessary to estimate it with the data available at each moment.
3. Analysis of the COVID-19 Pandemic in Spain during the Course of the Disease
In order to have enough data for the estimates to have a significant value, we consider official data [1,27] provided by the Spanish Government from 11 March 2020, when the disease had been in the country for several weeks (or months, this is still unknown). We differentiate several stages in the evolution of the epidemic as the data have changed, either due to changes in case reporting criteria or due to changes in the trend of the disease.
3.1. First Stage: 11–21 March 2020
We consider data supplied by the Ministry of Health of the Spanish Government up to 21 March 2020. Table 1 shows the status of the epidemic up to that date. During the first days, official data were completed with data from the GitHub Enterprise group [32]. To fit an SIRD model that approximates the known values, the following data have been taken: , and . The rest of the parameters have been estimated as follows:

Table 1.
Number of infected, recovered, and deceased people in Spain from 11–21 March 2020.
- The discussion of the above section allows us to consider the Recovered/Deceased fraction as , in accordance with the figures from 11 March 2020 (see Table 1). Taking 0.3 as the Recovered/Deceased fraction, we can estimate that days.
- From Equation (5) and considering , we obtain and .
- From Equation (7), we estimate once and are known. So, .
In this work, we have chosen to use the MATLAB Ode Solver ode45 [33] to solve the system (1)–(4). The results obtained are shown in Figure 2. In this first stage, when the epidemic is beginning to spread, the estimates show great uncertainty, although the forecasts are bleak: the number of infected people is around 800,000. It is surely this fact that led the Spanish authorities to take severe isolation measures [17]. It is true that there are more optimistic estimates, but also more pessimistic ones. The results obtained show a possible scenario. Figure 2 shows how the evolution of the epidemic may have progressed if no action had been taken and if the efficacy of the treatments had not improved. The figures about those recovered and deceased do not yet show a clear trend and we will not comment on them.
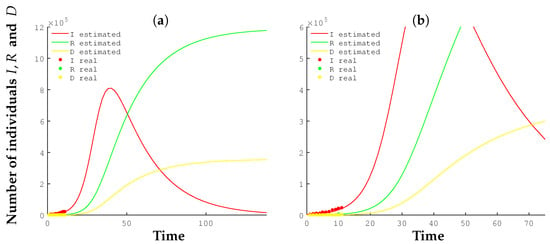
Figure 2.
(a) Comparison of real data with the predictions of the SIRD model on 21 March 2020. (b) Zoomed-in graph of real data.
In Figure 2 and below, the evolution of the number of susceptible people is not shown because it is an unknown figure introduced by us to adjust the other variables that are of most interest in terms of allowing us to influence the subsequent development of the epidemic.
3.2. Second Stage: 22–31 March 2020
At this stage, we consider the data provided by the Ministry of Health of the Spanish Government up to 31 March 2020 (see Table 2). The values we have taken at this stage to adjust the aforementioned SIRD model have been as follows: and . The estimation of the other parameters has been carried out analogously to the previous section:

Table 2.
Official data provided by the Spanish Government from 22–31 March 2020.
- We observed in the data that the Recovered/Deceased fraction follows the sequence tending towards 0.3 and 20 days.
The results obtained using the MATLAB Ode Solver considered in the first stage are shown in Figure 3. It is observed that the influence of the quarantine imposed by the Spanish Government begins to be noticed and the figures, although still worrying, are no longer so alarming.
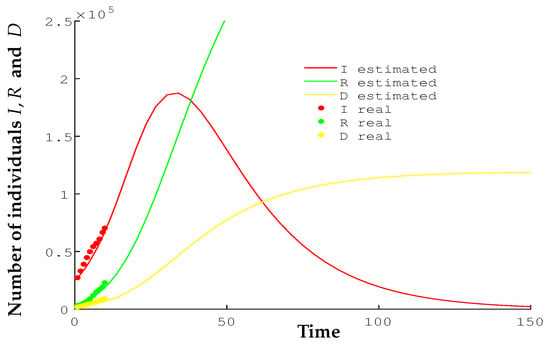
Figure 3.
Comparison of the real data with the estimations of the SIRD model during the second stage.
Obviously, the approximations show trends that the model variables follow according to the aforementioned conditions. It is important to note that we are estimating the values of the variables that will later be officially counted according to the conditions described. In the event that these conditions change, the values of the variables would undergo changes. However, the information provided will continue to be useful for making medical and political decisions, since the observed trends are representative of the situation. In addition, the cases that are officially detected are those of people who have a serious evolution or an uncertain prognosis, for whom hospitalization is therefore required or at least require that a follow-up be carried out by Family Medicine Units. In summary, these are the cases that must be attended to urgently and followed up on. In the evolution of an epidemic caused by the action of a little-known virus, it is important to anticipate the ICU beds that may be needed, and more so in this case, where the evolution of those infected with severe cases of COVID-19 require ICU care.
3.3. Third Stage: 1–13 April 2020
At this stage, we will consider the data in Table 3.

Table 3.
Official data provided by the Spanish Government from 1–13 April 2020.
The values that we have taken in this stage to adjust the SIRD model, described in previous paragraphs, have been , and . The other parameters have been estimated as follows:
- The Recovered/Deceased fraction has been observed to follow the sequence:Consequently, we have estimated the value 0.22, which produces good approximations for the data that are already known. Taking 0.22 as the Recovered/Deceased fraction, we can estimate that 20 days.
The results obtained using the MATLAB Ode Solver considered in previous stages are shown in Figure 4. These results are conditioned by the number of tests carried out, which provide us with the number of infected people, the number of patients discharged (in many cases the patients continue their convalescence at home, due to the saturation of hospitals), and the effectiveness of treatments.
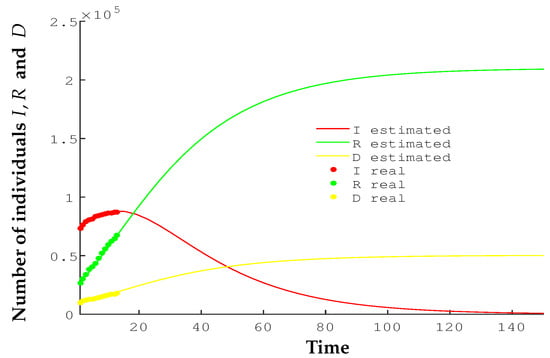
Figure 4.
Comparison of the real data with the estimates of the SIRD model during the third stage.
In the current part of the process in which we find ourselves, that is, fully immersed in the course of the epidemic, there are many doubts about it; if we take into account the number of hidden carriers of the disease, the data obtained would change shape very significantly [16]. However, the estimates that have been obtained are very useful for managing actions in the short term. There may be 7 million people infected in Spain, as indicated in the previous reference, but at the moment what is of interest is managing cases with severe symptoms. These patients who require a follow-up are those detected among the people who are cared for in health centers and hospitals, and their tests indicate that they are infected and are included in the official figures of those infected. SIRD models can also estimate the magnitude of the death toll. Figure 4 indicates that the number of deceased people may be between 40,000 and 50,000 people with the data available on 13 April 2020.
The number of deaths will be known more accurately once the epidemic has been overcome and comparative analyses of the data on deaths are carried out for the months during which the epidemic has remained active and the same months in previous years. However, the data provided by the models can help make decisions that modify the final figure.
3.4. Fourth Stage: 14–23 April 2020
We consider the data in Table 3, adding the values in Table 4. We carry out estimations with the parameters of the third stage. At this stage, the Spanish Government has reported an increase in the number of tests carried out [1,27], which largely disarrange the parameters of the model considered in previous stages.

Table 4.
Official data provided by the Spanish Government from 14–23 April 2020.
Figure 5 shows the evolution of the pandemic during this stage. A more detailed analysis indicates that on 14 April, there was a slight mismatch; which was accentuated on 15 April, with an upward trend in real data with respect to those expected by the SIRD measure. On 16 April, the change in trend was already evident in the data; during the days after 16 April, the change in the trend of the data was confirmed.
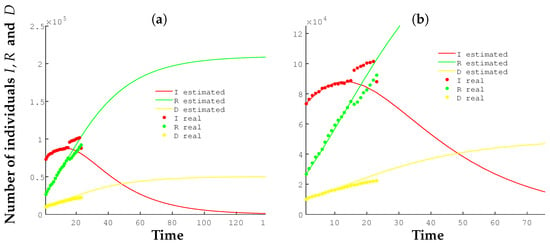
Figure 5.
(a) Comparison of the state of the real data with the predictions of the SIRD model on 23 April 2020. (b) Zoomed-in graph of real data.
Given the circumstances, the model needs to be revised. The Spanish authorities have clarified [1,27] the way of accounting for the data and the types of tests being carried out. Figure 6 shows the official data regarding the increase in the number of people infected and the types of tests performed.
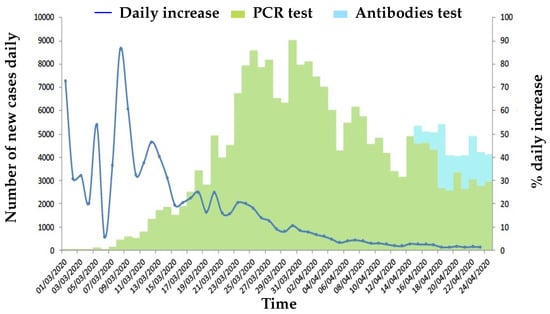
Figure 6.
Types of tests carried out and the % increase in the number of infected people on 23 April 2020. Source: Spanish Government [1] on 24 April 2020.
3.5. Types of COVID-19 Screening Tests
- The Polymerase Chain Reaction technique (PCR test) amplifies the genetic material of the virus (RNA and DNA) to detect it. So far, it is the most reliable method, but it requires analysis in a laboratory.
- The test for coronavirus antibodies (antibody test) does not detect the virus, but it detects the antibodies that kill it. It is done with a blood test, which can be performed quickly and on a massive scale.
In the days prior to 23 April, PCR tests were performed in conjunction with other, less-reliable types of tests not reported by the health authorities. A small number of antibody tests were also carried out, indicating whether a person has had the disease but not whether they are currently suffering from it. As of 14 April, the antibody tests were increased to carry out analyses of the prevalence of the disease and find out how many people in the total population have already had the infection. In the opinion of the Spanish authorities, this way of accounting for those affected makes it difficult to compare the data with previous data, since patients who currently have the disease and those who have already had it without being detected are counted, which undermines the trends observed. The Government has stated that from 14 April, only those infected confirmed by PCR test will be counted.
At this point of the investigation we have two alternatives: to model the total data with all the tests or to model only the official data that offer a positive result with the PCR test. In this work, we adopt the second option, which focuses on modeling the epidemiological data that are useful for making short-term decisions and being able to influence the evolution of the epidemic.
3.6. Fifth Stage: 23 April to 2 May 2020
At this stage, we will recover the data from 1 April, assuming that the data from 14–23 April are outside the model, but as we have already explained, they are not relevant in our study because our objective is to detect trends to modify the evolution of the epidemic in the short term. Therefore, we add the data from Table 3 to those of Table 5.

Table 5.
Official data provided by the Spanish Government of Spain from 23 April–2 May 2020.
Figure 7 shows the model estimates compared to the actual data according to the following parameters: , , , and . On this occasion, we have noted an improvement in medical treatments, patient care in less-saturated ICUs, and also a greater number of days that a patient remains in the hospital in order to provide longer care. So, 24 days and the Recovered/Deceased fraction .
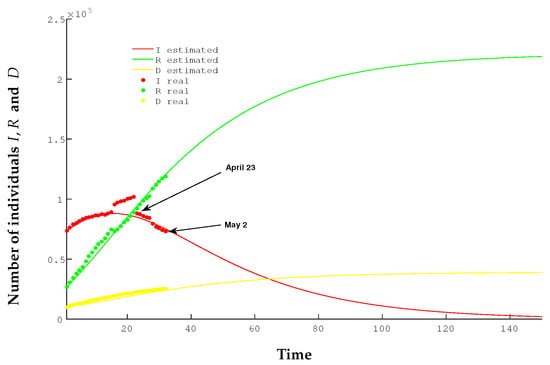
Figure 7.
Comparison of the real data with the estimates of the SIRD model during the fifth stage.
The SIRD model shows good behavior with these parameters. The estimate of deaths in this new situation is now around 38,000 people, far from the catastrophic figures of the beginning of the epidemic.
4. Discussion
The SIRD model that we have presented, like other models, is strongly dependent on the initial data used to adjust the parameters. For this reason, political authorities should publish the data without any kind of censorship or manipulation. Considering different initial data, we are able to estimate how catastrophic it would have been if the Spanish Government had not taken measures of social isolation on 14 March 2020 [17]. The displayed data in Figure 2 indicate that the number of people infected with active disease would have been around 800,000, while once the isolation measures were taken, they slowed down at the end of March. The maximum number of people infected with active disease and positive PCR was 87,280 (see Table 3) and it was reached on 12 April 2020. Approximately only 11% of those were probably infected without isolation measures. The delay in noticing the effect of the measures is largely due to the incubation period of the virus, estimated between 10 and 14 days after infection [34].
The model also depends on the exposed people to the virus by means of the variable S of susceptible people. At each stage of the pandemic, depending on the strictness of the isolation measures, this variable may be greatly higher or lower. In this sense, an exposure rate could be included in the model. However, when we vary the initial data of variable S of people susceptible to being infected, the results do not differ from obtained data.
The precision of the estimated parameters is determined by the theoretical reasoning of Section 2.2 and Section 2.3, and by the good behavior of the model against the observed data. In this sense, some studies [20,21] using Bayesian techniques, show a similar behavior in the estimates.
Figure 8 shows the evolution of the reproduction number during the latency period of the first wave of the COVID-19 pandemic. If we consider the stages in which we have focused our study, a strong decrease in this parameter can be observed during stages 2 and 3 (from 22 March–13 April) when the harsh quarantine measures imposed by the Spanish Government [17,18,19] had an effect. At this point, the incubation period must be taken into account, which means that the effects of the taken measures have several days of delay. From the fourth stage (13 April), the decrease is less due to relaxation of the isolation measures. Taking this parameter into account, we obtain useful information that allows us to take preventive measures in order to minimize the damage that the pandemic may cause.
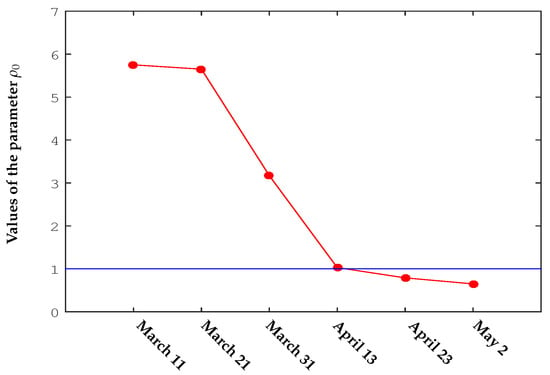
Figure 8.
Values of the parameter (reproduction number) over time in Spain during the first wave of the COVID-19 Pandemic.
5. Conclusions
An analysis has been performed on the evolution of the epidemic caused by the SARS-CoV-2 virus in Spain during the months of March and April, when the epidemic was in its most active phase. We observed good short-term predictions using the SIRD model, which have been described in previous sections. It has been discussed that short-term predictions are useful to influence the evolution of the epidemic and thus carry out actions that help reduce its harmful effects. For example, we confirmed the estimates made [16] regarding the usefulness of the quarantine imposed by the Spanish Government to reduce the number of deaths.
From the first days of April a decreasing number of actively infected patients was observed. In the days following the end of this study, it is expected that the epidemic will diminish if adequate isolation measures are maintained. A change in conditions could have a rebound effect on the number of people infected and the evolution could take, as of today, an uncertain path.
A more reliable representation of the behavior of the epidemic is to present its evolution in pieces, that is, to change the parameters as conditions have changed in relation to isolation measures, improvement of medical treatments, etc. If we take the parameters that best fit the constraints imposed in each case, a more appropriate global behavior can be observed. Figure 9 shows the fit of a piecewise SIRD model at each stage that has been described considering changes in conditions during the evolution of the epidemic.
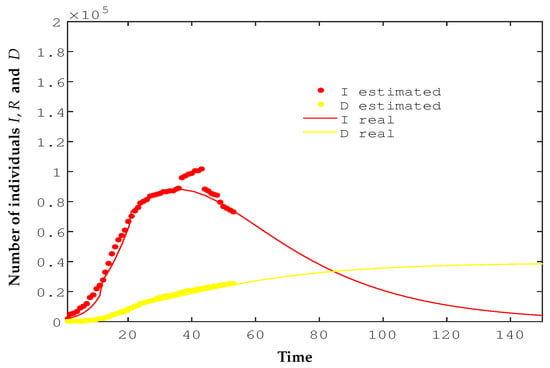
Figure 9.
Comparison of real data with the estimates of the piecewise SIRD model during the evolution of the epidemic.
Models are generated according to the data collected under certain conditions, which, as we have seen throughout the development of the epidemic, are changing. The number of diagnostic tests performed is not the same every day and treatments gradually become more effective, which affects the number of discharges. In addition, we remember with pain those hard weeks when ICUs were overflowing and many patients waited at home for the test to be performed, which also alters the exact date of positive diagnoses. On the other hand, it should be remembered that the data arrive a few days late, they are communicated the day after they are collected, and the virus also has an incubation period of 10 to 15 days. If these constraints are taken into account, the estimates made largely describe the evolution of the epidemic.
We present a model that allows us to adjust the parameters in real time when the disease is latent. Given the simplicity of the calculation of its parameters, one quickly obtains estimates on the number of infected people. In this way, adequate institutional actions could apply to minimize infections and to prevent overloading the health system. Another advantage of our model is its simplicity that permits an easy adaptation for similar infections.
Funding
This research was supported by the Institut de Matemàtiques i Aplicacions de Castelló, Departament de Matemàtiques, Universitat Jaume I, Spain.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used in this paper are publicly available in the references.
Acknowledgments
The author is grateful for several useful comments from unknown reviewers.
Conflicts of Interest
The author declares no conflict of interest.
References
- Spanish-Government. Web of Instituto de Salud Carlos III. Available online: https://covid19.isciii.es (accessed on 20 April 2020).
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology, 2nd ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Brauer, F.; Feng, Z.; Castillo-Chávez, C. Discrete epidemic models. Math. Biosci. Eng. 2010, 7, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Haefner, J.W. Modeling Biological Systems; Springer: New York, NY, USA, 2005. [Google Scholar]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: New York, NY, USA, 2015. [Google Scholar]
- Sameni, R. Mathematical Modeling of Epidemic Diseases; A Case Study of the COVID-19 Coronavirus. arXiv 2020, arXiv:2003.11371. [Google Scholar]
- Fernández-Villaverde, J.; Jones, C.I. Estimating and Simulating a SIRD Model of COVID-19 for Many Countries, States, and Cities; Working Paper 27128; National Bureau of Economic Research: Cambridge, MA, USA, 2020. [Google Scholar]
- Kermack, A.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. Lond. 1927, 115, 700–721, reprinted in Bull. Math. Biol. 1991, 53, 33–55. [Google Scholar]
- Belser, J.A.; Tumpey, T.M. The 1918 flu, 100 years later. Science 2018, 359, 255. Available online: https://science.sciencemag.org/content/359/6373/255 (accessed on 23 April 2020). [CrossRef] [PubMed]
- Morens, D.M.; Fauci, A.S. The 1918 Influenza Pandemic: Insights for the 21st Century. J. Infect. Dis. 2007, 195, 1018–1028. [Google Scholar] [CrossRef] [PubMed]
- Pulido, S. The Spanish Flu: The 1918 Pandemic that Did not Start in Spain. Available online: https://gacetamedica.com/investigacion/la-gripe-espanola-la-pandemia-de-1918-que-no-comenzo-en-espana-fy1357456/ (accessed on 20 April 2020). (In Spanish).
- Remuzzi, A.; Remuzzi, G. COVID-19 and Italy: What next? Lancet 2020, 395, 1225–1228. [Google Scholar] [CrossRef]
- Nokkaew, A.; Modchang, C.; Amornsamankul, S.; Lenbury, Y.; Pimpunchat, B.; Triampo, W. Mathematical modeling of infectious disease transmission in macroalgae. Adv. Differ. Equ. 2017, 2017, 1–8. [Google Scholar] [CrossRef]
- Prem, K.; Liu, Y.; Russell, W.; Kucharski, A.J.; Eggo, R.M.; Davies, N. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study. Lancet Public Health 2020. [Google Scholar] [CrossRef]
- Tang, B.; Xia, F.; Tang, S.; Bragazzi, N.L.; Li, Q.; Sun, X.; Liang, J.; Xiao, Y.; Wu, J. The effectiveness of quarantine and isolation determine the trend of the COVID-19 epidemics in the final phase of the current outbreak in China. Int. J. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Flaxman, S.; Mishra, S.; Gandy, A.; Unwin, H.J.T.; Coupland, H.; Mellan, T.A.; Zhu, H.; Berah, T.; Eaton, J.W.; Guzman, P.N.P.; et al. Report 13: Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in 11 European countries. arXiv 2020, arXiv:2004.11342. [Google Scholar]
- Spanish-Government. Royal Decree 463/2020, of March 14, Declaring the State of Alarm for the Management of the Health Crisis Situation Caused by COVID-19. Available online: https://www.boe.es/eli/es/rd/2020/03/14/463 (accessed on 20 March 2020). (In Spanish)
- Spanish-Government. Royal Decree 476/2020, of March 27, Extending the State of Alarm Declared by Royal Decree 463/2020, of March 14, Declaring the State of Alarm for the Management of the Situation of Health Crisis Caused by COVID-19. Available online: https://www.boe.es/eli/es/rd/2020/03/27/476/con (accessed on 20 April 2020). (In Spanish)
- Spanish-Government. Royal Decree 487/2020, of April 10, Which Extends the State of Alarm Declared by Royal Decree 463/2020, of March 14, Which Declares the State of Alarm for the Management of the Situation of Health Crisis Caused by COVID-19. Available online: https://www.boe.es/eli/es/rd/2020/04/10/487 (accessed on 20 April 2020). (In Spanish)
- Berihuete, A.; Sánchez-Sánchez, M.; Suárez-Llorens, A. A Bayesian Model of COVID-19 Cases Based on the Gompertz Curve. Mathematics 2021, 9, 228. [Google Scholar] [CrossRef]
- Taghizadeh, L.; Karimi, A.; Heitzinger, C. Uncertainty quantification in epidemiological models for the COVID-19 pandemic. Comput. Biol. Med. 2020, 125, 104011. [Google Scholar] [CrossRef] [PubMed]
- Umar, M.; Sabir, Z.; Zahoor Raja, M.A.; Shoaib, M.; Gupta, M.; Sánchez, Y.G. A Stochastic Intelligent Computing with Neuro-Evolution Heuristics for Nonlinear SITR System of Novel COVID-19 Dynamics. Symmetry 2020, 12, 1628. [Google Scholar] [CrossRef]
- Aràndiga, F.; Baeza, A.; Cordero-Carrión, I.; Donat, R.; Martí, M.C.; Mulet, P.; Yáñez, D.F. A Spatial-Temporal Model for the Evolution of the COVID-19 Pandemic in Spain Including Mobility. Mathematics 2020, 8, 1677. [Google Scholar] [CrossRef]
- De la Sen, M.; Ibeas, A.; Agarwal, R.P. On Confinement and Quarantine Concerns on an SEIAR Epidemic Model with Simulated Parameterizations for the COVID-19 Pandemic. Symmetry 2020, 12, 1646. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Silva, C.J.; Torres, D.F.M. Fractional model of COVID-19 applied to Galicia, Spain and Portugal. Chaos Solitons Fractals 2021, 144, 110652. [Google Scholar] [CrossRef] [PubMed]
- Cherniha, R.; Davydovych, V. A Mathematical Model for the COVID-19 Outbreak and Its Applications. Symmetry 2020, 12, 990. [Google Scholar] [CrossRef]
- Spanish-Government. Web of Ministerio de Sanidad, Consumo y Bienestar Social. Available online: https://www.mscbs.gob.es (accessed on 20 April 2020). (In Spanish)
- Diekmann, O.; Heesterbeek, J.A.P. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Heesterbeek, J.A.P. A Brief History of R0 and a Recipe for its Calculation. Acta Biotheor. 2002, 50, 189–204. [Google Scholar] [CrossRef]
- Thevarajan, I.; Nguyen, T.H.O.; Koutsakos, M.; Druce, J.; Caly, L.; van de Sandt, C.E.; Jia, X.; Nicholson, S.; Catton, M.; Cowie, B.; et al. Breadth of concomitant immune responses prior to patient recovery: A case report of non-severe COVID-19. Nat. Med. 2020, 26, 453–455. [Google Scholar] [CrossRef]
- Spanish-Government. Coronavirus Disease, COVID-19; Alerts Coordination Center and Health Emergencies. Available online: https://www.mscbs.gob.es/profesionales/saludPublica/ccayes/alertasActual/nCov-China/documentos/20200326_ITCoronavirus.pdf (accessed on 20 April 2020). (In Spanish)
- GitHub Enterprise. GitHub CSSEGISandData. Available online: https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series (accessed on 20 April 2020).
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- McAloon, C.; Collins, A.; Hunt, K.; Barber, A.; Byrne, A.W.; Butler, F.; Casey, M.; Griffin, J.; Lane, E.; McEvoy, D.; et al. Incubation period of COVID-19: A rapid systematic review and meta-analysis of observational research. BMJ Open 2020, 10, e039652. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).