Rockburst Hazard Prediction in Underground Projects Using Two Intelligent Classification Techniques: A Comparative Study

Abstract

Rockburst is a complex phenomenon of dynamic instability in the underground excavation of rock. Owing to the complex and unclear rockburst mechanism, it is difficult to accurately predict and reasonably assess the rockburst potential. With the increasing availability of case histories from rock engineering and the advancement of data science, the data mining algorithms provide a good way to predict complex phenomena, like rockburst potential. This paper investigates the potential of J48 and random tree algorithms to predict the rockburst classification ranks using 165 cases, with four parameters, namely maximum tangential stress of surrounding rock, uniaxial compressive strength, uniaxial tensile strength, and strain energy storage index. A comparison of developed models’ performances reveals that the random tree gives more reliable predictions than J48 and other empirical models (Russenes criterion, rock brittleness coefficient criterion, and artificial neural networks). Similar comparisons with convolutional neural network resulted at par performance in modeling the rockburst hazard data.

1. Introduction

During underground operations, rockburst is a sudden and violent release of elastic energy stored in rock and coal masses. This causes rock fragments to eject, potentially causing injury, collapse, and deformation of supporting structures, as well as damage to facilities [1,2,3]. Related activity occurs in open cuts in the mass of the joint rock [4,5]. For both the civil and mining engineering industries, its economic consequences are important. The mechanism is not yet well understood owing to the difficulty and uncertainty of the rockburst. In order to mitigate the risks caused by rockburst, such as damage to equipment, access closure, delays, and loss of property and life, it is important to accurately predict or estimate the realistic potential of rockburst for the safety and efficient construction and serviceability of underground projects.

Conventional mechanics-based methods fail to provide precise rockburst hazard detection due to the highly complex relationship between geological, geometric, and mechanical parameters of rock masses in underground environments. Further, mechanics-based methods have several underlying assumptions, which, if flouted, may yield biased model predictions. This has forced many researchers in recent years to investigate alternative methods for better hazard prediction and detection of the rockburst phenomenon. Several researchers suggested several indicators to assess burst potential. The strain energy storage index (W_et), proposed by Kidybinski [6], is the ratio of strain energy stored (W_sp) to strain energy dissipated (W_st).Wattimena et al. [7] used elastic strain energy density as a burst potential measure. The rock brittleness coefficient, which is based on the ratio of uniaxial compressive stress (UCS) to tensile stress, is another widely used burst liability index [8]. A tangential stress criterion, the ratio between tangential stress around underground excavations (σ_θ), and UCS of rock (σ_c), can be employed to assess the risk of rock bursts [9]. Energy-based burst potential index was developed by Mitri et al. [10] to diagnose burst proneness. However, many techniques have been developed in the last few decades to predict or assess rockburst, but there has been no advancement or a widely accepted technique preferred over other rockburst methods.

Over the past few decades, data mining techniques have been shown to be efficient in getting complex non-linear relationships between predictor and response variables and may be used to identify sites that are prone to rockburst events, as case history information is increasingly available. A number of approaches have been suggested by several researchers to predict the rockburst, such as Support Vector Machine (SVM) [11], Artificial Neural Networks (ANNs) [12], Distance Discriminant Analysis (DDA) [13], Bayes Discriminant Analysis (BDA) [14], and Fisher Linear Discriminant Analysis (LDA) [15], and moreover, some systems are based upon hybrid (Zhou et al. [16]; Adoko et al. [17]; Liu et al. [18]) or ensemble (Ge and Feng [19]; Dong et al. [20]) learning methods in long-term prediction of rockburst and their prediction accuracies are compared. Zhao and Chen [21], recently developed and compared a data-driven model based on a convolutional neural network (CNN) to a traditional neural network. In rockburst prediction, this proposed CNN model has a high potential compared to the conventional neural network. These algorithms used a number of rockburst indicators as input features, and the size of their training samples varied. While most of the aforementioned techniques have been effective in predicting rockburst hazard, they do have shortcomings. For example, the optimal structure (e.g., number of inputs, hidden layers, and transfer functions) must be specified a priori in the ANN method. This is usually accomplished by a process of trial and error. The black box nature of the ANN model, as well as the fact that the relationship between the system’s input and output parameters is described in terms of a weight matrix and biases that are not available to the user, is another major limitation [22]. Table 1 summarizes the main rockburst prediction studies that used machine learning (ML) methods with input parameters and accuracy.

Table 1. Study of the rockburst classification ML algorithm with influence factors and accuracy values.

Algorithm	D	σθ	σc	σt	Wet	σθ/σc	σc/σt	Accuracy (%)	Dataset	Reference
Support vector machine	✗	✓	✓	✓	✓	✗	✗	100	16	Zhao [11]
Distance discriminant analysis	✗	✗	✗	✗	✓	✓	✓	100	15	Gong and Li [13]
v-support vector regression	✗	✓	✓	✓	✓	✓	✓	93.75	45	Zhu et al. [23]
AdaBoost	✗	✓	✗	✗	✓	✓	✓	87.8–89.9	36	Ge and Feng [19]
Bayes discriminant analysis	✗	✗	✗	✗	✓	✓	✓	100	21	Gong et al. [14]
Fisher linear discriminant analysis	✗	✗	✗	✗	✓	✓	✓	100	15	Zhou et al. [15]
Heuristic algorithms and support vector machines	✓	✓	✓	✓	✓	✓	✓	66.67–90	132	Zhou et al. [16]
Adaptive neuro fuzzy inference system	✗	✓	✓	✓	✓	✓	✓	66.5–95.6	174	Adoko et al. [17]
Random forest	✗	✓	✓	✓	✓	✗	✗	100	46	Dong et al. [20]
Cloud model	✗	✓	✓	✓	✓	✓	✓	90–100	162	Liu et al. [18]
Decision tree model	✗	✗	✗	✗	✓	✓	✓	73–93	108 and 132	Pu et al. [24]
Artificial neural network and convolutional neural network	✗	✓	✓	✓	✓	✗	✗	89.29–100	165	Zhao and Chen [21]

Note: D = depth, m; σ_θ = maximum tangential stress of surrounding rock, MPa; σ_θ/σ_c = stress concentration factor; σ_c/σ_t = rock brittleness (B); σ_c = uniaxial compressive strength of rock, MPa; σ_t = uniaxial tensile strength of rock, MPa; W_et = strain energy storage index.

The majority of the established models (Table 1) are black boxes, meaning they do not show a clear and understandable relationship between input and output. These studies attempted to solve the problems of rockburst, but they were never entirely successful. In certain instances, a particular procedure can be appropriate, but not in others. Notably, precision ranges from 66.5 to 100%, which is a major variance in rockburst prediction. Rockburst prediction is a complex and nonlinear process that is hindered by model and parameter uncertainty, as well as limited by inadequate knowledge, lack of information characterization, and noisy data. Machine learning has been widely recognized in mining and geotechnical engineering applications for dealing with nonlinear problems and developing predictive data-mining models [25,26,27,28,29,30,31].

In this study, the random tree and J48 algorithms have been specifically selected on the basis of these considerations because they are primarily used in civil engineering but have not yet been thoroughly evaluated with each other and because of their open-source availability. The primary aim of this research was to reveal and compare the suitability of random tree and J48 algorithms in underground projects for rockburst hazard prediction. First, rockburst hazards classification cases are collected from the published literature. Next, these two algorithms are used to predict the rockburst hazard classification. Finally, their detailed performance is evaluated and compared with empirical models.

2. Materials and Methods

2.1. Influence Factors and Data Assemblage

Several factors such as the geological structures of the rock mass, the conditions of geo-stress, rock mass strength, the method of excavation and excavation size, and rock blasting are all related to the occurrence of rockbursts [9,15,32]. However, due to the limitations present in the reported parameters in previous field studies, all variables cannot be taken into account. Therefore, to create the new models, only parameters recorded in all field studies are used here. Previous studies used uniaxial compressive and tensile strength of the rock mass, maximum tangential stress of the surrounding rock, and strain energy storage index as main parameters. The existing rockburst cases were collected as supportive data for the development of the prediction model. This study used the rockburst database from different types of underground projects from all over the world previously collected by Pu et al. [24] and Zhou et al. [16] and recently referenced by Zhao and Chen [21]. The dataset contains 165 rockburst events of underground engineering projects which have four influence factors and a corresponding rank of rockburst. In general, the projects chosen experienced the most significant rockburst activity.

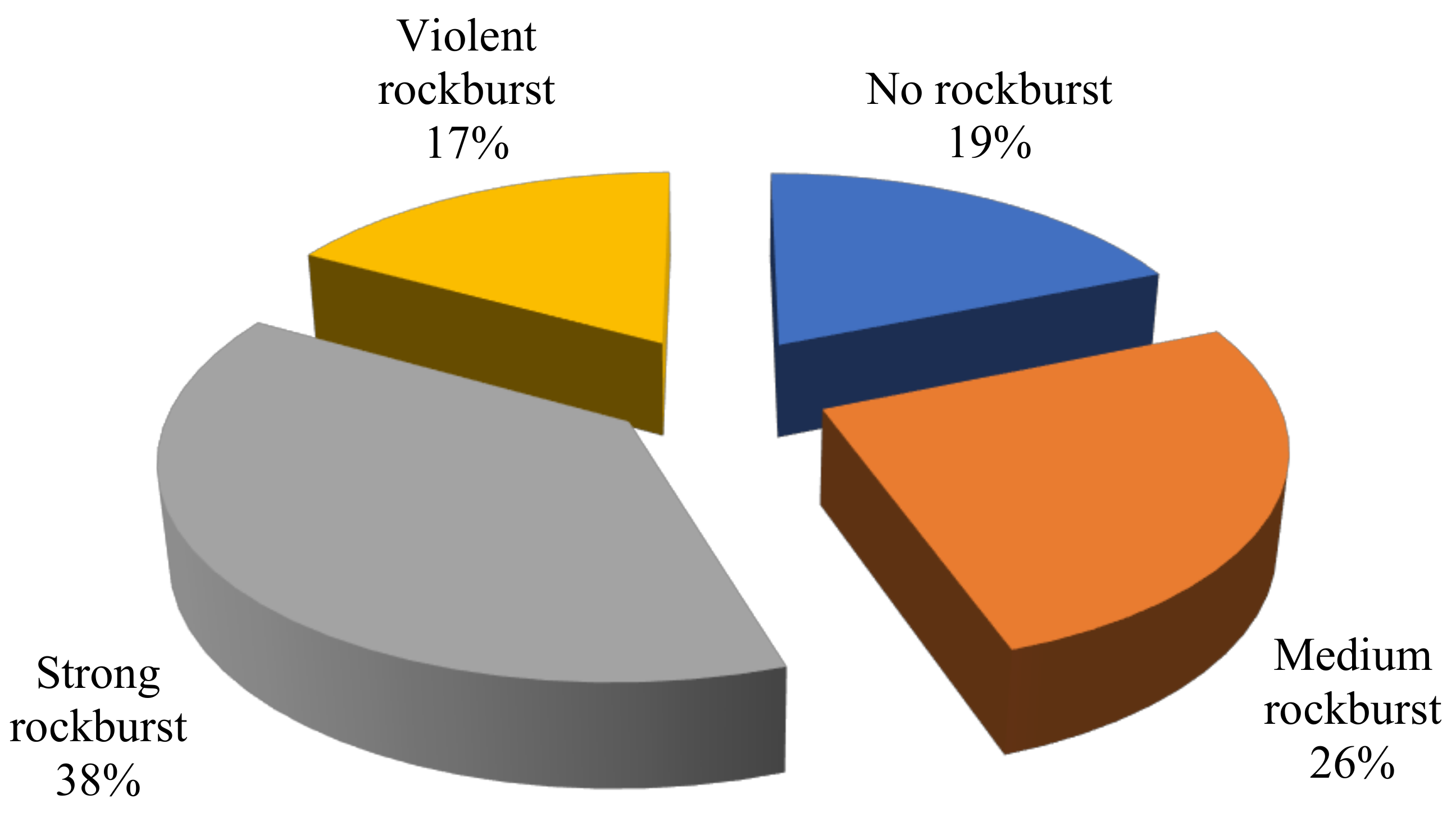
The way data are divided into training and research sets has a major influence on the results of data mining techniques [33]. The statistical analysis’ main goal was to ensure that the subsets’ statistical properties were as similar as possible and thus represented the same statistical population. To fairly compare the predictive performance of the proposed J48 and random tree models in this study, the dataset used for the training (137 cases) and testing (28 cases) was kept the same in the prediction of rockburst hazard. As per Cai et al. [34] the rockburst database has four rankings to determine the risk for the rockburst. They are as follows, with increasing severity: no rockburst (NR), moderate rockburst (MR), strong rockburst (SR) and violent rockburst (VR). The specific grading criteria are shown in Table 2 [34]. Figure 1 shows the distribution of rockburst data as a pie chart showing the portion of four rockburst hazard forms in underground projects, classified as no rockburst (NR, 31 cases), moderate rockburst (MR, 43 cases), strong rockburst (SR, 63 cases) and violent rockburst (VR, 28 cases).

Table 2. Grading criteria of rockburst intensity.

Rockburst Grade	No Rockburst	Moderate Rockburst	Strong Rockburst	Violent Rockburst
σθ/σc	<0.3	0.3–0.5	0.5–0.7	>0.7
σc/σt	>40	26.7–40	14.5–26.7	<14.5
Wet	>5	3.5–5.0	2.0–3.5	<2.0

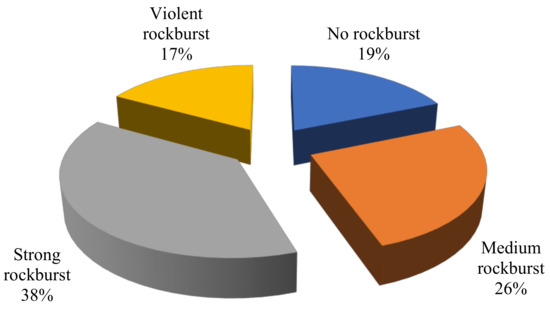
Figure 1. Distribution of observed rockburst hazard in underground projects.

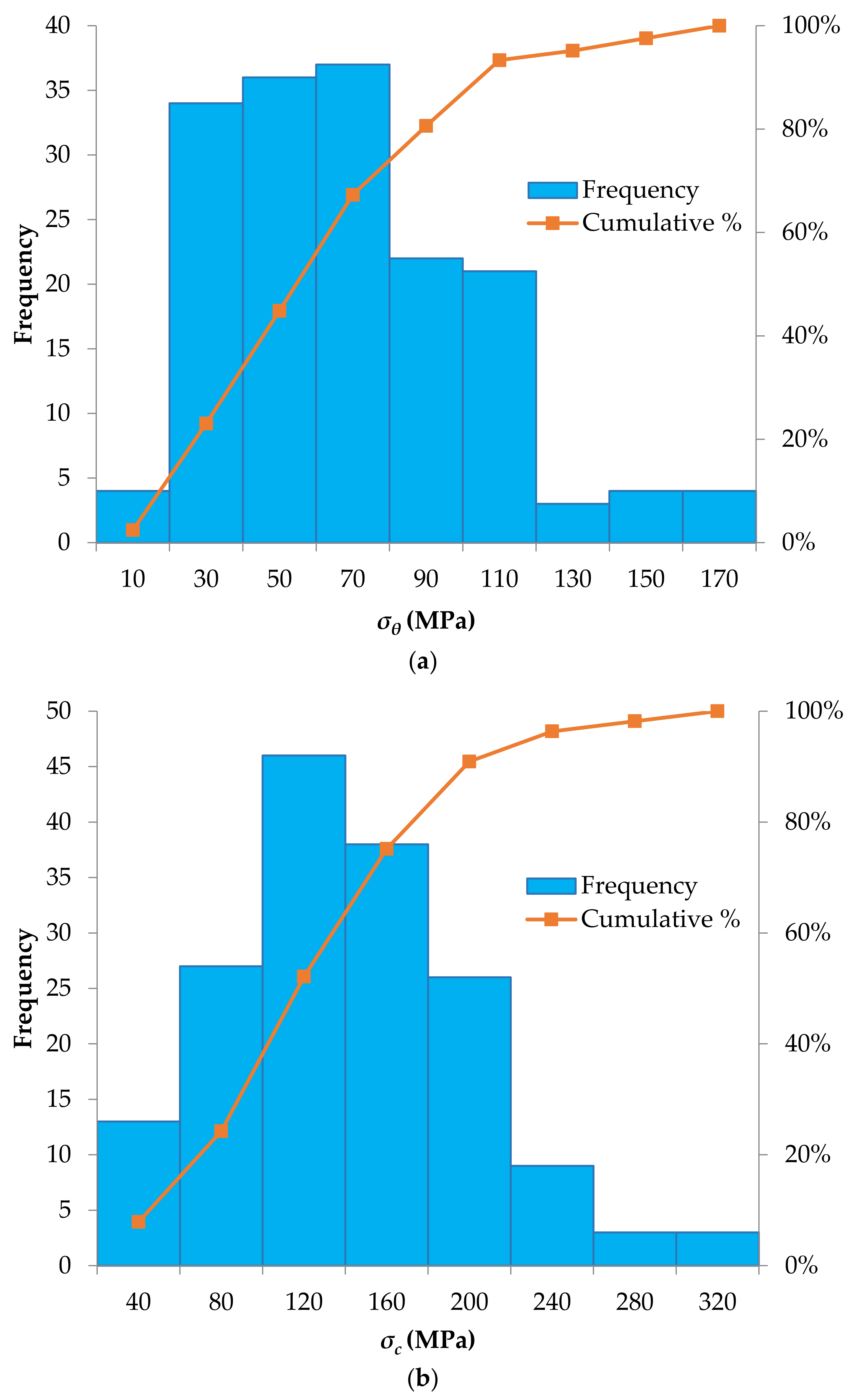
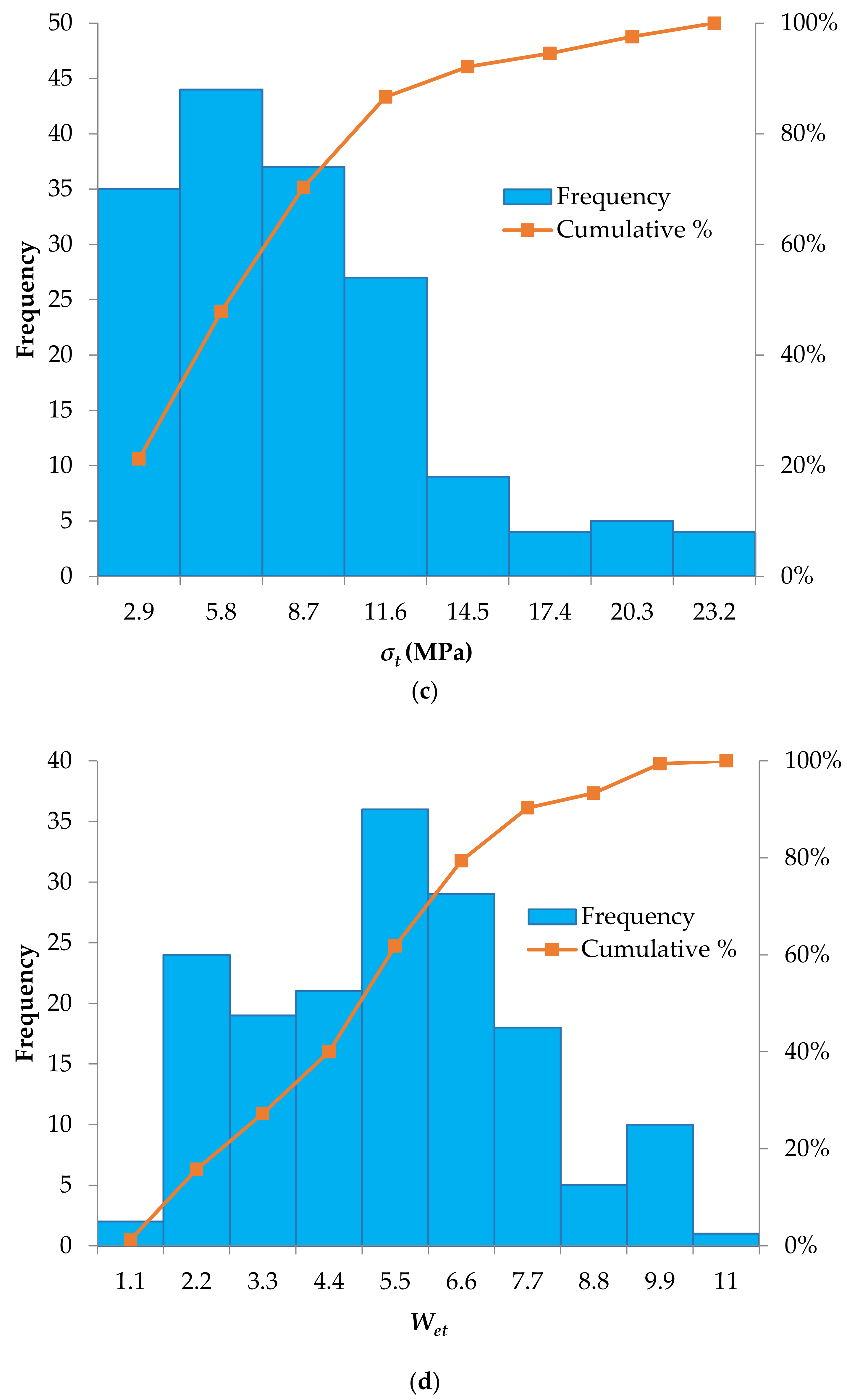
The database contains maximum tangential stress of surrounding rock σ_θ (MPa), uniaxial compressive strength σ_c (MPa), uniaxial tensile strength σ_t (MPa), and strain energy storage index W_et. The histograms, cumulative distribution functions and descriptive statistics (such as minimum and maximum values, mean and standard deviations) of the selected rockburst parameters with the established J48 and random tree models are provided in Figure 2 and Table 3 (the complete database is available in Appendix A, Table A1). It should be noted that in ranges with more dense data, the established models are more accurate.

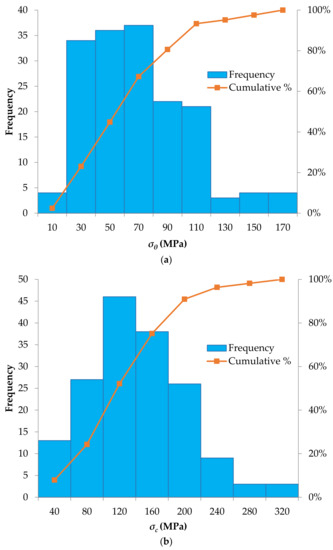
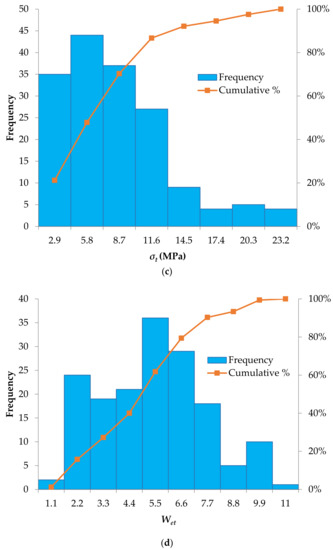
Figure 2. Histograms of the input parameters considered to predict the rockburst hazard: (a) Maximum tangential stress of surrounding rock (σ_θ; MPa), (b) Uniaxial compressive strength, (σ_c; MPa), (c) Uniaxial tensile strength (σ_t; MPa), (d) Strain energy storage index (W_et).

Table 3. Descriptive statistics of the rockburst dataset.

Statistical Parameter	Dataset	Maximum Tangential Stress of Surrounding Rock, σθ (MPa)	Uniaxial Compressive Strength, σc (MPa)	Uniaxial Tensile Strength, σt (MPa)	Strain Energy Storage Index, Wet
Minimum	Training	2.6	18.32	0.38	0.85
	Testing	11	18.32	0.38	1.6
	Total	2.6	18.32	0.38	0.85
Maximum	Training	167.2	306.58	22.6	10.57
	Testing	167.2	263	11.3	9.3
	Total	167.2	306.58	22.6	10.57
Mean	Training	56.17	122.31	7.14	4.69
	Testing	78.65	128.98	6.50	5.68
	Total	59.99	13.44	7.03	4.86
Standard deviation	Training	33.62	59.73	5.09	2.15
	Testing	42.32	64.98	2.97	2.19
	Total	36.11	60.5	4.79	2.18

Rockburst events typically occur in rock masses characterised by brittle behaviour (low deformability), massive and relatively homogeneous structure, high intact rock strength and high in-situ stress states. That said, it is hard to accept that rockburst events were registered in some case-studies involving rock masses with low or very low values of uniaxial compressive strength (see for instance case-studies no. 4, 6, 26, 27, 39, 44, 52, 53, 60, 67, 83, 90, 121, 137). Very probably, in these cases other factors such as large in-situ stress attended to provide high energy releases.

2.2. Methodology

2.2.1. J48

The J48 algorithm is the implementation of the C4.5 algorithm [35]. Waikato Environment for Knowledge Analysis (WEKA) software’s implementation of the C4.5 random tree learner is the J48 algorithm (J48 also implements a later and slightly modified version named C4.5 revision 8, which was the last public version of this algorithm family before C5.0 was released for commercial implementation) [36].

The random trees are generated with C4.5. A tree-like structure serves as a random support system in the random tree. A root node, internal nodes, and leaf nodes build the tree structure. The root node contains all of the input data. A random function is associated with an internal node that may have two or more branches. The label class is represented by the leaf node, which is the output of the input vector. The main advantage of random trees is that they are simple to build and the resulting trees are easy to understand [37]. The C4.5 algorithm has recently been used to determine the potential for seismic soil liquefaction [28,29] and landslide susceptibility [37]. The J48 random tree algorithm takes the following steps [38].

Step 1: Compute the Entropy(S) of the training dataset S as follows:

$$Entropy\left(S\right)=-{\displaystyle \sum _{i=1}^K\left[\left(\frac{freq\left(C_i,S\right)}{\left|S\right|}\right){\log }_2\left(\frac{freq\left(C_i,S\right)}{\left|S\right|}\right)\right]}$$

(1)

where |S| is the number of samples in the training dataset, C_i is a dependent variable, i = 1, 2, …, K, K is the number of classes for the dependent variable, and freq(C_i, S) is the number of samples included in class C_i.

Step 2: Calculate the Information Gain X(S) for the partition’s X test attribute:

$$GainX\left(S\right)=Entropy\left(S\right)-{\displaystyle \sum _{i=1}^L\left[\left(\frac{\left|S_i\right|}{\left|S\right|}\right)Entropy\left(S_i\right)\right]}$$

(2)

where L is the number of test outputs, X, S_i is the subset of S corresponding to the output of ith, and |S_i| is the number of dependent variables of the subset S_i. A subset that provides maximum information gain will be selected as the threshold for a particular partition attribute. The node branch will consist of the two partitions S and S–S_i. The tree is a leaf if the cases are from the same class; hence, the leaf is returned by defining the same dependent variables (class).

Step 3: Calculate the Split Info (X) acquisition’s partition information value for S partitioned to L subsets:

$$SplitInfo\left(X\right)=-{\displaystyle \sum _{i=1}^L\left[\frac{\left|S_i\right|}{\left|S\right|}{\log }_2\frac{\left|S_i\right|}{\left|S\right|}+\left(1-\frac{\left|S_i\right|}{\left|S\right|}\right){\log }_2\left(1-\frac{\left|S_i\right|}{\left|S\right|}\right)\right]}$$

(3)

Step 4: Calculate the Gain Ratio(X):

$$GainRatio\left(X\right)=\frac{InformationGainX\left(S\right)}{SplitInfo\left(X\right)}$$

(4)

Step 5: The root node will be the attribute with the highest gain ratio, and the same calculation from step 1 to step 4 will be repeated for each intermediate node until all instances are exhausted and it reaches the leaf node as defined in step 2.

2.2.2. Random Tree (RT)

RT splits the data set into sub-spaces and fits the constant to each sub-space. A single tree model tends to be very unstable and provides lower prediction accuracy. However, very accurate results can be obtained by bagging RT as a random tree algorithm [39]. RT has a high degree of versatility and quick training capabilities [40]. More comprehensive details of the RT can be found in Sattari et al. [41] and Kiranmai and Laxmi [42]. Table 4 presents the different variations between the J48 and random tree data mining algorithms.

Table 4. Differences between J48 and random tree algorithms.

Properties	J48	Random Tree
Attributes available at each decision node	All	Random Subset
Selection of attributes at each decision node	Highest information gain among all	Best among a random subset
Number of trees	One	One
Data samples used for training	All	All
Final result of Classification	Based on the leaf node reached	Based on the leaf node reached

3. Construction of Prediction Model

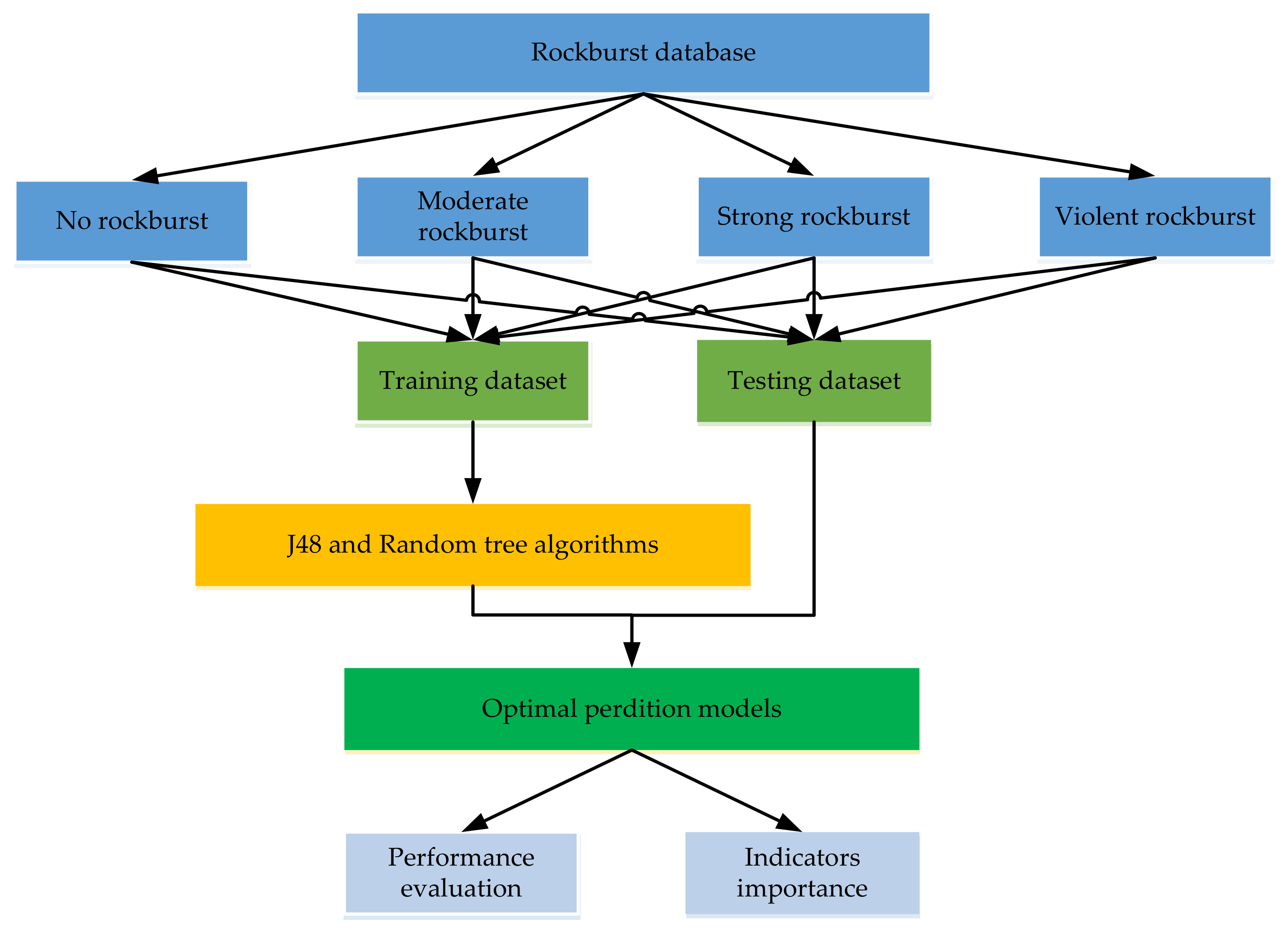
The construction method of the prediction model is presented in Figure 3. The data is divided in two sub-datasets, i.e., training and testing. A training dataset of 137 cases is chosen to train the model and the remaining 28 cases are used to test the model. A hold-out technique is used to tune the hyper parameters of the model. The prediction model is fitted using the optimal configuration of hyperparameters, based on the training dataset. Different performance indexes such as classification accuracy (ACC), kappa statistic, producer accuracy (PA), and user accuracy (UA) are used to evaluate model performance. Last, the optimum model is calculated by evaluating the comprehensive performance of these models. If the predicted performance of this model is appropriate, then it can be adopted for deployment. In WEKA, the entire method of calculation is carried out.

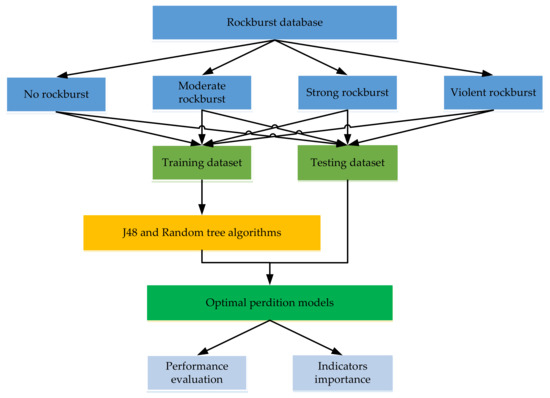
Figure 3. Construction process of prediction model.

3.1. Hyperparameter Optimization

Tuning is the process of maximizing a model’s performance and avoiding overfitting or excessive variance. This is achieved in machine learning by choosing suitable “hyperparameters”. Choosing the right set of hyperparameters is critical for model accuracy, but can be computationally challenging. Hyperparameters are different from other model parameters in that they are not automatically learned by the model through training methods, instead, these parameters must be set manually. Critical hyperparameters in random tree and J48 algorithms are tuned to determine the optimum value of algorithm parameters such as the minimum number of instances per leaf and the confidence factor. For both algorithms, the trial and error approach is used to evaluate these parameters in a particular search range in order to achieve the best classification accuracy. The search range of the same hyperparameters is kept consistent. Furthermore, according to the maximum accuracy, the optimal values for each set of hyperparameters are obtained. In this analysis, the optimum values for the J48 algorithm were found as: the minimum number of instances was 1 and the confidence factor was 0.25, the tree size was 63, the number of leaves was 32, and in the case of a random tree, the tree size was 103 and the minimum total weight of the instances in a leaf was 1.

3.2. Model Evaluation Indexes

J48 and random tree algorithms are used as described in Section 2.2 in order to construct a predictive model for the classification of a rockburst hazard. The uncertainty matrix is a projected results visualization table where each row of the matrix represents the cases in the actual class, while each column displays the cases in the predicted class. It is normally constructed with m rows and m columns, where m is equal to the number of classes. The accuracy, kappa, producer accuracy, and user accuracy found for each class of the confusion matrix sample are used to test the predictive model’s efficacy. Let x_ij (i and j = 1, 2, …, m) be the joint frequency of observations designated to class i by prediction and class j by observation data, x_i+ is the total frequency of class i as obtained from prediction, and x _{+ j} is the total frequency of class j based on observed data (see Table 5).

Table 5. Confusion matrix.

Predicted	Actual				Total	UA (%)
	1	2	…	m
1	x11	x21	…	x1m	x1+	(x11/x1+) × 100%
2	x21	x22	…	x2m	x2+	(x22/x2+) × 100%
…	…	…	…	…	…	…
m	xm1	xm2	…	xmm	xm+	(xmm/xm+) × 100%
Total	x+1	x+1	…	x+m
PA (%)	(x11/x+1) × 100%	(x22/x+2) × 100%	…	(xmm/x+m) × 100%

Classification accuracy (ACC) is determined by summing correctly classified diagonal instances and dividing them by the total number of instances. The ACC is given as:

$$ACC=\left(\frac{1}{n}{\displaystyle \sum _{i=1}^m{x}_{ii}}\right)\times 100\%$$

(5)

Cohen’s kappa index, which is a robust index that considers the likelihood of an event classification by chance, measures the proportion of units that are correctly categorized units proportions after removing the probability of chance agreement [43]. Kappa can be calculated using the following formula:

$$Kappa=\frac{n{\displaystyle {\sum }_{i=1}^m{x}_{ii}-{\displaystyle {\sum }_{i=1}^m\left(x_{i+}\cdot x_{+i}\right)}}}{n^2-{\displaystyle {\sum }_{i=1}^m\left(x_{i+}\cdot x_{+i}\right)}}$$

(6)

where n is the number of instances, m is the number of class values, x_ii is the number of cells in the main diagonal, and x_i+, x_+i are the cumulative counts of the rows and columns, respectively.

Landis and Koch [44] suggested a scale to show the degree of concordance (see Table 6). A kappa value of less than 0.4 indicates poor agreement, while a value of 0.4 and above indicates good agreement (Sakiyama et al. [45]; Landis and Koch [44]). The producer’s accuracy of class i (PA_i) can be measured using Congalton and Green’s formula [46].

$${\mathrm{PA}}_i=\left(\frac{x_{ii}}{x_{+m}}\right)\times 100\%=\left(\frac{x_{ii}}{{\displaystyle {\sum }_{i=1}^m{x}_{im}}}\right)\times 100\%$$

(7)

and user’s accuracy of class i (UA_i) can be found as:

$${\mathrm{UA}}_i=\left(\frac{x_{ii}}{x_{m+}}\right)\times 100\%=\left(\frac{x_{ii}}{{\displaystyle {\sum }_{i=1}^m{x}_{mj}}}\right)\times 100\%$$

(8)

Table 6. Strength agreement measure related to kappa statistic.

Interpretation	Almost Perfect	Substantial	Moderate	Fair	Slight	Poor
Kappa statistic	0.81–1.00	0.61–0.80	0.41–0.60	0.21–0.40	0.00–0.20	−1.00–0.00

The J48 and random tree models are studied for the suitability of predicting rockburst. Comparison is made with the traditional empirical criteria of the rockburst including the Russenes criterion [47], the rock brittleness coefficient criterion [48], ANN [21], and CNN [21] models using performance measures i.e., ACC, PA, UA, and kappa.

4. Results and Discussion

The performance of both models was tested to predict rockburst hazard using various evaluation criteria as mentioned in Section 3. Based on the statistical assessment criteria, it was observed that both models had very high predictive accuracy capability (J48: 92.857%; Random tree: 100%). The result of the kappa coefficient showed that both of these models are almost perfect but the random tree model performed best, owing to having the highest kappa coefficient value (1.0), followed by the J48 (0.904). With comparisons of the results from the four models, it is found that the prediction accuracy (ACC) and kappa coefficient of random tree and CNN models are equivalent, which is higher than that of other models shown in Table 7.

Table 7. Performance metrics of each model for test data.

Method	ACC (%)	Kappa
Russenes criterion [47]	42.867	0.222
Rock brittleness coefficient criterion [48]	53.571	0.352
ANN [21]	89.286	0.856
CNN [21]	100	1.000
J48 (present study)	92.857	0.904
Random tree (present study)	100	1.000

Note: Bold values indicate the highest value for each model.

In terms of the producer accuracy (PA) value, the random tree model also had the highest PA (100%) for all ranks of rockburst, followed by the J48. PA and UA show that some of the features are better classified than others (see Table 8). As can been seen from the Table 8, in the J48 model, both “no rockburst” and “moderate rockburst” both have at par PA values (100%) compared to “strong rockburst” (88.889%) and “no rockburst” (83.333%). While in the J48 model, both “no rockburst” and “violent rockburst” have at par UA values (100%) compared to “moderate rockburst” (88.889%) and “strong rockburst” (87.5%). The results showed that there was a statistically significant difference between the random tree and the J48 models, and it was found that the performance of the J48 is just secondary to the random tree model in prediction of rockburst hazard.

Table 8. Confusion matrices and performance measures based on testing dataset of rockburst.

Predicted	Observed				Total	UA (%)	Predicted	Observed				Total	UA (%)
	NR	MR	SR	VR				NR	MR	SR	VR
Russenes criterion [47]							CNN [21]
NR	2	0	0	0	2	100	NR	6	0	0	0	6	100
MR	1	1	1	1	4	25	MR	0	7	0	0	7	100
SR	0	4	6	2	12	50	SR	0	0	9	0	9	100
VR	3	2	2	3	10	30	VR	0	0	0	6	6	100
Total	6	7	9	6	28		Total	6	7	9	6	28
PA (%)	33.333	14.286	66.667	50			PA (%)	100	100	100	100
Rock brittleness coefficient criterion [48]							J48 (present study)
NR	1	0	0	0	1	100	NR	6	0	0	0	6	100
MR	2	3	1	0	6	50	MR	0	7	1	0	8	87.5
SR	2	3	8	3	16	50	SR	0	0	8	1	9	88.889
VR	1	1	0	3	5	60	VR	0	0	0	5	5	100
Total	6	7	9	6	28		Total	6	0	0	0	6
PA (%)	16.667	42.857	88.889	50			PA (%)	100	100	88.889	83.333
ANN [21]							Random Tree (present study)
NR	6	0	0	0	6	100	NR	6	0	0	0	6	100
MR	0	7	1	0	8	87.5	MR	0	7	0	0	7	100
SR	0	0	7	1	8	85.5	SR	0	0	9	0	9	100
VR	0	0	1	5	6	83.333	VR	0	0	0	6	6	100
Total	6	7	9	6	28		Total	6	7	9	6	28
PA (%)	100	100	77.778	83.333			PA (%)	100	100	100	100

Note: NR: no rockburst; MR: moderate rockburst; SR: strong rockburst; VR: violent rockburst.

To illustrate and verify the performances of J48 and random tree models, the prediction capacity of these models is compared with the other models including the Russenes criterion [47], the rock brittleness coefficient criterion [48], ANN [21], and CNN [21]. The confusion matrix and the performance indices for traditional empirical criteria of the rockburst including Russenes criterion [47], the rock brittleness coefficient criterion [48], ANN [21], and CNN [21] models are presented in Table 8. The comparison of these models reveals that J48 and random tree models can be applied efficiently, but the random model exhibits the best and at par performance with the CNN [21] model and after that the J48 model. The random tree model can predict “no rockburst”, “moderate rockburst”, “strong rockburst” and “violent rockburst” cases with overall accuracy of 100%.

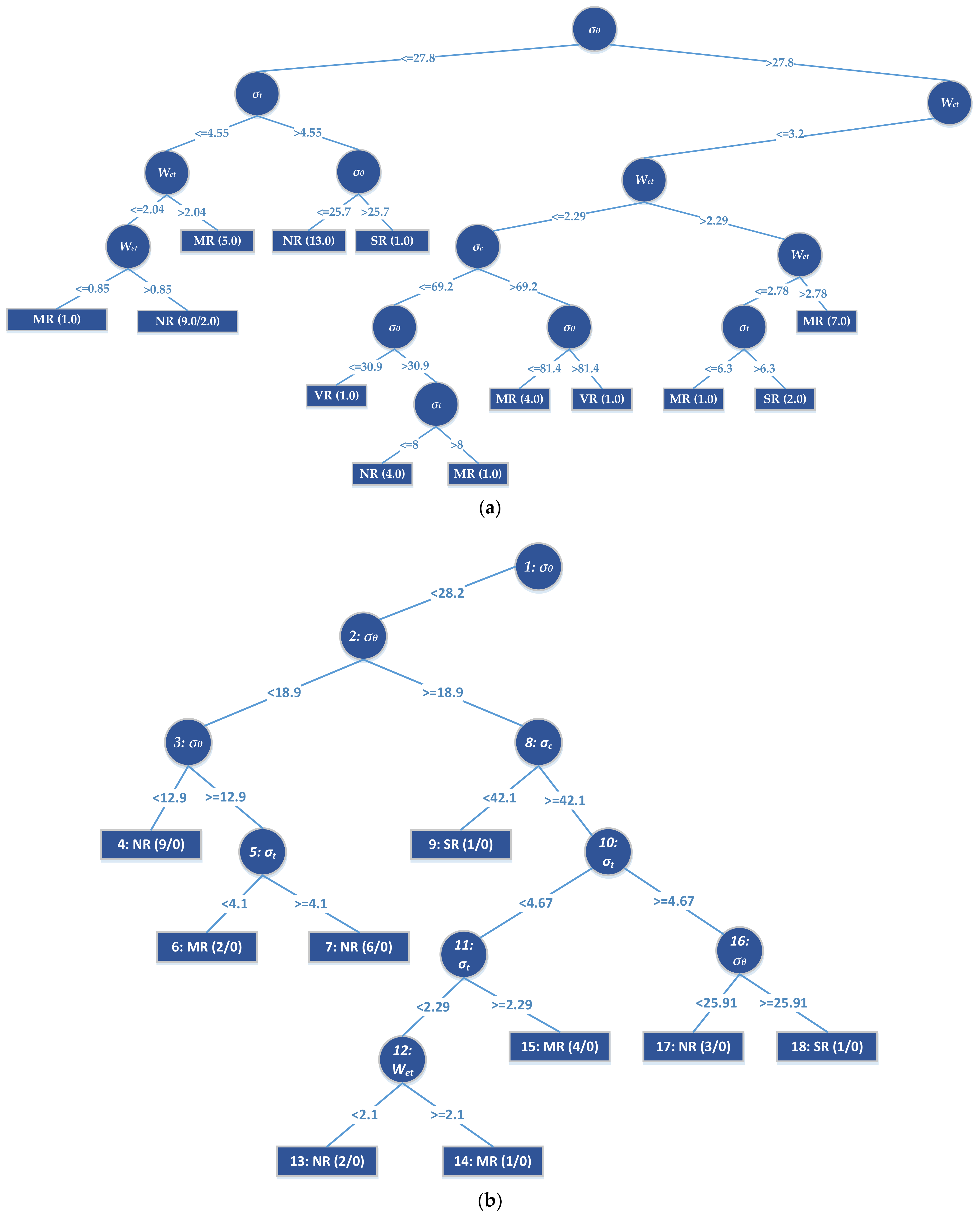
Although existing models such as SVM do not provide explicit equations for professionals, the established J48 and random tree models (see Figure 4) can be used by civil and mining engineering professionals with the aid of a spreadsheet to analyze potential rockburst events without going into the complexities of model development. Furthermore, the J48 and random tree approaches do not require data normalization or scaling, which is an advantage over most other approaches.

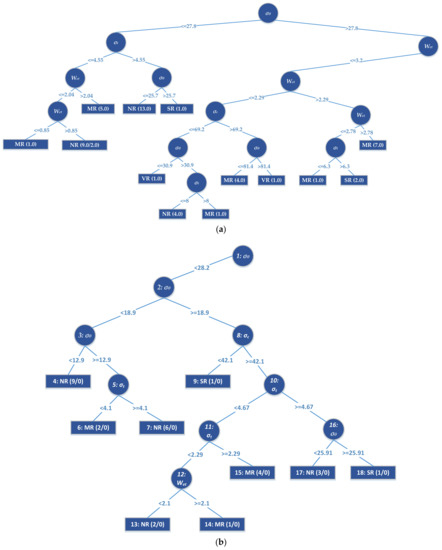
Figure 4. Part of (a) J48 and (b) random tree models.

In general, both of the established models performed well in the testing data phase, while overall performance of the random tree model showed better performance (see Table 7 and Table 8) and it is shown that the random tree model is preferred over other models. It was found that for a larger dataset with almost no sampling bias (i.e., disparity in class ratio between population and sample) in the training and testing phases, predictive performance should be further examined. Though the dataset (165) used in this study is small, the J48 and random tree models can always be updated to yield better results, as new data become available. Study results suggest that proposed models show improved predictive performance compared to the majority of existing studies. This, in turn, will ensure the reduction in the loss of property, human lives, and injuries from a practical viewpoint.

5. Conclusions and Limitations

In underground mining and civil engineering projects, models for predicting rockburst can be valuable tools. This study compared J48 and random tree models for predicting rockburst. Four variables (σ_θ, σ_c, σ_t, and W_et) were selected as influence factors for predicting rockburst using a dataset of 165 rockburst events compiled from recent published research, which was used to construct the decision tree models. The following conclusions can be drawn, based on the results of the study:

• The performance measures of the testing dataset for the J48 and random tree algorithms conclude that it is rational and feasible to choose the maximum tangential stress of surrounding rock σ_θ (MPa), the uniaxial compressive strength σ_c (MPa), the uniaxial tensile strength σ_t (MPa), and the strain energy storage index W_et as indexes for predicting rockburst.
• The classification accuracy of J48 and random tree models in the test phase is 92.857% and 100%, respectively, which shows that the random tree model is an accurate and efficient approach to predicting the potential for rockburst classification ranks.
• The kappa index of the developed J48 and random tree models is in the range of 0.904–1.000, which means that the correlation between observed and predicted values is nearly perfect.
• The comparison of models’ performances reveals that the random tree model gives more reliable predictions and their application is easier owing to a clear graphical outcome that can be used by civil and mining engineering professionals.

Although the proposed method yields adequate prediction results, certain limitations should be discussed in the future.

(1) The sample size is restricted and unbalanced. The number and quality of datasets have a significant impact on the prediction performance of random tree and J48 algorithms. In general, the generalization and reliability of all data-driven models are affected by the size of the dataset. Although the random tree and J48 algorithms perform well, larger datasets can yield better prediction results. Furthermore, the dataset is unbalanced, particularly for samples with violent rockburst (17%) and samples with no rockburst (19%). As a result, establishing a larger and more balanced rockburst database is essential.

(2) Other variables may have an effect on the prediction outcomes. Numerous factors influence the risk of a rockburst, including rock properties, energy, excavation depth, and support structure, among others. Although the four indicators used in this study can define the required conditions for rockburst hazard assessment to some degree, some other indicators, such as the buried depth of the tunnel (H), failure duration time, and energy-based burst potential index, may also have an impact on rockburst hazard. As a consequence, it is crucial to look into the effects of these variables on the prediction outcomes.