Abstract
When early failures in rolling bearings occur, we need to be able to extract weak fault characteristic frequencies under the influence of strong noise and then perform fault diagnosis. Therefore, a new method is proposed: complete ensemble intrinsic time-scale decomposition with adaptive Lévy noise (CEITDALN). This method solves the problem of the traditional complete ensemble intrinsic time-scale decomposition with adaptive noise (CEITDAN) method not being able to filter nonwhite noise in measured vibration signal noise. Therefore, in the method proposed in this paper, a noise model in the form of parameter-adjusted noise is used to replace traditional white noise. We used an optimization algorithm to adaptively adjust the model parameters, reducing the impact of nonwhite noise on the feature frequency extraction. The experimental results for the simulation and vibration signals of rolling bearings showed that the CEITDALN method could extract weak fault features more effectively than traditional methods.
1. Introduction
Rolling bearings are the most commonly used and extremely vulnerable core supporting components in rotating machinery. If they fail, they directly affect the safe and stable operation of the whole unit [1,2,3,4]. Fault detection through analyzing the vibration signals of rolling bearings is currently one of the most common methods used for bearing analysis. By installing an acceleration sensor near the bearing housing, the vibration signal generated by the rotating rolling bearing is collected and analyzed to determine the condition of the bearing. Affected by many environmental factors (such as vibration caused by the non-linearity of bearing stiffness, vibration caused by the corrugation of machining surface, vibration caused by the eccentricity of bearings, etc.) during the signal acquisition process, the fault signal of rotating machinery usually contains a large amount of noise. Meanwhile, the fault information is difficult to identify due to its unobvious early default characteristics. Additionally, the rotating machinery fault signal usually shows non-smooth, non-linear characteristics, because the dynamic signal will be non-smooth when a bearing fault occurs during operation, such as friction, cracks, oil film vortex, oil film oscillation, etc. Therefore, non-smoothness can characterize the presence of faults. Meanwhile, when a fault occurs and develops, the damping, stiffness, and elastic force of the bearing change, and the dynamic signal also exhibits nonlinear characteristics. The traditional time-domain analysis methods and Fourier transform-based analysis methods can capture only the overall statistical characteristics of the signal, but not the time-frequency detail characteristics of the signal, and cannot handle nonlinear, non-stationary signals. With the continuous development of signal processing technology, modern time-frequency analysis methods have made great progress in their ability to extract fault features from non-stationary, non-linear signals [5,6,7].
There are many weak signal processing methods available, and wavelet transform (WT) is often effective in analyzing non-stationary and non-linear signals [8,9]. However, WT has some shortcomings, such as the choice of certain wavelet basis functions. In recent years, some adaptive signal decomposition methods have been applied to the analysis of the vibration signals of bearings, such as empirical mode decomposition (EMD) [10] and local mean decomposition (LMD) [11]. Intrinsic time-scale decomposition (ITD) is another adaptive signal decomposition method that was proposed by Frei and Osorio [12] and first applied in medical diagnosis. ITD uses linear interpolation to construct the baseline signal, instead of averaging the envelope using cubic spline interpolation as in EMD. As a result, ITD has a clear advantage in terms of operational efficiency. Each proper rotational component (PRC) retains almost all of the polar information of the original signal. As a result, ITD is now widely used to extract the fault characteristics of rolling bearings, as the ITD process happens to be a demodulation process. On the basis of the above advantages, scholars introduced the ITD method from the medical field into mechanical signal fault diagnosis. For example, Lin and Chang proposed a rolling bearing fault diagnosis method based on an enhanced kurtosis spectrum and intrinsic time-scale decomposition [13]. Duan and Yao et al. proposed to apply intrinsic time-scale decomposition to the fault diagnosis of gearboxes under variable operating conditions [14]. Xing and Qu et al. proposed a gear fault diagnosis method with variable working conditions based on intrinsic time-scale and singular value decomposition [15]. Zhang and Liu et al. proposed a diesel engine fault diagnosis method with complete ensemble intrinsic time-scale decomposition [16]. Hu and Xiang proposed the application of the ensemble intrinsic time-scale decomposition of fan gear [17]. Tong and Cao et al. proposed an improved intrinsic time-scale decomposition with wavelet packet transform and singular-value decomposition to perform fault diagnosis on rolling bearings [18]. Liu and Zhang et al. proposed using intrinsic time-scale decomposition to diagnose diesel-engine faults [19]. Bi and Ma et al. proposed detecting gasoline-engine knock using the improved intrinsic time-scale decomposition of complete integration [20]. Yu and Liu proposed sparse coding based on intrinsic time-scale decomposition to diagnose weak bearing faults [21]. Yuan and Peng proposed smooth intrinsic time-scale decomposition for the fault diagnosis of rolling bearings [22]. Lei and Zhou et al. used intrinsic time-scale decomposition to monitor tool wear during milling [23]. Ma and Zhan et al. proposed complete ensemble intrinsic time-scale decomposition with adaptive noise (CEITDAN), which was applied to the feature extraction of rolling bearings [24]. According to the research findings of previous ITD methods in the process of signal decomposition based on ITD research. Through the analysis of previous studies, their proposed methods improve the problem of the modal blending of ITD methods, expand the application scope of ITD methods, and improve the effect of feature extraction, but there are still certain shortcomings, such as the fact that a certain amount of nonwhite noise components are still retained in the signals after the noise reduction in these methods. They did not find an effective method to filter out the nonwhite noise components in the signal (e.g., industrial frequency interference, colored noise caused by a drive motor, etc.), which can be contained between the feature frequencies and interfere with the extraction of the feature frequencies, making it difficult to locate them accurately. Additionally, the existence of these noises will cause the calculation of feature parameters such as the entropy value to have large errors, thus reducing the fault diagnosis accuracy.
For the current bearing fault signal processing method for use after noise reduction, where there is still a residual nonwhite noise component interference problem, this paper is inspired by the literature [25] and aims to propose a fault diagnosis method for the signal-to-noise ratio (SNR) −25 dB. This paper aims to improve the noise reduction after the nonwhite noise interference fault diagnosis, reducing the problem of fault diagnosis accuracy. Therefore, this article proposes a method that involves using variable-parameter analog noise (i.e., Lévy noise) to replace traditional white noise. This can effectively filter out noise in the decomposition process and improve the influence of the nonwhite noise part of noise on feature frequency extraction; this is called complete ensemble intrinsic time-scale decomposition with adaptive Lévy noise (CEITDALN). Lévy noise is a digital noise model that contains four parameters. Changes in the parameters can cause dramatic changes in the noise model [26]. Therefore, in order to avoid the difficulty of artificially setting parameters, this paper proposes an improved coyote algorithm to adaptively adjust the noise intensity coefficient and Lévy noise parameters in the CEITDALN method. The energy of the maximal center frequency band of the kurtosis spectrum was used as the objective function of the optimization algorithm to achieve the best feature extraction.
The rest of the article is organized as follows: Section 2 introduces related works such as CEITDAN and the theory of the coyote optimization algorithm. Section 3 introduces CEITDALN and the improved coyote optimization algorithm. Section 4 uses analog signals to verify the effectiveness of the proposed method and introduces the engineering application platform. Through the above platform, the effectiveness of the proposed method is further proved. Section 5 concludes this article.
2. Related Work
2.1. CEITDAN
CEITDAN’s decomposition method superimposes a component decomposed by ITD from white noise with a certain signal-to-noise ratio (we add a white noise whose standard deviation is normalized and whose noise amplitude can be adjusted adaptively, thus ensuring that the SNR of each decomposition stage is fixed) onto the original signal and uses the average residue component obtained by the ITD to obtain the first rotation component. It then subtracts the first rotation component from the original signal.
The residual component is obtained, white noise is added to the residual component, and the same operation is performed until the residual component is a monotonic function or there are less than three extreme points. A proper rotation component can accurately define the instantaneous information of the signal and is repeated several times in this manner.
Step 1. The first round of noise addition: is the first-order proper rotation component decomposed by ITD from white noise with a certain SNR (here, we use the coefficient to control the SNR of each unchanged decomposition stage), where is the number of noise additions superimposed onto the original signal . The average value is used as the residue component of the method; then, the first-order component of the origin signal is obtained as follows:
is the corresponding order of ITD white noise. is used as , is the noise-adding amplitude coefficient, is the quotient of standard deviation, represents the residue component obtained by the ITD of signal , and is the signal with white noise. The proper components at this time are as follows:
Step 2. The second round of noise addition: The second-order PRCs of white noise are superimposed onto , and the first-order components of the mixed signal are obtained by ITD. The average is used as the second residue component of this method’s residue component, as follows:
The second-order proper component obtained at this time is as follows:
Step 3. The-th round of noise addition: The -th-order PRCs of white noise are superimposed onto the remaining terms . Then, the first-order component of the signal with adaptive white noise is obtained by ITD, and the average value is taken as the -th-order residue component of the method, as follows:
The PRC obtained at this point is:
Step 4. Repeat Steps 1 to 3 several times until the residual component is a monotonic function or the number of extreme points in this residual component is fewer than three. The final remaining term is as follows:
At this point, the entire CEITDAN decomposition process ends.
The final shifted terms are as follows:
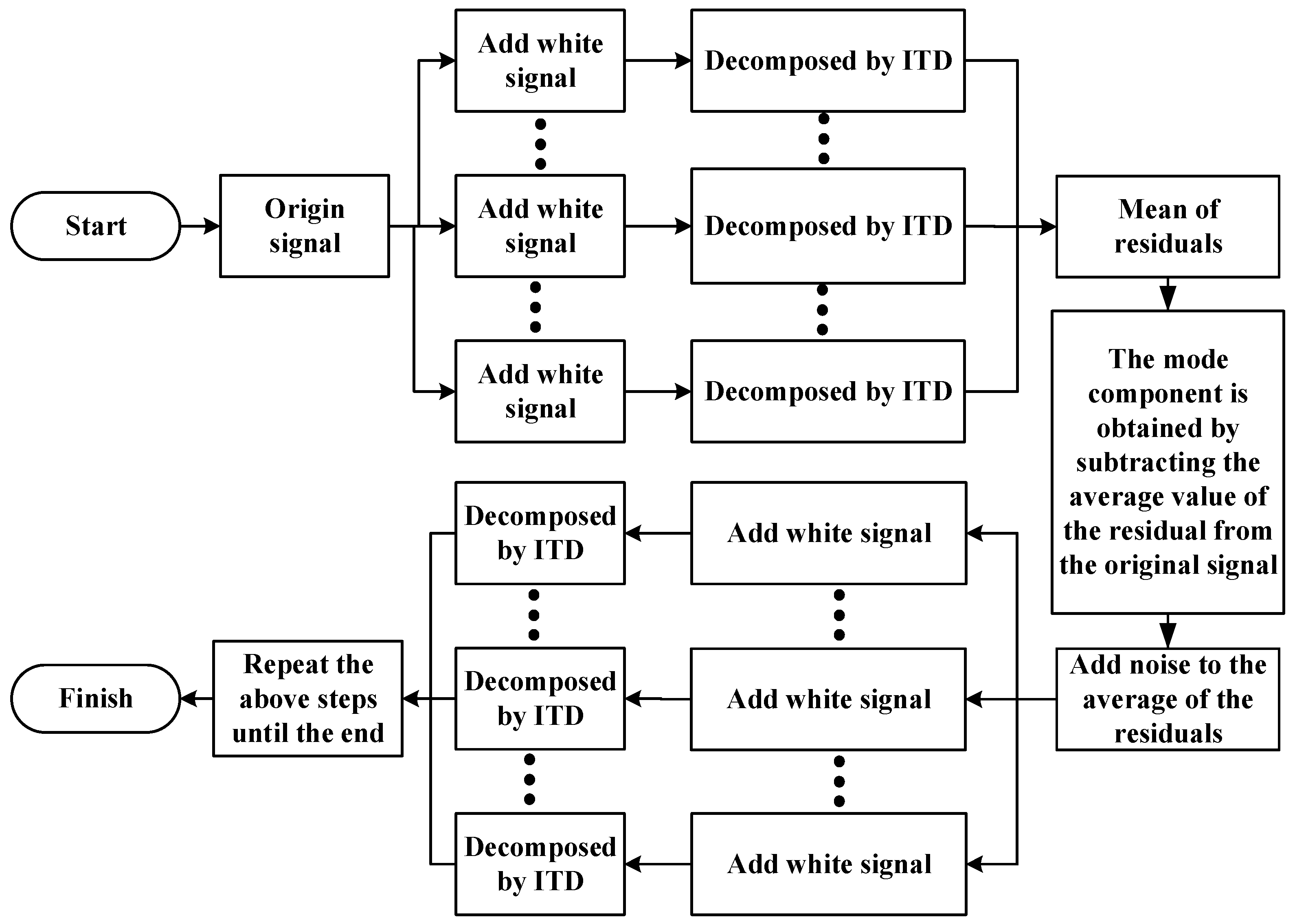
The flowchart of this method is shown in Figure 1:

Figure 1.
CEITDAN flowchart.
2.2. Group Optimization Algorithm Theory
The coyote optimization algorithm (COA) was proposed by Pierezan et al. [27] in 2018. It is a new intelligent optimization algorithm that simulates the phenomena of coyotes living in groups, including their growth, life, and death and being driven away and accepted by groups. It obtains better optimization results in the optimization of benchmark functions. The COA divides a population into several subgroups through random grouping, determines the alpha wolf and cultural trend of the subgroup, and randomly selects two coyotes. These four factors influence coyote growth. It reforms the growth process through coyote social adaptability. The birth of a coyote is affected by two randomly selected parent coyotes and environmental variation. In terms of social adaptability, if a newborn coyote is better than an old and poor coyote, the old coyote dies. Otherwise, the newborn coyote dies. According to a certain probability among subgroups, some coyotes are driven out of the group and accepted by other groups, thereby changing the coyote grouping status through the continuous evolution of this process of growth, death, driving away, and acceptance. It obtains the coyote that is most suitable for the social environment as the best solution to an optimization problem.
In the COA, each coyote represents a candidate solution. Each solution vector is composed of the social state factor of the coyote. These status factors include coyote internal factors and external factors. Each state factor represents a decision variable, and state factors constitute a solution vector containing decision variables. Every coyote is measured in terms of its social adaptability. The COA is mainly divided into four steps: randomly initializing the coyote group and randomly grouping them, the coyotes growing up in the group, the life and death of the coyotes, and coyotes being driven away and accepted.
Step 1: Parameters such as coyote population , number of coyote individuals per group , dimension , and termination condition were set.
Step 2: Randomly initialize the coyote pack; the -th coyote individual in pack at time is defined as:
where and denote the upper and lower bounds of the -th dimensional values, respectively, and is a randomly generated real number in the range of .
Step 3: Evaluation of coyote adaptability:
where , implies in the coyote’s adaptation to the environment (cost of the objective function ).
Step 4: Coyotes sometimes break away or are expelled from their original pack, forming a pack shift; the probability of the occurrence of this is defined as :
Step 5: Find the head wolf in the current pack and calculate the cultural trend of the current coyote pack:
where denotes the median of the -th dimensional variable for all coyotes within the group at moment when is odd.
Step 6: Simulating the birth-at-death practice in genetics, the age (in years) of the coyote was written as . The birth of a new coyote () was written as a combination of the social status of both parents (randomly selected) plus environmental influences:
where and are random coyotes from within the wolf pack, and are two random dimensions of the problem, and and are both random numbers within generated by uniform probability. The discrete probability and the association probability affect the cultural diversity of individuals in the coyote pack. and are defined as:
Assuming that indicates that the coyotes in the group are less adaptive than the pups and that represents the number of coyotes in the current group, if is 1 and holds—i.e., if the number of coyotes in a group is 1 and the pups are more adaptive than only one coyote—the pups survive and the oldest coyote in the group dies; in the remaining cases, the pups die.
Step 7: Calculate the effect of the head wolf and group cultural trends on the renewal of individuals within the coyote pack corresponding to the current moments and :
where and represent the random coyotes in the current pack, respectively.
Step 8: All coyote individuals in the coyote pack were updated in turn to obtain new coyote individuals , the size of the adaptation of the new coyote to the original coyote was selected by merit, and the optimal coyote was retained:
where and are uniform probability generated real numbers in the range of representing the magnitude of the weight of individual coyotes influenced by the cultural trend of wolves versus the group.
Step 9: Update the ages of individual coyotes by simulating the growth of individuals over time.
Step 10: Judge the termination condition, and if it is reached, output the social state of the coyote with the best adaptation ability; otherwise, return to Step 3 to continue.
The above steps show that COA has the following advantages: (a) COA has a good search model and framework. The coyotes are randomly divided into multiple subgroups. After all the coyotes grow up, cultural exchanges are carried out through repelling and acceptance. Compared with algorithms such as particle swarm optimization (PSO), this search model and framework has stronger exploration capabilities. (b) COA guides the growth of coyotes through wolves and cultural trends. The algorithm has a strong local search ability. (c) The emergence of newborn COA coyotes comes from the combined effect of two randomly selected parent coyotes and random variations in the social environment, meaning that the algorithm has a certain global search capability. (d) COA updates each coyote in the group. Compared with the similar structure of SFLA, the COA update method is simple. (e) COA is randomly grouped after initialization. The coyotes in the group are randomly driven out and accepted, so that there is an exchange of information between groups.
3. Proposed Method
3.1. Improved CEITDAN Based on Lévy Noise
The core idea of the CEITDAN algorithm is to add groups of white noise. During the decomposition process, the noise component in the noisy signal is cancelled out to achieve the purpose of noise reduction. However, the signal noise obtained by actual engineering is more complicated. There is both white and colored noise. Therefore, when white noise in the noisy signal does not exist as the main noise component, it is still difficult to extract the characteristic frequency after filtering by this method. For this reason, this article proposes a new noise addition. Instead of a single white noise, digital noise is added that can be adjusted to different noise types by changing parameters, improving the filtering effect, named complete ensemble intrinsic timescale decomposition with adaptive Lévy noise.
Lévy noise is also called stable noise [28]. Since the distribution and probability density functions of Lévy noise do not have explicit expressions, the characteristic function of the distribution of Lévy noise is as follows:
where is the characteristic index. The smaller is, the more obvious the noise impulse and tailing characteristics are. is the Cauchy distribution and is the Gaussian distribution; is the symmetry parameter that determines the symmetry of the noise distribution. When , the distribution is symmetrical; is the dispersion coefficient that represents the range of the Lévy distribution—that is, the degree of dispersion. is the position parameter that is used to determine the center of the distribution. In this paper, on the basis of the Chambers–Mallows–Stuck (CMS) method, the Lévy stable random variable can be expressed by the following formula:
When ,
In the above formula, is uniformly distributed in the interval and obeys an exponential distribution with an average value of 1. and can be calculated according to the following formula:
When ,
The proposed method in this paper is based on the above-mentioned Lévy noise. Therefore, the CEITDAN method was rewritten as follows.
Let the PR component calculated by pooled averaging be . is the -th PR component, is the Lévy noise and satisfies a normal distribution, and is the original signal. The CEITDALN algorithm proceeds as follows:
- (1)
- Using ITD to decompose each , followed by averaging the first residual component, the first residual component, , is:
- (2)
- By eliminating from the most primitive signal, the first PR signal is obtained as:
- (3)
- Construct the set residual signal and decompose it to obtain as:
- (4)
- When , analogous to the above calculation, find and then find :
- (5)
- The algorithm terminates when the -pole is less than 3. The final decomposition results in:
In the following, the time complexity of the proposed method is analyzed for this paper. Firstly, the problem size of the method is . The time complexity of the method is denoted as . According to the definition of the Cox–de Boor recursion, additive operations and multiplicative operations are required for all the baseline functions, and additive operations are required for the debase lining, so the time complexity of the proposed method is , where and denote the addition of time complexity and multiplication time complexity, respectively; is the number of PRCs.
3.2. Improved COA Based on GBO Optimization
As the coyote algorithm was proposed recently, there are still the problems mentioned above. Therefore, the gradient-based optimizer (GBO) method proposed in [29] was introduced into the coyote optimization algorithm. The gradient search rule (GSR) in the GBO method can speed up the convergence speed of the coyote optimization algorithm and enhance the exploration trend. The local escaping operator (LEO) can effectively solve the problem of local optimal solutions. Therefore, this article proposes using the GBO method to improve the COA method and named it GBO-COA.
The GBO method comes from a combination of the gradient method and the population optimization algorithm. It explores the search domain by specifying the search direction by Newton’s method and using gradient search rules and local escape operators. In the gradient search rule, better search and better positions are achieved by controlling the movement of vectors. The method uses GSR to increase the speed of convergence. Considering that many of the optimization probabilities in Newton’s gradient-based method [30] cannot be solved by differential calculations, the numerical gradient method is used instead of the direct function derivation method. The solution of GSR requires the calculation of both the first derivatives according to the Newtonian method in [31] and the Taylor series. Additionally, there is the following central difference formula [32]:
According to Newton’s method and Formula (31), the new can be defined as:
In the GBO algorithm, adjacent locations are replaced by two other vectors in the population. The GSR is modified using an adaptive factor to improve the ability of GBO to balance global and local searches.
In Formulas (33) to (35), and are 0.2 and 1.2, respectively; is the number of iterations and is the total number of iterations. In order to balance global and local search capabilities, parameter changes were based on the change in sine function . This parameter is dynamically adjusted at each iteration and can be set to a larger value at the early iterations in order to increase the population diversity. Then, as the number of iterations increases, the value is gradually reduced to speed up convergence. The generated solution should be able to explore the search space around the corresponding best solution. This helps the GSR method to get rid of any local optima, as it increases the diversity of the population to search for the best solution obtained. Thus, GSR follows as:
where is a decimal number in the range of . and are the worst and best solutions obtained in the optimization process, respectively. is an N-dimensional random number; , , , and are different integers randomly selected from . is the step size, affected by and .
The GBO algorithm uses the best space and moves the current space in the direction as the direction movement (DM). Therefore, an appropriate local search trend was generated in this process that could improve the speed of the GBO algorithm.
where is the random number of and is a random parameter that guarantees that each space has non-synchronization length.
In summary, the optimal space is:
The GBO algorithm also used LEO operators to improve the efficiency in solving complex problems. This operator can effectively change the position of to produce a solution . In the , solutions included and , two random schemes and , and a randomly generated scheme (). The generation of solution is as follows in Algorithm 1:
| Algorithm 1. Generation of solution |
| If If Else END END |
In the above formula, is the uniform random number of ; is the random number that obeys the normal distribution; the average is 0; the standard deviation is 1; is the probability; and , , and are three random numbers. The formula definition is:
where is a random number in the range of and is a constant in the range of .
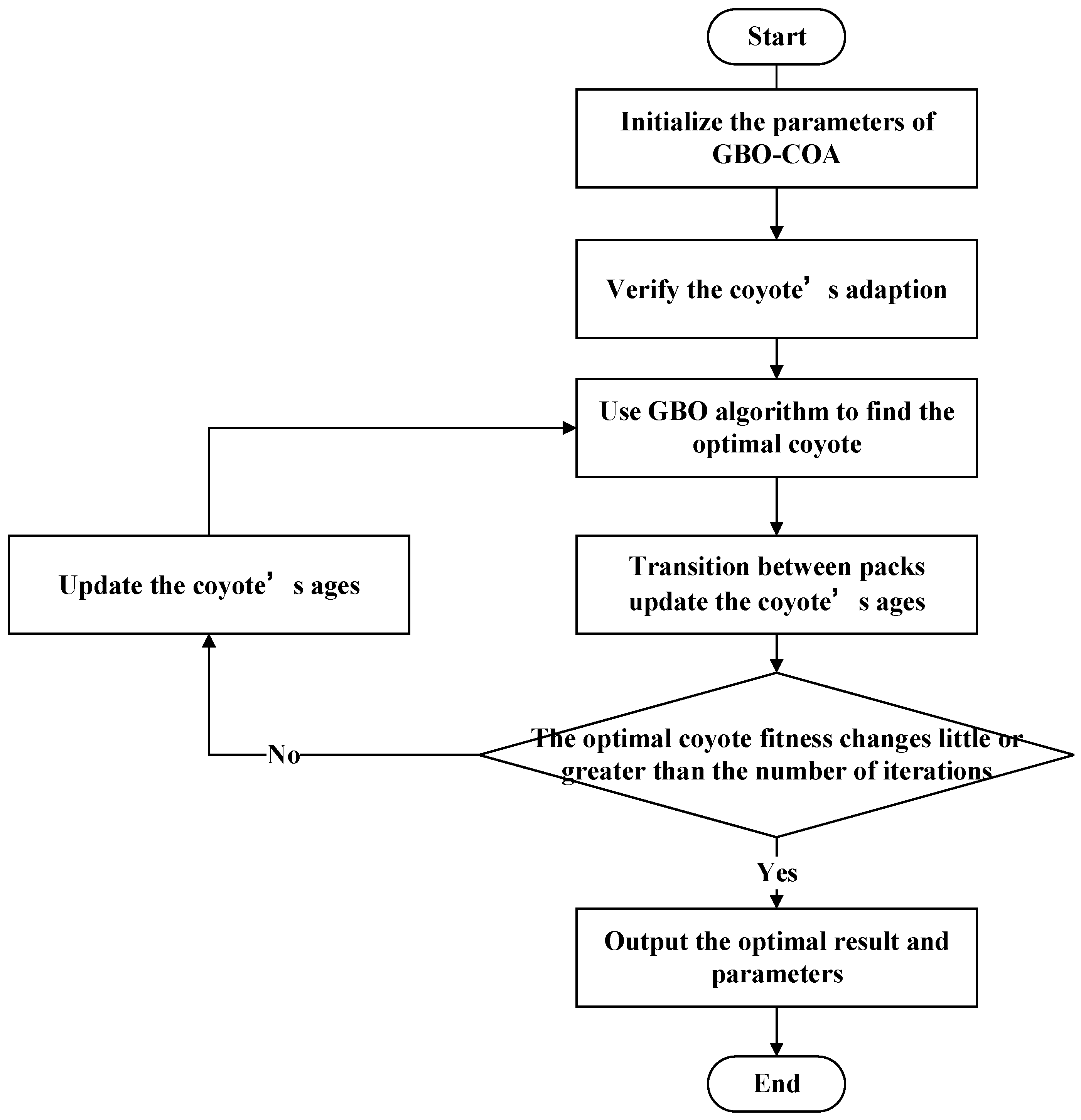
The traditional COA has shown strong optimization capabilities in solving optimization problems [27]. However, the COA method also suffers from the following deficiencies. For example, the following problems exist in solving complex optimization problems. (a) The growth process of coyotes in COA is influenced by the difference between the calculated group and the group breeding trend, and the convergence of the algorithm is slow when two coyotes are randomly selected in the group. (b) Guided by the group wolf and the group culture trends, it may appear that the group wolf and the group culture trends are locally optimal solutions, causing the algorithm to fall into a local optimum. (c) COA uses a dynamic greedy algorithm. To a certain extent, it speeds up the convergence speed, but the probability of falling into a local optimum increases. The GSR and LEO used by the GBO algorithm can improve the detection ability of COA very well. Considering the advantages and disadvantages of the COA and GBO methods, this paper proposes using the GBO method instead of the COA method to calculate the growth, life, and death of coyotes in order to improve the convergence speed and solve the local optimum stagnation problem. In contrast, the GBO method can produce smooth transitions in the exploration phase, thereby improving the speed of convergence and the ability to avoid local optima. Therefore, the combination of GBO and COA can improve the performance of COA. Figure 2 shows the flowchart of GBO-COA.

Figure 2.
GBO-COA flowchart.
3.3. Proposed Method
This paper proposes an adaptive intrinsic time-scale decomposition algorithm based on Lévy noise instead of white noise. Parameters were optimized using the improved coyote optimization algorithm, avoiding the drawbacks caused by the artificial setting of parameters. The method flow is shown in Figure 3.

Figure 3.
Fault diagnosis flowchart.
CEITDALN includes an improved coyote optimization algorithm to adaptively adjust Lévy noise parameters and add noise intensity parameters. The most important aspect in the adaptive algorithm is defining a suitable objective function [33]. Therefore, the CEITDALN method generates multiple components in the process of decomposing the signal. If mode components are analyzed and decomposed one by one, this wastes a great amount of time. Therefore, traditional time domain parameters and other objective functions are not applicable in this method, and it is necessary to select an objective function that can judge multiple mode components after decomposition. By consulting the related literature, this paper proposes a brand-new objective function: calculating the spectral kurtosis of the input signal [34]. The center frequency band is found, and the energy of the center frequency band of the decomposed component is calculated. Maximal energy is taken as the optimization target.
4. Results
4.1. Case A: Numerical Simulation Analysis
In this section, the CEEMDAN, CEITDAN and CEITDALN methods are used to decompose the analogue signals of bearing faults to compare the effectiveness of the CEITDALN method proposed in this paper in filtering. In order to objectively evaluate the effectiveness of the CEITDALN method, two metrics—the orthogonality measure and the energy conservation measure—were introduced to quantitatively evaluate the decomposition performance of the different methods [35,36]. Theoretically, the mode components of different decomposition algorithms should all be completely orthogonal. The orthogonality index is equal to zero. However, due to computer errors and environmental disturbances, the orthogonality index cannot be zero [35]. Therefore, in practical analysis, the closer the orthogonality index is to zero, the more desirable the decomposition result is. In addition, the decomposition result should satisfy the law of energy conservation, and the energy conservation exponent should be equal to 1. However, in practice, the same from computer errors can lead to some loss of signal energy, so the value of the energy conservation exponent should be close to 1 in practical applications, indicating less signal loss in the decomposition, while when the ECI is greater than 1, it indicates the presence of spurious components [37]. Here, we compare these three methods using the orthogonal index (OI), root mean square error (RMSE), energy conservation index (ECI) and improved SNR (ISNR). The definitions of OI, ECI, and ISNR are as follows.
where represents the original signal, represents the i-th mode component decomposed by different methods, and indicates residual error.
This paper also uses the improved SNR to compare the superiority of the method proposed in this paper in the envelope spectrum, calculated as follows:
where ISNR is the improved signal-to-noise ratio. stands for total regional power, and its calculation formula is as follows:
where is appropriately selected according to the number of sampling points and the size of the sampling rate.
In order to verify the effectiveness of the proposed method, a bearing failure model was used to simulate the generated shock signal. The structure of the simulation signal is as follows [24]:
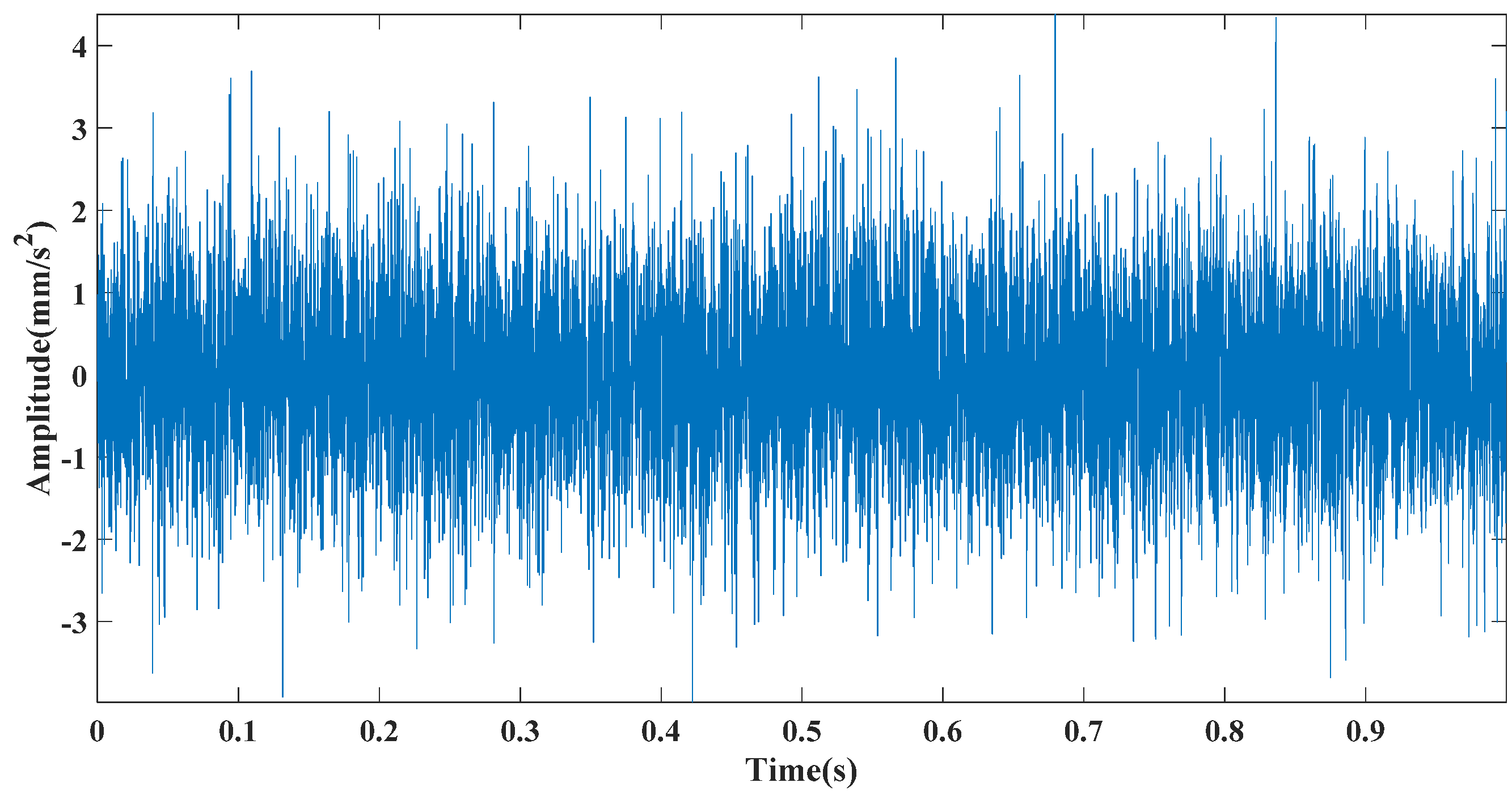
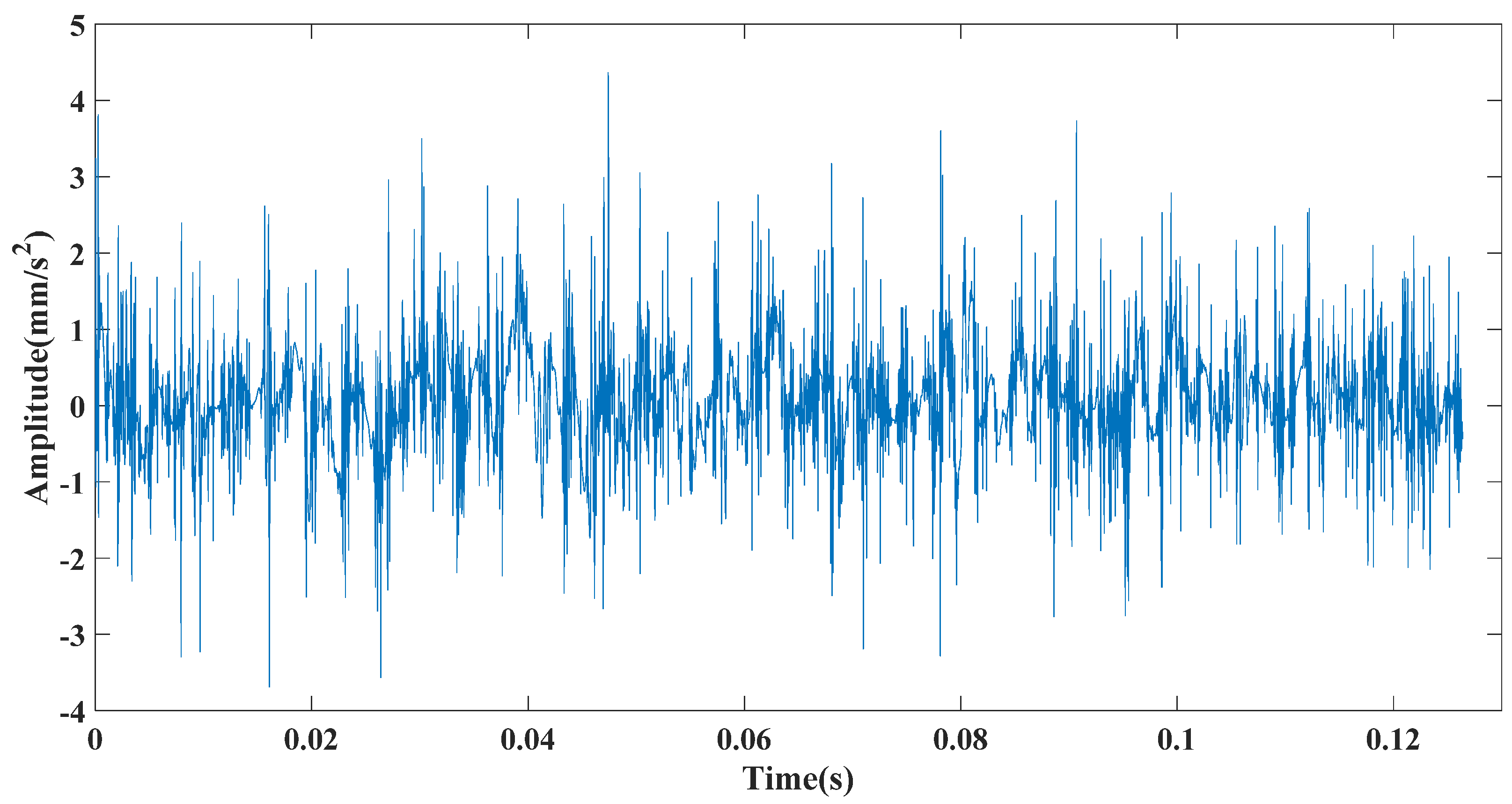
where is the periodic fault shock; is the frequency conversion, and ; is 1; C is the attenuation coefficient (); is the resonance frequency (); and is the characteristic frequency of the inner ring fault (). is the slight sliding of the shock with respect to period , after which the sliding follows a normal distribution with a mean of 0 (standard deviation is 0.5% of the frequency conversion). is Gaussian white noise with an SNR of −35 dB, and is the sampling frequency (). The number of analysis data points was 8192, as shown in Figure 4. Figure 5 shows the decomposition result of CEEMDAN, CEITDAN, and CEITDALN.

Figure 4.
Analog signal time domain.

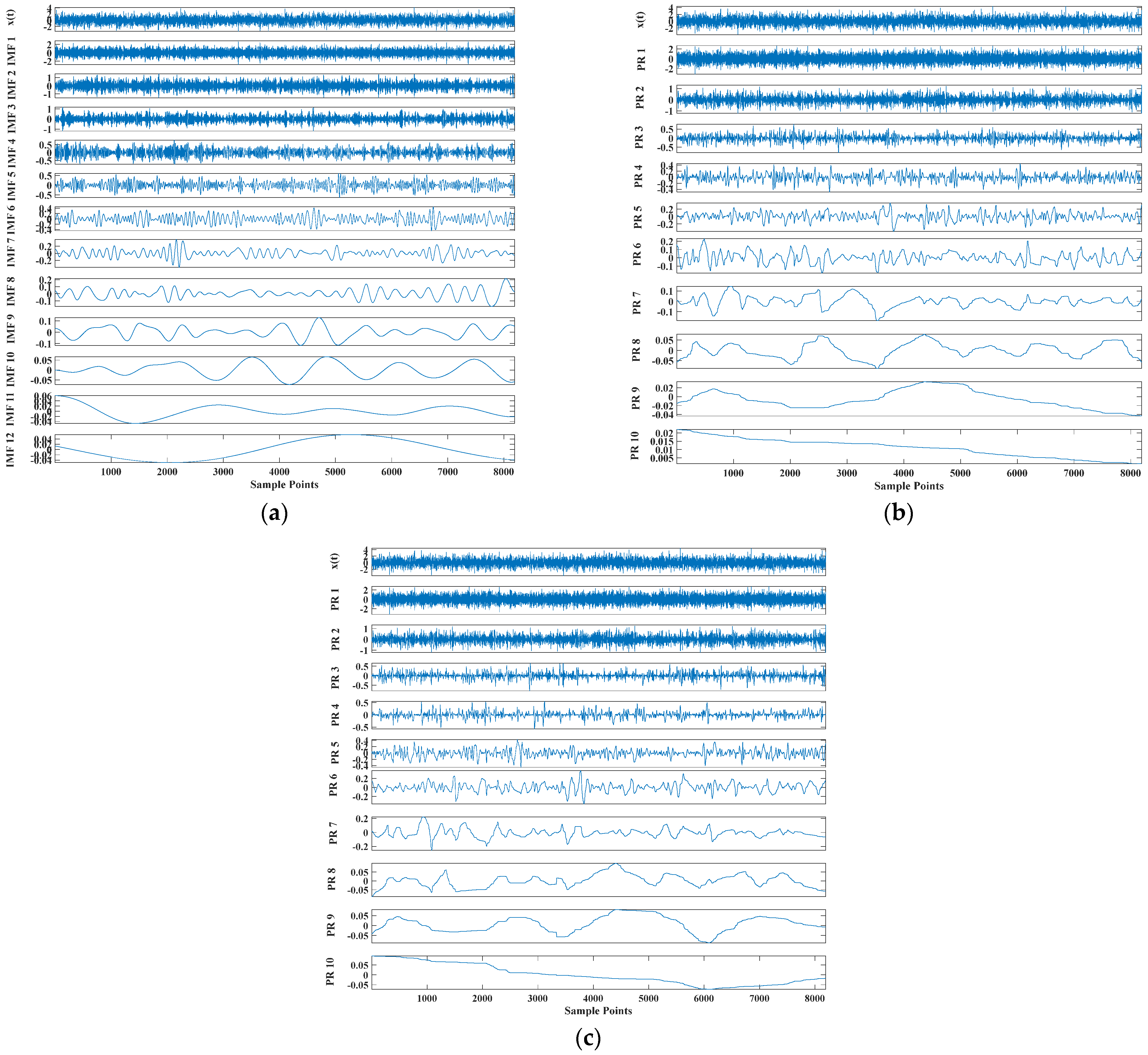
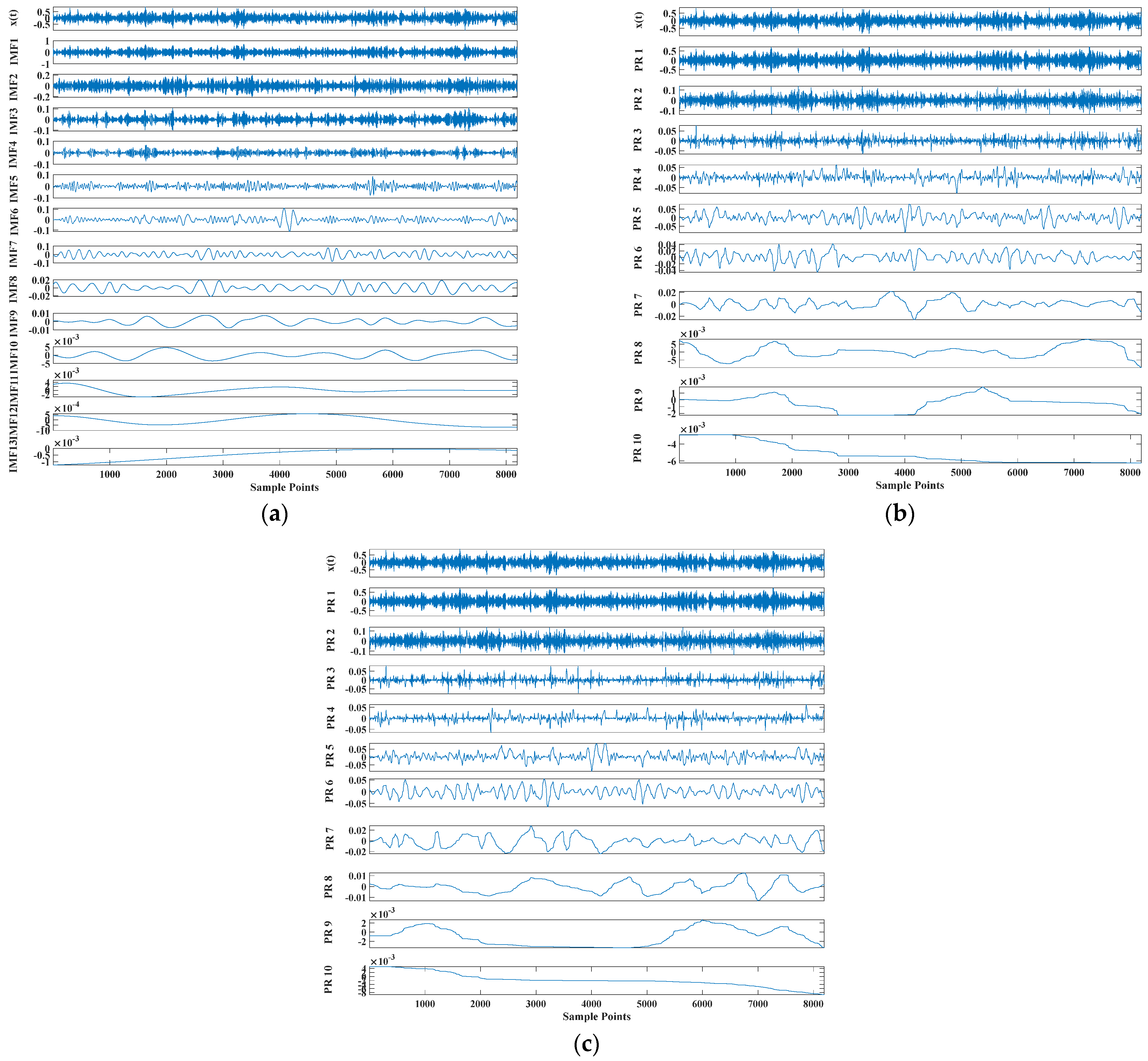
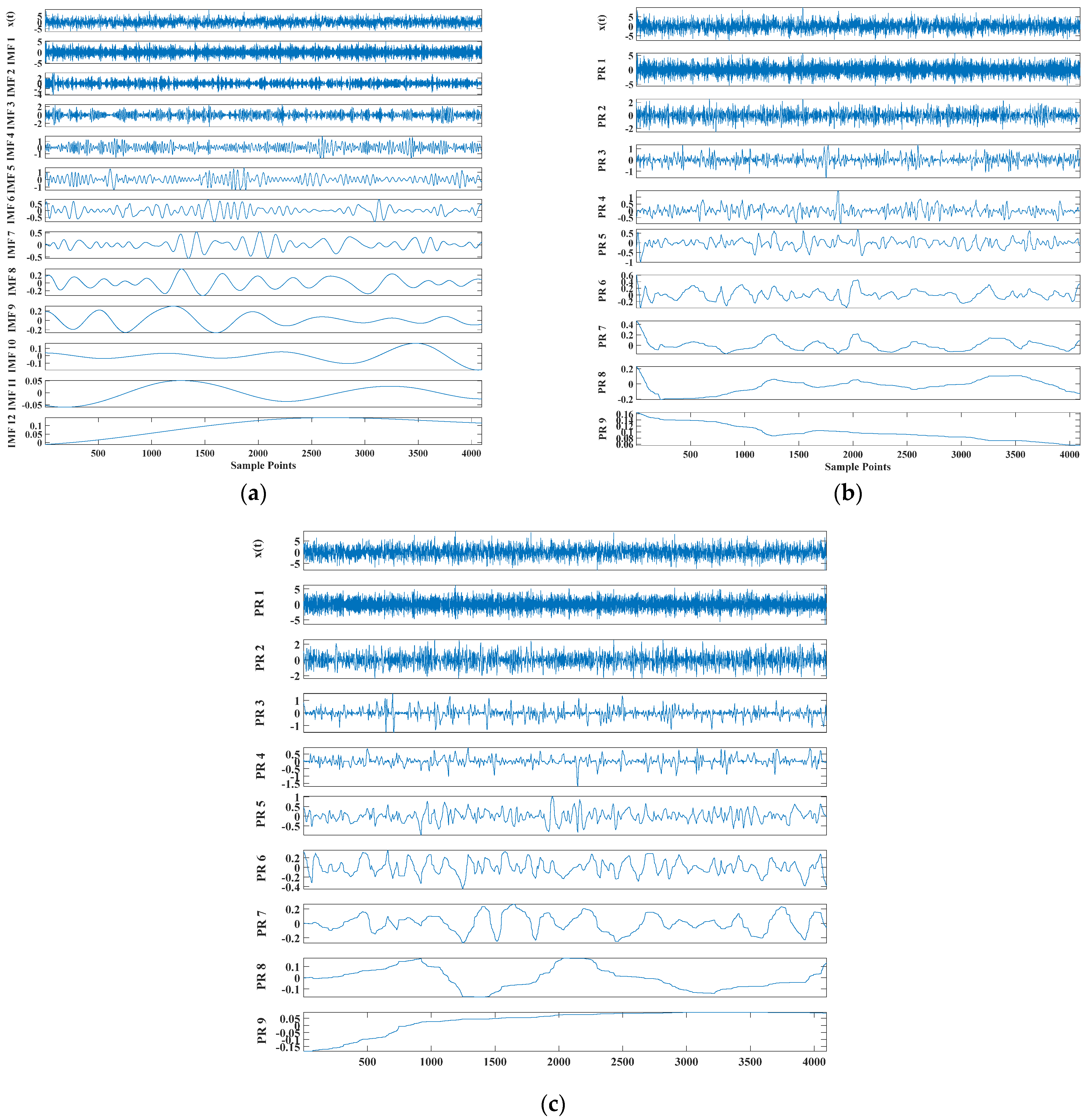
Figure 5.
Comparison results of three decomposition methods: (a) CEEMDAN, (b) CEITDAN and (c) CEITDALN.
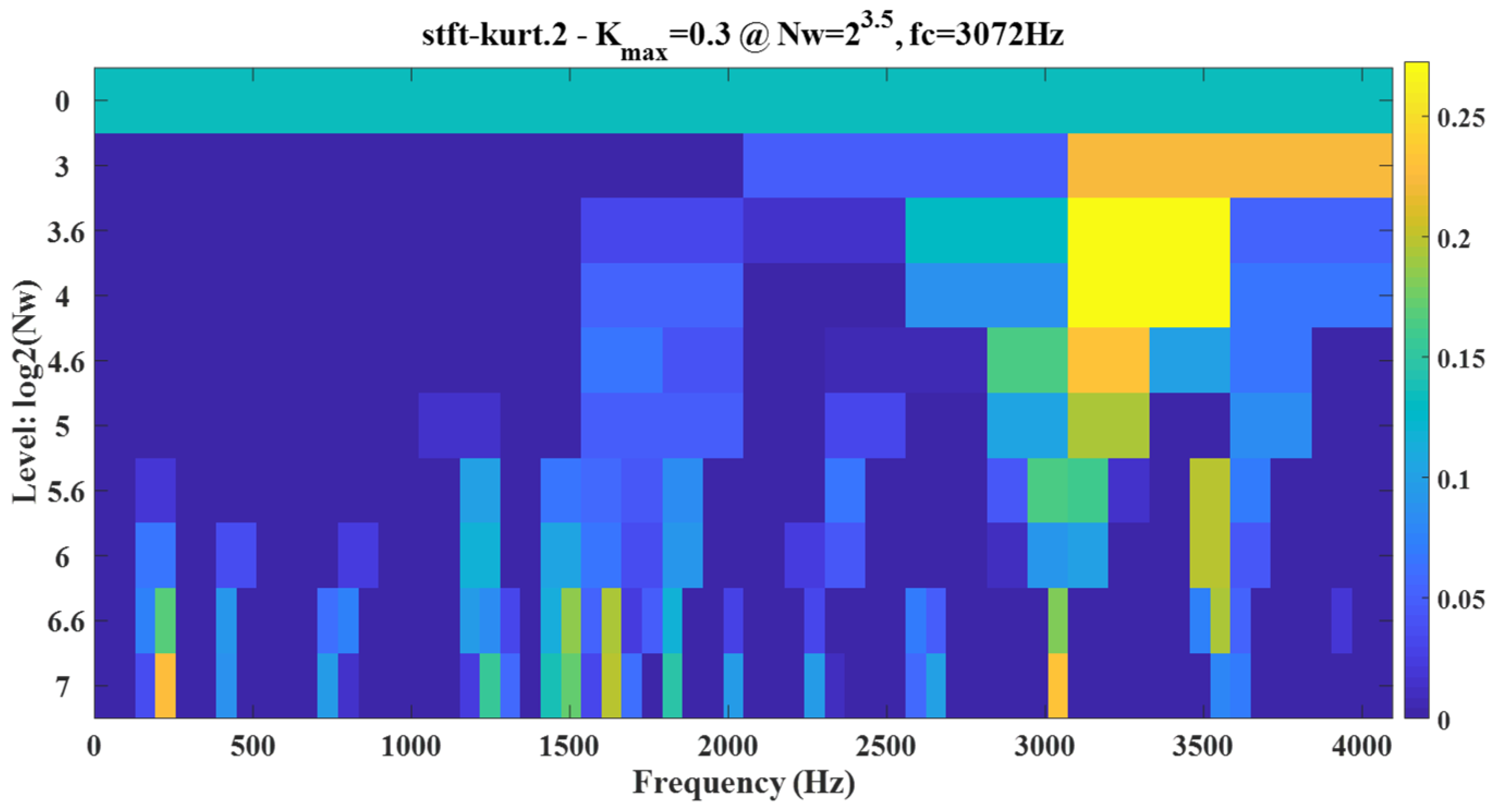
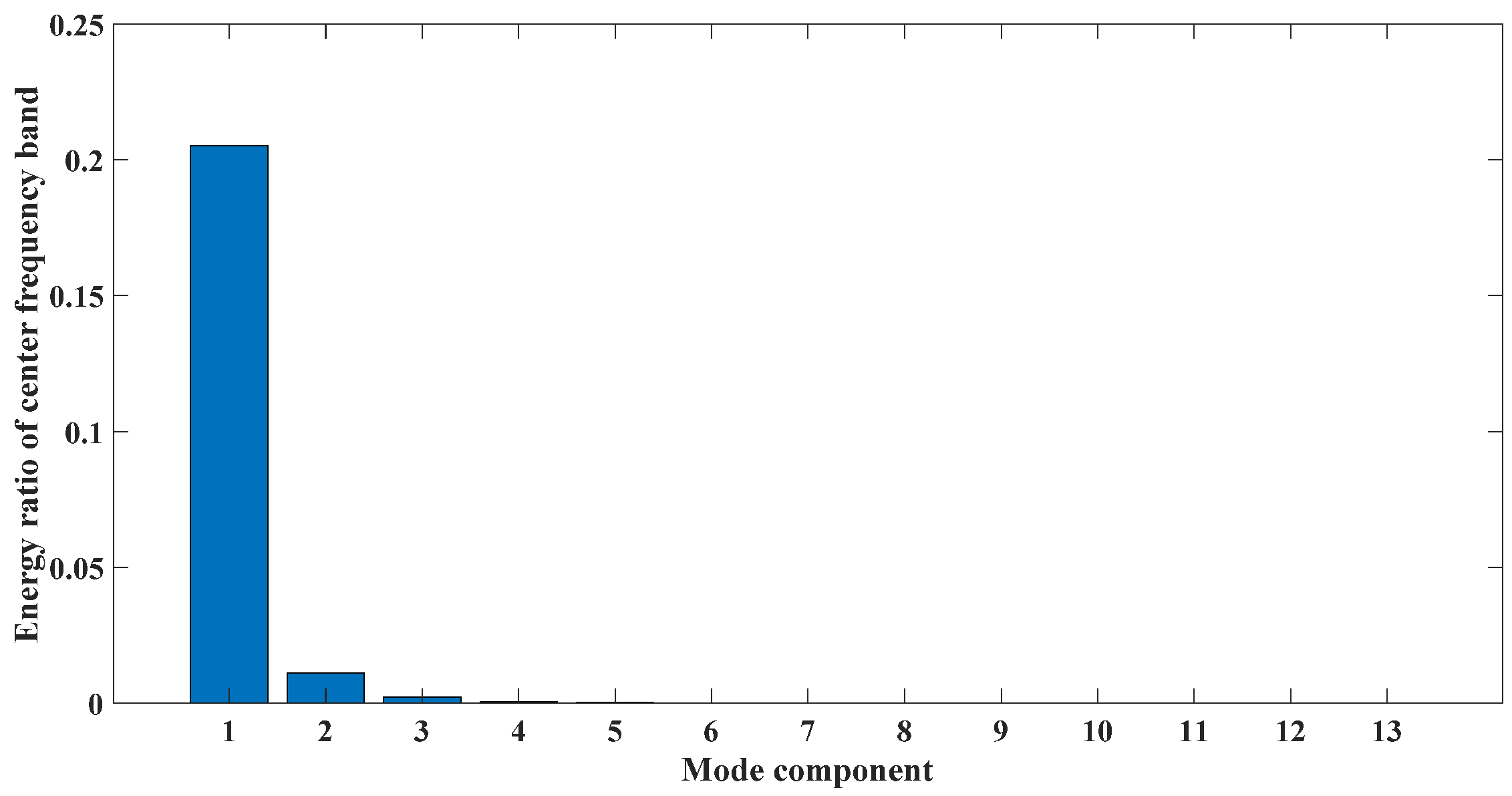
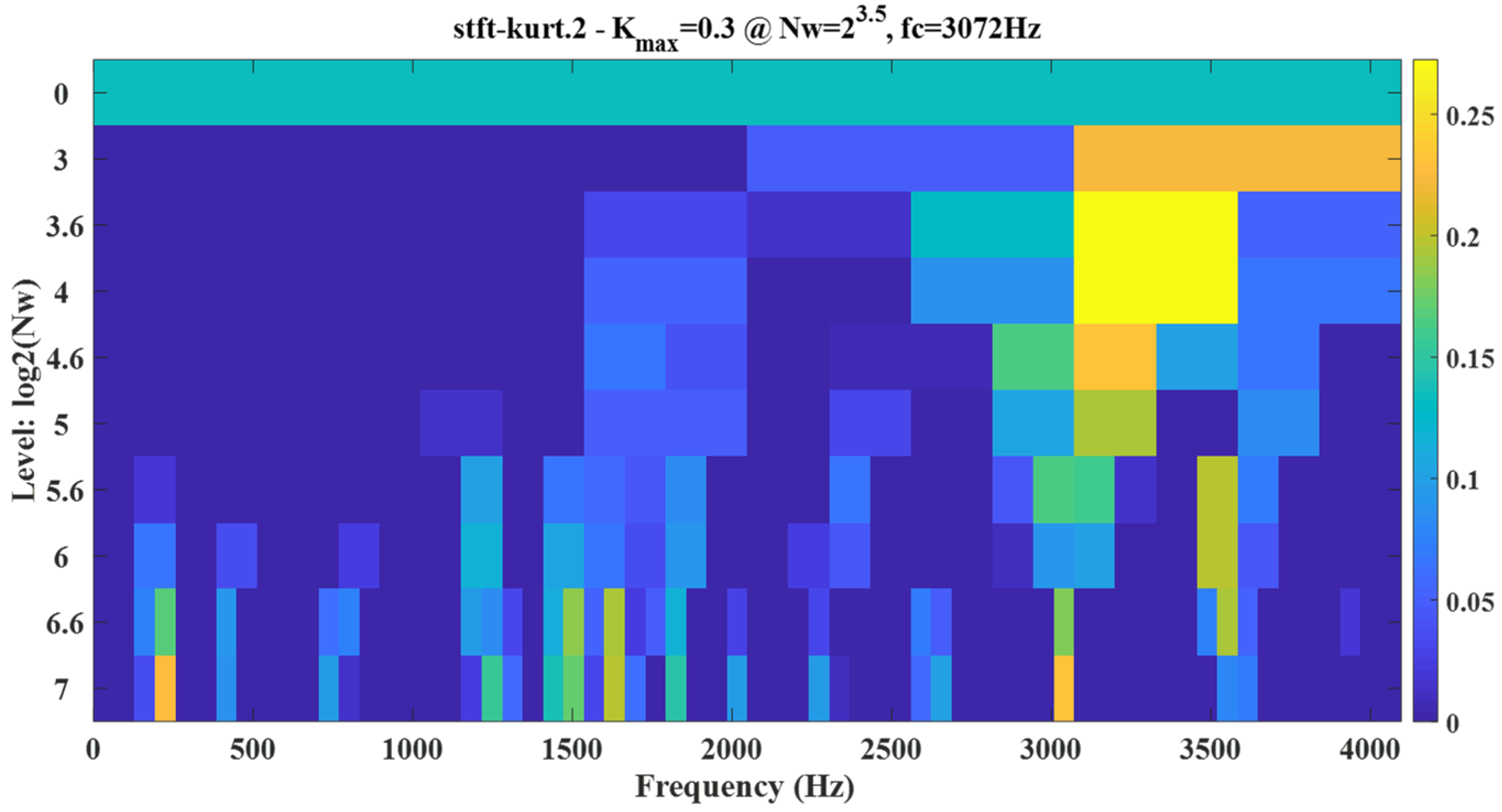
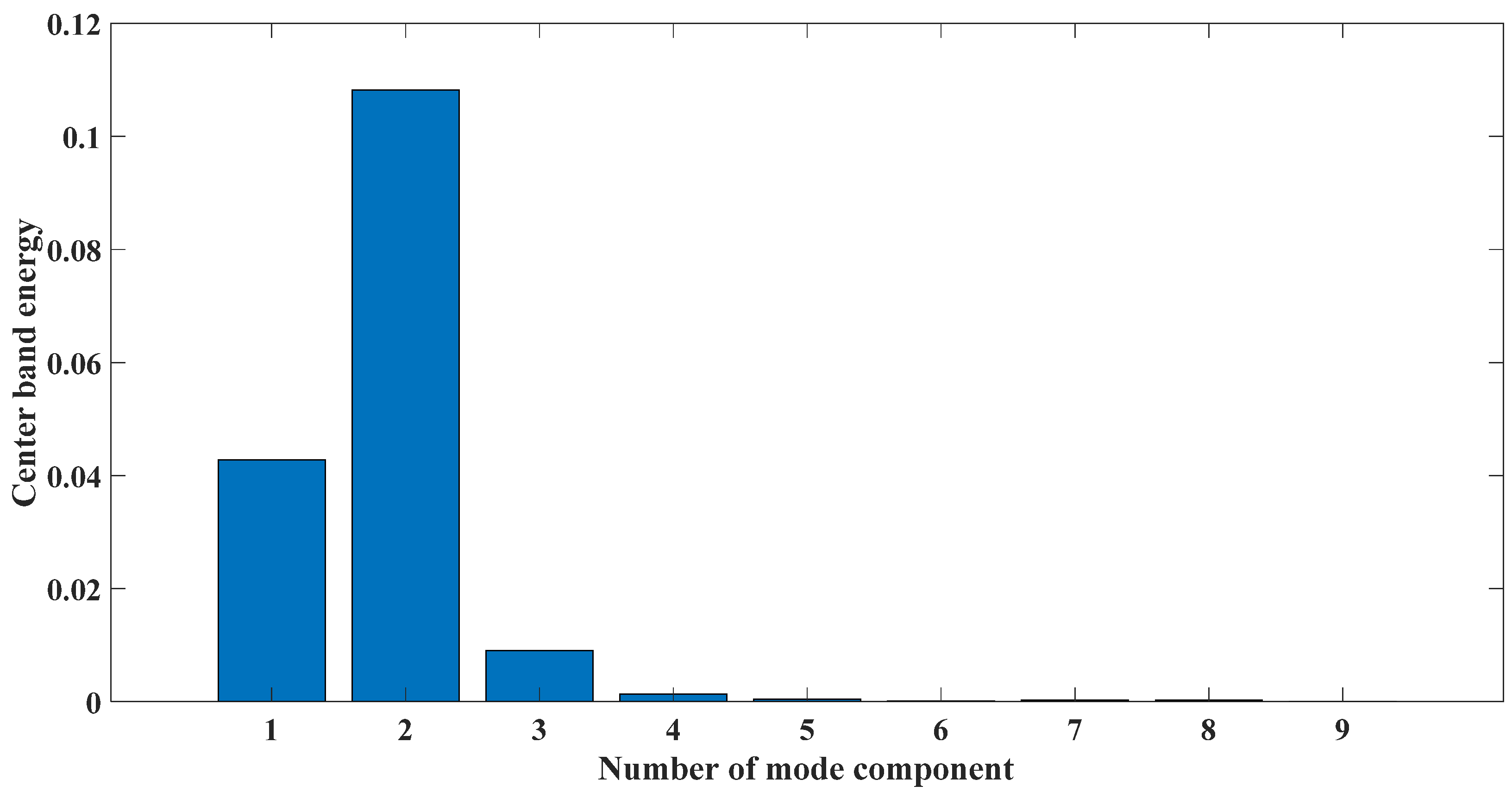
Figure 5 shows that the CEEMDAN method decomposed a total of 12 mode components, and CEITDAN and CEITDALN decomposed 10 rotation components. Fewer model components can save subsequent analysis time for decomposition results. More accurate mode components show that the number of false components was reduced. Figure 6 shows the kurtosis spectrum required in the fault diagnosis scheme proposed in this paper to extract the center frequency of the signal. We extracted the signal component on the basis of the central frequency for reconstruction. The results in Figure 6 show that the center frequency was consistent with the analog signal, so it could be used for a follow-up analysis. Figure 7 shows the center frequency of the different rotation components in the decomposition result of the CEITDALN method. The center frequencies of the first three components accounted for the largest proportion. Therefore, the first three components were selected for signal reconstruction, and the envelope spectrum was drawn.

Figure 6.
Determination of the center frequency of the kurtosis spectrum.

Figure 7.
Energy ratio of the center frequency band.
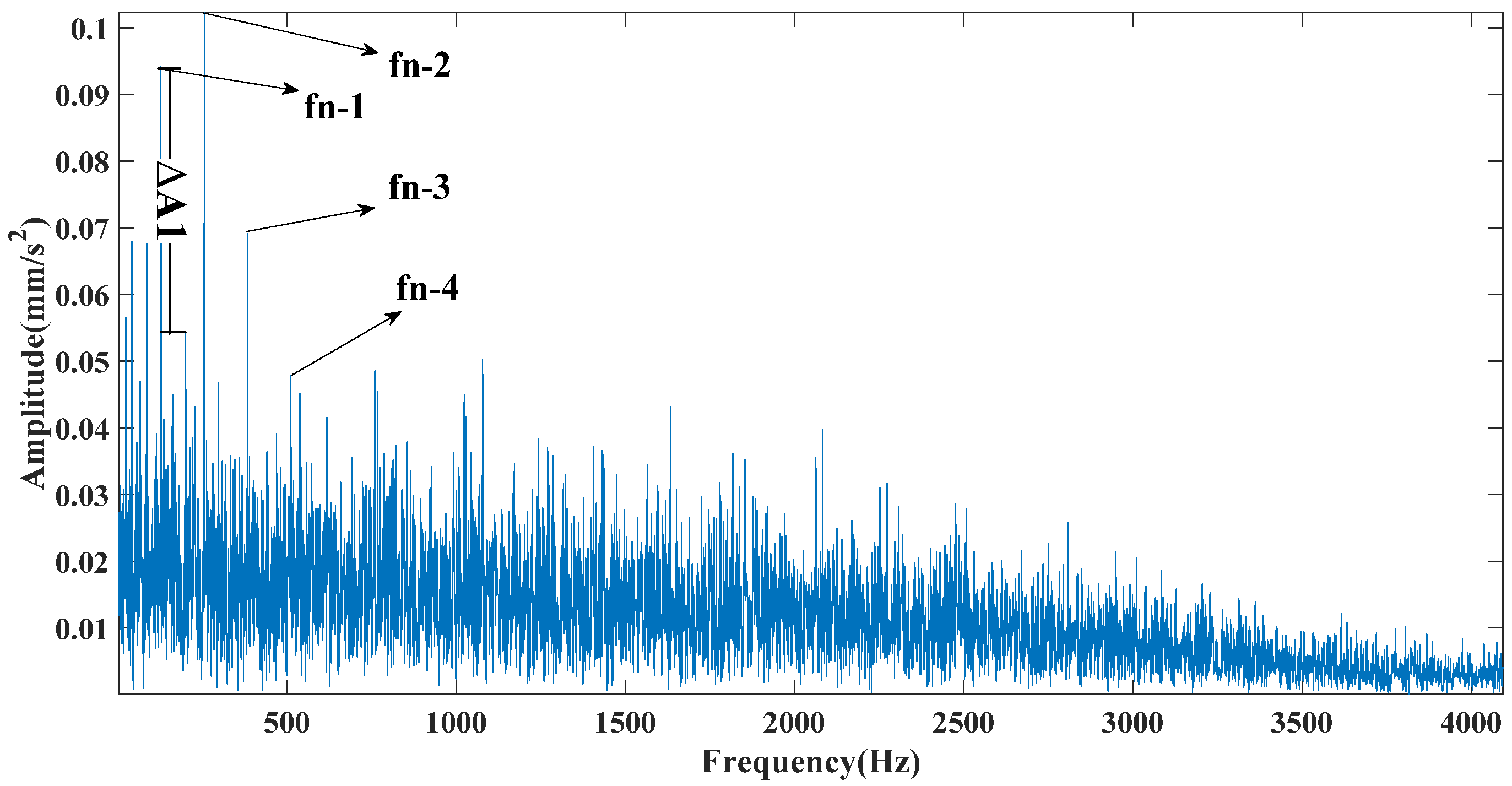
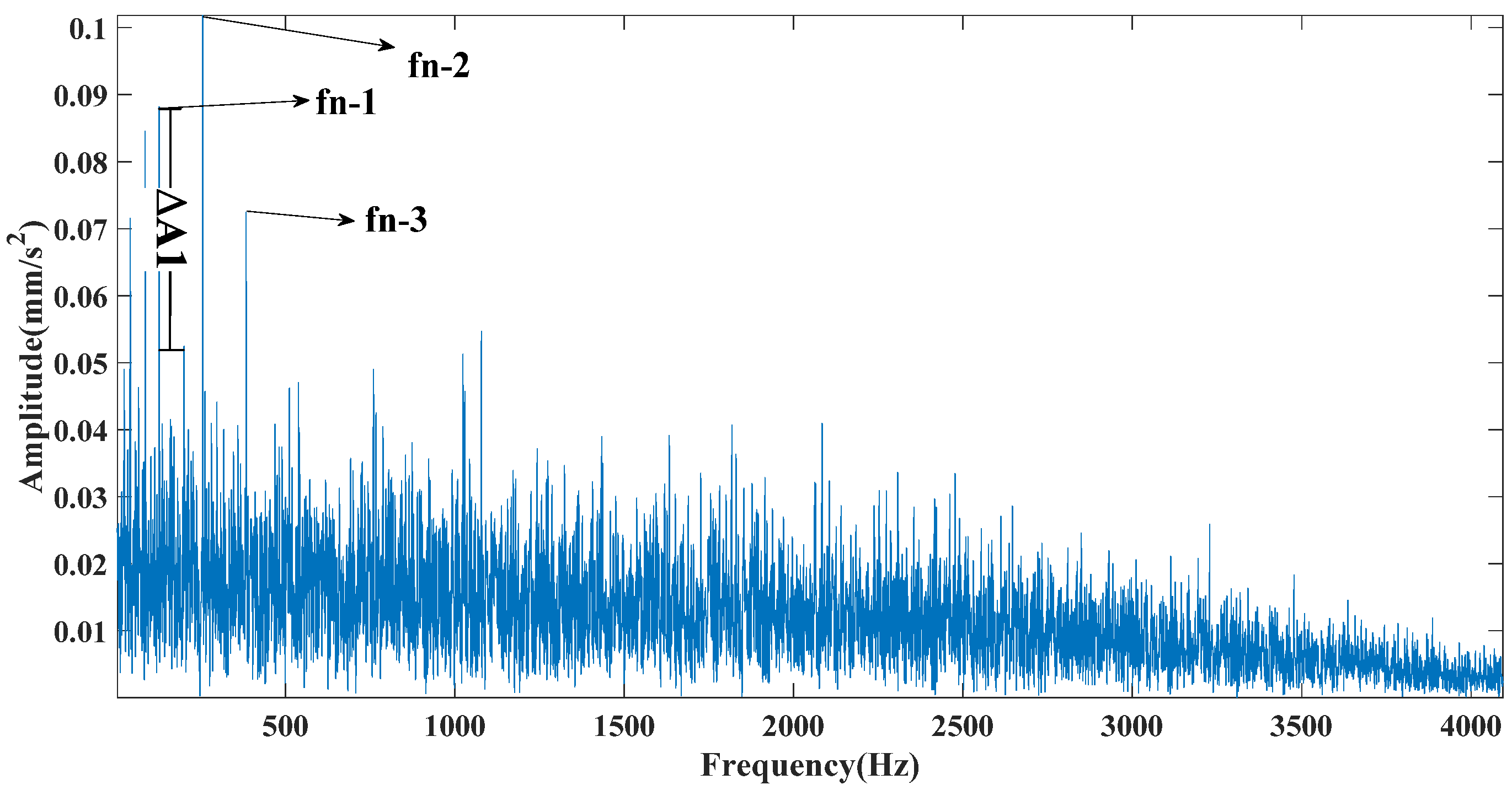
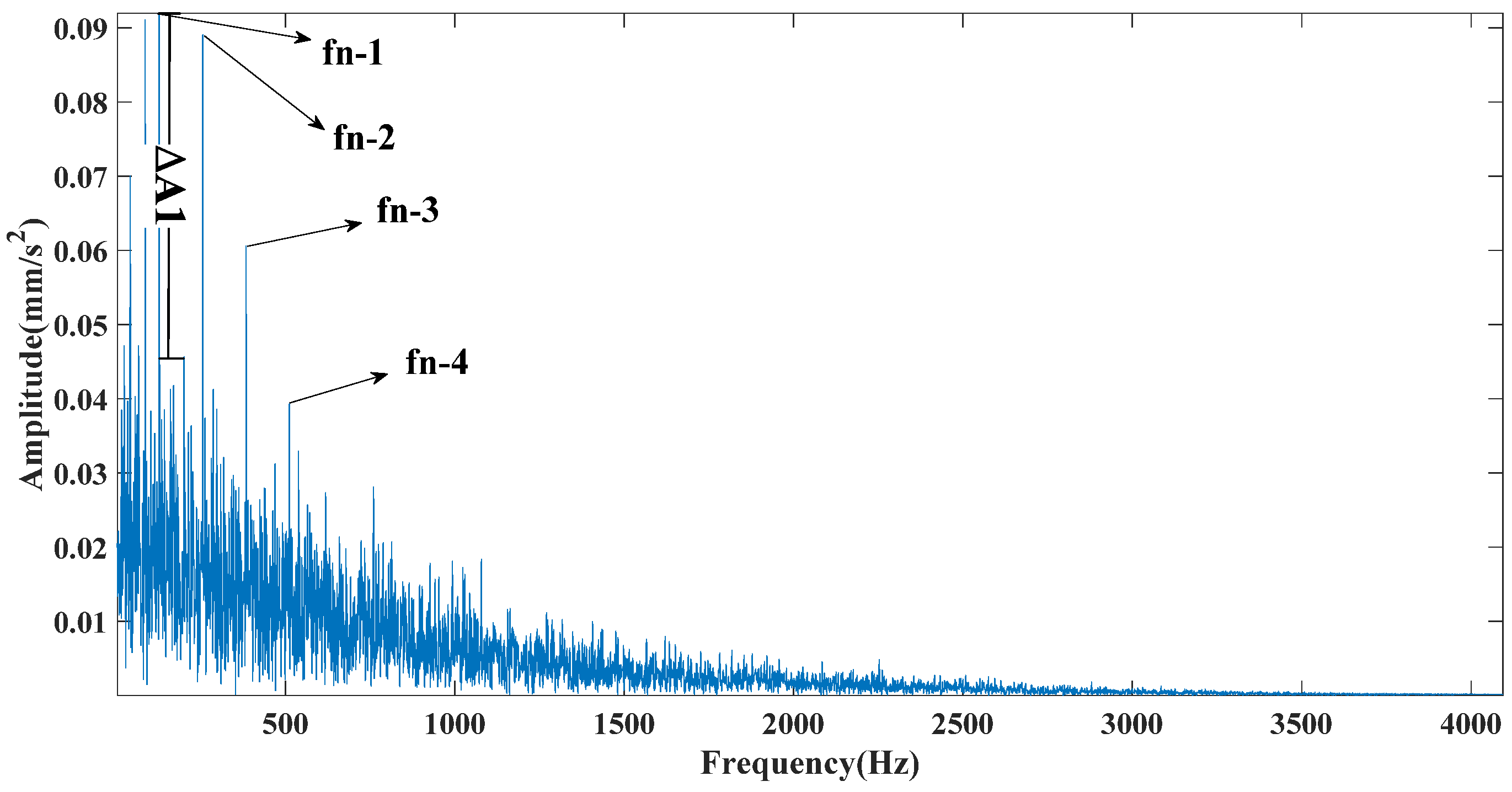
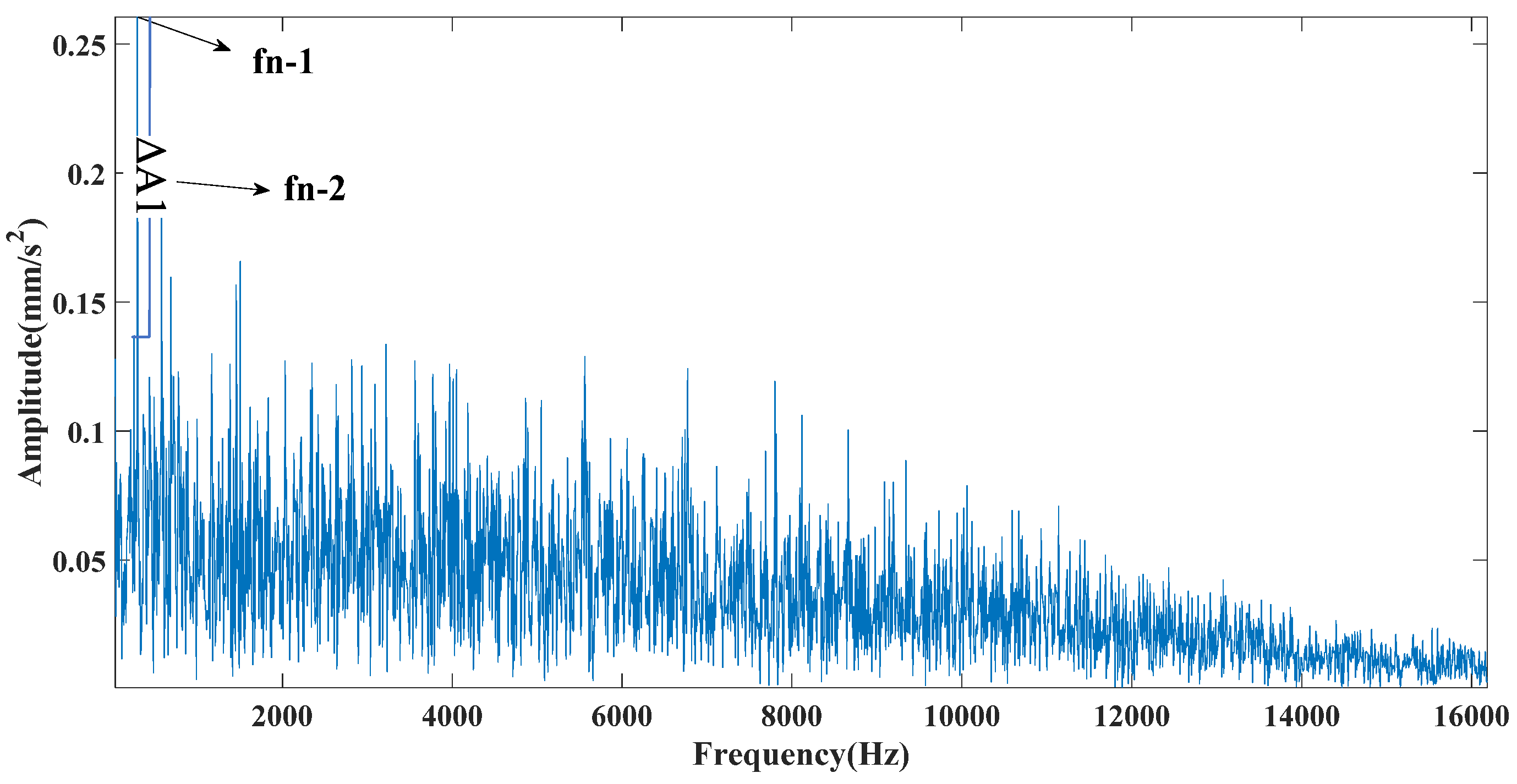
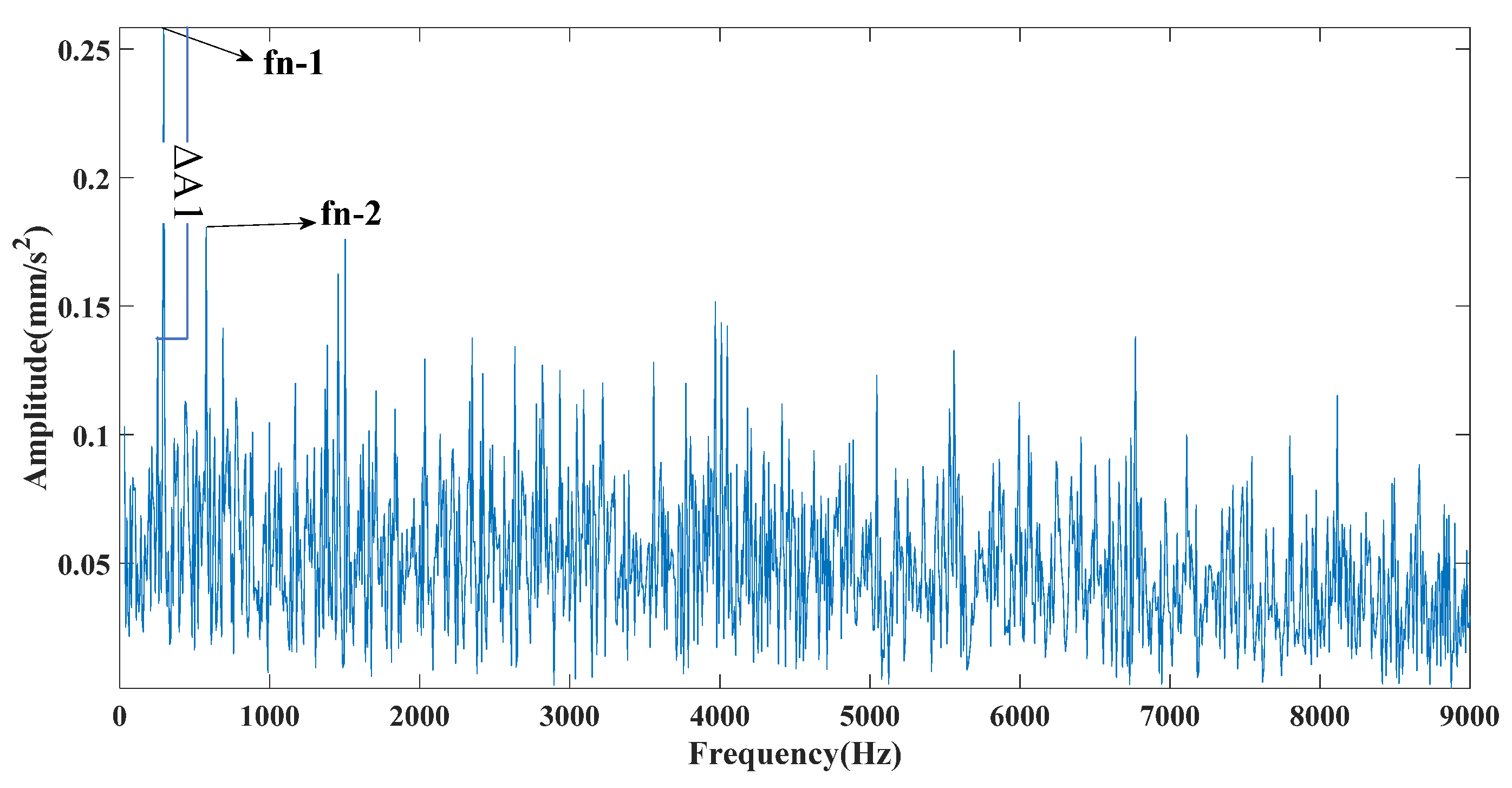
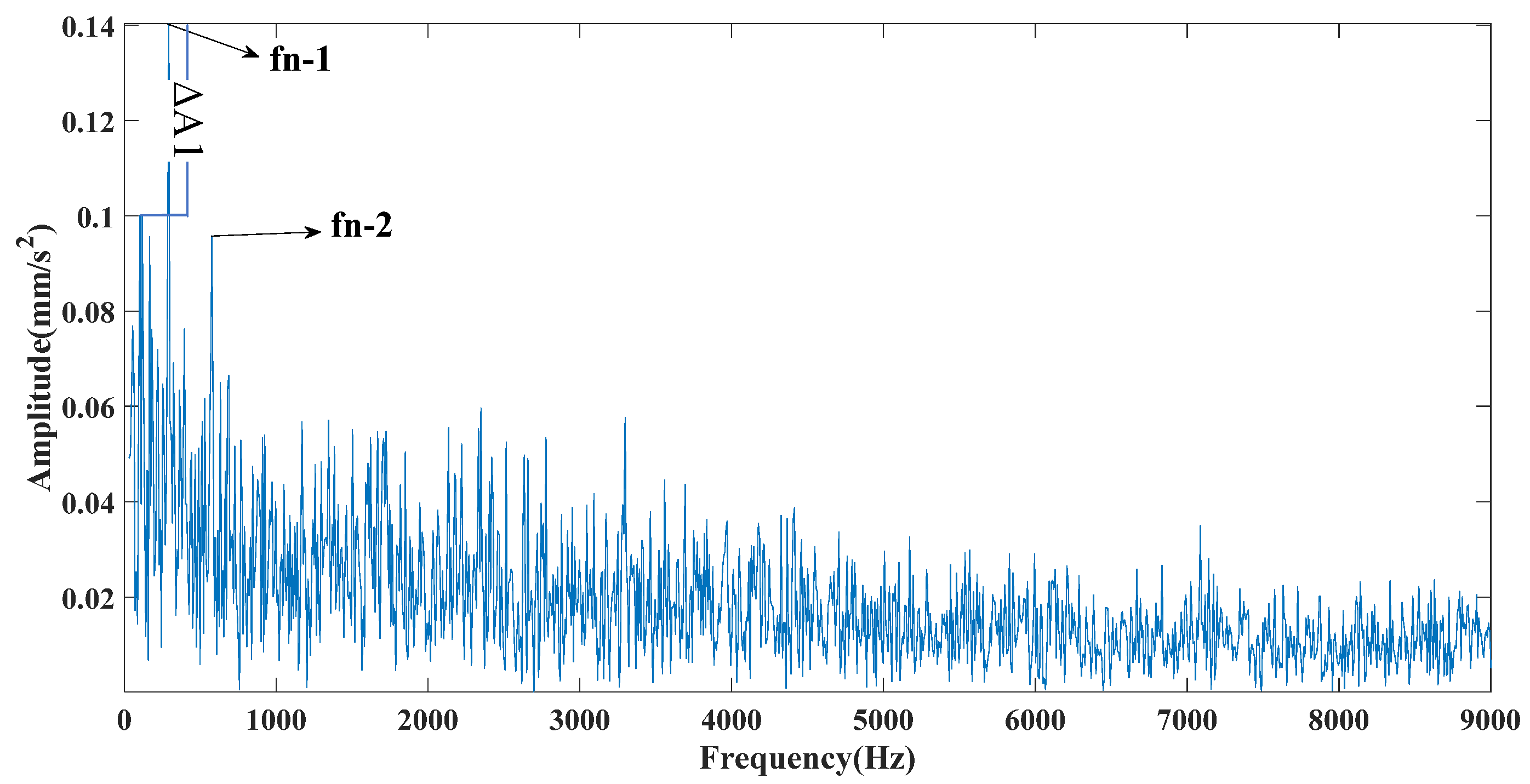
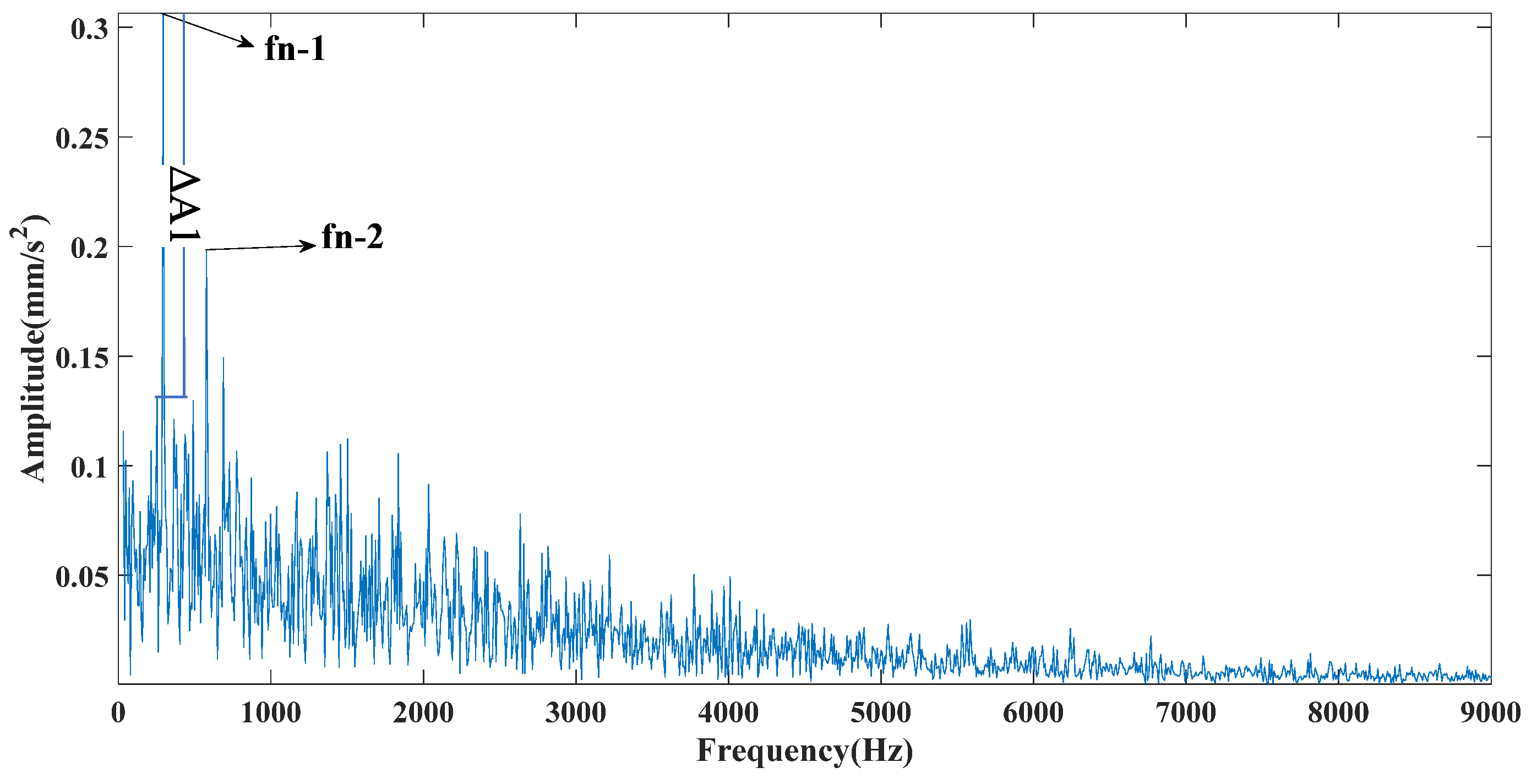
Figure 8, Figure 9 and Figure 10 are the envelope spectra of the signals obtained by the CEEMDAN, CEITDAN, and CEITDALN methods, respectively. In the above figure, fn-1 is the fault characteristic frequency, fn-2 is twice the fault characteristic frequency, and the rest can be deduced by analogy. The CEEMDAN and CEITDAN methods had similar denoising capabilities to strong noisy signals. However, the difference between the peak value of the fault characteristic frequency position and the noise peak value of the CEITDAN method was slightly larger than that of the CEEMDAN method. The CEITDALN method had the largest difference and the most obvious fault characteristic frequency. At the same time, the filtering effect of the high-frequency part was obvious compared with those of the CEEMDAN and CEITDAN methods. This did not affect the extraction of the fault characteristic frequency because the proposed method has good application prospects in fault diagnosis.

Figure 8.
CEEMDAN envelope spectrum.

Figure 9.
CEITDAN envelope spectrum.

Figure 10.
CEITDALN envelope spectrum.
In order to further compare the advantages and disadvantages of the three methods, OI, ECI, and ISNR were compared with the signal output SNR, as shown in Table 1. Table 1 shows that all the indicators of the proposed method were better than those of the other methods. Therefore, the effectiveness of the proposed method is proven.

Table 1.
Comparison table of indicators for different decomposition algorithms.
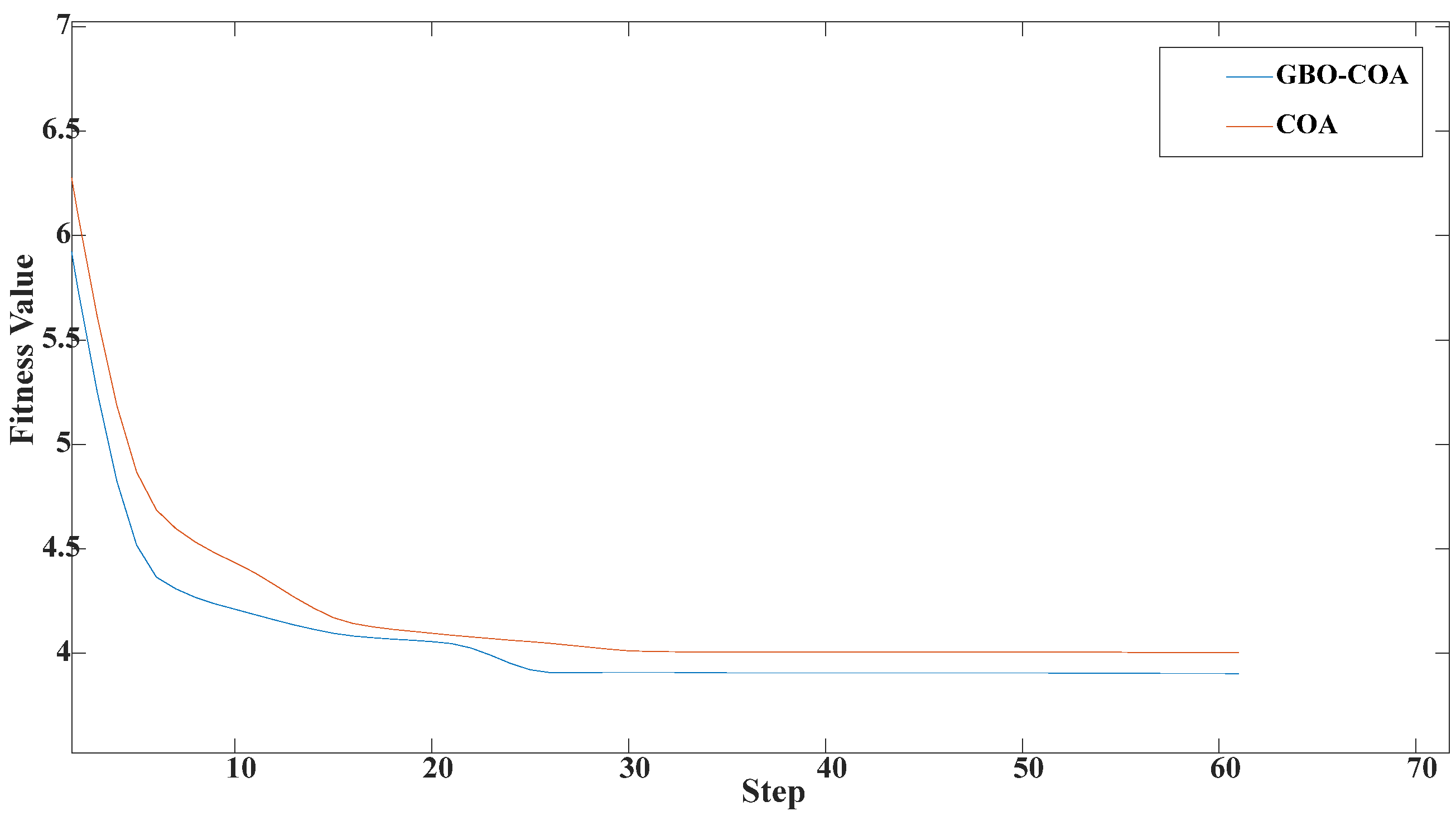
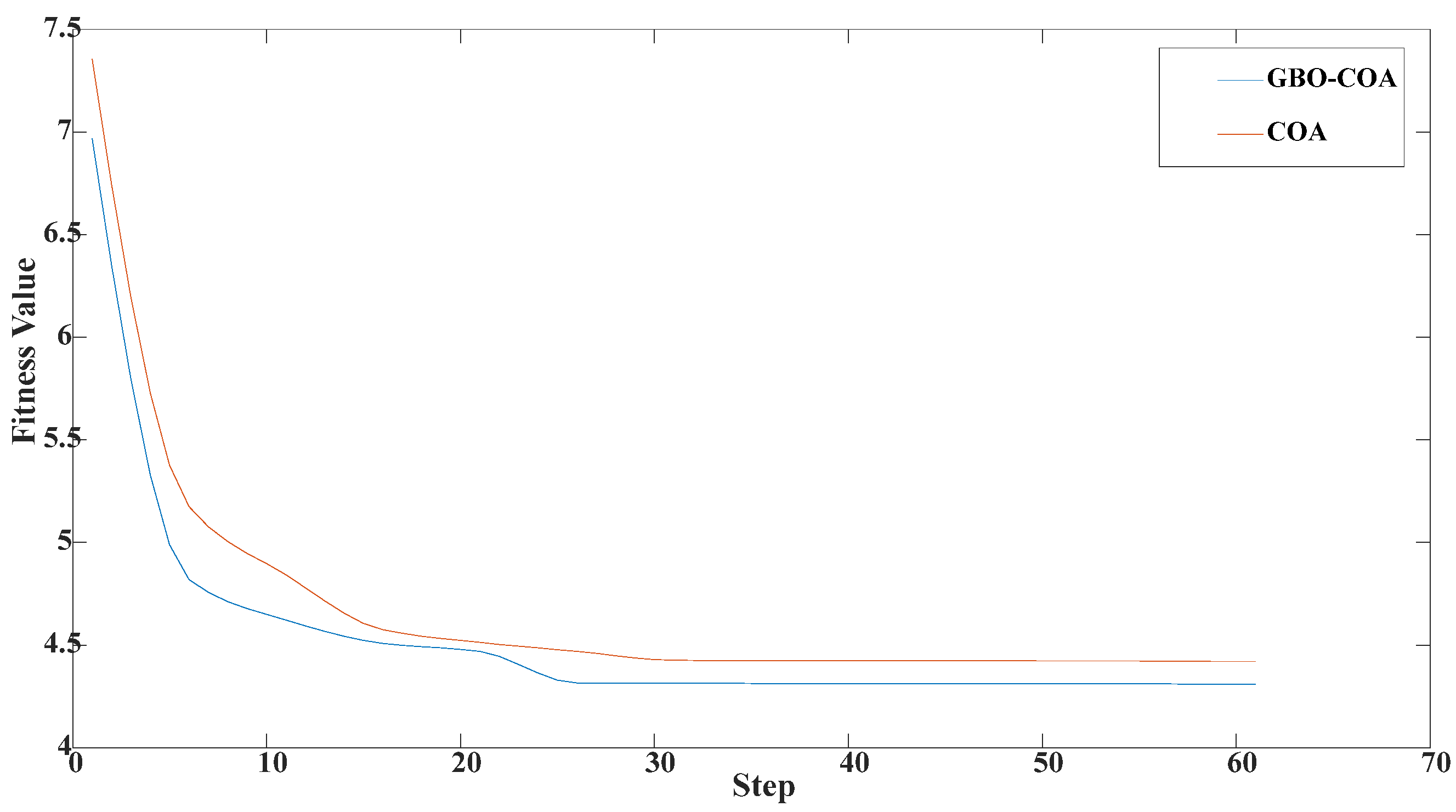
Figure 11 illustrates the improvement effect of the proposed COA. The method for optimizing the fitness value and the number of iteration steps was used for comparison. The smaller the optimization fitness value is, the faster the method’s optimization speed is, and the easier it is to quickly achieve convergence. Therefore, the GBO-COA method proposed in this paper is better than the traditional COA method, as the proposed method performed well in the simulation results and can be used in engineering practice to decompose strong noisy signals and perform fault diagnosis.

Figure 11.
Fitness value of the improved optimization algorithm and the number of iterations.
4.2. Case B: Experiment Analysis
In this section, we describe the fault signal acquisition and the test equipment used (Figure 12). The test platform part consists of the test bench and control system, which is mainly composed of the tested bearings, accompanying test bearings, test spindle, bearing outer ring fixture, drive unit, and loading system. During the test, there are four sets of bearings, divided into two sets of bearings under test and two sets of accompanying bearings. Two sets of loading systems apply loads to the test bearings, respectively. The drive unit provides the power for the whole test bench, and the loading system provides radial force for the test bearings, which causes the spindle to drive the bearings to rotate and obtains the vibration signal of the bearings during the rotation process through vibration sensors. The drive unit can provide the bearing speed in the range of 1000 rpm~20,000 rpm, which is continuous. The loading system has a loading range of 0~6 KN and a loading accuracy of and is continuously adjustable. The operating limit temperature of the test bench is 250 °C [38].

Figure 12.
Experimental rig for real measurements.
Table 2 shows the test bearing parameters. The sampling frequency was 18,400 Hz, and the data length was 8192 points. The bearing rotation speed was 3000 rpm. On the basis of Table 2, the fault characteristic frequency of the inner loop was calculated as Equation (50), and the result was 407 Hz. Due to computer error, the inner loop fault frequency in the envelope spectrum was 408 Hz.
where is the number of rolling bodies, is the inner ring rotation frequency, is the rolling body diameter, is the pitch diameter, and is the contact angle.

Table 2.
Test bearing parameters.
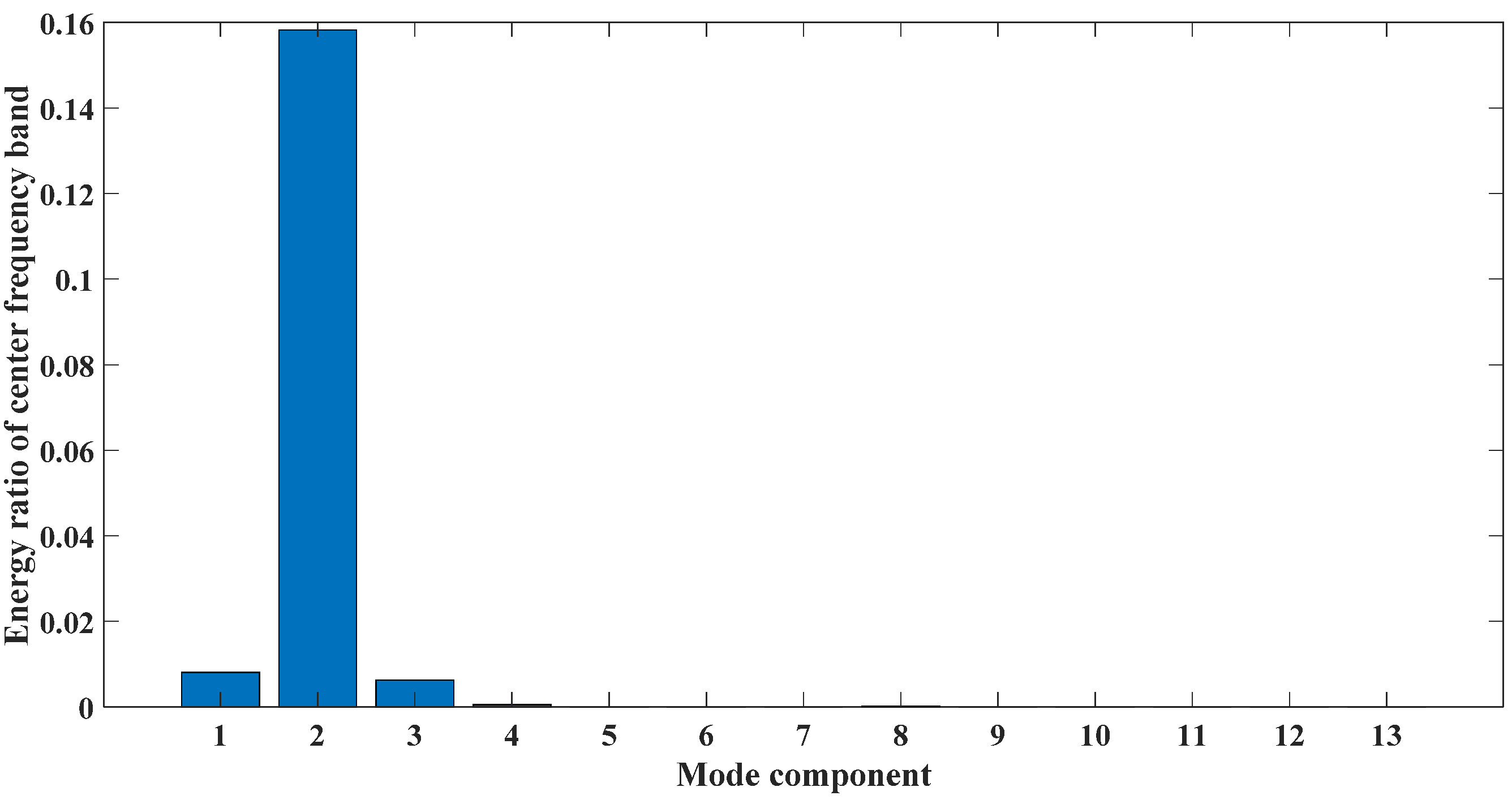
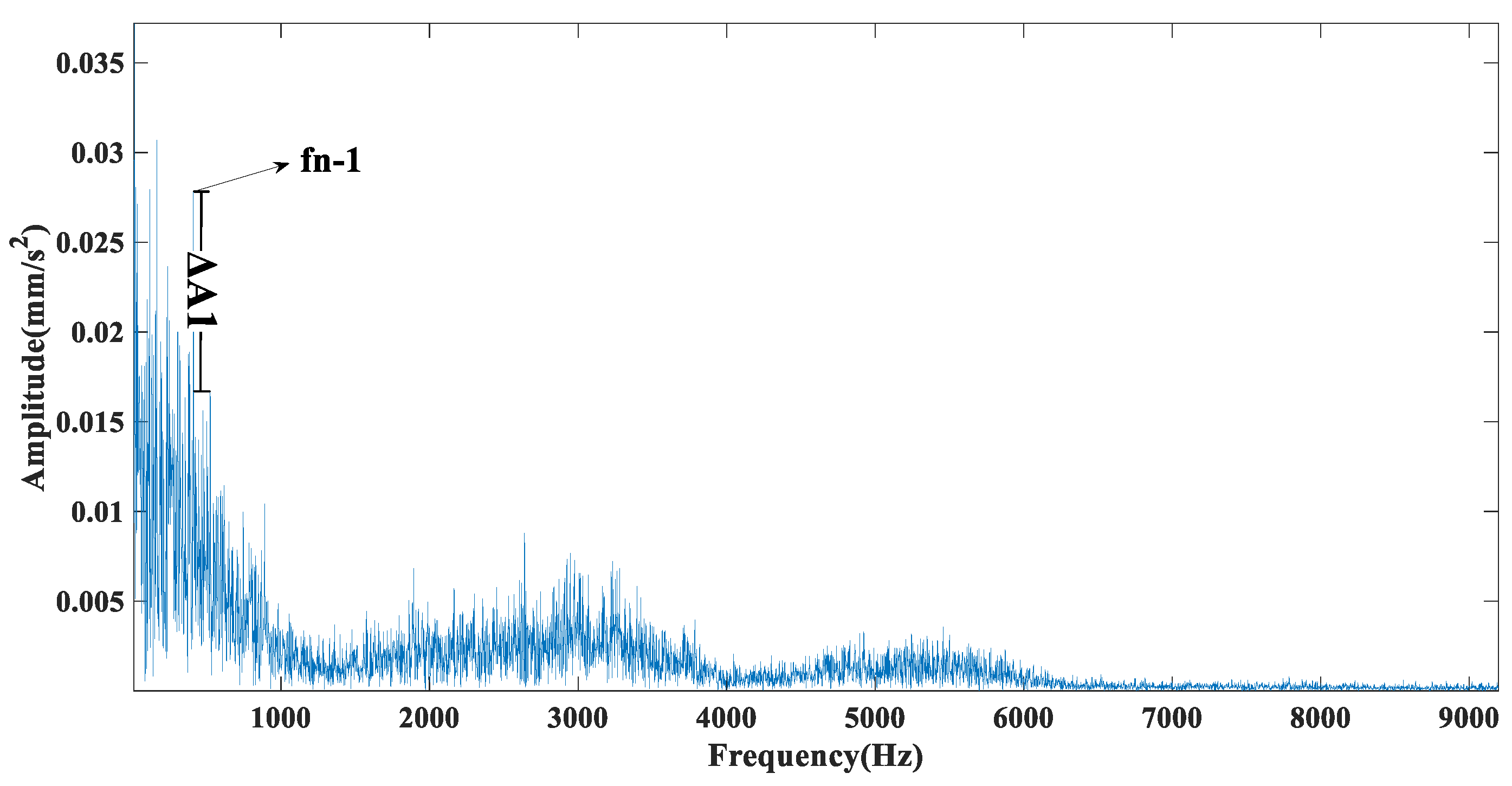
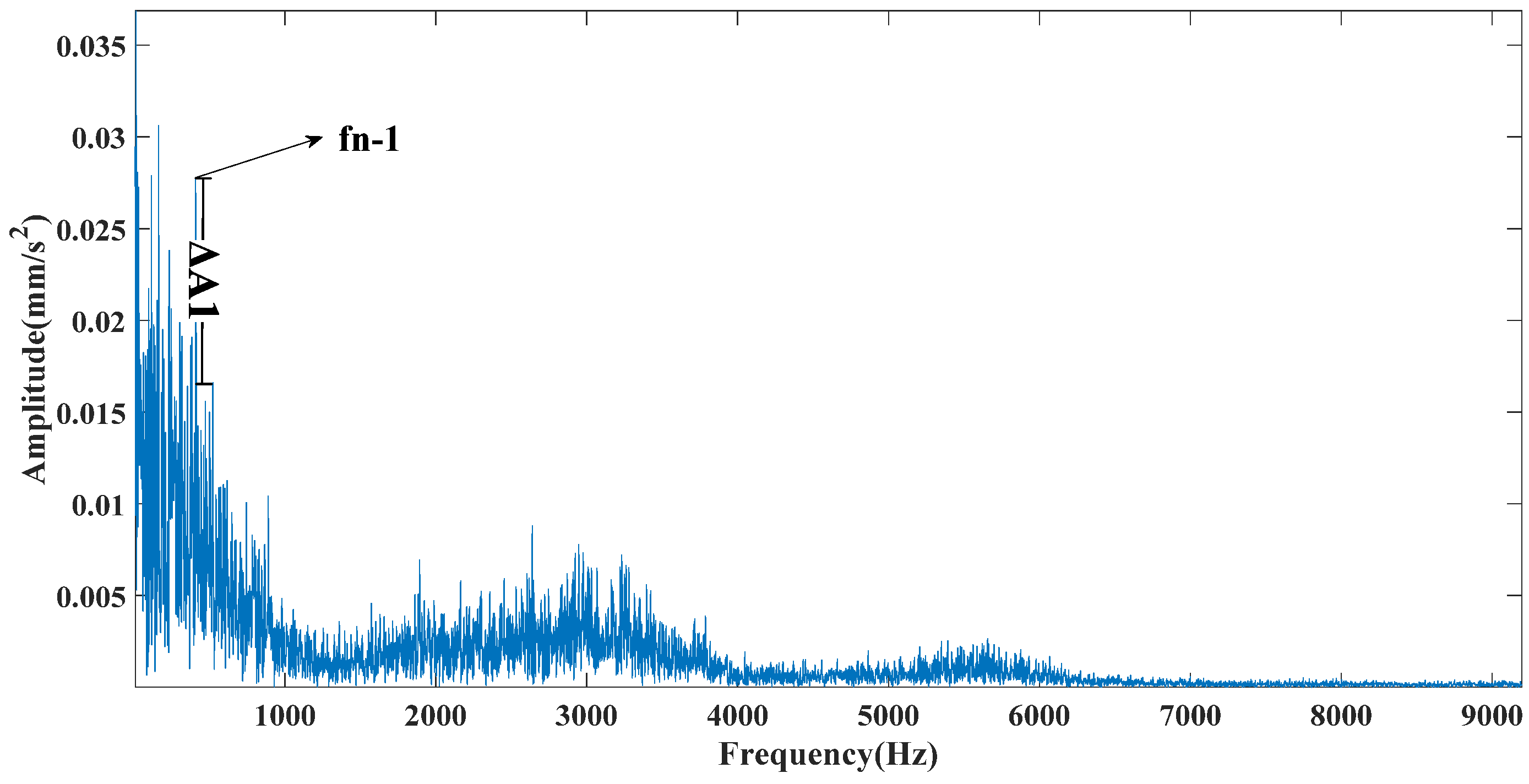
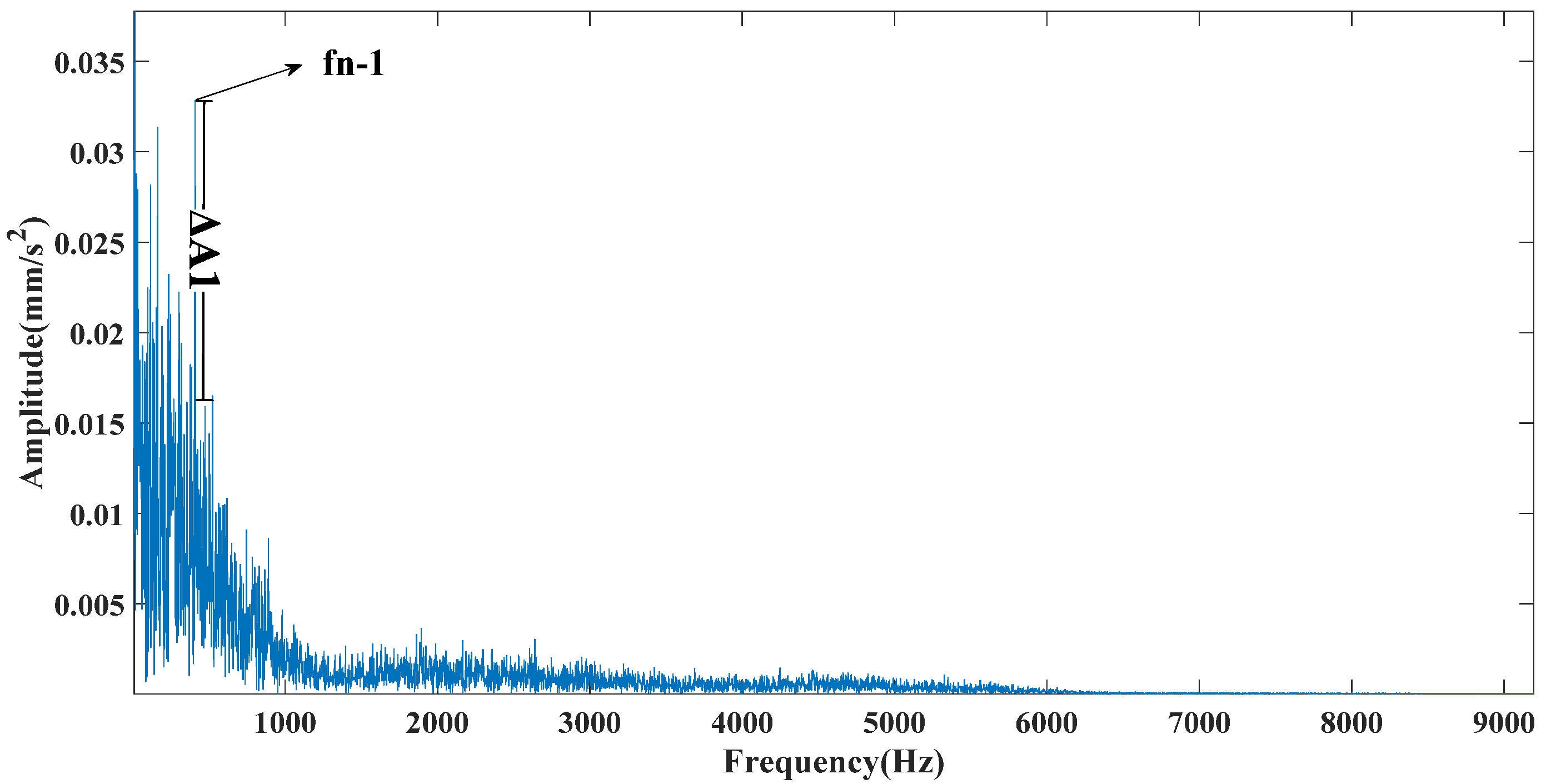
Figure 13 shows that the CEEMDAN method decomposed a total of 13 mode components. The CEITDAN and CEITDALN methods decomposed 10 mode components, respectively. This is consistent with the previous part of the analog signal results, because the three types are relatively stable in decomposing strong noise signals. The CEEMDAN method led to the appearance of false modes due to envelope fitting. The CEITDAN and CEITDALN methods showed better results in terms of signal decomposition. Figure 14 shows the kurtosis spectrum required by CEITDALN in the decomposition process to extract the center frequency and optimize the parameters. Figure 15 shows the percentage of the center frequency contained in the different rotation components of the CEITDALN method. Different from the analog signal, the second rotation component accounted for the largest proportion of the center frequency in the actual engineering signal. However, the results of the first three components were consistent with those of the analog signal. Figure 16, Figure 17 and Figure 18 show the signal envelope spectrum after decomposition by the CEEMDAN, CEITDAN, and CEITDALN methods, respectively. In the above figure, fn-1 is the fault characteristic frequency, fn-2 is twice the fault characteristic frequency, and the rest can be deduced by analogy. Figure 16 and Figure 17 show that, after the signal processing of the CEEMDAN and CEITDAN methods, the fault characteristic frequency could be observed. However, the difference between the peak values of the characteristic frequency and of the noise was small. High-frequency noise was not completely filtered out, and there was some retention. In the CEITDALN method shown in Figure 18, all the high-frequency noise was filtered out and the peak difference was the largest. The extraction of characteristic frequencies was the most obvious. In engineering applications, it is generally only necessary to observe the fault characteristic frequency of onefold frequency. A more intuitive consideration of the filtering method involves the degree of noise filtering. The results shown by the method in this paper can be used in engineering practice.

Figure 13.
Comparison results of three decomposition methods: (a) CEEMDAN, (b) CEITDAN, and (c) CEITDALN.

Figure 14.
Determination of the center frequency of the kurtosis spectrum.

Figure 15.
Energy ratio of the center frequency band.

Figure 16.
CEEMDAN envelope spectrum.

Figure 17.
CEITDAN envelope spectrum.

Figure 18.
CETIDALN envelope spectrum.
In order to objectively compare the three methods, this section still uses the same indicators as those in the analog signal section. However, due to the actual signal, the input SNR and output SNR could not be accurately calculated. Therefore, only four indicators—OI, ECI, ISNR, and RMSE—were used, as shown in Table 3. The results were consistent with those of analog signals, and the proposed method showed a strong applicability in index comparison. Figure 19 shows the comparison between the improved COA and the traditional COA algorithms in optimizing the fitness value. Although the basic value was improved, the improved method proposed in this paper maintained the characteristic of faster convergence compared with the traditional method.

Table 3.
Comparison table of indicators for different decomposition algorithms.

Figure 19.
Fitness value of the improved optimization algorithm and the number of iterations.
In order to more fully reflect the effectiveness of the proposed method in this paper, we use the same experimental platform for troubleshooting different bearing faults, including outer ring faults. The outer ring fault characteristic frequency was calculated as shown in Equation (51). The experimental bearing outer ring failure characteristic frequency was calculated as 292 Hz.
where is the number of rolling bodies, is the inner ring rotation frequency, is the rolling body diameter, is the pitch diameter, and is the contact angle.
According to the previous comparison of the CEITDAN and CEEMDAN methods, it can be seen that the proposed method has a better effect, but in order to have more convincing experimental results, this paper introduces wavelet threshold noise reduction to compare with the proposed method, and considering that the fault diagnosis results are more strict on time requirements, it is also necessary to add a time complexity index to evaluate the different methods. The results are as follows.
Figure 20 shows the decomposition results of the three methods for the bearing outer ring fault signal. From the figure, it can be seen that the signal decomposition effect of the proposed method in this paper is better than the other two, which is consistent with the performance of the simulated signal and the experimental signal of the inner ring fault in the previous paper. Figure 21 shows the time domain diagram of the signal after wavelet threshold noise reduction, and a subsequent envelope spectrum transformation of the noise reduction signal will be performed to obtain the fault characteristic frequency. Figure 22 shows the center band energy of the cliff spectrum used in the proposed method. It can be seen that the mode component contains the greatest center band energy, so this component is selected for the signal envelope spectrum transformation to obtain the fault characteristic frequency. Figure 23, Figure 24, Figure 25 and Figure 26 show the results of the envelope spectrum transformation for different methods. In the above figure, fn-1 is the fault characteristic frequency, fn-2 is twice the fault characteristic frequency, and the rest can be deduced by analogy. In Figure 23, Figure 24 and Figure 25, it can be seen that the filtering effect is not satisfactory, the difference between the fault characteristic frequency and the noise is small, and it is difficult to extract the fault characteristic frequency quickly and accurately. However, the gap between the peak of the characteristic frequency and the peak of the noise is large in Figure 26, and the high-frequency noise is completely filtered out cleanly, showing the same better application effect as the previous paper. Table 4 shows a summary table of the comparison indexes of different methods, and it is obvious from the table that the proposed method in this paper has a better effect than other methods in practical applications.

Figure 20.
Comparison results of three decomposition methods: (a) CEEMDAN, (b) CEITDAN, and (c) CEITDALN.

Figure 21.
Time domain diagram after wavelet threshold noise reduction.

Figure 22.
Energy ratio of the center frequency band.

Figure 23.
CEEMDAN envelope spectrum.

Figure 24.
CEITDAN envelope spectrum.

Figure 25.
Wavelet threshold noise reduction envelope spectrum.

Figure 26.
CETIDALN envelope spectrum.

Table 4.
Comparison table of indicators for different decomposition algorithms.
In summary, the method proposed in this paper maintained a good applicability in engineering practice, solving the problem of excessive signal noise and the influence of nonwhite noise on fault diagnosis. In the traditional decomposition method, the frequency bands of nonwhite noise are mostly concentrated in a specific frequency band. Therefore, it is necessary to analyze the decomposition results. We filtered out mode components that were not white noise. In the proposed method, nonwhite noise could be partially offset and preprocessed in the decomposition process, reducing the proportion of nonwhite noise components in the decomposition results. This improves the signal-to-noise ratio and diagnosis accuracy and has a strong practicability and operability.
5. Conclusions
This study solves the problem of the traditional CEITDAN method not being able to offset the effects of strong and nonwhite noise. The method proposed in this paper was verified by analog and actual engineering signals. This paper compares the proposed method and the traditional method using both qualitative analysis (the number of feature frequencies extracted from the envelope spectrum and the degree of noise interference included) and quantitative analysis (ECI, OI, RMSE and ISNR), and finds that the proposed method outperforms the traditional method in the fault diagnosis process. The results show that this method has a good performance because it has a certain reference and validity for signal processing and fault diagnosis. The CEITDALN method proposed in this paper changes the traditional decomposition algorithm by adding white noise to groups, adding analog noise in the form of adjustable parameter transformation noise. This can better cancel noise in strong noise signals in the process of signal decomposition. The proportion of nonwhite noise in the signal decomposition result was reduced, reducing the impact of nonwhite noise on the accuracy of the decomposition results. The method performs well in both analog and measured signals and can be further used in signal processing and fault diagnosis in actual projects. In the future, we will conduct in-depth research on the endpoint effects of the ITD method itself to solve the problem of curve distortion and further improve the accuracy and visualization of signal decomposition.
Author Contributions
Conceptualization, J.M.; methodology, J.M.; software, G.Z.; validation, J.M. and L.Z.; formal analysis, S.Z.; investigation, J.M.; resources, L.Z.; data curation, J.M.; writing—original draft preparation, J.M.; writing—review and editing, L.Z. and C.L.; visualization, C.L.; supervision, C.L.; project administration, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Laha, S.K. Enhancement of fault diagnosis of rolling element bearing using maximum kurtosis fast nonlocal means denoising. Measurement 2017, 100, 157–163. [Google Scholar] [CrossRef]
- Zheng, J.J.; Yuan, Y.; Zou, L.; Deng, W.; Guo, C.; Zhao, H.M. Study on a novel fault diagnosis method based on VMD and BLM. Symmetry 2019, 11, 747. [Google Scholar] [CrossRef]
- Zhou, L.M.; Wang, F.L.; Zhang, C.C.; Zhang, L.; Li, P. Evaluation of rolling bearing performance degradation using wavelet packet energy entropy and RBF neural network. Symmetry 2019, 11, 1064. [Google Scholar] [CrossRef]
- Yuan, R.; Lv, Y.; Song, G. Multi-fault diagnosis of rolling bearings via adaptive projection intrinsically transformed multivariate empirical mode decomposition and high order singular value decomposition. Sensors 2018, 18, 1210. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, R.; Gupta, V.K.; Kankar, P.K. Bearing fault diagnosis based on multi-scale permutation entropy and adaptive neuro fuzzy classifier. J. Vib. Control 2013, 21, 461–467. [Google Scholar] [CrossRef]
- Ge, M.; Wang, J.; Ren, X. Fault Diagnosis of Rolling Bearings Based on EWT and KDEC. Entropy 2017, 19, 633. [Google Scholar] [CrossRef]
- Ge, M.; Wang, J.; Xu, Y.C. Rolling bearing fault diagnosis based on EWT Sub-modal Hypothesis test and ambiguity correlation classification. Symmetry 2018, 10, 730. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Rolling element bearing fault diagnosis using wavelet transform. Neurocomputing 2011, 74, 1638–1645. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R. Enhancing Weak Defect Features Using Undecimated and Adaptive Wavelet Transform for Estimation of Roller Defect Size in a Bearing. Tribol. Trans. 2017, 5, 60. [Google Scholar] [CrossRef]
- Yang, P.; Yang, Q. Empirical Mode Decomposition and Rough Set Attribute Reduction for Ultrasonic Flaw Signal Classification. Int. J. Comput. Intell. Syst. 2014, 7, 481–492. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Yang, Y.; Xu, M.; Huang, W. Early Fault Diagnosis of Rotating Machinery by Combining Differential Rational Spline-Based LMD and K-L Divergence. IEEE Trans. Instrum. Meas. 2017, 66, 3077–3090. [Google Scholar] [CrossRef]
- Frei, M.G.; Osorio, I. Intrinsic time-scale decomposition: Time-frequency-energy analysis and real-time filtering of non-stationary signals. Proc. R. Soc. A 2007, 463, 321–342. [Google Scholar] [CrossRef]
- Bo, L.; Peng, C. Fault diagnosis of rolling bearing using more robust spectral kurtosis and intrinsic time-scale decomposition. J. Vib. Control 2014, 22, 2921–2937. [Google Scholar] [CrossRef]
- Duan, L.; Yao, M.; Wang, J.; Bai, T.; Yue, J. Integrative intrinsic time-scale decomposition and hierarchical temporal memory approach to gearbox diagnosis under variable operating conditions. Adv. Mech. Eng. 2016, 8, 1–14. [Google Scholar] [CrossRef]
- Xing, Z.; Qu, J.; Chai, Y.; Tang, Q.; Zhou, Y. Gear fault diagnosis under variable conditions with intrinsic time-scale decomposition-singular value decomposition and support vector machine. J. Mech. Sci. Technol. 2017, 31, 545–553. [Google Scholar] [CrossRef]
- Zhang, J.H.; Liu, Y. Application of complete ensemble intrinsic time-scale decomposition and least-square SVM optimized using hybrid DE and PSO to fault diagnosis of diesel engines. Front. Inf. Technol. Electron. Eng. 2017, 18, 272–286. [Google Scholar] [CrossRef]
- Hu, A.; Xiang, L.; Gao, N. Fault diagnosis for the gearbox of wind turbine combining ensemble intrinsic time-scale decomposition with Wigner bi-spectrum entropy. J. Vibroeng. 2017, 19, 1759–1770. [Google Scholar] [CrossRef]
- Tong, Q.; Cao, J.; Han, B.; Wang, D.; Lin, Y.; Zhang, W.; Wang, J. A fault diagnosis approach for rolling element bearings based on dual-tree complex wavelet packet transform-improved intrinsic time-scale decomposition. Singular value decomposition, and online sequential extreme learning machine. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Qin, K.; Xu, Y. Diesel engine fault diagnosis using intrinsic time-scale decomposition and multistage Adaboost relevance vector machine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 881–894. [Google Scholar] [CrossRef]
- Bi, F.; Ma, T.; Liu, C.; Tian, C. Knock detection in spark ignition engines based on complementary ensemble improved intrinsic time-scale decomposition (CEIITD) and Bi-spectrum. J. Vibroeng. 2018, 20, 936–953. [Google Scholar] [CrossRef]
- Yu, J.; Liu, H. Sparse coding shrinkage in intrinsic time-scale decomposition for weak fault feature extraction of bearings. IEEE Trans. Instrum. Meas. 2018, 67, 1579–1592. [Google Scholar] [CrossRef]
- Yuan, Z.; Peng, T.; An, D.; Cristea, D.; Pop, M.A. Rolling bearing fault diagnosis based on adaptive smooth ITD and MF-DFA method. J. Low Freq. Noise Vib. Active Control 2019, 39, 968–986. [Google Scholar] [CrossRef]
- Lei, Z.; Zhou, Y.; Sun, B.; Sun, W. An intrinsic timescale decomposition-based kernel extreme learning machine method to detect tool wear conditions in the milling process. Int. J. Adv. Manufac. Technol. 2019, 106, 1203–1212. [Google Scholar] [CrossRef]
- Ma, J.; Zhan, L.; Li, C.; Li, Z. An improved intrinsic time scale decomposition method based on adaptive noise and its application in bearing fault feature extraction. Meas. Sci. Technol. 2020, 32, 025103. [Google Scholar] [CrossRef]
- Ciabattoni, L.; Ferracuti, F.; Freddi, A.; Monteriu, A. Statistical spectral analysis for fault diagnosis of rotating machines. IEEE Trans. Ind. Electr. 2017, 65, 4301–4310. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Yang, H. Lévy noise induced stochastic resonance in an FHN model. Sci. China Technol. Sci. 2016, 59, 371–375. [Google Scholar] [CrossRef]
- Pierezan, J.; Coelho, L.S. Coyote optimization algorithm: A new metaheuristic for global optimization problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 2633–2640. [Google Scholar]
- Zhang, G.; Hu, D.; Zhang, T. The analysis of stochastic resonance and bearing fault detection based on linear coupled bistable system under levy noise. Chin. J. Phys. 2018, 56, 2718–2730. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Bazaraa, M.S.; Sherali, H.D.; Shetty, C.M. Nonlinear Programming: Theory and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Weerakoon, S.; Fernando, T.G. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Patil, P.; Verma, U. Numerical Computational Methods; Alpha Science International Ltd.: Oxford, UK, 2006. [Google Scholar]
- Yi, J.H.; Wang, J.; Wang, G.G. Improved probabilistic neural networks with self-adaptive strategies for transformer fault diagnosis problem. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterizing non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Wang, L.; Shao, Y. Fault feature extraction of rotating machinery using a reweighted complete ensemble empirical mode decomposition with adaptive noise and demodulation analysis. Mech. Syst. Signal Process. 2020, 138, 106545. [Google Scholar] [CrossRef]
- Huang, D.R. A sufficient condition of monotone cubic splines. Math. Number Sin. 1982, 2, 214–217. [Google Scholar]
- Chen, Q.; Huang, N.; Riemenschneider, S.; Xu, Y. A B-spline approach for empirical mode decompositions. Adv. Comput. Math. 2006, 24, 171–195. [Google Scholar] [CrossRef]
- Zhan, L.W.; Ma, F.; Zhang, J.J.; Li, C.W.; Li, Z.H.; Wang, T.J. Fault feature extraction and diagnosis of rolling bearings based on enhanced complementary empirical mode decomposition with adaptive noise and statistical time-domain features. Sensors 2019, 19, 4047. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).