Computational Intelligent Paradigms to Solve the Nonlinear SIR System for Spreading Infection and Treatment Using Levenberg–Marquardt Backpropagation
Abstract
1. Introduction
- A novel integrated design of an intelligent computing scheme is introduced via modeling competency of Levenberg–Marquardt backpropagation neural network applied to scrutinize the dynamics of both the categories of SIR systems represented with set of nonlinear ordinary differential equations.
- The designed LMB neural networks operate effectively on a dataset generated from numerical Adam method for different variants of the nonlinear modeling and treatment-based SIR systems.
- The performance via comparative investigations from reference results of Adam method on correlation, error histograms, regression and mean square error (MSE) metrics establish the worth of designed Levenberg–Marquardt backpropagation neural networks.
- Advantage of the proposed LMB neural network methodology is the smooth implementation, simplicity of the concept, stability and exhaustive applicability.
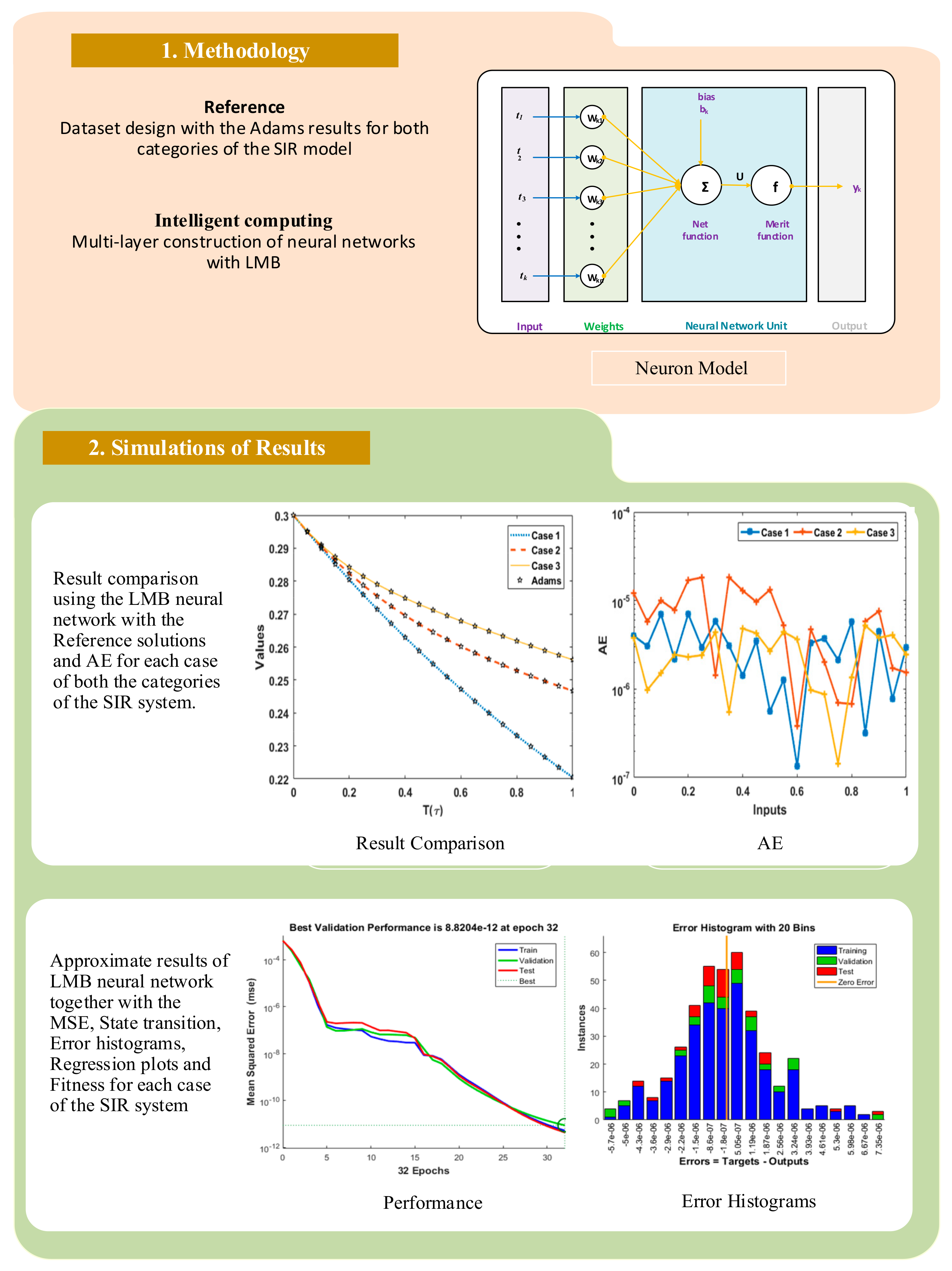
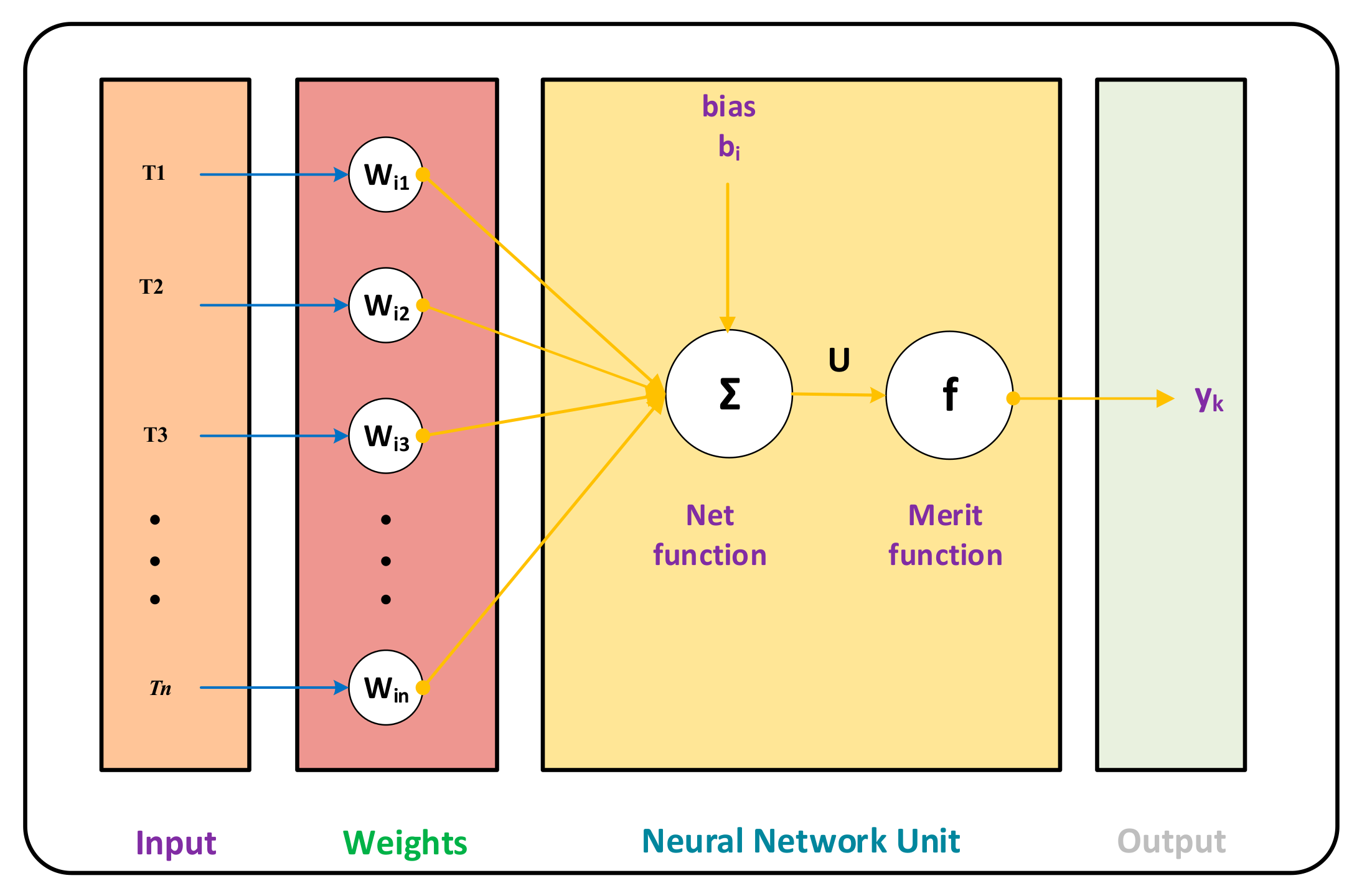
2. Methodology
- Essential descriptions are given to make or formulate the LMB neural networks dataset by the used of standard numerical methods—i.e., Runge–Kutta or Adam numerical solvers.
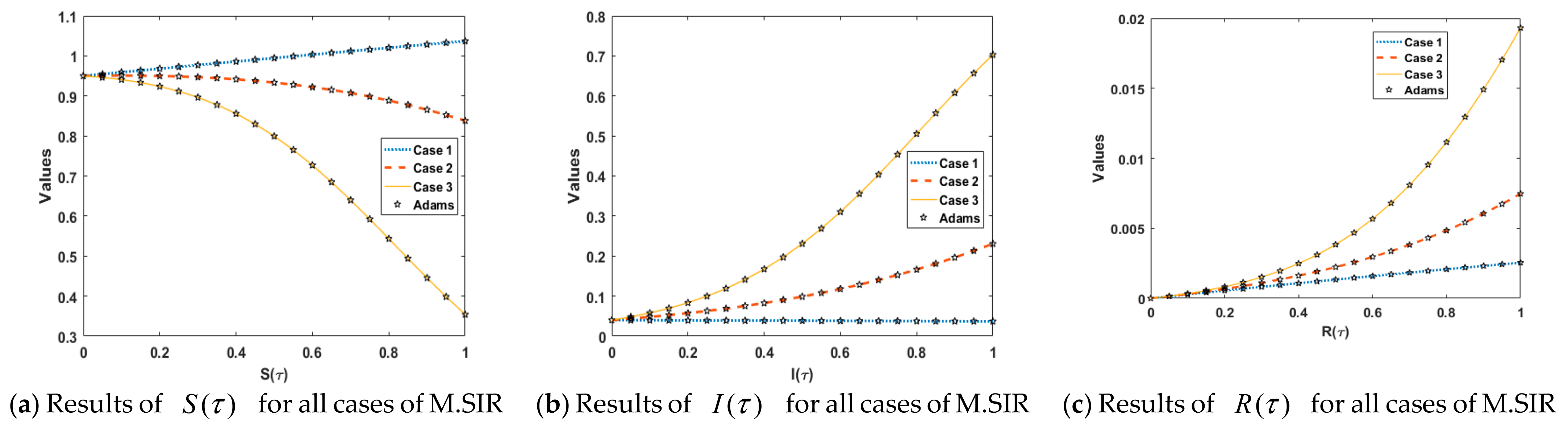
- Implementation procedure approved for LMB neural networks is introduced to find the approximate solution of both modified SIR (M.SIR) and SIR treatment (T.SIR) models presented in set of Equations (1) and (2).
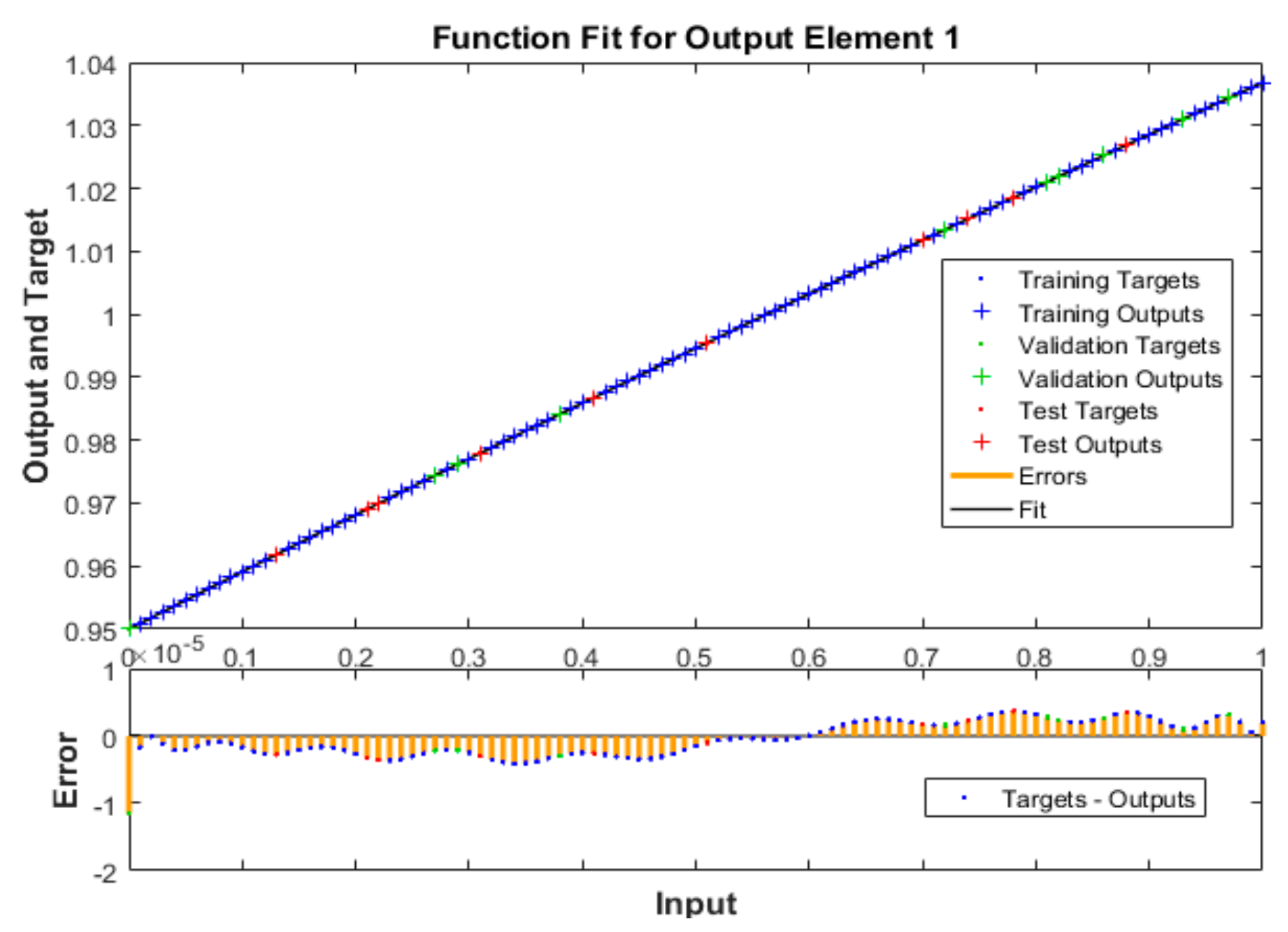
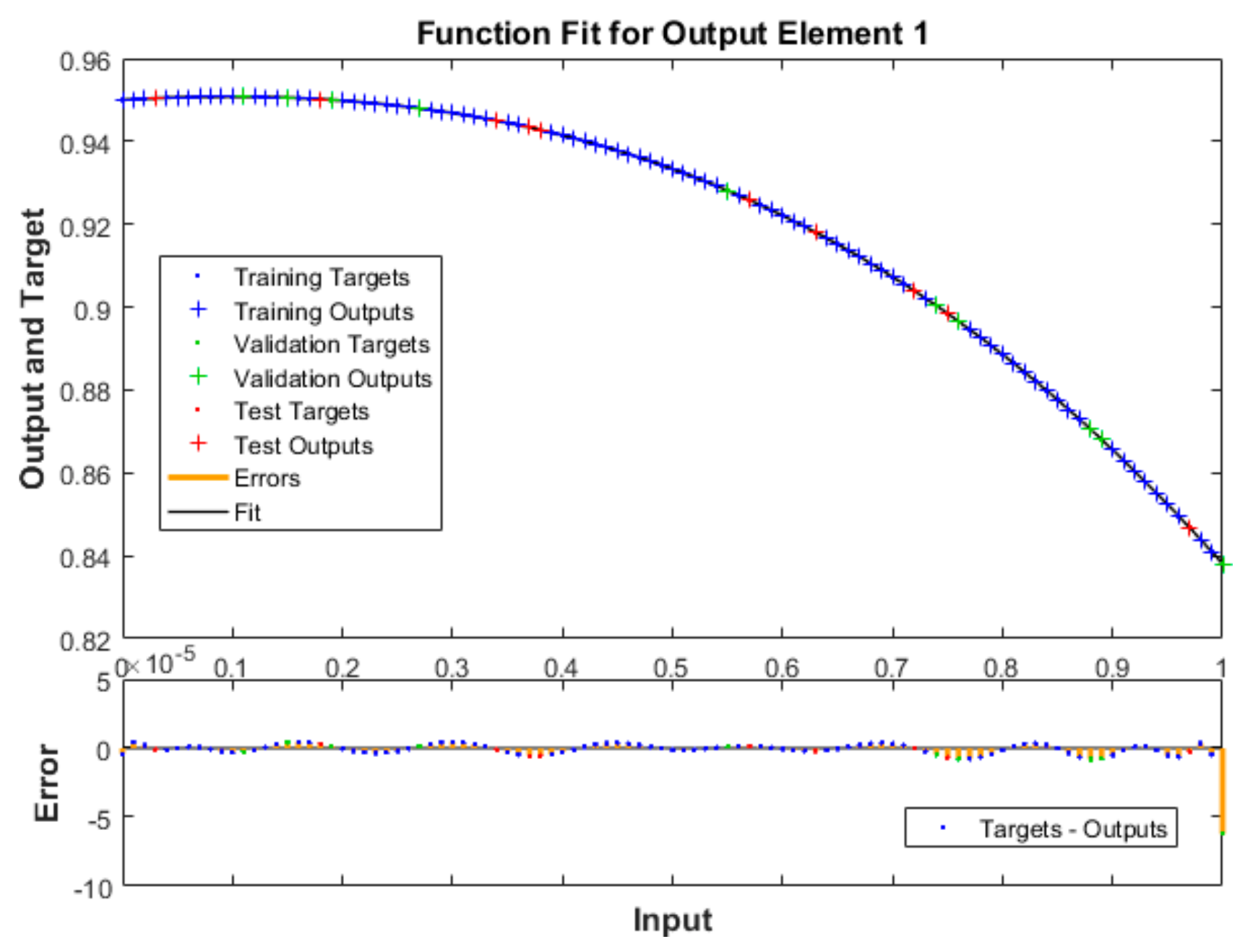
3. Numerical Measures with Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Diekmann, O.; Heesterbeek, J.A. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation; John Wiley & Sons: Hoboken, NJ, USA, 2000; Volume 5. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2001; Volume 40, Available online: https://link.springer.com/book/10.1007/978-1-4614-1686-9 (accessed on 10 January 2021).
- Murray, J.D. Mathematical Biology; Springer: New York, NY, USA, 1993. [Google Scholar]
- Bhattacharya, P.; Paul, S.; Biswas, P. Mathematical Modeling of Treatment SIR Model with Respect to Variable Contact Rate. Int. Proc. Econ. Dev. Res. 2015, 83, 34. [Google Scholar]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Dietz, K. The first epidemic model: A historical note on PD En’ko. Aust. J. Stat. 1988, 30, 56–65. [Google Scholar] [CrossRef]
- Wickwire, K. Mathematical models for the control of pests and infectious diseases: A survey. Theor. Popul. Biol. 1977, 11, 182–238. [Google Scholar] [CrossRef]
- Zhang, H.; Jiao, J.; Chen, L. Pest management through continuous and impulsive control strategies. Biosystems 2007, 90, 350–361. [Google Scholar] [CrossRef] [PubMed]
- Ögren, P.; Martin, C.F. Vaccination strategies for epidemics in highly mobile populations. Appl. Math. Comput. 2002, 127, 261–276. [Google Scholar] [CrossRef]
- Goufo, D.; Noutcjie, S.C.O.; Mugisha, S. A fractional SEIR epidemic model for spatial and temporal spread of measles in metapopulations. In Abstract and Applied Analysis; Hindawi: London, UK, 2014; Volume 2014. [Google Scholar]
- Mickens, R.E. A discrete-time model for the spread of periodic diseases without immunity. Biosystems 1992, 26, 193–198. [Google Scholar] [CrossRef]
- Fister, K.R.; Lenhart, S.; McNally, J.S. Optimizing chemotherapy in an HIV model. Electron. J. Differ. Equ. 1998, 32, 1–12. [Google Scholar]
- Müller, J. Optimal vaccination patterns in age-structured populations. SIAM J. Appl. Math. 1998, 59, 222–241. [Google Scholar] [CrossRef]
- Joshi, H.R. Optimal Control of an HIV Immunology Model. Optim. Control Appl. Methods 2002, 23, 199–213. [Google Scholar] [CrossRef]
- Boudjema, I.; Touaoula, T.M. Global stability of an infection and vaccination age-structured model with general nonlinear incidence. J. Nonlinear Funct. Anal. 2018, 2018, 33. [Google Scholar]
- Yan, M.; Shi, R.; Ji, Z. Analysis of an SIR epidemic model with saturation incidence rate in an environmentally-driven infectious disease. J. Nonlinear Funct. Anal. 2015, 2015, 10. [Google Scholar]
- Humphries, T.; Loreto, M.; Halter, B.; O’Keeffe, W.; Ramirez, L. Comparison of regularized and superiorized methods for tomographic image reconstruction. J. Appl. Numer. Optim. 2020, 2, 77–99. [Google Scholar]
- Sabir, Z.; Saoud, S.; Raja, M.A.Z.; Wahab, H.A.; Arbi, A. Heuristic computing technique for numerical solutions of nonlinear fourth order Emden–Fowler equation. Math. Comput. Simul. 2020, 178, 534–548. [Google Scholar] [CrossRef]
- Sabir, Z.; Umar, M.; Guirao, J.L.G.; Shoaib, M.; Raja, M.A.Z. Integrated intelligent computing paradigm for nonlinear multi-singular third-order Emden–Fowler equation. Neural Comput. Appl. 2021, 33, 3417–3436. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Umar, M.; Shoaib, M. Design of neuro-swarming-based heuristics to solve the third-order nonlinear multi-singular Emden–Fowler equation. Eur. Phys. J. Plus 2020, 135, 1–17. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Khalique, C.M.; Unlu, C. Neuro-evolution computing for nonlinear multi-singular system of third order Emden-Fowler equation. Math. Comput. Simul. 2021, 185, 799–812. [Google Scholar] [CrossRef]
- Bukhari, A.H.; Sulaiman, M.; Raja, M.A.Z.; Islam, S.; Shoaib, M.; Kumam, P. Design of a hybrid NAR-RBFs neural network for nonlinear dusty plasma system. Alex. Eng. J. 2020, 59, 3325–3345. [Google Scholar] [CrossRef]
- Guirao, J.L.A.; Sabir, Z.; Saeed, T. Design and Numerical Solutions of a Novel Third Order Nonlinear Emden–Fowler Delay Differential Model. Math. Probl. Eng. 2020. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Umar, M.; Shoaib, M. Neuro-swarm intelligent computing to solve the second-order singular functional differential model. Eur. Phys. J. Plus 2020, 135, 474. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z. Intelligent computing for numerical treatment of nonlinear prey–predator models. Appl. Soft Comput. 2019, 80, 506–524. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, M.; Amin, F.; Guirao, J.L.G.; Raja, M.A.Z. Stochastic numerical technique for solving HIV infection model of CD4+ T cells. Eur. Phys. J. Plus 2020, 135, 403. [Google Scholar] [CrossRef]
- Umar, M.; Raja, M.A.Z.; Sabir, Z.; Alwabli, A.S.; Shoaib, M. A stochastic computational intelligent solver for numerical treatment of mosquito dispersal model in a heterogeneous environment. Eur. Phys. J. Plus 2020, 135, 1–23. [Google Scholar] [CrossRef]
- Umar, M.; Amin, F.; Wahab, H.A.; Baleanu, D. Unsupervised constrained neural network modeling of boundary value corneal model for eye surgery. Appl. Soft Comput. 2019, 85, 105826. [Google Scholar] [CrossRef]
- Almalki, M.M.; Alaidarous, E.S.; Maturi, D.A.; Raja, M.A.Z.; Shoaib, M. A Levenberg–Marquardt Backpropagation Neural Network for the Numerical Treatment of Squeezing Flow with Heat Transfer Model. IEEE Access 2020, 8, 227340–227348. [Google Scholar] [CrossRef]
- Ilyas, H.; Ahmad, I.; Raja, M.A.Z.; Tahir, M.B.; Shoaib, M. Intelligent Computing for the Dynamics of Fluidic System of Electrically Conducting Ag/Cu Nanoparticles with Mixed Convection for Hydrogen Possessions. Int. J. Hydrogen Energy 2021, 46, 4947–4980. [Google Scholar] [CrossRef]
- Jadoon, I.; Ahmed, A.; Rehman, A.; Shoaib, M.; Raja, M.A.Z. ntegrated meta-heuristics finite difference method for the dynamics of nonlinear unipolar electrohydrodynamic pump flow model. Appl. Soft Comput. 2020, 97, 106791. [Google Scholar] [CrossRef]
- Sabir, Z.; Wahab, H.A.; Umar, M.; Sakar, M.G.; Raja, M.A.Z. Novel Design of Morlet Wavelet Neural Network for Solving Second Order Lane–Emden Equation. Math. Comput. Simul. 2020, 172, 1–14. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.; Shoaib, M. A Novel Design of Fractional Meyer Wavelet Neural Networks with Application to the Nonlinear Singular Fractional Lane-Emden Systems. Alex. Eng. J. 2021, 60, 2641–2659. [Google Scholar] [CrossRef]
- Mehmood, A.; Zameer, A.; Ling, S.H.; Rehman, A.U.; Raja, M.A.Z. Integrated Computational Intelligent Paradigm for Nonlinear Electric Circuit Models Using Neural Networks, Genetic Algorithms and Sequential Quadratic Programming. Neural Comput. Appl. 2020, 32, 10337–10357. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Mehmood, A.; Niazi, S.A.; Shah, S.M. Computational intelligence methodology for the analysis of RC circuit modelled with nonlinear differential order system. Neural Comput. Appl. 2018, 30, 1905–1924. [Google Scholar] [CrossRef]
- Sabir, Z.; Manzar, M.A.; Raja, M.A.Z.; Sheraz, M.; Wazwaz, A.M. Neuro-heuristics for nonlinear singular Thomas-Fermi systems. Appl. Soft Comput. 2018, 65, 152–169. [Google Scholar] [CrossRef]
- Sabir, Z.; Baleanu, D.; Shoaib, M.; Raja, M.A.Z. Design of stochastic numerical solver for the solution of singular three-point second-order boundary value problems. Neural Comput. Appl. 2020, 33, 2427–2443. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.G.; Shoaib, M. A Neuro-Swarming Intelligence-Based Computing for Second Order Singular Periodic Non-linear Boundary Value Problems. Front. Phys. 2020, 8, 224. [Google Scholar] [CrossRef]
- Guerrero Sánchez, Y.; Sabir, Z.; Günerhan, H.; Baskonus, H.M. Analytical and approximate solutions of a novel nervous stomach mathematical model. Discret. Dyn. Nat. Soc. 2020, 2020, 1–9. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Shoaib, M.; Gupta, M.; Sánchez, Y.G. A Stochastic Intelligent Computing with Neuro-Evolution Heuristics for Nonlinear SITR System of Novel COVID-19 Dynamics. Symmetry 2020, 12, 1628. [Google Scholar]
- Sánchez, Y.G.; Sabir, Z.; Guirao, J.L.G. Design of A Nonlinear SITR Fractal Model Based on The Dynamics of a Novel Coronavirus (COVID-19). Fractals 2020, 28, 2040026. [Google Scholar] [CrossRef]
- Onal, M.; Esen, A. A Crank-Nicolson Approximation for the Time Fractional Burgers Equation. Appl. Math. Nonlinear Sci. 2020, 5, 177–184. [Google Scholar] [CrossRef]
- Topsakal, M.; Taşcan, F. Exact Travelling Wave Solutions for Space-Time Fractional Klein-Gordon Equation and (2 + 1)-Dimensional Time-Fractional Zoomeron Equation via Auxiliary Equation Method. Appl. Math. Nonlinear Sci. 2020, 5, 437–446. [Google Scholar] [CrossRef]
- Durur, H.; Tasbozan, O.; Kurt, A. New Analytical Solutions of Conformable Time Fractional Bad and Good Modified Boussinesq Equations. Appl. Math. Nonlinear Sci. 2020, 5, 447–454. [Google Scholar] [CrossRef]
- Ghosh, S.; Mukhopadhyay, S.; Vajravelu, K. MHD 3-Dimensional Nanofluid Flow Induced by a Power-Law Stretching Sheet with Thermal Radiation, Heat and Mass Fluxes. Appl. Math. Nonlinear Sci. 2020, 1. [Google Scholar] [CrossRef]
- Dewasurendra, M.; Vajravelu, K. On the Method of Inverse Mapping for Solutions of Coupled Systems of Nonlinear Differential Equations Arising in Nanofluid Flow, Heat and Mass Transfer. Appl. Math. Nonlinear Sci. 2018, 3, 1–14. [Google Scholar] [CrossRef]
- Lakshminarayana, P.; Vajravelu, K.; Sucharitha, G.; Sreenadh, S. Peristaltic Slip Flow of a Bingham Fluid in an Inclined Porous Conduit with Joule Heating. Appl. Math. Nonlinear Sci. 2018, 3, 41–54. [Google Scholar] [CrossRef]
- Sabir, Z.; Sakar, M.G.; Yeskindirova, M.; Saldir, O. Numerical Investigations to Design a Novel Model Based on the Fifth Order System of Emden–Fowler Equations. Theor. Appl. Mech. Lett. 2020, 10, 333–342. [Google Scholar] [CrossRef]
- Martínez, M.E.I.; Antonino-Daviu, J.A.; De Córdoba, P.F.; Conejero, J.A. Higher-Order Spectral Analysis of Stray Flux Signals for Faults Detection in Induction Motors. Appl. Math. Nonlinear Sci. 2020, 5, 1–14. [Google Scholar] [CrossRef]
- Chen, G.; Chen, C.; Yuan, Y.; Zhu, L. Modelling and Simulation Analysis of High-Pressure Common Rail and Electronic Controlled Injection System for Diesel Engine. Appl. Math. Nonlinear Sci. 2020. [Google Scholar] [CrossRef]
- Muhammadhaji, A.; Halik, A. Persistence and extinction of a stochastic delay competitive system under regime switching. J. Nonlinear Funct. Anal. 2019, 2019, 36. [Google Scholar]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.G.; Shoaib, M. Integrated Intelligent Computing with Neuro-Swarming Solver for Multi-Singular Fourth-Order Nonlinear Emden–Fowler Equation. Comput. Appl. Math. 2020, 39, 1–18. [Google Scholar] [CrossRef]



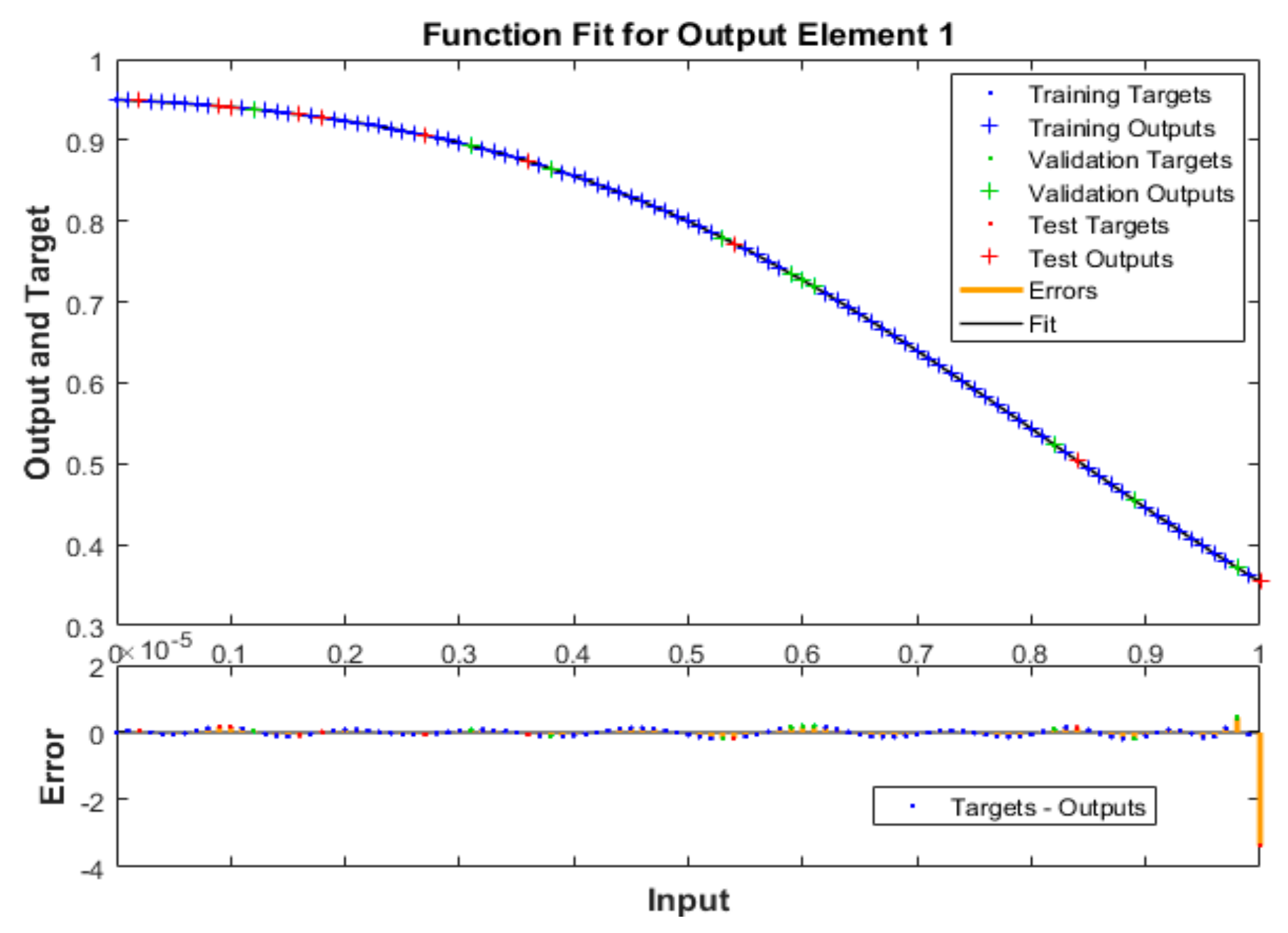
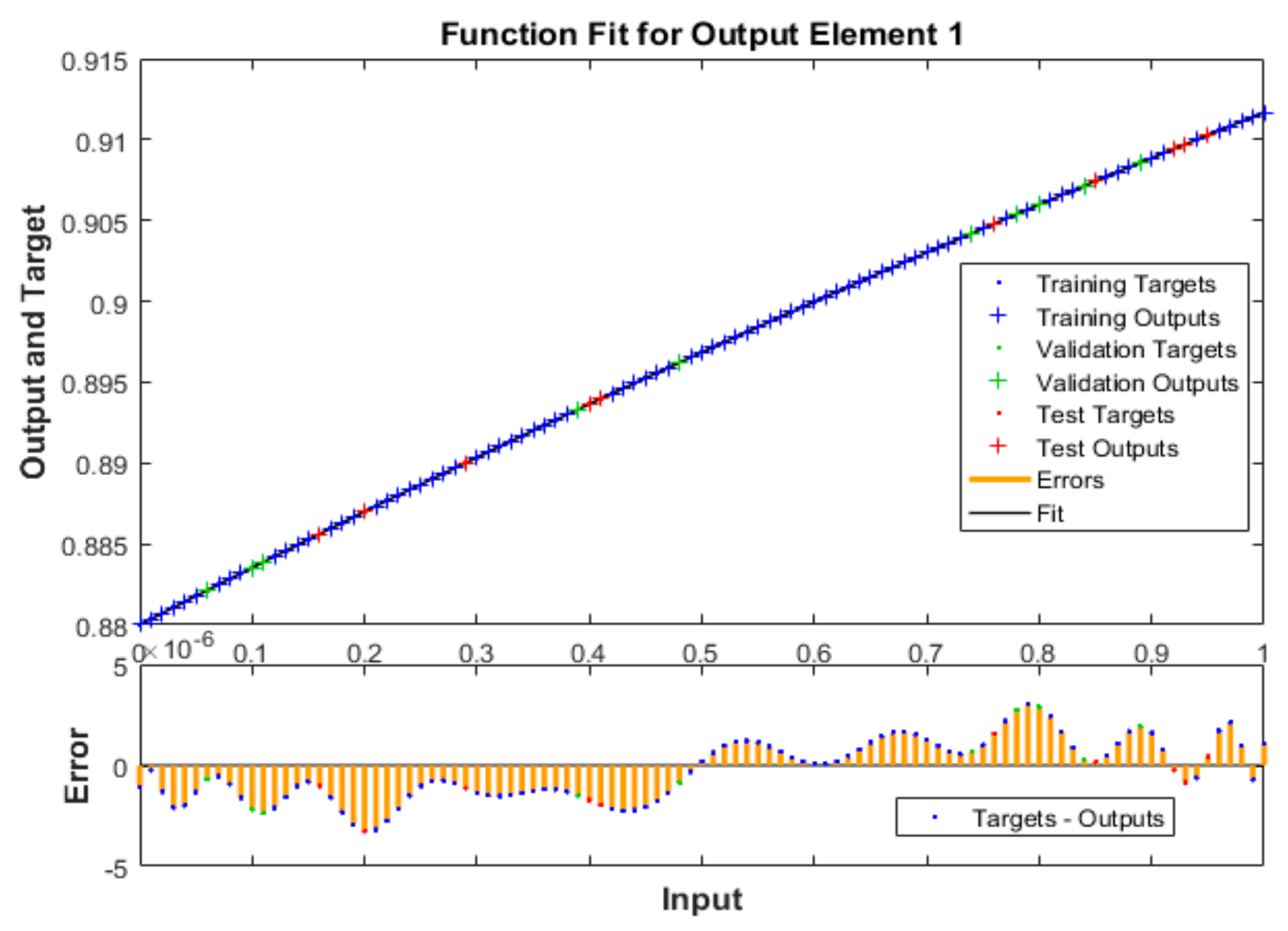
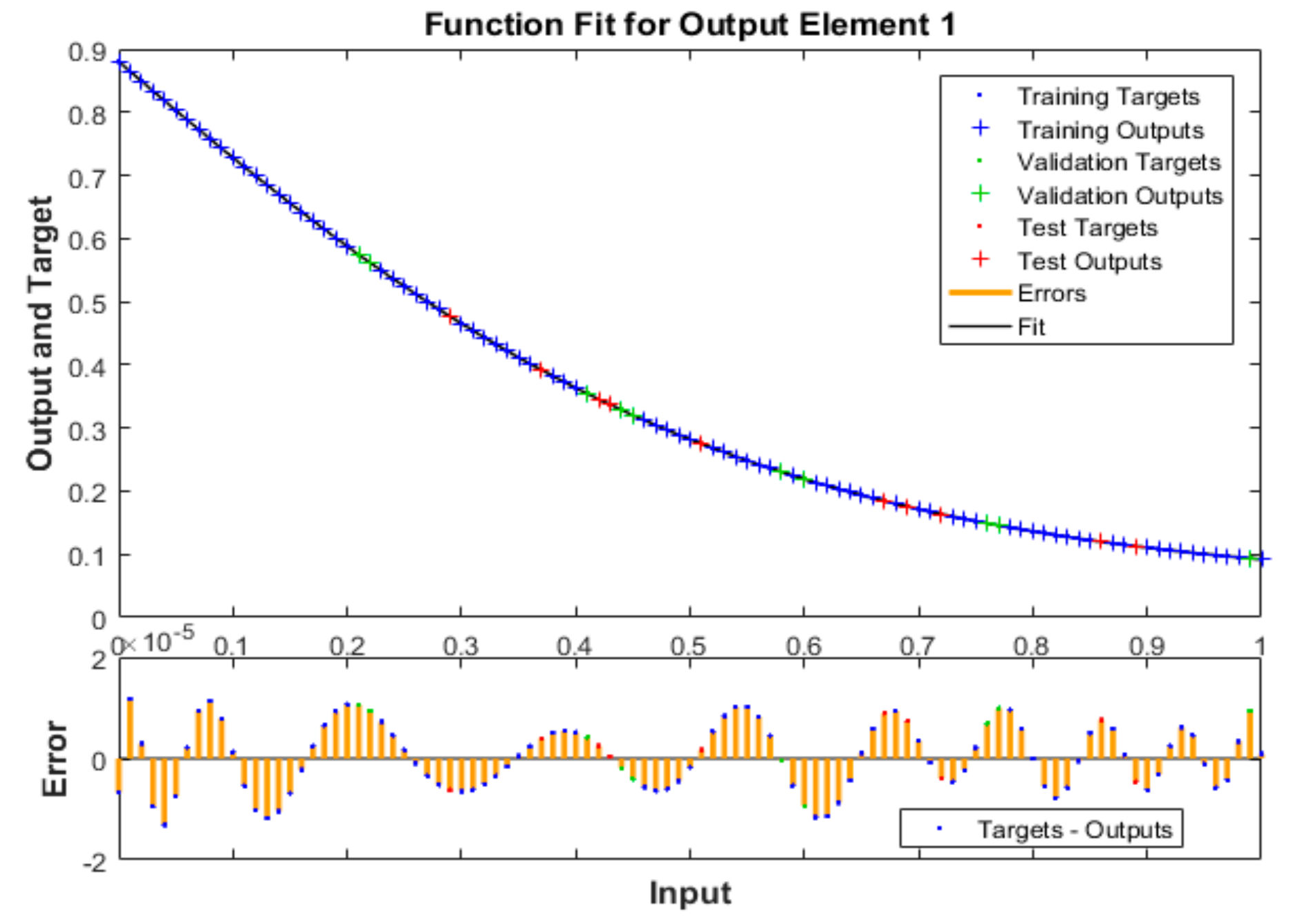

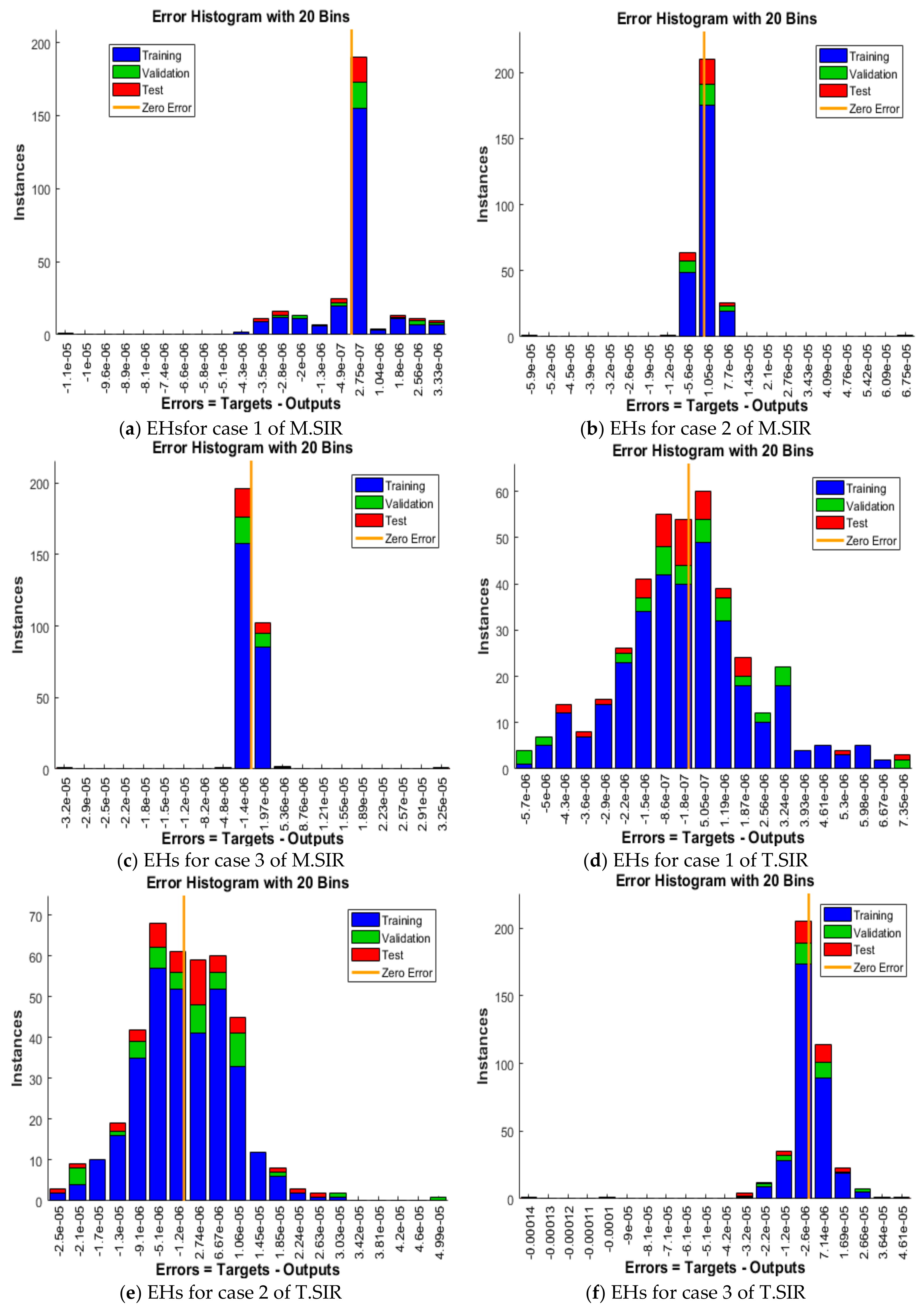
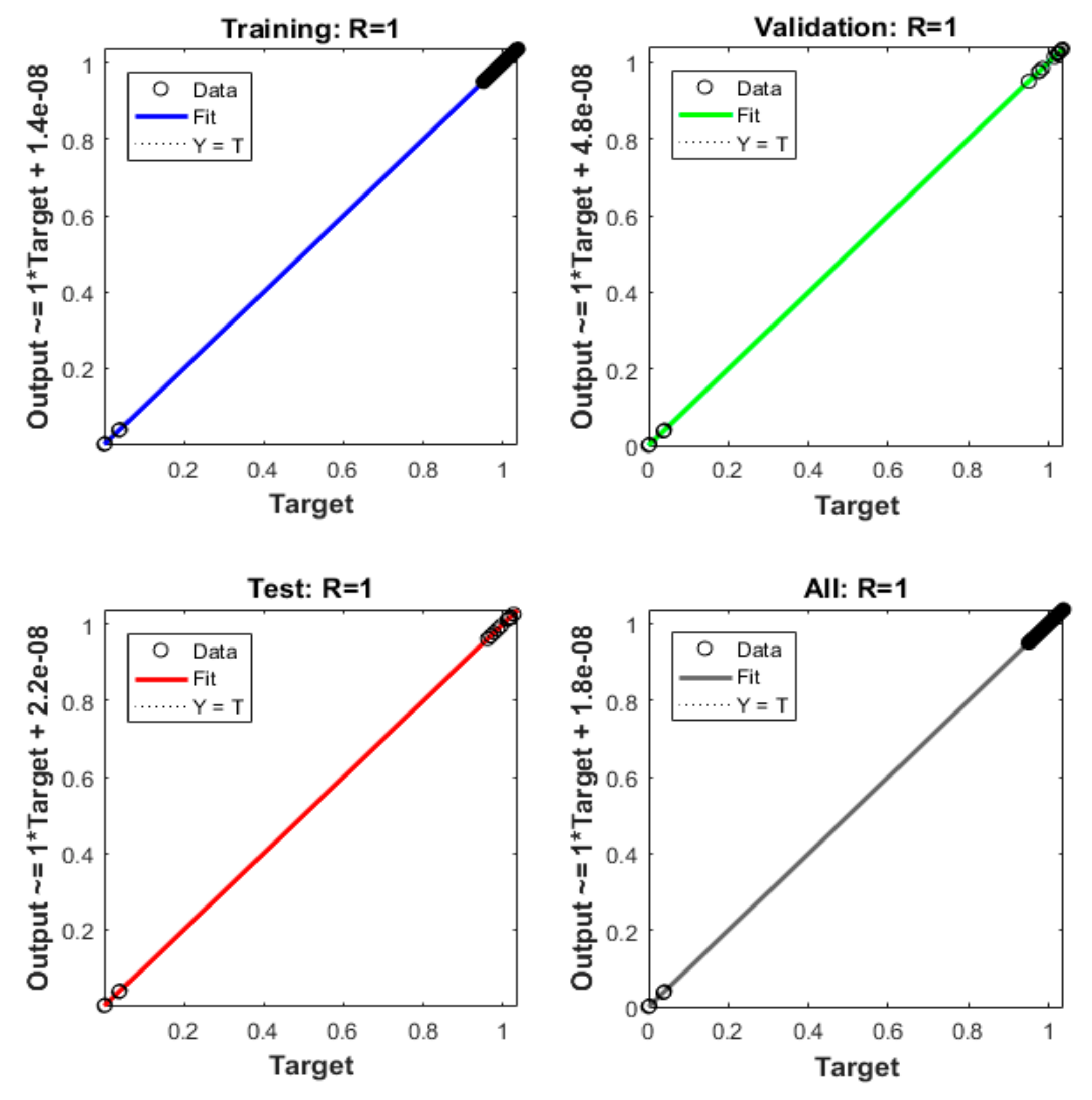



| Case | MSE | Performance | Gradient | Mu | Epoch | Time | ||
|---|---|---|---|---|---|---|---|---|
| Training | Validation | Testing | ||||||
| 1 | 1.90 × 10−12 | 6.21 × 10−12 | 2.71 × 10−12 | 1.90 × 10−12 | 9.49 × 10−08 | 1.00 × 10−13 | 25 | 1 |
| 2 | 9.04× 10−12 | 3.16 × 10−10 | 1.50 × 10−11 | 9.04 × 10−12 | 9.76 × 10−08 | 1.00 × 10−11 | 36 | 1 |
| 3 | 6.80 × 10−13 | 2.61 × 10−12 | 7.86 × 10−11 | 6.80 × 10−08 | 9.83 × 10−08 | 1.00 × 10−11 | 89 | 1 |
| Case | MSE | Performance | Gradient | Mu | Epoch | Time | ||
|---|---|---|---|---|---|---|---|---|
| Training | Validation | Testing | ||||||
| 1 | 5.26 × 10−12 | 8.82× 10−12 | 4.36 × 10−12 | 5.26 × 10−12 | 9.98 × 10−08 | 1.00 × 10−12 | 32 | 1 |
| 2 | 8.05× 10−11 | 1.83 × 10−10 | 1.00 × 10−10 | 8.50 × 10−12 | 9.83 × 10−08 | 1.00 × 10−10 | 551 | 3 |
| 3 | 6.89× 10−11 | 4.24 × 10−10 | 6.81 × 10−10 | 6.90 × 10−11 | 9.94 × 10−08 | 1.00 × 10−09 | 265 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umar, M.; Sabir, Z.; Zahoor Raja, M.A.; Gupta, M.; Le, D.-N.; Aly, A.A.; Guerrero-Sánchez, Y. Computational Intelligent Paradigms to Solve the Nonlinear SIR System for Spreading Infection and Treatment Using Levenberg–Marquardt Backpropagation. Symmetry 2021, 13, 618. https://doi.org/10.3390/sym13040618
Umar M, Sabir Z, Zahoor Raja MA, Gupta M, Le D-N, Aly AA, Guerrero-Sánchez Y. Computational Intelligent Paradigms to Solve the Nonlinear SIR System for Spreading Infection and Treatment Using Levenberg–Marquardt Backpropagation. Symmetry. 2021; 13(4):618. https://doi.org/10.3390/sym13040618
Chicago/Turabian StyleUmar, Muhammad, Zulqurnain Sabir, Muhammad Asif Zahoor Raja, Manoj Gupta, Dac-Nhuong Le, Ayman A. Aly, and Yolanda Guerrero-Sánchez. 2021. "Computational Intelligent Paradigms to Solve the Nonlinear SIR System for Spreading Infection and Treatment Using Levenberg–Marquardt Backpropagation" Symmetry 13, no. 4: 618. https://doi.org/10.3390/sym13040618
APA StyleUmar, M., Sabir, Z., Zahoor Raja, M. A., Gupta, M., Le, D.-N., Aly, A. A., & Guerrero-Sánchez, Y. (2021). Computational Intelligent Paradigms to Solve the Nonlinear SIR System for Spreading Infection and Treatment Using Levenberg–Marquardt Backpropagation. Symmetry, 13(4), 618. https://doi.org/10.3390/sym13040618









