A Survey on Knowledge Graph Embeddings for Link Prediction

Abstract

Knowledge graphs (KGs) have been widely used in the field of artificial intelligence, such as in information retrieval, natural language processing, recommendation systems, etc. However, the open nature of KGs often implies that they are incomplete, having self-defects. This creates the need to build a more complete knowledge graph for enhancing the practical utilization of KGs. Link prediction is a fundamental task in knowledge graph completion that utilizes existing relations to infer new relations so as to build a more complete knowledge graph. Numerous methods have been proposed to perform the link-prediction task based on various representation techniques. Among them, KG-embedding models have significantly advanced the state of the art in the past few years. In this paper, we provide a comprehensive survey on KG-embedding models for link prediction in knowledge graphs. We first provide a theoretical analysis and comparison of existing methods proposed to date for generating KG embedding. Then, we investigate several representative models that are classified into five categories. Finally, we conducted experiments on two benchmark datasets to report comprehensive findings and provide some new insights into the strengths and weaknesses of existing models.

1. Introduction

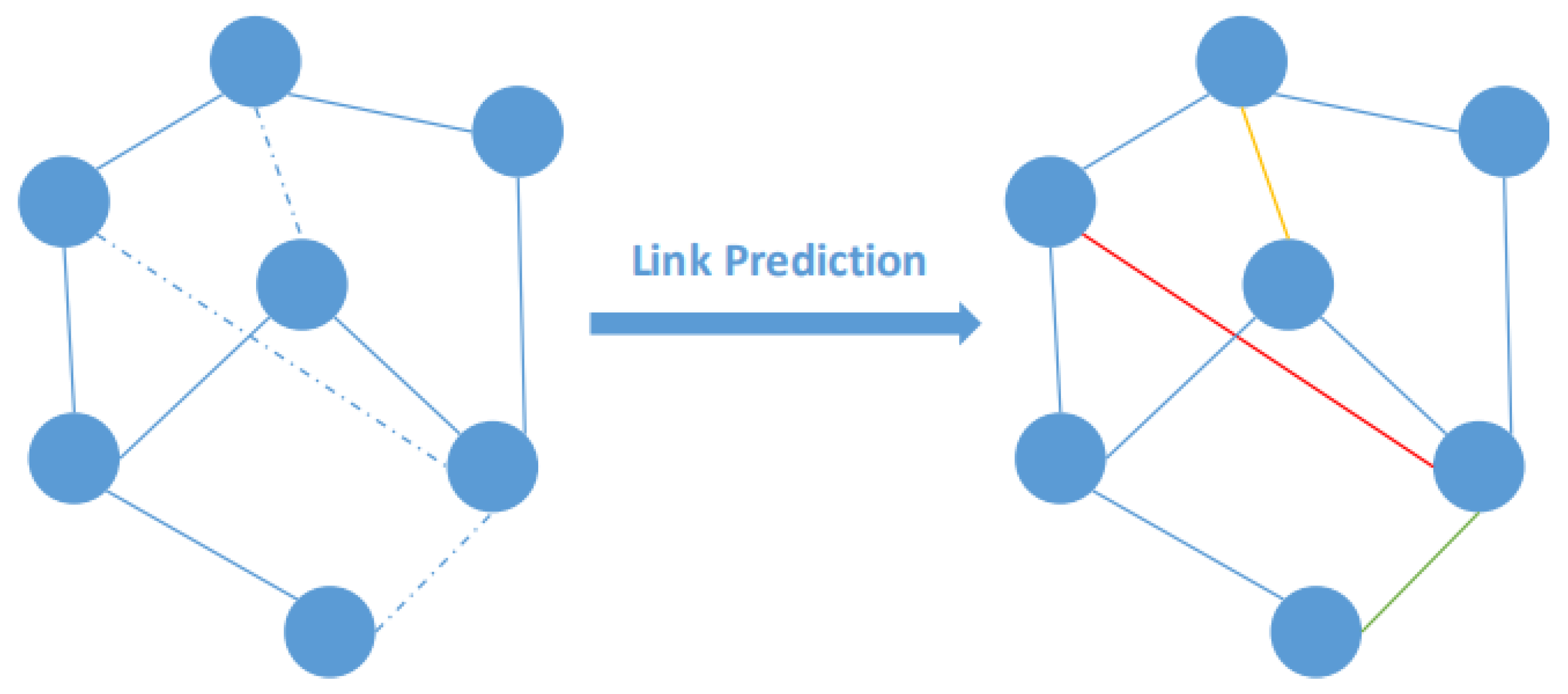
Knowledge graphs (KGs) have been widely used to store structured semantic information for tasks of artificial intelligence. Technically speaking, a knowledge graph is based on big data, which is one of the forms of big data applications. Many open KGs have been constructed, e.g., Freebase [1], DBpedia [2] and YAGO [3]. They often contain a large number of facts constructed using billions of entities and relations, which are represented as nodes and the edges linking these nodes, respectively. Each fact is represented as a triple $\left(h,r,t\right)$, where h is a head entity, t is a tail entity and r is the relation between them. KGs have been applied in many areas, such as question answering [4], recommendation systems [5] and information retrieval [6]. However, KGs have self-defects; they are always incomplete. First, existing KGs are often incomplete, as it is difficult to incorporate all the concepts that humans have [6]. Second, real-world data are often dynamic and evolving, which leads to difficulty in constructing correct and complete KGs [7]. Therefore, it is a challenging task to automatically construct a more complete KG, which is often formulated as the link-prediction problem [8]. The goal of link prediction is to predict missing information (links or relations) between the entities in KGs. Figure 1 shows an illustrated example of link prediction. The solid lines in the left figure are existing relations, and the dotted lines are possible relations. The different colors in the right figure represent various possible relations, which are calculated by the link-prediction task.

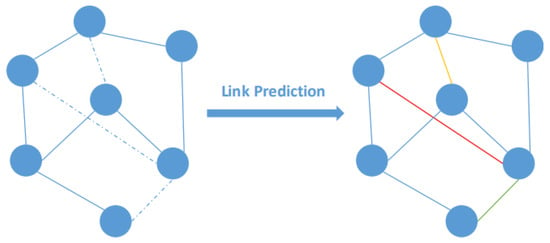
Figure 1. An example of link prediction.

To solve the link-prediction problem, various techniques have been proposed, including decomposition-based methods, path-based methods and embedding-based methods [9]. Decomposition-based models are based on potential semantic information, and their entity–relation triples are encoded in tensors [10]. They may involve many parameters, and such models may have low efficiency and poor scalability. Path-based models consider a path from a to b via a sequence of edges; the earliest models include random walks and the path-ranking algorithm (PRA) [11]. The larger the step size is, the larger the optimal solution space, but the computational complexity is higher. To address the above issues, embedding-based methods transform a KG into a low-dimensional vector space while preserving its underlying semantics [12]. Among them, knowledge graph embedding (KGE) models, which learn semantic representations of entities and relations, have significantly advanced the state of the art in the past few years [13]. Therefore, this paper focuses on a comprehensive survey of KGE models for link prediction.

KGE models embed entities and relations into a low-dimensional vector space while preserving the structure of the KG and its underlying semantic information. These models can be effectively applied to link prediction [14]. In this paper, we comprehensively survey existing KGE models and categorize them into three groups: translational-distance-based models, semantic-matching-based models and neural-network-based models. The first group is also denoted as a group of additive models, such as TransE [13], TransH [15], TransM [16] and TransR [17]. Inspired by word2vec [18], which allows word vectors to capture the semantic information of words with translation invariance, TransE [13] regards the relations in KGs as translation vectors. Given a triple $\left(h,r,t\right)$, the relation r translates the head entity h to the tail entity t. It defines a scoring function to measure the correctness of the triple in the embedding space. However, these models are reported to have low expressive power without capturing semantic information [19]. The second group of multiplicative models includes DistMult [20] and Complex [21], which can outperform the additive models by capturing more semantic information [19]. These models first embed entities and relations into a unified continuous vector space and then define a scoring function to measure its authenticity. However, these early models only consider each individual fact, while their intrinsic associations are neglected, which is not sufficient for capturing deeper semantics for better embedding. The third group are neural-network-based models, such as ConvE [22], ConvKB [23], HypER [24], CompGCN [25], SACN [26] and CNN-BiLSTM [27]. These models consider the type of entity or relation, temporal information, path information and substructure information. The use of convolutional neural networks or attention mechanisms also helps to generate better embeddings.

At present, there are many surveys of KGE models, such as [6,28,29,30,31,32,33]. They summarized, analyzed and compared the relevant KGE models from different angles, such as the models themselves, the training strategies, and the research directions. Rossi et al. [28] classified models into three categories: tensor decomposition models, geometric models and deep learning models. For these three categories, they selected typical models for detailed description, experimental result analysis and comparison. However, there is no overall classification and summary of the KGE models proposed in recent years in this paper, and the selected models are few, which cannot cover all types of KGE models. In particular, many KGE models fusing external information have been proposed in recent years, in which this information is diversified. However, this model does not better classify and summarize from the perspective of integrated information. In addition, the experiment of this survey was not reproduced in a unified environment configuration but used different coding frameworks, such as Python and C++. Dai et al. [19] described these models with two categories: triplet fact-based representation learning models and description-based representation learning models. Regarding additional information, they considered only these two aspects and also did not provide an overall table. They also conducted experiments on representative models and provided a detailed comparison, which is similar to Rossi et al. [28]’s. Ji et al. [31] divided the research on KGs into four categories: knowledge representation learning, knowledge acquisition, temporal KGs and knowledge-aware applications. We synthesized the previous surveys’ ideas; we summarize these models of KG embedding proposed over nearly three years into a classification table, which is intuitive, and we analyze the correlations among these models from a more fine-grained perspective, which involves our five main lines. In addition, our experiments on some representative models were conducted in a unified environment, including the server type and programming language (pytorch). Finally, we compare and analyze the results in detail, including the performance and training time. In this survey paper, the focus is on the analysis of different embedding approaches, and their advantages and drawbacks in handling different challenges are highlighted. Moreover, a review of the applications of representative KGE models is provided, with experiments conducted specifically on the link-prediction task. The contributions of this paper are summarized as follows:

• This paper provides a theoretical analysis and comparison of existing KGE methods for generating KG embeddings for link prediction in KGs.
• Several representative models in each category are also analyzed and compared along five main lines.
• We conducted experiments on two benchmark datasets to report comprehensive findings and provide new insights into the strengths and weaknesses of existing models. We also provide new insights into existing techniques that are beneficial for future research.

The main contents of the rest of the article are as follows: Section 2 introduces the concept of the knowledge graph and knowledge graph embedding, as well as the definition of the link-prediction task; Section 3 mainly presents the two types of categories of models and a detailed introduction on representative models; Section 4 presents the experiment and comparative analysis of representative models; Section 5 is the conclusion.

2. Preliminaries and Problem Definition

2.1. Preliminaries

In essence, knowledge graphs (KGs) are semantic networks that reveal the correlations between entities, which have the abilities of analysis and reasoning like human beings. A knowledge graph is similar to a knowledge base, describing information from different perspectives. The knowledge graph tends to consider the graph structure, while the knowledge base tends to be displayed in the textual form of reasoning and explanation [31]. Their differences and connections are shown in Figure 2 and Figure 3. Previous literature has proposed many definitions of KGs. In this paper, we cite a widely accepted definition proposed in [31], shown as Definition 1. Following previous literature, we mathematically define a KG as $G=\left(\upsilon ,\epsilon \right)$, where $\upsilon =\left\{v_1,v_2,\cdots ,v_{\left|\upsilon \right|}\right\}$ is a set of nodes (entities) and $\epsilon \subseteq \upsilon \times \upsilon$ is a set of edges (relations) [34]. An adjacency matrix $A\in R^{\left|\upsilon \right|\times \left|\upsilon \right|}$ shows where $A\left[i\right]\left[j\right]=0$ if $\left(v_i,v_j\right)\notin \epsilon$; otherwise, $A\left[i\right]\left[j\right]\in R_{+}$ represents the weight of the edge. A degree matrix $D\in R^{\left|\upsilon \right|\times \left|\upsilon \right|}$ is a diagonal matrix where $D\left[i\right]\left[i\right]={\sum }_{j=1}^{\left|\upsilon \right|}A\left[i\right]\left[j\right]$ represents the degree of $v_i$.

Figure 2. Knowledge base.

Figure 3. Knowledge graph.

A knowledge graph is composed of facts in the world, which exists in the form of triples $\left(h,r,t\right)$, with h, r and t representing the head entity, relation and tail entity, respectively. The relations in the world are plural. For example, some relations are symmetric (e.g., marriage) while others are antisymmetric (e.g., filiation); some relations are the inverse of other relations (e.g., hypernym and hyponym); and some relations may be composed by others (e.g., my mother’s husband is my father). It is critical to find ways to model and infer these patterns, i.e., symmetry/antisymmetry, inversion and composition, from observed facts in order to predict missing links [35].

In order to improve knowledge graphs, we use knowledge graph embedding (KGE) technology, which represents entities and relations as low-dimensional continuous vectors. We cite the definition of a KGE proposed in [31] as shown in Definition 2.

Definition 1 (Knowledge Graph (KG)). 

A knowledge graph is a multirelational graph composed of entities and relations that are regarded as nodes and different types of edges, respectively.

Definition 2 (Knowledge Graph Embedding (KGE)). 

Knowledge graph embedding is a technology for mapping the content of entities and relations in a knowledge graph to continuous low-dimensional vector space.

2.2. Link Prediction

Link prediction is one of the most common tasks for evaluating the performance of KGE, which has no formal definition. It has two subtasks: entity prediction, also called entity ranking, for predicting missing entities, i.e., predicting h given $\left(?,r,t\right)$ or t given $\left(h,r,?\right)$, and relation prediction for predicting missing relations, i.e., predicting r given $\left(h,?,t\right)$, where “?” represents a missing entity or relation for a triple $\left(h,r,t\right)$. For link-prediction models, the goal is to predict the missing relations among entities using the existing relations in a KG. It replaces the relation of each test triple with all the relations in the KG to obtain the negative samples. It is also defined as an entity-sorting task. Then, it determines whether the new triple, which is not observed in the KG, is valid according to the scoring function. In KGE technology, the entities are generally regarded as vectors, while the relations are regarded as operations in the vector space, which are used to calculate the relationships between entities. First, the entities and relations are mapped into a continuous low-dimensional vector space. Then, a scoring function is defined to measure the reliability of the triples, and a higher score indicates that the triple is more likely to be true. Finally, a loss function is defined to optimize the total reliability of all the triples in the KG. For evaluation, it is a common practice to record the ranks of the correct answers in such ordered lists to see whether the correct answers are ranked before the incorrect ones. The commonly used evaluation metrics in the study are the mean rank (the average of the predicted ranks), mean reciprocal rank (the average of the reciprocal ranks), and Hits@n (the proportion of ranks larger than n).

2.3. Research Questions

As described above, there are many models for KGE, but there are still many challenges in obtaining better entity and relation embeddings for link prediction. Some (but not all) of the challenges found in the survey are as follows:

• It is difficult to model the heterogeneity of graphs.
• There are few studies on dynamic graphs, which are better able to reflect the real world.
• How to incorporate prior knowledge to obtain deep semantics should be determined.
• How to capture multi-hop neighbor information should be determined.
• It has been argued that many models struggle to perform on hierarchical graphs such as WN18RR [8].

This paper focuses on the classification and comparative analysis of various models, aiming to determine the differences and breakthrough points of challenges to provide better guidance for future research.

3. Embedding Models for Link Prediction

We first performed a comprehensive investigation on the KGE models proposed in recent years. Then, we explored the three categories of KGE models for link prediction based on the investigation, including translation-distance-based models, semantic-matching-based models and neural-network-based models. These three categories reflect the mainstream models of KGE development in three main stages. The detailed models proposed in recent years and their categories are shown in Table 1. Then, we analyze how they work, and the challenges and the differences between them. Finally, in order to better study the correlations between various models (possibly cross-category models), we classify all these models from a more fine-grained perspective, proposing five main lines. The five main lines can help readers to more intuitively understand the more in-depth correlations between the models.

Table 1. Models and their categories.

Categories	Subcategories	Models
Based on translation distance	TransE and its extensions	TransE [13], TransH [15], TransM [16], TransR [17], TransD [36], TransA [37], TranSparse [38], ManifoldE [39], STransE [40], TransX-FT [41], TransX-DT [42], TransHR [43], CirE [44], GTrans [45], TransCore [46], TransF [47], TransGH [48], AEM [49], EMT [50], TransX-SYM [51], TransMS [52], KGLG [53], TransL [54].
	Gaussian embedding	KG2E [55], TransG [56].
	Others	KGE Continual Learning [57], TorusE [58], QuatE [59], RotatE [35], HAKE [60], DeCom [61], MobiusE [62], QuaR [63].
Based on semantic information	No additional information	RESCAL [64], DistMult [20], Hole [65], ComplEx [21], ANALOGY [66], ComplEx-N3 [67], TuckER [68], TriModel [69], CrossE [70], HolEx [71], MEI [72].
	Fusing additional information	Entity/relation types: TKRL [73], SSE [74], Att-Model+Types [75], ETE [76], TransT [77], Bilinear+TR [78], TransET [79], KGE via weighted score [80], RecKGC [81], RPE [82]. Relation paths: PTransE [83], Att-Model+Types [75], TransP [84], PaSKoGE [85], PTransD [86], DPTransE [87], abstract paths for KGC [88], ELPKG [9], PTranSparse [89], CoKE [90], RPE [82], RW-LMLM [91], KBAT [92], GAATs [93], path-based reasoning [27]. Textual descriptions: DKRL [94], SSP [95], KDCoE [96], CATT [97], textural association [98], pen-world extension for KGC [99], EDGE [100], TransW [101]. Logic rules: KALE [102], lppTransX [103], BiTransX+ [104], ELPKG [9], X-lc [105], RUGE [106], TARE [107], logic rule powered KGE [108], SoLE [109], GPFL [110], CBR [111], probabilistic case-based reasoning [112]. Entity attributes: KBLRN [113], TransEA [114], LiteralE [115], MARINE [116], AKRL [117]. Temporal: Time-aware link prediction [118], co-evolution of event and KGs [119], Know-Evolve [120], iTransA [121], HyTE [122], ATiSE [123], QCHyTE [124], TDG2E [125], T-GAP [126], TeMP [127]. Structure: GAKE [128], APP [129], ORC [130], KGC by embedding correlations [131], TCE(2017) [132], TCE(2018) [133], Graph2Seq [134], HRS [135], SA-KGE [136], TransS [137], S2E [138], AKSE [139], AggrE [140]. Constraints: ComplEx+NNE+AER [141], RPE [82], CoRelatE [142]. Negative sampling: TransR-PNC [143], TSLRF [144], TransE-ANS [145]. Fake triples: KGE via fake triples [146], AWML [147]. Order: RKGE [148], RW-LMLM [91]. Concepts: TransC [149], KEC [150], TransFG [151]. Background: SimplE [152], SimplE+ [153].
Based on neural network	No additional information	SME [154], NTN [155], MLP [156], NAM [157], R-GCNs [158], DSKG [159], SENN [160], TBNN [105], NTransGH [161], ConvE [22], ConvKB [23], ConnectER [162], FRS [163], HypER [24], CompGCN [25], TransGate [106], R-MeN [164], TransGCN [165], VR-GCN [166], InteractE [167], KBAT [92], BDRAN [168], BDR+CA [169], wRAN [170], RA-GCN [171], path-based reasoning [72], MultiView [172], KGEL [173], GAEAT [174], GRL [175].
	Fusing additional information	ProjE [176], ProjFE [177], ProjR [178], SACN [26], CNN-BiLSTM [27], ConMask [179], MIA Model [180], TKGE [181], a semi-supervised model for KGE [182], GAN based on Wasserstein [183], LAN [184], TransAt [185], KANE [186], context-aware temporal KGE [187], CACL [188], DKGE [189], G-DRNN [190], MTKGNN [191], LogicENN [192], TECRL [193], PATHCON [194], HARP [195].

3.1. Translation-Distance-Based Models

These models are additive models, which usually use distance-based functions to define the scoring function for link prediction. After the relation is translated, the distance is used to measure the credibility between two entities. For this category, we divide these models into three subcategories: TransE and its extensions, Gaussian embedding and others. The models of TransE and its extensions are those that extend TransE [13]. TransE [13] is one of the earliest models for link prediction, which uses the relation for translating the head entity to a tail entity. There are many extensions of TransE. The models of Gaussian embedding are those considering the uncertainties of entities and relations by using a probability function. The models of others are those similar to TransE; they do not belong to distance-based models in essence, but their idea is the same as that of TransE, such as using rotations, Lie groups, quaternions and MobiusE rings for translation.

TransE [13] is a well-known, early and simple model that regards a relation as a translation from a head entity to a tail entity. It uses a distance scoring function as follows: $f\left(h,t\right)={∥h+r-t∥}_{\frac{1}{2}}$. TransE is the earliest translation-based embedding model, and it has difficulty dealing with multirelational graphs; it is limited by its simple translation operation as well as its lack of a discrimination policy for all kinds of relations. In recent years, many variants of TransE have been proposed, such as TransH [15] and TransR [17]. TransH introduces a hyperplane, and TransR uses a relation-specific space to handle different relations, excavating more semantic information. The TransHR [43] model focuses on the embedding of hyperrelational data. These models are similar in nature; the only improvement is in translating the head entities to tail entities.

TransMS [52] regards the head entity, relation and tail entity as a subject, predicate and object, respectively, as in a sentence. In this way, it considers the semantics between the head entity and the relation as well as the semantics between the relation and the tail entity, which is not done in previous models. It uses the nonlinear function $p\left(e,r\right)$ (this is the tanh function) instead of a linear function to translate the semantics, that is, to translate both h and r to t, obtaining the final tail-entity embedding vector as $t_{\perp }=P\left(p\left(h,r\right),t\right)$ and obtaining the head-entity embedding vector from the converse semantic transfer $h_{\perp }=P\left(p\left(-t,r\right),h\right)$. In addition, it defines the bias vector $\alpha ·g\left(h,t\right)$ to transmit the semantic information of both h and t to r, where $\alpha$ is an added dimension for relations and $g\left(h,t\right)$ is a function concerning h and t, and then obtains the final relation embedding vector as $r_{\perp }=G\left(r,\partial ·g\left(h,t\right)\right)$. It chooses the tanh function as the nonlinear function $p\left(e,r\right)$, so the entity and relation embedding vectors are as Equations (1)–(3):

$$h_{\perp }=\tanh \left(-t\otimes r\right)\otimes h=-\tanh \left(t\otimes r\right)\otimes h$$

(1)

$$t_{\perp }=\tanh \left(h\otimes r\right)\otimes t$$

(2)

$$r_{\perp }=r+\partial ·\left(h\otimes t\right)$$

(3)

Finally, the score function is defined as in Equation (4):

$${∥-tanh\left(t\otimes r\right)\otimes h+r+\partial ·\left(h\otimes t\right)-tanh\left(h\otimes r\right)\otimes t∥}_2^2$$

(4)

Gaussian embedding models consider the uncertainties of entities and relations and model them as random variables. There are two models of this kind: KG2E [55] and TransG [56]. KG2E regards entities and relations as random vectors drawn from multivariate Gaussian distributions and scores a triple using the distance between the two random vectors. The TransG model also models entities with Gaussian distributions, using a mixture of Gaussian distributions to obtain multiple semantics. Gaussian embedding models take the uncertainties of the entities and relations into account, but this results in a complex model. Other methods such as TorusE [58], QuatE [59], RotatE [35] and MobiusE [62], using Lie groups, quaternions, rotations and MobiusE rings, are similar to TransE [13]. They do not belong to distance-based models in essence, but their idea is the same as that of TransE. Given a triple $\left(h,r,t\right)$, they all map the head entity h to the tail entity t through the relation r, but the specific mapping operations about r are different, so this paper puts them in this category.

RotatE [35] can model and infer various relation patterns, including symmetry (antisymmetry), inversion and composition. Specifically, it defines each relation as a rotation from the head entity to the tail entity in a complex vector space. It provides a novel self-adversarial negative-sampling technique for efficiently and effectively training RotatE. Inspired by Euler’s identity, RotatE maps the head and tail entities h and t to complex embeddings such as $\mathbf{h},\mathbf{t}\in {\mathbb{C}}^k$; then, it defines a mapping function induced by each relation r as an elementwise rotation from the head entity h to the tail entity t. For the triple $(h,r,t)$, RotatE yields $\mathbf{t}=\mathbf{h}\circ \mathbf{r},$, where $\left|r_i\right|=1$ and ∘ is the Hadamard (or elementwise) product. For each element in the embedding, we have $t_i=h_i{r}_i$. Here, this method constrains the modulus of each element of $\mathbf{r}\in {\mathbb{C}}^k,$ i.e., $r_i\in \mathbb{C}$, to be $\left|r_i\right|=1$. By doing so, $r_i$ takes the form $e^{i{\theta }_{r,i}}$, which corresponds to a counterclockwise rotation by ${\theta }_{r,i}$ radians about the origin of the complex plane and affects only the phases of the entity embeddings in the complex vector space. This is the origin of the “rotation”. The distance function of RotatE is $d_r(\mathbf{h},\mathbf{t})=\parallel \mathbf{h}\circ \mathbf{r}-\mathbf{t}\parallel$. By defining each relation as a rotation in the complex vector space, RotatE can model and infer all three types of relation patterns introduced above. It summarizes the pattern modeling and inference abilities of several models as shown in Table 2.

Table 2. The pattern modeling and reasoning ability of several models.

Model	Symmetry	Antisymmetry	Inversion	Composition
SE	✕	✕	✕	✕
TransE	✕	✓	✓	✓
TransX	✓	✓	✕	✕
DistMult	✓	✕	✕	✕
ComplEx	✓	✓	✓	✕
RotatE	✓	✓	✓	✓

HAKE [60] considers the semantic hierarchy of entities by using polar coordinates, in which concentric circles can naturally reflect the hierarchy. Additionally, it considers whether the entities are at the same level of the hierarchy, which consists of two parts, the modulus and the phase, used to distinguish the two types of entities. The modulus focuses on entities at different levels of the hierarchy; modulus information is used to model the entities as follows: $h_m\circ r_m=t_m,h_m,t_m\in R^k,r_m\in R_{+}^k$. Here, $h_m,r_m,t_m$ are the head-/tail-entity embedding and the relation embedding, and ∘ is the Hadamard (or elementwise) product. The corresponding distance function is $d_{r,m}\left(h_m,t_m\right)={∥h_m\circ r_m-t_m∥}_2$. The phase focuses on entities at the same level of the hierarchy; phase information is used to distinguish the entities as follows: $\left(h_p+r_p\right)mod2\pi =t_p,h_p,r_p,t_p\in {[0,2\pi )}^k$. Here, $h_p,r_p,t_p$ are the head-/tail-entity embedding and the relation embedding. The corresponding distance function is $d_{r,p}\left(h_p,t_p\right)={∥sin\left(\left(h_p+r_p-t_p\right)/2\right)∥}_1$. The above two parts correspond to the radial and angular parts of polar coordinates, respectively. This method maps each entity e to $\left[e_m;e_p\right]$, where $e_m,e_p$ are generated by the two parts and $\left({\left[h_m\right]}_i,{\left[h_p\right]}_i\right)$ is a 2D point in polar coordinates. The final score function is as in Equation (5):

$$\begin{array}{cc}\hfill f_r(h,t)& =d_r(h,t)=-d_{r·m}(h,t)-\lambda d_{r,p}(h,t)\hfill \\ & =-{∥h_m\circ r_m-t_m∥}_2-\lambda {∥sin\left(\left(h_p+r_p-t_p\right)/2\right)∥}_h\hfill \end{array}$$

(5)

All of these translation-based models use the margin-based pairwise ranking loss function to measure the scores of triples $\left(\mathbf{h},\mathbf{r},\mathbf{t}\right)$ as the $L_n$ distance between $\mathbf{h}+\mathbf{r}$ and $\mathbf{t}$. Therefore, the differences among these models are in how they translate a head entity $\mathbf{h}$ to a tail entity $\mathbf{t}$ by the relation $\mathbf{r}$. Their loss function is as in Equation (6):

$$\mathsf{\Lambda }=\sum _{\left(h,r,t\right)\in D}\sum _{\left(h^{{}^{\prime }},r^{{}^{\prime }},t^{{}^{\prime }}\right)\in D^{{}^{\prime }}}{\left[f_t\left(\mathbf{h},\mathbf{t}\right)+\gamma -f_r\left({\mathbf{h}}^{{}^{\prime }},{\mathbf{t}}^{{}^{\prime }}\right)\right]}_{+}$$

(6)

where ${\left[\chi \right]}_{+}$ denotes the positive value of $\chi$, and $\gamma >0$ is a margin hyperparameter. Although the embedding operation of this type of model is relatively simple, the expressiveness is not sufficient due to the direct addition of $\mathbf{h}+\mathbf{r}$ and the lack of different semantic information.

3.2. Semantic Information-Based Models

Semantic information-based models usually use similarity-based functions to define scoring functions for traditional semantic-matching models or introduce additional information to mine more knowledge for recently proposed models. Thus, these models are divided into two subcategories: models with additional information and models without additional information. The latter traditional models match the latent semantics of entities and relation embeddings to measure the plausibility of a triple. The traditional semantic-based models focus only on the information of the triple itself and do not fuse any additional information, as DistMult [20] and Complex [21] do. These models suffer from higher computational complexity. The former recently proposed models fuse various additional information to obtain better performance to mine deeper semantic information at the bottoms of graphs. The additional information includes path information, order information, concepts, entity attributes, entity types and so on.

TransW [101] uses word embeddings to compose knowledge graph embeddings and learns a function mapping from the word embedding space to the knowledge embedding space. Entities and relations are represented in the form of linear combinations of word embeddings in this model, which can detect unknown facts, as Equations (7)–(9):

$$h=\sum _{i=0}^n{h}_i\otimes w_{hi}+b_h$$

(7)

$$t=\sum _{i=0}^m{t}_i\otimes w_{ti}+b_t$$

(8)

$$r=\sum _{i=0}^p{r}_i\otimes w_{ri}+b_r$$

(9)

where $n,m,p$ are the numbers of words in entities h and t and relations r; ${\mathbf{h}}_i,{\mathbf{r}}_i,{\mathbf{t}}_i$ are the word embeddings for the i-th word in the corresponding $h,r,t$, respectively; $w{}_{hi},w{}_{ri},w{}_{ti}$ are the i-th connection vectors for $\mathbf{h},\mathbf{r},\mathbf{t}$, respectively; ⊗ denotes the Hadamard product; and $b_h,b_r,b_t\in R^k$ are the bias parameters. The score function is as in Equation (10):

$${∥\left(\sum h_i\otimes w_{hi}+b_h\right)+\sum r_i\otimes w_{ri}-\left(\sum t_i\otimes w_{ti}+b_t\right)∥}_{\frac{l_1}{2}}^2$$

(10)

The TransC [149] model combines structural information with entity concepts (referring to the categories of entities) to improve KGE models and introduces a novel type of semantic similarity to measure the distinctness of entity semantics by using the concept information. The relations in this model consist of two concept sets: the head concept set $C_r^{head}$ and tail concept set $C_r^{tail}$. The semantic similarity of a relation and a head entity and of the relation and a tail entity is used to measure the distinction of entity semantic with concept information that is defined as in Equations (11) and (12), separately:

$$sim\left(r_{head},h\right)=\frac{\left|C_r^{head}\cup C_h\right|}{\left|C_r^{head}\right|}$$

(11)

$$sim\left(r_{tail},h\right)=\frac{\left|C_r^{tail}\cup C_t\right|}{\left|C_r^{tail}\right|}$$

(12)

The semantic similarity of the head entity and tail entity is as in Equation (13):

$$sim\left(h,t\right)=\frac{\left|C_h\cup C_t\right|}{\left|C_h\right|}$$

(13)

TransC regards each entity concept as a concept vector and each entity as a set of concept vectors, and the likelihood of a vector representation for the triple $\mathrm{P}\left(fact,h,r,t\right)$ (it represents the possibility that triple $\left(h,r,t\right)$ is a fact, which means that the triple (h, r, t) satisfies the $h+r\approx t$ principle) is defined as in Equation (14):

$$\mathrm{P}\left(fact,h,r,t\right)=\sum _{i=1}^{\left|C_h\right|}\sum _{j=1}^{\left|C_t\right|}{w}_{h,i}{w}_{t,j}{f}_r\left(h_i,t_j\right)$$

(14)

where $\left|C_h\right|$, $\left|C_t\right|$ are the number of concepts of the head entity h and tail entity t; $\left\{w_{h,1},\dots ,w_{h,\left|C_h\right|}\right\},\left\{w_{t,1},\dots ,w_{t,\left|C_t\right|}\right\}$ are the distributions of random variables of h and t; and $f_r\left(h_i,t_j\right)$ is the likelihood of the component with the i-th concept vector $h_i$ of the head entity h and the j-th concept vector $t_j$ of the tail entity t. The score function is defined as follows: $f_r\left(h_i,t_j\right)={∥h_i+r-t_j∥}_l.$

PTransE [83] is a translation-based model, and it introduces contextual information by using multiple-step relation paths to extend TransE, which treats relation paths as transformations of representation learning between entities. TransE regards a relation as a translation vector of the head- and tail-entity vector. Its scoring function is defined as $E\left(h,r,t\right)=∥h+r-t∥$. PTransE integrates another score item into the triple’s score for the multiple-step relation path, given as $G\left(h,r,t\right)=E\left(h,r,t\right)+E\left(h,P,t\right)$. $E\left(h,r,t\right)$ is defined as in TransE, modeling the relations in the triple $\left(h,r,t\right)$ between entities and relations directly; $E\left(h,P,t\right)$ models multiple-step relationships between the entities and relations of each triple $\left(h,r,t\right)$ in a multiple-step path, defined as $E\left(h,P,t\right)=\frac{1}{Z}{\displaystyle \sum _{p\in P\left(h,t\right)}}R\left(p\left|h,t\right.\right)E\left(h,p,t\right)$, where ${\displaystyle \sum _{{}_{p\in P\left(h,t\right)}}}R\left(p\left|h,t\right.\right)$ is a normalized factor, for measuring the reliability of the relational path, and PTransE proposes a path-constraint resource allocation (PCRA) algorithm for it. $E\left(h,p,t\right)$ is used as a scoring function to define the triple $\left(h,r,t\right)$, differing from TransE in leveraging a semantic combinatorial model recurrent neural network (RNN) to combine the relational path p, defined as $E\left(h,p,t\right)=∥p-\left(t-h\right)∥=∥p-r∥=E\left(p,r\right)$. Moreover, PTransE considers the relation path in only one direction. To address this problem, bidirectional relations including both the forward and the inverse direction are added to the KGs, such as $e_1\underset{T}{\overset{BornInCity}{\to }}{e}_2\underset{T}{\overset{CityOfCountr{y}^{-1}}{\to }}{e}_3$ (BornInCity and CityOfCountry both represent relations, both constituting bidirectional relations. CityOfCountry is the inverse relation of BornInCity. If A is the BornInCity of B, then B is the CityOfCountry of A.). To improve the computational efficiency, the path length is limited to a maximum of three steps, and only the relationship paths with reliability scores greater than 0.01 will be selected.

Bilinear+TR [78] improves RESCAL [64] by introducing a regularization factor into the loss function, which is used to take entity types into account. In RESCAL, entities are expressed as vectors $x\in {\mathbb{R}}^d$, and relations are expressed as matrices $W\in {\mathbb{R}}^{d\times d}$. Then, the triple $(h,r,t)$ is represented as a score given by $s_c(s,r,t)=x_s^T{W}_r{x}_t$. This is similar to tensor factorization; these vectors and matrices are learned by a loss function that compares a correct triple with an incorrect triple. RESCAL uses a max-margin loss function as in Equations (15) and (16):

$$J\left(\mathsf{\Theta }\right)=\sum _{i=1}^N\sum _{t^{\prime }\in N\left(t\right)}mm\left(\sigma \left(s_{c_i}\right),\sigma \left(s_{c_i}^{\prime }\right)\right)$$

(15)

$$mm\left(\sigma \left(s_{c_i}\right),\sigma \left(s_{c_i}^{\prime }\right)\right)=max\left[0,1-\sigma \left(s_{c_i}\right)+\sigma \left(s_{c_i}^{\prime }\right)\right]$$

(16)

where there are N positive instances, and the positive and negative instances are scored as $s_{c_i}=s_c\left(s_i,r_i,t_i\right)$ and $s_{c_i}^{\prime }=s_c\left(s_i,r_i,t_i^{\prime }\right)$, respectively. $N_t$ is the set of incorrect targets, and $\sigma$ is the sigmoid function. In bilinear+TR, let $s_{cat}$ be the type of entity s and $r_{cat}$ be the relation between s and $s_{cat}$. For a query q with head entity s and tail entity t, the regularizer is defined as in Equation (17):

$$R(\mathsf{\Theta },q):=$$

$$\sum _{\genfrac{}{}{0pt}{}{s_{cat}^{\prime }\in N\left(s_{cat}\right)}{s_{cat}\in T\left(s_{cat}\right)}}\mathrm{mm}\left({\sigma }_{s_c}\left(s,r_{cat},s_{cat}\right),{\sigma }_{s_c}\left(s,r_{cat},s_{cat}^{\prime }\right)\right)$$

$$+\sum _{\genfrac{}{}{0pt}{}{t_{cat}^{\prime }\in N\left(t_{cat}\right)}{t_{cat}\in T\left(t_{cat}\right)}}\mathrm{mm}\left({\sigma }_{s_c}\left(t,r_{cat},t_{cat}\right),{\sigma }_{s_c}\left(t,r_{cat},t_{cat}^{\prime }\right)\right)$$

(17)

where $T\left(s_{cat}\right)$ and $T\left(t_{cat}\right)$ are the sets of correct categories for head s and tail t, respectively. mm is the maximum margin loss described above. Then, the complete objective function is minimized as in Equation (18):

$$J\left(\mathsf{\Theta }\right)=\sum _{i=1}^N\sum _{t_i^{\prime }\in T\left(q_i\right)}mm\left(q_i,t_i,t_i^{\prime }\right)+\alpha R\left(\mathsf{\Theta },q_i\right)$$

(18)

where the hyperparameter $\alpha$, $\alpha \ge 0$, controls the impact of the regularizer terms and $T\left(q_i\right)$ is the set of negative targets for query $q_i$, where $q_i$ corresponds to query $\left(s_i,r_i,?\right)$.

RW-LMLM is a novel approach for link prediction that consists of a random walk algorithm for KGs (RW) and a language model-based link-prediction model (LMLM). The paths output from RW are regarded as pseudosentences for LMLM training. RW can capture the semantic and syntactic information in KGs by considering the entities, relations and order information of the paths, in contrast to DeepWalk (which considers only the entities and relations). Therefore, the entities in the paths are in head-to-tail form, and the relations are in the middle, for example, $e_0\stackrel{r_0}{⟶}{e}_1\stackrel{r_1}{⟶}\cdots \stackrel{r_{l-1}}{⟶}{e}_l$. LMLM uses a multilayer transformer decoder language model instead of word2vec models (continuous bag-of-words encoders or skip-grams). The standard language model usually defines a probability distribution over a sequence of tokens: $P\left(w_1,w_2,\dots ,w_n\right)={\prod }_{i}P\left(w_i\mid w_1,\dots ,w_{i-1}\right)$. The goal of language modeling is to maximize this probability. The conditional probabilities $P\left(w_i\mid w_1,\dots ,w_{i-1}\right)$ can be learned by neural networks. The objective of RW-LMLM is to maximize the following probability as in Equation (19):

$$P\left(e_1,e_2,\dots ,e_l\right)=\prod _{i=1}^{l}P\left(e_i\mid \left(e_0,r_0\right),\dots ,\left(e_{i-1},r_{i-1}\right)\right)$$

(19)

LiteralE [115] introduces the literature information, giving priority to numerical literature. A general model with additional information adds a text-dependent merging term to the output of the scoring function to merge text indirectly. LiteralE directly incorporates literature information through a learnable parameterized function. There are two forms of triples in LiteralE: relations between entities and relations of entities and literals. This method obtains global information via the latent feature model, learning low-dimensional, latent representations, that is, embeddings. To evaluate the results, the basic dataset was extended here by adding literal information, and experiments were carried out on the basic models DistMult, ComplEx and ConvE. Except for embedding entities for transformation through a core function $g:R^H\times R^{N_d}\to R^H$, the scoring function is the same as in the basic models; that is, it transforms the entities into $e_i^{lit}=g\left(e_i,l_i\right)$. The definition of function g is critical for LiteralE. In addition to having learnability and flexibility, it should also be able to independently determine whether additional information is useful so that a judgment of whether to merge or ignore it can be made. To define g, LiteralE is inspired by the RNN gating strategy, and the gated recurrent unit (GRU) strategy is used to transform entities to ensure that the output vector and entity embedding have the same dimension. However, the model introduces a certain parameter overhead, which is proportional to the number of relationships in the KG.

Since the traditional model was put forward, semantic-matching-based models have been continuously mining deeper semantic information, including path information, entity types, contextual information and so on, to obtain more accurate representations for KGE.

3.3. Neural Network-Based Models

Neural networks have been a promising solution in many fields and have the abilities of self-study, associative storage and high-speed optimization. Traditional distance-based and semantic-matching-based models cannot meet the requirements of KGE. Recently, to obtain better and more effective entity and relation embeddings, a neural-network model was also introduced into KGE to propagate neighborhood information. These models are also divided into two subcategories: models with additional information and models without additional information. The additional information also includes path information, order information, concepts and so on.

ConvE [22] is the first model to use the convolutional neural network (CNN) framework for KG completion. Compared with fully connected neural networks, CNNs capture complex relationships with very few parameters by learning nonlinear features. ConvE uses embedded 2D convolution to predict missing links in KGs, which is the simplest multilayer convolutional network structure in these models for link prediction. Notably, 2D convolution outperforms 1D convolution in terms of extracting feature interactions between two embeddings. ConvE obtains local relationships in different dimensions between entities through a convolution layer and a fully connected layer, which ignores the global relationships between triple embeddings of the same dimension. ConvE first reshapes the head-entity embedding and relation embedding, concatenating them into an input matrix for the 2D convolution layer, which then returns a feature map tensor. Then, the tensor is vectorized and projected into k-dimensional space through a linear transformation parameterized by the matrix W and is finally matched with the tail-entity embedding through an inner product. Its scoring function is as in Equation (20):

$${\psi }_r\left(e_s,e_o\right)=f\left(vec\left(f\left(\left[\overline{e_s};\overline{r_r}\right]*w\right)\right)W\right)e_o$$

(20)

where $r_r\in R^k$ is a relation parameter depending on r, and $\overline{e_s}$ and $\overline{r_r}$ are the 2D reshapings of the head-entity embedding and relation embedding, respectively. The most important characteristic of ConvE is that the score it produces is defined by an embedded 2D convolution. Moreover, ConvE introduces a 1-N scoring program that takes a head-entity–relation pair and matches all the tail entities simultaneously, which is different from other models that use the 1-1 scoring program; thus, much evaluation time is saved.

Removing the reshaping operation from ConvE, ConvKB [23] uses 1D convolution to maintain the translation characteristics of TransE, which is sufficient for capturing the global relationships and transitional characteristics between entities. It represents the k-dimensional embedding of each triple $\left(v_h,v_r,v_t\right)$ as a three-column matrix $A=\left[v_h,v_r,v_t\right]\in R^{k\times 3}$ and then feeds it into the convolutional layer, where there are multiple filters of the same 1 × 3 shape with the ability to extract the global relationships among the same-dimensional entries of an embedding triple. These filters operate on each row of the input matrix to obtain different feature maps: $\mathbf{v}=\left[v_1,v_2,\dots ,v_k\right]\in R^k$, where $v_i=g\left(\omega ·A_{i,:}+b\right)$, $A_{i,:}\in R^{1\times 3}$ is the i-th row of A; $\omega \in R^{1\times 3}$ is the filter used to examine the global relationships between the same-dimensional entries of embedding triples and to retrieve the transitional characteristics in transition-based models; $b\in R$ represents the bias; and g is the activation function. Then, these feature maps are concatenated into a triple feature vector and calculated with a weight vector $\mathbf{w}$ via the dot product to obtain the score of the triple, which is used to determine the validation of the triple. Its scoring function is as in Equation (21):

$$f\left(h,r,t\right)=concat\left(g\left(\left[v_h,v_r,v_t\right]*\mathsf{\Omega }\right)\right)·\mathbf{w}$$

(21)

where $\mathsf{\Omega }$ is a set of filters, $\mathsf{\Omega }$ and $\mathbf{w}$ are shared parameters, * is the convolution operator, and $concat$ is the concatenation operator.

HypER [24] introduces hypernetworks based on ConvE to generate convolutional filter weights for each relation. The hypernetworks can be used to achieve weight sharing across layers and dynamically synthesize weights given inputs. The differences between HypER and ConvE are as follows: (1) ConvE uses 2D filters to construct convolution operators for the entity and relation embeddings after reshaping and concatenating, while HypER uses 1D relation-specific filters to handle entity embeddings, which simplifies the interaction between entities and relational embeddings. (2) The interaction between entities and relations in ConvE is affected by how they are reshaped and concatenated before being fed into the convolutional layers, while HypER uses a convolution operator for head-entity embeddings with a set of relation-specific filters $F_r$, which is created by hypernetwork H from the relation embeddings. The hypernetwork is a fully connected layer. (3) The feature maps obtained from ConvE and HypER by the convolution operator are all projected into a k-dimensional space and vectorized; however, the difference is that ConvE uses a linear transformation parameterized by $\mathbf{w}$, while HypER uses a weight matrix W to which the ReLU activation function is applied. (4) Finally, both methods calculate the tail-entity embeddings via the inner product to obtain a scoring vector for matching. The scoring function is as in Equation (22):

$$\begin{array}{c}{\varphi }_r\left(e_1,e_2\right)=f\left(vec\left(e_1*F_r\right)W\right)e_2=\\ f\left(vec\left(e_1*ve{c}^{-1}\left(w_{r}H\right)\right)W\right)e_2\end{array}$$

(22)

where the $vec$ operator transforms the matrix to a vector, the $ve{c}^{-1}$ operator reshapes a vector to a matrix, and the nonlinearity f is chosen to be a rectified linear unit (ReLU).

In summary, the vector embedding of each relation is projected through a fully connected layer in HypER, the result of which is reshaped, and then, a set of convolutional filter weight vector relations is provided for each layer. HypER implements nonlinear (quadratic) combinations of entity and relation embeddings rather than the linear combinations (weighted sums) in ConvE, which gives HypER the advantages of a much richer expressive capacity and fewer parameters. HypER can also be regarded as a factorization model.

Previous models introduced contextual information directly through one-way paths or text information, which ignores the important effects of various connection patterns between entities and unnecessary paths or unimportant words; this weakens the embedding of entities, resulting in the insufficient capture of the relationships between triples. R-GCN [158] utilizes a relational graph convolutional network (GCN) to model highly multiple-relational data explicitly, restoring the information of the 1-hot neighborhood facts around the entity. For link-prediction tasks, a relational graph convolutional network (R-GCN) can be regarded as an autoencoder consisting of an encoder and a decoder. The encoder generates a latent feature representation of the entity, while the decoder scores the triple according to the representation generated by the encoder. In the encoder, there is an R-GCN using the idea of a graph convolutional network, which can fully encode the structural information of the entities by considering all types of relations among the entity connections, including the in and out relations. The forward update of the entity is as in Equation (23):

$$h_i^{\left(l+1\right)}=\sigma \left(\sum _{r\in R}\sum _{j\in N_i^r}\frac{1}{c_{i,r}}{W}_r^{\left(l\right)}{h}_j^{\left(l\right)}+W_0^{\left(l\right)}{h}_i^{\left(l\right)}\right)$$

(23)

where $N_i^r$ is the set of neighbors of node i under relation $r\in R$ and $c_{i,r}$ is a problem-specific normalization constant that can be learned or set to a number in advance (such as $c_{i,r}=\left|N_i^r\right|$). In an R-GCN, a base decomposition and block diagonal decomposition are proposed to solve the problem of the height parameters. In the decoder, the DistMult factorization model is selected as the scoring function, and each relationship is associated with a diagonal matrix. Then, the scoring function of the triples is as follows: $f\left(s,r,o\right)=e_s^T{R}_r{e}_o$.

ProjE [176] complements the missing information in a KG by learning the joint embedding of the entities and edges and making modifications to the loss function, thus improving the KGE model through trivial changes to the network architecture and eliminating complex feature engineering. By means of a learned combinatorial operator, the embedding vectors of head entities and relations are combined into a target vector, which also distributes the projection of the candidate entities to obtain the order list, and the top-ranking candidates are the correct entities. Compared with TransE, ProjE saves many transformation matrix calculations because of the combination operations, which are defined as $e\oplus r=D_{e}e+D_{r}r+b_c$, where $D_e,D_r$ are diagonal matrices that serve as the global entity and relationship weights, respectively, and $b_c\in R^k$ is the combination bias. Then, the embedding projection function is defined as $h\left(e,r\right)=g\left(W^{c}f\left(e\oplus r\right)+b_p\right)$, where f and g are activation functions, $W^c\in R^{s\times k}$ is the candidate-entity matrix (s is the number of candidate entities), $b_p$ is the projection bias, and $h\left(e,r\right)$ represents the ranking score vector, whose elements measure the similarity between the candidate entity in $W^c$ and the combined input embedding $e\oplus r$. TransE defines the combination operation as addition and the similarity operation as distance. Similarly, ProjE defines the combination operation as a global linear layer and the similarity operation as a dot product. Moreover, it uses a collective ranking loss for the list of candidate entities (or relations) with two proposed methods: ProjE-pointwise and ProjE-listwise. The former uses sigmoid and tanh as the activation functions for g and f, respectively. Therefore, the ranking score is defined as $h{\left(e,r\right)}_i=sigmoid\left(W_{\left[i,:\right]}^{c}tanh\left(e\oplus r\right)+b_p\right)$, where $W_{\left[i,:\right]}^c$ represents the $i^{th}$ candidate in the candidate-entity matrix. The latter uses softmax and tanh as the activation functions, and its ranking score is defined as in Equation (24):

$$h{\left(e,r\right)}_i=\frac{exp\left(W_{\left[i,:\right]}^{c}tanh\left(e\oplus r\right)+b_p\right)}{{\sum }_{j}exp\left(W_{\left[i,:\right]}^{c}tanh\left(e\oplus r\right)+b_p\right)}$$

(24)

ProjE improves the loss function to Equation (25):

$$\mathsf{\Gamma }=-\sum _{i\in \left\{i\left|y_i=1\right.\right\}}log\left(h{\left(e,r\right)}_i\right)-\sum _m{E}_{j\sim P_y}log\left(1-h{\left(e,r\right)}_j\right)$$

(25)

where e and r are the input embedding vectors, $y\in R^s$ is a binary label vector such that $y_i=1$ means that candidate i is a positive label, and m is the number of negative samples drawn from a negative candidate distribution $E_{j\sim P_y}$.

ProjR [178] takes into account the diversity of structures and represents entities in terms of their different relational contexts and different entity locations; it combines TransR and ProjE to obtain these two representations by defining a unique combination operator for each relation. It can model N-1, N-N, 1-N-1 and one-relation circle structures with the advantage of a combination operator design. Before the similarity operator, TransR projects the representation of the head and tail entities into the relation-specific space through a relational projection matrix. ProjE projects the candidate-entity vectors into the representation space of the input entity relation pairs. Similarly, ProjR defines the scoring function in two parts: a combination operator and a similarity operator. To obtain representations of entities in different relational contexts, a combination operation $C_r\left(h\right)$ is applied to each relation r: $C_r\left(h\right)=c_{hr}=tanh\left(D_r^{e}h+D_r^{r}r+b_c\right)$, where $D_r^e\in R^{d\times d}$ is a diagonal matrix defined for the linear transformation of the head entity under relation r, $D_r^r\in R^{d\times d}$ is a diagonal matrix defined for the linear transformation of relation r, $b_c\in R^d$ is a global bias vector, and $tanh\left(z\right)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$ is a nonlinear activation function in which the output is restricted to (−1, 1). To obtain the representations of entities at different entity locations, the tail-entity vector $\mathbf{t}\in R^d$, rather than projection, is used directly for the similarity operation as $S\left(h,r,t\right)=\sigma \left(\mathbf{t}·c_{hr}\right)$, where $\sigma \left(z\right)=\frac{1}{1+e^{-z}}$ is used to restrict the final output to (0, 1) as the confidence score.

On the basis of ProjE, ProjFE [177] improves the combination operator by adding the fuzzy-membership degree, which is used to measure the degree of confidence that an entity belongs to a certain concept, to improve the performance of the model with different degrees of positive and negative samples. Because a large number of translation-matrix calculations are omitted, the model has a very small number of parameters. Unlike previous models, ProjFE uses binary vectors to represent fuzzy embeddings for projection work. ProjFE has the same combination operations as ProjE, except that it adds the fuzzy-membership degree ${\mu }_e,{\mu }_r$ for fuzzy entities and relationships, where the fuzzy-membership degree is defined as $\mu =e-{\left(\frac{x-a}{\sigma }\right)}^2,x\in \left(0,\infty \right),a=\left(a_1,a_2,...,a_n\right),a_i\in \left[0.5,1\right]$. The combination operator is defined as $\mathbf{e}\oplus \mathbf{r}={\mu }_e{D}_e\mathbf{e}+{\mu }_r{D}_r\mathbf{r}+b_c=\left(e-{\left(\frac{x_e-a}{\sigma }\right)}^2\right)D_e\mathbf{e}+\left(e-{\left(\frac{x_r-a}{\sigma }\right)}^2\right)D_r\mathbf{r}+b_c$. The scoring function of ProjFE is defined as in Equation (26):

$$S{\left(e\right)}_i=s\left({\mu }_c{D}_{c}r\left(e\oplus r\right)+b_s\right)=$$

$$sigmoid\left(\left(e-{\left(\frac{x_c-a}{\sigma }\right)}^2\right)W_{\left[i,:\right]}^{c}ReLU\left(\mathbf{e}\oplus \mathbf{r}\right)+b_s\right)$$

(26)

where $D_c$ is a candidate-entity matrix, ${\mu }_c$ is the candidate fuzzy degree, $b_s$ is the calculated bias, and $W_{\left[i,:\right]}^c$ is the matrix of the $i^{th}$ candidate entity.

Kipf et al. proposed a simple but effective hierarchical-propagation rule running directly on a graph with a neural-network model, a GCN. This is the idea of a local first-order approximation derived from spectral convolution that motivates the convolution structure. It can be scaled linearly on the edge of the graph to learn hidden layer representations for encoding the local graphical structures and features of nodes. Its hierarchical-propagation rules are as follows: $H^{\left(l+1\right)}=\sigma \left({\overline{D}}^{-\frac{1}{2}}\overline{A}{\overline{D}}^{-\frac{1}{2}}{H}^{\left(l\right)}{W}^{\left(l\right)}\right)$, where $\overline{A}=A+I_N$ is the adjacency matrix of a graph with self-connections, $I_N$ is the identity matrix, and ${\overline{D}}_{ii}={\sum }_j\overline{A_{ij}}$ and $W^{\left(l\right)}$ is a layer-specific trainable weight matrix. The GCN is a spectral method, and the convolution theorem on the graph is used to define the graph convolution in the spectral domain. Many spatial methods have been proposed, and their main idea is to define node similarity by an aggregation function in the node domain.

Weighted GCN, known as SACN [26], is an end-to-end structure-aware convolutional network that takes into account node connectivity, node attributes and relation types simultaneously. The model also defines an encoder and decoder. In the encoder part, by introducing weights for different types of relations, SACN improves the GCN model to obtain a weighted graph convolutional network (WGCN). It makes different trade-offs for different types of relations when aggregating, so the multirelational graph can be regarded as multiple single-relational graphs, where each subgraph contains a specific type of relation. The decoder, called Conv-TransE, removes the reshaping operation from the input entity and relation embeddings and lets the convolutional filters operate directly on input entities and relations in the same dimension. Thus, the translation properties of TransE remain, while the same prediction performance as ConvE is maintained. Furthermore, SACN treats entity attributes as another type of node, called attribute nodes, which have similar representations and operations as nodes. Its propagation process is defined for node $v_i$ as in Equation (27):

$$h_i^{l+1}=\sigma \left(\sum _{j\in N_i}{\alpha }_t^l{h}_j^l{W}^l+h_i^l{W}^l\right)$$

(27)

CompGCN [25] is a novel GCN that uses composition operators from KGE methods by jointly embedding both entities and relations in a relational graph. For a given entity, it considers the outgoing edges of the original, inverse and self relations simultaneously via the $\varphi$ composition operator, defined as $e_o=\varphi \left(e_s,e_r\right)$, where the $\varphi$ operator is restricted to nonparameterized operations. The updating process in CompGCN is as follows: $h_v=f\left(\sum _{\left(u,r\right)\in \mathrm{N}\left(v\right)}{W}_{\lambda \left(r\right)}\varphi \left(e_u,e_r\right)\right)$, where $e_u$ and $e_r$ are the initial features for entity u and relation r, $\mathrm{N}\left(v\right)$ is the set of immediate neighbors of v for the outgoing edges, and $w_{\lambda \left(r\right)}\in R^{d_1\times d_2}$ is a relation-type specific parameter for the original $w_O$, inverse $w_I$, and self $w_S$ relations, separately. Simultaneously, the relation embedding is transformed to $h_r=w_{rel}{z}_r$, where $w_{rel}\in R^{d_1\times d_2}$ is a transformation matrix that projects relations to the same space as entities; $z_r$ is defined as a set of learnable basis vectors as $z_r={\displaystyle \sum _{b=1}^{\mathrm{B}}}{\alpha }_{br}{v}_b$, where ${\alpha }_{br}\in R$ is the relation- and basis-specific learnable scale weight. In this paper, the $\varphi$ operator is calculated as follows, inspired by TransE, DistMult and HolE, to obtain the score:

Subtraction: $\varphi \left(e_s,e_r\right)=e_s-e_r$.

Multiplication: $\varphi \left(e_s,e_r\right)=e_s*e_r$.

Circular correlation: $\varphi \left(e_s,e_r\right)=e_s·e_r$.

CompGCN is a general GCN-based model that addresses the shortcomings of overparameterization by sharing a relation embedding calculated using basis decomposition across layers.

3.4. Connections between Typical Models

The category above is macrolevel, and there may be progressive correlations between these models of different categories. Based on the coarse-grained categories above, we made a more fine-grained category describing some representative models along five main lines. In this way, we can understand the relationships between these models in depth. These models include the representative models of the previous categories, including CNN-based models, GCN-based models, TransE extensions and so on, some of which also contain additional information.

In the first line, the introduced models are based on a CNN, as shown in Figure 4.

Figure 4. Main line 1: based on a CNN.

In the second line, the introduced models contain contextual information, as shown in Figure 5. The detailed descriptions are as follows:

Figure 5. Main line 2: contextual information.

In the third line, the introduced models all concern tensor or matrix production, as shown in Figure 6. The detailed descriptions are as follows:

Figure 6. Main line 3: tensor or matrix production.

In the fourth line, the introduced models are all based on a GCN, as shown in Figure 7. The detailed descriptions are as follows:

Figure 7. Main line 4: based on a GCN.

In the fifth line, the introduced models are all extensions of TransE, as shown in Figure 8. The detailed descriptions are as follows:

Figure 8. Main line 5: extensions of TransE.

4. Experiments

4.1. Experimental Settings

We conducted all the experiments targeting the link-prediction task in a unified environment with a T640 Dell server, the Ubuntu 16.04 system, and an NVIDIA-SMI 418.67 GPU. The implementation of these model architectures was based on the PyTorch framework. We also used the code provided in the original paper with the same settings to obtain the best results.

4.2. Dataset

We selected two datasets for our experiments, FB15k and FB15-237, which are the standard datasets commonly used in this field. FB15k is a subset of Freebase, a large-scale knowledge graph containing general knowledge facts. FB15k-237 is a subset of FB15k, where inverse relations are deleted. Therefore, these datasets could be used to evaluate the performance of the model more comprehensively. The details of these two datasets are shown in Table 3.

Table 3. Statistics of the experimental datasets.

Dataset	Entity	Relation	Triple	Train	Valid	Test
FB15k	14,951	1345	592,213	483,142	50,000	59,071
FB15k-237	14,541	237	310,116	272,115	17,535	20,466

4.3. The Implemented Models

Based on the previous categories of the existing models and the analysis of the five main lines, we selected several representative models for conducting the experiments, including CNN-based, GCN-based, semantic-matching and TransE extensions, some of which also fuse some important additional information. Therefore, these selected models are representative for gaining deep insight into the existing models, and they are conventional, recently proposed or highly cited. The implemented models are described below.

SACN [26] exploits a graph convolutional neural network and integrates relation type information as well as node attribute information, which is not limited to the traditional method of embedding based only on triple information. HypER [24] improves the ConvE model by providing a simple calculation method for sparsity and leveraging a parameter binding mechanism, which uses a hypernetwork to perform weight sharing. Bilinear+TR [78] introduces a type regularizer into the loss function, which fully considers the type information of entities. RW-LMLM [91] considers paths with three aspects of information: entities, relations and order information. It draws on the random walk algorithm and semantic-based models. LiteralE [115] introduces textual information as the attribute information of entities. SimplE [152] encodes background knowledge into an embedding by parameter sharing. It embeds relations and their inverse relations separately. HAKE [60] refers to the idea of polar coordinates, and it considers the hierarchical information of semantics. RotatE [35] replaces the traditional translation operation with a rotation operation, which can be used to distinguish various relations, such as symmetry, antisymmetry and composition. ConvE [22] is the first model to utilize the CNN framework for KG completion. It uses embedded 2D convolution to predict missing links in KGs. DistMult [20] and ComplEx [21] are traditional semantic-matching models based on tensor decomposition. ComplEx models asymmetric relations. The information on these models is summarized in Table 4.

Table 4. Implemented models.

Categories	Model	Embedding Space	Additional Information	Scoring Function
Based on	RotatE	Complex	None	$-∥h\circ r-t∥$
translation		space
distance	HAKE	Vector	None	$\begin{array}{c}{∥h_m\circ r_m-t_m∥}_2+\\ \lambda {∥sin\left(\left(h_p+r_p-t_p\right)/2\right)∥}_1\end{array}$
		space
Based on	RW-LMLM	Matrix	Order	$softmax\left(h_n^i{W}_h{W}_E^T\right)$
semantic		space	information
information	SimplE	Vector	Background	$\frac{1}{2}\left(⟨h_{e_i},v_r,t_{e_j}⟩+⟨h_{e_j},v_{r^{-1}},t_{e_i}⟩\right)$
		space	knowledge
	LiteralE	Vector	Literal	$f_X\left(g\left(e_i,l_i\right),g\left(e_j,l_j\right),r_k\right)$
		space	information
	Bilinear+TR	Tensor	Entity	$x_S^T{W}_r{x}_t$
		space	types
	ComplEx	Complex	None	$Re\left(⟨h,r,t⟩\right)$
		space
	DistMult	Vector	None	$\left(⟨h,r,t⟩\right)$
		space
Based on	SACN	Vector	Relation	$f\left(vec\left(\mathbf{M}\left(e_s,e_r\right)\right)\mathbf{W}\right)e_o$
neural		space	types
network	ConvE	Vector	None	$f\left(vec\left(f\left(\left[\overline{e_s};\overline{r_r}\right]*w\right)\right)W\right)e_o$
		space
	HypER	Vector	None	$f\left(vec\left(e_1*ve{c}^{-1}\left(w_{r}H\right)\right)W\right)e_2$
		space

4.4. Performance Analysis

As shown in Table 5, RotatE [35] and HypER [24] outperform the other models, which indicates that the rotation operation used in translational-distance models and the hypernetwork used in CNN-based models play important roles in improving performance. RotatE uses the complex space and mines different types of relations (symmetry/antisymmetry, inversion and composition); thus, different aspects of semantic information are modeled well by this integration strategy. HypER and ConvE [22] are based on a CNN; the former improves the latter by a hypernetwork, which can be used to perform weight sharing across layers and dynamically synthesize weights given inputs. RW-LMLM [91] takes into account both the order information and random walk algorithm, and it has the capability of dealing with underlying semantic information. SACN [26] also performs well among these models; it uses the relation types and entity attributes in the GCN model structure. On the whole, the top-performing models are all based on neural networks (GCNs or CNNs), from which we can conclude that the advanced neural-network structure, with its ability to generate rich and expressive feature embeddings, is helpful in the KGE task. The performance of conventional models such as translation models (TransE) and semantic models (DistMult and ComplEx) is not good. SimplEx [152] has low performance for FB15k-237 and high performance for FB15k because FB15k contains inverse relations and SimplEx can model the inverse relations appropriately. For HAKE [60], we believe that the polar coordinates may have great benefits because of their particular structure, which enables them to mine considerable hidden semantic structure information. In terms of Bilinear+TR [78] and LiteralE [115], we can see that adding the entity type, text and other information helps to improve performance.

Table 5. Results for FB15k-237 (left) and FB15k (right).

Model	FB15k-237				FB15k
	Hits@1	Hits@3	Hits@10	MRR	Hits@1	Hits@3	Hits@10	MRR
RotatE	0.2471	0.3802	0.5370	0.3432	0.7387	0.8240	0.8797	0.7905
HAKE	0.2561	0.3871	0.5488	0.3523	0.5745	0.7614	0.8482	0.6809
Bilinear+	0.1288	0.1524	0.1912	0.1503	0.1522	0.1584	0.1695	0.1604
TR-TransE
Bilinear+	0.2370	0.3549	0.4855	0.3246	0.4119	0.5683	0.6586	0.5064
TR-bilinear
DistMult	0.2129	0.3215	0.4635	0.2953	0.3055	0.4230	0.5149	0.3785
ComplEx	0.2014	0.3165	0.4526	0.2851	0.4407	0.5366	0.6168	0.5028
LiteralE+	0.2192 ↓	0.3285 ↓	0.4651 ↓	0.3013 ↓	0.2730 ↓	0.3537 ↓	0.4431 ↓	0.3323 ↓
text+DistMult
LiteralE+	0.2209	0.3279	0.4628	0.3022	0.2917 ↓	0.3820 ↓	0.4758 ↓	0.3555 ↓
DistMult
LiteralE+	0.1936 ↓	0.3029 ↓	0.4397 ↓	0.2753 ↓	0.5138	0.6102	0.6963	0.5777
ComplEx
LiteralE+	0.2092 ↓	0.3277 ↓	0.4675 ↓	0.2963 ↓	0.6055 ↓	0.7014 ↓	0.7768 ↓	0.6667 ↓
ConvE
SimplE	0.0895	0.1701	0.3170	0.1623	0.6593	0.7758	0.8434	0.7283
RW-LMLM	0.2249	0.3396	0.4859	0.3109	0.6767	0.7947	0.8648	0.7466
ConvE	0.2212	0.3371	0.4787	0.3070	0.6250	0.7254	0.7956	0.6874
SACN	0.2522	0.3699	0.5154	0.3400	-	-	-	-
HypER	0.2482	0.3629	0.5080	0.3335	0.7005	0.8167	0.8799	0.7668

As for LiteralE [115], it does not obtain only good results. For FB15k, only ComplEx obtains good results upon adding literal information, while for FB15-237, only DistMult improves slightly after adding literal information. For ConvE, a neural-network model, adding literal data does not achieve better results but worse results. LiteralE combines literal vectors (only numerical information is involved in this model) and an entity embedding as the input for training. DistMult uses a simple bilinear formula and matrix multiplication to learn embeddings. Its scoring function can only capture pairwise interactions of the same dimension between entities. Therefore, this simple embedding can only deal with symmetric relations. We suspect that this is the reason that literal information does not work. However, for FB15k-237, the result of DistMult is slightly improved due to the deletion of the inverse relationship. Because ComplEx introduces a complex vector space and can deal with asymmetric relations, it has a good response to literal information for FB15k but not FB15k-237. For ConvE, we believe that the neural-network model is able to aggregate the domain information well, so it is not sensitive to the addition of literal vectors. It performs even worse, which we guess is because of the large number of parameters from LiteralE and itself. In addition, we added textual information on the basis of numerics for LiteralE (LiteralE+text+DistMult), and the experimental results show that the performance was similarly worse. We speculate that simply adding textual information to the entity embedding of the input for training does not play a very important role. We should continuously aggregate effective domain information in the process of training and try to reduce the number of parameters. Moreover, the text information should not be only numerical information but should also include the entity type, entity attribute, path and other additional information.

Compared with traditional models, the latest models have their own advantages. Generally, they have achieved better results, benefiting from their own unique model structures and sampling technologies or adding important additional information. It is safe to conclude that the models using additional information and taking advantage of neural networks have better performance.

4.5. Training Time Analysis

Different model architectures critically affect the computational workload. Concerning the training time consumption, we analyzed these models in detail. The results obtained are consistent with the previous model description. See Table 6. Generally, the time efficiencies of the models based on neural networks are relatively low due to the introduction of more parameters.

Table 6. Training time used for FB15k.

Categories	Models	Training Time
Based on	HAKE	4.8908 h
translation distance	RotatE	6.9708 h
Based on	Bilinear+TR_bilinear	1.8083 h
semantic	Bilinear+TR_transE	1.8935 h
information	SimplE	4.4111 h
	LiteralE-ComplEx	11.1810 h
	DistMult	31.5515 h
	RW-LMLM	33.6141 h
	ComplEx	38.1560 h
	LiteralE-DistMult	42.3798 h
	LiteralE-text-DistMult	44.9654 h
Based on	HypER	8.9695 h
neural	ConvE	50.8799 h
network	LiteralE-ConvE	60.1813 h

• For CNN-based models, the initial model ConvE, which introduces numerous parameters because it uses an embedded 2D convolution, is very time-consuming for training. Similarly, for LiteralE, the introduction of additional information and its complex model structure lead to some additional parameter overhead. While HypER utilizes a 1D relation-specific filter and a nonlinear (quadratic) combination of entity and relation embeddings via hypernetworks to perform weight sharing, it has many fewer parameters than ConvE, so it saves much training time.
• Semantic matching models such as DistMult and ComplEx all suffer from longer training times.
• Translational distance models such as HAKE and RotatE all have shorter training times because the translational-distance model has a relatively simple model structure and scoring function without too many parameters.
• The bilinear+TR model has the shortest training time, with a type regularizer incorporated into the loss function, which fully considers the type information of entities. The times of the linear models are short, but their performance is not good.
• LiteralE introduces some overhead in terms of the number of parameters compared to the base method, leading to a long training time. This is due to the choice of the core function g, which takes an entity’s embedding and a literal vector as inputs and maps them to a vector of the same dimension as the entity embedding. Thus, it can make much effort in this step to choose a better function.

4.6. Suggestions for Improvement

Based on the previous model descriptions and experimental results, we can conclude that for factorization-based models, the sparsity and parameters are the key factors to be considered. It is revealed that reducing the computational complexity brought about by sparsity and conducting parameter sharing will greatly improve the overall performance. For translational-distance models, translating the head entity to the tail entity is critical for obtaining a concise and efficient scoring function. Additional efforts in the embedding space will also make a difference. Furthermore, it is nontrivial to exploit deeper semantic information and a better model structure to help improve the performance of models by using a neural network and adding additional information.

5. Conclusions

Knowledge graph embedding (KGE), as the technology of embedding entities and relations into a low-dimensional continuous vector space, has made remarkable progress in offering precise, effective and structural representation of information in many fields. This paper reviewed the main technologies of KGE, categorized the existing models into two types based on whether or not they use additional information besides facts, and then overviewed the advantages and disadvantages of representative models in each category. We focused on the task of link prediction and carried out experiments on several typical models in a unified environment. Through the analysis of the experimental results, we found that different model architectures enjoyed unique advantages in different facets. According to our research on KGE models and the analysis and comparison of the experimental results, we can roughly summarize two points about how to improve the performance of KGE models, as follows:

• Neural network models with excellent structure and a small number of parameters have good performance. Especially, the graph convolution neural network has a strong ability to mine the underlying semantics of knowledge graphs. In addition, if the node information of a multi-hop domain can be aggregated, the accuracy of the model in specific tasks can be greatly improved.
• Models with additional information, such as node attributes, node types, relationship types, prior knowledge and so on, have better performance.

We hope that this survey can provide researchers with new insights and a stepping stone to help them conduct research better. Of course, there are some limitations in our survey. Due to space constraints, we will conduct in-depth research into the following aspects in future research:

• This survey only focused on the link prediction of KGE; we will research more tasks of knowledge graph completion in the future, such as entity prediction, entity classification and triple classification.
• This survey only used two datasets (FB15k and FB15k-237) for the experiments; we will use more knowledge graph datasets, such as WN18, WN18RR and FB13.
• This survey only focused on static graphs; we will explore new model architectures, such as dynamic graphs and heterogeneous graphs.
• The categories we proposed for KGE models may not be the perfect ones; we will attempt to mine new category strategies for KGE models.