Abstract
The framework of this paper is intertemporal choice, which traditionally has been studied with preference relations and discount functions. However, the interest of econophysics in this topic makes time become a central magnitude. Therefore, the aim of this paper is to introduce the concept of delay function and, by using this tool, to analyze the concept of impatience and the different types of inconsistency. In behavioral finance, consistency is correlated with the concept of symmetry because, in this case, the indifference between two rewards does not change when the same delay is added to their respective availability dates. Moreover, we have shown the way to derive a discount (respectively, delay) function starting from the expression of its corresponding delay (respectively, discount) function by requiring some suitable conditions for this construction. Finally, we have deduced the concept of instantaneous variation rate and Prelec’s measure of inconsistency in terms of the delay function.
Keywords:
econophysics; intertemporal choice; delay function; inconsistency; increasing impatience; moderately decreasing impatience; strongly decreasing impatience JEL Classification:
C91; D81; D99
1. Introduction
Intertemporal choice involves making decisions between several alternatives whose monetary amounts take place at different instants of time. From the point of view of economics, Samuelson [1] carried out the first study on intertemporal choice when introducing the so-called Discounted Utility (DU) model. However, the latest studies in the field of behavioral economics, econophysics, and neuroeconomics have revealed several limitations of the DU model.
In effect, among the former disciplines, econophysics is achieving a great relevance due to the high number of techniques from physics which are being applied to economics: theoretical macroeconomics (wealth distributions), microstructure of financial markets (order book modeling), econometrics of financial bubbles and crashes, etc. [2]. More specifically, within this wide field of research, physics has been applied to finance (returns of financial assets—fat tails, volatility clustering, autocorrelation, etc.) [3,4]. However, in this paper we are interested in the description of intertemporal choice from the perspective of “time” (see, e.g., the work by Zauberman [5,6,7]) which is the main instrumental variable in econophysics. In effect, one of the main concepts of intertemporal choice is discount function which is present in several physical processes characterized by the loss of properties of a given system. For example, the reduction through time of temperature in a system or the decrease of individuals in an organism can be described in the same way as the loss of acquisitive power suffered by a monetary unit (i.e., temporal discounting).
In this context, Cajueiro [8] demonstrated that the q-exponential function, present in the deformed algebra inspired in the Tsallis’ nonextensive thermodynamics, could be used to model discount functions in intertemporal choices. The introduction of this discount function is justified when analyzing some situations of decreasing impatience which lead to the phenomenon of dynamic inconsistency.
In effect, the impatience has been defined by Takahashi [9] as a strong preference for small, immediate rewards over large, delayed ones. In the study of this concept, many researchers have shown that subjects discount delayed losses less fast than they do delayed gains [10,11]. These results were completed with further analysis based on the asymmetry observed in making decisions of discounting tasks about gains and losses [12,13]. Specifically, clinical studies have been conducted with magnetic resonance imaging which are consistent with the idea that an asymmetric activity pattern underlies the process of discounting future gains and future losses [14].
However, it is also important to take into account the situations in which the subject changes his/her initial decision when the reward is delayed over the time, that is to say, people may exhibit inconsistency when making intertemporal choices.
The main measure of inconsistency was given by Prelec [15] who considered that the degree of decreasing impatience was represented by the convexity of the Napierian logarithm of the discount function. The drawback of this index is the difficulty in measuring it, whereby Rohde [16,17], starting from an indifference pair, defined the so-called hyperbolic which allows us to distinguish between strongly and moderately decreasing impatience. Anchugina et al. [18] extended the Prelec’s result from the mixture of two functions to a finite number of DI functions.
On the other hand, in the Multifractal Model of Asset Returns (MMAR), introduced by Mandelbrot [19], the multifractality of returns results from a deformation of time [20] because the so-called business time is dictated by the density of transactions. In the same way, the magnitude “time” in intertemporal choice has been deformed to explain certain variations of impatience (inconsistency). For example, Cajueiro [8] and Takahashi [21] deformed time in the hyperbolic discount function, giving rise to the aforementioned q-exponential discounting. Several analyses in econophysics have shown the relation between the roles of psychophysical effects of time perception and the anomalies in intertemporal choice. In effect, [22] introduces a discussion of the current influence of time perception on intertemporal choice by exploring different representations. In particular, Lu and Li [23] study the psychophysics presented in the consumer’s preferences. On the other hand, recent studies by Takahashi et al. [24] used Tsallis’ statistics-based econophysics to show that the q-exponential discount function may continuously parameterize a subject’s consistency in intertemporal choice. This result was generalized by Cruz and Muñoz [25] to any discount function, based on the deformed algebra developed in the Tsallis’ nonextensive thermostatistics. Later, Cruz and Ventre [26] and Cruz et al. [27] deformed time by means of the Steven’s “power” law in a subadditive discount function in order to obtain S-inverse curves. In this context, Webb [28] provides a novel model to study the inverse-S discounting behavior. Indeed, the analysis of time with delay functions will help us to better understand those mechanisms of intertemporal choice centered on time such as deformation of time or several types of decreasing impatience.
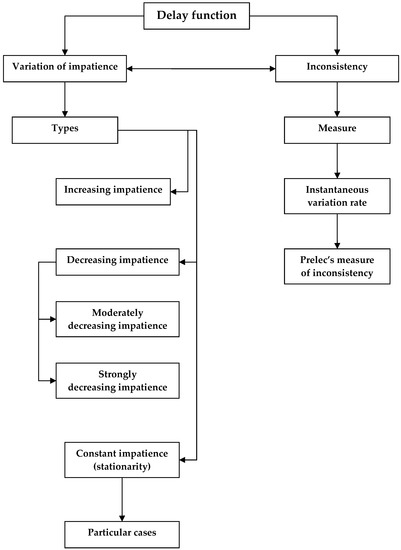
This paper is organized as follows. In the current section we have contextualized the topic of inconsistency within the fields of econophysics and intertemporal choice. In Section 2, the concept of impatience and the different types of inconsistency are analyzed starting from the concept of delay function. In Section 3, we show the way to derive a discount (respectively, delay) function starting from the expression of its corresponding delay (respectively, discount) function by requiring some suitable conditions for this construction. In Section 4, we use the concept of delay function to derive the so-called instantaneous variation rate and Prelec’s index. Next, in Section 5 we introduce a set of characterizations of the different types of impatience starting from the definition of delay function. Finally, Section 6 summarizes and concludes.
2. The Delay Function
The aim of this paper is to analyze the concept of impatience and the different types of inconsistency by using the so-called delay function which will be defined in this section. Therefore, the delay function becomes a new element for the mathematical treatment of intertemporal choice. Consequently, it is necessary to derive the expression of the discount function underlying to the intertemporal choice process, starting from the concept of delay function and vice versa. Additionally, it is well known that preferences can be embedded in this framework. In this way, several scholars have paid attention to the different mathematical conditions to be satisfied by these preference relations (for a summary, see the paper by Baucells and Heukamp [29]). Consequently, intertemporal choice can be viewed from three different perspectives.
In effect, intertemporal choice can be treated by means of discount functions or, alternatively, with preference relations. However, as shown by Figure 1, intertemporal choice can also be related to delay functions by arising the need for the development of some procedures to generate both discount and delay functions starting from a preference relation (steps (1) and (2)) and a delay from a discount function, and vice versa (step (3)).
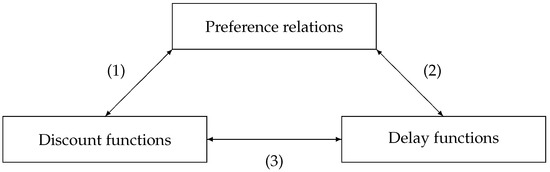
Figure 1.
Relationship among different concepts of intertemporal choice. Source: own elaboration.
The economic literature on the first step is very prolific, the most famous representation theorem being due to Fishburn and Rubinstein [30]: if order, monotonicity, continuity, impatience, and separability hold, and the set of rewards X is an interval, then there are continuous real-valued functions u on X and F on the time interval T such that
Additionally, and u is increasing, whilst F is decreasing and positive.
In what follows, we are going to introduce the concept of delay function [31]. Let s be a small reward and l a large reward. A delay function, denoted by , gives the delay which makes the subject indifferent between the amount s at each time t and the amount l at time (see Figure 2), viz:
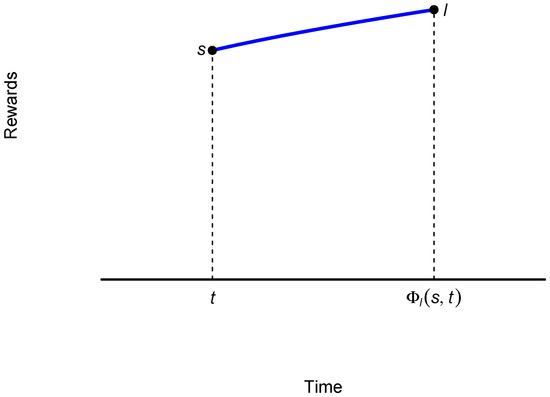
Figure 2.
Plotting a delay function. Source: own elaboration.
More formally, let be the set of rewards and be the set of times corresponding to the dated rewards involved in an intertemporal choice process.
Definition 1.
If , a delay function or a time compensation function is a continuous map
such that
denoted by , satisfying the indifference relation .
A delay function expresses the time point at which a reward equals a certain lower reward.
Example 1.
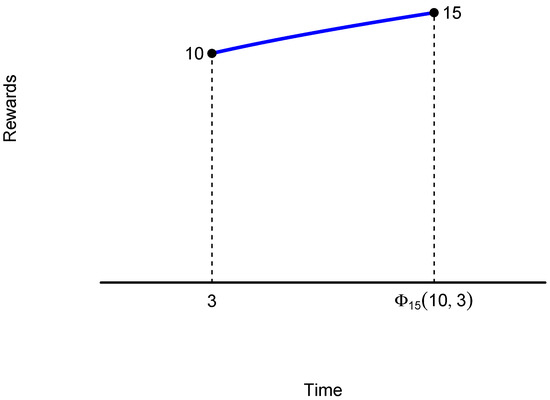

Figure 3.
Plotting the indifference relation of Example 1. Source: own elaboration.
The following paragraph continues with Definition 1. In order to make financial sense, a delay function must satisfy the following conditions:
- (i)
- (in particular, ).
- (ii)
- is strictly increasing with respect to t.
- (iii)
- is strictly increasing with respect to l.
- (iv)
- is strictly decreasing with respect to s.
Observe that the conditions (i) and (ii) guarantee that, if , then . Takeuchi [32] instead introduces the so-called equivalent delay function
such that
Observe that this last definition is more limited than Definition 1 since, in an equivalent delay function, always . A delay function allows to characterize the concepts of decreasing and increasing impatience (see Section 5). Before this, in Section 3 and Section 4, we are going to develop the step (3) of Figure 1. Firstly however, we need to introduce the following definition.
Definition 2.
A discount function is a continuous map
such that
satisfying the following conditions:
- (i)
- , for every .
- (ii)
- , for every .
- (iii)
- is strictly decreasing with respect to z.
- (iv)
- is strictly increasing with respect to m.
In particular, if , we will say that F is separable. Obviously, in this case, condition (iv) of Definition 2 is not necessary. The discount function indicates the present value of a reward available at a certain time point.
3. Discount and Delay Functions
The aim of this section is to derive a discount (respectively, delay) function starting from the expression of its corresponding delay (respectively, discount) function by previously requiring some suitable conditions for these constructions.
3.1. Discount from Delay Functions
In this subsection, we are going to introduce the methodology to derive discount functions starting from delay functions. Let be a delay function and define . Suppose that, for every , the partial delay function
such that
is surjective. Observe that, moreover, this function is bijective since, by condition (iii) of Definition 1, is injective. In this case, we define
such that
and
Remark 1.
Observe that, by Definition 1, Equation (2) can be written as which is the intuitive idea underlying the concept of discount function.
On the other hand, Equation (2) can be rewritten as follows:
Now, we can enunciate the following proposition.
Proposition 1.
Function F, defined as , is a discount function.
Proof.
Firstly, let us see that F is well defined. In effect, for every , the partial delay function is bijective (see the beginning of Section 3.1) whereby its reciprocal, , is also a bijective function.
Secondly, let us show that the four conditions of Definition 2 hold:
- (i)
- (ii)
- This condition is Equation (1): For every ,
- (iii)
- Assume . By condition (iv) of Definition 1, is strictly decreasing with respect to z and thenand, by Equation (3),Consequently, is strictly decreasing with respect to z.
- (iv)
- Assume . By condition (iii) of Definition 1, is strictly increasing with respect to m and thenand, by Equation (3),Consequently, is strictly increasing with respect to m.
This completes the proof of this proposition. □
Example 2.
Let us consider the following delay function
where . One may easily check that the four conditions of Definition 1 hold. In this case, we can obtain the discount function defined by
and
In effect, we can write:
where we obtain
Example 3.
Let us consider the following delay function
One may easily check that the four conditions of Definition 1 hold. In this case, we can obtain the discount function defined by
and
In effect, we can write:
where we obtain
Once we have deduced how to obtain a discount function starting from its corresponding delay function, we will then introduce the characterization of the indifference of rewards by using a delay function and also the particular case in which the discount function is separable. In effect, the indifference of rewards can be characterized by the following proposition.
Proposition 2.
The rewards and are indifferent if, and only if, the following equation holds:
where ∘ is the composition of functions.
Proof.
As ,
which completes the proof. □
Therefore, we have shown that the indifference of rewards is characterized by the delay function.
Remark 2.
Observe that expression (4) is consistent since . Moreover, observe that, given two amounts x and y, the indifference must be restricted to those times r such that the delay function can be decomposed as the composition of the reciprocal of and , applied to time r.
Example 4.
With the delay function of Example 2, one has
One may easily show that
Therefore,
Definition 3.
A delay function Φ is said to be linear if, for every and every ,
Proposition 3.
A delay function Φ is linear if, and only if, its corresponding discount function F is separable.
Proof.
In effect, for every ,
If is linear, then
or
and, consequently, as and is bijective, one has
where . From this, the discount function is separable. □
Corollary 1.
If the delay function Φ is linear, then if, and only if, .
Proof.
In this case, by Equation (2), one has
and so
where we obtain
which is the expression of the well-known discount ratio for separable discount functions. □
Example 5.
The delay function of Example 3 satisfies the condition of linearity. Obviously, in this case, implies and then
3.2. Delay from Discount Functions
Before presenting the methodology to obtain a delay function starting from the expression of its corresponding discount functions, we are going to introduce the following concepts of regular and singular discount functions, which are necessary to develop this subsection.
Definition 4.
A discount function F is said to be regular if, for every , —that is to say, if . Contrarily, a discount function F is said to be singular if
Given a regular discount function
and given and l, with , is defined such that (see Figure 4)
from which we obtain
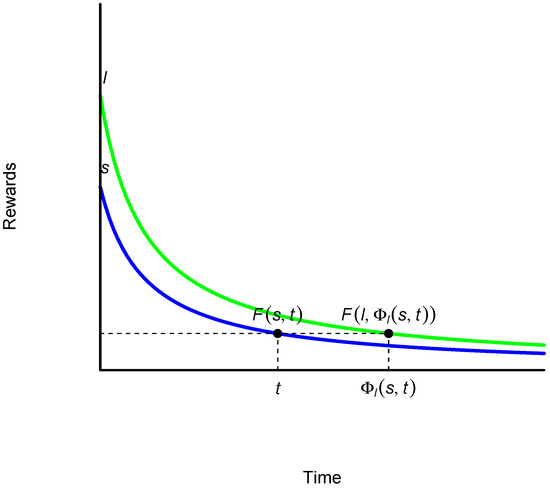
Figure 4.
Case of a regular discount function. Source: own elaboration.
In the particular case in which F is separable, can be obtained as follows:
Remark 3.
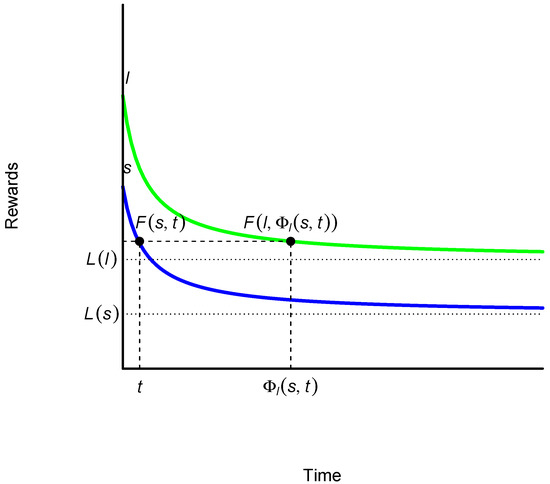
Observe that, if F is singular,
and
Obviously, (see the two dotted horizontal lines in Figure 5). In this case, the procedure described in Definition 4 is only possible for those values of t such that

Figure 5.
Case of a singular discount function. Source: own elaboration.
The question arising now is whether the delay function corresponding to a discount function—which comes from a delay function—is the starting delay function. The answer is affirmative since, given a delay function , its associated discount function is given by
In order to determine the delay function corresponding to the just-obtained discount function, we start from the indifference and then
4. Measures of Inconsistency with Delay Functions
4.1. The Instantaneous Variation Rate
In this section, we are going to derive the expression of the so-called instantaneous variation rate corresponding to the interval , denoted as , by using delay functions. This parameter is a measure of inconsistency introduced by Cruz and Muñoz [33] based exclusively on time. But before, we are going to introduce some comments to relate the instrumental variables used here with physics. In finance, the force of discounting is measured by the instantaneous discount rate, given by
Observe that the discount rate is the derivative of the Napierian logarithm of the discount function because, in finance, we are interested in relative magnitudes. In effect, take into account that can be written as
On the other hand, the acceleration of discounting necessarily involves the derivative of which leads to, among other measures, the degree of convexity by Prelec.
Observe that all aforementioned physical and financial processes describe the temporal evolution of a system. Figure 6 schematizes the content of Section 4 and Section 5 of this paper.
In effect, consider the indifference relation:
where and, consequently, . If the availability of the reward s is delayed until moment , with , the delay now satisfies the following indifference relation:
If the discount function underlying the intertemporal choice is separable, the first indifference
can be written as
The same reasoning can be applied to the second indifference
resulting in
Then,
Successive algebraic operations lead to
and
where we obtain
Letting (which, by continuity, implies ):
or, equivalently,
The left-hand side of Equation (7) represents the instantaneous variation rate, denoted by . Thus, Equation (7) can be written as
Observe that v depends on l, s, and t. However, it is easy to demonstrate that v is only a function of t and , as stated at the beginning of this subsection. In effect, take into account that, in case of separability, the following equality holds:
4.2. Prelec’s Measure of Inconsistency
In this subsection, we are going to derive the expression of Prelec’s measure of inconsistency by using delay functions. In effect, Equation (7) can be written as
By subtracting 1 to both sides of Equation (9), one has
As , then and so Equation (10) can be written as
By dividing both sides of Equation (11) by , one has
Letting , the left-hand side of Equation (12) is
Observe that the left-hand side of Equation (13) is Prelec’s measure of inconsistency, denoted by . Consequently, this parameter can be written as a function of the delay function as follows:
Example 6.
Let us consider the hyperbolic discount function
where . In this case, the delay function is
Simple calculations lead to
- .
- .
- .
Finally, if the discount function is separable, the following equality holds:
Therefore,
- .
- .
- .
Example 7.
Let us consider the discount function
In this case,
Simple calculations lead to
- .
- .
- .
- .
5. Types of Impatience with Delay Functions
In this section, we are going to characterize the different types of impatience. More specifically, the concepts of strongly and moderately decreasing and increasing impatience will be defined by using the concept of delay function. To do this, let us start from an arbitrary indifference pair [34]:
and
where , , , and . Recall that the different types of impatience can be defined in the following way:
- Decreasing impatience holds if .
- Increasing impatience holds if .
- Constant impatience (stationarity) holds if .
By applying Definition 1, one has
As
then . On the other hand,
As
then holds. Therefore, the different types of impatience can be described by using the notation provided by the delay function:
- (i)
- Decreasing impatience holds if . In this case,So,
- -
- More specifically, moderately decreasing impatience holds if also . Simple algebra shows that this condition is equivalent to
- -
- On the other hand, strongly decreasing impatience holds if also . Now, this condition is equivalent to
- (ii)
- Increasing impatience holds if
- (iii)
- Finally, constant impatience (stationarity) holds if
5.1. Characterizing Constant, Decreasing, and Increasing Impatience
Throughout this section, we are going to introduce different results which relate the different types of impatience to the involved delay function implicit in the process of intertemporal choice. Firstly, delay functions satisfying constant impatience or stationarity are the solutions of the following functional equation:
where . The general solution of the functional Equation (15) is
where necessarily satisfies the following conditions:
- .
- is strictly increasing with respect to l.
- is strictly decreasing with respect to s.
In summary, given two rewards s and l (), a delay function satisfying constant impatience or stationarity (15) can be expressed as
where satisfies the former three conditions. Therefore, the indifference relation remains as
Now, we are going to demonstrate that function (16) satisfies the conditions required to be considered a delay function:
- , since .
- is strictly increasing with respect to t, since obviously implies
- is strictly increasing with respect to l, since impliesand so .
- is strictly decreasing with respect to s, since impliesand so .
Example 8.
Let us consider the following discount function [35]:
and the indifference relation:
So,
where we obtain
If , then we can write
and, consequently, is stationary.
Finally, making in Equation (16), then and, therefore, the expression of a stationary discount function can be derived:
5.2. Particular Cases
In this subsection, we are going to show that, depending on the shape of , it is possible to generate different patterns of delay functions starting from a strictly increasing function. In effect, if g is a strictly increasing function, the following specific cases can be considered to generate delay functions:
- , where we obtain . In this case, if , thenwhere we obtainand, therefore,which is stationary.
- Another way to generate delay functions is by consideringwhere we obtainIf , thenwhere we obtainand, therefore,which is stationary.
- Another way to generate delay functions iswhere f is an increasing function. In this case,and then,where finally
Example 9.
Let us consider the delay function
where
and
Therefore,
and the discount function corresponding to this delay function is
5.3. Characterizing Strongly and Moderately Decreasing Impatience
According to Theorem 1 in [36], an individual exhibits strongly decreasing impatience if, and only if, for every , and , implies . By applying the definition of delay function to the indifference, one has
Moreover, the preference can be written as follows:
and, consequently,
Now, we are going to analyze a specific delay function exhibiting strongly decreasing impatience. To do this, let denote the general solution of the functional equation:
In this case, it can be shown that
where necessarily must satisfy the following conditions:
- .
- is strictly increasing with respect to l.
- is strictly decreasing with respect to s.
Therefore, given two rewards l and s (), a specific delay function reflecting strongly decreasing is
Now, we are going to analyze the discount functions exhibiting moderately decreasing impatience. In effect, according to Corollary 1 in [36], an individual exhibits moderately decreasing impatience if, and only if, for every , , and , implies but . By applying the definition of delay function to the indifference, one has
Moreover, the preferences can be written as follows:
and
Therefore,
and
6. Conclusions
This paper analyzed the concept of impatience and the different types of inconsistency from the point of view of a delay function. It is well known that intertemporal choice can be treated by means of discount functions or, alternatively, with preference relations, but in this paper, we derived the expression of the discount function, underlying the process of intertemporal choice, starting from the concept of delay function. To do this, given a dated reward and an amount l (), a delay function assigns a time, denoted by , such that .
Firstly, with this novel methodology, we showed the way to derive the discount function associated to a given delay function satisfying some suitable conditions. This discount function is defined such that and is given by Equation (3). It was demonstrated that satisfies the conditions to be a discount function. As a consequence of this result, we characterized the indifference between rewards by using the delay function.
Secondly, we obtained the delay function corresponding to a discount function by considering the definitions of regular and singular discount functions. In effect, the delay function derived from a discount function is defined by Equation (6). We demonstrated that the delay function coming from a discount function, which also derives from a delay function, is the original delay function.
Thirdly, we derived the expression of the so-called instantaneous variation rate and then the measure of inconsistency by Prelec, using the delay function associated to the process of intertemporal choice.
Once we displayed the existing relationship between delay and discount functions, we introduced some characterizations of the different types of inconsistency (increasing impatience, and moderately and strongly decreasing impatience) starting from the concept of delay function. Finally, different methodologies to generate delay functions were proposed as a first step to continue the implementation of delay functions in modeling intertemporal choice from an empirical point of view. Obviously, this work will be left for further research.
Author Contributions
Conceptualization, S.C.R.; methodology, I.G.F.; formal analysis, I.G.F.; investigation, S.C.R.; resources, S.C.R.; writing—original draft preparation, S.C.R.; writing—review and editing, I.G.F.; supervision, I.G.F.; funding acquisition, S.C.R. All authors have read and agreed to the published version of the manuscript.
Funding
The author gratefully acknowledges financial support from the Spanish Ministry of Economy and Competitiveness [National R&D Project “La sostenibilidad del Sistema Nacional de Salud: reformas, estrategias y propuestas”, reference: DER2016-76053-R].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Samuelson, P.A. A note on measurement of utility. Rev. Econ. Stud. 1937, 4, 155–161. [Google Scholar] [CrossRef]
- Chakraborti, A.; Muni Toke, I.; Patriarca, M.; Abergel, F. Econophysics review 1: Empirical facts. Quant. Financ. 2011, 11, 991–1012. [Google Scholar] [CrossRef]
- Chakraborti, A.; Muni Toke, I.; Patriarca, M.; Abergel, F. Econophysics review 2: Agent-based models. Quant. Financ. 2011, 11, 1013–1041. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Stanley, H.E. Introduction to Econophysics: Correlations and Complexity in Finance; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Zauberman, G. The intertemporal dynamics of consumer lock-in. J. Consum. Res. 2003, 30, 405–419. [Google Scholar] [CrossRef]
- Kim, B.K.; Zauberman, G. Perception of anticipatory time in temporal discounting. J. Neurosci. Psychol. Econ. 2009, 2, 91–101. [Google Scholar] [CrossRef]
- Zauberman, G.; Kim, B.K.; Malkoc, S.A.; Bettman, J.R. Discounting time and time discounting: Subjective time perception and intertemporal preferences. J. Mark. Res. 2009, 46, 543–556. [Google Scholar] [CrossRef]
- Cajueiro, D. A note on the relevance of the q-exponential function in the context of intertemporal choices. Phys. A Stat. Mech. Appl. 2006, 364, 385–388. [Google Scholar] [CrossRef]
- Takahashi, T.; Han, R.; Nakamura, F. Time discounting: Psychophysics of intertemporal and probabilistic choices. J. Behav. Econ. Financ. 2012, 5, 10–14. [Google Scholar] [CrossRef][Green Version]
- Loewenstein, G. Anticipation and the valuation of delayed consumption. Econ. J. 1987, 97, 666–684. [Google Scholar] [CrossRef]
- Read, D. Intertemporal choice. In Blackwell Handbook of Judgment and Decision Making; Koehler, D., Harvey, N., Eds.; Blackwell: Oxford, UK, 2004; pp. 424–443. [Google Scholar]
- Baker, F.; Johnson, M.W.; Bickel, W.K. Delay discounting in current and never-before cigarette smokers: Similarities and differences across commodity, sign, and magnitude. J. Abnorm. Psychol. 2003, 112, 382–392. [Google Scholar] [CrossRef]
- Thaler, R. Some empirical evidence on dynamic inconsistency. Econ. Lett. 1981, 8, 201–207. [Google Scholar] [CrossRef]
- Xu, L.; Liang, Z.Y.; Wang, K.; Li, S.; Jiang, T. Neural mechanism of intertemporal choice: From discounting future gains to future losses. Brain Res. 2009, 1261, 65–74. [Google Scholar] [CrossRef]
- Prelec, D. Decreasing impatience: A criterion for non-stationary time preference and hyperbolic discounting. Scand. J. Econ. 2004, 106, 511–532. [Google Scholar] [CrossRef]
- Rohde, K.I.M. The hyperbolic factor: A measure of time inconsistency. J. Risk Uncertain. 2010, 41, 125–140. [Google Scholar] [CrossRef]
- Rohde, K.I.M. An Index to Measure Decreasing Impatience. In Proceedings of the 2015 Risk, Uncertainty and Decision Conference, Milano, Italy, 1–3 June 2015. [Google Scholar]
- Anchugina, N.; Ryan, M.; Slinkoc, A. Mixing discount functions: Implications for collective time preferences. Math. Soc. Sci. 2019, 102, 1–14. [Google Scholar] [CrossRef]
- Mandelbrot, B.; Fisher, A.; Calvet, L. A Multifractal Model of Asset Returns; Cowles Foundation Discussion Paper #1164; Yale University: New Haven, CT, USA, 1997. [Google Scholar]
- Slanina, F. Essentials of Econophysics Modelling; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Takahashi, T. A comparison of intertemporal choices for oneself versus someone else based on Tsallis’ statistics. Phys. A Stat. Mech. Appl. 2007, 385, 637–644. [Google Scholar] [CrossRef]
- Jin, S. The influence of time perception on intertemporal preference and its psychological mechanism. Open J. Soc. Sci. 2020, 8, 236–249. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Y. Psychophysics of consumer’s sequence preference of e-commerce loan repayments. J. Phys. Conf. Ser. 2019, 1302, 042025. [Google Scholar] [CrossRef]
- Takahashi, T.; Oono, H.; Radford, M. Empirical estimation of consistency parameter in intertemporal choice based on Tsallis’ statistics. Phys. A Stat. Mech. Appl. 2007, 381, 338–342. [Google Scholar] [CrossRef]
- Cruz Rambaud, S.; Muñoz Torrecillas, M.J. A generalization of the q-exponential discounting function. Phys. A Stat. Mech. Appl. 2013, 392, 3045–3050. [Google Scholar] [CrossRef]
- Cruz Rambaud, S.; Ventre, V. Deforming time in a nonadditive discount function. Int. J. Intell. Syst. 2017, 32, 467–480. [Google Scholar] [CrossRef]
- Cruz Rambaud, S.; González Fernández, I.; Ventre, V. Modeling the inconsistency in intertemporal choice: The generalized Weibull discount function and its extension. Ann. Financ. 2018, 14, 415–426. [Google Scholar] [CrossRef]
- Webb, C.S. Trichotomic discounted utility. Theory Decis. 2019, 87, 321–339. [Google Scholar] [CrossRef]
- Baucells, M.; Heukamp, F.H. Probability and time trade-off. Manag. Sci. 2012, 58, 831–842. [Google Scholar] [CrossRef]
- Fishburn, P.C.; Rubinstein, A. Time preference. Int. Econ. Rev. 1982, 23, 677–694. [Google Scholar] [CrossRef]
- Ericson, K.M.; Noor, J. Delay Functions as the Foundations of Time Preference: Testing for Separable Discounted Utility; Working paper of the Boston University; Boston University: Boston, MA, USA, 2015. [Google Scholar]
- Takeuchi, K. Non-parametric test of time consistency: Present bias and future bias. Games Econ. Behav. 2011, 71, 456–478. [Google Scholar] [CrossRef]
- Cruz Rambaud, S.; Muñoz Torrecillas, M.J. Capitalization Speed of a Financial Law. In Proceedings of the Fourth Italian-Spanish Conference on Financial Mathematics, Alghero, Italy, 28 June–1 July 2001. [Google Scholar]
- Rohde, K.I.M. Measuring decreasing and increasing impatience. Manag. Sci. 2019, 65, 1700–1716. [Google Scholar] [CrossRef]
- Lisei, G. Su un’equazione funzionale collegata alla scindibilità delle leggi finanziarie. Giornalle dell’Istituto Italiano Degli Attuari 1979, XLII, 19–24. [Google Scholar]
- Cruz Rambaud, S.; González Fernández, I. A measure of inconsistencies in intertemporal choice. PLoS ONE 2019, 14, e0224242. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).