Abstract
This article is concerned with the nanofluid flow in a rotating frame under the simultaneous effects of thermal slip and convective boundary conditions. Arrhenius activation energy is another important aspect of the present study. Flow phenomena solely rely on the Darcy–Forchheimer-type porous medium in three-dimensional space to tackle the symmetric behavior of viscous terms. The stretching sheet is assumed to drive the fluid. Buongiorno’s model is adopted to see the features of Brownian diffusion and thermophoresis on the basis of symmetry fundamentals. Governing equations are modeled and transformed into ordinary differential equations by suitable transformations. Solutions are obtained through the numerical RK45-scheme, reporting the important findings graphically. The outputs indicate that larger values of stretching reduce the fluid velocity. Both the axial and transverse velocity fields undergo much decline due to strong retardation produced by the Forchheimer number. The thermal radiation parameter greatly raises the thermal state of the field. The temperature field rises for a stronger reaction within the fluid flow, however reducing for an intensive quantity of activation energy. A declination in the concentration profile is noticed for stronger thermophoresis. The Forchheimer number and porosity factors result in the enhancement of the skin friction, while both slip parameters result in a decline of skin friction. The thermal slip factor results in decreasing both the heat and mass flux rates. The study is important in various industrial applications of nanofluids including the electro-chemical industry, the polymer industry, geophysical setups, geothermal setups, catalytic reactors, and many others.
1. Introduction
Flow analysis comprised of the slip boundary is of utmost interest; especially in the recent past, it has gained importance as compared to no-slip boundary conditions because no-slip is no more beneficial for the procedures that involve suspensions, polymer solutions, foams in which fluid behaves as a particulate, emulsions, etc. Therefore, the importance of partial slip and full slip boundary conditions appears to be more prominent. It has great importance in the electro-chemical and polymer industries. The early indication about this kind of formulation was reported by Akbar et al. [1] and Turkyilmazoglu [2,3] in their articles based on the influence of partial slip in nanofluid flow analysis. Besides them, Mustafa and Khan [4] reported the association of slip conditions with convective conditions in Magnetohydrodynamic (MHD)nanofluid flow towards a stretching disk in a rotating frame. The nanoparticles were assumed to be FeO.
The most recent and famous class of fluids is defined as nanofluids. These types of fluids are actual suspensions, having tiny particles of highly conductive metals, which are convenient to enhance the thermophysical properties such as the density, conductivity, and heat and mass flux rates for the given base fluids. The first indication on this type of formulation was reported by Choi [5] in his study focusing on the colloidal mixture of nano-size metallic particles in typical base fluids such as oil, glycol, and water. Within a short span of time, the formulation received importance in various industrial and engineering setups due to its variety of enhanced physical properties. Later on, Dogonchi et al. [6] reported an important study of MHD Cu-water-type nanofluid flow using the CVFEMmethod. The flow was assumed to be flowing through a cavity. Furthermore, Rasool et al. [7] reported Marangoni effects in the flow of nanofluids towards different surfaces. Sarafraz et al. [8] reported some good results on diurnal thermal interpretation in an ETSCtube using a graphene-based nano-suspension. In another study, Sarafraz et al. [9] reported thermal assessment in graphene-water-based nanofluid over glycol (WEG60:40). Goodarzi et al. [10] analyzed the natural convection and heat flux phenomena in MWCNT, Cu, and Al2O3-based nanofluids. Sarafraz et al. [11] discussed the potential of nanofluids and solar collectors in thermal energy production systems used in smart cities. Sarafraz et al. [12] reported some major findings and performed smart optimization using tube solar collectors and the response surface method (RSM) over heat pipes. Tlili et al. [13] discussed the impact of MHD in nanofluid flow across a cylindrical channel. Furthermore, Tlili et al. [14] reported some good results of entropy optimization and MHD in stagnation point nanofluid flow using a stretching sheet. Some recent and advanced studies on the effects of different nanoparticles in nanofluids’ flow can be seen in [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] and the references cited therein.
The rotating frame equipped with a stretching surface is quite famous in engineering and geophysical procedures. For example, rotor systems, gas turbines, food treatments, and disk cleaners are very dependent on the rotating frame having stretching surfaces. However, less attention is paid to this aspect of fluid flow and heat transfer analysis using a porous medium. One of the pioneer studies on this topic was given by Wang [30]. The classical perturbation technique was used in this study. In recent studies, Rashid et al. [31] reported Darcy–Forchheimer flow of nanofluids bounded by a rotating frame having a stretching sheet. The solutions were obtained by the NDSolve numerical method using Mathematica-based code. Hayat et al. [32] reported Maxwell-type flow of nanofluids using the same rotating frame. In this study, this involved the optimal homotopy technique for finding the solutions. In another study, Hayat et al. [33] reported the impact of heat absorption, heat generation, and thermal radiation on the Darcy-type flow of nanofluids. Homotopy Analysis Method (HAM)was used for the final convergent solutions. Similarly, Hayat et al. [34] reported Jeffrey-type nanofluid flow bounded by a rotating frame with a stretching surface. The study revealed some good results in the context of relation time parameters.
Some procedures such as heat transfer design, geophysical setups, geothermal setups, and catalytic reactors are best known for the involvement of porous medium in their structure. The mathematical term used for the porosity factor is known as the “Darcy–Forchheimer model”, named after Darcy and Forchheimer, who reported this model in early 1901. The model received importance in the late 1990s, when most of the studies were reported on Darcy-type medium used in fluid flow analysis. This importance was reported especially in the procedures like grain storage, ground water purification systems, beds of fossils, structuring the thermal insulation materials, water motion in reservoirs, units that are solely prepared for energy storage and many others. Some important studies have been reported recently. For example, Jumah et al. [35] reported Darcy-type flow using mixed convective conditions. Rasool et al. [36,37,38,39] reported recent findings on Darcy-type nanofluid flow bounded by various surfaces including MHD and the Riga pattern. The results have been obtained by using HAM and numerical RK45 methods.
Models based on oil storage and geothermal procedures involve many typical and extended chemical reaction systems. The creation and consumption of chemical reactants is classified under various situations both within the liquid and mass transport mechanism. The pioneer study was reported by Bestman [40] considering the effect of activation energy on the Darcy-type model in fluid flow analysis. Later on, Makinde et al. [41] reported some good results considering time-dependent heat and mass convection together with activation energy and resistance force. Mustafa et al. [42] reported some good results on MHD nanofluid flow subject to activation energy and chemical reaction. Recently, Rasool et al. [43,44] reported some good findings on the nanofluids’ flow subject to chemical reaction and convective boundary conditions using the Riga pattern. The solutions were obtained using HAM [45,46,47,48,49,50,51,52,53,54].
The thermal radiation effect is naturally accounted for in fluid flow analysis due to the temperature difference between the ambient fluid and continuum because it varies the structure of the boundary layer associated with the temperature distribution attribute. Thus, a decent number of applications are found in many engineering and industrial setups that involve the radiative heat transfer mechanism. Procedures such as gas turbines, nuclear power plants, nuclear reactors, and many satellites. The pioneer study was given by Nayak [55], showing that as long as the radiative effect was minimum, the more the cooling achieved due to viscoelastic MHD-type fluid flow. Furthermore, Nayak et al. [56] regarded the influence of thermal radiation as an important factor while considering a flow over a plate surface. Bhatti et al. [57] gave the thermal radiation impact on MHD fluid flow analysis in a metachronal wavy channel.
In the above literature, one can see that most emphasis was given to studies based on nanofluids’ flow through different channels. However, the literature lacks articles based on the formulations that involve thermal slip, convective conditions, and the Darcy channel all together. In this study, for the first time, the model involves the Darcy–Forchheimer relation, thermal and velocity slip, together with the convective boundary. The impact of Arrhenius activation energy is yet another novel aspect of this study. Overall, the article is organized as follows: Firstly, we assumed a non-Newtonian, incompressible Darcy–Forchheimer MHD nanofluid flow bounded in a rotating frame via a stretching surface. Secondly, the modeled problems were converted into ordinary problems using transformations. Thirdly, the numerical RK45 scheme was applied to solve the problems, and finally, the solutions were plotted graphically for better understanding of the audience.
2. Formulation
Here, we investigated a Darcy–Forchheimer nanofluid flow in a three-dimensional rotating frame. Thermal radiation, thermal slip, velocity slip, and chemical reaction with Arrhenius activation energy were the important factors involved in this study. The concentration of nanoparticles was associated with the Brownian motion parameter and thermophoresis. The stretching surface was considered adjacent to the plane . Ω = Ωk is the rotation velocity where k is the unit vector in the direction parallel to the z-axis. Assuming a small Reynolds number and a transverse magnetic field having strength applied alongside/parallel to the z-axis with partial slip, thermal radiation, and activation energy, the governing equations (see for example [4,42,53]) take the following form:
with:
Define,
Using (7) in (1)–(6), we get,
along with:
where is the MHD parameter, is the stretching ratio, is the velocity slip, is the velocity slip, is the thermal slip, is the Forchheimer number, is the Prandtl number, is the Biot number, is the thermal radiation, is the non-dimensional activation energy parameter, is the temperature difference, is the chemical reaction parameter, is the rotational factor/parameter, , , , and . Physical quantities are given below:
- (1)
- Skin friction:
- (2)
- Local Nusselt and Sherwood numbers:where,
3. Methodology
The numerical RK45 scheme using the shooting technique was applied for final solutions of the nonlinear problems. An initial guess was made carefully to solve the problem numerically. The iterations was performed repeatedly unless a difference up to or less than was achieved for the most suitable convergence. These results were quite efficient and accurate compared to the analytic solutions reported in previous literature.
4. Analysis of the Solutions
Here, we interpret the results and findings plotted graphically in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28. In particular, Figure 1 gives the impact of the rotational parameter on the axial velocity field. Physically, the stretching rate is directly related to the rotational parameter. For larger values, stretching reduces, which effectively results in a declining change in the fluid velocity. Figure 2 presents the impact of on transverse velocity field. A similar, but more prominent impact is noticed in this case. The higher the value of , the lesser is the stretching rate, which certainly affects the fluid motion. Figure 3 and Figure 4 present the influence received by the axial and transverse velocity field due to the magnetic parameter. Physically, a strong and intensive Lorentz force generated by the MHD results in sudden bumps and retardation in the fluid flow directions, which leads to a reducing trend in both the axial and transverse velocity fields. However, the impact is quite prominent in the case of transverse velocity. Figure 5 and Figure 6 represent the influence of the Forchheimer parameter on the velocity field. Both the axial and transverse velocity fields decline greatly due to the strong retardation produced by the Forchheimer number. Physically, the Forchheimer number is directly related to the resistance offered to the fluid motion due to the porous media. A similar declination is noted in fluid motion due to the velocity slip parameters and , respectively, given in Figure 7 and Figure 8. The impact of non-dimensional parameter on the thermal distribution is given in Figure 9. An enhancement in the field is noticed for elevated values of . Physically, the stretching rate is inversely related to the chemical reaction. For larger , the stretching rate is less, which reduces the fluid flow, creating more relaxation to the fluid packets, leading to a rise in the temperature field. Figure 10 presents the impact of the thermal radiation parameter on the temperature field. It greatly raises the thermal state of the field due to the natural heat source attributes. The resistive force is enhanced due to the porous medium, and consequently, the temperature rises. Figure 11 and Figure 12 are related to the chemical reaction part involved in the governing equations. An opposite trend in the temperature profile is found for both the chemical reaction parameter and the Arrhenius activation energy parameter, respectively. The temperature field rises for a stronger reaction within the fluid flow, however reducing for an intensive quantity of activation energy. Both the Brownian diffusion and thermophoresis increase for the thermal distribution. The unpredictable motion of particles due to Brownian diffusion increases strongly for the given strong thermophoretic force resulting in a clear rise in the temperature field, as displayed in Figure 13 and Figure 14. Curiously, the rising values of the Biot number produce more and stronger convective heating at the surface given the greater gradient temperature at the wall. Thus, a rise in the thermal field is noticed as shown in Figure 15. A similar rising trend in the thermal field is noticed due to the stronger thermal slip parameter shown in Figure 16. Figure 17, Figure 18, Figure 19 and Figure 20 are the influences offered by thermophoresis, Brownian diffusion, Arrhenius activation energy, and the Schmidt factor to the concentration of nanoparticles in the base fluid. Stronger Brownian diffusion results in a higher concentration of the nanoparticles due to enhanced motion as shown in Figure 17; however, a declination is noticed for stronger thermophoresis due to the unpredictable motion of the fluid particles, leaving more gaps within the fluid shown in Figure 18. The Arrhenius activation energy gives rise to the concentration field shown in Figure 19. The inverse relation between kinematic viscosity and Brownian diffusion gives rise to the higher concentration field given in Figure 20. Figure 21, Figure 22 and Figure 23 are the density graphs, whereas streamlines are drawn in Figure 24, Figure 25 and Figure 26 at different values assigned to and . Figure 27 and Figure 28 are called the stream density graphs. The information about the skin friction at the solid surface is compiled in Table 1. Both the Forchheimer number and porosity factors result in the enhancement of the skin friction, while both slip parameters result in a decline of the skin friction. The information about heat flux and mass flux is tabulated in Table 2. The activation energy enhances the heat flux with a clear reduction in mass flux. The thermal slip factor results in a decline of both the heat and mass flux rates.
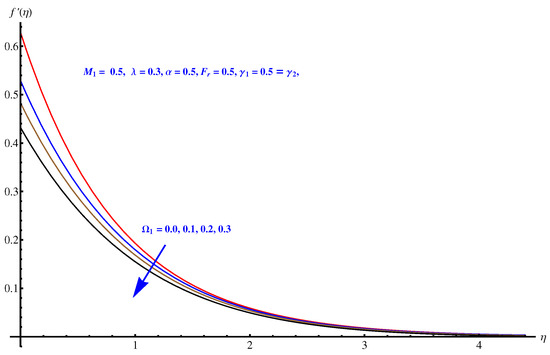
Figure 1.
Rotational parameter versus axial velocity field.
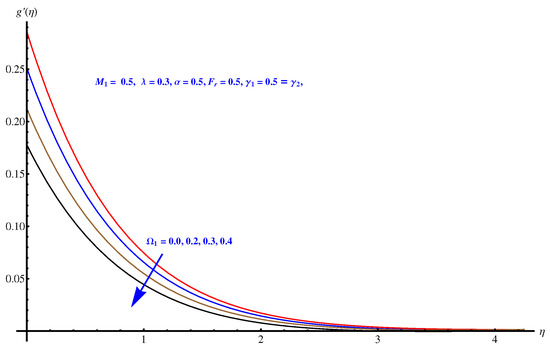
Figure 2.
Rotational parameter versus transverse velocity field.
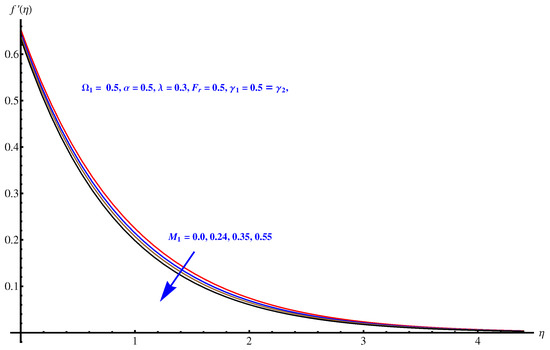
Figure 3.
Magnetic parameter versus axial velocity field.
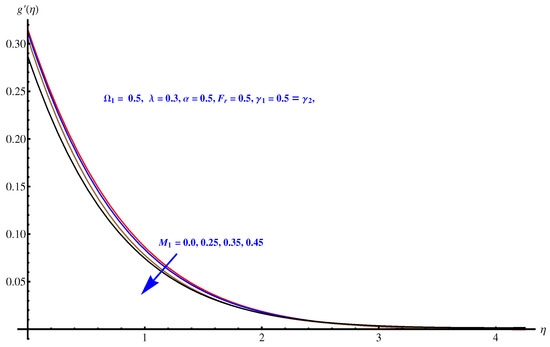
Figure 4.
Magnetic parameter versus transverse velocity field.

Figure 5.
Forchheimer parameter versus axial velocity field.
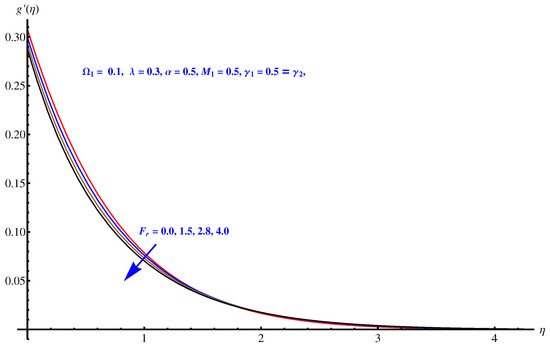
Figure 6.
Forchheimer parameter versus transverse velocity field.
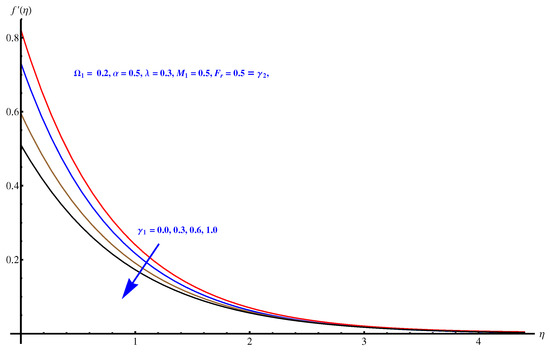
Figure 7.
Slip parameter versus axial velocity field.
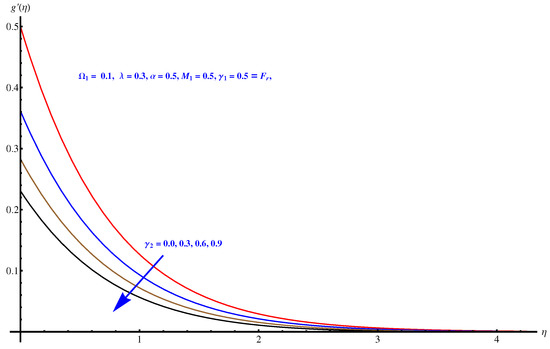
Figure 8.
Slip parameter versus transverse velocity field.
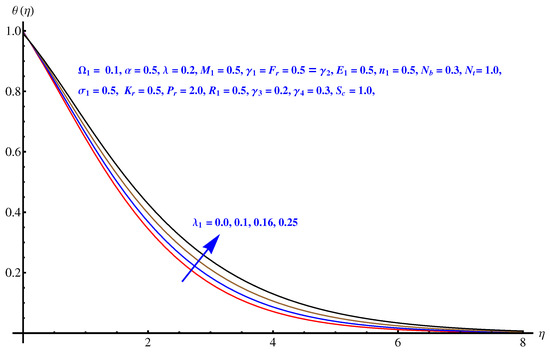
Figure 9.
Non-dimensional parameter versus temperature field.
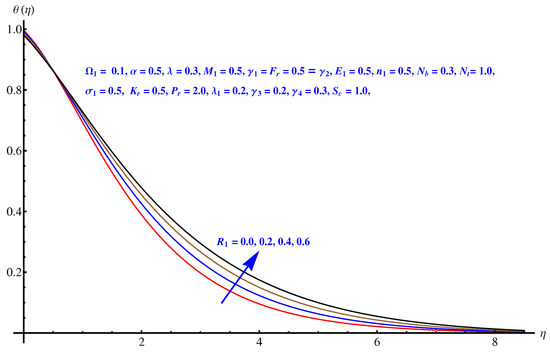
Figure 10.
Radiation parameter versus temperature field.
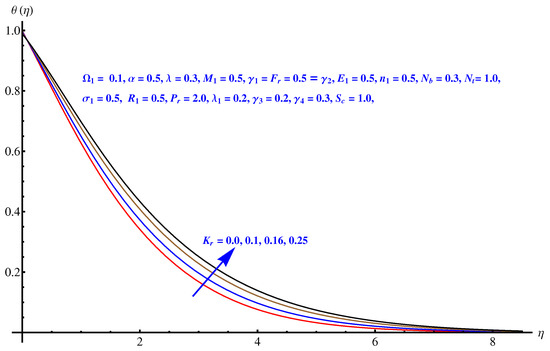
Figure 11.
Chemical reaction parameter versus temperature field.
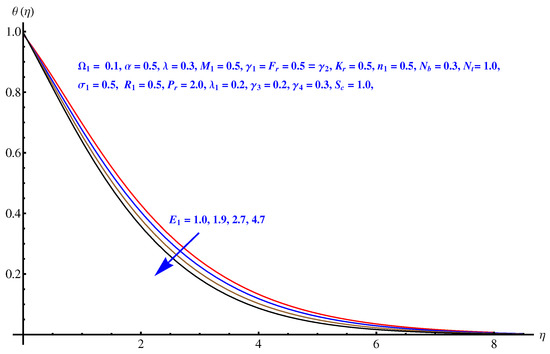
Figure 12.
Arrhenius activation energy parameter versus temperature field.
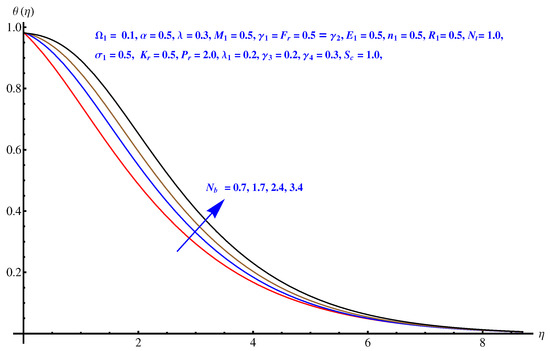
Figure 13.
Brownian diffusion versus temperature field.
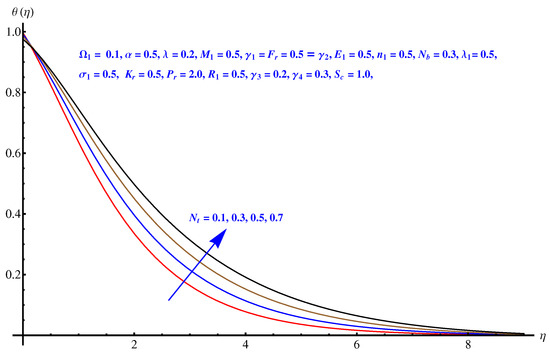
Figure 14.
Thermophoresis versus temperature field.
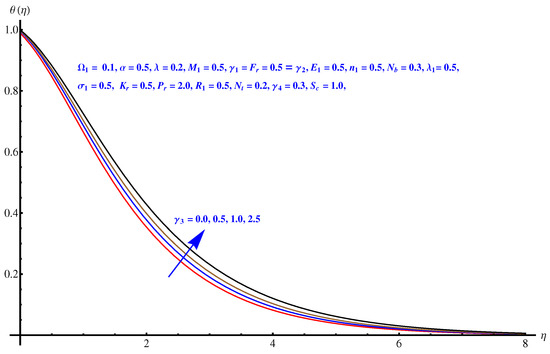
Figure 15.
Biot number versus temperature field.
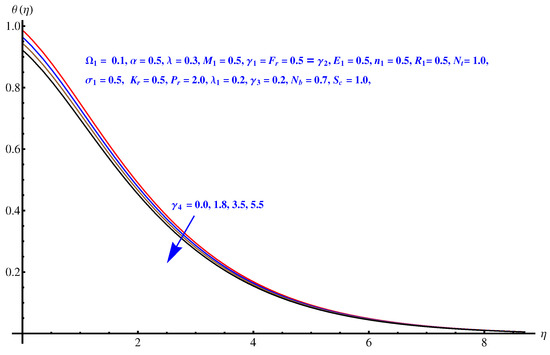
Figure 16.
Thermal slip versus temperature field.
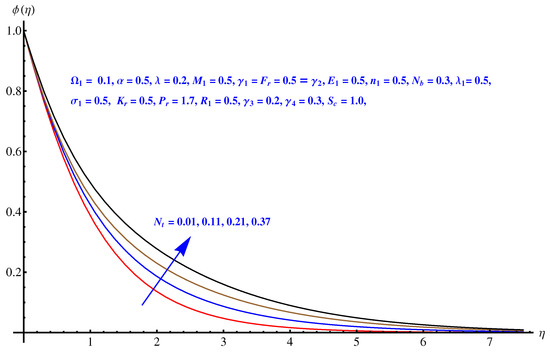
Figure 17.
Thermophoresis versus concentration field.
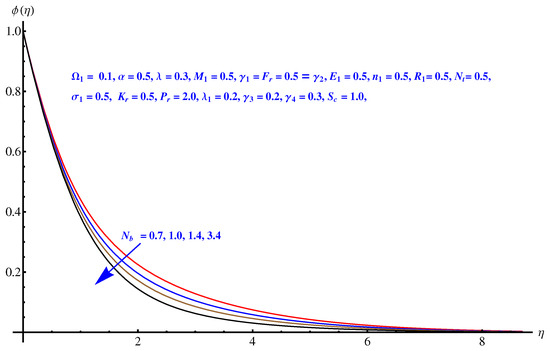
Figure 18.
Brownian diffusion versus concentration field.
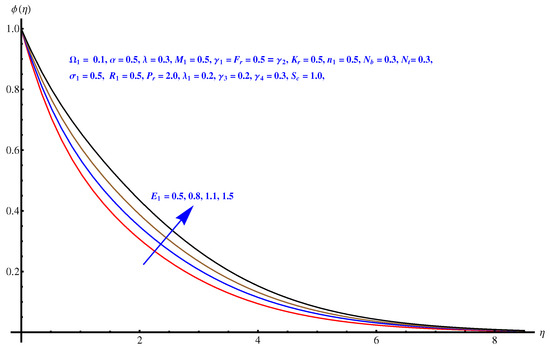
Figure 19.
Activation energy versus concentration field.
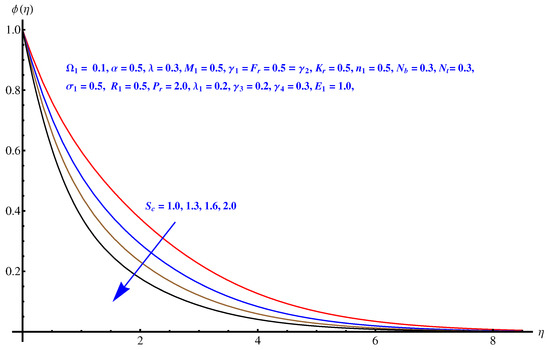
Figure 20.
Schmidt parameter versus concentration field.
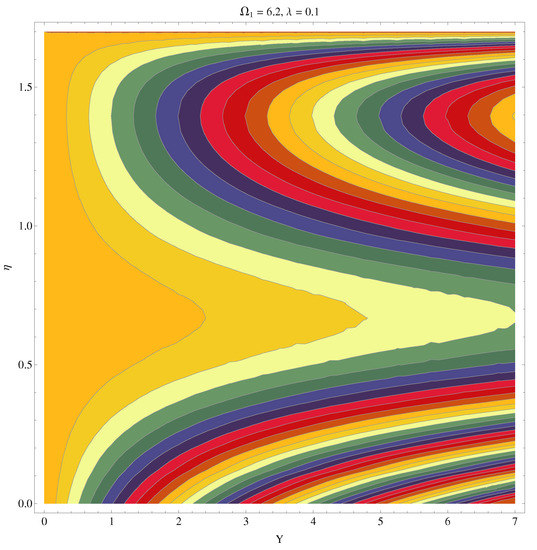
Figure 21.
Contour graph at and .
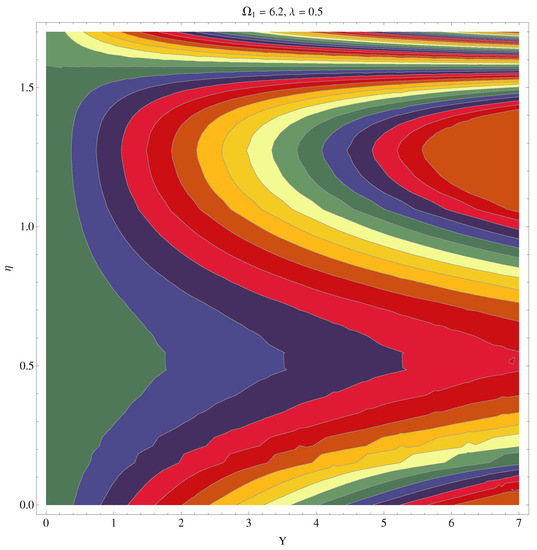
Figure 22.
Contour graph at and .
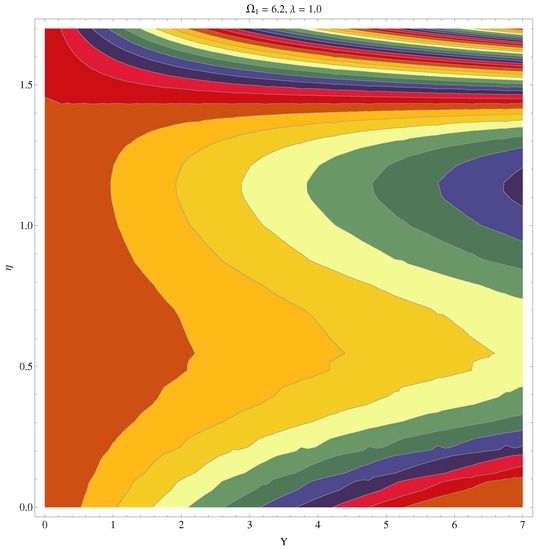
Figure 23.
Contour graph at and .

Figure 24.
Streamlines at .
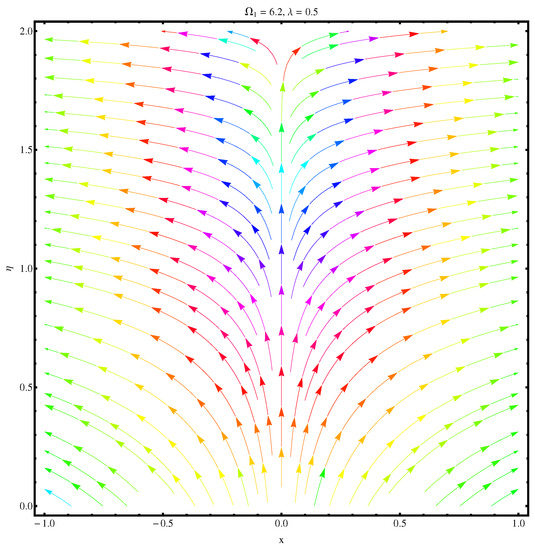
Figure 25.
Streamlines at and .
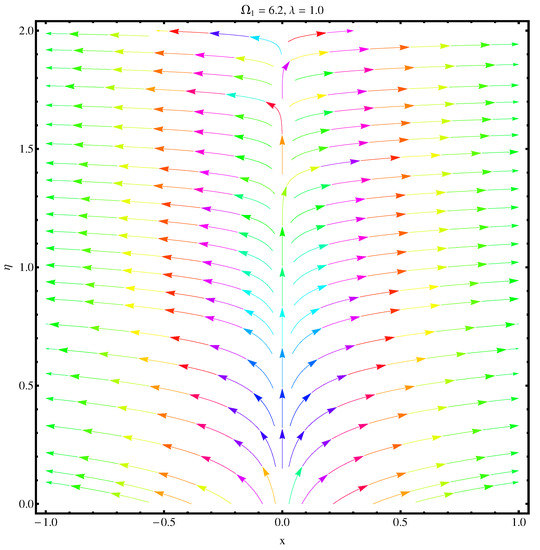
Figure 26.
Streamlines at and .
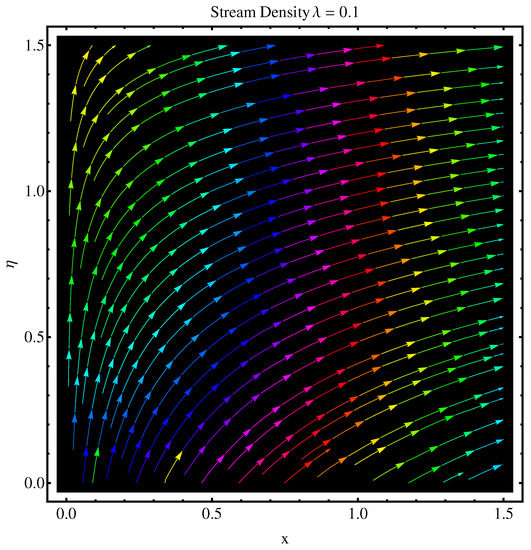
Figure 27.
Stream density at .
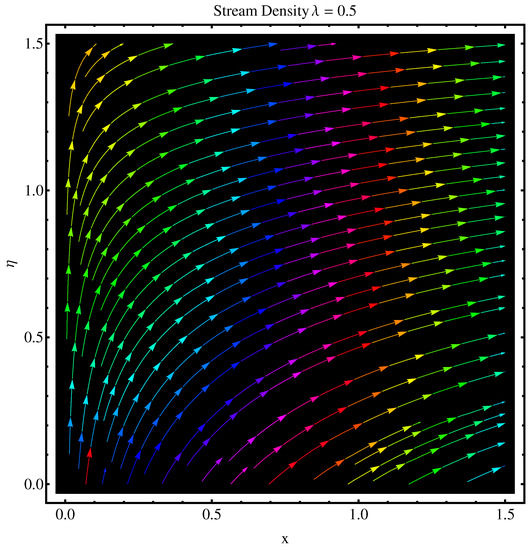
Figure 28.
Stream density at .

Table 1.
Numerical data of skin friction.

Table 2.
Numerical data of local Nusselt and Sherwood numbers .
5. Concluding Remarks
In this article, we chose a nanofluid flow in a rotating channel considering slip and convective boundary conditions simultaneously. The solutions were found using a numerical scheme. The salient findings are listed below:
- Lorentz force generated by the MHD resulted in reducing trend in both the axial and transverse velocity fields.
- Both the axial and transverse velocity fields greatly declined for larger values of the Forchheimer number.
- The thermal radiation parameter greatly raised the thermal state of the field.
- The chemical reaction part involved in the governing equations showed the opposite trend in the temperature profile for both the chemical reaction parameter and the Arrhenius activation energy parameter, respectively.
- Both the Brownian diffusion and thermophoresis were rising factors for the thermal distribution.
- The augmented Biot number resulted in a rise in the thermal field.
- The augmented thermal slip parameter enhanced the temperature field.
- Stronger Brownian diffusion resulted in a higher concentration of the nanoparticles.
- A declination was noticed for stronger thermophoresis.
- The Arrhenius activation energy gave rise to the concentration field.
- Both the Forchheimer number and porosity factor resulted in enhancement of the skin friction, while both slip parameters resulted in a decline of the skin friction.
- The activation energy enhanced heat flux with a clear reduction in mass flux. The thermal slip factor resulted in a decline of both the heat and mass flux rates.
Author Contributions
Writing, original draft, A.S. and G.R.; conceptualization, A.S. and G.R.; software, A.S. and G.R.; validation, A.S. and G.R.; writing, original draft, A.S., G.R., and C.M.K.; methodology, A.S., G.R., and C.M.K.; concept, A.S., G.R., and C.M.K.; formal analysis, A.S., G.R., and C.M.K.; funding, C.M.K.; review and revision, A.S., G.R., and C.M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding
Acknowledgments
Chaudry Masood Khalique thanks North-West University for its continued support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Akbar, N.S.; Khan, Z.H.; Nadeem, S. Copper nanoparticle analysis for peristaltic flow in a curved channel with heat transfer characteristics. J. Mol. Liq. 2014, 196, 21. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Multiple solutions of heat and mass transfer of MHD slip flow for the viscoelastic fluid over a stretching sheet. Int. J. Therm. Sci. 2011, 50, 2264. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Dual and triple solutions for MHD slip flow of non-Newtonian fluid over a shrinking surface. Comput. Fluids 2012, 70, 53. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A. Numerical study of partial slip effects on MHD flow of nanofluids near a convectively heated stretchable rotating disk. J. Mol. Liq. 2017, 234, 287. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparti-cles. In Proceedings of the ASME International Mechanical Engineering Congress & Exposisition, American Society of Mechanical Engineers, San Francisco, CA, USA, 12–17 November 1995; Volume 66, pp. 99–105. [Google Scholar]
- Dogonchi, A.S.; Chamkha, A.J.; Ganji, D.D. A numerical investigation of magneto-hydrodynamic natural convection of Cu-water nanofluid in a wavy cavity using CVFEM. J. Therm. Anal. Calorim. 2019, 135, 2599–2611. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Shafiq, A. Marangoni effect in second grade forced convective flow of water based nanofluid. J. Adv. Nanotechnol. 2019, 1, 50–61. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Safaei, M.R. Diurnal thermal evaluation of an evacuated tube solar collector (ETSC) charged with graphene nanoplatelets-methanol nano-suspension. Renew. Energy 2019, 142, 364–372. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Safaei, M.R.; Tian, Z.; Goodarzi, M.; Filho, E.P.B.; Arjom, M. Thermal Assessment of Nano-Particulate Graphene-Water/Ethylene Glycol (WEG 60:40) Nano-Suspension in a Compact Heat Exchanger. Energies 2019, 12, 1929. [Google Scholar] [CrossRef]
- Goodarzi, H.; Akbari, O.A.; Sarafraz, M.M.; Karchegani, M.M.; Safaei, M.R.; Shabani, G.A.S. Numerical Simulation of Natural Convection Heat Transfer of Nanofluid With Cu, MWCNT, and Al2O3 Nanoparticles in a Cavity With Different Aspect Ratios. J. Thermal Sci. Eng. Appl. 2019, 11, 061020. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Tlili, I.; Baseer, M.A.; Safaei, M.R. Potential of Solar Collectors for Clean Thermal Energy Production in Smart Cities using Nanofluids: Experimental Assessment and efficiency improvement. Appl. Sci. 2019, 9, 1877. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Tlili, I.; Tian, Z.; Bakouri, M.; Safaei, M.R. Smart optimization of a thermosyphon heat pipe for an evacuated tube solar collector using response surface methodology (RSM). Phys. A Stat. Mech. Appl. 2019, 534, 122146. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Ramadan, K. MHD flow of nanofluid flow across horizontal circular cylinder: Steady forced convection. J. Nanofluids 2019, 8, 179–186. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Ramadan, K. Entropy generation due to MHD stagnation point flow of a nanofluid on a stretching surface in the presence of radiation. J. Nanofluids 2018, 7, 879–890. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Shafiq, A. Second grade nanofluidic flow past a convectively heated vertical Riga plate. Phys. Scr. 2019, 94, 125212. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, S.; Muhammad, T.; Alsaedi, A.; Ayub, M. Radiative flow of Powell-Eyring nanofluid with convective boundary conditions. Chin. J. Phys. 2017, 55, 1523–1538. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Khalique, C.M. Marangoni forced convective Casson type nanofluid flow in the presence of Lorentz force generated by Riga plate. Discret. Contin. Dyn. Syst. Ser. S 2019, in press. [Google Scholar]
- Sohail, M.; Naz, R.; Abdelsalam, S.I. On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic microorganisms through 3D flows. Phys. Scr. 2019, 95. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R. Modified heat and mass transmission models in the magnetohydrodynamic flow of Sutterby nanofluid in stretching cylinder. Phys. A Stat. Mech. Appl. 2020, in press. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Tlili, I. Marangoni convective nano-fluid flow over an electromagnetic actuator in the presence of first order chemical reaction. Heat Transf. Asian Res. 2019. [Google Scholar] [CrossRef]
- Lund, L.A.; Zurni, O.; Khan, I. Analysis of dual solution for MHD flow of Williamson fluid with slippage. Heliyon 2019, 5, e01345. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability analysis of Darcy–Forchheimer flow of Casson type nanofluid over an exponential sheet: Investigation of critical points. Symmetry 2019, 11, 412. [Google Scholar] [CrossRef]
- Lund, L.A.; Zurni, O.; Khan, I.; Dero, S. Multiple solutions of Cu-C6H9NaO7 and Ag-C6H9NaO7 nanofluids flow over nonlinear shrinking surface. J. Cent. South Univ. 2019, 26, 1283. [Google Scholar] [CrossRef]
- Goodarzi, M.; Tlili, I.; Tian, Z.; Safaei, M. Efficiency assessment of using graphene nanoplatelets-silver/water nanofluids in microchannel heat sinks with different cross-sections for electronics cooling. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Tlili, I. Effects MHD and Heat Generation on Mixed Convection Flow of Jeffrey Fluid in Microgravity Environment over an Inclined Stretching Sheet. Symmetry 2019, 11, 438. [Google Scholar] [CrossRef]
- Tlili, I.; Alkanhal, T.A. Nanotechnology for water purification: Electrospun nanofibrous membrane in water and wastewater treatment. J. Water Reuse Desalin. 2019, 24. [Google Scholar] [CrossRef]
- Shafiq, A.; Khan, I.; Rasool, G.; Seikh, A.H.; Sherif, E.M. Significance of double stratification in stagnation point flow of third-grade fluid towards a radiative stretching cylinder. Mathematics 2019, 7, 1103. [Google Scholar] [CrossRef]
- Shafiq, A.; Zari, I.; Rasool, G.; Tlili, I.; Khan, T.S. On the MHD Casson axisymmetric Marangoni forced convective flow of nanofluids. Mathematics 2019, 7, 87. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Khan, I.; Baleanu, D.; Nisar, K.S.; Shahzadi, G. Entropy generation and consequences of MHD in Darcy–Forchheimer nanofluid flow bounded by non-linearly stretching surface. Symmetry 2020, 29, 5. [Google Scholar] [CrossRef]
- Wang, C.Y. Stretching a surface in a rotating fluid. Zeitschrift für Angewandte Mathematik und Physik 1988, 39, 177–185. [Google Scholar] [CrossRef]
- Rashid, S.; Hayat, T.; Qayyum, S.; Ayub, M.; Alsaedi, A. Three dimensional rotating Darcy–Forchheimer flow with activation energy. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A. Three dimensional rotating flow of Maxwell nanofluid. J. Mol. Liq. 2017, 229, 495–500. [Google Scholar] [CrossRef]
- Hayat, T.; Shah, F.; Khan, M.I.; Alsaedi, A. Framing the performance of heat absorption/generation and thermal radiation in chemically reactive Darcy–Forchheimer flow. Results Phys. 2017, 7, 3390–3395. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Imtiaz, M.; Alsaedi, A. Three-dimensional rotating flow of Jeffrey fluid for Cattaneo-Christov heat flux model. AIP Adv. 2016, 6, 025012. [Google Scholar] [CrossRef]
- Jumah, R.Y.; Fawzi, A.; Abu-Al-Rub, F. Darcy–Forchheimer mixed convection heat and mass transfer in fluid saturated porous media. Int. J. Numer. Methods Heat Fluid Flow 2001, 11, 600–618. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Durur, H. Darcy–Forchheimer relation in Magnetohydrodynamic Jeffrey nanofluid flow over stretching surface. Discret. Contin. Dyn. Syst. Ser. S 2019, accepted. [Google Scholar]
- Rasool, G.; Shafiq, A.; Khalique, C.M.; Zhang, T. Magnetohydrodynamic Darcy Forchheimer nanofluid flow over nonlinear stretching sheet. Phys. Scr. 2019, 94, 105221. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T. Darcy–Forchheimer nanofluidic flow manifested with Cattaneo-Christov theory of heat and mass flux over non-linearly stretching surface. PLoS ONE 2019, 14, e0221302. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Chamkha, A.J.; Shafiq, A.; Tlili, I.; Shahzadi, G. Entropy Generation and Consequences of Binary Chemical Reaction on MHD Darcy–Forchheimer Williamson Nanofluid Flow Over Non-Linearly Stretching Surface. Entropy 2020, 22, 18. [Google Scholar] [CrossRef]
- Bestman, A.R. Natural convection boundary layer with suction and mass transfer in a porous medium. Int. J. Energy Res. 1990, 14, 389–396. [Google Scholar] [CrossRef]
- Makinde, O.D.; Olanrewaju, P.O.; Charles, W.M. Unsteady convection with chemical reaction and radiative heat transfer past a flat porous plate moving through a binary mixture. Afr. Mat. 2011, 22, 65–78. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. Buoyancy effects on the MHD nanofluid flow past a vertical surface with chemical reaction and activation energy. Int. J. Heat Mass Transf. 2017, 108, 1340–1346. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T. Characteristics of chemical reaction and convective boundary conditions in Powell-Eyring nanofluid flow along a radiative Riga plate. Heliyon 2019, 5, e01479. [Google Scholar] [CrossRef] [PubMed]
- Rasool, G.; Zhang, T.; Shafiq, A.; Durur, H. Influence of chemical reaction on Marangoni convective flow of nanoliquid in the presence of Lorentz forces and thermal radiation: A numerical investigation. J. Adv. Nanotechnol. 2019, 1, 32–49. [Google Scholar] [CrossRef]
- Shafiq, A.; Hammouch, Z.; Turab, A. Impact of radiation in a stagnation point flow of Walters’ B fluid towards a Riga plate. Therm. Eng. Prog. 2018, 6, 27–33. [Google Scholar] [CrossRef]
- Nayak, M.K.; Shaw, S.; Makinde, O.D.; Chamkha, A.J. Effects of homogenous-Heterogeneous reactions on radiative NaCl-CNP nanofluid flow past a convectively heated vertical Riga plate. J. Nanofluids 2018, 7, 657–667. [Google Scholar] [CrossRef]
- Naseem, A.; Shafiq, A.; Zhaoa, L.; Farooq, M.U. Analytical investigation of third grade nanofluidic flow over a riga plate using Cattaneo-Christov model. Results Phys. 2018, 9, 961–969. [Google Scholar] [CrossRef]
- Shafiq, A.; Hammouch, Z.; Sindhu, T.N. Bioconvective MHD flow of tangent hyperbolic nanofluid with newtonian heating. Int. J. Mech. Sci. 2017, 133, 759–766. [Google Scholar] [CrossRef]
- Liao, S.J. Homotopy Analysis Method in Nonlinear Differential Equations; Springer & Higher Education Press: Berlin /Heidelberg, Germany, 2012. [Google Scholar]
- Shafiq, A.; Jabeen, S.; Hayat, T.; Alsaedi, A. Cattaneo-Christov heat flux model for squeezed flow of third grade fluid. Surf. Rev. Lett. 2017, 1750098. [Google Scholar] [CrossRef]
- Naseem, F.; Shafiq, A.; Zhao, L.; Naseem, A. MHD biconvective ‡ow of Powell Eyring nanofluid over stretched surface. AIP Adv. 2017, 7, 065013. [Google Scholar] [CrossRef]
- Shafiq, A.; Sindhu, T.N. Statistical study of hydromagnetic boundary layer flow of Williamson fluid regarding a radiative surface. Results Phys. 2017, 7, 3059–3067. [Google Scholar] [CrossRef]
- Mabood, F.; Shafiq, A.; Hayat, T.; Abelman, S. Radiation effects on stagnation point flow with melting heat transfer and second order slip. Results Phys. 2017, 7, 31–42. [Google Scholar] [CrossRef]
- Hayat, T.; Jabeen, S.; Shafiq, A.; Alsaedi, A. Radiative squeezing flow of second grade fluid with convective boundary conditions. PLoS ONE 2016, 11, e0152555. [Google Scholar] [CrossRef] [PubMed]
- Nayak, M.K. Chemical reaction effect on MHD viscoelastic fluid over a stretching sheet through porous medium. Meccanica 2016, 51, 1699. [Google Scholar] [CrossRef]
- Nayak, M.K.; Dash, G.C.; Singh, L.P. Unsteady Radiative MHD Free Convective Flow and Mass Transfer of a Viscoelastic Fluid Past an Inclined Porous Plate. Arab. J. Sci. Eng. 2015, 40, 3029. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Zeeshan, A.; Ellahi, R. Heat transfer with thermal radiation on MHD particle–fluid suspension induced by metachronal wave. Pramana J. Phys. 2017, 89, 48. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).