Abstract
A coherent optical (CO) orthogonal frequency division multiplexing (OFDM) scheme gives a scalable and flexible solution for increasing the transmission rate, being extremely robust to chromatic dispersion as well as polarization mode dispersion. Nevertheless, as any coherent-detection OFDM system, the overall system performance is limited by laser phase noises. On the other hand, extreme learning machines (ELMs) have gained a lot of attention from the machine learning community owing to good generalization performance, negligible learning speed, and minimum human intervention. In this manuscript, a phase-error mitigation method based on the single-hidden layer feedforward network prone to the improved ELM algorithm for CO-OFDM systems is introduced for the first time. In the training step, two steps are distinguished. Firstly, pilots are used, which is very common in OFDM-based systems, to diminish laser phase noises as well as to correct frequency-selective impairments and, therefore, the bandwidth efficiency can be maximized. Secondly, the regularization parameter is included in the ELM to balance the empirical and structural risks, namely to minimize the root mean square error in the test stage and, consequently, the bit error rate (BER) metric. The operational principle of the real-complex (RC) ELM is analytically explained, and then, its sub-parameters (number of hidden neurons, regularization parameter, and activation function) are numerically found in order to enhance the system performance. For binary and quadrature phase-shift keying modulations, the RC-ELM outperforms the benchmark pilot-assisted equalizer as well as the fully-real ELM, and almost matches the common phase error (CPE) compensation and the ELM defined in the complex domain (C-ELM) in terms of the BER over an additive white Gaussian noise channel and different laser oscillators. However, both techniques are characterized by the following disadvantages: the CPE compensator reduces the transmission rate since an additional preamble is mandatory for channel estimation purposes, while the C-ELM requires a bounded and differentiable activation function in the complex domain and can not follow semi-supervised training. In the same context, the novel ELM algorithm can not compete with the CPE compensator and C-ELM for the 16-ary quadrature amplitude modulation. On the other hand, the novel ELM exposes a negligible computational cost with respect to the C-ELM and PAE methods.
1. Introduction
For optical fiber transmissions, intersymbol interference originated by polarization-mode dispersion and chromatic dispersion becomes relevant as the bit rate achieves the order of various tens of Gbps [1]. As an efficient alternative to mitigate this issue, coherent optical (CO) orthogonal frequency division multiplexing (OFDM) systems have attracted the attention of the scientific community because intersymbol interference may be eliminated as long as the guard interval occupies enough space of the OFDM symbol period [2]. Additionally, next-generation Tbps, bandwidth variable elastic optical systems can be a direct consequence of the CO-OFDM technology by its high receiver sensitivity as well as its effective transmission rate. Nevertheless, both coherent detection and OFDM are prone to phase noise due to the phase mismatch between the laser oscillators at the transmitter and receiver sides and the relatively long OFDM symbol duration compared to that of the single carrier communications. In the CO-OFDM signal, laser phase noise produces two clearly effects, termed as common phase error (CPE) and inter-carrier interference (ICI) [3]. CPE is relatively easy to diminish contrasted with ICI since the former induces the same rotation in all constellation symbols during the OFDM symbol, instead the latter behaves like Gaussian noise and depends on the subcarrier frequency. Fortunately, the CPE may be controlled through the pilot-assisted equalization (PAE) method [4,5,6,7], which is usually inserted in OFDM modems in order to correct the multipath channel effects. Here, the channel frequency response for data subcarriers is estimated by interpolation from the values provided by pilot subcarriers. Other phase-noise reduction techniques, such as the pilot-added scheme [8] that realizes ideal CPE compensation and the RF-pilot-based mechanism [9] that completely removes phase noise fluctuations (pioneering studies for optical OFDM transmissions), employ not only various pilots dedicated to phase-noise issue but also some preambles for channel equalization purposes. By comparing with the PAE technique, the spectral efficiency of these methods hence suffer a diminution. In a general sense, optimal approaches for suppressing the laser phase noise for CO-OFDM systems are still required in order to enhance the bit error rate (BER) especially in the situation of the low-cost broad-linewidth lasers are used.
Huang et al. [10] introduced the extreme leaning machine (ELM) algorithm in 2006, which is a novel technique of machine learning focused on single-hidden layer feedforward networks (SLFNs). The ELM is well-known for their fast training capability and remarkable performance. The main feature of this algorithm is that the parameters of the input-hidden-layer are randomly originated and do not necessitate to be adjusted. Therefore, the output weights in the training process simplify into a regularized least problem, and of which result comes from a closed equation. Enhancements and extensions of the standard ELM such as improving the stability [11] and compactness [12] of the ELM, ELMs for online sequential [13] and imbalanced [14] data, Bayesian [15], fuzzy [16], Wavelet [17], or complex [18,19] ELMs have been demonstrated excellent generation performance, superior efficiency, and less computational complexity, by giving solutions for regression and classification problems in diverse practical areas (medical, remote sensing, control and robotics, image/video processing, time series analysis, text classification and understanding, telecommunication, chemical process, and computer vision). Hence, the issues of convergence ability, generalization, over-fitting, local minima, and/or parameter adjustment (learning rate, learning epochs, among others) presented in support vector machines as well as back-propagation artificial neural networks do not happen in ELMs [10,20].
The merits owned by the ELM algorithm make it a suitable alternative to perform channel equalization in OFDM schemes in wireless [13,21,22] and optical fiber [23,24] communications. On the one hand, a fully real-valued ELM to perform equalization and symbol detection processes in OFDM-based systems is introduced in Reference [21]. In the following, the methodology and results of this study are briefly exposed. After the fast Fourier transform (FFT) module at the demodulator, data are separated into training and testing parts, where the first set is used to estimate the channel response thanks to the Moore-Penrose generalized inverse of the hidden layer output matrix. Consequently, pilot subcarriers are not exploited. Over a time-varying Rayleigh fading channel for the quadrature phase-shift keying (QPSK), 16-ary quadrature amplitude modulation (16QAM), and 64-ary QAM modes, the ELM exhibits significant improvement in terms of the symbol error rates and has lower computations than the following learning-based equalization schemes—the fully complex-valued ELM [25], complex-valued radial basis function network [25], complex-valued minimal resource allocation network [25], k-nearest neighbor approach [25], and back propagation [26] and stochastic gradient [27] neural networks. For QPSK-OFDM networks, an online fully-complex ELM based channel estimation and equalization scheme robust to fading channels based on the 802.11g standard and the nonlinear distortion originated from a high-power amplifier is proposed by Liu et al. [13]. By combining the least square-based decision-directed channel estimation and the ELM algorithm, the received/equalized pilots may be employed to train the SSFN without pre-training and feedback connection between the transmitter and receiver. The ELM defined in the complex domain demonstrates the best BER metric contrasting with the minimum mean-square error and least square channel estimators as well as a deep neural network-based scheme. Methods that amalgamate real and complex ELM regressors for equalization and minimum-distance based symbol slicers for symbol detection are presented in Reference [22] for QPSK-OFDM communications over strong frequency selective channels. To find the output weights matrix, pilot signals are utilized. With the assistance of 1000 hidden neurons, simulations establish that compared to the previous ELM based methods [13,21], the multiple split-complex ELM owns the benefit of higher detection accuracy with a slight complexity increase. On the other hand, the multi-layer perceptron, generalized radial basis function, and robust ELM are proposed in Reference [23] for mitigating nonlinearities in CO-OFDM systems under the 16QAM signaling. All of these equalizers are trained with the Wilcoxon learning algorithm in order to the outliers do not depend on the training data. While the Wilcoxon robust ELM possesses a good generalization capability and fast training speed, the Wilcoxon generalized radial basis function gives the highest value of Q-factor among the rest of the algorithms as well as non-robust approaches based on minimization of least square error principle. ELMs in the real and complex planes for decreasing the chromatic dispersion effect in direct-detection OFDM-based radio-over-fiber systems are revealed by Zabala-Blanco et al. [24]. Immediately, its ELM algorithm is summarized. Based on the comb-type pilot arrangement in an OFDM packet, pilot subcarriers are exploited during each OFDM symbol period in order to obtain a real-time equalization without reducing the effective bit rate. To prevent time limitations and algebraic requirements related to the hidden layer output matrix in the training process, the singular value decomposition approach is adopted [20]. Simulated results report that for the QPSK constellation subject to an additive white Gaussian noise (AWGN) channel, the fully-complex ELM outperforms the fully-real ELM and feasible PAE [4,7] in terms of the BER as well as the complexity modem.
As seen, none of the works of ELM oriented to OFDM have proved its competency in tackling face the laser phase noise in a CO signal, which is one of the major limitations. By considering the overall OFDM frame, as well as the ELM potential against multipath fading channels, we introduce for the first time the SLFN prone to an improved ELM algorithm as equalizer for CO-OFDM systems with wide radio-frequency (RF) linewidths. The architecture of the artificial neural network is given by three layers: the first has two real-inputs (one for each component of the constellation symbol), the second possesses an activation function defined in the real domain for all hidden nodes, and the third supplies a single complex-output. The main contributions of the paper can be summarized as:
- We propose a modified ELM under supervised learning for maximizing the system performance (the BER minimization) of a phase-uncorrelated OFDM signal in the optical domain based on the adoption of the pilot subcarriers as training samples, as well as the consideration of the regularization parameter in the learning stage.
- Taking into account the RF phase error as well as the subcarrier modulation format, we find the sub-optimal ELM parameters (the number of hidden nodes, penalty coefficient, and activation function) that yield the best BER via extensive simulations. This result is explained by the evaluation of the error vector magnitude (EVM) metric in the training as well as testing steps, which can properly quantify the root mean square error for complex numbers in the telecommunication industry.
- We verify that when the Moore–Penrose generalized inverse of the hidden layer output matrix takes into account the regularization parameter, the ELM significantly improves in terms of stability and precision. As a result, the distortion induced by the laser oscillators is less within the constellation symbols.
- For several signal to noise ratio (SNR) levels and RF-linewidth values, we respectively observe the superiority, and competitiveness of the novel ELM algorithm in terms of the BER metric among the benchmark PAE and a fully-real ELM, and the sophisticated ELM defined in the complex plane and non-effective bandwidth CPE compensator for binary phase-shift keying (BPSK) and QPSK modes.
The content of the rest of the paper is organized as follows: Section 2 exposes in detail the foundations of this work (ELMs and OFDM-based CO systems). Section 3 presents the novel ELM algorithm for reducing the RF phase-noise effect in the BER performance. Furthermore, Section 4 shows the numerical-optimization process of the ELM parameters and compares its performance and computational cost with several state-of-the art phase-error mitigation mechanisms. Finally, Section 5 provides some concluding remarks.
2. Background
In this Section, we outline the standard ELMs with the regularization parameter as well as the optical OFDM schemes subject to coherent detection because they are the bases of this work.
2.1. Extreme Learning Machine
The ELM refers to an attractive learning algorithm for SLFNs, which has fast training speed together with good generalization performance [10]. It is characterized by the random assignment of the weights of the input layer as well as the threshold values in the hidden layer and, hence, the training problem is translated into finding the minimum norm least-squares solution of a linear system. The basic ELM may be written as follows [20]:
where H is the output matrix of the hidden layer, is the output weight matrix, T is the matrix of the target output, refers to the activation function, denotes the weight vector between the jth hidden node and the input nodes, represents the n-dimensional input vector of the ith data (n corresponds to the dimension of the input layer), the term means the inner product between and , is the bias of the jth hidden neuron, refers to the output weight vector between the jth hidden node and the output neurons, and denotes the m-dimensional target vector resulted from . Notice that (i) may be any piecewise functions (including discontinuous, differential, nondifferential functions), see Table 1, (ii) as well as can be generated from any continuous probability distribution, such as the uniform distribution on , and (iii) the upper bound of L hidden neurons is given by N distinct observations in order to get an arbitrarily small error . The last observation means that with probability one, as long as demonstrated mathematically in References [10,20]. Here, implies the Frobenius norm. Results of Figure 4 furthermore prove this note. As seen, the basic ELM is trained by N discrete samples and composed by L hidden nodes.

Table 1.
Popular activation functions in extreme learning machines (ELMs).
Following the Moore-Penrose generalized inverse matrix theory and adding a positive constant in order to improve the stability and precision of the ELM, may be find as follows [14]:
where implies the generalized inverse of H, I denotes an identity square matrix of order equals to L if or N otherwise, and C represents the penalty coefficient on the training errors. Therefore, the training algorithm of the improved ELM possesses the following steps:
- Setting the hidden neurons L, the activation function , and the regularization parameter C.
- Randomly choosing the input weights as well as biases .
- Finding the output layer weights via Equation (2), where N samples are known.
This approach eliminates long learning procedures where the hidden layer of SLFNs require to be tuned. Contrasted with classical computational intelligence methods, the ELM gives better generalization performance at an extremely fast training speed and with fewer user interventions.
2.2. Coherent Optical OFDM Network
CO-OFDM is realized via the OFDM modulation in the optical domain accompanied by the coherent detection. As mentioned in the Section 1, it exposes excellent results in terms of the receiver sensitivity and spectral efficiency. Figure 1a shows a simplified model of a CO-OFDM system [28], which consists of five parts: an OFDM modulator, a RF to optical upconverter, a fiber link, an optical to RF down-converter, and an OFDM demodulator.
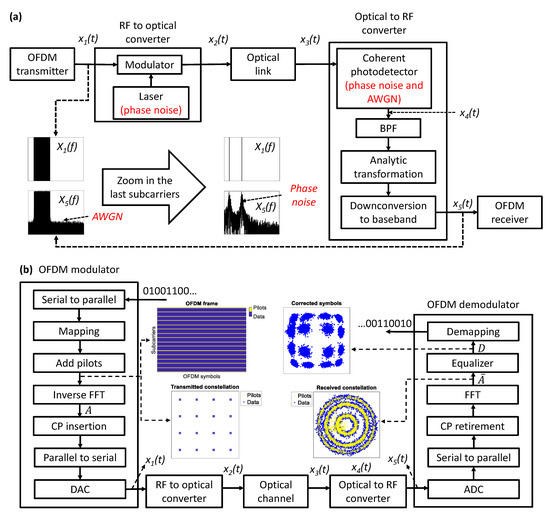
Figure 1.
(a) Block diagram of a coherent optical orthogonal frequency division multiplexing (CO-OFDM) system, where its five parts are noticed. BPF: band pass filter. (b) Structure of the generic OFDM modem whose differences occur in the pilots’ information as well as the equalization stage. ADC: analog-to-digital converter.
At the transmitter end, the input serial data bits are transformed into data pipes and mapped onto corresponding constellation symbols. pilot subcarriers, termed as reference tones, are periodically inserted along the data streams. The digital time-domain signal is obtained by utilizing the inverse FFT, which is subsequently added with a cyclic prefix (CP) to combat with inter-symbol interference resulted from multipath channels, and converted into real-time waveform by using an ideal digital-to-analog converter (DAC) under a fixed sampling rate [29,30], refer to the OFDM transmitter (Figure 1b). The baseband signal of an OFDM symbol can be written as:
where and respectively represent the transmitted data and subcarrier frequency at the kth subcarrier and implies the total number of subcarriers. In terms of the subcarrier index, should be either modulated or unmodulated . As mentioned, reference tones are periodically added among data subcarriers throughout the OFDM symbols, see the OFDM frame of Figure 1b for clarification purposes. establishes the separation between adjacent subcarriers in order to that subcarriers become orthogonal to each other, where T defines the duration of a single OFDM symbol.
The optical-upconversion stage is then realized, where the phase noise variation due to laser oscillator occurs. The modulated signal by a single-frequency laser results in References [4,31]:
where denotes the amplitude of the optical tone, refers to the optical carrier frequency, and is the laser phase noise. is frequency noise with zero mean and autocorrelation function equals to , where and are respectively the laser linewidth parameter and Dirac delta function. The optical OFDM signal convoys via the fiber optical previously being combined with a local oscillator at the coherent receiver, the received signal acquires the form of [8]:
with and * being the impulse response of the optical channel and convolution operation, respectively. Each fiber span consists of chromatic dispersion, numerous stages of high birefringence devices, and polarization dependent on loss elements [28,32]. Taking into account that the phase error resulted by the effect of the fiber chromatic dispersion (the fiber-link penalty in terms of phase noise) results in a time-invariant phase rotation [4,33] that may be eliminated with a single complex multiplication at the OFDM receiver [34,35], a flat channel response is possible to assume that is, . This situation makes strict sense if the RF is much greater than the bandwidth of the OFDM signal [24,30], which is very common for OFDM signals in the optical domain. Besides, our study is focused on the introduction of the improved ELM to enhance the CO-OFDM performance affected by laser phase noises; consequently, linear distortions (chromatic dispersion) and non-linear impairments (fiber non-linearity, intra-channel nonlinearity, among others) [36] are discarded. As future research, results in the case of optical channel model presence by including both linearities and non-linearities must be considered, where the impact of the chromatic dispersion and fiber nonlinearities in the BER depends on the subcarrier position. By considering that the coherent detection implies of heterodyning the optical signal with a continuous-wave optical field previously it falls on the photodetector, the electrical current may be written as [7,32]:
where R corresponds to the responsivity of the photodiode, , and respectively denote the amplitude, frequency, and phase noise of the local oscillator, ℜ is the real part function, implies the RF, and is the RF phase noise, whose linewidth comes from the addition of the laser linewidth and local oscillator linewidth, which in turn is evident via subcarriers characterized by Lorentzian spectra (see Figure 10) [4,31]. Additionally, refers to the AWGN signal for accounting thermal and shot noises, still present in a perfect receiver [37]. After secreting the low frequencies, transforming to an analytic representation with the assistance of the Hilbert transform, and converting to the baseband frequency, the normalized input to the OFDM demodulator is given by [7]:
where represents the baseband AWGN signal, which may be clearly observed through the SNR at the frequency domain (see Figure 9).
By assuming a perfect time and frequency synchronization at the demodulation process, the OFDM symbol is under-sampled with the fixed sampling rate to simulate the ADC process, CP is removed, and FFT is performed, see Figure 1b. The kth received information symbol can be expressed as follows [24,38]:
where refers to the dc component of the RF phase noise, which is known as CPE term, represents the ICI coupling coefficient between two subcarriers with distance of k, and denotes AWGN on the kth subcarrier. is defined as follows [30]:
with being the discrete-time converted RF phase variation. In order to consider all subcarriers of the OFDM symbol, Equation (9) may be expressed in a compact matrix form as:
A certain number of subcarriers across the OFDM spectrum is dedicated for the time-varying channel estimation. As mentioned in the Introduction, the channel frequency response for data subcarriers is usually estimated through linear interpolation from the values given by pilots [39], technique knows as PAE. This kind of equalization has demonstrated high performance and low complexity [4,6,7]. Here, the power of pilot subcarriers comes from the average power of the constellation while the quadrature component (the imaginary part of the symbol in the constellation diagram) of pilots is fixed to 0 for simplicity purposes [5]. In other words, all reference tones are located in a single point of the constellation in the PAE technique. Fortunately, at the same time, this equalizer reduces phase noise for small OFDM symbols [7,40], especially when CPE dominates over ICI in terms of their relative powers.
3. Proposed Extreme Learning Machine Algorithm for Laser Phase-Noise Reduction Purposes
An equalizer based on the standard ELM can be robust against the multipath effects introduced by the wireless channel [13,21,22]. In our work, the improved ELM algorithm is used to increase the RF-linewidth tolerance in CO-OFDM signals, by considering pilot and data subcarriers as training and testing samples, respectively. This noise-mitigation mechanism takes the next advantages: (i) the ELM learning results in a determined linear system [20] and (ii) the position and information for all OFDM pilots are known in the receiver during one symbol period [37]. Unlike the PAE, in the ELM equalizer to obtain a superior accuracy in the testing stage and, hence, a minimum BER, the reference tones must share the in-phase (the real part of the symbol in the constellation diagram) and quadrature components of the M-ary subcarrier modulation format, which in turn must be equal or greater than these. It is desired that each constellation point has the same number of pilot subcarriers so that the BER does not increase for certain data streams. For instance, a QPSK mode requires at least 4 pilots, where both data and pilots are modulated in {1 + 1j, 1 − 1j, −1 − 1j, and −1 + 1j} (its constellation alphabet). By considering practical relationships between data and pilots for spectral efficiency purposes, the proposed equalizer is not useful in the situation of a few tones together with high constellations; here, PAE should be considered [4,6,7]. Notice that in the ELM algorithm as in the PAE method, no additional blocks in the modem as well as no extra overhead in the signal are necessary for getting the phase-error mitigation and channel correction. Namely, the effective transmission rate does not decrease. On the contrary, the spectral efficiency is affected by the use of specific phase-noise mechanisms [8,9]. The reason behind these benefits comes from the exploitation of the common OFDM in the equalizer stage.
In this work, the ELM architecture consists of 2 real input (one for the real part and one for the imaginary part of the points in the constellation), L neurons in the hidden layer defined in the real domain, and 1 complex output (the constellation symbol), see Figure 2 where constants and variables may be identified. After the FFT module, pilot and data subcarriers are separated as well as serialized to accelerate and reinforce the learning procedure. The real-complex (RC) ELM by assuming the pilot subcarriers as training data is introduced for the first time since it could be directly extended to a semisupervised machine learning algorithm [41,42] for enhancing the system performance, but its realization is left for future research. Remember that the origin of phase error in the diverse subcarriers comes from the same oscillators and, hence, the inclusion of some data in the training step should be an overall positive impact. In addition, the conditions of the input weight vectors and biases based on a certain activation function in the complex plane (a fully-complex ELM) [18,19] do not occur in the RC-ELM where a real activation function is considered, by facilitating its realization. Consequently, the output weights thanks to pilot subcarriers acquire the form of:
where ℑ corresponds to the imaginary part of a complex function and i varies from 0 to . Expression (11) synthesizes the learning step, where the number of hidden nodes L, the input weights and biases according to any continuous probability distribution, the activation function , and the regularization parameter C must be firstly specified. As will be observed in Section 4.1, the consideration of C becomes very important because it allows to reduce the impact of the laser phase noise on the BER. The testing performance is then given by the product between the hidden layer output matrix of the modulated symbols with the output weight vector obtained from pilots, namely:
where . As seen, in order to do not reduce the spectral efficiency as well as to achieve a real-time estimation and mitigation of the laser phase noise, the reference tones are only used for properly following the channel impulse response. Finally, points in the constellation are demapped with gray coding and rectangle decision areas.
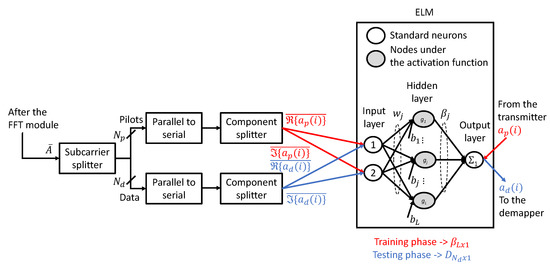
Figure 2.
Structure of the ELM equalizer.
4. Results and Discussion
Based on the setting of References [4,6,7,24,37,43] (common values for CO-OFDM signals), the employed parameters in this work are summarized in Table 2. Various constellations are considered in order to rigorously analyze the benefits and limitations of the SLFN subject to the RC-ELM algorithm to diminish amplitude and phase noises. Note that since the bit rate, number of data and pilots, and CP are fixed, the bandwidth of the OFDM signal at the OFDM-demodulator input (before the ADC) is directly related with the subcarrier modulation format. In fact, the following relationship exists: . Consequently, the OFDM symbol periods correspond to s for BPSK, s for QPSK, and s for 16QAM. By considering a hard-decision forward error correction (FEC) threshold of [2], the RF-linewidth values are adopted according to the subcarrier modulation format in order to properly evaluate the system performance. For practical purposes, the RF linewidth is utilized in the rest of manuscript. Remember that this linewidth comes from the addition of linewidths of the transmitted and received lasers () [31]. Monte Carlo simulation is utilized for determining the performance [44], namely by contrasting the originated and received information in independent runs several times and, then, by computing its arithmetic average.

Table 2.
Parameters used for the CO-OFDM signal.
4.1. Parameters’ Optimization of the Extreme Learning Machine
Initially, we discover the parameters (the number of hidden nodes, regularization parameter, and activation function) of the proposed ELM to avoid the system degradation owing to laser phase noise. AWGN is discarded for the moment.
Taking into account the SIG activation function, Figure 3 depicts the contour plots of the BER metric as a function of the regularization parameter and number of hidden neurons according to (a–c) BPSK, (d–f) QPSK, and (g–i) 16QAM constellations. This function guarantees the universal approximation capability of SLFNs under any learning algorithm, such as the ELM [10,20]. Throughout the manuscript, the input weights and biases are generated from the range based on uniform distribution [24,41]. For each subcarrier modulation format, three outcomes are observed by varying the RF linewidth. As mentioned, the linewidth parameter depends on the number of points in the constellation to determine the system performance around the FEC limit. The BER deteriorates as the bandwidth narrows and the laser phase noise increases, just meaning that a format with higher bit-rate efficiency needs more pure subcarriers at the frequency domain. In detail, the penalty of the adoption of a certain subcarrier modulation format in the BER metric is explained later through normalized linewidths for realizing overall conclusions. For each symbol constellation and phase-noise level, the superior success rate in the testing stage happens in an irregular region dependent on the ELM parameters. In general terms, for coefficient penalties between and and number hidden nodes greater than the number learning samples (pilot subcarriers), the system performance exhibits important enhancement. The highlighted zone in terms of the BER extends for broad lasers. In the following, as well as are adopted as sub-optimal parameters in order to convert these invariants to the symbol constellation and/or mixed linewidth, and get away from the boundaries of the BER degradation.
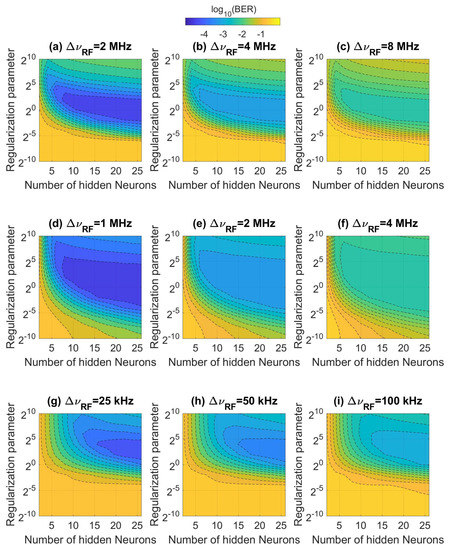
Figure 3.
According to diverse radio-frequency (RF) linewidths and (a–c) binary phase-shift keying (BPSK), (d–f) quadrature phase-shift keying (QPSK), and (g–i) 16QAM subcarrier modulation formats, the BER in terms of the regularization parameter and number of hidden neurons by considering the SIG activation function.
As mentioned in Section 2.1, for further enhancing the ELM behavior, the regularization parameter is added, which is utilized to balance structural and empirical risks. In the absence of this (, refer to the Equation (2)), for (a) BPSK, (b) QPSK, and (c) 16QAM subcarrier modulation formats, Figure 4 depicts the BER against the number of hidden nodes with the combined linewidth as parameter. In other words, here, the inverse of the hidden layer output matrix is determined by employing the singular value method, which averts matrix requirements as well as time consumption [20]. For 16 hidden neurons, the signal deterioration is maximum. Instead, the better performances respectively occur with 4 and 10 hidden nodes for BPSK/QPSK and 16QAM constellations. By contrasting Figure 3 and Figure 4, it is clear that the penalty-coefficient insertion in a standard ELM improves its learning capability, which is more notorious as the constellation points augment, but with the obvious cost of increasing its complexity. Evidently, results of Figure 3 with and Figure 4 where expose similar behaviors. Taking into account the 16QAM signaling and 50-kHz mixed linewidth, for instance, the (BER) goes from −2.6 with 10 hidden neurons and without regularization parameter to −3.2 subject to 18 hidden nodes and a positive constant equals to . Namely, there is a (BER) improvement of −0.6, but the dimension of the hidden layer output matrix and its Moore–Penrose generalized inverse possesses an increase of 8 rows and 8 columns and additionally the summation of the C rectangular matrix must be computed in the learning procedure, refer to expression (2). Note that in our previous study (ELMs to reduce phase error in radio-over-fiber OFDM schemes with direct detection [24]), does not consider the regularization parameter and, consequently, its inclusion could be explored in a next paper. Indeed, this constant is either discarded or not optimized in the rest of the manuscripts about OFDM schemes with the ELM algorithm as equalizer [13,21,22,23]. In the next Subsection, an analysis of the complexity of the proposed ELM and other phase-error mitigation mechanisms is presented.
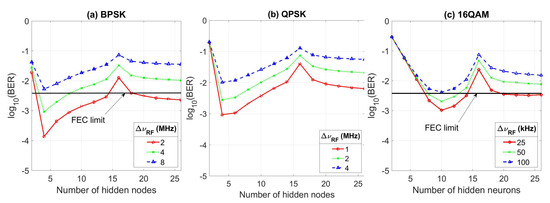
Figure 4.
According to (a) BPSK, (b) QPSK, and (c) 16QAM constellations, the bit error rate (BER) in terms of the number of hidden nodes with the combined linewidth as parameter. The penalty coefficient is not considered.
Figure 5 afterward illustrates the BER as a function of the RF linewidth with the most used activation function as parameter (see Table 1) for the studied subcarrier modulation formats. The impact of the activation function on the system performance augments as the constellation symbols increase and/or phase noise becomes more predominant, where the SIG function outperforms the rest of the functions. The HT function, which is also SIG (s-shaped), has practically the same behavior that the SIG function. In the same context, the worst activation function depends on the number of points in the constellation. For example, the HL and TB functions provide poor results for the BPSK and QPSK modes, respectively. If the equalizer outcome will be a real number, these observations could be attributed to the testing root mean square error, which is commonly used to quantify the effectiveness of any classifier or regressors [10,11,12,14,15,16,17,20,41,42]. Unfortunately, the proposed phase-noise suppression technique provides an output in the complex plane (the points in the constellation). The root mean square EVM is hence employed. It manages to measure how far a symbol constellation is from its perfect location in telecommunication networks [45,46]. In Figure 6, histogram constellations together with EVM values at training as well as testing stages are displayed. For the sake of illustration, the subcarrier modulation format and combined linewidth correspond to 16QAM and 100 kHz, respectively. It can be seen that EVMs in the testing phase explain the superiority in terms of the BER of SIG and HT functions, whose constellations manifest low dispersion. At the same time, the poor results by the use of TB and RB functions make sense, whose constellation shapes do not remain. To further gain insight on the explanation behind these performances, the histogram constellation in the learning stage for each activation function is exposed. While SIG and HT functions present the most regular constellations, the other functions are characterized by scattered symbols; the EVM metric obviously affirms this note. In the rest of the paper, the SIG as activation function is adopted.
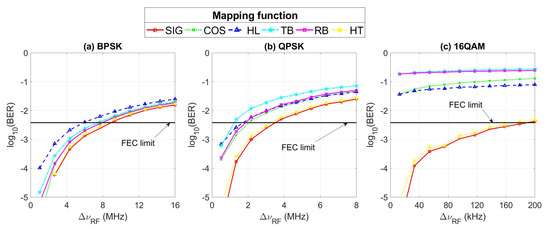
Figure 5.
For the different modulations: (a) BPSK, (b) QPSK, and (c) 16QAM, the system performance as a function of the RF linewidth with the activation function as parameter.

Figure 6.
For (i) SIG, (ii) COS, (iii) HL, (iv) TB, (v) RB, and (vi) HT activation functions, histogram constellations together EVM values at training and testing stages. The subcarrier modulation format and combined linewidth correspond to 16QAM and 100 kHz, respectively.
Finally, the BER in terms of the product between the RF linewidth and the OFDM symbol period for the studied subcarrier modulation formats is displayed in Figure 7. This normalization is done in order to clearly establish the cost of increasing the spectral efficiency on the system performance as long as the bit rate remains constant. For BERs below the FEC threshold (a successfully communication), the RF linewidth decreases by a factor close to 2 and 20 times from BPSK to QPSK and from QPSK to 16 QAM, respectively. These relationships tend to reduce as the BER reaches the FEC limit, which can be attributed to the ELM behavior as the constellation alphabet and phase-noise level augment. Because the system performance of phase-uncorrelated OFDM signals depends on the relationship between the RF linewidth and OFDM symbol period for a certain subcarrier modulation format [2,3,7], this outcome and the rest of observations along the paper are useful for the design and implementation of CO-OFDM schemes.
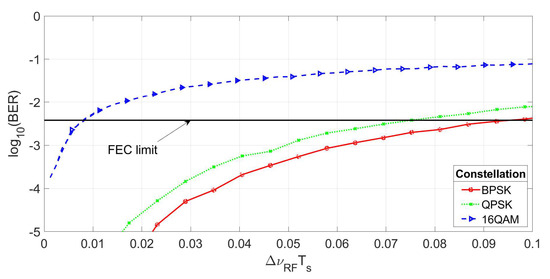
Figure 7.
The BER in terms of the normalized RF linewidth according to the the modulation modes.
4.2. Performance Evaluation
In order to analyze the behavior of the RC-ELM, in Figure 8, we display the BER at SNRs ranging from 0 to 25 dB with the RF linewidth as parameter for five techniques that reduce the laser phase noise: feasible PAE [4,6,7], fully-real ELM (R-ELM) [24], ELM in the complex plane (C-ELM) [24], new ELM algorithm, and conventional CPE compensation [8,40]. One again, (a) BPSK, (b) QPSK, and (c) 16QAM subcarrier modulation formats are taking into account for a complete study of CO-OFDM signals. As mentioned at the end of Section 2.2, the PAE is included in most OFDM modems since it can control frequency-selective impairments by the linear-interpolation of pilot subcarriers in the frequency domain [5] and, furthermore, PAE is able to diminish the low frequencies of phase-noise spectrum. Taking into account that ELMs are suitable for channel estimation and correction purposes [9,13,21,22], ELMs in real and complex planes are recently introduced to eliminate the chromatic-dispersion effect in direct-detection OFDM-based radio-over-fiber systems with the QPSK signaling [24], where the C-ELM is distinguished by low complexity as well as high precision. and SIG activation function, and and HT activation function are adopted for the R-ELM and C-ELM, respectively. These parameters are the ones that obtain the BER enhancement. Notice that here, the penalty coefficient () does not exist in the inverse matrix calculation (). With the cost of some preambles to assistant frame synchronization as well as channel estimation (an extra bandwidth consumption), the CPE term (see Equation (8)) may be effectively mitigated by approximating the mean phase rotation of each OFDM symbol from reference tones and rotating the received constellation points back [9], namely the pilots are only destined for reducing phase noise. As upper and lower bounds, the system performance without phase-error reduction (the worst case) and no susceptible to phase noise (the ideal situation) are depicted, respectively. These limits correspond to theoretical results [3] and are only represented with the black color.
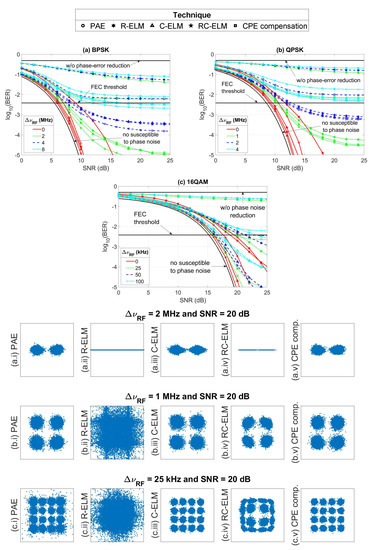
Figure 8.
By considering diverse phase-noise compensation techniques for the studied subcarrier modulation formats, the BER against the SNR with the RF linewidth as parameter. For an SNR of 20 dB and different combined linewidths, Subfigures show constellations.
As expected, the BER enhances as AWGN disappears and/or the combined parameter narrows. The reasons behind these facts result evident via the power spectral densities of the received OFDM-based CO signal, exposed in Figure 9 and Figure 10. The former comes from a phase-noise free simulation, while the latter is a theoretical result without considering CP and AWGN [4,43]. For demonstration purposes, a zoom-in some QPSK subcarriers is depicted, whose OFDM symbol period corresponds to s. On the one hand, the OFDM and AWGN signals overlap inversely proportional to the SNR value, see Figure 9. On the other hand, as the RF-linewidth widens, the phase-noise strength in any subcarrier bandwidth increases, refer to Figure 10. Consequently, a spectrally purer and more powerful CO-OFDM signal leads to the best system performance.
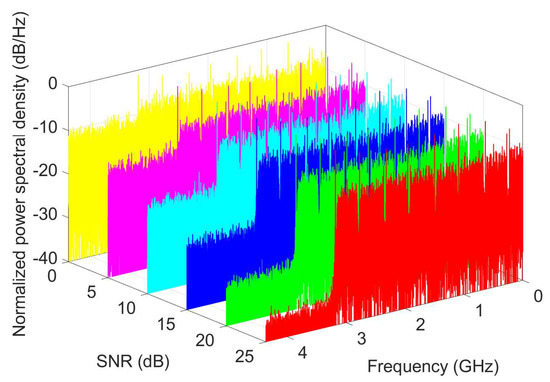
Figure 9.
Taking into account a phase-noise free QPSK-OFDM signal, its positive spectrum as a function of the SNR values.
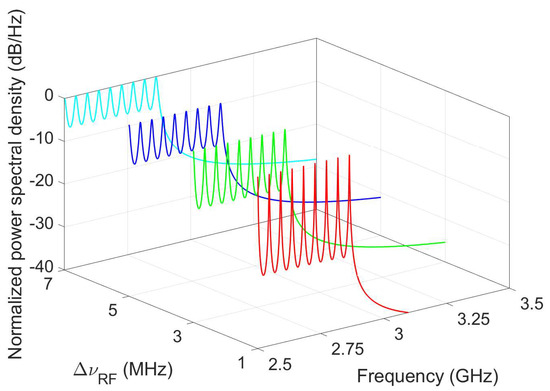
Figure 10.
By considering an unmodulated QPSK-OFDM signal without CP and AWGN, its frequency profile in the last subcarriers as the combined linewidth increases.
In terms of the phase-error reduction, the classic CPE compensation, C-ELM, and proposed method outperform the benchmark PAE, showing more advantages for inefficient spectrally constellations, high SNR values, and regular RF linewidths. In this context, the former is a bit more effective for all CO-OFDM signals, and the C-ELM and RC-ELM expose negligible differences for BPSK and QPSK subcarrier modulation formats. This competitiveness does not happen for the 16QAM constellation, where the C-ELM must be highlighted by its superiority. Finally, even without AWGN, the R-ELM presents incapacity to follow phase noise fluctuations in a single OFDM symbol. For example, the (BER) corresponds to −2.65, −2.8, and 2.85 by using the CPE compensation, C-ELM, and RC-ELM, respectively, according to an SNR equals to 15 dB and a 2-MHz combined linewidth for the QPSK format (see blue curves in Figure 8b). Meanwhile, the FEC limit remains unreachable in the case of adoption of the PAE and R-ELM, whose (BERs) respectively result in −1.9 and −0.6. Notice that if the ratio between data and pilots tends to be 1, the BERs provided by PAE and CPE compensation techniques could be similar (the interpolation and mean operations to obtain the corrected symbols converge to the same result). Because this situation does not happen in our work (refer to Table 1), their BER values differ even under an AWGN channel without phase noise. In the absence of phase noise, the required SNR to overcome the FEC threshold increases as the constellation symbols augments, simply meaning that higher spectral efficiency formats have poorer sensitivity. Instead, without any phase-noise reduction technique, the BER reaches its maximum value for any SNR value (refer to the uncorrected constellation of Figure 1b), by showing that phase error is especial detrimental.
A better understanding of the performance behavior may be accomplished by studying the constellations (after the PAE, R-ELC, C-ELM, RC-ELM, or CPE compensation) for (a) BPSK, (b) QPSK, and (c) 16QAM subcarrier modulation formats, refer to Figure 8. For that end, the SNR value is fixed to 20 dB and the RF-linewidth parameter varies as a function of the modulation in order to clearly perceive the system deterioration. Looking at the point dispersion, it can be seen that whereas for the CPE compensation, the constellation shape remains notorious, the R-ELM practically leads to a stain. The PAE, C-ELM, and CPE compensation produce quasi-circular constellations for all subcarrier modulation formats. Their symbols then suffer a uniform distortion and standard decision regions do not affect the system performance. On the other hand, the constellation shape of the novel ELM changes as a function of its number of symbols. The constellation degradation only happens in the real dimension for BPSK. While the variance noise comes from a non-Gaussian distribution in the QPSK constellation. Finally, the constellation dispersion in 16QAM is determined by the symbol power as follows: the inner points seem to possess a Gaussian degradation, in contrast to the symbol shapes in the periphery that are elliptical with semi-minor and semi-major axes dependent on the magnitude of the complex point. Consequently, in order to broaden the laser oscillators in CO-OFDM schemes, the RC-ELM should be included the demapping process by providing non-rectangular boundaries. However, this improved ELM is left as a pending task.
4.3. Complexity Analysis
Another important issue to analyze is the complexity of the novel ELM. The complexity of the equalization process directly determines the implementation cost of the CO-OFDM scheme with respect to the power consumption and needed hardware. Following the procedure used in studies about ELMs for equalizing OFDM signals [21,24], we develop a comparison of the complexity for the five methods (PAE, R-ELM, C-ELM, RC-ELM, and CPE compensation) in terms of the training, testing, and total times elapsed in the phase-noise correction stage, where the OFDM demodulator would expose modifications in its realization. At the same time, this complexity-evaluation form is usually adopted in standard and modified ELMs [10,18,19,41]. Training and testing phases only make sense when artificial neural networks are employed. In the OFDM transmitter, the in-phase and quadrature components of the reference tones depend on the adopted equalizer as mentioned above; nevertheless, any configuration of the pilots demands the same computational time. By considering the QPSK signaling affected by a combined linewidth of 4 MHz without AWGN for demonstration purposes, 100 trials are carried out and, then, the mean results expressed in seconds are illustrated in Table 3. The CPE compensator is faster than all other techniques. It however necessitates an extra preamble for each OFDM packet for equalization purposes, which is not included in the system model. Consequently, the fully-complex ELM only formed by 2 hidden neurons consumes the minimum resources. On the contrary, the processing time of the R-ELM is the longest due to its composition: two real-valued ELMs of 10 hidden nodes each. Compared with the C-ELM, the augmentation for the benchmark PAE and introduced ELM in the CPU time is near to 1.4 and 2.8 times, respectively. The computational cost of the RC-ELM is expected by the consideration of the regularization parameter as well as the architecture characterized by 24 hidden nodes in order to the BER minimization. Regarding the ELM algorithms, the computational time for learning is higher than the testing step. It may be explained by the Moore-Penrose generalized inverse of the hidden layer output matrix that requires the training phase (see Section 3). The previous observations are obviously software/hardware dependent. A MATLAB R2018a environment running in an Intel Core i5 processor at 2.6 GHz clock speed and 4GB RAM is used.

Table 3.
Average complexity time in seconds.
5. Conclusions
In this manuscript, we introduced a new ELM with its hidden layer defined in the real plane based on the adoption of pilot subcarriers as training set and the inclusion of the regularization parameter in the learning algorithm. The RC-ELM successfully diminishes the distortion caused by the laser phase noises and AWGN in 10 Gbps CO-OFDM networks subject to a negligible computational cost. The obtained results showed that the novel ELM improves the SNR and RF-linewidth requirements below the FEC limit with respect to the feasible PAE and R-ELM for BPSK, QPSK, and 16QAM subcarrier modulation formats. Furthermore, the RC-ELM almost matched in terms of the BER metric the classic CPE and C-ELM, but these techniques present implementation drawbacks. We also demonstrated that (i) the penalty coefficient allows to increase the ELM effectiveness, and (ii) the system performance obtained from an ELM with complex outputs can be explained by quantifying its training and testing root mean square errors through the EVM metric.
Author Contributions
Conceptualization, D.Z.-B.; methodology, D.Z.-B.; software, D.Z.-B. and M.M.; formal analysis, D.Z.-B.; investigation, D.Z.-B.; writing–original draft preparation, D.Z.-B.; writing–review and editing, D.Z.-B., M.M., C.A.A.-M., A.D.F., P.P.J. and I.S.; project administration, D.Z.-B.; funding acquisition, D.Z.-B. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Vicerrectoría de Investigación y Posgrado (VRIP) and Faculty of Engineering Science of the Universidad Católica del Maule.
Acknowledgments
This work was supported by the Laboratory of Technological Research in Pattern Recognition (LITRP), FONDECYT Postdoctorado No. 3190147, CONICYT PFCHA/Beca de Doctorado Nacional/2019 21190489, SENESCYT “Convocatoria abierta 2014-primera fase, Acta CIBAE-023-2014”.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADC | Analog-to-digital converter |
| AWGN | Additive white Gaussian noise |
| BER | Bit error rate |
| BPF | Band pass filter |
| BPSK | Binary phase shift keying |
| C-ELM | Extreme learning machine in the complex plane |
| CO | Coherent optical |
| COS | Cosine |
| CP | Cyclic prefix |
| CPE | Common phase error |
| DAC | Digital-to-analog converter |
| ELMs | Extreme learning machines |
| EVM | Error vector magnitude |
| FEC | Forward error correction |
| FFT | Fast Fourier transform |
| HL | Hard limit |
| HT | Hyperbolic tangent |
| ICI | Inter-carrier interference |
| OFDM | Orthogonal frequency division multiplexing |
| PAE | Pilot-assisted equalization |
| QAM | Quadrature amplitude modulation |
| QPSK | Quadrature phase-shift keying |
| RC | Real-complex |
| RF | Radio frequency |
| SIG | Sigmoid |
| SLFNs | Single-hidden layer feedforward networks |
| SNR | Signal to noise ratio |
| RB | Radial basis |
| R-ELM | Fully-real extreme learning machine |
| TB | Triangular basis |
References
- Wang, Y.; Wang, D.; Ma, J. On the Performance of coherent OFDM Systems in free-space optical communications. IEEE Photonics J. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Gonzalez-Guerrero, L.; Shams, H.; Fatadin, I.; Fice, M.J.; Naftaly, M.; Seeds, A.J.; Renaud, C.C. Single sideband signals for phase noise mitigation in wireless THz-over-fibre systems. J. Lightw. Technol. 2018, 36, 4527–4534. [Google Scholar] [CrossRef]
- Mathecken, P.; Riihonen, T.; Werner, S.; Wichman, R. Performance analysis of OFDM with Wiener phase noise and frequency selective fading channel. IEEE Trans. Commun. 2011, 59, 1321–1331. [Google Scholar] [CrossRef]
- Zabala-Blanco, D.; Campuzano, G.; Aldaya, I.; Castanon, G.; Vargas-Rosales, C. Impact of partial phase decorrelation on the performance of pilot-assisted millimeter-wave RoF-OFDM systems. Phys. Commun. 2018, 26, 106–115. [Google Scholar] [CrossRef]
- Garcia Armada, A.; Calvo Ramon, M. Rapid prototyping of a test modem for terrestrial broadcasting of digital television. IEEE Trans. Consum. Electron. 1997, 43, 1100–1109. [Google Scholar] [CrossRef]
- Ferreira, A.; Dias, B.; de Oliveira, J.A.; Alves, A.; Marconi, J.D.; Campuzano, G.; Pita, J.; Aldaya, I. Optimization of OFDM parameters for 10-Gbps long reach coherent PONs. In Proceedings of the 2019 21st International Conference on Transparent Optical Networks (ICTON), Angers, France, 9–13 July 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Zabala-Blanco, D.; Azurdia-Meza, C.A.; Montejo-Sánchez, S.; Dehghan Firoozabadi, A. OFDM tolerance to additive white Gaussian and laser phase noises in optical heterodyning systems accompanied by the feasible pilot-assisted equalization. Opt. Rev. 2020. [Google Scholar] [CrossRef]
- Yi, X.; Shieh, W.; Ma, Y. Phase noise effects on high spectral efficiency coherent optical OFDM transmission. J. Lightw. Technol. 2008, 26, 1309–1316. [Google Scholar] [CrossRef]
- Randel, S.; Adhikari, S.; Jansen, S.L. Analysis of RF-pilot-based phase noise compensation for coherent optical OFDM systems. IEEE Photonics Technol. Lett. 2010, 22, 1288–1290. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Chen, Z.X.; Zhu, H.Y.; Wang, Y.G. A modified extreme learning machine with sigmoidal activation functions. Neural Comput. Appl. 2013, 22, 541–550. [Google Scholar] [CrossRef]
- Luo, J.; Vong, C.; Wong, P. Sparse Bayesian extreme learning machine for multi-classification. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 836–843. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Mei, K.; Zhang, X.; Ma, D.; Wei, J. Online extreme learning machine-based channel estimation and equalization for OFDM systems. IEEE Commun. Lett. 2019, 23, 1276–1279. [Google Scholar] [CrossRef]
- Luo, X.; Jiang, C.; Wang, W.; Xu, Y.; Wang, J.H.; Zhao, W. User behavior prediction in social networks using weighted extreme learning machine with distribution optimization. Future Gener. Comput. Syst. 2019, 93, 1023–1035. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, J.; Liang, J.; Wang, H. Multi-fault rapid diagnosis for wind turbine gearbox using sparse Bayesian extreme learning machine. IEEE Access 2019, 7, 773–781. [Google Scholar] [CrossRef]
- Kale, A.P.; Sonavane, S. PF-FELM: A robust PCA feature selection for fuzzy extreme learning machine. IEEE J. Sel. Top. Signal Process. 2018, 12, 1303–1312. [Google Scholar] [CrossRef]
- Shafiullah, M.; Abido, M.A.; Al-Hamouz, Z. Wavelet-based extreme learning machine for distribution grid fault location. IET Gener. Transm. Distrib. 2017, 11, 4256–4263. [Google Scholar] [CrossRef]
- Li, M.B.; Huang, G.B.; Saratchandran, P.; Sundararajan, N. Fully complex extreme learning machine. Neurocomputing 2005, 68, 306–314. [Google Scholar] [CrossRef]
- Huang, G.B.; Li, M.B.; Chen, L.; Siew, C.K. Incremental extreme learning machine with fully complex hidden nodes. Neurocomputing 2008, 71, 576–583. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef]
- Muhammad, I.G.; Tepe, K.E.; Abdel-Raheem, E. QAM equalization and symbol detection in OFDM systems using extreme learning machine. Neural Comput. Appl. 2013, 22, 491–500. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, Q.; Jing, Y. Channel equalization and detection with ELM-based regressors for OFDM systems. IEEE Commun. Lett. 2020, 24, 86–89. [Google Scholar] [CrossRef]
- Kaur, G.; Kaur, G. Performance analysis of Wilcoxon-based machine learning nonlinear equalizers for coherent optical OFDM. Opt. Quantum Electron. 2018, 50, 256. [Google Scholar] [CrossRef]
- Zabala-Blanco, D.; Mora, M.; Azurdia-Meza, C.A.; Dehghan Firoozabadi, A. Extreme learning machines to combat phase noise in RoF-OFDM schemes. Electronics 2019, 8, 921. [Google Scholar] [CrossRef]
- Michell, T. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Moustafa, M.M.A.; El-Ramly, S.H.A. Channel estimation and equalization using backpropagation neural networks in OFDM systems. In Proceedings of the IFIP International Conference on Wireless and Optical Communications Networks, Cairo, Egypt, 28–30 April 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Shieh, W.; Bao, H.; Tang, Y. Coherent optical OFDM: Theory and design. Opt. Express 2008, 16, 841–859. [Google Scholar] [CrossRef] [PubMed]
- Mun, K.; Jung, S.; Kang, S.; Han, S. Channel equalization and phase noise compensation free DAPSK-OFDM transmission for Coherent PON System. IEEE Photonics J. 2017, 9, 1–9. [Google Scholar] [CrossRef]
- Peng, W. Analysis of laser phase noise effect in direct- detection optical OFDM transmission. J. Lightw. Technol. 2010, 28, 2526–2536. [Google Scholar] [CrossRef]
- Gallion, P.; Mendieta, F.J.; Leconte, R. Single-frequency laser phase-noise limitation in single-mode optical-fiber coherent-detection systems with correlated fields. J. Opt. Soc. Am. 1982, 72, 1167–1170. [Google Scholar] [CrossRef]
- Agrawal, G.P. Fiber-Optic Communication Systems; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 222. [Google Scholar]
- Yi, X.; Shieh, W.; Tang, Y. Phase estimation for coherent optical OFDM. IEEE Photonics Technol. Lett. 2007, 19, 919–921. [Google Scholar] [CrossRef]
- Lowery, A.J.; Du, L.B. Optical orthogonal division multiplexing for long haul optical communications: A review of the first five years. Opt. Fiber Technol. 2011, 17, 421–438. [Google Scholar] [CrossRef]
- Jansen, S.L.; Morita, I.; Schenk, T.C.; Tanaka, H. Long-haul transmission of 16 × 52.5 Gbits/s polarization-division- multiplexed OFDM enabled by MIMO processing (Invited). J. Opt. Netw. 2008, 7, 173–182. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics; Elsevier: Amsterdam, The Netherlands, 2015; Volume 648. [Google Scholar]
- Zhang, L.; Ming, Y.; Li, J. Suppression of laser phase noise in direct-detection optical OFDM transmission using phase-conjugated pilots. Opt. Commun. 2017, 403, 197–204. [Google Scholar] [CrossRef]
- Mandelli, S.; Gatto, A.; Magarini, M.; Boffi, P.; Martelli, P.; Pecorino, S.; Spalvieri, A. Phase noise impact on directly detected optical OFDM transmission in uncompensated links. In Proceedings of the 18th International Conference on Transparent Optical Networks (ICTON), Trento, Italy, 10–14 July 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Hanzo, L.; Munster, M.; Choi, B.; Keller, T. OFDM and MC-CDMA for Broadband Multi-User Communications, WLANs and Broadcasting; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Zhu, J.; Omomukuyo, O.; Venkatesan, R.; Li, C.; Dobre, O.A. RF-pilot phase noise compensation for long-haul coherent optical OFDM systems. In Proceedings of the IEEE 14th Canadian Workshop on Information Theory (CWIT), St. John’s, NL, Canada, 14 September 2015; pp. 127–130. [Google Scholar] [CrossRef]
- Huang, G.; Song, S.; Gupta, J.N.D.; Wu, C. Semi-supervised and unsupervised extreme learning machines. IEEE Trans. Cybern. 2014, 44, 2405–2417. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wen, Y.; Yang, L. Lagrangian supervised and semi-supervised extreme learning machine. Appl. Intell. 2019, 49, 303–318. [Google Scholar] [CrossRef]
- Wei, C.; Lin, C.; Huang, H.; Liang, W.; Chi, S. Estimation and suppression of dispersion-induced phase noise in W-band direct-detection OFDM radio-over-fiber systems. J. Lightw. Technol. 2014, 32, 3874–3884. [Google Scholar] [CrossRef]
- Guimaraes, D.A. Digital Transmission: A Simulation-Aided Introduction With VISSIM/COMM; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Freiberger, K.; Enzinger, H.; Vogel, C. A noise power ratio measurement method for accurate estimation of the error vector magnitude. IEEE Trans. Microw. Theory Tech. 2017, 65, 1632–1645. [Google Scholar] [CrossRef]
- Wu, K.; Ren, G.; Wang, Q. Error vector magnitude analysis of uplink multiuser OFDMA and SC-OFDMA systems in the presence of nonlinear distortion. IEEE Commun. Lett. 2017, 21, 172–175. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).