Abstract
A problem with the thermogravitational energy transference of a hybrid nanofluid (Al2O3-SiO2/H2O) in a porous space with a central heat-conducting body has been presented and numerical analysis has been performed. Governing equations, transformed in terms of non-dimensional parameters, have been solved by a developed numerical algorithm based on the finite difference technique. The behavior of streamlines and isotherms was investigated, and the impact of various important characteristics is discussed. The variation in the average and local Nusselt numbers was studied; by selecting various appropriate nano-sized particle combinations in hybrid nanosuspension, the desired energy transport strength could be obtained. The results were compared and successfully validated with previous reported numerical and experimental data from the literature.
1. Introduction
Chambers and closed spaces can be found in various industrial systems and equipment, heat exchangers, nuclear power, renewable energy units, etc. (Izadi et al. [1]). The low chemico-physical characteristics of usual Newtonian liquids demand that researchers develop new cooling liquids. As a result of solutions to the considered problem, the idea of suspending nano-sized metallic particles in the water was proposed by Choi [2], who introduced the term “nanofluid” for the first time in 1995. Since then, nanoliquids have provoked significant attention from scientists and engineers. The broad range of current and future applications involving nanosuspensions can be viewed in the monographs by Das et al. [3], Minkowicz et al. [4], Shenoy et al. [5], and Nield and Bejan [6]; and in the review manuscripts by Ambreen and Kim [7], Hemmat Esfe et al. [8], Pandya et al. [9], Ahmadi et al. [10], Pordanjani et al. [11], Mahian et al. [12,13], Keshteli and Sheikholeslami [14], Groşan et al. [15], Sajid and Ali [16], etc.
Nowadays, many published papers are devoted to experimental or numerical analyses of heat transfer processes within hybrid nanosuspensions that can be considered as a new kind of working liquid including two or three solid materials [17,18,19,20]. The solid nano-sized particles employed for the energy transport augmentation of working liquids are: Al2O3–Cu/water, Fe3O4–graphene, graphene, Al2O3–SiO2, etc. In the last few years, such hybrid nanosuspensions have been employed in different engineering and industrial applications, including heat exchangers, solar collectors, chemical reactors, heat sinks, air conditioning systems, and others. Comprehensive reviews of hybrid nanofluids have been presented by Devi and Devi [21,22], Sarkar et al. [23], Akilu et al. [24], Sidik et al. [25], Sundar et al. [26], Babu et al. [17], Hayat and Nadeem [27], Yousef et al. [28], Sajid and Ali [29], Chamkha et al. [30], Izadi et al. [31,32], Suresh et al. [33,34], Soltani and Akbari [35], Leong et al. [36], Waini et al. [37,38,39], and Aly and Pop [40].
Hayat and Nadeem [27] numerically studied 3D hybrid nanosuspension motion over a linearly stretching surface under the effect of rotation, thermal radiation and internal heat generation/absorption. The formulated boundary-layer equations were transformed to ordinary differential equations that were solved numerically. It was found that the energy transport strength at the surface can be improved by using the hybrid nanosuspension. Chamkha et al. [30] numerically investigated the transient natural convection in a semicircular chamber with solid walls of finite thickness. Non-primitive variables with cylindrical coordinates were employed for analysis. The developed finite difference code allowed the analyzing of the impacts of many different parameters, including the Rayleigh number, heat conductivity ratio, nanoadditives concentration, and time. It was revealed that the combination of two kinds of nanoparticles can improve the energy transport strength. The influence of combined magnetohydrodynamic and ferrohydrodynamic effects on hybrid nanosuspension motion in a porous chamber with isothermal surfaces was investigated by Izadi et al. [32]. The Brinkman–Forchheimer approach was employed for the description of nanosuspension transport within porous material. The authors showed that a rise in the heat conductivity ratio leads to the intensification of heat transference. An experimental analysis of the hybrid nanosuspension flow in a circular tube with fixed thermal flux at the borders was conducted by Suresh et al. [34]. The authors defined correlations for the average Nusselt number and liquid friction factor that illustrate a rise in these parameters with the nanoadditives concentration and reduction with the Reynolds number. Ghalambaz et al. [41] computationally scrutinized the thermal convective energy transport of a hybrid nanoliquid in a square porous cavity with vertical solid walls of finite thickness under the influence of a local thermal non-equilibrium approach to the transport processes within the porous material. The finite element method was used for analysis. The authors ascertained that the addition of nano-sized particles of Ag and MgO to water results in a reduction in the mean Nusselt number.
Nowadays, many papers are devoted to convective energy transport in hybrid nanoliquids in the case of motion along the stretching/shrinking sheets under the influence of various factors [37,38,39,40].
The aim of the present analysis was to computationally investigate natural convection in a porous closed space saturated with a hybrid nanosuspension under the effects of an internal heat-conducting block and horizontal temperature difference. Considering the literature survey performed, thermogravitational convection in a porous chamber with an internal solid body filled with a hybrid nanofluid is analyzed for the first time in this manuscript. Moreover, here, non-primitive variables were employed for the description of convective transport within a double-connected region. Such an approach included a mathematical equation related to the definition of the stream function value at the surface of the inner solid block. Therefore, the developed numerical technique for the nanoliquid within a clear medium presented in [42] was generalized here for the case of the porous medium and hybrid nanoliquid. In addition, a detailed analysis of the nanoadditives’ concentration with the permeability of the porous material allows an opportunity to understand how to intensify the convective transport within such a domain of interest.
2. Control Equations and Conditions
Free convection in a porous chamber filled with a hybrid nanoliquid with a bottom border the size of L was scrutinized. Figure 1 demonstrates the proposed enclosure and some boundary conditions. The considered region contained a porous medium. The bottom and upper borders were thermally insulated, while the left boundary was hot (Th) and the right border was cold (T = Tc). The thermal-conducting body was placed in the center of the region. The hybrid nanofluid included two kinds of solid nano-sized additives; their characteristics are demonstrated in Table 1. Heat equilibrium between the liquid phase and nano-sized particles was assumed.

Figure 1.
Engineering sketch and mathematical conditions.

Table 1.
The physicochemical characteristics of the host liquid, Al2O3 and SiO2 nano-sized particles, solid matrix of porous material and central block material [30,41,43].
The Brinkman porous approach was used for the momentum transport inside the porous chamber. The dimensional control equations can be written as [30,41]:
In the case of the internal heat-conducting block, an additional heat conduction equation has been included in the following form [42,43]
The nanosuspension chemical characteristics were [30,31,32]:
- hybrid nanosuspension density,
- hybrid nanofluid buoyancy coefficient
- hybrid nanofluid heat capacitance
- hybrid nanofluid thermal conductivity
- hybrid nanofluid viscosity
- porous medium thermal conductivity saturated with hybrid nanofluid
- and porous medium heat capacity ratio
The written basic Equations (1)–(5) have been transformed into a dimensionless form using
stream function ψ and vorticity . As a result, Equations (1)–(5) are
In the case of the internal heat-conducting solid body, we should add to the previous system of equations the following non-dimensional heat conduction equation
Additional conditions are
Here λ = λmhnf/λb is the thermal conductivity ratio and H1(ϕ), H2(ϕ), H3(ϕ,ε), H4 are given by
An investigation of the energy transport strength can be performed using the local (Nu) and mean Nusselt numbers
3. Computational Technique and Validation
Equations (7)–(10) with additional relations (11) were calculated on the basis of the finite difference technique [30,44,45]. Finite differences of the second order were used for the spatial derivatives and the first order finite differences were used for the time derivatives. The convective terms were approximated on the basis of the monotonic Samarskii scheme, while the diffusive terms were approximated using the central differences. It should be noted that the difference Poisson equation for the stream function was worked out by the successive over-relaxation method. The optimal value of the relaxation parameter was defined by numerical experiments. The parabolic equations for vorticity and temperature were solved using the local one-dimensional Samarskii scheme and the obtained system of one-dimensional difference equations were solved by means of the Thomas algorithm. It should be noted that the numerical analysis of convective heat transfer within a double-connected region was performed employing non-primitive variables, and as a result, a special numerical algorithm has been developed for the definition of the stream function value at the inner block surface. A detailed description of this technique can be found in [42,46]. The described numerical approach was implemented using the C++ programming language.
The developed numerical program was validated using the computational data of Das and Reddy [47] and Garoosi and Rashidi [48] for free convection in a differentially heated chamber with a centered heat-conducting body. Figure 2 and Figure 3 show a good comparison for the isolines of stream function and temperature between the obtained results and numerical data [47,48] for different Rayleigh numbers.

Figure 2.
Isolines of ψ and θ for a Rayleigh number (Ra) = 106, : a shows the numerical data of [47], b shows the obtained results, c shows the numerical data of [48].

Figure 3.
Isolines of ψ and θ for Ra = 106, : a shows the numerical data of [47], b shows the obtained results, c shows the numerical data of [48].
A grid sensitivity study was performed for free convection in a porous chamber filled with a hybrid nanosuspension at Ra = 106, P = 6.82, Da = 10−3, ε = 0.8, . Steel was the material of the internal block, and the dimensionless size of the internal block δ = 0.5. Three different grids of 100 × 100 points, 200 × 200 points, and 400 × 400 points were investigated. Figure 4 demonstrates the influence of the mesh characteristics on the time profiles of the mean Nusselt number of the heated border.

Figure 4.
Time profiles of the mean Nusselt number for different mesh parameters.
As a result of this mesh analysis, the grid of 200 × 200 points has been selected for studying.
4. Results and Discussion
Numerical research was conducted on the Rayleigh number (Ra = 106), Prandtl number (Pr = 6.82), Darcy number (Da = 10−4–10−1), porosity (ε = 0.8), nanoparticles’ volume fraction, and internal block material () (glass, steel, copper). The influence of these mentioned parameters on the hybrid nanofluid circulation and energy transference within the enclosure was tested. The isolines of ψ and θ and profiles of Nu and were investigated in Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.
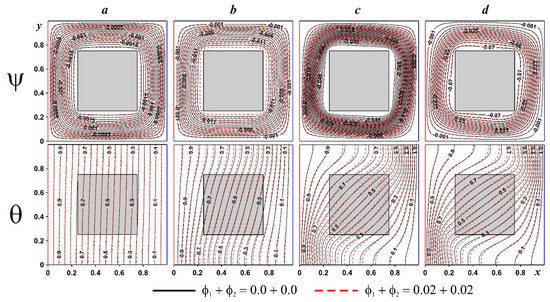
Figure 5.
Isolines of ψ and θ for the steel internal block: a shows a Darcy number (Da) = 10−4, b shows Da = 10−3, c shows Da = 10−2, d shows Da = 10−1.
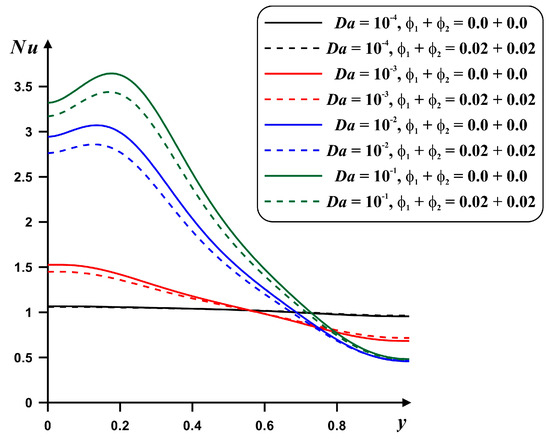
Figure 6.
Profiles of the local Nusselt number (Nu) for the steel internal block, various Darcy numbers and nanoparticles’ concentration.
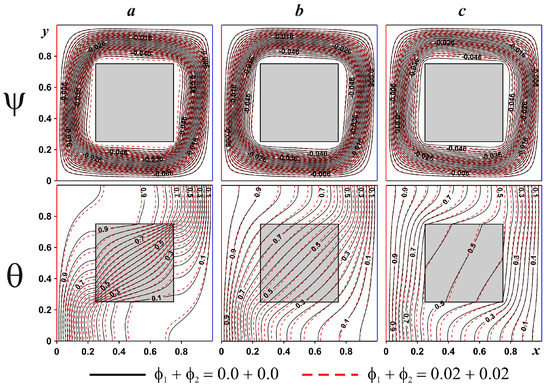
Figure 7.
Isolines of ψ and θ for Da = 10−2: a shows the glass internal block, b shows the steel internal block, c shows the copper internal block.

Figure 8.
Profiles of the mean Nusselt number for various Darcy numbers and nanoadditives’ concentrations: a shows for the glass internal block, b shows for the steel internal block, c shows for the copper internal block.
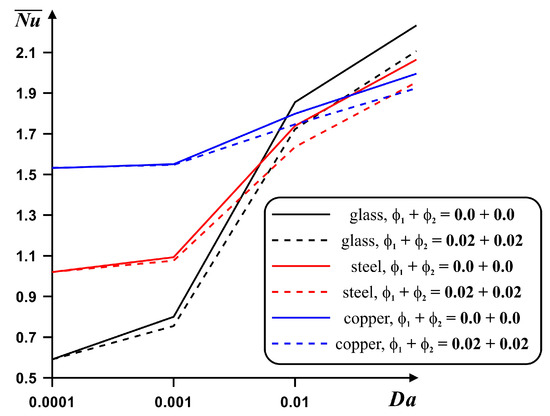
Figure 9.
Profiles of average Nu for various Darcy numbers, nanoadditives’ concentrations and internal solid block materials.
Figure 5 demonstrates the isolines of ψ and θ within the chamber for various Darcy numbers and nano-sized additives’ concentrations. For low Da numbers (Da = 10−4), a weak clockwise circulation appeared inside the region, while the temperature field illustrated the dominant heat conduction. A rise in Da resulted in a strengthening of liquid motion, causing a small distortion of isotherms. The latter reflected an interaction between the hot liquid in the upper part with a cold right wall and the cold liquid in the bottom part with a hot left border. A further increase in the porous medium’s permeability caused a strengthening of the convective circulation and more essential distortion of the temperature pattern, with a generation of boundary layers by the isothermal borders. It is worth highlighting that for Da ≥ 10−2, the streamlines illustrated a formation of irregular circulation where one could find the boundary layer separation near the surface of the internal block from the leeward side. The addition of nano-sized particles reflected the appearance of some differences in the temperature field, while the isolines of stream function had weak changes. The isotherms described a less strong cooling of the lower zone and less intensive heating of the upper zone with nano-sized particles. It is important to emphasize the temperature changes within the solid block when the nanoparticles’ volume fraction was increased. In the considered case, nanoadditives were introduced for 2% of Al2O3 and 2% of SiO2.
Figure 6 represents Nu profiles dependent on the vertical coordinate for various Da numbers. As has been mentioned above, a low Da (Da = 10−4) characterized a constant magnitude of Nu where the heat convection was very low. For Da = 10−3, Nu diminished with the y-coordinate owing to a reduction in the temperature gradient from the bottom border, where an interaction between the cold liquid and hot wall occurred, to the upper one, where it was possible to reveal an enlargement of the thermal boundary layer. For Da ≥ 10−2, Nu rose with y for a short zone (y < 0.2) and after that Nu decreased. The small increase in Nu that occurred for y < 0.2 can be explained by a vertical displacement of the interaction zone between the cold liquid and hot surface of the bottom part. Moreover, a rise in the Darcy number (Da ≥ 10−2) did not cause any essential changes in the upper part of the hot wall, while Nu increased in the bottom part with Da. The addition of nanoadditives characterized a diminution of Nu in the lower zone and an increase in Nu in the top part for Da < 10−2. For Da ≥ 10−2, Nu decreased with φ. Moreover, Nu increased with the growth in Da in the lower part of the cavity and it decreased with Da in the upper part. This confirms that heat transport is enhanced there due to the heated left border.
Figure 7 represents the isolines of ψ and θ for different internal block materials: glass, steel, and copper. The flow structure did not change with the internal block material. One can find only low suppression of internal circulation for copper in comparison with steel and glass. The temperature pattern depended on the solid block material. In the case of the glass solid block with low thermal conductivity, the temperature within this block changed from 0.1 to 0.9, with essential heating in the top left corner and significant cooling in the lower right corner. For the steel solid block, one could find that the isotherms within the solid block had not some distortions due to the similar thermal conductivity. Namely, the material of the porous medium solid matrix was aluminum and the nanosuspension heat conductivity within the porous domain was similar to the thermal conductivity of the solid block material. Therefore, isotherms in the case of steel did not have any distortions at the internal block surface. In the case of the copper solid block, which had a high thermal conductivity, there was significant heating/cooling of this central block.
The behavior of average Nu with various Da, nanoadditives’ concentrations and internal solid block materials is presented in Figure 8. The mean Nu increased with Da. For high considered Da (10−2), a rise in the internal solid block material’s heat conductivity resulted in a reduction in the mean Nu. Such behavior is explained by a stronger interaction between the cold nanosuspension and hot wall in the bottom part. It should be noted also that with an increase in the solid block’s heat conductivity, the transition for two zones of Da, namely, (10−3, 10−2) and (10−2, 10−1), became inconspicuous. A rise in the concentration of nano-sized particles characterized a diminution of average Nu and this reduction became great for high Da. Additionally, a rise in the nanoadditives’ concentration for low Darcy numbers (10−4,10−3) of the considered internal solid block materials did not have a strong influence on average Nu.
Figure 9 demonstrates the influence of all the considered parameters on the mean Nu. A rise in the solid block material’s thermal conductivity for Da < 0.005 resulted in an increase in the mean Nu. While for Da > 0.005, one could find non-linear behavior, for Da > 0.05, one could find the opposite situation. The thermal transference strength increased with Da, and such a rise was strong in the case of internal solid blocks with low thermal conductivities. The addition of nanoadditives suppressed the convective energy transport.
5. Conclusions
The thermogravitational energy transference of hybrid water-based nanosuspension in a porous chamber with an internal thermal-conducting block has been scrutinized computationally. Transport equations based on the single-phase nanofluid approach and Brinkman porous model were worked out using the finite difference technique. The impacts of the Darcy number, nanoadditives concentration and internal solid block material on the liquid motion structure and heat transference patterns were investigated. The obtained results show that: (1) a rise in Da accelerates the convective circulation and energy transport; (2) the addition of nano-sized solid particles suppresses the flow strength and thermal transference intensity; (3) a growth in the internal solid block material’s thermal conductivity intensifies the thermal transmission for Da < 0.005, but for Da > 0.05, an increase in the considered heat conductivity reduces the energy transference intensity.
Author Contributions
Conceptualization, M.A.S., D.S.C. and I.P.; methodology, M.A.S., D.S.C. and I.P.; software, M.A.S.; validation, M.A.S.; investigation, M.A.S., D.S.C. and I.P.; writing—original draft preparation, M.A.S., D.S.C. and I.P.; writing—review and editing, M.A.S., D.S.C. and I.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work of Mikhail A. Sheremet was supported by the Russian Science Foundation (Project No. 17-79-20141).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Izadi, S.; Armaghani, T.; Ghasemiasl, R.; Chamkha, A.J.; Molana, M. A comprehensive review on mixed convection of nanofluids in various shapes of enclosures. Powder Technol. 2019, 343, 880–907. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, FED 231/MD, San Francisco, CA, USA, 12–17 November 1955; Volume 6, pp. 99–105. [Google Scholar]
- Das, S.K.; Choi, S.U.S.; Yu, W.; Pradeep, Y. Nanofluids: Science and Technology; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Minkowycz, W.J.; Sparrow, E.M.; Abraham, J.P. Nanoparticle Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Shenoy, A.; Sheremet, M.; Pop, I. Convective Flow and Heat Transfer from Wavy Surfaces: Viscous Fluids, Porous Media and Nanofluids; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ambreen, T.; Kim, M.-H. Influence of particle size on the effective thermal conductivity of nanofluids: A critical review. Appl. Energy 2020, 264, 114684. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Hassan Kamyab, M.; Valadkhani, M. Application of nanofluids and fluids in photovoltaic thermal system: An updated review. Sol. Energy 2020, 199, 796–818. [Google Scholar] [CrossRef]
- Pandya, N.S.; Shah, H.; Molana, M.; Tiwari, A.K. Heat transfer enhancement with nanofluids in plate heat exchangers: A comprehensive review. Eur. J. Mech./B Fluids 2020, 81, 173–190. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ghazvini, M.; Sadeghzadeh, M.; Nazari, M.A.; Ghalandari, M. Utilization of hybrid nanofluids in solar energy applications: A review. Nano-Struct. Nano-Objects 2019, 20, 100386. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Aghakhani, S.; Afrand, M.; Mahmoudi, B.; Mahian, O.; Wongwises, S. An updated review on application of nanofluids in heat exchangers for saving energy. Energy Convers. Manag. 2019, 198, 111886. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estelle, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid flows—Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estelle, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S.; et al. Recent advances in modeling and simulation of nanofluid flows—Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Keshteli, A.N.; Sheikholeslami, M. Nanoparticle enhanced PCM applications for intensification of thermal performance in building: A review. J. Mol. Liq. 2019, 274, 516–533. [Google Scholar] [CrossRef]
- Groşan, T.; Sheremet, M.A.; Pop, I. Heat transfer enhancement in cavities filled with nanofluids. In Advances Heat Transfer Fluids: From Numerical to Experimental Techniques; Minea, A.A., Ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 267–284. [Google Scholar]
- Sajid, M.U.; Ali, H.M. Recent advances in application of nanofluids in heat transfer devices: A critical review. Renew. Sustain. Energy Rev. 2019, 103, 556–592. [Google Scholar] [CrossRef]
- Ranga Babu, J.A.; Kiran Kumar, K.; Srinivasa Rao, S. State-of-art review on hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Hybrid nanofluids for heat transfer applications—A state of the art review. Int. J. Heat Mass Transf. 2018, 125, 82–103. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Entropy generation of nanofluid and hybrid nanofluid flow in thermal systems: A review. J. Mol. Liq. 2020, 302, 112533. [Google Scholar] [CrossRef]
- Salman, S.; Abu Talib, A.R.; Saadon, S.; Hameed Sultan, M.T. Hybrid nanofluid flow and heat transfer over backward and forward steps: A review. Powder Technol. 2020, 363, 448–472. [Google Scholar] [CrossRef]
- Devi, S.U.; Devi, S.A. Numerical investigation of three-dimensional hybrid Cu–Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Devi, S.U.; Devi, S.A. Heat transfer enhancement of Cu–Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energ. Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Akilu, S.; Sharma, K.V.; Baheta, A.T.; Mamat, R. A review of thermophysical properties of water based composite nanofluids. Renew. Sustain. Energ. Rev. 2016, 66, 654–678. [Google Scholar] [CrossRef]
- Sidik, N.A.; Adamu, I.M.; Jamil, M.M.; Kefayati, G.H.; Mamat, R.; Najafi, G. Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review. Int. Commun. Heat Mass Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa, A.C. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor—A review. Renew. Sustain. Energ. Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Results Phys. 2017, 7, 2317–2324. [Google Scholar] [CrossRef]
- Yousefi, M.; Dinarvand, S.; Yazdi, M.E.; Pop, I. Stagnation-point flow of an aqueous titania-copper hybrid nanofluid toward a wavy cylinder. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1716–1735. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M. Thermal conductivity of hybrid nanofluids: A critical review. Int. J. Heat Mass Transf. 2018, 126, 211–234. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Miroshnichenko, I.V.; Sheremet, M.A. Numerical analysis of unsteady conjugate natural convection of hybrid water-based nanofluid in a semicircular cavity. J. Therm. Sci. Eng. Appl. 2017, 9, 041004. [Google Scholar] [CrossRef]
- Izadi, M.; Mohebbi, R.; Karimi, D.; Sheremet, M.A. Numerical simulation of natural convection heat transfer inside a ┴ shaped cavity filled by a MWCNT-Fe3O4/water hybrid nanofluids using LBM. Chem. Eng. Process. Process Intensif. 2018, 125, 56–66. [Google Scholar] [CrossRef]
- Izadi, M.; Oztop, H.F.; Sheremet, M.A.; Mehryan, S.A.M.; Abu-Hamdeh, N. Coupled FHD-MHD free convection of a hybrid nanoliquid in an inversed T-shaped enclosure occupied by partitioned porous media. Numer. Heat Transf. A 2019, 76, 479–498. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3–Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloid. Surf. A-Phys. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Effect of Al2O3–Cu /water hybrid nanofluid in heat transfer. Exp. Therm. Fluid Sci. 2012, 38, 54–60. [Google Scholar] [CrossRef]
- Soltani, O.; Akbari, M. Effects of temperature and particles concentration on the dynamic viscosity of MgO-MWCNT/ethylene glycol hybrid nanofluid: Experimental study. Phys. E Low Dimens. Syst. Nanostruct. 2016, 84, 564–570. [Google Scholar] [CrossRef]
- Leong, K.Y.; Ahmad, K.K.; Ong, H.C.; Ghazali, M.J.; Baharum, A. Synthesis and thermal conductivity characteristic of hybrid nanofluids–a review. Renew. Sustain. Energ. Rev. 2017, 75, 868–878. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–290. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Flow and heat transfer along a permeable stretching/shrinking curved surface in a hybrid nanofluid. Phys. Scr. 2019, 94, 105219. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow and heat transfer over a nonlinear permeable stretching/shrinking surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3110–3127. [Google Scholar] [CrossRef]
- Aly, E.; Pop, I. MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3012–3038. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Sheremet, M.A.; Mehryan, S.A.M.; Kashkooli, F.M.; Pop, I. Local thermal non-equilibrium analysis of conjugate free convection within a porous enclosure occupied with Ag-MgO hybrid nanofluid. J. Therm. Anal. Calorim. 2019, 135, 1381–1398. [Google Scholar] [CrossRef]
- Pop, I.; Sheremet, M.A.; Grosan, T. Thermal convection of nanoliquid in a double-connected chamber. Nanomaterials 2020, 10, 588. [Google Scholar] [CrossRef]
- Sivaraj, C.; Sheremet, M.A. MHD natural convection in an inclined square porous cavity with a heat conducting solid block. J. Magn. Magn. Mater. 2017, 426, 351–360. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Oztop, H.F.; Abu-Hamdeh, N. Natural convection of nanofluid inside a wavy cavity with a non-uniform heating: Entropy generation analysis. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 958–980. [Google Scholar] [CrossRef]
- Astanina, M.S.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. MHD natural convection and entropy generation of ferrofluid in an open trapezoidal cavity partially filled with a porous medium. Int. J. Mech. Sci. 2018, 136, 493–502. [Google Scholar] [CrossRef]
- Shulepova, E.V.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Mixed convection of Al2O3–H2O nanoliquid in a square chamber with complicated fin. Int. J. Mech. Sci. 2020, 165, 105192. [Google Scholar] [CrossRef]
- Das, M.K.; Reddy, S.K. Conjugate natural convection heat transfer in an inclined square cavity containing a conducting block. Int. J. Heat Mass Transf. 2006, 49, 4987–5000. [Google Scholar]
- Garoosi, F.; Rashidi, M.M. Two phase flow simulation of conjugate natural convection of the nanofluid in a partitioned heat exchanger containing several conducting obstacles. Int. J. Mech. Sci. 2017, 130, 282–306. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).