Abstract
In this article, vibration of viscoelastic axially functionally graded (AFG) moving Rayleigh and Euler–Bernoulli (EB) beams are investigated and compared, aiming at a performance improvement of translating systems. Additionally, a detailed study is performed to elucidate the influence of various factors, such as the rotary inertia factor and axial gradation of material on the stability borders of the system. The material properties of the beam are distributed linearly or exponentially in the longitudinal direction. The Galerkin procedure and eigenvalue analysis are adopted to acquire the natural frequencies, dynamic configuration, and instability thresholds of the system. Furthermore, an exact analytical expression for the critical velocity of the AFG moving Rayleigh beams is presented. The stability maps and critical velocity contours for various material distributions are examined. In the case of variable density and elastic modulus, it is demonstrated that linear and exponential distributions provide a more stable system, respectively. Furthermore, the results revealed that the decrease of density gradient parameter and the increase of the elastic modulus gradient parameter enhance the natural frequencies and enlarge the instability threshold of the system. Hence, the density and elastic modulus gradients play opposite roles in the dynamic behavior of the system.
1. Introduction
Axially moving beams are broadly explored in various engineering industries, such as telescopic robotic manipulators, band-saw blades, crane hoist cables, high-speed magnetic tapes, and thread lines in the textile industry. For this reason, numerous researchers have devoted considerable attention to the accurate mathematical modeling and dynamic behavior of these applicable structures [1,2,3,4]. Wickret [5] analyzed the nonlinear vibrations of pre-tensioned traveling beams and explained the influence of initial tension and flexural stiffness on the free vibration response. Ghayesh and Amabili [6] numerically solved the forced nonlinear vibrations of axially moving beams and extracted the bifurcation points and steady-state response of the considered system. Chen and Yang [7] inspected the parametric dynamics of axially moving viscoelastic systems with hybrid supports subjected to a fluctuating axial velocity. In the mentioned paper, the natural frequencies, mode shapes, and critical velocity of the system were obtained for different system parameters. Gou and co-workers [8] modeled the coupled thermo-elastic dynamic of axially moving beams. They deduced that the stability borders of these systems are highly dependent on the coupled thermo-elastic factor and beam translation speed. Oz and Pakdemirli [9] considered the vibration mechanism of moving beams with a time-dependent velocity. Their results disclosed that when the amplitude of velocity fluctuations of the system ascends, the stability regions expand. Employing the artificial parameter method, Yang et al. [10] discussed different aspects of the vibrational behavior of moving beams. Additionally, they acquired the closed-form approximated solutions for the natural frequencies of axially moving beams and determined the dynamic stability of these systems systemically. Vibrational performance and stability conditions of accelerating viscoelastic beams surveyed by Chen et al. [11]. They discovered that in the first subharmonic resonance, decreasing the initial stress and increasing the average axial velocity had the same influence on the instability threshold of the beam. Kiani [12] focused on the transverse free vibration instability of nanobeams with axial motion resting on an elastic substrate. He scrutinized the influence of shear and surface energies on the divergence and flutter boundaries. In contrast to the case of Euler–Bernoulli beams with axial motion, the literature on the Rayleigh and Timoshenko moving beams is limited [13,14,15,16,17]. Within this context, Zhou and Chang [18] studied the vibration, stability, and gyroscopic characteristics of rotating Rayleigh beams. They found that by increasing the rotational inertia of the beam, the stability is reduced. Dehrouyeh-Semnani et al. [19] carried out a numerical investigation on the vibration characteristics of axially moving microbeams based on the Timoshenko beam theory. Their numerical results obtained the size-dependent frequencies and critical velocities of the system for clamped-clamped and supported boundary conditions.
Preventing instability and unwanted vibration is a crucial requirement in the engineering design of axially moving continua. Heretofore, engineers have suggested various active and passive vibration control methods to annihilate the excessive vibrations of axially moving structures [20,21]. For instance, Li et al. [22] addressed the active nonlinear dynamic control of axially moving strings using boundary velocity feedback. They showed that the vibrations of the string could be effectively dampened through negative linear velocity feedback at either the upstream or downstream of the system. Zhang et al. [23] attended the passive and adaptive vibration attenuation of axially moving beams attached to nonlinear energy sinks. Their results indicated that the performance of the nonlinear absorbers could be appropriately promoted by adjusting the mass parameter. In all the studies mentioned above, the constituent materials of the moving systems are homogenous and isotropic. During recent years, with the aid of modulating materials properties, engineers improved the mechanical behavior of the moving systems [24,25,26]. In this sense, employing the multiple scales method, the nonlinear forced vibration of axially moving sandwich viscoelastic beams was studied by Li et al. [27]. They obtained the dynamic response and instability boundaries of the considered beam for various values of the core layer thickness and initial tension. Ghayesh [28] concentrated on the dynamic behavior of the moving laminated composite beams and determined the critical velocity, natural frequencies, and mode shapes of the considered system. Lv et al. [29] numerically and analytically inspected the nonlinear lateral dynamics of viscoelastic sandwich beams with varying axial motion and tension. They concluded that applying higher initial tension in the system diminishes the natural frequencies.
To eliminate the structural limitations, researchers introduced novel composite materials known as functionally graded (FG) materials. FG materials are fabricated by smooth and continuous variations of two or more constituent materials in a preferred direction from one surface to another [30,31,32,33]. Compared to the conventional isotropic and laminated materials, FG materials are utilized broadly in the complex engineering applications due to their supreme mechanical characteristics such as lower stress concentration, higher corrosion, and fracture resistance [34,35]. Although FG materials have great potential in the design and development of advanced axially moving components, there are limited studies in this area. In this regard, Piovan and Sampaio [36] carried out the vibration analysis of sliding beams made of FG materials during deploying and retrieving. They supposed that the material characteristics of the system alter according to a power-law function. Furthermore, they evaluated the influence of the acceleration and material constituents on the dynamic response of the system. Sui et al. [37] assessed the lateral dynamics of FG Timoshenko beams with axial motion. They determined the critical velocity and natural frequencies of the considered beam in terms of the length to thickness ratio and FG power index. Kiani [38] presented an analytical study on the transverse and longitudinal vibrations of FG nanobeams within the framework of nonlocal Rayleigh theory. He described the influence of scale parameter and power FG index on the instability threshold of the system. Recently, Yan et al. [39] accomplished the nonlinear vibration of FG beams with axial motion by considering the influence of geometric nonlinearity and axial force. They reported the conditions of occurrence of subharmonic resonance in the system by utilizing the direct multiscale method.
Based on the authors’ knowledge, the previous studies performed on the dynamics of axially moving FG beams considered the gradation of mechanical characteristics of the system along the thickness direction. Despite the importance of metrical gradation through the axial direction, dynamic analysis of moving AFG Rayleigh beams has not been described in the literature. Motivated by this issue, in the current study, the stability enhancement of supported axially moving Rayleigh and EB beams utilizing AFG materials is comprehensively investigated numerically and analytically. Additionally, an in-depth clarification of the effect of various essential parameters such as rotary inertia factor and axial grading of materials on the dynamic features of the axially moving beams, as well as their physical interpretations are presented. It is supposed that the material characteristics of the moving beam are varying exponentially or linearly in the longitudinal direction. The dynamic equation of the considered system is derived from Hamilton’s principle. Then, the reduced-order equation of the system is obtained by implementing Galerkin method, and an eigenvalue problem is carried out. The instability regions of axially moving AFG beam are detected. To confirm the accuracy of the used approach, a comparison study with the available results in the literature is conducted. Time response, natural frequencies, and critical velocity of the considered system are acquired numerically. Additionally, an exact analytical expression is obtained for the critical divergence velocity of AFG moving Rayleigh beams. Finally, the influence of key factors on the vibrational response and instability boundaries of the system are elucidated.
2. Mathematical Modeling
In Figure 1, a viscoelastic AFG moving beam is depicted. It is supposed that the beam with simply supported boundary conditions moves with a constant velocity V and is subjected to axial tension load P. Length, cross-sectional area. as well as moment of inertia of the beam are denoted by L, A, and I, respectively.
Figure 1.
Schematic of a moving beam composed of axially functionally graded materials.
The density, ρ(x), and elastic modulus, E(x), of the beam vary along the axial direction linearly or exponentially as follows:
where:
in which αρ and αE represent the density and elastic modulus gradient parameters, respectively. They can be declared as follows:
It is found that at x = 0, E = E0, and ρ = ρ0. Furthermore, E = EL and ρ = ρL at x = L. The potential and kinetic energies of the system can be expressed as [5,18,40]:
in which prime and overdot indicate spatial and temporal derivatives, respectively. Additionally, w(x, t) presents the lateral displacement of the system, and M is the bending moment and can be calculated by as follows [41]:
where ζ is the viscoelastic coefficient.
According to Hamilton’s principle, one can write [42,43]:
By substituting Equations (7)–(9) into Equation (10), the dynamic equation of motion of the considered system can be acquired as:
To obtain the dimensionless dynamic equation of the system, the subsequent dimensionless variables are introduced:
where:
Substituting the dimensionless parameters of Equations (12) and (13) into Equation (11) leads to the subsequent dimensionless dynamic equation:
in which the overdot and prime denote the differentiation with respect to the dimensionless coordinates. Additionally, the dimensionless parameters in Equation (14) are defined as:
It should be mentioned that β and kf are the rotary inertia factor and the flexural stiffness of the considered system, respectively. It is worth noting that the governing equation of the system reduces to that of AFG moving EB beam by setting β = 0. Furthermore, if the viscoelastic coefficient of the system is supposed to be zero (μ = 0), the dynamic equation degenerates to that of a moving elastic AFG Rayleigh beam.
3. Discretization Technique
With the aim of discretizing the dynamic equation of the system, the lateral displacement of the beam is considered as [44,45,46]:
in which qr, n, and φr are dimensionless generalized coordinate, the number of basic functions, and acceptable mode shape for the transverse displacement of the system, respectively. The normalized mode shapes of a simply supported beam are given by [47]:
By applying the Galerkin discretization procedure, one can obtain the discretized form of the dynamic equation of the system as follows:
where q, M, C, and K are the vector of generalized coordinates, mass, damping, and stiffness matrices, respectively, and are given by:
4. Stability Examination
The second-order differential equations of Equation (18) can be reduced to the following first-order ones as:
where:
Assuming Z(τ) = Aeiωτ yields the following eigenvalue problem:
where I indicates the unity matrix and D = −B−1E. Moreover, ω is the complex-valued natural frequency of the AFG moving Rayleigh beams and can be determined in terms of different key factors such as rotary inertia factor, flexural stiffness, and density and elastic modulus gradient parameters. The stability of the AFG moving Rayleigh beams is profoundly affected by the sign of imaginary and real parts of the natural frequency. Imaginary and real parts of the natural frequency are related to damping and the frequency of oscillation of the system, respectively. When the real part of one of the frequency branches becomes zero while its imaginary part is negative (Re(ω) = 0, Im(ω) < 0), the instability via a pitch-fork bifurcation occurs in the system. The minimum velocity at which the divergence instability happens is recognized as the critical velocity. Furthermore, when the imaginary part of at least one of the frequency branches is negative while its real part is positive (Real(ω) > 0, Image(ω) < 0), the system experiences flutter instability via a Hopf bifurcation [9].
5. Results and Discussion
Firstly, in the case of isotropic system, the results are acquired and compared with the literature. Then, the effect of density and elastic modulus gradations separately and simultaneously on the vibrational frequencies, the dynamic response, and the stability regions of AFG moving Rayleigh and EB simply supported beams are explored and highlighted. It should be mentioned that the dynamic response of the system can be determined numerically by employing the fourth-order Runge–Kutta technique.
5.1. Model Verification
To examine the correctness of the present solution, the real part of the fundamental frequency of an isotropic moving EB simply supported beam under a compressive load versus dimensionless axial velocity is plotted in Figure 2 for various values of flexural stiffness. As revealed in this figure, the results of the current investigation are in good agreement with those presented by Oz and Pakdemirli [9]. According to Figure 2, by increasing kf, the fundamental frequency of the isotropic system rises.
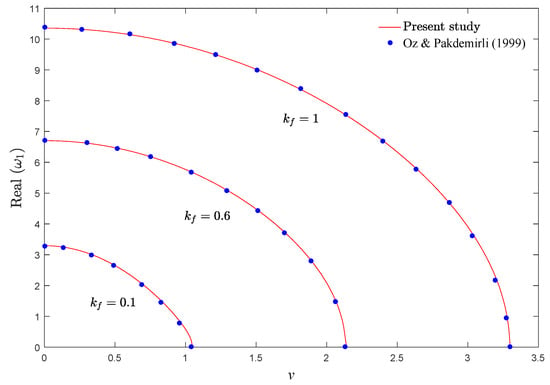
Figure 2.
Fundamental frequency of an isotropic moving EB simply supported beam against dimensionless axial velocity, μ = 0.
In Figure 3, the real part of the three vibrational frequencies of isotropic moving simply supported Rayleigh beam under tension load is displayed. The obtained outcomes are in a close agreement with the results obtained by Chang et al. [18]. It should be noted that, to obtain the presented results in Figure 2 and Figure 3, nine terms in Equation (16) are considered. To this end, due to the accuracy of the acquired results, applying nine vibrational bending modes is reasonable for the subsequent computations.
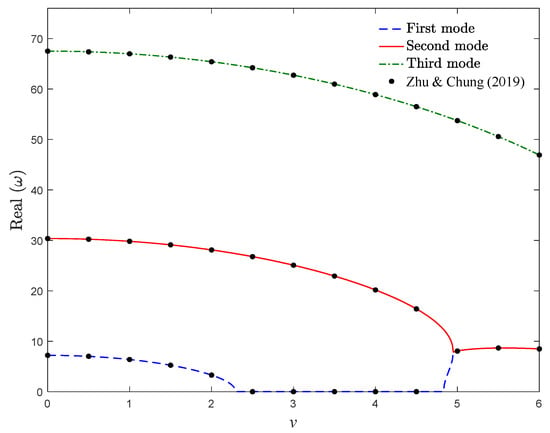
Figure 3.
Natural frequencies of an isotropic moving Rayleigh beam against dimensionless axial velocity for β = 0.001, kf = 0.8, μ = 0.
5.2. Effect of Elastic Modulus Variation
In Figure 4a,b, real and imaginary parts of the first two vibrational frequencies of the system versus the axial velocity are displayed, respectively, for the exponential and linear variations of elastic modulus when kf = 0.5. As it is obvious, the vibrational frequencies of the considered system are purely real when the axial velocity is zero. Afterward, by increasing the velocity, the real part of the vibrational frequencies of the system declines gradually, while their imaginary part is still equal to zero. At the critical axial velocity (vd), the real part of system frequencies vanished, and the system loses its stability and consequently undergoes the divergence phenomenon. The induced divergence instability in moving structures due to ascending the axial velocity is analogous to that of buckling in classical beams under the compression load [48]. By further increasing the axial velocity, the fundamental frequency of the considered structure becomes purely imaginary, while the second natural frequency declines monotonically. Due to gyroscopic effects in the system, at higher velocities, the beam regains its stability again. In other words, the initiation and termination of divergence instability are correlated to the vanishing of real and imaginary parts of the fundamental vibrational frequency, respectively. Eventually, real parts of the two vibrational frequencies merge into each other via a Paidoussis coupled-mode flutter bifurcation while their imaginary parts divide into two branches with negative and positive values. This phenomenon is related to the flutter instability in the system, and the corresponding velocity is known as the flutter velocity (vf). In fact, in addition to the velocities lower than critical divergence velocity (v < vd), a narrow range of axial velocity (between the termination point of the divergence instability and the initiation of flutter instability) exists in which the system is stable at this operational velocity range. It is worth mentioning that the system is no longer stable beyond the critical flutter velocity. As a result, the moving beam experiences a stability evolution of “stable – first mode divergence – stable – coupled-mode flutter”.
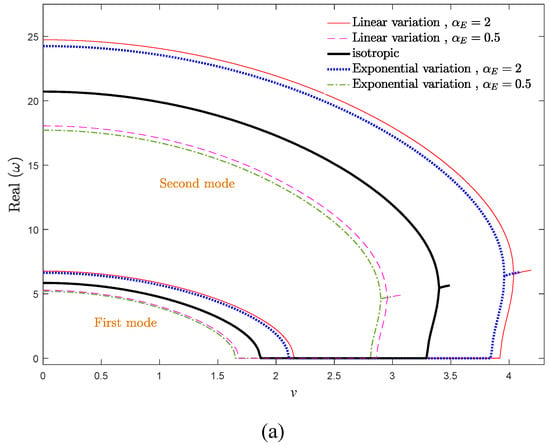
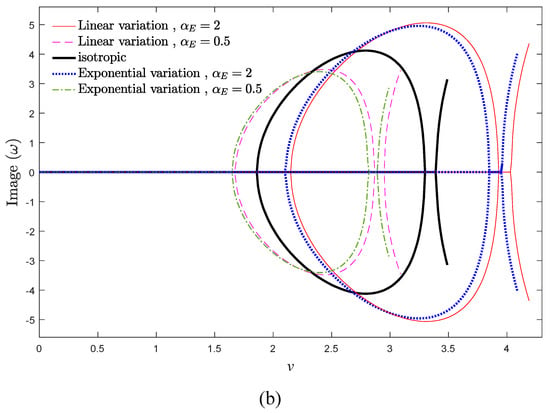
Figure 4.
(a) Real and (b) imaginary parts of two vibrational frequency of the system against the axial velocity for β = 0, αρ = 1, kf = 0.5, μ = 0.
According to Figure 4a, the real part of system frequencies ascends by increasing the elastic modulus gradient parameter, especially frequencies of the higher modes. Additionally, increasing αE leads to ascending the critical divergence and flutter velocities of axially AFG moving EB beams. In other words, it is feasible to hinder the occurrence of undesirable divergence phenomenon by increasing the elastic modulus gradient in moving structures. Since αE has an increasing role in the stiffness matrix; hence, any increment in αE leads to a stiffer system and also wider stability regions. In other words, increasing αE induces the stiffness-hardening effect in the system. Another important feature in Figure 4a,b is that the velocity bandwidth corresponding to the divergence and flutter phenomena in the system (vd < v < vf) would be expanded slightly by increasing αE. Moreover, based on these figures, compared with the exponential variation of elastic modulus, the linear variation leads to a more stable system. As demonstrated in Figure 4b, the damping ratio of the system is higher for αE > 1 and linear variation of elastic modulus. Accordingly, it is possible to determine the instability thresholds and vibrational behavior of the system by fine-tuning of the elastic modulus gradient parameter.
To better understand the dynamic behavior of the considered structure, the time history of the first generalized coordinate of the system in various velocities are displayed in Figure 5 for kf = 0.5, β = 0, αρ = 1, and αE = 2. Unit static displacement and zero initial velocity for the first mode ( and ) are considered for the initial conditions of the system. According to Figure 4a, for v = 1, Real(ω) > 0 and Image(ω) = 0; hence, the system is dynamically stable and generates stable harmonic oscillations. By increasing v, the effective stiffness of the system declines due to the centrifugal force effects. For v = 2.5, the real part of the fundamental frequency of the considered system equals zero, and the beam undergoes instability. In this condition, the dynamic response of the system dramatically grows without oscillation, and the static instability occurs in the system. Increasing the velocity to v = 4 leads to vanishing the imaginary part of frequency, and the beam regains its stability. As the velocity increases, when v = 5, the real part of the frequency grows, while the imaginary part of the vibrational frequency becomes zero. As a result, the oscillation amplitude of the system amplified exponentially by the time. In this case, unlike the divergence instability, the AFG moving beam experiences the flutter instability with growing oscillation. Therefore, the flutter instability is more dangerous than the divergence instability for axially moving structures.
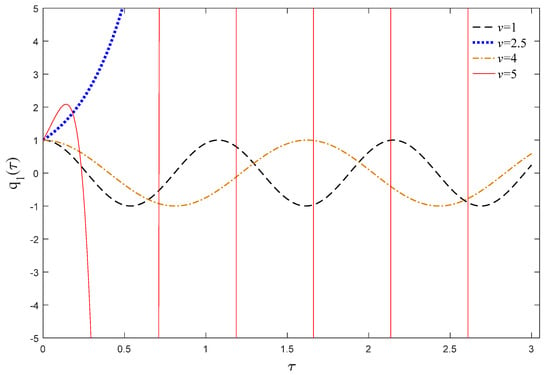
Figure 5.
Dynamic response of an AFG moving EB beam for β = 0, αE = 2, αρ = 1, kf = 0.5, μ = 0.
To better understand the stable configuration of the system, stability maps of the system in vd–kf and vd–αE planes are drawn in Figure 6a,b, respectively. The indicated curves in the stability maps separated the stable and unstable regions, in which, above of each curve, the structure is in the divergence condition. The critical divergence velocity of the system in Figure 4 is consistent with Figure 6. According to Figure 6a, the greater the flexural stiffness, the more stable the system becomes. Therefore, one can conclude that increasing the flexural stiffness parameter has a stabilizing effect on the axially moving systems. Additionally, by increasing αE, the stability regions of the system expanded. Based on Figure 6a, the linear variation of elastic modulus expands the stability regions of the system more than the exponential one. Moreover, the effect of the elastic modulus gradient is more prominent at higher values of kf, and the stability borders separate from each other.
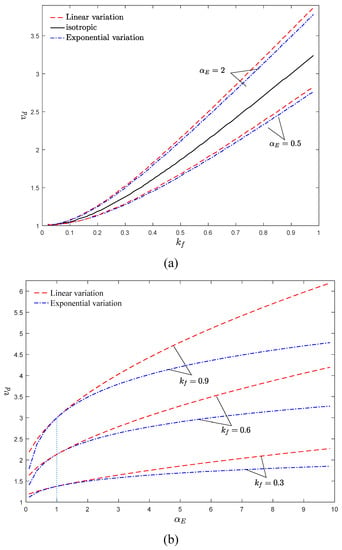
Figure 6.
Critical divergence velocity of an AFG EB beam against (a) dimensionless flexural stiffness and (b) elastic modulus gradient parameter for αρ = 1, μ = 0.
According to Figure 6b, compared with the conventional isotropic axially moving beam (αE = 1), the AFG system is more stable when αE > 1 and ascending αE promotes the stability of the system. It is evident that the critical divergence velocity of the system increases by kf, which can be attributed to the stabilizing effects of the flexural stiffness. By approaching the value of elastic modulus gradient parameter to one (isotropic condition), the stability boundaries of the system are close to each other for linear and exponential distributions, and these boundaries separate from each other by increasing or decreasing of αE. Additionally, except at αE = 1, the system is more stable for the linear distribution of elastic modulus in comparison with the exponential one.
5.3. Effect of Density Variation
To study the influence of the density gradient parameter on the system dynamics, the evolution of real and imaginary parts of two vibrational frequencies versus the axial velocity is demonstrated in Figure 7a,b for various values of αρ. The influence of αρ is more tangible in the vibrational frequencies of higher modes. As displayed, the natural frequencies of the system have a descending trend by increasing the density gradient parameter. Hence, the influence of αρ and αE variations on the vibrational behavior of the system are opposite to each other. Furthermore, the stability region of the system shrinks by ascending the density gradient parameter. Moreover, in contrast to the case of variable elastic modulus scrutinized in the former section, in the case of variable density, the critical divergence and flutter velocities of the exponential distribution is higher than that of the linear distribution.
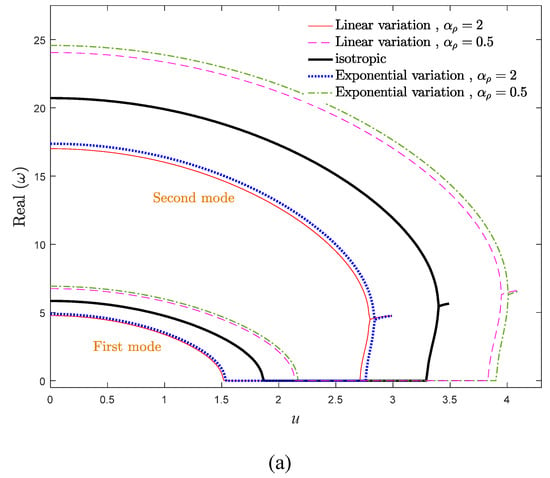
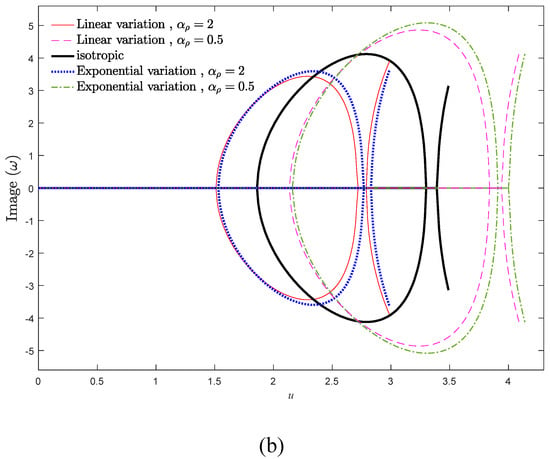
Figure 7.
(a) Real and (b) imaginary parts of two vibrational frequencies of the system against the axial velocity for β = 0, αE = 1, kf = 0.5, μ = 0.
The density gradient parameter is contributed in the mass, damping, and stiffness matrices, which associated with mass-addition effect, gyroscopic effect, and stiffness-hardening effect, respectively. According to Figure 7a,b, one can conclude that the mass-addition effect is dominant in the system. Another important feature in the frequency diagrams of AFG moving beams is that compared with the case of elastic modulus grading, the system experiences a wider range of vibrational frequencies in the case of density gradation. For this reason, from the perspective of designing, the case of density variation is more effective in avoiding the resonance phenomenon. By scrutinizing Figure 4 and Figure 7, it can be observed that axially grading the materials changes the critical velocities of the system, while it does not alter the order and the type of the system bifurcation series. Accordingly, one can conclude that the quantitative values of natural frequencies and critical velocities are strictly dependent on axial grading of materials, but the qualitative stability of the system does not vary by the axial gradation of materials. Based on Figure 4 and Figure 7, it can be mentioned that the vibrational behavior of the axially moving systems is highly dependent on the αρ and αE, as well as the type of their distributions.
To better describe the dynamic behavior of AFG moving beams, the stability maps in vd–αρ and vd–β planes are plotted in Figure 8a,b, respectively. As demonstrated in Figure 8a, the AFG moving beam is more stable for αρ < 1 in comparison with the isotropic one. It is crucial to mention that the stability borders of exponential and linear distributions approach to each other for the density gradient parameters close to one (i.e., the isotropic case). Moreover, the critical velocity of the structure is higher for the exponential distribution of density in comparison with the linear one, especially for the higher and lower values of αρ. In other words, the difference between the stability borders of linear and exponential distributions can be magnified by selecting a higher or lower density gradient.
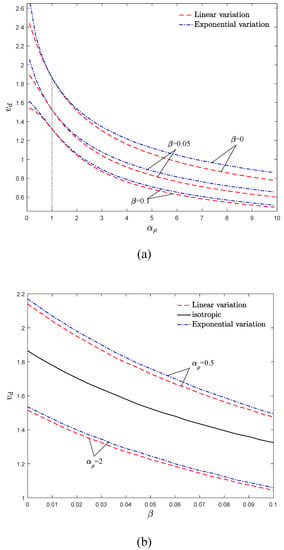
Figure 8.
Critical divergence velocity of an AFG Rayleigh beam against (a) density gradation parameter and (b) rotary inertia factor for kf = 0.5 and αE = 1, μ = 0.
According to Figure 8a,b, since increasing the rotary inertia factor displaces the stability boundaries toward smaller velocities, EB theory predicts less stability for the axially moving structures in comparison with Rayleigh beam theory. Additionally, for any constant values of β, the stability regions of the system shrink by increasing αρ. Generally, compared with the stability maps in vd–kf and vd–αE planes analyzed in the former section, it can be declared that the stability maps in vd–β and vd–αρ are overall descending with increasing β and αρ. This implies that increasing β and αρ can destabilize the system and leads to the decrement of the critical divergence velocity of the structure. It should be mentioned that the indicated stability borders in Figure 7 and Figure 8 are in agreement. Based on Figure 7 and Figure 8, the critical velocity of the structure is substantially dependent on αρ. This dependency is more pronounced for the higher and lower values of αρ.
5.4. Effect of Simultaneous Elastic Modulus and Density Variations
According to previous sections, it can be concluded that the variations of elastic modulus and density along the axial direction of the structure have remarkable effects on the vibrations of axially moving beams. Additionally, it is demonstrated that mitigating the excessive oscillations is feasible by adjusting αE and αρ, separately. Based on Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, variations of elastic modulus and density along the longitudinal direction of the beam have opposite effects on the stability of the system. As a result, these parameters can provide additional degrees of freedom to modify the dynamic characteristics of axially moving structures. In other words, it is possible to significantly improve the performance of axially moving systems by simultaneous fine-tuning αE and αρ. Therefore, determining the role of simultaneous gradation of the material properties on the stability of the moving structures is of great significance. In this section, stability characteristics of the system are explored by considering the coupled variation of density and elastic modulus through the axial direction (simultaneous mass-addition and stiffness-hardening effects). Additionally, the exact analytical expression is presented for critical divergence velocity. Furthermore, a comparison is carried out between different solution procedures.
When the system experiences the divergence phenomenon, the effective stiffness of the system equals zero. In other words, at the divergence threshold, the lowest vibrational frequency of the structure becomes zero. Consequently, the critical velocity of the system is related to the first mode and obtained by reducing Equation (16) to the following equation:
in which the subscript one represents the first natural mode. Considering linear variations for material properties of the system leads to the following equation:
Equation (27) confirms that the critical velocity of the AFG moving system is dependent on the β, αE, αρ, as well as kf of the system. To better inspect the stability of the two-dimensional contour plot for the critical divergence velocity in αE–αρ and kf–β planes are drawn in Figure 9a,b, respectively. As shown in Figure 9a, the critical divergence velocity of the system enhances by increasing the αE and decreasing αρ and vice versa. As illustrated in Figure 9b, the critical divergence velocity of the system increases by decreasing the rotatory inertia factor and increasing the dimensionless flexural stiffness and vice versa. Additionally, it can be deduced that the influence of the flexural stiffness and the rotary inertia factor on the stability of the system is opposite to each other. In other words, contrary to the effect of αρ and β, increasing the elastic modulus gradient parameter and dimensionless flexural stiffness enhance the buckling strength of the system. Accordingly, simultaneously selecting larger values of αE and kf as well as choosing smaller values of β and αρ leads to a more stable system and, consequently, improves the performance of the axially moving structures.
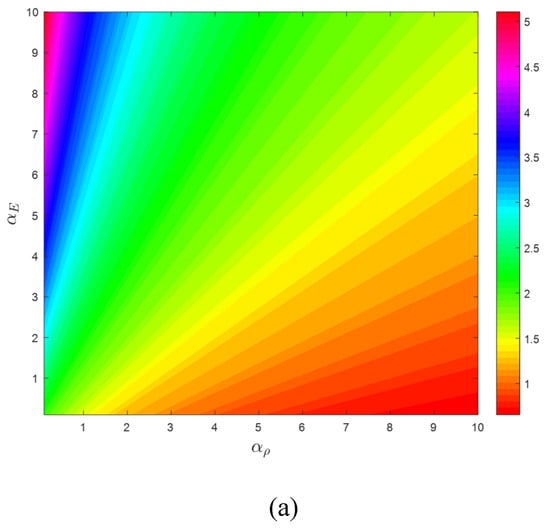
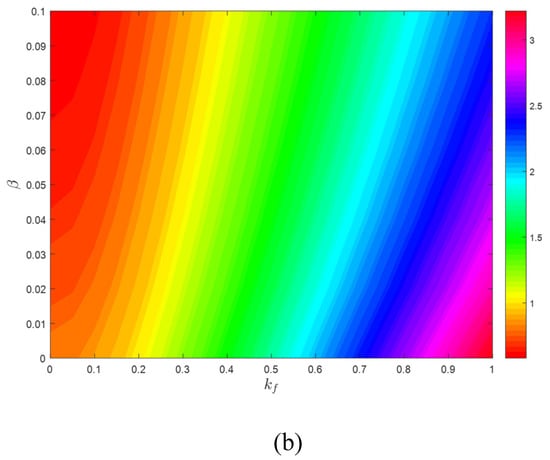
Figure 9.
Effect of (a) elastic modulus and density gradations and (b) dimensionless flexural stiffness and rotary inertia factor on the dimensionless stability of the structure, μ = 0.
In Figure 10a–d), the instability thresholds of the system when the elastic modulus and density gradient parameters are equal (αE = αρ = α) are demonstrated, and the validity of the analytical expressions are examined. According to these figures, the critical divergence velocities acquired by the numerical approaches are in a close agreement with those acquired analytically. As seen in Figure 10a, increasing the material gradient parameter, α, leads to a slight decrease in the critical divergence velocity of the structure. Therefore, compared with the stability maps in previous sections (Figure 6 and Figure 8), it can be inferred that the density gradation (mass-addition effect) shows a dominant role in the stability of the system, and elastic modulus gradation (stiffness-hardening effect) has less effect on the vibrational behavior of the structure. It should be mentioned that compared with previous sections, as density and elastic modulus vary simultaneously, stability borders are closer to each other and are less sensitive to the axial material gradation when the effect of flexural stiffness is highlighted. According to Figure 10b, the stability regions of the system shrink by increasing the gradient parameter, and the curves have a descending trend. Moreover, in the higher values of dimensionless flexural stiffness, variation in the gradient parameter has a minor influence on the instability threshold of AFG moving beam; this point can be helpful at the design stage. As depicted in Figure 10c,d, the stability regions shrink by increasing the gradient parameter and rotary inertia factor. Compared with the isotropic case, when α < 1, the axially moving beam is more stable. Furthermore, at sufficiently high gradient parameter, the divergence velocity of the structure experiences small changes.
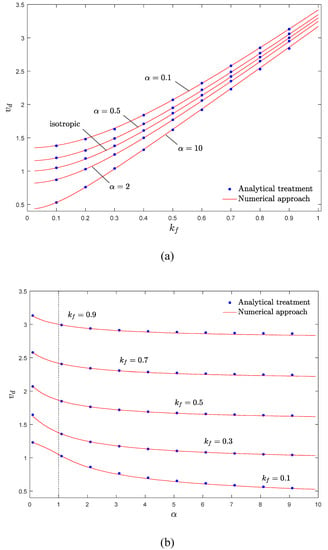
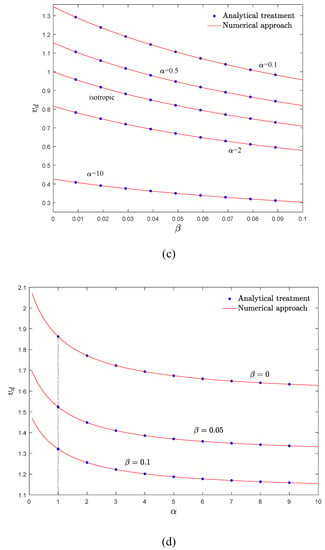
Figure 10.
Critical divergence velocity of an AFG moving Rayleigh beam against (a) dimensionless flexural stiffness (b) gradient parameter (c) rotary inertia factor (d) gradient parameter, μ = 0.
The critical velocity of the system in the three-dimensional space of α, β, and kf is plotted in Figure 11. It is detected that the instability threshold of moving beams is entirely dependent on the axial material gradation, dimensionless flexural stiffness, and rotary inertia factor. As it is obvious, the variation of the material gradient parameter and the rotary inertia factor have the same effects on the stability boundaries, and by increasing each of these parameters, the divergence strength of the system diminishes. While ascending the flexural stiffness enhances the stability of the structure. Consequently, in the simultaneous presence of higher values of dimensionless flexural stiffness, lower values of the material gradient, and rotary inertia factor, the performance of axially moving systems would be improved. Therefore, these parameters could be introduced as the key factors for the vibration control of moving continua. Generally, AFG moving beams are more flexible to adjust their vibrational behavior in comparison with isotropic ones. As a result, it can be claimed that, compared with isotropic materials, AFG ones have a better performance in axially moving structures.
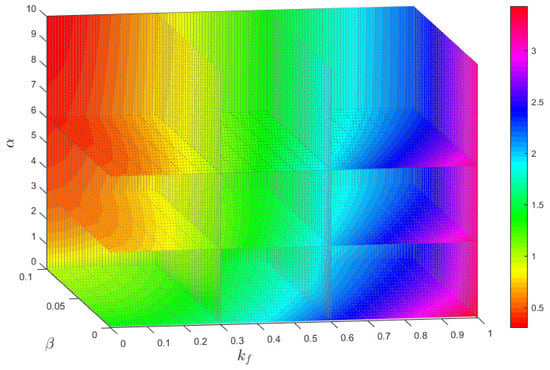
Figure 11.
Effect of dimensionless flexural stiffness, rotary inertia factor, and material gradation parameter on the critical divergence velocity of the AFG moving Rayleigh beams, μ = 0.
5.5. Effect of Viscoelastic Material
Finally, to explore the influence of viscoelastic materials on the dynamics of the moving beam, real and imaginary parts of the two vibrational frequencies of the system are plotted versus the velocity in Figure 12a,b, respectively, for μ = 0.001. The critical divergence velocity of the structure does not change by ascending the viscosity coefficient. This point can be verified by the analytical solution presented in the previous section. Since the viscoelastic structure is non-conservative, the vibrational frequencies are complex before the buckling, especially the frequency of higher modes. According to Figure 12b, imaginary parts of the frequency curves lose their symmetry toward the x-axis when the system is viscoelastic. Additionally, it can be understood that the viscoelastic structure experiences the stability evolution of “stable-first mode flutter-second mode divergence”. As a result, it can be established that compared with the isotropic and axially graded systems, utilizing viscoelastic materials change the stability evolution of the axially moving continua. Generally, it can be stated that the qualitative stability of the beams with axial motion is dependent on the effect of viscoelastic materials, while, axial gradation of materials plays a significant role in determining quantitative values of the critical velocity and the natural frequencies of the structure.
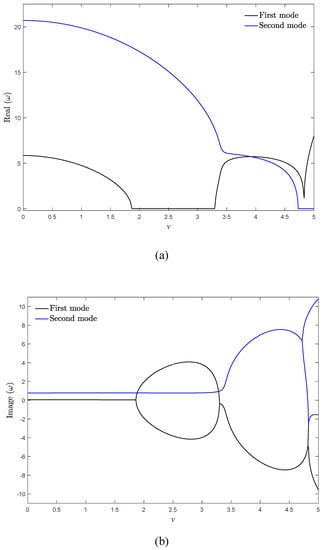
Figure 12.
(a) Real and (b) imaginary parts of two vibrational frequencies of a viscoelastic moving beam for kf = 0.5, αE = αρ = 1, β = 0, μ = 0.001.
6. Conclusions
In this study, structural dynamics and possible vibrational instabilities of AFG moving beams are investigated analytically and numerically in detail. Linear and exponential distributions for the axial grading of material properties are considered for the system. By applying the Galerkin discretizing technique and eigenvalue analysis, the natural frequencies, dynamic response, divergence and flutter instability boundaries of the system are obtained for coupled effects of beam velocity, dimensionless flexural stiffness, viscosity coefficient, and axial material gradation. Closed-form mathematical expression is derived for the critical divergence velocity of the system. Stability maps and two-dimensional contour plots of critical divergence velocity are plotted for Rayleigh and EB beams. The main outcomes of the current study may be narrated as follows:
- Increasing the density/elastic modulus gradient parameter has a destabilizing/stabilizing effect on axially moving beams. Compared with isotropic axially moving beams, the system is more stable when density/elastic modulus decreases/increases along the axial direction.
- In the case of density/elastic modulus variation, exponential/linear distribution leads to a more stable system.
- In the case of simultaneous axial variation of elastic modulus and density, the effect of density gradation on the vibrational configuration of the system is dominant.
- The higher flexural stiffness, and the lower rotary inertia factor, the more stable the structure becomes. Moreover, the influence of axial material gradation on the stability boundaries of the system is more tangible at higher and lower values of flexural stiffness and rotary inertia factor.
- Compared with isotropic and moving axially graded beams, utilizing the viscoelastic material changes the stability evolution of the system.
It is demonstrated that compared with isotropic moving beams, axially moving beams present a better performance by designating appropriate viscoelastic AFG materials.
Author Contributions
Conceptualization, A.S. and D.w.J.; methodology, M.H.; software, M.H.; validation, M.S., K.K.Ż. and H.M.-S.; formal analysis, M.S.; investigation, A.S.; resources, M.H. and H.M.-S.; data curation, M.S.; writing—original draft preparation, M.H.; writing—review and editing, K.K.Ż. and H.M.-S.; visualization, H.M.-S.; supervision, D.w.J., K.K.Ż.; project administration, D.w.J.; funding acquisition, K.K.Ż. and D.w.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the 2020 scientific promotion funded by Jeju National University.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Chen, L.-Q. Analysis and control of transverse vibrations of axially moving strings. Appl. Mech. Rev. 2005, 58, 91–116. [Google Scholar] [CrossRef]
- Marynowski, K.; Kapitaniak, T. Dynamics of axially moving continua. Int. J. Mech. Sci. 2014, 81, 26–41. [Google Scholar] [CrossRef]
- Stylianou, M.; Tabarrok, B. Finite element analysis of an axially moving beam, part II: Stability analysis. J. Sound Vib. 1994, 178, 455–481. [Google Scholar] [CrossRef]
- Sreeram, T.; Sivaneri, N. FE-analysis of a moving beam using Lagrangian multiplier method. Int. J. Solids Struct. 1998, 35, 3675–3694. [Google Scholar] [CrossRef]
- Wickert, J. Non-linear vibration of a traveling tensioned beam. Int. J. Non-Linear Mech. 1992, 27, 503–517. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M. Post-buckling bifurcations and stability of high-speed axially moving beams. Int. J. Mech. Sci. 2013, 68, 76–91. [Google Scholar] [CrossRef]
- Chen, L.-Q.; Yang, X.-D. Vibration and stability of an axially moving viscoelastic beam with hybrid supports. Eur. J. Mech. A Solids 2006, 25, 996–1008. [Google Scholar] [CrossRef]
- Guo, X.-X.; Wang, Z.-M.; Wang, Y.; Zhou, Y.-F. Analysis of the coupled thermoelastic vibration for axially moving beam. J. Sound Vib. 2009, 325, 597–608. [Google Scholar] [CrossRef]
- Öz, H.; Pakdemirli, M. Vibrations of an axially moving beam with time-dependent velocity. J. Sound Vib. 1999, 227, 239–257. [Google Scholar] [CrossRef]
- Yang, T.; Fang, B.; Yang, X.-D.; Li, Y. Closed-form approximate solution for natural frequency of axially moving beams. Int. J. Mech. Sci. 2013, 74, 154–160. [Google Scholar] [CrossRef]
- Chen, L.-Q.; Yang, X.-D.; Cheng, C.-J. Dynamic stability of an axially accelerating viscoelastic beam. Eur. J. Mech. A Solids 2004, 23, 659–666. [Google Scholar] [CrossRef]
- Kiani, K. Divergence and flutter instabilities of nanobeams in moving state accounting for surface and shear effects. Comput. Math. Appl. 2019, 77, 2764–2785. [Google Scholar] [CrossRef]
- Kiani, K. Longitudinal, transverse, and torsional vibrations and stabilities of axially moving single-walled carbon nanotubes. Curr. Appl. Phys. 2013, 13, 1651–1660. [Google Scholar] [CrossRef]
- Chang, J.-R.; Lin, W.-J.; Huang, C.-J.; Choi, S.-T. Vibration and stability of an axially moving Rayleigh beam. Appl. Math. Model. 2010, 34, 1482–1497. [Google Scholar] [CrossRef]
- Zinati, R.F.; Rezaee, M.; Lotfan, S. Nonlinear Vibration and Stability Analysis of Viscoelastic Rayleigh Beams Axially Moving on a Flexible Intermediate Support. Iran. J. Sci. Technol. Trans. Mech. Eng. 2019, 1–15. [Google Scholar] [CrossRef]
- Tang, Y.-Q.; Chen, L.-Q.; Yang, X.-D. Natural frequencies, modes and critical speeds of axially moving Timoshenko beams with different boundary conditions. Int. J. Mech. Sci. 2008, 50, 1448–1458. [Google Scholar] [CrossRef]
- An, C.; Su, J. Dynamic response of axially moving Timoshenko beams: Integral transform solution. Appl. Math. Mech. 2014, 35, 1421–1436. [Google Scholar] [CrossRef]
- Zhu, K.; Chung, J. Vibration and stability analysis of a simply-supported Rayleigh beam with spinning and axial motions. Appl. Math. Model. 2019, 66, 362–382. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Dehrouyeh, M.; Zafari-Koloukhi, H.; Ghamami, M. Size-dependent frequency and stability characteristics of axially moving microbeams based on modified couple stress theory. Int. J. Eng. Sci. 2015, 97, 98–112. [Google Scholar] [CrossRef]
- Fard, M.; Sagatun, S. Exponential stabilization of a transversely vibrating beam via boundary control. J. Sound Vib. 2001, 240, 613–622. [Google Scholar] [CrossRef]
- Zhang, Y.-W.; Hou, S.; Xu, K.-F.; Yang, T.-Z.; Chen, L.-Q. Forced vibration control of an axially moving beam with an attached nonlinear energy sink. Acta Mech. Solida Sin. 2017, 30, 674–682. [Google Scholar] [CrossRef]
- Li, T.-C.; Hou, Z.-C.; Li, J.-F. Stabilization analysis of a generalized nonlinear axially moving string by boundary velocity feedback. Automatica 2008, 44, 498–503. [Google Scholar] [CrossRef]
- Zhang, Y.-W.; Zhang, Z.; Chen, L.-Q.; Yang, T.-Z.; Fang, B.; Zang, J. Impulse-induced vibration suppression of an axially moving beam with parallel nonlinear energy sinks. Nonlinear Dyn. 2015, 82, 61–71. [Google Scholar] [CrossRef]
- Sarparast, H.; Ebrahimi-Mamaghani, A. Vibrations of laminated deep curved beams under moving loads. Compos. Struct. 2019, 226, 111262. [Google Scholar] [CrossRef]
- Sedighi, H.M.; Daneshmand, F.; Abadyan, M. Dynamic instability analysis of electrostatic functionally graded doubly-clamped nano-actuators. Compos. Struct. 2015, 124, 55–64. [Google Scholar] [CrossRef]
- Hosseini, R.; Hamedi, M.; Mamaghani, A.E.; Kim, H.C.; Kim, J.; Dayou, J. Parameter identification of partially covered piezoelectric cantilever power scavenger based on the coupled distributed parameter solution. Int. J. Smart Nano Mater. 2017, 8, 110–124. [Google Scholar] [CrossRef]
- Li, Y.; Dong, Y.; Qin, Y.; Lv, H. Nonlinear forced vibration and stability of an axially moving viscoelastic sandwich beam. Int. J. Mech. Sci. 2018, 138, 131–145. [Google Scholar] [CrossRef]
- Ghayesh, M.H. On the natural frequencies, complex mode functions, and critical speeds of axially traveling laminated beams: Parametric study. Acta Mech. Solida Sin. 2011, 24, 373–382. [Google Scholar] [CrossRef]
- Lv, H.; Li, Y.; Li, L.; Liu, Q. Transverse vibration of viscoelastic sandwich beam with time-dependent axial tension and axially varying moving velocity. Appl. Math. Model. 2014, 38, 2558–2585. [Google Scholar] [CrossRef]
- Esfahani, S.; Khadem, S.E.; Mamaghani, A.E. Size-dependent nonlinear vibration of an electrostatic nanobeam actuator considering surface effects and inter-molecular interactions. Int. J. Mech. Mater. Des. 2019, 15, 489–505. [Google Scholar] [CrossRef]
- Mirtalebi, S.H.; Ebrahimi-Mamaghani, A.; Ahmadian, M.T. Vibration Control and Manufacturing of Intelligibly Designed Axially Functionally Graded Cantilevered Macro/Micro-tubes. IFAC Pap. 2019, 52, 382–387. [Google Scholar] [CrossRef]
- Ebrahimi-Mamaghani, A.; Mirtalebi, S.H.; Ahmadian, M.-T. Magneto-mechanical stability of axially functionally graded supported nanotubes. Mater. Res. Express 2020, 6, 1250–1255. [Google Scholar] [CrossRef]
- Ebrahimi-Mamaghani, A.; Sotudeh-Gharebagh, R.; Zarghami, R.; Mostoufi, N. Thermo-mechanical stability of axially graded Rayleigh pipes. Mech. Based Des. Struct. Mach. 2020, 1–30. [Google Scholar] [CrossRef]
- Safarpour, M.; Rahimi, A.; Alibeigloo, A.; Bisheh, H.; Forooghi, A. Parametric study of three-dimensional bending and frequency of FG-GPLRC porous circular and annular plates on different boundary conditions. Mech. Based Des. Struct. Mach. 2019, 1–31. [Google Scholar] [CrossRef]
- Safarpour, M.; Rahimi, A.; Alibeigloo, A. Static and free vibration analysis of graphene platelets reinforced composite truncated conical shell, cylindrical shell, and annular plate using theory of elasticity and DQM. Mech. Based Des. Struct. Mach. 2019, 1–29. [Google Scholar] [CrossRef]
- Piovan, M.T.; Sampaio, R. Vibrations of axially moving flexible beams made of functionally graded materials. Thin Walled Struct. 2008, 46, 112–121. [Google Scholar] [CrossRef]
- Sui, S.; Chen, L.; Li, C.; Liu, X. Transverse vibration of axially moving functionally graded materials based on Timoshenko beam theory. Math. Probl. Eng. 2015, 2015, 391452. [Google Scholar] [CrossRef]
- Kiani, K. Longitudinal and transverse instabilities of moving nanoscale beam-like structures made of functionally graded materials. Compos. Struct. 2014, 107, 610–619. [Google Scholar] [CrossRef]
- Yan, T.; Yang, T.; Chen, L. Direct Multiscale Analysis of Stability of an Axially Moving Functionally Graded Beam with Time-Dependent Velocity. Acta Mech. Solida Sin. 2020, 33, 150–163. [Google Scholar] [CrossRef]
- Rezaee, M.; Lotfan, S. Non-linear nonlocal vibration and stability analysis of axially moving nanoscale beams with time-dependent velocity. Int. J. Mech. Sci. 2015, 96, 36–46. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear forced dynamics of an axially moving viscoelastic beam with an internal resonance. Int. J. Mech. Sci. 2011, 53, 1022–1037. [Google Scholar] [CrossRef]
- Mamaghani, A.E.; Zohoor, H.; Firoozbakhsh, K.; Hosseini, R. Dynamics of a Running Below-Knee Prosthesis Compared to Those of a Normal Subject. J. Solid Mech. Vol. 2013, 5, 152–160. [Google Scholar]
- Mirtalebi, S.H.; Ahmadian, M.T.; Ebrahimi-Mamaghani, A. On the dynamics of micro-tubes conveying fluid on various foundations. SN Appl. Sci. 2019, 1, 547. [Google Scholar] [CrossRef]
- Mamaghani, A.E.; Khadem, S.; Bab, S. Vibration control of a pipe conveying fluid under external periodic excitation using a nonlinear energy sink. Nonlinear Dyn. 2016, 86, 1761–1795. [Google Scholar] [CrossRef]
- Mamaghani, A.E.; Khadem, S.E.; Bab, S.; Pourkiaee, S.M. Irreversible passive energy transfer of an immersed beam subjected to a sinusoidal flow via local nonlinear attachment. Int. J. Mech. Sci. 2018, 138, 427–447. [Google Scholar] [CrossRef]
- Ebrahimi-Mamaghani, A.; Sotudeh-Gharebagh, R.; Zarghami, R.; Mostoufi, N. Dynamics of two-phase flow in vertical pipes. J. Fluids Struct. 2019, 87, 150–173. [Google Scholar] [CrossRef]
- Esfahani, S.; Khadem, S.E.; Mamaghani, A.E. Nonlinear vibration analysis of an electrostatic functionally graded nano-resonator with surface effects based on nonlocal strain gradient theory. Int. J. Mech. Sci. 2019, 151, 508–522. [Google Scholar] [CrossRef]
- Wickert, J.; Mote, C., Jr. Classical vibration analysis of axially moving continua. J. Appl. Mech. 1990, 57, 738–744. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).