Abstract
The DR-SCIR network public opinion propagation model was employed to study the characters of S-state users stopping transmitting information for the first time and secondary transmission of immune users. The model takes into account symmetry and complexity such as direct immunization and social reinforcement effect, proposes the probability of direct immunity Psr and the probability of transform from the immune state to the hesitant state Prc, and divides public opinion information into positive public opinion and negative public opinion based on whether the public opinion information is confirmed. Simulation results show that, when direct immunity Psr = 0.5, the density of I-state nodes in the model decreased by 54.12% at the peak index; when the positive social reinforcement effect factor b = 10, the density of I-state nodes in the model increased by 16.67% at the peak index; and when the negative social reinforcement effect factor b = -10, the density of I-state nodes in the model decreased by 55.36% at the peak index. It shows that increasing the positive social reinforcement effect factor b can promote the spread of positive public opinion, reducing the negative social reinforcement effect factor b can control the spread of negative public opinion, and direct immunization can effectively suppress the spread of public opinion. This model can help us better analyze the rules of public opinion on social networks, so as to maintain a healthy and harmonious network and social environment.
1. Introduction
In recent years, with the rapid development of communication technology, the way of socializing has gradually shifted to online platforms, resulting in a large amount of online public opinion information. Public opinion refers to information that is spread through informal channels and widely circulated [1]. Even considering the same facts, information, and events, different stakeholders may interpret, understand, and communicate them in completely different ways based on the interests, values, norms, and strategies of each group [2]. This leads to different influences of individual propensity on the spread of public opinion, which may form a bifurcation of public opinion [3]. The continuous development of the technology and scale of social networks has promoted the relevant theories and methods for researching social network public opinion propagation, such as cellular automata [4,5,6], multi-agent theory [7,8], game theory [9,10], and epidemiology. Due to the similarities between the spread of public opinion on social networks and the spread of epidemic diseases, most research on the spread of public opinion on social network is based on epidemiological transmission models. Typical epidemic transmission models include SI model, SIS model, and SIR model, as well as their improved models [11,12,13,14]. Yan et al. proposed the SIRS model; they assumed individuals in the immune state R will lose their immunity with a certain probability and recover to the susceptible state S [15]. Adisak proposed the SEIRS propagation model and derived the model’s immune balance point, that is, the epidemic threshold; analyzed the global stability of the system’s immune balance point when the basic regeneration number was lower than 1 and greater than 1; and verified the impact of the number of infected bodies and the duration of the outbreak on the spread of the disease by simulation [16]. Kimura considered the influence of node influence and time delay on information dissemination, and established an information dissemination model. The simulation analysis shows that nodes with large node influence have a promoting effect on information dissemination [17]. Liu et al. proposed a SEIR model with an improved hesitation mechanism based on the average field theory and applied it to the rumor propagation process. The equilibrium point and the basic regeneration number of the model were derived through the average field theory, and the feedback mechanism cannot change the basic regeneration number but can reduce continuity and suppress the spread of rumors by simulation [18]. Galuba linearized the information in the network and established a linear threshold model to obtain different influences of different users’ influence on information transmission [19]. Lü established an information dissemination model based on memory effects and social reinforcement effects and found that the small-world networks have a better information dissemination capabilities [20]. Ma et al. used a generation function and a cavity method to study the effects of bipolar social reinforcement on rumors. By simulating the spread of public opinion on social networks, it was found that increasing negativity or increasing positivity can restrain the spread of rumors [21].
In terms of immunity to the spread of public opinion, Wang proposed the SIRaRu rumor propagation model, which shows that there are extended thresholds for both homogeneous and heterogeneous networks, and obtained the immune threshold and propagation threshold for both networks. Wang showed that the network topology has significant influence on the rumor spreading [22]. Moreno explored the spread of rumors in a scale-free network and found that the scale-free nature of the network suppressed the spread of rumors [23]. Pastor studied the control effects of three control strategies in uniform networks and scale-free networks based on the SIS epidemic model, and found that random control strategies are only effective in uniform networks, while the target control strategy has better control effect in both networks [24]. Gu established a rumor-based SEIR propagation model based on online networks and proposed a strategy for suppressing rumor propagation based on important acquaintances immune. The simulation results showed that the model is more in line with the propagation characteristics of real online social networks, and the important acquaintance immune strategies can effectively solve the problem of online social networks rumor suppression problem [25]. Cohen studied the nature of acquaintance control strategies based on traditional rumor propagation models, proposed a control strategy that is broad, especially effective for scale-free networks, and obtained the threshold of its complete immunity [26].
However, the current research has not considered the impact of the combined effects of the direct immune effect on susceptible users and the social reinforcement effect on immune users in the process of public opinion propagation. Actually, on the public opinion propagation network, the government’s regulatory role can promptly release the real information and guide users to directly transform to the immune state after contacting with public opinion information for the first time. At the same time, under the function of social reinforcement effects, immune users may re-broadcast the message when they received it from friends many times. Therefore, we propose the DR-SCIR public opinion propagation model with direct immune effect and social reinforcement effect based on the SCIR network model in this paper. We define a two-way social reinforcement effect with a threshold, and take the credibility of public opinion information as a factor that affects the social reinforcement effect factor b. The greater the credibility is, the easier the information will be transmitted, and the larger the social reinforcement effect factor b is; otherwise, the less credible the information is, the less likely it is to spread further, and the smaller the social reinforcement effect factor b is. At the same time, considering the degree of Internet users’ reception, a threshold for social reinforcement effect is set (this article assumes the threshold is 3). Only after the number of times the user contacts the same public opinion information exceeds the threshold, the social reinforcement effect will act on the immune users. At the same time, the supervision of public opinion by relevant departments is considered, and the direct immunity probability is proposed to make the network have a direct immune effect.
The rest of the paper is organized as follows. Section 2 introduces the SCIR model for public opinion propagation. Section 3 proposes the DR-SCIR public opinion propagation model with direct immune effect and social reinforcement effect, introduces the specific definition of direct immune effect and social strengthening effect, and proposes the transform probability of each part in the propagation model. Section 4 evaluates the feasibility and effectiveness of the model, analyzes its influence on the spread of public opinion by changing the parameters, and compares the control effects of different models. Section 5 is the conclusion of the thesis.
2. SCIR Public Opinion Propagation Model
The SIR epidemic spread model divides network nodes into three states: susceptible state S, infected state I, and immune state R [27,28,29,30,31]. To study the dissemination rules of public opinion propagation, the researchers introduced the contact state C based on the SIR model, and built the SCIR public opinion propagation model. Network users can be divided into four states: unknown state S, which indicates that the user has not been exposed to the information, but is likely to spread the information; hesitation state C, which indicates that the user has obtained the information from the neighbor nodes, but has not yet decided whether to spread it; propagation state I, which represents the state that the user already knows the public opinion information and then spread itl and immune state R, which represents the state that the user already knows the information and will not transmit it [32,33]. The SCIR propagation model is shown in Figure 1.
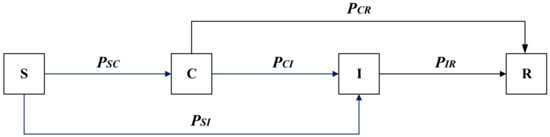
Figure 1.
The SCIR propagation model.
The differential equation for the SCIR propagation model can be written as
indicates the probability that the user has contacted the public opinion but has no decision on whether to spread it, that is, the internal contact rate; indicates the probability that the unknown person contacts the public opinion and spreads it, that is direct repost rate; indicates the probability that the hesitant contacts and spreads the public opinion, that is, the indirect repost probability; PIR indicates the probability that the communicator does not believe the public opinion for some reason, thus turns to be immune, that is, the repost immunity rate; and indicates the probability that the hesitant contacts the information, and then converts to immune directly without propagating, that is the indirect immunity rate.
3. DR-SCIR Public Opinion Propagation Model
3.1. Direct Immune
Common immune strategies in complex network theory include three types: random immunity, target immunity, and acquaintance immunity. Random immunity is also called uniform immunity. A part of the nodes in the network are randomly selected for immunization [34,35]. The chance of each node being immunized is equal, and it does not vary according to the level of the risk of infection. Target immunity is also called selective immunity, which is an immunization strategy designed for the uneven characteristics of scale-free networks. It mainly immunizes nodes with large degrees in the network and, once the nodes with large degrees are immunized, it means that their connected edges can be removed from the network, which can greatly reduce the possible connection paths for transmission [36]. However, this method needs to know the global information of the network, which is difficult for large social networks. Acquaintance immunity is also called neighbor immunity, by immunizing neighbor nodes that are randomly connected to nodes with a large degree, which do not need to know the global information.
Huang verified that, in the rumor propagation model, both random immunity and target immunity can greatly affect the spread of rumors [37]. Considering there are relevant departments in the real social network that can guide the spread of public opinion by publishing real information and other methods, this paper uses a random immune strategy to apply direct immunity to the users in susceptible state.
Specifically, the effect of direct immunization on susceptible users makes it easy for them to directly transform to the immune state with probability when they contact the public opinion information for the first time after the relevant department releases real information, thereby controlling the spread of public opinion and reducing the influence for society. The direct immune mechanism can be expressed by the following formula:
3.2. Social Reinforcement Effect
Public opinion has gone through several stages of development in a communication system and its authenticity has not been proven. In social networks, the main points of public opinion are: (i) essence, i.e., emphasize the unproven nature of the content; (ii) constitutional characteristics, i.e., realism and fiction coexist, and psychological reality and symbolism coexist; (iii) scale, i.e., the amount of communication must reach a certain amount of public opinion; (iv) content, i.e., information that can arouse people’s interest; (v) emotion, i.e., express the sentiment of the communicator; and (vi) background of the production, i.e., many complicated factors promote rumors.
Public opinion information can be divided into rumors and reliable information according to whether its authenticity is confirmed. For example, during the transmission of COVID-19 in China, epidemic prevention materials such as masks are very scarce. Messages appearing on the Internet that alcohol can sterilize surgical masks for reuse. Experts from the National Health Commission point out that alcohol can damage the internal structure of masks and make it impossible to block the entry of viruses. The former is a typical rumor, while the latter is proven to be reliable information. This article defines rumors as negative public opinion and reliable information as positive public opinion. To maintain the health and stability of the network and society, the negative public opinion should be suppressed from spreading on the Internet, and the positive public opinion should be expanded.
Social reinforcement effect refers to the cumulative effect that individuals are repeatedly prompted by their peers before they adopt opinions or make behavioral decisions, thereby affecting their final decision. Social psychology has shown that any information that meets people’s subjective wishes, subjective impressions, or subjective prejudices is most easily transmitted. At the same time, positive and optimistic public opinion is more likely to be transmitted than negative and dark public opinion. Therefore, in the process of public opinion propagation on the real network, the effect of social reinforcement effect on public opinion dissemination can be divided into positive social reinforcement effect and negative social reinforcement effect [38].
It is assumed that the social reinforcement effect acts on the immune users and considers the actual situation of public opinion transmission at the same time. Assuming only when the immune users receive the same public opinion information from their friends for a certain number of times do immune users have possibility to escape from the immune state and retransmit public opinion, and the probability of positive social reinforcement effect will increase with the increase of the number of exposures until the upper limit of the probability of transmission is reached, the probability of negative social reinforcement effect will decrease to zero as the number of exposures increases.
Lu et al. considered the impact of information accumulation on users, and defined the social reinforcement effect for the S-state node. Considering the complexity of social networks, this paper defines two-way social reinforcement effects with thresholds for positive and negative public opinion for R-state nodes [20]. Assume that the probability that the social reinforcement effect causes the immune user to transform to a hesitant state is , where m represents the cumulative quantity, that is, the number of times that the public opinion is received. We consider the threshold of the cumulative quantity m based on the model. Only if the cumulative quantity , the probability exists. It is expressed as:
where represents the initial propagation probability. is the upper limit of the propagation probability, considering that immune users themselves have a certain resistance to the propagation of public opinion information, even under the effect of social reinforcement effects, the probability of repost will not be very high, so we assume the upper limit of the probability of transmission . represents the social reinforcement effect factor. is a function related to , represents the positive influence of the social reinforcement effect, and at that time; and represents the negative influence of the social reinforcement effect, and at that time. Then, we can get:
3.3. DR-SCIR Network Public Opinion Propagation Model
Due to the complexity of actual social networks, we make the following assumptions on the designed model before conducting research [39,40,41,42]:
- (i)
- Assume that the total number of users remains constant during the spread of public opinion, corresponding to the network is the total number of nodes N remains unchanged, that is, at any time t, there will be:
- (ii)
- In the process of public opinion propagation, the topology of the entire social network remains the same, that is, the friend relationship between users in the social network remains constant.
- (iii)
- Users treat the information from different friends equally, that is, under the effect of social reinforcement effect, the weight of the impact of each time they receive the information is the same.
Based on the above assumptions, considering the combined effects of direct immunity and social reinforcement effects, we propose the DR-SCIR public opinion propagation model. Based on the SCIR model, we add two types of public opinion transmission possibilities: the unknown person S directly changes to the immunizer R with probability , and the immune person R changes to hesitant C with probability . DR-SCIR public opinion propagation model is shown in Figure 2.
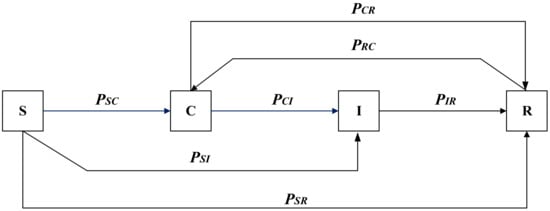
Figure 2.
DR-SCIR public opinion propagation model.
The differential equation for the DR-SCIR public opinion propagation model is
where indicates the probability that the unknown state S will directly change to the immune state R when it is exposed to public opinion under the supervision of the authority, that is, the direct immune probability. indicates the probability that the immune state R will transform to the hesitant state C under the effect of social reinforcement effect, .
3.4. Transition Probability
Transition rules for each node are defined as follows:
- (i)
- When the unknown state S contacts the propagation state I, there will be three transition states for S: the first one is to transform to the hesitant state C with probability , the second one is to transform to the propagation state I with probability , and the last one is to transform to the immune state R with probability .
- (ii)
- When the hesitation state C contacts the propagation state I, one part will transforms to the propagation state I with probability , and the other part will transforms to the immune state R with probability .
- (iii)
- The propagation state I will transforms to the immune state R with probability .
- (iv)
- The immune state R will transform to the hesitant state C with probability under the function of social reinforcement effect.
When the node is at time t, the transition probability calculation process of each state is as follows:
- (i)
- Suppose node j is in state S at time t; the relationship between propagation probabilities is given byConsidering as the number of nodes at state I in the neighborhood of node j at time t, we can write the above probabilities as follows,Thus,Supposing node j has k edges and is a random variable obeying the binomial distribution,where is the probability of connecting from node in state S with k edges to node in state I at time t:is a degree correlation function, which represents the conditional probability that a node with degree k is adjacent to a node with degree k1. represents the probability that a node with k1 edges is in the propagation state I under the condition that it is connected to a susceptible node with degree k.Use to represent the density of nodes in state I with degree of k1 at time t, and then is approximately:Then, the average probability that the S state node with degree k becomes state C within the time period is:Substituting Equation (12) into Equation (13), there is:Similarly, the average probability that the S state node with degree k becomes state I within the time period is:Similarly, the average probability that the S state node with degree k becomes state R within the time period is:Thus, the average probability that the S state node with degree k maintains its state in the time period is:
- (ii)
- Suppose node j is in state C at time t; the relationship between propagation probabilities is given bySpecifically, there areThus, the average probability that the C state node with degree k maintains its state in the time period is:
- (iii)
- Suppose node j is in state I at time t; the relationship between propagation probabilities are as followings,Thus, the average probability that the I state node with degree k maintains its state in the time period is:
- (iv)
- Suppose node j is in state I at time t; the relationship between propagation probabilities is given by,Considering as the number of nodes at state I in the neighborhood of node j at time t,Supposing node j has k edges and is a random variable obeying the binomial distribution,where is the probability of connecting from node in state R with k edges to node in state I at time t:represents the probability that a node with k1 edges is in the propagation state I under the condition that it is connected to an immune node with degree k.Use to represent the density of nodes in state I with degree of k1 at time t; then, is approximately:Then, the average probability that the R state node with degree k becomes state C within the time period is:Substituting Equation (28) into Equation (29), there is:Thus, the average probability that the R state node with degree k maintains its state in the time period is:
4. Simulation Analysis
4.1. Simulation Dataset
The characteristics of social networks are consistent with BA scale-free networks, such as the typical power-law distribution characteristic [43]. At present, most research on the spread of public opinion in social networks is based on BA scale-free networks. We generated a random network, a NW small-world network, and a BA scale-free network, and they were all with 1000 nodes. Then, we analyzed the characteristics of the above three networks. Figure 3 is a schematic diagram of random network, NW small-world network, and BA scale-free network, and the corresponding characteristic parameters are shown in Table 1.
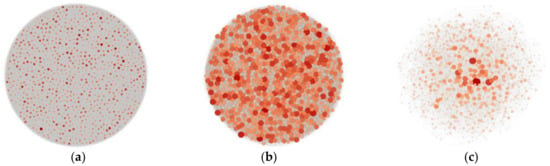
Figure 3.
Schematic diagram of three networks: (a) random network; (b) NW network; and (c) BA network.

Table 1.
Characteristic parameters of three networks.
It can be seen that the degree of BA scale-free network follows the power-law distribution approximately, reflecting the scale-free characteristics. The maximum and minimum degrees have a large gap, while the average degree and clustering coefficient are small, which reflect the characteristic of the small world. All these characteristics are similar to real social networks. The average path of the NW small-world network is small, but the average degree is large, and the degree of nodes approximately follows the Poisson distribution and the gap between the maximum degree and minimum degree is small. Random network has the largest number of connected edges, average degree, and clustering coefficient, and it has the smallest average path length, which has the biggest difference from the real social network. Considering the generality and applicability of the model, BA network was selected as the simulation data.
To verify the effectiveness and feasibility of the DR-SCIR public opinion propagation model with direct immune effect and social reinforcement effect, we established a BA network with 1000 nodes to simulate the real social network. To make the propagation evolution process of nodes in different states in the network reach a stable state, the number of iterations was set to 100.
4.2. Impact of Propagation Probability Upper Limit T on Propagation
To analyze the effect of the reinforcement effect on network propagation, that is, the impact of the transformation from the immune state R to the hesitant state C on the propagation of public opinion, we observed its impact on each state node by changing the upper limit T of the propagation probability in the medium. Assume that the node with the highest degree of selection in the initial state is the propagation state I [44,45], and the other node states are all unknown state S. Set the initial parameters PCR = 0.2, PSC = 0.7, PCI = 0.5, PIR = 0.2, PSI = 0.2, PSR = 0.1, , and b = 10. The influence of different values of the upper limit T of the propagation probability on the density of various nodes is shown in Figure 4.
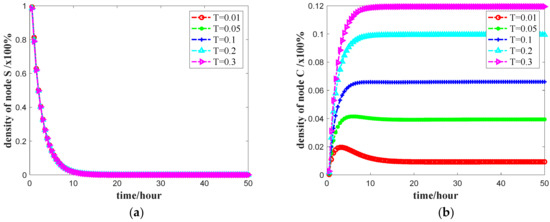
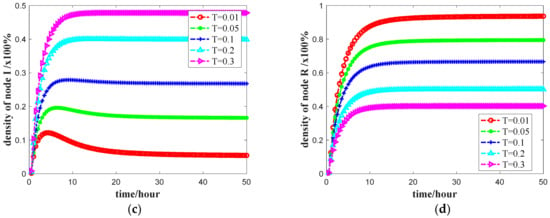
Figure 4.
The number of four states nodes against time t with varying upper limit T: (a) density change of S state node; (b) density change of C state node; (c) density change of I state node; and (d) density change of R state node. The final propagation scope with T = 0.01, 0.05, 0.1, 0.2, and 0.3, respectively. Other parameters are the same as the default settings.
Figure 4 shows that, in the early stage of the propagation, the number of users in the S state decreases sharply, and the number of users in the C, I, and R states increases rapidly. With the increase of the upper limit of the propagation probability T, the time for the C, I, and R state nodes to reach a stable state decreases as well. In the steady state, the proportion of the R state nodes decreases, while the proportion of the C, I state nodes increases, indicating that the larger is T, the more users are in the state of C and I at the same time, so that public opinion can spread on the network for a longer time. This is because T changes the final state. The larger is T, the greater is the social reinforcement effect in the final state. It is more likely that a R state node will transform to the C state, which makes it easier for public opinion to spread on the network.
4.3. Impact of Positive Social Reinforcement Effect Factor b on Propagation
To analyze the impact of the positive social reinforcement effect factor b on the density of various nodes, set b = 0, b = 1, b = 2, b = 5, and b = 10 and perform 100 iterations based on the basic parameters. The simulation results are shown in Figure 5.
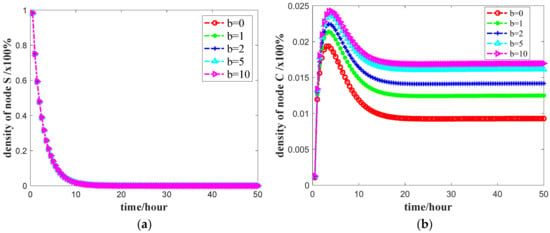
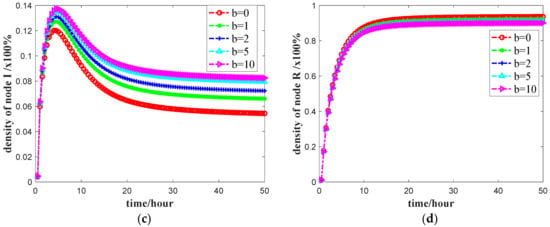
Figure 5.
The number of four states nodes against time t with varying positive social reinforcement effect factor b: (a) density change of S state node; (b) density change of C state node; (c) density change of I state node; and (d) density change of R state node. The final propagation scope with b = 0, 1, 2, 5, and 10, respectively. Other parameters are the same as the default settings.
Figure 5b,c shows that, with the increase of the positive social reinforcement effect factor b, the growth rates of the number in the hesitation state C and the propagation state I during the propagation process are increased as well, while the number of users in the I and C states is higher in the steady state. When b = 10, the node densities of C and I states increased by 24.62% and 16.67% at the peak, respectively, and increased by 82.58% and 53.16% at the steady state. These results all show that the positive social reinforcement effect factor b is positively related to the number of users in the C state and I state: a higher positive social reinforcement effect factor b makes a larger number of users in the C state and I state. Figure 5d shows that the number of users R who are in the immune state during the transmission is relatively smaller with the increase of positive b. When b = 10, the density of R-state nodes decreases by 4.40% in steady state. In summary, the positive social reinforcement effect factor b can affect the spread of public opinion apparently. The larger is b, the stronger is the impact, which reduces the number of users in the C and I states and increases the number of users in the R state, and also promotes the spread of positive public opinion. The above shows that the positive social reinforcement effect factor b is proportional to the density of nodes in the C and I states, and inversely proportional to the density of nodes in the R state. At the same time, the higher is the density of C and I state nodes, the wider is the scope of public opinion information transmission on the network. Therefore, relevant departments can increase the positive social reinforcement effect factor b by publishing real information and other means, thereby promoting the spread of positive public opinion.
4.4. Impact of Negative Social Reinforcement Effect Factor b on Propagation
To analyze the impact of the negative social reinforcement effect factor b on the density of various nodes, set b = 0, b = –1, b = –2, b = –5, and b = –10 and perform 100 iterations based on the basic parameters. The simulation results are shown in Figure 6.
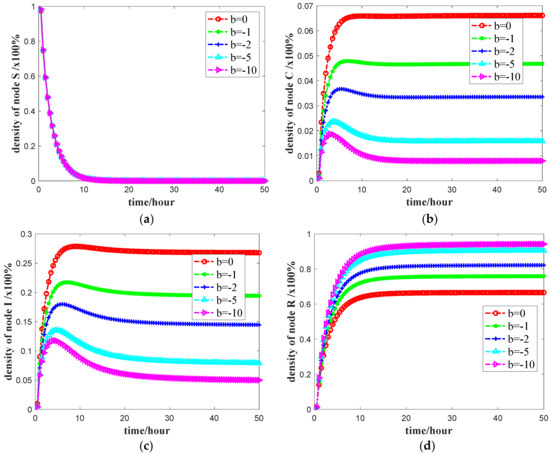
Figure 6.
The number of four states nodes against time t with varying negative social reinforcement effect factor b: (a) density change of S state node; (b) density change of C state node; (c) density change of I state node; and (d) density change of R state node. The final propagation scope with b = 0, –1, –2, –5, and –10 respectively. Other parameters are the same as the default settings.
Figure 6b,c shows that, as the absolute value of the negative social reinforcement effect factor b increases, the growth rate of the number of users in the hesitation state C and propagation state I decreases during the propagation process and the number of them in the steady state is smaller. In the steady state, the node densities in the C and I states at b = –10 are reduced by 72.55% and 81.57%, respectively, compared to b = 0, showing that the negative social reinforcement effect factor b is negatively related to the number of users in the C and I states, and a larger negative value of the negative social reinforcement effect factor b results a lower number of users in the C and I states. Figure 6d also shows that, in the steady state, the node densities in the R states at b = –10 are increased by 41.46% compared to b = 0, showing that listing the absolute value of the negative direction b can increase the number of users in the immune state R. In summary, the larger is the absolute value of the negative social reinforcement effect factor b, the greater is its influence on the spread of public opinion. It causes fewer users in the C and I states and more users in the R state, and plays a significant role in suppressing the spread of negative public opinion.
4.5. Impact of Direct Immunization on Propagation
To analyze the influence of the regulatory role of relevant departments on the spread of Internet public opinion, that is, the impact of the transform from an unknown state S to an immune state R on the spread of public opinion in the presence of direct immunity [46,47], we can observe the effect of direct immunity on each state node by changing , ,, , and . The simulation results are shown in Figure 7.
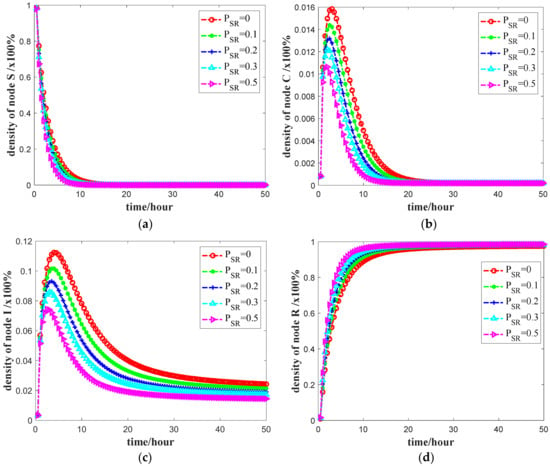
Figure 7.
The number of four states nodes against time t with varying PSR: (a) density change of S state node; (b) density change of C state node; (c) density change of I state node; and (d) density change of R state node. The final propagation scope with PSR = 0, 0.1, 0.2, 0.3, and 0.5, respectively. Other parameters are the same as the default settings.
Figure 7a shows that, in the early stage of public opinion propagation, the number of users in the state S drops sharply. At this time, increasing the probability of direct immunization can speed up the decrease. From the results in Figure 7b,c, we can know that an increase in the probability of direct immunization can significantly reduce the peaks of the number of users in the hesitation state C and the propagation state I during the transmission process, which indicates that the direct immunization can effectively suppress the spread of public opinion. Figure 7d shows that, by listing the probability of direct immunization, the number of users in the immune state R increases more quickly, and the spread expansion of public opinion can be suppressed. At the same time, the greater is the probability of direct immunization, the shorter is the time it takes for users in the four states to reach the final stable state, indicating that direct immunization can also suppress the time for public opinion to spread. In summary, direct immunization can effectively suppress the depth and breadth of public opinion in social networks, thereby effectively reducing the impact of negative public opinion on society.
4.6. Comparative Analysis of SIR Model, SCIR Model and DR-SCIR Model
To further analyze the impact of the combined effects of social reinforcement effect and direct immunity on the spread of social network public opinion, we compared the SIR model, SCIR model, and DR-SCIR model. The changes in the density of various nodes are shown in Figure 8.
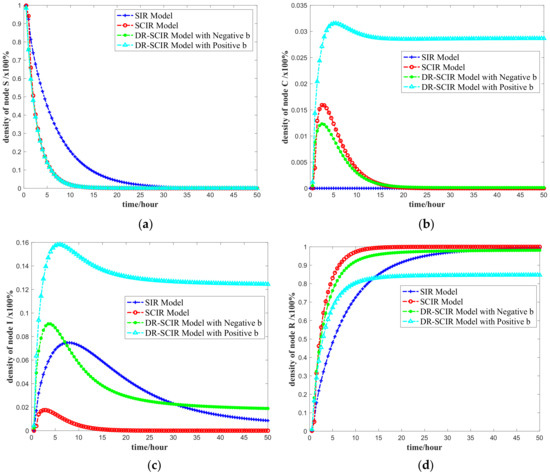
Figure 8.
The number of four states nodes against time t with different models: (a) density change of S state node; (b) density change of C state node; (c) density change of I state node; and (d) density change of R state node. The final propagation scope with SIR model, SCIR model, DR-SCIR model with negative b, and DR-SCIR model with positive b, respectively. Other parameters are the same as the default settings.
Figure 8a shows that, in the early stage of public opinion propagation, the number of users in the S state of the SCIR model and the DR-SCIR model decreases much more quickly than that of the SIR model, which reflects the characteristic of the rapid propagation of public opinion in the early stage. Figure 8b shows that there is no hesitation state C in the SIR model; in the SCIR model, the number of users in the hesitant state C approaches 0 after public opinion spreads for a period of time. The DR-SCIR network with a positive social reinforcement effect promotes the spread of positive public opinion that increases the number of users in the hesitant state C, while the DR-SCIR model with a negative social reinforcement effect suppresses the propagation of negative public opinion. Compared with the SCIR model, the number of users in the hesitant state C is smaller in the DR-SCIR model with a negative social reinforcement effect, and it can be reduced to 0 earlier, thereby preventing the spread of negative public opinion. Figure 8c shows that, due to the complexity of the DR-SCIR model, the number of users in the I state in the initial stage of public opinion propagation increases more quickly, and it can better reflect the explosive transmission characteristic of public opinion, which is consistent with the characteristic of real Internet public opinion propagation. When the network is in the stable state, the number of users in the propagation state I is higher in the DR-SCIR network with a positive social reinforcement effect than the other networks, indicating that the DR-SCIR model with a positive social reinforcement effect hopes to spread positive public opinion on the network. The above simulation results show that, compared with the SIR and SCIR models, the model with a social reinforcement effect takes into account the information credibility and the user’s acceptance of the information, and reflects the complexity of public opinion dissemination. The direct immune effect reflects the controllability of the depth and breadth of public opinion transmission.
5. Conclusions
Since the existing public opinion propagation models do not consider the relevant departments’ control of public opinion information and the impact of secondary transmission of immune users on public opinion propagation, they have difficulty describing the rules of public opinion propagation accurately. After considering the relevant department’s supervision of the spread of public opinion that makes the network have a direct immune effect and the impact of social reinforcement effects on immune users comprehensively, we propose the DR-SCIR network public opinion propagation model with direct immunity and social reinforcement effects based on the SCIR model. The simulation results show that the combined effect of direct immunity and social reinforcement effect can promote the spread of positive public opinion and inhibit the spread of negative public opinion, indicating that there is a link between users’ behavior and the spread of public opinion. At the same time, we can get that the direct immunity can effectively suppress the spread of public opinion. The simulation results show that the positive social reinforcement effect factor b is proportional to the density of nodes in the C and I states, and inversely proportional to the density of nodes in the R state. The larger is b, the stronger is the impact, and the wider is the scope of public opinion information transmission on the network. Therefore, relevant departments can increase the positive social reinforcement effect factor b by publishing real information and other means, thereby promoting the spread of positive public opinion. The larger is the absolute value of the negative social strengthening effect factor b caused fewer users in the C and I state and more users in the R state, and the greater is its influence on the spread of public opinion. The greater is the probability of direct immunization, the smaller is the peak value of the number of users in the hesitation state C and the propagation state I, and the more quickly the number of users in the immunization state R increases, the less time it takes for the users in the four states to reach the final stable state, which indicates that direct immunization can effectively suppress the depth and breadth of public opinion in social networks. The model can better analyze the rules of public opinion transmission on social networks, and enable relevant departments to formulate effective immunization strategies to supervise and control the spread of public opinion in different states, and avoid large-scale outbreaks of negative public opinion.
When designing the threshold m of social strengthening effect, we only assume that m is a certain value, and do not consider the ability of different users to accept information. Future experiments may consider determining the value of m based on factors such as user interests, so as to establish a more accurate public opinion propagation model, and provide a reference for relevant departments to supervise the online public opinion.
Author Contributions
Conceptualization, W.L. and Y.W.; Formal analysis, T.G. and W.L.; Methodology, T.G. and Y.W.; Software, T.G.; Validation, T.G. and Y.W.; Writing—original draft preparation, T.G.; Writing—review and editing, B.C. and T.G.; and Supervision, W.L. and B.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China(Grant No. 6147108); the Equipment Development Department Research Foundation of China (Grant No. 61400010303); the Natural Science Research Project of Liaoning Education Department of China (Grant No. JDL2019019); the Surface Project for Natural Science Foundation in Guangdong Province of China (Grant No. 2019A1515011164); and the Science and Technology Plan Project in Zhanjiang (Grant No. 2018A06001).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Singh, A.; Singh, Y.N. Nonlinear Spread of Rumor and Inoculation Strategies in the Nodes with Degree Dependent Tie Strength in Complex Networks. Acta. Phys. Pol. B 2013, 44. [Google Scholar] [CrossRef]
- Lim, S.; Berry, F.S.; Lee, K. Stakeholders in the Same Bed with Different Dreams: Semantic Network Analysis of Issue Interpretation in Risk Policy Related to Mad Cow Disease. J. Public Adm. Res. Theory 2015, 26, 79–93. [Google Scholar] [CrossRef]
- Chen, T.G.; LI, Q.Q.; Fu, P.H. Public Opinion Polarization by Individual Revenue from the Social Preference Theory. Int. J. Environ. Res. Public Health 2020, 17, 946. [Google Scholar] [CrossRef] [PubMed]
- Kawachi, K.; Seki, M.; Yoshida, H.; Otake, Y.; Warashina, K.; Ueda, H. A rumor transmission model with various contact interactions. J. Theor. Biol. 2008, 253, 55–60. [Google Scholar] [CrossRef] [PubMed]
- De Arruda, G.F.; Rodrigues, F.A.; Moreno, Y. Fundamentals of spreading processes in single and multilayer complex networks. Phys. Rep. 2018, 756, 1–59. [Google Scholar] [CrossRef]
- Malecki, K.; Jankowski, J.; Szkwarkowski, M. Modelling the Impact of Transit Media on Information Spreading in an Urban Space Using Cellular Automata. Symmetry 2019, 11, 428. [Google Scholar] [CrossRef]
- Bodaghi, A.; Goliaei, S.; Salehi, M. The number of followings as an influential factor in rumor spreading. Appl. Math. Comput. 2019, 357, 167–184. [Google Scholar] [CrossRef]
- Lu, P.; Deng, L.; Liao, H. Conditional effects of individual judgment heterogeneity in information dissemination. Physica A 2019, 523, 335–344. [Google Scholar] [CrossRef]
- Ebel, H.; Bornholdt, S. Coevolutionary games on networks. Phys. Rev. E 2002, 66, 056118. [Google Scholar] [CrossRef]
- Szabo, G.; Fath, G. Evolutionary games on graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef]
- Olinky, R.; Stone, L. Unexpected epidemic thresholds in heterogeneous networks: The role of disease transmission. Phys. Rev. E 2004, 70, 030902. [Google Scholar] [CrossRef] [PubMed]
- Boguna, M.; Pastor-Satorras, R.; Vespignani, A. Absence of epidemic threshold in scale-free networks with degree correlations. Phys. Rev. Lett. 2003, 90, 028701. [Google Scholar] [CrossRef] [PubMed]
- Moreno, Y.; Gomez, J.B.; Pacheco, A.F. Epidemic incidence in correlated complex networks. Phys. Rev. E 2003, 68, 035103. [Google Scholar] [CrossRef] [PubMed]
- Moreno, Y.; Nekovee, M.; Vespignani, A. Efficiency and reliability of epidemic data dissemination in complex networks. Phys. Rev. E 2004, 69, 055101. [Google Scholar] [CrossRef] [PubMed]
- Yan, G.; Fu, Z.Q.; Ren, J.; Wang, W.X. Collective synchronization induced by epidemic dynamics on complex networks with communities. Phys. Rev. E 2007, 75, 016108. [Google Scholar] [CrossRef]
- Denphedtnong, A.; Chinviriyasit, S.; Chinviriyasit, W. On the dynamics of SEIRS epidemic model with transport-related infection. Math. Biosci. 2013, 245, 188–205. [Google Scholar] [CrossRef]
- Kimura, M.; Satio, K.; Ohara, K. Learning information diffusion model in a social network forpredicting influence of nodes. Intell. Data Anal. 2011, 15, 633–652. [Google Scholar] [CrossRef]
- Liu, X.; Li, T.; Tian, M. Rumor spreading of a SEIR model in complex social networks with hesitating mechanism. Adv. Differ. Equ. 2018, 2018, 391. [Google Scholar] [CrossRef]
- Galuba, W.; Aberer, K.; Chakraborty, D. Outtweeting the Twitterers—Predicting Information Cascades in Microblogs. In Proceedings of the 3rd Workshop on Online Social Networks (WOSN 2010), Boston, MA, USA, 22 June 2010; p. 3. [Google Scholar]
- Lu, L.; Chen, D.B.; Zhou, T. The small world yields the most effective information spreading. New J. Phys. 2011, 13, 123005. [Google Scholar] [CrossRef]
- Ma, J.; Li, D.D.; Tian, Z.H. Rumor spreading in online social networks by considering the bipolar social reinforcement. Physica A 2016, 447, 108–115. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, L.; Huang, R. SIRaRu rumor spreading model in complex networks. Physica A 2014, 398, 43–55. [Google Scholar] [CrossRef]
- Moreno, Y.; Nekovee, M.; Pacheco, A. Dynamics of Rumor Spreading in Complex Networks. Phy. Rev. E 2004, 69, 066130. [Google Scholar] [CrossRef] [PubMed]
- Pastor-Satorras, R.; Vespignani, A. Immunization of complex networks. Phy. Rev. E 2002, 65, 036104. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.R.; Xia, L.L. The propagation and inhibition of rumors in online social network. Acta Phys. Sin. 2012, 61, 544–550. [Google Scholar]
- Cohen, R.; Havlin, S.; Daniel, B.A. Efficient immunization strategies for computer networks and populations. Phys. Rev. Lett. 2003, 91, 247901. [Google Scholar] [CrossRef]
- Moore, C.; Newman, M.E. Epidemics and percolation in small-world networks. Phy. Rev. E 2000, 61, 5678–5682. [Google Scholar] [CrossRef]
- Eguiluz, V.M.; Klemm, K. Epidemic threshold in structured scale-free networks. Phys. Rev. Lett. 2002, 89, 108701. [Google Scholar] [CrossRef]
- Liu, Z.H.; Hu, B.B. Epidemic spreading in community networks. EPL (Europhys. Lett.) 2005, 72, 315–321. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Chen, Y.; Wang, Q.; Cheng, J.; Cui, H. SIHR rumor spreading model in social networks. Physica A 2012, 391, 2444–2453. [Google Scholar] [CrossRef]
- Liu, Q.; Li, T.; Sun, M. The analysis of an SEIR rumor propagation model on heterogeneous network. Physica A 2017, 469, 372–380. [Google Scholar] [CrossRef]
- Hosseini, S.; Azgomi, M.A. A model for malware propagation in scale-free networks based on rumor spreading process. Comput. Netw. 2016, 108, 97–107. [Google Scholar] [CrossRef]
- Xia, L.L.; Jiang, G.P.; Song, B.; Zhu, G.H. Rumor Spreading Model Considering the Importance and Fuzziness of Information. In Proceedings of the IEEE International Conference on P2P, Parallel, Grid, Cloud and Internet Computing (3PGCIC), Guangdong, China, 8–10 October 2014; pp. 3463–3470. [Google Scholar]
- Fu, X.; Small, M.; Walker, D.M.; Zhang, H. Epidemic dynamics on scale-free networks with piecewise linear infectivity and immunization. Phy. Rev. E 2008, 77, 036113. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.M.; Chen, B.; Chen, X.S.; Gao, X.E. Cascading Failure Model for Command and Control Networks Based on an m-Order Adjacency Matrix. Mob. Inf. Syst. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Maeda, H.; Wu, J.; Sawa, T.; Matsumura, Y.; Hori, K. Tumor vascular permeability and the EPR effect in macromolecular therapeutics: A review. J. Control. Release 2000, 65, 271–284. [Google Scholar] [CrossRef]
- Huang, J.; Jin, X. Preventing rumor spreading on small-world networks. J. Syst. Sci. Complex. 2011, 24, 449–456. [Google Scholar] [CrossRef]
- Wang, H.; Han, J.-H.; Deng, L.; Cheng, K.-Q. Dynamics of rumor spreading in mobile social networks. Acta Phys. Sin. 2013, 62, 110505. [Google Scholar]
- Nekovee, M.; Moreno, Y.; Bianconi, G.; Marsili, M. Theory of rumour spreading in complex social networks. Physica A 2007, 374, 457–470. [Google Scholar] [CrossRef]
- Chen, B.; Yu, H.; Wang, Y.; Gao, X.; Xu, Y. Multilevel Command and Control Supernetwork Modeling Based on Attribute Synergy Prioritization. IEEE Access 2019, 7, 32693–32702. [Google Scholar] [CrossRef]
- Zhu, H.M.; Kong, Y.H.; Wei, J.; Ma, J. Effect of users’ opinion evolution on information diffusion in online social networks. Physica A 2018, 492, 2034–2045. [Google Scholar] [CrossRef]
- Cui, W.; Gong, X.Q.; Liu, C.; Xu, D.; Chen, X.J.; Fang, D.Y.; Tang, S.J.; Wu, F.; Chen, G.H. Node Immunization with Time-Sensitive Restrictions. Sensors 2016, 16, 2141. [Google Scholar] [CrossRef]
- Albert, B. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar]
- Zhou, Y.S.; Wu, C.J. Identifying Rumor Source of Online Social Networks in the SEIR Model. In Proceedings of the International Conference on Cloud Computing and Security, Haikou, China, 8–10 June 2018; pp. 384–394. [Google Scholar]
- Zhou, Y.S.; Wu, C.J.; Zhu, Q.Y.; Xiang, Y.; Loke, S.W. Rumor Source Detection in Networks Based on the SEIR Model. IEEE Access 2019, 7, 45240–45258. [Google Scholar] [CrossRef]
- Chen, B.; Guo, Y.; Gao, X.; Wang, Y. A Novel Multi-Attribute Decision Making Approach: Addressing the Complexity of Time Dependent and Interdependent Data. IEEE Access 2018, 6, 55838–55849. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chen, S.; Pan, C.; Chen, B. Measure of invulnerability for command and control network based on mission link. Inf. Sci. 2018, 426, 148–159. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).