Abstract
The aim of this study was to develop a novel intuitionistic Type-2 fuzzy inference system (IT-2 FIS) which adopts a parameterized Yager-generating function and particle swarm optimization (PSO). In IT-2 FIS, the intuitionistic Type-2 is set as a fuzzy symmetrical triangular number in which the hesitation degree adopts the Yager-generating function, and the parameters of the proposed IT-2 FIS adopting the PSO are tuned. The intuitionistic and Type-2 fuzzy sets have been proven to be the most effective for handling more uncertainty. Therefore, this study proposes an intuitionistic Type-2 set with a Yager-generating function to enhance the conventional fuzzy inference system. Moreover, PSO can improve the fuzzy inference system by searching for the optimal parameters of IT-2 FIS. In this study, linguistic variables were represented by triangular fuzzy numbers (TFS). Two numerical examples were examined: capacity-planning and medical diagnosis problems. An approaching capacity-loadings example was used to verify that the proposed IT-2 FIS could effectively estimate the results of the capacity loadings. In the medical diagnosis problem, IT-2 FIS could obtain a higher correct rate by revealing experts’ knowledge. In both examples, the proposed IT-2 FIS provided more objective estimated values than traditional fuzzy inference systems (FIS) and Type-2 FIS.
1. Introduction
Fuzzy inference systems are based on fuzzy IF-THEN rules that connect the fuzzy input and output variables. Therefore, a fuzzy inference system (FIS) can be used as a prediction model that inputs or outputs data with a high uncertainty. In expert systems with approximate reasoning process fields, FIS is one of the popular systems that can approach a single output (scalar) by a vector of several inputs using fuzzy logic [1]. The fuzzy inference process, which effectively maps pattern discerning or decision-making, includes four phases of FIS, which are determining membership functions, constructing reasoning systems (inference rules), and calculating aggregation and defuzzification processes, respectively [1,2].
Olvera-García [3] proposed a new evaluation model using fuzzy inferences combined with the Analytic Hierarchy Process (AHP), to provide a new air quality index. The second phase of the FIS consists of assigning a weight to each environmental parameter, using a priority analysis based on the AHP. The experimental results showed that the proposed air quality index obtained a good performance when compared with those presented in the literature. When weights were assigned based on the importance level in atmospheric pollution, the new evaluation model could provide better assessments. Blanes-Vidal et al. [4] used neuro-fuzzy inference systems (NFIS) to develop a novel approach for exposure assessment, in which the inputs of the model were easily obtainable proximity measures and the output was the residential exposure to air pollutants. The results indicated that, when emission-dispersion data are not available, NFIS is a useful tool for estimating individual air pollution exposures in epidemiological studies on large populations. Kang et al. [5] used an FIS in which fuzzy theory was applied for diagnosing performance degradation in feed water heaters among power-generation facilities. According to the experimental results, inferences could be made with a consideration of uncertainties based on fuzzy theory. Milan et al. [6] used FIS to automatically determine groundwater withdrawal. In order to determine the best scenario with the highest prediction performance for water withdrawal from an aquifer, the FIS model approached predictive variables under different scenarios. The proposed model was able to predict the optimal amount of groundwater withdrawal and could replace numerical optimization methods. Toseef and Khan [7] used FIS as the main decision-making engine for the diagnosis of crop diseases in Pakistan. The proposed system was tested on a pool of 100 real crop problems, and its inference engine showed an excellent performance in predicting the right disease, with up to a 99% accuracy. Jamshidi et al. [8] used FIS to approach health-risk levels. The input variables, including PM2.5, PM10, and total suspended particles (TSP), as well as the health-risk level, as the output variable, were fuzzed by using a fuzzy inference system. This method could be used effectively in other workplaces, such as hospitals and health-care facilities. Wang et al. [9] developed the Genetic Algorithm and Rough Set Incorporated Neural Fuzzy Inference System (GARSINFIS), which is an integrated autonomous computational model for underpricing forecasting in initial public offerings. The experimental results showed a higher yield of initial returns for initial public offerings, by following the advice provided by GARSINFIS in comparison to any other benchmarking model. Hence, the GARSINFIS model was capable of offering investors highly interpretable and reliable decision support to gain the money-left-on-the-table in initial public offerings. Maciel and Ballini [10] proposed interval-valued fuzzy inference system (iFIS) modeling to predict interval-valued time series. The fuzzy c-means clustering algorithm was used in interval-valued data with adaptive distances for antecedent identification. In order to fit a linear regression model to symbolize the interval data, the center-range methodology estimated the parameters of the linear consequents. The results indicated that iFIS could obtain a better performance than traditional alternative approach methods.
A summary of the research that has investigated FIS as a classification technique since 2016 is shown in Table 1, illustrating that FIS has been widely applied in various fields and that combining FIS with other techniques usually results in a better performance.

Table 1.
Recent developments in the fuzzy inference system (FIS).
This research developed a novel Type-2 fuzzy inference system (IT-2 FIS) for enhancing traditional FIS in uncertain environments. In various situations [11,12,13], the Type-2 fuzzy set has been shown to express uncertainty information effectively. The Type-2 fuzzy set can obtain a higher computational power and better description of uncertainty than traditional FIS. Moreover, traditional degrees of the fuzzy membership function have been determined to be valued between 0 and 1. Atanassov [14] proposed an intuitionistic fuzzy set (IFS) that could express various degrees of membership, non-membership, and hesitation in a fuzzy set for more clearly express uncertain environments. However, degrees of hesitation are not easy to clearly determine. This study adopts the parameterized Yager-generating function to determine degrees of hesitation in a Type-2 fuzzy set. With the help of Atanassov’s intuitionistic fuzzy complement with Yager-generating functions [15], the hesitation can be determined to promote efficiency of the proposed fuzzy inference system, and this has been successfully examined in [16,17]. In this study, the parameterized Yager-generating function could tune to optimal target values based on particle swarm optimization (PSO). Therefore, the concept of IFS combined with a Type-2 fuzzy set would obtain a better description of uncertainty, and this study develops an intuitionistic Type-2 FIS with PSO.
The main contributions of this paper are as follows:
- (1)
- A novel Type-2 fuzzy inference system (IT-2 FIS) for enhancing traditional FIS in uncertain environments is developed. The proposed IT-2 FIS adopts the parameterized Yager-generating function to determine the degrees of hesitation in Type-2 fuzzy set, and optimal target values based on particle swarm optimization.
- (2)
- The proposed IT-2 FIS is capable of dealing with complex capacity loading and medical diagnosis problems in which various uncertain variables and incomplete knowledge are involved. It is more suitable for revealing expert knowledge and constructing fuzzy models in a human tractable form.
The rest of this paper is organized as follows: The proposed IT-2 FIS with the novel intuitionistic Type-2 set and PSO is introduced in Section 2; in Section 3, two numerical examples of capacity-planning and medical diagnosis problems are utilized to demonstrate the performance of different fuzzy inference systems; finally, conclusions are made in Section 4.
2. IT-2 FIS with a Novel Intuitionistic Type-2 Fuzzy Set
This study developed an IT-2 FIS with a novel intuitionistic Type-2 set. Figure 1 and the following steps illustrate the designed system. First, the intuitionistic Type-2 fuzzy sets are determined and the parameters of the intuitionistic Type-2 fuzzy sets are continuously tuned by the PSO algorithm. Secondly, the fuzzy IF-THEN rules are structured by experts as conventional FIS, and the novel intuitionistic Type-2 fuzzy set with Yager-generating functions is used to substitute traditional triangular fuzzy numbers (TFSs). Thirdly, the intuitionistic fuzzy Type-2 set is type-reduced to obtain the interval consequent set. Fourthly, the interval consequent set is transformed to a crisp value, using the defuzzification technique, and the defuzzification return to the PSO mechanism is calculated with the fitness values for the optimal novel intuitionistic Type-2 fuzzy set, until the maximum number of iterations is reached.
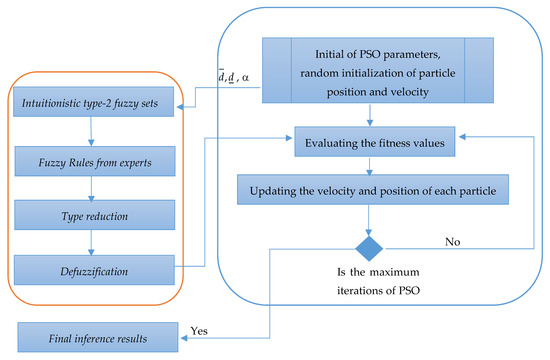
Figure 1.
Flowchart of the Type-2 fuzzy inference system (IT-2 FIS).
2.1. Intuitionistic Type-2 Fuzzy Sets with Yager-Generating Functions (Fuzzy Input)
Intuitionistic Type-2 fuzzy sets with Yager-generating functions were employed in all the definitions of fuzzy input in the proposed IT-2 FIS. Firstly, an intuitionistic Type-2 membership function, , is determined, and this particular set includes a non-membership function. Hence, the intuitionistic Type-2 membership function can be expressed as , where x ∈ X and u ∈ Jx ⊆ [0, 1] are calculated as follows:
in which 0 ≤ + ≤ 1, with the help of Atanassov’s intuitionistic fuzzy complement with Yager-generating functions. In Yager-generating functions for each value of parameter α ∈ (0, ∞), a particular fuzzy complement can be defined, which includes non-membership and hesitation degree. can become based on Yager-generating functions, and the hesitation degree is . In a traditional fuzzy operator, the hesitation degree has not been reasonably considered and defined, and it is usually ignored. The parametric intuitionistic fuzzy complement therefore can more effectively define the value of the hesitation degree based on historical or observational data or experiments. Therefore, this study adopts the parametric intuitionistic fuzzy complement to define the hesitation degree for fuzzy inference system.
The Footprint of Uncertainty (FOU) represents that proposed intuitionistic Type-2 fuzzy set that consists of a bounded region, and it is determined as a union of all primary membership. FOU characterizes intuitionistic Type-2 fuzzy sets:
The upper membership functions (UMF) and lower membership functions (LMF), which are associated with FOU, as proposed by [18], model the uncertainties in the shape and position of the traditional fuzzy set by using two traditional membership functions. FOU represents the entire Type-2 fuzzy set, and uniform shading denotes the interval sets for the secondary membership functions. Meanwhile, the membership function, non-membership function, and hesitation degree are determined as intuitionistic fuzzy sets. , , and are the upper bounds of the membership, non-membership, and hesitation membership functions, respectively. All membership functions are determined as triangular fuzzy numbers , where c is the mode, is the spread of membership functions, and these membership functions can associate with the upper bound of ,, and . Furthermore, the novel intuitionistic Type-2 membership function includes the membership function and hesitation degree, which are denoted as follows:
where is the updated version of the upper membership function. The lower membership function is associated with the . All membership functions are determined as triangular fuzzy numbers (), where c is the mode, is the spread of membership functions, and these membership functions can associate with the lower bound of , , and . is the updated version of the lower membership function, which can also be denoted as follows:
In this study, the intuitionistic Type-2 fuzzy sets were as shown in Figure 2.
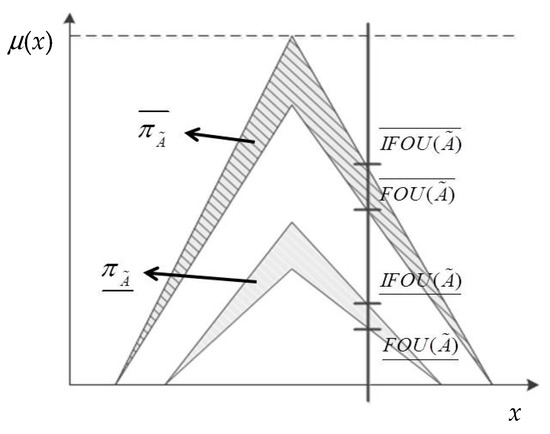
Figure 2.
Illustration of intuitionistic Type-2 fuzzy sets.
2.2. Fuzzy IF-THEN Rules
General fuzzy rules are IF-THEN rules, in which the lth rule has the form “Rl: IF x1 is and x2 is and … and xq is , THEN y is Gl”, where xi represents the inputs, represents the antecedent sets (i = 1, …, q), y is the map of input xi, and Gl is the linguistic variable. The lth rule can also take the form “Rl: IF x1 is and x2 is and … and xq is , THEN y is ”. The input and output sets can be replaced by intuitionistic Type-2 sets. The structure of this intuitionistic fuzzy Type-2 rule is exactly the same as that of a fuzzy Type-1 rule; the only difference is in the nature of the membership functions using the upper and lower membership functions of intuitionistic Type-2 fuzzy sets.
2.3. Type Reduction and Defuzzification
The output of the intuitionistic fuzzy Type-2 inference engine is type-reduced as Type-2 FIS. The type-reduction method is most commonly employed in Type-2 FIS and can determine the center of the set. The type-reduction method can be expressed as follows:
where Ycos is an interval set determined by two end points, yl and yr; fi ∈ = []; yi ∈ Yi = []; Yi is the centroid of the intuitionistic fuzzy Type-2 interval set of ; and, i = 1, …, M. Due to Ycos being an interval set, it can be defuzzified by using the average of yl and yr. The defuzzified output of intuitionistic fuzzy interval Type-2 is as follows:
2.4. Particle Swarm Optimization in the Proposed FIS
PSO was developed by Kennedy [19] and is a type of stochastic optimization technology. PSO is adopted to identify the three parameters of , and α in the proposed IT-2 FIS. Li et al. [20] mentioned that PSO can model the social behavior of bird flocking and used a population-based search as a genetic algorithm. Based on exploiting a population, the PSO can probe a promising region of the search space. The PSO has been successfully applied in searching optimal parameters [21,22]. The PSO mainly search optimal parameters of intuitionistic Type-2 fuzzy sets, and the performance of PSO is accurate rate of IT-2 FIS based on upper and lower spread of membership functions and α in the proposed IT-2 FIS. Algorithm 1 describes particle swarm optimization in the IT-2 FIS. In this study, the notation for the PSO algorithm is as follows:
| Population_size | is initial population size; |
| pbest | is the best movement; |
| gbest | is the best position movement; |
| vid | is a modification of velocity; |
| xid | is the position of the ith particle; |
| rand(.) | represents random variables with a uniform distribution |
| C1 and C2 | are two acceleration constants that regulate the velocities to the best global and local positions; |
| K | is the current generation number; |
| wk | is the inertia weight; |
| wmax | is the initial weight; |
| wmin | is the final weight; |
| kmax | is the maximum number of generations; |
| is the spread of membership functions which can associate with the upper bound; | |
| is the spread of membership functions which can associate with the lower bound; | |
| α | is tuned parameter of Yager-generating functions. |
| Algorithm 1 Particle swarm optimization in an IT-2 FIS | |
| 1. | Initial populations (Randomly) |
| 2. | Iteration = 0 |
| 3. | Setting Population_size, x = (, α) |
| 4. | Setting C1, C2, wmax, wmin |
| 5. | While (Iteration < Maximum number of iterations) do |
| 6. | If f(xi) < pbest then |
| 7. | pbest = xi |
| 8. | end if |
| 9. | If pbes < gbest then |
| 10. | gbest = pbest |
| 11. | end if |
| 12. | Calculating the modification of velocity and position of the ith particle |
| 13. | |
| 14. | Calculating inertia weight |
| 15. | Calculating new position of the particle |
| 16. | Iteration++ |
| 17. | End while |
| 18. | Return, and α |
3. Numerical Examples
Two numerical examples were examined—capacity-planning and medical diagnosis problems. In the first example, the fuzzy IF-THEN rules are employed to approach capacity loadings. The fuzzy IF-THEN rules of capacity loadings refer to Pai et al. [23], who successfully adopted traditional FIS to approach the actual capacity loadings. Therefore, the example that approached capacity loadings was used to verify that the proposed IT-2 FIS could effectively estimate the results of the capacity loadings. In the second example, the medical diagnosis problem was examined—which is a standard classification problem—by using fuzzy IF-THEN rules. The fuzzy IF-THEN rules could simulate the decision of a radiologist who is an expert at determining the stage of breast cancer. The medical diagnosis problem was also used to verify that the proposed IT-2 FIS could obtain a higher accuracy by revealing expert knowledge. Two different types of problems (estimating values and classification) were examined, and the two examples were real cases from the manufacturing and medical industries, respectively. In IT-2 FIS, the parameters of PSO are shown in Table 2 for the two numerical examples.

Table 2.
Parameters of PSO in IT-2 FIS.
3.1. Proposed FIS in Capacity-Planning Problems
The capacity-planning is accurately approached as an actual quantity in advance, which can bring many benefits, such as reducing the inventory, improving the quality, allowing on-time deliveries, and reducing the processing time. In the proposed FIS, two stages of approximate reasoning are performed. These data are collected by product-assembly companies in he manufacturing industry. In stage one, the proposed FIS can approach the total capacity requirements (TCR) quantity (production requirement + set up resources) based on the demand (D) and failure rate (FR). Generally, the TCR is estimated by managerial experience in real environment. In stage two, the proposed FIS can approach the capacity loadings (CL) during the production planning period. The fuzzy inputs of D, set-up resources (SR), and capacity constraints (CC) in stage two are considered in capacity-planning systems [23]. A numerical experiment verified that the proposed FIS can effectively approach the capacity loadings. Linguistic variables are presented as Figure 3, Figure 4 and Figure 5. This study adopted triangular fuzzy sets (TFSs) as linguistic variables, making the study differ from the work of Pai et al. [23], because the proposed FIS adopted the TFSs in this study to promote the performance. The term of “NB” is very less, “NM” is much less, “NS” is less, “O” is normal, “PS” is more, “PM” is much more, and “PB” is very much more in Figure 3, Figure 4 and Figure 5. The bill of material (BOM) is illustrated in Figure 6.
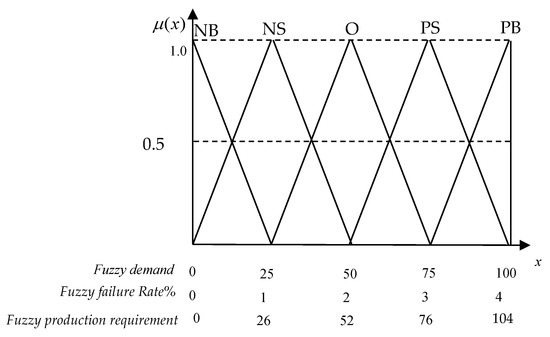
Figure 3.
The compatibilities of the demand (D) and failure rate (FR).
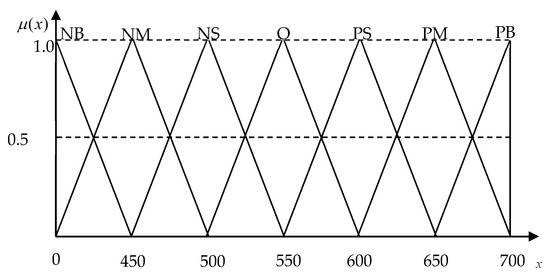
Figure 4.
The compatibilities of the fuzzy total capacity requirements (TCR) and the fuzzy capacity requirements (CR).
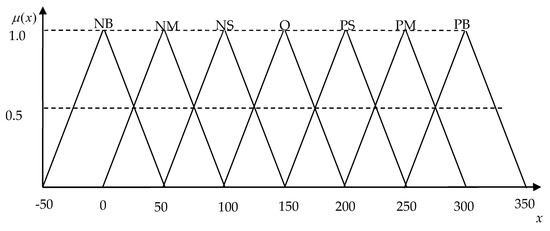
Figure 5.
The compatibilities of the fuzzy capacity loadings (CL).
Figure 6.
Bill of material [23].
The TCR production quantity is inferred in stage one. The input data are the fuzzy D and fuzzy FR of four periods. The rules of the total capacity requirements (TCR) can be referred to in [23], and Figure 7 displays the surface of the fuzzy IF-THEN rules of the total capacity requirement. Table 3 displays the inference results of TCR, which also show the defuzzification of upper membership functions (UMF) and lower membership functions (LMF) of TCR by using Type-2 FIS, and the proposed FIS. The rules of the production requirement with traditional TFSs, fuzzy Type-2 (UMF and LMF) sets, and intuitionistic Type-2 (UMF, LMF, and α1) fuzzy sets are shown in Table 3. The output of this stage is the TCR of each period, and it shows the approaching values under FIS, Type-2 FIS, and the proposed FIS. The UMF and LMF of the CR for the four periods are presented in Table 3, and the TCR is shown in Table 3, after the exploration of BOM.
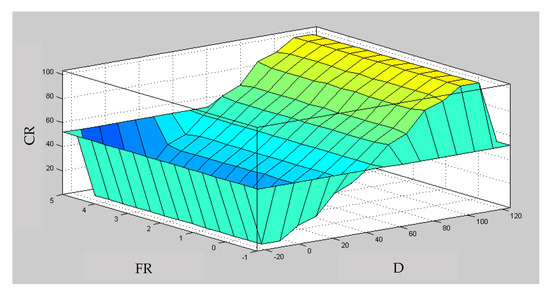
Figure 7.
The surface of the fuzzy IF-THEN rules of the TCR.

Table 3.
The fuzzy D, fuzzy FR, and set-up resources (SR) of four periods with various FIS.
In stage two, the CL is inferred. The rules of the CL [23] are illustrated in Figure 8. The input data of this stage are the fuzzy TCR and fuzzy CC with their UMF and LMF (Type-2 fuzzy sets). The outputs of stage two are the fuzzy CL of four periods. Figure 9 shows the training error of proposed IT-2 FIS via using proposed PSO. The performance has convergence with excellent stability in the capacity-planning problem. Table 4, Table 5 and Table 6 indicate the defuzzified CL of the four periods by Equation (12). The positive numbers in Table 4, Table 5 and Table 6 represent the overloading of the capacity, and the negative numbers are the underloading of the capacity. The proposed IT-2 FIS can provide a more objective estimated value than the traditional FIS because of the fuzzy bounds (UMF and LMF). In the simulated results, period 4 considered the underloading of the capacity for tuning material and production projects.
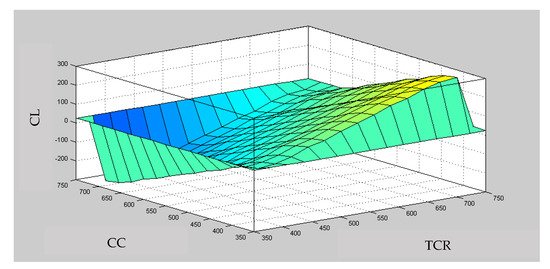
Figure 8.
The surface of rules of the CL.
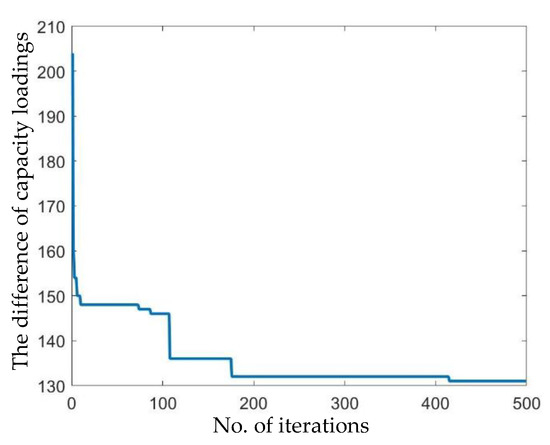
Figure 9.
The training error of proposed IT-2 FIS in capacity-planning problem.

Table 4.
Defuzzified capacity loadings of four periods with FIS.

Table 5.
Defuzzified capacity loadings of four periods with Type-2 FIS.

Table 6.
Defuzzified capacity loadings of four periods with proposed IT-2 FIS.
In this capacity-planning case, the [23] has verified traditional FIS could approach capacity loadings well. Hence, the performance evaluation is difference with results of traditional FIS (capacity loadings is −46, −162, 127, and 7, with period is 1 to 4). Table 7 shows the result of proposed IT-2 FIS is significantly similarity the FIS by T-test and verifies that the proposed IT-2 FIS could successfully estimate the capacity-planning problem, too. A comparison of FIS, Type-2 FIS, and the proposed FIS revealed a number of phenomena. First, the proposed FIS could obtain reasonable capacity loading approach values, similar to [23], in capacity-planning problems. Second, since the proposed FIS could appropriately tune the parameters of the Yager-generating functions using the PSO algorithm, it could obtain a more suitable fuzzy input than FIS or Type-2 FIS, while the case has actual target values. Third, the proposed FIS could be an effective alternative capacity-loading inference system.

Table 7.
The T-test CL estimate for difference (FIS to Type-2 FIS and FIS to proposed IT-2 FIS).
3.2. Proposed FIS in a Medical Diagnosis Problem
The identification of micro-calcifications can be used in the effective detection of breast cancer, which has been verified in the medical field. The procedure of mammography, a specific type of X-ray radiograph, can digitally capture the contrasting imageries of both micro-calcifications and normal breast tissues. However, different examiners of the same digitized images may arrive at divergent diagnoses due to the varying experience and background of each examiner, as well as his/her own subjectivity. In this numerical example, this study conducted a discussion with a professional physician and investigated the variables of micro-calcifications, calcification density, and calcification abnormal shape to establish the fuzzy decision rules (Table 8). The “H”, “M”, and “L” respectively represent high (0.5, 0.75, 0.75), median (0.25, 0.5, 0.75), and lower (0.25, 0.25, 0.5) bounds, which are shown in Figure 10. Figure 11 displays the fuzzy decision terms, which are “3” (0, 0.2, 0.4), “4A” (0.2, 0.4, 0.6), “4B” (0.4, 0.6, 0.8), and “4C” (0.6, 0.8, 1), respectively. The fuzzy decision terms mean the breast cancer stages. The “3” stage is when the tumor size is bigger than 50 mm. The “4A”, “4B”, and “4C” mean different degrees of direct extension to the chest wall. Figure 12 shows the training error of proposed IT-2 FIS via using proposed PSO. The performance also has convergence with excellent stability in a breast cancer diagnosis problem. In the medical diagnosis case, correct rate is measure index. The actual results are shown in Table 9, and the accurate rate of the proposed IT-2 FIS is 100%, which is better than the traditional FIS (50%) and type-2 FIS (80%) in cases A to J. The results show that cases B, C, E, G, and I were incorrect estimations of stages for breast cancer by using traditional FIS; and cases B and G were incorrect estimation of stages for breast cancer by using Type-2 FIS.

Table 8.
Fuzzy decision rules of breast cancer diagnosis problems.
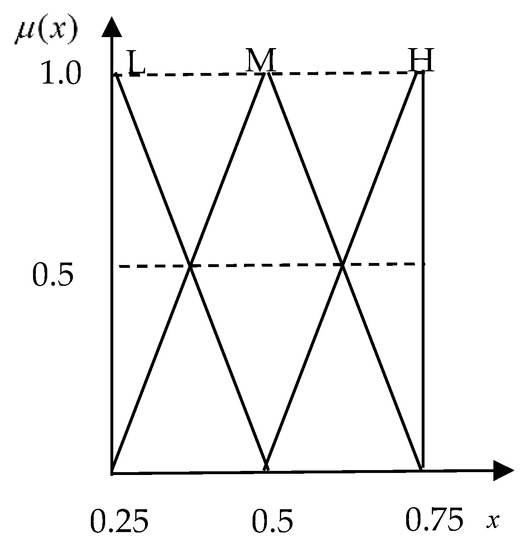
Figure 10.
The compatibilities of the fuzzy variables.
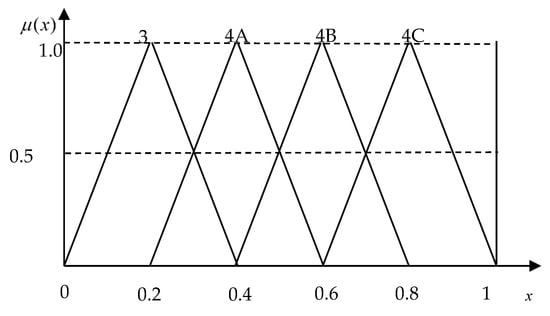
Figure 11.
The compatibilities of the fuzzy decision.
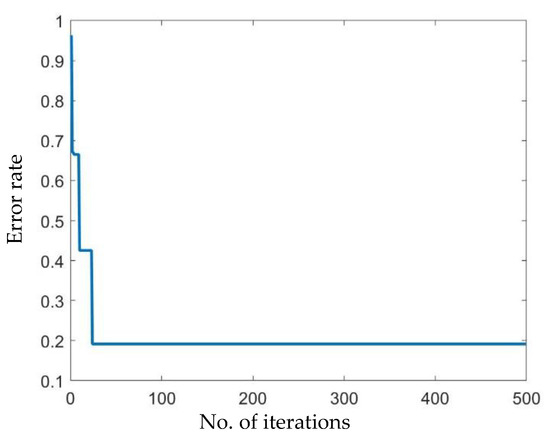
Figure 12.
The training error of proposed IT-2 FIS in a breast cancer diagnosis problem.

Table 9.
Comparison of FIS, Type-2 FIS, and intuitionistic Type-2 FIS in a breast cancer diagnosis problem.
Finally, the T-test was implemented to test the breast cancer diagnosis results. The test results, presented in Table 10, show significant differences among the FIS and proposed IT-2 FIS models, indicating the breast cancer diagnosis results of the proposed IT-2 FIS model are better than the traditional FIS based on accurate rate. In this example, IT-2 FIS is successfully applied in breast cancer diagnosis problems. The IT-2 FIS is capable of dealing with complex breast cancer diagnosis. Through the IT-2 FIS, managers can obtain more objective estimated values and higher accurate rates than those obtained with traditional FIS and type-2 FIS in medical diagnosis.

Table 10.
The T-test estimate for difference in a breast cancer diagnosis problem.
4. Conclusions
In this study, the proposed IT-2 FIS, which adopts intuitionistic Type-2 fuzzy sets with Yager-generating functions as the fuzzy input, was successfully applied in two numerical examples. The proposed IT-2 FIS is capable of dealing with complex capacity loading and medical diagnosis problems where various uncertain variables and incomplete knowledge are involved. It is more suitable for revealing experts’ knowledge and constructing fuzzy models in a human tractable form. Through the proposed IT-2 FIS, managers can obtain more flexible approach values compared to traditional FIS and Type-2 FIS in numerical examples. This study was the first to use novel intuitionistic Type-2 fuzzy sets with Yager-generating functions and PSO. However, this study did not examine the ability of the proposed IT-2 FIS to approach other types of actual problems. For instance, the time-series financial data (can refer to [24,25]) may also be examined by using proposed IT-2 FIS in future research. Another unexamined issue is the appropriateness of combining the proposed IT-2 FIS with other approaches, such as different linguistic models, to deal with uncertain data. The state-of-the-art FIS may also adopt the Yager-generating functions and PSO to enhance their fuzzy inference system. The others heuristic algorithm also could be adopted to search optimal parameters of IT-2 FIS, such as improved PSO Algorithm. All issues are worth further investigation.
Author Contributions
Conceptualization and methodology, C.-M.Y.; methodology and writing—original draft preparation, K.-P.L.; writing—review and editing, G.-S.L.; data curation, C.-H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology of the Republic of China, Taiwan, grant numbers MOST-108-2221-E-029-020 and MOST-107-2622-E-029-010-CC3.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zadeh, L. Fuzzy sets as a basis for theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Ocampo, W.; Ferré, N.; Domingo, J.; Schuhmacher, M. Assessing water quality in rivers with fuzzy inference systems: A case study. Environ. Int. 2006, 32, 733–742. [Google Scholar] [CrossRef] [PubMed]
- Olvera-García, M.Á.; Carbajal-Hernández, J.J.; Sánchez-Fernández, L.P.; Hernández-Bautista, I. Air quality assessment using a weighted Fuzzy Inference System. Ecol. Inform. 2016, 33, 57–74. [Google Scholar] [CrossRef]
- Blanes-Vidal, V.; Cantuaria, M.L.; Nadimi, E.S. A novel approach for exposure assessment in air pollution epidemiological studies using neuro-fuzzy inference systems: Comparison of exposure estimates and exposure-health associations. Environ. Res. 2017, 154, 196–203. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.K.; Kim, H.; Heo, G.; Song, S.Y. Diagnosis of feed water heater performance degradation using fuzzy inference system. Expert Syst. Appl. 2017, 69, 239–246. [Google Scholar] [CrossRef]
- Milan, S.G.; Roozbahani, A.; Banihabib, M.E. Fuzzy optimization model and fuzzy inference system for conjunctive use of surface and groundwater resources. J. Hydrol. 2018, 566, 421–434. [Google Scholar] [CrossRef]
- Toseef, M.; Khan, M.J. An intelligent mobile application for diagnosis of crop diseases in Pakistan using fuzzy inference system. Comput. Electron. Agric. 2018, 153, 1–11. [Google Scholar] [CrossRef]
- Jamshidi, H.R.; Karimi, A.; Haghshenas, M.; Haghshenasb, M. Risk assessment of particulate matters in a dentistry school using fuzzy inference systems. Measurement 2018, 116, 257–263. [Google Scholar] [CrossRef]
- Wang, D.; Qian, X.; Quek, C.; Tan, A.-H.; Miao, C.; Zhang, X.; Ng, G.S.; Zhou, Y. An interpretable neural fuzzy inference system for predictions of underpricing in initial public offerings. Neurocomputing 2018, 319, 102–117. [Google Scholar] [CrossRef]
- Maciel, L.; Ballini, R. A fuzzy inference system modeling approach for interval-valued symbolic data forecasting. Knowl. -Based Syst. 2019, 164, 139–149. [Google Scholar] [CrossRef]
- Mendel, J.M. Advances in type-2 fuzzy sets and systems. Inf. Sci. 2007, 177, 84–110. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.; Liu, F. Interval type-2 fuzzy logic systems Made Simple. IEEE Trans. Fuzzy Syst. 2006, 14, 808–821. [Google Scholar] [CrossRef]
- Mendel, J.M.; Liu, X. Simplified interval type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 2013, 21, 1056–1069. [Google Scholar] [CrossRef]
- Atanassov, K.T. More on intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 33, 37–45. [Google Scholar] [CrossRef]
- Yager, R.R. On some new classes of implication operators and their role in approximate reasoning. Inform. Sci. 2004, 167, 193–216. [Google Scholar] [CrossRef]
- Chaira, T. A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images. Appl. Soft Comput. 2011, 11, 1711–1717. [Google Scholar] [CrossRef]
- Lin, K.-P. A Novel Evolutionary Kernel Intuitionistic Fuzzy C-means Clustering Algorithm. IEEE Trans. Fuzzy Syst. 2014, 22, 1074–1087. [Google Scholar] [CrossRef]
- Mendel, J.M.; Liang, Q. Pictorial comparisons of type-1 and type-2 fuzzy logic systems. In Proceedings of the IASTED International Conference on Intelligent Systems & Control, Santa Barbara, CA, USA, 28–30 October 1999. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Li, X.; Ming, S.; Lixing, D. Particle swarm optimization-based LS-SVM for building cooling load prediction. J. Comput. 2010, 5, 614–621. [Google Scholar] [CrossRef]
- Bhandari, V.S.; Kulkarni, S.H. Optimization of heat sink for thyristor using particle swarm optimization. Results Eng. 2019, 4, 100034. [Google Scholar] [CrossRef]
- Isietm, M.; Gadala, M. Sensitivity analysis of control parameters in particle swarm optimization. J. Comput. Sci. 2020, 41, 101086. [Google Scholar] [CrossRef]
- Pai, P.F.; Chang, P.T.; Wang, S.S.; Lin, K.P. A fuzzy logic-based approach in capacity-planning problems. Int. J. Adv. Manuf. Technol. 2004, 23, 806–811. [Google Scholar]
- Bekiros, S.D. Fuzzy adaptive decision-making for boundedly rational traders in speculative stock markets. Eur. J. Oper. Res. 2010, 202, 285–293. [Google Scholar]
- Gradojevic, N. Non-linear, hybrid exchange rate modeling and trading profitability in the foreign exchange market. J. Econ. Dyn. Control 2007, 31, 557–574. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).