A New Dataset and Deep Residual Spectral Spatial Network for Hyperspectral Image Classification
Abstract
1. Introduction
- Spectral-based classification methods: Using a convolutional neural network (CNN), the input is a 1-D vector obtained from the spectral band of each pixel. For this type of methods, a stacked autoencoder (SAE) was proposed as a feature extractor to capture the representative stacked spectral and spatial features with a greedy layerwise pretraining strategy. Subsequently, denoising SAE [14], and Laplacian SAE [15] were successively proposed. However, since these models have the requirement that the input must be 1-D data, spatial information is ignored. Besides, there are so many parameters produced by fully connected (FC) layers in these networks that a large number of available samples are required to train the network.
- Spatial-based classification methods: These methods consider the neighboring pixels of a target pixel in the original remote sensing images in order to extract the spatial feature representation. Therefore, a 2-D CNN architecture is adopted, where the input data is a patch of P×P neighboring pixels. In order to extract high-level spatial features, multi-scale structure methods have been proposed. For example, in [16] the neighboring pixels of each target pixel of the HSI are fed to the network. Compared with SAE, these types of methods use the spatial information to improve the classification performance. However, it should be noted that such methods usually require a pre-processing of the spectral information (such as PCAs [17,18] or autoencoders [19,20]) to reduce the number of bands used for classification, which will lose some of the spectral information.
- Spectral-spatial classification methods: By using a combination of spatial and spectral information [21], these types of methods can significantly improve the classification accuracy. Each of the target pixel is associated with a P×P spatial neighborhood and B spectral bands (P×P×B). Then they are processed by means of 3-D CNNs in order to learn the local signal changes in both the spatial and the spectral domain of the hyperspectral data cubes. In these types of methods, [22] proposed a 3-D CNN to take full advantage of the structural characteristics of the 3-D hyperspectral remote sensing data.
- A new HSI dataset named Shandong Feicheng was presented, which is larger in scale and is more complex in data compared with other public HSI datasets. State-of-the-art methods were tested on the proposed dataset.
- We proposed a novel HSI classification framework DRSSN. Taking the advantage of the structure of shortcut connection and 2-D convolution, it is much deeper to extract features with better discrimination while reducing overfitting.
- A novel sample balanced loss was proposed to alleviate insufficient training caused by sample size unbalance between easily and hard classified samples. Experimental results proved its validity.
2. Materials and Methods
2.1. Datasets
2.2. Network Architecture
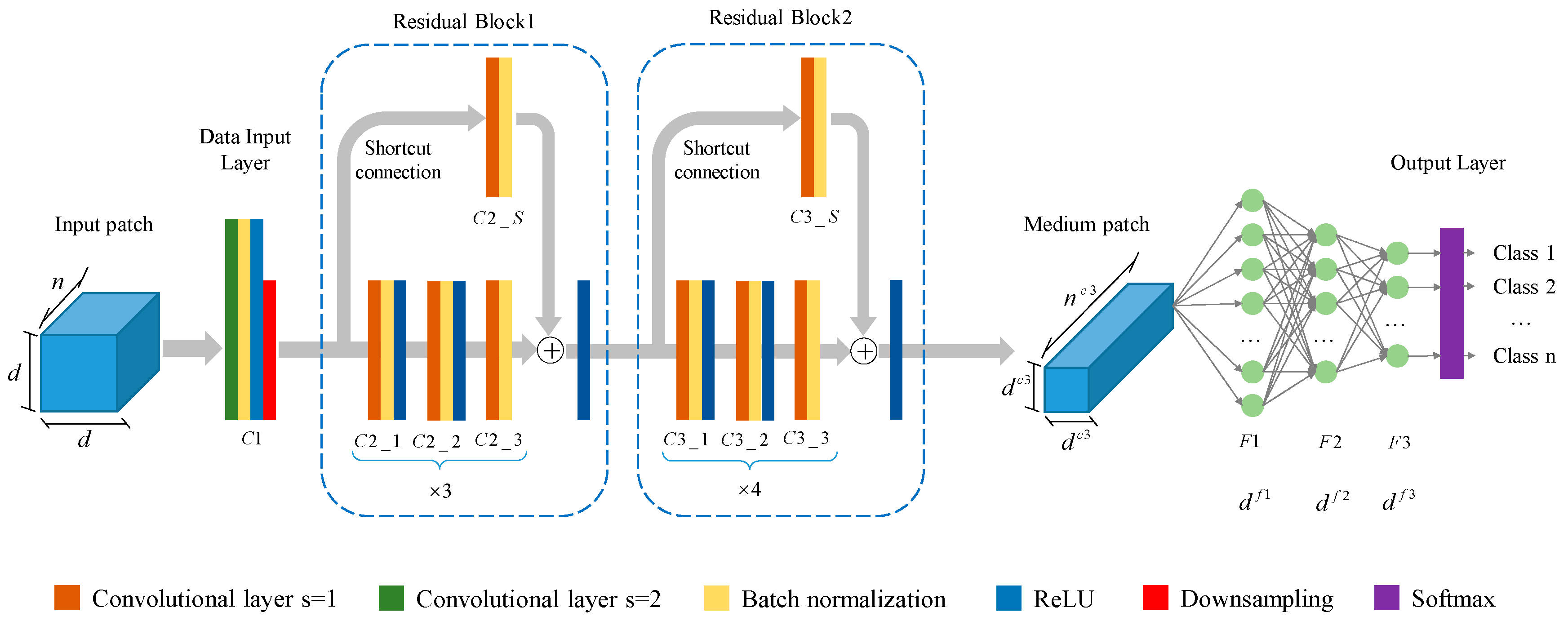
2.2.1. Details of DRSSN Framework
2.2.2. Data Preprocessing
2.3. Sample Balanced Loss
3. Results
3.1. Implementation Details
3.2. Experimental Results and Analysis
3.3. Ablation Study
4. Discussion
4.1. The Effect of Window Size
4.2. The Effect of Focusing Parameter
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X.; Du, B. Hyperspectral Remote Sensing Image Subpixel Target Detection Based on Supervised Metric Learning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4955–4965. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of spectral–temporal response surfaces by combining multispectral satellite and hyperspectral UAV imagery for precision agriculture applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Makki, I.; Younes, R.; Francis, C.; Bianchi, T.; Zucchetti, M. A survey of landmine detection using hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2017, 124, 40–53. [Google Scholar] [CrossRef]
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, A.J. Advanced Spectral Classifiers for Hyperspectral Images: A review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.; Plaza, J.; Plaza, A. Cloud implementation of the K-means algorithm for hyperspectral image analysis. J. Supercomput. 2017, 73, 1–16. [Google Scholar] [CrossRef]
- Marinoni, A.; Gamba, P. Unsupervised Data Driven Feature Extraction by Means of Mutual Information Maximization. IEEE Trans. Comput. Imaging 2017, 3, 243–253. [Google Scholar] [CrossRef]
- Marinoni, A.; Iannelli, G.C.; Gamba, P. An Information Theory-Based Scheme for Efficient Classification of Remote Sensing Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5864–5876. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bruzzone, L. Kernel-based methods for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1351–1362. [Google Scholar] [CrossRef]
- Bazi, Y.; Melgani, F. Gaussian Process Approach to Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 186–197. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral–Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Jia, K.; Lin, S.; Gao, S.; Zhan, S.; Shi, B.E. Laplacian Auto-Encoders: An explicit learning of nonlinear data manifold. Neurocomputing 2015, 160, 250–260. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Ma, L.; Jiang, H.; Zhao, H. Deep residual networks for hyperspectral image classification. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1824–1827. [Google Scholar]
- Kang, X.; Xiang, X.; Li, S.; Benediktsson, J.A. PCA-based edge-preserving features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Agarwal, A.; El-Ghazawi, T.; El-Askary, H.; Le-Moigne, J. Efficient hierarchical-PCA dimension reduction for hyperspectral imagery. In Proceedings of the 2007 IEEE International Symposium on Signal Processing and Information Technology, Giza, Egypt, 15–18 December 2007; pp. 353–356. [Google Scholar]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Hyperspectral image classification with independent component discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef]
- Wang, J.; Chang, C.-I. Independent component analysis-based dimensionality reduction with applications in hyperspectral image analysis. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1586–1600. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- Zhong, Z.; Member, S.; Li, J.; Member, S.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Gundogdu, E.; Koç, A.; Alatan, A.A. Infrared object classification using decision tree based deep neural networks. In Proceedings of the 2016 24th Signal Processing and Communication Application Conference (SIU), Zonguldak, Turkey, 16–19 May 2016; pp. 1913–1916. [Google Scholar]
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging Spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote Sens. Environ. 1998, 65, 227–248. [Google Scholar] [CrossRef]
- Kunkel, B.; Blechinger, F.; Lutz, R.; Doerffer, R.; van der Piepen, H.; Schroder, M. ROSIS (Reflective Optics System Imaging Spectrometer)—A Candidate Instrument for Polar Platform Missions. In Optoelectronic Technologies for Remote Sensing from Space; Seeley, J., Bowyer, S., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 1988; Volume 0868, pp. 134–141. [Google Scholar]
- Girshick, R.; Donahue, J.; Dar rell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition; in CVPR. 2016. Available online: http://openaccess.thecvf.com/content_cvpr_2016/html/He_Deep_Residual_Learning_CVPR_2016_paper.html (accessed on 28 February 2020).
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Jiang, Y.; Wang, P.; Shen, Q.; Shen, C. Hyperspectral Classification Based on Lightweight 3-D-CNN With Transfer Learning. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5813–5828. [Google Scholar] [CrossRef]

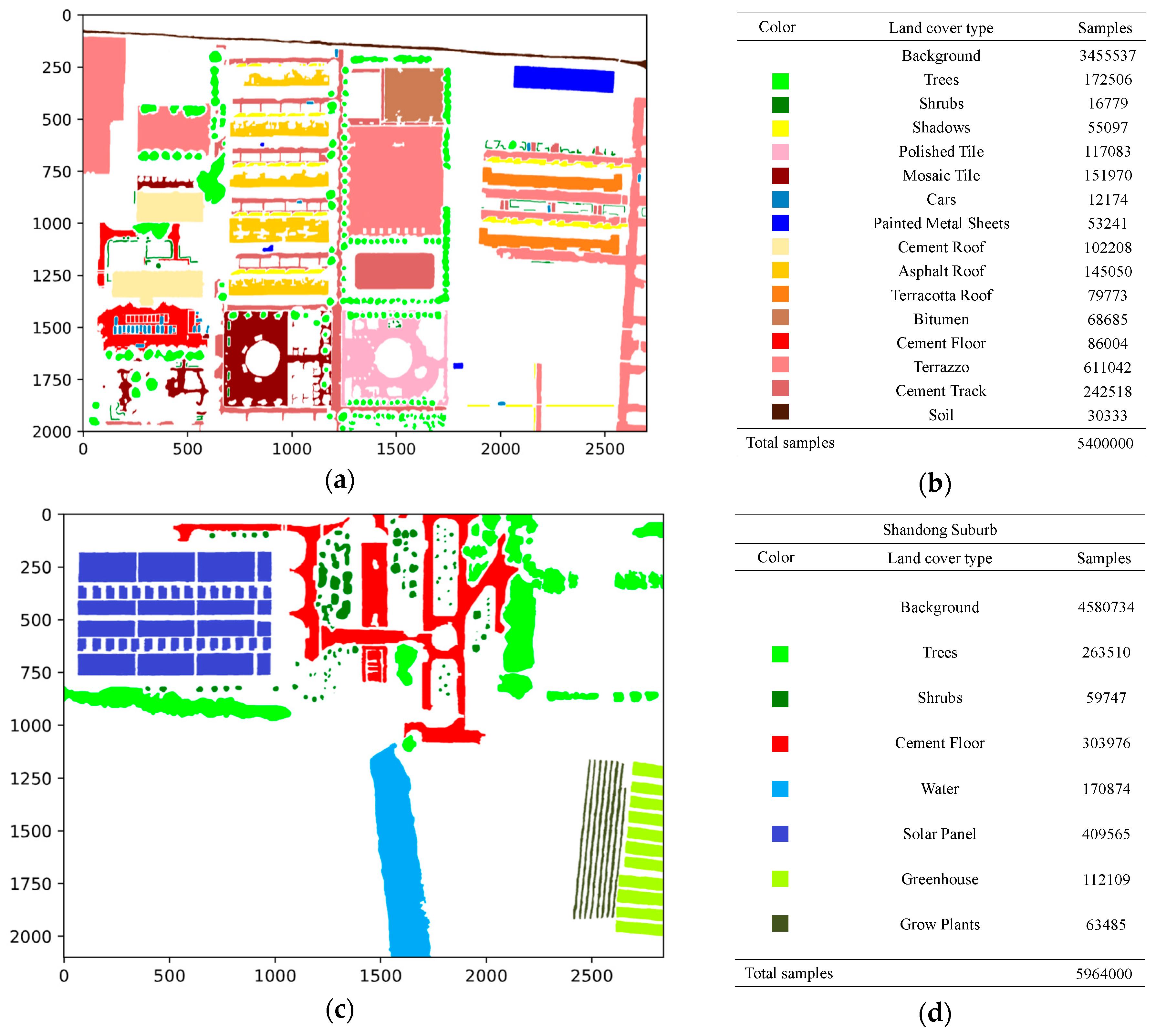
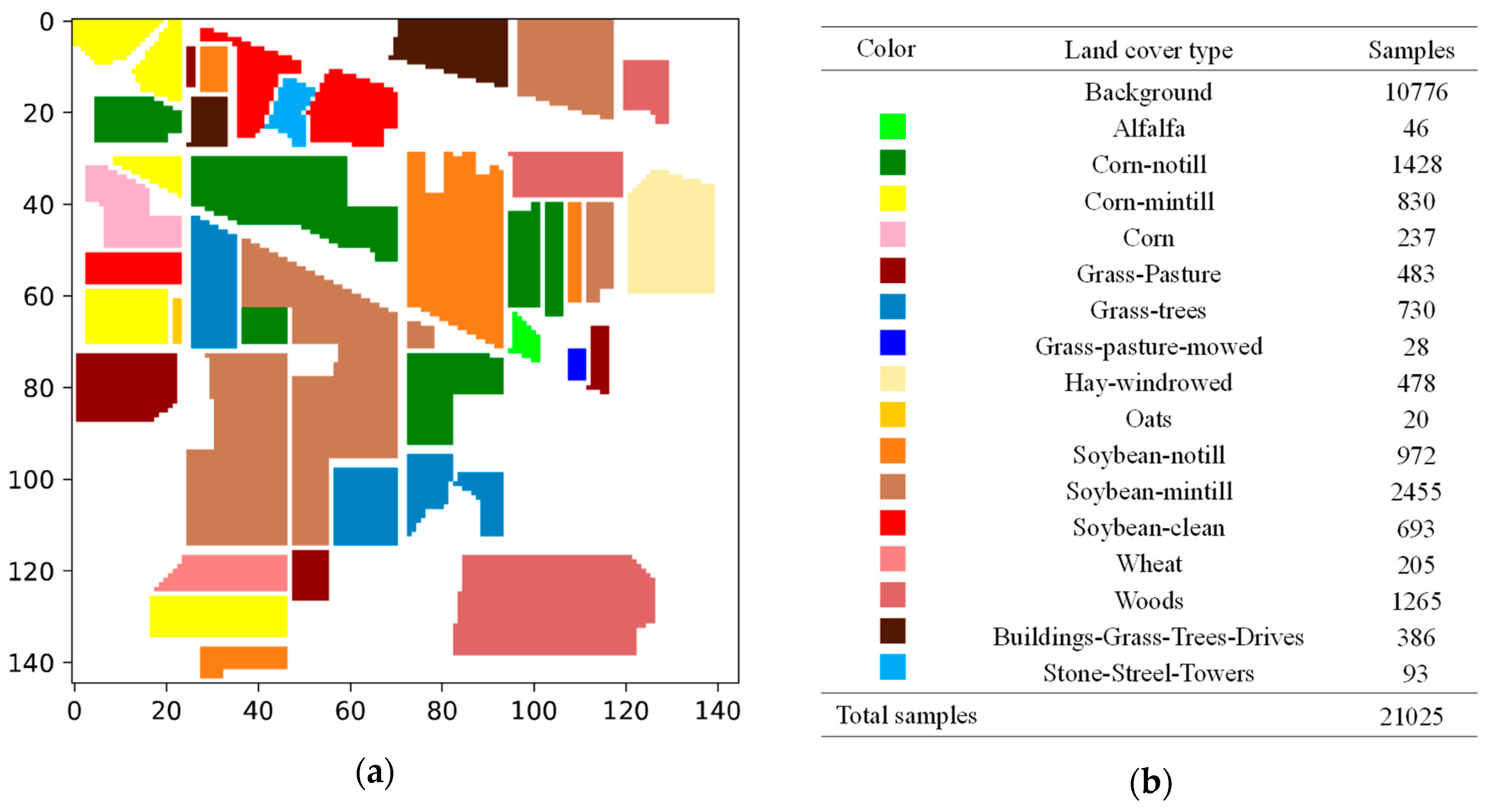

| Dataset | Image Size | Spectral Bands | Classes | Labeled Pixels | Intra-Class Variance | Inter-Class Variance |
|---|---|---|---|---|---|---|
| Indian Pines | 145 × 145 | 220 | 16 | 10,249 | 7.78 × 108 | 6.51 × 108 |
| Pavia University | 630 × 340 | 103 | 9 | 42,776 | 1.25 × 109 | 5.33 × 109 |
| Shandong Downtown | 2000 × 2700 | 63 | 19 | 3,327,729 | 1.51 × 109 | 1.96 × 106 |
| Shandong Suburb | 2100 × 2840 | 8.85 × 108 | 1.45 × 105 |
| DRSSN Topologies | |||||
|---|---|---|---|---|---|
| Kernel Size () | Batch Norm | ReLU | Pooling ) | ||
| Data Input Layer | C1 | Yes | Yes | ||
| Residual Block 1 | C2_1 | ) | Yes | Yes | No |
| C2_2 | Yes | Yes | No | ||
| C2_3 | Yes | No | No | ||
| C2_S | Yes | No | No | ||
| Residual Block 2 | C3_1 | ) | Yes | Yes | No |
| C3_2 | Yes | Yes | No | ||
| C3_3 | Yes | No | No | ||
| C3_S | Yes | No | No | ||
| Kernel Size ) | Dropout | ReLU | |||
| F1 | Yes | Yes | |||
| F2 | Yes | Yes | |||
| F3 | Yes | Yes | |||
| Indian Pines | ||||
|---|---|---|---|---|
| Category | Samples | Intra-class Variance (×106) | Accuracy (%) | Classification Difficulty |
| Grass-Pasture | 483 | 200.84 | 99.24 | Easily classified samples |
| Grass-trees | 730 | 150.57 | 99.51 | |
| Corn | 237 | 2864.47 | 97.79 | Hard classified samples |
| Soybean-notill | 972 | 640.86 | 98.74 | |
| Alfalfa | 46 | 48.96 | 97.82 | |
| Grass-pasture-mowed | 28 | 25.38 | 98.70 | |
| Indian Pines | ||||||
|---|---|---|---|---|---|---|
| Reference [21] Versus the Proposed DRSSN | Reference [22] Versus the Proposed DRSSN | |||||
| [21] | d = 29 | Samples | [22] | d = 27 | Samples | |
| Alfalfa | 99.13 (1.06) | 100.00 (0.00) | 33 | 97.82 | 97.39 (3.98) | 10 |
| Corn-notill | 98.17 (0.67) | 98.94 (1.06) | 200 | 99.17 | 99.42 (0.38) | 286 |
| Corn-mintill | 98.92 (0.68) | 99.70 (0.52) | 200 | 99.53 | 99.12 (0.78) | 166 |
| Corn | 100.00 (0.00) | 100.00 (0.00) | 181 | 97.79 | 98.43 (1.84) | 48 |
| Grass-Pasture | 99.71 (0.21) | 99.48 (0.90) | 200 | 99.24 | 98.20 (1.59) | 97 |
| Grass-trees | 99.40 (0.52) | 99.66 (0.59) | 200 | 99.51 | 99.59 (0.47) | 146 |
| Grass-pasture-mowed | 100.00 (0.00) | 100.00 (0.00) | 20 | 98.70 | 98.21 (4.99) | 6 |
| Hay-windrowed | 100.00 (0.00) | 100.00 (0.00) | 200 | 99.85 | 99.92 (0.25) | 96 |
| Oats | 100.00 (0.00) | 100.00 (0.00) | 14 | 98.50 | 100.00 (0.00) | 4 |
| Soybean-notill | 98.62 (1.39) | 98.97 (0.73) | 200 | 98.74 | 99.22 (0.66) | 195 |
| Soybean-mintill | 96.15 (0.57) | 99.49 (0.44) | 200 | 99.30 | 99.78 (0.17) | 491 |
| Soybean-clean | 99.33 (0.18) | 100.00 (0.00) | 200 | 98.43 | 98.97 (0.90) | 119 |
| Wheat | 99.90 (0.20) | 100.00 (0.00) | 143 | 100.00 | 99.71 (0.55) | 41 |
| Woods | 98.96 (0.46) | 100.00 (0.00) | 200 | 99.31 | 99.79 (0.25) | 253 |
| Buildings-Grass-Trees-Drives | 100.00 (0.00) | 100.00 (0.00) | 200 | 99.20 | 99.17 (1.15) | 78 |
| Stone-Streel-Towers | 100.00 (0.00) | 97.22 (4.81) | 75 | 97.82 | 98.15 (2.77) | 19 |
| OA (%) | 98.37 (0.17) | 99.53 (0.19) | 99.19(0.26) | 99.41 (0.15) | ||
| AA (%) | 99.27 (0.11) | 99.59 (0.40) | 98.93(0.59) | 99.07 (0.52) | ||
| Kappa (%) | 98.15 (0.19) | 99.47 (0.22) | 99.07(0.30) | 99.33 (0.17) | ||
| Total samples | 2466 | 2055 | ||||
| Pavia University | ||||||
|---|---|---|---|---|---|---|
| Reference [21] Versus the Proposed DRSSN | Reference [22] Versus the Proposed DRSSN | |||||
| [21] | d = 27 | Samples | [22] | d = 27 | Samples | |
| Asphalt | 96.31 (0.19) | 97.08 (1.17) | 200 | 99.92 | 99.88 (0.08) | 664 |
| Meadows | 97.54 (0.39) | 99.28 (0.18) | 200 | 99.96 | 99.97 (0.02) | 1865 |
| Gravel | 96.84 (0.29) | 99.66 (0.60) | 200 | 98.46 | 99.47 (0.50) | 210 |
| Trees | 97.58 (0.41) | 98.69 (0.60) | 200 | 99.69 | 98.84 (0.26) | 307 |
| Painted metal sheets | 99.65 (0.15) | 99.94 (0.12) | 200 | 99.99 | 99.79 (0.14) | 135 |
| Bare Soil | 99.33 (0.25) | 99.78 (0.22) | 200 | 99.94 | 100.00 (0.00) | 503 |
| Bitumen | 98.90 (1.14) | 100.00 (0.00) | 200 | 99.82 | 99.62 (0.30) | 133 |
| Self-Blocking Bricks | 98.89 (0.47) | 99.02 (0.39) | 200 | 99.22 | 99.76 (0.14) | 369 |
| Shadows | 99.58 (0.09) | 99.49 (0.32) | 200 | 99.95 | 99.00 (0.73) | 95 |
| OA (%) | 97.80 (0.22) | 99.00 (0.16) | 99.79 (0.09) | 99.80 (0.05) | ||
| AA (%) | 98.29 (0.25) | 99.22 (0.12) | 99.66 (0.17) | 99.59 (0.12) | ||
| Kappa (%) | 97.44 (0.29) | 98.68 (0.21) | 99.72 (0.12) | 99.74 (0.06) | ||
| Total samples | 1800 | 4281 | ||||
| Shandong Downtown | ||||
|---|---|---|---|---|
| Category | [21] | [22] | DRSSN | Samples |
| Trees | 84.71 (3.55) | 87.75 (9.74) | 96.28 (1.55) | 200 |
| Shrubs | 83.83 (7.12) | 43.73 (4.56) | 96.65 (1.33) | 200 |
| Shadows | 87.38 (1.07) | 96.82 (2.30) | 97.78 (1.37) | 200 |
| Polished-Tile | 96.09 (1.69) | 98.64 (0.31) | 98.94 (0.35) | 200 |
| Mosaic-Tile | 84.11 (7.09) | 98.01 (0.75) | 98.41 (0.30) | 200 |
| Cars | 78.43 (4.70) | 84.24 (4.44) | 97.38 (0.51) | 200 |
| Painted-Metal-Sheets | 98.42 (1.14) | 99.83 (0.08) | 99.87 (0.12) | 200 |
| Cement-Roof | 47.22 (1.42) | 86.99 (3.72) | 96.84 (0.54) | 200 |
| Asphalt-Roof | 87.07 (3.41) | 89.57 (2.91) | 97.74 (0.67) | 200 |
| Terracotta-Roof | 92.02 (1.77) | 92.90 (0.51) | 99.15 (0.43) | 200 |
| Bitumen | 98.62 (0.59) | 99.61 (0.17) | 99.68 (0.10) | 200 |
| Cement-Floor | 93.13 (1.50) | 97.21 (0.62) | 96.89 (0.93) | 200 |
| Terrazzo | 75.97 (6.72) | 78.00 (6.74) | 85.33 (1.57) | 200 |
| Cement-Track | 62.71 (8.37) | 73.03 (5.42) | 82.34 (1.30) | 200 |
| Soil | 93.33 (3.98) | 99.29 (0.53) | 99.06 (0.92) | 200 |
| OA (%) | 79.76 (1.52) | 85.82 (2.07) | 92.02 (0.45) | |
| AA (%) | 84.20 (2.85) | 88.37 (2.13) | 96.16 (0.21) | |
| Kappa (%) | 77.20 (1.66) | 83.92 (2.24) | 90.84 (0.50) | |
| Total samples | 3000 | |||
| Shandong Suburb | ||||
|---|---|---|---|---|
| Category | [21] | [22] | DRSSN | Samples |
| Trees | 78.79 (9.78) | 62.08 (7.32) | 83.13 (1.89) | 200 |
| Shrubs | 34.81 (5.26) | 37.55 (1.48) | 84.26 (1.90) | 200 |
| Cement-Floor | 96.85 (0.63) | 98.84 (0.93) | 99.85 (0.19) | 200 |
| Water | 98.71 (1.31) | 99.83 (0.10) | 99.72 (0.19) | 200 |
| Solar-Panel | 96.64 (1.89) | 99.80 (0.24) | 99.85 (0.11) | 200 |
| Greenhouse | 90.89 (3.09) | 96.05 (0.89) | 99.67 (0.11) | 200 |
| Grow-Plants | 94.84 (2.33) | 93.55 (1.41) | 99.53 (0.18) | 200 |
| OA (%) | 90.32 (2.77) | 89.13 (1.07) | 95.95 (0.37) | |
| AA (%) | 84.50 (1.78) | 83.96 (1.29) | 95.15 (0.42) | |
| Kappa (%) | 88.17 (3.28) | 86.71 (1.28) | 94.99 (0.45) | |
| Total samples | 1400 | |||
| SSN Topologies | |||||
|---|---|---|---|---|---|
| ) | Batch Norm | ReLU | Pooling ) | ||
| Data Input Layer | C1 | Yes | Yes | ||
| Residual Block 1 | C2_1 | ) | Yes | Yes | No |
| C2_2 | Yes | Yes | No | ||
| C2_3 | Yes | No | No | ||
| Residual Block 2 | C3_1 | ) | Yes | Yes | No |
| C3_2 | Yes | Yes | No | ||
| C3_3 | Yes | No | No | ||
| Kernel Size ) | Dropout | ReLU | |||
| F1 | Yes | Yes | |||
| F2 | Yes | Yes | |||
| F3 | Yes | Yes | |||
| Pavia University | ||
|---|---|---|
| Class | SSN | DRSSN |
| Asphalt | 96.58 (1.18) | 97.08 (1.17) |
| Meadows | 99.22 (0.17) | 99.28 (0.18) |
| Gravel | 99.31 (0.79) | 99.66 (0.60) |
| Trees | 98.46 (0.45) | 98.69 (0.60) |
| Painted metal sheets | 99.82 (0.36) | 99.94 (0.12) |
| Bare Soil | 99.95 (0.06) | 99.78 (0.22) |
| Bitumen | 99.76 (0.23) | 100.00 (0.00) |
| Self-Blocking Bricks | 98.80 (0.59) | 99.02 (0.39) |
| Shadows | 99.41 (0.43) | 99.49 (0.32) |
| OA (%) | 98.85 (0.15) | 99.00 (0.16) |
| AA (%) | 99.04 (0.14) | 99.22 (0.12) |
| Kappa (%) | 98.48 (0.20) | 98.68 (0.21) |
| DRSSN | |||
|---|---|---|---|
| Number of Residual Blocks | One | Two | Three |
| OA (%) | 98.66 (0.21) | 99.00 (0.16) | 98.86 (0.18) |
| AA (%) | 99.14 (0.07) | 99.22 (0.12) | 99.02 (0.15) |
| Kappa (%) | 98.23 (0.28) | 98.68 (0.21) | 98.50 (0.24) |
| Pavia University | ||
|---|---|---|
| Class | Cross Entropy Loss | Sample Balanced Loss |
| Asphalt | 95.88 (1.06) | 97.08 (1.17) |
| Meadows | 99.10 (0.33) | 99.28 (0.18) |
| Gravel | 99.47 (0.37) | 99.66 (0.60) |
| Trees | 98.85 (0.46) | 98.69 (0.60) |
| Painted metal sheets | 99.58 (0.45) | 99.94 (0.12) |
| Bare Soil | 99.79 (0.15) | 99.78 (0.22) |
| Bitumen | 99.82 (0.15) | 100.00 (0.00) |
| Self-Blocking Bricks | 99.17 (0.50) | 99.02 (0.39) |
| Shadows | 99.32 (0.57) | 99.49 (0.32) |
| OA (%) | 98.73 (0.22) | 99.00 (0.16) |
| AA (%) | 99.00 (0.21) | 99.22 (0.12) |
| Kappa (%) | 98.33 (0.29) | 98.68 (0.21) |
| Pavia University | ||
|---|---|---|
| Class | Without Dropout | With Dropout |
| Asphalt | 96.45 (1.63) | 97.08 (1.17) |
| Meadows | 99.09 (0.30) | 99.28 (0.18) |
| Gravel | 99.47 (0.37) | 99.66 (0.60) |
| Trees | 98.15 (0.83) | 98.69 (0.60) |
| Painted metal sheets | 99.88 (0.15) | 99.94 (0.12) |
| Bare Soil | 99.67 (0.48) | 99.78 (0.22) |
| Bitumen | 99.82 (0.36) | 100.00 (0.00) |
| Self-Blocking Bricks | 98.52 (0.56) | 99.02 (0.39) |
| Shadows | 99.07 (0.62) | 99.49 (0.32) |
| OA (%) | 98.70 (0.21) | 99.00 (0.16) |
| AA (%) | 98.90 (0.16) | 99.22 (0.12) |
| Kappa (%) | 98.28 (0.27) | 98.68 (0.21) |
| Pavia University | ||||
|---|---|---|---|---|
| Class | Window Size | |||
| 15 × 15 | 21 × 21 | 27 × 27 | 33 × 33 | |
| Asphalt | 92.96 (1.36) | 95.57 (1.26) | 97.08 (1.17) | 98.13 (1.19) |
| Meadows | 97.24 (0.30) | 98.96 (0.31) | 99.28 (0.18) | 99.29 (0.29) |
| Gravel | 95.61 (1.37) | 98.44 (0.77) | 99.66 (0.60) | 98.66 (0.78) |
| Trees | 98.72 (0.33) | 98.72 (0.34) | 98.69 (0.60) | 98.38 (0.54) |
| Painted metal sheets | 99.82 (0.24) | 99.94 (0.12) | 99.94 (0.12) | 100.00 (0.14) |
| Bare Soil | 98.42 (1.02) | 99.89 (0.19) | 99.78 (0.22) | 99.88 (0.23) |
| Bitumen | 98.19 (0.66) | 99.40 (0.54) | 100.00 (0.00) | 100.00 (0.00) |
| Self-Blocking Bricks | 95.39 (1.29) | 98.80 (0.58) | 99.02 (0.39) | 98.48 (0.29) |
| Shadows | 99.92 (0.17) | 99.49 (0.32) | 99.49 (0.32) | 99.15 (0.25) |
| OA (%) | 96.75 (0.32) | 98.54 (0.31) | 99.00 (0.16) | 99.06 (0.23) |
| AA (%) | 97.36 (0.33) | 98.80 (0.19) | 99.22 (0.12) | 99.26 (0.14) |
| Kappa (%) | 95.74 (0.42) | 98.08 (0.41) | 98.68 (0.21) | 98.76 (0.32) |
| Running Time(s/epoch) | 1.27 (0.02) | 1.55 (0.01) | 2.49 (0.01) | 5.37 (0.02) |
| Pavia University | |||||
|---|---|---|---|---|---|
| Class | Focusing Parameter | ||||
| 0.5 | 1 | 1.5 | 2 | 2.5 | |
| Asphalt | 96.75 (1.26) | 97.08 (1.17) | 96.85 (1.34) | 96.46 (1.43) | 98.82 (0.38) |
| Meadows | 99.15 (0.17) | 99.28 (0.18) | 98.96 (0.49) | 98.94 (0.30) | 98.82 (0.38) |
| Gravel | 99.47 (0.56) | 99.66 (0.60) | 99.27 (0.31) | 99.43 (0.48) | 99.16 (0.43) |
| Trees | 98.49 (0.51) | 98.69 (0.60) | 98.49 (0.59) | 98.20 (0.68) | 98.07 (0.43) |
| Painted metal sheets | 99.70 (0.33) | 99.94 (0.12) | 99.88 (0.15) | 99.88 (0.15) | 99.82 (0.24) |
| Bare Soil | 99.94 (0.08) | 99.78 (0.22) | 99.89 (0.19) | 99.86 (0.17) | 99.59 (0.44) |
| Bitumen | 100.00 (0.00) | 100.00 (0.00) | 99.70 (0.47) | 99.70 (0.33) | 99.58 (0.45) |
| Self-Blocking Bricks | 99.17 (0.27) | 99.02 (0.39) | 98.89 (0.39) | 98.93 (0.64) | 98.87 (0.70) |
| Shadows | 99.41 (0.51) | 99.49 (0.32) | 99.83 (0.34) | 99.66 (0.32) | 99.58 (0.38) |
| OA (%) | 98.89 (0.20) | 99.00 (0.16) | 98.79 (0.25) | 98.70 (0.24) | 98.51 (0.25) |
| AA (%) | 99.12 (0.13) | 99.22 (0.12) | 99.08 (0.17) | 99.01 (0.19) | 98.83 (0.16) |
| Kappa (%) | 98.53 (0.26) | 98.68 (0.21) | 98.40 (0.33) | 98.29 (0.31) | 98.04 (0.33) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Y.; Zeng, D.; Chen, F.; Wang, Y.; Zhang, Z. A New Dataset and Deep Residual Spectral Spatial Network for Hyperspectral Image Classification. Symmetry 2020, 12, 561. https://doi.org/10.3390/sym12040561
Xue Y, Zeng D, Chen F, Wang Y, Zhang Z. A New Dataset and Deep Residual Spectral Spatial Network for Hyperspectral Image Classification. Symmetry. 2020; 12(4):561. https://doi.org/10.3390/sym12040561
Chicago/Turabian StyleXue, Yiming, Dan Zeng, Fansheng Chen, Yueming Wang, and Zhijiang Zhang. 2020. "A New Dataset and Deep Residual Spectral Spatial Network for Hyperspectral Image Classification" Symmetry 12, no. 4: 561. https://doi.org/10.3390/sym12040561
APA StyleXue, Y., Zeng, D., Chen, F., Wang, Y., & Zhang, Z. (2020). A New Dataset and Deep Residual Spectral Spatial Network for Hyperspectral Image Classification. Symmetry, 12(4), 561. https://doi.org/10.3390/sym12040561







