Abstract
This study is carried out to scrutinize the gyrotactic bioconvection effects on modified second-grade nanofluid with motile microorganisms and Wu’s slip (second-order slip) features. The activation energy and thermal radiation are also incorporated. The suspended nanoparticles in a host fluid are practically utilized in numerous technological and industrial products such as metallic strips, energy enhancement, production processes, automobile engines, laptops, and accessories. Nanoparticles with high thermal characteristics and low volume fraction may improve the thermal performance of the base fluid. By employing the appropriate self-similar transformations, the governing set of partial differential equations (PDEs) are reduced into the ordinary differential equations (ODEs). A zero mass flux boundary condition is proposed for nanoparticle diffusion. Then, the transmuted set of ODEs is solved numerically with the help of the well-known shooting technique. The numerical and graphical illustrations are developed by using a collocation finite difference scheme and three-stage Lobatto III as the built-in function of the bvp4c solver via MATLAB. Behaviors of the different proficient physical parameters on the velocity field, temperature distribution, volumetric nanoparticles concentration profile, and the density of motile microorganism field are deliberated numerically as well as graphically.
1. Introduction
In recent years, the tremendous progress in research and wide-ranging solicitations of functional nanoparticles have been noticed. Nanoparticles have numerous potential applications in the many fields such as the biomedical field, microbiology, supramolecular and colloid chemistry, material sciences, petroleum sciences, social sciences, etc. Nanoparticles have further physical features that must be determined for an undivided depiction, for example surface characteristics, sizes, and shapes. Nanoparticles belong to a broad interdisciplinary field in pharmaceutical medicines, thermal systems, electronics, nuclear reactors, the chemical industry, etc. Nanoparticles are also expressed in ink, polymer, and natural fluids such as blood. In general, nanoparticles-based technologies are focused on opportunities for improving the efficiency, sustainability, and speed of already existing processes. A nanofluid is an advanced type of fluid that contains nanometer-sized particles. As a result of their sub-nanoscopic size, they have unique material features and manufactured nanomaterials that may find practical applications in a mixture of areas, including catalysis, environmental remediation, medicine, and engineering. Beneath that classification, nanosubstances needs simply one of their quality scopes to be in the range of 1–100 nm to be classified as nanoparticles, even if its other dimensions are exterior to that range. Choi [1] proposed the idea of nanofluids. Numerous researchers have gained interest in the study of nanofluids due to their significant technical processes and applications. The coefficient of heat transfer between the medium and the soil is considered to be important. Nanofluids are commonly used in automotive and industrial cooling, tumor care, tracking, cooling towers, new fuel types, micro electron cooling, imaging, the heating/cooling of home appliances, and many more. Buongiorno [2] presented a two-phase model depicting the salient features of Brownian diffusion and thermophoresis. He determined that the properties of thermophoretic and Brownian motion are enough to establish a viable model. Khan et al. [3] discussed the characteristics of Brownian motion and thermophoresis in Jeffery nanofluid flow by a stretched surface. The article reveals the impacts of drag force and heat transfer rate for numerous physical variables. Nanofluid heat transfer in a porous duct in the presence of Lorentz forces by using the lattice Boltzmann method was examined by Li et al. [4]. Several researchers made serious attempts on nanofluids subjected to different configurations [5,6,7,8,9,10,11,12]. Alamri et al. [13] described the impacts of a second-order slip on plane Poiseuille nanofluid flow under the influence of Stefan blowing in a channel. Kumar [14] explored the behavior of heat transmit flow of non-Newtonian nanofluid through a stretching sheet. Farahangmehr et al. [15] scrutinized numerically the continuous boundary layer of an incompressible viscous nanofluid with heat and mass transfer over the horizontal surface. Tlili et al. [16] discussed boundary layer flow in the presence of convection and mass transfer features of the Buongiorno nanofluid model over a wedge with Navier slip and Biot number. Khan et al. [17] inspected the mass and heat transfer mechanism in Carreau nanofluid flow across a wedge. The unsteady slip flow of Carreau nanofluid over a moving/ static wedge was numerically investigated by Masood et al. [18]. Khan et al. [19] examined the significance of activation energy and nonlinear thermal radiation on modified second grade fluid flow in the presence of nanoparticles. Rehman et al. [20] scrutinized the impacts of heat transfer and heterogeneous–homogeneous reactions in modified second-grade nanofluid over a stretching sheet. Khan et al. [21] investigated the multi-dimensional axisymmetric flow and convection of the modified second-grade fluid through the nonlinear radially expanding oscillatory surface. Hassan et al. [22] investigated the mass and heat transport aspects in viscoelastic nanofluid flows under the presence of velocity slip conditions. Afterwards, the methods of combining second-grade fluid and a power law model resulted in the generalized second-grade fluid as described by Man and Sun [23].
Bioconvection caused by the density differences of motile microorganisms is effectively assorted in the field of environmental systems, biofuels, and industry. The presence of these microorganisms increases the primary density of the fluid and creates a density gradient by swimming, which leads to bioconvection. This interesting observation inevitably leads to an unstable, lower density surface. Microorganisms are typically classified according to the impellent force of various types due to gyrotactic, oxytactic, and gravitactic microorganisms. There are some distinct and similar characteristics of nanoparticles and motile microorganisms. Immunology microsystems (i.e., biomaterials, tissue engineering, protein engineering, synthetic biology, and drug delivery systems) such as enzyme biosensors are typically involved in bioconvection applications. Kuznetsov [24] therefore suggested that the growth of microorganisms in the biomicrosystems plays a major role in the processing and aggregation of mass transport. Khan et al. [25] analyzed the influence of bio-convection in a rheology of magnetized nanofluid. Waqas et al. [26] investigated the heat and mass transfer phenomenon of Williamson’s nanofluid flow in the existence of gyrotactic motile microorganisms. Waqas et al. [27] considered viscous nanofluid flow across a flexible stretching disk with a mixture of microorganisms. Waqas et al. [28] also visualized the flow of modified second-grade nanofluid in the presence of motile microorganisms with heat and mass transfer rates across the stretching boundary. Waqas et al. [29] examined the magnetohydrodynamics (MHD) flow of rate-type nanofluid in the presence of gyrotactic microorganisms with activation energy. Recently, Waqas et al. [30] securitized the novel biofuel significance in viscoelastic nanofluid under the bioconvection process.
This research paper provides a more compelling approach to the nanoliquid heat and mass transfer phenomena through the bioconvection of self-motile microorganisms, which helps to avoid the agglomeration of nanoparticles. New results are established with inclusion of Wu’s slip (second-order velocity slip), activation energy, and the thermal radiation. The manuscript is organized as follows. Section 1 describes the introduction, Section 2 contains a mathematical model, Section 3 yields the numerical solution, Section 4 present the graphical analysis, and the conclusions of the graphical and tabular results are exhibited in Section 5. Observation of the results shows that the buoyancy ratio parameter , bioconvection Rayleigh number , and Wu’s slip parameter inhibit the fluid flow and cause a reduction in the velocity. However, the parameters and augmented the thermal distribution.
2. Mathematical Model
Let us consider the two-dimensional, steady-state modified second-grade nanofluid with activation energy and gyrotactic motile microorganisms. Moreover, the flow is incompressible across a stretching surface. Additionally, non-linear thermal radiation and Wu’s slip (second-order velocity slip) are taken into consideration. Let us assume that the surface stretches as , where is the power law exponent parameter, and is symbolized for stretching strength. Furthermore, is the flow velocity, the temperature of the fluid is , and the volume fraction for nanoparticles and the motility of the microorganisms are symbolized as , respectively. The Cauchy stress tensor for modified second-grade fluid is taken as [31]
Here, is the identity tensor, is the pressure, is viscosity coefficient, are the conventional stress coefficients, is the material parameter, is the velocity gradient for the symmetric part of second invariant, and are termed as kinematical tensors and defined as
where .
Man and Sun [23] studied the Cauchy stress tensor and described two models as terminated in modified forms of second-grade fluid and power law fluid model, which are:
Model (a):
Model (b):
Model (a) is about second-grade fluid.
Model (b) is representing the power-law index model.
The boundary layer formulation for mass conservation, momentum, energy, concentrations of nanoparticles, and motile microorganisms’ distributions are [32,33,34]:
The boundary conditions entertained the following relations:
The temperature of the surface is assumed as , while the volume fraction for nanoparticles and the density of the microorganisms at the surface are denoted as respectively. are the free-stream temperature, concentration of nanoparticles, and the density of the microorganisms. Some researcher used the as [35,36]:
where notifies the Knudsen number, and stand for constant numbers, and expresses the free path associated with the molecular mean motion. In the above equations, is the material-related parameter, represents the power law index, represents the motile microorganism particles density, represents the nanoparticles density, represents the average volume of the microorganism, represents the gravity, notifies the temperature of the nanofluid, reflects the nanoparticles’ volume resistance, stands for the friction coefficient, represents the heat capability of fluids, represents the impressive heat capacity of the nanomaterial, symbolizes the Brownian diffusivity, represents the Stefan Boltzmann constant, represents the mean absorption coefficient, stands for the thermophoresis diffusion coefficient, reflects the activation energy coefficient, reflects the reaction rate constant, represents the chemotaxis constant, describes the superlative cell swimming rapidity, and is the microorganism’s diffusion coefficient. Equations (5)–(9) are non-dimensionalized by the following variables [22]:
Equation (5) is satisfied. The re-established dimensionless form of Equations (6)–(9) respectively yield:
Similarly, the boundary conditions (10) and (11) are transformed as follows:
where is the generalized second-grade fluid parameter, is the mixed convection parameter, is the buoyancy ratio parameter, is the bioconvection Rayleigh number, is the Prandtl number, is the radiation parameter, is the Brownian motion constraint, is the thermophoresis parameter, the temperature ratio parameter is is the Lewis number, is the motile microorganism difference parameter,
is the activation energy, is the bioconvection Lewis number, is the Peclet number, is the first-order velocity slip, the second-order velocity slip is represented as , and the Biot number is symbolized as .
In order to express the consequences of wall shear stress, we have following mathematical relations:
where is the wall shear stress. By using the following dimensionless variable, Equation (21) yields:
Moreover, the local Sherwood number, motile density number, and local Nusselt number are stated as follows:
The above quantities in dimensionless forms are:
3. Numerical Procedure
The system of the non-linear coupled ordinary differential Equations (15)–(18) with the boundary conditions (19) and (20) has been computed by bvp4c [37,38] in MATLAB with a tolerance level of . In the bvp4c routine, a three-stage Lobatto-IIIA method is employed in the development of this collocation technique. The bvp4c function of computational software MATLAB only resolves the first-order ordinary differential equations. To approximate the solution of the distorted non-linear ODEs (ordinary differential equations), appropriate initial guesses satisfying the pertinent boundary conditions are required. For further approximation, the initial guess is modified with the help of shooting technique. Let us consider
The associated boundary conditions are:
4. Graphical Analysis
This section is set to explain the emerging consequences of the involved parameters on the physical quantities of interest. Similar to the traditional way, the involved parameters have been assigned some fixed values such as , and , and . Furthermore, the complete analysis has been performed in view of the shear thinning case second-grade fluid , and shear thickening case The variation in the impact of the buoyancy ratio parameter over velocity distribution is drawn in Figure 1a. It illustrates that the velocity component decreases on the rising variation of the buoyancy ratio parameter with the power law index . The physically buoyancy ratio parameter is the phenomenon of upthrust of fluid to objects, which exerts pressure on it. The discussion of the buoyancy ratio parameter rose to another next level when it was considered for the temperature profile. The behavior of temperature distribution in relation to the variation of the buoyancy ratio parameter can be traced from Figure 1b. It can be noticed that the curve of temperature profile rises when the buoyancy ratio parameter is increased. Regarding the concentration profile, the buoyancy ratio parameter has a unique trend, as graphed by Figure 1c. It can be viewed that the concentration profile gets an uplifting effect with the buoyancy ratio parameter. When the buoyancy ratio parameter is varied by higher values, the concentration distribution shows a rising inclination in the graph, which depicts that the fluid is concentrating more and more in the boundary layer region. The motility profile is the characteristic of moving microorganisms mixed in the fluid. Figure 1d is the description of this whole effect. It can be noticed that when the buoyancy ratio parameter is enhanced, then the motility of the microorganism also increases; i.e., the motile particles become more active. The bioconvection Rayleigh number is a dimensionless parameter that is used to measure the fluid instability due to the density differences as described in study [39]. The effect of on velocity distribution is considered to be very interesting, as it is the effect of instability that is caused by the dense layer of microorganisms at the top of the fluid. This top dense layer breaks, and ultimately, the microorganisms fell down. Then, they move up to attain their motive (gravitative, phototactic, chemotactic, etc.). Figure 2a is the exhibition of the result between the Rayleigh number and velocity distribution. It displays that when the bioconvection Rayleigh number is uplifted, it causes a reduction in the velocity distribution. The investigation of on the temperature profile for the power law index is illustrated by Figure 2b. The conduct of on thermal distribution disclosed that the temperature profile rises when we give a higher value to the Rayleigh number. The concentration profile is one of the main characteristics of the Rayleigh number, as it causes the instability of the fluid. Figure 2c depicts that tends to grow the concentration of nanoparticles in fluids. Actually, this is one of the main interests of our work to control the sedimentation of added/mixed nanoparticles. Figure 2d illustrates the behavior of a motile microorganism versus the bioconvection Rayleigh number. It can be noticed that the density function of the motile microorganism is increased with higher Rayleigh number values. Generally, the motile microorganism characteristics of the mobile particles in a fluid are used for an increased heat transfer phenomenon. The behavior of stretching parameter has been examined in Figure 3a. Regarding increments in the stretching parameter , the velocity of the fluid particles diminishes. Here, the power law index is applied on discussed respectively. We can say that physically, the stretching parameter provides more strength to velocity distribution . The impact of the stretching parameter on the concentration function with the same fixed values of the power law index parameter is plotted in Figure 3b. The plot depicts that when is taken to be , the concentration profile increases as we raise the stretching parameter , but a contrasting effect is observed when we take , so that the volumetric nanoparticle concentration distribution shows a retarding effect for increasing the value of stretching parameter . The phenomenon of the motile microorganism of the fluid for the flow of a modified second-grade nanofluid is measured on assorted values of stretching parameter for three individual values of the power law index . The complete sketch is figured out in Figure 3c. When the power law index is taken to be , then the motility of the liquid intensifies for rising values of stretching parameter , but when , the trend for the concentration of motile microorganisms goes down as we uplift the stretching parameter . Hence, we conclude that the profile of increases for shear thickening and decreases for modified second-grade and shear thinning fluids, as described in Figure 3d. The effect of the first-order velocity slip parameter with the power law index on velocity is sketched via Figure 4a. The first-order velocity slip parameter is also a medium characteristic affecting the fluid of the velocity distribution. The sketched graph shows that for all the three chosen cases of power law index , when we uplift the first-order velocity slip, it causes a reduction in the velocity distribution. Figure 4b illustrates the behavior of the second-order velocity slip parameter on velocity distribution for an addition with power law index . Actually, this slip parameter is a medium characteristic that affects fluid flow. The velocity distribution retards when we vary with higher values. Generally, gives a slope of second order for the fluid flow with different characteristics, which reduces the velocity distribution. Hence, enhancement in the value of causes decay in the velocity contour. The mixed convection parameter is the phenomenon of the combined interaction of the pressure forces and buoyant forces altogether. For power law index , the effect of becomes more influential for velocity distribution. The impact of on the velocity profile in the presence of three different priorities for the power law index, i.e., , is depicted via Figure 4c. It can be visualized that when the mixed convection is intensified, it boosts up the velocity profile of the fluid in the presence of all the values of . Figure 4d elucidates the behavior of Lewis number on the non-dimensional temperature function . It is inspected that the curve of the temperature distribution rises with the growing Lewis number values for three cases of the power law index . The impact of the Lewis number on the concentration profile is exhibited in Figure 5b. It is found that the concentration profile shows retardation with the rise of Lewis number for various power law index values: . The variation of dimensionless temperature distribution versus Prandtl number is delineated in Figure 6a. It is observed that the shows a diminishing pattern for larger Prandtl numbers, . The thermal boundry layer thickness is contracted as the fluid charactaricstics change from shear thinning to shear thickninng. This is explained by the fact that the thermal diffusivity decreases, and therefore, the thermal distribution declines. The effect of temperature ratio parameter on the temperature profile in the presence of the power law index is drawn graphically through Figure 6b. It is depicted that the strengthening of the temperature ratio parameter tends to improve the temperature of the flowing fluid. When it is gradually rises, the fluid also become hot. The radiation parameter is the phenomenon of the emission of heat waves. The effect of radiation parameter on the temperature in the presence of three different values of power law index is sketched by Figure 6c. The sketched information reveals that the power law index varied from to and the larger value of the radiation parameter causes an enhancement of the temperature function. Generally, it can be said that when the radiation parameter increases, it directly increases the temperature of the fluid. The effect of Biot number on the temperature field can be predicted in the presence of the power law index. The predicted result between the Biot number and temperature profile is sketched by Figure 7a. The figure represents that when the Biot number is raised, it causes the temperature profile of the liquid to rise as well. Generally, we can say that the increment in the value of the Biot number enhances the temperature of the fluid. The Biot number is also marked as a key influence on the variation of the concentration profile. Figure 7b illustrates the effect of the Biot number on the concentration profile in the presence of the power law index. The value of the power law index is varied from to , and the effect is noticed when the Biot number is uplifted; thus, it increases the concentration profile. Figure 8a visualizes the perception of the Prandtl number on the concentration of nanoparticles. As we vary the Prandtl number, the concentration field reduces from shear thinning to shear thickening. This is caused by the fact that the rise in Prandtl number stands for a reduction in thermal diffusivity, which creates a decline in the concentration region. Figure 8b illustrates the impact of activation energy on concentration distribution in the presence of the power law index. The sketched information indicates that the activation energy has a unique effect on the concentration field. It is seen that when the amount of activation energy is increased, it directly enhances the concentration of nanoparticles in the fluid flow. Figure 9a depicts the influence of Peclet number against the density of the motile microorganism profile. It is observed that an increment in the value of the Peclet number causes decay in motility distribution. In addition, the motile microorganism profile declines as we enhance the value of the bioconvection Lewis number as interpreted through Figure 9b. In Table 1, the present numerical results are verified by comparing the exact and numerical solutions as available in the existing literature for special cases by Masood et al. [33]. The numerical values of the local skin friction and local Nusselt number are tabulated in the absence of nanoparticles. Both solutions are noticed to be in strong agreement, and this verifies our numerical technique. Table 2 describes the effects of the local skin friction coefficient for the shear thinning and shear thickening fluid against the different prominent parameters such as stretching parameter , mixed convection parameter , buoyancy ratio parameter , bioconvection Rayleigh number , and Wu’s slip (second-order velocity slip) parameters and , respectively. The increasing behavior of is observed for as compared to when it decreases. As the value of the slip parameters enhances, the value for the skin friction coefficient declines. Table 3, Table 4 and Table 5 show the local Nusselt number , local Sherwood number , and the density of the local motile microorganism respectively against the dimensionless parameters such as . The uplifted behavior of , , and is seen for as compared to .
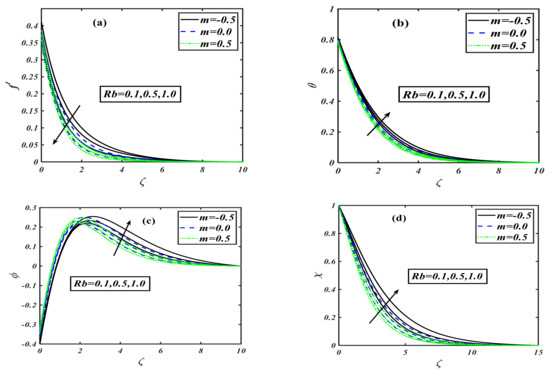
Figure 1.
(a–d): Variations of for various values of when .

Figure 2.
(a–d): Variations of for various values of when .
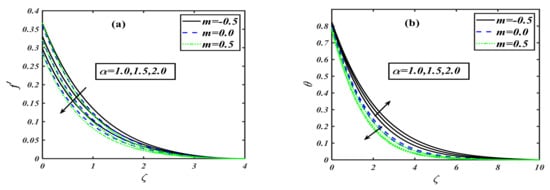
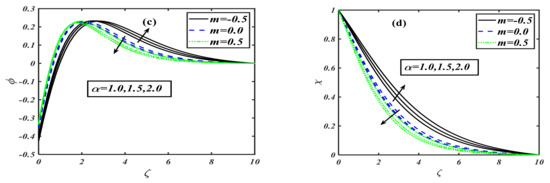
Figure 3.
(a–d): Variations of for various values of when .

Figure 4.
(a–c): Variations of for various parameters when .
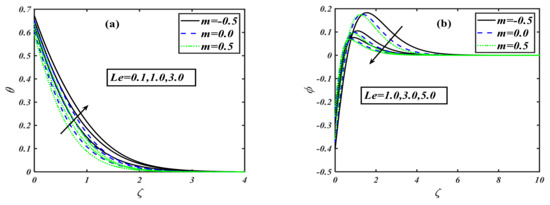
Figure 5.
(a,b): Variations of for various values of when .
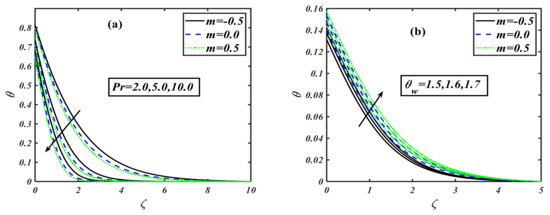
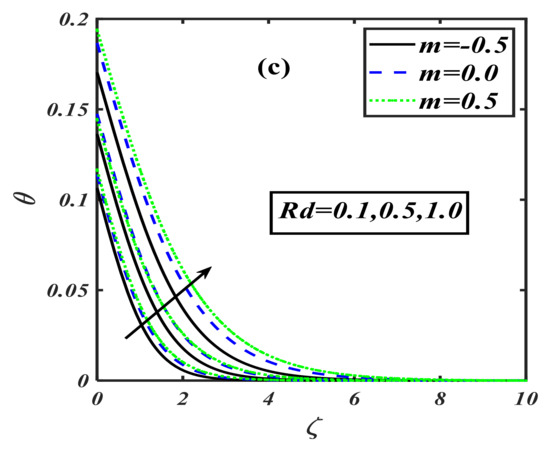
Figure 6.
(a–c): Variations of for various parametrs when .
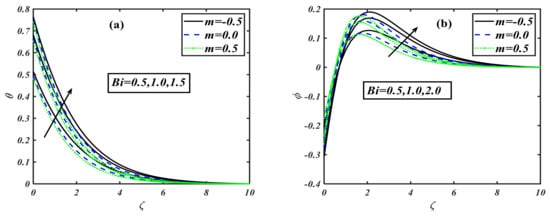
Figure 7.
(a,b): Variations of for various values of when .
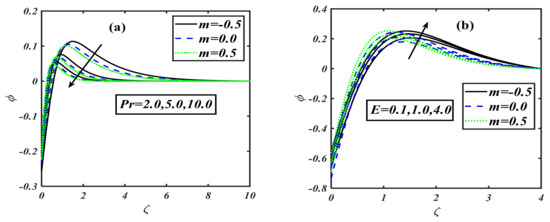
Figure 8.
(a,b): Variations of for various values of parameters when .
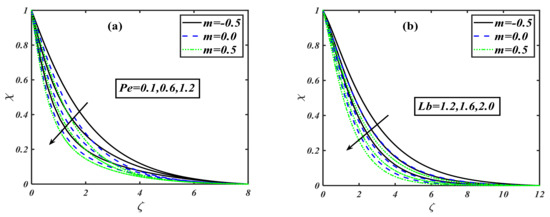
Figure 9.
(a,b): Variations of for various values of parameters when .

Table 1.
Comparison for the results of and in the case of second-grade fluid , .

Table 2.
Variations in against , , , , , and .

Table 3.
Variations in against , , , , , , and .

Table 4.
Variations in against , , , , , , , and .

Table 5.
Variations in against , , and .
5. Conclusions
In this article, we have developed the numerical investigation of the non-linear radiation and the activation energy effects on the bioconvection of generalized second-grade nanofluid flow across a stretching surface with convective condition, zero nanoparticles mass flux condition, and Wu’s slip (second-order slip) on the boundary. One of the most prominent features of generalized second-grade fluid is that it depicts the effects of shear thinning and shear thickening as well as stress effects. For , the fluid is shear thickening, while for , the fluid is shear thinning, and when , it becomes a second-grade fluid. The tables and graphs depict the sensitivity of heat transfer and flow characteristics of nanofluids. Some major remarks are listed below:
The first-order and second-order slip parameters reduced the velocity profile for both shear thinning and shear thickening, but the opposite behavior is observed for larger values of the mixed convection parameter.
The temperature distribution exhibits an improvement when the values of the temperature ratio parameter and the Lewis number are hosted.
The increment in stretching parameter discloses interesting effects. It is noticed that for shear thickening , the associated thermal boundary layer become thicker, and for the shear thinning cases , this boundary layer becomes thinner. However, the momentum boundary layer is reduced for both the cases.
The nanoparticles concentration profile declines as the Lewis number and Brownian motion parameter values increase.
As the buoyancy ratio parameter, the bioconvection Rayleigh number, and thermophoresis parameter values intensify, the temperature function is boosted up as well.
Mounting Prandtl number values reduce the thermal distribution, but the radiation parameter enhances the temperature distribution.
The volumetric nanoparticles concentration profile retards as the Prandtl number rises, but it can be more effectively boosted up in the presence of activation energy.
The gyrotactic microorganism concentration profile retards by enlarging the Peclet number and bioconvection Lewis number.
Author Contributions
Y.L.; H.W.; M.I.; U.F.; F.M. and I.T. modeled the problem, numerically computed results, discussed the results physically, computed the tabulated results, wrote the manuscript and proof read it. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia under grant no. (KEP-16-130-40). Therefore, the authors acknowledge with thanks DSR technical and financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, S.U.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. Argonne Natl. Lab. Il USA 1995, 1–8. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Waqas, M.; Alsaedi, A.; Khan, M.I. Effectiveness of radiative heat flux in MHD flow of Jeffrey-nanofluid subject to Brownian and thermophoresis diffusions. J. Hydrodyn. 2019, 31, 421–427. [Google Scholar] [CrossRef]
- Li, Z.; Sheikholeslami, M.; Mittal, A.S.; Shafee, A.; Haq, R.U. Nanofluid heat transfer in a porous duct in the presence of Lorentz forces using the lattice Boltzmann method. Eur. Phys. J. Plus 2019, 134, 30. [Google Scholar] [CrossRef]
- Aziz, A.; Muhammad, T.; Alsaedi, A.; Hayat, T. An optimal study for 3D rotating flow of Oldroyd-B nanofluid with convectively heated surface. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 236. [Google Scholar] [CrossRef]
- Li, Z.; Sheikholeslami, M.; Shafee, A.; Ramzan, M.; Kandasamy, R.; Al-Mdallal, Q.M. Influence of adding nanoparticles on solidification in a heat storage system considering radiation effect. J. Mol. Liquids. 2019, 273, 589–605. [Google Scholar] [CrossRef]
- Safaei, M.R.; Karimipour, A.; Abdollahi, A.; Nguyen, T.K. The investigation of thermal radiation and free convection heat transfer mechanisms of nanofluid inside a shallow cavity by lattice Boltzmann method. Phys. A Stat. Mech. Its Appl. 2018, 509, 515–535. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Alsabery, A.I.; Hashim, I. Internal heat generation effect on transient natural convection in a nanofluid-saturated local thermal non-equilibrium porous inclined cavity. Phys. A Stat. Mech. Its Appl. 2018, 509, 275–293. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Keramati, H.; Shafee, A.; Li, Z.; Alawad, O.A.; Tlili, I. Nanofluid MHD forced convection heat transfer around the elliptic obstacle inside a permeable lid drive 3D enclosure considering lattice Boltzmann method. Phys. A: Stat. Mech. Its Appl. 2019, 523, 87–104. [Google Scholar] [CrossRef]
- Farshad, S.A.; Sheikholeslami, M. Simulation of nanoparticles second law treatment inside a solar collector considering turbulent flow. Physics A 2019, 525, 1–12. [Google Scholar] [CrossRef]
- Khan, S.U.; Waqas, H.; Shehzad, S.A.; Imran, M. Theoretical analysis of tangent hyperbolic nanoparticles with combined electrical MHD, activation energy and Wu’s slip features: A mathematical model. Phys. Scr. 2019, 94, 125211. [Google Scholar] [CrossRef]
- Li, F.; Sheikholeslami, M.; Dara, R.N.; Jafaryar, M.; Shafee, A.; Nguyen-Thoi, T.; Li, Z. Numerical study for nanofluid behavior inside a storage finned enclosure involving melting process. J. Mol. Liquids. 2020, 297, 111939. [Google Scholar] [CrossRef]
- Alamri, S.Z.; Ellahi, R.; Shehzad, N.; Zeeshan, A. Convective radiative plane Poiseuille flow of nanofluid through porous medium with slip: An application of Stefan blowing. J. Mol. Liq. 2019, 273, 292–304. [Google Scholar] [CrossRef]
- Kumar, K.G. Exploration of flow and heat transfer of non-Newtonian nanofluid over a stretching sheet by considering slip factor. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Farhangmehr, V.; Moghadasi, H.; Asiaei, S. A nanofluid MHD flow with heat and mass transfers over a sheet by nonlinear boundary conditions: Heat and mass transfer’s enhancement. J. Cent. South Univ. 2019, 26, 1205–1217. [Google Scholar] [CrossRef]
- Tlili, I.; Hamadneh, N.N.; Khan, W.A. Thermodynamic Analysis of MHD Heat and Mass Transfer of Nanofluids Past a Static Wedge with Navier Slip and Convective Boundary Conditions. Arab. J. Sci. Eng. 2019, 44, 1255–1267. [Google Scholar] [CrossRef]
- Khan, M. Effects of multiple slip on flow of magneto-Carreau fluid along wedge with chemically reactive species. Neural Comput. Appl. 2018, 30, 2191–2203. [Google Scholar] [CrossRef]
- Khan, M.; Azam, M.; Alshomrani, A.S. Unsteady slip flow of Carreau nanofluid over a wedge with nonlinear radiation and new mass flux condition. Results Phys. 2017, 2261–2270. [Google Scholar] [CrossRef]
- Khan, S.U.; Tlili, I.; Waqas, H.; Imran, M. Effects of nonlinear thermal radiation and activation energy on modified second-grade nanofluid with Cattaneo–Christov expressions. J. Therm. Anal. Calorim. 2020, 139, 1–12. [Google Scholar] [CrossRef]
- Rahman, M.; Manzur, M.; Khan, M. Mixed convection heat transfer to modified second grade fluid in the presence of thermal radiation. J. Mol. Liq. 2016, 223, 217–223. [Google Scholar] [CrossRef]
- Khan, M.; Rahman, M.; Manzur, M. Axisymmetric flow and heat transfer to modified second grade fluid over a radially stretching sheet. Results Phys. 2017, 7, 878–889. [Google Scholar] [CrossRef]
- Waqas, H.; Imran, M.; Khan, S.U.; Shehzad, S.A.; Meraj, M.A. Slip flow of Maxwell viscoelasticity-based micropolar nanoparticles with porous medium: a numerical study. Appl. Math. Mech. 2019, 40, 1255–1268. [Google Scholar] [CrossRef]
- Man, C.S.; Sun, Q.X. On the significance of normal stress effects in the flow of glaciers. J. Glacial. 1987, 33, 268–273. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Thermo-bioconvection in a suspension of oxytactic bacteria. Int. Commun. Heat Mass Transf. 2005, 32, 991–999. [Google Scholar] [CrossRef]
- Khan, S.U.; Waqas, H.; Bhatti, M.M.; Imran, M. Bio-convection in the Rheology of Magnetized Couple Stress Nanofluid Featuring Activation Energy and Wu’s Slip. J. Non Equilib. Thermodyn. 2020, 28, 81–95. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Imran, M.; Bhatti, M.M. thermally developed Falkner–Skan bio-convection flow of a magnetized nanofluid in the presence of a motile gyrotactic microorganism: Buongiorno’s nanofluid model. Phys. Scr. 2019, 94, 115304. [Google Scholar] [CrossRef]
- Waqas, H.; Shehzad, S.A.; Khan, S.U.; Imran, M. Novel Numerical Computations on Flow of Nanoparticles in Porous Rotating Disk with Multiple Slip Effects and Microorganisms. J. Nanofluids 2019, 8, 1423–1432. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Hassan, M.; Bhatti, M.M.; Imran, M. Analysis on the bio-convection flow of modified second-grade nanofluid containing gyrotactic microorganisms and nanoparticles. J. Mol. Liq. 2019, 291, 111231. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Shehzad, S.A.; Imran, M. Radiative flow of Maxwell nanofluid containing gyrotactic microorganism and energy activation with convective Nield conditions. Heat Transf. Asian Res. 2019, 48, 1663–1687. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Tlili, I.; Muhammad, A.; Mustafa, S.S. Significance of Bioconvective and thermally dissipation flow of viscoelastic nanoparticles with activation energy features: Novel biofuel significance. Symmetry 2020, 12, 214. [Google Scholar] [CrossRef]
- Khan, M.; Manzur, M.; Rahman, M. On axisymmetric flow and heat transfer of Cross fluid over a radially stretching sheet. Results Phys. 2017, 7, 3767–3772. [Google Scholar] [CrossRef]
- Aksoy, Y.; Pakdemirli, M.; Khalique, C.M. Boundary layer equations and stretching sheet solutions for the modified second grade fluid. Int. J. Eng. Sci. 2007, 45, 829–841. [Google Scholar] [CrossRef]
- Khan, M.; Rahman, M.U. Flow and heat transfer to modified second grade fluid over a non-linear stretching sheet. Aip Adv. 2015, 19, 087157. [Google Scholar] [CrossRef]
- Rahman, M.; Khan, M.; Manzur, M. Boundary layer flow and heat transfer of a modified second grade nanofluid with new mass flux condition. Results Phys. 2018, 10, 594–600. [Google Scholar] [CrossRef]
- Fang, T.; Yao, S.; Zhang, J.; Aziz, A. Viscous flow over a shrinking sheet with a second order slip flow model. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1831–1842. [Google Scholar] [CrossRef]
- Nandeppanavar, M.M.; Vajravelu, K.; Abel, M.S.; Siddalingappa, M.N. Second order slip flow and heat transfer over a stretching sheet with non-linear Navier boundary condition. Int. J. Therm. Sci. 2012, 58, 143–150. [Google Scholar] [CrossRef]
- Khan, M.; Irfan, M.; Khan, W.A. Numerical assessment of solar energy aspects on 3D magneto-Carreau nanofluid: A revised proposed relation. Int. J. Hydrogen Energy 2017, 22054–22065. [Google Scholar] [CrossRef]
- Hayat, T.; Ali, S.; Farooq, M.A.; Alsaedi, A. On comparison of series and numerical solutions for flow of Eyring-Powell fluid with Newtonian heating and internal heat generation/absorption. PLoS ONE 2015, 10. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Kuznetsov, A.V. Bio-thermal convection caused by combined effects of swimming of oxytactic bacteria and inclined temperature gradient in a shallow fluid layer. Int. J. Numer. Methods Heat Fluid Flow 2010, 20, 157–173. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).