Influence of Ramped Wall Temperature and Ramped Wall Velocity on Unsteady Magnetohydrodynamic Convective Maxwell Fluid Flow
Abstract
1. Introduction
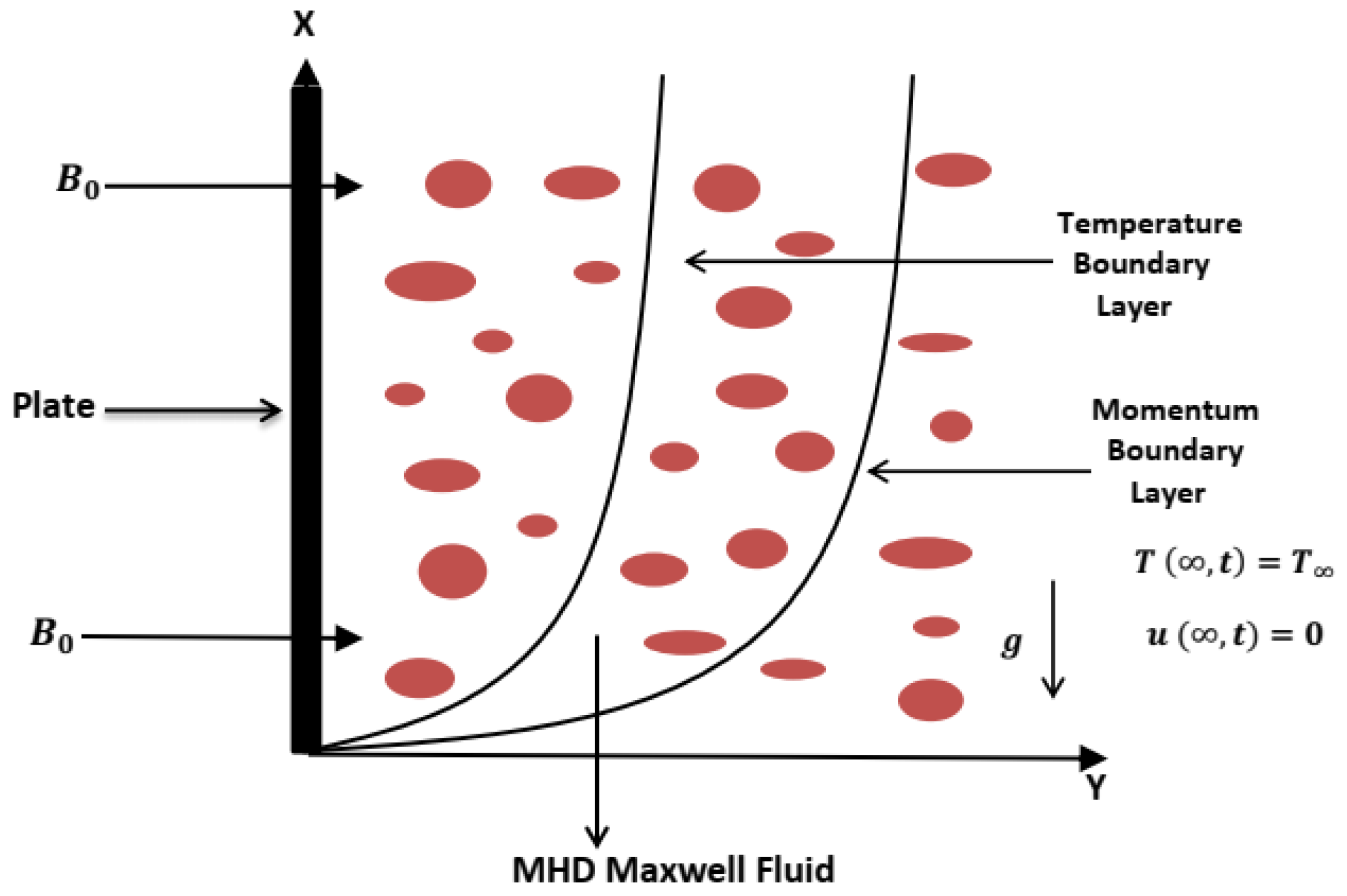
2. Mathematical Modeling
3. Analytical Solutions
4. Special Cases
4.1. Case 1
4.2. Case 2
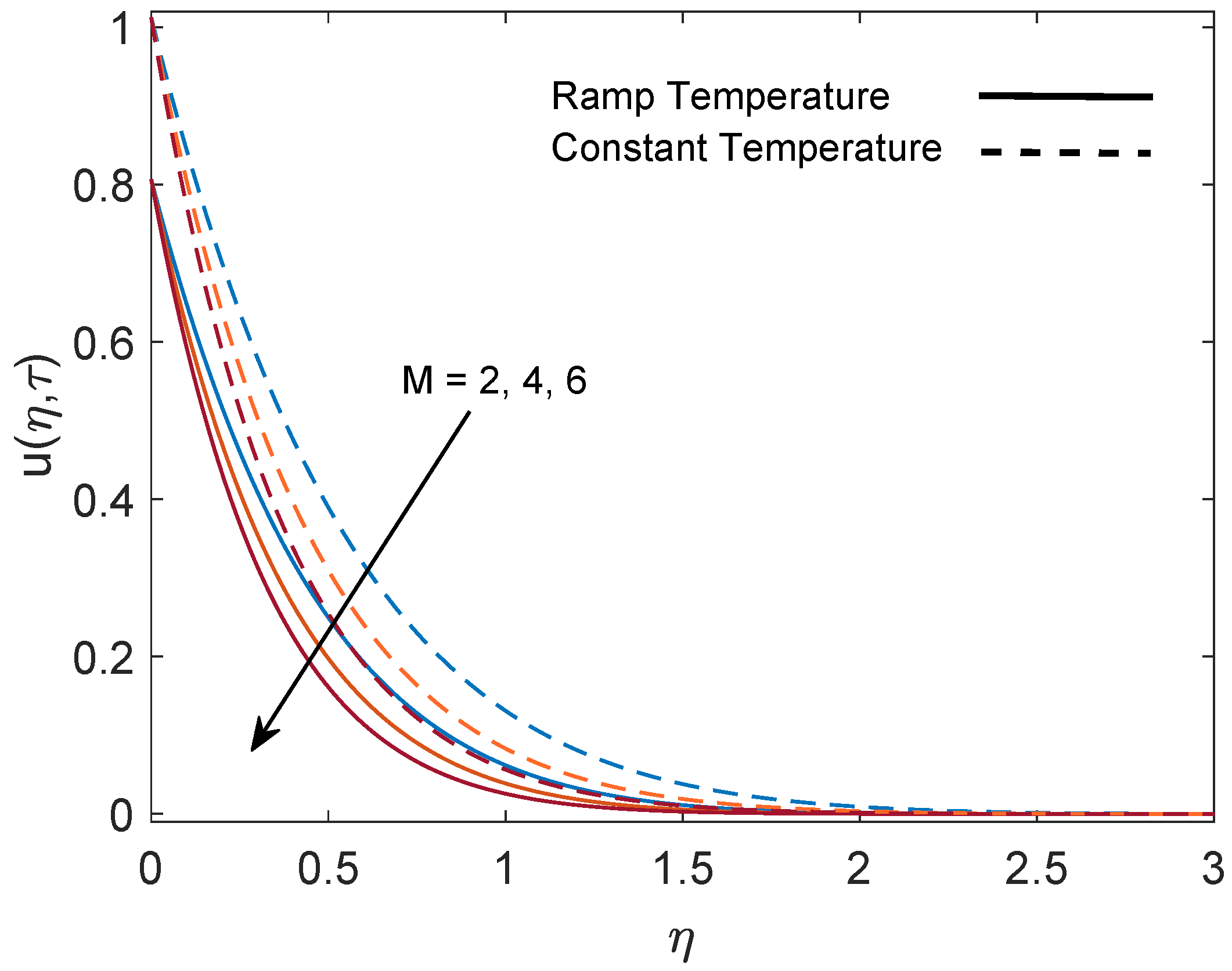
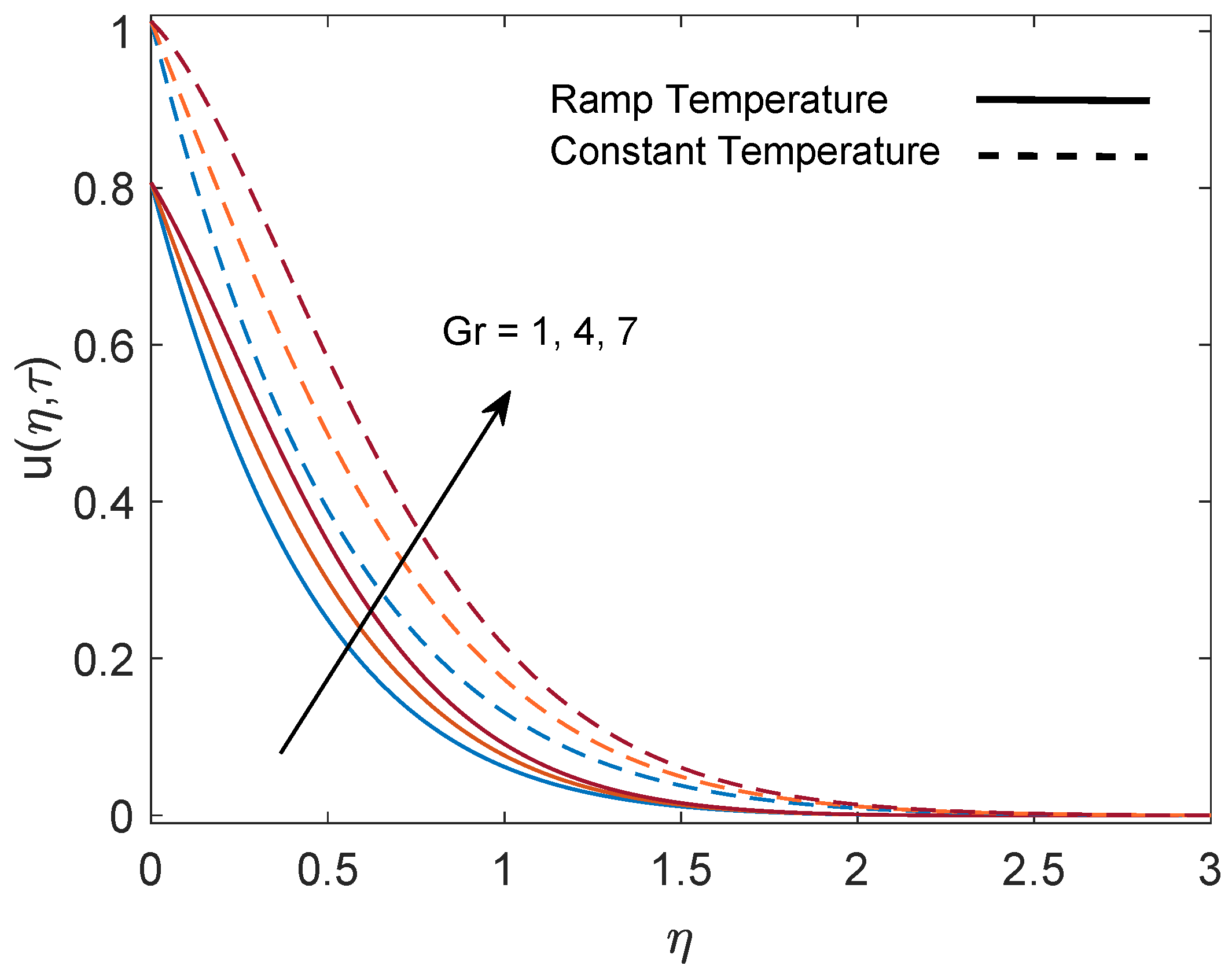
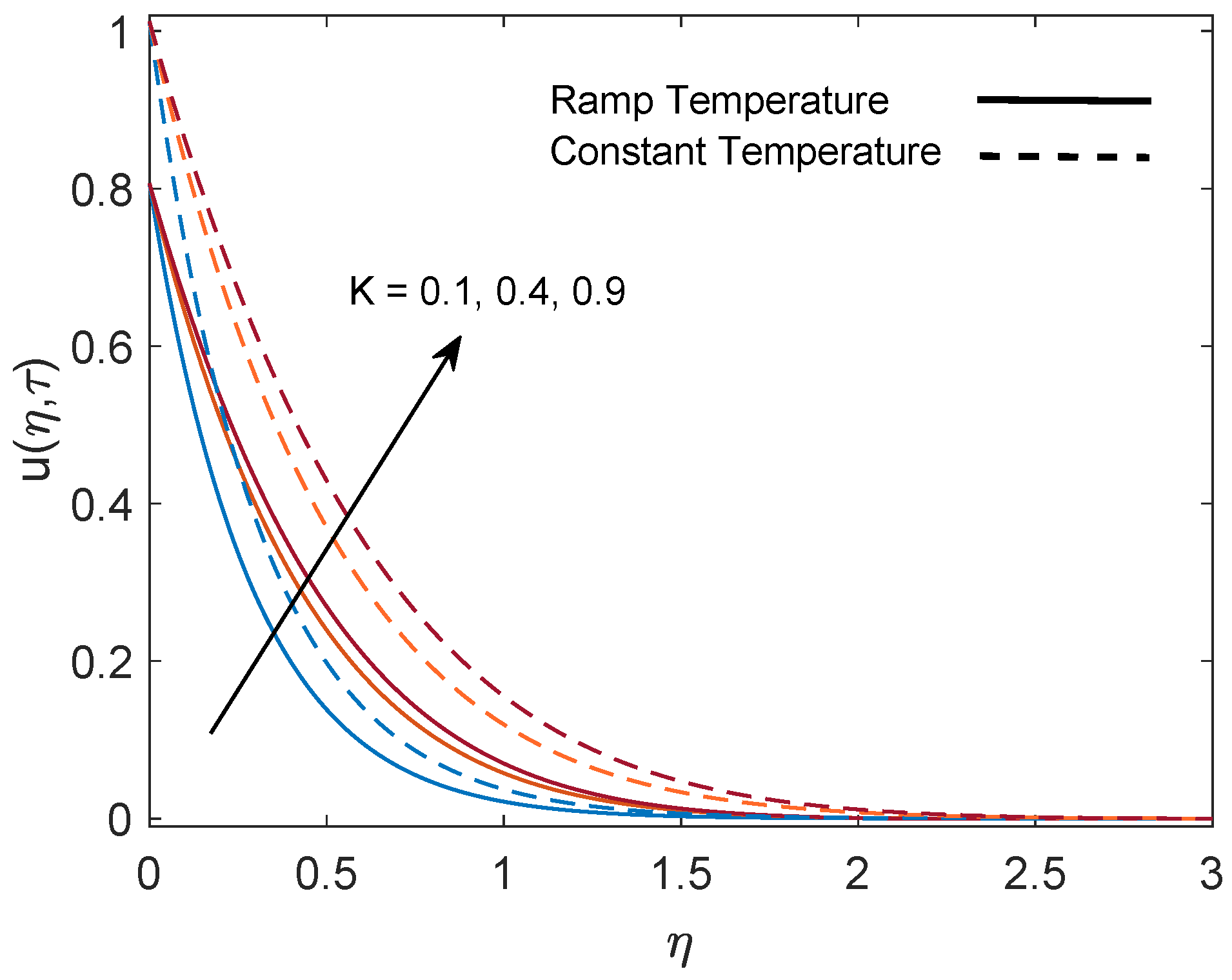
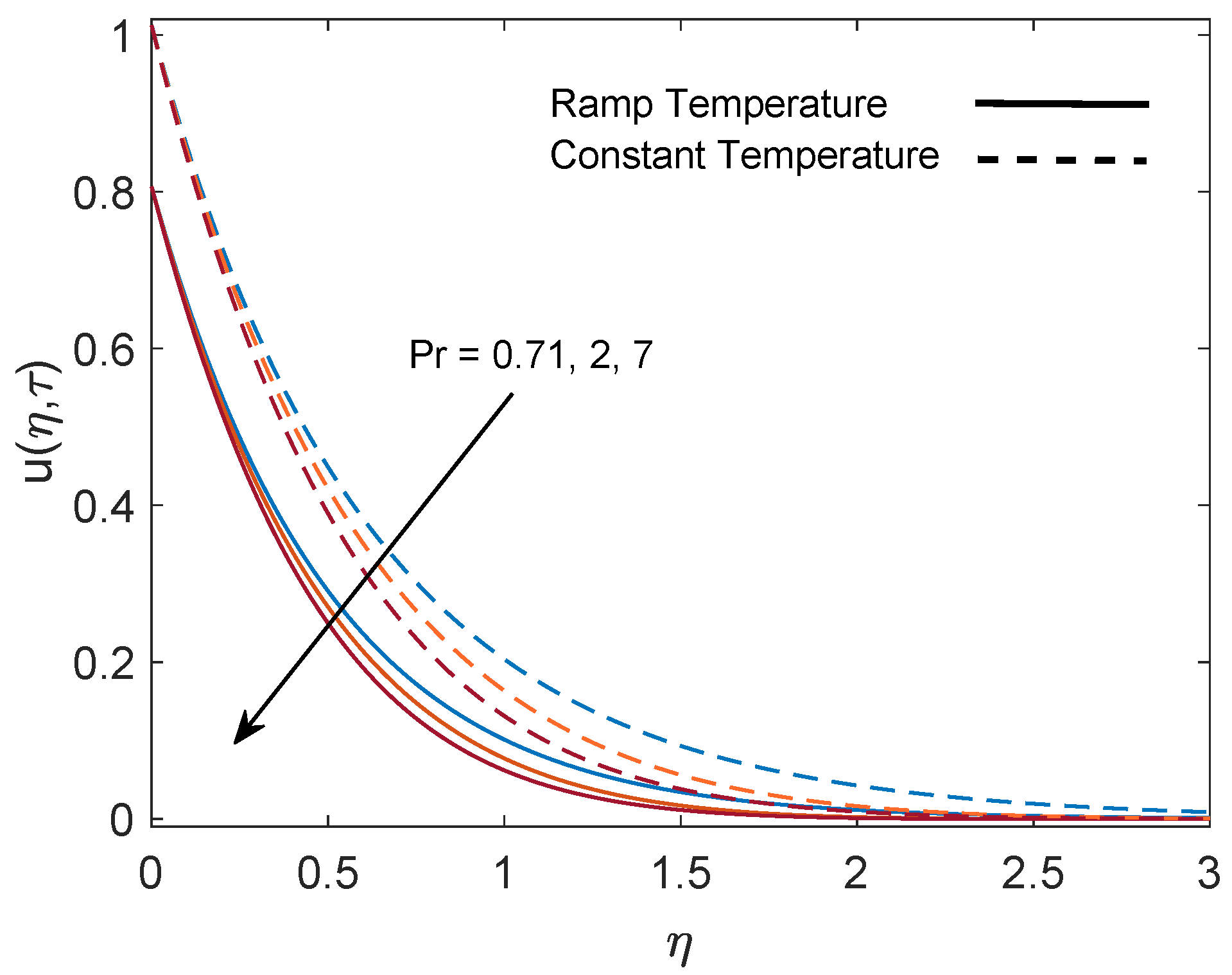
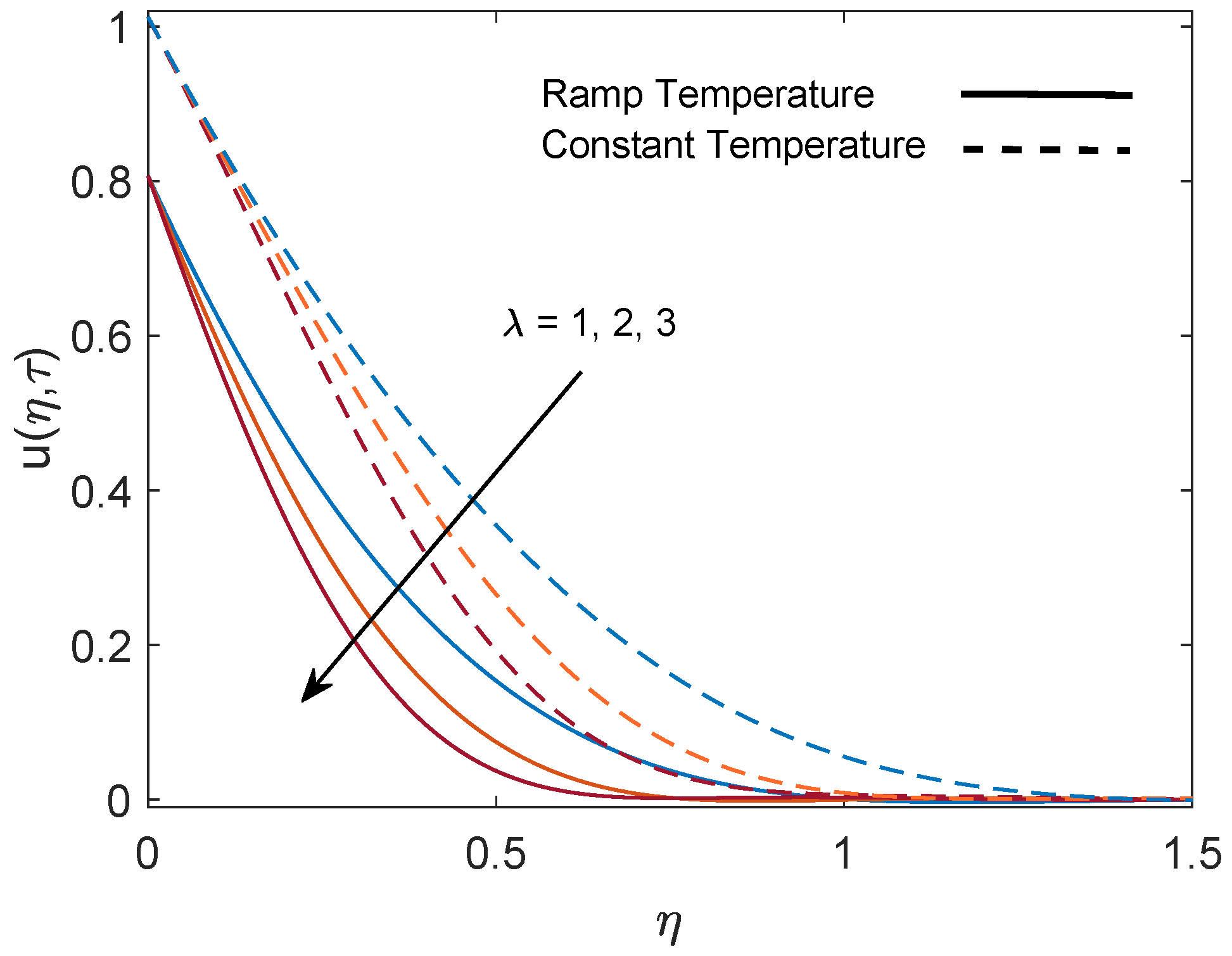
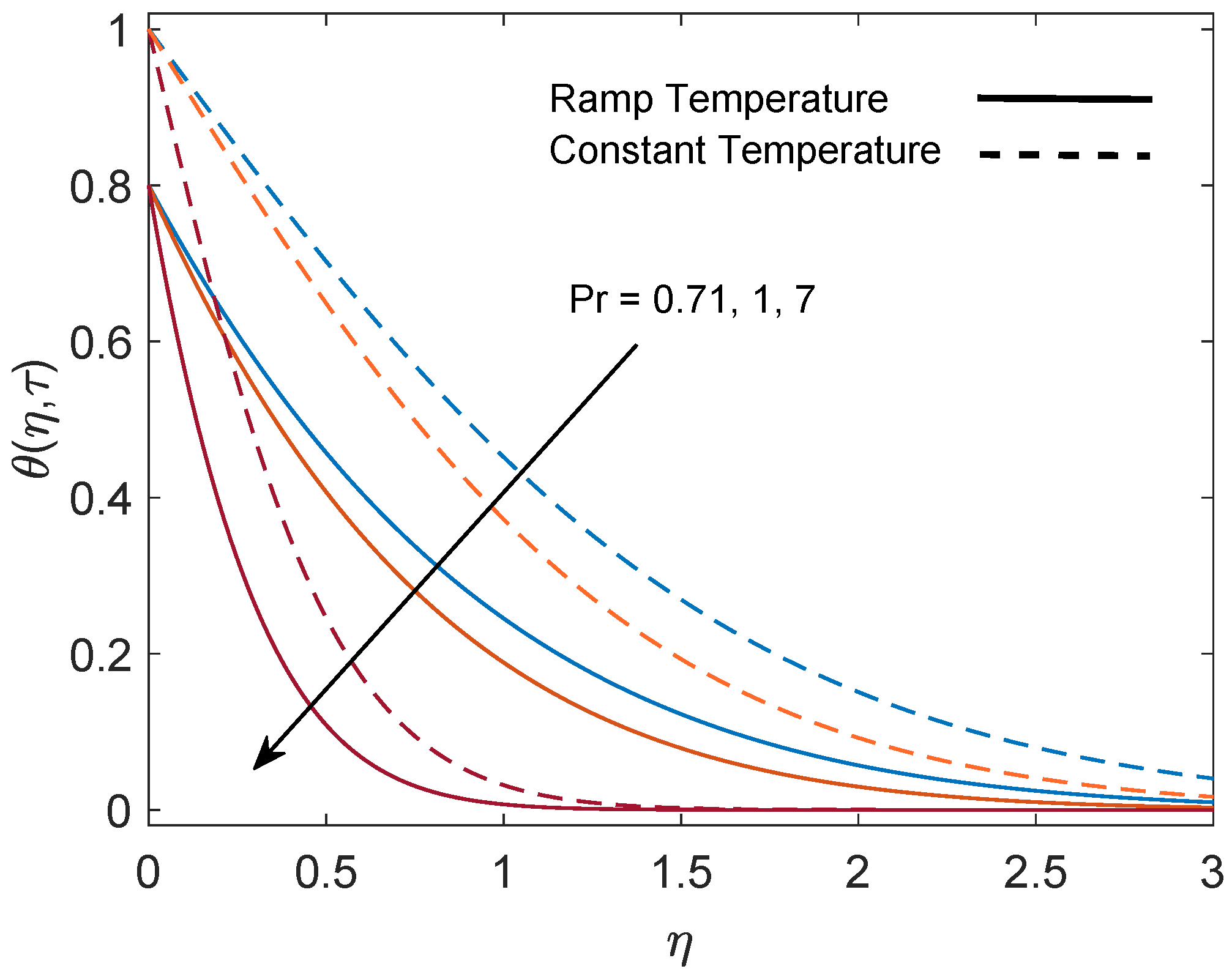
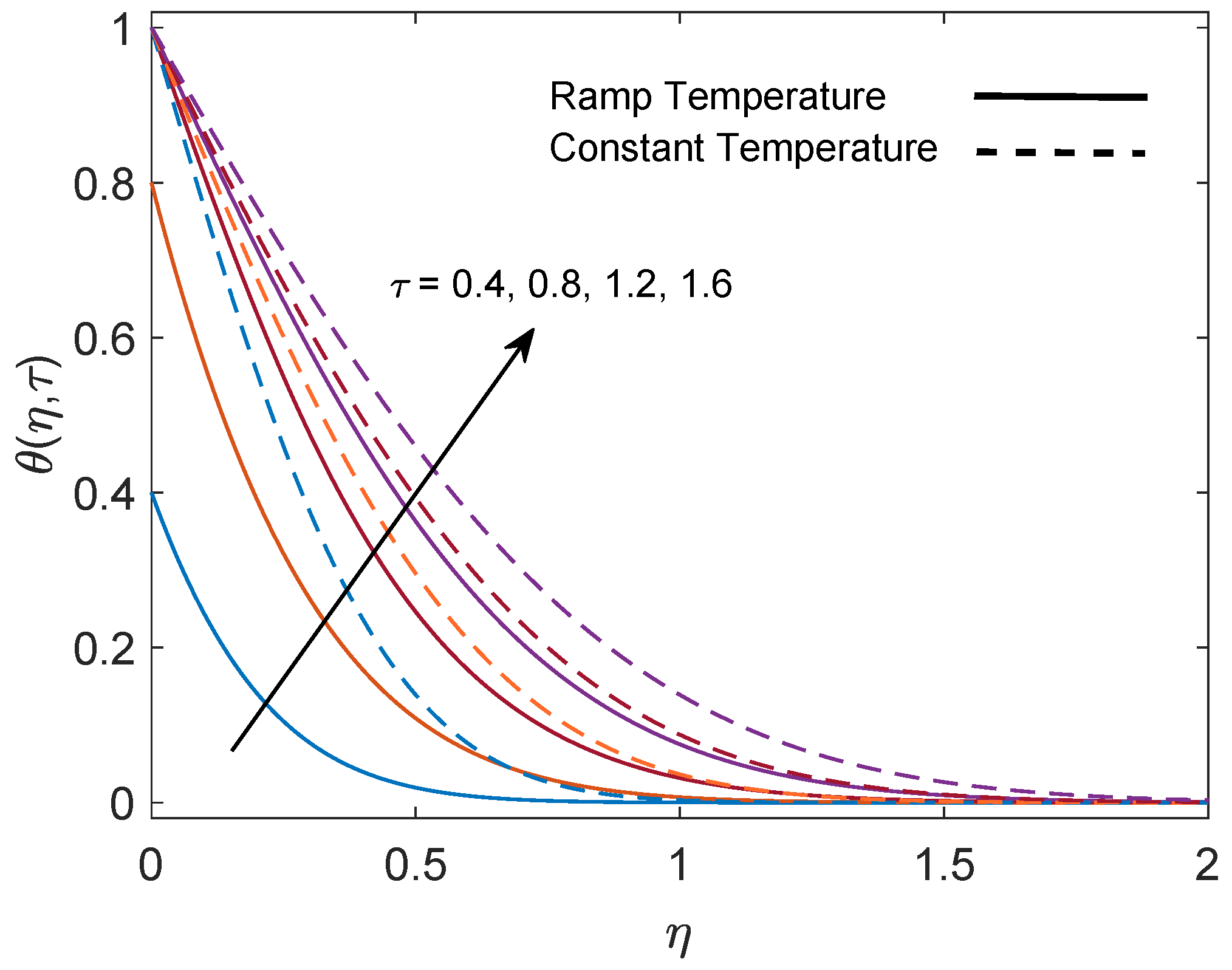
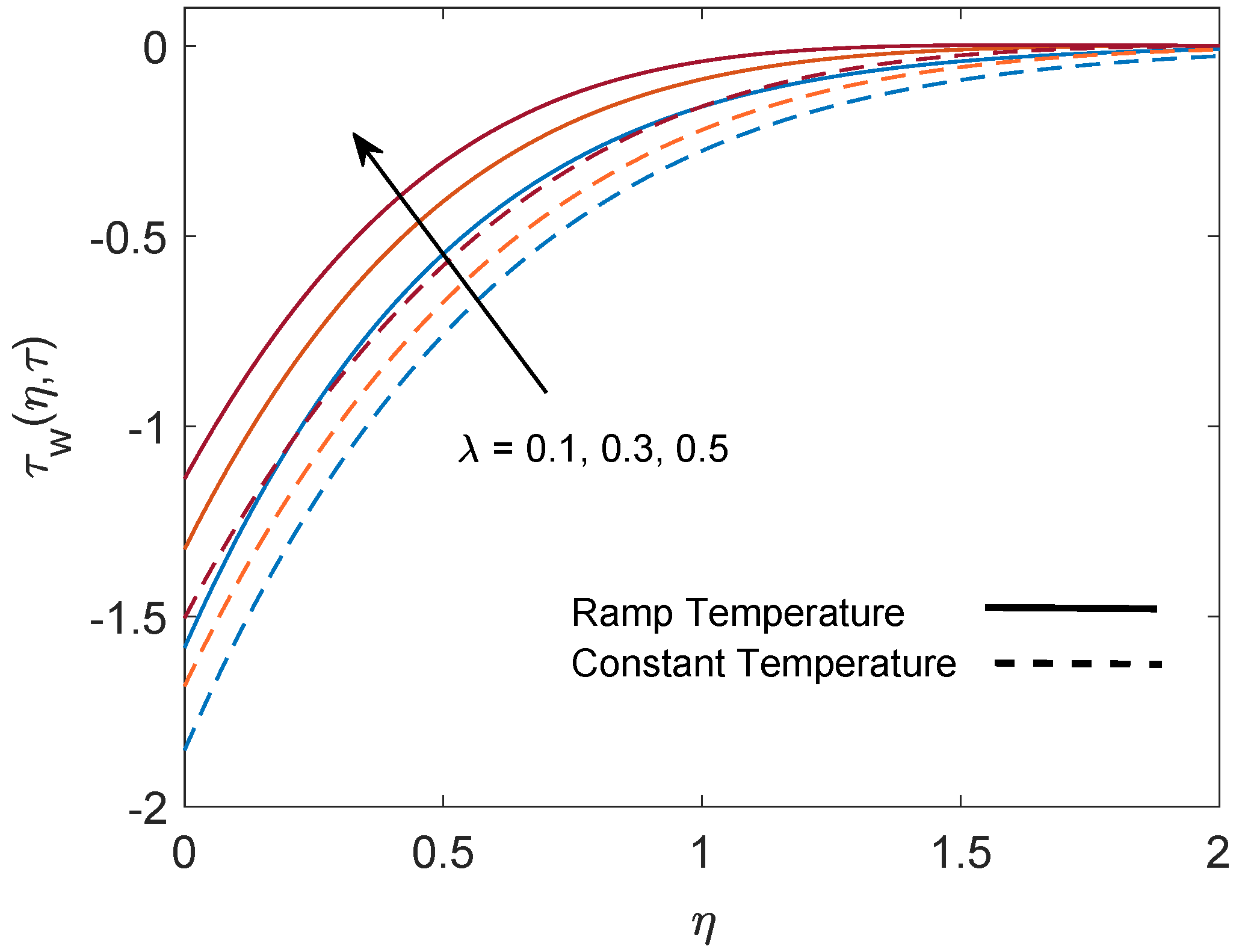
5. Parametric Study
6. Conclusions
- Momentum boundary layer thickness increases with increasing values of the parameters Gr (due to the strong buoyancy force) and K (due to the decrease in viscous force). Meanwhile, it reduces with increasing values of M (due to the strong drag force) and (due to the increase in resistance).
- An elevation in the relaxation time leads to a decrease in velocity on the plate (in terms of skin friction).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Fluid density | |
| Maxwell parameter | |
| Dimensionless time | |
| Dynamic viscosity | |
| u | Fluid velocity |
| Space variable | |
| Electrical conductivity | |
| Coefficient of thermal expansion | |
| Porosity parameter | |
| Permeability parameter | |
| g | Acceleration due to gravity |
| T | Fluid temperature |
| Free stream temperature | |
| S | Shear stress |
| k | Thermal conductivity |
| Heat capacitance | |
| Wall temperature | |
| Gr | Grashof number |
| M | Magnetic parameter |
| K | Dimensionless porosity parameter |
| Pr | Prandtl number |
| s | Laplace parameter |
| Laplace transform coefficient |
References
- Nadeem, S.; Mehmood, R.; Akbar, N.S. Non-orthogonal stagnation point flow of a nano non-Newtonian fluid towards a stretching surface with heat transfer. Int. J. Heat Mass Transf. 2013, 57, 679–689. [Google Scholar] [CrossRef]
- Ghosh, A.; Sana, P. On hydromagnetic flow of an Oldroyd-B fluid near a pulsating plate. Acta Astronaut. 2009, 64, 272–280. [Google Scholar] [CrossRef]
- Kucuk, F.; Karakas, M.; Ayestaran, L. Well testing and analysis techniques for layered reservoirs. SPE Form. Eval. 1986, 1, 342–354. [Google Scholar] [CrossRef]
- Mohyuddin, M.R.; Hayat, T.; Mahomed, F.; Asghar, S.; Siddiqui, A.M. On solutions of some non-linear differential equations arising in Newtonian and non-Newtonian fluids. Nonlinear Dyn. 2004, 35, 229–248. [Google Scholar] [CrossRef]
- Vajravelu, K.; Cannon, J.; Rollins, D.; Leto, J. On solutions of some non-linear differential equations arising in third grade fluid flows. Int. J. Eng. Sci. 2002, 40, 1791–1805. [Google Scholar] [CrossRef]
- Maxwell, J.C. Iv. on the dynamical theory of gases. Philos. Trans. R. Soc. Lond. 1867, 157, 49–88. [Google Scholar]
- Fetecau, C.; Fetecau, C. A new exact solution for the flow of a Maxwell fluid past an infinite plate. Int. J. Non-Linear Mech. 2003, 38, 423–427. [Google Scholar] [CrossRef]
- Fetecau, C.; Jamil, M.; Fetecau, C.; Siddique, I. A note on the second problem of Stokes for Maxwell fluids. Int. J. Non-Linear Mech. 2009, 44, 1085–1090. [Google Scholar] [CrossRef]
- Jordan, P.; Puri, A.; Boros, G. On a new exact solution to Stokes’ first problem for Maxwell fluids. Int. J. Non-Linear Mech. 2004, 39, 1371–1377. [Google Scholar] [CrossRef]
- Noor, N.F.M. Analysis for MHD flow of a Maxwell fluid past a vertical stretching sheet in the presence of thermophoresis and chemical reaction. World Acad. Sci. Eng. Technol. 2012, 64, 1019–1023. [Google Scholar]
- Ramesh, G.; Gireesha, B. Influence of heat source/sink on a Maxwell fluid over a stretching surface with convective boundary condition in the presence of nanoparticles. Ain Shams Eng. J. 2014, 5, 991–998. [Google Scholar] [CrossRef]
- Cao, Z.; Zhao, J.; Wang, Z.; Liu, F.; Zheng, L. MHD flow and heat transfer of fractional Maxwell viscoelastic nanofluid over a moving plate. J. Mol. Liq. 2016, 222, 1121–1127. [Google Scholar] [CrossRef]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Al-Mdallal, Q.M. Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Sci. Rep. 2017, 7, 2445. [Google Scholar] [CrossRef] [PubMed]
- Jamil, M.; Fetecau, C.; Khan, N.A.; Mahmood, A. Some exact solutions for helical flows of Maxwell fluid in an annular pipe due to accelerated shear stresses. Int. J. Chem. React. Eng. 2011, 9. [Google Scholar] [CrossRef]
- Jamil, M.; Fetecau, C.; Fetecau, C. Unsteady flow of viscoelastic fluid between two cylinders using fractional Maxwell model. Acta Mech. Sin. 2012, 28, 274–280. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C. The Rayleigh–Stokes-Problem for a fluid of Maxwellian type. Int. J. Non-Linear Mech. 2003, 38, 603–607. [Google Scholar] [CrossRef]
- Vieru, D.; Zafar, A.A. Some Couette flows of a Maxwell fluid with wall slip condition. Appl. Math. Inf. Sci. 2013, 7, 209–219. [Google Scholar] [CrossRef]
- Sobral Filho, D.C. A new proposal to guide velocity and inclination in the ramp protocol for the treadmill ergometer. Arq. Bras. De Cardiol. 2003, 81, 48–53. [Google Scholar]
- Myers, J.; Bellin, D. Ramp exercise protocols for clinical and cardiopulmonary exercise testing. Sport Med. 2000, 30, 23–29. [Google Scholar] [CrossRef]
- Bruce, R. Evaluation of functional capacity and exercise tolerance of cardiac patients. Mod. Concepts Cardiovasc. Dis. 1956, 25, 321. [Google Scholar]
- Kundu, B. Exact analysis for propagation of heat in a biological tissue subject to different surface conditions for therapeutic applications. Appl. Math. Comput. 2016, 285, 204–216. [Google Scholar] [CrossRef]
- Malhotra, C.P.; Mahajan, R.L.; Sampath, W.; Barth, K.L.; Enzenroth, R.A. Control of temperature uniformity during the manufacture of stable thin-film photovoltaic devices. Int. J. Heat Mass Transf. 2006, 49, 2840–2850. [Google Scholar] [CrossRef]
- Eichhorn, R. Discussion: “Free Convection From a Vertical Flat Plate With Step Discontinuities in Surface Temperature” (Hayday, AA, Bowlus, DA, and McGraw, RA, 1967, ASME J. Heat Transfer, 89, pp. 244–249). J. Heat Transf. 1967, 89, 249–250. [Google Scholar] [CrossRef]
- Schetz, J. On the approximate solution of viscous-flow problems. J. Appl. Mech. 1963, 30, 263–268. [Google Scholar] [CrossRef]
- McIntosh, R.; Waldram, S. Obtaining more, and better, information from simple ramped temperature screening tests. J. Therm. Anal. Calorim. 2003, 73, 35–52. [Google Scholar] [CrossRef]
- Chandran, P.; Sacheti, N.C.; Singh, A.K. Natural convection near a vertical plate with ramped wall temperature. Heat Mass Transf. 2005, 41, 459–464. [Google Scholar] [CrossRef]
- Seth, G.; Ansari, M.S.; Nandkeolyar, R. MHD natural convection flow with radiative heat transfer past an impulsively moving plate with ramped wall temperature. Heat Mass Transf. 2011, 47, 551–561. [Google Scholar] [CrossRef]
- Seth, G.; Hussain, S.; Sarkar, S. Hydromagnetic natural convection flow with heat and mass transfer of a chemically reacting and heat absorbing fluid past an accelerated moving vertical plate with ramped temperature and ramped surface concentration through a porous medium. J. Egypt. Math. Soc. 2015, 23, 197–207. [Google Scholar] [CrossRef]
- Seth, G.; Sharma, R.; Sarkar, S. Natural Convection Heat and Mass Transfer Flow with Hall Current, Rotation, Radiation and Heat Absorption Past an Accelerated Moving Vertical Plate with Ramped Temperature. J. Appl. Fluid Mech. 2015, 8, 7–20. [Google Scholar]
- Seth, G.; Sarkar, S. MHD natural convection heat and mass transfer flow past a time dependent moving vertical plate with ramped temperature in a rotating medium with Hall effects, radiation and chemical reaction. J. Mech. 2015, 31, 91–104. [Google Scholar] [CrossRef]
- Seth, G.; Mahato, G.; Sarkar, S. Effects of Hall current and rotation on MHD natural convection flow past an impulsively moving vertical plate with ramped temperature in the presence of thermal diffusion with heat absorption. Int. J. Energy Technol. 2013, 5, 1–12. [Google Scholar]
- Narahari, M.; Bég, O.A.; Ghosh, S.K. Mathematical modelling of mass transfer and free convection current effects on unsteady viscous flow with ramped wall temperature. World J. Mech. 2011, 1, 176–184. [Google Scholar] [CrossRef]
- Khan, I. A note on exact solutions for the unsteady free convection flow of a Jeffrey fluid. Z. Für Naturforschung A 2015, 70, 397–401. [Google Scholar] [CrossRef]
- Mohd Zin, N.A.; Khan, I.; Shafie, S. Influence of thermal radiation on unsteady MHD free convection flow of Jeffrey fluid over a vertical plate with ramped wall temperature. Math. Probl. Eng. 2016, 2016, 6257071. [Google Scholar] [CrossRef]
- Ahmed, N.; Dutta, M. Transient mass transfer flow past an impulsively started infinite vertical plate with ramped plate velocity and ramped temperature. Int. J. Phys. Sci. 2013, 8, 254–263. [Google Scholar]
- Maqbool, K.; Mann, A.; Tiwana, M. Unsteady MHD convective flow of a Jeffery fluid embedded in a porous medium with ramped wall velocity and temperature. Alex. Eng. J. 2018, 57, 1071–1078. [Google Scholar] [CrossRef]
- Tiwana, M.H.; Mann, A.B.; Rizwan, M.; Maqbool, K.; Javeed, S.; Raza, S.; Khan, M.S. Unsteady Magnetohydrodynamic Convective Fluid Flow of Oldroyd-B Model Considering Ramped Wall Temperature and Ramped Wall Velocity. Mathematics 2019, 7, 676. [Google Scholar] [CrossRef]
- Khan, I.; Ali, F.; Shafie, S. Exact Solutions for Unsteady Magnetohydrodynamic oscillatory flow of a maxwell fluid in a porous medium. Z. Für Naturforschung A 2013, 68, 635–645. [Google Scholar] [CrossRef]
- Khan, I.; Shah, N.A.; Mahsud, Y.; Vieru, D. Heat transfer analysis in a Maxwell fluid over an oscillating vertical plate using fractional Caputo-Fabrizio derivatives. Eur. Phys. J. Plus 2017, 132, 194. [Google Scholar] [CrossRef]
- Le Page, W.R. Complex Variables and the Laplace Transform for Engineers; Courier Corporation: Chelmsford, MA, USA, 1980. [Google Scholar]
- Legua, M.; Morales, I.; Ruiz, L.S. The heaviside function and Laplace transforms. In Proceedings of the 10th WSEAS International Confenrence on Applied Mathematics, Dallas, TX, USA, 1–3 November 2006. [Google Scholar]
- Al-Humaidi, B.; Al-Lail, M.; Chaudhry, M.A. Iterated integrals of the generalized complementary error function. Far East J. Math. Sci. (FJMS) 2012, 63, 25–43. [Google Scholar]
- Durbin, F. Numerical inversion of Laplace transforms: An efficient improvement to Dubner and Abate’s method. Comput. J. 1974, 17, 371–376. [Google Scholar] [CrossRef]
- Seth, G.; Nandkeolyar, R.; Ansari, M.S. Effect of rotation on unsteady hydromagnetic natural convection flow past an impulsively moving vertical plate with ramped temperature in a porous medium with thermal diffusion and heat absorption. Int. J. Appl. Math. Mech. 2011, 7, 52–69. [Google Scholar]
- Gargano, F.; Ponetti, G.; Sammartino, M.; Sciacca, V. Route to chaos in the weakly stratified Kolmogorov flow. Phys. Fluids 2019, 31, 024106. [Google Scholar] [CrossRef]
- Vadasz, P.; Olek, S. Route to chaos for moderate Prandtl number convection in a porous layer heated from below. Transp. Porous Media 2000, 41, 211–239. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anwar, T.; Kumam, P.; Watthayu, W.; Asifa. Influence of Ramped Wall Temperature and Ramped Wall Velocity on Unsteady Magnetohydrodynamic Convective Maxwell Fluid Flow. Symmetry 2020, 12, 392. https://doi.org/10.3390/sym12030392
Anwar T, Kumam P, Watthayu W, Asifa. Influence of Ramped Wall Temperature and Ramped Wall Velocity on Unsteady Magnetohydrodynamic Convective Maxwell Fluid Flow. Symmetry. 2020; 12(3):392. https://doi.org/10.3390/sym12030392
Chicago/Turabian StyleAnwar, Talha, Poom Kumam, Wiboonsak Watthayu, and Asifa. 2020. "Influence of Ramped Wall Temperature and Ramped Wall Velocity on Unsteady Magnetohydrodynamic Convective Maxwell Fluid Flow" Symmetry 12, no. 3: 392. https://doi.org/10.3390/sym12030392
APA StyleAnwar, T., Kumam, P., Watthayu, W., & Asifa. (2020). Influence of Ramped Wall Temperature and Ramped Wall Velocity on Unsteady Magnetohydrodynamic Convective Maxwell Fluid Flow. Symmetry, 12(3), 392. https://doi.org/10.3390/sym12030392





