Charged Particle Oscillations in Transient Plasmas Generated by Nanosecond Laser Ablation on Mg Target
Abstract
1. Introduction
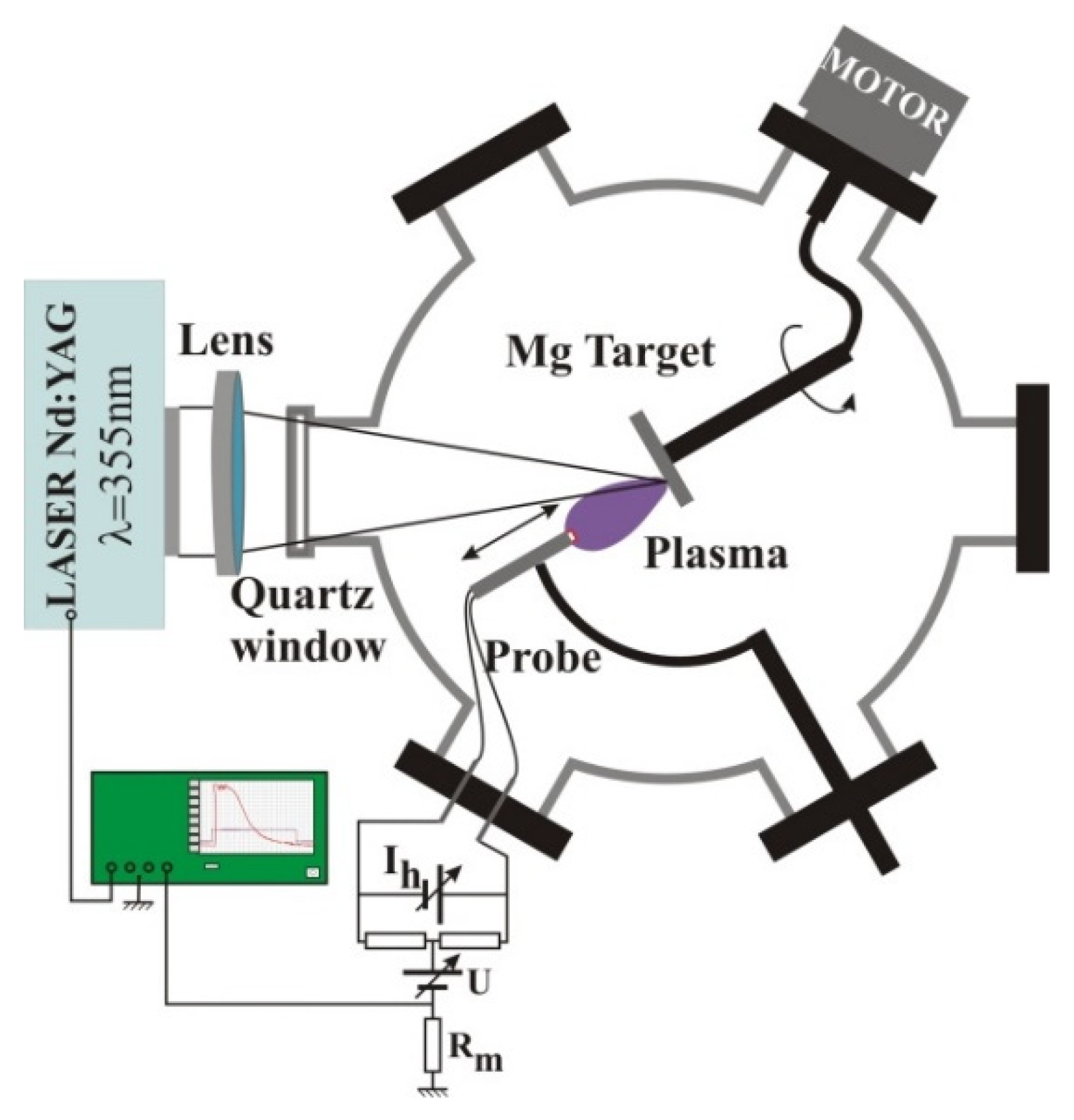
2. Experimental Setup
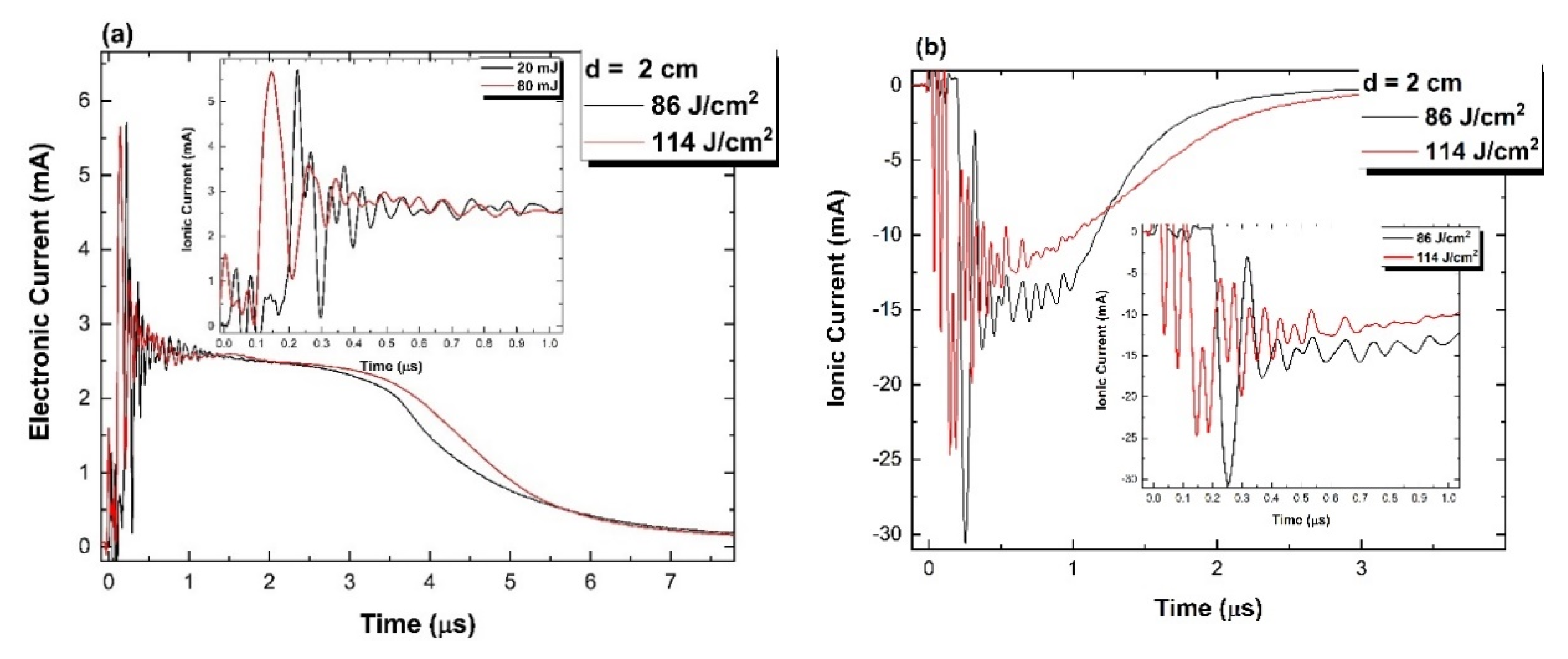
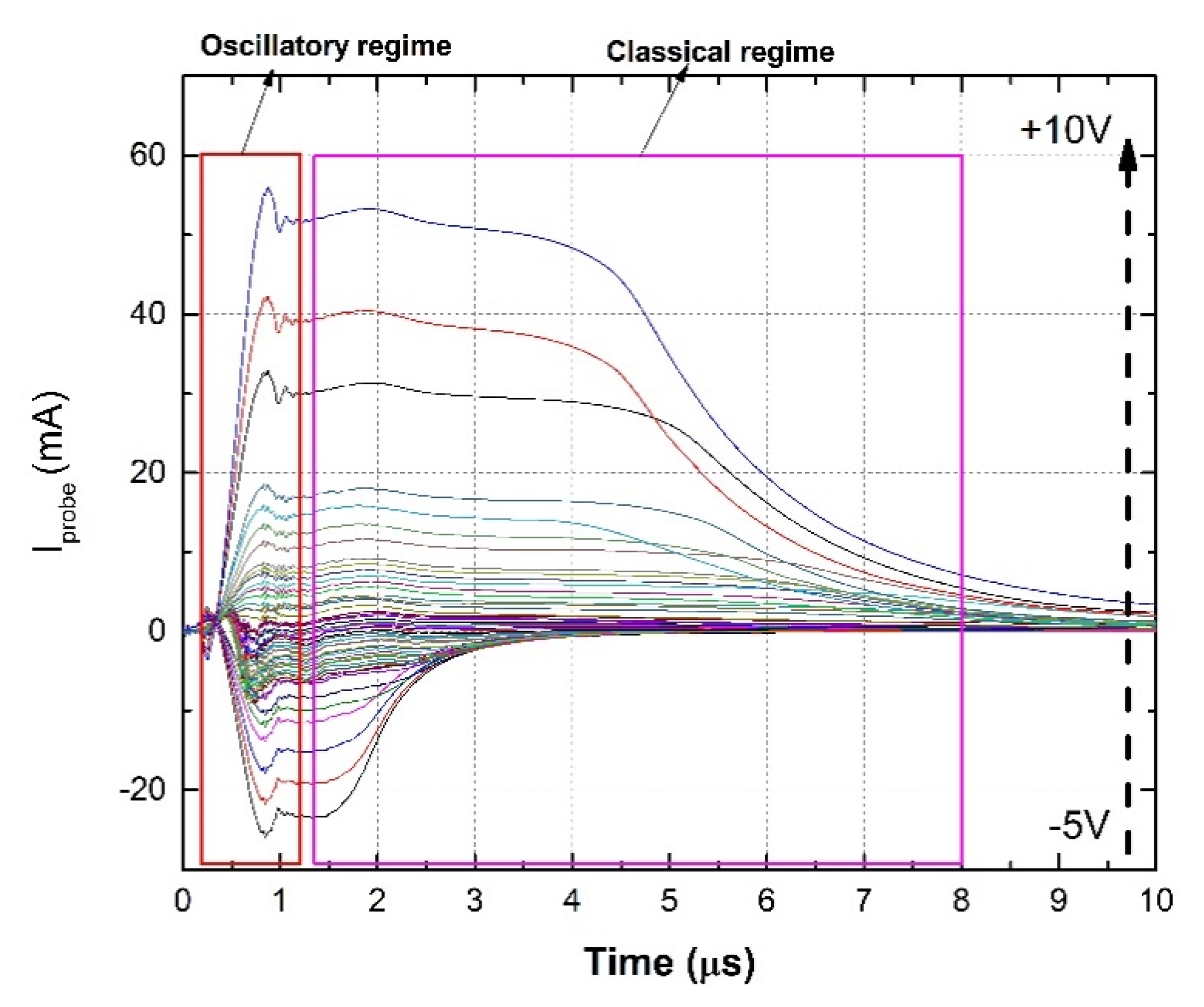
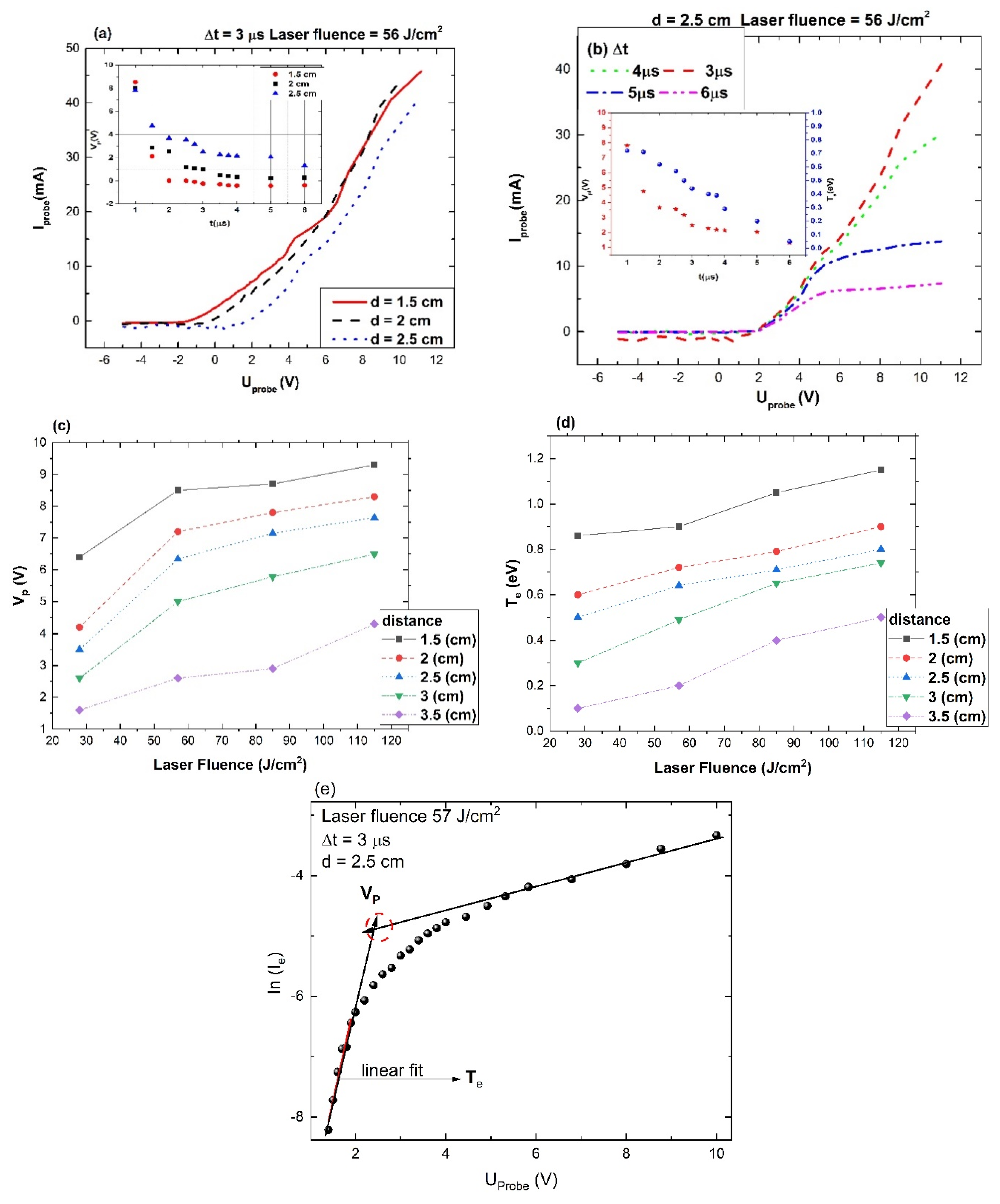
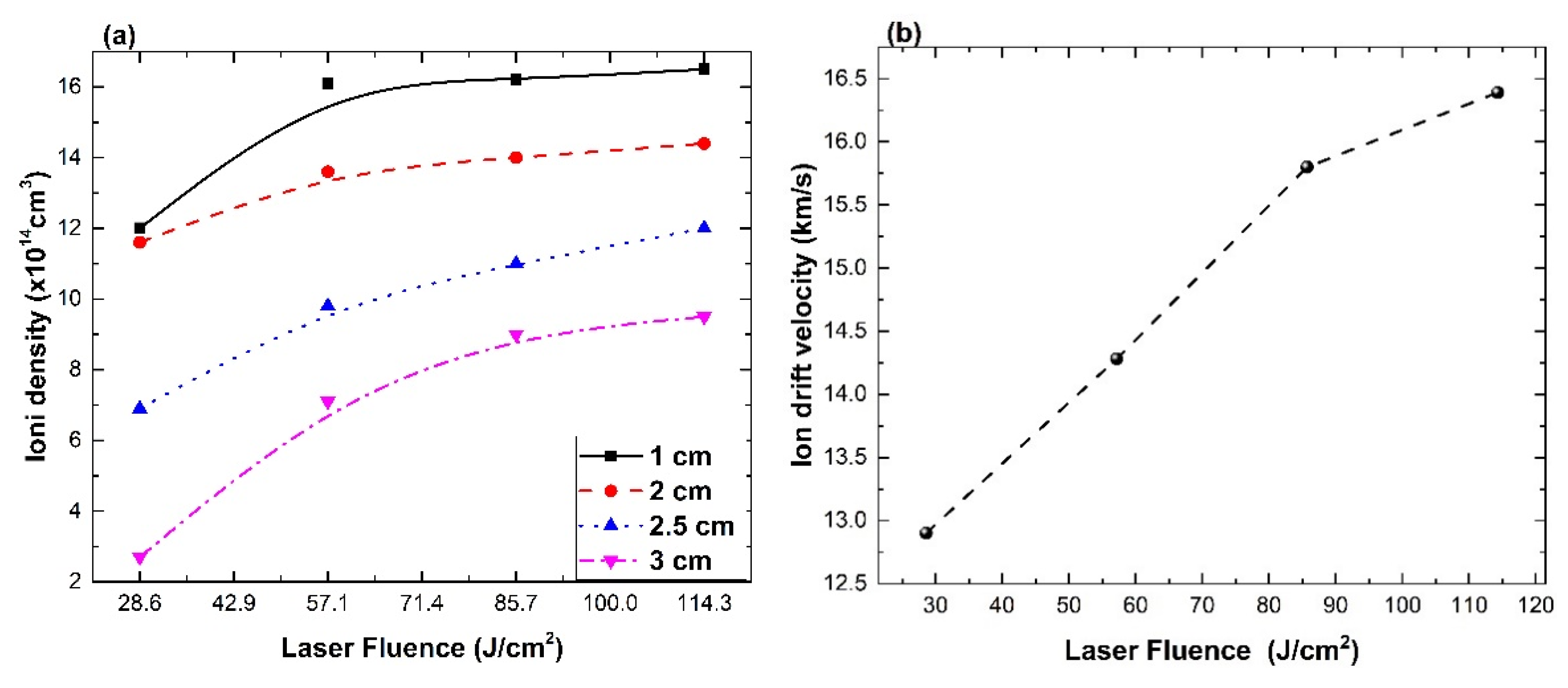
3. Langmuir Probe Measurements
4. Mathematical Model
4.1. Ablation Plasma as a Fractal Medium
4.2. Scale Covariant Derivative and Geodesics Equations
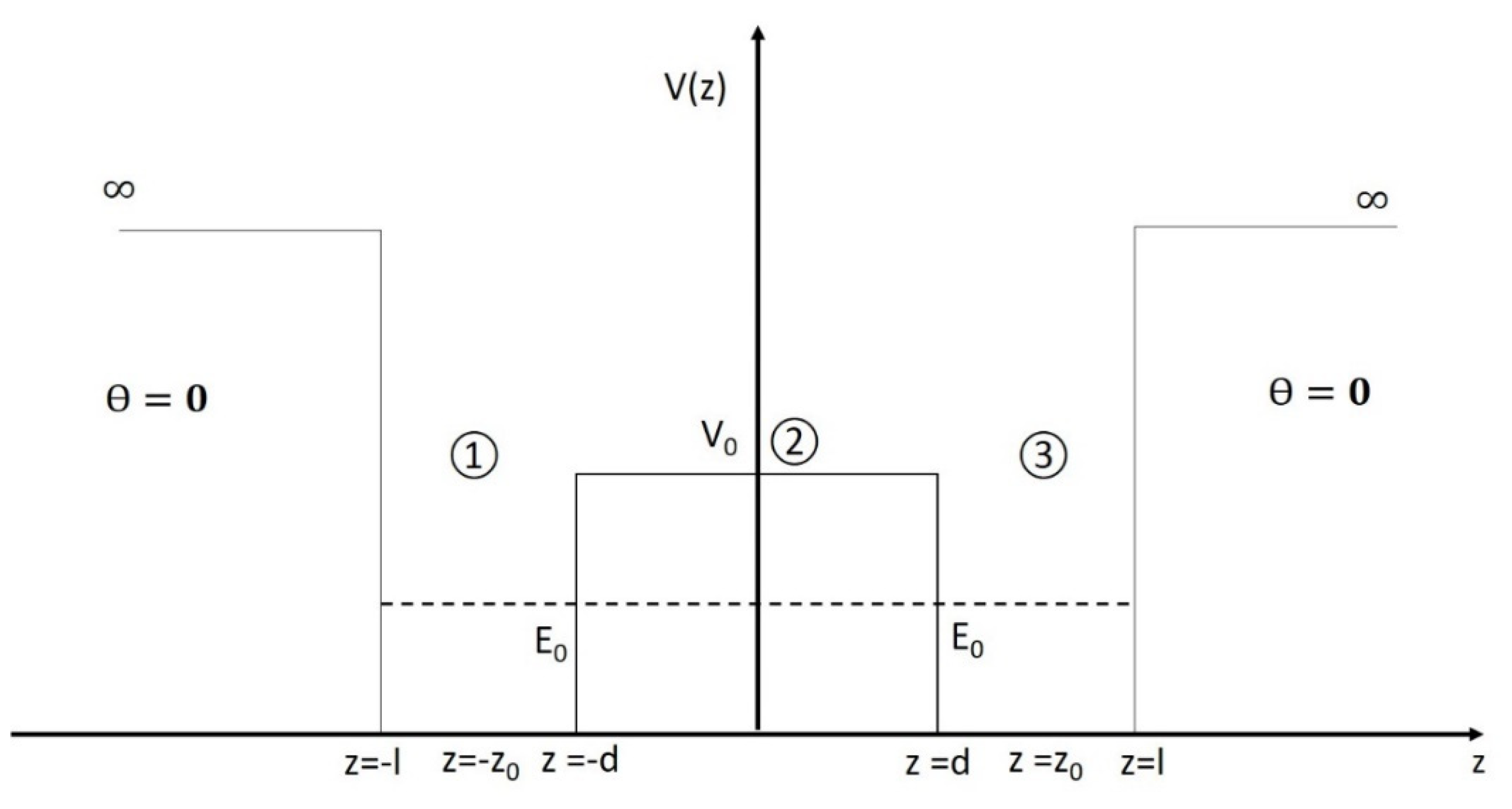
4.3. Ablation Plasma Behavior through a Special Tunneling Effect of Fractal Type
4.4. Mutual Conditionings of the Plasma Structures through Joint Invariant Functions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dijkkamp, D.; Venkatesan, T.; Wu, X.D.; Shaheen, S.A.; Jisrawi, N.; Min-Lee, Y.H.; McLean, W.L.; Croft, M. Preparation of Y-Ba-Cu oxide superconductor thin films using pulsed laser evaporation from high Tc bulk material. Appl. Phys. Lett. 1987, 51, 619–621. [Google Scholar] [CrossRef]
- Bulai, G.; Trandafir, V.; Irimiciuc, S.A.; Ursu, L.; Focsa, C.; Gurlui, S. Influence of rare earth addition in cobalt ferrite thin films obtained by pulsed laser deposition. Ceram. Int. 2019, 45, 20165–20171. [Google Scholar] [CrossRef]
- Craciun, D.; Socol, G.; Stefan, N.; Dorcioman, G.; Hanna, M.; Taylor, C.R.; Lambers, E.; Craciun, V. Applied Surface Science The effect of deposition atmosphere on the chemical composition of TiN and ZrN thin films grown by pulsed laser deposition. Appl. Surf. Sci. 2014, 302, 124–128. [Google Scholar] [CrossRef]
- Yang, Q.I.; Zhao, J.; Zhang, L.; Dolev, M.; Fried, A.D.; Marshall, A.F.; Risbud, S.H.; Kapitulnik, A. Pulsed laser deposition of high-quality thin films of the insulating ferromagnet EuS. Appl. Phys. Lett. 2014, 104, 082402. [Google Scholar] [CrossRef]
- Craciun, V.; Doina, C. Reactive pulsed laser deposition of TiN. Appl. Surf. Sci. 1992, 54, 75–77. [Google Scholar] [CrossRef]
- Dorcioman, G.; Socol, G.; Craciun, D.; Argibay, N.; Lambers, E.; Hanna, M.; Taylor, C.R.; Craciun, V. Applied Surface Science Wear tests of ZrC and ZrN thin films grown by pulsed laser deposition. Appl. Surf. Sci. 2014, 306, 33–36. [Google Scholar] [CrossRef]
- Amoruso, S.; Bruzzese, R.; Velotta, R.; Spinelli, M.; Vitiello, M.; Wang, X. Characterization of LaMnO3 laser ablation in oxygen by ion probe and opticalemission spectroscopy. Appl. Surf. Sci. 2005, 248, 45–49. [Google Scholar] [CrossRef]
- Irimiciuc, S.; Bulai, G.; Agop, M.; Gurlui, S. Influence of laser-produced plasma parameters on the deposition process: In situ space- and time-resolved optical emission spectroscopy and fractal modeling approach. Appl. Phys. A 2018, 124, 1–14. [Google Scholar] [CrossRef]
- Aragón, C.; Aguilera, J.A. Characterization of laser induced plasmas by optical emission spectroscopy: A review of experiments and methods. Spectrochim. Acta Part B 2008, 63, 893–916. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Nica, P.E.; Agop, M.; Focsa, C. Target properties–plasma dynamics relationship in laser ablation of metals: Common trends for fs, ps and ns irradiation regimes. Appl. Surf. Sci. 2019, 506, 144926. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Gurlui, S.; Bulai, G.; Nica, P.; Agop, M.; Focsa, C. Langmuir probe investigation of transient plasmas generated by femtosecond laser ablation of several metals: Influence of the target physical properties on the plume dynamics. Appl. Surf. Sci. 2017, 417, 108–118. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Mihaila, I.; Agop, M. Experimental and theoretical aspects of a laser produced plasma. Phys. Plasmas 2014, 21, 093509. [Google Scholar] [CrossRef]
- Chen, J.; Lippert, T.; Ojeda-G-P, A.; Stender, D.; Schneider, C.W.; Wokaun, A. Langmuir probe measurements and mass spectrometry of plasma plumes generated by laser ablation of La0.4Ca0.6MnO3. J. Appl. Phys. 2014, 116, 073303. [Google Scholar]
- Kumari, S.; Kushwaha, A.; Khare, A. Spatial distribution of electron temperature and ion density in laser induced ruby (Al2O3:Cr3+) plasma using Langmuir probe. J. Instrum. 2012, 7, C05017. [Google Scholar] [CrossRef]
- Schou, J.; Toftmann, B.; Amoruso, S. Dynamics of a laser-produced silver plume in an oxygen background gas. In High-Power Laser Ablation V; International Society for Optics and Photonics: New Mexico, NM, USA, 2004; Volume 5448, pp. 22–26. [Google Scholar]
- Harilal, S.S.; Bindhu, C.V.; Tillack, M.S.; Najmabadi, F.; Gaeris, A.C. Internal structure and expansion dynamics of laser ablation plumes into ambient gases. J. Appl. Phys. 2003, 93, 2380–2388. [Google Scholar] [CrossRef]
- Harilal, S.S.; Issac, R.C.; Bindhu, C.V.; Nampoori, V.P.N.; Vallabhan, C.P.G. Temporal and spatial evolution of C2 in laser induced plasma from graphite target. J. Appl. Phys. 1996, 80, 3561. [Google Scholar] [CrossRef]
- Vivien, C.; Hermann, J.; Perrone, A.; Boulmer-Leborgne, C. A study of molecule formation during laser ablation of graphite in low-pressure ammonia. J. Phys. D 1999, 32, 518–528. [Google Scholar] [CrossRef]
- Thestrup, B.; Toftmann, B.; Schou, J.; Doggett, B.; Lunney, J.G. Ion dynamics in laser ablation plumes from selected metals at 355 nm. Appl. Surf. Sci. 2002, 197, 175–180. [Google Scholar] [CrossRef]
- Harilal, S.S.; Bindhu, C.V.; Nampoor, V.P.N.; Vallabhan, C.P.G. Temporal and spatial Behavior of electron density and temperature in a laser-produced plasma from YBa2Cu3O7. Appl. Spectrosc. 1998, 52, 449–455. [Google Scholar] [CrossRef]
- Nica, P.; Agop, M.; Gurlui, S.; Focsa, C. Oscillatory Langmuir probe ion current in laser-produced plasma expansion. EPL 2010, 89, 65001. [Google Scholar] [CrossRef]
- Tang, E.; Xiang, S.; Yang, M.; Li, L. Sweep Langmuir Probe and Triple Probe Diagnostics for Transient Plasma Produced by Hypervelocity Impact. Plasma Sci. Technol. 2012, 14, 747–753. [Google Scholar] [CrossRef][Green Version]
- Singh, S.C.; Fallon, C.; Hayden, P.; Mujawar, M.; Yeates, P.; Costello, J.T. Ion flux enhancements and oscillations in spatially confined laser produced aluminum plasmas. Phys. Plasmas 2014, 21, 093113. [Google Scholar] [CrossRef]
- Bulgakov, A.V.; Bulgakova, N.M. Dynamics of laser-induced plume expansion into an ambient gas during film deposition. J. Phys. D 1999, 28, 1710–1718. [Google Scholar] [CrossRef]
- Focsa, C.; Gurlui, S.; Nica, P.; Agop, M.; Ziskind, M. Plume splitting and oscillatory behavior in transient plasmas generated by high-fluence laser ablation in vacuum. Appl. Surf. Sci. 2017, 424, 299–309. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Agop, M.; Nica, P.; Gurlui, S.; Mihaileanu, D.; Toma, S.; Focsa, C. Dispersive effects in laser ablation plasmas. Jpn. J. Appl. Phys. 2014, 53, 116202. [Google Scholar] [CrossRef]
- Irimiciuc, Ş.; Enescu, F.; Agop, A.; Agop, M. Lorenz Type Behaviors in the Dynamics of Laser Produced Plasma. Symmetry 2019, 11, 1135. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Gurlui, S.; Nica, P.; Focsa, C.; Agop, M. A compact non-differential approach for modeling laser ablation plasma dynamics. J. Appl. Phys. 2017, 12, 083301. [Google Scholar] [CrossRef]
- Marine, W.; Bulgakova, N.M.N.M.; Patrone, L.; Ozerov, I. Electronic mechanism of ion expulsion under UV nanosecond laser excitation of silicon: Experiment and modeling. Appl. Phys. A 2004, 79, 771–774. [Google Scholar] [CrossRef][Green Version]
- Merlino, R.L. Understanding Langmuir probe current-voltage characteristics. Am. J. Phys. 2007, 75, 1078. [Google Scholar] [CrossRef]
- Nottale, L. Scale Relativity and Fractal Space-Time: An Approach to Unifying Relativity and Quantum Mechanics; Imperial College Press: London, UK, 2011. [Google Scholar]
- Merches, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific: Singapore, 2016. [Google Scholar]
- Agop, M.; Paun, V.P. On the New Paradigm of Fractal Theory; Fundamental and applications, Romanian Academy Publishing House: Bucharest, Romania, 2017. [Google Scholar]
- Agop, M.; Merches, I. Operational Procedures Describing Physical Systems; CRC Press, Taylor and Francis Group: London, UK, 2019. [Google Scholar]
- El-Nabulsi, R.A. Some implications of position dependent mass quantum fractional Hamiltonian in Quantum mechanics. Eur. Phys. J. Plus 2019, 134, 192. [Google Scholar] [CrossRef]
- Wójcik, D.; Białynicki-Birula, I.; Życzkowski, K. Time Evolution of Quantum Fractals. Phys. Rev. Lett. 2000, 85, 5022. [Google Scholar] [CrossRef]
- Laskin, N. Fractals and quantum mechanics. Chaos 2000, 4, 780–790. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Golmankhaneh, A.K.; Balean, D. About Schrödinger Equation on Fractals CurvesImbedding inR3. Int. J. Theor. Phys. 2015, 54, 1275–1282. [Google Scholar] [CrossRef]
- Chuprikov, N.L.; Spiridonov, O.V. A new type of solution of the Schrödinger equationon a self-similar fractal potential. J. Phys. A 2008, 41, 409801. [Google Scholar] [CrossRef]
- Dhillon, H.S.; Kusmartsev, F.V.; Kürten, K.E. Fractal and Chaotic Solutions of the Discrete Nonlinear Schrödinger Equation in Classical and Quantum Systems. J. Nonlinear Math. Phys. 2001, 8, 38–49. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Path Integral Formulation of Fractionally Perturbed Lagrangian Oscillators on Fractal. J. Stat. Phys. 2018, 172, 1617–1640. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; WH Freeman Publisher: New York, NY, USA, 1993. [Google Scholar]
- Stoka, M.I. Integral Geometry; Romanian Academy Publishing House: Bucharest, Romania, 1967. [Google Scholar]
- Stoler, D. Equivalence Classes of Minimum Uncertainty Packets. Phys. Rev. D 1970, 1, 3217. [Google Scholar] [CrossRef]
- Stoler, D. Equivalence Classes of Minimum-Uncertainty Packets. II. Phys. Rev. D 1972, 4, 1925. [Google Scholar] [CrossRef]
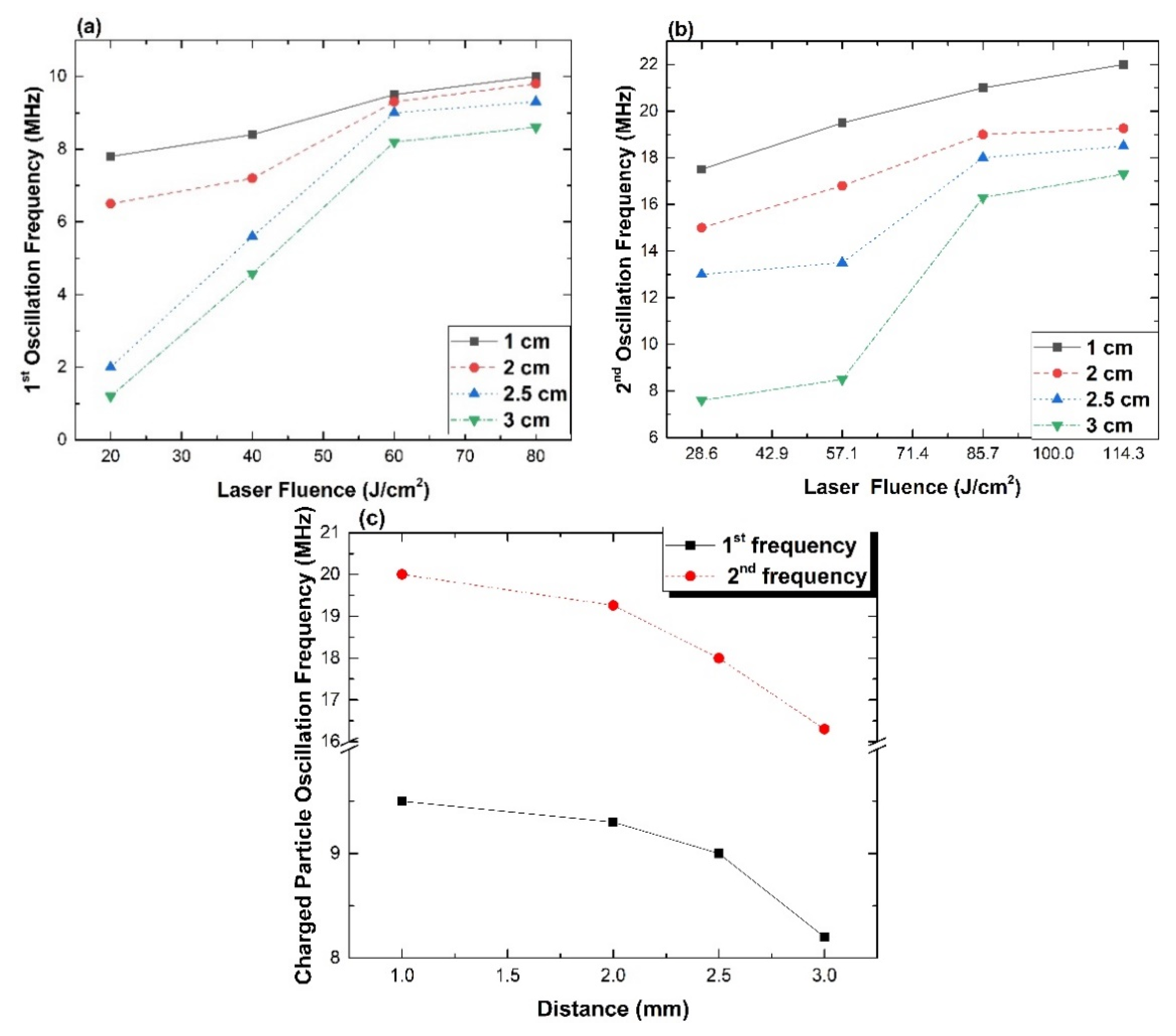
| (a) | 1st Structure Experimental Data (MHz) | 1st Structure Simulated Data (MHz) | ||||||
| Fluence (J/cm2) | 1 cm | 2 cm | 2.5 cm | 3 cm | 1 cm | 2 cm | 2.5 cm | 3 cm |
| 28 | 17.5 ± 0.2 | 15 ± 0.8 | 13 ± 0.5 | 7.6 ± 0.6 | 18.5 ± 0.3 | 16.1 ± 0.1 | 13.5 ± 0.2 | 9.4 ± 0.2 |
| 57 | 19.5 ± 0.3 | 16.8 ± 0.6 | 13.5 ± 0.7 | 8.5 ± 0.7 | 21.7 ± 0.2 | 18.2 ± 0.4 | 14.2 ± 0.6 | 10.6 ± 0.35 |
| 85 | 21 ± 0.7 | 19 ± 0.4 | 18 ± 0.5 | 16.3 ± 0.1 | 22.4 ± 0.05 | 20.2 ± 0.6 | 17.7 ± 0.5 | 16.3 ± 0.2 |
| 115 | 22 ± 0.1 | 19.26 ± 0.2 | 18.5 ± 0.3 | 17.3 ± 0.2 | 22.8 ± 0.5 | 20.9 ± 0.3 | 18.4 ± 0.2 | 17.4 ± 0.1 |
| (b) | 2nd Structure Experimental Data (MHz) | 2nd Structure Simulated Data (MHz) | ||||||
| Fluence (J/cm2) | 1 cm | 2 cm | 2.5 cm | 3 cm | 1 cm | 2 cm | 2.5 cm | 3 cm |
| 28 | 7.8 ± 0.1 | 6.5 ± 0.3 | 2 ± 0.4 | 1.2 ± 0.6 | 7.4 ± 0.6 | 6.44 ± 0.1 | 2.4 ± 0.3 | 2.2 ± 0.1 |
| 57 | 8.4 ± 0.2 | 7.2 ± 0.1 | 5.6 ± 0.1 | 4.58 ± 0.2 | 8.68 ± 0.6 | 7.28 ± 0.04 | 5.68 ± 0.05 | 4.35 ± 0.05 |
| 85 | 9.5 ± 0.4 | 9.3 ± 0.5 | 9 ± 0.3 | 8.2 ± 0.2 | 8.96 ± 0.6 | 9.08 ± 0.1 | 8.78 ± 0.04 | 8.14 ± 0.04 |
| 115 | 10 ± 0.5 | 9.8 ± 0.5 | 9.3 ± 0.4 | 8.6 ± 0.3 | 9.12 ± 0.6 | 9.36 ± 0.06 | 8.99 ± 0.05 | 8.4 ± 0.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agop, M.; Mihaila, I.; Nedeff, F.; Irimiciuc, S.A. Charged Particle Oscillations in Transient Plasmas Generated by Nanosecond Laser Ablation on Mg Target. Symmetry 2020, 12, 292. https://doi.org/10.3390/sym12020292
Agop M, Mihaila I, Nedeff F, Irimiciuc SA. Charged Particle Oscillations in Transient Plasmas Generated by Nanosecond Laser Ablation on Mg Target. Symmetry. 2020; 12(2):292. https://doi.org/10.3390/sym12020292
Chicago/Turabian StyleAgop, Maricel, Ilarion Mihaila, Florin Nedeff, and Stefan Andrei Irimiciuc. 2020. "Charged Particle Oscillations in Transient Plasmas Generated by Nanosecond Laser Ablation on Mg Target" Symmetry 12, no. 2: 292. https://doi.org/10.3390/sym12020292
APA StyleAgop, M., Mihaila, I., Nedeff, F., & Irimiciuc, S. A. (2020). Charged Particle Oscillations in Transient Plasmas Generated by Nanosecond Laser Ablation on Mg Target. Symmetry, 12(2), 292. https://doi.org/10.3390/sym12020292






