1. Introduction
Air pollution is a matter of concern among the public, particularly for those who live in mega-urban and industrial cities, which may have serious effects on humans and the natural environment in the future [
1]. Air pollution forecasting is a high-priority in air quality research since it is related to public health effects and the natural environment [
2,
3,
4]. The most widely important classical methods of time series are the autoregressive integrated moving average (ARIMA) models [
5], the artificial neuron network (ANN) models [
6,
7,
8], and the fuzzy time series (FTS) [
9,
10,
11,
12,
13,
14,
15,
16,
17].
The FTS model is first introduced by Song and Chissom [
18,
19] based on a fuzzy set theory proposed by Zadeh [
20]. Chen [
21] developed the FTS model of Song and Chissom based on fuzzy logic group relations tables for reducing the computational complexity in the model. Huarng [
22,
23] developed Chen’s [
21] model by determining the effective length of intervals. Yolcu et al. [
24] developed the ratio-based method based on a constrained optimization to select the length of intervals. Yu [
25] improved a predicting model based on weighted fuzzy relations, which produced better forecasting results than the Chen [
21] model. Cheng et al. [
26] introduced the trend weighted FTS model for TAIEX forecasting by assign proper weights to individual fuzzy relationships. Effindy et al. [
27] modified a weighted FTS model for enrollment forecasting. They adopted the weighted model by adding the difference between the observed dataset across a midpoint of intervals. Tsaur [
28] proposed the FTS model based on Markov chain, which is used for obtaining the largest probability using the transition probability matrix. He also used a random length of interval for the universe of discourse, which leads to a negative effect by abnormal observations and outliers. Sadaei et al. [
29] developed a refined exponentially weighted FTS for forecasting the load data, which is developed prediction preciseness. More specifically, the effective interval length has been investigated by several studies based on different methods. For example, Huarng [
22,
23] proposed two methods for determining the effective length of intervals, which are based on averages and distribution. Yolcu et al. [
24] developed Huarng’s model [
22] based on constrained optimization for determining the effective length of intervals. Eğrioğlu et al. [
30] proposed a new method of fuzzy time series using a single variable constrained optimization to determine the best length of interval for the best forecasting accuracy. Chen et al. [
31] proposed a new FTS forecasting model integrated with the granular computing approach and entropy method for stock price data. Talarposhti et al. [
32] proposed a hybrid approach using optimization techniques and intelligence algorithm to determine the proper length of intervals for predicting the stock market. Cheng et al. [
33] employed a rough set and utilized an adaptive expectation model to propose a new fuzzy time series to forecast the closing price. Rahim et al. [
34] developed a type 2 FTS model using the sliding window technique for determining the appropriate length of intervals. Bose et al. [
35] proposed a new partitioning method with the rough-fuzzy method for developing the fuzzy time series model.
Apart from that, Zuo et al. [
36] developed a combining topological optimization technique in order to figure out the optimization problem in the product manufacturing process. Ning et al. [
37] proposed a new method based on a chip formation model and an iterative gradient search method using Kalman filter algorithm. This optimization method has been used to inversely identify the Johnson-Cook model constants of ultra-fine-grained titanium. Ning and Liang [
38] introduced a developed inverse identification technique for Johnson-Cook model constants based on the use of temperature and force data for predicting machining forces. The development of the model has been done by using an iterative gradient search method based on the Kalman filter algorithm. These types of optimization techniques can be adopted for improving the forecasting models.
More specifically, The FTS models have been utilized for forecasting environmental problems such as air quality 9-17], which are considered for predicting air pollution since the time series of air pollution may include uncertainty data and may not verify some of the statistical assumptions. Nevertheless, utilizing the FTS models in the field of air pollution is still very rare. For example, Cheng et al. [
17] introduced a trend weighted FTS model to predict daily O3 concentrations. Dincer and Akkuş [
12] predicted the SO2 concentrations based on a robust FTS model, which has provided good forecasting results. Koo et al. [
39] made a comparison study using FTS and other statistical models for predicting air pollution events. They concluded that the proposed model outperformed the other models. Wang et al. [
40] proposed a hybrid FTS method with data re-processing approaches for forecasting the main air pollutants. Yang et al. [
41] proposed a forecasting system based on a combination of the fuzzy theory and advanced optimization algorithm for air pollution forecasting.
As previously mentioned, the FTS models have been utilized to solve various domain forecasting problems. However, several FTS have some issues, such as using an arbitrary length of intervals for the universe of discourse, repeated fuzzy relationships, or considering the weights of fuzzy logical relationships. According to the literature review above, some researchers proposed a partition method with complexity computations, and some have not evaluated their models, by comparison with the other recent models. Particularly, the FTS-based Markov chain model has a deficiency in determining the effective length of the interval, which was negatively affected by abnormal observations and outliers. Therefore, determining the optimal length of intervals and assigning the proper weights to present is an interesting issue that needs to be addressed. This motivated us to investigate the optimal partition number of the universe of discourse. This study proposes the FTS Markov chain (FTSMC) model based on the grid method with the optimal number of the partitions of the universe of discourse to provide significantly improved performance in the model accuracy for air pollution forecasting. The major contribution of this study is to propose an improved model with an appropriate partition number and to implement the model for forecasting APIs as a new forecasting model in air quality research.
4. The Implementation of the Algorithm
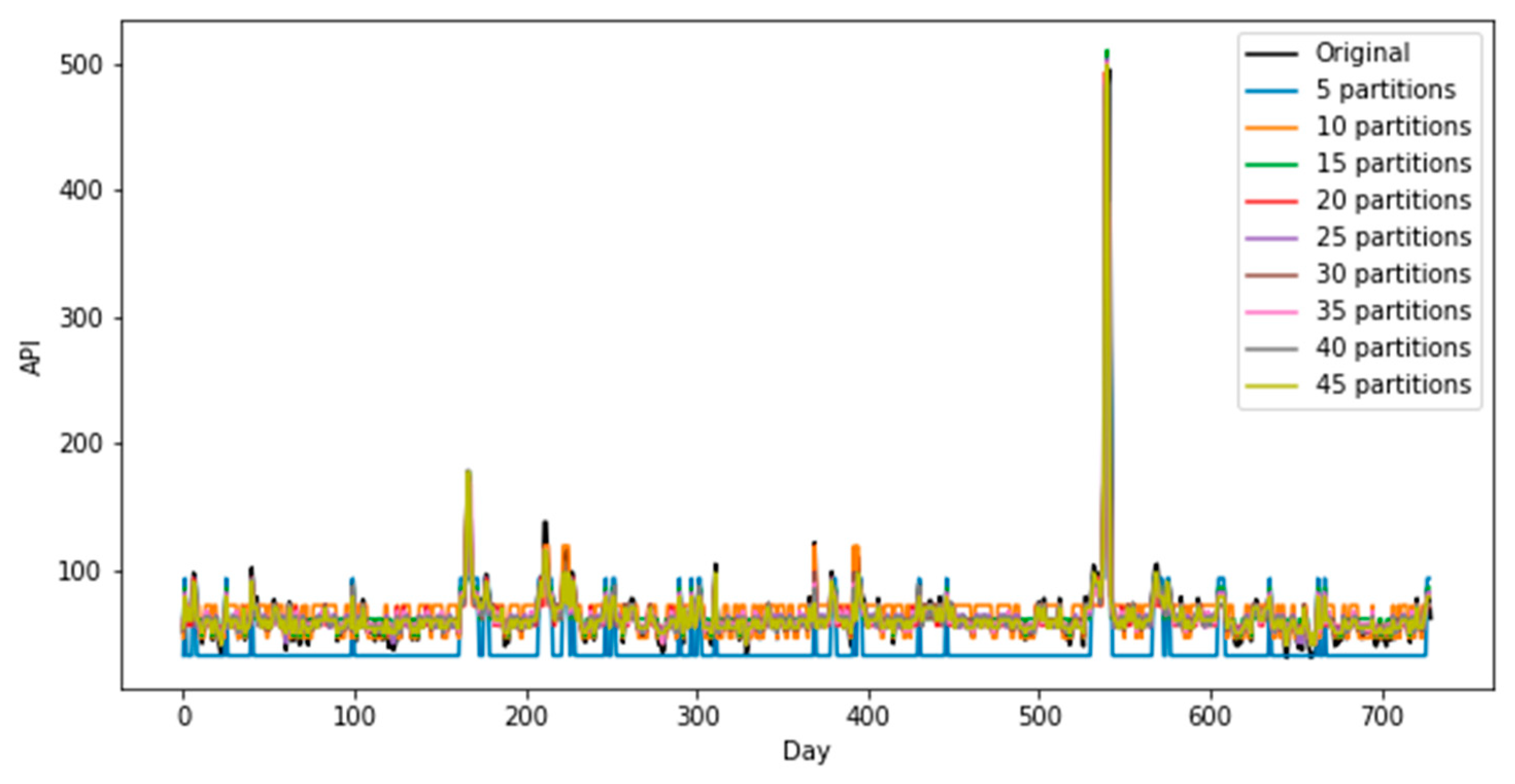
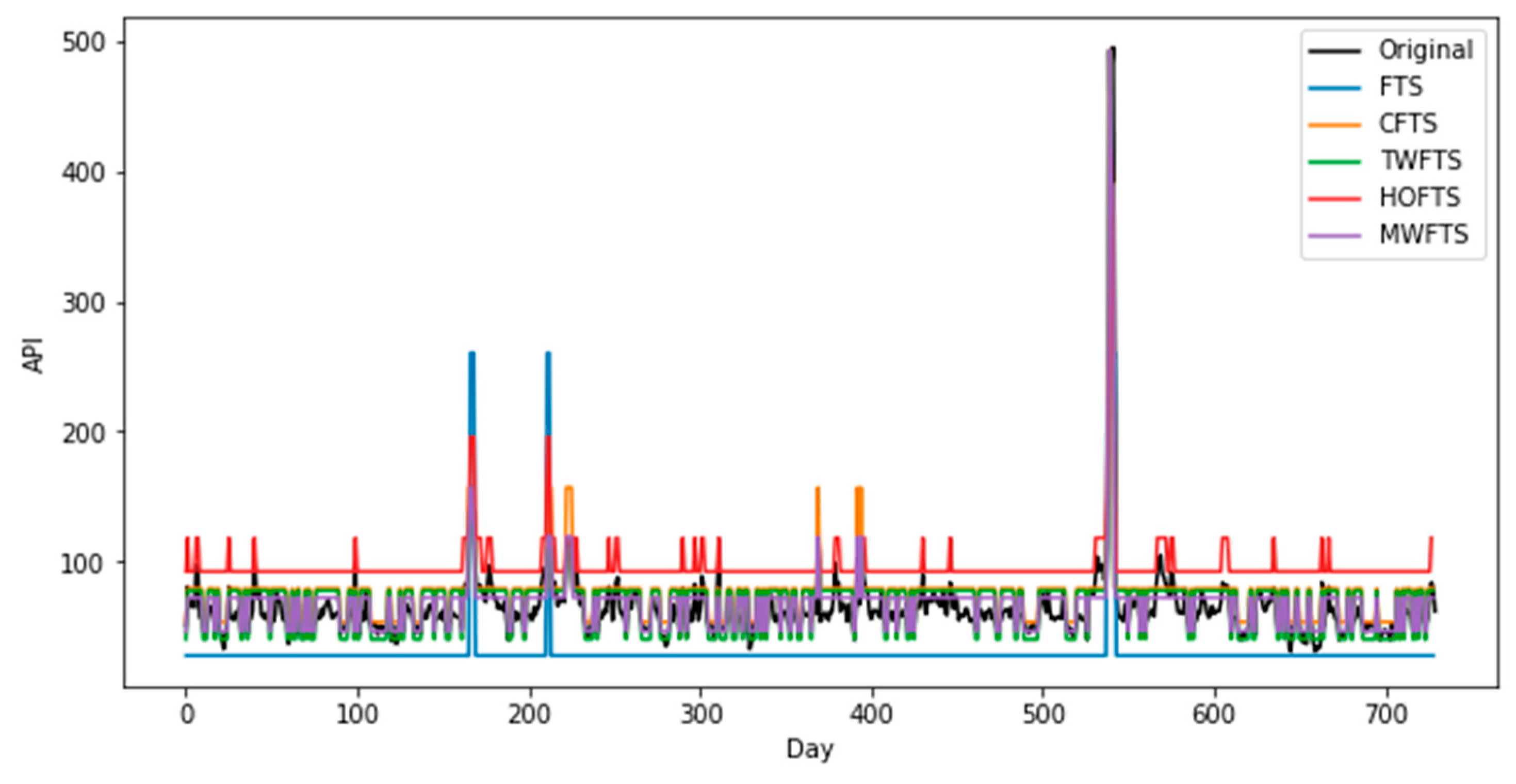
In this section, we will provide a result of the proposed model using the daily API data, whose plots for training data and testing data are given in
Figure 4, respectively.
The implementation of the proposed model’s algorithm can be done based on pyFTS [
46] as follows:
- Step 1.
Define
for the APIs values.
- Step 2.
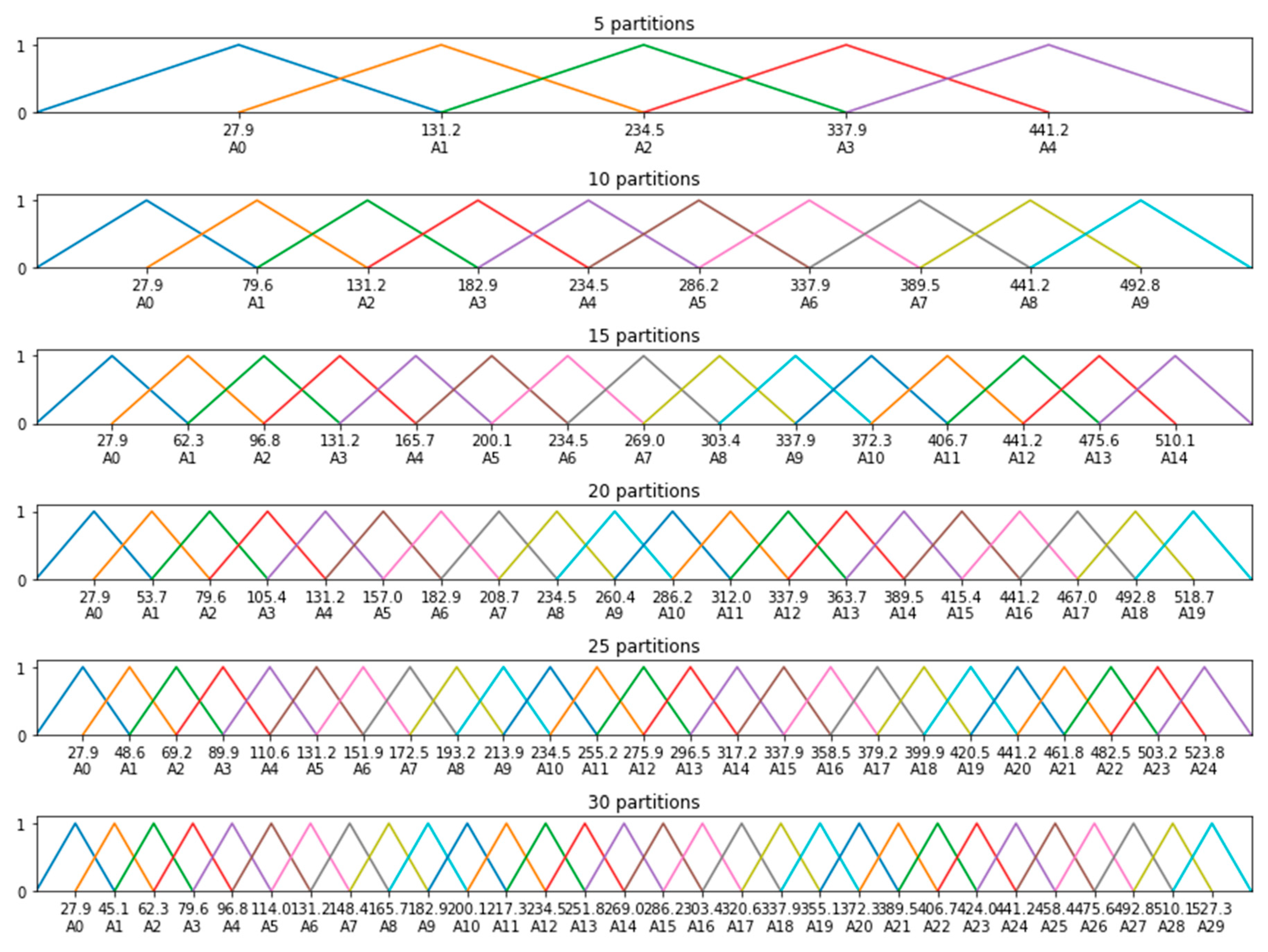
Partitioning
based on different numbers of partitions from 1 to 50. However, to prevent the redundancy where it will be too long, we have only mentioned numbers 5, 10, 15, …, 30 to present the partitioning as shown in
Figure 5.
- Step 3.
Fuzzy sets are defined. Fuzzy sets
are determined based on the intervals
that already have formed using the grid method in the previous step with the function membership. Then, the fuzzy sets
can be written as follows using Equation (2).
Table 1 reveals the fuzzy sets
, (
). The greater the value of
indicates that the fuzzy set of API values will move from the lowest to the highest fuzzy set of API values.
- Step 4.
Transform APIs values into fizzy numbers and find the fuzzy logic relationships (FLRs), as shown in
Table 2.
Table 3 reveals the actual API values that have been transferred to the FTS values. Then, the FLRs of these values are determined. Since
has the maximum membership degree in fuzzy set
, observation 51 is transferred to a fuzzy set
. Similarly, the API values have been fuzzified.
- Step 5.
Fuzzy logical relationships (FLRs) are determined, and frequencies (count) matrix of fuzzy relation between observations are determined. This step shows the FLRGs can be grouped into the fuzzy logic relationship groups (FLRGs).
It can be seen from
Table 4 that thirteen groups of the FTS values are presented, which is found with several FLRs. From
Table 4, transition frequency matrix or frequencies (count) matrix of fuzzy relation between observations can be determined, which could be a matrix
.
- Step 6.
Assign the Markov weights based on the matrix of frequencies from Step 5 by using Equation (4), as shown in
Table 4. Then, transition process diagram could be established using the weights to visualize the Markov weighted Matrix.
Table 5 demonstrates the number of transitions of the FTS and Markov weight elements for each group. The obtained Markov weights using the grid partition method can be used for establishing the transition probability matrix
, which can be used for calculating the forecasting values in the next step. For instance, in the case of FLRG, it is
, 𝐴8. Then, value
and
. Thus,
and
, otherwise
.
- Step 7.
Calculate the forecasted values by using Equation (5) or (6) based on Markov weights. For example, the forecast value for the day (2012/1/2) is calculated by using Equation (6).
- Step 8.
The forecasted values are adjusted by using Equation (7). For example, in Step 7, we have found the forecast value is 56.66.
6. Conclusions
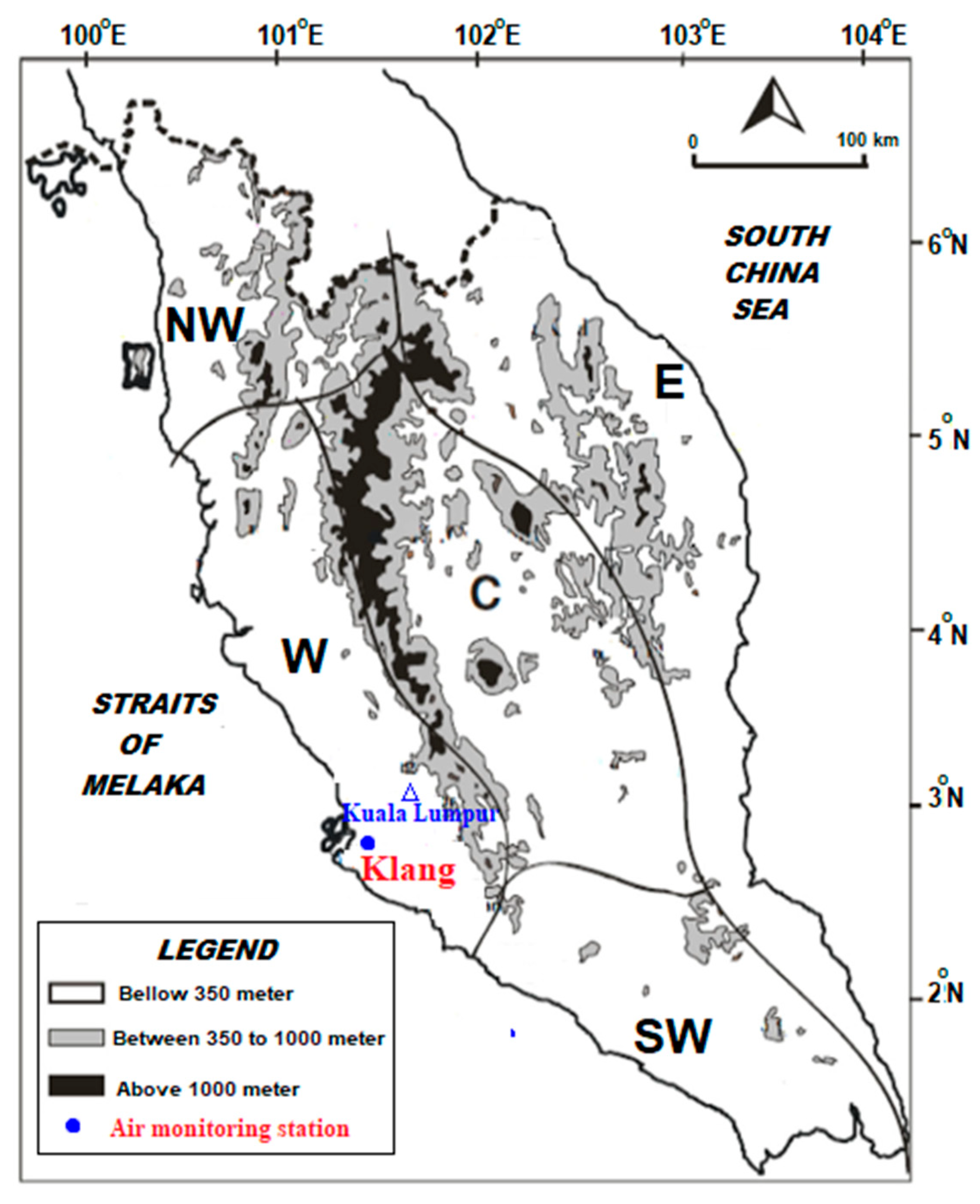
This study proposed the FTSMC model based on the optimal partition number for forecasting the air pollution in Malaysia using daily API data gathered from Klang for a period of three years. In this study, the Markov weights of the fuzzy logical relationships (FLRs) in the FLRG have been calculated based on the Markov transition probability. The grid partition method has been used to determine the optimal partition number of . Then, the evaluation of the proposed model has been performed using a different number of partitions, which is chosen in order to avoid the arbitrary choosing of intervals. This is considered the first study that has ever properly defined the number of partitions in the FTSMC model. Although, the optimal number of partitions could be developing the model performance. In the proposed forecasting method, fitting the optimal number of partitions provided an improvement in the forecasting accuracy. In forecasting the daily API data, it shows that the proposed model has produced a higher prediction accuracy as compared to some FTS models. This indicated that the model could be used for forecasting air pollution data, in addition to various time-series data. For future studies, the proposed model could be performed to provide accurate results of air pollution for the sub-index variables such as PM2.5, PM10, O3, SO2, NO2, and CO, including the weather factors, such as wind speed and temperature, to provide a comprehensive exanimation of the air pollution problem. In addition, the proposed model can be developed by utilizing optimization methods such as Kalman filter, topology method, and Bayesian method, which are recommended to be employed in future works to provide an accurate forecasting model to predict air pollution. Additionally, it can be developed by combining the model with clustering and machine learning techniques in order to improve the model forecasting accuracy.