Abstract
During the last few decades, domination theory has been one of the most active areas of research within graph theory. Currently, there are more than 4400 published papers on domination and related parameters. In the case of total domination, there are over 580 published papers, and 50 of them concern the case of product graphs. However, none of these papers discusses the case of rooted product graphs. Precisely, the present paper covers this gap in the theory. Our goal is to provide closed formulas for the total domination number of rooted product graphs. In particular, we show that there are four possible expressions for the total domination number of a rooted product graph, and we characterize the graphs reaching these expressions.
Let G be a graph. The open neighborhood of a vertex is defined to be . A set is a dominating set of G if for every vertex . Let be the set of dominating sets of G. The domination number of G is defined to be,
A set is a total dominating set, TDS, of a graph G without isolated vertices if every vertex is adjacent to at least one vertex in S. Let be the set of total dominating sets of G.
The total domination number of G is defined to be,
By definition, , so that .
We define a -set as a set with . The same agreement will be assumed for optimal parameters associated with other characteristic sets defined in the paper. For instance, a -set will be a set with .
The theory of domination in graphs has been extensively studied. For instance, there are more than 4400 papers already published on domination and related parameters. In particular, we cite the following books [1,2]. In the case of total domination, there are over 580 published papers and one book [3]. Among these papers on total domination in graphs, there are over 50 which concern the case of product graphs. Surprisingly, none of these papers discusses the case of rooted product graphs. The present paper covers that gap in the theory.
In order to present our results, we need to introduce some additional notation and terminology. The closed neighborhood of is defined to be . A vertex is universal if , while it is a leaf if . The set of leaves of G will be denoted by . A support vertex is a vertex v with . The set of support vertices of G will be denoted by . If v is a vertex of a graph G, then the vertex-deletion subgraph is the subgraph of G induced by . By analogy, we define the subgraph for an arbitrary subset
The concept of rooted product graph was introduced in 1978 by Godsil and McKay [4]. Given a graph G of order and a graph H with root vertex v, the rooted product graph is defined as the graph obtained from G and H by taking one copy of G and copies of H and identifying the vertex of G with the root vertex v in the copy of H for every . If H or G is a trivial graph, then is equal to G or H, respectively. In this sense, hereafter we will only consider graphs G and H with no isolated vertex.
Figure 1 shows an example of a rooted product graph. In this case, the set of black-coloured vertices forms a TDS of and
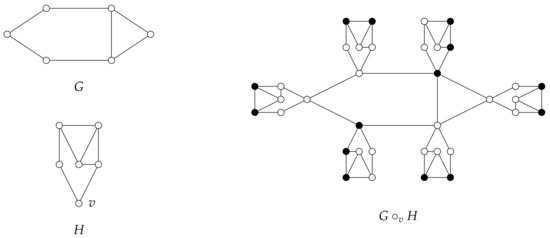
Figure 1.
The set of black-coloured vertices forms a -set.
For every , will denote the copy of H in containing x. The restriction of any set to will be denoted by , and the restriction to will be denoted by ; i.e., and . In some cases, we will need to define from the sets as .
Since , we have that for every set ,
A basic problem in the study of product graphs consists of finding closed formulas or sharp bounds for specific invariants of the product of two graphs and expressing these in terms of parameters of the graphs involved in the product. In this sense, for recent results on rooted product graphs, we cite the following works [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. As we can expect, the products of graphs are not alien to applications in other fields. In particular, in [5] the authors show that several important classes of chemical graphs can be expressed as rooted product graphs, and as described in [20], there exist a number of molecular graphs of high-tech interest that can be generated using the rooted product of graphs.
1. Closed Formulas for the Total Domination Number
The following three lemmas will be the main tools to deduce our results.
Lemma 1.
Given a graph H with no isolated vertex and any , the following statements hold.
- (i)
- (ii)
- If then the following statements hold.
- (a)
- for every -set S.
- (b)
- There exists a -set S such that .
- (iii)
- If , then for every -set S.
Proof.
Let and S a -set. For every we have that is a TDS of H, which implies that . Therefore, (i) follows.
Now, in order to prove (ii), we assume that . If there exists a vertex , then S is also a TDS of H, which is a contradiction. Therefore, and so (a) follows. In addition, for any , the set is a -set not containing v. Therefore, (b) also follows.
Finally, we proceed to prove (iii). If there exists a -set D such that , then D is also a TDS of , and so . Therefore, we conclude that if , then for every -set D, which completes the proof. □
Lemma 2.
Let H be a graph and . If v is not a universal vertex and does not have isolated vertices, then
Furthermore, if , then
Proof.
Assume that v is not a universal vertex and does not have isolated vertices. Let S be a -set and . Since is a TDS of H, we have that , as required.
Now, assume . In this case, by Lemma 1 (ii) we have that for every -set D, which implies that D is a TDS of , and so . Therefore, the result follows. □
Lemma 3.
Given a -set S and a vertex , the following statements hold.
- (i)
- (ii)
- If , then .
Proof.
Let . Notice that every vertex in is adjacent to some vertex in . For any , the set is a TDS of , and so . Therefore, (i) follows.
Finally, assume that . If there exists a vertex , then is a TDS of , which is a contradiction. Therefore, , and so (ii) follows. □
Given a -set S, we define the following subsets of associated with S.
These sets will play an important role in the inference results. By Lemma 3, . In particular, if , then , and as we will show in the proof of Theorem 2, if , then . As we can expect, these are the extreme values of .
Theorem 1.
For any graphs G and H with no isolated vertex and any ,
Furthermore, if , then
Proof.
The lower bound follows from Lemma 3, as for any -set S,
Now, we proceed to prove the upper bound. Let such that is a -set for every . It is readily seen that D is a TDS of . Hence,
From now on, assume . Notice that, by assumption, does not have isolated vertices.
Let such that is a -set for every and is a -set. Clearly, W is a TDS of , which implies that
Therefore, the result follows. □
The following lemma is another important tool for determining all possible values of .
Lemma 4.
Given a -set S with , the following statements hold.
- (i)
- If , then
- (ii)
- If , then , and as a consequence,
Proof.
First, we proceed to prove (i). Given a fixed , let such that for every the set is induced by . Obviously, D is a TDS of . Hence, Therefore, Theorem 1 leads to
In order to prove (ii), assume that , and let . By Lemma 3 we have that . So, and is a TDS of . Hence, , and so Lemma 1 leads to . Therefore, by Theorem 1 we have that .
Moreover, since for every , we have that is a dominating set of G. Hence,
Therefore, the result follows. □
Next we give one of the main results of this section, which states the four possible values of .
Theorem 2.
Let G and H be two graphs with no isolated vertex. For any ,
Proof.
Let S be a -set and consider the subsets associated with S. We distinguish the following cases.
Case 1. . In this case, for any we have that , and as a consequence, . Thus, Theorem 1 leads to the equality .
Case 2. . If , then from Lemma 4 (i) we have that .
From now on we assume that . Hence, Lemma 4 (ii) leads to
We only need to prove that only can take the extreme values. To this end, we shall need to introduce the following notation. Let and .
Subcase 2.1. There exists such that is a -set containing . From a fixed vertex and any -set D, we can construct a set as follows. If , then is induced by , while if , then is induced by . Notice that W is a TDS of , which implies that . Therefore, .
Subcase 2.2. or for any , either is not a -set or . If , then every vertex satisfies one of the following conditions.
- (a)
- is a -set such that .
- (b)
- is not a TDS of and .
Notice that we do not consider the case where is not a TDS of and , as in this case we can replace S with the -set for some -set . In such a case, if , then we proceed as in Subcase 2.1, while if , then x satisfies (a).
Let us construct a TDS X of G as follows.
- -
- .
- -
- For any which satisfies condition (a) and , we choose one vertex and set .
- -
- For any with , we choose one vertex and set .
We proceed to show that X is a TDS of G. If , then either or . If , then , which implies that . Obviously, if , then , by definition of X. Now, let . If , then by definition. If , then x satisfies condition (b). This implies that . Hence, there exists a vertex , as desired.
Therefore, X is a TDS of G, which implies that . Thus,
which completes the proof. □
Later on, we will characterize the graphs that reach each of the previous expressions. However, we have to admit that when applying some of these characterizations we will need to calculate the total domination number of or which may not be easy. Before giving the above mentioned characterizations, we shall show a simple example in which we can observe that these expressions of are realizable.
Example 1.
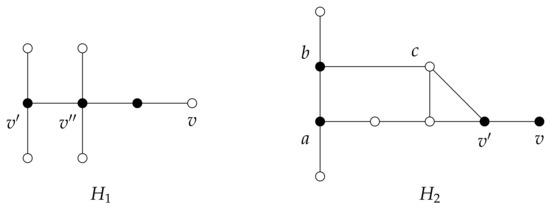
Let G be a graph with no isolated vertex. If H is one of the graphs shown in Figure 2, then the resulting values of for some specific roots are described below.

Figure 2.
The set of black-coloured vertices forms a -set for . The set forms a -set, while forms a -set.
For these cases, it is not difficult to construct a -set. For instance, a -set S can be formed as follows. Given a fixed -set X, we take S in such a way that the set is induced by for every , and induced by for every .
As we have observed in Lemma 2, if is not a universal vertex and does not have isolated vertices, then . Next we show that the extreme case characterizes the graphs with .
Theorem 3.
Given two graphs G and H with no isolated vertex and , the following statements are equivalent.
- (i)
- (ii)
- v is a universal vertex of H or
Proof.
First, assume that (i) holds. Let S be a -set. If v is a universal vertex of H, then we are done. Assume that is not a universal vertex. In this case, Lemma 3 leads to and for every . Thus, is a dominating set of G and for any we have that does not have isolated vertices and is a TDS of , which implies that Hence, Lemma 2 leads to Therefore, (ii) follows.
Conversely, assume that (ii) holds. If v is a universal vertex of H, then is a TDS of , which implies that . Thus, by Theorem 1 we conclude that .
From now on, we assume that v is not a universal vertex. For any , let be a -set and . Observe that is a TDS of , which implies that . By Theorem 1 we conclude that , which completes the proof. □
Lemma 5.
Let G and H be two graphs with no isolated vertex and . If , then
Proof.
By Theorem 1 we have that . Let S be a -set. If , then we are done. Suppose that . Hence, there exists such that , which implies that by Lemma 3. Since , Lemma 4 (ii) leads to , and by Lemma 4 (i) we deduce that . □
Lemma 6.
Let G and H be two graphs with no isolated vertex and . If v belongs to every -set, then
Proof.
We first consider the case where . By Lemma 1 we deduce that , and so Lemma 5 leads to the result. Now, assume that and let S be a -set. If , then we are done. Thus, we assume that . In such a case, there exists , and since , it follows that . Therefore, , and by Lemma 4 (i) we deduce that , which completes the proof. □
We are now ready to characterize the graphs with
Theorem 4.
Let G and H be two graphs with no isolated vertex and . The following statements are equivalent.
- (i)
- (ii)
- , and in addition, or there exists a -set D such that .
Proof.
First, assume that (i) holds. Since , by Lemma 6, , so that from Lemma 5 we deduce that and Lemma 1 leads to . Hence, by Lemma 2 it follows that and by Theorem 3 we obtain that .
Now, let S be a -set. Since , Lemma 3 leads to and . Additionally, by Lemma 4 we deduce that , and by Lemma 3 we have that for every . Hence, is a dominating set of G and . Thus, , which implies that is a -set and for every we have that . Therefore, there exists such that is a -set or is a -set, which implies that (ii) holds.
Conversely, assume that (ii) holds. As above, let S be a -set. Since , by Theorem 1,
Suppose that . In such a case, , which implies that , and so . Let be the bipartition of the vertex set of G, i.e., every edge has one endpoint in A and the other one in B. Thus, for every we define a subset as follows. If , then is a -set which contains x, while if , then is a -set. Hence, is a TDS of and so , which is a contradiction. From now on we assume that .
If there exists a vertex , then by Lemma 3 we have that , which implies that is a TDS of . Hence, , which is a contradiction with the assumption . Therefore, , and by Lemma 4 we deduce that
It is still necessary to prove that If , then we are done. Assume . Now we take a -set X and for every we define a set as follows. If , then is a -set such that , while if , then is a -set. Notice that is a TDS of . Therefore, as required. □
Next we proceed to characterize the graphs with Notice that it is excluded the case . In such a case, , and so , which implies that the characterization of this particular case can be derived by elimination from Theorems 3 and 4. Analogously, the case is excluded, as it was discusses in Theorem 4.
Theorem 5.
Let and H be two graphs with no isolated vertex such that , and let . The following statements are equivalent.
- (i)
- (ii)
- and for every -set D.
Proof.
First, assume that (i) holds. Since, , we have that . Thus, by Lemma 6, and then by Lemma 5 we deduce that and Lemma 1 leads to .
Suppose that there exists a -set containing v. Let X be a -set. For every we define a set as follows. If , then is a -set such that , while if , then is a -set. Notice that is a TDS of . Therefore, which is a contradiction, as . Therefore, for every -set D, which implies that (ii) follows.
Conversely, assume that (ii) holds. Since , by Theorem 1 we have that Let S be a -set. If , then , and so , which is a contradiction, as . Hence, from now on we assume that .
If there exists a vertex , then for any vertex , the set is a -set, which is a contradiction. Thus, , and so by Lemma 3, is a dominating set of G. Moreover, by Lemma 4 and Theorem 2 we deduce that either or . Now, let where if and . Let such that and for every . Obviously, is a total dominating set of G, and so Therefore, the result follows. □
From Theorem 2 we learned that there are four possible expressions for . In the case of the first three expressions, the graphs (and the root) reaching the equality were characterized in Theorems 3–5. In the case of the expression , the corresponding characterization can be derived by elimination from the previous results, although it must be recognized that the formulation of such a characterization is somewhat cumbersome. To conclude this section, we will just give a couple of examples where this expression is obtained.
The following result shows an example where , which covers the cases in which v is a neighbor of a support vertex, excluding the case where v is the only leaf adjacent to its support.
Proposition 1.
Let G and H be two graphs with no isolated vertex and . If there exists such that , then
Proof.
Assume first that . Let D be a -set. Since , we have that . Hence, D is a TDS of H, and so . Therefore, Lemma 5 leads to or Now, suppose that Let S be a -set. By Lemma 3, and for every , which is a contradiction, as and . Therefore, .
Now, if , then . Hence, for every -set S and every vertex , we have that is a TDS of . Thus, , which implies that , as required. □
We next consider another example where
Proposition 2.
Let G and H be two graphs with no isolated vertex and . If and v does not belong to any -set, then
Proof.
If , then by Lemma 5 we have that or Now, assume that v does not belong to any -set. If , then . Hence, by Lemma 4 (ii) there exists , which is a contradiction as from any the set is a -set containing x. Therefore, . □
2. An Observation on the Domination Number
It was shown in [15] that there are two possibilities for the domination number of a rooted product graph. Since the graphs reaching these expressions have not been characterized, we consider that it is appropriate to derive a result in this direction. Specifically, we will provide a characterization in Theorem 7.
Theorem 6.
[15] For any nontrivial graphs G and H and any ,
In order to derive our result, we need to introduce the following two lemmas.
Lemma 7.
[21] Let H be a graph. For any vertex ,
Lemma 8.
For any -set D and any vertex ,
Furthermore, if , then .
Proof.
Let . Notice that every vertex in is adjacent to some vertex in . Since is a dominating set of , we have that , as required.
Now, assume that . If , then is a dominating set of , which is a contradiction as . Therefore, the result follows.
Theorem 7.
For any pair of nontrivial graphs G and H, and any ,
Proof.
By Theorem 6 we only need to prove that if and only if .
We first assume . Let such that is a -set for every , and is a -set. It is readily seen that D is a dominating set of , which implies that , and by Theorem 6 we conclude that the equality holds.
Conversely, assume . Let S be a -set. Since , there exists such that . Hence, by Lemma 8, and . This implies that is a dominating set of , and so . By Lemma 7 we conclude that , which completes the proof. □
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Domination in Graphs: Advanced Topics.; Chapman and Hall/CRC Pure and Applied Mathematics Series; Marcel Dekker, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Fundamentals of Domination in Graphs; Chapman and Hall/CRC Pure and Applied Mathematics Series; Marcel Dekker, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Henning, M.; Yeo, A. Total Domination in Graphs. Springer Monographs in Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Godsil, C.D.; McKay, B.D. A new graph product and its spectrum. Bull. Austral. Math. Soc. 1978, 18, 21–28. [Google Scholar] [CrossRef]
- Azari, M.; Iranmanesh, A. Chemical Graphs Constructed from Rooted Product and Their Zagreb Indices. MATCH Commun. Math. Comput. Chem. 2013, 70, 901–919. [Google Scholar]
- Cabrera Martínez, A. Double outer-independent domination number of graphs. Quaest. Math. 2020. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Cabrera García, S.; Carrión García, A.; Hernández Mira, F.A. Total Roman domination number of rooted product graphs. Mathematics 2020, 8, 1850. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Cabrera García, S.; Carrión García, A.; Grisales del Rio, A.M. On the outer-independent Roman domination in graphs. Symmetry 2020, 12, 1846. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Estrada-Moreno, A.; Rodríguez-Velázquez, J.A. Secure total domination in rooted product graphs. Mathematics 2020, 8, 600. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Montejano, L.P.; Rodríguez-Velázquez, J.A. Total weak Roman domination in graphs. Symmetry 2019, 11, 831. [Google Scholar] [CrossRef]
- Chris Monica, M.; Santhakumar, S. Partition dimension of rooted product graphs. Discrete Appl. Math. 2019, 262, 138–147. [Google Scholar] [CrossRef]
- Hernández-Ortiz, R.; Montejano, L.P.; Rodríguez-Velázquez, J.A. Italian domination in rooted product graphs. Bull. Malays. Math. Sci. Soc. 2020. [Google Scholar] [CrossRef]
- Hernández-Ortiz, R.; Montejano, L.P.; Rodríguez-Velázquez, J.A. Secure domination in rooted product graphs. J. Comb. Optim. to appear.
- Klavžar, S.; Yero, I.G. The general position problem and strong resolving graphs. Open Math. 2019, 17, 1126–1135. [Google Scholar] [CrossRef]
- Kuziak, D.; Lemanska, M.; Yero, I.G. Domination-Related parameters in rooted product graphs. Bull. Malays. Math. Sci. Soc. 2019, 39, 199–217. [Google Scholar] [CrossRef]
- Kuziak, D.; Yero, I.G.; Rodríguez-Velázquez, J.A. Strong metric dimension of rooted product graphs. Int. J. Comput. Math. 2016, 93, 1265–1280. [Google Scholar] [CrossRef]
- Jakovac, M. The k-path vertex cover of rooted product graphs. Discrete Appl. Math. 2015, 187, 111–119. [Google Scholar] [CrossRef]
- Lou, Z.; Huang, Q.; Huang, X. On the construction of Q-controllable graphs. Electron. J. Linear Algebra 2017, 32, 365–379. [Google Scholar] [CrossRef]
- Yang, Y.; Klein, D.J. Resistance distances in composite graphs. J. Phys. A 2014, 47, 375203. [Google Scholar] [CrossRef]
- Farrell, E.J.; Rosenfeld, V.R. Block and articulation node polynomials of the generalized rooted product of graphs. J. Math. Sci. India 2000, 11, 35–47. [Google Scholar]
- Sampathkumar, E.; Neeralagi, P.S. Domination and neighbourhood critical, fixed, free and totally free points. Sankhya 1992, 54, 403–407. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).