Abstract
Reliable information on transition matrix elements of various property operators between molecular electronic states is of crucial importance for predicting spectroscopic, electric, magnetic and radiative properties of molecules. The finite-field technique is a simple and rather accurate tool for evaluating transition matrix elements of first-order properties in the frames of the Fock space relativistic coupled cluster approach. We formulate and discuss the extension of this technique to the case of transitions between the electronic states associated with different sectors of the Fock space. Pilot applications to the evaluation of transition dipole moments between the closed-shell-like states (vacuum sector) and those dominated by single excitations of the Fermi vacuum (the sector) in heavy atoms (Xe and Hg) and simple molecules of heavy element compounds (I and TlF) are reported.
1. Introduction
In recent years, there has been a marked increase of interest in highly accurate theoretical data on excited electronic states and electronic transitions in molecules of heavy element compounds. Such data are of key importance for ultra-low temperature physics [1,2,3,4], searches for violation of time-reversal and spatial-parity symmetries of fundamental interactions in low-energy spectroscopic experiments [5] and high-resolution spectroscopy of short-lived radioactive atoms and molecules [6]. The preparation of experimental studies and interpretation of their results require detailed knowledge of energetic, electric, magnetic, radiative and other molecular properties. Besides the information on pure electronic state properties, transition property values, i.e., matrix elements of property operators between the electronic state wavefunctions, is necessary to predict the excited-state dynamics.
The Fock space version of the relativistic coupled cluster method (FS RCC) is one of the most powerful tools of electronic structure modelling for heavy element compounds, widely used for obtaining accurate and reliable information on excited state potential energy surfaces and transition energies in molecules [7,8,9,10]. The prediction of expectation and transition values of various property operators within the FS RCC framework is usually a more complicated task than energy spectra calculations. Due to the exponential form of the wave operators, the expressions for property matrix elements between the FS CC wavefunctions in terms of cluster amplitudes and model eigenvectors have the form of (quasi-) nonterminating series. Truncating these series, one arrives at computational schemes which had been successfully applied to ab initio calculations of transition probabilities in small systems (see, e.g., [11,12,13] and references therein). The simplest scheme of this kind includes abandoning of all the amplitude-dependent terms, and estimating the required property matrix elements between the FS (R)CC wavefunctions by the transition amplitudes between the corresponding model space functions (e.g., left and right eigenvectors of the effective Hamiltonian) [14,15]. This scheme describes properly indirect influence of the couplings between the model space and its orthogonal complement (usually referred to as outer space manifold) on the transition property values. The latter circumstance is of a critical importance for the qualitatively correct description of transition properties in presence of weakly avoided crossings. At the same time, the accuracy of this approach remains limited due to the complete neglect of outer-space contributions to effective property operators.
Apparently the most universal and rigorous approach to evaluating transition matrix elements of first-order properties [16,17,18,19] is based on the use of the constrained-variational technique of Jørgensen et al. [20]. This approach implies solving the so-called equations for each pair of states generated in a single FS CC calculation and leads to rather involved computations; to our knowledge, until now it has only limited implementation within the non-relativistic FS CC framework (for a recent review, see [21]).
A practical solution of the problem might consist in combining the potential surfaces, constructed using multireference coupled cluster methods, with the transition property surfaces obtained within the multireference configuration interaction (MRCI) schemes (see, e.g., [22]). Although the accuracy of MRCI estimates of some transition properties (in particular, transition dipoles) is generally sufficient for practical purposes, mismatches of avoided crossings and/or conical intersection’s positions in MRCI and coupled cluster calculations can give rise to serious distortion of corresponding matrix elements between vibronic states. Another serious problem can arise from typically large number of electrons and shells which should be explicitly included into the correlation treatment for heavy element compounds, since the MRCI method is not size-consistent.
The expectation values of numerous important properties can be straightforwardly determined via using the finite-field technique, i.e., by numerical differentiation of the calculated energies with respect to the amplitude of appropriate perturbation (see [23,24,25,26,27] for recent applications). The extension of this approach to evaluating the transition matrix elements of first-order property operators proposed in [28,29] is based on the analysis of variations of the effective Hamiltonian eigenvectors induced by appropriate external field. Although no explicit information on the composition of the wavefunctions outside of the model space is used, the resulting transition matrix element estimates implicitly include the leading contributions from couplings between the model space and the outer space manifolds to the effective property operator [28] (see also Appendix A), thus generally having a significantly better accuracy than those obtained as property matrix elements between effective Hamiltonian eigenvectors. Note, however, that, in contrast to the finite-field coupled-cluster method for expectation values, its counterpart for off-diagonal matrix elements does not ensure the convergency of the results to exact values with appropriate extension of FS (R)CC computational scheme (inclusion of higher excitations in the cluster operator, approaching the complete basis set limit, etc.). The transition matrix elements are determined simultaneously for all pairs of states obtained in FS (R)CC effective Hamiltonian calculations. Applications of the finite-field technique to atomic and molecular relativistic calculations of transition probabilities and off-diagonal magnetic hyperfine interactions were described by the authors of [4,29,30,31] and the authors of [32,33], respectively.
Up to now, the applications of the finite-field technique were restricted to the cases of single Fock space sector and complete model spaces. If the model spaces are incomplete and the model states belong to the same Hilbert space but to different Fock space sectors, the straightforward use of the finite-field procedure in its present form [29] would always lead to unphysical zero values of the corresponding off-diagonal matrix elements. In the present paper, we describe the extension of the technique to the complicated cases mentioned above, focusing on the calculations of transition matrix elements between the closed-shell-like ground state and excited states dominated by single excitations (–-type transitions). Pilot applications to transition dipole moment calculations in heavy atoms and diatomic molecules of heavy element compounds are reported.
2. Theory
Consider a first-order property operator D defining the dependence of the total many-electron Hamiltonian H on some external field strength parameter F, . Let us choose a field-independent model space as the linear span of several Slater determinants and denote the projectors onto and its orthogonal complement by P and Q, respectively. Within the FS RCC approach, the field-dependent many-electron problem is solved through constructing the wave operator and the effective Hamiltonian . The diagonalizaition of operating within ,
yields low-lying (target) eigenvalues , of the total Hamiltonian H, whereas the wave operator should reconstruct the target eigenfunctions of the total Hamiltonian from the corresponding eigenvectors of (model eigenstates), . The wave operator is assumed to be a single normal-ordered exponential of a cluster operator T (linear combination of excitation operators, usually classified according to their total ranks k and the numbers of annihilated holes and particles ):
Naturally, both and depend on the parameter F.
If is a complete model space, i.e., it is spanned by all possible distributions of a certain number of particles between active spinors, one can adopt the intermediate normalization of the wave operator,
(in other words, and T are open operators). In this case, the effective Hamiltonian eigenfunctions are simply the model space projections of the full wavefunctions, , and is non-Hermitian. We suppose that are normalized, so that the norms of the full Hamiltonian eigenvectors exceed 1.
It is convenient to express the transition property matrix elements
in terms of the eigenvectors of and the effective property operator . We adopt the following definition of [34]:
where is the “left” counterpart of the wave operator ,
( denotes the orthogonal projector onto the subspace spanned by the target eigenfunctions of H and the inversion is restricted to the model space). The matrix elements (4) are related to those of the effective operator (5) by [34]:
Here, are the left eigenfunctions of , biorthonormalized to its right eigenfunctions, .
The derivative of the effective Hamiltonian with respect to the parameter F does not coincide with the effective property operator [28]:
Rewriting Equation (8) in terms of matrix elements as
one can notice that the additional term vanishes for the diagonal matrix elements but survives for the off-diagonal ones. However, a simple perturbation theory analysis [28] demonstrates that the approximation of by the effective Hamiltonian derivative incorporates the leading contributions from the couplings to the orthogonal complement of . Combined with the off-diagonal Hellmann–Feynman theorem [35] for the effective Hamiltonian, this approximation yields
The finite-field technique is based on estimating the derivative matrix element in the rhs of (10) within the central finite-difference approximation, evaluating and diagonalizing the effective Hamiltonians and for two small finite values of the field strength parameter:
Absolute values of transition matrix elements can be immediately obtained from Equations (7) and (11):
for all pairs of target states simultaneously.
It is worth underlining that the choice of the wave operator normalization is essential for the reliability of the basic approximation (10). If the condition (3) is fulfilled for any value of field strength parameter, has no closed component. Taking into account the exponential form of and Equation (6), one can represent the operator determining the error of our basic approximation (see Equation (9)) by the series
and notice that in the case of intermediate normalization the first term (which can be large even in the case when all amplitudes for are small) vanishes.
The situation with incomplete model spaces and transitions between the states associated with different Fock space sectors seems to be more complicated. For the sake of simplicity, let us focus on the case of transitions from the closed-shell like state to those dominated by the creation of single hole-particle pairs and described within the valence-universal FS (R)CC approach for the sector; the generalization to other cases of “intersector” transitions is straightforward. The model space should include the vacuum closed-shell state and the subspace spanned by all possible combinations of one active hole and one active particle; the corresponding projectors are denoted by and ,
The conventional valence-universal FS (R)CC formulation supposes that the sector [7,36] is fully decoupled from the vacuum sector,
so that the model wavefunctions and for the ground state i and an excited state j are strictly orthogonal for any field strengths F and and the finite-field estimate of transition property matrix elements within seems to be senseless. Note that the intermediate normalization of is incompatible with the connectivity of the effective Hamiltonian for incomplete model spaces [37,38]. Two types of cluster components contributing to are usually introduced: single excitations creating an active hole and an active particle, (Figure 1a), and single de-excitations destructing such pairs, (Figure 1b). The model-space part of the wave operator
(see Figure 1) explicitly contains the terms linearly and quadratically dependent on cluster amplitudes.
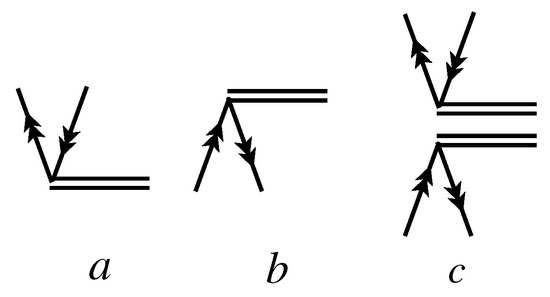
Figure 1.
Goldstone diagrams representing components of the wave operator contributing to . Double arrows correspond to active holes/particles, while double horizontal lines denote cluster amplitudes.
Let us perform a posteriori transformation of the effective Hamiltonian (15),
corresponding to the restoration of the intermediate normalization of the wave operator,
(cf. [39]). Taking into account Equation (16) and the normalized exponential form of the original wave operator, one readily realizes that
where is the purely open () part of the cluster operator and stands for the sum of terms of second and higher orders in cluster amplitudes. In a strict analogy to Equation (13), the first term in the similar expansion of should disappear. One can thus expect that the model-space finite-field transition property estimates obtained according to Equations (11) and (12) with the eigenfunctions of the transformed Hamiltonian are generally as accurate as in the case of transitions within a single sector.
The computational efforts for transforming the effective Hamiltonian (or its eigenvectors) are negligible since the number of amplitudes required for constructing is small. Although in the case of the scalar property operator the CC equations are to be solved at least twice, for and , the choice of a common (field-independent) set of one-electron spinors enables one to avoid the doubling of the amount of computations at least for one-electron properties, using the same transformed and sorted two-body integrals and other intermediate data in both calculations. Furthermore, due to the smallness of the step size , the amplitudes obtained with one field strength value provide an excellent initial guess for computing the amplitudes for another field strength, reducing dramatically the number of iterations. Unfortunately, the substantial increase of computational work is unavoidable when the applied field lowers the symmetry of the system under study.
Let us notice finally that the simplest finite-field scheme does not make use of the information concerning the dependence of the cluster amplitudes on F which can be readily extracted from the results of calculations. Obviously, one could employ this information to estimate the derivative in the rejected term in the rhs of Equation (9) and to evaluate approximately this term, truncating in some way the expansions in powers of the cluster operator.
3. Pilot Applications to Transition Dipole Moment Calculations
In this section, we apply the finite-field FS RCC scheme to evaluate transition dipole moments in heavy atoms (Xe, Hg) and molecules containing heavy atoms (, TlF). The calculations described below employed the accurate relativistic shape-consistent semilocal pseudopotential model [40,41,42] for heavy atoms; the inner core shells with principal quantum numbers 1–3 for fifth-row atoms and 1–4 for sixth-row atoms were excluded from the explicit treatment. The light fluorine atom was treated in the nonrelativistic all-electron manner. The cluster operator expansions were always restricted to single and double excitations (FS RCCSD). One-electron spinors were generated by solving the two- or four-component spin–orbit-coupled SCF equations. The component of spinors were expanded in contracted Gaussian basis sets. All explicitly treated electrons were correlated. The valence-universal approach to constructing the effective Hamiltonian for the sector for the neutral systems with zero or small electron affinities gives rise to certain difficulties in choosing the set of active “particle” spinors. Normally one faces a rather objectionable choice between problematically large amplitudes of if the active particle spinors are compact (e.g., taken from the solutions of the SCF problem for a positive ion) and large amplitudes when these spinors are diffuse (obtained as virtual SCF spinors for the neutral system). We bypassed this difficulty via choosing quite large sets of active particle spinors and using the adjustable denominator shift technique [43] to suppress the possible divergencies in the presence of intruder states (more specifically, we employed the simulated imaginary shifts [32]). To conserve the core separability of the original FS RCC scheme, shifts were never applied to the energy denominators in the equations for amplitudes; a balanced treatment of excitation and deexcitation contributions to implied the use of non-shifted equations for amplitudes as well. Shift amplitudes ( in Equation (8) of [32]) were always defined by a single parameter , universal denominator shift amplitude for all double excitations in the , and sectors; for single excitations in the and sectors, we used . The shift attenuation parameter (m in Equation (8) of [32]) was assumed equal to 3.
The construction of spinors and evaluation of one- and two-electron integrals was performed using the DIRAC19 program package [15,44], whereas all FS RCC calculations were carried out with the help of the EXP-T code [45,46,47]. The VIBROT code [48] was used to solve the vibrational problem and compute the excited-state lifetime of TlF.
3.1. Transition Dipoles for Excitations of Closed-Shell Atoms
Experimental-based estimates of transition dipole moments in heavy-element-containing species accurate to about 1% and better are generally available only for atoms and atomic ions. Reliable estimates of transition dipole moments for several transitions in atomic Xe and Hg (Table 1 and Table 2) were obtained from Einstein coefficients from Sansonetti and Martin [49]. Our FS RCC calculations for Xe employed the adaptation of the aug-cc-pVQZ-PP basis of Peterson et al. [50,51] to the pseudopotential [42], augmented by the -like functions to improve the description of spin-orbit splittings, core-valence correlation functions from aug-cc-pwCVTZ-PP set [52] and additional diffuse functions in order to better reproduce the Rydberg nature of the excited states. The total basis size was [] (see Supplementary Materials for details). The one-electron spinors were obtained by solving the SCF equation for the ground-state configuration of the neutral atom () or positive ion (); the corresponding results are marked in Table 1 by the symbols (Xe) or (Xe). Three pairs of highest-energy spinors occupied in the neutral Xe and 43 pairs of lowest-energy unoccupied spinors were considered as active. Rather small shift amplitudes ( a.u.) were found to be sufficient to ensure the numerical stability of solving the FS RCC equations.

Table 1.
Transition dipole moments (a.u.) for excitations from the ground state of the Xe atom according to the finite-field FS RCC calculations () and the corresponding dipole matrix elements between the model space vectors ().

Table 2.
Transition dipole moments (a.u.) for excitations from the ground state of the Hg atom according to the finite-field FS RCC calculations () and the corresponding dipole matrix elements between the model space vectors ().
The resulting finite-field transition dipole moment estimates along with the experimental-based values and matrix elements of the dipole operator between the FS RCC model states, , are listed in Table 1. The deviation of from the empirical values never exceeds 0.04 a.u.; for intensive transitions, the error is within 4 %. It is worth noting that only slightly depend on the choice of one-electron spinors (which, in turn, defines the model space). The dipole matrix elements between the eigenvectors, despite their strong dependence on this choice, can be considered as less accurate but rather reasonable preliminary estimates of the transition dipole moments.
Similar calculations were carried out for the Hg atom. The employed primitive Gaussian basis set [] was essentially an uncontracted version of the augmented quadruple zeta basis [53] adapted to the use with the shape-consistent pseudopotential [42]. We performed two series of calculations with one-electron spinors taken from the neutral atom (configuration ) or positive ion () SCF problem. Six Kramers pairs of highest occupied spinors and 31 pairs of lowest unoccupied spinors spanned active-hole and active-particle subspaces, respectively. The same shift amplitudes as in the case of the xenon atom were used. The results compared to the experimental values are listed in Table 2.
The finite-field scheme underestimates the transition moment by 16% and the transition moment by 11%. This level of accuracy is actually close to that reported in [29] for the finite-field calculations within the sector. It might be worth noting that the difference between the finite-field estimates of and according to Equation (11) were quite large (up to 20 %). This can be presumably attributed to significant differences in the norms of the ground-state and excited-state wavefunctions outside of the model space (see Equation (7)), in other words, to a non-balanced description of these states within the chosen model space. The results are stable with respect to further extensions of active spinor subspaces. A possible way of improving the estimates in such cases might consist in accounting for the dependence of the wave operator on the external field strength Equation (9). Similarly to the case of Xe, the values for Hg exhibit only a very weak dependence on the choice of the SCF problem for generating one-electron spinors.
3.2. Transition Dipole Moment Functions in and
Optical transitions in the iodine molecule are among the most studied molecular electronic transitions in heavy element compounds (see [54] for a recent review). The rather intensive transition is of particular interest for testing relativistic transition dipole calculation techniques since it corresponds to the forbidden singlet-triplet () excitation at the non-relativistic (or scalar relativistic) limit. The empirical dependence of the transition dipole moment on the internuclear separation derived from a large amount of experimental data by Tellinghuisen [55] is expected to be accurate within a few percent at least in the vicinity of the ground-state equilibrium point. Our calculations were performed using the [] basis set for iodine constructed in the same way as for Xe, except for the absence of Rydberg-like functions which are not needed to describe the valence-like states under study. The active space comprised five Kramers pairs of occupied spinors and 17 pairs of virtual spinors. The shift amplitude values corresponded to a.u.
The finite-field FS RCC transition dipole moment curve (Figure 2) exhibits a good agreement with its empirical counterpart for moderate internuclear separations where the single-reference treatment of the ground state remains reasonable, i.e., approximately for Å. At larger R, an unusually rapid increase of amplitudes of double excitations in the vacuum sector (first of all, -like ones), see the dotted curve in Figure 2, gradually lowers the efficiency of the single-reference description of the ground state. The deviation of values from their empirical counterparts in the vicinity of the ground-state equilibrium point is about 4%. Except for the domain of large R, our results also agree with those of quasirelativistic many-body multipartitioning perturbation theory calculations [56] which ensured equal-footing and inherently multireference treatment of both states involved. In contrast with the atomic cases, the quality of transition dipole estimates by the dipole matrix elements between the model space vectors seems fully unacceptable for benchmark calculations.
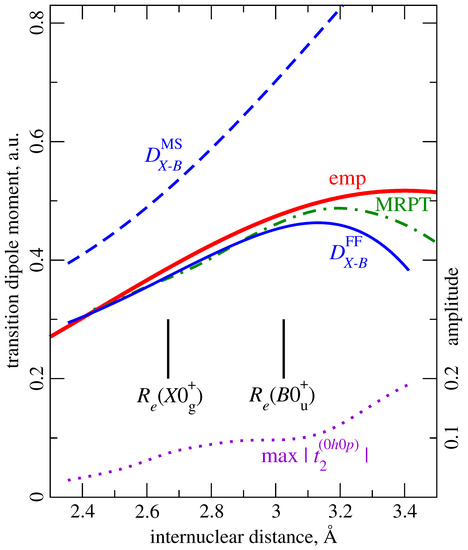
Figure 2.
transition dipole moment function of the molecule: bold red line, empirical function from Tellinghuisen [55]; solid and dashed blue lines: finite-field () and model-state () FS RCC estimates, respectively; green dot-dashed line, quasirelativistic multireference perturbation theory data [56]; dotted violet line, the dependence of the largest amplitude in () on the internuclear separation.
The transition between the ground and second excited (sometimes also referred to as ) states of the thallium monofluoride molecule attracts great attention due to its possible use for laser cooling of TlF, which is considered as a perspective system for searches for “new physics” in tabletop-scale experiments (see [2] and references therein). The lifetime of the lowest vibrational level () of the state, ns, was measured by Hunter et al. [2]. It should be noted that the accuracy of the lifetime measurements in [2] is of an unprecedented level for molecules of heavy element compounds. Due to nearly coinciding equilibrium separations and vibrational frequencies of this state with those of the ground one and the negligible probability of its radiative decay into the first excited state (energy factor of the branching rate is about 10), one can immediately obtain an estimate of the transition dipole at : a.u. The computational study of radiative transitions in TlF was performed recently by Liu et al. [57] using the scalar relativistic multireference configuration interaction method with subsequent incorporation of the direct spin-orbit interactions between low-lying scalar eigenstates (MRCI + SO). The resulting lifetime (85 ns) and the transition dipole moment value at (0.321 a.u.) agree perfectly with their experimental counterparts.
The present calculation used the [] Tl basis set with core-valence-correlation and diffuse functions from Zaitsevskii and Eliav [43] and the standard aug-cc-pVQZ fluorine basis [58,59], the solutions of the ground-state SCF problem as one-electron spinors, the model space defined by 4 pairs of active hole spinors and 16 pairs of active particle spinors, and the same shift parameters as for the I molecule. Our estimate of vertical transition moment (0.297 a.u.) is quite close to both experimental-based and MRCI + SO values. In accordance with the MRCI + SO data [57], as function of the internuclear separation is rather flat near the equilibrium points and becomes decreasing at larger R; the difference between and its MRCI + SO counterpart becomes more significant at short R (see Figure 3). Combining the present transition dipole moment and energy difference function along with the accurate RCCSD(T) ground state potential from Zaitsevskii and Eliav [43], we evaluated the radiative lifetime of according to the Tellinghuisen’s formula [60]. The resulting value, 112 ns, is only slightly longer than the measured one.
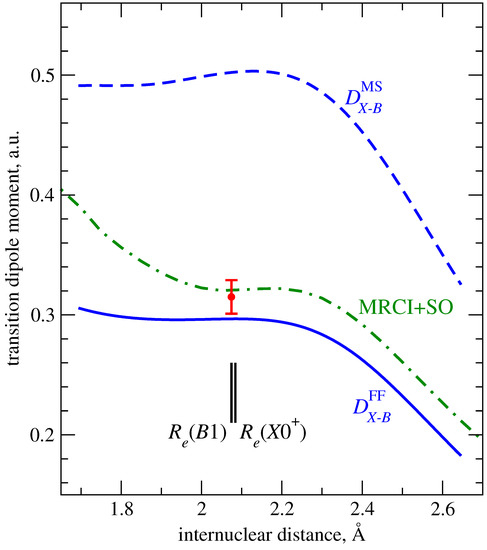
Figure 3.
Transition dipole moment function for the electronic transition in the molecule: red circle, estimate based on the experimental lifetime measurements [2]; solid and dashed blue lines, and functions from the present FS RCC calculations; green dot-dashed line, MRCI + SO calculations [57].
Similar to the case of transition in I, the dipole matrix elements between the model states provide much worse estimates of the transition moment (however, the correct trend is reproduced).
4. Concluding Remarks
The simple finite-field technique of molecular transition property matrix element calculations within the framework of the Fock space relativistic coupled cluster method, deriving the matrix element estimates from the analysis of variations of the model-space projections of electronic eigenstates under the influence of an external field, is extended to the case of transitions between the states associated with different Fock space sectors. In contrast to the case of transitions between the states of the same sector, these projections are not immediately obtained as eigenstates of FS RCC effective Hamiltonian; an additional transformation of these eigenstates is required. The transformation matrix is readily constructed from the cluster amplitudes corresponding to the excitations which are closed with respect to the direct sum of the involved model subspaces of the Fock space. Pilot applications to off-diagonal electric dipole matrix elements for excitations of closed-shell-like ground states in systems containing heavy-element atoms yielded the estimates approximately at the same level of accuracy as for “single-sector” transitions, normally within 10 % for intensive transitions. This level of accuracy is comparable with the experimental one for the molecular measurements. The reliability of results is clearly superior to that achieved in calculation of dipole matrix elements between the eigenvectors of FS RCC effective Hamiltonians.
Due to the use of field-independent model spaces and one-electron spinors for solving the many-electron problem for a molecule in the finite-strength external field, the additional work required to evaluate transition property values remains moderate. However, in applications to highly symmetric systems and in the cases when one focuses on a small number of transitions but has to estimate off-diagonal matrix elements of numerous or multicomponent (tensor) properties the technique can become computationally extensive, so that the development of relativistic counterparts of analytical methods for transition density matrix construction remains desirable.
An important advantage of the finite-field technique consists in the possibility to simultaneously evaluate the transition matrix elements for all pairs of states corresponding to eigenvalues of the FS RCC effective Hamiltonian. This advantage can be decisive for studying intensity distributions in dense spectra, especially in those of actinide and lanthanide compounds. The work on assessment of reliability of the technique as a tool for describing the excitations in molecules and cluster models of crystals containing f-elements [61] is in progress in our group.
Supplementary Materials
The employed basis sets and numerical results are available online at https://www.mdpi.com/2073-8994/12/11/1845/s1. Table S1: FS RCC excitation energy and finite-field estimate of transition dipole moment for the transition in I as functions of the internuclear separation R. Table S2: FS RCC excitation energy and finite-field estimate of transition dipole moment for the transition in TlF as functions of the internuclear separation R. Table S3: Contracted Gaussian basis set for xenon. The DIRAC mol format is assumed. Table S4: Gaussian basis set for mercury. Table S5: Contracted Gaussian basis set for iodine. Table S6: Contracted Gaussian basis set for thallium.
Author Contributions
A.Z., A.V.O., and E.E. equally contributed to the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the Russian Science Foundation (Grant No. 20-13-00225).
Acknowledgments
Thanks are due to Bing Yan and Haifeng Xu for supplying us with detailed numerical data concerning their study [57] and to Anatoly V. Titov for critical reading of the manuscript. This work was carried out using computing resources of the federal collective usage centre Complex for Simulation and Data Processing for Mega-science Facilities at NRC “Kurchatov Institute”, http://ckp.nrcki.ru/, and computers of Quantum Chemistry Lab at NRC “Kurchatov Institute”—PNPI.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Perturbative Analysis of the Effective Property Operator and Effective Hamiltonian Derivative
At the lowest orders of the perturbation theory with some field-independent zero-order Hamiltonian commuting with P and degenerate within , the (right) wave operator satisfying the normalization condition (3) can be written as
Here, G denotes the resolvent, , where is the zero-order energy of model states, and we split the perturbation into the field-independent part, , and the field-dependent part . The derivatives of these operator with respect to F for are
The left wave operator corrections for are given by
The second-order effective Hamiltonian has the form
and its derivative with respect to F at ,
coincides exactly with the first-order approximation to the effective property operator
The differentiation of the third-order correction for the field-dependent effective Hamiltonian,
yields
This expression does not coincide with that for the second-order one for the field-free effective property operator:
but the difference is restricted to only one class of renormalization-type terms (underlined).
References
- Krems, R.; Friedrich, B.; Stwalley, W.C. (Eds.) Cold Molecules: Theory, Experiment, Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar] [CrossRef]
- Hunter, L.R.; Peck, S.K.; Greenspon, A.S.; Alam, S.S.; DeMille, D. Prospects for laser cooling TlF. Phys. Rev. A 2012, 85, 012511. [Google Scholar] [CrossRef]
- Pazyuk, E.A.; Zaitsevskii, A.V.; Stolyarov, A.V.; Tamanis, M.; Ferber, R. Laser synthesis of ultracold alkali metal dimers: optimization and control. Russ. Chem. Rev. 2015, 84, 1001–1020. [Google Scholar] [CrossRef]
- Isaev, T.A.; Zaitsevskii, A.V.; Eliav, E. Laser-coolable polyatomic molecules with heavy nuclei. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 225101. [Google Scholar] [CrossRef]
- DeMille, D.; Doyle, J.M.; Sushkov, A.O. Probing the frontiers of particle physics with tabletop-scale experiments. Science 2017, 357, 990–994. [Google Scholar] [CrossRef] [PubMed]
- Garcia Ruiz, R.F.; Berger, R.; Billowes, J.; Binnersley, C.L.; Bissell, M.L.; Breier, A.A.; Brinson, A.J.; Chrysalidis, K.; Cocolios, T.E.; Cooper, B.; et al. Spectroscopy of short-lived radioactive molecules. Nature 2019, 581, 396–400. [Google Scholar] [CrossRef] [PubMed]
- Kaldor, U. The Fock space coupled cluster method: Theory and application. Theor. Chim. Acta 1991, 80, 427–439. [Google Scholar] [CrossRef]
- Visscher, L.; Eliav, E.; Kaldor, U. Formulation and implementation of the relativistic Fock-space coupled cluster method for molecules. J. Chem. Phys. 2001, 115, 9720. [Google Scholar] [CrossRef]
- Lyakh, D.I.; Musiał, M.; Lotrich, V.F.; Bartlett, R.J. Multireference nature of chemistry: The coupled-cluster view. Chem. Rev. 2012, 112, 182–243. [Google Scholar] [CrossRef]
- Eliav, E.; Kaldor, U. Relativistic four-component multireference coupled-cluster methods: towards a covariant approach. In Recent Progress in Coupled Cluster Methods: Theory and Applications; Pittner, J., Charsky, P., Paldus, J., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 113–144. [Google Scholar] [CrossRef]
- Sahoo, B.K.; Majumder, S.; Merlitz, H.; Chaudhuri, R.; Das, B.P.; Mukherjee, D. Electric dipole transition amplitudes for 207Pb+. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 355–363. [Google Scholar] [CrossRef]
- Sahoo, B.K.; Das, B.P. Transition properties of low-lying states in atomic indium. Phys. Rev. A 2011, 84, 012501. [Google Scholar] [CrossRef]
- Bhattacharya, D.; Vaval, N.; Pal, S. Electronic transition dipole moment: A semi-biorthogonal approach within valence universal coupled cluster framework. Int. J. Quantum Chem. 2014, 114, 1212–1219. [Google Scholar] [CrossRef]
- Hehn, A.; Visscher, L. Transition dipole moment calculations within the Fock space relativistic coupled cluster approach (implementation in the DIRAC code). Unpublished, private communication, 2011. [Google Scholar]
- DIRAC, a Relativistic ab Initio Electronic Structure Program, Release DIRAC19. 2019. Available online: http://dx.doi.org/10.5281/zenodo.3572669 and http://www.diracprogram.org (accessed on 19 October 2020).
- Szalay, P.G. Analytic energy derivatives for coupled-cluster methods describing excited states: General formulas and comparison of computational costs. Int. J. Quantum Chem. 1995, 55, 151–163. [Google Scholar] [CrossRef]
- Kállay, M.; Gauss, J. Calculation of excited-state properties using general coupled-cluster and configuration-interaction models. J. Chem. Phys. 2004, 121, 9257–9269. [Google Scholar] [CrossRef]
- Bag, A.; Manohar, P.U.; Vaval, N.; Pal, S. First- and second-order electrical properties computed at the FSMRCCSD level for excited states of closed-shell molecules using the constrained-variational approach. J. Chem. Phys. 2009, 131, 024102. [Google Scholar] [CrossRef]
- Bhattacharya, D.; Vaval, N.; Pal, S. Electronic transition dipole moments and dipole oscillator strengths within Fock-space multi-reference coupled cluster framework: An efficient and novel approach. J. Chem. Phys. 2013, 138, 094108. [Google Scholar] [CrossRef]
- Jørgensen, P.; Helgaker, T. Møller–Plesset energy derivatives. J. Chem. Phys. 1988, 89, 1560–1570. [Google Scholar] [CrossRef]
- Pal, S. Fock space multi-reference coupled-cluster method for energies and energy derivatives. Mol. Phys. 2010, 108, 3033–3042. [Google Scholar] [CrossRef]
- Tomza, M.; Skomorowski, W.; Musiał, M.; González-Férez, R.; Koch, C.P.; Moszynski, R. Interatomic potentials, electric properties and spectroscopy of the ground and excited states of the Rb2 molecule: ab initio calculations and effect of a non-resonant field. Mol. Phys. 2013, 111, 1781–1797. [Google Scholar] [CrossRef]
- Prasannaa, V.S.; Abe, M.; Das, B.P. Permanent electric dipole moment of strontium monofluoride as a test of the accuracy of a relativistic coupled-cluster method. Phys. Rev. A 2014, 90, 052507. [Google Scholar] [CrossRef]
- Skripnikov, L.V. Combined 4-component and relativistic pseudopotential study of ThO for the electron electric dipole moment search. J. Chem. Phys. 2016, 145, 214301. [Google Scholar] [CrossRef]
- Hao, Y.; Iliaš, M.; Eliav, E.; Schwerdtfeger, P.; Flambaum, V.V.; Borschevsky, A. Nuclear anapole moment interaction in BaF from relativistic coupled-cluster theory. Phys. Rev. A 2018, 98, 032510. [Google Scholar] [CrossRef]
- Abe, M.; Prasannaa, V.S.; Das, B.P. Application of the finite-field coupled-cluster method to calculate molecular properties relevant to electron electric-dipole-moment searches. Phys. Rev. A 2018, 97, 032515. [Google Scholar] [CrossRef]
- Denis, M.; Hao, Y.; Eliav, E.; Hutzler, N.R.; Nayak, M.K.; Timmermans, R.G.E.; Borschesvky, A. Enhanced , -violating nuclear magnetic quadrupole moment effects in laser-coolable molecules. J. Chem. Phys. 2020, 152, 084303. [Google Scholar] [CrossRef]
- Zaitsevskii, A.; Pychtchev, A.P. On the finite-field transition dipole moment calculations by effective Hamiltonian methods. Eur. Phys. J. D 1998, 4, 303–308. [Google Scholar] [CrossRef]
- Zaitsevskii, A.V.; Skripnikov, L.V.; Kudrin, A.V.; Oleinichenko, A.V.; Eliav, E.; Stolyarov, A.V. Electronic transition dipole moments in relativistic coupled-cluster theory: the finite-field method. Opt. Spectrosc. 2018, 124, 451–456. [Google Scholar] [CrossRef]
- Znotins, A.; Kruzins, A.; Tamanis, M.; Ferber, R.; Pazyuk, E.A.; Stolyarov, A.V.; Zaitsevskii, A. Fourier-transform spectroscopy, relativistic electronic structure calculation, and coupled-channel deperturbation analysis of the fully mixed A1 and b3Πu states of Cs2. Phys. Rev. A 2019, 100, 042507. [Google Scholar] [CrossRef]
- Krumins, V.; Kruzins, A.; Tamanis, M.; Ferber, R.; Pashov, A.; Oleynichenko, A.V.; Zaitsevskii, A.; Pazyuk, E.A.; Stolyarov, A.V. The branching ratio of intercombination A1Σ+∼b3Π→a3Σ+/X1Σ+ transitions in the RbCs molecule: Measurements and calculations. J. Quant. Spectrosc. Radiat. Transf. 2020, 256, 107291. [Google Scholar] [CrossRef]
- Oleynichenko, A.V.; Skripnikov, L.V.; Zaitsevskii, A.; Eliav, E.; Shabaev, V.M. Diagonal and off-diagonal hyperfine structure matrix elements in KCs within the relativistic Fock space coupled cluster theory. Chem. Phys. Lett. 2020, 756, 137825. [Google Scholar] [CrossRef]
- Bormotova, E.A.; Stolyarov, A.V.; Skripnikov, L.V.; Titov, A.V. Ab initio study of R-dependent behavior of the hyperfine structure parameters for the (1)1,3Σ+ states of LiRb and LiCs. Chem. Phys. Lett. 2020, 760, 137998. [Google Scholar] [CrossRef]
- Hurtubise, V.; Freed, K.F. The Algebra of Effective Hamiltonians and Operators: Exact Operators. In Advances in Chemical Physics; John Wiley & Sons, Ltd.: New York, NY, USA, 1992; pp. 465–541. [Google Scholar] [CrossRef]
- Epstein, S.T. Note on perturbation theory. Am. J. Phys. 1954, 22, 613–614. [Google Scholar] [CrossRef]
- Rittby, C.M.L.; Bartlett, R.J. Multireference coupled cluster theory in Fock space with an application to s-tetrazine. Theor. Chim. Acta 1991, 80, 469–482. [Google Scholar] [CrossRef]
- Mukherjee, D. The linked-cluster theorem in the open-shell coupled-cluster theory for incomplete model spaces. Chem. Phys. Lett. 1986, 125, 207–212. [Google Scholar] [CrossRef]
- Lindgren, I.; Mukherjee, D. On the connectivity criteria in the open-shell coupled-cluster theory for general model spaces. Phys. Rep. 1987, 151, 93–127. [Google Scholar] [CrossRef]
- Chowdhuri, R.; Mukhopadhyay, D.; Mukherjee, D. An Explicitly Connected Many-Body Perturbation Theory for Incomplete Model Space. In Aspects of Many-Body Effects in Molecules and Extended Systems; Springer: Berlin/Heidelberg, Germany, 1989; Volume 50, pp. 165–183. [Google Scholar] [CrossRef]
- Mosyagin, N.S.; Petrov, A.N.; Titov, A.V.; Tupitsyn, I.I. Generalized RECPs accounting for Breit effects in Uranium, Plutonium and superheavy elements 112, 113, 114. Progr. Theor. Chem. Phys. 2006, B 15, 229–251. [Google Scholar] [CrossRef]
- Mosyagin, N.S.; Zaitsevskii, A.; Titov, A.V. Shape-consistent relativistic effective potentials of small atomic cores. Int. Rev. At. Mol. Phys. 2010, 1, 63–72. [Google Scholar]
- Mosyagin, N.S.; Titov, A.V. Generalized Relativistic Effective Core Potentials. Available online: http://www.qchem.pnpi.spb.ru/recp (accessed on 19 October 2020).
- Zaitsevskii, A.; Eliav, E. Padé extrapolated effective Hamiltonians in the Fock space relativistic coupled cluster method. Int. J. Quantum Chem. 2018, 118, e25772. [Google Scholar] [CrossRef]
- Saue, T.; Bast, R.; Gomes, A.S.P.; Jensen, H.J.A.; Visscher, L.; Aucar, I.A.; Di Remigio, R.; Dyall, K.G.; Eliav, E.; Fasshauer, E.; et al. The DIRAC code for relativistic molecular calculations. J. Chem. Phys. 2020, 152, 204104. [Google Scholar] [CrossRef]
- Oleynichenko, A.; Zaitsevskii, A.; Eliav, E. EXP-T, an Extensible Code for Fock Space Relativistic Coupled Cluster Calculations. 2020. Available online: http://www.qchem.pnpi.spb.ru/expt (accessed on 17 October 2020).
- Oleynichenko, A.V.; Zaitsevskii, A.; Eliav, E. Towards high performance relativistic electronic structure modelling: The EXP-T program package. arXiv 2020, arXiv:2004.03682. [Google Scholar]
- Oleynichenko, A.V.; Zaitsevskii, A.; Skripnikov, L.V.; Eliav, E. Relativistic Fock space coupled cluster method for many-electron systems: non-perturbative account for connected triple excitations. Symmetry 2020, 12, 1101. [Google Scholar] [CrossRef]
- Sundholm, D. VIBROT. Available online: http://www.chem.helsinki.fi/~sundholm/software/GPL/ (accessed on 19 October 2020).
- Sansonetti, J.E.; Martin, W.C. Handbook of basic atomic spectroscopic data. J. Phys. Chem. Ref. Data 2005, 34, 1559–2259. [Google Scholar] [CrossRef]
- Peterson, K.A. Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16-18 elements. J. Chem. Phys. 2003, 119, 11113. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New basis set exchange: An open, up-to-date resource for the molecular sciences community. J. Chem. Inf. Model. 2019, 47, 1045–1052. [Google Scholar] [CrossRef]
- Peterson, K.A.; Yousaf, K.E. Molecular core-valence correlation effects involving the post-d elements Ga–Rn: Benchmarks and new pseudopotential-based correlation consistent basis sets. J. Chem. Phys. 2010, 133, 174116. [Google Scholar] [CrossRef]
- Peterson, K.A.; Puzzarini, C. Systematically convergent basis sets for transition metals. II. Pseudopotential-based correlation consistent basis sets for the group 11 (Cu, Ag, Au) and 12, (Zn, Cd, Hg) elements. Theor. Chem. Acc. 2005, 114, 283–296. [Google Scholar] [CrossRef]
- Lukashov, S.; Petrov, A.; Pravilov, A. Electronic States of Iodine Molecule and Optical Transitions between Them. In The Iodine Molecule; Springer: Cham, Switzerland, 2018; pp. 21–56. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Intensity analysis of overlapped discrete and continuous absorption by spectral simulation: The electronic transition moment for the B-X system in I2. J. Chem. Phys. 2011, 134, 084301. [Google Scholar] [CrossRef]
- Zaitsevskii, A.; Pazyuk, E.A.; Stolyarov, A.V.; Teichteil, C.; Vallet, V. Theoretical spectroscopy of molecular iodine. 1. Ab initio study on the , and B′1u − radiative transition intensities. Mol. Phys. 2000, 98, 1973–1979. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, X.; Xiao, L.; Xu, H.; Yan, B. Electronic structure and spectroscopy of the low-lying electronic states of thallium fluoride: MRCI + Q study including spin-orbit coupling. J. Quant. Spectrosc. Radiat. Transf. 2020, 243, 106817. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796. [Google Scholar] [CrossRef]
- Tellinghuisen, J. A simple sum rule for total radiative decay rates in diatomics. Chem. Phys. Lett. 1984, 105, 241–243. [Google Scholar] [CrossRef]
- Lomachuk, Y.V.; Maltsev, D.A.; Mosyagin, N.S.; Skripnikov, L.V.; Bogdanov, R.V.; Titov, A.V. Compound-tunable embedding potential: which oxidation state of uranium and thorium as point defects in xenotime is favorable? Phys. Chem. Chem. Phys. 2020, 32, 17922–17931. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).