Abstract
Object selection is the basis of natural user–computer interaction (NUI) in a virtual environment (VE). Among the three-dimensional object selection techniques employed in virtual reality (VR), bare hand-based finger clicking interaction and ray-casting are two convenient approaches with a high level of acceptance. This study involved 14 participants, constructed a virtual laboratory environment in VR, and compared the above two finger-based interaction techniques in terms of aspects of the task performance, including the success rate, total reaction time, operational deviation, and accuracy, at different spatial positions. The results indicated that the applicable distance range of finger clicking interaction and finger ray-casting was 0.2 to 1.4 m and over 0.4 m, respectively. Within the shared applicable distance, the finger clicking interaction achieved a shorter total reaction time and higher clicking accuracy. The performance of finger clicking interaction varied remarkably at the center and edge of the horizontal field of view, while no significant difference was found among ray-casting at various horizontal azimuths. The current findings could be directly applied to the application of bare-hand interaction in VR environments.
1. Introduction
With the popularization of low-cost gesture recognition and tracking technologies, and the rapid increasing of virtual reality commercial applications, the natural user–computer interaction (NUI) in a virtual environment (VE) has become a hot topic. NUI allows for communicating with computers in a way that is more suitable for humans, such as voice, gesture, gaze, etc. When operators in VE systems perform tasks such as selecting from virtual menus or inspecting physical or virtual information, it is necessary to begin by selecting an interactive object, before performing a series of subsequent operations. Therefore, object selection is fundamental to the human–computer interaction within VE.
Existing three-dimensional (3D) object selection techniques in VE primarily include grasping, clicking, pointing, circular selection, and indirect selection [1]. The grasping metaphor is based on virtual-hand technology, which directly maps the movement of the physical hand to the movement of the virtual hand to realize the target selection [2]. Finger touch contact is the most comprehensible and intuitional interaction approach, which, to some extent, may simulate mouse clicking in a graphical user interface (GUI) [3]. However, since grasping and clicking interaction are confined to the users’ physical limits, some studies have attempted to adopt nonlinear mapping techniques to break through the limitations [4]. Ray-based pointing is an intuitive and natural interaction technique [5], which is analogous to the techniques integrated by home entertainment systems [6] and the absolute ray-casting technology employed in the real world [7], which use the metaphor of ray-casting to locate targets [8,9]. Additionally, the ray-casting interaction allows users to interact with objects beyond physical accessibility. Circular gesture selection is another long-distance selection technique, which matches gesture trajectory mapping and object labels for target selection [10]. In addition to the hand-related selection, there are several auxiliary alternative interaction approaches, such as selection based on eye fixation [11]. The above techniques, that is grasping, clicking, circular selection, and fixation, are all direct selection approaches used for direct interaction with visual targets, while indirect selection focuses on selecting objects through menus or semantics [12].
In addition to the differences in the information input and output, the interaction in virtual reality (VR) and a traditional 2D display varies greatly in terms of the work position. The information input of two-dimensional GUI mostly depends on a mouse and keyboard, requiring fine hand movements within a small range, so operators commonly have a sitting posture. Conversely, since interaction in VE involves six degrees of freedom input control, the range of motion includes the entire close-body 3D space. In this case, interactive activities in VE include body rotation, large-scale arm movement, and small-scale walking [13], stimulating users to take a standing position. In the case of standing work, the interactive mode in VR environments should meet the requirements for both convenience and usability. Convenience calls for the elimination of the extra burden on users caused by external equipment to reduce the restraint that users suffer from in the standing position. Usability requires quick and accurate object selection, which could minimize the cognitive load imposed by the interaction process.
Compared with other techniques in VE, such as wands and data gloves, the bare-hand interaction is more convenient and has a low burden. The most common and mature bare-hand interaction technologies are those based on the leap motion controller (LMC), which is an infrared gesture recognition device. LMC is a commonly used low-cost gesture capture device [14], providing access to a skeleton model of tracked hand to realize hand recognition and tracking. LMC supports both static and dynamic gesture recognition [15,16,17] and can be attached to head-mounted display (HMD) devices to map the user’s hand to the virtual hand and achieve real-time acquisition of the hand posture [18,19]. In the VR applications based on HMD and LMC, some of them use the index finger to select the virtue objects [20,21,22,23], others use the hand ray-casting [9,24]. Thus far, there are some studies that have focused on the user preference for different hand interaction methods in VE. Based on HMD and LMC, Liang et al. compared ray-casting, virtual hand, and hand-extension techniques and found that direct finger clicking is superior in terms of both speed and accuracy [25]. By comparing the different triggering methods of index finger and palm pointing, Jeffrey et al. reported that index finger pointing is more usable than palm-based techniques in triggering an operation [26]; and the study on the five common interactions (1D and 2D sliders, buttons, selection of icons at a distance, and grasp and release of virtual objects) showed that users preferred ray-casting emitted by a finger rather than that emitted by a controller [27]. In summary, finger-based clicking and ray-casting are preferred bare-hand techniques in VE, that can satisfy the requirements for convenience and usability.
The interaction in VE is carried out within the 3D space. Norman pointed out that it is erroneous to copy the traditional interaction and NUI of 3D systems, which could cause a lot of confusion [28]. The visual interface of VE can provide a horizontal and vertical field of view (FOV) [29]. The perceived degrees of freedom provided by VR HMD, for instance, include the position of x, y, and z axis coordinates, pitch, yaw, and roll rotation, as well as the horizontal and vertical convergence [30]. Such stereoscopic vision, which increases the dimension of the depth display, is the most essential difference between the 3D and 2D display [31], and relative work has reported that people tend to adopt distinct perception strategies within different deep spaces [32]. In addition to the display position, the size of the selected target in the 3D virtual space also has a significant impact on the operational performance [33].
Among the existing research on hand interaction, most studies have focused on gesture recognition [34,35] or interaction methods for specific tasks [27,32]. In the three-dimensional interface of VE, which involves depth dimensions, we need to understand the relationship between hand interaction mode and depth space. Previous studies suggested that the two most preferred object selection techniques under VE are finger clicking and ray-casting interaction. However, it is necessary to investigate the applicable depth range of these two interaction techniques, and whether they have distinct requirements for the size of interactive targets, which have not been sufficiently investigated in previous studies. Based on the results of applicability, specific design guidelines for implementing finger clicking and ray-casting interaction in VE could be established. Therefore, this study aims to explore the applicability of finger clicking and finger ray-casting techniques within VE. By conducting experiments under the same experimental conditions, we measured and compared the operational performance of these two interaction techniques with targets at different depths, location, and of different sizes, and speculated their applicable thresholds based on the experimental results.
2. Materials and Methods
2.1. Participants and Apparatus
The experimental program was written and implemented using a PC computer, equipped with an AMD R9 3900X processor, 2080Ti graphics card, and HTC Vive Pro headset. The HMD headset had a binocular resolution of 2880 × 1600 px and a refresh rate of 90 Hz and provided a FOV of 110 degrees. LMC, with a sampling rate of 120 Hz, was mounted on the front of the HMD for recognizing the location and posture of hands.
The experimental VE was built with the unity engine, which copied and simulated the environmental scene in the real laboratory where the experiment was conducted. It is difficult for users to search and locate targets in VE if there are no depth clues [36]. Therefore, in addition to the setting of the scene perspective, a grid map was added to the floor to enhance the participants’ perception of depth. In VR, the virtual scene can be set to be fixed or follow the head movement of users. Since fixed physical space is used more commonly among geographic visualization systems, the simulated scene in the current experiment was fixed so that operators could move in the virtual scene whilst all of the virtual objects remained still. In addition, participants could see their virtual hands in real-time during the experiment, and the position and size of the hands were identical to those in reality. The control-display (C/D) ratio of the interaction in reality and VE was 1:1.
A total of 14 participants participated in the experiments, including seven males and seven females, aged between 21 and 28 years old. All were right-hand dominant with normal or corrected-to-normal vision. All of the participants received a monetary reward for their participation. After entering the laboratory, participants were first required to get familiar with the VR headset and adjust the head strap and its interpupillary distance to the most comfortable setting. Then, they were required to take a training session, where they kept practicing until they were fully proficient in the operation of bare-hand interaction. The experiment consisted of two parts, with finger clicking and finger ray-casting as the interaction techniques, respectively. To eliminate the study and fatigue effect, participants were divided into two groups, one of which started with the finger clicking experiment, while the other one began with the finger ray-casting experiment.
2.2. Experiment 1: Finger Clicking Experiment
In each trial of the finger clicking experiment, a red ball appeared in the virtual scene as the experimental stimulus, and participants were required to click the emerged balls with the index finger of their right hand. Before each trial, participants had to move their hands back to the preset initial position, which could be confirmed through a cross line on the opposite wall, so as to ensure that the interaction motion in all trials started at the same spatial location.
Three independent variables were included in this study. The first variable is the deviation azimuth of the horizontal FOV, which involved three levels of −30, 0 and 30 degrees. The 0-degree level was located at the mid-sagittal plane of participants and clockwise was adopted as the positive direction. The second independent variable was the size of the stimulus, with a FOV of 1.2, 2.9, and 7 degrees, respectively. The smallest stimulus is approximately equal to the width of the index finger pad exhibited by a man when he stretches his finger forward. The third independent variable is the distance between the stimulus and participants. In a range of 200 to 2600 mm, we examined 13 distances, with an interval of 200 mm. The experimental settings are shown in Figure 1. The setting of the experimental stimulus referred to the results of a pilot study.
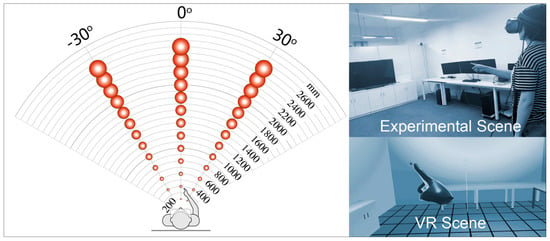
Figure 1.
Experimental settings of the finger clicking experiment.
The gesture selection task could be divided into two steps: Pointing and confirming. During the process of confirming, the direction of finger pointing may alter, which is known as the Heisenberg effect [37]. To address this issue, the situation when the 3D coordinate set of the finger and stimulus intersected was identified as successful clicking, without demanding for an additional operation. After clicking was completed, the visual stimulus disappeared, and participants moved their hands back to the initial position and prepared for the next trial. Participants could move freely within a small range and were required to verbally report “skip” when targets were found to be too far or too difficult to click, after which the tester triggered the next trial manually and recorded the condition. Participants were required to keep practicing until they were sufficiently familiar with the operational procedure, after which they were allowed to proceed to the formal experiment.
Within each trial during the formal experiment, the position and size of the stimulus were collected, and the time differences between the moment when the stimuli appeared and when they were clicked were recorded as the total reaction time (TRt). Moreover, the distance between the point where the finger successfully clicked the stimulus and the nearest point between the stimulus and participant was collected as the operational deviation, as illustrated in Figure 2. Since we compared the performance among different trials, the system delay was not considered in this study. In this experiment, the stimuli were presented 4 s after each trial when targets were successfully clicked, and a single session took about 12 to 13 min to accomplish. In the finger clicking experiment, performance data of 1638 effective trials were obtained from the 14 participants.
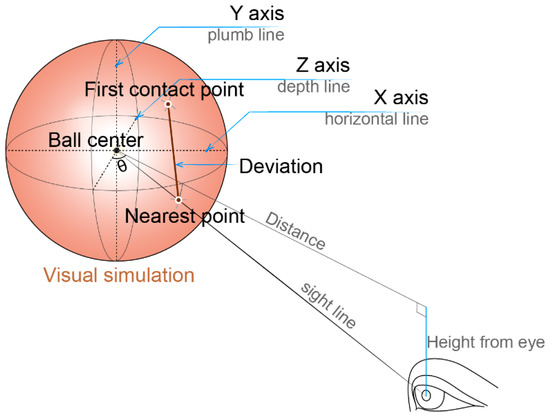
Figure 2.
Operational deviation in the finger clicking experiment.
2.3. Experiment 2: Finger Ray-Casting Experiment
The hardware and virtual scene used in experiment 2 were the same as that in experiment 1. Similarly, in the finger ray-casting experiment, an experimental stimulus, that is, a red ball, appeared in the virtual space for each trial. In order to avoid the Heisenberg effect when the same hand was used for selecting and operation confirmation, participants were required to use their dominant hand for selecting and the other hand for confirming. Specifically, participants stretched their right arm forward, with their index finger and thumb completely open, and then pressed the space bar on the keyboard with the other hand. The precise gesture was captured by LMC, and a visible virtual ray was emitted from the two nodes at the root and top of the index finger. When the virtual ray was in contact with the red ball, participants had to press the space bar instantly with their left hands. Participants could see their virtual hands and emitted virtual rays in real-time during the experiment.
In a pilot study, we found that the bare-hand ray along the direction of the index finger could cause considerable shakes, which was also reported by a prior study [27]. The possible reason for this is that when participants stretched their hands forward, the root node of the index finger could be occluded by the top node, thus resulting in a large recognition error. Therefore, in the current experiment, a virtual ray was emitted along the connecting line of the top nodes of the index finger and thumb, improving the stability of gesture recognition. Although some studies have considered other body parts, such as the chin [38] or eye center [39] for controlling the direction of the hand ray, those approaches require additional equipment. Since this experiment focused on examining the applicable area of finger ray-casting interaction, only bare hand-based techniques were considered to emit virtual rays.
Three independent variables were included in experiment 2. The first variable was the deviation azimuth of the horizontal FOV, which included three levels, that is, −30, 0, and 30 degrees. The second independent variable was of different stimulus sizes, with a visual angle of 1.2, 2.9, and 7 degrees, respectively. The third independent variable was the distance between the stimulus and participants, involving 15 levels. Except for the 13 distances used in experiment 1, we additionally added two distances, including 3000 and 5000 mm. The experimental settings are shown in Figure 3.
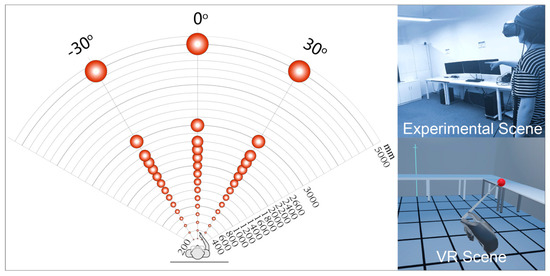
Figure 3.
Experimental settings of the ray-casting experiment.
Before experiment 2, participants were also required to perform a training session until they became fully familiar with the task operation, after which the formal experiment and data collecting started. In experiment 2, stimuli were also presented 4 s after each successful clicking, and a single session took about 18 to 20 min to finish. In the formal experiment, the data of 1890 effective trials were collected from 14 participants. For each trial, the time interval between the appearance of the stimulus and successful interaction was collected as TRt and the distance between the contact point of the ray and ball and the nearest point of the ball to the participants were collected as the TRt and operational deviation, respectively. System delays were also neglected in this experiment.
3. Results
3.1. Interactive Performance Data of Finger Clicking Experiment
We analyzed the relationship between the position of the visual stimulus, including the horizontal azimuth angle of the stimulus and the distance between the stimulus and participants, and the performance of the finger clicking operation. The mean values of performance indexes are plotted in Figure 3, with the horizontal axis indicating the horizontal viewing angle (−30, 0, and 30 degrees) and the vertical axis representing the distance between the stimulus and participants (0.2–2.6 m). Figure 4a–d visualizes the mean success rate of clicking, TRt, operational deviation, and relative accuracy at different spatial positions, respectively. The TRt, operational deviation, and relative clicking accuracy in the situation where clicking was not completed successfully were excluded.
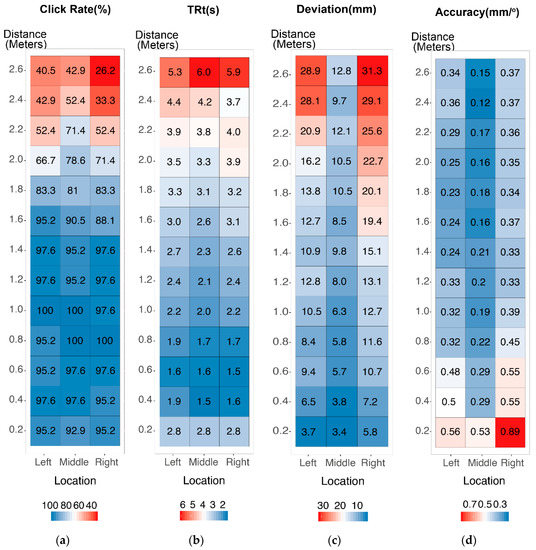
Figure 4.
Performance of the finger clicking experiment. (a) Mean success rate of clicking; (b) mean total reaction time; (c) mean operational deviation; and (d) mean relative clicking accuracy.
As shown by the mean success rate of clicking in Figure 4a, the success rate reached more than 90% within 1.4 m, and the willingness to click started to significantly decrease from 1.8 m. Since the success rate at a distance of 2.0 m or more was extremely low, it is of little significance to discuss accuracy or reaction time data. It could be considered that at a distance of 1.8 m away from the operators, it is not suitable to set interactive objects, which requires the clicking interaction. Based on the above results, we will only discuss the reaction time and accuracy data within a distance of 1.8 m.
When it comes to the mean TRt data, as illustrated in Figure 4b, it could be found that, except for the distance within 0.2 m, TRt progressively increased along with the depth increment, and the reaction between 0.4 and 0.8 m achieved the best performance. This is an interaction distance demanding merely a small-scale arm movement or leaning forward without any walking. TRt is the time between the emergence of the stimulus and the successful clicking, containing the reaction time before triggering the gesture and the motion time required for hand movement. When only one visual target was displayed, the visual reaction time was about 150 to 225 ms. Therefore, since the mean TRt was approximately 3000 ms, hand movement could be considered as the primary contributor to TRt data. The operation at 0 degrees of the center horizontal FOV achieved a significantly faster speed than that at 30 degrees left or right, while clicks at the 30 degrees right position achieved a shorter operational duration than that of the opposite position horizontally.
Clicking deviation represents the distance between the contacting point and the nearest point. As shown in Figure 4c, the operational deviation increased as the depth of stimulus became greater. Since the actual size difference in the stimulus with a similar visual size was great, we divided the operational deviation by the diameter of the corresponding stimulus to achieve the relative clicking accuracy at different spatial positions, as shown in Figure 4d. The results showed that within the close-body distance range of 0.2 to 0.6 m, the closer the stimulus was to the participants, the higher the relative accuracy value was, while the accuracy was low and without a significant changing trend when the distance was greater than 0.8 m. In addition, the clicking accuracy was higher at 0 degrees of the horizontal FOV than at 30 degrees deviated to the right or left. Moreover, the accuracy at the position of −30 degrees (left) was higher than that at the position of 30 degrees (right). A possible interpretation is that when clicking on the left side, the right-hand participants’ forearm and palm were in a straight posture, while there was an angle between the forearm and palm when they clicked on the right side, causing more shakes.
An F-test and t-test were performed for investigating the task performance using the stimulus of different angles of view (i.e., different visual sizes), and the results are plotted in Figure 5. No significant result was found in terms of the success rate, where F (2114) = 1.265 and p = 0.286 > 0.05, as shown in Figure 5a. Whether participants had a willingness to click was primarily determined by the distance between them and the stimulus. Regarding the comparison among clicking deviation values, significant differences were found among different stimulus sizes, where F (2114) = 29.486 and p = 0.000 < 0.01. Furthermore, significant differences were also found for TRt data, where F (2114) = 4.655 and p = 0.011 < 0.05, as displayed in Figure 5b. The results of the t-test indicated that the TRt data of 1.2 and 2.9 degrees were significantly different, where t (76) = 2.145 and p = 0.035 < 0.05; TRt data of 1.2 and 7 degrees were also significantly different, where t (76) = 2.788 and p = 0.007 < 0.01. However, no significant difference was found between 2.9 and 7 degrees, where t (76) = 0.686 and p = 0.495 > 0.05. It can be seen that when the stimulus size increased within the size range providing an angle of view of over 2.9 degrees, there was no significant change in TRt.
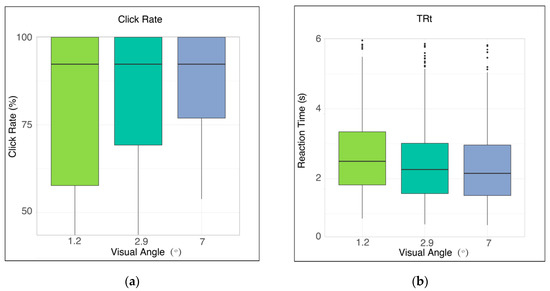
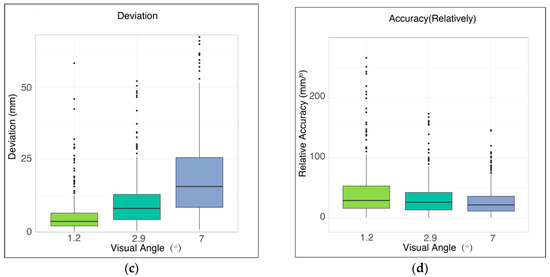
Figure 5.
Finger clicking performance using different stimulus sizes. (a) Success rate of clicking with three stimulus sizes; (b) total reaction time of clicking with three stimulus sizes; (c) operational deviation with three stimulus sizes; and (d) relative clicking accuracy with three stimulus sizes.
Significant differences were found among operational deviation values using different stimulus sizes, where F (2114) = 29.486 and p = 0.000 < 0.01, as shown in Figure 5c. Additionally, the results of the relative accuracy were also found to be significant, where F (2114) = 9.722 and p = 0.000 < 0.01, as plotted in Figure 5d. The t-test showed that the relative accuracy data using stimulus sizes of 1.2 and 2.9 degrees were significantly different, where t (76) = 2.807 and p = 0.006 < 0.01; the accuracies using stimulus sizes of 1.2 and 7 degrees were also significantly different, where t (76) = 3.864 and p = 0.000 < 0.01. In comparison, no significant result was found when using stimulus sizes of 2.9 and 7 degrees, where t (76) = 1.452 and p = 0.151 > 0.05. Overall, it can be observed that the clicking accuracy was closely associated with the stimulus size, although no marked change in the accuracy was found when the stimulus size was larger than 2.9 degrees.
When comparing the operational time when using the stimulus size of 1.2 degrees at the center position of 0 degrees and the stimulus size of 2.9 degrees at the left or right position of ±30 degrees, we found no significant difference, where t = 1.351 and p = 0.178 > 0.05; a similar comparison of the clicking accuracy also found no remarkable result, where t = −0.375 and p = 0.708 > 0.05. Moreover, although the t-test showed no significantly different operational times when using a stimulus size of 2.9 degrees at the center position and stimulus size of 7 degrees at the left or right marginal position, where t = −0.145 and p = 0.885 > 0.05, the comparison result of the relative accuracy was significant, where t = −3.790 and p = 0.000 < 0.01. It could be considered that when the stimulus size increased to a certain degree, the relative accuracy was linked to the appearance position, rather than its size.
We performed a one-way ANOVA analysis on the TRt and clicking accuracy separately, with different participants as the independent variable. Significant differences of both indexes were found among participants and the results indicated that the mean value of TRt changed from 1.73 to 3.32 s, where F (13, 1312) = 14.043 and p = 0.000 < 0.01, and the mean value of operational deviation changed from 0.11 to 0.36 mm, where F (13, 1312) = 5.899 and p = 0.000 < 0.01. The current findings indicate that there were significant differences in the performance of finger clicking interaction among individuals.
3.2. Interactive Performance Data of Finger Ray-Casting Experiment
Firstly, the relation between the spatial position of the visual stimulus and the operational performance of finger ray-casting interaction was analyzed. Figure 6 shows the mean value of the operational performance as a function of the position of the stimulus, with the horizontal axis indicating the horizontal viewing angle (−30, 0, and 30 degrees) and the vertical axis representing the distance between the experimental stimulus and participants (0.2–5 m). Data of trials where stimuli were not successfully clicked were excluded when visualizing the mean value of TRt and the operational accuracy.
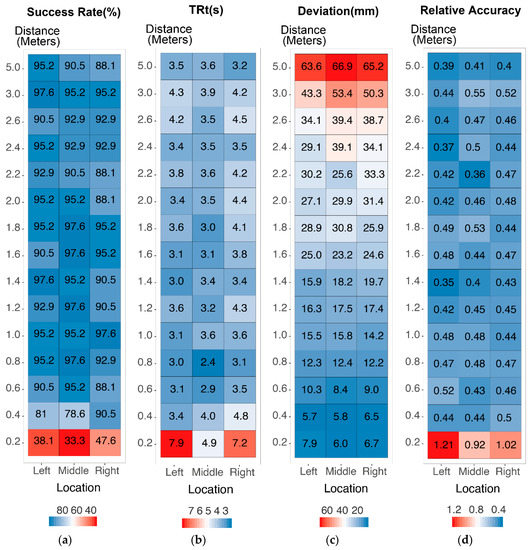
Figure 6.
Performance of the finger ray-casting experiment. (a) Mean success rate of operation; (b) mean total reaction time; (c) mean operational deviation; and (d) mean relative operational accuracy.
It could be seen that the performances of both the success rate and TRt were significantly worse at a distance of 0.2 m, while no significant change trend following the increased distance was found at other spatial positions. The operational deviation shown in Figure 6c, that is, the average value of the distance between the position of each click and the closest point of the stimulus, was found to increase when the stimulus moved further from the participants. The calculation of the relative operational accuracy, as shown in Figure 6d, is similar to that of the relative clicking accuracy in experiment 1. We found that the change in the relative accuracy was consistent with that in the TRt and success rate, that is, the performance was significantly worse at 0.2 m and exhibited no significant change trend when interaction distances equaled or were greater than 0.4 m. Therefore, it could be considered that the applicable distance range of finger ray interaction is greater than or equal to 0.4 m.
From Figure 6a,b,d, it could be found that there were no significant differences in the success rate, TRt, and relative operational accuracy, which is obviously distinct from the results of the finger clicking experiment. Ray interaction required participants to control the position, azimuth, and pitching of hands. However, when interacting with the stimulus at various positions, the position and pitch angle of their hands were relatively stable, with merely the azimuth angle changing from time to time.
Figure 7 shows the ray-casting operational performance with stimuli of three different angles of view (1.2, 2.9, and 7 degrees). To compare the success rate among stimuli with different angle views, we performed an ANOVA analysis and the results were significant, where F (2132) = 27.782 and p = 0.000 < 0.01, as plotted in Figure 7a. A t-test was then performed for each pair. The results of the comparison between 1.2 and 2.9 degrees were significant, where t (88) = −5.590 and p = 0.000 < 0.01; besides, the comparison of 1.2 and 7 degrees was also significant, where t (88) = −6.529 and p = 0.000 < 0.01. However, no significant difference was found between 2.9 and 7 degrees, where t (88) = −0.736 and p = 0.464 > 0.05. When comparing the TRt among the three stimulus sizes, the result of ANOVA was F (2132) = 105.499 and p = 0.000 < 0.01, as shown in Figure 7b. The pairwise t-test showed that TRt using a stimulus of 1.2 and 2.9 degrees were significantly different, where t (88) = 10.086 and p = 0.000 < 0.01; the comparisons between 1.2 and 7 degrees were also significant, where t (88) = 14.383 and p = 0.000 < 0.01. Significant results were found in the comparison between 2.9 and 7 degrees, where t (88) = 3.749 and p = 0.000 < 0.01. Regarding the comparison of the absolute operational accuracy using three stimulus sizes, the result of ANOVA was F (2132) = 35.632 and p = 0.000 < 0.01, as shown in Figure 7c. The t-test was performed on each pair and the result of the comparison between 1.2 and 2.9 degrees was t (88) = −4.965 and p = 0.000 < 0.01; the result of the comparison between 1.2 and 7 degrees was t (88) = −8.026 and p = 0.000 < 0.01, and the results of the comparison between 2.9 and 7 degrees was t (88) = −4.166 and p = 0.000 < 0.01, which indicated significant differences between pairs. The result of the ANOVA performed on the relative operational accuracy with different stimulus sizes was F (2132) = 2.492 and p = 0.087 > 0.05, as shown in Figure 7d. This result indicated that the relationship between the relative operational accuracy and stimulus size was not significant, and the stimulus size may merely affect the interaction duration.
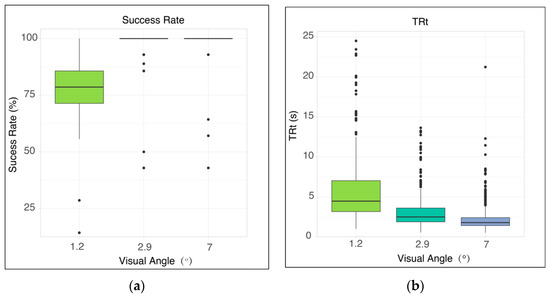
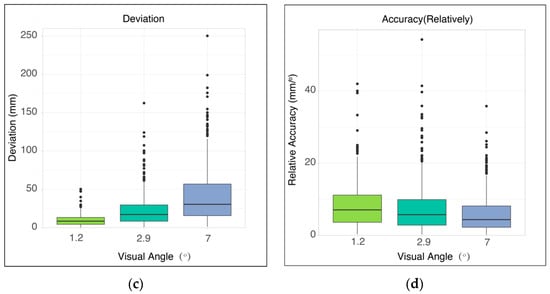
Figure 7.
Finger ray-casting performance using different stimulus sizes. (a) Success rate of the operation with three stimulus sizes; (b) total reaction time with three stimulus sizes; (c) operational deviation with three stimulus sizes; and (d) relative operational accuracy with three stimulus sizes.
The performance of the ray-casting interaction was also compared among participants. The results showed that the mean TRt varied from 2.53 to 4.73 s, where F (13, 1581) = 9.635 and p = 0.000 < 0.01, and the mean operational accuracy varied from 0.17 to 0.28 mm, where F (13, 1581) = 5.275 and p = 0.000 < 0.01, showing significant differences. Therefore, the current results indicated that significant individual differences may exist when adopting the finger ray-casting interaction.
3.3. Fitts’ Law
3.3.1. Adaptation on the Finger Clicking Experiment
Fitts’ Law is a well-known psychological predictive model [40]. In two-dimensional tasks, Fitts’ formula can reflect the relationship between the difficulty of operation and the movement time in a human–computer interface, which has been unanimously recognized by the academic community [41]. Studies have been conducted to extend Fitts’ Law to a 3D interface [42,43], and have suggested that an effective target width W in 3D space is related to the viewing angle, and A is related to the movement amplitude [44]. Additionally, some scholars have reported that the movement time is correlated with the horizontal deviation angle, which can also be supported by the relationship between TRt and horizontal azimuth identified in this study, as illustrated by Figure 7b. Therefore, Fitts’ Law should be modified for the interaction in a 3D environment [45]. The standard experimental paradigm of Fitt’s law is to measure the movement duration between the clicking on two visual targets. This study was a little different from it. In experiment 1, the participants responded to the visual stimuli and started moving the dominant hand from the leg side to the chest position. The duration time could be counted as the start gesture time. Then, the hand moved from the chest position to the visual target, the visual stimuli disappeared when touching. Therefore, the TRt in this experiment includes three time periods: The visual response time, the start gesture time, and the pointing time. The visual response time which includes the response time of the visual system to the light pulse (about 100 ms), the central nervous system processing time (about 70 ms), and the activation effector time (about 70 ms) [46], and the start gesture time could be treated as the same in different experimental trails. Therefore, the difference among the trails was mainly determined by the pointing time which is related to the distance (A) and the width (We) of the visual stimuli in each trial. In this study, ID could be computed through Formula (1), where We is the viewing angle of the stimulus from the initial position and A is the movement amplitude estimated by the moving distance. Since there was both translation and sway of the task-related arm in this study, we regraded the distance covered by the arm which naturally moves by 180 degrees to be approximately 1.2 m, and calculated the corresponding approximate amplitude A in each trial at an equal angle.
The correlation analysis was performed on the observation values within the range of 0.2 to 1.4 m, which is the range of distance achieving a 95% success rate. The results showed a significant correlation between TRt and ID, where r = 0.726 and p = 0.000 < 0.01; no significant correlation was found between TRt and the cosine of deviation angle, where r = 0.230 and p = 0.095 > 0.05. We performed regression on TRt, ID, and the correction of the horizontal deviation angle, and obtained the following results:
where θ is the correction of the deviation angle. The adjusted R2 of this model is 0.563. The parameter significance of ID, correction of the angle, and constant terms is 0.000, 0.015, and 0.003, respectively, all of which are significant. The TRt in this formula includes, except for the movement time, the response and recognition time of the system, and the reaction time of participants. However, since the other three temporal parameters had much lower values than the movement time, TRt could be used to approximately replace the movement time. It could be found that the finger clicking interaction in 3D space roughly conforms to Fitts’ Law, and it is statistically significant to adopt the deviation angle to correct the movement time.
3.3.2. Adaptation on the Finger Ray-Casting Experiment
Studies have reported that the ray-casting interaction also obeys Fitts’ Law [47]. Similar to the finger clicking experiment, regardless of the system response time, the ray-casting processing could be decomposed into four parts: The visual response time, the start ray gesture time, the ray aiming time, and the interaction confirmation time. The visual response time, the start ray gesture time, and the interaction confirmation time can be approximately considered equally between trails, therefore, the TRt difference was mainly determined by the ray aiming time. As mentioned earlier, in 3D space, the effective size W is related to the viewing angle, and A is related to the motion amplitude [45]. With the use of finger ray-casting in this experiment, we regarded the viewing angle of the stimulus as the effective size of what was employed in experiment 1. Moreover, since the motion amplitude of the arm was also roughly the same as that in experiment 1, which is the amplitude from the natural downward to the front raised position, it could be regarded as 90 degrees. As shown in Figure 5, the TRt and accuracy of ray-casting interaction were not related to the horizontal azimuth angle of the stimulus, so no angle correction was required in this part. According to Formula (1) in experiment 1, the correlation between ID and TRt is r = 0.764, which is a significant positive correlation. The regression equation obtained when ID is used to predict TRt is
The R2 of this regression equation is 0.584, which proves that ID has the main effect on TRt. In summary, Fitts’ Law could be used to predict the interactive TRt in the bare hand-based ray interaction.
4. Discussion
4.1. Applicability of Techniques
From the previous analysis, it could be found that the suitable depth range for direct finger clicking interaction is 0.2 to 1.8 m, the suitable depth range for finger ray-casting is above 0.4 m, and 0.4 to 1.8 m is the suitable depth range for both interaction techniques. Within this shared suitable range, we compared the performance difference achieved by the two approaches with different stimulus sizes, as shown in Figure 8. The results showed that the increased operational accuracy and speed emerged, along with the enhanced target size, when using either one of the techniques. Regarding the operational time, we found that the ray interaction was more sensitive to the stimulus size. Moreover, we also found that it was more difficult to use the ray-based selection when the target size was within 1.2 degrees and the 7-degree visual target induced both a shorter consumed time and better operational accuracy. Moreover, the performance change in the finger clicking interaction was not significant when the stimulus size increased up to 2.9 degrees. Conversely, the TRt and operational accuracy of finger ray-casting remained variable when the stimulus became larger than 2.9 degrees. By analyzing the operational accuracy data, we found that, regardless of the stimulus size, the accuracy of finger clicking interaction remained better than that of finger ray-casting, with less operational deviation.
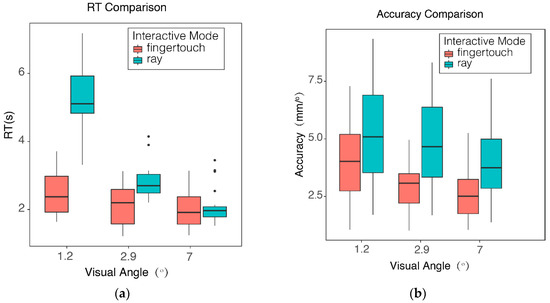
Figure 8.
Performance comparison of finger clicking and finger ray-casting techniques. (a) RT comparison of the two interactive mode with three stimulus sizes; (b) Accuracy comparison of the two interactive mode with three stimulus sizes.
Since finger clicking requires the entire belly surface to contact the interactive object, this may leave people with a feeling of operating roughly. In contrast, ray interaction has the semantics of aiming, and requires contact between the end of the ray and targets, thus inducing a subjective feeling of interacting precisely. However, the performance data obtained in this study indicate that finger the clicking interaction is better than the finger ray-casting interaction within the shared suitable depth range in terms of the operating time and accuracy. In the process of ray interaction, muscle fatigue commonly appears, caused by handshaking, which may result in a reduced accuracy [48]. To address this issue, some investigations have proposed improving the ray-casting interaction performance by changing the C/D gain [5,49], but the mismatch of virtual and real worlds may cause problems in the interaction experience.
To conclude, the recommended depth range (comfort zone) for finger clicking interaction is 0.4 to 1.4 m and the maximum range is between 0.2 and 1.8 m, and the suitable range for finger ray-casting is above 0.4 m. Within a short distance, since the reaction time of finger clicking interaction is shorter and the operational accuracy is better, implementing direct clicking techniques is recommended. For medium and long distances, the ray-based interaction technique appears to be a better choice.
4.2. Size Adjustment of an Interactive Object Within the Horizontal FOV
The human FOV is about 200 degrees horizontally and 130 degrees vertically [50]. Since HTC Vive Pro provides a FOV of approximately 110 degrees (the FOV parameters of other mainstream HMDs are similar), and the embedded sponge pads may increase the distance between eyes and lenses, the actual FOV of a single eye that we measured by the kinetic perimetry paradigm is about 92 degrees (temporal 49 degrees and nasal 43 degrees). Figure 9 shows the binocular FOV in HMD represented by polar coordinates. The monocular visual field is physically restricted within a circular when wearing HTC Vive Pro and the maximum binocular visual field is the blue-colored range presented in Figure 9. Therefore, the visual content in virtual information should also be placed within this visual range. In addition, as can be concluded from the aforementioned performance analysis, the finger clicking interaction is sensitive to the special position of the stimulus, so the size of an interactive object situated far from the center visual field should be increased when adopting finger clicking techniques, while it is less critical to the ray-based interaction. Therefore, when designing the interaction within a near-field (within 1.8 m), interactive controls and elements in the surrounding area should be set larger to ensure the efficient operation of various programs in HMD based on the direct finger contact interaction. Drasdo has proposed that the marginal elements are visually smaller than the central display elements, which decrease according to the function of cos2(θ), where θ is the angle of eccentricity [51]. However, using HMD in real-life conditions is often accompanied by head movement and eye movement, so the change amplitude of targets is much smaller than what occurs when using a fixed viewpoint. Based on the results of the current research, we could conclude that the target 30 degrees that deviated from the center visual field should be enlarged by 2.4 times in size, which could serve as a design reference for considering the enlargement ratio of visual elements in future work.
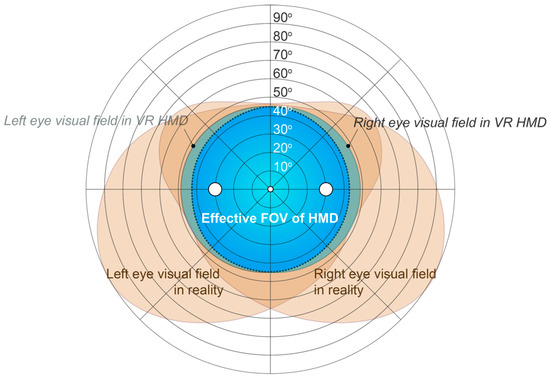
Figure 9.
Design reference for finger clicking interactive controls in a head-mounted display (HMD).
4.3. Psychological Coordinates
When we attempt to locate a target, the target first enters the early stages of the visual cortex through the eyes, and the information in the parietal and premotor region then experiences a transformation of external coordinates. At the neuron level, information is transformed into two main psychological coordinate systems through the initial retinal coordinates, that is, body-centered and world-centered coordinates. Visual information is then transformed into motor coordinates [52,53] and a psychological coordinate system can be estimated through external people’s external motor performance [54]. Studies have shown that changes in the target depth and direction may lead the brain to adopt different spatial labeling strategies [55].
Judging from the results of the current experiments, differences appeared in the spatial strategies adopted by participants when they implemented the two interaction techniques. In the finger clicking experiment, the closer the stimuli were to the participants, the shorter the TRt, and the operational accuracy of the center area was higher than that of the surrounding area, which all reflect the characteristics of head-centered target positioning. In this situation, participants focused on the contact relationship between themselves and the stimulus, and the visual and proprioceptive coordinate system occupied a dominant position in the information processing process. Studies have shown that laying out virtual interfaces that need to be clicked and operated according to the egocentric coordinate system within the near vision field can improve the interaction performance [56], which is consistent with the results of this study. In the ray-casting interaction, although the nearest (0.2 m) target was found to be difficult to operate, no changes were found in the TRt and operational accuracy with variable depth and position within the distance range ray interaction. Additionally, in the finger ray-casting interaction, since the participants’ position remained unchanged, their visual attention was allocated to the observation of the contact relationship between visual stimuli and the virtual ray, making the space-centered coordinate system dominant. Therefore, it could be concluded that this technique is more suitable for object interaction within a medium or long distance.
Under the conditions of this experiment, when the participants observe the visual stimuli, both eyes gaze on the stimuli which appear in the binocular visual field. The horopter will show a Hering-Hillebrand horopter deviation when it is tested by the equidistance matching horopter paradigm. That is, the curvature of the horopter increases proportionally along with the gaze distance. At a certain distance (from 3 to 6 m), the horopter becomes a plane. The magnitude of the change varies among the participants; therefore, the equidistant depth was still employed as the depth independent variable in this experiment. However, during the debugging and implementation of the experimental program, participants could tell that the visual stimuli in the left or right visual field are closer than the middle one at the same depth beyond 3 m.
5. Conclusions and Future Work
In the VR-based 3D object selection interaction, finger clicking interaction and finger ray-casting based on bare hands are highly accepted and convenient interaction techniques. When implementing the finger clicking technique, the interactive elements should be placed within the range of 0.2 to 1.4 m from users and should be no further than 1.8 m. From a performance perspective, the target size for finger clicking interaction in VR should be larger than 1.2 degrees, and that at the off-center position should be larger than that at the center FOV. When the finger ray-casting interaction is used, interactive elements should be further than 0.4 m from users and larger than 2.9 degrees, because the larger the size, the better the operational performance.
Priority should be given to the finger clicking interaction when the interaction occurs within a distance of 1.4 m, where the finger clicking technique performs better than the ray-casting interaction in terms of both the TRt and accuracy. However, if the ray-casting interaction is required when conducting a medium or long-distance interaction, using a larger-size visual target may achieve better operational performance. Furthermore, the performances achieved by these two techniques were found to be significantly variable among different individuals. Therefore, when planning the interaction techniques in virtual reality and augmented reality, interactive controls could be placed within the near-body distance and implement the finger clicking approach, and finger ray-casting could be adopted when interacting with medium or long-distance virtual or physical targets.
The current study adopted three stimulus sizes with proportionally increased viewing angles to investigate the interaction techniques based on finger clicking and ray-casting. Future work could refine the distribution of the stimulus size and the critical threshold may be defined. In addition, the stimulus distribution along the vertical FOV could be added to investigate the changes in performance with a deviation of the viewing angle. The study was carried out in the condition of VR, but the research results can also be applied in AR (augmented reality) or MR (mixed reality).
Author Contributions
Conceptualization, X.Z. and L.J.; experimental design and programming, W.X. and L.J.; data processing, X.Z. and H.Q.; visualization, X.Z. and W.X.; writing—original draft preparation, X.Z.; writing—review and editing, H.Q. and C.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported in part by the National Natural Science Foundation of China (Nos. 71901061 and 71871056) and the Fundamental Research Funds for the Central Universities (No. 2242019k1G016).
Acknowledgments
The authors would like to thank the graduate students from the department of industrial design in Southeast University for the selfless support in the experimental process, especially Hao Ming.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Froehlich, B.; Bowman, D.A. 3D User Interfaces. IEEE Eng. Med. Boil. Mag. 2009, 29, 20–21. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Liang, J.; Green, M. JDCAD: A highly interactive 3D modeling system. Comput. Graph. 1994, 18, 499–506. [Google Scholar] [CrossRef]
- Lee, S.-B.; Jung, I.-H. A Design and Implementation of Natural User Interface System Using Kinect. J. Digit. Contents Soc. 2014, 15, 473–480. [Google Scholar] [CrossRef][Green Version]
- Poupyrev, I.; Billinghurst, M.; Weghorst, S.; Ichikawa, T. The Go-Go Interaction Technique. In Proceedings of the 9th Annual ACM Symposium on User Interface Software and Technology—UIST ’96; Association for Computing Machinery (ACM): New York, NY, USA, 1996; pp. 79–80. [Google Scholar]
- Chen, H.-J.; Lin, C.J.; Lin, P.-H. Effects of control-display gain and postural control method on distal pointing performance. Int. J. Ind. Ergon. 2019, 72, 45–53. [Google Scholar] [CrossRef]
- Patel, S.N.; Abowd, G.D. A 2-Way Laser-Assisted Selection Scheme for Handhelds in a Physical Environment. Computer Vision 2003, 2864, 200–207. [Google Scholar]
- Parker, J.K.; Mandryk, R.L.; Nunes, M.N.; Inkpen, K. TractorBeam Selection Aids: Improving Target Acquisition for Pointing Input on Tabletop Displays. In Proceedings of the Computer Vision; Springer: Berlin/Heidelberg, Germany, 2005; pp. 80–93. [Google Scholar]
- Bowman, D.A.; Wingrave, C.A.; Campbell, J.M.; Ly, V.Q.; Rhoton, C.J. Novel Uses of Pinch Gloves™ for Virtual Environment Interaction Techniques. Virtual Real. 2002, 6, 122–129. [Google Scholar] [CrossRef]
- Bowman, D.A.; Hodges, L.F. An Evaluation of Techniques for Grabbing and Manipulating Remote Objects in Immersive Virtual Environments. In Proceedings of the 1997 Symposium on Interactive 3D Graphics—SI3D ’97; Association for Computing Machinery (ACM): New York, NY, USA, 1997. [Google Scholar]
- Chang, Y.S.; Nuernberger, B.; Luan, B.; Hollerer, T. Evaluating gesture-based augmented reality annotation. In Proceedings of the 2017 IEEE Symposium on 3D User Interfaces (3DUI), Los Angeles, CA, USA, 18–19 March 2017; pp. 182–185. [Google Scholar]
- Schweigert, R.; Schwind, V.; Mayer, S. EyePointing. In Proceedings of the Mensch und Computer—MuC ’19; Association for Computing Machinery (ACM): New York, NY, USA, 2019; pp. 719–723. [Google Scholar]
- McMahan, R.P.; Kopper, R.; Bowman, D.A. Chapter 12: Principles for Designing Effective 3D Interaction Techniques. In Handbook of Virtual Environments: Design, Implementation, and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 285–311. [Google Scholar]
- Argelaguet, F.; Andujar, C. A survey of 3D object selection techniques for virtual environments. Comput. Graph. 2013, 37, 121–136. [Google Scholar] [CrossRef]
- Bachmann, D.; Weichert, F.; Rinkenauer, G. Review of Three-Dimensional Human-Computer Interaction with Focus on the Leap Motion Controller. Sensors 2018, 18, 2194. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Cai, X.; Wang, L.; Tian, H. Interactive Design of 3D Dynamic Gesture Based on SVM-LSTM Model. Int. J. Mob. Hum. Comput. Interact. 2018, 10, 49–63. [Google Scholar] [CrossRef]
- Liu, L.; Huai, Y.; Long, L.; Yongjian, H. Dynamic Hand Gesture Recognition Using LMC for Flower and Plant Interaction. Int. J. Pattern Recognit. Artif. Intell. 2018, 33, 1950003. [Google Scholar] [CrossRef]
- Ameur, S.; Ben Khalifa, A.; Bouhlel, M.S. A comprehensive leap motion database for hand gesture recognition. In Proceedings of the 7th International Conference on Sciences of Electronics, Technologies of Information and Telecommunications (SETIT), Hammamet, Tunisia, 18–20 December 2016. [Google Scholar]
- Lee, J.H.; An, S.-G.; Kim, Y.; Bae, S.-H.; Gajos, K.; Mankoff, J.; Harrison, C. Projective Windows. In Proceedings of the Adjunct Publication of the 30th Annual ACM Symposium on User Interface Software and Technology—UIST ’17; Association for Computing Machinery (ACM): New York, NY, USA, 2017; pp. 169–171. [Google Scholar]
- Luo, Y.; Gao, B.; Deng, Y.; Zhu, X.; Jiang, T.; Zhao, X.; Yang, Z. Automated brain extraction and immersive exploration of its layers in virtual reality for the rhesus macaque MRI data sets. Comput. Animat. Virtual Worlds 2018, 30, e1841. [Google Scholar] [CrossRef]
- Morse, P.; Reading, A.M.; Lueg, C.P.; Kenderdine, S. TaggerVR: Interactive Data Analytics for Geoscience—A Novel Interface for Interactive Visual Analytics of Large Geoscientific Datasets in Cloud Repositories. In 2015 Big Data Visual Analytics (BDVA); Institute of Electrical and Electronics Engineers (IEEE): New York NY, USA, 2015; pp. 1–2. [Google Scholar]
- Shen, J.; Luo, Y.; Wu, Z.; Tian, Y.; Deng, Q. CUDA-based real-time hand gesture interaction and visualization for CT volume dataset using leap motion. Vis. Comput. 2016, 32, 359–370. [Google Scholar] [CrossRef]
- Li, J.; Cho, I.; Wartell, Z. Evaluation of Cursor Offset on 3D Selection in VR. In Proceedings of the Symposium on Spatial User Interaction—SUI ’18; Association for Computing Machinery (ACM): New York, NY, USA, 2018; pp. 120–129. [Google Scholar]
- Bachmann, D.; Weichert, F.; Rinkenauer, G. Evaluation of the Leap Motion Controller as a New Contact-Free Pointing Device. Sensors 2014, 15, 214–233. [Google Scholar] [CrossRef]
- Steed, A.; Parker, C. Evaluating Effectiveness of Interaction Techniques across Immersive Virtual Environmental Systems. Presence Teleoperators Virtual Environ. 2005, 14, 511–527. [Google Scholar] [CrossRef]
- Difeng, Y.; Liang, H.-N.; Lu, F.; Nanjappan, V.; Papangelis, K. Target Selection in Head-Mounted Display Virtual Reality Environments. J. Univers. Comp. Sci. 2018, 24, 1217–1243. [Google Scholar]
- Lin, J.; Harris-Adamson, C.; Rempel, D. The Design of Hand Gestures for Selecting Virtual Objects. Int. J. Hum. Comp. Interact. 2019, 35, 1729–1735. [Google Scholar] [CrossRef]
- Figueiredo, L.; Rodrigues, E.; Teixeira, J.; Teichrieb, V.; Teixeira, J.M.; Teichrieb, V. A comparative evaluation of direct hand and wand interactions on consumer devices. Comput. Graph. 2018, 77, 108–121. [Google Scholar] [CrossRef]
- Norman, D.A. The way I see it: Natural user interfaces are not natural. Interactions 2010, 17, 6–10. [Google Scholar] [CrossRef]
- El Jamiy, F.; Marsh, R. Survey on depth perception in head mounted displays: Distance estimation in virtual reality, augmented reality, and mixed reality. IET Image Process. 2019, 13, 707–712. [Google Scholar] [CrossRef]
- Alger, M. Visual Design Methods for Virtual Reality. Available online: http://aperturesciencellc.com/vr/CARD.pdf (accessed on 10 October 2020).
- Loup-Escande, E.; Jamet, E.; Ragot, M.; Erhel, S.; Michinov, N. Effects of Stereoscopic Display on Learning and User Experience in an Educational Virtual Environment. Int. J. Hum. Comp. Interact. 2016, 33, 115–122. [Google Scholar] [CrossRef]
- Previc, F.H. The neuropsychology of 3-D space. Psychol. Bull. 1998, 124, 123–164. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.; Liang, H.-N.; Lu, X.; Fan, K.; Ens, B. Modeling endpoint distribution of pointing selection tasks in virtual reality environments. ACM Trans. Graph. 2019, 38, 1–13. [Google Scholar] [CrossRef]
- Cheok, M.J.; Omar, Z.; Jaward, M.H. A review of hand gesture and sign language recognition techniques. Int. J. Mach. Learn. Cybern. 2017, 10, 131–153. [Google Scholar] [CrossRef]
- Zengeler, N.; Kopinski, T.; Handmann, U. Hand Gesture Recognition in Automotive Human–Machine Interaction Using Depth Cameras. Sensors 2018, 19, 59. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.; Kim, H.; Kim, B.; Kim, J.-I. Artificial Landmarks to Facilitate Spatial Learning and Recalling for Curved Visual Wall Layout in Virtual Reality. In Proceedings of the IEEE International Conference on Big Data and Smart Computing (BigComp), Shanghai, China, 15–18 January 2018. [Google Scholar]
- Marichal, T.; Bedoret, D.; Mesnil, C.; Pichavant, M.; Goriely, S.; Trottein, F.; Cataldo, D.D.; Goldman, M.; Lekeux, P.; Bureau, F. Interferon response factor 3 is essential for house dust mite–induced airway allergy. J. Allergy Clin. Immunol. 2010, 126, 836–844. [Google Scholar] [CrossRef] [PubMed]
- Hincapié-Ramos, J.D.; Ozacar, K.; Irani, P.P.; Kitamura, Y. GyroWand: An Approach to IMU-Based Raycasting for Augmented Reality. IEEE Eng. Med. Boil. Mag. 2016, 36, 90–96. [Google Scholar] [CrossRef]
- Sanz, F.A.; Andújar, C. Efficient 3D pointing selection in cluttered virtual environments. IEEE Eng. Med. Boil. Mag. 2009, 29, 34–43. [Google Scholar] [CrossRef]
- Fitts, P.M. The information capacity of the human motor system in controlling the amplitude of movement. J. Exp. Psychol. 1954, 47, 381–391. [Google Scholar] [CrossRef]
- MacKenzie, I.S. Fitts’ Law as a Research and Design Tool in Human-Computer Interaction. Hum. Comp. Interact. 1992, 7, 91–139. [Google Scholar] [CrossRef]
- Grossman, T.; Balakrishnan, R. Pointing at Trivariate Targets in 3D Environments. In Proceedings of the 2004 Conference on Human Factors in Computing Systems—CHI ’04; Association for Computing Machinery (ACM): New York, NY, USA, 2004; pp. 447–454. [Google Scholar]
- Cha, Y.; Myung, R. Extended Fitts’ law in Three-Dimensional Pointing Tasks. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2010, 54, 972–976. [Google Scholar] [CrossRef]
- Wingrave, C.A.; Bowman, D.A. Baseline factors for raycasting selection. In Proceedings of the HCI International, 2005; pp. 61–68. [Google Scholar]
- Murata, A.; Iwase, H. Extending Fitts’ law to a three-dimensional pointing task. Hum. Mov. Sci. 2001, 20, 791–805. [Google Scholar] [CrossRef]
- Huesmann, L.R.; Card, S.K.; Moran, T.P.; Newell, A. The Psychology of Human-Computer Interaction. Am. J. Psychol. 1984, 97, 625. [Google Scholar] [CrossRef]
- Teather, R.J.; Stuerzlinger, W. Pointing at 3D targets in a stereo head-tracked virtual environment. In Proceedings of the IEEE Symposium on 3D User Interfaces (3DUI), Singapore, 19–20 March 2011. [Google Scholar]
- Olsen, D.R., Jr.; Nielsen, T. Laser Pointer Interaction. In Proceedings of the 27th International Conference on Human Factors in Computing Systems—CHI 09; Association for Computing Machinery (ACM): New York, NY, USA, 2001; pp. 17–22. [Google Scholar] [CrossRef]
- Bateman, S.; Mandryk, R.L.; Gutwin, C.; Xiao, R. Analysis and comparison of target assistance techniques for relative ray-cast pointing. Int. J. Hum. Comput. Stud. 2013, 71, 511–532. [Google Scholar] [CrossRef]
- Patterson, R.; Winterbottom, M.D.; Pierce, B.J. Perceptual Issues in the Use of Head-Mounted Visual Displays. Hum. Factors J. Hum. Factors Ergon. Soc. 2006, 48, 555–573. [Google Scholar] [CrossRef]
- Drasdo, N. The neural representation of visual space (reply). Nat. Cell Biol. 1978, 276, 422. [Google Scholar] [CrossRef]
- Andersen, R.A.; Snyder, L.H.; Li, C.-S.; Stricanne, B. Coordinate transformations in the representation of spatial information. Curr. Opin. Neurobiol. 1993, 3, 171–176. [Google Scholar] [CrossRef]
- Andersen, R.A.; Buneo, C.A. Intentional Maps in Posterior Parietal Cortex. Annu. Rev. Neurosci. 2002, 25, 189–220. [Google Scholar] [CrossRef]
- Bosco, A.; Piserchia, V.; Fattori, P. Multiple Coordinate Systems and Motor Strategies for Reaching Movements When Eye and Hand Are Dissociated in Depth and Direction. Front. Hum. Neurosci. 2017, 11, 1–15. [Google Scholar] [CrossRef]
- Ens, B.; Hincapié-Ramos, J.D.; Irani, P. Ethereal Planes. In Proceedings of the 2nd ACM Symposium on Computing for Development—ACM DEV ’12; Association for Computing Machinery (ACM): New York, NY, USA, 2014; pp. 2–12. [Google Scholar]
- Ens, B.; Finnegan, R.; Irani, P.P. The personal cockpit. In Proceedings of the 32nd Annual ACM Conference on Human Factors in Computing Systems—CHI ’14; Association for Computing Machinery (ACM): New York, NY, USA, 2014; pp. 3171–3180. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).