Reinforcement Learning Approach to Design Practical Adaptive Control for a Small-Scale Intelligent Vehicle
Abstract
:1. Introduction
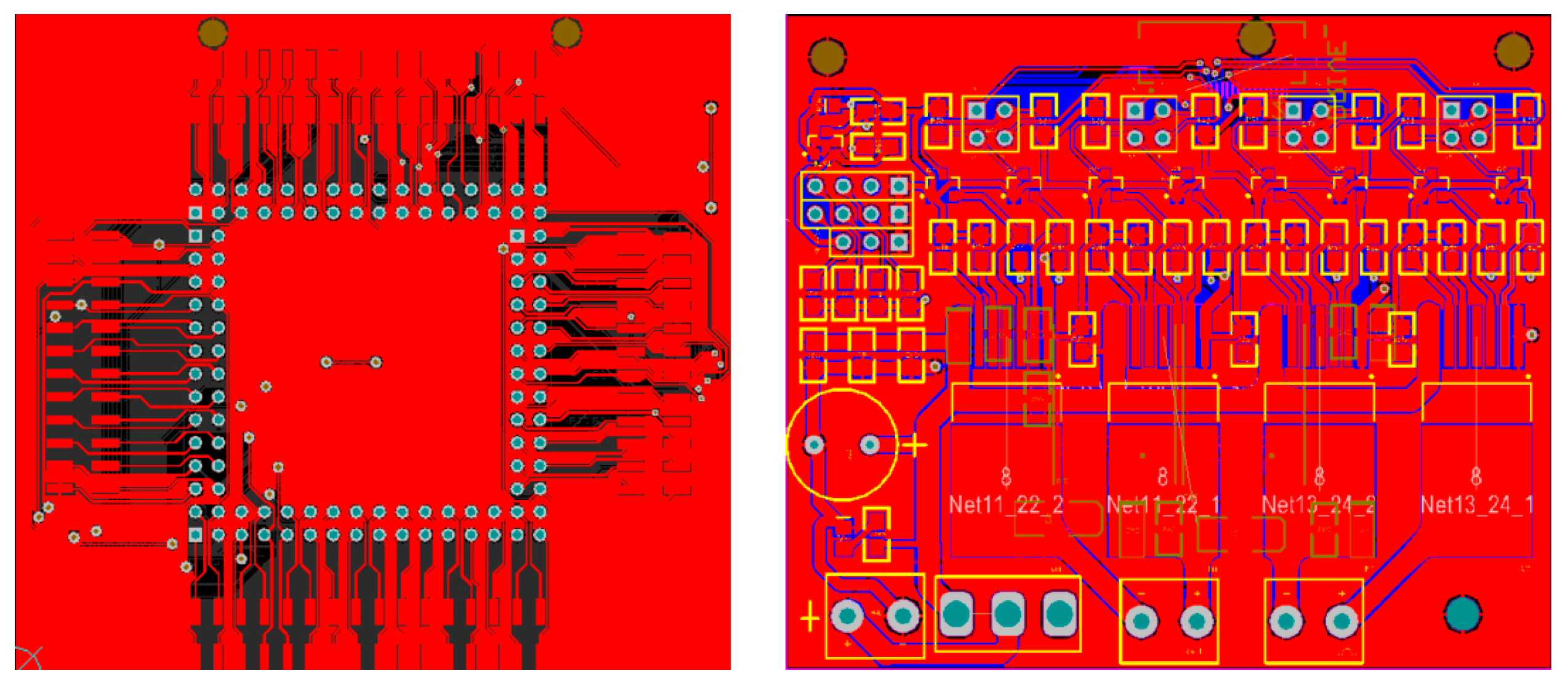
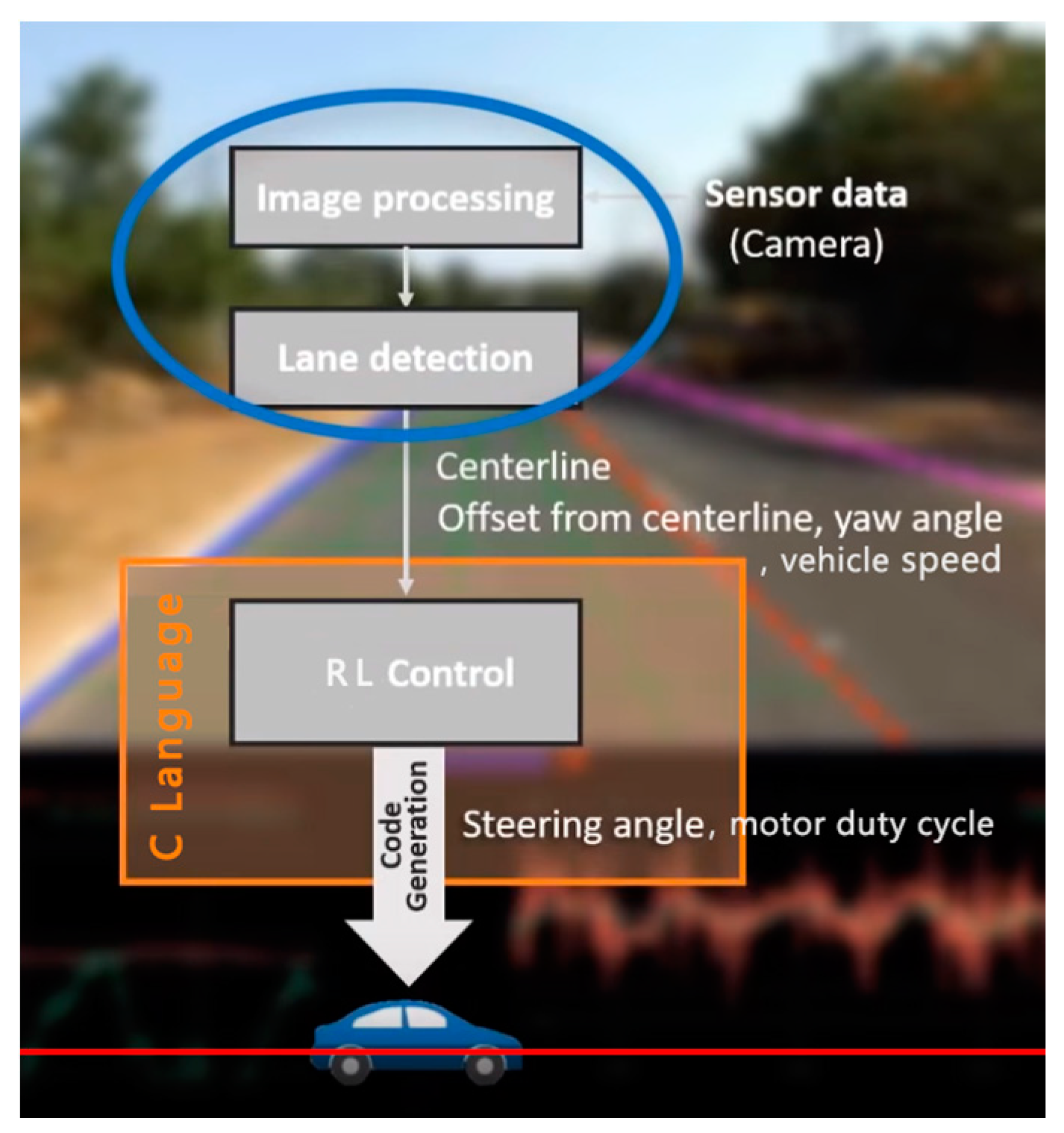
2. Experimental Setup
3. Control Strategy Based on Reinforcement Learning
3.1. Problem Formulation
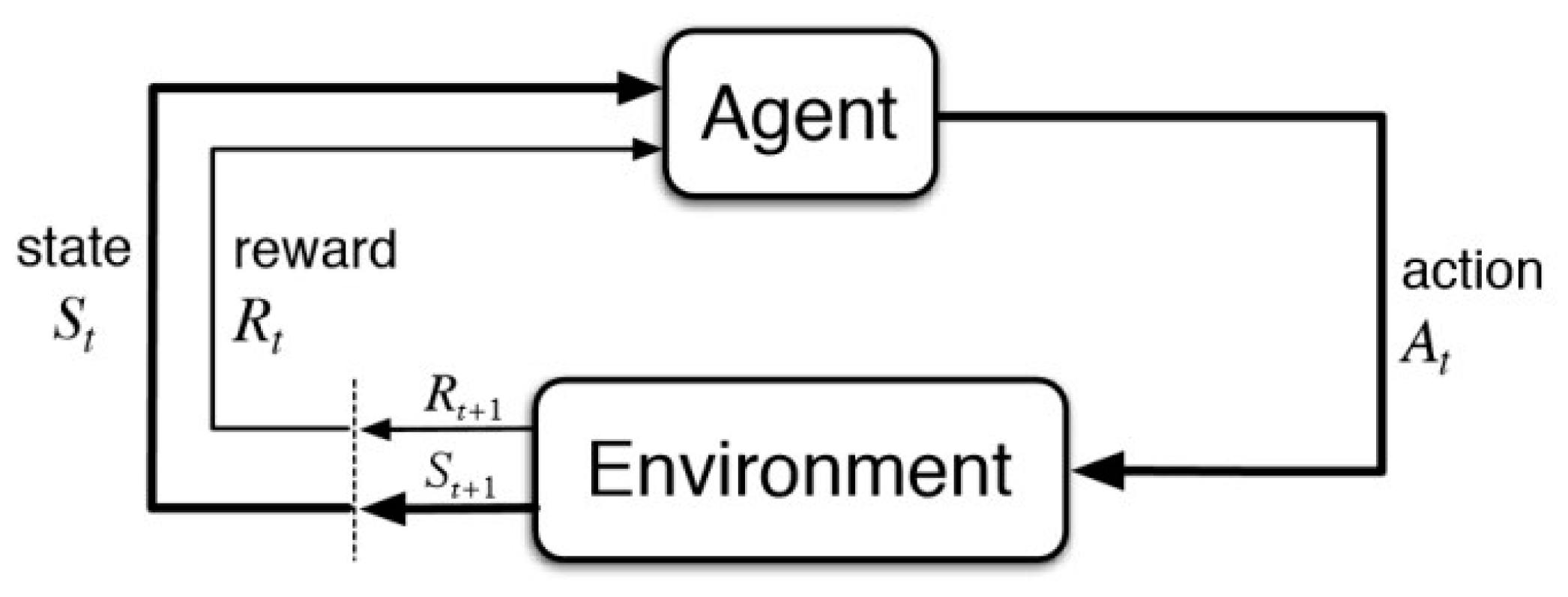
3.2. The Key Concept of Reinforcement Learning
3.3. The Q-Learning Algorithm
| Algorithm 1. The Q-learning algorithm pseudo code. |
3.4. The Sarsa Algorithm
| Algorithm 2. The Sarsa algorithm pseudo code. |
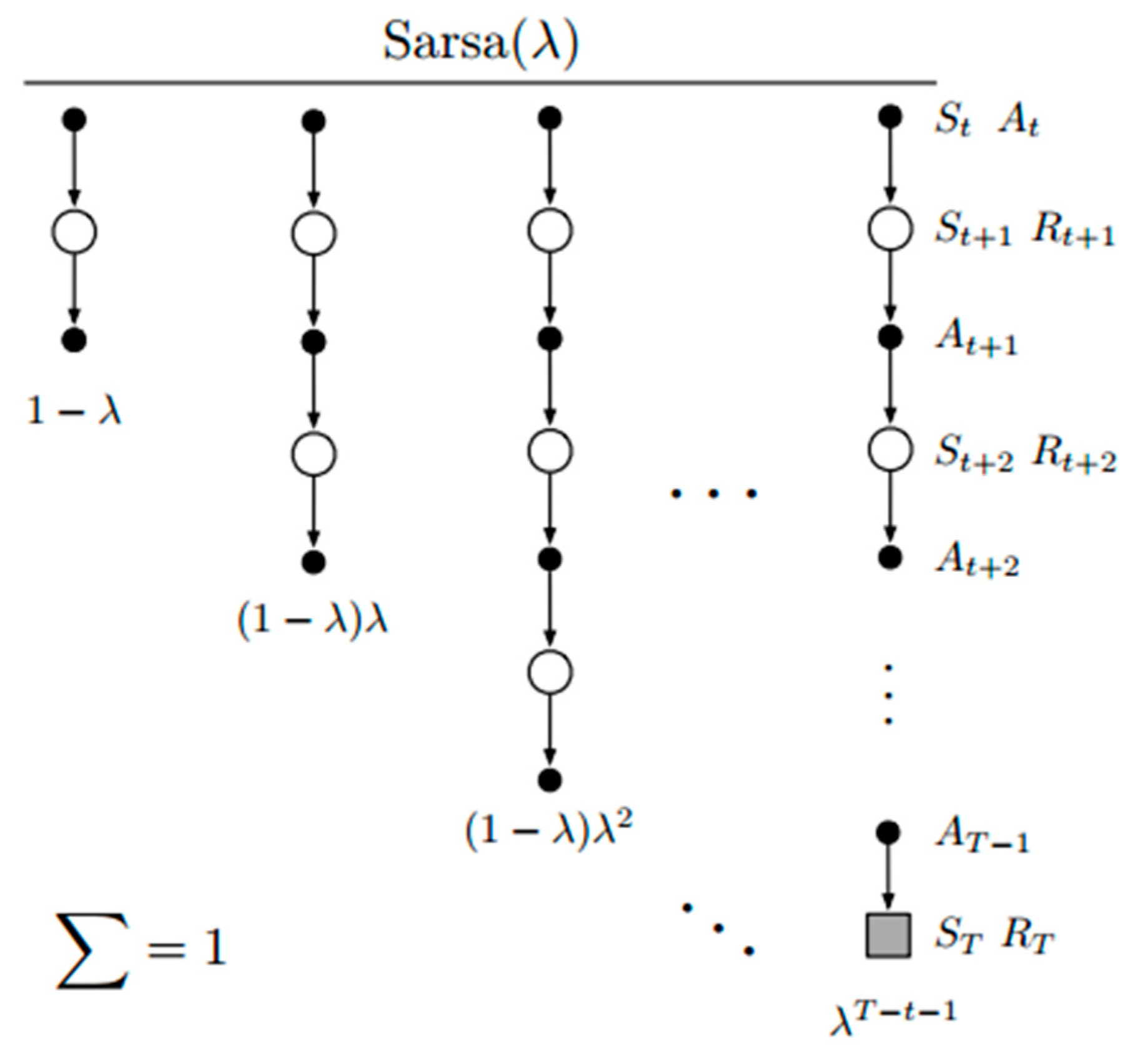
3.5. The Sarsa (λ) Algorithm
| Algorithm 3. The Sarsa (λ) algorithm pseudo code. |
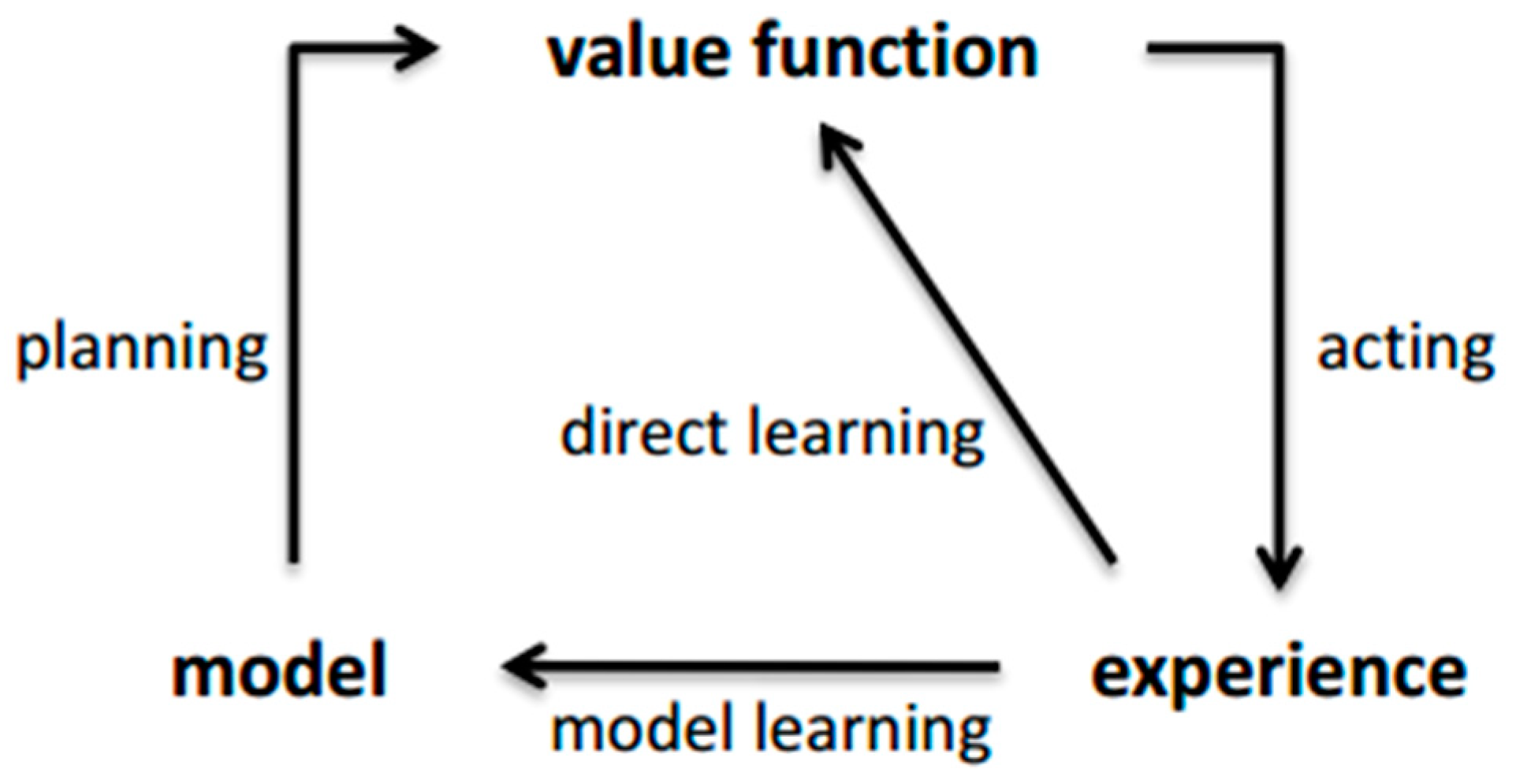
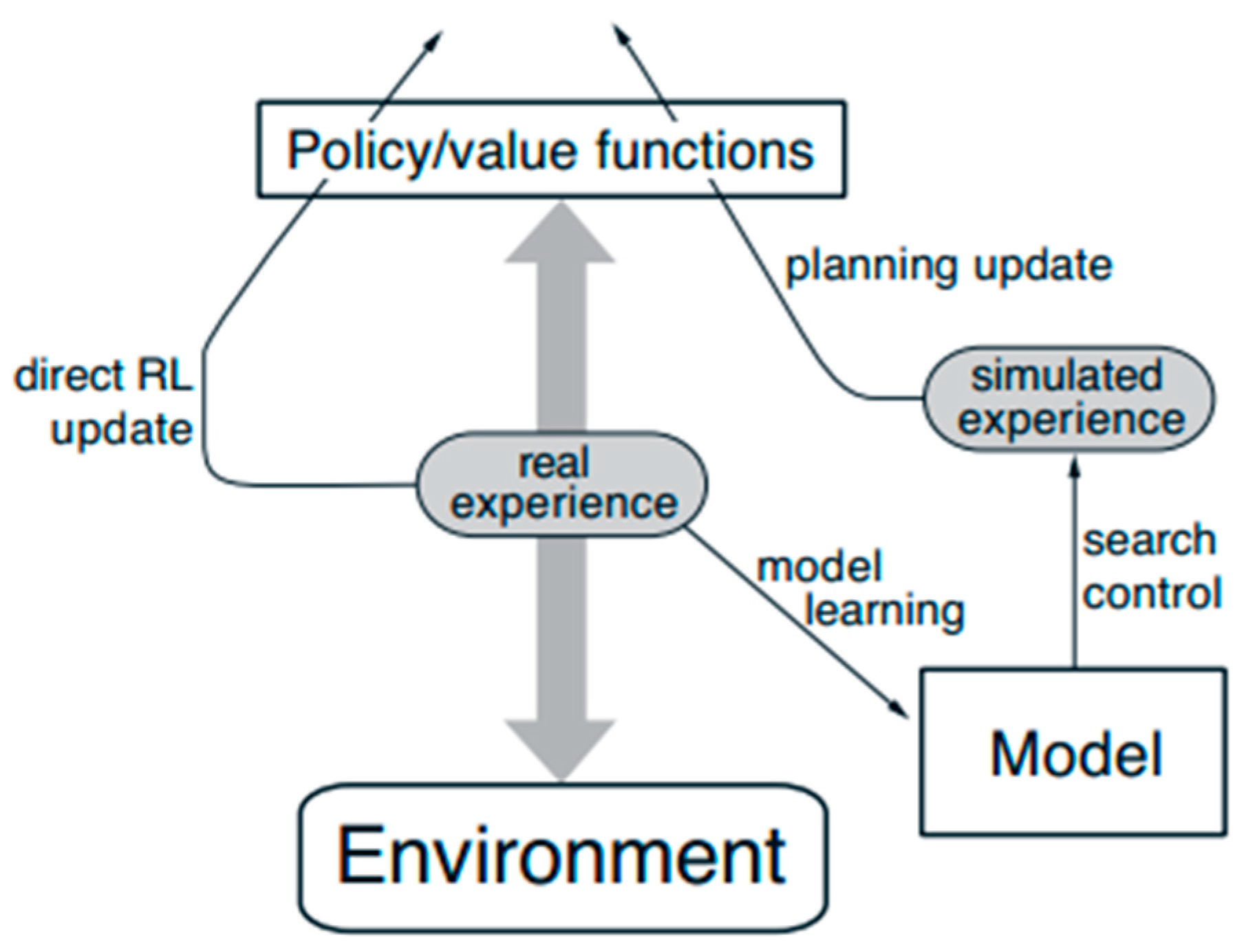
3.6. Dyna-Q Algorithm
| Algorithm 4. The Dyna-Q algorithm pseudo code. |
4. Experimental Results and Discussion
4.1. Tracking Control at Constant Vehicle Velocity
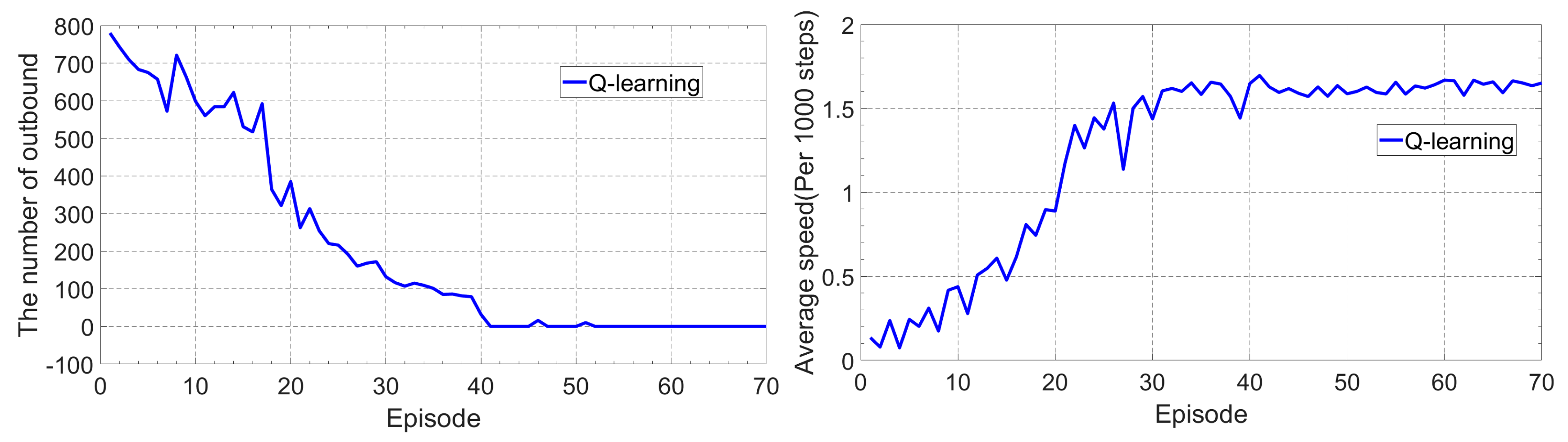
4.2. Tracking Control While Learning to Increament the Vehicle Speed
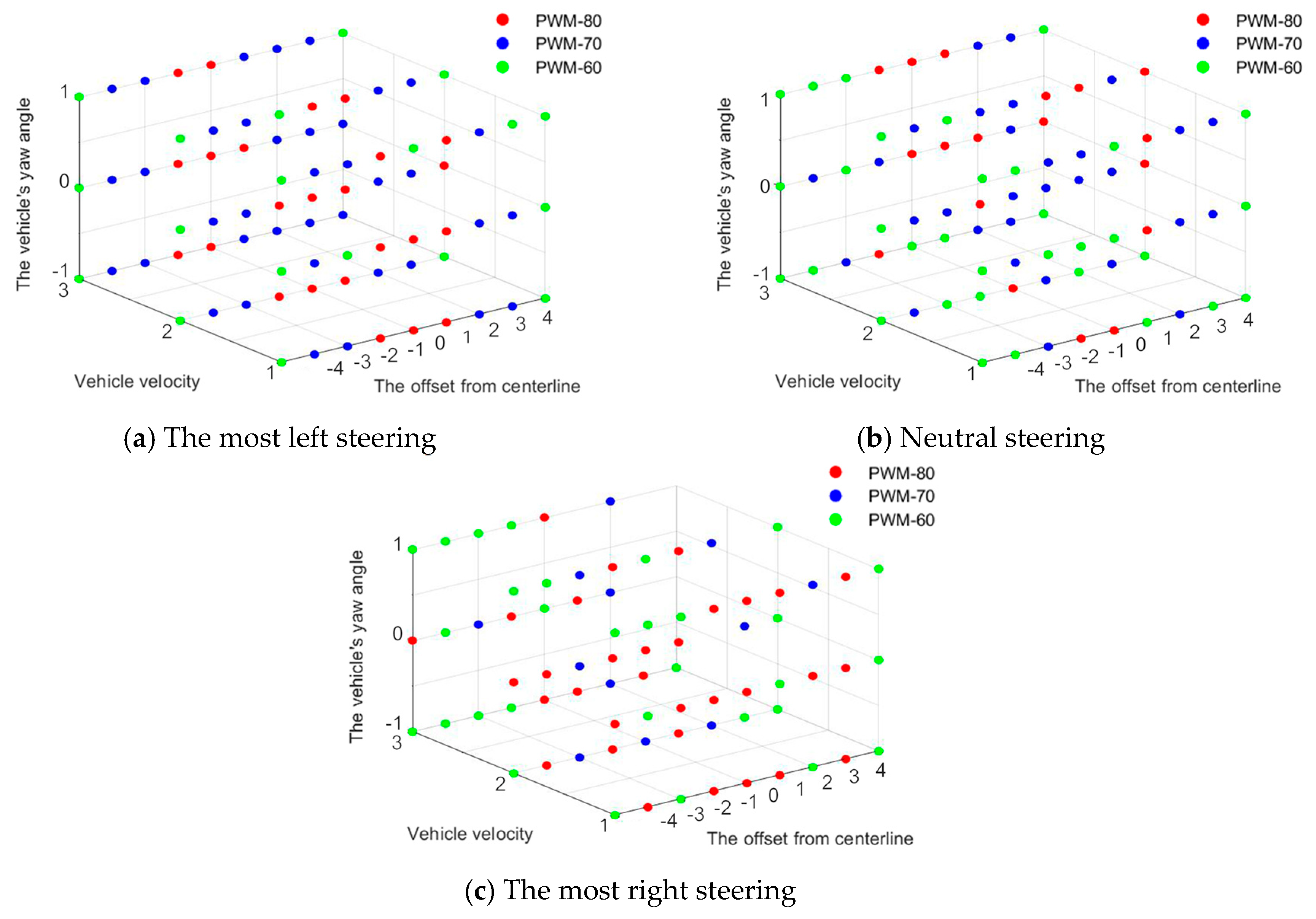
4.3. Steering Control at Adaptive Velocity
5. Conclusions
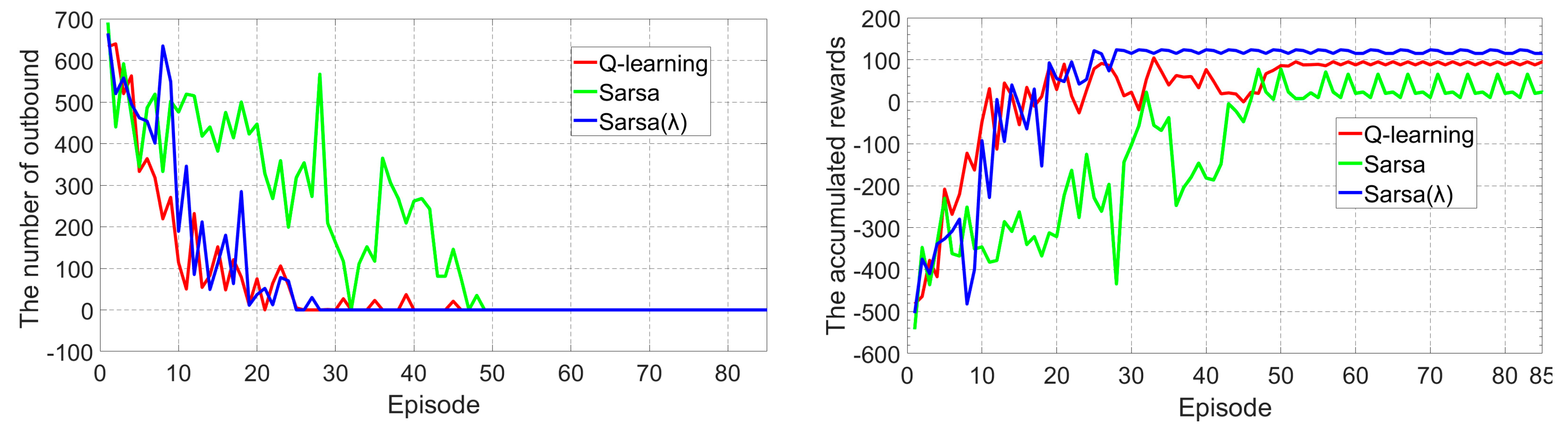
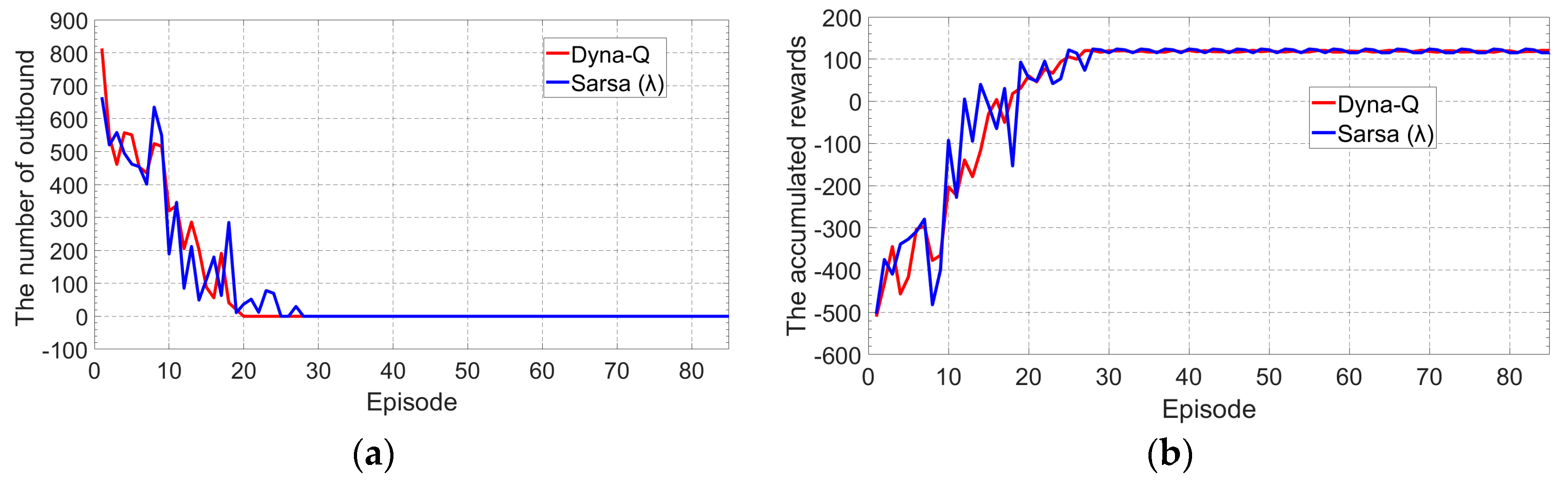
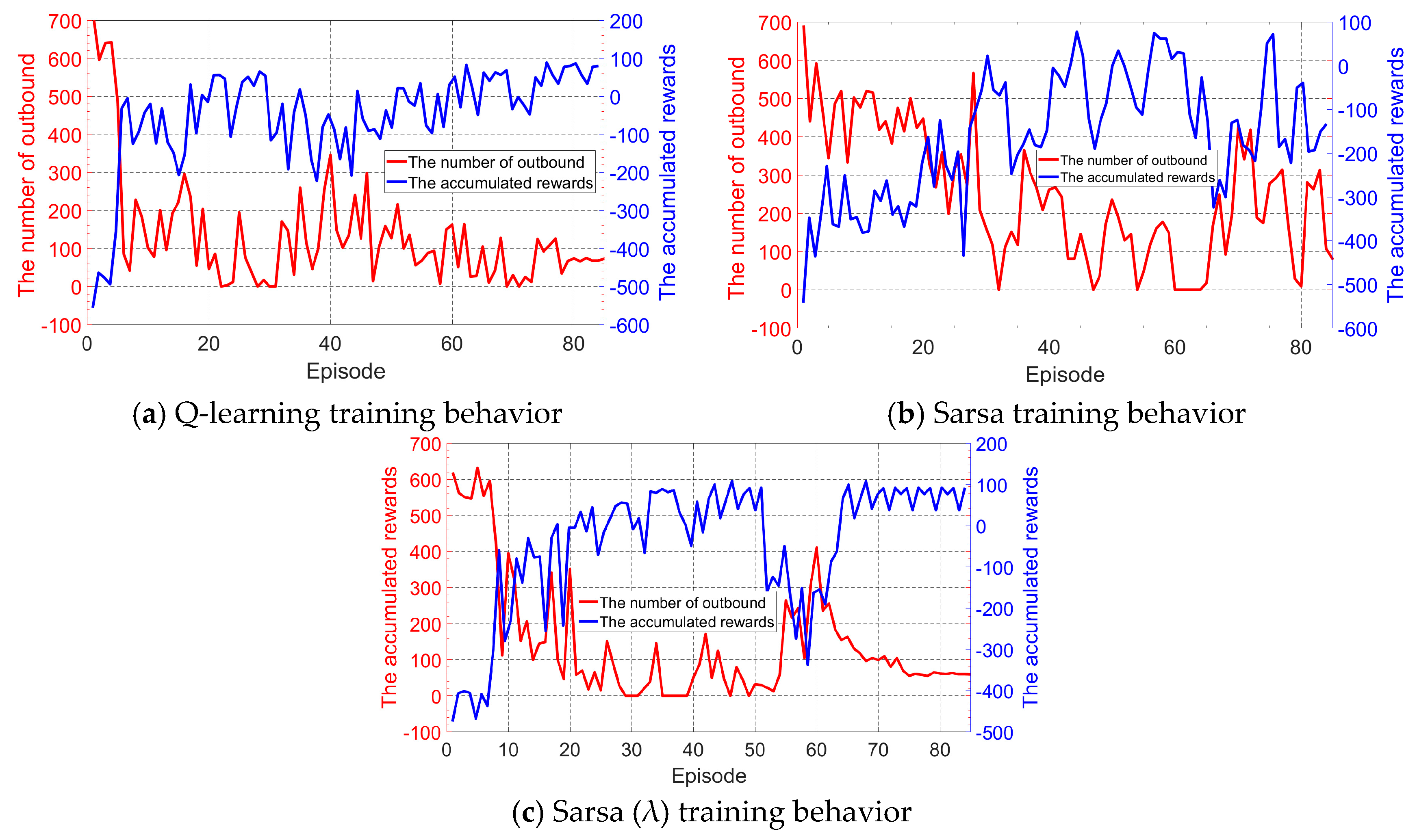
- The Q-learning and Sarsa (λ) algorithms can achieve a better tracking behavior than the conventional Sarsa, although they all can converge within a small number of training episodes. In addition, the converging speed and the final tracking behavior of Sarsa (λ) seems to be better than Q-learning by a small margin, but Q-learning outperforms Sarsa (λ) in terms of computational complexity and thus is more suitable for the vehicle’s real time learning and control.
- The Dyna-Q method, which can learn both in the model and in the environment interaction, performs similarly with the Sarsa (λ) algorithms, but with a significant reduction of computational time.
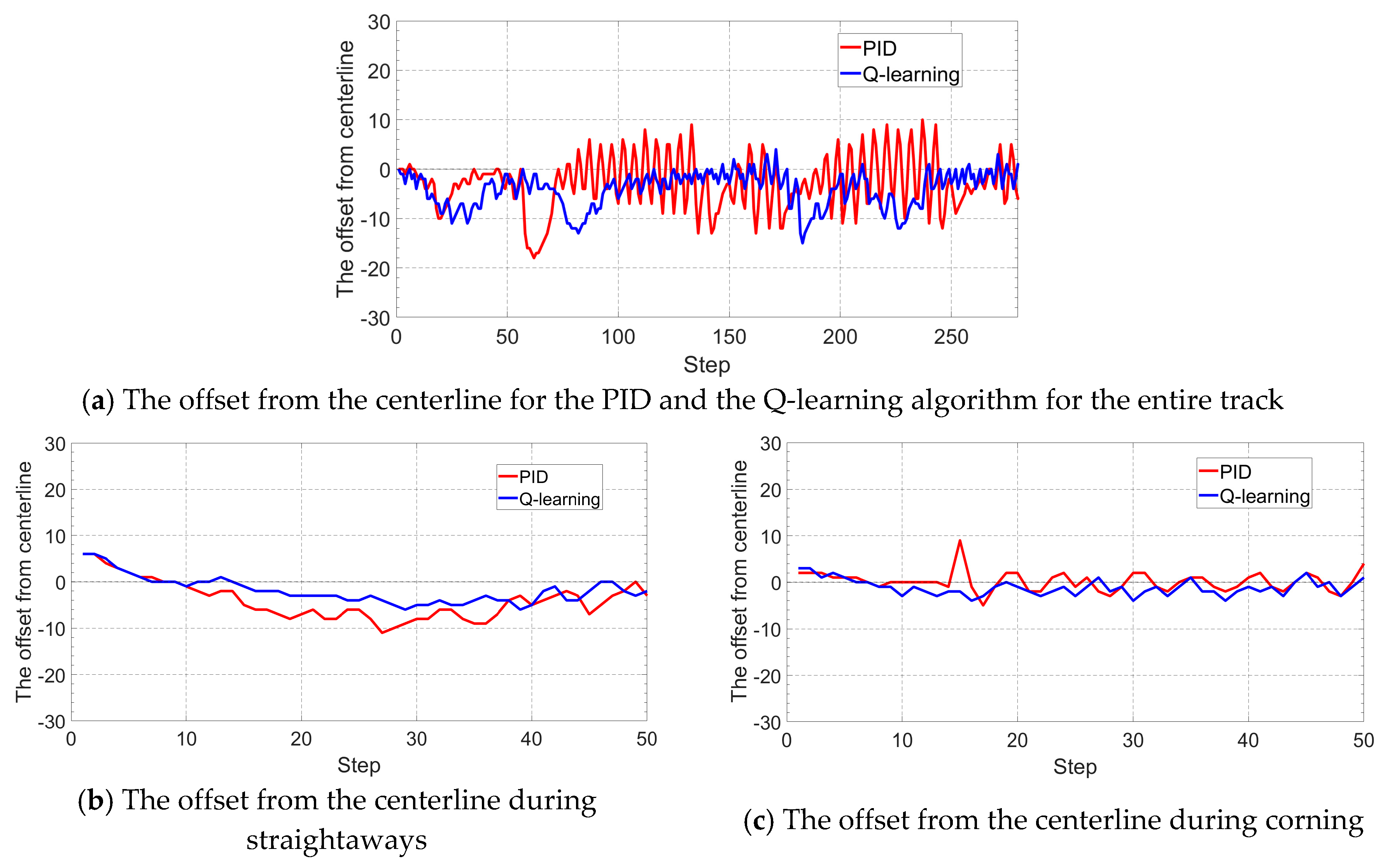
- The Q-learning algorithm with a good balance between the converging speed, the computational complexity, and the final control behavior is seen to perform better compared with a fine-tune PID controller in terms of adaptability and tuning efficiency, and the Q-learning method can also be easily applied to control problems with over one control actions, putting it as more suitable for the self-driving vehicle control whose steering angle and vehicle speed needs to be regulated simultaneously.
Author Contributions
Funding
Data Availability
Conflicts of Interest
References
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Broggi, A.; Cerri, P.; Debattisti, S.; Laghi, M.C.; Medici, P.; Molinari, D.; Panciroli, M.; Prioletti, A. PROUD—Public Road Urban Driverless-Car Test. IEEE Trans. Intell. Transp. Syst. 2015, 16, 3508–3519. [Google Scholar] [CrossRef]
- Li, L.; Huang, W.; Liu, Y.; Zheng, N.; Wang, F. Intelligence Testing for Autonomous Vehicles: A New Approach. IEEE Trans. Intell. Veh. 2016, 1, 158–166. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, M.; Zhang, F.; Jin, S.; Zhang, J.; Zhao, X. Patavtt: A hardware-in-the-loop scaled platform for testing autonomous vehicle trajectory tracking. J. Adv. Transp. 2017, 1–11. [Google Scholar] [CrossRef]
- From the Lab to the Street: Solving the Challenge of Accelerating Automated Vehicle Testing. Available online: http://www.hitachi.com/rev/archive/2018/r2018_01/trends2/index.html/ (accessed on 1 September 2019).
- Ruz, M.L.; Garrido, J.; Vazquez, F.; Morilla, F. Interactive Tuning Tool of Proportional-Integral Controllers for First Order Plus Time Delay Processes. Symmetry 2018, 10, 569. [Google Scholar] [CrossRef]
- Liu, X.; Shi, Y.; Xu, J. Parameters Tuning Approach for Proportion Integration Differentiation Controller of Magnetorheological Fluids Brake Based on Improved Fruit Fly Optimization Algorithm. Symmetry 2017, 9, 109. [Google Scholar] [CrossRef]
- Chee, F.; Fernando, T.L.; Savkin, A.V.; Heeden, V.V. Expert PID Control System for Blood Glucose Control in Critically Ill Patients. IEEE Trans. Inf. Technol. Biomed. 2003, 7, 419–425. [Google Scholar] [CrossRef]
- Savran, A. A multivariable predictive fuzzy PID control system. Appl. Soft Comput. 2013, 13, 2658–2667. [Google Scholar] [CrossRef]
- Lopez_Franco, C.; Gomez-Avila, J.; Alanis, A.Y.; Arana-Daniel, N.; Villaseñor, C. Visual Servoing for an Autonomous Hexarotor Using a Neural Network Based PID Controller. Sensors 2017, 17, 1865. [Google Scholar] [CrossRef]
- Moriyama, K.; Nakase, K.; Mutoh, A.; Inuzuka, N. The Resilience of Cooperation in a Dilemma Game Played by Reinforcement Learning Agents. In Proceedings of the IEEE International Conference on Agents (ICA), Beijing, China, 6–9 July 2017. [Google Scholar]
- Meng, Q.; Tholley, I.; Chung, P.W.H. Robots learn to dance through interaction with humans. Neural Comput. Appl. 2014, 24, 117–124. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, L.; Li, N.; Wang, W.; Zhong, S.; Hu, K. Minimizing mean weighted tardiness in unrelated parallel machine scheduling with reinforcement learning. Comput. Oper. Res. 2012, 39, 1315–1324. [Google Scholar] [CrossRef]
- Iwata, K. An Information-Theoretic Analysis of Return Maximization in Reinforcement Learning. Neural Netw. 2011, 24, 1074–1081. [Google Scholar] [CrossRef] [PubMed]
- Jalalimanesh, A.; Haghighi, H.S.; Ahmadi, A.; Soltani, M. Simulation-based optimization of radiotherapy: Agent-based modelling and reinforcement learning. Math. Comput. Simul. 2017, 133, 235–248. [Google Scholar] [CrossRef]
- Fernandez-Gauna, B.; Marques, I.; Graña, M. Undesired state-action prediction in multi-Agent reinforcement learning for linked multi-component robotic system control. Inf. Sci. 2013, 232, 309–324. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018; pp. 97–113. [Google Scholar]
- Liu, T.; Zou, Y.; Liu, D.; Sun, F. Reinforcement Learning–Based Energy Management Strategy for a Hybrid Electric Tracked Vehicle. Energies 2015, 8, 7243–7260. [Google Scholar] [CrossRef]
- Sistani, M.B.N.; Hesari, S. Decreasing Induction Motor Loss Using Reinforcement Learning. J. Autom. Control Eng. 2016, 4, 13–17. [Google Scholar] [CrossRef]
- Shen, H.; Tan, Y.; Lu, J.; Wu, Q.; Qiu, Q. Achieving Autonomous Power Management Using Reinforcement Learning. ACM Trans. Des. Autom. Electron. Syst. 2013, 18, 1–24. [Google Scholar] [CrossRef]
- Anderlini, E.; Forehand, D.I.M.; Stansell, P.; Xiao, Q.; Abusara, M. Control of a Point Absorber using Reinforcement Learning. IEEE Trans. Sustain Energy 2016, 7, 1681–1690. [Google Scholar] [CrossRef]
- Sun, J.; Huang, G.; Sun, G.; Yu, H.; Sangaiah, A.K.; Chang, V. A Q-Learning-Based Approach for Deploying Dynamic Service Function Chains. Symmetry 2018, 10, 646. [Google Scholar] [CrossRef]
- Aissani, N.; Beldjilali, B.; Trentesaux, D. Dynamic scheduling of maintenance tasks in the petroleum industry: A reinforcement approach. Eng. Appl. Artif. Intell. 2009, 22, 1089–1103. [Google Scholar] [CrossRef]
- Habib, A.; Khan, M.I.; Uddin, J. Optimal Route Selection in Complex Multi-stage Supply Chain Networks using SARSA(λ). In Proceedings of the 19th International Conference on Computer and Information Technology, North South University, Dhaka, Bangladesh, 18–20 December 2016. [Google Scholar]
- Li, Z.; Lu, Y.; Shi, Y.; Wang, Z.; Qiao, W.; Liu, Y. A Dyna-Q-Based Solution for UAV Networks Against Smart Jamming Attacks. Symmetry 2019, 11, 617. [Google Scholar] [CrossRef]
- Mit-Racecar. Available online: http//www.Github.com/mit-racecar/ (accessed on 28 April 2019).
- Berkeley Autonomous Race Car. Available online: http//www.barc-project.com/ (accessed on 28 April 2019).
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the Game of Go without Human Knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Pandey, P.; Pandey, D.; Kumar, S. Reinforcement Learning by Comparing Immediate Reward. Int. J. Comput. Sci. Inf. Secur. 2010, 8, 1–5. [Google Scholar]
- Liu, T.; Hu, X.; Li, S.E.; Cao, D. Reinforcement Learning Optimized Look-Ahead Energy Management of a Parallel Hybrid Electric Vehicle. IEEE/ASME Trans. Mechatron. 2017, 22, 1497–1507. [Google Scholar] [CrossRef]




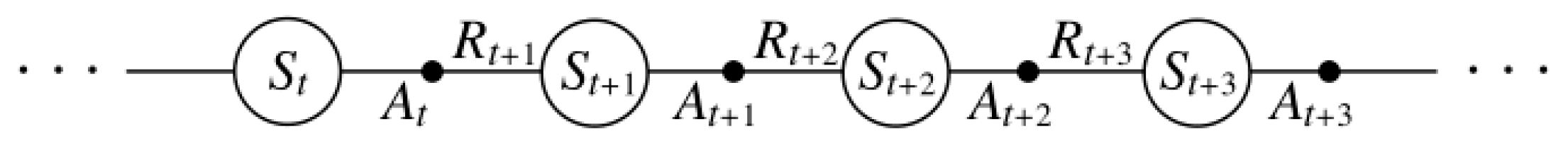
| Q-Learning | Sarsa | Sarsa (λ) | Dyna-Q | |
|---|---|---|---|---|
| Minimum episodes to converge | 45 | 50 | 28 | 20 |
| Final accumulated reward per episode | 9511 | 6578 | 12,204 | 12,506 |
| Single step calculation time (%) * | 100 | 100 | 1335 | 766 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Li, J.; Yang, J.; Bai, H.; Li, S.; Sun, Y.; Yang, X. Reinforcement Learning Approach to Design Practical Adaptive Control for a Small-Scale Intelligent Vehicle. Symmetry 2019, 11, 1139. https://doi.org/10.3390/sym11091139
Hu B, Li J, Yang J, Bai H, Li S, Sun Y, Yang X. Reinforcement Learning Approach to Design Practical Adaptive Control for a Small-Scale Intelligent Vehicle. Symmetry. 2019; 11(9):1139. https://doi.org/10.3390/sym11091139
Chicago/Turabian StyleHu, Bo, Jiaxi Li, Jie Yang, Haitao Bai, Shuang Li, Youchang Sun, and Xiaoyu Yang. 2019. "Reinforcement Learning Approach to Design Practical Adaptive Control for a Small-Scale Intelligent Vehicle" Symmetry 11, no. 9: 1139. https://doi.org/10.3390/sym11091139
APA StyleHu, B., Li, J., Yang, J., Bai, H., Li, S., Sun, Y., & Yang, X. (2019). Reinforcement Learning Approach to Design Practical Adaptive Control for a Small-Scale Intelligent Vehicle. Symmetry, 11(9), 1139. https://doi.org/10.3390/sym11091139





