Personalized Product Evaluation Based on GRA-TOPSIS and Kansei Engineering
Abstract
:1. Introduction
- We define a matrix variate (Kansei decision matrix, KDM) to describe the satisfaction of user requirements. The KDM taking a user’ requirements as the PIS, and the farthest from requirements constitute the NIS. To extend MCDM methods to user-specific subjective product evaluation, we replace the decision matrix with KDM.
- Taking the KDM as input, the entropy method is used to acquire the objective weights. Moreover, adopt AHP to get subjective weights. Then, the game theory is used to optimize the two types of weights to obtain comprehensive weights, which is one of the inputs of KE-GRA-TOPSIS.
- We combine AHP and KE to construct user requirements into a hierarchy (evaluation system). Specifically, we adopt AHP to establish a hierarchical structure, and KE is used to obtain criteria and indexes.
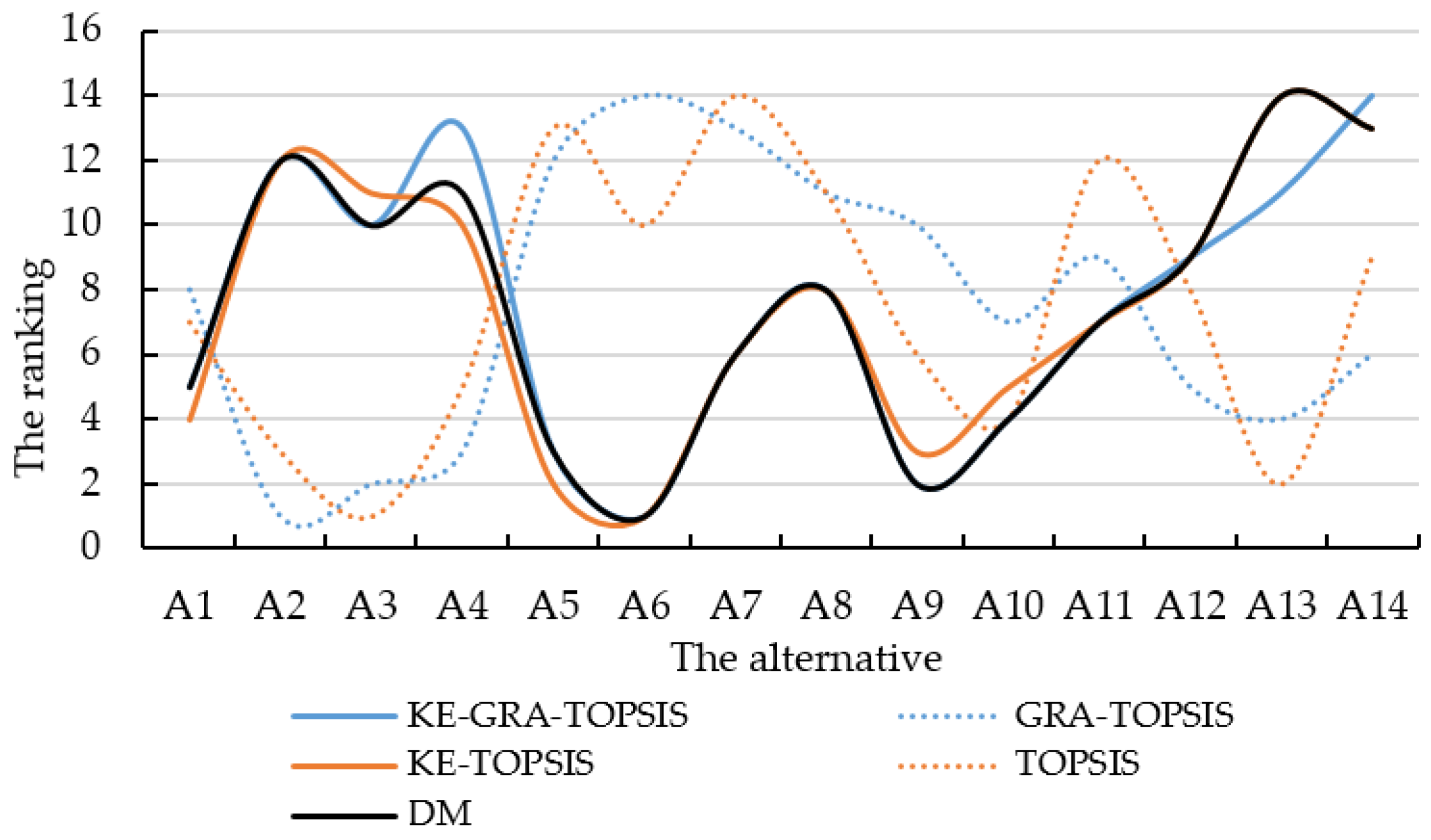
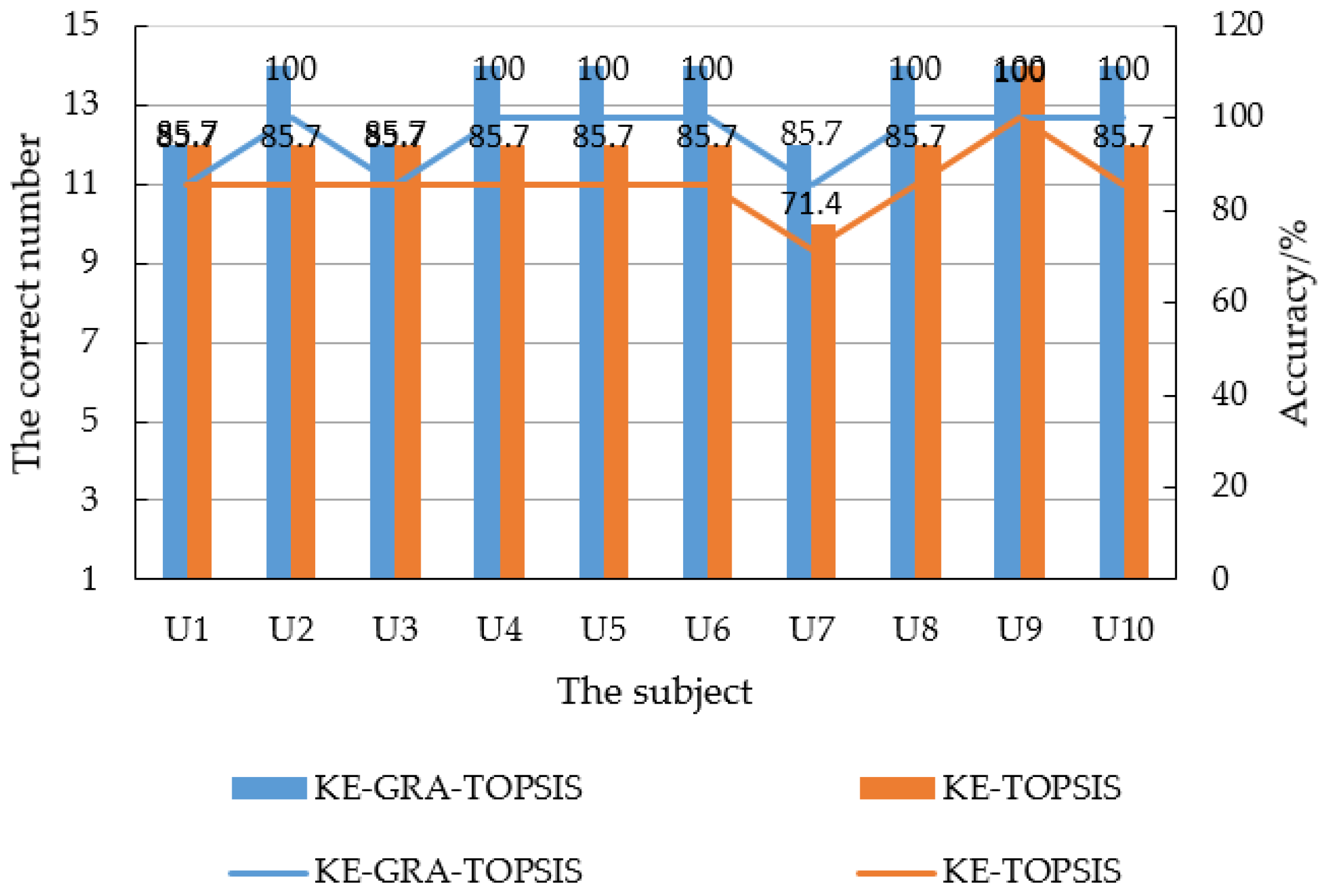
- Taking the electric drill as an example, we compared DM’s choice with the ranking results of KE-GRA-TOPSIS, KE-TOPSIS, KE-GRA, GRA-TOPSIS, and TOPSIS methods. It is shown that KE-GRA-TOPSIS outperforms other methods in terms of accuracy.
2. Methods
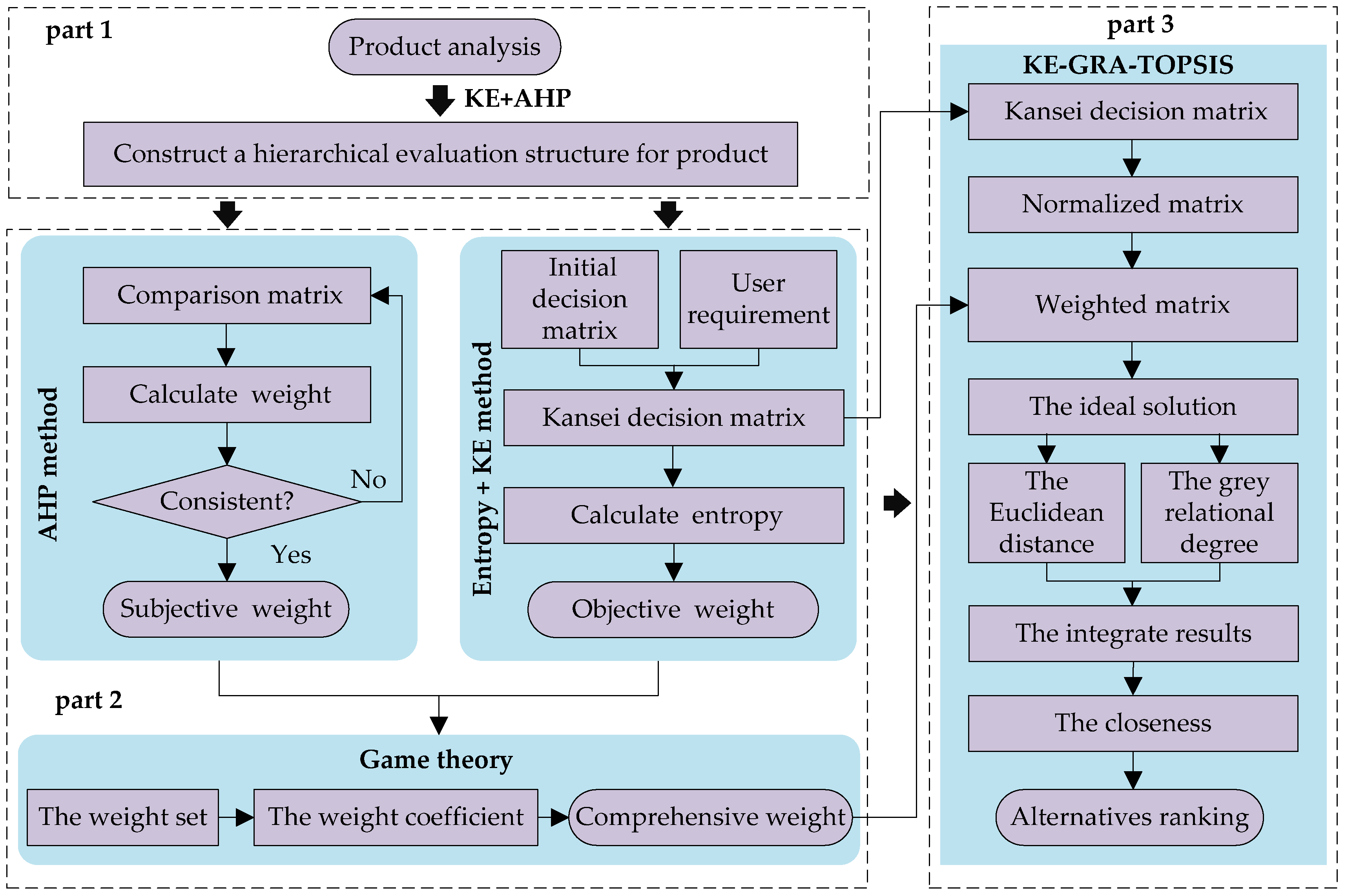
2.1. Research Framework
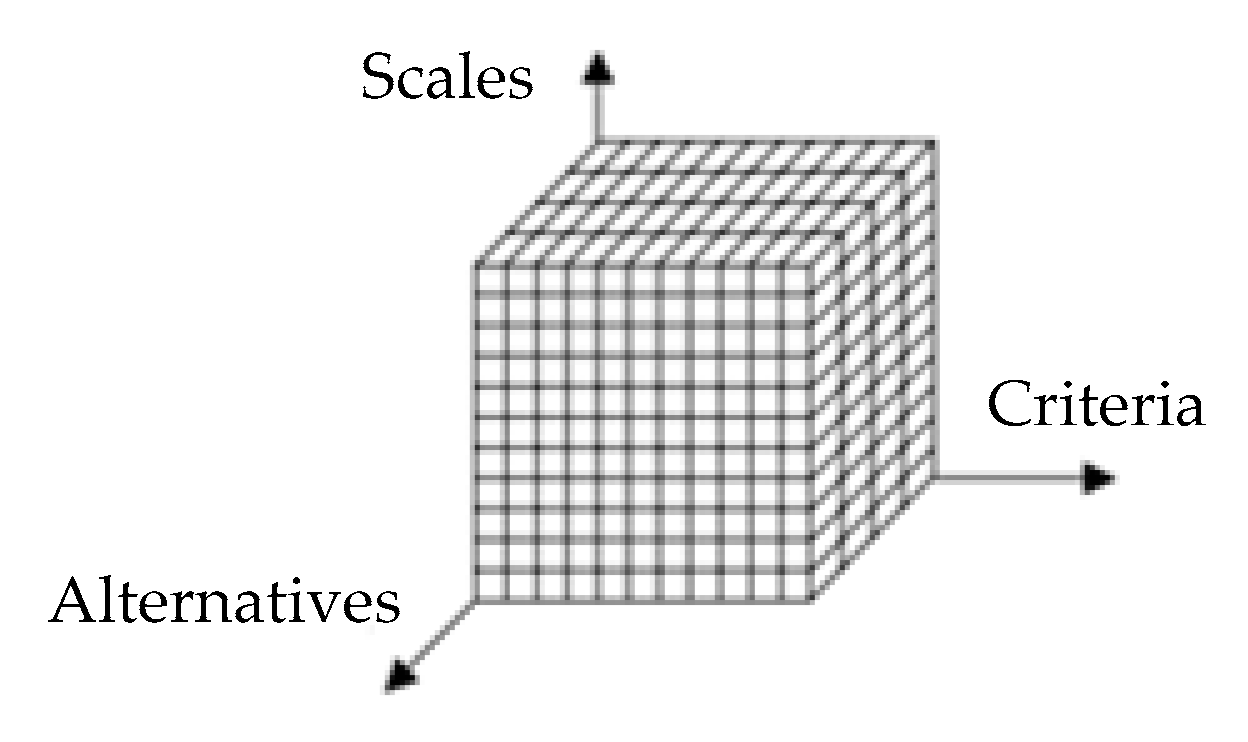
2.2. KE Method
2.3. AHP Method
2.4. Entropy Method
2.5. Game Theory
2.6. GRA-TOPSIS Method
3. Empirical Study
3.1. Evaluation System and Alternatives
3.2. Criteria Weighting
3.3. Alternative Ranking
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Story, V.M.; Boso, N.; Cadogan, J.W. The form of relationship between firm-level product innovativeness and new product performance in developed and emerging markets. J. Prod. Innov. Manag. 2015, 32, 45–64. [Google Scholar] [CrossRef]
- Bányai, T. Economic aspects of decision making in production processes with uncertain component quality. Eng. Econ. 2019, 30, 4–13. [Google Scholar] [CrossRef]
- Kuo, Y.-F.; Wu, C.-M. Satisfaction and post-purchase intentions with service recovery of online shopping websites: Perspectives on perceived justice and emotions. Int. J. Inf. Manag. 2012, 32, 127–138. [Google Scholar] [CrossRef]
- Lin, C.-T.; Chen, C.-W.; Wang, S.-J.; Lin, C.-C. The influence of impulse buying toward consumer loyalty in online shopping: A regulatory focus theory perspective. J. Ambient Intell. Humaniz. Comput. 2018. [Google Scholar] [CrossRef]
- Chou, J.-R. A Kansei evaluation approach based on the technique of computing with words. Adv. Eng. Inform. 2016, 30, 1–15. [Google Scholar] [CrossRef]
- Nagamachi, M. Kansei engineering: A new ergonomic consumer-oriented technology for product development. Int. J. Ind. Erg. 1995, 15, 3–11. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making; Springer: Berlin/Heidelberg, Germany, 1981; Volume 186, pp. 58–191. [Google Scholar]
- Lei, J.; Chang, W.; Zhou, S.; Li, X.; Wei, F. Study on the Quality Evaluation Model of Diesel Engine with ANP and TOPSIS Method. In Proceedings of the 2018 Annual Reliability and Maintainability Symposium (RAMS), Reno, NV, USA, 22–25 January 2018; pp. 1–6. [Google Scholar]
- Hu, Y.-C. Classification performance evaluation of single-layer perceptron with Choquet integral-based TOPSIS. Appl. Intell. 2008, 29, 204–215. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, Z.; Huang, S. The use of improved TOPSIS method based on experimental design and Chebyshev regression in solving MCDM problems. J. Intell. Manuf. 2017, 28, 229–243. [Google Scholar] [CrossRef]
- Ertuğrul, İ. Fuzzy group decision making for the selection of facility location. Group Decis. Negot. 2011, 20, 725–740. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Lee, P.-C.; Ting, H.-I. Dynamic multi-attribute decision making model with grey number evaluations. Expert Syst. Appl. 2008, 35, 1638–1644. [Google Scholar] [CrossRef]
- Oztaysi, B. A decision model for information technology selection using AHP integrated TOPSIS-Grey: The case of content management systems. Knowl. Based Syst. 2014, 70, 44–54. [Google Scholar] [CrossRef]
- Wachowicz, T.; Błaszczyk, P. TOPSIS based approach to scoring negotiating offers in negotiation support systems. Group Decis. Negot. 2013, 22, 1021–1050. [Google Scholar] [CrossRef]
- Sakthivel, G.; Ilangkumaran, M.; Nagarajan, G.; Priyadharshini, G.V.; Dinesh Kumar, S.; Satish Kumar, S.; Suresh, K.S.; Thirumalai Selvan, G.; Thilakavel, T. Multi-criteria decision modelling approach for biodiesel blend selection based on GRA–TOPSIS analysis. Int. J. Ambient Energy 2014, 35, 139–154. [Google Scholar] [CrossRef]
- Şengül, Ü.; Eren, M.; Shiraz, S.E.; Gezder, V.; Şengül, A.B. Fuzzy TOPSIS method for ranking renewable energy supply systems in Turkey. Renew. Energy 2015, 75, 617–625. [Google Scholar] [CrossRef]
- Chen, M.-F.; Tzeng, G.-H. Combining grey relation and TOPSIS concepts for selecting an expatriate host country. Math. Comput. Model. 2004, 40, 1473–1490. [Google Scholar] [CrossRef]
- Pham, T.Y.; Ma, H.M.; Yeo, G.T. Application of Fuzzy Delphi TOPSIS to locate logistics centers in Vietnam: The Logisticians’ perspective. Asian J. Shipp. Logist. 2017, 33, 211–219. [Google Scholar] [CrossRef]
- Jain, V.; Sangaiah, A.K.; Sakhuja, S.; Thoduka, N.; Aggarwal, R. Supplier selection using fuzzy AHP and TOPSIS: A case study in the Indian automotive industry. Neural Comput. Appl. 2018, 29, 555–564. [Google Scholar] [CrossRef]
- Zolfani, S.H.; Yazdani, M.; Zavadskas, E.K. An extended stepwise weight assessment ratio analysis (SWARA) method for improving criteria prioritization process. Soft Comput. 2018, 22, 7399–7405. [Google Scholar] [CrossRef]
- Ginevičius, R. A new determining method for the criteria weights in multicriteria evaluation. Int. J. Inf. Technol. Decis. Mak. 2011, 10, 1067–1095. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Krylovas, A.; Zavadskas, E.K.; Kosareva, N.; Dadelo, S. New KEMIRA method for determining criteria priority and weights in solving MCDM problem. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 1119–1133. [Google Scholar] [CrossRef]
- Dos Santos, B.M.; Godoy, L.P.; Campos, L.M. Performance evaluation of green suppliers using entropy-TOPSIS-F. J. Clean. Prod. 2019, 207, 498–509. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, H.; Gao, F.; Zhang, Q.; Zhang, J.; Zhou, Y. Multi-attribute decision making on reverse logistics based on DEA-TOPSIS: A study of the Shanghai End-of-life vehicles industry. J. Clean. Prod. 2019, 214, 730–737. [Google Scholar] [CrossRef]
- Alemi-Ardakani, M.; Milani, A.S.; Yannacopoulos, S.; Shokouhi, G. On the effect of subjective, objective and combinative weighting in multiple criteria decision making: A case study on impact optimization of composites. Expert Syst. Appl. 2016, 46, 426–438. [Google Scholar] [CrossRef]
- Wu, D.; Wang, N.; Yang, Z.; Li, C.; Yang, Y. Comprehensive Evaluation of Coal-Fired Power Units Using Grey Relational Analysis and a Hybrid Entropy-Based Weighting Method. Entropy 2018, 20, 215. [Google Scholar] [CrossRef]
- Sun, L.; Liu, Y.; Zhang, B.; Shang, Y.; Yuan, H.; Ma, Z. An integrated decision-making model for transformer condition assessment using game theory and modified evidence combination extended by D numbers. Energies 2016, 9, 697. [Google Scholar] [CrossRef]
- Esposito, C.; Ficco, M.; Palmieri, F.; Castiglione, A. Smart cloud storage service selection based on fuzzy logic, theory of evidence and game theory. IEEE Trans. Comput. 2016, 65, 2348–2362. [Google Scholar] [CrossRef]
- Liu, T.; Deng, Y.; Chan, F. Evidential supplier selection based on DEMATEL and game theory. Int. J. Fuzzy Syst. 2018, 20, 1321–1333. [Google Scholar] [CrossRef]
- Kirubakaran, B.; Ilangkumaran, M. Selection of optimum maintenance strategy based on FAHP integrated with GRA–TOPSIS. Ann. Oper. Res. 2016, 245, 285–313. [Google Scholar] [CrossRef]
- Lai, C.; Chen, X.; Chen, X.; Wang, Z.; Wu, X.; Zhao, S. A fuzzy comprehensive evaluation model for flood risk based on the combination weight of game theory. Nat. Hazards 2015, 77, 1243–1259. [Google Scholar] [CrossRef]
- Tang, J.; Zhu, H.-L.; Liu, Z.; Jia, F.; Zheng, X.-X. Urban sustainability evaluation under the modified TOPSIS based on grey relational analysis. Int. J. Environ. Res. Public Health 2019, 16, 256. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.; Li, S.; Hu, J. Product Innovation Design Based on Deep Learning and Kansei Engineering. Appl. Sci. 2018, 8, 2397. [Google Scholar] [CrossRef]
- Osgood, C.E.; Suci, G.J. Factor analysis of meaning. J. Exp. Psychol. 1955, 50, 325–338. [Google Scholar] [CrossRef] [PubMed]
- Osgood, C.E.; Suci, G.J.; Tannenbaum, P.H. The Measurement of Meaning; University of Illinois Press: Urbana, IL, USA, 1957. [Google Scholar]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Tasur, S. The multiple criteria evaluation of grey relation model. J. Grey Syst. 1994, 6, 87–108. [Google Scholar]
- Chan, J.W.; Tong, T.K. Multi-criteria material selections and end-of-life product strategy: Grey relational analysis approach. Mater. Des. 2007, 28, 1539–1546. [Google Scholar] [CrossRef]
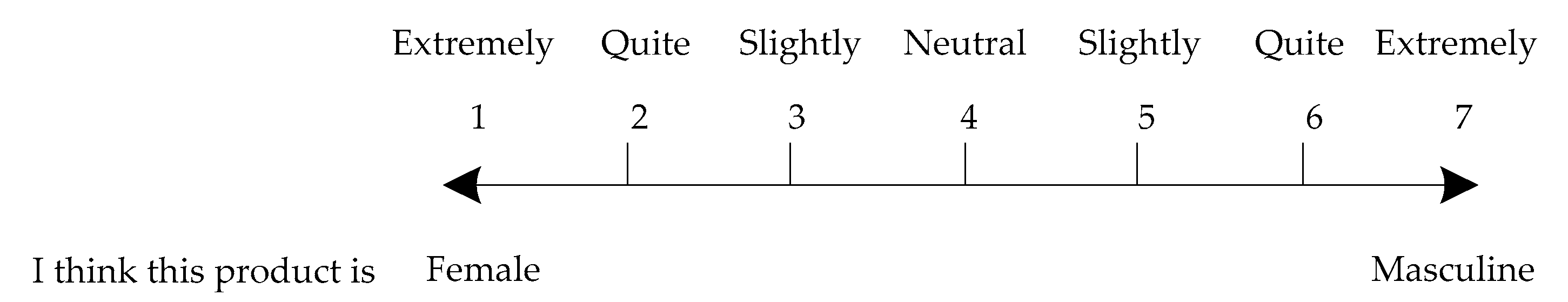





| Author, Year and Reference | Methods | Summary |
|---|---|---|
| Hu (2007) [9] | TOPSIS/ Genetic algorithm | -Proposed a TOPSIS based single-layer perceptron. -The genetic algorithm is used to determine the weights. -Taken the Choquet integral-based Manhattan distance into account. |
| Wang et al. (2014) [10] | TOPSIS | -Introduced TOPSIS into equipment selection problem under the manufacturing environment. |
| Ertuğrul (2010) [11] | Fuzzy TOPSIS | -Adopted fuzzy TOPSIS for facility location selection. -The fuzzy number represents the rating of alternatives’ criteria. -The closeness is determined by FNIS and FPIS. |
| Lin et al. (2008) [12] | GRA-TOPSIS | -GRA-TOPSIS can deal with uncertain information. -Used the Minkowski distance to calculate the closeness. |
| Oztaysi (2014) [13] | GRA-TOPSIS/AHP | -Calculated the subjective weights by AHP. -Used GAR-TOPSIS to evaluate the foreign trade company. |
| Pham et al. (2017) [18] | Fuzzy TOPSIS/ Fuzzy Delphi/Delphi | -Used Delphi method to identify criteria. -Established the triangular fuzzy number and calculate the weights of each criterion by the fuzzy Delphi method. -Adopted fuzzy TOPSIS to evaluate the logistics center. |
| Santos et al. (2019) [24] | Fuzzy TOPSIS/Entropy | -Calculated the objective weights by entropy. -Established the fuzzy decision matrix, FPIS, and FNIS. -Fuzzy TOPSIS is used to rank green supplier. |
| Wang et al. (2019) [25] | TOPSIS/DEA | -DEA is used to determine the relative efficiency of similar units. -Adopted TOPSIS to evaluate the End-of-life vehicle. |
| Wu et al. (2018) [27] | AHP/GRA/Entropy | -AHP is used to establish a hierarchy and calculate subjective weights. -Calculated objective weights based on entropy. -Proposed a new formula to combine the objective and subjective weights. -Adopted GRA to evaluate the coal-fired power unit. |
| Sun et al. (2016) [28] | Fuzzy set theory/Fuzzy AHP/Entropy/ Game theory | -Adopted the fuzzy set theory to get the basic probability assignments. -The objective and subjective weights are calculated by fuzzy AHP and entropy, and then they are integrated by game theory. -Proposed a modified evidence combination to obtain the assessment result. |
| Liu et al. (2018) [30] | Evidence theory/Game theory/Entropy/Analytic network process (ANP) | -The subjective and objective weights are obtained by ANP and entropy respectively. -Game theory is used to obtain comprehensive weights.-Evidence theory is used for supplier selection. |
| Kirubakaran (2015) [31] | GRA-TOPSIS/FAHP | -Adopted FAHP to compute the criteria weights. - GRA–TOPSIS is used to rank alternatives. |
| Lai et al. (2015) [32] | Fuzzy comprehensive evaluation (FCE)/Game theory/ AHP/Entropy | -The subjective and objective weights are obtained by AHP and entropy respectively. Then, game theory is used to optimize them. -FCE is adopted to evaluate flood risk. |
| Tang et al. (2019) [33] | GRA-TOPSIS/Entropy | -Entropy is employed to obtain the objective weights of criteria. -GRA-TOPSIS is adopted to evaluate urban sustainability. |
| Definition | oij |
|---|---|
| Factor i is as important as factor j | 1 |
| Factor i is slightly more important than factor j | 3 |
| Factor i is obviously more important than factor j | 5 |
| Factor i is strongly more important than factor j | 7 |
| Factor i is extremely more important than factor j | 9 |
| The median of the adjacent judgments above | 2,4,6,8 |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
| a1 | a2 | a3 | a4 | a5 | a6 | w1 | |
|---|---|---|---|---|---|---|---|
| a1 | 1 | 1/3 | 2 | 1/2 | 2 | 1/2 | 0.1221 |
| a2 | 3 | 1 | 3 | 2 | 3 | 1 | 0.2852 |
| a3 | 1/2 | 1/3 | 1 | 1/2 | 1 | 1/3 | 0.0807 |
| a4 | 2 | 1/2 | 2 | 1 | 2 | 1/2 | 0.1647 |
| a5 | 1/2 | 1/3 | 1 | 1/2 | 1 | 1/3 | 0.0807 |
| a6 | 2 | 1 | 3 | 2 | 3 | 1 | 0.2666 |
| Alternative | Mean of the Evaluation | |||||
|---|---|---|---|---|---|---|
| Female- Masculine | Unique- Ordinary | Simple- Refined | Modern- Traditional | Light- Steady | Technical- Artificial | |
| A1 | 3.3 | 2.7 | 3.2 | 1.5 | 5 | 3.1 |
| A2 | 5.5 | 3 | 5 | 2.2 | 5.5 | 2.5 |
| A3 | 3.5 | 5.5 | 2.5 | 2 | 3.3 | 3.3 |
| A4 | 6.5 | 2.5 | 5.5 | 6 | 5.3 | 3.8 |
| A5 | 5 | 2.7 | 6 | 5.5 | 4.7 | 4.7 |
| A6 | 1.5 | 3.5 | 1.7 | 3.3 | 3 | 2.7 |
| A7 | 5.2 | 3 | 5.3 | 5.3 | 4.8 | 6 |
| A8 | 6.2 | 3.6 | 6.3 | 5.5 | 5.3 | 5.8 |
| A9 | 2.5 | 5.1 | 3 | 2.6 | 4.9 | 2 |
| A10 | 2.5 | 4.7 | 1.5 | 2.5 | 4.8 | 3.1 |
| A11 | 6.1 | 2 | 6.3 | 6.3 | 5.6 | 4.6 |
| A12 | 6.5 | 2.6 | 6.5 | 5.8 | 5.3 | 3.5 |
| A13 | 3.6 | 3 | 2.1 | 3.1 | 4.5 | 3.1 |
| A14 | 6.2 | 3.6 | 5 | 5.6 | 6 | 5.5 |
| Female- Masculine | Unique- Ordinary | Simple- Refined | Modern- Traditional | Light- Steady | Technical- Artificial | |
|---|---|---|---|---|---|---|
| E | 0.9729 | 0.9953 | 0.976 | 0.9919 | 0.9933 | 0.9942 |
| w | 0.355 | 0.0614 | 0.3141 | 0.1064 | 0.0872 | 0.0758 |
| Alternative | D+ | D− | v+ | v− |
|---|---|---|---|---|
| A1 | 0.0515 | 0.0522 | 0.404 | 0.6598 |
| A2 | 0.042 | 0.0637 | 0.405 | 0.6556 |
| A3 | 0.0427 | 0.0643 | 0.4191 | 0.6249 |
| A4 | 0.0495 | 0.0726 | 0.3998 | 0.6733 |
| A5 | 0.057 | 0.0511 | 0.3952 | 0.6832 |
| A6 | 0.0707 | 0.0594 | 0.4153 | 0.6464 |
| A7 | 0.0516 | 0.0548 | 0.3957 | 0.6816 |
| A8 | 0.0572 | 0.0671 | 0.3962 | 0.6851 |
| A9 | 0.0581 | 0.0545 | 0.41 | 0.6495 |
| A10 | 0.0569 | 0.0601 | 0.4134 | 0.6418 |
| A11 | 0.0607 | 0.065 | 0.3915 | 0.6988 |
| A12 | 0.0585 | 0.0723 | 0.3987 | 0.6793 |
| A13 | 0.0439 | 0.0668 | 0.4151 | 0.6343 |
| A14 | 0.0455 | 0.0693 | 0.3978 | 0.6781 |
| Alternative | KE-GRA-TOPSIS 1 | KE-TOPSIS | KE-GRA | |||
|---|---|---|---|---|---|---|
| s+ | s− | s+ | s− | s+ | s− | |
| A1 | 0.8464 | 0.8312 | 0.7288 | 0.7184 | 0.964 | 0.9441 |
| A2 | 0.7805 | 0.9078 | 0.5946 | 0.8775 | 0.9664 | 0.9381 |
| A3 | 0.8019 | 0.8895 | 0.6039 | 0.8848 | 1 | 0.8942 |
| A4 | 0.8274 | 0.9817 | 0.7009 | 1 | 0.954 | 0.9634 |
| A5 | 0.875 | 0.8403 | 0.807 | 0.7031 | 0.943 | 0.9776 |
| A6 | 0.9954 | 0.8716 | 1 | 0.8181 | 0.9909 | 0.925 |
| A7 | 0.8368 | 0.865 | 0.7293 | 0.7547 | 0.9442 | 0.9753 |
| A8 | 0.8774 | 0.9522 | 0.8093 | 0.9242 | 0.9455 | 0.9803 |
| A9 | 0.8999 | 0.8395 | 0.8214 | 0.7497 | 0.9784 | 0.9294 |
| A10 | 0.8958 | 0.8726 | 0.805 | 0.8269 | 0.9866 | 0.9183 |
| A11 | 0.8963 | 0.9475 | 0.8584 | 0.895 | 0.9342 | 1 |
| A12 | 0.8894 | 0.9836 | 0.8273 | 0.9951 | 0.9515 | 0.9721 |
| A13 | 0.8056 | 0.9136 | 0.6207 | 0.9195 | 0.9906 | 0.9076 |
| A14 | 0.7965 | 0.9619 | 0.6437 | 0.9534 | 0.9493 | 0.9704 |
| Alternative | The Closeness | Ranking | |||||
|---|---|---|---|---|---|---|---|
| KE-GRA-TOPSIS | KE-TOPSIS | KE-GRA | KE-GRA-TOPSIS | KE-TOPSIS | KE-GRA | DM | |
| A1 | 0.5045 | 0.5036 | 0.5052 | 5 | 4 | 7 | 5 |
| A2 | 0.4623 | 0.4039 | 0.5074 | 12 | 12 | 6 | 12 |
| A3 | 0.4741 | 0.4056 | 0.5279 | 10 | 11 | 1 | 10 |
| A4 | 0.4574 | 0.4121 | 0.4975 | 13 | 10 | 8 | 11 |
| A5 | 0.5101 | 0.5344 | 0.491 | 3 | 2 | 12 | 3 |
| A6 | 0.5332 | 0.55 | 0.5172 | 1 | 1 | 4 | 1 |
| A7 | 0.4917 | 0.4915 | 0.4919 | 6 | 6 | 11 | 6 |
| A8 | 0.4795 | 0.4669 | 0.491 | 8 | 8 | 13 | 8 |
| A9 | 0.5174 | 0.5228 | 0.5128 | 2 | 3 | 5 | 2 |
| A10 | 0.5066 | 0.4933 | 0.5179 | 4 | 5 | 3 | 4 |
| A11 | 0.4861 | 0.4896 | 0.483 | 7 | 7 | 14 | 7 |
| A12 | 0.4748 | 0.454 | 0.4946 | 9 | 9 | 9 | 9 |
| A13 | 0.4686 | 0.403 | 0.5218 | 11 | 14 | 2 | 14 |
| A14 | 0.453 | 0.403 | 0.4945 | 14 | 13 | 10 | 13 |
| Alternative | KE-GRA-TOPSIS | GRA-TOPSIS | KE-TOPSIS | TOPSIS | DM |
|---|---|---|---|---|---|
| A1 | 5 | 8 | 4 | 7 | 5 |
| A2 | 12 | 1 | 12 | 3 | 12 |
| A3 | 10 | 2 | 11 | 1 | 10 |
| A4 | 13 | 3 | 10 | 5 | 11 |
| A5 | 3 | 12 | 2 | 13 | 3 |
| A6 | 1 | 14 | 1 | 10 | 1 |
| A7 | 6 | 13 | 6 | 14 | 6 |
| A8 | 8 | 11 | 8 | 11 | 8 |
| A9 | 2 | 10 | 3 | 6 | 2 |
| A10 | 4 | 7 | 5 | 4 | 4 |
| A11 | 7 | 9 | 7 | 12 | 7 |
| A12 | 9 | 5 | 9 | 8 | 9 |
| A13 | 11 | 4 | 14 | 2 | 14 |
| A14 | 14 | 6 | 13 | 9 | 13 |
| Accuracy/% | 78.6 | 0 | 57.2 | 7.2 |
| Participant | Requirements | Ranking |
|---|---|---|
| P1 | [2 3 5 2 2 4] | |
| P2 | [6 5 4 5 6 3] | |
| P3 | [5 3 6 5 6 3] | |
| P4 | [3 6 2 3 4 5] | |
| P5 | [3 7 2 3 3 3] | |
| P6 | [5 3 5 5 5 5] | |
| P7 | [3 4 3 3 3 4] | |
| P8 | [5 3 5 6 7 6] | |
| P9 | [7 4 5 5 5 2] | |
| P10 | [1 6 2 4 2 5] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, H.; Li, S.; Wei, H.; Hu, J. Personalized Product Evaluation Based on GRA-TOPSIS and Kansei Engineering. Symmetry 2019, 11, 867. https://doi.org/10.3390/sym11070867
Quan H, Li S, Wei H, Hu J. Personalized Product Evaluation Based on GRA-TOPSIS and Kansei Engineering. Symmetry. 2019; 11(7):867. https://doi.org/10.3390/sym11070867
Chicago/Turabian StyleQuan, Huafeng, Shaobo Li, Hongjing Wei, and Jianjun Hu. 2019. "Personalized Product Evaluation Based on GRA-TOPSIS and Kansei Engineering" Symmetry 11, no. 7: 867. https://doi.org/10.3390/sym11070867
APA StyleQuan, H., Li, S., Wei, H., & Hu, J. (2019). Personalized Product Evaluation Based on GRA-TOPSIS and Kansei Engineering. Symmetry, 11(7), 867. https://doi.org/10.3390/sym11070867





