Abstract
In this paper, a new hybrid method including simulation optimization and artificial intelligence based simulation is created to solve the inventory routing problem (IRP) in which three different routing strategies are evaluated for uneven demand patterns including intermittent, erratic, and lumpy demand. The proposed method includes two phases. In the first phase, a nondominated sorting genetic algorithm II based simulation is employed to perform a multi-objective search for the IRP where the objectives of the method are total supply chain cost minimization and average service level maximization. In the second phase, artificial neural network based simulation is used to adjust the reorder point and order-up-to-level by forecasting the customer demand at each replenishment time. The results of the study demonstrated that the average service level is at least 98.54% in the supply chain. From this, it can be concluded that the proposed method can provide a tremendous opportunity to improve the average service level under uncertain environments. In addition, it is determined that different routing strategies can be selected for different demand patterns according to the considered performance measures.
1. Introduction
To remain competitive in today’s business world, companies must cope with the increasing customer expectations and with growing markets. Products must be obtained at the right place, in the right quantity, and at the right time. Furthermore, companies have to consider risks formed by the sudden fluctuations in global and local economies. Thus, the success measures of the companies include many different factors, such as higher quality, lower costs, and shorter lead time. At this point, supply chain management (SCM) has become an important necessity for companies [1]. Successful SCM requires many decisions including the flow of information, product, and funds [2]. This paper focuses on inventory control and routing, which are the core topics in SCM. The performance of the supply chain is closely linked to the performance of inventory control and routing. In addition, simultaneous consideration of inventory control and routing offers a tremendous opportunity for companies to gain competitive advantage in the supply chain. The simultaneous consideration of inventory control and routing is known as the inventory routing problem (IRP). In IRP, customer demands are met while satisfying the objectives related to the inventory control and the routing. In this case, determining customer demand is a challenging task for the supply chain to eliminate uncertainty and make itself stable. Inaccurate demand forecasting can increase the total supply chain cost. Therefore, demand forecasting is critical for any supply chain to make correct decisions and to achieve benefits in regularly changing business scenarios [3]. Accurate forecasting of demand under uncertain environments also improves supply chain activities [4]. In literature, many studies are related to customer demand forecasting based on casual models, such as regression, and time-series methods, such as moving-average [5]. Although these methods perform well, they have some limitations. For example, accurate forecasting is generally guaranteed when a large amount of data is used in these methods. Therefore, there is a need to develop a more efficient and precise method for demand forecasting. At this point, artificial intelligence (AI) techniques can be employed for demand forecasting.
AI is interested in intelligent behavior in artifacts. At this point, the perception, learning, reasoning, communicating, and acting in complex environments can be considered intelligent behaviors [6]. Today’s complex environment needs intelligent behaviors in systems to combine knowledge, methodologies, and procedures from various sources. AI adapts itself and learns to do better problem solving in stochastic and dynamic environments. To increase the performance of AI techniques, many methodologies that find actual and potential uses within simulation environments were developed [7]. A combination of AI and simulation improves the functionality of the simulation due to a more realistic perspective. Furthermore, it provides an intelligent and accurate system for decision-making process in SCM.
In this paper, simulation optimization (SO) and AI based simulation models are developed to solve the IRP. The main contributions of this paper can be summarized as follows: (i) the application of a nondominated sorting genetic algorithm II (NSGA-II) to determine the parameters of IRP considering two objective functions; (ii) the application of a Genetic Algorithm (GA) to determine the de-noising degree, the number of neurons in hidden layers, and the training algorithm; (iii) the implementation of de-noising with the Maximal Overlap Discrete Wavelet Transform (MODWT) to improve the customer demand data; and (iv) the application of a Genetic Algorithm based Artificial Neural Network (GA-ANN) to forecast uneven customer demand patterns. Integration of NSGA-II based SO and GA-ANN based simulation is necessary to provide a better coordination level in the supply chain. This integration directly affects the synchronization and overall supply chain performance.
The remainder of the study is proposed as follows. Section 2 presents the literature review related to IRP, artificial intelligence techniques for forecasting, and some studies related to hybrid structures for supply chain. The proposed method is presented in Section 3. In Section 4, an analysis of IRP is given. Finally, Section 5 presents concluding remarks for the results obtained in this research.
2. Literature Review
Over the years, several computing methods have been used synergistically rather than exclusively in order to improve supply chain performance. The construction of complementary hybrid methods provides a powerful solution methodology in real-world problems. In this paper, hybrid inventory and routing based methods are analyzed. Further, demand forecasting, which has generated an increasing interest nowadays because of an increase in competition, is considered. Accurate demand forecasting provides valuable information about local and global markets. Companies can make informed decisions about the markets’ potential. In addition, demand forecasting gives information about business growth and pricing strategies. It helps companies reduce risks involved in business activities and cope with uncontrollable and competitive forces. Therefore, demand forecasting is the main requirement for the competitive survival of business. It can also provide an insight into the expansion of decisions and capital investment.
In literature, various methods have been used to model different demand patterns. Traditional forecasting methods can be successfully used when the demand of an item is smooth and continuous. However, forecasting is hardly difficult with traditional methods when the demand of item has changing values [8]. At this point, the artificial neural network (ANN) method is a logical choice to handle these limitations [9]. ANN can capture interactions between the non-zero demand and the inter-arrival rate of demand events [10]. We summarized some of the papers associated with forecasting of different demand patterns using ANN. For erratic demand patterns, Molina et al. [11] showed the comparison of ANN methods and an autoregressive integrated moving average method to forecast the demand medicines. In the paper, the demand of two drugs in a public hospital was analyzed with an erratic nature. For intermittent demand patterns, Kourentzes [10] proposed the ANN method, which allows interactions between the interdemand intervals and the demand of intermittent items. Lolli et al. [12] used the ANN method trained by back-propagation and extreme learning machines. In addition, different input patterns and architectures were used to compare the forecasting results of proposed ANN methods for intermittent demand. Kaya and Turkyilmaz [8] employed the ANN, support vector regressions, and decision tree techniques. In their paper, the intermittent package of R software was employed to produce artificial demand data. For lumpy demand patterns, Gutierrez et al. [13] presented a lumpiness factor and a coefficient of skewness as two measures to characterize the lumpy demand of an electronics distributor. Similarly, Gutierrez et al. [14] applied the ANN method to forecast lumpy demand. Amin-Naseri and Tabar [9] used the recurrent ANN for lumpy demand forecasting of spare parts. Croston’s method and Syntetos & Boylan’s approximation were also used to evaluate the proposed method.
In SCM, demand forecasting is one of the most significant topics for a company’s survival and sustainability. Unsatisfactory demand forecasting will hurt company profitability and market competitiveness. Therefore, various methods are proposed to forecast demand in supply chains. Zhang et al. [15] presented a decomposition-and-ensemble principle for erratic demand forecasting. Support vector machines were used to model and formulate the erratic demand series. Durmusoglu and Satoglu [16] presented a complete road map in erratic demand environment for the hybrid cellular manufacturing systems. Prestwich et al. [17] used several intermittent demand patterns and proposed several new error measures with almost no infinities, and with correct forecaster ranking. Ramaekers and Janssens [18] used the SO to develop a framework for intermittent demand. In their study, the simulation model, developed via Microsoft Excel spreadsheets, aimed to determine the optimal inventory system. Demand forecasting and an order decision were made at each review-time. Lei et al. [19] presented a new forecasting algorithm using the material intermittent demand data. Then, the results were compared with the exponential smoothing method. Jung et al. [20] presented a new bootstrap method. They deployed a simple experiment that utilizes artificial data to compare the results of the suggested method and the conventional Markov bootstrap method. Verganti [21] investigated the demand management mechanisms by means of quantitative analyses. The ability of order overplanning was also explored to cope with uncertain lumpiness. Bartezzaghi et al. [22] evaluated the behavior of forecasting techniques, especially an exponentially weighted moving average, early sales, and order overplanning, under the lumpy demand pattern. Dellino et al. [23] formulated a multi-objective optimization problem considering key performance indicators in the fresh food supply chain. The dataset was provided by a set of small- and medium-sized retailers. In their study, the decision support system focused on order planning and sales forecasting. Li and Lim [24] proposed a greedy aggregation–decomposition method that includes three parts. In the first part, daily total demand was forecasted. In the second part, the demand size and interval were forecasted. Finally, the total demand was allocated at each store considering the forecasting in the first and the second part. At this point, the first part was for aggregation while the other parts were for decomposition. Fu et al. [25] used a hybrid of a recurrent neural network and Syntetos-Boylan approximation for semiconductor product demand forecasting. The proposed method can handle the intermittent demand occurrence and the deficient downstream information in the supply chain.
The forecasting of demand can be considered the primary revenue source of the company since all departments establish themselves with respect to the results obtained from demand forecasting. In addition to this, the integration of inventory control and routing directly influences the synchronization and overall supply chain performance. In IRP, the supply chain can be managed as an interdependent and interconnected structure. At this point, simulation ensures the flexibility to model the supply chain under an interdependent and interconnected structure. Furthermore, it provides an essential level of realism. Simulation allows the user to change parameters easily within the method. The outcomes for different alternatives are evaluated in the supply chain via simulation [26,27,28]. In addition to simulation, optimization methods allow researchers to determine the best possible alternatives [29]. Hence, integrating simulation and optimization into the IRP ensures a remarkable solution method. It also provides a structured approach to the system of design and configuration [30]. SO can be used to cope with uncertainties since it allows us to model and evaluate the uncertainties in the system. Furthermore, SO can handle the multidimensional natures of the uncertainties. However, the experience and knowledge of a model developer are important in order to handle the uncertainties in supply chain successfully. The robustness of the optimal solution is also important in SO. Dellino and Kleijnen [31] presented a methodology in order to incorporate robustness issues in SO. In their study, a metamodel was employed to create a robust SO that accounted for uncertainties during the optimization process. Briefly, managing uncertainties, such as uncertain demand and uncertain lead time, has always been a major concern in IRP because ignoring uncertainties can cause sub-optimal or infeasible solutions in the supply chain. Thus, SO is an exciting and fast developing area for both research and practice in the IRP. For example, Jarugumilli et al. [32] modified the A* algorithm to determine heuristic solutions and developed a simulation framework to validate heuristic performance for the IRP. In the study, a single vehicle was used to transport a single product. A periodic review model was selected to control inventory. In addition, various design factors related to demand, the shortage cost, the holding cost, and the transportation cost were determined for the experimental design. Cáceres-Cruz et al. [33] utilized a hybrid algorithm integrating Monte Carlo simulation with a metaheuristic under stochastic demands with stock-outs. The proposed approach considered diverse inventory control policies for each customer. In the study, a single-period IRP included multiple retailers and a single distribution depot. Abdollahi et al. [34] proposed an SO to solve the IRP that includes one distributor and N retailers. In the study, some risk factors were employed to design the method under a maximum level inventory policy. Homogeneous vehicles were employed to distribute one type of product. Unsatisfied demand was backlogged. Juan et al. [35] presented an algorithm that combines the Monte Carlo simulation and multi-start randomized heuristics to solve the single-period IRP.
Lately, the advance of information systems and the availability of data have greatly increased. Therefore, the integration of inventory and routing has been growing constantly, enhanced by the advances in information technology. In recent years, various IRP methods have been created to cope with growing competitive markets and to handle the additional constraints. The possibilities of combining methods are also so vast for the IRP in supply chain. In addition, hybrid methodology provides a remarkable solution to promptly cope with any changes in supply chain. However, the design of a hybrid methodology that includes simulation, optimization methods, and an AI based method can be difficult for a complex supply chain problem. Therefore, a hybrid methodology including SO and AI-based simulation forms the motivation of our study. In this paper, SO and AI based simulation are developed to solve the IRP under different demand patterns including intermittent, erratic, and lumpy. Firstly, the SO is used to conduct a “what-if” scenario analysis considering the occurrence of unplanned events in the supply chain. Then, AI is employed to forecast the demand and simulation embraces proposed by the supply chain with their complicated and nonlinear relationships. In this paper, three issues are mainly considered: What is the effect of integration of NSGA-II based SO and GA-ANN based simulation on performance of the supply chain members? Which parameters are widely chosen by GA? Is there a difference among supply chain members when using different customer demand patterns? Our proposed method adds a new dimension to the supply chain modeling approaches. It provides an attractive opportunity to represent the ambiguity in the supply chain with real life uncertainty.
3. Proposed Method
Syntetos et al. [36] presented a categorization scheme in which the average inter-demand interval (ADI) and the squared coefficient of variation (CV2) of demand are compared with cutoffs of 1.32 for ADI and 0.49 for CV2. Details about the categorization can be found in Syntetos et al. [36]. The data used in this paper is taken from Chen et al. [37], whose dataset is available for one year. Data is adapted considering three different uneven demand patterns. In erratic demand, ADI is less than 1.32 and CV2 is greater than 0.49. The mean of customer order quantity in erratic demand is 12 units. In intermittent demand, the ADI is greater than 1.32 and the CV2 is less than 0.49. The mean of the customer order quantity in intermittent demand is 368 units. In lumpy demand, the ADI is greater than 1.32, the CV² is greater than 0.49. The mean of customer order quantity in lumpy demand is 368 units.
The proposed system, including Phase 1 and Phase 2, allows the controlling of continuous changes of the method representing the current state of the inventory and routing system. In Phase 1, SO is used to optimize the initial inventory, reorder point, and order-up-to level in a two echelon supply chain. Note that five distribution centers and one supplier are used to minimize the network traffic in simulation and to prevent network overloading. Integrating optimization and simulation is a highly demanded method in problem solving due to the need for high computational power, even by today’s standards. The interactions and uncertainties related to the proposed system can be easily captured by SO. However, the design of SO is crucial. The possibilities for combining simulation and optimization are vast, so a good overview of methods is necessary. In this study, NSGA-II is used as the optimization method. In NSGA-II, the population is initialized considering the problem range and constraint. Then, non-dominated sorting is applied. Next, the value of crowding distance is calculated and genetic operators are applied to individuals. Finally, offspring population and current generation population are combined to create the new generation. Details about the NSGA-II can be found in [38,39]. In our proposed NSGA-II, population size is 20, crossover probability is 0.08, and mutation probability is 0.05. Note that, the parameters of NSGA-II are specified by a trial and error method. NSGA-II was coded using C# (Visual Studio Community 2017). The simulation model was developed by using Simio (Version: 7.121.12363).
In SO methods, the total supply chain cost (TSCC) is minimized while the average service level is maximized. In the proposed methods, each objective function along the Pareto-front is only improved by degrading the other objective function. In this case, none of the Pareto-optimal solutions is exactly better than the other solutions, and, therefore, one of them can be considered an acceptable solution. We select the lowest cost solution when Pareto-optimal solutions are found. The general structure of Phase 1 is depicted in Figure 1. Note that the SO method runs during the half year in Phase 1. Then, the AI and data driven simulation in Phase 2 runs for the next half year.
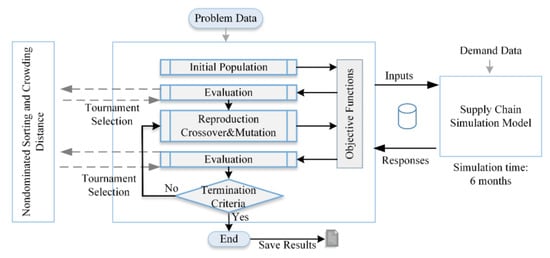
Figure 1.
The general structure of Phase 1.
In Phase 2, first de-noising with MODWT is done to improve the data quality. The outliers and systematic noises are identified to improve the demand data. After preprocessing of the data, AI and data driven simulations are used in the supply chain system. AI is utilized at each replenishment time to provide accurate demand forecasting. The forecasted demand is used to calculate the reorder point and order-up-to-level at each replenishment time (R) for each supply chain member. Note that only R is considered as a fixed value and assumed to be 5 days. At each replenishment time, the demand of supply chain members is forecasted by the GA-ANN. In this forecasting process, GA is used for optimizing the parameters of the ANN. The procedure of GA is initialized by defining chromosome structure to represent a set of parameters. Then, selection, crossover, and mutation operators are repeatedly applied to create new chromosomes in the GA. In our proposed GA, the number of iterations is 50, population size is 20, crossover probability is 0.08, and mutation probability is 0.05. Note that the parameters of GA are specified by a trial and error method. The general structure of Phase 2 is depicted in Figure 2.
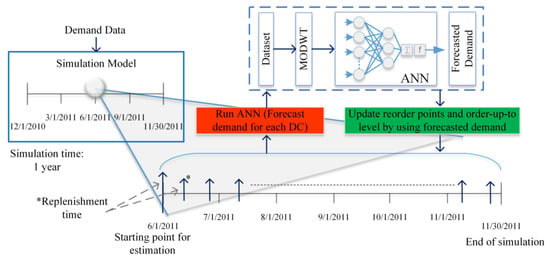
Figure 2.
The general structure of Phase 2. Maximal Overlap Discrete Wavelet Transform (MODWT); Artificial Neural Network (ANN).
The possibilities for combining methods are vast for the supply chain. At this point, one of the most important points is to have a good overview of the AI and simulation that can be used to realize the supply chain effectively. For example, Kilmer [40] used the baseline ANN metamodel approach to develop an (s, S) inventory computer simulation. In addition, the details of the SO and metamodels can be found in Dellino et al. [31].
In this paper, the ANN is utilized as an AI method. To make forecasts, multilayer feedforward networks, in which the connection of layers and units within a layer are created in a feedforward manner, are developed. In the proposed ANN, connections are only available between successive layers. Thus, no connections exist among neurons. The proposed ANN consists of four layers. The first layer is the input layer that connects to the input variables. The second and third layer are called hidden layers that are between the input and output layers. Thus, we used two hidden layers. The last layer is the output layer that connects to the output variables. Information is transmitted through the connections between layers. In the ANN, performance directly depends on the configuration of parameters such as the input variables, the number of neurons, the number of layers, the training algorithm, the type of the activation function, the number of epochs, and weights. The values of parameters can vary according to the type of the problems. The determination of ANN architecture is very crucial to improve the method of performance. In the literature, no certain method is available to perform well for all types of problems. Therefore, researchers have tried to find a systematic method for ANN development. In this paper, GA optimized the de-noising degree. In addition, some of the main parameters of the ANN, including the number of neurons in hidden layers and training algorithm, are optimized by the GA. The initial pool of the training algorithm is the same as the Dosdoğru [41], except for bayesian regularization. Note that log-sigmoid is utilized as an activation function in the proposed ANN method. For ANN, the overall dataset is divided into three subsets including training (70%), validation (15%) and testing (15%). In the proposed ANN, the training data is employed to train the network. Validation data is used to tune and improve the network. Finally, testing data is utilized to test the accuracy of the network. In the ANN, the mean absolute percent error (MAPE) is utilized to evaluate the forecasting performance. The MAPE is calculated as follows:
where , is the forecasted demand and is the actual demand.
3.1. Inventory Control Policy
In this paper, a periodic (R, s, S) inventory control is considered. The inventory level is controlled at equal intervals of time R. If the inventory level falls below a reorder point (s), the supply chain member is replenished up to an order-up-to level (S). If the inventory level is more than the reorder point at time R, no replenishment order is placed.
In Phase 1, the initial inventory, reorder point and order-up-to level are optimized by the SO method. In Phase 2, reorder point () and order-up-to level () are calculated at each replenishment time for each supply chain member using the output of GA-ANN. Taylor III [42] presented the formula for the reorder point with variable demand and variable lead time as follows:
where denotes the average daily demand, represents the average lead time, denotes the standard deviation of demand during lead time, and Z is the number of standard deviations corresponding to the service level probability. This formula is adapted, and the average daily demand is changed with the forecasted demand (, obtained via GA-ANN) as follows. The 95% service level ( is used for the reorder point ():
Using the calculated reorder point, the order-up-to level () is computed as follows:
3.2. Routing Strategies
Various routing policies are used to achieve a variety of supply chain objectives. At this point, an incorrect policy can hurt the customer service level while increasing the cost. Therefore, many different policies have been developed to provide ongoing and consistent customer satisfaction while increasing profit. In the literature, the strategies are generally represented as simple policies. On the other hand, strategy based policies enable practical application on the IRP side. Therefore, we used three different strategies.
Strategy 1 assigns a route for a vehicle considering the TSCC. Under intense competition, marginal profit is becoming thinner and thinner in recent years, so companies should reduce total cost. The costs incurred in IRP can play a major role while deciding on which IRP model to use in the supply chain. Therefore, the largest TSCC is assigned first in Strategy 1.
Strategy 2 assigns a route for the vehicle considering the least inventory first principle. The least inventory first principle is defined as the policy under which the vehicle goes next to the not-yet-visited supply chain member with the smallest inventory position. At the beginning of each replenishment time, the distribution center (DC)s‘ orders are ordered from smallest to largest by considering the DCs’ inventory levels. This means that the order of DC with the smallest inventory level has the highest delivery priority.
In Strategy 3, the vehicle starts its route according to the predetermined priority rule. Priority order, from highest to lowest, in proposed methods is given as DC1, DC2, DC3, DC4, and DC5, respectively. Note that the vehicle considers the shortest paths when more than one route is available between these destinations for all strategies considered.
In this study, order splitting is not allowed, and vehicles are loaded and routed considering same strategy based policies. Thus, each vehicle starts and continues its route according to the loaded order. The vehicle considers the shortest paths while returning back to the Supplier. We used a single uncapacitated vehicle and vehicle speed considered to be uniform (80, 90) meters per hour. In all strategies, each DC is visited at most once in each review period. Vehicle load changes during transportation. Quantity to be delivered to each DC is determined according to the value of replenishment order. Routing based cost is calculated using the following equation:
where is the capital cost per vehicle, is the fixed cost of initiating delivery, and is the fixed cost of each customer stop. Transportation cost per unit distance is denoted as . The supplier to the round trip distance is represented as ( denotes the number of DC in the system, and represents the Supplier). Finally, denotes the set of DCs that is to be delivered at delivery d. Thus, denotes each DC that is to be delivered at delivery d.
3.3. Performance Measurements
In order to evaluate the performance of the methods, we used various measures including cost based analysis, quantity based analysis, lead time based analysis, routing based analysis, and average service level. In cost based analysis, the expected total cost for all supply chain members is the sum of the inventory based cost and routing based cost.
where is the unmet customer order quantity of over period and is the remaining inventory quantity of over period .is the average holding cost rate of for each unit of inventory. is specified as the lost sales cost rate of for each unit of stockout. is the processing cost of . is the processing time of . The order cost per use of is represented as which is the cost charged for any order of irrespective of the time spent in there. The order processing cost of is represented as . Note that the order processing cost includes cost per use and the order processing cost rate, which is proportional to the order processing time. The cost parameters in proposed supply chain are given in Table 1.

Table 1.
The cost parameters in the proposed supply chain.
In routing based analysis, the space utilization per delivery is calculated using following formula:
where is the total transportation time of vehicle loaded with orders per each delivery, and denotes the quantity of transporting orders at time during a delivery.
Finally, the average service level is calculated as follows:
4. Results and Discussion
The determination of ANN parameters is important since performance of the ANN directly depends on the configuration of parameters in layers. Therefore, GA is used to determine the optimal parameters including the number of neurons in hidden layers, training algorithm, and de-noising degree. Note that, at first, pre-analysis is made to determine the upper bound of the number of neurons in the hidden layer. The model runs with different number of hidden neurons. It is determined that using more than 20 neurons did not increase performance at all. Therefore, the upper bound of the number of neurons in the hidden layers is fixed at 20 in GA. The values of the parameters determined by GA generally change according to the strategy type and supply chain member. The number of neurons in the first and second hidden layers is between 3 and 20 in erratic demand. The number of neurons in the first hidden layers is between 2 and 20 in intermittent demand while the number of neurons in the second hidden layers is between 3 and 20 in intermittent demand. The number of neurons in the first hidden layers is between 6 and 20 in lumpy demand while the number of neurons in the second hidden layers is between 3 and 20 in lumpy demand. The minimum (min) and maximum (max) value of the determined hidden neurons for the ANN is given in Table 2. The de-noising degree values vary between 2 and 3. Furthermore, the training algorithm is optimized by GA, which generally selects the conjugate gradient backpropagation with Powell-Beale restarts and one step secant method.

Table 2.
The determined number of hidden neurons for the ANN.
In this section, we only analyzed the results of Phase 2 due to the space limitations. In Phase 2, the reorder point and order-up-to levels are calculated at each replenishment time using the forecasted customer demand. The estimated value of the reorder point in erratic demand varies between 13 units and 82 units, while the estimated value of the order-up-to level in erratic demand varies between 18 units and 101 units. The estimated value of reorder point in intermittent demand varies between 348 units and 2905 units, while the estimated value of order-up-to level in intermittent demand varies between 348 units and 3297 units. The estimated value of the reorder point in lumpy demand varies between 196 units and 2265 units, while the estimated value of the order-up-to level in lumpy demand varies between 395 units and 2549 units. The minimum (min) and maximum (max) values of the estimated reorder point and order-up-to levels are given in Table 3.

Table 3.
The descriptive statistics of the determined reorder point and order-up-to level.
In order to draw conclusions and make decisions correctly and efficiently from the AI based simulation method, we used different analyses. For example, the average service level for each strategy under different demand patterns is given in Table 4. Taking a glance at the average service levels of strategies reveals that the proposed method helps properly control the supply chain so that good customer service is maintained.

Table 4.
Average service level for each strategy under different demand patterns.
4.1. Cost Based Analysis
In today’s competitive world, the competition is not only between the companies in the local market but also between companies in the global market. To remain competitive and grow sales, the supply chain should be controlled considering performance measurements. The criteria for the supply chain performance measurement can be different for companies since the participants and the structure of the network can vary according to the view of its own vision. When the TSCC is considered, Strategy 2 can be selected for lumpy demand patterns (Table 5). Thus, the least inventory is controlled in supply chain to cope with the fluctuating nature of lumpy demand. Strategy 3 can be chosen for intermittent demand and erratic demand pattern when the TSCC is taken into account.

Table 5.
The total supply chain cost (TSCC) for each demand pattern and each strategy.
4.2. Quantity Based Analysis
Quantity based analysis includes partially lost order quantity, totally lost order quantity, and totally met order quantity, as given in Table 6. Note that the values in the table include the sum of all DCs results for each demand pattern during six months. According to the results of quantity based analysis, Strategy 2 gives better results in lumpy demand while Strategy 3 provides satisfying results in erratic demand and intermittent demand. The nature of lumpy demand causes difficulties in controlling inventory level, and, therefore, focusing on the smallest inventory improves the partially lost order quantity and totally lost order quantity. On the other hand, giving priority to DCs improves the lost order quantities in erratic demand and intermittent demand.

Table 6.
Quantity based analysis.
4.3. Routing Based Analysis
In an economic environment of fierce competition, routing is a very challenging problem. Hence, we paid particular attention to the modeling phase for an accurate capture of supply-chain behavior. We address the IRP from the perspective of different demand patterns considering strategy based policies. Various analyses are employed to determine the better routing strategy for each demand pattern. As a routing based analysis, the ratio of the transported quantity for the DCs is given in Table 7. To calculate the ratio, the transported quantity from the supplier to each DC is divided by the total transported quantity from supplier to all DCs. For example, the transported quantity from supplier to DC1 comprised 19.4 percent of the total transported quantity in Strategy 1 for the erratic demand pattern.

Table 7.
The ratio of transported quantity for distribution center (DC)s.
The minimum (min), mean, and maximum (max) values for space utilization per delivery are given in Table 8. Note that mean represents the average of the space utilization per delivery for the DCs. The space utilization per delivery varies between seven units and 1609 units for demand patterns in Strategy 1. The space utilization per delivery varies between nine units and 2986 units for demand patterns in Strategy 2. The space utilization per delivery varies between seven units and 1874 units for demand patterns in Strategy 3. In Table 8, the total number of deliveries in Phase 2 is also given for each demand pattern. Different routing strategies can be selected for demand patterns according to the routing based analysis. When the mean space utilization per delivery is taken into account in erratic demand, Strategy 1 and Strategy 2 give better results than Strategy 3. Strategy 1 can be chosen in lumpy demand with respect to the mean space utilization per delivery. In intermittent demand, Strategy 3 can be selected according to the mean space utilization per delivery.

Table 8.
The space utilization per delivery for strategies.
4.4. Lead Time Based Analysis
The lead time period length ratio to review period length varies with respect to the demand patterns and supply chain members, and its minimum (min) and its maximum (max) values are given in Table 9. In Strategy 1, the lead time of the supply chain members comprised a minimum of 10.3 percent of the review period and a maximum of 72.9 percent of the review period. In Strategy 2, the lead time of supply chain members comprised a minimum of 10.5 percent of the review period and a maximum of 78.3 percent of the review period. In Strategy 3, the lead time of the supply chain members comprised a minimum of 9.8 percent of the review period and a maximum of 69.6 percent of the review period.

Table 9.
The lead time period length ratio to review period length.
In the literature, SO methods (e.g., [32,33,34,35]) and AI based methods (e.g., [24,25]) are widely used to solve the supply chain problems. However, there is still lack of studies that show the integration of the SO method and AI based methods to solve the IRP. In addition, there is a need to determine the values of the IRP parameters for each demand pattern. This paper fulfils a part of this gap by integrating NSGA-II based discrete event simulation and AI based discrete event simulation methods. In this paper, various analyses are applied to evaluate the SO and AI based methods, since the structure of the supply chain should be perfectly understood to determine an effective method. In addition, we provide a comparative analysis related to the demand patterns. Decision makers can select the most suitable strategy that suits their needs.
5. Conclusions
In today’s world, the importance of SCM is increasing due to the fiercer competition in local and global economies. Integrating inventory and routing decisions has become an especially important necessity in SCM. It is very critical for any company to cope with its competitors in a changing business environment. However, there is no standard method to handle the IRP. A detailed literature review showed that simulation, optimization methods, or AI based methods play a significant role in the solving of IRP. Therefore, we developed a new hybrid method to solve stochastic and dynamic IRP. The proposed method includes two phases. Firstly, the NSGA-II based SO is used to model the supply chain system under a multi-objective search. Then, the ANN based demand forecasting and simulation is employed to improve the efficiency of the supply chain system.
Customers are not willing to wait anymore due to the changing competitive environments in the supply chain, and, therefore, customer demand is generally considered lost sales in many practical settings. In addition, companies should reduce total cost to cope with today’s management challenges. For these reasons, the quantity based analysis and cost based analysis can be used to select the strategy for demand patterns. It became evident from the results that Strategy 2 gives better results for the lumpy demand pattern when the quantity based analysis and cost based analysis are considered. Strategy 3 can be chosen for erratic and intermittent demand patterns with respect to the quantity based analysis and cost based analysis.
In conclusion, this paper presents a new hybrid method for IRP with uneven customer demand patterns. Combining the respective strengths of SO and AI based simulation provides a competitive advantage under a dynamic and stochastic environment. In the literature, SO is widely used to solve problems in the supply chain [32,33,34,35]. In addition to this, we demonstrated that integration of SO and AI based simulation also provides satisfying results in the supply chain. The proposed method can encourage further development of the hybrid SO and AI based simulations. In future work, parameters of the ANN can be determined by integrating other AI methods, such as particle swarm optimization. In addition, big data can be integrated with the proposed method to improve the performance of the supply chain members. Sentiment analysis can be used especially to improve the accuracy of demand forecasting. For future work, the proposed method can be also applied to other problems, such as the dynamic vehicle routing problem [43] and dual-channel supply chain [44].
Author Contributions
Conceptualization, A.B., A.T.D., M.G. and R.E.; methodology, software and validation, A.B., A.T.D. and M.G.; formal analysis, A.T.D. and M.G.; investigation, A.B.; writing—original draft preparation and writing—review and editing, A.B., A.T.D. and M.G.; supervision, M.G. and R.E.
Funding
This research received no external funding.
Acknowledgments
Aslı Boru gratefully acknowledges the Scientific and Technological Research Council of Turkey (TÜBİTAK) for the 2211-C PhD scholarship program.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gumus, A.T.; Guneri, A.F.; Keles, S. Supply chain network design using an integrated neuro-fuzzy and MILP approach: A comparative design study. Expert Syst. Appl. 2009, 36, 12570–12577. [Google Scholar] [CrossRef]
- Chopra, S.; Meindl, P. Supply Chain Management: Strategy, Planning, and Operation, 3rd ed.; Pearson Education, Inc.: Bergen, NJ, USA, 2016. [Google Scholar]
- Bhadouria, S.; Jayant, A. Development of ANN models for demand forecasting. Am. J. Eng. Res. 2017, 6, 142–147. [Google Scholar]
- Jaipuria, S.; Mahapatra, S.S. An improved demand forecasting method to reduce bullwhip effect in supply chains. Expert Syst. Appl. 2014, 41, 2395–2408. [Google Scholar] [CrossRef]
- Efendigil, T.; Önüt, S.; Kahraman, C. A decision support system for demand forecasting with artificial neural networks and neuro-fuzzy models: A comparative analysis. Expert Syst. Appl. 2009, 36, 6697–6707. [Google Scholar] [CrossRef]
- Nilsson, N.J. Artificial Intelligence: A New Synthesis; Morgan Kaufmann: Burlington, MA, USA, 1998. [Google Scholar]
- Doukidis, G.I.; Angelides, M.C. A framework for integrating artificial intelligence and simulation. Artif. Intell. Rev. 1994, 8, 55–85. [Google Scholar] [CrossRef]
- Kaya, G.O.; Turkyilmaz, A. Intermittent demand forecasting using data mining techniques. Appl. Comput. Sci. 2018, 14, 38–47. [Google Scholar] [CrossRef]
- Amin-Naseri, M.R.; Tabar, B.R. Neural network approach to lumpy demand forecasting for spare parts in process industries. In Proceedings of the International Conference on Computer and Communication Engineering, Kuala Lumpur, Malaysia, 13–15 May 2008; pp. 1378–1382. [Google Scholar] [CrossRef]
- Kourentzes, N. Intermittent demand forecasts with neural networks. Int. J. Prod. Econ. 2013, 143, 198–206. [Google Scholar] [CrossRef]
- Molina, A.; Ponte, B.; Parreño, J.; De la Fuente, D.; Costas, J. Forecasting Erratic Demand of Medicines in a Public Hospital: A Comparison of Artificial Neural Networks and ARIMA Models. 2016. Available online: https://pdfs.semanticscholar.org/c92d/4828504d270b9f0d7c000062a2ad4ad0fd68.pdf (accessed on 5 February 2019).
- Lolli, F.; Gamberini, R.; Regattieri, A.; Balugani, E.; Gatos, T.; Gucci, S. Single-hidden layer neural networks for forecasting intermittent demand. Int. J. Prod. Econ. 2017, 183, 116–128. [Google Scholar] [CrossRef]
- Gutierrez, R.S.; Solis, A.O.; Bendore, N.R. Lumpy Demand Characterization and Forecasting Performance: AN Exploratory Case Study. 2004. Available online: http://utminers.utep.edu/solis/wdsi%202004,%202006%20&%202007/Lumpy%20demand%20forecasting%20WDSI%202004%20proceedings.pdf (accessed on 5 February 2019).
- Gutierrez, R.S.; Solis, A.O.; Mukhopadhyay, S. Lumpy demand forecasting using neural networks. Int. J. Prod. Econ. 2008, 111, 409–420. [Google Scholar] [CrossRef]
- Zhang, R.; Bao, Y.; Zhang, J. Forecasting erratic demand by support vector machines with ensemble empirical mode decomposition. In Proceedings of the 3rd International Conference on Information Sciences and Interaction Sciences, Chengdu, China, 23–25 June 2010; pp. 567–571. [Google Scholar] [CrossRef]
- Durmusoglu, M.B.; Satoglu, S.I. Axiomatic design of hybrid manufacturing systems in erratic demand conditions. Int. J. Prod. Res. 2011, 49, 5231–5261. [Google Scholar] [CrossRef]
- Prestwich, S.; Rossi, R.; Tarim, S.A.; Hnich, B. Mean-based error measures for intermittent demand forecasting. Int. J. Prod. Res. 2014, 52, 6782–6791. [Google Scholar] [CrossRef]
- Ramaekers, K.; Janssens, G.K. Optimal policies for demand forecasting and inventory management of goods with intermittent demand. J. Appl. Oper. Res. 2014, 6, 111–123. [Google Scholar]
- Lei, M.; Li, S.; Tan, Q. Intermittent demand forecasting with fuzzy markov chain and multi aggregation prediction algorithm. J. Intell. Fuzzy Syst. 2016, 31, 2911–2918. [Google Scholar] [CrossRef]
- Jung, G.; Park, J.; Kim, Y.; Kim, Y.B. A modified bootstrap method for intermittent demand forecasting for rare spare parts. Int. J. Ind. Eng. 2017, 24, 245–254. [Google Scholar]
- Verganti, R. Order overplanning with uncertain lumpy demand: A simplified theory. Int. J. Prod. Res. 1997, 35, 3229–3248. [Google Scholar] [CrossRef]
- Bartezzaghi, E.; Verganti, R.; Zotteri, G. A simulation framework for forecasting uncertain lumpy demand. Int. J. Prod. Econ. 1999, 59, 499–510. [Google Scholar] [CrossRef]
- Dellino, G.; Laudadio, T.; Mari, R.; Mastronardi, N.; Meloni, C. A reliable decision support system for fresh food supply chain management. Int. J. Prod. Res. 2018, 56, 1458–1485. [Google Scholar] [CrossRef]
- Li, C.; Lim, A. A greedy aggregation–decomposition method for intermittent demand forecasting in fashion retailing. Eur. J. Oper. Res. 2018, 269, 860–869. [Google Scholar] [CrossRef]
- Fu, W.; Chien, C.-F.; Lin, Z.-H. A hybrid forecasting framework with neural network and time-series method for intermittent demand in semiconductor supply chain. In IFIP International Federation for Information Processing; Springer Nature Switzerland AG: Basel, Switzerland, 2018; pp. 65–72. [Google Scholar] [CrossRef]
- Wu, G.-D.; Tang, D.-Z. Inter-organizational cooperative innovation of project-based supply chains under consideration of monitoring signals. Int. J. Simul. Model. 2015, 14, 539–550. [Google Scholar] [CrossRef]
- Al-Hawari, T.; Ahmed, A.; Khrais, S.; Mumani, A. Impact of assignment, inventory policies and demand patterns on supply chain performance. Int. J. Simul. Model. 2013, 12, 164–177. [Google Scholar] [CrossRef]
- Costantino, F.; Di Gravio, G.; Shaban, A.; Tronci, M. Inventory control system based on control charts to improve supply chain performances. Int. J. Simul. Model. 2014, 13, 263–275. [Google Scholar] [CrossRef]
- Gocken, M.; Dosdogru, A.T.; Boru, A. Optimization via simulation for inventory control policies and supplier selection. Int. J. Simul. Model. 2017, 16, 241–252. [Google Scholar] [CrossRef]
- Ammeri, A.; Hachicha, W.; Chabchoub, H.; Masmoudi, F. A comprehensive litterature review of mono-objective simulation optimization methods. Adv. Prod. Eng. Manag. 2011, 6, 291–302. [Google Scholar]
- Dellino, G.; Kleijnen, J.P.C.; Meloni, C. Robust simulation-optimization using metamodels. In Proceedings of the 2009 Winter Simulation Conference, Austin, TX, USA, 13–16 December 2009; pp. 540–550. [Google Scholar]
- Jarugumilli, S.; Grasman, S.E.; Ramakrishnan, S. A simulation framework for real-time management and control of inventory routing decisions. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; pp. 1485–1492. [Google Scholar]
- Cáceres-Cruz, J.; Juan, A.A.; Bektas, T.; Grasman, S.E.; Faulin, J. Combining Monte Carlo simulation with heuristics for solving the inventory routing problem with stochastic demands. In Proceedings of the 2012 Winter Simulation Conference, Berlin, Germany, 9–12 December 2012; pp. 1–9. [Google Scholar]
- Abdollahi, M.; Arvan, M.; Omidvar, A.; Ameri, F. A simulation optimization approach to apply value at risk analysis on the inventory routing problem with backlogged demand. Int. J. Ind. Eng. Comput. 2014, 5, 603–620. [Google Scholar] [CrossRef]
- Juan, A.A.; Grasman, S.E.; Caceres-Cruz, J.; Bektaş, T. A simheuristic algorithm for the single-period stochastic inventory-routing problem with stock-outs. Simul. Model. Pract. Theory 2014, 46, 40–52. [Google Scholar] [CrossRef]
- Syntetos, A.A.; Boylan, J.E.; Croston, J.D. On the categorization of demand patterns. J. Oper. Res. Soc. 2005, 56, 495–503. [Google Scholar] [CrossRef]
- Chen, D.; Sain, S.L.; Guo, K. Data mining for the online retail industry: A case study of RFM model-based customer segmentation using data mining. J. Database Mark. Cust. Strategy Manag. 2012, 19, 197–208. [Google Scholar] [CrossRef]
- Sarkar, D.; Modak, J.M. Pareto-optimal solutions for multi-objective optimization of fed-batch bioreactors using nondominated sorting genetic algorithm. Chem. Eng. Sci. 2005, 60, 481–492. [Google Scholar] [CrossRef]
- Yusoff, Y.; Ngadiman, M.S.; Zain, A.M. Overview of NSGA-II for optimizing machining process parameters. Procedia Eng. 2011, 15, 3978–3983. [Google Scholar] [CrossRef]
- Kilmer, R.A. Applications of artificial neural networks to combat simulations. Math. Comput. Model. 1996, 23, 91–99. [Google Scholar] [CrossRef]
- Dosdoğru, A.T. Comparative study of hybrid artificial neural network methods under stationary and nonstationary data in stock market. Manag. Decis. Econ. 2019. [Google Scholar] [CrossRef]
- Taylor, B.W., III. Introduction to Management Science; Pearson Education, Inc.: London, UK, 2013. [Google Scholar]
- Kucharska, E. Dynamic vehicle routing problem—Predictive and unexpected customer availability. Symmetry 2019, 11, 546. [Google Scholar] [CrossRef]
- Fang, D.; Ren, Q. Optimal decision in a dual-channel supply chain under potential information leakage. Symmetry 2019, 11, 308. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).