Abstract
With the development of modern society, there are not only many voice calls being made over wireless communication systems, but there is also a great deal of demand for data services. There are increasing demands from the general public for more information data, especially for high-speed services with elevated Gbps levels. As is well known, higher sending power is needed once data rates increase. In order to solve this problem, virtual cellular networks (VCNs) can be employed in order to reduce these peak power shifts. If a VCN works well, mobile ports will receive their own wireless signals via individual cells, and then, the signals will access core networks with the help of a central terminal. Power control can improve the power capacity in multi-hop networks. However, the use of power control will also have a negative impact on network connectivity, delay, and capacity. In order to address the problem, this paper compares specific control methods and capacities in multi-hop networks. Distributed chicken game algorithm power control (DCGAPC) methods are presented in order to reach acceptable minimum levels of network delay and maximum network capacity and connectivity. Finally, a computer simulation is implemented, and the results are shown.
1. Introduction
In the middle and late 20th century, mobile networks played a vital role in modern life. Similar to other technologies, wireless communication systems were first used by national governments, emergency services, and especially for military purposes. With the development of internet networks, an increase in both the data transmitting rate and the system capacity was needed in order to meet the increase in demand. Taking peak data rates as an example, there has been an increase in demand in IMT-2000 (International Mobile Telecom-2000) from 2 Mbps to more than 1 Gbps. Satisfying these demands is going to be the most important task in future 5G and even 6G wireless communication systems.
In order to meet the above requirements, certain problems need to be addressed. As well as data rate increases, there will soon also be greater peak power requirements. Consequently, the conception of multi-hop virtual cellular networks was proposed [1]. If a virtual cellular network (VCN) works well, mobile ports will receive their own wireless signals via individual cells, and then, the signals will access core networks with the help of a central terminal.
Power control plays a vital role in multi-hop networks in that it can efficiently use and manage wireless resources. Some power control algorithms have been proposed in recent years. In multi-hop networks, there is no base station, and communication between hops relies on a hopping scheme. At the same time, there is a great dynamic change of topological structure in the network, meaning that each hop should use a strategy that will allow them to gain maximum capacity.
Behzad and Rubin [2,3,4] researched throughput based on power control in multi-hop networks. Other previous studies [5,6,7,8,9,10] have investigated capacity based on the influence of interference on hops. Recently, scientists have discovered that game theory may be used to optimize the power control of multi-hop networks [11,12]. In this paper, a new power control system based on chicken game theory [13] is introduced, and a computer simulation [14,15] proves that the method is more efficient than others.
2. System Model
Figure 1 shows a typical ad hoc network, composed of virtual cells (VCs). In this model, many central ports act as gateways to networks. Every VC has its own gateway, and the location of the wireless ports are randomly distributed. Groups of VCs can work as a virtual base station.
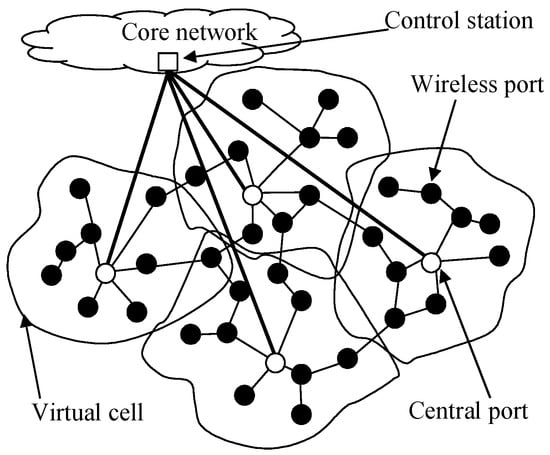
Figure 1.
Multi-hop (ad hoc) networks.
Because there is some shadowing decay, distance loss, and multi-path fading in networks, high transmission power is required by many VCs when they exchange messages directly with central ports. Multi-hop networks could reduce this problem. The signals in the network could be relayed via these VCs [16,17,18,19,20,21]. A number of VCs can communicate smoothly with central ports with any downlink [21,22,23,24,25,26] or uplink [27,28,29,30,31,32,33] transmission of data.
In order to judge the quality of the transmit power reduction, the numerical equations of transmit power are obtained below [34]. The ideal transmit power control (TPC) based on the signal-to-noise power ratio (SNR) measurements with ideal rake combining [35] is assumed here. A Rayleigh fading channel with an L-path is also assumed. In relation to a multi-hop relay with no diversity, the transmit power Pt(i) from port #i is shown in Equation (1). The system’s supposition is that there is ideal rake combining, and the TPC works well enough to accurately value sending power. In addition, a fading channel with Rayleigh [35] is supposed as the L-path, so no diversity is applied in multi-hop relay networks [36,37,38,39,40,41,42]. Transmit power Pt(i) from port #i is expressed below:
In Equation (1), Preq is the required received signal power. Between nodes #i and #j, there is some definition, including shadowing decay ηi,j (dB), l-th path plurality path gain ξi,j, path loss exponent α, and the distance di,j. If the ensemble average operation is E[*], then the result is independent plurality gaussian variables in which the zero-mean [43] is {ξi,j}. In order to unify this article, “i” and “j” are used to symbolize nodes #i and #j.
To establish the complete, transmit power following the multi-hop maximum ratio combining (MHMRC) [29,30,31,32,33] route, an n-hop connection from the wireless terminal to the central port is investigated, where port #i = 0 is the mobile terminal, port #i = n is the central port, and port #i = 1~n − 1 is the intermediate port. The received power Pr(1) from the mobile terminal #i = 0 is given by
Therefore, the mobile terminal transmit power Pt(0) can be written as
For convenience during the numeric computation, Equation (3) has been included, although it should be noted that it is exactly the same as Equation (1) except that i = 0. This is because, if the numerical calculations start from 0, then the totaling is easier; it means that 1 is 1, and the current number does not need to be subtracted by 1.
As for the ports where #i = 2~(n − 1), the receiving power Pr(i) of port #i is the total of all the received power from all the previous ports and is derived by
The summed transmit power Ptotal is calculated by totaling the transmit powers as follows:
Because Pr(i) = Preq, by using TPC, the transmit power Pt(i − 1) of port #(i − 1) is derived via
Once the power Pr(i) received from previous ports #0~#(i − 1) at port #i is larger than the required received power Preq, i.e., Pr(i) ≥ Preq, port #(i − 1) can be fired from the constructed route, i.e., Pt(i − 1) = 0. The transmit power Pt(i − 2) of port #(i − 2) is given as:
Applying this route modification method, the number of these hops decreases, and consequently, the time of the delay also reduces.
The average normalized power Pnorm using MHMRC diversity [9] is described as the average total transmit power following the route normalized by that of a single-hop case, i.e., Pnorm = E[Ptotal]/E[Psingle-hop], where Ptotal is calculated by Equation (5) and Psingle-hop is calculated by Equation (1) with i = 0 (mobile terminal) and j = n (central port). Therefore, Pnorm is derived as follows:
The sending power Pt(j) is derived from Equation (3) for port #j = 0 and from Equation (6) for ports #j = 1~n − 1, displacing i − 1 by j. Pt(j) is derived recursively from Equation (6). Due to Pt(0)∝Preq, it can be easily accepted that Pt(j)/Preq is not a function of Preq. Consequently, Pnorm is an independent variable relative to Preq. In Equation (8), considering the fact that two operations of expectation and addition have been done, the algorithm complexity of Pnorm is O(n3).
Figure 2 draws the normalized average power as a function of N with ρ as a factor for α = 3.5, σ = 7 dB, L = 2, and K = 50. It can be seen that the MHMRC (Multi-Hop Maximum Ratio Combining) [9] reduces the sum transmit power for all ρ values. The power decrease by MHMRC is bigger when ρ reduces. As for ρ ≥ 0.5, the MHMRC diversity gain reduces and becomes very small once ρ = 1.
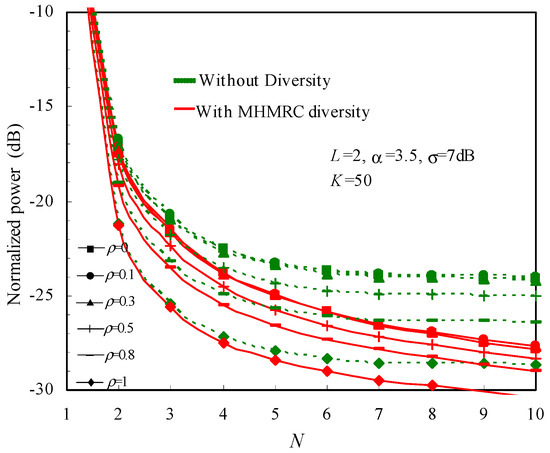
Figure 2.
Impact of ρ on the transmit power.
While ρ = 1, both the routing construction channel and the data’s communication channel experience the same fading. The data’s communication routing is equal to the minimum transmit power routing. The fading correlation property between the control channel and the data’s communication channel can be derived as follows:
where is the carrier frequency separation between the two independent channels and is the delay spreading of the fading channel. Once L = 2 and = 0.165, the frequency separation should be KHz for ρ = 0.5.
3. Distributed Chicken Game Algorithm Power Control
In traditional wireless communication protocols, due to the constraints of their use, their structure is not very flexible. They cannot operate in certain averse conditions and are unable to adapt to dynamic situations. Consequently, this problem causes the system to use spectrum and energy inefficiently. A hybridizing layer design is adaptable, because it means that it has the capability to investigate and reply to variations in the channel. The distributed chicken game algorithm power control (DCGAPC) layer design model can be seen in Figure 3. In this model, the realization of the power control module is in the physical layer, and the module can receive interference messages via an adjacent node table, which is located in the internet layer so that the sending power can be computed.
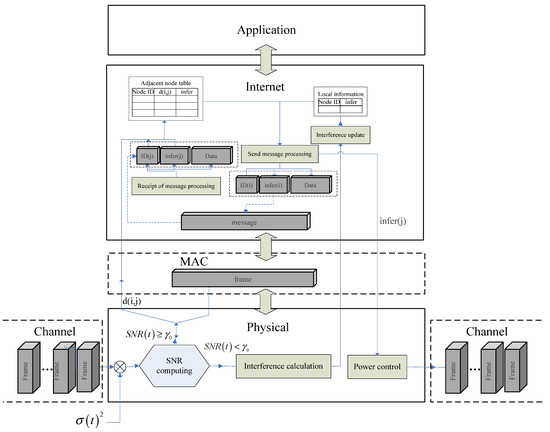
Figure 3.
The distributed chicken game algorithm power control (DCGAPC) layer design model. ID: identification; SNR: signal-to-noise ratio.
The DCGAPC algorithm is proposed as a cross-layer design method. The power control module includes SNR computing, interference calculations, and power control. Figure 3 shows the hybridizing layer of the proposed method. The SNR computing module calculates and derives a specific transmission distance based on the received signal strength (RSS), which comes from its own physical layer. The native information form is constructed at the network layer. The interference calculation module gets local interference power and transmits it to the interference update module that is located in the network layer. Once the node intends to send a message, the send message processing module, which is located in the networks layer, will find its own native information form and then calculate the sending power with the max payoff. In the next step, the send message processing module calculates and derives the payoff value of the sending power and puts the value to the power control module located in the physical layer. After this power control unit has done its calculations based on the DCGAPC algorithm, the wireless communication system sends the message with this calculated power level.
When the nodes receive message frames, the SNR computing module determines whether the message is a valid message by calculating the SNR of the received signal. If the message is valid, it can be transmitted to the upper layers to travel between two nodes. If the message is interference, then the nodes will abandon it and operate the interference module to update the information in nodes, which are located in the internet layer. Whenever nodes need to send messages, they calculate the interference of the destiny node based on the adjacent node table and then send the interference to the power control module for calculating.
If the power control of nodes in multi-hop networks are considered as a problem using the chicken game, then its basic expression is . represents the number of all the nodes in the network, and the strategy of the specific node i is denoted as . All nodes in the network select their strategies to maximize their gain based on diverse gain function [39]:
where represents the transmitting power selected by node I and denotes the transmitting power selected by other nodes except node i.
The quality of wireless networks is often influenced by factors such as signal modulation and coding. The income function can ignore the signal modulation:
To state this explicitly, the classical Gauss channel capacity formula is used, where is the profit coefficient and is the price linear functional variable of the sending power:
where is the path gain when the sending power of the node is .
Because is a simple linear function, its algorithm complexity depends on its base function Pnorm and is not any more complex than Pnorm. Therefore, the complexity of the proposed algorithm should be O(n3).
4. Simulation Analyses
In order to use the power control proposed in this article, the adjacent node form (Table 1) has to be established in order to record the identification (ID) of the nodes, interference of adjacent nodes, and the gain.

Table 1.
Adjacent node table.
The algorithm proposed in this paper should work as follows: First, every node writes the local interference power value into the HELLO message and then broadcasts it to its neighbors. Once a node receives a HELLO message, it computes the income according to Equation (11) and updates its neighboring node’s information table. When a mobile port needs to transmit information, the node checks the native form and then chooses the maximum income for calculating the sending power based on Equation (8) in order to send the information. Virtually, Equation (11) is computed according to Equation (12), and the transmit power is calculated from Equation (8) based on Equations (1)–(9). The Algorithm 1 can be written as below:
| Algorithm 1 Power control |
| 1: Initialize the local table. |
| 2: FUNCTION INIT () |
| 3: {if t = 0 Then Pi = Pmax; Piinfer = 0; |
| Initialize (native_form); |
| 4: Endif;} |
| 5: update the local table once system get a new message. |
| FUNCTION Deal Message (HI/HELLO) |
| 6: {if I get HELLO Then update(native_form); Endif;} |
| 7: determine whether system need to transmit the message according to evaluate the cost from native form. |
| 8: FUNCTION Send Message (M) |
| 9: {if i transmits M Then u < = find_payoff(native_form); |
| 10: Pi < = calculate_trans_power(u); |
| 11: If M = message then add_infer_area (Piinfer); |
| 12: Endif; |
| 13: Endif;} |
In the simulation test, there are three ways used to control power:
- Maximum energy power control algorithm (MAXPCA), by which all the nodes in the networks choose the highest transmission power;
- Minimum energy power control algorithm (MINPCA), by which all the nodes in the networks choose the lowest sending power;
- Distributed chicken game algorithm to power control (DCGAPC), which is the method proposed in this article.
The factors for the numerical computation simulation test can be seen in Table 2.

Table 2.
Computation conditions.
In all figures, the Monte–Carlo computation process was used to calculate the numerical simulation results. All data were computed using the C programming language, and then, these numerical data were drawn into a statistical curve using professional tools, such as MATLAB and Microsoft VISIO.
During the test of the performance of the routing method, the following performance parameters in the simulation experiment were also investigated:
- Reachability—ratio of the figures of the correct messages received compared to the figure of the actual messages received.
- Average latency—how long it takes for a broadcast message to be sent from the source node to all nodes in the network.
- Capacity—maximum data transmission rate for the link with the lowest processing power in the network.
- Energy efficiency—the ratio of the sum figure of the messages received compared to the energy consumed in broadcasting each unit.
Due to the hidden terminal problem, with the increase of the node’s DCGAPC, message collision is aggravated, so the broadcast success rate is reduced, which can be seen in Table 3.

Table 3.
Average successful received number of messages.
The MINPCA can decrease the power consumption of all the nodes: however, it cannot decrease the interference caused by hidden terminals. Moreover, because of the simple use of low-power transmissions, the received signal-to-noise power ratio (SNR) is relatively small, so its anti-interference ability is weak. Consequently, the average number of successfully received messages is less than the other two algorithms. When the DCGAPC is heavy, the broadcast success rate is worse than the other two methods. The broadcast success rate of DCGAPC is basically the same as that of MAXPCA.
Figure 4 shows the success rates of the three algorithms. When the DCGAPC is heavy, the broadcast success rate of MINPCA is worse than that of the other two methods. The broadcast success rate of DCGAPC is basically the same as that of MAXPCA. The broadcast success rate using MINPCA can reduce the power consumption of nodes, but it cannot reduce the interference caused by hidden terminals. Furthermore, because of the simple use of low-power transmissions, the received SNR is relatively small, so its anti-interference ability is also weak.
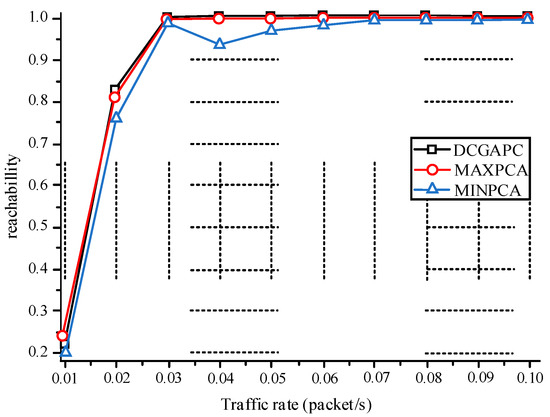
Figure 4.
Comparison of the success rate of algorithm broadcasting.
Figure 5, Figure 6 and Figure 7 show the interference distributions of the three algorithms. MAXPCA produces the most interference with e−7~e−8 level/magnitude. However, MINPCA generates less interference with e−10~e−11 level/magnitude due to its low sending power. DCGAPC shows the least interference, with only e−11 level/magnitude. Because this algorithm can regulate the sending power via the condition of the channels, its interference is less than the other two methods.
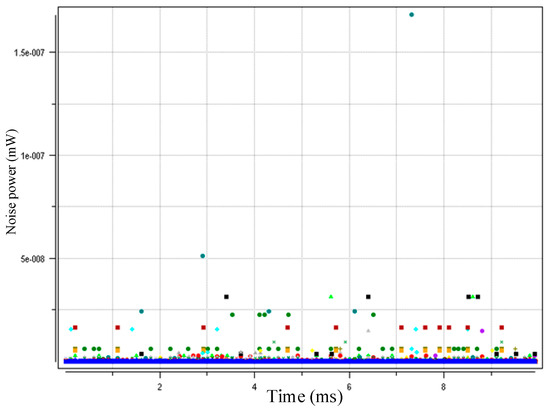
Figure 5.
MAXPCA algorithm interference distribution (50 nodes).
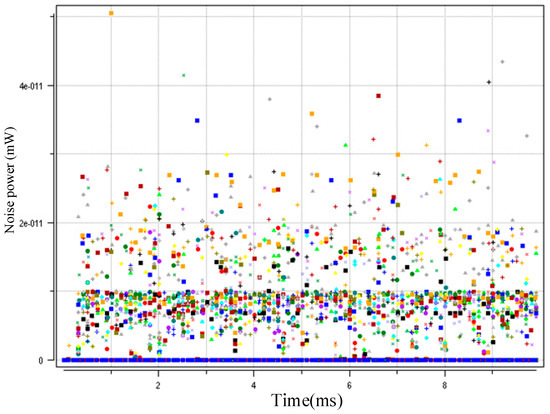
Figure 6.
DCGAPC algorithm interference distribution (50 nodes).
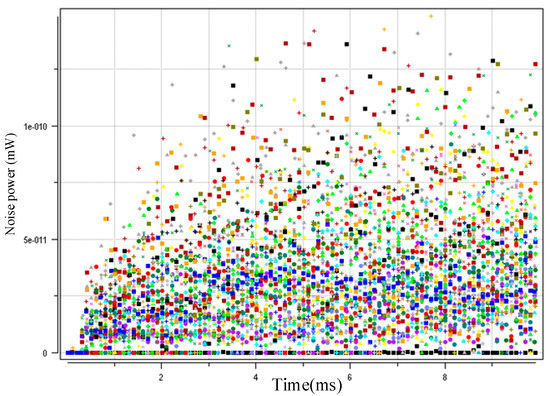
Figure 7.
MINPCA algorithm interference distribution (50 nodes).
Because DCGAPC can deal with interference and has a lower delay, the number of message collisions and channel contentions are all less than MAXPCA, as can be seen in Figure 5, Figure 6 and Figure 7. Figure 8 shows the delay in the three algorithms, and Figure 9 shows their system capacity. In Figure 8, the capacity of the three algorithms increases linearly when the business load increases. Capacity is at its peak when the load reaches 0.04 (s/packet).
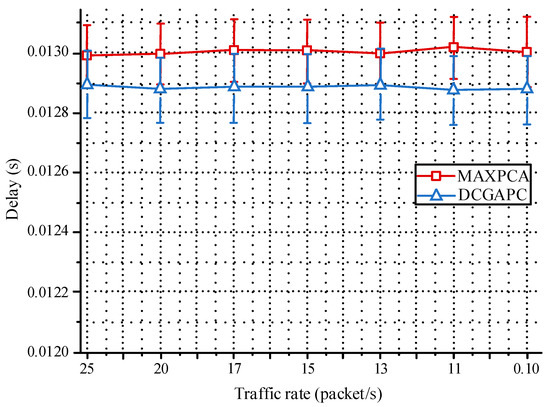
Figure 8.
Average delay comparison of the three algorithms.
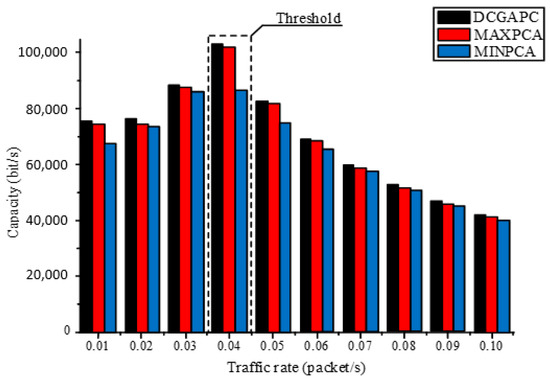
Figure 9.
Capacity comparison of the three algorithms under different service loads.
In Figure 8, Figure 9 and Figure 10, the confidence intervals are also shown. Although the simulation uses the same confidence interval with each of the three different algorithms, the DCGAPC shows more efficiency. Typically, when dynamic Tx power is applied to DCGAPC, the transmission range of each node tends to be changed (the same as energy consumption). Thus, a DCGAPC should have increased efficiency.
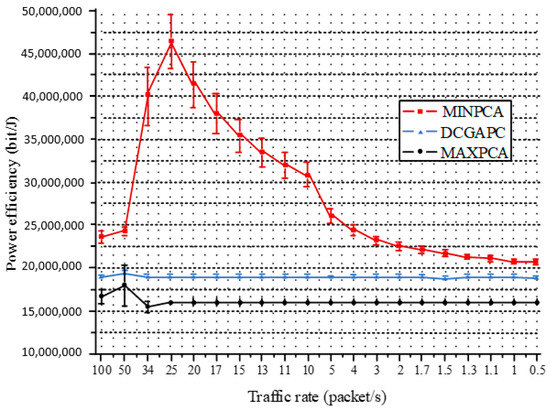
Figure 10.
Comparison of energy efficiency in the three algorithms.
After this peak value, the capacities of the three algorithms decline, irrespective of the load increases. This decline is due to the broadcast storm produced by a broadcast when the load reaches the threshold 0.04 (s/packet). It is well known that the broadcast storm problem can lead to the failure of the broadcast in all three algorithms.
Figure 10 shows the power efficiency of the three algorithms. MINPCA requires the minimum sending power, so its power efficiency is optimal. MAXPCA has the lowest efficiency, followed by DCGAPC.
5. Conclusions
Power control is an important and complex problem, and merely reducing sending power cannot perfectly control interference and achieve optimal capacity. In this article, the novel algorithm, DCGAPC, was proposed. The method fully considered the channel capacity, network radius, and the optimization of the transmitting power of the nodes. It used the DCGAPC layer design model, power control module including SNR computing, interference calculation, and power control. The modeling indicated that MAXPCA has the maximum capacity and the lowest energy efficiency, and MINPCA has optimal energy efficiency, the lowest capacity, and the largest delay. However, it has been shown that the DCGAPC algorithm suggested in this article can regulate sending power via the condition of the channels. Therefore, its interference is lower than both the MAXPCA and MINPAC methods.
Author Contributions
J.W. designed the measurement scheme, carried out the simulations, and wrote the paper; N.Z. supervised the work, arranged the architecture, and contributed to the writing of the paper; and Y.Z., J.G., and T.M.S. performed the field test and analyzed the data.
Funding
This research was financially supported by the Project for the National Natural Science Foundation of China (61402069), the 2017 Project for the Natural Science Foundation of Liaoning province (20170540059), and the General project of the National Social Science Fund (2019AG00482).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kudoh, E.; Adachi, F. Study of a multi-hop communication in a virtual cellular system. In Proceedings of the WPMC—Wireless Personal Multimedia Communiations, Yokosuka, Japan, 19–22 October 2003. [Google Scholar]
- Behzad, A.; Rubin, I. Impact of power control on the performance of Ad hoc wireless networks. In Proceedings of the INFOCOM 2005, Miami, FL, USA, 13–17 March 2005; pp. 102–113. [Google Scholar]
- Wang, J.; Zou, N.; Zhang, Y.; Li, P. Study on Downlink Performance of Multiple Access Algorithm based on Antenna Diversity. ICIC Express Lett. 2015, 9, 1221–1225. [Google Scholar]
- Xu, H.; Guo, C.; Zhang, L. Optimal Power Control in Wireless Powered Sensor Networks: A Dynamic Game-Based Approach. Sensors 2017, 17, 547. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Shao, F.; Ye, S.; Zheng, W. LSRR-LA: An Anisotropy-Tolerant Localization Algorithm Based on Least Square Regularized Regression for Multi-Hop Wireless Sensor Networks. Sensors 2018, 18, 3974. [Google Scholar] [CrossRef] [PubMed]
- Katranaras, E.; Imran, M.A.; Tzaras, C. Uplink capacity of a variable density cellular system with multicell processing. IEEE Trans. Commun. 2009, 57, 2098–2108. [Google Scholar] [CrossRef]
- Wang, C.L.; Ku, S.J. Novel Conversion Matrices for Simplifying the IFFT Computation of an SLM-Based PAPR Reduction Scheme for OFDM Systems. IEEE Trans. Commun. 2009, 57, 1903–1907. [Google Scholar] [CrossRef]
- Lu, G.; Wu, P.; Aronsson, D. Peak-to-Average Power Ratio Reduction in OFDM Using Cyclically Shifted Phase Stages. IET Commun. 2007, 1, 1146–1151. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, S.; Zhang, J. Multi-hop maimal ratio combining (MHMRC) diversity based on virtual cellular network. J. Jilin Univ. 2011, 41, 533–536. [Google Scholar]
- Sklar, B. A primer on turbo code concepts. IEEE Commun. Mag. 1997, 35, 94–101. [Google Scholar] [CrossRef]
- Lin, S.; Costello, D.J., Jr. Error Control Coding: Fundamentals and Applications; Prentice Hill: Upper Saddle River, NJ, USA, 1983. [Google Scholar]
- Li, S.E.; Li, R.; Wang, J.; Hu, X.; Cheng, B.; Li, K. Stabilizing Periodic Control of Automated Vehicle Platoon with Minimized Fuel Consumption. IEEE Trans. Transp. Electrif. 2017, 3, 259–271. [Google Scholar] [CrossRef]
- Zou, Q.-F.; Tan, X.-Z.; Liu, M.; Ma, L. Low complexity frequency domain iterative equalization based on minimum mean square error for single carrier systems. Jilin Daxue Xuebao (Gongxueban) 2015, 45, 2062–2068. [Google Scholar]
- Tian, P.; Xiao, X.; Wang, K.; Ding, R. A Hierarchical Energy Management System Based on Hierarchical Optimization for Microgrid Community Economic Operation. IEEE Trans. Smart Grid 2016, 7, 2230–2241. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Yang, S.; Deng, F. Weighted Optimization-Based Distributed Kalman Filter for Nonlinear Target Tracking in Collaborative Sensor Networks. IEEE Trans. Cybern. 2017, 1, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Li, M.; Feng, J. Multi-Feedback Interference Cancellation Algorithms for OFDM Systems over Doubly-Selective Channels. Algorithms 2015, 8, 484–513. [Google Scholar] [CrossRef]
- Vasudevan, K. Coherent Detection of Turbo-Coded OFDM Signals Transmitted Through Frequency Selective Rayleigh Fading Channels with Receiver Diversity and Increased Throughput. Wirel. Pers. Commun. 2015, 82, 1623–1642. [Google Scholar] [CrossRef]
- Shu, S.; Qu, D.; Li, L.; Jiang, T. Invertible Subset QC-LDPC Codes for PAPR Reduction of OFDM Signals. IEEE Trans. Broadcast. 2015, 61, 290–298. [Google Scholar] [CrossRef]
- Zhao, D.-W.; Zhao, H.-L.; Ma, Y.-K.; Jia, M. Enhanced scaled selection combiner for decode-and-forward systems with adaptive modulation. Jilin Daxue Xuebao (Gongxueban) 2016, 46, 671–677. [Google Scholar]
- Wan, L.; Zhou, H.; Xu, X.; Huang, Y.; Zhou, S.; Shi, Z.; Cui, J.-H. Adaptive Modulation and Coding for Underwater Acoustic OFDM. IEEE J. Ocean. Eng. 2015, 40, 327–336. [Google Scholar] [CrossRef]
- Marina, M.; Arno, T.; Emmeric, T.; Vallozzi, L.; Vermeeren, G.; Joseph, W.; Rogier, H.; Martens, L. Diversity Performance of Off-Body MB-OFDM UWB-MIMO. IEEE Trans. Antennas Propag. 2015, 63, 3187–3197. [Google Scholar] [CrossRef]
- Chai, E.; Shin, K. Low-Overhead Control Channels in Wireless Networks. IEEE Trans. Mob. Comput. 2015, 14, 2303–2315. [Google Scholar] [CrossRef]
- Wang, J.; Cao, F.; Zou, N. Multi carrier system joint receiving method based on MAI and ICI. Jilin Daxue Xuebao (Gongxueban) 2018, 41, 301–305. [Google Scholar]
- Al-Awami, A.; Saif, W.A.; Zerguine, A.; Zidouri, A.; Cheded, L. An Adaptive Equalizer Based on Particle Swarm Optimization Techniques. In Proceedings of the ISSPA 2007, Sharjah, UAE, 12–15 February 2007; pp. 12–15. [Google Scholar]
- Hu, M.; Li, Y.; Lu, X.; Zhang, H. Tone Reservation to Minimize Nonlinearity Impact on OFDM Signals. IEEE Trans. Veh. Technol. 2015, 64, 4310–4314. [Google Scholar] [CrossRef]
- Bishwarup, M.; Timothy, T.; Visotsky, E.; Vook, F.W.; Ghosh, A.; Nam, Y.-H.; Li, Y.; Zhang, C.; Zhang, M.; Luo, Q.; et al. 3D channel model in 3GPP. IEEE Commun. Mag. 2015, 53, 16–23. [Google Scholar]
- Guido, R.; Conforti, D. A hybrid genetic approach for solving an integrated multi-objective operating room planning and scheduling problem. Comput. Oper. Res. 2017, 87, 270–282. [Google Scholar] [CrossRef]
- Qiu, X.; Sha, X.-J.; Mei, L. Hybrid carrier CDMA multi-antenna system based on weighted-type fractional Fourier transform. Jilin Daxue Xuebao (Gongxueban) 2013, 43, 218–222. [Google Scholar]
- Guillermo, D.; Rey, P.A.; Wolff, P. Solving the operating room scheduling problem with prioritized lists of patients. Ann. Oper. Res. 2016, 258, 395–414. [Google Scholar]
- Guo, M.; Wu, S.; Li, B.; Song, J.; Rong, Y. Integrated scheduling of elective surgeries and surgical nurses for operating room suites. Flex Serv. Manuf. J. 2016, 28, 166–181. [Google Scholar] [CrossRef]
- Wang, S.; Roshanaei, V.; Aleman, D.M.; Urbach, D.R. A discrete event simulation evaluation of distributed operating room scheduling. IIE Trans. Healthc. Syst. Eng. 2016, 6, 236–245. [Google Scholar] [CrossRef]
- Mauve, M.; Widmer, J.; Hartenstein, H. A survey on position-based routing in mobile ad hoc networks. IEEE Netw. 2001, 30–39. [Google Scholar] [CrossRef]
- Huang, C.; Yates, R. Rate of convergence for minimum power assignment algorithms in cellular radio systems. Wirel. Netw. 1998, 4, 223–231. [Google Scholar] [CrossRef]
- Holland, G.; Vaidya, N. A rate adaptive MAC protocol for multi-hop wireless networks. In Proceedings of the 7th Annual International Conference on Mobile Computing and Networking, ACM MobiCom, Rome, Italy, 16–21 July 2001. [Google Scholar]
- Daou, I.; Kudoh, E.; Adachi, F. Transmit power efficiency of multi-hop MRC diversity for a virtual cellular network. IEICE Trans. Commun. 2005, E88-B, 3643–3648. [Google Scholar] [CrossRef]
- Daou, I.; Kudoh, E.; Adachi, F. Transmit power efficiency of multi-hop hybrid selection/MRC diversity for a DS-CDMA virtual cellular network. In Proceedings of the 62th IEEE VTC, Dallas, TX, USA, 25–28 September 2005. [Google Scholar]
- Luo, J.; Ye, D.; Xue, L.; Fan, M. A survey of multicast routing protocols for mobile Ad-Hoc networks. IEEE Commun. Surv. Tutor. 2009, 11, 78–91. [Google Scholar]
- Adachi, F. Wireless past and future-evolving mobile communication systems. IEICE Trans. Fundam. 2001, E84-A, 55–60. [Google Scholar]
- Sun, Q.; Zeng, X.; Chen, N. A Cross-layer Designed Power Control Algorithm for Wireless Ad Hoc Networks. In Proceedings of the 10th IEEE International Conference on High Performance Computing and Communications, Dalian, China, 25–27 September 2008; pp. 478–485. [Google Scholar]
- Lee, W.C.Y. Mobile Cellular Telecommunication Systems; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Han, G.Y.; Song, J. Extensions of the I-MMSE Relationship to Gaussian Channels with Feedback and Memory. IEEE Trans. Inf. Theory 2016, 62, 5422–5445. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Zhang, S. Pseudorange Measurement Method Based on AIS Signals. Sensors 2017, 17, 1183. [Google Scholar] [CrossRef]
- Zheng, K.; Hu, Q.; Zhang, J.B. Positioning Error Analysis of Ranging-Mode Using AIS Signals in China. J. Sens. 2016, 2016, 6928961. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).