Abstract
In view of the dynamic change of customer requirements (CRs) during the process of product use, in this paper we propose a Bayesian Nash equilibrium configuration model for product variant design driven by CRs. By analyzing CRs, the complete variant requirements of the products can be obtained. Combined with modularization and parameterization variant design methods, a parametric variant instance is proposed. Since cost and delivery time are affected by the product variant design, firms and customers are established as two decision-making bodies, and Bayesian Nash theory is introduced to the product configuration. The theory takes the product cost and customer satisfaction as the payoff function of the game, and based on the threshold value search of the customer satisfaction it determines the strategy set of the two parties. The Nash equilibrium solution equation is established and solved by a simulated annealing algorithm. The optimal product configuration scheme satisfying the interests of both sides of the game is obtained. Finally, the automatic guided vehicle (AGV) is taken as an example to illustrate the effectiveness and practicability of the method.
1. Introduction
With a rise in individualized services during product usages, research on customer requirements has become a key issue in product development. Through the analysis of customer requirements, a firm can not only more clearly understand the customer’s preferences for various product features, but also better judge different customization solutions [1]. A firm’s ability to quickly respond to CRs is key to winning the market. However, with the gradual understanding of products, CRs are dynamic, and may vary drastically from time to time [2]. The firms need to solve the changing CRs quickly and make interdependencies explicit by using information technology in order to support product development [3]. Currently, product configuration technology is the main way to solve CRs at present. Customer satisfaction maximization and firm product cost minimization are the main concerns in product configuration decisions. These factors are often contradictory and cannot all be satisfied in the same configuration scheme.
It is, therefore, difficult for firms to improve customer satisfaction and decrease costs simultaneously, which means that a firm faces two problems—the first problem is how to meet the dynamic CRs; the other is how to choose a reasonable solution to make decisions regarding the configuration scheme. In order to solve this problem, in this paper we propose a Bayesian Nash equilibrium configuration model of product variant design driven by CRs. The model is oriented to a modular product, realizing product configuration based on individualized CRs during the stage of product concept design and establishing the balance of interests between customers and firms. Modular product design offers a large number of advantages for addressing product architecture. Moreover, it enables mass customization, reduces development cost, and allows efficient work in loosely coupled organizations [4].
The present paper is organized as follows. Section 2 reviews the related work in this field. In Section 3, product variant design driven by CRs is studied. Section 4 introduces the configuration model based on the Bayesian Nash equilibrium. A case study is given in Section 5 and the conclusions are drawn in Section 6.
2. Research Background
There are two issues related to the configuration model of CRs: Solutions to CRs and decision-making concerning the scheme.
2.1. Solutions to Customer Requirements (CRs)
The issue of how to meet the dynamic requirements of customers has attracted much interest in recent years. The solution to this problem is to improve product variants on the basis of the original product. At present, the main methods are variant design and product innovation design. Since product innovation design has the characteristics of long development time and high cost, it is not suitable for rapid response to customer requirements. It is sometimes difficult to directly evaluate the correlation degree between the engineering characteristics (ECs) and CRs as ECs are too simple [5]. Product variant design is achieved by improving on the original product, with strong purpose and short development time [6]. In recent years, domestic and foreign experts have studied more and more modularization variant design. Lo et al. [7] proposed a novel methodology, i.e., QFD(Quality Function Deployment)-based 3D morphological charts, to support the variant design of simple and technically mature products. Yu et al. [8] developed a joint optimization model of complex product variant design responding to customer requirement changes. Levandowski et al. [9] presented a variant design approach for engineering-to-order configuration design. Vianello et al. [10] focused on investigating the characteristics of engineering changes. Luh et al. [11] proposed an information model to analyze and improve complex design processes and product architecture. Feng et al. [12] proposed a new variant design method of mechanical parts based on extensible logic theory. The above studies focused on the technological development of parameterized variant design, but lacked consideration of the decision-making factor the variant configuration scheme.
2.2. Decision-Making of the Scheme
Product configuration is a method to achieve mass customization [13]. It connects components in a pre-defined component library according to customer requirements to find solutions that meet the requirements [14,15].
Baldwin et al. [16] believe that a modular system consists of some such units (or modules). They can be designed separately and integrated to perform specific functions. However, how to choose the optimal solution among a large number of configuration design scheme is usually the focus of researchers. For modular products, the design can be completed according to the variant or configuration of modules at all stages of the life cycle. To obtain a satisfactory multi-objective design, decision-making in the early phases of the design process is important when considering the multiple sources of uncertainty [17]. Bimal et al. [18] proposed a non-linear and explicit customer satisfaction model based on neuro-fuzzy method. Ma et al. [19] used the subjective uncertainty of engineers and customers’ preferences to implement the quantitative evaluation function solution principle through the decision method of fuzzy morphology matrix. Wang [20] proposed a new model for differentiated pricing and setting service time in order to solve the customer’s pursuit of the maximum profit of multi-fleet ferry service. Gebauer et al. [21] proposed a differentiated service model in order to generate more benefits in the manufacturing industry. However, they only considered a single-factor problem in their decision-making model, while the problems of firm product cost and customer satisfaction are not independent in firm product decision-making. It is, thus, obviously not comprehensive to consider a single problem to make a product configuration decision.
Bayesian Nash equilibrium is a way to make a decision between two parties. Hartline et al. [22] discussed the classical economic theory of Bayesian from the perspective of algorithms and approximations. In order to study quantum strategies in incomplete games, Alid-Vaccarezza et al. [23] proposed a game theory form based on multi-sector probability matrix. Hougaard et al. [24] proposed Nash equilibria to resolve the minimum cost spanning tree model. Solmeyer et al. [25] used a Bayesian framework to study quantum games with incomplete information. Sadeghi et al. [26] constructed a game theory-based mathematical model to deal with the problem of product portfolio management based on the perspective of customer and firm. Mu et al. [27] proposed a Stackelberg game model enabling customer and providers to maximize their own benefit under the industrial product-service system for a computer numerical control machine tool.
According to the above review, the Bayesian Nash equilibrium can fully consider the interest relationship of two factors, and has a good effect on the decision-making problem of the scheme.
3. Product Variant Design Driven by CRs
The model proposed in this article consists of two main processes: product variant design and the Bayesian Nash equilibrium allocation model. Firstly, firms need to analyze the dynamic CRs and transform them into corresponding variant requirements, and then the designers can make the parameterized and modularized variant design based on this analysis. Finally, the new modules are added to the module library to prepare for the Bayesian Nash equilibrium configuration model.
3.1. Customer Dynamic Requirements Acquisition and Transformation
As CRs become more and more important, during the process of product use, customers will put forward the requirement of upgrading and updating. The dynamic change of CRs often leads to changes in product structure, size, etc.
The dynamic change of CRs refers to the change of requirements that have been put forward by customers in terms of product functions, performance, and structure, including the addition, deletion, and modification of product functions and structures. Through the “requirement-structure” analysis method (such as QFD [28,29]), designers can complete the transformation of customer requirements to product characteristic parameters. Module and module characteristic values that require a variant design can be determined by product characteristic parameters. The transformation of customer requirements can be expressed as:
where CRs is the customer requirements, Rf is the fth characteristic parameter of the product, and valuef is the corresponding value of the fth characteristic parameter (expressed by a parameter or option value), f = 1, 2, …, n.
CRs→<R1,value1>∨<R2,value2>∨…∨<Rf,valuef>…∨<Rn,valuen>,
3.2. Modularization and Parameterized Variant Design Method
The product variant design is based on the firm product family structure. The product is divided into a series of module units based on the function and structure analysis. Each module contains several module instances with the same function and with a similar structure. The product’s modular product family structure is divided into three levels: the product layer, the module layer, and the instance layer. Modular variants and parametric variants are two main factors of product variant design. The specific form is shown in Figure 1.
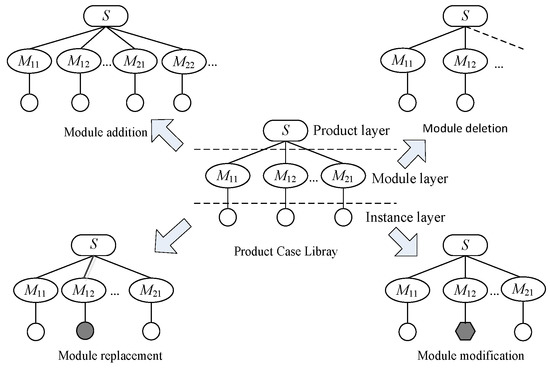
Figure 1.
Modular and parameterized product variant design method.
Modular variants result in diversified product instance designs by adding, deleting, and replacing product modules. The addition and deletion of the modules are used in the module layer, which is mainly applied to the modification of the optional functional modules. The replacement of modules is used in the instance layer, and the variant design of the product is realized by selecting an instance of the customer requirement in the module instance library to replace the original module instance (i.e., the replacement of the instance).
The parametric variant design acts on the instance layer. By analyzing the dimensional relationship and the constraint relationship between the module components, the parameters of the module that need to be modified can be determined and the dimensional constraint relationship network can be established. The variant parameters are transmitted in the size constraint relationship network. The resulting new module instance can replace the original module instance to match with CRs.
The modular variant design can change the topological structure of the product and increase the product diversity. The parameterized variant design can be combined with the computer-aided design (CAD) system, and the new module instance can be quickly generated through minor modifications of the variant parameters. In this paper, we combine the two variant design methods and propose a virtual parametric variant instance. A module of parametric variant design is added as a virtual instance to the module instance library. The product modules can be divided into basic modules (main modules for realizing product functions) and optional modules (functional modules that can be added or deleted according to CRs). It is assumed that the modules involved in the product variant include M1 basic modules and M2 optional modules. The instance library of the module can be expressed as:
In this formula, Mij represents the jth module of the ith type module, where i = 1 represents a basic module, and i = 2 represents an optional module. Pijk represents the kth instance of the module, where k = 1,2,..., Nij, and Nij is the number of instances of the module. The instance library of module Mij contains (Nij − 1) existing common instances and a virtual parametric variant instance . The expression of the product instance library is shown in Figure 2.
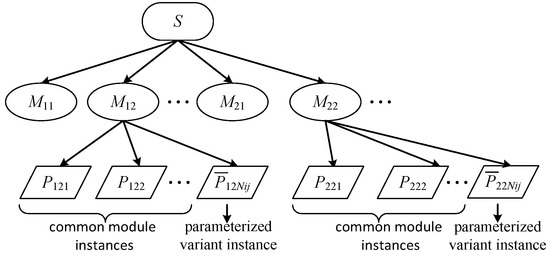
Figure 2.
Expression of the product instance library.
4. Configuration Model Based on the Bayesian Nash Equilibrium
Although the variant design of the product can satisfy the CRs, the cost increases at the same time and the delivery time is extended. The customer is more concerned with the degree of satisfaction for requirements and whether the order can be completed on schedule. The firm pays more attention to the cost, but the customer satisfaction and the cost are negatively correlated.
Due to the lack of customers’ awareness of the cost of firm products, customers and firms pursue their own interests and are in a game state, just like the relationship between doctors and patients [30]. Zandt et al. established the Bayesian game of strategic complementarity, which can realize the strategic complementarity between two players [31]. Therefore, in order to establish a model with a win–win solution between the customer and the firm (as shown in Figure 3), this paper proposes a Bayesian Nash equilibrium configuration model of the product variant design.
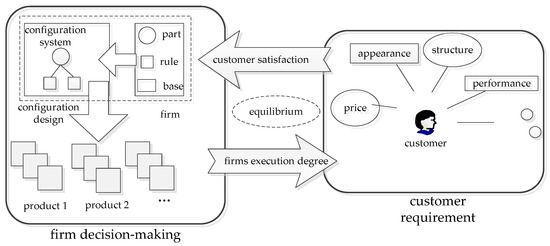
Figure 3.
Equilibrium strategies model of firms and customers.
4.1. The Model of the Bayesian Nash Equilibrium Theory
Non-cooperative game refers to a strategic interaction situation in which the players in the game choose their respective strategies to maximize their own interests. Nash equilibrium is a profile of strategies that in which each player’s strategy is a best response to the other players’ ones [32,33].
If we interpret the process of product configuration as a game, the customer and the firm are the players of the game. The strategy sets are the product model library configured by existing instance modules and the variant design module, and the payoffs are customer satisfaction and the firm product cost. Therefore, the Bayesian Nash equilibrium configuration model is described as follows:
G={Pg,Xm,Um(SR,Cp)}.
Here, Pg (g = 1,2) is gth player, Xm (m = 1,2,...) is set of strategies, and Um (SR,Cp) is the payoff set corresponding to the strategy set Xm. SR is the degree of customer satisfaction, and Cp is the product cost.
4.2. Determination of Product Strategy Set
The product characteristic parameter vector is R = (R1,R2,…,Rn). The corresponding weight vectors are W = (ω1,ω2,…,ωn). The customer satisfaction matrix CS between module instances and product characteristic parameters is constructed as follows:
where Sijkf is the customer satisfaction of product characteristic parameter Rf for the kth instance of module Mij. Here, i = 1,2; j = 1,2,…,Mi; k = 1,2,…Nij; f = 1,2,…n. If a module is not related to the product characteristic parameter Rf, the customer satisfaction of the characteristic parameter Rf for all instances of the module set to 0.
Based on the dynamic change of CRs, the modularity and parameterized variant design method is adopted to analyze the determination of the product module depending on the customer satisfaction matrix CS.
The increase of a function or a structure can be implemented by adding a module Mij in the module layer, that is, <Mij, add >. The customer satisfaction of the characteristic parameter for module instance is expressed as Sijkf = 1. The deletion of optional modules matched with the CRs in the module layer can reduce the cost or delivery time of the product.
According to the relationship between customer satisfaction and the value of product characteristic parameters, the product characteristic parameters can be divided into three categories: larger-the-better, smaller-the-better, and target-the-better [34]. According to the type of the product characteristic parameter Rd and the value of valued, the function of the customer satisfaction and the product characteristic parameter value can be established as shown in Figure 4, where Q is the overflow value of the customer satisfaction. The value can be determined by the designer according to the actual situation. If the product characteristic parameter value is discrete, the product designer can determine the correlation between the product characteristic parameter value and the customer satisfaction according to the actual situation.
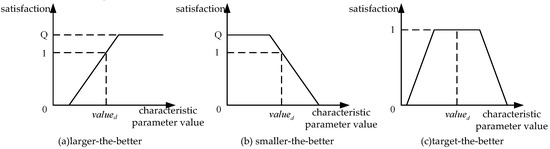
Figure 4.
Customer satisfaction and product characteristic parameter value function.
Customer satisfaction of the characteristic parameter, which is expressed as SM = {sij1f,sij2f,sij3f, ...,1}, can be obtained according to the value of its own characteristic parameters of each instance in the instance library of the module Mij. The virtual variable instances can completely satisfy the CRs, so the satisfaction is set to 1. The description of this process is shown as follows:
In the process of product configuration, the complexity of each module in design and process is different, and therefore the delivery time is different. For customized products, delivery time has a critical influence on customer satisfaction. If the product is completed within the expected time of the customer, the satisfaction of the product itself will not be affected. When the customer’s delivery time is exceeded, customer satisfaction decreases in direct proportion with time. The function of the customer satisfaction impact factor and delivery time is shown in Figure 5.
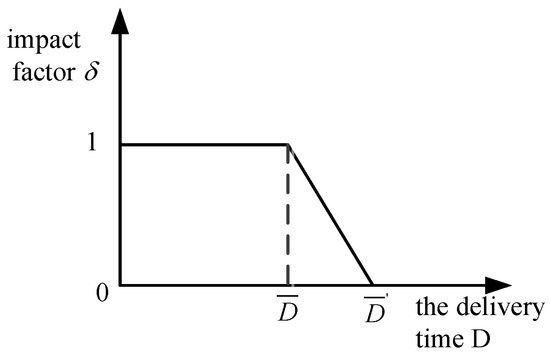
Figure 5.
Customer satisfaction impact factor and delivery time function.
The construction of the delivery time function is given as follows:
where aijk is a binary decision variable, aijk = 1 represents the kth instance of module Mij was selected, otherwise, aijk = 0, k = 1,2, …, Nij. dijk is the delivery time of the kth instance of module Mij, is the expected product delivery time, and is the last tolerated delivery time. Among them, the delivery time of the virtual parameterized variant instance includes the design cycle and manufacturing cycle of the new instance, and its value can be obtained based on the historical data of the firm.
Thus, the customer satisfaction of the product configuration model is:
where ωf is the weight of the characteristic parameter Rf,.
The maximum satisfaction value can be obtained from Equation (4); the customer satisfaction threshold, S△, is set according to the empirical value. The product model satisfying the condition, Si ≥ S△, is searched in the product configuration model. The searched product model constitutes a product strategy set Xm = {x1,x2,…,xm}.
4.3. Construction of Payoff Function
In this paper, customer satisfaction and enterprise product cost are defined as payoff function U1 and U2 of customers and enterprises respectively. Among them, customer satisfaction and product cost are required to be close to maximization and minimization.
SRi is the customer satisfaction with strategy xi, CPi is the product cost with strategy xi. In order to improve the accuracy of the payoff value and facilitate the comparison of payoff values, when the satisfaction is 1, the customer’s payoff is set to 10, then the payoff function of the customer to strategy xi is:
If CAi is the additional cost of product xi and Cr is the cost of customer requirements, then the payoff function of firm to strategy xi is:
where cijk is the cost of the kth module Mij. The cost of virtual parameterized variant instances includes the design cost and manufacturing cost, and its value can be obtained based on firm historical data. ri is the acceptance coefficient of the firm to the cost.
This paper defines that when the price of strategy xi is equal to or lower than the rated value, the firm accepts the strategy; otherwise the firm does not accept the strategy. Therefore, if , ri = 1; otherwise, ri = 0.
Integrating Equations (6) and (7), taking firms and customers as two decision-making bodies, the game payoff function is then established as:
Configuration constraints:
where the constraint conditions are that the basic modules of M1 must be selected, and Z modules (Z ≤ M2) are selected in the optional modules of M2. Then each module selects an instance accordingly.
For the above game model, a value of the payoff function is obtained only when ri = 1; otherwise, the value is 0.
4.4. Game Tree and Payoff Matrix
In the product configuration game model, based on the satisfaction of CRs and the weight of the module instance, the customer’s payoff in the strategy can be calculated. Therefore, the probability of customers accepting this strategy is determined. Since the customer’s decision is diverse and dynamic, the customer has the right to choose whether to accept or refuse the product strategy proposal provided by the firm. The firm must also consider whether to implement this strategy based on its own cost. Figure 6 is the game tree and payoff matrix in the product configuration process. If both the customer and the firm in the game accept the strategy, both sides of the game are willing to facilitate this strategy. However, in the course of the game, if one side of the game parties expresses opposition to this strategy, the payoffs of both sides of the game are 0, namely, the cooperation between the two parties fails. When solving the Nash equilibrium solution, it is considered that the two sides of the game accept the strategy, that is, assuming that the two sides cooperate successfully.
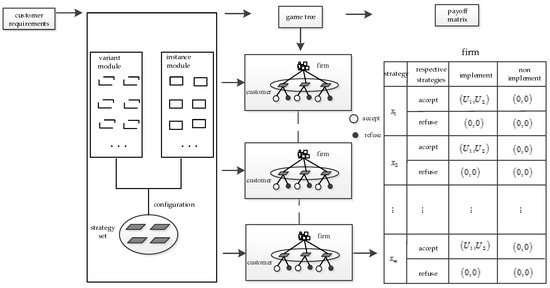
Figure 6.
Game tree and payoff matrix in product configuration.
4.5. Calculation of Nash Equilibrium Based on an Improved Simulated Annealing (SA)
SA is a stochastic optimization algorithm for iterative solutions, which is used for combinatorial optimization [35]. Considering the advantages of SA, such as high quality, strong initial value robustness, and easy general implementation [36], this paper adopts an SA algorithm to realize the Nash equilibrium solution of the model. The solution principle and the actual search solution are shown in Table 1. In the search, the neighborhood search method is adopted to improve the stability of understanding, increase the memory function, and record the historical optimal solution.

Table 1.
Comparison between the material annealing process and the optimization problem solving process.
The SA algorithm is used to solve the Nash equilibrium solution. As shown in Figure 7, the specific steps mainly include: initialization, setting the state generation, receiving, and temperature updating functions, setting the cycle termination criteria, and outputting the algorithm search results.
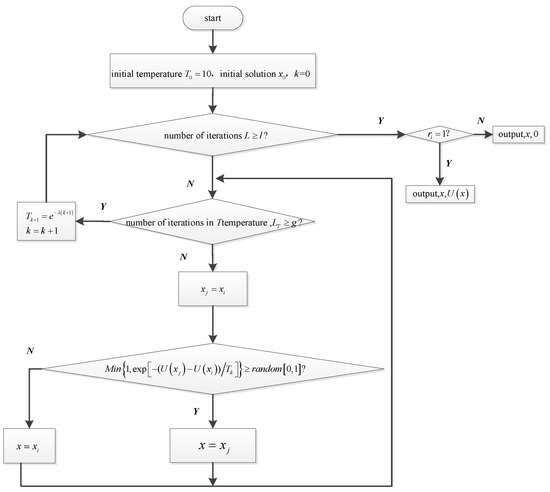
Figure 7.
Nash equilibrium solution process based on simulated annealing (SA).
Based on the non-cooperative game, the modular configuration process of product variant design under the dynamic customer requirements is also the process of maximizing the interests of both sides of the game. According to the game model, if the strategy chosen by the decision sides is the best strategy relative to other strategies, the system achieves the Nash equilibrium, namely, U(x*) ≤ U(x); x∈Xm.
Therefore, we used the SA algorithm to solve the Nash equilibrium solution and design the following parameters:
1) Objective function:
2) Temperature update function: , .
3) New state receiving function: .
4) The number of iterations of the outer loop is L = l, and the number of iterations at a specific temperature is LT = g.
Based on the SA solution process, we obtain the payoff values U1 and U2 of the customer and firm, as well as the comprehensive payoff U(xi). Then the strategy xi of the minimum value of U(xi) is a Nash equilibrium solution. If the customer’s satisfaction with the product is higher and the cost is relaxed, the firm can increase the value of the threshold S△ in the selection process of the strategy set, and further search to obtain a new Nash equilibrium solution.
5. Case Study
Automatic guided vehicle (AGV) is a transport vehicle with safety protection and transfer function applied to warehousing and manufacturing industries. This article takes the variant design configuration scheme of AGV as an example to illustrate the feasibility of the proposed method (Figure 8). Due to limited knowledge of AGV products, customers generally put forward new requirements from the function and performance of products. It is assumed that the following requirement changes are put forward in the process of use; the rated load of the AGV is larger, the continuous running time is longer, the stopping precision is higher, and the automatic charging function is added. The cost of CRs is about 45 thousand yuan, the expected delivery time is 20 days, and the last tolerated delivery time is 30 days.
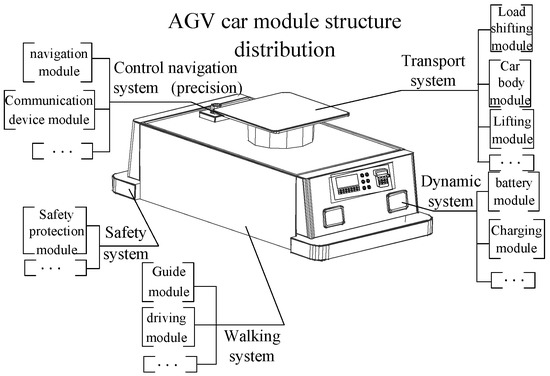
Figure 8.
Automatic guided vehicle (AGV) car module structure distribution.
5.1. Transformation of CRs
The variable module can be determined by the technician analysis and transformed into the corresponding characteristic parameter values of the product: R1 <rated load, 500 kg>R2 <continuous running time, 10 h>R3 <stop precision, ±5 mm>and R4 <automatic charging function, add>. At the same time, it inherits the unchanged characteristic parameters of the product such as R5 <body shape, L1800 × W650 × H1020>.
5.2. Variant Design Modules
Through the analysis of variant design modules and instances as well as the analysis of the firm product module, the modules’ related information and attributes involved in the dynamic change of CRs are shown in Table 2. According to the estimation method for determining product cost and time in the mass customization process [37,38] and based on the cost and time of the components and parts, the firm can establish the product cost and time as an exact value.

Table 2.
AGV modules’ related information and attributes.
5.3. Determination of Strategy Sets
Taking the product characteristic parameter R1 <rated load, 500 kg> as an example, the characteristic parameter R1 is the larger-the-better type of parameter, and the designer can construct the customer satisfaction function as shown in Figure 3a. According to the characteristic parameter R1 locking to the car body module, the satisfaction of the module instance to the characteristic parameter R1 is SM = {0.6, 0.9, 1.1, 1}. The value of customer satisfaction with the characteristic parameter R1 is set to 0 in the other unrelated modules. Similarly, the customer satisfaction matrix CS between module instances and characteristic parameters of the product can be constructed as shown below.
The analytic hierarchy process (AHP) can be used to determine the weight of each characteristic parameter as ω1 = 0.241, ω2 = 0.176, ω3 = 0.172, ω4 = 0.196, and ω5 = 0.215. From the data in Table 1, it can be seen that the parameterized variant instances of the module meet the requirements well, but at the same time the cost and delivery time of other modules increase. By considering the cost and delivery time, a Nash equilibrium game model between customer and firm payoff is established. The customer satisfaction threshold of the AGV is set by the firm designer to S△= 0.84 according to past experience. After verification, there are nine configuration schemes that meet the requirements. The corresponding strategy sets are X4 = {x1, x2, x3, x4, x5, x6, x7, x8, x9} as shown in Table 3.

Table 3.
Product strategy sets.
5.4. Calculation of Nash Equilibrium Based on SA
According to the AGV strategy set, the simulated annealing algorithm (SA) is applied to solve the Nash equilibrium solution of the product configuration, and a product that meets the interests of both the customer and the firm is obtained. In this paper, the temperature update function index in the algorithm is λ = 0.5, the number of iterations of the outer loop is L = 200, and the number of iterations at a specific temperature is LT = 50. Thereafter, by setting the corresponding satisfaction threshold, the simulated annealing algorithm is used to calculate the optimal strategy scheme, which is repeated many times, and the solution is set as a constraint to find the next one. The results are listed in Table 4.

Table 4.
Nash equilibrium solution for the configuration of the AGV.
Five strategies of AGV variant design and their corresponding payoff values are listed in Table 4. According to the payoff value, the comprehensive payoff of strategy x1 is the minimum (0.252). Therefore, it is the Nash equilibrium solution, and the configuration scheme x7(P111, , P132, P211) is the best one.
Analyzing the equilibrium payoff of each strategy (Table 5), it can be seen that the comprehensive payoff of x9 is larger than those of the other strategies. From the composition of the module, the strategy does not include other variation modules, and the inherent modules themselves are expensive, resulting in high costs. Due to the limitation of module parameters, customer satisfaction has not been significantly improved. Relatively speaking, there are few competitive advantages and it is unlikely for firms to choose this strategy.

Table 5.
Payoff matrix of the AGV.
The satisfaction of strategy x1 is the highest, and the virtual variant instance module is adopted. Compared with x7 the cost is high, but it is more suitable for pursuing high-quality customers.
All of the above schemes meet the configuration requirements. Customers can also make artificial decisions on five products according to their own requirements. Firms can also make decisions on the main products of the future market of the AGV according to customer satisfaction and implementation capacity. Of course, customers can also adjust their weights to the Nash equilibrium model according to their special requirements, and gain the product that both customers and firms are satisfied with.
6. Conclusions
In order to quickly respond to the dynamic changes of firms, firms must analyze the issue of product design from two perspectives: technology and decision-making. On this basis, a Bayesian Nash equilibrium decision-making model is established by introducing the product variable design method.
The main contributions of this paper are given below:
- Based on the variant requirements of products, a virtual parameterized variable example is presented to realize the product variant design which combines modularization and parameterization.
- A Bayesian Nash equilibrium game model with customer satisfaction and reduced cost as the objectives is established based on the configuration decision problem of the product variant module, and the equilibrium solution of the scheme decision is realized.
Author Contributions
Conceptualization, Q.Y. and R.S.; methodology, Q.Y.; software, X.B. and C.F; validation, X.B., F.S.; data curation, X.B.; writing—original draft preparation, X.B.; writing—review and editing, Q.Y., R.S and C.F.
Funding
This research was funded by the National Natural Science Foundation of China (NSFC, grant no. 5177516), and the China Scholarship Council (CSC, grant no. 201706695019).
Acknowledgments
The authors especially thank the editors and reviewers for their kindly review and helpful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Du, X.; Jiao, J.; Tseng, M.M. Understanding customer satisfaction in product customization. Int. J. Adv. Manuf. Technol. 2006, 31, 396–406. [Google Scholar] [CrossRef]
- Chen, C.; Wang, L. Integrating rough set clustering and grey model to analyse dynamic customer requirements. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2008, 222, 319–332. [Google Scholar] [CrossRef]
- Oddsson, G.; Ladeby, K.R. From a literature review of product configuration definitions to a reference framework. Artif. Intel. Eng. Des. Anal. Manuf. 2014, 28, 413–428. [Google Scholar] [CrossRef]
- Bonvoisin, J.; Halstenberg, F.; Buchert, T.; Stark, R. A systematic literature review on modular product design. J. Eng. Des. 2016, 27, 488–514. [Google Scholar] [CrossRef]
- Jia, W.; Liu, Z.; Lin, Z.; Qiu, C.; Tan, J. Quantification for the importance degree of engineering characteristics with a multi-level hierarchical structure in QFD. Int. J. Prod. Res. 2016, 54, 1627–1649. [Google Scholar] [CrossRef]
- Ma, J.; Kremer, G.E. A systematic literature review of modular product design (MPD) from the perspective of sustainability. Int. J. Adv. Manuf. Technol. 2016, 86, 1509–1539. [Google Scholar] [CrossRef]
- Lo, C.H.; Tseng, K.C.; Chu, C.H. One-Step QFD based 3D morphological charts for concept generation of product variant design. Expert Syst. Appl. 2010, 37, 7351–7363. [Google Scholar] [CrossRef]
- Yu, G.; Yang, Y.; Liu, A. Joint optimization of complex product variant design responding to customer requirement changes. J. Intell. Fuzzy Syst. 2016, 30, 397–408. [Google Scholar]
- Levandowski, C.E.; Jiao, J.R.; Johannesson, H. A two-stage model of adaptable product platform for engineering-to-order configuration design. J. Eng. Des. 2015, 26, 220–235. [Google Scholar] [CrossRef]
- Vianello, G.; Ahmed-Kristensen, S. A comparative study of changes across the lifecycle of complex products in a variant and a customised industry. J. Eng. Des. 2012, 23, 99–117. [Google Scholar] [CrossRef]
- Luh, D.B.; Ko, Y.T.; Ma, C.H. A structural matrix-based modelling for designing product variety. J. Eng. Des. 2011, 22, 1–29. [Google Scholar] [CrossRef]
- Feng, Y.X.; Hao, H.; Tan, J.R.; Hagiwara, I. Variant design for mechanical parts based on extensible logic theory. Int. J. Mech. Mater. Des. 2010, 6, 123–134. [Google Scholar] [CrossRef]
- Simpson, T.W.; Siddique, Z.; Jiao, R.J. Product Platform and Product Family Design: Methods and Applications; Springer: New York, NY, USA, 2005. [Google Scholar]
- Tseng, H.E.; Chang, C.C.; Chang, S.H. Applying case-based reasoning for product configuration in mass customization environments. Expert Syst. Appl. 2005, 29, 913–925. [Google Scholar] [CrossRef]
- Li, B.; Chen, L.; Huang, Z. Product configuration optimization using a multiobjective genetic algorithm. Int. J. Adv. Manuf. Technol. 2006, 30, 20–29. [Google Scholar] [CrossRef]
- Baldwin, C.Y.; Clark, K.B. Managing in an age of modularity. Harv. Bus. Rev. 1997, 75, 84–93. [Google Scholar] [PubMed]
- Inoue, M.; Lindow, K.; Stark, R.; Tanaka, K.; Nahm, Y.-E.; Ishikawa, H. Decision-making support for sustainable product creation. J. Adv. Eng. Inform. 2012, 26, 782–792. [Google Scholar] [CrossRef]
- Nepal, B.; Yadav, O.P.; Murat, A. A fuzzy-AHP approach to prioritization of CS attributes in target planning for automotive product development. Expert Syst. Appl. 2010, 37, 6775–6786. [Google Scholar] [CrossRef]
- Ma, H.; Chu, X.; Xue, D.; Chen, D. A systematic decision making approach for product conceptual design based on fuzzy morphological matrix. Expert Syst. Appl. 2017, 81, 444–456. [Google Scholar] [CrossRef]
- Wang, D.; Hong, K.L. Multi-fleet ferry service network design with passenger preferences for differential services. Transp. Res. Part B Methodol. 2008, 42, 798–822. [Google Scholar] [CrossRef]
- Gebauer, H.; Gustafsson, A.; Witell, L. Competitive advantage through service differentiation by manufacturing companies. J. Bus. Res. 2011, 64, 1270–1280. [Google Scholar] [CrossRef]
- Hartline, J.D. Bayesian mechanism design. Found. Trends Theor. Comput. Sci. 2013, 8, 143–263. [Google Scholar] [CrossRef]
- Alid-Vaccarezza, M.; Soto, M.E. Bayesian Nash equilibria using extended Werner-like states. Quantum Inf. Process. 2016, 15, 4337–4346. [Google Scholar] [CrossRef]
- Hougaard, J.L.; Tvede, M. Truth-telling and Nash equilibria in minimum cost spanning tree models. European. J. Oper. Res. 2012, 222, 566–570. [Google Scholar] [CrossRef]
- Solmeyer, N.; Dixon, R.; Balu, R. Characterizing the Nash equilibria of a three-player Bayesian quantum game. Quantum Inf. Process. 2017, 16, 146. [Google Scholar] [CrossRef]
- Sadeghi, A.; Zandieh, M. A game theory-based model for product portfolio management in a competitive market. Expert Syst. Appl. 2011, 38, 7919–7923. [Google Scholar] [CrossRef]
- Mu, H.; Jiang, P.; Leng, J. Costing-based coordination between mt-iPSS customer and providers for job shop production using game theory. Int. J. Prod. Res. 2017, 55, 430–446. [Google Scholar] [CrossRef]
- Sousa-Zomer, T.T.; Miguel, P.A.C. A QFD-based approach to support sustainable product-service systems conceptual design. Int. J. Adv. Manuf. Technol. 2016, 88, 701–717. [Google Scholar] [CrossRef]
- Chan, L.K.; Wu, M.L. Quality Function Deployment: A Literature Review. Eur. J. Oper. Res. 2002, 143, 463–497. [Google Scholar] [CrossRef]
- Wang, S.S.; Kong, Z.K.; Xie, C.; Xiang, J. Bayesian Nash Equilibrium Analysis of Medical Market under Asymmetry Information. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 2–14 October 2008. [Google Scholar]
- Zandt, T.V.; Vives, X. Monotone equilibria in Bayesian games of strategic comple-mentarities. J. Econ. Theory. 2007, 134, 339–360. [Google Scholar] [CrossRef]
- Nishimura, K.; Friedman, J. Existence of Nash equilibrium in n person games without quasiconcavity. Int. Econ. Rev. 1981, 22, 637–648. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Kiet, S.; Zhuang, J. A mixed complementarity-based equilibrium model of natural gas markets. Oper. Res. 2005, 53, 799–818. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, H.; Xu, Z.; Wu, Z. Research on Demand-overflowing Customer Satisfaction Model. China Mech. Eng. 2013, 24, 2880–2884. [Google Scholar]
- Allahyari, S.; Salari, M.; Vigo, D. A hybrid metaheuristic algorithm for the multi-depot covering tour vehicle routing problem. Eur. J. Oper. Res. 2015, 242, 756–768. [Google Scholar] [CrossRef]
- Oliveira, H.; Petraglia, A. Establishing Nash equilibria of strategic games: A multistart fuzzy adaptive simulated annealing approach. Appl. Soft Comput. 2014, 19, 188–197. [Google Scholar] [CrossRef]
- Wei, G.; Qin, Y. Framework of Rapid Product Cost Estimation Based on the Modular Product Family. In 2011 International Conference in Electrics, Communication and Automatic Control Proceedings; Chen, R., Ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wang, H.; Sun, B.; Zhang, Q.; Wang, J.; Wei, X. Variant configuration design upporting personalization product customization. Chin. J. Mech. Eng. 2006, 42, 90–97. (In Chinese) [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).