Fixed-Discs in Rectangular Metric Spaces

Abstract

In this manuscript, we present some results related to fixed-discs of self-mappings in rectangular metric spaces. To do this, we give new techniques modifying some classical notions such as Banach contraction principle, α-admissible mappings and Brianciari type contractions. We give necessary illustrative examples to show the validity of our obtained theoretical theorems. Our results are generalizations of some fixed-circle results existing in the literature.

1. Introduction and Preliminaries

It is well known that some applications of the Banach fixed point theorem and its generalizations have been widely studied in various disciplines of mathematics, engineering, economics and statistics. An interesting application of the Banach fixed point theorem has been obtained in the study of the graph neural network model [1]. On the other hand, the number of the fixed points of an activation function used in a neural network is important (see [2] and the references therein). There are some applications of the notion of a fixed point (resp. fixed circle) in neural networks. For example, some activation functions with a fixed circle have been used in complex valued Hopfield neural networks [3]. Discontinuous activation functions are also extensively used in neural networks. Some applications of fixed points and fixed circles have been obtained in discontinuous activation functions (see [4,5,6,7] and the references therein). In addition, some of popular activation functions existing in the literature have fixed discs (see [8,9]).

A recent approach is to consider the geometric properties of fixed points when the number of fixed points is not unique. In this context, the fixed-circle problem has been investigated in metric spaces via different contractive conditions (see [4,5,10,11,12] for more details). Since there exist some examples of an S-metric which is not generated by any metric, the fixed-circle problem has also been considered in S-metric spaces and some new fixed-circle results have been obtained (see [13,14,15,16,17]). In some of these studies, fixed-disc results have been appeared consequently.

Motivated by these studies, our aim in this paper is to consider the fixed-disc problem as a generalization of the fixed-circle (resp. fixed-point) problem.

The notion of a metric space has been extended and generalized in variant directions. One of these generalizations is made by Branciari [18] where the triangle inequality was replaced by a rectangular one. Last years, many (common) fixed point results have been established in these spaces. For more details, see [19,20,21,22,23,24,25,26,27,28,29,30]. In the sequel, denote by $\mathbb{N}$ the set of all positive integer numbers.

Definition 1.

[18] (Rectangular (or Branciari) metric space) Given a nonempty set X. The function $d_R:X\times X\to \left[0,\infty \right)$ satisfying:

• (R₁) $\theta =\vartheta$ if and only if $d_R(\theta ,\vartheta )=0$;
• (R₂) $d_R(\theta ,\vartheta )=d_R(\vartheta ,\theta )$;
• (R₃) $d_R(\theta ,\vartheta )\le d_R(\theta ,\xi )+d_R(\xi ,\eta )+d_R(\eta ,\vartheta )$

for any $\theta ,\vartheta \in X$ and all distinct elements $\xi ,\eta \in X\backslash \{\theta ,\vartheta \}$, is called a rectangular metric. Here, the pair $(X,d_R)$ is said a rectangular metric $\left(RM\right)$ space.

An S-metric space generalizes a metric space [31].

Definition 2.

[31] Given a nonempty set X and $\mathcal{S}:X^3\to [0,\infty )$. Let $\xi ,\eta ,\theta ,a\in X$ be such that

1. 

$\mathcal{S}(\xi ,\eta ,\theta )=0$ if and only if $\xi =\eta =\theta$,

2. 

$\mathcal{S}(\xi ,\eta ,\theta )\le \mathcal{S}(\xi ,\xi ,a)+\mathcal{S}(\eta ,\eta ,a)+\mathcal{S}(\theta ,\theta ,a)$.

Such $\mathcal{S}$ is said to be an S-metric on X.

The relationships between an S-metric space and a metric space are as follows:

Lemma 1.

[32] Let $(X,d)$ be a metric space. Then,

1. 

the function given as ${\mathcal{S}}_d(\xi ,\eta ,\theta )=d(\xi ,\theta )+d(\eta ,\theta ),$ for all $\xi ,\eta ,\theta \in X$, is an S-metric on X.

2. 

${\xi }_n\to \xi$ in $(X,d)$ if ${\xi }_n\to \xi$ in $(X,{\mathcal{S}}_d)$.

3. 

$\left\{{\xi }_n\right\}$ is Cauchy in $(X,d)$ iff $\left\{{\xi }_n\right\}$ is Cauchy in $(X,{\mathcal{S}}_d).$

4. 

$(X,d)$ is complete iff $(X,{\mathcal{S}}_d)$ is complete.

We write ${\mathcal{S}}_d$ as an S-metric generated by d [33]. In [32,33], there are some examples of S-metrics which are not generated by any metric. On the other hand, Gupta [34] claimed that each S-metric on X defines a metric $d_S$ on X:

$$d_S(\xi ,\eta )=S(\xi ,\xi ,\eta )+S(\eta ,\eta ,\xi ),$$

(1)

for all $\xi ,\eta \in X$. However, since the triangle inequality does not hold for all elements of X everywhere, the function $d_S$ defined in Equation (1) is not always a metric (see [33] for more details). If the S-metric is generated by a metric d on X, then $d_S$ is a metric on X. Indeed, $d_S(\xi ,\eta )=4d(\xi ,\eta )$, while, if the S-metric is not generated by any metric, then $d_S$ can or can not be a metric on X. Such $d_S$ is called the metric generated by $\mathcal{S}$ if it is a metric.

In [17], the notion of a circle was defined on an S-metric space as follows:

Definition 3.

[17] Let $(X,\mathcal{S})$ be an S-metric space and ${\xi }_0\in X$, $r\in [0,\infty )$. The circle centered at ${\xi }_0$ with radius r is given as

$$C_{{\xi }_0,r}^S=\{\xi \in X:\mathcal{S}(\xi ,\xi ,{\xi }_0)=r\}.$$

In [14], the investigation of circles on metric and S-metric spaces has been considered.

Proposition 1.

[14] Let $\mathcal{S}$ be an S-metric generated by a metric d on a nonempty set X. Hence, each circle $C_{{\xi }_0,r}^S$ on $(X,\mathcal{S})$ corresponds to the circle $C_{{\xi }_0,\frac{r}{2}}$ on $(X,d)$.

Corollary 1.

[14] Let $\mathcal{S}$ be an S-metric generated by a metric d on a nonempty set X. The circle $C_{{\xi }_0,r}$ on $(X,d)$ corresponds to the circle $C_{{\xi }_0,2r}^S$ on $(X,\mathcal{S})$.

Proposition 2.

[14] Let $(X,d_S)$ be a metric space such that $d_S$ is generated by an S-metric $\mathcal{S}$. Then, any circle $C_{{\xi }_0,r}$ on $(X,d_S)$ corresponds to the circle $C_{{\xi }_0,\frac{r}{2}}^S$ on $(X,\mathcal{S})$.

Corollary 2.

[14] The circle $C_{{\xi }_0,r}^S$ on an S-metric space $(X,\mathcal{S})$ corresponds to the circle $C_{{\xi }_0,2r}$ on $(X,d_S)$ where $d_S$ is the metric generated by $\mathcal{S}$.

Considering the above literature, the study of new fixed-disc results and fixed-circle results on a rectangular metric space gains an importance because a rectangular metric is a generalization of a metric and there exist some examples of a rectangular metric that is not a metric (see the following two examples).

At first, we define the concepts of a circle and a disc on a rectangular metric space $(X,d_R)$. Let $r\ge 0$ and ${\xi }_0\in X$. The circle $C_{{\xi }_0,r}^R$ and the closed disc $D_{{\xi }_0,r}^R$ are

$$C_{{\xi }_0,r}^R=\left\{\xi \in X:d_R(\xi ,{\xi }_0)=r\right\}$$

and

$$D_{{\xi }_0,r}^R=\left\{\xi \in X:d_R(\xi ,{\xi }_0)\le r\right\}.$$

Following [29], we present the following.

Example 1.

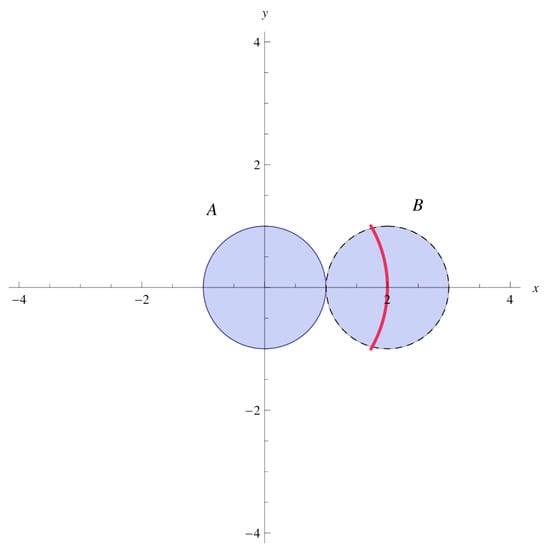
Let $A=\left\{(\xi ,\eta )\in {\mathbb{R}}^2:{\xi }^2+{\eta }^2\le 1\right\}$, $B=\left\{(\xi ,\eta )\in {\mathbb{R}}^2:{(\xi 2)}^2+{\eta }^2<1\right\}$, $X=A\cup B$ and $\rho :X\times X\to [0,\infty )$ be given as

$$\rho ((\xi ,\eta ),(\theta ,\vartheta ))=\sqrt{{(\xi \theta )}^2+{(\eta \vartheta )}^2}.$$

Given the rectangular metric $d_R:X\times X\to [0,\infty )$ as

$$d_R((\xi ,\eta ),(\theta ,\vartheta ))=\left\{\begin{array}{ccc}0& ,& (\xi ,\eta )=(\theta ,\vartheta ),\\ \rho \left(\right(\xi ,\eta ),(\theta ,\vartheta \left)\right)& ,& (\xi ,\eta )\in A,(\theta ,\vartheta )\in B,\\ 4& ,& \mathit{otherwise}.\end{array}\right.$$

Note that $d_R$ is not a metric. Indeed, if we take $(0,0),(1,0),(2,0)\in X$, then we get

$$d_R((0,0),(1,0))=4\le d_R((0,0),(2,0))+d_R((2,0),(1,0))=3,$$

which is a contradiction. In this rectangular metric space, the circle $C_{(0,0),2}^R$ is shown in Figure 1.

Figure 1. The red arc is the circle $C_{(0,0),2}^R$.

Following [35], we state the following example.

Example 2.

Consider $V=\{0,2\},W=\{\frac{1}{n}:n\in \mathbb{N}\}$ and $X=V\cup W$. Given the rectangular metric $d_R:X\times X\to [0,\infty )$ as

$$d_R(\xi ,\eta )=\left\{\begin{array}{c}0,\xi =\eta ,\hfill \\ 1,\xi \ne \eta \mathit{and}(\xi ,\eta \in V\mathit{or}\xi ,\eta \in W,)\hfill \\ \eta ,\xi \in V,\eta \in W,\hfill \\ \xi ,\xi \in W,\eta \in V.\hfill \end{array}\right.$$

Here, $d_R$ is not a metric. Indeed, if we take $0,2,\frac{1}{4}\in X$, then we get

$$d_R(0,2)=1\le d_R\left(0,\frac{1}{4}\right)+d_R\left(\frac{1}{4},2\right)=\frac{1}{4}+\frac{1}{4}=\frac{1}{2},$$

which is a contradiction. Given $r\ge 0$ and ${\xi }_0\in X$, we have

$$D_{{\xi }_0,r}^R=\left\{\xi \in X:d_R(\xi ,{\xi }_0)\le r\right\}.$$

In the case that $r\ge 1$, we have $D_{{\xi }_0,r}^R=X$, while, in the case that $0<r<1$ and ${\xi }_0\in V$, $D_{{\xi }_0,r}^R=\left\{{\xi }_0\right\}\cup (W \left\{1\right\})$.

In this paper, we provide some results on fixed-discs for different contraction mappings in the setting of rectangular metric spaces. The given results are supported by several examples. To derive new fixed-disc results, we modify some known techniques and introduce new contractive conditions such as an $\alpha$-${\xi }_0$-contractive condition, an $F_d$-contractive condition, a Ćirić type $F_d$-contractive condition, a Branciari $F_d$-contraction and a Branciari $F_d$-rational contraction on a rectangular metric space. Using these new contractive conditions, we prove some fixed-disc (fixed-circle) theorems and discuss some related results.

2. Main Results

Throughout the paper, T is a self-mapping on a rectangular metric space $(X,d_R)$. Put

$$r=\underset{\xi \in X}{inf}\{d_R(\xi ,T\xi )\mid T\xi \ne \xi \}.$$

(2)

We give new contractive conditions to establish some fixed-disc results. The definition of a fixed-disc is given in the following.

Definition 4.

The disc $D_{{\xi }_0,r}^R$ is said the fixed disc of T if $T\xi =\xi$ for all $\xi \in D_{{\xi }_0,r}^R$.

2.1. New Contractions via $\alpha$-${\xi }_0$-Admissible Maps

Definition 5.

T is an ${\xi }_0$-contractive mapping if there are ${\xi }_0\in X$ and $0<k<1$ such, that for every $\xi \in X$, we have

$$d_R(\xi ,T\xi )\le k{d}_R({\xi }_0,\xi ).$$

(3)

Now, we prove that, if T is an ${\xi }_0$-contractive mapping, then it fixes a disc.

Theorem 1.

Each ${\xi }_0$-contraction T with ${\xi }_0\in X$ fixes the disc $D_{{\xi }_0,r}^R.$

Proof. 

First of all, assume that $r=0$. In this case, $D_{{\xi }_0,r}^R=\left\{{\xi }_0\right\}$ and using the ${\xi }_0$-contractive hypothesis, we get that $T{\xi }_0={\xi }_0.$

Assume that $r>0.$ We claim that T fixes the disc $D_{{\xi }_0,r}^R.$ Let $\xi \in D_{{\xi }_0,r}^R$ be such that $T\xi \ne \xi$. By Equation (2), we have $r\le d_R(\xi ,T\xi ).$ On the other hand, using the ${\xi }_0$-contractive property of T, we obtain

$$0<d_R(\xi ,T\xi )\le k{d}_R({\xi }_0,\xi )\le kr<r,$$

which is a contradiction. Thus, $T\xi =\xi$ for every $\xi \in D_{{\xi }_0,r}^R$, that is, T fixes the disc $D_{{\xi }_0,r}^R$. □

Now, we introduce the concept of $\alpha$-${\xi }_0$-contractive self-maps.

Definition 6.

T is said to be an α-${\xi }_0$-contractive self-mapping if there are $\alpha :X\times X\to (0,\infty )$ and ${\xi }_0\in X$ such that

$$\alpha ({\xi }_0,T\xi )d_R(\xi ,T\xi )\le k{d}_R({\xi }_0,\xi );0<k<1,$$

(4)

for all $\xi \in X$.

Now, we introduce $\alpha$-${\xi }_0$-admissible maps.

Definition 7.

$\alpha :X\times X\to (0,\infty )$ and ${\xi }_0\in X.$ T is called α-${\xi }_0$-admissible if for each $\xi \in X,$

$$\alpha ({\xi }_0,\xi )\ge 1\Rightarrow \alpha ({\xi }_0,T\xi )\ge 1.$$

Theorem 2.

Let T be an α-${\xi }_0$-contractive self mapping. Assume that T is α-${\xi }_0$-admissible, and, if $\xi \in D_{{\xi }_0,r}^R$, we have $\alpha ({\xi }_0,\xi )\ge 1$. Then, T fixes the disc $D_{{\xi }_0,r}^R.$

Proof. 

In the case $r=0$, we have $D_{{\xi }_0,r}^R=\left\{{\xi }_0\right\}$. The $\alpha$-${\xi }_0$-contractive hypothesis yields that $T{\xi }_0={\xi }_0.$ Assume that $r>0.$ Let $\xi \in D_{{\xi }_0,r}^R$ such that $T\xi \ne \xi$. We have $r\le d_R(\xi ,T\xi ).$ We also have $\alpha ({\xi }_0,\xi )\ge 1$ and T is $\alpha$-${\xi }_0$-admissible, so the $\alpha$-${\xi }_0$-contractive property of T implies that

$$0<d_R(\xi ,T\xi )<\alpha ({\xi }_0,T\xi )d_R(\xi ,T\xi )\le k{d}_R({\xi }_0,\xi )\le kr<r,$$

which is a contradiction. Thus, $T\xi =\xi$, that is, T fixes the disc $D_{{\xi }_0,r}^R$. □

In [36], Wardowski initiated a new class of functions.

Definition 8.

[36] Let $\mathbb{F}$ be the set of all functions $F:(0,\infty )\to \mathbb{R}$ such that

• (F₁) F is strictly increasing;
• (F₂) For every positive sequence $\left\{{\lambda }_n\right\}$, we have

  $$\underset{n\to \infty }{lim}{\lambda }_n=0\mathit{iff}\underset{n\to \infty }{lim}F\left({\lambda }_n\right)= \infty ;$$
• (F₃) There is $u\in (0,1)$ in order that $\underset{\lambda \to 0^{+}}{lim}{\alpha }^{u}F\left(\lambda \right)=0$.

The concept of $F_d$-contractive mappings is as follows:

Definition 9.

If there exist $F\in \mathbb{F}$, $t>0,$ a function $\alpha :X\times X\to (0,\infty )$ and ${\xi }_0\in X$ such that for all $\xi \in X$, the following holds

$$d_R(\xi ,T\xi )>0\Rightarrow t+\alpha ({\xi }_0,T\xi )F\left(d_R(\xi ,T\xi )\right)\le F\left(d_R({\xi }_0,\xi )\right).$$

(5)

Then, T is said to be an $F_d$-contractive self-map on X.

Theorem 3.

Let T be an $F_d$-contractive self-mapping with ${\xi }_0\in X$ and T be α-${\xi }_0$-admissible. Suppose that, if $\xi \in D_{{\xi }_0,r}^R,$ we have $\alpha ({\xi }_0,\xi )\ge 1$. Then, T fixes the disc $D_{{\xi }_0,r}^R.$

Proof. 

If $r=0$, then we have $D_{{\xi }_0,r}^R=\left\{{\xi }_0\right\}$ and using the $F_d$-contractive property, one can easily deduce that $T{\xi }_0={\xi }_0.$ Thus, T fixes the disc $D_{{\xi }_0,r}^R.$ Now, we assume that $r>0.$ Let $\xi \in D_{{\xi }_0,r}^R$ where $T\xi \ne \xi$. Therefore, by (2), we have $r\le d_R(\xi ,T\xi ).$ Moreover, we have $\alpha ({\xi }_0,\xi )\ge 1$ and T is $\alpha$-${\xi }_0$-admissible. Thus, using the $F_d$-contractive property of T, we get

$$F\left(d_R(\xi ,T\xi )\right)<t+\alpha ({\xi }_0,T\xi )F\left(d_R(\xi ,T\xi )\right)\le F\left(d_R({\xi }_0,\xi )\right)\le F\left(r\right)\le F\left(d_R(\xi ,T\xi )\right).$$

It is a contradiction because F is strictly increasing, and $t>0$. Hence, we deduce that $T\xi =\xi$, that is, the disc $D_{{\xi }_0,r}^R$ is fixed by T. □

Definition 10.

If there are $F\in \mathbb{F}$, $t>0$ and ${\xi }_0\in X$ such that, for each $\xi \in X$,

$$d_R(\xi ,T\xi )>0⟹t+\alpha ({\xi }_0,T\xi )F\left(d_R(\xi ,T\xi )\right)\le F\left(M(\xi ,{\xi }_0)\right),$$

(6)

where

$$M(\xi ,\eta )=max\left\{d_R(\xi ,\eta ),d_R(\xi ,T\xi ),d_R(\eta ,T\eta ),\frac{1}{2}\left[d_R(\xi ,T\eta )+d_R(\eta ,T\xi )\right]\right\}.$$

(7)

Then, T is called a Ćirić type $F_d$-contraction on X.

Proposition 3.

If T is a Ćirić type $F_d$-contraction self-map with ${\xi }_0\in X$ such that $\alpha ({\xi }_0,T{\xi }_0)\ge 1$, then we have $T{\xi }_0={\xi }_0$.

Proof. 

Assume that $T{\xi }_0\ne {\xi }_0$. By Equations (6) and (7), we have

$$\begin{array}{ccc}\hfill d_R({\xi }_0,T{\xi }_0)& >& 0⟹t+\alpha ({\xi }_0,T{\xi }_0)F\left(d_R({\xi }_0,T{\xi }_0)\right)\le F\left(M({\xi }_0,{\xi }_0)\right)\hfill \\ & =& F\left(max\left\{\begin{array}{c}{d}_R({\xi }_0,{\xi }_0),d_R({\xi }_0,T{\xi }_0),d_R({\xi }_0,T{\xi }_0),\\ \frac{1}{2}\left[d_R({\xi }_0,T{\xi }_0)+d_R({\xi }_0,T{\xi }_0)\right]\end{array}\right\}\right)\hfill \\ & =& F\left(d_R({\xi }_0,T{\xi }_0)\right),\hfill \end{array}$$

which is a contradiction because of $t>0$. Then, we have $T{\xi }_0={\xi }_0$. □

A generalization of Theorem 3 is as follows:

Theorem 4.

Let T be a Ćirić type $F_d$-contraction with ${\xi }_0\in X$.Assume that T is α-${\xi }_0$-admissible and if, for every $\xi \in D_{{\xi }_0,r}^R$, we have $d_R({\xi }_0,T\xi )\le r$. Then, T fixes the disc $D_{{\xi }_0,r}^R.$

Proof. 

If $r=0$, clearly $D_{{\xi }_0,r}^R=\left\{{\xi }_0\right\}$ is a fixed-disc (point). Consider $r>0.$ Let $\xi \in D_{{\xi }_0,r}^R$. For Equation (2), we have $d_R(\xi ,T\xi )\ge r$. Thus, using Equations (6), (7) and the fact that T is $\alpha$-${\xi }_0$-admissible and F is increasing, we get

$$\begin{array}{ccc}\hfill F\left(d_R(\xi ,T\xi )\right)& <& \alpha ({\xi }_0,T\xi )F\left(d_R(\xi ,T\xi )\right)+t\le F\left(M(\xi ,{\xi }_0)\right)\hfill \\ & =& F\left(max\left\{d_R(\xi ,{\xi }_0),d_R(\xi ,T\xi ),d_R({\xi }_0,T{\xi }_0),\frac{1}{2}\left[d_R(\xi ,T{\xi }_0)+d_R({\xi }_0,T\xi )\right]\right\}\right)\hfill \\ & =& F\left(max\left\{r,d_R(\xi ,T\xi ),0,r\right\}\right)\le r,\hfill \end{array}$$

which leads to a contradiction. Hence, $d_R(\xi ,T\xi )=0$ and so $T\xi =\xi$, i.e., T fixes the disc $D_{{\xi }_0,r}^R$. □

2.2. Branciari Type $F_d$-Contractions

Definition 11.

T is said to be a Branciari $F_d$-contraction mapping if there are $F\in \mathbb{F}$, $t>0$ and ${\xi }_0\in X$ so that

$$d_R(\xi ,T\xi )>0\Rightarrow t+F\left(d_R(\xi ,T\xi )\right)\le F\left(d_R({\xi }_0,\xi )\right)$$

(8)

for all $\xi \in X$.

Theorem 5.

Let T be a Branciari $F_d$-contraction self-mapping with ${\xi }_0\in X$.Then, T fixes the disc $D_{{\xi }_0,r}^R$.

Proof. 

Suppose that $r=0$. Therefore, we get $D_{{\xi }_0,r}^R=\left\{{\xi }_0\right\}$ and, using the Branciari $F_d$-contractive property, we can easily see $T{\xi }_0={\xi }_0$. Hence, T fixes the center of the disc $D_{{\xi }_0,r}^R$ and the whole disc $D_{{\xi }_0,r}^R$. Let $r>0$ and $\xi \in D_{{\xi }_0,r}^R$ with $T\xi \ne \xi$. By Equation (2), we have $r\le d_R(T\xi ,\xi )$. Because of the Branciari $F_d$-contractive property, there are $F\in \mathbb{F}$, $t>0$ and ${\xi }_0\in X$ so that

$$t+F\left(d_R(\xi ,T\xi )\right)\le F\left(d_R({\xi }_0,\xi )\right)\le F\left(r\right)\le F\left(d_R(\xi ,T\xi )\right)$$

for all $\xi \in X$. It is a contradiction with $t>0$. Hence, $T\xi =\xi$, that is, T fixes the disc $D_{{\xi }_0,r}^R$. □

Now, we introduce a new rational type contractive condition.

Definition 12.

T is said to be a Branciari $F_d$-rational contraction if there exist $F\in \mathbb{F}$, $t>0$ and ${\xi }_0\in X$ such that

$$d_R(\xi ,T\xi )>0\Rightarrow t+F\left(d_R(\xi ,T\xi )\right)\le F\left(M_R(\xi ,{\xi }_0)\right),$$

(9)

for all $\xi \in X$, where

$$M_R(\xi ,\eta )=max\left\{\begin{array}{c}{d}_R(\xi ,\eta ),d_R(\xi ,T\xi ),d_R(\eta ,T\eta ),\\ \frac{d_R(\xi ,T\xi )d_R(\eta ,T\eta )}{1+d_R(\xi ,\eta )},\frac{d_R(\xi ,T\xi )d_R(\eta ,T\eta )}{1+d_R(T\xi ,T\eta )}\end{array}\right\}.$$

Theorem 6.

Let T be a Branciari $F_d$-rational contraction self-mapping with ${\xi }_0\in X$ and $T{\xi }_0={\xi }_0$. Then, T fixes the disc $D_{{\xi }_0,r}^R$.

Proof. 

Suppose that $r=0$. Thus, we have $D_{{\xi }_0,r}^R=\left\{{\xi }_0\right\}$. Using the hypothesis $T{\xi }_0={\xi }_0$, T fixes the disc $D_{{\xi }_0,r}^R$. Let $r>0$ and $\xi \in D_{{\xi }_0,r}^R$ with $T\xi \ne \xi$. By Equation (2), we have $r\le d_R(T\xi ,\xi )$. Because of the Branciari $F_d$-rational contractive property, there are $F\in \mathbb{F}$, $t>0$ and ${\xi }_0\in X$ so that

$$t+F\left(d_R(\xi ,T\xi )\right)\le F\left(M_R(\xi ,{\xi }_0)\right)$$

for all $\xi \in X$. Then,

$$\begin{array}{ccc}\hfill t+F\left(d_R(\xi ,T\xi )\right)& \le & F\left(M_R(\xi ,{\xi }_0)\right)\hfill \\ & =& F\left(max\left\{\begin{array}{c}{d}_R(\xi ,{\xi }_0),d_R(\xi ,T\xi ),d_R({\xi }_0,T{\xi }_0),\\ \frac{d_R(\xi ,T\xi )d_R({\xi }_0,T{\xi }_0)}{1+d_R(x,{\xi }_0)},\frac{d_R(\xi ,T\xi )d_R({\xi }_0,T{\xi }_0)}{1+d_R(T\xi ,T{\xi }_0)}\end{array}\right\}\right)\hfill \\ & \le & F(max\{r,d_R(\xi ,T\xi )\})=F\left(d_R(\xi ,T\xi )\right),\hfill \end{array}$$

a contradiction. Hence, $T\xi =\xi$. Consequently, T fixes the disc $D_{{\xi }_0,r}^R$. □

2.3. Some Remarks

Let $D_{{\xi }_0,r}^R$ be any disc on a rectangular metric space X. We note that all bijective self-mappings $T:X\to X$ that fix the disc $D_{{\xi }_0,r}^R$ form a group under composition of functions. That is, the set

$$\mathcal{D}\left(D_{{\xi }_0,r}^R\right)=\left\{T:X\to X\mid T\mathrm{is}\mathrm{a}\mathrm{bijection}\mathrm{and}\mathrm{the}\mathrm{disc}{D}_{{\xi }_0,r}^R\mathrm{is}\mathrm{fixed}\mathrm{by}T\right\}$$

is a group under the operation of composition of functions. Besides this main fact, we can give the following remarks considering all of the obtained theorems in the previous sections.

(1) If the given rectangular metric is a metric, then all of the obtained results can be considered in a metric space.

(2) Although the triangle condition $\left(R_3\right)$ is not used actively in the proofs of the above results. Examples 1 and 2 given in Section 1, show the importance of studying new fixed-circle (or fixed-disc) theorems in rectangular metric spaces.

(3) If we take the function $\alpha :X\times X\to (0,\infty )$ as $\alpha (\xi ,\eta )=1$ for all $(\xi ,\eta )\in X\times X$ in Definition 9, then we get Definition 11. In this case, Theorem 3 coincides with Theorem 5.

(4) If the function $\alpha :X\times X\to (0,\infty )$ is given as $\alpha (\xi ,\eta )\in (0,1]$ for all $(\xi ,\eta )\in X\times X$, then every Branciari $F_d$-contraction is an $F_d$-contraction. Indeed, we get

$$\begin{array}{ccc}\hfill d_R(\xi ,T\xi )& >& 0\Rightarrow t+\alpha ({\xi }_0,T\xi )F\left(d_R(\xi ,T\xi )\right)\hfill \\ & \le & t+F\left(d_R(\xi ,T\xi )\right)\le F\left(d_R({\xi }_0,\xi )\right)\hfill \end{array}$$

for all $\xi \in X$.

(5) If the function $\alpha :X\times X\to (0,\infty )$ is given as $\alpha (\xi ,\eta )\ge 1$ for all $(\xi ,\eta )\in X\times X$, then every $F_d$-contraction is a Branciari $F_d$-contraction. Indeed, we get

$$\begin{array}{ccc}\hfill d_R(\xi ,T\xi )& >& 0\Rightarrow t+F\left(d_R(\xi ,T\xi )\right)\hfill \\ & \le & t+\alpha ({\xi }_0,T\xi )F\left(d_R(\xi ,T\xi )\right)\le F\left(d_R({\xi }_0,\xi )\right)\hfill \end{array}$$

for all $\xi \in X$.

(6) Note that the radius r of the fixed-disc is independent from the center ${\xi }_0$ in Theorem 3 (resp. Theorem 1, Theorem 2, Theorem 4, Theorem 5 and Theorem 6) (see Example 6 for an example of Theorem 3).

(7) The contractive conditions given in previous subsections have been modified from some classical contractions used to find some fixed-point theorems. For example the notion of an ${\xi }_0$-contractive mapping, introduced in Definition 5, has been modified using the Banach contraction principle [37].

(8) All of the obtained fixed-disc results can also be considered as the fixed-circle results.

(9) If the given rectangular metric is a metric, then this metric generate an S-metric as defined in Lemma 1. Then, all of the obtained results can be considered in an S-metric space. In this case, some relationships between circles on a rectangular metric and an S-metric space can be obtained using the similar arguments given in Proposition 1 and Corollary 1.

(10) If an S-metric generates a metric $d_S$, then it generates a rectangular metric space since every metric is a rectangular metric. Then, the obtained fixed-circle results on S-metric spaces (see [13,14,15,16,17]) can be considered in a rectangular metric space. Some relationships between circles on a rectangular metric and an S-metric space can be obtained using the similar arguments given in Proposition 2 and Corollary 2.

2.4. Illustrative Examples

In this section, we give four illustrative examples for obtained theorems throughout the previous subsections.

Example 3.

Consider the rectangular metric space given in Example 2. Given $T:A\cup B\to A\cup B$ defined by

$$T\xi =\left\{\begin{array}{ccc}\xi & ,& \xi \in \left\{0\right\}\cup B,\\ \frac{\xi }{4}& ,& \xi =2,\end{array}\right.$$

for all $\xi \in A\cup B$.

The${\mathit{\xi }}_{\mathit{0}}$-contractive self-mapping$\mathit{T}\mathit{:}$ The mapping T is an ${\xi }_0$-contraction with ${\xi }_0=0$ and $k=\frac{1}{2}$. Indeed, we get the following cases:

• Case 1:Let $\xi \in \left\{0\right\}\cup B$. Then, we have

  $$d_R(\xi ,T\xi )=0\le \frac{1}{2}{d}_R(0,\xi ).$$
• Case 2: Let $\xi =2$. Then, we have

  $$d_R(\xi ,T\xi )=d_R\left(2,\frac{1}{2}\right)=\frac{1}{2}\le \frac{1}{2}{d}_R(0,2)=\frac{1}{2}.$$

Then, T verifies the condition of Theorem 1.

The$\mathit{\alpha }$-${\mathit{\xi }}_{\mathit{0}}$-contractive and$\mathit{\alpha }$-${\mathit{\xi }}_{\mathit{0}}$-admissible self-mapping$\mathit{T}\mathbf{:}$ If we take ${\xi }_0=0$ and the function $\alpha :X\times X\to (0,\infty )$ defined as $\alpha (\xi ,\eta )=1$, then T verifies the condition of Theorem 2 similar to the above cases.

The${\mathit{F}}_{\mathit{d}}$-contractive and$\mathit{\alpha }$-${\mathit{\xi }}_{\mathit{0}}$-admissible self-mapping$\mathit{T}\mathbf{:}$ If we take $F=ln\xi$, $t=ln4$, ${\xi }_0=0$ and $\alpha :X\times X\to (0,\infty )$ such that $\alpha (\xi ,\eta )=2$, then T satisfies the condition of Theorem 3. Indeed, we get

$$d_R(\xi ,T\xi )=d_R\left(2,\frac{1}{2}\right)=\frac{1}{2}>0,$$

for $\xi =2$. Then, we have

$$\begin{array}{ccc}\hfill t+\alpha ({\xi }_0,T\xi )F\left(d_R(\xi ,T\xi )\right)& =& ln4+2ln\frac{1}{2}=0\hfill \\ & \le & ln1=F\left(d_R(0,2)\right)=F\left(d_R({\xi }_0,\xi )\right).\hfill \end{array}$$

The Ćirić type${\mathit{F}}_{\mathit{d}}$-contractive and$\mathit{\alpha }$-${\mathit{\xi }}_{\mathit{0}}$-admissible self-mapping$\mathit{T}\mathbf{:}$ If we take $F=ln\xi$, $t=ln4$, ${\xi }_0=0$ and $\alpha :X\times X\to (0,\infty )$ given as $\alpha (\xi ,\eta )=2$, then T verifies the conditions of Proposition 3 and Theorem 4. Indeed, we get

$$d_R(\xi ,T\xi )=d_R\left(2,\frac{1}{2}\right)=\frac{1}{2}>0,$$

for $\xi =2$. Then, we have

$$\begin{array}{ccc}\hfill t+\alpha ({\xi }_0,T\xi )F\left(d_R(\xi ,T\xi )\right)& =& ln4+2ln\frac{1}{2}=0\hfill \\ & \le & ln1=F\left(M(2,0)\right)=F\left(M(\xi ,{\xi }_0)\right).\hfill \end{array}$$

The Branciari${\mathit{F}}_{\mathit{d}}$-contractive self-mapping$\mathit{T}\mathbf{:}$ If we take $F=ln\xi$, $t=ln2$ and ${\xi }_0=0$, then T verifies the condition of Theorem 5. Indeed, we get

$$d_R(\xi ,T\xi )=d_R\left(2,\frac{1}{2}\right)=\frac{1}{2}>0,$$

for $\xi =2$. Then,

$$\begin{array}{ccc}\hfill t+F\left(d_R(\xi ,T\xi )\right)& =& ln2+ln\frac{1}{2}=0\hfill \\ & \le & ln1=F\left(d_R(0,2)\right)=F\left(d_R({\xi }_0,\xi )\right).\hfill \end{array}$$

The Branciari${\mathit{F}}_{\mathit{d}}$-rational contractive self-mapping$\mathit{T}\mathbf{:}$ If we take $F=ln\xi$, $t=ln2$ and ${\xi }_0=0$, then T verifies the condition of Theorem 6. Indeed, we get

$$d_R(\xi ,T\xi )=d_R\left(2,\frac{1}{2}\right)=\frac{1}{2}>0,$$

for $\xi =2$. Then, we have

$$\begin{array}{ccc}\hfill t+F\left(d_R(\xi ,T\xi )\right)& =& ln2+ln\frac{1}{2}=0\hfill \\ & \le & ln1=F\left(M_R(2,0)\right)=F\left(M_R(\xi ,{\xi }_0)\right).\hfill \end{array}$$

In addition, we obtain

$$r=\underset{\xi \in X}{inf}\left\{d_R(\xi ,T\xi ):\xi \ne T\xi \right\}=\frac{1}{2}.$$

Consequently, T fixes the disc

$$D_{0,\frac{1}{2}}^R=\left\{0\right\}\cup (B \left\{1\right\}).$$

In the following, the converse statement of Theorem 1 does not hold everywhere.

Example 4.

Let us consider the rectangular metric space given in Example 1. Take $T:A\cup B\to A\cup B$ as

$$T\xi =\left\{\begin{array}{ccc}\xi & ,& \xi \in D_{(0,0),2}^R,\\ \frac{\xi }{2}& ,& \xi \in A,\\ \xi 2& ,& \xi \in B D_{(0,0),2}^R,\end{array}\right.$$

then we find

$$\begin{array}{ccc}\hfill r& =& \underset{\xi \in X}{inf}\left\{d_R(\xi ,T\xi ):\xi \ne T\xi \right\}\hfill \\ & =& \underset{\xi \in X}{inf}\left(\left\{d_R(\xi ,T\xi ):\xi \in A \left\{0\right\}\right\}\cup \left\{d_R(\xi ,T\xi ):\xi \in B D_{(0,0),2}^R\right\}\right)\hfill \\ & =& min\left\{4,2\right\}=2.\hfill \end{array}$$

The mapping T fixes $D_{(0,0),2}^R$, but T is not an ${\xi }_0$-contractive mapping with any k$(0<k<1)$. Indeed, if $\xi \in A$ then $\frac{\xi }{2}\in A$ and hence

$$d_R(\xi ,T\xi )=4\le k\left(d_R(0,\xi )\right)=4k,$$

a contradiction.

In the following, the converse statements of Theorem 1, Theorem 2, Theorem 3, Theorem 4, Theorem 5 and Theorem 6 are not always true.

Example 5.

Let $(X,d_R)$ be a rectangular metric space and ${\xi }_0\in X$ be any point. If we define $T:X\to X$ as

$$T\xi =\left\{\begin{array}{ccc}\xi & ,& \xi \in D_{{\xi }_0,r}^R,\\ {\xi }_0& ,& \xi \notin D_{{\xi }_0,r}^R,\end{array}\right.$$

for each $\xi \in X$ with $r>0$; then, T fixes the disc $D_{{\xi }_0,r}^R$, but T does not satisfy the conditions (3), (4), (5), (6), (8) and (9).

In the following example, we see that the radius r of the fixed disc is independent from ${\xi }_0$ in Theorem 3.

Example 6.

Let $X=\mathbb{C}$ be the family of all complex numbers and $d_R:\mathbb{C}\times \mathbb{C}\to \left[0,\infty \right)$ be defined as $d_R(\xi ,\eta )=\left|\xi \eta \right|$ for all $\xi ,\eta \in \mathbb{C}$. Then, $(\mathbb{C},d_R)$ is a rectangular metric space. Take

$$T\xi =\left\{\begin{array}{ccc}\xi +\frac{1}{\xi }& ,& 2<\left|\xi \right|<3,\\ \xi & ,& \mathit{otherwise},\end{array}\right.$$

for all $\xi \in \mathbb{C}$. Then,

$$r=\underset{\xi \in X}{inf}\left\{d_R(\xi ,T\xi ):\xi \ne T\xi \right\}=\frac{1}{3}.$$

In addition, if we take $F=ln\xi$, $t=ln2$, ${\xi }_0=0$ and $\alpha :X\times X\to (0,\infty )$ given as $\alpha (\xi ,\eta )=1$, then T verifies the condition of Theorem 3. Hence T fixes the disc

$$D_{0,\frac{1}{3}}^R=\left\{\xi \in \mathbb{C}:\left|\xi \right|\le \frac{1}{3}\right\}.$$

Now, if we take $F=ln\xi$, $t=ln2$, ${\xi }_0= 1$ and $\alpha :X\times X\to (0,\infty )$ as $\alpha (\xi ,\eta )=1$, again T satisfies the condition of Theorem 3. Hence, T fixes the disc

$$D_{ 1,\frac{1}{3}}^R=\left\{\xi \in \mathbb{C}:\left|\xi +1\right|\le \frac{1}{3}\right\}.$$

Consequently, the radius r of the fixed disc is independent from the center ${\xi }_0$.

3. Conclusions and Perspectives

In the present paper, we gave some fixed-disc results using different techniques. As we have noted, the radius r of a fixed disc in all of our obtained theorems is independent from the center ${\xi }_0$. As a future work, it will be an interesting problem to study the geometric properties of all the points ${\xi }_0$ satisfying the hypotheses of Theorem 1 (resp. Theorem 2, Theorem 3, Theorem 4, Theorem 5 and Theorem 6) for a fixed self-mapping T.