A Numerical Simulation of Silver–Water Nanofluid Flow with Impacts of Newtonian Heating and Homogeneous–Heterogeneous Reactions Past a Nonlinear Stretched Cylinder
Abstract
:1. Introduction
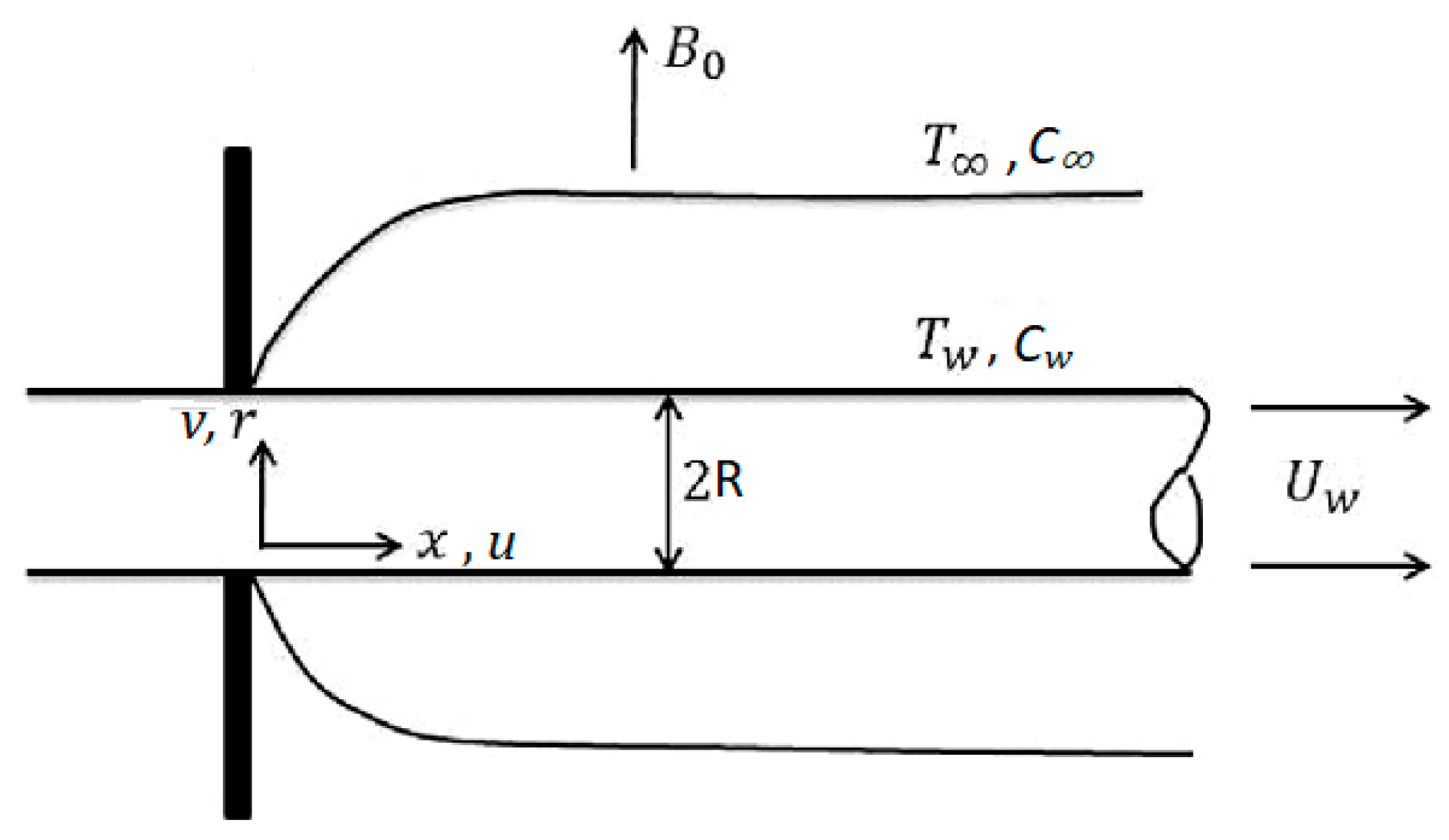
2. Mathematical Modeling
3. Numerical Scheme
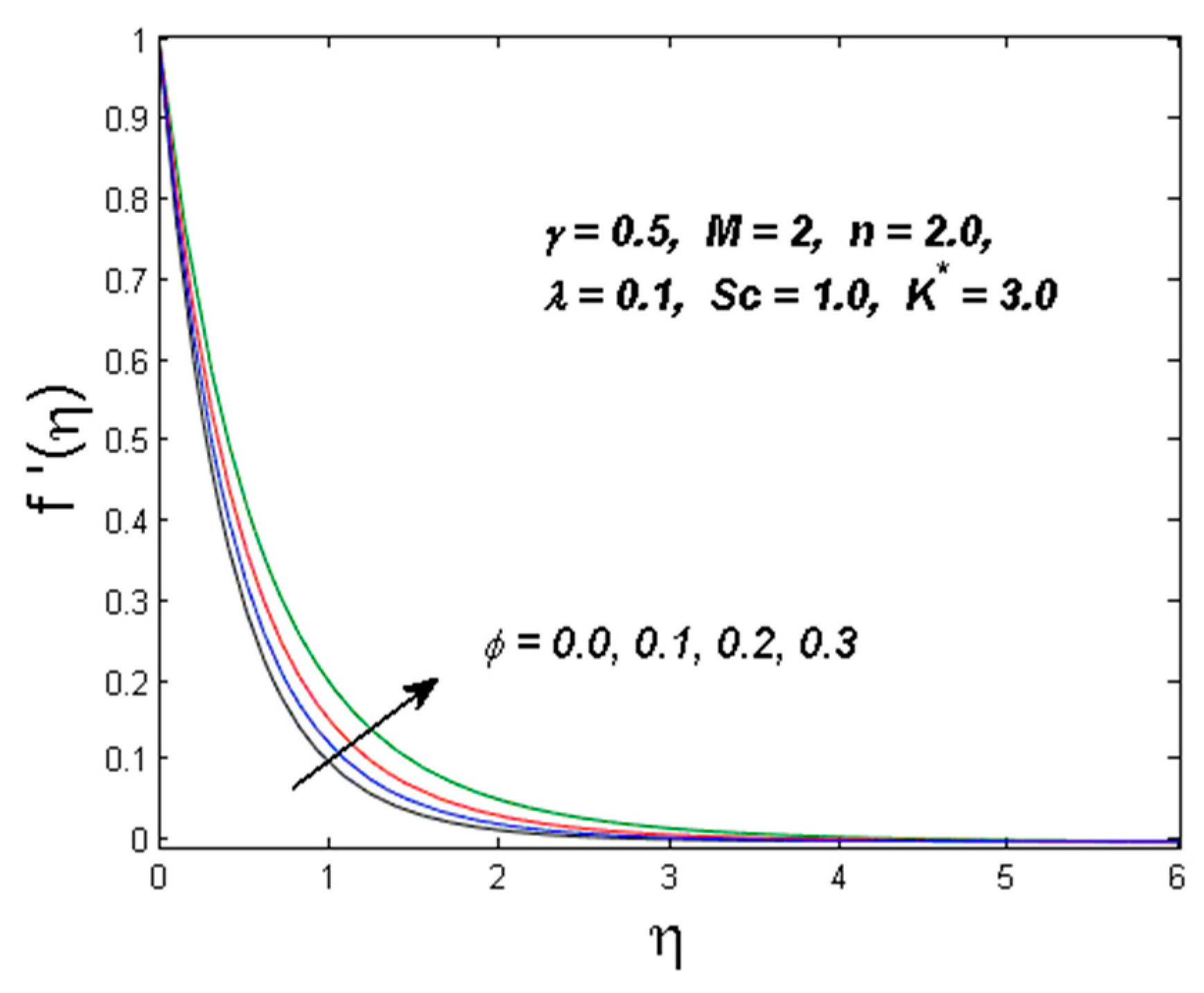
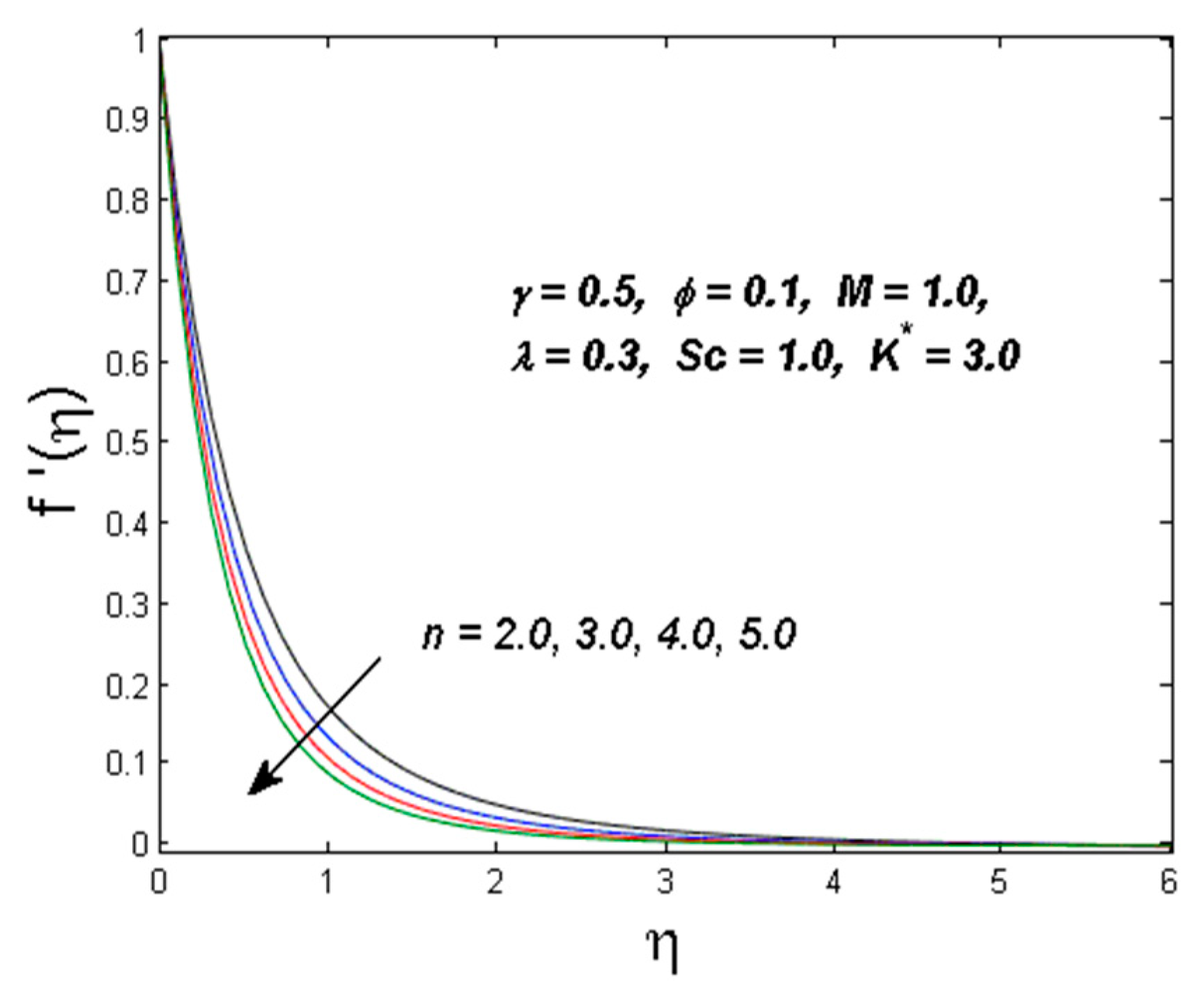
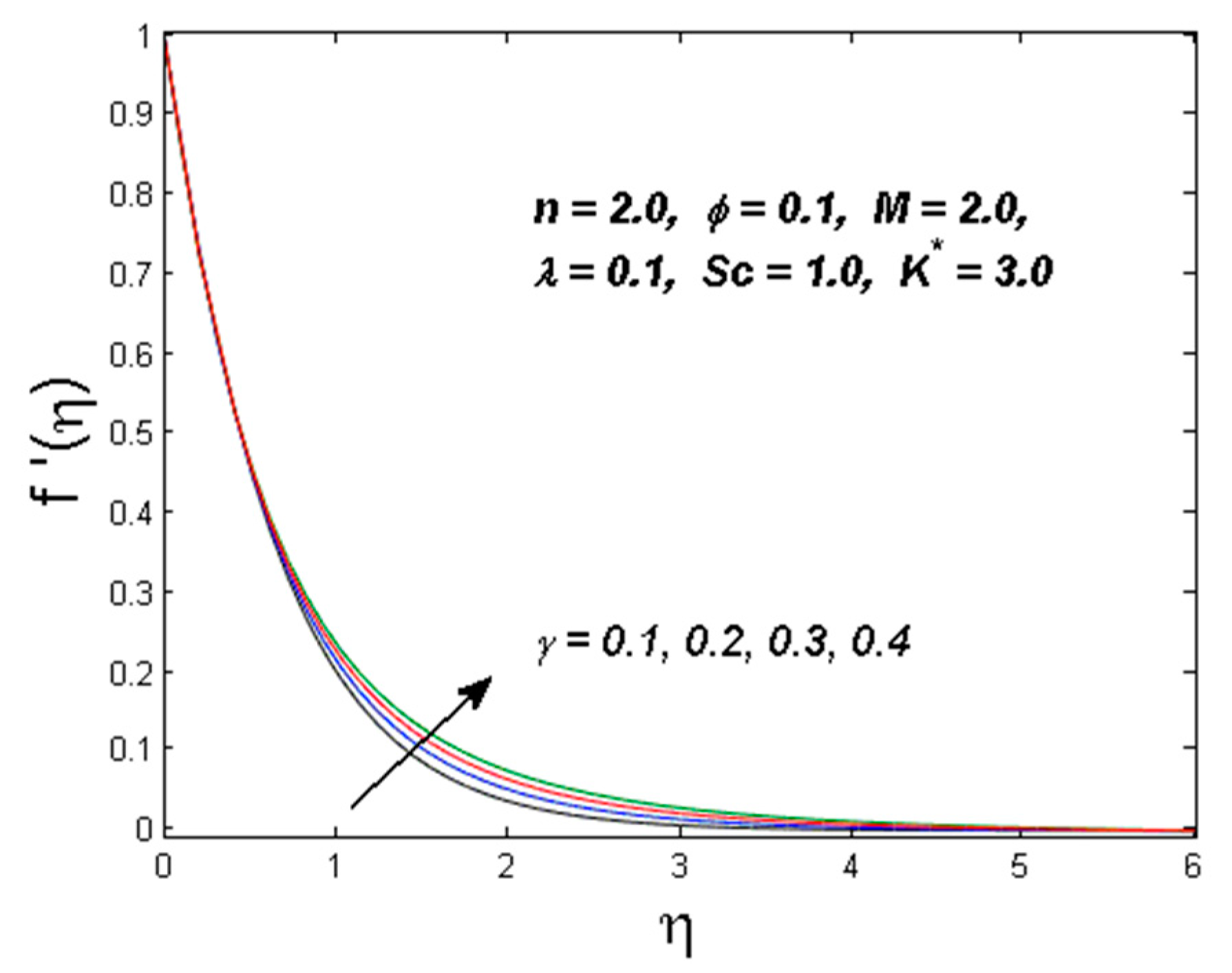
4. Results and Discussion
5. Final Comments
- The temperature profile is a growing function of radiation and magnetic parameters.
- For larger values of the curvature parameter, augmented velocity is observed.
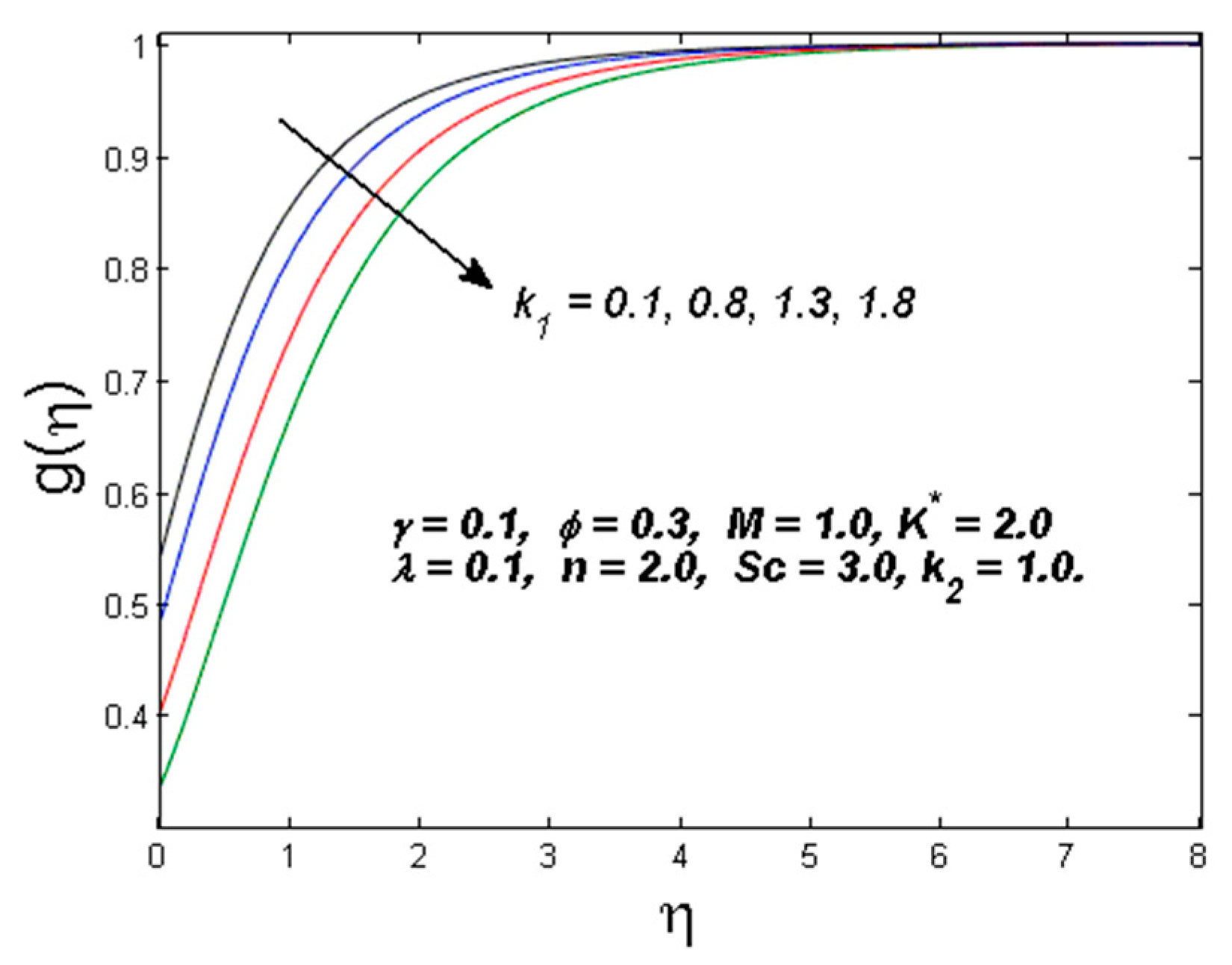
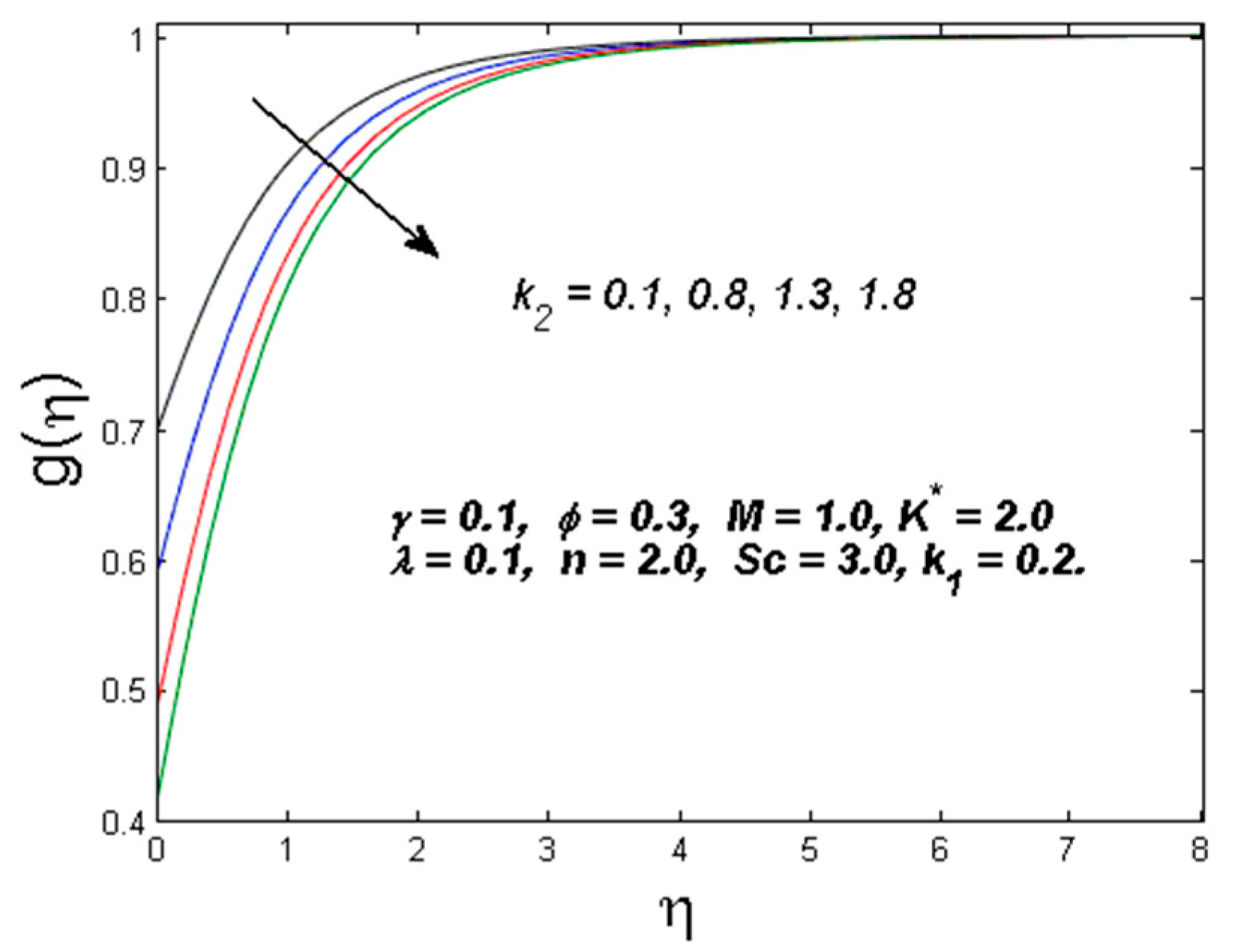
- The concentration of the fluid decreases for growing values of homogeneous–heterogeneous reactions.
- For escalated values of the magnetic parameter, velocity and temperature distributions show the opposite trend.
- The skin friction and local Nusselt number show opposite behavior for curvature and nonlinearity parameters.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| U | along x-axis fluid velocity [m/s] |
| V | along r-axis fluid velocity [m/s] |
| Uw | Stretching velocity [m/s] |
| Ue | Free stream velocity [m/s] |
| Magnetic parameter | |
| , | Density of fluid and solid particle respectively [kg/m3] |
| nanofluid volume fraction | |
| surface shear stress [N/m2] | |
| T∞ | Ambient temperature [K] |
| conjugate parameter | |
| electric conductivity of fluid and nanofluid respectively [S/m] | |
| curvature parameter | |
| kf | thermal conductivities of fluid [] |
| ks | thermal conductivities of nanomaterial [] |
| ratio of mass diffusion coefficients | |
| qr | radiative heat flux [] |
| hf | convective heat transfer coefficient |
| Cf | Skin friction coefficient |
| Nux | Nusselt number |
| T | Temperature [K] |
| Tf | convective fluid temperature [K] |
| hs | heat transfer coefficient |
| Nanofluid dynamic viscosity [] | |
| Rex | local Reynolds number |
| mean absorption coefficient | |
| Stefan-Boltzmann constant | |
| DA, DB | diffusion coefficients |
| qw | surface heat flux |
| Sc | Schmidt number |
| Rate constants | |
| K* | Radiation parameter |
| Fluid dynamic viscosity [] | |
| Nanofluid thermal diffusivity | |
| k1 | Strength of homogeneous reaction |
| nanofluid kinematic viscosity | |
| k2 | strength of heterogeneous reaction |
| R | radius of cylinder [m] |
| B | Magnetic field strength [A/m] |
| Nr | temperature ratio parameter |
| A1, B1 | concentrations of chemical species |
| Nonlinearity exponent |
References
- Choi, S.U.S. Enhancing conductivity of fluids with nanoparticles, ASME Fluid Eng. Division 1995, 231, 99–105. [Google Scholar]
- Minkowycz, W.J.; Sparrow, E.M.; Abraham, J.P. (Eds.) Nanoparticle Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2012; Volume 4. [Google Scholar]
- Kakac, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- Li, Z.; Sheikholeslami, M.; Shafee, A.; Ramzan, M.; Kandasamy, R.; Al-Mdallal, Q.M. Influence of adding nanoparticles on solidification in a heat storage system considering radiation effect. J. Mol. Liq. 2019, 273, 589–605. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shafee, A.; Ramzan, M.; Li, Z. Investigation of Lorentz forces and radiation impacts on nanofluid treatment in a porous semi annulus via Darcy law. J. Mol. Liq. 2018, 272, 8–14. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Ahmad, S.; Chung, J.D.; Farooq, U. Upshot of binary chemical reaction and activation energy on carbon nanotubes with Cattaneo-Christov heat flux and buoyancy effects. Phys. Fluids 2017, 29, 123103. [Google Scholar] [CrossRef]
- Ramzan, M.; Ullah, N.; Chung, J.D.; Lu, D.; Farooq, U. Buoyancy effects on the radiative magneto Micropolar nanofluid flow with double stratification, activation energy and binary chemical reaction. Sci. Rep. 2017, 7, 12901. [Google Scholar] [CrossRef] [PubMed]
- Suleman, M.; Ramzan, M.; Zulfiqar, M.; Bilal, M.; Shafee, A. Entropy analysis of 3D non-Newtonian MHD nanofluid flow with nonlinear thermal radiation past over exponential stretched surface. Entropy 2018, 20, 930. [Google Scholar] [CrossRef]
- Farooq, U.; Lu, D.C.; Ahmed, S.; Ramzan, M.; Chung, J.D.; Chandio, F.A. Computational analysis for mixed convective flows of viscous fluids with nanoparticles. J. Therm. Sci. Eng. Appl. 2019, 11, 021013. [Google Scholar] [CrossRef]
- Ramzan, M.; Sheikholeslami, M.; Saeed, M.; Chung, J.D. On the convective heat and zero nanoparticle mass flux conditions in the flow of 3D MHD Couple Stress nanofluid over an exponentially stretched surface. Sci. Rep. 2019, 9, 562. [Google Scholar] [CrossRef] [PubMed]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Mann, A.B. On MHD radiative Jeffery nanofluid flow with convective heat and mass boundary conditions. Neural Comput. Appl. 2019, 30, 2739–2748. [Google Scholar] [CrossRef]
- Ramzan, M.; Sheikholeslami, M.; Chung, J.D.; Shafee, A. Melting heat transfer and entropy optimization owing to carbon nanotubes suspended Casson nanoliquid flow past a swirling cylinder—A numerical treatment. AIP Adv. 2018, 8, 115130. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Ullah, N.; Chung, J.D.; Farooq, U. A numerical treatment of radiative nanofluid 3D flow containing gyrotactic microorganism with anisotropic slip, binary chemical reaction and activation energy. Sci. Rep. 2017, 7, 17008. [Google Scholar] [CrossRef] [PubMed]
- Ramzan, M.; Bilal, M.; Kanwal, S.; Chung, J.D. Effects of variable thermal conductivity and non-linear thermal radiation past an Eyring Powell nanofluid flow with chemical reaction. Commun. Theor. Phys. 2017, 67, 723. [Google Scholar] [CrossRef]
- Muhammad, T.; Lu, D.C.; Mahanthesh, B.; Eid, M.R.; Ramzan, M.; Dar, A. Significance of Darcy-Forchheimer porous medium in nanofluid through carbon nanotubes. Commun. Theor. Phys. 2018, 70, 361. [Google Scholar] [CrossRef]
- Azam, M.; Shakoor, A.; Rasool, H.F.; Khan, M. Numerical simulation for solar energy aspects on unsteady convective flow of MHD Cross nanofluid: A revised approach. Int. J. Heat Mass Transf. 2019, 131, 495–505. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Kataria, H.R.; Mittal, A.S. Effect of thermal diffusion and heat-generation on MHD nanofluid flow past an oscillating vertical plate through porous medium. J. Mol. Liq. 2018, 257, 12–25. [Google Scholar] [CrossRef]
- Makinde, O.D.; Animasaun, I.L. Bioconvection in MHD nanofluid flow with nonlinear thermal radiation and quartic autocatalysis chemical reaction past an upper surface of a paraboloid of revolution. Int. J. Therm. Sci. 2016, 109, 159–171. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Bilal, M.; Chung, J.D.; Farooq, U. A numerical investigation of 3D MHD rotating flow with binary chemical reaction, activation energy and non-Fourier heat flux. Commun. Theor. Phys. 2018, 70, 089. [Google Scholar] [CrossRef]
- Rana, P.; Shukla, N.; Gupta, Y.; Pop, I. Analytical prediction of multiple solutions for MHD Jeffery–Hamel flow and heat transfer utilizing KKL nanofluid model. Phys. Lett. A 2019, 383, 176–185. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Lu, D.; Farooq, U. Impact of generalized Fourier’s and Fick’s laws on MHD 3D second grade nanofluid flow with variable thermal conductivity and convective heat and mass conditions. Phys. Fluids 2017, 29, 093102. [Google Scholar] [CrossRef]
- Yuan, M.; Mohebbi, R.; Rashidi, M.M.; Yang, Z.; Sheremet, M.A. Numerical study of MHD nanofluid natural convection in a baffled U-shaped enclosure. Int. J. Heat Mass Transf. 2019, 130, 123–134. [Google Scholar]
- Rahimah, J.; Nazar, R.; Pop, I. Magnetohydrodynamic boundary layer flow and heat transfer of nanofluids past a bidirectional exponential permeable stretching/shrinking sheet with viscous dissipation effect. J. Heat Transf. 2019, 141, 012406. [Google Scholar]
- Benos, L.; Sarris, I.E. Analytical study of the magnetohydrodynamic natural convection of a nanofluid filled horizontal shallow cavity with internal heat generation. Int. J. Heat Mass Transf. 2019, 130, 862–873. [Google Scholar] [CrossRef]
- Sajjadi, H.; Delouei, A.A.; Izadi, M.; Mohebbi, R. Investigation of MHD natural convection in a porous media by double MRT lattice Boltzmann method utilizing MWCNT–Fe3O4/water hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 132, 1087–1104. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, Z.; Jian, Y. Heat transfer of the MHD nanofluid in porous microtubes under the electrokinetic effects. Int. J. Heat Mass Transf. 2019, 130, 821–830. [Google Scholar] [CrossRef]
- Ibrahim, M.G.; Hasona, W.M.; ElShekhipy, A.A. Concentration-dependent viscosity and thermal radiation effects on MHD peristaltic motion of Synovial Nanofluid: Applications to rheumatoid arthritis treatment. Comput. Methods Programs Biomed. 2019, 170, 39–52. [Google Scholar] [CrossRef] [PubMed]
- Merkin, J.H. Natural-convection boundary-layer flow on a vertical surface with Newtonian heating. Int. J. Heat Fluid Flow 1994, 15, 392–398. [Google Scholar] [CrossRef]
- Kamran, M.; Wiwatanapataphee, B. Chemical reaction and Newtonian heating effects on steady convection flow of a micropolar fluid with second order slip at the boundary. Eur. J. Mech. B/Fluids 2018, 71, 138–150. [Google Scholar] [CrossRef]
- Mehmood, R.; Rana, S.; Nadeem, S. Transverse thermopherotic MHD Oldroyd-B fluid with Newtonian heating. Results Phys. 2018, 8, 686–693. [Google Scholar] [CrossRef]
- Shafiq, A.; Hammouch, Z.; Sindhu, T.N. Bioconvective MHD flow of tangent hyperbolic nanofluid with Newtonian heating. Int. J. Mech. Sci. 2017, 133, 759–766. [Google Scholar] [CrossRef]
- Khan, A.; Khan, D.; Khan, I.; Ali, F.; Karim, F.U.; Imran, M. MHD flow of Sodium Alginate-based Casson type nanofluid passing through a porous medium with Newtonian heating. Sci. Rep. 2018, 8, 8645. [Google Scholar] [CrossRef] [PubMed]
- El-Hakiem, M.A.; Ramzan, M.; Chung, J.D. A numerical study of magnetohydrodynamic stagnation point flow of nanofluid with Newtonian heating. J. Comput. Theor. Nanosci. 2016, 13, 8419–8426. [Google Scholar] [CrossRef]
- Ramzan, M.; Yousaf, F. Boundary layer flow of three-dimensional viscoelastic nanofluid past a bi-directional stretching sheet with Newtonian heating. AIP Adv. 2015, 5, 057132. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Hussain, T.; Hayat, T.; Ramzan, M.; Alsaedi, A. Boundary layer flow of third grade nanofluid with Newtonian heating and viscous dissipation. J. Cent. South Univ. 2015, 22, 360–367. [Google Scholar] [CrossRef]
- Ramzan, M. Influence of Newtonian heating on three dimensional MHD flow of couple stress nanofluid with viscous dissipation and Joule heating. PLoS ONE 2015, 10, e0124699. [Google Scholar] [CrossRef] [PubMed]
- Upreti, H.; Pandey, A.K.; Kumar, M. MHD flow of Ag-water nanofluid over a flat porous plate with viscous-Ohmic dissipation, suction/injection and heat generation/absorption. Alex. Eng. J. 2018, 57, 1839–1847. [Google Scholar] [CrossRef]
- Qasim, M.; Khan, Z.H.; Khan, W.A.; Shah, I.A. MHD boundary layer slip flow and heat transfer of ferrofluid along a stretching cylinder with prescribed heat flux. PLoS ONE 2014, 9, e83930. [Google Scholar] [CrossRef] [PubMed]

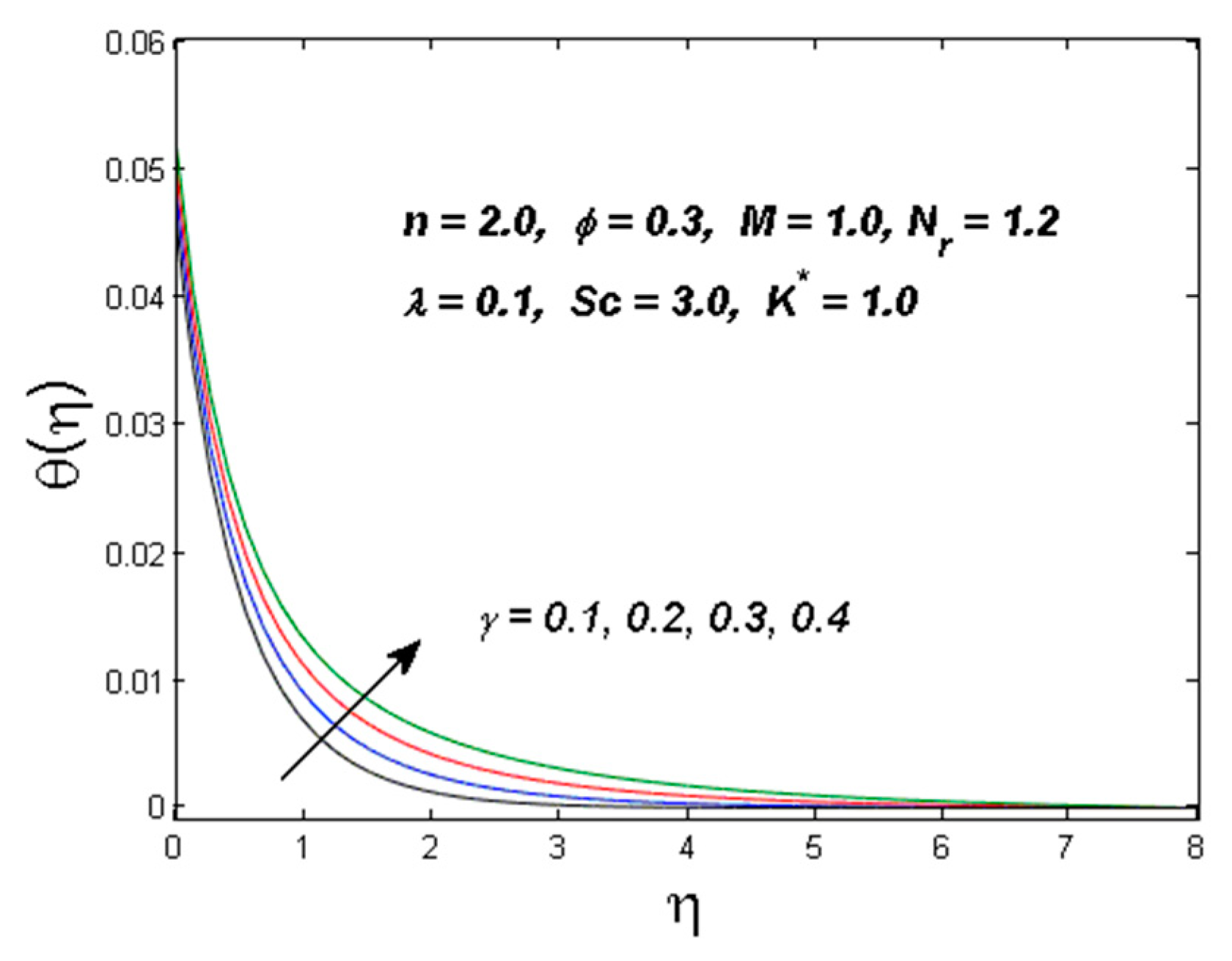
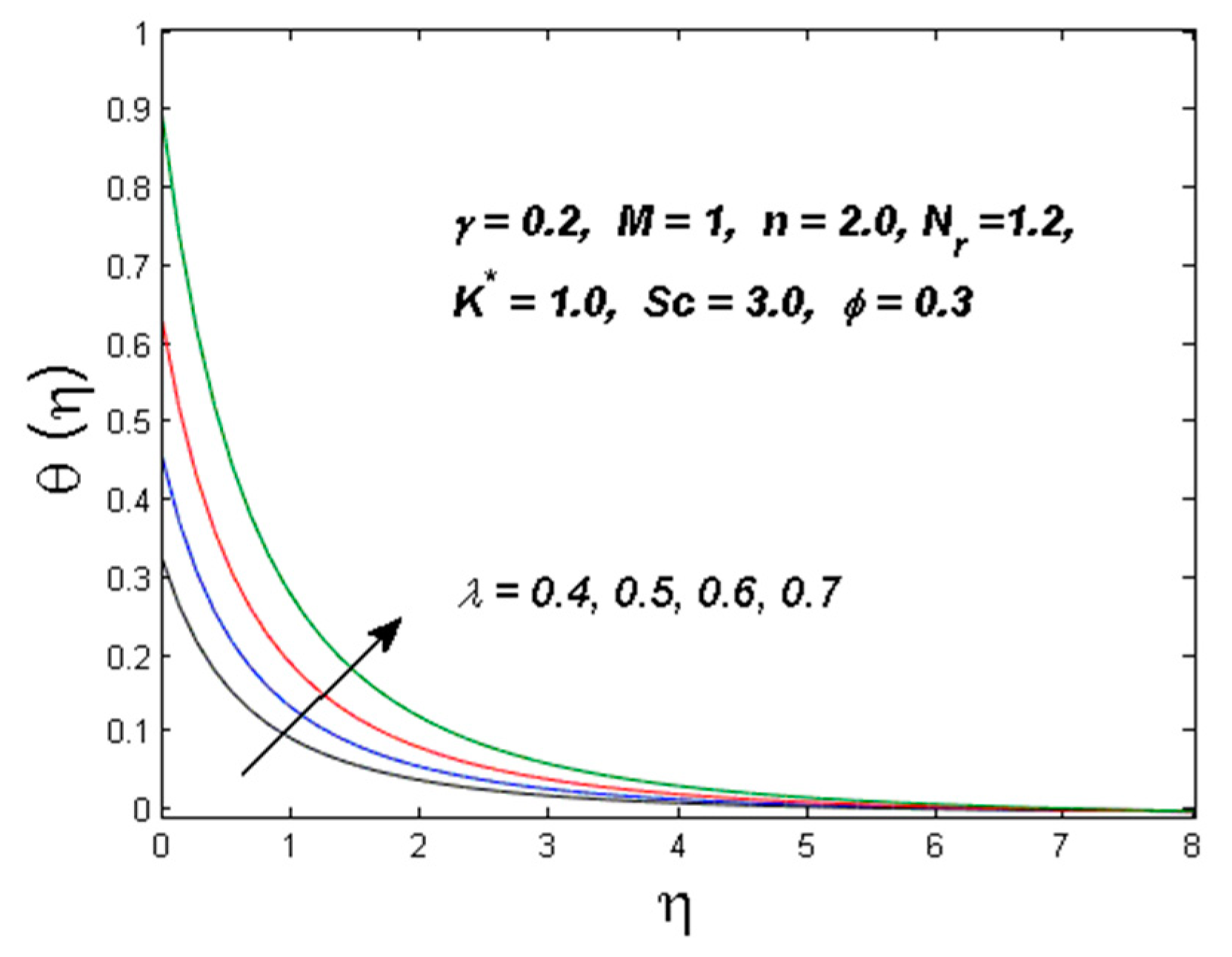
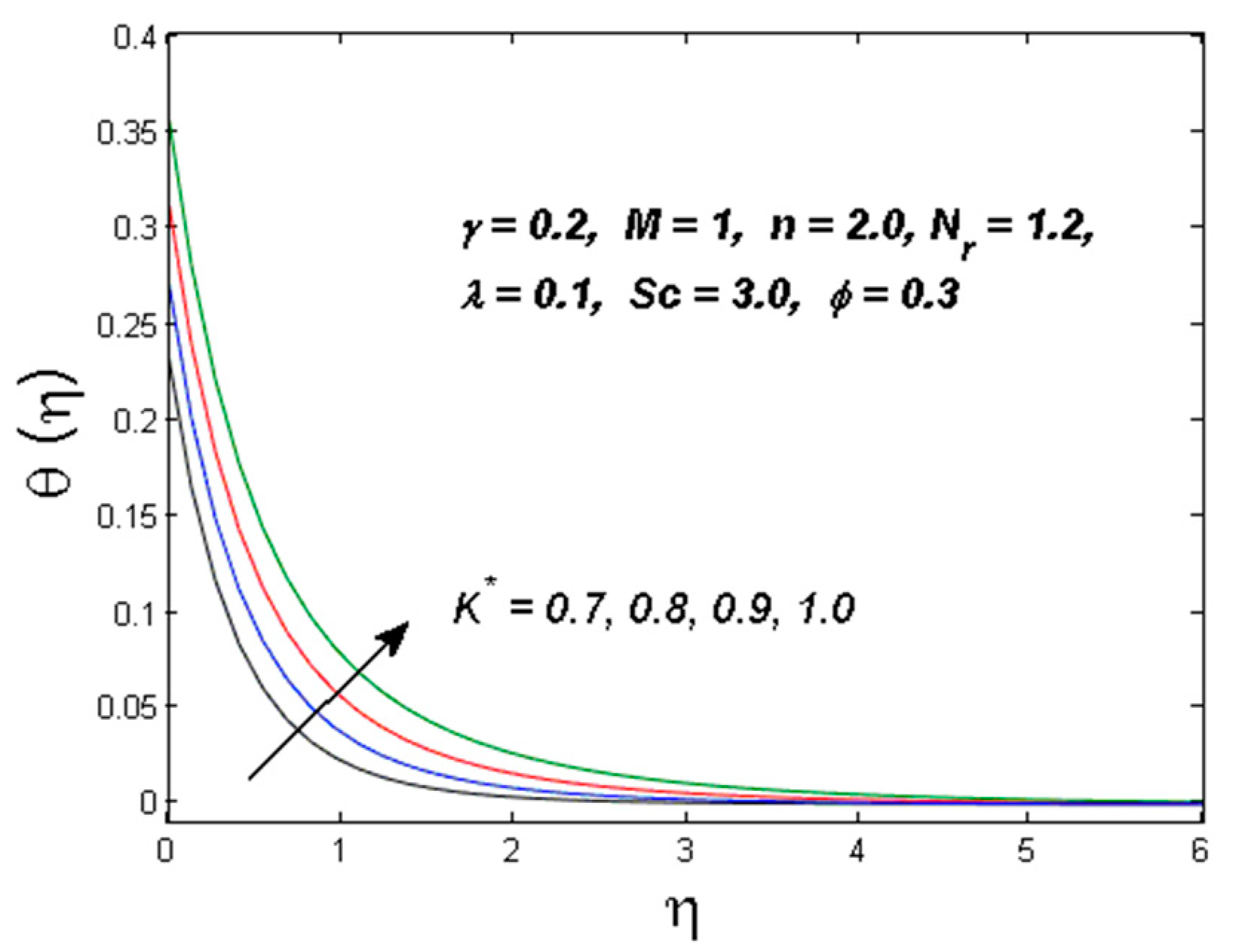
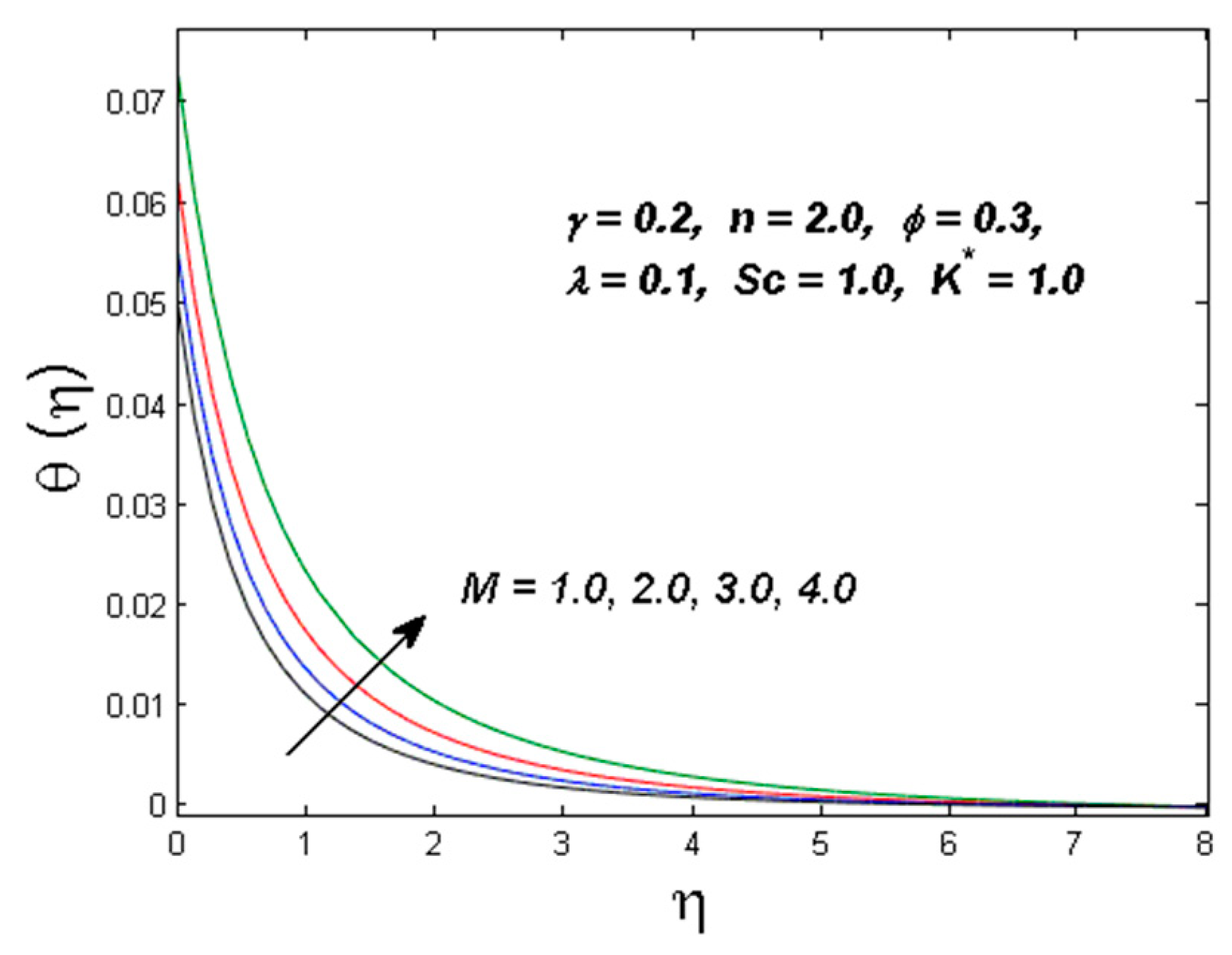
| Physical Properties | Water | Ag |
|---|---|---|
| Cp (J/kg K) | 4179 | 235.0 |
| (kg/m3) | 997.1 | 10,500.0 |
| K (W/mK) | 0.61300 | 429.0 |
| Pr | |||
|---|---|---|---|
| Qasim et al. [38] | Present Result | ||
| 0.0 | 0.72 | 1.23664 | 1.236651 |
| 1.0 | 1.00000 | 1.000000 | |
| 6.7 | 0.33330 | 0.333310 | |
| 10 | 0.26876 | 0.268770 | |
| 1.0 | 0.72 | 0.87018 | 0.870190 |
| 1.0 | 0.74406 | 0.744070 | |
| 6.7 | 0.29661 | 0.296620 | |
| 10 | 0.24217 | 0.242180 | |
| n | M | Nr | K* | ||||
|---|---|---|---|---|---|---|---|
| 1.0 | 0.1 | 0.1 | 1.0 | 1.2 | 1.0 | 1.92700 | 0.32149 |
| 2.0 | 0.1 | 0.1 | 1.0 | 1.2 | 1.0 | 2.45720 | 0.30963 |
| 3.0 | 0.1 | 0.1 | 1.0 | 1.2 | 1.0 | 2.89050 | 0.30305 |
| 2.0 | 1.0 | 0.1 | 1.0 | 1.2 | 1.0 | 2.81410 | 0.28200 |
| 2.0 | 2.0 | 0.1 | 1.0 | 1.2 | 1.0 | 3.18730 | 0.26410 |
| 2.0 | 3.0 | 0.1 | 1.0 | 1.2 | 1.0 | 3.54330 | 0.25369 |
| 2.0 | 1.0 | 0.1 | 1.0 | 1.2 | 1.0 | 2.81410 | 0.28200 |
| 2.0 | 1.0 | 0.2 | 1.0 | 1.2 | 1.0 | 3.42830 | 0.31250 |
| 2.0 | 1.0 | 0.3 | 1.0 | 1.2 | 1.0 | 4.04270 | 0.34319 |
| 2.0 | 1.0 | 0.1 | 1.0 | 1.2 | 1.0 | 2.81410 | 0.28200 |
| 2.0 | 1.0 | 1.0 | 2.0 | 1.2 | 1.0 | 2.99960 | 0.28387 |
| 2.0 | 1.0 | 1.0 | 3.0 | 1.2 | 1.0 | 3.17070 | 0.28553 |
| 2.0 | 1.0 | 1.0 | 1.0 | 0.1 | 1.0 | 2.81410 | 0.28200 |
| 2.0 | 1.0 | 1.0 | 1.0 | 0.7 | 1.0 | 2.81410 | 0.28200 |
| 2.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 2.81410 | 0.28200 |
| 2.0 | 1.0 | 1.0 | 1.0 | 1.2 | 1.0 | 2.81410 | 0.28200 |
| 2.0 | 1.0 | 1.0 | 1.0 | 1.2 | 2.0 | 2.81410 | 0.28200 |
| 2.0 | 1.0 | 1.0 | 1.0 | 1.2 | 3.0 | 2.81410 | 0.28200 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suleman, M.; Ramzan, M.; Ahmad, S.; Lu, D.; Muhammad, T.; Chung, J.D. A Numerical Simulation of Silver–Water Nanofluid Flow with Impacts of Newtonian Heating and Homogeneous–Heterogeneous Reactions Past a Nonlinear Stretched Cylinder. Symmetry 2019, 11, 295. https://doi.org/10.3390/sym11020295
Suleman M, Ramzan M, Ahmad S, Lu D, Muhammad T, Chung JD. A Numerical Simulation of Silver–Water Nanofluid Flow with Impacts of Newtonian Heating and Homogeneous–Heterogeneous Reactions Past a Nonlinear Stretched Cylinder. Symmetry. 2019; 11(2):295. https://doi.org/10.3390/sym11020295
Chicago/Turabian StyleSuleman, Muhammad, Muhammad Ramzan, Shafiq Ahmad, Dianchen Lu, Taseer Muhammad, and Jae Dong Chung. 2019. "A Numerical Simulation of Silver–Water Nanofluid Flow with Impacts of Newtonian Heating and Homogeneous–Heterogeneous Reactions Past a Nonlinear Stretched Cylinder" Symmetry 11, no. 2: 295. https://doi.org/10.3390/sym11020295
APA StyleSuleman, M., Ramzan, M., Ahmad, S., Lu, D., Muhammad, T., & Chung, J. D. (2019). A Numerical Simulation of Silver–Water Nanofluid Flow with Impacts of Newtonian Heating and Homogeneous–Heterogeneous Reactions Past a Nonlinear Stretched Cylinder. Symmetry, 11(2), 295. https://doi.org/10.3390/sym11020295






