Abstract
Subcooled flow boiling is one of the major issues in the nuclear and power generation industries. If the fluid inlet temperature in the boiling area is less than the boiling temperature, the boiling process is called subcooled boiling. The symmetry of a physical system is a constant property of the system and is fixed by deformation. Using magnetohydrodynamic (MHD) forces and broken symmetry induced by nanosized particles, fluid and thermal systems can be more controlled. In this study, the effect of a magnetic field and nanoparticles on subcooled flow boiling in a vertical tube was investigated. For this purpose, a one-dimensional numerical code was used to simulate the flow and variations of various parameters that have been investigated and evaluated. The results showed that as the flow entered the heated area, the vapor volume fraction, Froude number, fluid cross-sectional area forces, mixture velocity, fluid velocity, bubble departure diameter, liquid and vapor Reynolds numbers, squared ratio of the Froude number to the Weber number, and fluid cross-sectional area forces coefficient increased. In the same region, the Eötvös number, root mean square (RMS) of the fluid cross-sectional area force, sound velocity, liquid superficial velocity, critical tube diameter, bubble departure frequency, and density of the active nucleation site were reduced. It was also observed that after the heated area and under the influence of the magnetic field and the nanoparticles, the values of the vapor volume fraction, Froude number, fluid cross-sectional area force, mixture velocity, fluid velocity, vapor, liquid Reynolds number, and squared ratio of the Froude number to the Weber number were decreased. Moreover, there was no significant effect on the Eötvös number, liquid superficial velocity, Taylor bubble Sauter mean diameter, bubble departure diameter, critical tube diameter, bubble departure frequency, or density of the active nucleation site.
1. Introduction
Heat transfer problems have always been an interesting topic for researchers [1,2,3,4,5]. Among them, flow boiling has been extensively studied in recent decades. In this regard, we can refer to the studies of Sadeghi et al. [6,7], Sadeghi and Shadloo [8], Suriyawong et al. [9], Suriyawong and Wongwises [10], Trisaksri and Wongwises [11], and Duangthongsuk et al. [12]: they used numerical simulation and the lattice Boltzmann method to investigate and analyze bubbling flow and bubble formation. As the nuclear industry progresses, new solutions and research are being developed to increase the cooling rate of equipment. Boiling and the resulting heat transfer are phenomena that are important not only in nuclear reactions but also in the critical state of power generation equipment. During the boiling process, the heat transfer coefficient is very high, so this process can expel high heat from the system. The maximum heat flux that can be applied to the system without damaging it is called critical heat flux. Flow boiling includes saturated flow boiling and subcooled flow boiling. If the inlet fluid temperature in the boiling region is lower than the boiling temperature, the boiling process is called subcooled boiling. In subcooled flow boiling, steam bubbles begin to form and grow on the heated surface. Bubbles are formed when the wall temperature is higher than the liquid saturation temperature at the local pressure, although the liquid temperature farther from the wall is lower than the saturation temperature [13]. The bubbles can slip on the surface or move away from the surface and condense in the subcooled liquid beyond the wall. This causes mass transfer in addition to heat transfer. Therefore, given the importance of the subject, much research has been done by researchers on subcooled flow boiling, which will be discussed next.
Zeitoun and Shoukri [14] studied axial volume fraction profiles in low-pressure subcooled flow boiling using gamma attenuation techniques for different levels of mass flux, wall heat flux, and inlet subcooling. The predictions of the proposed model with respect to the distribution of the axial volume fraction in low-pressure subcooled flow boiling were in good agreement with the experimental data. In addition, the researchers conducted numerous studies [15,16,17] systematically on the applied relationships for saturated boiling heat transfer in vertical tubes. Ribatski et al. [18] performed an experimental study. They studied nuclear boiling on a vertical array of horizontal pipes. They also proposed a general relationship with the predicted nuclear boiling point heat transfer coefficient in the stated case. The new relationship was compared to the data independently of the article. Kljenak et al. [19] modeled subcooled boiling in a vertical channel. They improved subcooled boiling by coupling a two-dimensional two-fluid model and a three-dimensional bubble-tracking model. Their results of the calculated and measured volume fractions at different points along the channel were in good agreement with each other. Yun et al. [20] analyzed the subcooled boiling flow of water in coaxial tubes. They showed the dependence of the percentage of the vapor volume fraction and the joint surface density on thermal conditions and mass flux. In addition, they revealed that with increasing heat flux, bubble velocity increased. Yan et al. [21] experimentally investigated the effect of heat flux and mass flux on the heat transfer coefficient and the Nusselt number of subcooled boiling in a vertical tube. In 2015, Jamalabadi [22] thoroughly investigated the effects of joule heating on a rectangular orifice in a microchannel, with an emphasis on thermal boundary conditions. This microchannel was filled with electrolyte-containing nanobubbles. Numerical studies of the temperature and velocity fields were performed to illustrate the different aspects of fluid flow and thermal design in rectangular microchannels. Additionally, relationships were obtained for increasing the maximum temperature for several geometrical parameters and thermal boundary conditions. This was accomplished to gain an understanding of the best cooling scenario for a microfluidic rectangular orifice. This study provided useful information for optimizing a thermoelectric bioMEMS (micro-electromechanical systems) device, and it had the benefits of nanobubble injection for temperature control.
Shadloo et al. [23] investigated the smooth particle hydrodynamics (SPH) method in fluid streams for industrial applications. They explained the differences, similarities, advantages, and disadvantages using numerical strategies in computational fluid dynamics. The SPH method can deal with substantial fluid area deformations and extensive motions of several solid areas, and it can accurately solve fast dynamic currents and interfacial deformations such as complex free surfaces, multiphases, and fluid–structure surfaces. In contrast, this method is not a proper choice for issues such as high Reynolds turbulent flows, steady flows, slow dynamic flows, and complex currents without a common surface. Chen et al. [24] experimentally investigated the volume fraction variations in the subcooled boiling process under horizontal forced vibrations. They used an annular test section for subcooled boiling tests under atmospheric pressure. The annular test section was attached to an eccentric-cam vibrator that could generate horizontal forced vibrations with the help of a low-speed motor. Their experimental results showed that volume fraction and fluid temperature could be different in the subcooled boiling area under forced horizontal vibration. These changes could be explained by slight variations in the thermal boundary layers and the enhancement of heat transfer under vibration. By studying nanofluid boiling, several researchers also found that the injection of nanoparticles in some cases increased the heat transfer coefficient in the boiling flows. A nanofluid is a fluid that results from the distribution of solid particles less than 100 nm in fluid used in thermal equipment. These particles are usually made of metals or metal oxides. Due to the higher thermal conductivity of these particles compared to conventional fluids in heat transfer, nanofluids are expected to have better thermal efficiency than the corresponding base fluid.
Using laboratory work, Boudouh et al. [25] found that local heat flux, local vapor quality, and the nanofluid heat transfer coefficient were increased with enhanced nanofluid concentration in boiling. Henderson et al. [26] investigated the boiling of nanofluidic flow with refrigerant-based fluid. They observed that if the nanoparticles were well-dispersed in the fluid that would increase the transfer coefficient. In an experimental work, Kim et al. [27] showed that using alumina nanoparticles in boiling currents in a tube increased the critical heat flux. Abedini et al. [28] modeled nanofluidic subcooled boiling in a tube. In that work, while considering nanoparticles to be a homogeneous fluid and obtaining effective nanofluidic properties, they applied a two-phase perspective to perform the modeling. They stated that with the addition of alumina nanoparticles, the heat transfer coefficient increased. This increment was due to the increase in single-phase heat transfer and bubble detachment. Chehade et al. [29] collected various relationships to obtain the heat transfer coefficient in flow boiling and in channels with different shapes. They indicated that in nanofluid boiling, the local heat transfer coefficient and local heat flux are affected by the concentration of nanoparticles. Mali et al. [30] reviewed the enhancement of flow boiling heat transfer with nanofluids.
In addition, the importance of effective thermal conductivity and the viscosity of nanofluids has been highlighted in various studies. Bang [31] investigated the effect of deposition of Al2O3 nanoparticles on the critical heat flux of R-123 and the flow boiling heat transfer. In their experimental work, they measured and compared the critical heat flux (CHF) of each plate with different mass fluxes. Their results showed that in the nanoparticle-coated tube, CHF was increased by up to 17% compared to the uncoated state. Rashidi et al. [32] studied entropy generation in a circular tube heat exchanger using nanofluids. The primary purpose of that paper was to compare the single-phase and two-phase modeling methods for forced displacement of water/TiO2 nanoparticles. The intended geometry was a horizontal tube with boundary conditions of a constant wall heat flux and a turbulent flow regime. In their results, the entropy production values for heat dissipation and turbulence for single-phase and mixed models were very close. However, as the volume fraction of nanoparticles increased, differences between the models appeared. It was found that the entropy production of turbulent nanofluid flow was mainly due to the component of frictional entropy production fluctuations. The importance of this component for higher amounts of nanoparticle volume fractions and Reynolds numbers has increased significantly.
Karimzadehkhouei et al. [33] investigated the heat transfer of a subcooled flow boiling in γ-Al2O3/water nanofluids in horizontal microtubes and the effect of surface properties and the deposition of nanoparticles. The nanoparticles were added to distilled water (base fluid) in five different mass fractions (low mass fraction of 0.05 wt % and 0.02 wt %; high mass fraction of 0.5 wt.%, 1 wt % and 1.5 wt %). According to the results, the heat transfer coefficients of subcooled flow boiling were similar to those of pure water with a low mass fraction, and those for the nanofluids with high mass fractions decreased. Therefore, nanoparticle concentration is also an essential parameter in the inefficiency of heat transfer at higher concentrations. High concentrations of nanoparticles cause deposition and accumulation on the inner surface of microtubes, which should be considered. Abedini et al. [34] studied the vapor volume fraction in subcooled nanofluid boiling numerically. A mixture model was used to study the subcooled boiling of alumina–water nanoparticles in vertical annular and vertical tubes. They proved that this model predicted the local flow characteristics of the subcooled flow boiling, such as axial volume fraction and temperature distribution, well. In addition, under constant nanoparticle inlet velocity conditions, increasing the concentration of nanoparticles decreased the axial volume fraction of vapor resulting from the decrease in wall temperature. However, at a constant inlet mass flux, the axial vapor volume fraction was higher than the constant inlet velocity state, which could have been due to a lower velocity with a constant inlet mass flux.
Nasiri et al. [35] investigated nanofluidic flow and heat transfer around a horizontal cylinder at a Reynolds numbers above 250. They applied a weakly compressible smoothed particle hydrodynamics (WCSPH) method. Simulations were performed for Prandtl numbers of 0.01–40 with volume concentrations of 0%–4% for nanoparticles. The velocity fields and Nusselt profiles were calculated from numerical works and were in good agreement with the experimental values. According to the results, the nanofluid flow heat transfer characteristics improved compared to the pure fluids. This improvement was better for currents with higher Rayleigh numbers and higher particle volumes. Sarafraz et al. [36] analyzed the thermal and hydraulic properties of water–zirconium nanofluids under convective boiling flow inside a heat exchanger. Their experimental results showed that the boiling thermal performance and heat transfer coefficient of zirconium nanofluids were acceptable; therefore, they can be used as a coolant inside two-phase heat exchanger systems. In their study, the heat transfer coefficient improved by 35.8%, although the pressure drop increased. In another study, Sarafraz et al. [37] experimentally evaluated the formation of water bubbles in a boiling stream in an annulus tube. They surveyed the effects of various variables such as total dissolved solids (TDSes) in mass fractions, the water flow rate, the heat flux applied to the heat transfer coefficient, and bubble behavior. They showed that the presence of TDS materials increased the angle of contact and the bubble diameter and improved the system heat transfer coefficient. It was observed that at a heat flux of 15 Kw/m2 and a temperature of 50 °C, the first nuclear boiling in the tube appeared, and the contact angles of water with the presence of 300 mg/L and 1200 mg/L of TDS material were 74° and 124°, respectively. The heat transfer was improved due to the presence of TDS materials.
Mostafazadeh et al. [38] simulated the heat transfer and laminar flow of a nanofluid in a vertical channel, taking into account the effects of radiation, single-phases and two-phases, surface temperature conditions, and plate heat flux conditions. Their main purpose was to investigate the effects of the Grashof number, radiation parameter, and volume fraction of nanoparticles on heat transfer characteristics. They showed that by increasing the Grashof number in both heat flux and constant temperature, the nanofluid velocity increased, and by increasing the volume fraction in the two expressed states, the nanofluid velocity and temperature decreased. Toghyani et al. [39] investigated nanofluids as working fluids in an arabolic trough solar collector used for solar cooling and hydrogen production. It was observed that the rate of hydrogen production was increased with increasing intensities of solar radiation (by increasing the radiation intensity from 389.3 to 929.7 W/m2, the production of hydrogen increased by 20 kg), as the Rankin cycle gave more power to the polymer electrolyte membrane (PEM) electrolyzer. The efficiency of the hybrid system increased by approximately 9% when the ambient temperature was enhanced from 5 to 40 °C. When higher nanofluid volume fractions were used, the power generated by the Rankin cycle and the hydrogen produced by the electrolyzer increased. The overall energy and exergy efficiency of the hybrid system at a solar radiation intensity of 600 W/m2 with a nanoparticle volume fraction of zero were 1.55 and 1.4 times higher, respectively, than the nanoparticle volume fraction of 0.03.
Understanding symmetry in physical systems makes it easier to explain physical phenomena and leads to simplifications in the mathematical explanation of the nature of the problem. The broken symmetry of a thermophysical system can be used in an area with different sizes to control the physical properties of that area. Symmetric breaking occurs suddenly in a particle system that is subjected to variations in size or inhomogeneous thermophysical properties. The symmetry of a physical system is a constant property of a system that is fixed by deformation. When magnetohydrodynamic (MHD) forces and broken symmetry induced by nanosized particles are used, fluid and thermal systems can be more controlled. Although the applied magnetic field can be symmetric, the random nature of the nanofluid and the occurrence of two-phase phenomena cause asymmetric effects.
In recent years, studies have investigated the effect of electric and magnetic fields separately or in combination with flow boiling. Cotton et al. [40] investigated a two-phase flow pattern map for annular channels under direct current (DC)-applied voltage for use in an electrohydrodynamic (EHD) convective boiling analysis. For this purpose, they applied HFC-134a in a single-phase countercurrent flow heat exchanger under an electric field. In their results, EHD affected the forced convective flow when the Masuda number was proportional to the square of the Reynolds number of the liquid. In that work, the importance of determining the flow regime was demonstrated. In addition, the average Nusselt number and overall pressure drop with and without applying voltage at a constant heat flux have been studied and analyzed. Lee et al. [41] studied the critical heat flux in boiling flows of nanofluids with magnetic nanoparticles with low mass fluxes. The main feature of this study was the use of a new nanofluid called magnetic nanofluid. This nanofluid is a suspension of magnetized nanoparticles in pure fluid. Magnetic nanoparticles can be controlled, and this has two significant consequences: First, nanoparticles can be collected by applying a magnetic field. Second, the concentration of nanoparticles can be varied within the fluid. Aminfar et al. [42] modeled nanofluidic flow boiling using a two-phase Euler–Euler perspective. They used magnetic nanoparticles in this modeling. They also investigated the effect of a magnetic field by applying it to a subcooled boiling flow.
Sharma and Sharma [43] explored unsteady MHD flows in two viscous immiscible incompressible electrically conducting fluids and the heat transfer across a horizontal channel with constant temperature permeable plates in the presence of a transverse magnetic field. The velocity and temperature fields were displayed, and the numerical values of the shell friction and Nusselt number were obtained. The influences of various parameters (such as the viscosity ratio, phase angle, Hall parameter, thermal conductivity ratio, and Prandtl number) on the velocity field, temperature field, shell friction, and Nusselt number were expressed. Mirzaee et al. [44] investigated the effects of electromagnetohydrodynamics (EMHD) on the shape of a vapor bubble in upward heated vertical flow. It was observed that the Lorentz force could decrease and delay bubble production. It also affected the slip speed, flow forces, viscous dissipation, and joule heating. Shell friction and joule heating were shown to increase with magnetic fields were applied. Sheikholeslami and Bhatti [45] surveyed an active method for improving nanofluid heat transfer using EHD. In that study, the effect of coulomb force on forced convection heat transfer of nanofluids using Fe3O4-ethylene glycol nanoparticles was investigated. The finite element method was used to obtain the effects of the Fe3O4 volume fraction, Reynolds number, and applied voltage. Nanofluid viscosity was considered to be a function of the electric field, according to the experimental data. Their results showed that the coulomb force helped the convection to increase the temperature gradient with increasing voltage. The greatest improvement in the Nusselt number was due to an electric field at a lower lip velocity.
A CHF enhancement analysis was performed through the deposition of magnetic nanoparticles in the subcooled boiling zone of the flow (by Choi et al.) [46]. Magnetite nanoparticles (Fe3O4) were equally exposed in the test areas. The increase in CHF through the nanoparticle deposition ranged from 0%–40%. CHF was enhanced with increasing mass flux, which resulted in lower output quality. It was also observed that increments of CHF in low mass fluxes in a slug flow were relatively lower than in high mass fluxes in a vapor clot. Bhatti et al. [47] investigated mass and energy transfer by applying a magnetic field on a two-phase peristaltic motion (suspension of particle fluids) across the planar channel. It was perceived that the velocity tended to increase due to the larger electric field and the electro-osmotic parameter, although the magnetic field and the two-phase volume fraction induced an apparent resistance to the current. The effect of an electric field and the electro-osmotic parameter showed inverse behavior on the temperature and the distribution of the two-phase flow concentration. Therefore, the chemical reaction parameter significantly reduced the concentration distribution.
Jamalabadi [48] examined the effects of EMHD on subcooled boiling in a vertical annulus tube. Gravitational and EMHD forces were included in the momentum equation, and viscose dissipation, joule heating, and radiation were included in the energy equation. He showed that EMHD could reduce the phase transfer rate and change the velocity difference between the phases, volume forces, and dissipative components. The friction coefficient and joule heating were also increased by EMHD forces. Dogonchi et al. [49] numerically investigated the natural convection of magnetohydrodynamics in Cu–water nanofluids in a wavy cavity using a finite element control volume method. The effective viscosity and thermal conductivity of the nanofluids were defined by relationships in which Brownian motion effects on thermal conductivity were considered. In that paper, the influence of various parameters such as the Rayleigh number, wave contraction ratio, Hartmann number, and undulation number were calculated and presented. Average and local Nusselt numbers were also computed and reported.
Unni et al. [50] simulated the magnetohydrodynamic flow of two fluids. They used two-dimensional isothermal flow and investigated two fluids with different viscosities and electrical conductivities. At first, the problem was analytically solved. Open Foam software was applied to solve the problem. Since there are only two-dimensional single-fluid MHD modules (mhdFoam) and multifluid flow solver modules in Open Foam, they provided a combination of these two solvents and validated it with the analytical solution results. Aminfar et al. [51] experimentally investigated the effect of a magnetic field on the critical heat flux of ferrofluid flow boiling in a vertical tube. CHF variations were studied by applying an external magnetic field, and it was observed that the CHF was increased when nanofluids were used as the working fluid, especially at lower volume concentrations of nanoparticles. In addition, the adsorption of nanoparticles into the magnets and increases in the wettability of the plate resulted in increased CHF.
Jamalabadi [52] investigated the effects of MHD forces and nanoparticles on the subcooled flow boiling inside an annular tube. The effect of magneto hydrodynamics on the base fluid (liquid water) was measured, and different concentrations of nanoparticles were used as working fluids. It was deduced from their results that by applying the Lorentz force, the peak velocities were reduced. The convective heat transfer coefficient was improved slightly using Lorentz force. Using the Lorentz force enabled an estimation of the Reynolds number of liquid and gas. In addition, when the particle fraction increased from 0%–10%, the vapor fraction decreased, and as the nanoparticle concentration increased, the maximum temperature decreased. Jamalabadi [53] presented a mathematical model to determine the effect of EMHD forces on vibrations caused by the steady flow of liquid water and vapor in a heated vertical channel. It was observed that vibrations caused by fluid were increased with an augmentation of EMHD forces. Moreover, an increasing Lorentz force controlled the fluid coefficient, the cross-section, the water hammer forces, the two-phase oscillation frequency, and the variable velocities, while the root mean square of the fluid force increased. These results indicated that the bubble disintegration frequency, surface tension force, nucleation site density, bubble departure diameter, sound velocity, and superficial velocity were not affected by Lorentz force.
In the present study, the effect of MHD forces on a two-phase boiling flow in a vertical path with nanoparticles was investigated. Four different states for the boundary conditions of the problem were considered (under the influence of magnetic fields with different powers). The results of the problem solving for each state were validated with empirical data. In addition, variations of various parameters such as the Froude number, fluid cross-sectional area force, water hammer force, bubble departure diameter and frequency, Eötvös number, critical pipe diameter, fluid and mixture velocity, sound velocity, heat transfer coefficient, Reynolds numbers of the vapor and liquid, volume fraction, and Weber number were studied (under the influence of various magnetic fields). Due to previous studies, no extensive work was undertaken to examine all these parameters.
2. Materials and Methods
The geometry of the problem is shown in Figure 1. As can be seen in this figure, the inlet flow with the nanoparticles was inserted into the vertical annular tube in subcooled and near-saturation conditions. The inner diameter of the tube was 12.7 mm, the outer diameter of the tube was 25.4 mm, and its length was 114.6 cm. The right-side wall of the tube was subjected to a constant heat flux at a distance of 34 to 64.6 cm, and other surfaces of the pipe were considered to be adiabatic. Solving the problem for different values of the mass flux, outlet pressure, inlet velocity, heat flux, inlet temperature difference, and saturation state were performed in four different states, which are compiled in Table 1. In computational fluid dynamics problems, the inlet velocity is often specified, and the outlet pressure is set to zero. For channel flow, the fluids are controlled through a pressure gradient (P_in and P_out as needed) or an inlet velocity with an outflow condition or are otherwise in a periodic domain. This is a common method since only the pressure gradient is of interest. Consequently, the inlet pressure computed by the numerical method was equal to the total pressure loss at the given flow rate. However, to display here the effects of both parameters, (the outlet pressure and the inlet speed), both of them are varied.
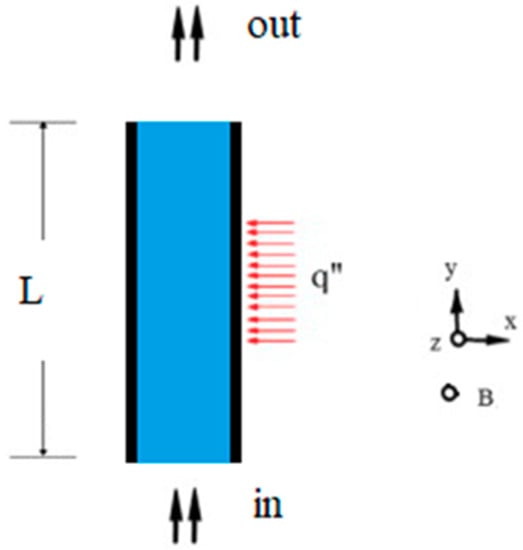
Figure 1.
Schematic of the geometry investigated: vertical pipe with heat flux applied to the right side of the pipe.

Table 1.
Problem boundary conditions and their values for four different states.
The flow of nanofluids is also affected by magnetic fields with different strengths. The size of the magnetic field and the properties of the nanofluids are presented in Table 2 and Table 3, respectively. According to aforementioned studies, when the pipe length is larger than the diameter, one-dimensional modeling leads to acceptable results [14]. Therefore, in this study, an in-house code was used to solve the two-phase welding current with nanoparticles affected by the magnetic field in a one-dimensional mode. Due to the accuracy of the results, this eventuated in less computational time than the three-dimensional one would have.

Table 2.
Various magnetic field values applied in vertical flow.

Table 3.
Nanoparticle specifications.
For validation, the percentage of relative error resulting from the mesh-independent solution is given in Table 4. As can be seen in this table, the percentage of relative error decreased with decreasing grid size. Therefore, the grid size was considered to be 0.01 to solve the present study. In accordance with other studies and due to the importance of the volume fraction, the variation of this parameter along the channel for all four states was investigated and is presented in Figure 2. It can be seen that the results of the numerical and experimental modeling [14] were in good agreement, and the results of the solution were reliable. The calculation showed that the error amount was less than 5% for the four modes in Figure 2.

Table 4.
Mesh-independent solution for case 4.
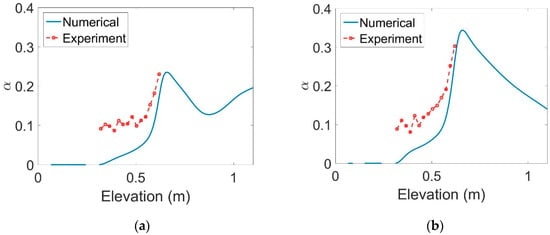
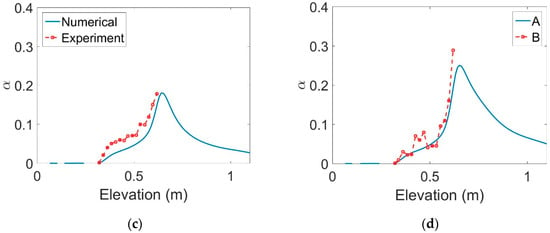
Figure 2.
Validation of numerical results with experimental data for the four modes stated in Table 1: (a) case 1, (b) case 2, (c) case 3, and (d) case 4.
3. Governing Equations
The equations for mass, momentum, and energy conservation were applied in each phase. From a microscopic perspective, each phase was not independent of the others and needed to be coupled at the common-level expressions of mass, momentum, and energy transfer. The liquid phase was dominant and continuous, whereas the vapor bubbles were assumed to be a dispersed phase.
The conservation of mass is as follows:
The conservation of momentum is
The conservation of energy is
In the mass conservation equation, Γ is the mass transfer rate due to condensation or deposition between phases in a subcooled liquid: here, to simplify the problem, the mass generation of the vapor phase () is only considered in the bulk fluid. In addition, the wall vapor condensation rate is equivalent to , and α is the volume fraction of vapor and is expressed as 1 − α for the liquid. It is also considered to be the first left-hand side to be zero because of problem-solving under steady conditions.
In the momentum equation, the last component on the right represents forces other than pressure and frictional forces such as magnetic force. Interfacial forces are considered to be external forces for each phase, and the transient component of the equation is ignored. Here, and are the wall friction coefficient and interfacial drag force coefficient, respectively, in each phase; is the shear stress at the boundary layer; and is the electrical conductivity.
In the energy equation, the first component of the left-hand side is ignored due to the steady-state solution. Here, is radiation heat flux, is wall heat transfer, is heat transfer between phases, and is external work applied to the desired volume.
Nanofluid Properties
The mixture of water and nanoparticles was considered to be perfectly uniform and homogeneous. Because of the low volume of vapor in subcooled flow boiling and due to consideration of the nanofluid as single-phase, the equations were solved only for two water and vapor fluids. The properties of the nanofluids can be calculated from the following equations.
Density is
viscosity is
And specific heat capacity is
4. Results and Discussion
The volume fraction is an essential factor in two-phase flows, and flow patterns (bubbles, slugs, churn, and annular) play a crucial role in determining the volume fraction. In bubble and slug flows that have a low volume fraction, the volume fraction increases as the slip velocity between the gas and liquid increases. In addition, with increasing internal pressure gradients (which is inversely related to pipe diameter) and Lorentz forces, the volume fraction decreases. Although the slip velocity between phases affects the volume fraction, the volume fraction is independent of gas velocity at very low flow rates. Variations in the vapor volume fraction along the channel length for the four different states presented in Table 1 are shown in Figure 3. As can be seen in Figure 3, at a distance of 34 to 64.6 cm from the pipe inlet, when a constant heat flux was applied to the flow, the vapor volume fraction increased. However, after this interval, the amount of vapor phase decreased due to the increase in MHD forces, which is given in Table 2.
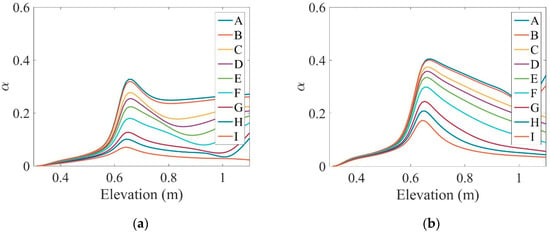
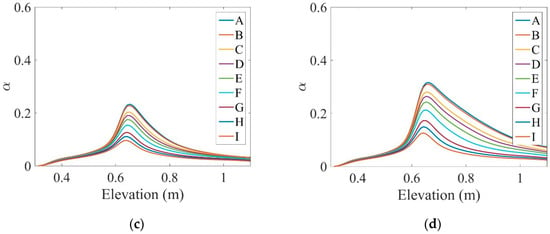
Figure 3.
Changes in the vapor volume fraction along the pipe length for the four modes stated in Table 1: (a) case 1, (b) case 2, (c) case 3, and (d) case 4.
One of the critical nondimensional numbers in the determination of a vertical pipe regime is the Froude number (), which represents the ratio of fluid inertia to gravity in two-phase continuum mechanics. The Froude number variations along the channel length for the four different states stated in Table 1 are shown in Figure 4a. This number is used to measure the effect of gravity on the repulsion of one phase over another or to describe the relative velocity between phases. When the relative velocity between the phases is large, it causes instability between the momentum fluxes. Therefore, according to Figure 4a, the Froude number was unchanged at the beginning of the tube and in the region where heat flux was applied to the flow: as the flow rate increased, it increased. Then, under the influence of the magnetic field force, its value decreased, indicating more flow control. At the different values of the magnetic field presented in Table 2, the Froude number was smaller than 1, indicating that only small surface waves could move upstream. In fact, the decrease in the Froude number along the fluid path reflected the effect of the magnetic field in reducing the effects of surface waves.
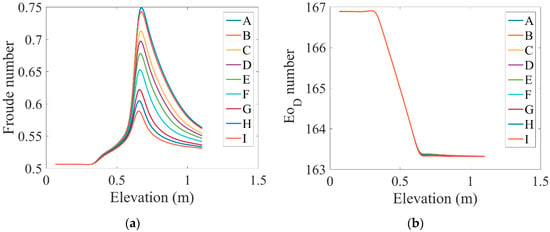
Figure 4.
Dimensional number changes of (a) Froude and (b) Eötvös along the channel length for the four different states shown in Table 1 under the influence of the magnetic field.
Another dimensionless number that is important on the surface between the liquid and gas or on the surface between the two immiscible liquids is the Eötvös number (Eo) or Bond number (Bo), which represents the ratio of body forces to surface tension forces. It is important to determine the shape of bubbles or droplets moving in the fluid. The variations in the Eo number () along the pipe length for the four states are shown in Figure 4b. The surface tension force and magnetic field force affected the two-phase joint boundary. The surface tension force was a function of curvature of the two-phase joint boundary. As can be seen, the Eo number in the heated area decreased, indicating that body forces were the dominant force and that the use of MHD forces had no significant effect on it, so that at different values of the magnetic field the changes were the same and the profiles overlapped.
In Figure 5a, variations in the fluid cross-sectional area force along the channel length and under the influence of different values of the magnetic field are presented. At first, this parameter was constant, and when it reached the heated area, the oscillation sources increasd with the change of flow from single-phase to multiphase. The vibration induced by the two-phase flow was a function of various parameters caused by the flow motion regime, interactions between the two phases, thermophysical properties, and mass sink/sources due to evaporation and condensation. Vibrations caused by the flow were the result of the fluid impact force. It was observed that when increasing the distance from the beginning of the tube to the middle of the heated section, the effect of fluid momentum multiplied several times. This force was calculated from the tube cross-sectional area and the Bernoulli pressure, which is a function of the mixture density and velocity. When the flow was influenced by different values of the magnetic field, the peak of the fluid force decreased as MHD forces opposed the fluid impact force.
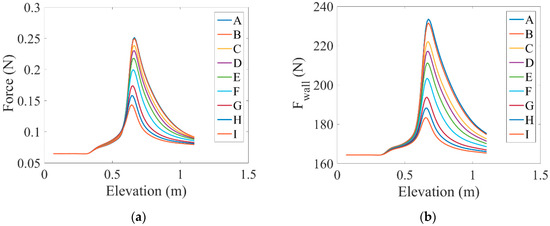
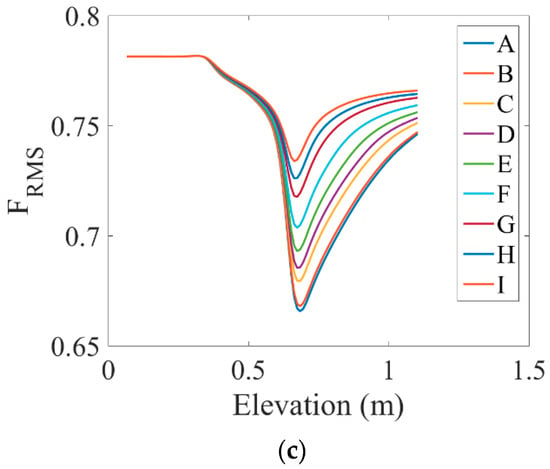
Figure 5.
Variations in (a) fluid cross-sectional area forces, (b) fluid wall forces, and (c) root mean squares of the force applied to the fluid cross-section along the channel length under the influence of different magnetic fields.
The fluid impact resulted in an increase in pressure of the water hammer and could affect the boundary wall of the tube. The changes in fluid wall forces along the length of the tube under the influence of different values of the magnetic field are plotted in Figure 5b. This force was perpendicular to the flow direction and resulted in corrosion of the pipe wall. The fluid wall forces could be obtained by multiplying the fluid mass flux and velocity of sound in the tube (). As shown, the wall tube forces increased in the heated area, and as the MHD forces increased, the peak of the wall tube forces decreased. As you can see, the amount of this force was much higher than the other forces shown in Figure 5, which indicated a more significant impact and importance of this force.
Variations in the root mean square (RMS) of forces applied to the fluid cross-section along the pipe length are shown in Figure 5c. According to this figure, as flow passed through the heated area, this force decreased, and as MHD forces increased, the RMS of the fluid cross-sectional area forces improved the flow performance. This kind of momentum instability tends to reduce the amount of MHD forces and is likely to affect the internal vibrations caused by the flow. The RMS force is linearly proportional to the total superficial velocity:
Variations in mixture velocity and fluid velocity along the tube length under the influence of different magnetic fields are shown in Figure 6a,b, respectively. As can be seen, in the heated section, both velocities increased, and this increment was higher for the mixed velocity due to the greater effect of higher gas velocity. According to the figure, using MHD forces reduced the peak velocity and created a smoother profile.
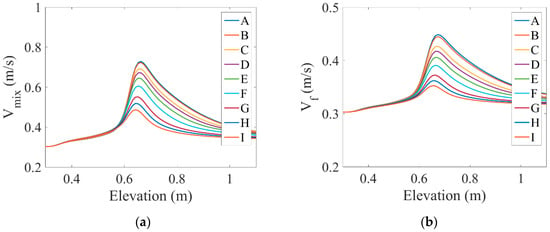
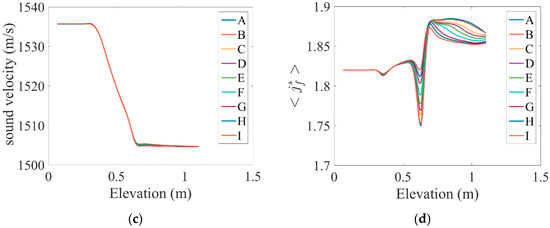
Figure 6.
Variations in the (a) mixture velocity, (b) fluid velocity, (c) speed of sound, and (d) fluid superficial velocity along the tube length under the influence of different values of the magnetic field.
Sound velocity plays a vital role in water hammer force. Figure 6c illustrates the changes in sound velocity along the length of the tube under the influence of different values of the magnetic field. According to this figure, as flow entered the heated section, the sound velocity decreased slightly, and the use of different amounts of MHD forces did not change the sound velocity.
Geometrical and working conditions can cause internal vibrations caused by two-phase flows. Most structural vibrations occur in the slug or churn flow regime due to large discontinuity in the momentum flux. Figure 6d shows variations in the liquid superficial velocity along the tube under the influence of different values of the magnetic field. Flow patterns are usually made based on the superficial velocity of the liquid (). As shown, the superficial velocity of the liquid decreased at the beginning of the heated section and then increased with increasing distance. This indicated that the entire tube could not be analyzed as a bubble–slug flow pattern and that MHD forces did not have a direct effect on the superficial velocity of the liquid.
Figure 7a shows the bubble Sauter mean diameter along the length of the tube under the influence of different values of the magnetic field. The bubble diameter in a given vapor volume fraction is related to the concentration of the interfacial area. The mean diameter of the bubble can be equal to half the maximum diameter of the bubble and can be evaluated from a critical Weber number and the relative velocity. As can be seen, the Sauter mean diameter of the Taylor bubble () suddenly decreased at the beginning of the tube, and the use of MHD forces did not have a significant effect on it.
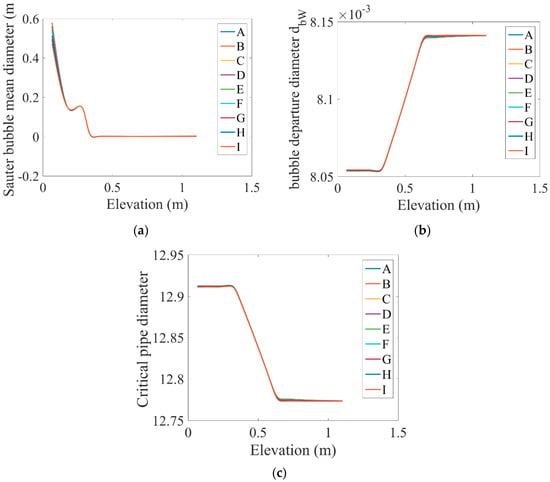
Figure 7.
Variations in the (a) Sauter mean diameter of the bubble, (b) the bubble departure diameter, and (c) the critical diameter of the tube along the channel length under the influence of different magnetic fields.
Subcooled flow boiling reduces bubble break-up on the tube wall. The theoretical solution of bubble dynamics is found from the balance between the surface tension and buoyancy pressure of the inside and outside bubble (). Figure 7b shows variations in the bubble departure diameter along the tube length under the influence of different values of magnetic fields. It was observed that as the current entered the heated area, the bubble departure diameter increased from the starting point to the endpoint of the heated area and maintained this value until the end of the tube. There is a relationship between the pressure frequency or momentum flux fluctuation and the tube natural frequency. Spacers have been shown to play a role in converting large turbulences into smaller ones, thereby reducing oscillatory energy. Since the diameter of the tubes was larger than the diameter of the Taylor bubble, this had little effect on the dominant frequency. According to the figure, the use of MHD forces had little effect on the bubble departure diameter.
Secondary flow, which forms unstable bubbles, results in increased liquid–vapor mixing and the break-up of Taylor bubbles in pipes that are large enough (larger than the critical diameter of the pipe), which can affect the vibrations caused by the flow. If the critical tube diameter ratio is less than 40, the flow regime can be considered to be bubble flow. The critical tube diameter is expressed as a function of the hydraulic diameter, surface tension of the liquid phase, gravity constant, and density difference between the vapor and liquid phases. Figure 7c shows the critical pipe diameter () changes along the pipe under the influence of different values of the magnetic field. It was observed that the critical tube diameter decreased after the heated area, and the use of MHD forces had no significant effect on it. According to this figure, the critical diameter of the tube was less than the critical value of 40, and the bubble regime needed to be applied.
Variations in the liquid and vapor Reynolds numbers along the tube under the influence of different values of the magnetic field are shown in Figure 8a,b. It can be observed that when the distance from the beginning of the tube to the entry of the flow into the heated area increased, the Reynolds number of the liquid and vapor increased as the velocity of the phases increased, which was higher for the vapor than for the liquid, because the higher vapor velocity was due to the void that was produced by boiling. In addition, as they were affected by MHD forces, the Reynolds numbers of the vapor and liquid were damped.
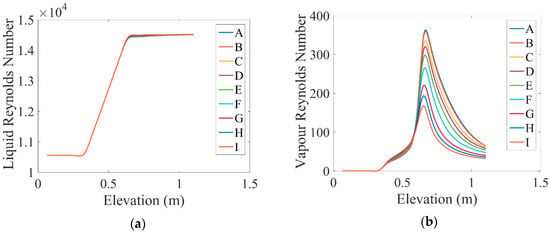
Figure 8.
Variations in the (a) liquid Reynolds number and (b) the vapor Reynolds number along the tube under the influence of different values of the magnetic field.
The Weber number () represents the ratio of the inertial force to the surface tension force: in Figure 9a, its variation along the tube under the influence of different values of the magnetic field is shown. The Weber number can be used for a Taylor bubble. Figure 9a reveals that as the flow entered the heated area, the Weber number increased as the inertial force increased. As a result, through the increase in MHD forces, the inertial force overcame the surface tension force, the inertial force decreased, and thus the Weber number decreased, too.
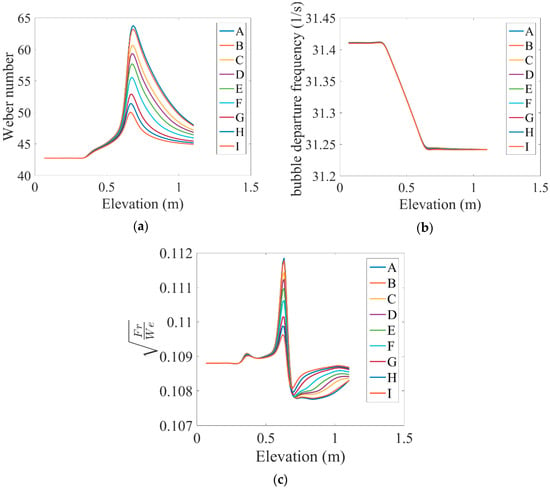
Figure 9.
Variations in the (a) Weber number, (b) bubble departure frequency, and (c) square root of the ratio of the Froude number to the Weber number along the pipe under the influence of different values of the magnetic field (presented in Table 2).
At high flow rates and in turbulent flows, bubble formation and bursting may cause vibrations. For an 80° contact angle, the calculated bubble departure diameter and the gravity constant lead to a measure of the bubble departure frequency (). Therefore, measuring the bubble departure frequency is an essential parameter in terms of gravity acceleration and bubble diameter and should be considered. Figure 9b shows the variation in the bubble departure frequency along the tube under the influence of different values of the magnetic field. This characteristic shows the rate of vapor bubble production in the nucleation boiling from the liquid to the vapor phase. It was observed that the bubble departure frequency in the heated area decreased as the bubble diameter increased, and the use of MHD forces had no effect on this behavior. Here, since the gas volume rate was low and the amplitudes of the surface waves and liquid slag were low, this reduced the sources of oscillation. It was observed that there existed a critical frequency, fc, of the momentum flux fluctuation at a given inlet velocity value (adjoining the annular flow region and at the limit between the slug and the annular).
The square root of the ratio of the Froude number to the Weber number indicates the effect of the surface tension and the gravity parameter on the frequency of the momentum fluxes, whose variations are plotted along the tube length in Figure 9c. In fact, this ratio was used to measure the frequency of two-phase oscillations. According to the figure, the size of this parameter increased before the heated area, and subsequently, the amplitude of this parameter decreased due to the MHD force.
Figure 10a indicates the radiation heat flux variations along the pipe length. As shown, the radiation heat flux at the beginning of tube and even in the heated region showed a constant value of zero and subsequently increased through the influence of MHD forces. In addition, variations in the convection heat transfer coefficient on the wall along the tube length are shown in Figure 10b. It was observed that this coefficient was almost constant in the two regions at the beginning and end of the tube, with the highest convection heat transfer followed by the highest convection heat transfer coefficient in the region of nucleation boiling. The use of MHD forces slightly increased the heat transfer coefficient.
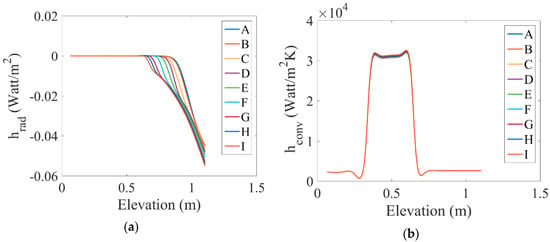
Figure 10.
(a) Radiation heat flux variations and (b) changes in the convection heat transfer coefficient along the tube length under the influence of different values of magnetic fields.
Changes in the volume fraction and the parameters of the base volume fraction along the tube length under the influence of different magnetic field values are shown in Figure 11a,b, respectively. Figure 11a shows that at the beginning of the pipe, the mentioned parameter was constant and increased as it entered the heated area. It was then controlled and reduced by the magnetic field. In Figure 11b, the base volume fraction parameter increased before the heated area, and then its amplitude was reduced by the MHD force. In addition, variations in the maximum volume fraction and the parameters of the critical volume fraction along the tube length are shown in Figure 11c,d for the various cases presented in Table 2. These two parameters decreased at the beginning of the heated area and increased with enhanced distance from the point of entry. As is shown, the MHD force had no significant effect on these two parameters.
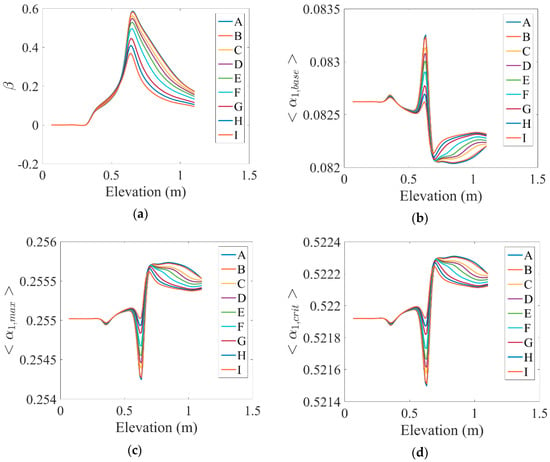
Figure 11.
Variations in the (a) volume fraction, (b) base volume fraction, (c) maximum volume fraction, and (d) critical volume fraction along the tube length under the influence of different values of the magnetic field.
The density changes of the active nucleation site along the tube length are shown in Figure 12. As can be seen, the density of the active nucleation site initially was maintained at a constant value, and then, upon entering the heated area at the farthest point where the heating continued (the point where the volume fraction was maximized), it was reduced and then became fixed. This behavior also showed that an increase in the MHD forces did not have a significant effect on the active nucleation site.
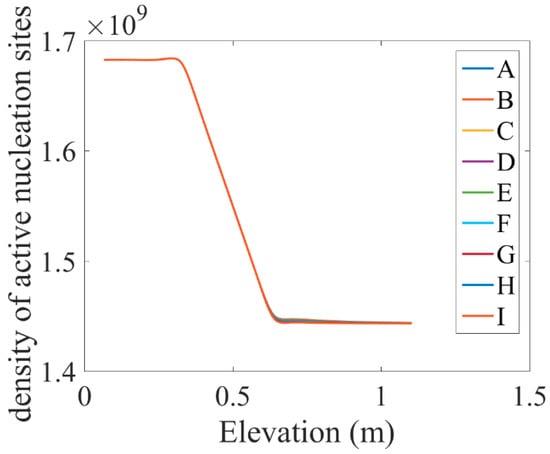
Figure 12.
Changes in the density of the active nucleation site along the tube length under the influence of different values of the magnetic field.
5. Conclusions
In this study, a one-dimensional numerical code was used to simulate a two-phase boiling flow in a vertical heated tube. The effects of MHD forces and nanoparticles on the flow were considered in this research, and the results of the parametric study show that the numerical results were close to the experimental results and were reliable. The following was observed.
At a distance of 34 to 64.6 cm from the tube inlet, when a constant heat flux was applied to the tube, vapor volume fraction increased, and then the amount of vapor phase decreased as MHD forces increased.
The Froude number was constant in the tube inlet and increased in the heated area as flow velocity increased. Then, under the influence of a magnetic field force, its value decreased, indicating that the flow was more controlled. The Froude number was smaller than one that would state that the movement of small surface waves could be ignored.
The Eötvös number decreased in the heated area, indicating that the surface tension was the dominant force and that the use of MHD forces had no significant effect on it.
Variations in the fluid cross-sectional area force were also constant initially, and when they reached the heated area, the source of oscillations increased with the change of flow from single-phase to multiphase. As the flow was affected by the magnetic field, the peak of the fluid force decreased.
The wall tube forces increased in the heated area, and with increasing MHD forces, the peak wall forces decreased.
By passing through the heated area, the RMS of the force applied to the fluid cross-section underwent a decreasing process, and with increasing MHD forces, the RMS of the fluid cross-sectional area force improved.
In the heated section, both the mixture velocity and fluid velocity were increased, and the peak velocity decreased with the use of MHD forces.
The liquid superficial velocity decreased at the beginning of the heated section and then increased with increasing distance. The MHD force did not have a direct effect on the superficial velocity of the liquid.
As the current entered the heated area, the bubble departure diameter increased from the starting point to the endpoint of the heated area, maintaining this value to the end of the tube. The use of MHD forces did not have a significant effect on the bubble departure diameter.
The critical tube diameter decreased after the heated area, and the use of MHD forces had no significant effect on it.
As the flow entered the heated area, the Weber number increased due to the increment in surface tension forces, and the Weber number also decreased with an enhanced MHD force.
The bubble departure frequency in the heated area decreased as the bubble diameter increased, and the use of MHD forces had no effect on this behavior.
The amount of radiation heat flux at the beginning of the pipe and even in the heated area was constant and equal to zero, and subsequently, the amount of radiation heat flux increased with the influence of MHD forces.
The convection heat transfer coefficient was almost constant in the two regions at the beginning and end of the pipe, and the highest convection heat transfer coefficient was in the heated area. The use of MHD forces slightly increased the convection heat transfer coefficient.
The density of the active nucleation site initially was maintained at a constant value and then decreased as it entered the heated zone at the point where the volume fraction was at its maximum value: after that, it became fixed. The increment in MHD forces did not have a significant effect on the density of the active nucleation site.
Author Contributions
Conceptualization, M.Y.A.J.; methodology, M.Y.A.J.; software, M.Y.A.J.; validation, M.Y.A.J.; formal analysis, M.G., R.A.; investigation, M.Y.A.J., M.G.; resources, M.Y.A.J.; data curation, M.Y.A.J., M.G., R.A.; writing—original draft preparation, R.A., writing—review and editing, S.W., M.A.; visualization, M.Y.A.J.; supervision, M.S.S.; project administration, M.Y.A.J., M.S.S.; funding acquisition, M.Y.A.J., M.S.S.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| A | area cross-section (m2) | z | coordinate system along the electric field (m) |
| B | magnetic flux (T) | Greek Symbols | |
| heat capacity (J/(kg K)) | Α | volume fraction (m2/s) | |
| d | diameter (m) | density (kg/m3) | |
| EO | Eötvös number | viscosity (kg/(m s)) | |
| f′i | friction coefficient at wall on phase i | σ | electric conductivity (S/m) |
| f′I,i | interfacial drag force coefficient on phase i | shear stress in boundary layer (Pa) | |
| F | force (N) | Subscripts | |
| Fr | Froude number | base | base |
| g | gravitational acceleration (m/s2) | bf | base fluid |
| G | mass velocity (kg/m2s), /A | conv | convection |
| h | heat transfer coefficient (watt/m2K) | crit | critical |
| superficial velocity (m/s) | D | diameter | |
| L | length (m) | f | fluid |
| mass flow rate (kg/s) | g | gas phase | |
| m′ | mass flow rate between phases (kg/s) | i | species i |
| P | pressure (Pa) | in | Inlet |
| qr | radiation heat flux (J/m2s) | mass | mass |
| q″ | wall heat transfer (J/m2s) | max | maximum |
| qi,j″ | heat transfer between phases (J/m2s) | mix | mixture |
| T | temperature (K) | np | nanoparticle |
| u | specific internal energy (J/kg) | out | outlet |
| v | velocity (m/s) | rad | radiation |
| w | external work applied on the volume (J/m3) | RMS | root mean square |
| We | Weber number | sat | saturation |
| x | coordinate system along the magnetic field (m) | wall | wall |
| y | coordinate system along the tube (m) |
References
- Bozorg, M.V.; Doranehgard, M.H.; Hong, K.; Xiong, Q. CFD study of heat transfer and fluid flow in a parabolic trough solar receiver with internal annular porous structure and synthetic oil–Al2O3 nanofluid. Renew. Energy 2020, 145, 2598–2614. [Google Scholar] [CrossRef]
- Daungthongsuk, W.; Wongwises, S. A critical review of convective heat transfer of nanofluids. Renew. Sustain. Energy Rev. 2007, 11, 797–817. [Google Scholar] [CrossRef]
- Izadi, A.; Siavashi, M.; Xiong, Q. Impingement jet hydrogen, air and CuH2O nanofluid cooling of a hot surface covered by porous media with non-uniform input jet velocity. Int. J. Hydrogen Energy 2019, 44, 15933–15948. [Google Scholar] [CrossRef]
- Trisaksri, V.; Wongwises, S. Critical review of heat transfer characteristics of nanofluids. Renew. Sustain. Energy Rev. 2007, 11, 512–523. [Google Scholar] [CrossRef]
- Zhong, H.; Xiong, Q.; Zhu, Y.; Liang, S.; Zhang, J.; Niu, B.; Zhang, X. CFD modeling of the effects of particle shrinkage and intra-particle heat conduction on biomass fast pyrolysis. Renew. Energy 2019, 141, 236–245. [Google Scholar] [CrossRef]
- Sadeghi, R.; Shadloo, M.S.; Hooman, K. Numerical investigation of the natural convection film boiling around elliptical tubes. Numer. Heat Transf. Part A Appl. 2016, 70, 707–722. [Google Scholar] [CrossRef]
- Sadeghi, R.; Shadloo, M.S.; Jamalabadi, M.Y.A.; Karimipour, A. A three-dimensional lattice Boltzmann model for numerical investigation of bubble growth in pool boiling. Int. Commun. Heat Mass Transf. 2016, 79, 58–66. [Google Scholar] [CrossRef]
- Sadeghi, R.; Shadloo, M. Three-dimensional numerical investigation of film boiling by the lattice Boltzmann method. Numer. Heat Transf. Part A Appl. 2017, 71, 560–574. [Google Scholar] [CrossRef]
- Suriyawong, A.; Saisorn, S.; Wongwises, S. Pool boiling heat transfer enhancement of distilled water with passive rotating blades installed above the heating surface. Exp. Therm. Fluid Sci. 2017, 87, 109–116. [Google Scholar] [CrossRef]
- Suriyawong, A.; Wongwises, S. Nucleate pool boiling heat transfer characteristics of TiO2–water nanofluids at very low concentrations. Exp. Therm. Fluid Sci. 2010, 34, 992–999. [Google Scholar] [CrossRef]
- Trisaksri, V.; Wongwises, S. Nucleate pool boiling heat transfer of TiO2–R141b nanofluids. Int. J. Heat Mass Transf. 2009, 52, 1582–1588. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Yiamsawasd, T.; Selim Dalkilic, A.; Wongwises, S. Pool-boiling heat transfer characteristics of Al2O3-water nanofluids on a horizontal cylindrical heating surface. Curr. Nanosci. 2013, 9, 56–60. [Google Scholar]
- Collier, J.G.; Thome, J.R. Convective Boiling and Condensation; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Zeitoun, O.; Shoukri, M. Axial void fraction profile in low pressure subcooled flow boiling. Int. J. Heat Mass Transf. 1997, 40, 869–879. [Google Scholar] [CrossRef]
- Kolev, N. How accurately can we predict nucleate boiling? Exp. Therm. Fluid Sci. 1995, 10, 370–378. [Google Scholar] [CrossRef]
- Pioro, I.; Rohsenow, W.; Doerffer, S. Nucleate pool-boiling heat transfer. I: Review of parametric effects of boiling surface. Int. J. Heat Mass Transf. 2004, 47, 5033–5044. [Google Scholar] [CrossRef]
- Steiner, D.; Taborek, J. Flow boiling heat transfer in vertical tubes correlated by an asymptotic model. Heat Transf. Eng. 1992, 13, 43–69. [Google Scholar] [CrossRef]
- Ribatski, G.; Jabardo, J.M.S.; Da Silva, E.F. Modeling and experimental study of nucleate boiling on a vertical array of horizontal plain tubes. Exp. Therm. Fluid Sci. 2008, 32, 1530–1537. [Google Scholar] [CrossRef]
- Kljenak, I.; Končar, B.; Mavko, B. Modelling of Subcooled Nucleate Boiling in a Vertical Channel with Coupling of Bubble-Tracking and Two-Fluid Models. In Proceedings of the Workshop on Modelling ad Measurements of Two-Phase Flow and Heat Transfer in Nuclear Fuel Assemblies, Stockholm, Sweden, 10–11 October 2006. [Google Scholar]
- Yun, B.; Bae, B.; Euh, D.; Park, G.; Song, C.-H. Characteristics of the local bubble parameters of a subcooled boiling flow in an annulus. Nucl. Eng. Des. 2010, 240, 2295–2303. [Google Scholar] [CrossRef]
- Yan, J.; Bi, Q.; Liu, Z.; Zhu, G.; Cai, L. Subcooled flow boiling heat transfer of water in a circular tube under high heat fluxes and high mass fluxes. Fusion Eng. Des. 2015, 100, 406–418. [Google Scholar] [CrossRef]
- Jamalabadi, M.A. Joule heating in low-voltage electroosmotic with electrolyte containing nano-bubble mixtures through microchannel rectangular orifice. Chem. Eng. Res. Des. 2015, 102, 407–415. [Google Scholar] [CrossRef]
- Shadloo, M.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Chen, S.-W.; Hibiki, T.; Ishii, M.; Mori, M.; Watanabe, F. Experimental investigation of void fraction variation in subcooled boiling flow under horizontal forced vibrations. Int. J. Heat Mass Transf. 2017, 115, 954–968. [Google Scholar] [CrossRef]
- Boudouh, M.; Gualous, H.L.; De Labachelerie, M. Local convective boiling heat transfer and pressure drop of nanofluid in narrow rectangular channels. Appl. Therm. Eng. 2010, 30, 2619–2631. [Google Scholar] [CrossRef]
- Henderson, K.; Park, Y.-G.; Liu, L.; Jacobi, A.M. Flow-boiling heat transfer of R-134a-based nanofluids in a horizontal tube. Int. J. Heat Mass Transf. 2010, 53, 944–951. [Google Scholar] [CrossRef]
- Kim, T.I.; Chang, W.J.; Chang, S.H. Flow boiling CHF enhancement using Al2O3 nanofluid and an Al2O3 nanoparticle deposited tube. Int. J. Heat Mass Transf. 2011, 54, 2021–2025. [Google Scholar] [CrossRef]
- Abedini, E.; Behzadmehr, A.; Sarvari, S.; Mansouri, S. Numerical investigation of subcooled flow boiling of a nanofluid. Int. J. Therm. Sci. 2013, 64, 232–239. [Google Scholar] [CrossRef]
- Chehade, A.A.; Gualous, H.L.; Le Masson, S.; Fardoun, F.; Besq, A. Boiling local heat transfer enhancement in minichannels using nanofluids. Nanoscale Res. Lett. 2013, 8, 130. [Google Scholar] [CrossRef] [PubMed]
- Mali, S.; Pise, A.; Acharya, A. Review on flow boiling heat transfer enhancement with nanofluids. IOSR J. Mech. Civ. Eng. 2014, 11, 43–48. [Google Scholar] [CrossRef]
- Bang, I.C. Effects of Al2O3 nanoparticles deposition on critical heat flux of R-123 in flow boiling heat transfer. Nucl. Eng. Technol. 2015, 47, 398–406. [Google Scholar]
- Rashidi, M.M.; Nasiri, M.; Shadloo, M.S.; Yang, Z. Entropy generation in a circular tube heat exchanger using nanofluids: Effects of different modeling approaches. Heat Transf. Eng. 2017, 38, 853–866. [Google Scholar] [CrossRef]
- Karimzadehkhouei, M.; Sezen, M.; Şendur, K.; Mengüç, M.P.; Koşar, A. Subcooled flow boiling heat transfer of γ-Al2O3/water nanofluids in horizontal microtubes and the effect of surface characteristics and nanoparticle deposition. Appl. Therm. Eng. 2017, 127, 536–546. [Google Scholar] [CrossRef]
- Abedini, E.; Zarei, T.; Rajabnia, H.; Kalbasi, R.; Afrand, M. Numerical investigation of vapor volume fraction in subcooled flow boiling of a nanofluid. J. Mol. Liq. 2017, 238, 281–289. [Google Scholar] [CrossRef]
- Nasiri, H.; Jamalabadi, M.Y.A.; Sadeghi, R.; Safaei, M.R.; Nguyen, T.K.; Shadloo, M.S. A smoothed particle hydrodynamics approach for numerical simulation of nano-fluid flows. J. Therm. Anal. Calorim. 2019, 135, 1733–1741. [Google Scholar] [CrossRef]
- Sarafraz, M.; Tlili, I.; Tian, Z.; Khan, A.R.; Safaei, M.R. Thermal analysis and thermo-hydraulic characteristics of zirconia–water nanofluid under a convective boiling regime. J. Therm. Anal. Calorim. 2019, 1–10. [Google Scholar] [CrossRef]
- Sarafraz, M.; Shadloo, M.S.; Tian, Z.; Tlili, I.; Alkanhal, T.A.; Safaei, M.R.; Goodarzi, M.; Arjomandi, M. Convective Bubbly Flow of Water in an Annular Pipe: Role of Total Dissolved Solids on Heat Transfer Characteristics and Bubble Formation. Water 2019, 11, 1566. [Google Scholar] [CrossRef]
- Mostafazadeh, A.; Toghraie, D.; Mashayekhi, R.; Akbari, O.A. Effect of radiation on laminar natural convection of nanofluid in a vertical channel with single-and two-phase approaches. J. Therm. Anal. Calorim. 2019, 138, 779–794. [Google Scholar] [CrossRef]
- Toghyani, S.; Afshari, E.; Baniasadi, E.; Shadloo, M. Energy and exergy analyses of a nanofluid based solar cooling and hydrogen production combined system. Renew. Energy 2019, 141, 1013–1025. [Google Scholar] [CrossRef]
- Cotton, J.; Robinson, A.; Shoukri, M.; Chang, J. A two-phase flow pattern map for annular channels under a DC applied voltage and the application to electrohydrodynamic convective boiling analysis. Int. J. Heat Mass Transf. 2005, 48, 5563–5579. [Google Scholar] [CrossRef]
- Lee, T.; Lee, J.H.; Jeong, Y.H. Flow boiling critical heat flux characteristics of magnetic nanofluid at atmospheric pressure and low mass flux conditions. Int. J. Heat Mass Transf. 2013, 56, 101–106. [Google Scholar] [CrossRef]
- Aminfar, H.; Mohammadpourfard, M.; Maroofiazar, R. Numerical study of non-uniform magnetic fields effects on subcooled nanofluid flow boiling. Prog. Nucl. Energy 2014, 74, 232–241. [Google Scholar] [CrossRef]
- Sharma, P.; Sharma, K. Unsteady MHD Two-Fluids Flow and Heat Transfer Through a Horizontal Channel. Int. J. Eng. Sci. Invent. Res. Dev. 2014, 1, 65–72. [Google Scholar]
- Mirzaee, M.; Hooshmand, P.; Ahmadi, H.; Balotaki, H.; KhakRah, H.; Abdollahzadeh Jamalabadi, M. Electromagnetohydrodynamic Effects on Steam Bubble Formation in Vertical Heated Upward Flow. Energies 2016, 9, 657. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bhatti, M. Active method for nanofluid heat transfer enhancement by means of EHD. Int. J. Heat Mass Transf. 2017, 109, 115–122. [Google Scholar] [CrossRef]
- Choi, Y.J.; Kam, D.H.; Jeong, Y.H. Analysis of CHF enhancement by magnetite nanoparticle deposition in the subcooled flow boiling region. Int. J. Heat Mass Transf. 2017, 109, 1191–1199. [Google Scholar] [CrossRef]
- Bhatti, M.; Zeeshan, A.; Ellahi, R.; Ijaz, N. Heat and mass transfer of two-phase flow with Electric double layer effects induced due to peristaltic propulsion in the presence of transverse magnetic field. J. Mol. Liq. 2017, 230, 237–246. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A. EMHD effects on subcooled boiling in a Vertical annulus. Multiph. Sci. Technol. 2018, 30, 4. [Google Scholar] [CrossRef]
- Dogonchi, A.; Chamkha, A.J.; Ganji, D. A numerical investigation of magneto-hydrodynamic natural convection of Cu–water nanofluid in a wavy cavity using CVFEM. J. Therm. Anal. Calorim. 2019, 135, 2599–2611. [Google Scholar] [CrossRef]
- Unni, S.; Bokade, V.; Bhandarkar, U.; Gopalakrishnan, S.; Bodi, K. Numerical simulation of two-fluid magnetohydrodynamic channel flows. Numer. Heat Transf. Part A Appl. 2018, 74, 1342–1352. [Google Scholar] [CrossRef]
- Aminfar, H.; Mohammadpourfard, M.; Maroofiazar, R. Experimental study on the effect of magnetic field on critical heat flux of ferrofluid flow boiling in a vertical annulus. Exp. Therm. Fluid Sci. 2014, 58, 156–169. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y. Magnetohydrodynamic and Nanoparticle Effects in Vertical Annular Subcooled Flow Boiling. Symmetry 2019, 11, 810. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A. Electromagnetohydrodynamic two-phase flow-induced vibrations in vertical heated upward flow. J. Comput. Des. Eng. 2019, 6, 92–104. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).