Abstract
Modern daily life activities result in a huge amount of data, which creates a big challenge for storing and communicating them. As an example, hospitals produce a huge amount of data on a daily basis, which makes a big challenge to store it in a limited storage or to communicate them through the restricted bandwidth over the Internet. Therefore, there is an increasing demand for more research in data compression and communication theory to deal with such challenges. Such research responds to the requirements of data transmission at high speed over networks. In this paper, we focus on deep analysis of the most common techniques in image compression. We present a detailed analysis of run-length, entropy and dictionary based lossless image compression algorithms with a common numeric example for a clear comparison. Following that, the state-of-the-art techniques are discussed based on some bench-marked images. Finally, we use standard metrics such as average code length (ACL), compression ratio (CR), pick signal-to-noise ratio (PSNR), efficiency, encoding time (ET) and decoding time (DT) in order to measure the performance of the state-of-the-art techniques.
1. Introduction
The utilization of the computer in modernized activities is increasing virtually everywhere. As a result, sending a plethora of data, especially images and videos over the cyber world, is the most challenging issue because of circumscribed bandwidth and storage capacity; and it is time-consuming and costly as reported in [1]. For instance, a conventional movie camera customarily uses 24 frames per second. However, recent video standards sanction 120, 240, or 300 frames per second. Video is a series of still images or frames passed per second and a color image contains three panels: red, green and blue. Suppose you would like to send or store a three-hour color movie file of 1200 × 1200 dimension and 50 frames are passed in every second. It takes approximately (1200 × 1200 × 3 × 84 × 50 × 10,800) bits = 17,797,851.5625 Megabits = 2172.5893 gigabytes storage if a pixel is coded in 8 bits, which is a sizably voluminous challenge to store in a computer or send over the cyber world. Here, three is the number of channels of a color image, that is, R, G, and B, and 10,800 is the total number of seconds. Additionally, the medium of transmission and latency are two major issues for data transmission. If the video file is sent over a medium of 100 Mbps, approximately (17,797,851.5625 Megabits)/100 = 177,978.5156 s = 49.4385 h is required because the medium can send 100 Megabits per second. For these reasons, compression is required and it is a paramount way to represent an image with fewer bits keeping its quality and an immensely colossal volume of data can be sent through an inhibited bandwidth at high speed over the cyber world reported in [2,3]. The general block diagram of an image compression procedure is shown in Figure 1.
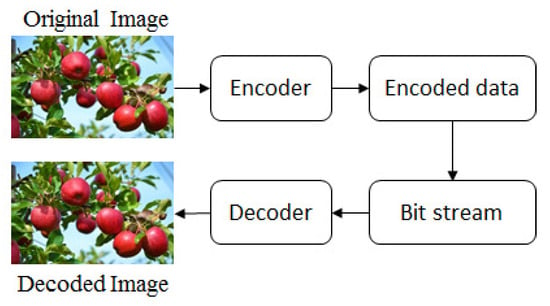
Figure 1.
General block diagram of an image compression procedure.
There are many image compression techniques and an image compression technique is verbally expressed to be the best when it contains less average code length, encoding and decoding time, and provides more compression ratio. Image compression algorithms are extensively applied in medical imaging, computer communication, military communication via radar, teleconferencing, magnetic resonance imaging (MRI), broadcast television and satellite images reported in [4]. Some applications of these require high-quality visual information and others need less quality, reported in [5,6].
From the perspectives, compression is divided into two types: lossless and lossy. All pristine data are recuperated correctly from an encoded data set in lossless, whereas the lossy technique retrieves virtually all data sempiternally eliminating categorical information, especially redundant information reported in [7,8]. Lossless is mostly utilized in facsimile transmissions of bitonal images, ZIP file format, digital medical imagery, internet telephony, and streaming video file reported in [9].
The foremost intention of implementing a compression algorithm is to diminish superfluous data reported in [10]. Run-length coding, for example, is a lossless procedure where a set of consecutive same pixels (runs of data) are preserved as a single value and a count stated in [11,12]. But, long runs of data does not subsist in authentic images mentioned in [13,14] which is the main quandary of run-length coding. Article [15] shows that a chain code binarization with run-length, and LZ77 provides a more satisfactory result than the traditional run-length technique from a compression ratio perspective. The authors in [16] show a different way of compression utilizing a bit series of a bit plane and demonstrate that it provides a better result than conventional run-length coding.
The entropy encoding techniques are proposed to solve the difficulties of a run-length algorithm. Entropy coding style encodes source symbols of an image with code words of different lengths. There are some well-recognized entropy coding methods: such as Shannon–Fano, Huffman and arithmetic coding. The first entropy coding technique is Shannon–Fano, which gives a better result than run-length reported in [17]. The authors in [18] show that Shannon–Fano coding provides 30.64% and 36.51% better results for image and text compression, respectively, compared to run-length coding. However, Nelso et al. stated in [19] that Shannon–Fano sometimes generates two different codes for the same symbol and does not ascertain optimal codes, which are the two main problems of the algorithm. From the perspectives, Shannon–Fano coding is an inefficient data compression technique reported in [20,21].
Huffman is another entropy coding algorithm that solves the quandaries of Shannon–Fano reported in [22,23]. In that technique, pixels that are happening more frequently are encoded, utilizing fewer bits shown in [24,25]. Although Huffman coding is a good compression technique, Rufai et al. proposed singular value decomposition (SVD) and Huffman coding based image compression procedure in [26], where SVD is used to decompose an image first and the rank is reduced by ignoring some lower singular values. Lastly, the processed representation is coded by Huffman coding, which shows a better result than JPEG2000 for lossy compression. In [27], three algorithms, Huffman, fractal algorithm and Discrete Wavelet Transform (DWT) coding, have been implemented and are compared to show the best coding procedure among them. It shows that Huffman works better to reduce redundant data and DWT improves the quality of a compressed image, whereas the fractal provides a better compression ratio. The main problem of Huffman coding is that it is very sensitive to noise. It can not reconstruct an image perfectly from an encoded image if any changes are happened reported in [28].
Another lossless entropy method is arithmetic coding, which gives a short average code compared to Huffman coding reported in [29]. In [30], Masmoudi et al. proposed a modified technique of arithmetic coding that encodes an image from top to bottom block-row wise and block by block from left to right in lieu of pixel by pixel using a statistical model. The precise probability between the current and its neighboring block are calculated by reducing the Kullback–Leibler gap. As a result, around 15.5% and 16.4% bitrates are decremented for static and adaptive order sequentially. Utilizing adaptive arithmetic coding and finite mixture models, a block-predicated lossless compression has been proposed in [31]. Here, an image is partitioned into non-overlapping blocks and encoded every block individually utilizing arithmetic coding. This algorithm provides 9.7% better results than JPEG-LS reported in [32,33] when the work is done in a predicted error domain in lieu of pixel domain. Articles [34,35] state that arithmetic coding provides better compression ratio. But, it takes so much time that is virtually unutilizable for dynamic compression. Furthermore, its use is restricted by patent. On the other hand, though Huffman coding provides marginally less compression but it utilizes very less time to encode an image than arithmetic coding. That’s why it is good for dynamic compression reported in [36,37]. Furthermore, an image encoded by arithmetic coding can corrupt the entire image for a single bit error because it has very impecunious error resistance reported in [26,38,39]. Contiguous to, the primary inhibition of entropy coding is that it increments the complexity of CPU stated in [40,41].
LZW (Lempel–Ziv–Welch) is a dictionary predicated compression technique that reads a sequence of pixels, and then groups the pixels into strings. Lastly, the strings are converted into codes. In that technique, a code table with 4096 common entries are utilized and the fixed codes 0–255 are assigned first in a table as an initial entry because an image can have a maximum of 256 different pixels from 0 to 255. It works better in case of text compression reported in [42]. However, Saravanan et al. propose an image coding procedure utilizing LZW, which compresses an image in two stages shown in [43]. Firstly, an image is encoded utilizing Huffman coding. Secondly, after concatenating all the code words, LZW is applied to compress the encoded image, which provides a better result. However, the main challenge of that technique is to manage the string table.
In this study, we use a common numeric data set and shows the step by step details of implementation procedures of the state-of-the-art data compression techniques mentioned. This demonstrates the comparisons among the methods and explicates the quandaries of the methods based on the results of some benchmarked images. The organization of this article is shown as follows: the encoding and decoding procedure; and the analysis of run-length, Shannon–Fano, Huffman, LZW and Arithmetic coding are discussed in Section 2. The experimental results of some bench-marked images are explained in Section 2.2, and concluding statements are presented in Section 3.
2. The State-of-the-Art Techniques
2.1. Run-Length Coding
Run-length coding is a lossless compression procedure that takes the occurrence of data in lieu of statistical information, and it is generally utilized in TIFF and PDF formats reported in [44]. In the encoding, a single value and the count of same consecutive values are preserved. For instance, the encoding procedure is shown based on the 50 elements (A = [6 7 6 6 6 7 7 7 7 7 7 7 7 7 5 4 4 4 4 7 7 7 7 7 7 7 7 7 5 5 5 7 7 3 3 3 2 2 2 5 5 5 5 5 5 5 5 5 1 1]).
2.1.1. Run-Length Encoding Procedure
- Calculate the difference (B = [1 −1 0 0 1 0 0 0 0 0 0 0 0 −2 −1 0 0 0 3 0 0 0 0 0 0 0 0 −2 0 0 2 0 −4 0 0 −1 0 0 3 0 0 0 0 0 0 0 0 −4 0 1]) using .
- Assign 1 to each non-zero data of B and we get B = [1 1 0 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 1].
- Save the positions of all ones into an array (position = [1 2 5 14 15 19 28 31 33 36 39 48 50]) and the corresponding data into (items = [6 7 6 7 5 4 7 5 7 3 2 5 1]) from A. The array position and items are stored or sent as the encoded list of the original 50 elements.
It shows that only twenty six elements are preserved in two matrices in lieu of 50 items, which designates that (26 × 8) = 208 bits are sent to the decoder in lieu of (50 × 8) = 400 bits. Thus, the average code length is 208/50 = 4.16 bits and ((8 − 4.16)/8) × 100 = 48% working memory is saved for the data set.
2.1.2. Run-Length Decoding Procedure
The two array named position and items are received for decoding, and the decoder follows the style shown below for decompression.
- Read each element from the array items and write the element repeatedly until its corresponding number in the position array is found.
As an example, the first 6 and 7 of the items array are written one times at index 1 and 2 in the new decoded list, respectively, whereas the next 6 and 7 are reiterated three times at the index 3 to 5 and nine times at the index 6 to 14 in the same decoded list, respectively. These processes will continue until the reading of all elements from the items is finished. Conclusively, we get the same list as the original list(A) after decoding.
2.1.3. Analysis of Run-Length Coding Procedure
Run-length coding works well when an image contains long runs of identical samples that customarily do not appear in an authentic image, which is the main quandary of run-length coding reported in [13,14]. For example, data (A) is rearranged with a slight change and the rearranged list is C = [1 6 7 6 6 7 7 7 4 7 7 7 7 5 7 4 4 7 4 7 7 7 7 7 7 7 5 7 7 5 5 7 7 3 3 2 3 2 2 5 5 5 5 6 5 5 5 5 5 1]. We apply run-length coding on C, and get [1 2 3 5 8 9 13 14 15 17 18 19 26 27 29 31 33 35 36 37 39 43 44 49 50 ] and [1 6 7 6 7 4 7 5 7 4 7 4 7 5 7 5 7 3 2 3 2 5 6 5 1 ] in position and item arrays. There is no compression here because the two arrays contain 50 elements together, which is precisely identically tantamount to the initial list (C).
2.2. Shannon–Fano Coding
Shannon–Fano is a lossless coding technique that takes sorted probabilities in the descending order of an image and separated them into two sets where the total sum of each set is almost equivalent, which is reported in [45]. The Shannon–Fano encoding procedure is shown as follows:
2.2.1. Shannon–Fano Encoding Style
- Find the distinct symbols (N) and their corresponding probabilities.
- Sort the probabilities in descending order.
- Divide them into two groups so that the entire sum of each group is as equal as possible, and make a tree.
- Assign 0 and 1 to the left and right group, respectively.
- Repeat steps 3 and 4 until each element becomes a leaf node on a tree.
Run-length coding does not perform any compression on array C. C contains seven different components (7,5,4,6,3,2,1) and their probabilities are 0.42,0.26,0.08,0.08,0.06,0.06 and 0.04, respectively. As indicated by the algorithm, the two groups left (0.42,0.08) and right (0.26,0.08,0.06,0.06,0.04) are made and the Shannon–Fano encoding system is applied as demonstrated in Figure 2.
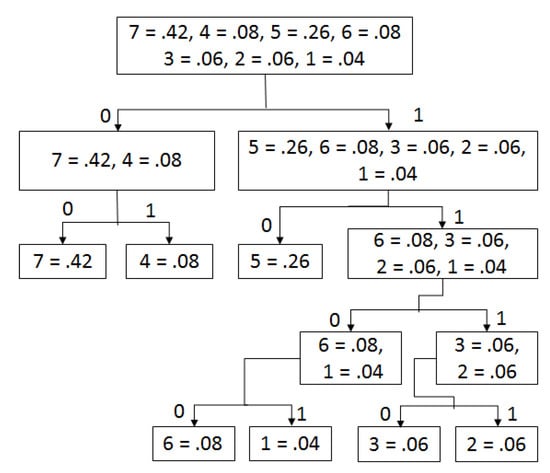
Figure 2.
Encoding procedure of Shannon–Fano.
Entropy, efficiency, ACL, CR, mean square error (MSE) and PSNR are determined using the following equations that are utilized to measure the performance of a compression algorithm, where , , OR, CO, and MAX represent probability of symbol, length of the code word of the symbol, original image, compressed image and the maximum variation of a dataset separately. The encoded results of the array (C) are appeared in Table 1, where represents an encoded code word of the symbol:

Table 1.
The results of Shannon–Fano encoding procedure.
Using Table 1, the Shannon–Fano coding provides [110111000011001100000000010000000010000101 0001000000000000001000001010000011101110111111101111111110101010110010101010101101] bitstream of data set (C), which is sent for decompression together with symbols and their probabilities. It appears that Shannon–Fano saves ((8 − 2.48)/8) × 100 = 69% storage, where run-length coding can save no memory for the same data set. Thus, Shannon–Fano provides 69% better results than run-length coding for the data set and the algorithm proficiency is 92.298%.
2.2.2. Shannon–Fano Decoding Style
In decoding, Shannon–Fano receive an encoded bitstream, items and their relating probabilities. It builds a similar tree to Figure 2 dependent on the probabilities, and the following procedure is used for decoding. Finally, we get the same data list as array C.
- Read each bit from an encoded bitstream and scan the tree until a leaf node is found. At the point when a leaf hub is discovered, read the symbol of the node as decoded value, and the process will proceed until scanning of the encoded bitstream is finished.
2.2.3. Analysis of Shannon–Fano Coding
In Shannon–Fano coding, we cannot be sure about the codes generated. There might be two different codes for the same symbol depending on the way we build our tree shown below through an example. Assume two groups (7 = 0.42 and 6 = 0.08) and (5 = 0.26, 4 = 0.08, 2 = 0.06, 3 = 0.06, 1 = 0.04) are made instead of (7 = 0.42 and 4 = 0.08) and (5 = 0.26, 6 = 0.08, 2 = 0.06, 3 = 0.06, 1 = 0.04) simply exchanging two probabilities between two groups appearing in bold. In addition, if we apply Shannon–Fano decoding on the received bitstream, we get (D = [1 4 7 4 4 7 7 7 6 7 7 7 7 5 7 6 6 7 6 7 7 7 7 7 7 7 5 7 7 5 5 7 7 2 2 3 2 3 3 5 5 5 5 4 5 5 5 5 5 1]) as decoded values. In the decoded list, the bold symbols represent the changed components of the original list that are considered as a loss. There are 14 elements in the decoded list that the Shannon–Fano’s rebuilt tree can not reproduce perfectly. Thus, it loses (14/50) × 100 = 28% data for only 50 elements.
2.3. Huffman Coding
Shannon–Fano coding sometimes produces the poorest code for some set of probabilities because it cannot produce an optimal tree. David A. Huffman illustrated a coding procedure that consistently makes an optimal tree and tackled the issues that exist in Shannon–Fano coding reported in [46,47]. Shannon–Fano coding is a top-down methodology, whereas Huffman coding uses the reverse route, from the leaves to the root. Huffman coding uses the statistical information of an image like Shannon–Fano coding. The encoding style of Huffman coding is given below. In addition, Figure 3 and Table 2 demonstrate a graphical representation of Huffman tree and the outcomes dependent on the same data used in Shannon–Fano coding.
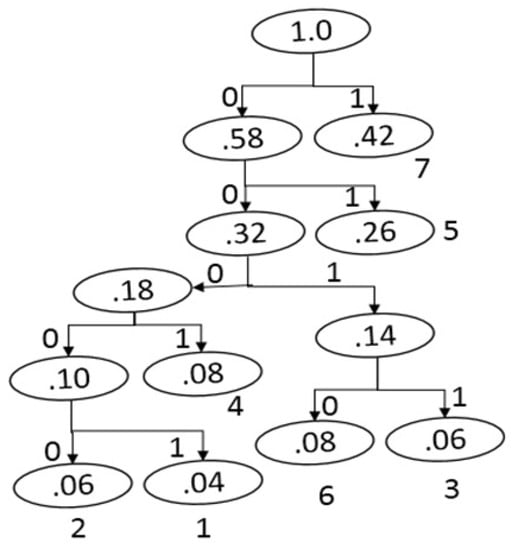
Figure 3.
Huffman tree for encoding.

Table 2.
Huffman encoding procedure.
2.3.1. Huffman Encoding Style
- List the probabilities of a gray-scale image in descending order.
- Form a new node of a tree with the sum of the two lowest probabilities on the list and rearrange them in the same order for the proceeding process. This process will continue until the end.
- Assign 0 and 1 to each left and right branch of the tree, respectively.
Based on Table 2, we get [0000100101001000101 11000111110110001000110001111111101110101110 011001 10000000110000000000010101010010010101010100001] as encoded bitstream for the data set (C) that is sent for decoding with symbols and their corresponding probabilities. In this way, Huffman coding saves 71% memory space, which is 69% and 2% more than Run-length and Shannon–Fano coding, respectively, and the efficiency of Huffman coding is 98.664%, which is 6.366% more than Shannon–Fano coding.
2.3.2. Huffman Decoding Style
Huffman coding provides an optimal prefix code. Huffman receives an encoded bitstream, items and their corresponding probabilities and uses the following methodology for decompression; and we get indistinguishable data as the original list (C):
- Recreates the equivalent Huffman tree built in the encoding step using the probabilities.
- Each bit is scanned from the encoded bitstream and traverses the tree node by node until a leaf node is reached. At the point when a leaf node is discovered, the symbol is predicted from the node. This process will proceed until finished.
2.3.3. Analysis of Huffman Coding
The main problem for Huffman coding is that it is very sensitive to noise. A minor change in any bit of the encoded bitstream would break the whole message reported in [28]. Assume that the decoder receives items, probabilities and the encoded bitstream with only three altered bits at the positions 5th, 19th, 54th. Then, we get [2676657477775744747777777355773323 2255556555551] as decoded values where bold elements (total 23) indicate loss of data. In addition, it produces only 47 elements rather than 50 elements. Thus, it devastates ((23 + 3)/50) × 100 = 52% data.
2.4. Lempel–Ziv–Welch (LZW) Coding
Lempel–Ziv–Welch (LZW) is generally used for lossless text compression invented by Abraham Lempel, Jacob Ziv, and Terry Welch. This strategy is easy to implement and broadly applied for Unix file compression, which was published in 1984 as an updated version of LZ78. It encodes a sequence of characters with a unique code using a table-based lookup algorithm. In this algorithm, the first 256 8-bit code, 0–255 are inserted into a table as an initial entry because an image contains 0–255 distinct pixels, and the following codes come from 256 to 4095, which will be embedded into the bottom of the table. This algorithm works better in case of text compression and provides most noticeably a terrible outcome for another sort of compression. The encoding procedure of the algorithm is shown as follows.
2.4.1. LZW Encoding Procedure
- Assign 0–255 in a table and set the first data from the input file to FD,
- Repeat steps 3 to 4 until reading is finished,
- ND = Read the next data,
- IF FD + ND is in the table,
- FD = FD + ND,
ELSE- Store the code for FD as encoded data and insert FD + ND to the table. In addition, set FD = ND.
Since the previously mentioned original list (C) contains only 7 (1–7) different values, only 1–7 are inserted into the table as an initial dictionary first. Applying the LZW encoding procedure on C shown in Table 3 and we get the decoded list that appears in Table 4. Finally, the encoded bitstream is sent to the decoder, where each piece of encoded data is converted into 6-bit binary on the grounds that the biggest value is 33 in the encoded list and just 6 bits are required to represent 33.

Table 3.
LZW encoding procedure.

Table 4.
Average code length and compression ratio.
Since the average code length is 3.84, as it appears in Table 4. Thus, LZW saves 36% memory, which is 28.7356% and 29.3103% more than Shannon–Fano and Huffman coding individually for the same dataset. Furthermore, the only encoded bitstream is sent to the decoder for decompression.
2.4.2. LZW Decoding Procedure
The Lempel–Ziv–Welch (LZW) decoding procedure uses the same initial dictionary used in the encoding step and decoding is done using the procedures shown below for image compression.
- Assign 0–255 in a table and scan the first encoded value and assign it to FEV. Later, send the translation of FEV to the output.
- Repeat steps 3 to 4 until the reading of the encoded file ends.
- NC = read next code from encoded file.
- IF (NC is not found in the table).
- Assign the translation of FEV to DS and perform DS = DS + NC
ELSE- Assign the translation of NC to DS, the first code of DS to NC, NC to FEV and add FEV+NC into the table. Furthermore, send DS to the output.
For instance, the mentioned encoded bitstream converts each six bits into decimal value and assign 1–7 as the initial dictionary shown in Table 5. The decoding demonstration for the encoded data is shown in Table 6, and we get a similar list as C after decoding.

Table 5.
Initial dictionary.

Table 6.
The decoding procedure of LZW coding.
2.4.3. Analysis of LZW Coding
Searching dictionary is a major challenge in the LZW compression technique because it is more complicated and time-consuming. Moreover, an image that does not carry much repetitive data at all cannot be reduced, and it is good for deducing file size that carries more repeated data reported in [48,49].
2.5. Arithmetic Coding
Arithmetic coding is a lossless data compression procedure where a set of symbols is presented using a fixed number of bits reported in [50,51]. It takes likelihood data from a dataset and applies the following procedures for encoding, where N and CF indicate number and cumulative frequency. In addition, UL, LL, LUL and LLL indicate upper, lower, last upper and the last lower limit of the current range, respectively.
2.5.1. Arithmetic Encoding Procedure
Arithmetic_encoding(N, CF)
- limit = UL − LL,
- UL = LL + limit * CF[N − 1],
- LL = LL + limit * CF[N].
The original array (C) contains 50 elements and showing the method of the encoding style of 50 items in a figure is very difficult. That’s why, the encoding style for ten items is shown. Suppose that the list is [2 3 4 3 4 4 4 1 4 1 ]. There are four different items (4 3 1 2) on the list, and their corresponding probabilities are 0.5, 0.2, 0.2, 0.1, individually. The four elements (4 3 1 2) contain 50%, 20%, 20% and 10% data, respectively. Thus, each limit is divided into 50%, 20%, 20% and 10% each time to encode each element, which is shown in Figure 4 for all ten elements.

Figure 4.
Arithmetic encoding procedure.
The tag value is calculated using Equation (7):
For the example shown in Figure 4, the LLL and LUL are 0.9551925 and 0.9551975. Thus, the tag is 0.955195. The bitstream of the tag value is 001111000110111. Thus, the average code length is 15/10 = 1.5 bits, and the compression ratio is 5.3333 where 15 is the length of the tag. Finally, the tag’s bitstream, symbols (4,3,1,2), and their corresponding probabilities (0.5, 0.2, 0.2, 0.1) are sent to the decoder for decompression. When Arithmetic coding is applied on data set (C), we get [00000101100110101110100101111100101010111011110011 11110101011001011100110011100000000101011010010110110111100001011] bitstream from the provided tag. Thus, average code length and compression ratio is 2.3000 bits and 3.4783 separately, which saves 71.25% of storage. It appears that run-length, Shannon–Fano, Huffman and LZW coding use 44.7115%, 7.2581%, 6.5041% and 33.908% more memory than arithmetic coding.
2.5.2. Arithmetic Decoding Procedure
The decoding procedure of arithmetic coding receives tag, symbols and their corresponding probabilities; and the tag is converted into its floating point number and follows the following methodology for decoding. For decompression, if the tag is in between in any range, then the symbol of the range is taken as the decoded value. The range (r) and Newtag (NT) is calculated using Equations (8) and (9), respectively.
Arithmetic_decoding(CF)
- if(CF[N] < = (tag − LL)/(UL − LL) < CF[N − 1]),
- (a)
- limit = UL − LL,
- (b)
- UL = LL + limit*CF[N − 1],
- (c)
- LL = LL + limit*CF[N],
- (d)
- return N.
The whole decoding procedure of the ten values is demonstrated in the following list using Figure 5, and we get the same list [2 3 4 3 4 4 4 1 4 1] as the original. Here, the floating value of the corresponding tag’s bitstream is 0.955195.
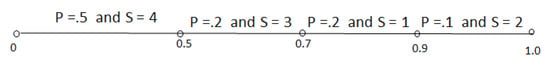
Figure 5.
Arithmetic decoding procedure.
- tag = 0.955195. Since 0.9 < = tag < = 1.0, Thus, decoded value is 2 because the symbol 2 is in range.
- NT1 = (tag − LL)/r = 0.55195 and it is in between 0.5 and 0.7, so the decoded value is 3.
- NT2 = (NT1 − LL)/r = 0.25975 and it is in between 0 and 0.5, so the decoded value is 4.
- NT3 = (NT2 − LL)/r = 0.5195 and it is in between 0.5 and 0.7, so the decoded value is 3.
- NT4 = (NT3 − LL)/r = 0.0975 and it is in between 0 and 0.5, so the decoded value is 4.
- NT5 = (NT4 − LL)/r = 0.195 and it is in between 0 and 0.5, so the decoded value is 4.
- NT6 = (NT5 − LL)/r = 0.39 and it is in between 0 and 0.5, so the decoded value is 4.
- NT7 = (NT6 − LL)/r = 0.78 and it is in between 0.7 and 0.9, so the decoded value is 1.
- NT8 = (NT7 − LL)/r = 0.4 and it is in between 0 and 0.5, so the decoded value is 4.
- NT9 = (NT8 − LL)/r = 0.8 and it is in between 0.7 and 0.9, so the decoded value is 1.
2.5.3. Analysis of Arithmetic Coding Procedure
The authors in [34,35] state that arithmetic coding provides a better compression ratio. However, it takes so much time that it is virtually not utilizable for dynamic compression. Furthermore, its use is restricted by the patent. On the other hand, though Huffman coding provides marginally less compression, it utilizes much less time to encode an image than arithmetic coding. This is why it is good for dynamic compression reported in [36,37]. Furthermore, an image encoded by arithmetic coding can corrupt the entire image for a single bit error because it has very impecunious error resistance reported in [26,38]. Another problem is that an entire code word must be taken to start interpreting a message. Contiguous to the primary inhibition of entropy coding is that it increments the complexity of CPU stated in [40,41]. Suppose the decoder receives the tag of the original 50 elements with only a first bit altered and we get [65427777727567777477777717765757772472757571571711] as a decoded list where the bold symbols indicate the altered values. In the list, 31 elements have been altered, which means (31/50) × 100 = 62% of the data have been corrupted.
3. Experimental Results and Analysis
The outcomes and investigation of the state-of-the-art methods have been demonstrated in this segment. The techniques have been applied on the different types of bench-marked images. In this paper, we have initially used three PC created photographs and the next twenty-two medical images from the DICOM Image dataset [52] of various sizes appeared in Figure 6. Encoding time, decoding time, average code length, compression ratio, PSNR and efficiency have been used to analyze the performance of the algorithms.
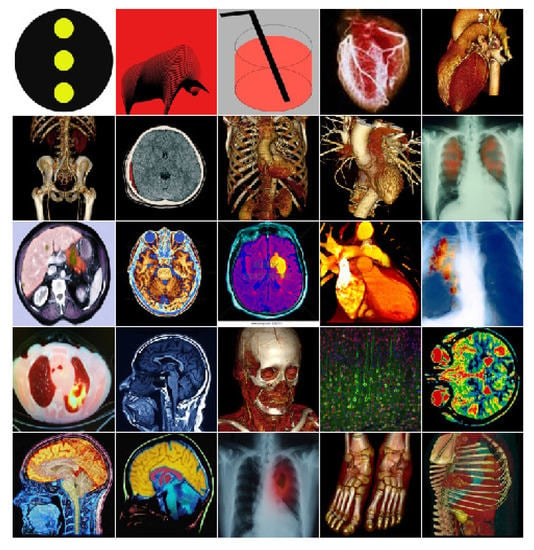
Figure 6.
Original image list.
The encoding and decoding time are the periods of time required to encode and decode an image. Average code length determines the number of bits used to store a pixel on average, and the compression ratio represents the ratio of original and compressed images. Pick signal-to-noise ratio ((PSNR)) is used to measure the quality of an image. Less encoding and decoding time, short average code length and higher compression ratio tell how much faster an algorithm is and how much less memory it uses. The higher efficiency and PSNR convey that an image contains high-quality information. The encoding time, decoding time, average code length, and compression ratio are shown in Table 7, Table 8, Table 9 and Table 10, whereas Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show the graphical representation of encoding time, decoding time, average code length, compression ratio and efficiency, respectively, based on the twenty-five images.

Table 7.
Encoding time comparison.

Table 8.
Decoding time comparison.

Table 9.
Comparison of average code length.

Table 10.
Comparison of compression ratio.
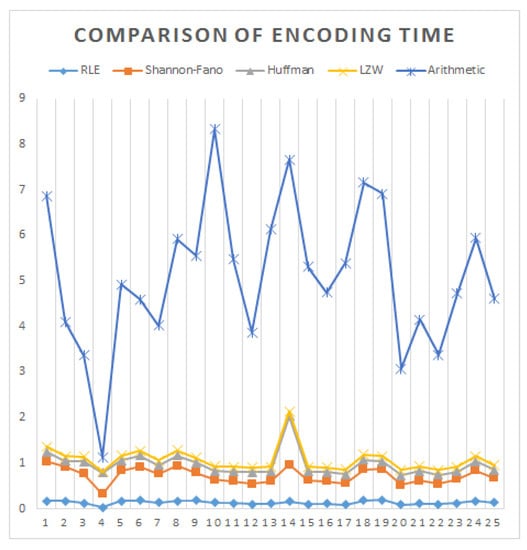
Figure 7.
Encoding time comparison of the images.
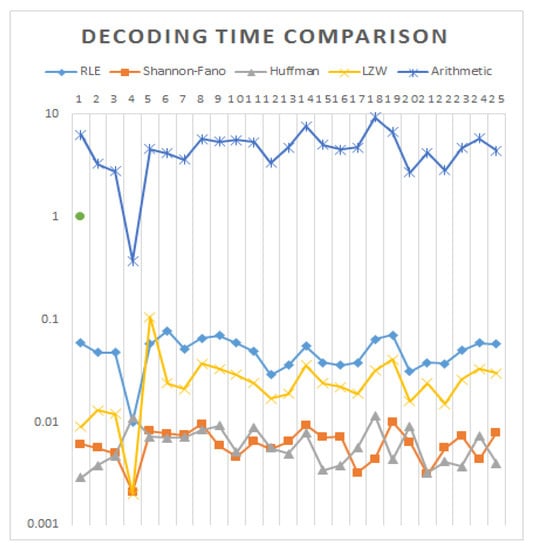
Figure 8.
Decoding time comparison of the images.
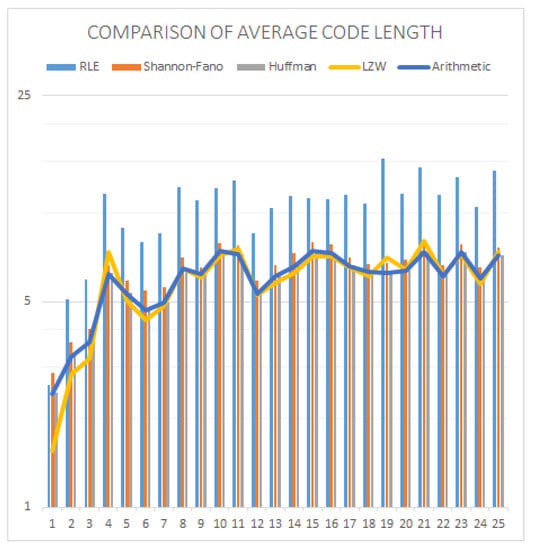
Figure 9.
Average code length comparison of the images.
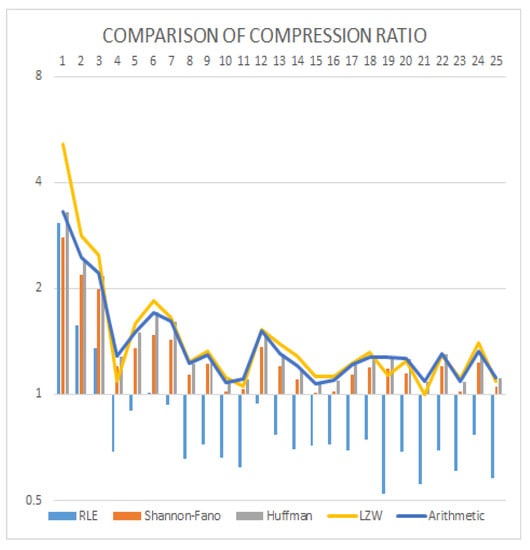
Figure 10.
Comparison of compression ratio.
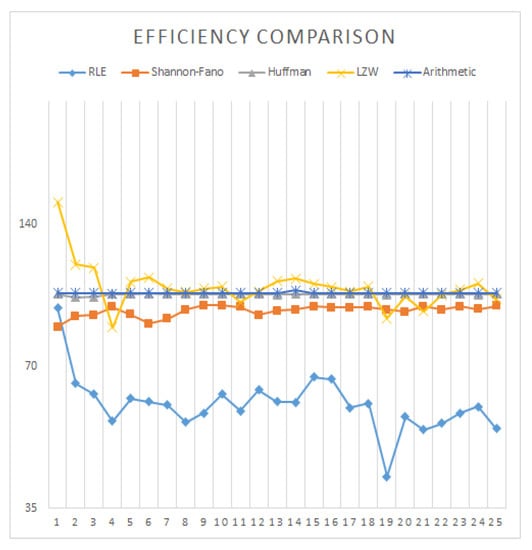
Figure 11.
Efficiency comparison.
Table 7 shows that arithmetic and run-length coding take the highest (4.0178) and lowest (0.1349) milliseconds on average, whereas Shannon–Fano, Huffman and LZW take 0.5873, 0.2488 and 0.1054 milliseconds individually to encode the images. It appears that arithmetic coding uses 96.6424%, 85.3825%, 93.8076% and 97.3767% more time than run-length, Shannon–Fano, Huffman and LZW coding, respectively. However, Huffman coding uses much less time (0.0062) on average in decoding, whereas arithmetic coding uses more time, which is demonstrated in Table 8. On the other hand, LZW uses more time than Shannon–Fano and Huffman coding but less than Arithmetic and Run-Length coding. Figure 7 and Figure 8 show the graphical representation of encoding and decoding time for comparison.
Table 9 and Table 10 show average code length and compression ratio, respectively. It looks that RLE uses 10.5618 bits per pixel, on average, which is 24.2553% more memory being used than the original images, which is the reason it is not used directly for real image compression. On the other hand, LZW uses the lowest number of bits (5.9365) per pixel, but the problem of LZW is that it sometimes uses more memory than an original, which happened for image 21 shown in Table 9. Arithmetic coding uses the second lowest number of bits per pixel on average. Thus, arithmetic coding is the best coding technique because it provides a better compression ratio than other state-of-the-art techniques without LZW shown in Table 10. Figure 9 and Figure 10 demonstrate the graphical representation of average code length and compression ratio separately for comparison.
All the state-of-the-art strategies are lossless. Thus, pick signal-to-noise ratio and mean squared error (MSE) for each algorithm are inf and zero, respectively, for every case. However, arithmetic and run-length coding on average have the highest (99.9899) and lowest (58.6783) efficiency than the other methods shown in Figure 11. Despite the fact that the proficiency of LZW coding at some point provides better outcomes and sometimes provides absolutely terrible outcome, which is why it is not used for image compression in real applications. The list of the decompression images is shown in Figure 12.
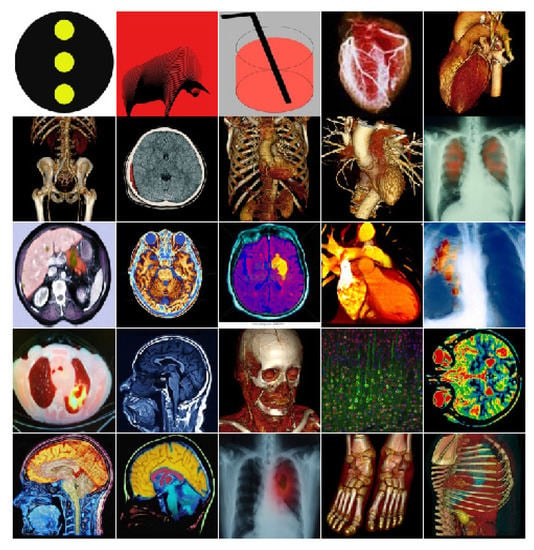
Figure 12.
Decompressed image list.
From the previously mentioned perspectives, it can tell that arithmetic coding is the best way when more compression is required; however, it isn’t useful for a real-time application in view of taking additional time in encoding and decoding steps. Searching in a dictionary is a big challenging issue for LZW coding, and it provides the worst results for an image compression. Shannon–Fano coding sometimes does not provide optimal code and provides two different codes for the same element, which is the reason it is obsolete now. Run-length coding is not good for a straightforward real image compression.
Thus, it very well may be reasoned that Huffman coding is the best algorithm for the recent technologies among the state-of-the-art lossless methods mentioned used in various applications. However, if we can decrease the encoding and decoding time in case of arithmetic coding, then it will be the best algorithm. On the other hand, Huffman coding will work more if we can decrease its average code length keeping its same encoding and decoding times. In this article, all the experiments are done using C, Matlab (version 9.4.0.813654 (R2018a). Natick, Massachusetts, USA: The MathWorks Inc.; 2018) and Python languages. For the coding environments, Spyder (Python 3.6), Codeblocks (17.12, The Code::Blocks Team) and Matlab are utilized. Furthermore, we utilized an HP laptop (Palo Alto, California, United States) that contained the Intel Core i3-3110M @2.40 GHz processor (Santa Clara, USA), 8 GB DDR3 RAM, 32 KB L1D-Cache, 32 KB L1I-Cache, 256 KB L2 Cache and 3 MB L3 Cache, where L1D, L1I, and L2 Caches contained 8-way set associative, 64-byte line size each, and L3 Cache contained 12-way set associative, 64-byte line size. According to the algorithms used for testing, the CPU-Time is , , , and for Run-length, Shannon–Fano, Huffman, LZW and Arithmetic coding, respectively, where P indicates the number of pixels and represents the number of different pixels of an image.
4. Conclusions
In this study, we presented a detailed analysis of some common lossless image compression techniques such as: the run-length, Shannon–Fano, Huffman, LZW and arithmetic coding. The relevance of these techniques comes from the fact that most of the other recently developed lossless (or lossy) algorithms use one of them as a part of its compression procedure. All the mentioned algorithms have been discussed using a common numeric data set. Both computer generated and actual medical images are used to assess the efficiency of such state-of-the-art methods. We also used standard metrics such as: encoding time, decoding time, average code length, compression ratio, efficiency and PSNR to measure the superiority of such techniques. Finally, we noticed that Huffman coding outperforms other state-of-the-art techniques in case of real time lossless compression applications.
Author Contributions
For the research article, M.A.R.; conceived and designed the experiments, M.A.R.; performed the experiments, M.A.R.; analyzed the data; M.A.R and M.H.; wrote the paper, M.H.; writing–review and editing, M.H.; supervision, M.H.; funding acquisition. This paper was prepared the contributions of all authors. All authors have read and approved the final manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bovik, A.C. Handbook of Image and Video Processing; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Sayood, K. Introduction to Data Compression; Morgan Kaufmann: Burlington, MA, USA, 2017. [Google Scholar]
- Salomon, D.; Motta, G. Handbook of Data Compression; Springer Science & Business Media: Berlin, Germnay, 2010. [Google Scholar]
- Ding, J.; Furgeson, J.C.; Sha, E.H. Application specific image compression for virtual conferencing. In Proceedings of the International Conference on Information Technology: Coding and Computing (Cat. No.PR00540), Las Vegas, NV, USA, 27–29 March 2000; pp. 48–53. [Google Scholar] [CrossRef]
- Bhavani, S.; Thanushkodi, K. A survey on coding algorithms in medical image compression. Int. J. Comput. Sci. Eng. 2010, 2, 1429–1434. [Google Scholar]
- Kharate, G.K.; Patil, V.H. Color Image Compression Based on Wavelet Packet Best Tree. arXiv 2010, arXiv:1004.3276. [Google Scholar]
- Haque, M.R.; Ahmed, F. Image Data Compression with JPEG and JPEG2000. Available online: http://eeweb.poly.edu/~yao/EE3414_S03/Projects/Loginova_Zhan_ImageCompressing_Rep.pdf (accessed on 1 October 2019).
- Clarke, R.J. Digital Compression of still Images And Video; Academic Press, Inc.: Orlando, FL, USA, 1995. [Google Scholar]
- Joshi, M.A. Digital Image Processing: An Algorithm Approach; PHI Learning Pvt. Ltd.: New Delhi, India, 2006. [Google Scholar]
- Golomb, S. Run-length encodings (Corresp). IEEE Trans. Inform. Theory 1966, 12, 399–401. [Google Scholar] [CrossRef]
- Nelson, M.; Gailly, J.L. The Data Compression Book; M & t Books: New York, NY, USA, 1996; Volume 199. [Google Scholar]
- Sharma, M. Compression using Huffman coding. IJCSNS Int. J. Comput. Sci. Netw. Secur. 2010, 10, 133–141. [Google Scholar]
- Burger, W.; Burge, M.J. Digital Image Processing: An Algorithmic Introduction Using Java; Springer: Berlin, Germany, 2016. [Google Scholar]
- Kim, S.D.; Lee, J.H.; Kim, J.K. A new chain-coding algorithm for binary images using run-length codes. Comput. Vis. Graphics Image Process. 1988, 41, 114–128. [Google Scholar] [CrossRef]
- Žalik, B.; Mongus, D.; Lukač, N. A universal chain code compression method. J. Vis. Commun. Image Represent. 2015, 29, 8–15. [Google Scholar] [CrossRef]
- Benndorf, S.; Siemens, A.G. Method for the Compression of Data Using a Run-Length Coding. U.S. Patent 8,374,445, 12 February 2013. [Google Scholar]
- Shanmugasundaram, S.; Lourdusamy, R. A comparative study of text compression algorithms. Int. J. Wisdom Based Comput. 2011, 1, 68–76. [Google Scholar]
- Kodituwakku, S.R.; Amarasinghe, U.S. Comparison of lossless data compression algorithms for text data. Indian J. Comput. Sci. Eng. 2010, 1, 416–425. [Google Scholar]
- Rahman, M.A.; Islam, S.M.S.; Shin, J.; Islam, M.R. Histogram Alternation Based Digital Image Compression using Base-2 Coding. In Proceedings of the 2018 Digital Image Computing: Techniques and Applications (DICTA), Canberra, Australia, 10–13 December 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Drozdek, A. Elements of Data Compression; Brooks/Cole Publishing Co.: Pacific Grove, CA, USA, 2001. [Google Scholar]
- Howard, P.G.; Vitter, J.S. Parallel lossless image compression using Huffman and arithmetic coding. Data Compr. Conf. 1992. [Google Scholar] [CrossRef]
- Pujar, J.H.; Kadlaskar, L.M. A new lossless method of image compression and decompression using Huffman coding techniques. J. Theor. Appl. Inform. Technol. 2010, 15, 15–21. [Google Scholar]
- Mathur, M.K.; Loonker, S.; Saxena, D. Lossless Huffman coding technique for image compression and reconstruction using binary trees. Int. J. Comput. Technol. Appl. 2012, 1, 76–79. [Google Scholar]
- Vijayvargiya, G.; Silakari, S.; Pandey, R. A Survey: Various Techniques of Image Compression. arXiv 2013, arXiv:1311.6877. [Google Scholar]
- Rahman, M.A.; Shin, J.; Saha, A.K.; Rashedul Islam, M. A Novel Lossless Coding Technique for Image Compression. In Proceedings of the 2018 Joint 7th International Conference on Informatics, Electronics & Vision (ICIEV) and 2018 2nd International Conference on Imaging, Vision & Pattern Recognition (ic4PR), Kitakyushu, Japan, 25–29 June 2018; pp. 82–86. [Google Scholar] [CrossRef]
- Rufai, A.M.; Anbarjafari, G.; Demirel, H. Lossy medical image compression using Huffman coding and singular value decomposition. In Proceedings of the 2013 21st Signal Processing and Communications Applications Conference (SIU), Haspolat, Turkey, 24–26 April 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Jasmi, R.P.; Perumal, B.; Rajasekaran, M.P. Comparison of image compression techniques using huffman coding, DWT and fractal algorithm. In Proceedings of the 2015 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 8–10 January 2015; pp. 1–5. [Google Scholar]
- Xue, T.; Zhang, Y.; Shen, Y.; Zhang, Z.; You, X.; Zhang, C. Adaptive Spatial Modulation Combining BCH Coding and Huffman Coding. In Proceedings of the 2018 IEEE 23rd International Conference on Digital Signal Processing (DSP), Shanghai, China, 19–21 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Witten, I.H.; Neal, R.M.; Cleary, J.G. Arithmetic Coding for Data Compression. Commun. ACM 1987, 30, 520–540. [Google Scholar] [CrossRef]
- Masmoudi, A.; Masmoudi, A. A new arithmetic coding model for a block-based lossless image compression based on exploiting inter-block correlation. Signal Image Video Process. 2015, 9, 1021–1027. [Google Scholar] [CrossRef]
- Masmoudi, A.; Puech, W.; Masmoudi, A. An improved lossless image compression based arithmetic coding using mixture of non-parametric distributions. Multimed. Tools Appl. 2015, 74, 10605–10619. [Google Scholar] [CrossRef]
- Weinberger, M.J.; Seroussi, G.; Sapiro, G. The LOCO-I lossless image compression algorithm: Principles and standardization into JPEG-LS. IEEE Trans. Image Process. 2000, 9, 1309–1324. [Google Scholar] [CrossRef]
- Li, X.; Orchard, M.T. Edge directed prediction for lossless compression of natural images. IEEE Trans. Image Proc. 2001, 6, 813–817. [Google Scholar]
- Sasilal, L.; Govindan, V.K. Arithmetic Coding-A Reliable Implementation. Int. J. Comput. Appl. 2013, 73, 7. [Google Scholar] [CrossRef]
- Ding, J.J.; Wang, I.H. Improved frequency table adjusting algorithms for context-based adaptive lossless image coding. In Proceedings of the 2016 IEEE International Conference on Consumer Electronics-Taiwan (ICCE-TW), Nantou, Taiwan, 27–29 May 2016; pp. 1–2. [Google Scholar]
- Rahman, M.A.; Fazle Rabbi, M.M.; Rahman, M.M.; Islam, M.M.; Islam, M.R. Histogram modification based lossy image compression scheme using Huffman coding. In Proceedings of the 2018 4th International Conference on Electrical Engineering and Information & Communication Technology (iCEEiCT), Dhaka, Bangladesh, 13–15 September 2018; pp. 279–284. [Google Scholar] [CrossRef]
- Pennebaker, W.B.; Mitchell, J.L. JPEG: Still Image Data Compression Standard; Springer Science & Business Media: New York, NY, USA, 1992. [Google Scholar]
- Clunie, D.A. Lossless compression of grayscale medical images: effectiveness of traditional and state-of-the-art approaches. In Proceedings of the Medical Imaging 2000: PACS Design and Evaluation: Engineering and Clinical Issues, San Diego, CA, USA, 12–18 February 2000; pp. 74–85. [Google Scholar] [CrossRef]
- Kim, J.; Kyung, C.M. A lossless embedded compression using significant bit truncation for HD video coding. IEEE Trans. Circuits Syst. Video Technol. 2010, 20, 848–860. [Google Scholar]
- Kato, M.; Sony Corp. Motion Video Coding with Adaptive Precision for DC Component Coefficient Quantization and Variable Length Coding. U.S. Patent 5,559,557, 24 September 1996. [Google Scholar]
- Lamorahan, C.; Pinontoan, B.; Nainggolan, N. Data Compression Using Shannon–Fano Algorithm. Jurnal Matematika dan Aplikasi 2013, 2, 10–17. [Google Scholar] [CrossRef]
- Yokoo, H. Improved variations relating the Ziv-Lempel and Welch-type algorithms for sequential data compression. IEEE Trans. Inform. Theory 1992, 38, 73–81. [Google Scholar] [CrossRef]
- Saravanan, C.; Surender, M. Enhancing efficiency of huffman coding using Lempel Ziv coding for image compression. Int. J. Soft Comput. Eng. 2013, 6, 2231–2307. [Google Scholar]
- Pu, I.M. Fundamental Data Compression; Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mobile Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Huffman, D.A. A method for the construction of minimum-redundancy codes. Proc. IRE 1952, 40, 1098–1101. [Google Scholar] [CrossRef]
- Hussain, A.J.; Al-Fayadh, A.; Radi, N. Image compression techniques: A survey in lossless and lossy algorithms. Neurocomputing 2018, 300, 44–69. [Google Scholar] [CrossRef]
- Zhou, Y.-L.; Fan, X.-P.; Liu, S.-Q.; Xiong, Z.-Y. Improved LZW algorithm of lossless data compression for WSN. In Proceedings of the 2010 3rd International Conference on Computer Science and Information Technology, Chengdu, China, 9–11 July 2010; pp. 523–527. [Google Scholar] [CrossRef]
- Ziv, J.; Lempel, A. A universal algorithm for sequential data compression. IEEE Trans. Inform. Theory 1977, 23, 337–343. [Google Scholar] [CrossRef]
- Rahman, M.A.; Jannatul Ferdous, M.; Hossain, M.M.; Islam, M.R.; Hamada, M. A lossless speech signal compression technique. In Proceedings of the 1st International Conference on Advances in Science, Engineering and Robotics Technology, Dhaka, Bangladesh, 3–5 May 2019. [Google Scholar]
- Langdon, G.G. An introduction to arithmetic coding. IBM J. Res. Dev. 1984, 28, 135–149. [Google Scholar] [CrossRef]
- Osirix-viewer.com. 2019. OsiriX DICOM Viewer | DICOM Image Library. Available online: https://www.osirix-viewer.com/resources/dicom-image-library/ (accessed on 10 April 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).