Abstract
This paper studies the stress state of a threaded fastening by using Finite Element (FE) models, applied to surgical screws in cortical bone. There is a general interest in studying the stress states induced in the different elements of a joint caused by the thread contact. Analytical models were an initial approach, and later FE models allowed detailed studies of the complex phenomena related to these joints. Different studies have evaluated standard threaded joints in machinery and structures, being the thread symmetric. However, surgical screws employ asymmetric thread geometry, selected to improve the stress level generated in the bone. Despite the interest and widespread use, there is scarce documentation on the actual effect of this thread type. In this work, we discuss the results provided by FE models with detailed descriptions of the contacts comparing differences caused by the materials of the joint, the thread geometry and the thread’s three-dimensional helical effects. The complex contacts at the threaded surfaces cause intense demand on computational resources that often limits the studies including these joints. We analyze the results provided by one commercial software package to simplify the threaded joints. The comparison with detailed FE models allows a definition of the level of uncertainty and possible limitations of this type of simplifications, and helps in making suitable choices for complex applications.
1. Introduction
Threaded parts are the most widely deployed mechanical joint in machinery design. The most common threads for machinery are symmetric ones, typically metric and Whitworth, see Figure 1b,c. A key characteristic of a joint is the load distribution pattern through the threads along the depth path of the joint. This pattern helps when analyzing the joint’s performance in some applications, especially if the material characteristics of the joint parts are rather different from those of the fastener part. That is the case of surgical screws, applied to fasten bone plates to heal broken bones in reduction procedures. Screws and plates are usually made of stainless steel or titanium and both have similar success rates in fracture fixation applications. In terms of deployment, there is a preference for stainless steel orthopaedic devices in the USA and for titanium in Europe [1]. For screws, stainless steel allows better torque control but the tissue integration with titanium shows smaller inflammatory responses [1,2]. Since we focus this work on the thread geometry, we chose stainless steel as the reference material to perform this study, without lack of generality.
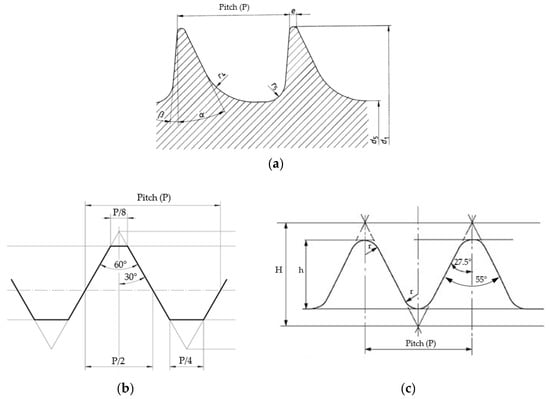
Figure 1.
Drawing of the threads according to (a), ISO5835-HA; (b), metric ISO68; (c), Withworth BS84.
Early analytical results [3,4,5] showed that the three threads just under the head, considering a bolt or screw for reference, take more than 50% of the applied load. These models were based on defining the rigidity of the parts of the joint and then analyzing the stresses caused in the geometrical sections of interest. These results were in line with common empirical experience of broken parts in failed joints. Analytical models were developed further to describe more complex joint effects such as the bending of the threads, compression of the nut, etc. [6,7,8], and provided more detailed descriptions such as the thread fillet stress, joint efficiency, etc. [9]. The state-of-the-art analytical models are implemented in the reference [10] with procedures to assess bolted joints, used as a de-facto standard guideline.
The numerical methods applied to mechanical calculations allowed major new approaches to more complex cases, and were immediately applied to the analysis of joints—always critical parts of any mechanical assembly. In the initial studies, using Finite Element (FE) methods the joints were modelled by using an axisymmetric description [11,12,13,14]. Typically, the authors revisited the state-of-the-art analytical models to cross check the results and search for possible influencing effects lying beneath the simplifications introduced, which the powerful numerical tools could directly address. The models also grew in complexity by introducing three-dimensional effects caused by the real helical geometry [15] and the pre-loading of the joint with a calculated torque [16,17,18] usually applied to bolts. Typically, geometric models are defined with sufficient detail so as to reproduce the thread effects in the parts. This search for detail has meant that the need for model definition and computing time is continuously increasing and the study of multi-joint assemblies has become a highly time-consuming problem that includes complex contact modelling.
The study of cases involving surgical screws usually focuses on analyzing the influence of the mechanical effects on more subtle biological or physiological processes, typically cellular osteosynthesis. Such studies clearly face the challenge of applying a complex detailed model and the calculation requirements can be unfeasibly demanding [19,20]. Sometimes the authors opt to use a highly simplified model [21], and commonly simplify the contact at the thread regions assuming cylindrical glued surfaces [22,23,24]. This selection may cause an immediate overestimation of the assembly stiffness and therefore hinder the study of some unnoticed effects. The optimal compromise would be the application of simple-to-implement methods that have limited computational cost but can provide realistic results. Software packages dedicated to developing FE models include tools to describe different joint formats efficiently. ANSYS (ANSYS Inc., PA, USA) offers a specific tool (version 17, 2017) for threaded joints, which, despite simple implementation [25], is not documented and leaves the user responsible for any type of application in case studies. This tool has been developed for symmetric threads (Metric and Whitworth).
This study focuses on analyzing joint models for threaded parts related to surgical applications when two different materials are in contact: bone and steel. We selected the reverse buttress-shaped HA thread as described for surgical screws according to ISO5835, ISO6475 and ISO9268. These screws are applied to cortical bones to fasten bone plates for reduction healing procedures. The HA thread is asymmetric (Figure 1a) and its design maximizes the contact area and minimizes the stress in the bone regions, while supporting the typical single direction loads of the application.
This work aims to contribute towards the knowledge of surgical threads studying them with 2D axisymmetric models, full 3D models and also testing the use of simplified bolt thread modelling software initially devoted to symmetric threads. If the use of this simplified modelling could be demonstrated, the studies including plates and bolts would be highly improved in terms of efficiency for both the model definition and the computing demand, while preserving the accuracy of the description. The work is organized as follows. Section 2 describes a detailed two-dimensional axisymmetric FE model to study specifically the load sharing in the threads and the stress state in the bone bulk regions next to the joint, depending on the thread types. Then, Section 3 analyses a three-dimensional model to compare any differences emerging from the volumetric geometry. Section 4 deals with the application and comparison of a simplified model that could be an option when describing the threaded joints if properly implemented. We also describe possible size-scale effects and computing time issues in Section 5.
2. Axisymmetric Two-Dimensional FE Model
To build a reference model for our studies we used an axisymmetric geometry based on the ISO68 ‘metric’ thread. This case study allows the results to be crosschecked with previous works based on analytic [8] and FE models [15]. Thus, we can compare the effect of having different materials in the joints by including the bone and finally we can modify the geometry to the asymmetric HA thread to compare the differences due to the geometry, while keeping the materials and contact definitions.
We used as our case study the geometry of ISO68 M2 and 2 mm diameter ISO5835-HA screws. For the joint, eight full threads of the screw inserted into the plate, with internal thread, were used. The plate has a depth equivalent to 10 threads, and a width equivalent to three times the screw’s nominal diameter. Therefore, the stress distributions can develop with no geometrical limitations.
The model was defined with a mesh of rectangular linear elements (PLANE 182 type in the software) with axisymmetric option. Due to the different geometrical characteristics of the symmetric and non-symmetric screws, we selected different element sizes in the contact region, which is especially important to define the curvatures of the HA thread properly, see Figure 2. We used 0.015 mm element size for the model of ISO68 threads producing 6500 elements, with a structured mesh; and 0.010 mm element size for the model of HA threads producing 36,000 elements. Mesh sensitivity analyses showed a correct convergence.
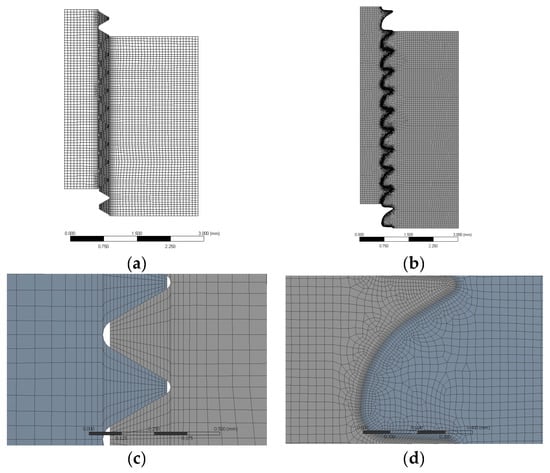
Figure 2.
Drawing of the geometry and mesh defined for the two-dimensional axisymmetric Finite Element (FE) models. Upper panels: general view of threads ISO68 (a) and ISO5845-HA (b). Note that the number of inserted threads is the same in both cases. Lower panels: detailed view of threads ISO68 (c) and ISO5845-HA (d). The scale is now the same and the different size is given by the thread pitch definition.
Contacts were modelled using frictional contacts whose coefficients are defined in Table 1. In addition, augmented Lagrange formulation was used in order to guarantee good convergence as well as low penetration in contacts. We checked that penetration was negligible in comparison with the local deformation values. Because of the high value of the friction coefficient, we used a full Newton method to solve the FE model but additionally applied an unsymmetrical solver to deal with the non-symmetric stiffness matrix. In the case of models where only steel is used, as friction coefficient is lower, the stiffness matrix could be considered symmetric, and the un-symmetrical solver is not needed.

Table 1.
Material properties and friction coefficients for the materials used in the FE model.
The material properties used in the models were defined for the surgical recommended AISI-316 stainless steel with elastic properties. The cortical bone was considered as isotropic following the works [19,20,21,24,26,27,28], which studied cases referring to human and also to animal bones, which are an important research field and source of intense research [29,30]. The thread contacts were defined as frictional type with friction coefficient value 0.1 for steel-steel [15] and 0.37 for bone-steel [31,32]. The material and tribological values used in our work are listed in Table 1.
To define the boundary conditions, a 200 N axial force was applied to the screw while the thread was fixed at its top as shown in Figure 3. This load value produces maximal tensional values in the bone about the material yield stress. We performed tests for ISO68 threads with steel-steel contact, ISO68 threads with steel-bone contact, and ISO5835-HA threads with steel-bone contact.
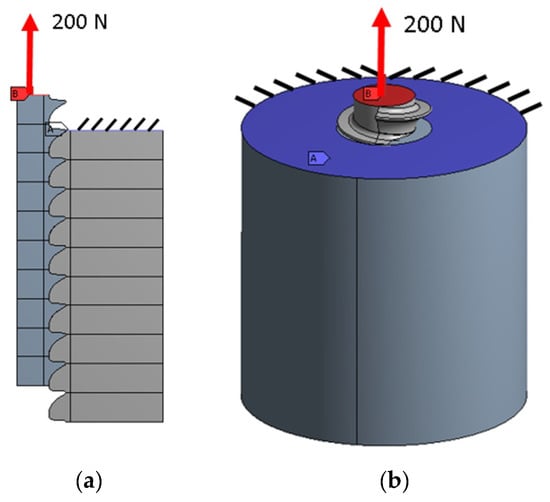
Figure 3.
Boundary conditions (BC) application over two-dimensional model (a) and three-dimensional model (b). The same BC are used in all models and geometries.
The results provided the contact stresses at the thread contact, tensional states and internal deformations. The contact load evaluated at each thread of the joint normalized with respect to the overall of 200 N applied to the screw was then plotted. In order to perform such a computation, we divided the whole contact definition as shown in Figure 4. Thus, one single contact surface for each thread is defined; all of them are defined with the same conditions. Defining contacts separately allows to compute the total load at each thread. Therefore, since contact pressure is computed during the solution process, the integral extended to each contact surface provides the total load supported by the thread. Figure 5 depicts the load normalized with respect to total applied load. As stated [3,4,5], the load of the first thread takes the highest value but it then diminishes continuously through the grip length. There are differences depending on the material combination due the trade-off effects caused by the different rigidities involved. The steel-steel and steel-bone cases differ up to 25% in the higher loads, when comparing the same ISO68 thread. The more compliant bone causes a more even sharing of load between threads. The HA thread causes a slightly higher load than the ISO68 for steel-bone contact but the differences are lower than 5% in the initial threads.
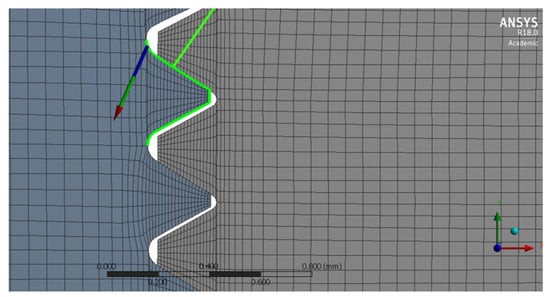
Figure 4.
Contact surface defined to post-process the load per thread values.
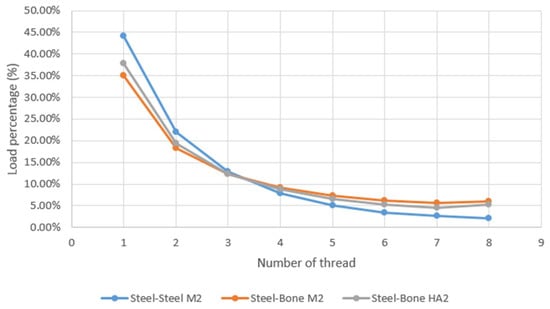
Figure 5.
Force measured on each thread relative to the applied force. This load is defined as the contact reaction on the thread. The results are for threads ISO68 for steel-steel and steel-bone contacts, and for HA thread with steel-bone contact, according to the legend.
A more interesting evaluation for the joint is the stress state caused by the loads. The von Mises stress measured in the bone bulk material was evaluated in a path parallel to the screw axis, at a certain radial distance, and as a function of the depth, see Figure 6. The tensional profile in the bulk material depends on the distance to the joint so different paths were analyzed, located at distances of 0.125 p, 0.25 p and 0.5 p from the outermost diameter of the internal thread, where p is the pitch value. Thus, the stress changes can be evaluated as a function of the depth and radial distance to the joint. The results showed that the stress level decreases when increasing radial position, as was to be expected. Thus, the discussion is focused on one of the distances (0.25 p) for the sake of simplicity, while other results are rather similar. In Figure 6, the stress level along the depth path at radial distance of 0.25 p is plotted. The depth is shown as a function of the pitch for a better comparison of both ISO68 and HA threads.
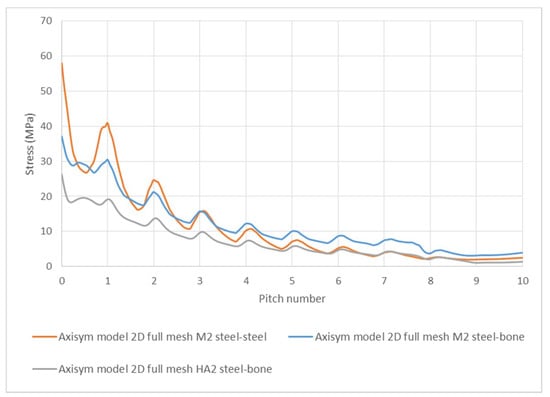
Figure 6.
Von Mises stress along a path in the bone defined parallel to the screw axis and separated 0.25p from the outermost diameter of the internal thread. The lines correspond to the calculations done with a two-dimensional axisymmetric FE model of ISO68 M2 thread with steel-steel and steel-bone contact, and 2mm HA thread with steel-bone contact.
The results show that the decrease of the stress is faster in depth for steel-bone contact than for steel-steel contact. This is caused by the higher compliance of the bone. Indeed, for equivalent size bolts and the same actuating force, the results show a lower stress level for the HA surgical bolts of approximately 40%. This effect is caused by the special design of the HA thread, which is better adapted to work with more compliant materials.
3. Comparison with a Three-Dimensional FE Model
The two-dimensional models may hinder the observation of effects caused by the helical geometry through the thread profile. Some authors have addressed this issue for the UNC-UNF Unified Coarse and Fine pitch threads [15] (both symmetric). However, it is interesting to study the possible effects caused by the asymmetric HA thread. A 3-dimensional FE model of the HA thread geometry was built by using a mesh of linear tetrahedral elements (SOLID185) with element size 0.02 mm at the complex contact regions with about 4.9 × 106 elements, see Figure 7. The materials were steel and bone as previously defined, and the contact definition was a frictional one with friction coefficient values as before, see Table 1. All remaining settings were imposed as in the two-dimensional case to generate a model suitable for comparing with the axisymmetric case.

Figure 7.
Drawing and detail of the screw and plate used for the three-dimensional FE model, showing the complex mesh defined, with a large density at the thread contact region: (a), global mesh view; (b), detailed view near the contact region.
The results of both the two-dimensional and three-dimensional models can be directly compared. The loads per thread slightly change up to 5% in the highest values. In Figure 8 the von Mises stress measured in the bone bulk material in a path parallel to the screw axis, at distance of 0.25 p is plotted. The X axis is measured in mm, where 0.6 is the thread pitch, and the two lines correspond to the results of the two-dimensional and three-dimensional models. The start point in the 3D model was selected to coincide with the 2D model due to the initial location of the helical trajectory. The three-dimensional model values differ by less than 5% at the initial threads, and the profiles mimic each other closely along the path. The profiles showed no important differences, either through the depth or the radial position, comparing paths at distances 0.125 p and 0.5 p. Therefore, the differences for both the load and the stress values are kept within 10% for two-dimensional and three-dimensional models. However, the model definition and computational cost is notably increased for the three-dimensional model, and it will be discussed in Section 5.
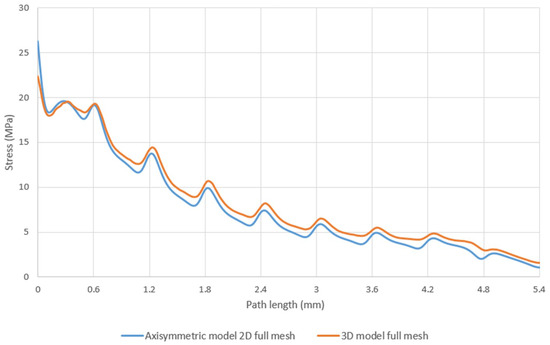
Figure 8.
Von Mises stress along a path in the bone defined parallel to the screw axis and separated 0.25 p from the outermost diameter of the internal thread. The lines correspond to two-dimensional and three-dimensional FE models for a HA 2 mm thread in steel-bone contact.
4. Simplified Bolt Thread Modelling
Considering the previous results obtained with FE models including detailed contacts, the performance of some implemented methods for simplifying joints in software packages can now be compared. ANSYS offers the so-called ‘simplified bolt thread modeling’. It can be applied to two-dimensional and three-dimensional models.
The geometrical definition is rather simple, requiring the definition of two cylinders: one for the screw and the drill hole for the plate. The diameter corresponds to the thread´s mean diameter value. For the mesh, at the ‘contact’ region, the element size must be so that there are at least four elements per pitch. The simplified model requires the input values for mean pitch diameter, pitch and thread angle to characterize the threaded joint at the defined region.
4.1. Comparison of a Symmetric ISO68 Thread
The simplified model is firstly compared with the two-dimensional FE model for the ISO68 thread and steel-bone contact, the materials and contacts defined as above, see Table 1. The simplified model substitutes the M2 screw with a cylinder of thread mean diameter 1.77 mm. The structured mesh was made of rectangular elements (PLANE 152) defined with 10 elements per thread pitch and therefore an element size of 0.04 mm. The recommended value is four elements [25], interpreted as a minimum, but having better detail of the stress maps was preferred. The mesh was built with 432,560 elements. The numerical model input values were the nominal M2 pitch diameter (1.742 mm), pitch (0.4 mm) and thread angle (60°).
The simplified model does not contain geometrical threads and so a straight comparison of load-per-thread is not possible. Instead, we used the stress state measured in the bone part. The stress was measured at paths located at radial distances 0.125 p, 0.25 p and 0.5 p, as described before. In Figure 9 the stress state is shown for the path at 0.25 p, for both the two-dimensional axisymmetric FE model and the simplified model. The threads reappear now in the results provided by the simplified model with clear stress peaks. There is a slight offset of the peak location between the models. This is simply connected to the relative position of the first thread in the two-dimensional model, while it may correspond to some average value in the simplified model. Therefore, this shift is of no interest for further discussions. The stress pattern is rather similar and the peak values differ by no more than 7%. The same behavior and similar values were observed at other radial distances, 0.125 p and 0.5 p.
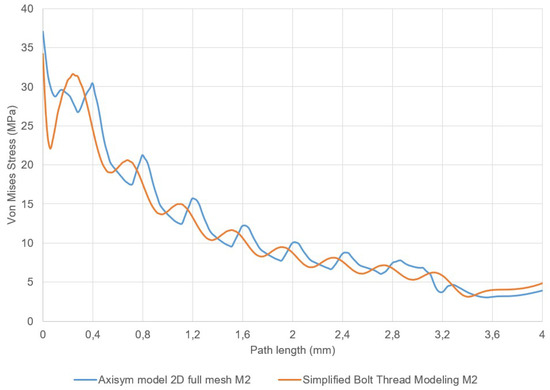
Figure 9.
Stress state (von Mises) along a path in the bone defined parallel to the screw axis and separated 0.25 p from the outermost diameter of the internal thread. The lines correspond to the two-dimensional FE model and the simplified model, for an ISO68 M2 thread in steel-bone contact. Thread pitch is 0.4 mm.
4.2. Comparison of an Asymmetric HA Thread
A second comparison case can be considered for the asymmetric HA threads. The simplified model was defined with values of mean thread diameter 1.65 mm, pitch diameter 1.41 mm and pitch 0.6 mm. The thread angle is not defined for asymmetric geometry. The results were evaluated with input angle values in the range of 35° to 60° and only slight differences were found, affecting the absolute value of the peaks and therefore not affecting the following discussion.
In Figure 10, the von Mises stress at the bone along a path defined at a distance of 0.25 p and thread angle 60° is plotted. The shift between peaks caused by an average effect was again observed, which is of no interest. Both the two-dimensional and the simplified model show the same stress pattern, the results from the simplified model being smoother and providing lower values, up to 8% difference, in the higher stress peaks. The stresses at other radial locations, 0.125 p and 0.5 p, showed similar results.
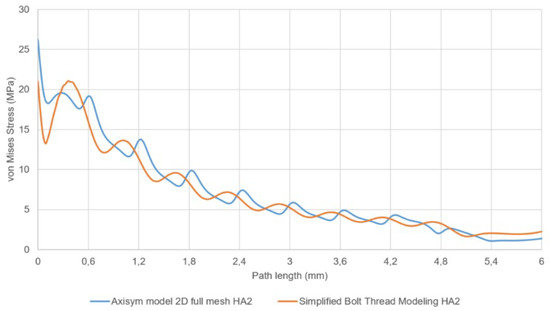
Figure 10.
Von Mises stress along a path in the bone defined parallel to the screw axis and separated 0.25 p from the outermost diameter of the internal thread. The lines correspond to the two-dimensional FE model and the simplified model, for an HA 2 mm thread in steel-bone contact. Thread pitch is 0.6 mm.
The results obtained for ISO68 M2 and HA 2 mm analyzed with the two-dimensional FE model and compared with the simplified model, with the proper parameterization, show deviations of stress of about 7–8%. However, we have found differences up to 40% comparing the stresses caused by threads M2 and HA (see Section 2, Figure 6). The different values defining the model thread parameters: thread diameter, pitch diameter and pitch make possible a proper stress evaluation, despite the fact that the geometry is rather different considering the character of ISO68 (symmetric) and HA (asymmetric) threads.
4.3. Scale Factor Effects
The previous discussions have been developed by using threads of 2 mm diameter as a reference case study. Further analysis can be made of any size-scale effect that may arise when applying the simplified model to other diameter values. We have evaluated the results of a second set of models developed for ISO68 M5 and HA 5 mm threads.
Figure 11 plots the results of stress along a path, similarly defined as before, at distance 0.25 p, the pitch value now being 1.75 mm. In these tests, a force of 500 N was applied. This value is rather low, compared to the case analyzed for 2 mm, in terms of the values of stress state produced. Therefore, the application of the model to different sizes and also different relative loads is tested simultaneously. As shown in the results, the stress state values are again rather similar for both the two-dimensional FE model and the simplified model, with differences in the same range for the higher peaks. Possible effects caused by the size-scale can then be excluded in the application of the simplified model preserving the conditions on mesh size.
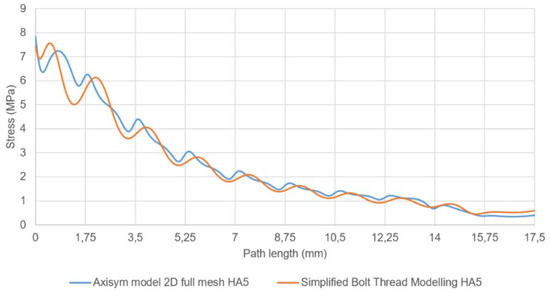
Figure 11.
Von Mises stress along a path in the bone defined parallel to the screw axis and separated 0.25 p from the outermost diameter of the internal thread. The lines correspond to the two-dimensional FE model and the simplified model, for values corresponding to a HA thread of 5 mm in steel-bone contact. Thread pitch is 1.75 mm.
5. Model Definition and Computing Time
When selecting alternative models for the definition of the joints in complex models, an evaluation of the level of time effort needed to build the model and the time required for the calculations is needed, and should be balanced with the quality and confidence of the expected results. These two aspects, time and quality, usually oppose each other. The time needed to build the model will depend on the expertise of the user, and the computing time on the complexity of the model. To compare both times in an objective way, the complexity of the model definition will be treated in this section, and also the computing time for the solver.
On the one hand, the necessities for the model definition will be explained in order of increasing difficulty:
- Simplified bolt thread modelling. Requires the implementation of a simple geometry (cylinder) to define the thread region, and three input parameters. The mesh needs a simple size control based on the pitch value, and easy to define.
- Detailed two-dimensional FE model. The geometry for the contact teeth must be fully defined as a CAD format. The contact regions depend on the number of threads, in this case eight individual contacts. The mesh requires attention: first, a simple size control by pitch, but also customized size controls in the thread edges and the fillets, which implies higher time effort for the definition of the mesh. Indeed, the two-dimensional analysis may not be at all adequate for the overall problem definition.
- Detailed three-dimensional FE models. Again, the geometry must be fully input in CAD format. The contact regions depend on the number of threads, and the individual thread-to-thread contacts. The mesh must be fully customized to obtain smooth transitions at the tiny features. Small element sizes and growing control are needed to have uniform elements, and to avoid deformed elements, which produce inaccurate results.
Therefore, the amount of time and attention required to implement the different options is rather different. The participation of trained personnel becomes critical for defining detailed models in order to apply proper modelling techniques.
On the other hand, the computing time is also a selection parameter. It will depend on the machines used for calculation, as a reference, in Table 2 we compare the time needed for the calculation of the different models developed for this work. The models using a two-dimensional description, either detailed FE models or simplified models, require relatively low calculation times. However, three-dimensional models are much more time demanding. Clearly the model selection will have a major impact on the evaluation of complex models.

Table 2.
CPU (Central Processing Unit) solving time of the models (Intel Core i7-4820K 3.70 GHz, 64 GB RAM).
6. Conclusions
This work has revisited the evaluation of loads and stress distributions caused by threaded joints, in this case focusing on surgical applications. These joints comprise materials of different rigidity (steel and bone) and asymmetric thread geometries. Therefore, the aim was to obtain information of two-dimensional axisymmetric FE models with detailed geometry and contact definitions, and then compare the differences caused by the asymmetric geometry with respect to the well-established symmetric threads. Comparing symmetric (ISO68) and asymmetric (ISO5835-HA) threads of similar diameter, it was found that the load values were quite similar (within 5%) while the stress state can differ up to 30%, with HA favoring the lower stress state values at the bone material. This result, despite being practically applied long ago, cannot be found quantified in any public document to the author’s knowledge.
The comparison of the two-dimensional and three-dimensional FE models showed that the geometrical influence of three-dimensional features is within a 5% limit. This value is beyond the interest for many complex applications. Indeed, the use of two-dimensional models gives an excellent ratio of accuracy in respect to the modeling and computing time.
The use of FE models with multi-joints can easily demand simplification of the joint definitions to obtain a feasible model. The results of detailed FE models were compared with the results provided by a simplified algorithm available in a widespread software tool. Despite the simple implementation of this model, the results differed by no more than 8% with respect to the reference FE models. In this context, it is important to recall the demands of the different options. The definition of very detailed models is time consuming, and the increasing number of elements to be characterized is also a source of errors. Indeed, the computing time is also an important point when selecting an appropriate model. The comparisons made between the different models and cases are useful input information in order to make educated choices from the options when defining threaded joints, considering the accuracy of the output results and the degree of difficulty and time required to build and solve the models.
Author Contributions
Conceptualization and Methodology, J.A.V., J.R.F. and E.C.; Software, Formal Analysis and Data Curation A.S. and J.A.L.-C.; Validation A.S., J.A.L.-C., J.R.F., P.I. and J.A.V.; Supervision J.A.V.; Writing—Original Draft Preparation P.I.; Writing—Review & Editing E.C.; Funding Acquisition J.R.F. and J.A.V.
Funding
This research was partially funded by Xunta de Galicia under the program Grupos de Referencia Competitiva with Ref. GRC2015/16. J.A. López-Campos also acknowledges the funding received from Xunta de Galicia under the program Axudas á etapa predoutoral with Ref. ED481A-2017/045. The work of J.R. Fernández was partially supported by Ministerio de Economía y Competitividad (Spain) under the research project MTM2015-66640-P (with FEDER Funds).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hayes, J.S.; Richards, R.G. The use of titanium and stainless steel in fracture fixation. Expert Rev. Med. Dev. 2010, 7, 843–853. [Google Scholar] [CrossRef] [PubMed]
- Kazmers, N.H.; Fragomen, A.T.; Rozbruch, S.R. Prevention of pin site infection in external fixation: A review of the literature. Strat. Trauma Limb. Reconstr. 2016, 11, 75–85. [Google Scholar] [CrossRef] [PubMed]
- Maduschka, L. Beanspruchung von Schraubenverbindungen und Zweckmäßige Gestaltung der Gewindeträger. Forschung Auf Dem Gebiet Des Ingenieurwesens A 1936, 7, 299–305. [Google Scholar] [CrossRef]
- Sopwith, D.G. The distribution of load in screw threads. Proc. Inst. Mech. Eng. 1948, 159, 373–383. [Google Scholar] [CrossRef]
- Goodier, J.N. The distribution of load on the threads of screws. Trans. ASME 1940, 62, A10–A16. [Google Scholar]
- Wang, W.; Marshek, K.M. Determination of the load distribution in a threaded connector having dissimilar materials and varying thread stiffness. J. Eng. Ind.-Trans. ASME 1995, 117, 1–8. [Google Scholar] [CrossRef]
- Chen, S.; Gao, L.; An, Q. Calculation method of load distribution on pipe threaded connections under tension load. Front. Mech. Eng. 2011, 6, 241–248. [Google Scholar]
- Yamamoto, A. The Theory and Computation of Thread Connection; Youkendo: Tokyo, Japan, 1980; pp. 39–54. (In Japanese) [Google Scholar]
- Heywood, R.B. Tensile fillet stresses in loaded projections. Proc. Inst. Mech. Eng. 1948, 159, 384–391. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure (The Association of German Engineers). Standard VDI 2230: Systematic Calculation of High Duty Bolted Joints; VDI: Berlin, Germnay, 2003. [Google Scholar]
- Grosse, I.R.; Mitchell, L.D. Non-linear axial stiffness characteristic of axisymmetric bolted joint. J. Mech. Des. 1990, 112, 442–449. [Google Scholar] [CrossRef]
- Wileman, J.; Choudhury, M.; Green, I. Computation of member stiffness in bolted connections. J. Mech. Des.-Trans. ASME 1991, 113, 432–437. [Google Scholar] [CrossRef]
- Chaaban, A.; Jutras, M. Static analysis of buttress threads using the finite element method. J. Press. Vessel. Technol. 1992, 114, 209–212. [Google Scholar] [CrossRef]
- Lehnhoff, T.F.; Wistehuff, W.E. Non-linear effects on the stress and deformations of bolted joints. J. Mech. Des. 1996, 118, 54–58. [Google Scholar]
- Chen, J.-J.; Shih, Y.-S. A study of the helical effect on the thread connection by three dimensional finite element analysis. Nucl. Eng. Des. 1999, 191, 109–116. [Google Scholar] [CrossRef]
- Citipitioglu, A.M.; Haj-Ali, R.M.; White, D.W. Refined 3D finite element modelling of partially restrained connections including slip. J. Constr. Steel Res. 2002, 58, 995–1013. [Google Scholar] [CrossRef]
- Ju, S.-H.; Fan, C.-Y.; Wu, G.H. Three dimensional finite elements of steel bolted connections. Eng. Struct. 2004, 26, 403–413. [Google Scholar] [CrossRef]
- Kim, J.; Yoon, J.-C.; Kang, B.-S. Finite element analysis and modelling of structure with bolted joints. Appl. Math. Model. 2007, 31, 895–911. [Google Scholar] [CrossRef]
- Battula, S. Experimental and numerical evaluation of the pull-out strength of self-tapping bone screw in normal and osteoporotic bone. Ph.D. Thesis, University of Akron, Akron, OH, USA, 2007. [Google Scholar]
- Hou, S.-M.; Hsu, C.-C.; Wang, J.L.; Chao, C.-K.; Lin, J. Mechanical tests and finite element models for bone holding power of tibial locking screws. Clin. Biomech. 2004, 19, 738–745. [Google Scholar] [CrossRef] [PubMed]
- Inzana, J.A.; Varga, P.; Windolf, M. Implicit modelling of screw threads for efficient finite element analysis of complex bone-implant systems. J. Biomech. 2016, 49, 1836–1844. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, S.J.; Wyss, U.P.; Pichora, D.R. Finite element stress analysis of a hybrid fracture fixation plate. Med. Eng. Phys. 1996, 18, 241–250. [Google Scholar] [CrossRef]
- Shah, S.; Kim, S.Y.R.; Dubov, A.; Schemitsch, E.H.; Bougherara, H.; Zdero, R. The biomechanics of plate fixation of periprosthetic femoral fractures near the tip of a total hip implant: Cables, screw, or both? Proc. Inst. Mech. Eng. H 2011, 225, 845–856. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Schmutz, B.; Wullschleger, M.; Pearcy, M.J.; Schuetz, M.A. Computational investigation of mechanical failures of internal plate fixation. Proc. Inst. Mech. Eng. H 2010, 224, 119–126. [Google Scholar] [CrossRef] [PubMed]
- ANSYS Inc. Ansys v17 User’s Manual; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Barbosa, P.; Arantes, S.; Domingues, S.; Rezende, R.; Zanetta-Barbosa, D.; Soares, C.J. Measurement of Elastic Modulus and Vickers Hardness of Surround Bone Implant Using Dynamic Microindentation—Parameters Definition. Braz. Dent. J. 2014, 25, 385–390. [Google Scholar]
- Gondret, F.; Larzul, C.; Combes, S.; Rochambeau, H. Carcass composition, bone mechanical properties, and meat quality traits in relation to growth rate in rabbits. J. Anim. Sci. 2005, 83, 1526–1535. [Google Scholar] [CrossRef] [PubMed]
- Perrella, M.; Franciosa, P.; Gerbino, S. FEM and BEM Stress Analysis of Mandibular Bone Surrounding a Dental Implant. Open Mech. Eng. J. 2015, 9, 282–292. [Google Scholar] [CrossRef]
- Wancket, L.M. Animal Models for Evaluation of Bone Implants and Devices. Vet. Pathol. 2015, 52, 842–850. [Google Scholar] [CrossRef] [PubMed]
- Histing, T.; Garcia, P.; Holstein, J.H.; Klein, M.; Matthys, R.; Nuetzi, R.; Steck, R.; Laschke, M.W.; Wehner, T.; Bindl, R.; et al. Small animal bone healing models: Standards, tips, and pitfalls results of a consensus meeting. Bone 2011, 49, 591–599. [Google Scholar] [CrossRef] [PubMed]
- Moazen, M.; Mak, J.H.; Jones, A.C.; Jin, Z.; Wilcox, R.K.; Tsiridis, E. Evaluation of a new approach for modelling the screw-bone interface in a locking plate fixation: A corroboration study. Proc. Int. Mech. Eng. H 2013, 227, 746–756. [Google Scholar] [CrossRef] [PubMed]
- Hayes, W.C.; Perren, S.M. Plate-bone friction in the compression fixation of fractures. Clin. Orthop. Relat. Res. 1972, 89, 236–240. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).