The Characteristic Polynomials of Symmetric Graphs

Abstract

In this paper, we study the way the symmetries of a given graph are reflected in its characteristic polynomials. Our aim is not only to find obstructions for graph symmetries in terms of its polynomials but also to measure how faithful these algebraic invariants are with respect to symmetry. Let p be an odd prime and $\Gamma$ be a finite graph whose automorphism group contains an element h of order p. Assume that the finite cyclic group generated by h acts semi-freely on the set of vertices of $\Gamma$ with fixed set F. We prove that the characteristic polynomial of $\Gamma$, with coefficients in the finite field of p elements, is the product of the characteristic polynomial of the induced subgraph $\Gamma \left[F\right]$ by one of $\Gamma \backslash F$. A similar congruence holds for the characteristic polynomial of the Laplacian matrix of $\Gamma$.

1. Introduction

The purpose of this paper is to address the question of how the symmetries of a graph are reflected in its algebraic invariants. In other words, we study the interaction between the algebraic invariants of a graph and its automorphism group. Indeed, our study will be limited to discussing how the information about graph periodicity is carried by its characteristic polynomials. This question is primarily motivated by the results about knots and spatial graph periodicity obtained in terms of their quantum invariants. We shall start by fixing some notation. Let n be a positive integer and $V=\{v_1,\dots ,v_n\}$ be a finite set. A weight on V is a symmetric function w: $V\times V\to {\mathbb{Z}}_{+}\cup \left\{0\right\}$. The pair $\Gamma =(V,w)$ is called a weighted graph. Indeed, a weighted graph can be seen as a finite graph possibly with multiple edges and loops. In particular, if the graph $\Gamma$ is simple, then the corresponding symmetric function w is defined by $w(u,v)=1$ if u and v are adjacent and 0 otherwise. Throughout this paper, wherever no confusion may arise, we will simplify notation and use the term graph instead of weighted graph. Given a graph $\Gamma$ with vertex set $V=\{v_1,\dots ,v_n\}$, the adjacency matrix of $\Gamma$ is the n-square matrix $A(\Gamma )=\left[w_{ij}\right]$ where $w_{ij}=w(v_i,v_j)$. Since the weight function w is symmetric, so is the matrix $A(\Gamma )$. It is worth mentioning here that while the matrix $A(\Gamma )$ depends on the ordering of the vertices, its characteristic polynomial, defined as $det(x{I}_n-A(\Gamma ))$, is known to be independent of that order. It is denoted hereafter by ${\phi }_{\Gamma }(x)$. On the other hand, if $D(\Gamma )=\left[d_{ij}\right]$ is the degree matrix of $\Gamma$, which is the diagonal n-square matrix defined by $d_{ii}=deg(v_i)$, then the Laplacian matrix of $\Gamma$ is defined by $L(\Gamma )=D(\Gamma )-A(\Gamma )$. The characteristic polynomial of $L(\Gamma )$ is also independent of the ordering of the vertices and is denoted hereafter by ${\psi }_{\Gamma }(x)$. Both polynomials ${\phi }_{\Gamma }(x)$ and ${\psi }_{\Gamma }(x)$ are well-known graph invariants which carry important information about the graph.

An automorphism of a weighted graph $\Gamma$ is a permutation $\sigma$ of the set of vertices V such that for any pair of vertices u and v, we have $w(\sigma (u),\sigma (v))=w(u,v)$. The set of all automorphisms of $\Gamma$ forms a group denoted here by $Aut(\Gamma )$.

Let $p\ge 2$ be an integer. A graph $\Gamma$ is said to be p-periodic if its automorphism group $Aut(\Gamma )$ contains an element h such that $h^p=Id$ and for any vertex v, we have $h^i(v)\ne v$ for all $1\le i\le p-1$. In other words, the finite cyclic group ${\mathbb{Z}}_p$ acts freely on the set of vertices of the graph. A graph $\Gamma$ is said to be semi-free p-periodic if $Aut(\Gamma )$ contains an element h such that $h^p=Id$ and the set of fixed vertices by h is non empty. This set of fixed vertices will be denoted hereafter by F. It is worth mentioning here that for simplicity we will sometimes abuse notation and denote by F the induced subgraph $\Gamma \left[F\right]$ as well. Notice that if $\Gamma$ is semi-free p-periodic then $\Gamma \backslash F$ is p-periodic.

Let r and s be two positive integers. The complete 4-partite graph $K_{r,s,p,p}$ is semi-free p-periodic with fixed subgraph F the complete bipartite graph $K_{r,s}$. The graph $\Gamma \backslash F$ is the complete bipartite graph $K_{p,p}$.

Given a p-periodic weighted graph $\Gamma$, we define its quotient graph $\overline{\Gamma }$ as the weighted graph $(\overline{V},\overline{w})$, where $\overline{V}$ is the quotient set of V under the action of h and $\overline{w}$ is the weight function on $\overline{V}$ defined by ${\displaystyle \overline{w}(\overline{u},\overline{v})=\sum _{i=0}^{p-1}w(u,h^i(v))}$, see [1].

The natural question of how the information about symmetries of graphs are carried by their algebraic invariants has been subject to relatively extensive study. In particular, several results about the characteristic polynomial of periodic graphs and graph coverings in general have been obtained, see [2,3,4] for instance. In [1], the first author suggested a more elementary approach by considering these polynomials with coefficients in the finite field of p elements ${\mathbb{F}}_p$. Actually, he studied the characteristic polynomial of p-periodic graphs and proved that ${\phi }_{\Gamma }(x)$ is determined by the characteristic polynomial of the quotient graph $\overline{\Gamma }$. More precisely, ${\phi }_{\Gamma }(x)\equiv {\phi }_{\overline{\Gamma }}(x^p)in{\mathbb{F}}_p\left[x\right]$. Furthermore, the polynomial ${\psi }_{\Gamma }(x)$ is divisible by $x^p$ in ${\mathbb{F}}_p\left[x\right]$. Other necessary conditions for a graph to be p-periodic have been also obtained in terms of the Tutte polynomial and its generalizations [1,5]. In this paper, we discuss the case of semi-free actions and show that some similar congruences hold.

Theorem 1.

Let p be an odd prime and Γ be a semi-free p-periodic graph with a fixed subgraph F. Then the following congruences hold in ${\mathbb{F}}_p\left[x\right].$

$${\phi }_{\Gamma }(x)\equiv {\phi }_F(x){\phi }_{\Gamma \backslash F}(x)\equiv {\phi }_F(x){\phi }_{\overline{\Gamma \backslash F}}(x^p).$$

Example 1.

The complete 4-partite graph $K_{2,2,3,3}$ admits a semi-free action of ${\mathbb{Z}}_3$, with the 4 vertices of degree 8 fixed. Hence $F=K_{2,2}$ and $\Gamma \backslash F=K_{3,3}$. Computations of the characteristic polynomials show that ${\phi }_{K_{2,2,3,3}}(x)=-108x^6-120x^7-37x^8+x^{10}$, ${\phi }_{K_{2,2}}(x)=-4x^2+x^4$ and ${\phi }_{K_{3,3}}(x)=-9x^4+x^6$. Thus, the congruences given in Theorem 1 hold modulo 3.

Theorem 2.

Let p be an odd prime and Γ be a semi-free p-periodic graph with a fixed subgraph F. Then ${\psi }_{\Gamma }(x)$ is divisible by ${\psi }_F(x)$ with quotient in ${\mathbb{F}}_p\left[x^p\right]$.

Example 2.

For the complete 4-partite graph $K_{2,2,3,3}$, we have modulo 3: ${\psi }_{K_{2,2,3,3}}(x)\equiv 2x+2x^2+x^3+2x^5+x^6+2x^8+x^9+x^{10}$; ${\psi }_{K_{2,2}}(x)\equiv 2x+2x^2+x^3+x^4$ and ${\psi }_{K_{3,3}}(x)\equiv x^6$. It can be easily checked that ${\psi }_{K_{2,2,3,3}}(x)\equiv {\psi }_{K_{2,2}}(x){\psi }_{K_{3,3}}(x-1)$ modulo 3. Hence, the condition given by Theorem 2 is satisfied.

2. Block Circulant Matrices

In this section we will introduce block circulant matrices and briefly explain how to compute their characteristic polynomials. More details can be found in [6]. Let p and s be two positive integers. For $0\le i\le p-1$, let $A_i$ be a s-square matrix. The block circulant matrix $C=C(A_0,\dots ,A_{p-1})$ is the $ps$-square matrix of the form:

$$\left[\begin{array}{ccccc}{A}_0& A_1& A_2& \cdots & A_{p-1}\\ A_{p-1}& A_0& A_1& \cdots & A_{p-2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ A_1& A_2& A_3& \cdots & A_0\end{array}\right].$$

The characteristic polynomial of the circulant matrix C, with coefficients in the finite filed ${\mathbb{F}}_p$, satisfies the following property.

Lemma 1.

Let p be an odd prime and $C=C(A_0,\dots ,A_{p-1})$ be a block circulant matrix. Then, ${\phi }_C(x)\in {\mathbb{F}}_p\left[x^p\right]$.

Proof. 

Let $\zeta$ be a $p^{th}$ primitive root of unity. For $0\le k\le p-1$, we define the s-square matrix ${\displaystyle T_k=\sum _{j=0}^{p-1}{\zeta }^{kj}{A}_j}$. Let ${\phi }_{T_k}(x)$ denotes the characteristic polynomial of the matrix $T_k$. The characteristic polynomial of the circulant matrix C is ${\displaystyle {\phi }_C(x)=\prod _{k=0}^{p-1}{\phi }_{T_k}(x)}$, see [6]. Since p is prime, the following homomorphism is well defined:

$$\begin{array}{cccc}\hfill f_p:& \mathbb{Z}\left[\zeta \right]\hfill & ⟶\hfill & {\mathbb{Z}}_p\hfill \\ & \sum n_i{\zeta }^i\hfill & ⟼\hfill & \overline{\sum n_i}.\hfill \end{array}$$

Furthermore, it extends to a homomorphism of rings $f_p:\mathbb{Z}\left[\zeta \right]\left[x\right]⟶{\mathbb{Z}}_p\left[x\right]$. Notice that for all $0\le k\le p-1$ we have $f_p({\phi }_{T_k}(x))=f_p({\phi }_{T_0}(x))$. Thus $f_p({\phi }_C(x))=f_p{({\phi }_{T_0}(x))}^p$. In conclusion, ${\phi }_C(x)$ is congruent to ${\phi }_{T_0}(x^p)$ modulo p. This completes the proof of the lemma. □

Let $\Gamma$ be a semi-free p-periodic graph with fixed set of vertices F. Assume that F is made up of r vertices $u_1,u_2,\dots ,u_r$. Since p is prime and $\Gamma \backslash F$ is p-periodic, the finite cyclic group ${\mathbb{Z}}_p=<h>$ acts freely on the set of vertices of $\Gamma \backslash F$. This set splits into a partition made up of s orbits, where s is the number of vertices of the quotient graph $\overline{\Gamma \backslash F}$. Since the action is free and p is prime, each orbit is made up of exactly p elements. Let us label the vertices of $\overline{\Gamma \backslash F}$ as $v_1,\dots ,v_s$. Let $\pi$ be the canonical surjection from $V\backslash F$ to $\overline{V\backslash F}$. We label the elements of ${\pi }^{-1}(v_i)$ as $v_i^0,\dots ,v_i^{p-1}$, so that $h(v_i^k)=v_i^{k+1}$ if $0\le k<p-1$ and $h(v_i^{p-1})=v_i^0$. The order of the vertices of $\overline{\Gamma \backslash F}$ extends to a natural order of the vertices of $\Gamma \backslash F$, namely, $v_1^0,v_2^0,\dots ,v_s^0,v_1^1,v_2^1,\dots ,v_s^1,v_1^2,\dots ,v_s^{p-1}$. Notice that for all $1\le i\le r$, $1\le k,k^{\prime }\le s$ and $0\le j\le p-1$, we have:

1.

$w(u_i,h^m(v_k^j))=w(u_i,v_k^j)$,

2.

$w(h^m(v_{k^{\prime }}^0),h^m(v_k^j))=w(v_{k^{\prime }}^0,v_k^j)$.

Consequently, if we consider the order of the vertices of $\Gamma$ obtained by placing the vertices of F first then those of $\Gamma \backslash F$ in the order described above, then the adjacency matrix of $\Gamma$ is of the following form:

$$A(\Gamma )=\left[\begin{array}{ccccc}A(F)& R& R& \cdots & R\\ R^t& A_0& A_1& \cdots & A_{p-1}\\ R^t& A_{p-1}& A_0& \cdots & A_{p-2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ R^t& A_1& A_2& \cdots & A_0\end{array}\right],$$

where $A(F)$ denotes the adjacency matrix of the subgraph F, R is an $r\times s$-matrix and for $0\le i\le p-1$, $A_i$ is a s-square matrix. Notice that the block circulant sub-matrix $(A_0,A_1,\dots ,A_{p-1})$ is indeed the adjacency matrix of the periodic graph $\Gamma \backslash F$. For instance the adjacency matrix of the semi-free 3-periodic graph displayed in Figure 1 is of the form.

$$\left[\begin{array}{ccccccc}0& 1& 0& 1& 0& 1& 0\\ 1& 0& 2& 0& 0& 0& 1\\ 0& 2& 0& 1& 1& 0& 1\\ 1& 0& 1& 0& 2& 0& 0\\ 0& 0& 1& 2& 0& 1& 1\\ 1& 0& 0& 0& 1& 0& 2\\ 0& 1& 1& 0& 1& 2& 0\end{array}\right].$$

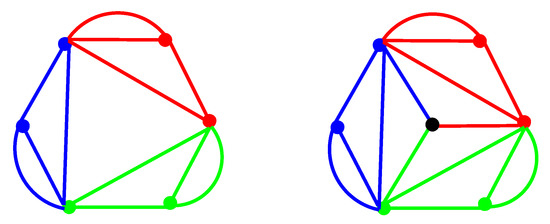
Figure 1. A 3-periodic graph (left) and a semi-free 3-periodic graph with a fixed vertex (right).

The adjacency matrix of the semi-free 3-periodic graph $K_{2,2,3,3}$, see Figure 2, can be written in the form:

$$\left[\begin{array}{cccccccccc}0& 0& 1& 1& 1& 1& 1& 1& 1& 1\\ 0& 0& 1& 1& 1& 1& 1& 1& 1& 1\\ 1& 1& 0& 0& 1& 1& 1& 1& 1& 1\\ 1& 1& 0& 0& 1& 1& 1& 1& 1& 1\\ 1& 1& 1& 1& 0& 1& 0& 1& 0& 1\\ 1& 1& 1& 1& 1& 0& 1& 0& 1& 0\\ 1& 1& 1& 1& 0& 1& 0& 1& 0& 1\\ 1& 1& 1& 1& 1& 0& 1& 0& 1& 0\\ 1& 1& 1& 1& 0& 1& 0& 1& 0& 1\\ 1& 1& 1& 1& 1& 0& 1& 0& 1& 0\end{array}\right].$$

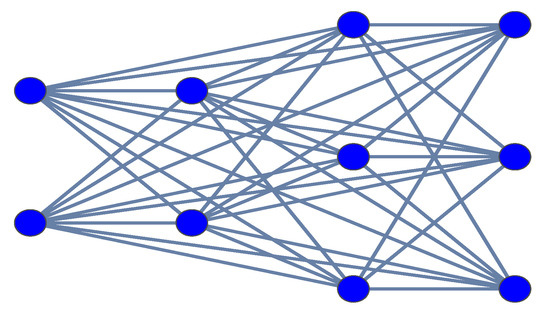
Figure 2. The complete 4-partite graph $K_{2,2,3,3}$.

3. Proofs

We will first prove Theorem 1. The proof of Theorem 2 will be based on similar arguments. Let us compute the characteristic polynomial of $\Gamma$, $det(A(\Gamma )-x{I}_n)$ by expanding with respect to the first row. The basic observation here is that since $w(u_1,h^m(v_k^j))=w(u_1,v_k^j)$ for $1\le m\le p$, the co-factors corresponding to each of these p entries are equal. Hence their contribution to the value of $det(A(\Gamma )-x{I}_n)$ will add to zero modulo p. We will prove that for the co-factors which correspond to deleting the first row of $A(\Gamma )$ and the columns $r+1,r+s+1,\dots ,r+(p-1)s+1$ of $A(\Gamma )$. The sub-matrices obtained by such operations will be denoted hereafter by ${\Delta }_{r+1},{\Delta }_{r+s+1},\dots ,{\Delta }_{r+(p-1)s+1}$, respectively. These sub-matrices are displayed below.

${\Delta }_{r+1}=\left[\begin{array}{ccccc}A(F)& S^{\prime }& S& \cdots & S\\ R^t& A_0^{\prime }& A_1& \cdots & A_{p-1}\\ R^t& A_{p-1}^{\prime }& A_0& \cdots & A_{p-2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ R^t& A_1^{\prime }& A_2& \cdots & A_0\end{array}\right]$, ${\Delta }_{r+s+1}=\left[\begin{array}{ccccc}A(F)& S& S^{\prime }& \cdots & S\\ R^t& A_0& A_1^{\prime }& \cdots & A_{p-1}\\ R^t& A_{p-1}& A_0^{\prime }& \cdots & A_{p-2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ R^t& A_1& A_2^{\prime }& \cdots & A_0\end{array}\right]$,

…, ${\Delta }_{r+(p-1)s+1}=\left[\begin{array}{ccccc}A(F)& S& S& \cdots & S^{\prime }\\ R^t& A_0& A_1& \cdots & A_{p-1}^{\prime }\\ R^t& A_{p-1}& A_0& \cdots & A_{p-2}^{\prime }\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ R^t& A_1& A_2& \cdots & A_0^{\prime }\end{array}\right]$

where, S is the matrix obtained from R by deletion of the first row. Moreover, if M is a matrix, then we denote by $M^{\prime }$ the matrix obtained from M by deletion of the first column.

Let us explain how to transform the first matrix ${\Delta }_{r+1}$ into ${\Delta }_{r+s+1}$ using elementary operations on rows and columns. These operations are known to keep the determinant unchanged up to a sign. First, we interchange column $r+i$ and $r+s+i$ for all $1\le i\le s-1$, then we apply $s-1$ column interchanges to move column $r+2s-1$ to column $r+s$, our matrix is then transformed into:

$\left[\begin{array}{ccccc}A(F)& S& S^{\prime }& \cdots & S\\ R^t& A_1& A_0^{\prime }& \cdots & A_{p-1}\\ R^t& A_0& A_{p-1}^{\prime }& \cdots & A_{p-2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ R^t& A_2& A_1^{\prime }& \cdots & A_0\end{array}\right].$

Now, we shall rearrange rows using elementary row operations. Indeed, using $(p-1)s$ interchanges of rows we will be able to transform our matrix into:

$\left[\begin{array}{ccccc}A(F)& S& S^{\prime }& \cdots & S\\ R^t& A_2& A_1^{\prime }& \cdots & A_0\\ R^t& A_1& A_0^{\prime }& \cdots & A_{p-1}\\ R^t& A_0& A_{p-1}^{\prime }& \cdots & A_{p-2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ \Gamma \end{array}\right].$

By interchanging column $r+i$ and column $r+p(s-1)+i-1$, for $1\le i\le s$, we obtain:

$\left[\begin{array}{ccccc}A(F)& S& S^{\prime }& \cdots & S\\ R^t& A_0& A_1^{\prime }& \cdots & A_2\\ R^t& A_{p-1}& A_0^{\prime }& \cdots & A_1\\ R^t& A_{p-2}& A_{p-1}^{\prime }& \cdots & A_0\\ ⋮& ⋮& ⋮& ⋮& ⋮\end{array}\right]$

Finally, we can perform $(p-3)s$ column operations to rearrange the matrix into the desired form:

$$\left[\begin{array}{ccccc}A(F)& S& S^{\prime }& \cdots & S\\ R^t& A_0& A_1^{\prime }& \cdots & A_{p-1}\\ R^t& A_{p-1}& A_0^{\prime }& \cdots & A_{p-2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ R^t& A_1& A_2^{\prime }& \cdots & A_0\end{array}\right].$$

Notice that the total number of rows and columns interchanges performed to transform ${\Delta }_{r+1}$ into ${\Delta }_{r+s+1}$ is $2(s-1)+(p-1)s+s+(p-3)s=2(s-1)+(2p-3)s$. Thus $|{\Delta }_{r+1}{|=(-1)}^s\left|{\Delta }_{r+s+1}\right|.$ Similarly, one can show that $|{\Delta }_{r+1}{|=(-1)}^{ms}\left|{\Delta }_{r+ms+1}\right|$, for $1\le m\le p-1$. It can be easily checked that

$${(-1)}^{r+1}{w}_{1r+1}|{\Delta }_{r+1}{|=(-1)}^{r+1+s}{w}_{1r+s+1}|{\Delta }_{r+s+1}{|=\cdots =(-1)}^{r+(p-1)s+1}{w}_{1r+s+1}\left|{\Delta }_{r+(p-1)s+1}\right|.$$

Hence, the contributions of these p sub-matrices to the value of the determinant add to zero modulo p. Consequently, to compute the ${\phi }_{\Gamma }(x)$ modulo p, one may consider only the co-factors corresponding to entries in the first row of F. With an elementary induction argument on the size of F, we can prove that ${\phi }_{\Gamma }(x)\equiv {\phi }_F(x){\phi }_{\Gamma \backslash F}(x)$ modulo p. Notice that since $\Gamma \backslash F$ is a p-periodic graph, we have ${\phi }_{\Gamma \backslash F}(x)\equiv {\phi }_{\overline{\Gamma \backslash F}}(x^p)$ modulo p, as proven in [1]. This completes the proof of Theorem 1.

The proof of Theorem 2 is also based on the study of block circulant matrices. Using the order of the vertices described above, the Laplacian matrix of $\Gamma$ is of the form:

$$L(\Gamma )=\left[\begin{array}{ccccc}l(F)& M& M& \cdots & M\\ M^t& B_0& B_1& \cdots & B_{p-1}\\ M^t& B_{p-1}& B_0& \cdots & B_{p-2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ M^t& B_1& B_2& \cdots & B_0\end{array}\right],$$

where $l(F)$ is an r-square matrix, M is an $r\times s$-matrix and for $0\le i\le p-1$, $B_i$ is a s-square matrix. In a similar way, we can prove that $det(L(\Gamma )-x{I}_n)$ is the product of $det(l(F)-x{I}_n)$ by $det(C(B_0,\dots ,B_{p-1})-x{I}_n)$. On the other hand, it can be easily seen that $l(F)$ and $L(F)$ coincide out of the diagonal. Furthermore, for any i, the diagonal entries are congruent modulo p, $d_{ii}(l(F))\equiv d_{ii}(L(F))$ modulo p. Thus, $det(l(F)-x{I}_n)\equiv det(L(F)-x{I}_n)$ modulo p. Consequently, ${\psi }_F(x)$ divides ${\psi }_{\Gamma }(x)$ in ${\mathbb{F}}_p\left[x\right]$.

Finally, by Lemma 1 $det(C(B_0,\dots ,B_{p-1})-x{I}_n)$ is a polynomial on $x^p$. This ends the proof of Theorem 2.

4. Conclusions

By using elementary properties of block circulant matrices, we established two obstruction criteria for a graph to be symmetric. More precisely, we proved that if a given graph $\Gamma$ is semi-free p-periodic with set of fixed vertices F, then its characteristic polynomial, with coefficients reduced modulo p, is the product of the characteristic polynomial of the induced subgraph $\Gamma \left[F\right]$ by the one of $\Gamma \backslash F$. We also proved that the characteristic polynomial of the Laplacian matrix of a semi-free p-periodic graph satisfies a similar necessary condition.