Abstract
In this paper, we study the way the symmetries of a given graph are reflected in its characteristic polynomials. Our aim is not only to find obstructions for graph symmetries in terms of its polynomials but also to measure how faithful these algebraic invariants are with respect to symmetry. Let p be an odd prime and be a finite graph whose automorphism group contains an element h of order p. Assume that the finite cyclic group generated by h acts semi-freely on the set of vertices of with fixed set F. We prove that the characteristic polynomial of , with coefficients in the finite field of p elements, is the product of the characteristic polynomial of the induced subgraph by one of . A similar congruence holds for the characteristic polynomial of the Laplacian matrix of .
1. Introduction
The purpose of this paper is to address the question of how the symmetries of a graph are reflected in its algebraic invariants. In other words, we study the interaction between the algebraic invariants of a graph and its automorphism group. Indeed, our study will be limited to discussing how the information about graph periodicity is carried by its characteristic polynomials. This question is primarily motivated by the results about knots and spatial graph periodicity obtained in terms of their quantum invariants. We shall start by fixing some notation. Let n be a positive integer and be a finite set. A weight on V is a symmetric function w: . The pair is called a weighted graph. Indeed, a weighted graph can be seen as a finite graph possibly with multiple edges and loops. In particular, if the graph is simple, then the corresponding symmetric function w is defined by if u and v are adjacent and 0 otherwise. Throughout this paper, wherever no confusion may arise, we will simplify notation and use the term graph instead of weighted graph. Given a graph with vertex set , the adjacency matrix of is the n-square matrix where . Since the weight function w is symmetric, so is the matrix . It is worth mentioning here that while the matrix depends on the ordering of the vertices, its characteristic polynomial, defined as , is known to be independent of that order. It is denoted hereafter by . On the other hand, if is the degree matrix of , which is the diagonal n-square matrix defined by , then the Laplacian matrix of is defined by . The characteristic polynomial of is also independent of the ordering of the vertices and is denoted hereafter by . Both polynomials and are well-known graph invariants which carry important information about the graph.
An automorphism of a weighted graph is a permutation of the set of vertices V such that for any pair of vertices u and v, we have . The set of all automorphisms of forms a group denoted here by .
Let be an integer. A graph is said to be p-periodic if its automorphism group contains an element h such that and for any vertex v, we have for all . In other words, the finite cyclic group acts freely on the set of vertices of the graph. A graph is said to be semi-free p-periodic if contains an element h such that and the set of fixed vertices by h is non empty. This set of fixed vertices will be denoted hereafter by F. It is worth mentioning here that for simplicity we will sometimes abuse notation and denote by F the induced subgraph as well. Notice that if is semi-free p-periodic then is p-periodic.
Let r and s be two positive integers. The complete 4-partite graph is semi-free p-periodic with fixed subgraph F the complete bipartite graph . The graph is the complete bipartite graph .
Given a p-periodic weighted graph , we define its quotient graph as the weighted graph , where is the quotient set of V under the action of h and is the weight function on defined by , see [1].
The natural question of how the information about symmetries of graphs are carried by their algebraic invariants has been subject to relatively extensive study. In particular, several results about the characteristic polynomial of periodic graphs and graph coverings in general have been obtained, see [2,3,4] for instance. In [1], the first author suggested a more elementary approach by considering these polynomials with coefficients in the finite field of p elements . Actually, he studied the characteristic polynomial of p-periodic graphs and proved that is determined by the characteristic polynomial of the quotient graph . More precisely, . Furthermore, the polynomial is divisible by in . Other necessary conditions for a graph to be p-periodic have been also obtained in terms of the Tutte polynomial and its generalizations [1,5]. In this paper, we discuss the case of semi-free actions and show that some similar congruences hold.
Theorem 1.
Let p be an odd prime and Γ be a semi-free p-periodic graph with a fixed subgraph F. Then the following congruences hold in
Example 1.
The complete 4-partite graph admits a semi-free action of , with the 4 vertices of degree 8 fixed. Hence and . Computations of the characteristic polynomials show that , and . Thus, the congruences given in Theorem 1 hold modulo 3.
Theorem 2.
Let p be an odd prime and Γ be a semi-free p-periodic graph with a fixed subgraph F. Then is divisible by with quotient in .
Example 2.
For the complete 4-partite graph , we have modulo 3: ; and . It can be easily checked that modulo 3. Hence, the condition given by Theorem 2 is satisfied.
2. Block Circulant Matrices
In this section we will introduce block circulant matrices and briefly explain how to compute their characteristic polynomials. More details can be found in [6]. Let p and s be two positive integers. For , let be a s-square matrix. The block circulant matrix is the -square matrix of the form:
The characteristic polynomial of the circulant matrix C, with coefficients in the finite filed , satisfies the following property.
Lemma 1.
Let p be an odd prime and be a block circulant matrix. Then, .
Proof.
Let be a primitive root of unity. For , we define the s-square matrix . Let denotes the characteristic polynomial of the matrix . The characteristic polynomial of the circulant matrix C is , see [6]. Since p is prime, the following homomorphism is well defined:
Furthermore, it extends to a homomorphism of rings . Notice that for all we have . Thus . In conclusion, is congruent to modulo p. This completes the proof of the lemma. □
Let be a semi-free p-periodic graph with fixed set of vertices F. Assume that F is made up of r vertices . Since p is prime and is p-periodic, the finite cyclic group acts freely on the set of vertices of . This set splits into a partition made up of s orbits, where s is the number of vertices of the quotient graph . Since the action is free and p is prime, each orbit is made up of exactly p elements. Let us label the vertices of as . Let be the canonical surjection from to . We label the elements of as , so that if and . The order of the vertices of extends to a natural order of the vertices of , namely, . Notice that for all , and , we have:
- 1.
- ,
- 2.
- .
Consequently, if we consider the order of the vertices of obtained by placing the vertices of F first then those of in the order described above, then the adjacency matrix of is of the following form:
where denotes the adjacency matrix of the subgraph F, R is an -matrix and for , is a s-square matrix. Notice that the block circulant sub-matrix is indeed the adjacency matrix of the periodic graph . For instance the adjacency matrix of the semi-free 3-periodic graph displayed in Figure 1 is of the form.
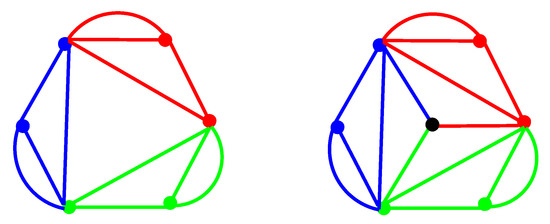
Figure 1.
A 3-periodic graph (left) and a semi-free 3-periodic graph with a fixed vertex (right).
The adjacency matrix of the semi-free 3-periodic graph , see Figure 2, can be written in the form:
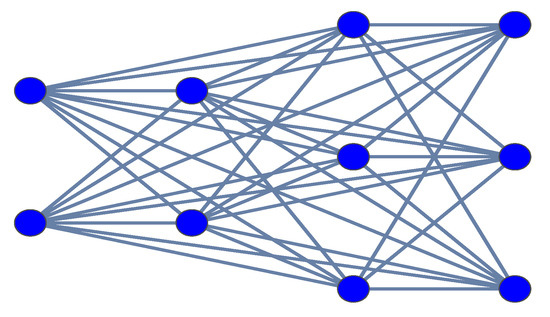
Figure 2.
The complete 4-partite graph .
3. Proofs
We will first prove Theorem 1. The proof of Theorem 2 will be based on similar arguments. Let us compute the characteristic polynomial of , by expanding with respect to the first row. The basic observation here is that since for , the co-factors corresponding to each of these p entries are equal. Hence their contribution to the value of will add to zero modulo p. We will prove that for the co-factors which correspond to deleting the first row of and the columns of . The sub-matrices obtained by such operations will be denoted hereafter by , respectively. These sub-matrices are displayed below.
where, S is the matrix obtained from R by deletion of the first row. Moreover, if M is a matrix, then we denote by the matrix obtained from M by deletion of the first column.
| , , |
| …, |
Let us explain how to transform the first matrix into using elementary operations on rows and columns. These operations are known to keep the determinant unchanged up to a sign. First, we interchange column and for all , then we apply column interchanges to move column to column , our matrix is then transformed into:
Now, we shall rearrange rows using elementary row operations. Indeed, using interchanges of rows we will be able to transform our matrix into:
By interchanging column and column , for , we obtain:
Finally, we can perform column operations to rearrange the matrix into the desired form:
Notice that the total number of rows and columns interchanges performed to transform into is . Thus Similarly, one can show that , for . It can be easily checked that
Hence, the contributions of these p sub-matrices to the value of the determinant add to zero modulo p. Consequently, to compute the modulo p, one may consider only the co-factors corresponding to entries in the first row of F. With an elementary induction argument on the size of F, we can prove that modulo p. Notice that since is a p-periodic graph, we have modulo p, as proven in [1]. This completes the proof of Theorem 1.
The proof of Theorem 2 is also based on the study of block circulant matrices. Using the order of the vertices described above, the Laplacian matrix of is of the form:
where is an r-square matrix, M is an -matrix and for , is a s-square matrix. In a similar way, we can prove that is the product of by . On the other hand, it can be easily seen that and coincide out of the diagonal. Furthermore, for any i, the diagonal entries are congruent modulo p, modulo p. Thus, modulo p. Consequently, divides in .
Finally, by Lemma 1 is a polynomial on . This ends the proof of Theorem 2.
4. Conclusions
By using elementary properties of block circulant matrices, we established two obstruction criteria for a graph to be symmetric. More precisely, we proved that if a given graph is semi-free p-periodic with set of fixed vertices F, then its characteristic polynomial, with coefficients reduced modulo p, is the product of the characteristic polynomial of the induced subgraph by the one of . We also proved that the characteristic polynomial of the Laplacian matrix of a semi-free p-periodic graph satisfies a similar necessary condition.
Author Contributions
Conceptualization, N.C.; Investigation, S.A.D., M.Y.T. and A.A.E.A.; Software, S.A.D., M.Y.T. and A.A.E.A.; Supervision, N.C.; Writing-review and editing, N.C.
Funding
This research was funded by United Arab Emirates University, Summer Undergraduate Research Experience (SURE PLUS) Grant .
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chbili, N. Graph polynomials and symmetries. J. Algebra Appl. 2018. [Google Scholar] [CrossRef]
- Feng, R.; Kwak, J.H.; Lee, J. Characteristic polynomials of graph coverings. Bull. Austral. Math. Soc. 2004, 69, 133–136. [Google Scholar] [CrossRef]
- Lee, J.; Kim, H.K. Characteristic polynomials of graphs having a semi-free action. Linear Algebra Appl. 2000, 307, 35–46. [Google Scholar] [CrossRef]
- Wang, K. Characteristic polynomials of symmetric graphs. Linear Algebra Appl. 1983, 51, 121–125. [Google Scholar] [CrossRef]
- Chbili, N. A note on the Tutte polynomial and automorphism group of a graph. Asian Eur. J. Math. 2014, 7, 1450001. [Google Scholar] [CrossRef]
- Friedman, B. Eigenvalues of composite matrices. Math. Proc. Camb. Philos. Soc. 1961, 57, 37–49. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).