Abstract
This paper explores numerically the benefits of water discharge prediction in the real time control (RTC) of water distribution networks (WDNs). An algorithm aimed at controlling the settings of control valves and variable speed pumps, as a function of pressure head signals from remote nodes in the network, is used. Two variants of the algorithm are considered, based on the measured water discharge in the device at the current time and on the prediction of this variable at the new time, respectively. As a result of the prediction, carried out using a polynomial with coefficients determined through linear regression, the RTC algorithm attempts to correct the expected deviation of the controlled pressure head from the set point, rather than the currently measured deviation. The applications concerned the numerical simulation of RTC in a WDN, in which the nodal demands are reconstructed stochastically through the bottom-up approach. The results prove that RTC benefits from the implementation of the prediction, in terms of the closeness of the controlled variable to the set point and of total variations of the device setting. The benefits are more evident when the water discharge features contained random fluctuations and large hourly variations.
1. Introduction
Nowadays, water utility managers often choose to perform active pressure control in their water distribution networks (WDNs) due to the many associated benefits [1], which include leakage and pipe burst reduction and the extension of network infrastructure useful life [2]. Another benefit of pressure control lies in the possibility of recovering energy from the WDN through turbines or similar devices [3,4]. After the WDN is subdivided in pressure zones [5], active pressure control requires a suitable pressure control device to be installed in the pipe(s) connecting each pressure zone to its source(s). Recent studies have proven that active pressure control can be more cost effective when the device setting is controlled in real time, in order to meet WDN demand variations in time [6]. In this context, the device controlled in real time can be a pressure control valve [7] or a variable speed pump [8], depending on whether the source node is under pressure surplus or deficit conditions compared to the pressure zone it feeds.
Remote real time control (RTC) is a kind of control in which the pressure head is monitored at remote critical node(s) in the WDN. By making use of suitable algorithms operating on the pressure head measurements, a programmable logic controller sets the new suitable device setting to maintain the minimum desired pressure at the remote node(s). In the scientific literature of WDNs, the first study on service pressure RTC was carried out by Campisano et al. [9], followed by many others [10,11,12,13,14,15]. Whereas the proportional algorithms of Campisano et al. [9,10,12] only used the pressure head measurement at the critical node, Creaco and Franchini [11] set up a more effective algorithm that also makes use of the water discharge measurement in the pipe fitted with the control device. Like the algorithm used by Campisano et al. [9,10,12], the algorithm of Creaco and Franchini [11] has a parameter that needs to be tuned to ensure the maximum regulation performance. Later, a parameter-less algorithm with only slightly worse performance than the algorithm of Creaco and Franchini [11] was proposed for the RTC of control valves [13] and variable speed pumps [14]. The algorithm of Page et al. [13,14] has the novel aspect of making use of the water discharge prediction in the pipe fitted with the control device. The prediction is carried out through water discharge measurements at small temporal steps (smaller than the RTC temporal step, which has order of magnitude of some minutes). However, a limit of this approach lies in the fact that it is effective only if the water discharge trend is smooth.
In this work, the water discharge prediction is implemented in a refined version of the algorithm of Creaco and Franchini [11]. Unlike the work of Page et al. [13,14], the prediction method operates on larger temporal steps than the control temporal step. Therefore, it is able to cope with the irregular trend of the pipe water discharge at fine temporal scale, due to the random nature of demand [15,16]. To show this, a stochastic bottom-up approach is used for nodal demand reconstruction in the applications, which concern the numerical simulation of RTC in a WDN.
2. Materials and Methods
In the following subsections, first the algorithm proposed by Creaco and Franchini [11] for control valve regulation is summarized, followed by its extension to variable speed pumps. Then, a novel upgrade of the algorithm is proposed, to include prediction at the new time. In both the cases of control valve and variable speed pump, the device setting is regulated in such a way to bring the pressure head at the control node close to the desired set point value. This node is selected as that which features the lowest pressure head among all the nodes sensitive to valve regulation [9].
2.1. Control Valve Regulation
The algorithm is described with reference to the schematic on the left side of Figure 1, in which a control valve is positioned in a pipe upstream from the control node B. At current time t1 (s), let the water discharge in the pipe, temporally averaged over the control temporal step Δt (s), be equal to Q (m3/s). The valve closure setting is then assumed to be equal to α1 (-), which can range from 0 (fully open valve) to 1 (fully closed valve). If ξ(α) is the valve curve, ξ1 (-) is the local head loss coefficient associated with α1. As shown in [5], the corresponding local head loss Δh1 (m) is then equal to:
where A (m2) is the pipe inner cross section area and g = 9.81 m/s2 is the gravity acceleration. In the downstream pipe end B, a temporally averaged pressure head value hB (m), far from the set point value hsp (m) by a quantity e (m), is observed. Incidentally, positive and negative values of e indicate larger and smaller values of hB (m) than hsp, respectively.
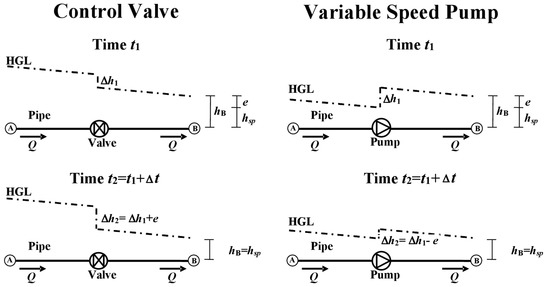
Figure 1.
Schematic for the description of the operation of logic controller for the control valve (left) and for the variable speed pump (right): situation at the current (above) and new (below) times. HGL stands for head grade line.
In order to bring the pressure head at node B close to the value hsp at new time t2 (s) (with t2 = t1 + Δt), the valve has to be regulated in such a way that the new head loss Δh2 (m) is equal to:
By making use of the relationship between head loss and head loss coefficient in Equation (1) and considering Equation (2), the head loss coefficient ξ2 (-) at time t2 has to be equal to:
which can be rewritten as:
In order to be able to tune the promptness of the control algorithm as well as to account for the fact that the system in Figure 1 is a simplified representation of a WDN, a correction coefficient K (-) is inserted in Equation (4), yielding the following Equation (5):
Indeed, coefficient K enables modulating the pressure head deviation e to correct. By using the relationship α(ξ) of the control valve, the valve setting α2 corresponding to ξ2 can be easily obtained. The setting variation from α1 to α2 has to be limited by the maximum correction allowed by the valve shutter velocity [9].
2.2. Variable Speed Pump Regulation
The algorithm is described with reference to the schematic on the right side of Figure 1, in which a variable speed pump is positioned in a pipe upstream from the control node B. At current time t1, let the water discharge in the pipe, temporally averaged over the temporal step Δt, be equal to Q. If β1 (-), which can range from 0 (pump speed equal to 0) to 1 (maximum pump speed), is the current speed setting for the pump, the head Δh1 provided by the pump is obtained through the pump curve:
where a (s2/m5), b (s/m2) and c (m) are the pump curve coefficients. Equation (6) was obtained by considering that a second order curve can fit effectively the curve data of head and water discharge from pump catalogues, and by applying the affinity laws for pumps [5].
Let the temporally averaged pressure head hB in the downstream pipe end B be far from the set point value hsp by a quantity e.
In order to bring the piezometric height at node B close to the value hsp at new time t2, the pump has to be regulated in such a way that the head is equal to:
An estimate for the new pump setting β2 (-) can then be calculated starting from the following equation, derived from Equation (7) and from Equation (6):
The positive solution for β2 in the previous equation is:
A corrective coefficient K is introduced in this case as well, so that the formula for the estimation of the new pump setting is:
The setting variation from β1 to β2 has to be limited by the maximum correction allowed by the variable speed drive.
2.3. Algorithm Refinement through State Prediction
As described in the sections above, variables Q and e appearing in Equations (5) and (10) are estimated at current time t1. However, the algorithm can be improved if it is aimed at eliminating the expected pressure head deviation at new time t2, rather than at eliminating the pressure head deviation at current time t1. Therefore, reference should be made to the predicted water discharge Qforecast [m3/s] and deviation eforecast [m]. Qforecast is the predicted water discharge at the new time; eforecast, instead, is the deviation that would be expected at time t2 if no setting variations were made from time t1.
Unlike Page et al. [13,14], no water discharge measurements inside the control temporal step Δt are used in this work for water discharge prediction. This choice was made because the water discharge features, at small temporal scale, not negligible random fluctuations [15,16] that can distort the prediction. These fluctuations are due to the random nature of demand [15,16]. A further risk connected to the use of discharge measurements at small temporal scale, that is below the control temporal step Δt, is the presence of not temporally averaged measurement errors. Therefore, a prediction algorithm is set up to estimate Qforecast, based on the value of the water discharge at time t1 and at other previous times. At time t1, based on the series of temporally averaged values Q = Q(t1), Q(t1 − Δt), Q(t1 − 2Δt), …, Q(t1 − (N − 1)Δt) derived from the available measurements, a regression is carried out to evaluate a smooth (fluctuation-free) trend of Q in the time interval from time t1 − (N − 1)Δt to time t1, with the following second order polynomial:
where coefficients r1 (m3/s) r2 (m3/s2) and r3 (m3/s3) are derived through the application of linear regression [17]. This polynomial is used for calculating Qforecast, that is Q(t2 = t1 + Δt).
At this stage, a caveat has to be made about the number N (-) of water discharge measurements to consider for estimating the coefficients of the polynomial in Equation (11). Indeed, this represents the number N of measurements that must be stored inside the logic controller to make the prediction. To estimate coefficients r1, r2 and r3, a value of N ≥ 3 must be considered. Incidentally, for r = 3, no best fit has to be searched for since only one parabola passes through three points. At each case study, an ad hoc analysis should be performed to understand the best window size N. As an explicative example of the prediction algorithm, let us consider a water discharge prediction at time t1, in the context of RTC with Δt = 180 s (see graphs in Figure 2, in which dots and lines represent the measured values of Q and the polynomials obtained through regression, respectively). As graph a) highlights, if the water discharge trend is smooth (regular trend of the dots), as is the case with the aggregation of stochastically reconstructed demands from very numerous users, N = 3 already gives excellent prediction results. When the trend features visible random fluctuations (irregular trend of the dots), as is the case with the aggregation of stochastically reconstructed demands from few users (e.g., see Figure 2b), a larger value of N has to be considered to obtain a polynomial that reflects reliably the global temporal trend of Q, though failing to catch its random fluctuations. A small value of N (e.g., N = 3), instead, makes the water discharge prediction too dependent on random fluctuations. At each case study, the optimal window size must be assessed with the objective to maximize the overall performance of water discharge prediction and, therefore, of RTC. In this context, the closeness of the controlled variable to the set point can be considered as an indicator of the RTC performance for the choice of N, as is shown in Appendix A.
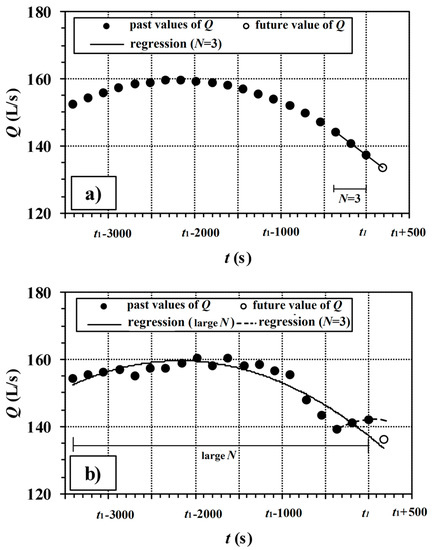
Figure 2.
Example of application of the polynomial regression method for water discharge prediction in smooth (a) and irregular (b) demand trends.
As for eforecast, which is associated with Qforecast, the two following expressions can be used in the case of control valve or variable speed pump, respectively:
The formulas in Equations (12) and (13) reflect how the pressure head at the critical node is expected to vary if the water discharge in the device changes from the value Q to the value Qforecast, in the absence of device setting variations. Potentially, two additional terms could be inserted in the right side of the expressions (12) and (13): the former associated with the predicted pressure-head variation upstream from the device (i.e., at the source) from time t1 to time t2; the latter associated with the predicted head loss variation in the WDN from time t1 to time t2. However, these terms are neglected in the present work because they are usually smaller than the contribution related to the variation in head loss (Equation (12)) or in head gain (Equation (13)) across the device. Furthermore, the assessment of these terms would require other variables to be monitored in the WDN. Ultimately, the presence of the corrective term K in Equation (5) and in Equation (10) enables taking account of all the effects not explicitly considered in the analysis.
3. Results
The applications concerned the numerical simulation of a network in Northern Italy, which serves about 30,000 inhabitants and has already been used for research in the field of pressure control [6,11,15]. The skeletonized layout is reported in Figure 3.
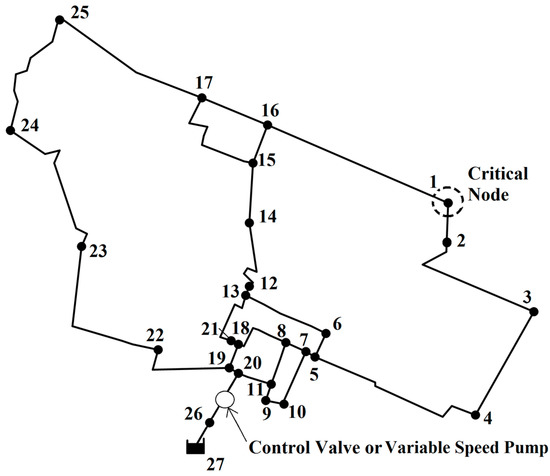
Figure 3.
Water distribution network considered for the applications.
The network has a single source node, 26 demanding nodes with ground elevation of 0 m a.s.l. and 32 pipes. The uniform ground elevation and the size make the network eligible for being considered as a single pressure zone.
More details about characteristics of the pipes, in terms of pipes and length, can be found in the referenced work.
Two scenarios were considered hereinafter. In scenario 1, the source node is considered to have a constant head of 40 m a.s.l. Furthermore, a DN350 plunger control valve is inserted in pipe 26-11, which connects the source node to the rest of the network. The valve curve ξ(α) considered for the plunger valve has the following form [10]:
where c1 = 0.75 and c2 = 3.25 are the coefficients calculated to best fit the data provided by a valve manufacturer. In Equation (14), α was allowed to range from 0 (fully open) to 0.95 (almost fully closed).
In scenario 2, the source node is considered to have a constant head of 1 m a.s.l. and a variable speed pump is inserted in pipe 26-11. The curve used for this device is the following:
with β allowed to range from 0.5 (minimum speed) to 1 (maximum speed).
In both scenarios, the critical node of the network, which features the lowest pressure head values along the day, is node 1. Therefore, node 1 was selected as control node. The RTC of the control valve and of the variable speed pump, in scenarios 1 and 2, respectively, was carried out to bring the pressure head at the control node to set point value hsp = 25 m.
For each node, the demand trend was obtained through the bottom-up approach by applying the methodology described in [15,16], which is based on demand pulse generation through the Poisson model. In the present work, the same pulse features as those associated with Dutch households with two to three inhabitants (reported in [16]), in terms of duration, intensity, and duration/intensity correlation, were considered. After being generated for five consecutive days and for all the network nodes, the demand pulses were aggregated over Δt = 180 s long temporal steps, to correspond to the temporal step adopted for RTC and for the extended period simulation [18] of the network. At this stage, a remark must be made about the choice of Δt = 180 s as control temporal step for RTC. In fact, this choice was made based on the findings in [15], which proved that 180 s guarantees the best trade-off between closeness of the controlled variable to the set point and number of actuator setting variations in this case study.
Each instant of network operation was simulated through the global gradient algorithm [19]. Incidentally, the combination of extended period simulation with nodal demands reconstructed with the bottom-up approach at medium temporal steps represents the best combination to simulate the behavior of RTC [15] and WDNs [16] in real time, in the trade-off between accuracy of the results and computational efficiency.
At each node and at each instant of simulation, the outflow to the users was evaluated with the pressure-driven approach through the Wagner et al. [20] formula, taking hsp as the pressure head for full demand satisfaction at all nodes. Furthermore, leakage qleak (m3/s) was related to the nodal pressure head h through the Tucciarelli et al. [21] formula:
where ∑L (m) is the total length of the pipes connected to the node. Furthermore, αleak (m2−γ/s) and γ (-) are the leakage coefficient and exponent, respectively. While γ depends on pipe material and leak opening shape [22], αleak depends on the number of leak openings along the pipe and then grows with pipe age. In this work, these parameters were assumed uniform over the network. γ was set to 1 (typical value for plastic pipes) while αleak was set to 9.4 × 10−9 m/s in order to have in the first scenario a leakage percentage rate close to 20% of the total outflow from the source, in the case of fully open control valve.
The total network demand D (L/s) trend at the Δt = 180 s temporal scale obtained with the bottom-up reconstruction is reported in graph a) in Figure 4 and Figure 5 for the five consecutive days of network operation. These graphs show that, despite the spatial and temporal aggregation, demand random fluctuations are still present, especially under low demand conditions. Furthermore, each daily trend of demand is slightly different from the others. These aspects are due to the stochastic method used for demand generation, which obtains nodal demands as the superimposition of demand pulses [15,16], consistently with real WDNs.
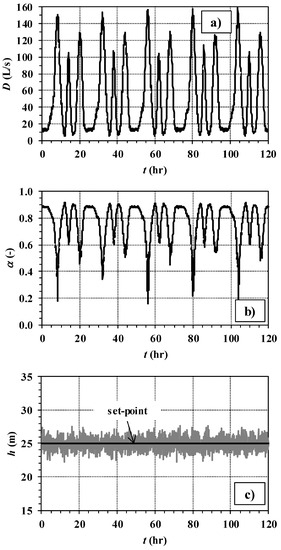
Figure 4.
Real time control (RTC) of control valve through LCb. In the five days of network operation, trends of total network demand (a), device setting (b) and controlled pressure head (c).
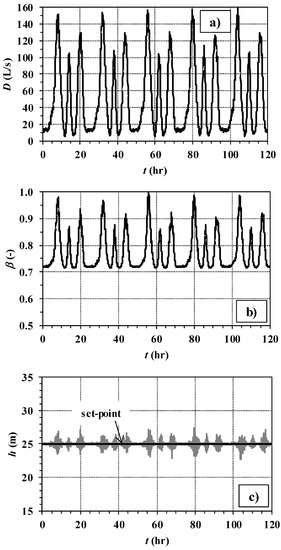
Figure 5.
RTC of variable speed pump through LCb. In the five days of network operation, trends of total network demand (a), device setting (b) and controlled pressure head (c).
For analyzing the performance of RTC, two indices were used. The former, indicated as mean|e|, concerns the closeness of the controlled variable at the generic i-th time, that is the pressure head hi at the control node, to the set point value hsp. It is calculated as:
where Ntot = 2400 is the number of temporal steps Δt in the five days of simulation.
The latter index, indicated as ∑|Δα| and ∑|Δ β| for the control valve and for the variable speed pump, respectively, is representative of the total variations of the device setting. In the two scenarios, it is calculated as:
where αi and β i are the values of valve setting α and pump setting β, respectively, at the generic i-th time. Generally speaking, a good controller is expected to keep the controlled variable close to the set point with small device setting variations, to avoid the wear of the control device. Therefore, it will feature a low value of both indices.
For both control valves (Equation (5)) and pumps (Equation (10)), the coefficient K of the logic controller was calibrated in such a way as to minimize mean|e|.
Globally, 4 simulations were carried out: simulations 1a and 1b, associated with scenario 1, and simulations 2a and 2b, associated with scenario 2. Simulations 1a and 2a were carried out considering the original RTC algorithm of Creaco and Franchini [11] with no water discharge prediction, hereinafter indicated as LCa (logic controller a). In simulations 1b and 2b, the refined RTC algorithm fitted with the water discharge prediction, hereinafter indicated as LCb (logic controller b), was used. In the application, the polynomial regression useful for the demand prediction was carried out on N = 20 time instants, following a preliminary analysis the results of which are reported in Appendix A.
The setting variation speed of both the control valve and the variable speed pump was set in such a way as to allow the maximum setting variation (0–0.95 and 0.5–1 for the former and the latter device, respectively) inside the control temporal step Δt = 180 s.
The results of the simulations in terms of optimal K, mean|e| and ∑|Δα| are reported in Table 1 and Table 2 for the control valve and the variable speed pump, respectively.

Table 1.
Results of simulations 1a and 1b related to scenario 1 (control valve), in terms of mean|e| and ∑|Δα| for the optimal value of K. LCa (logic controller a); LCb (logic controller b).

Table 2.
Results of simulations 2a and 2b related to scenario 2 (variable speed pump), in terms of mean|e| and ∑|Δβ| for the optimal value of K. LCa (logic controller a); LCb (logic controller b).
The results in Table 1 highlight, for the control valve controlled in real time, the superiority of LCb, in terms of both mean|e| and ∑|Δα|. In fact, accounting for the water discharge prediction enabled the controlled variable to stay, on average, closer to the set point with smaller control valve setting variations.
The results in Table 2 highlights, also for the variable speed pump controlled in real time, the better performance of LCb.
Other results of simulations 1b and 2b (with LCb) are reported in Figure 4 and Figure 5, respectively. In either Figure, graphs b and c report the trend of the device setting and of the controlled pressure head, respectively. Graph b) in Figure 4 shows, as expected, that the control valve tends to open (lower values of α, down to about 0.2) in correspondence to the morning, midday and evening demand peaks. Outside the peaks, instead, the control valve tends to close (higher values of α, up to about 0.9), in order to cause larger local head losses. Only minor oscillations are observed in the valve setting trend. Graph c shows that h is, on average, always close to the set point. However, up to 2.5 m large overshooting and undershooting are remarked. These oscillations take place due to the imperfect effectiveness of the prediction method. In fact, as was remarked above with reference to Figure 2b, the prediction method is not able to catch the random fluctuations of the water discharge, though being able to detect its overall trend.
In this context, it has to be stressed that it is unfeasible to totally eliminate the random oscillations of the pressure head at a remote node. In fact, this would require the prediction/time step to be reduced. However, the control time step cannot be reduced below a threshold value, which accounts for signal propagation from the control node to the valve, as was stated in [15].
The graphs in Figure 5 show that, contrary to α, the pump speed ratio β tends to increase during demand peaks and to decrease under low demand conditions. Furthermore, in the case of the variable speed pump, the oscillations of the controlled variable are smaller, especially under low demand conditions. This can be explained as follows. If we consider, for an assigned value of water discharge Q, the device settings bringing the controlled pressure head to the set point, a variation in Q, like that associated with a demand fluctuation, tends to produce a smaller change in terms of Δh for the pump (Equation (6)) than for the valve (Equation (1)). In other words, the pump tends to dampen the effects of water discharge variations better than the valve, especially under low-demand conditions (which require high valve closures and low pump speeds).
A sensitivity analysis is then carried out to investigate if the superiority of LCb persists when other values are used for the parameters in the bottom-up generation of nodal pulsed demands. In new simulations performed with the control valve, the pulse parameters associated with the Milford households [23] were used (see [16] for more details on the values of these parameters). Furthermore, a flatter trend was considered for the demand pattern throughout the day, leading to the total demand D shown in Figure 6a, where demand fluctuations are more evident than in Figure 4a and Figure 5a. The optimization of parameter K yielded, for both LCa and LCb, the optimal value of 0.3, in correspondence to which the two algorithms produce an almost identical value of mean|e| = 0.8. However, LCb is still superior in terms of ∑|Δα| (9.42 for LCb vs. 11.09 for LCa). Graphs b and c in Figure 6 show the trend of the valve closure setting and of the controlled pressure head for LCb under conditions of modified demand.
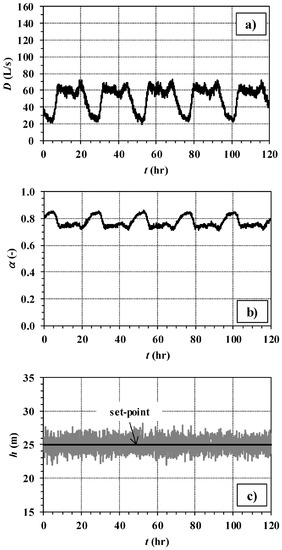
Figure 6.
RTC of control valve through LCb under conditions of modified demand. In the five days of network operation, trends of total network demand (a), device setting (b) and controlled pressure head (c).
Overall, the advantages of LCb are less evident in the case of the modified pulse parameter values, due to the more evident presence of random fluctuations, uncaptured by the water discharge prediction method (see Figure 2), in the total network demand (compare Figure 6a with Figure 4a and Figure 5a). This entails that, ceteribus paribus, the benefits of LCb will be more evident when the random fluctuations of demand are small compared to its hourly variations. Otherwise, the benefits of LCb will decrease due to the worse effectiveness of the prediction.
4. Conclusions
In this paper, two variants of the logic controller of [11] were numerically applied to the RTC of control valves and variable speed pumps, namely, its original version and the novel version fitted with the prediction of the water discharge through the device. Thanks to this prediction, the algorithm attempts to correct the expected deviation of the remotely controlled pressure head from the set point at the new time, rather than the measured one at the current time. In this work, water discharge prediction was carried out using a polynomial function constructed starting from the measured water discharges in the previous time instants. The results showed that this simple prediction method can represent the global temporal trend of the water discharge, even when nodal demands feature random fluctuations due to the stochastic reconstruction through the bottom-up approach. As a result, the performance of the RTC algorithm benefits from the implementation of the water discharge prediction method in terms of closeness of the controlled variable to the set point and of total variations of the device setting. The benefits stand out above all when the random fluctuations of demand are small compared to its hourly variations.
Future work will be dedicated to the setup of more complicated prediction methods, such as those based on probabilistic concepts. By enabling proper interpretation and representation of the random water discharge fluctuations, which arise because of the random nature of demand, these methods are expected to improve the effectiveness of the prediction and, as a result, the performance of RTC. Future work will also be dedicated to testing the RTC algorithms in other case studies, to explore the influence of network size and topography on the algorithm effectiveness.
Furthermore, in another development of this work, a different kind of device regulation will be used, which will consider an acceptable range of pressure heads at the critical node, rather than a single set point. This is expected to reduce the number of actuator setting variations and, ultimately, to extend the useful life of the device.
Acknowledgments
This research was conducted using the funds supplied by the University of Pavia.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
A preliminary analysis was carried out to select the optimal window size N on which to apply the regression in Equation (11). In this analysis, algorithm LCb was applied to the five days of network operation considering values of N ranging from 3 to 30. For each simulation in the analysis, mean|e| was calculated. The graph in Figure A1 reports the trend of mean|e| as a function of N (window size). The curve has a minimum at N = 20, indicating that, in the present case study, this is the optimal size of the window used for the prediction. This value was then adopted for all the simulations with LCb in the paper. However, as highlighted in the section entitled “Materials and Methods”, the optimal value of N may be different in different case studies from that considered in this paper. Furthermore, it is expected to vary as a function of the control temporal step Δt. Therefore, an ad hoc analysis should be performed for assessing this parameter in each case study.
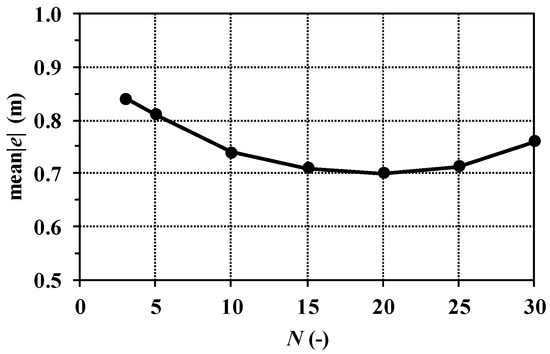
Figure A1.
Trend of mean|e| as a function of the window size N used for water discharge prediction.
References
- Farley, M.; Trow, S. Losses in Water Distribution Networks; IWA: London, UK, 2003. [Google Scholar]
- Vicente, D.; Garrote, L.; Sánchez, R.; Santillán, D. Pressure Management in Water Distribution Systems: Current Status, Proposals, and Future Trends. J. Water Resour. Plan. Manag. 2016, 142, 04015061. [Google Scholar] [CrossRef]
- Fecarotta, O.; Aricò, C.; Carravetta, A.; Martino, R.; Ramos, H.M. Hydropower Potential in Water Distribution Networks: Pressure Control by PATs. Water Resour. Manag. 2014, 29, 699–714. [Google Scholar] [CrossRef]
- Sinagra, M.; Sammartano, V.; Morreale, G.; Tucciarelli, T. A new device for pressure control and energy recovery in water distribution networks. Water 2017, 9, 309. [Google Scholar] [CrossRef]
- Walski, M.; Chase, D.; Savic, D.; Grayman, W.; Beckwith, S.; Koelle, E. Advanced Water Distribution Modelling and Management; Haestad: Waterbury, CT, USA, 2003. [Google Scholar]
- Creaco, E.; Walski, T. Economic Analysis of Pressure Control for Leakage and Pipe Burst Reduction. J. Water Resour. Plan. Manag. 2017, 143, 04017074. [Google Scholar] [CrossRef]
- Fontana, N.; Giugni, M.; Glielmo, L.; Marini, G. Real Time Control of a PRV in Water Distribution Networks for Pressure Regulation: Theoretical Framework and Laboratory Experiments. J. Water Resour. Plan. Manag. 2018, 144, 04017075. [Google Scholar] [CrossRef]
- Walski, T.; Creaco, E. Selection of Pumping Configuration for Closed Water Distribution Systems. J. Water Resour. Plan. Manag. 2016, 142, 04016009. [Google Scholar] [CrossRef]
- Campisano, A.; Creaco, E.; Modica, C. RTC of valves for leakage reduction in water supply networks. J. Water Resour. Plan. Manag. 2010, 136, 138–141. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C.; Vetrano, L. Calibration of proportional controllers for the RTC of pressures to reduce leakage in water distribution networks. J. Water Resour. Plan. Manag. 2012, 138, 377–384. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M. A new algorithm for the real time pressure control in water distribution networks. Water Sci. Technol. Water Supply 2013, 13, 875–882. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C.; Reitano, S.; Ugarelli, R.; Bagherian, S. Field-Oriented Methodology for Real-Time Pressure Control to Reduce Leakage in Water Distribution Networks. J. Water Resour. Plan. Manag. 2016, 142, 04016057. [Google Scholar] [CrossRef]
- Page, P.R.; Abu-Mahfouz, A.M.; Yoyo, S. Parameter-Less Remote Real-Time Control for the Adjustment of Pressure in Water Distribution Systems. J. Water Resour. Plan. Manag. 2017, 143, 04017050. [Google Scholar] [CrossRef]
- Page, P.R.; Abu-Mahfouz, A.M.; Mothetha, M.L. Pressure Management of Water Distribution Systems via the Remote Real-Time Control of Variable Speed Pumps. J. Water Resour. Plan. Manag. 2017, 143, 04017045. [Google Scholar] [CrossRef]
- Creaco, E.; Campisano, A.; Franchini, M.; Modica, C. Unsteady Flow Modeling of Pressure Real-Time Control in Water Distribution Networks. J. Water Resour. Plan. Manag. 2017, 143, 04017056. [Google Scholar] [CrossRef]
- Creaco, E.; Pezzinga, G.; Savic, D. On the choice of the demand and hydraulic modeling approach to WDN real-time simulation. Water Resour. Res. 2017, 53. [Google Scholar] [CrossRef]
- Freedman, D.A. Statistical Models: Theory and Practice; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Todini, E. A more realistic approach to the ‘extended period simulation’ of water distribution networks. In Proceedings of the Computing and Control for the Water Industry 2003, London, UK, 15–17 September 2003. [Google Scholar] [CrossRef]
- Todini, E.; Pilati, S. A gradient algorithm for the analysis of pipe networks. In Computer Application in Water Supply, System Analysis and Simulation; Coulbeck, B., Choun-Hou, O., Eds.; John Wiley & Sons: London, UK, 1988; Volume 1, pp. 1–20. [Google Scholar]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water distribution reliability: Simulation methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef]
- Tucciarelli, T.; Criminisi, A.; Termini, D. Leak Analysis in Pipeline System by Means of Optimal Value Regulation. J. Hydraul. Eng. 1999, 125, 277–285. [Google Scholar] [CrossRef]
- Van Zyl, J.E.; Cassa, A.M. Modeling elastically deforming leaks in water distribution pipes. J. Hydraul. Eng. 2013, 140, 182–189. [Google Scholar] [CrossRef]
- Buchberger, S.G.; Carter, J.T.; Lee, Y.H.; Schade, T.G. Random Demands, Travel Times and Water Quality in Dead-Ends; AWWARF Rep. No. 294; American Water Works Association Research Foundation: Denver, CO, USA, 2003. [Google Scholar]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).