Abstract
Constructed ponds and wetlands are widely used in urban areas for stormwater management, ecological conservation, and pollution treatment. The treatment efficiency of these systems is strongly related to the hydrodynamics and hydraulic residence time. In this study, we developed a physical model and used rhodamine-WT as a tracer to conduct flume experiments. An equivalent Reynolds number was assumed, and the flume was a 1/25-scale model. Emergent obstructions (EOs), submerged obstructions (SOs), and high- and low-density emergent vegetation were placed along the sides of the flume, and 49 tracer tests were performed. We altered the density, spatial extent, aspect ratio, and configurations of the obstructions and emergent vegetation to observe changes in the hydraulic efficiency of a deep-water wetland. In the cases of low-aspect-ratio obstructions, the effects of the EOs on the hydraulic efficiency were significantly stronger than those of the SOs. In contrast, in the cases of high-aspect-ratio obstructions, the improvement effects of the EOs were weaker than those of the SOs. The high-aspect-ratio EOs altered the flow direction and constrained the water conveyance area, which apparently caused a short-circuited flow phenomenon, resulting in a decrease in hydraulic efficiency. Most cases revealed that the emergent vegetation improved the hydraulic efficiency more than the EOs. The high-density emergent vegetation (HEV) improved the hydraulic efficiency more than the low-density emergent vegetation (LEV). Three cases involving HEV, two cases involving LEV, and one case involving EOs attained a good hydraulic efficiency (λ > 0.75). To achieve greater water purification, aquatic planting in constructed wetlands should not be overly dense. The HEV configuration in case 3-1 achieved optimum hydraulic performance for compliance with applicable water treatment standards.
1. Introduction
Wetlands process nutrients via siltation, absorption, and chemical or biological decomposition. These processes are significantly impacted by flow conditions and related residence times [1]. In addition, the residence time is highly correlated with the effectiveness of contaminant treatment [2]. Determining the treatment efficiency of wetlands can be helped by understanding the flow dynamics of water through a wetland [3]. The treatment efficiency can be improved by manipulating the hydraulic regime to improve the hydraulic efficiency [4,5]. Preferential flow, short-circuited flow, circular flow, and dead zones can reduce the treatment efficiency of wetlands [6,7]. These undesirable conditions result in low flow uniformity and low hydraulic efficiency [8]. Wetlands with emergent vegetation are significantly more efficient than wetlands with submerged vegetation and non-vegetated wetlands at removing nitrogen and salt [9]. Mathematical models have been used to simulate various densities, spatial extent, and orientations of obstructions in constructed wetlands [8]. The results indicated that the density and extent of the obstructions were positively correlated with the hydraulic efficiency. However, tracer experiments revealed several peak values of tracer concentration indicative of varied flow paths, particularly in the presence of emergent vegetation [10]. The tracer response curves with vegetation were inaccurate when utilizing mathematical models because they did not take into account the dispersion effects caused by vegetation [8]. Therefore, we performed tracer experiments to compare a wetland with various configurations of emergent obstructions (EOs), submerged obstructions (SOs), and high- and low-density emergent vegetation (EV); the residence time distribution (RTD) was obtained, and the hydraulic efficiency was calculated. In addition, we assessed how various aspect ratios and configurations of EOs, SOs, and EVs affected the flow conditions and whether they resulted in “good hydraulic efficiency (λ > 0.75)” [11].
2. Methods
2.1. Study Area
The study area was a farm pond located in Taoyuan County, Northern Taiwan (Figure 1a). The upstream section of the wetland was designed to hold shallow water with a meandering flow (called the Taiji area). The downstream section is a large area of deeper, open water, and it was suggested that the hydraulic performance of this deeper section could be improved [12]. In this study, we developed a flume experiment with tracer tests to study the effects of obstructions and vegetation on the hydraulic efficiency in the deeper downstream section.
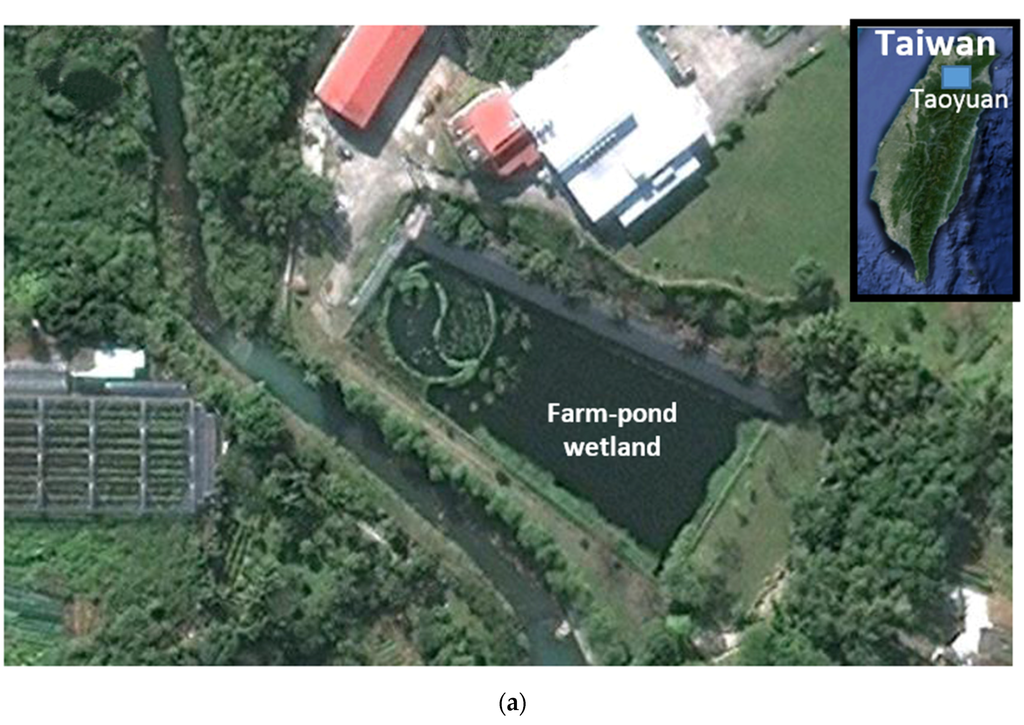
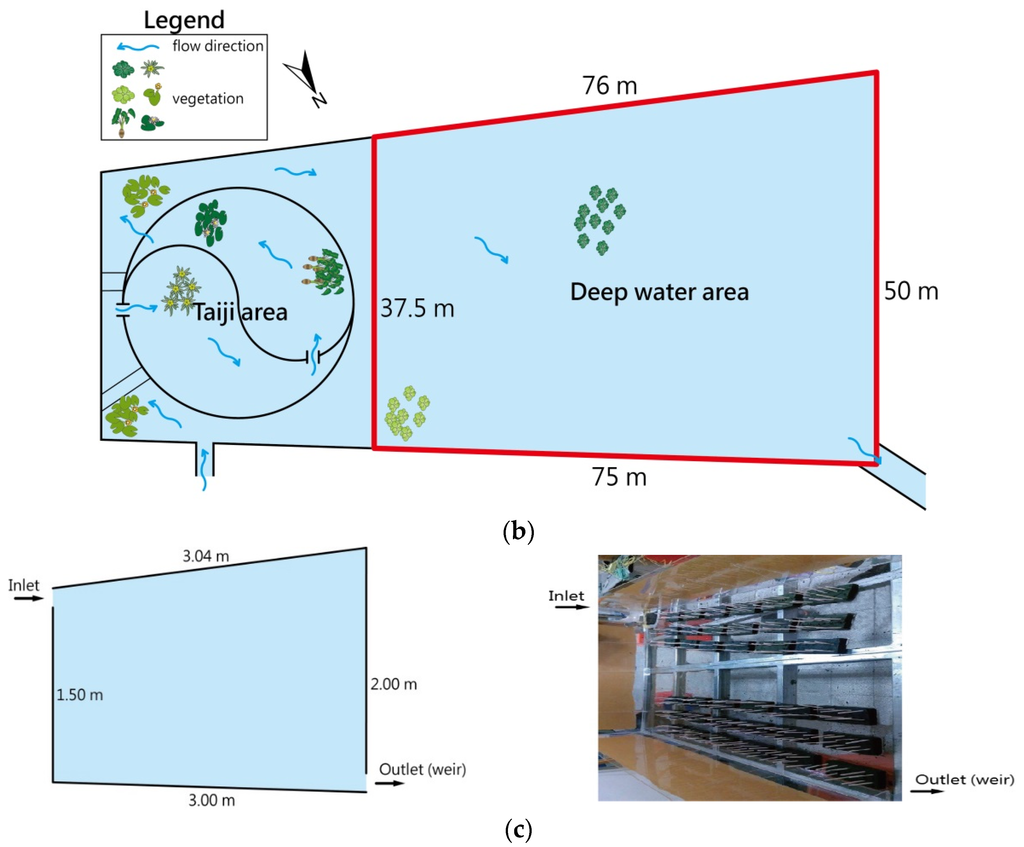
Figure 1.
(a) Study area location in Taoyuan County, Northern Taiwan; (b) farm pond (prototype) with dimensions of 50 m wide by 75 m long. The vegetation in the wetland consists of dominant emergent vegetation such as Cyperus papyrus and Cyperus malaccensis Lam. subsp. monophyllus and minor floating vegetation, such as Nuphar shimadai; and (c) flume model of the deep area (2 m wide by 3 m long) viewed from above (left) and a photograph of the flume and the distribution of the installed obstructions in a perspective view from the outlet (right).
2.2. Flume Experiment Setup
2.2.1. Physical Model
We constructed a small-scale physical model of the deep section of the farm-pond wetland. A physical model is a small-scale representation of a prototype, i.e., a real-world object or system. Physical models are often used to represent hydraulic flow situations. Both the boundary conditions and flow field must be scaled appropriately. Geometric similarity refers to the ratios of model dimensions to prototype dimensions (Equations (1) and (2)):
where Lm is the length of the model, Lp is the length of the prototype, Am is the area of the model, Ap is the area of the prototype, and λL is a scale factor for the length.
Kinematic similarity refers to the ratios of model flow parameters to prototype flow parameters (Equations (3) and (4)):
where vm is the velocity of the model fluid; vp is the velocity of the prototype fluid; Qm is the discharge of the model; Qp is the discharge of the prototype; Lm is the length of the model; Lp is the length of the prototype; Tm is the time when observing the model; Tp is the time when observing the prototype; and λL, λT, λv, and λQ are scale factors for the length, time, velocity, and discharge.
The combination of geometric and kinematic similarities yields the model-to-prototype ratios of length, time, velocity, and discharge. Dynamic similarity exists between geometrically and kinematically similar systems if the ratios of all forces in the model and prototype are the same (Equation (5)):
where Fm is the force of the model fluid; Fp is the force of the prototype fluid; Mm is the mass of the model fluid; Mp is the mass of the prototype fluid; am is the acceleration of the model fluid; ap is the acceleration of the prototype fluid; ρm is the density of the model fluid; ρp is the density of the prototype fluid; Lm is the length of the model; Lp is the length of the prototype; and λρ, λL, λT, λv, and λF are scale factors for the density, length, time, velocity, and force.
True dynamic similarity is achieved if and only if each dimensionless parameter has the same value in both the model and prototype [13]. There are many phenomena that might be important in hydraulic flow situations. In practice, only the most dominant mechanism is modeled. In wetlands, the viscous force is typically dominant due to the low flow velocity and low Reynolds number. When the dominant viscous forces in a model are tested, all of the other forces are neglected. The Reynolds number was used to evaluate the dynamic similarity in this study. Equivalence in Reynolds number was achieved between the on-site constructed wetland (prototype) and experimental flume (model) (Equation (6)):
where Rem is the Reynolds number of the model fluid, Rep is the Reynolds number of the prototype fluid, ρm is the density of the model fluid, ρp is the density of the prototype fluid, vm is the velocity of the model fluid, vp is the velocity of the prototype fluid, Lm is the length of the model, Lp is the length of the prototype, μm is the dynamic viscosity of the model fluid, and μp is the dynamic viscosity of the prototype fluid.
Since the fluid in both the model and prototype is water, μm = μp and ρm = ρp. All geometric and kinematic parameters were made equivalent, and corresponding angles of the prototype wetland and experimental flume were the same. We developed the experimental flume with a true model (not distorted) to avoid scale effects [13]. Thus, λv = 1/λL, λT = λL2 and λQ = λL by substituting Equation (6) into Equations (3) and (4). The model-to-prototype ratios of length, time, velocity, and discharge were determined to be 1/25, 1/625, 25, and 1/25, respectively (Table 1). The prototype measured 50 m wide by 75 m long (Figure 1b), the water level downstream was controlled at 2 m, and the discharge was set at 0.01 m3/s. Therefore, the flume model was 2 m wide by 3 m long (Figure 1c), the water level was 8 cm, and the discharge was 0.0004 m3/s.

Table 1.
Proportions of scale factors of the physical model used in the flume experiments.
2.2.2. Obstructions and Emergent Vegetation
The hydraulic efficiency indicates the behavior of fluid particle movement in a wetland. Adding obstructions and emergent vegetation can change the hydraulic efficiency considerably. The hydraulic performance associated with their presence was compared with a case without obstructions and vegetation. Forty-eight cases consisting of four obstruction types (emergent and submerged obstructions and high- and low-density emergent vegetation) as shown in Figure 2a and twelve obstruction configurations were developed as shown in Figure 2b. Grass bricks were placed as obstructions along the sides of the flume. These grass bricks were constructed with heights such that they either protruded above the water surface (emergent obstructions, or EOs) or did not (submerged obstructions, or SOs), and they were arranged as solid obstructions to block the flow of water. The bottoms of the grass bricks were fixed to the flume bottom. Plastic tubes with a diameter of 0.4 cm were used to simulate the stems of emergent vegetation. These tubes were erected on the SOs and protruded above the water surface. In contrast to the water-blocking effects of EOs, emergent vegetation allows water to pass through. Twelve obstruction configurations whose number of obstructions ranged from 1 to 3 were divided into two categories in terms of their aspect ratio. In the cases of high aspect ratios (cases 2-4, 2-5 and 2-6), the obstructions were 120 cm long by 20–60 cm wide by 11 cm high (EOs) and 120 cm long by 20–60 cm wide by 5 cm high (SOs). These aspect ratios ranged from 2 to 6. In the cases of low aspect ratios (cases 1-1, 1-2, 1-3, 2-1, 2-2, 2-3, 3-1, 3-2, and 3-3), the obstructions were 40–120 cm long by 10 cm wide by 11 cm high (EOs) and 40–120 cm long by 10 cm wide by 5 cm high (SOs). These aspect ratios ranged from 0.083 to 0.25. In addition, ten tubes were placed to represent low-density emergent vegetation (LEV), and twenty tubes were placed to represent high-density emergent vegetation (HEV). The vegetation spacing in the prototype ranged between 0.8 and 1.0 m to achieve good water purification and hydraulic performance [14]. In the 1/25-scale model, the tubes representing LEV and HEV were spaced 3.2 to 4 cm apart.
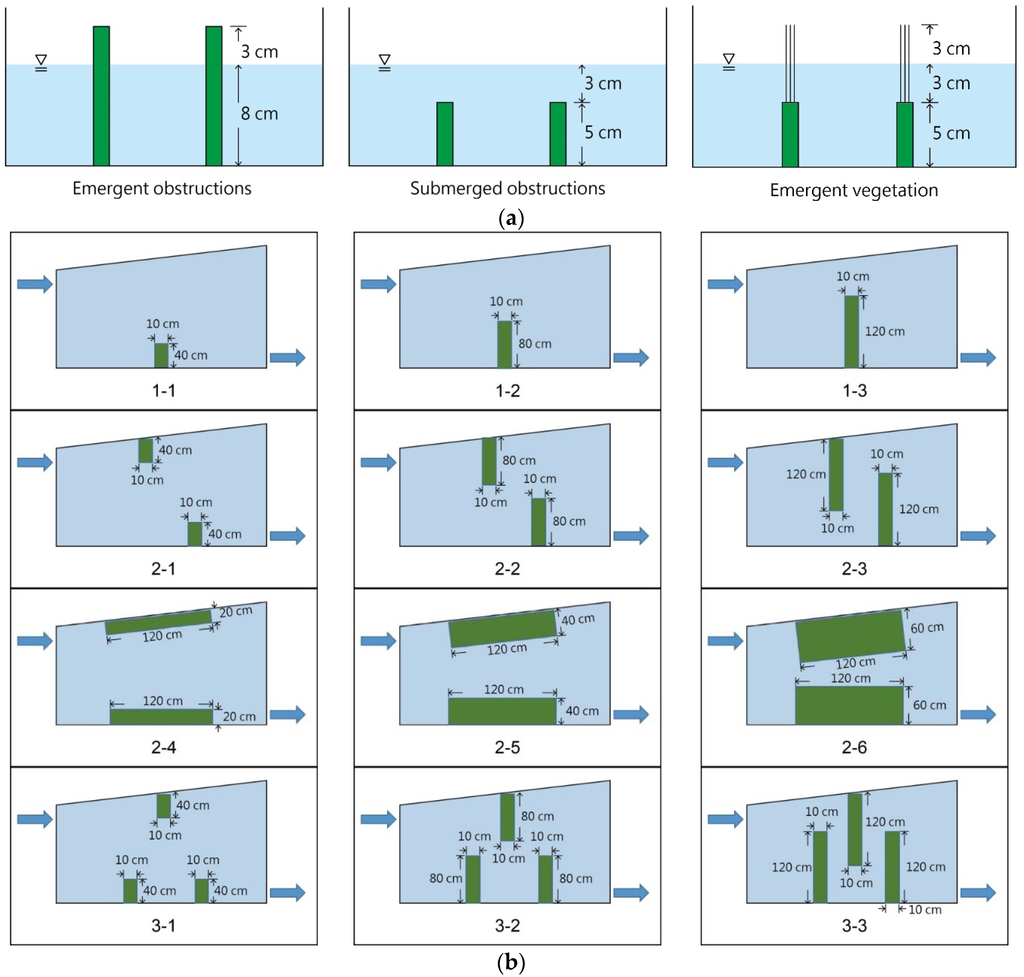
Figure 2.
(a) Sizes and placement of emergent obstructions (EOs), submerged obstructions (SOs), and high- and low-density emergent vegetation (EV) in the side view. The heights of the EOs and SOs are 11 cm and 5 cm, respectively, which yield a protrusion and submergence of 3 cm above and below the water surface, respectively. The emergent vegetation was erected on the SOs and protruded above the water surface; and (b) configuration and dimensions of obstructions. In cases 2-4, 2-5, and 2-6 (high aspect ratio), the obstructions were 120 cm long by 20–60 cm wide. In the other cases (low aspect ratio), the obstructions were 40–120 cm long by 10 cm wide.
2.2.3. Tracer and Detector
To observe the flow and diffusion of contaminants in the water body of the model, a tracer consisting of rhodamine-WT (RWT) was instantaneously added at the inlet. At the outlet, variations in the tracer concentration were measured over time to obtain the tracer response curve and residence time distribution curve (RTD) and, thus, to assess the overall hydraulic performance of the wetland. In addition, a triangular weir at the outlet was installed to measure the flow discharge. In front of this weir, a submerged underwater fluorescence meter (Cyclops-7) and an automatic recorder were installed to record changes in the tracer concentration over time. The top and sides of the instruments were covered with black plastic bags to avoid external interference. The measurement time increment was six seconds. The testing was ended when the tracer could no longer be detected. A complete test spanned approximately 40–60 min. Each test case was repeated three times to ensure the repeatability of the results. The concentration based on the measurements from the automatic recording detector was calculated using Equation (7) to derive the measured total amount of the fluorescence agent, thus enabling the recovery rate of the tracers to be calculated [15]:
where Mout is the mass of tracer at the outlet, Q is the discharge, C is the tracer concentration, t is the time of measurement, and T is the total time of the tracer experiment.
2.3. Residence Time, Effective Volume, and Hydraulic Efficiency
The residence time was estimated using the simplified hydraulic retention time (HRT) method, which yields the nominal retention time (tn; Equation (8)), and using the residence time distribution (RTD) method, which yields the mean residence time (tm; Equation (9)) [8]. The HRT was calculated by assuming an aquatic system with uniform, unrestricted water flow with no mixing and/or diffusion and a nominal retention time [16]. The RTD method is used to assess the mixing, diffusion, and RTD of a fluid in a reactor vessel; it models the flow conditions of a fluid in a reactor better than does the HRT method [17].
where V is the water volume, Q is the discharge, and tn is the nominal retention time.
where C is the containment concentration, t is the time of measurement, and tm is the mean residence time.
The parameter ev indicates the effective volume ratio of a detention system based on the ratio of tm to tn as per Equation (10) [18].
where tm is the mean residence time, tn is the nominal retention time, and ev is the effective volume ratio.
The hydraulic efficiency (λ) was calculated using Equation (11) [8]. The performance of wastewater treatment facilities such as constructed wetlands is closely related to their hydraulic efficiency [19,20,21]. The calculated hydraulic efficiency was assigned to one of three classes: good (λ > 0.75), satisfactory (0.5 ≤ λ ≤ 0.75), and poor (λ < 0.5) [11]:
where tp is the time of the peak concentration in the RTD curve measured at the outlet of the wetland or facility, tm is the mean residence time, tn is the nominal retention time, and λ is the hydraulic efficiency.
3. Results and Discussion
3.1. No Obstructions or Vegetation
The tracer response curve (RWT concentration vs. time) of the case without obstructions and vegetation is shown in Figure 3.The tracer recovery rate was approximately 72%. The largest peak in the RWT concentration occurred at t = 4.2 min. We noted several peaks in the RTD distribution, which have also been obtained in previous studies [9,10]. The calculated λ was approximately 0.21. This λ was compared with our previous study [22], which was from an on-site test and numerical simulation. The values of λ were all approximately 0.2–0.3 (Table 2), which indicates the reliability of the flume experiment. The nominal retention time (tn), mean residence time (tm), effective volume (ev) and hydraulic efficiency (λ) were calculated and are shown in Table 3. The hydraulic efficiency was classified as poor. The following tests were set up with internal obstructions and emergent vegetation.
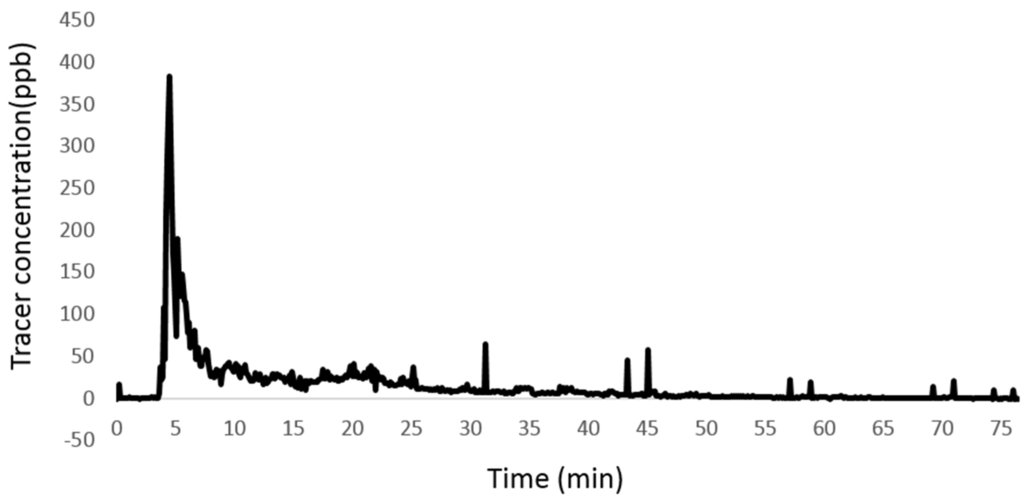
Figure 3.
Tracer response curve of the flume experiment without obstructions or vegetation.

Table 2.
Validation of the flume model based on comparisons with the on-site investigation and mathematical model simulation with no obstructions.

Table 3.
Nominal retention time, mean residence time, peak time, effective volume, and hydraulic efficiency of cases with emergent obstructions.
3.2. Installation of Obstructions
We installed obstructions consisting of emergent obstructions (EOs) and submerged obstructions (SOs) to improve the flow uniformity and hydraulic efficiency. The tracer recovery rates associated with the presence of the EOs and SOs were approximately 62% and 65%, respectively. After the EOs were installed, the nominal retention time (tn) decreased linearly with increases in the obstruction volume. The mean residence time (tm) appeared to increase with increases in the quantity and length of obstructions. Although the volume percentage corresponding to the case with high aspect ratios was rather high, tm did not significantly increase. The effective volume () increased with increases in the obstruction volume (Table 3). In the cases with low aspect ratios (cases 1-1, 1-2, 1-3, 2-1, 2-2, 2-3, 3-1, 3-2, 3-3), the hydraulic efficiency (λ) improved significantly when the number and lengths of obstructions were increased. Among all of the configurations, the group consisting of cases 3-1, 3-2, and 3-3 yielded the largest improvements in λ. Case 3-3 exhibited a λ of 0.87, i.e., good hydraulic efficiency. Cases 1-1, 1-2, and 1-3 yielded the second largest improvement in λ. Cases 2-1, 2-2, and 2-3 yielded the smallest improvements in λ, and only case 2-3 yielded satisfactory hydraulic efficiency. Among the cases with high aspect ratios, i.e., cases 2-4, 2-5 and 2-6, none of the λ values improved significantly; all yielded poor hydraulic efficiency. After installing the high-aspect-ratio EOs, we observed constrained water conveyance and a distinct short-circuited flow, i.e., an area with relatively high flow velocity. The short-circuited flow reduced the residence time and flow uniformity and thereby decreased the hydraulic performance and treatment efficiency.
After the SOs were placed, the nominal retention time (tn) decreased linearly with increases in the obstruction volume. In the cases with low aspect ratios, the mean residence time (tm) increased with increases in the number and lengths of obstructions (Table 4). In the cases with high aspect ratios, although the volume percentage was somewhat higher, the effective volume () increased with increases in the obstruction volume (Figure 4a). In the cases with low aspect ratios, the hydraulic efficiency (λ) increased as the number and lengths of obstructions increased, although, this effect was not highly significant (Figure 4b). The majority of the λ values were less than 0.75, representing poor hydraulic efficiency. The nominal retention time (tn) decreased linearly with increases in the obstruction volume. In the cases with low aspect ratios, the EOs yielded significantly greater improvements in hydraulic efficiency (λ) than did the SOs (Figure 4). In contrast, in the cases with high aspect ratios, the EOs yielded less improvement than did the SOs. The high-aspect-ratio EOs clearly altered the flow direction and constrained the water conveyance area more than did the low-aspect-ratio EOs, and this greater alteration may have caused the short-circuited flow. The short-circuited flow occurred in the areas with relatively high flow speeds, caused by lower friction and constrained conveyance water area. This creates a non-uniform flow condition, resulting in a decrease in the residence time and hydraulic efficiency, which also prevents a wetland from improving the water quality.

Table 4.
Nominal retention time, mean residence time, peak time, effective volume, and hydraulic efficiency of cases with submerged obstructions.
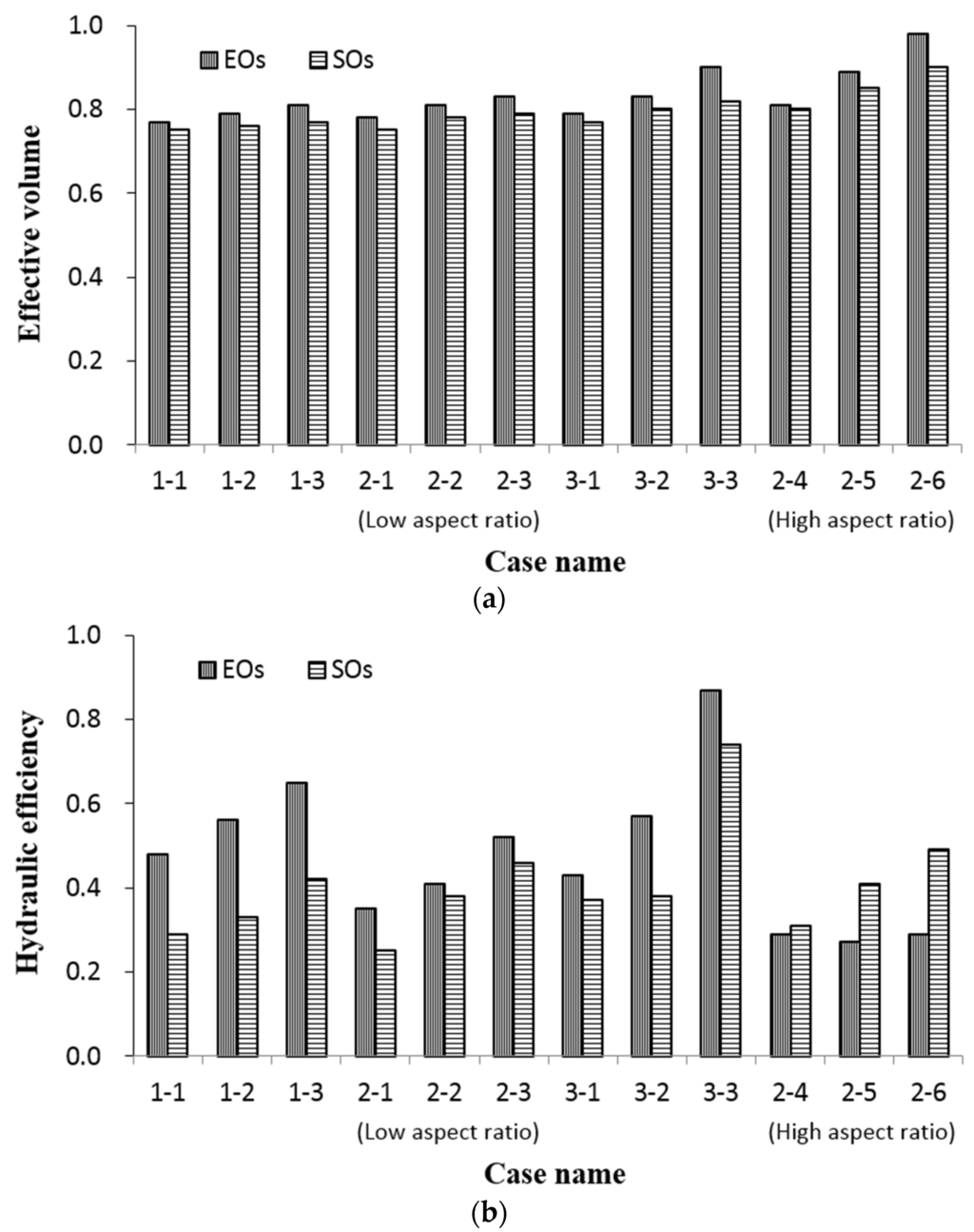
Figure 4.
(a) Effective volumes and (b) hydraulic efficiencies associated with emergent and submerged obstructions.
3.3. Installation of Emergent Vegetation
We installed HEV and LEV on the SOs. The tracer recovery rates associated with the HEV and LEV were approximately 54% and 60%, respectively. The nominal retention time (tn) associated with the HEV decreased linearly with increases in the obstruction volume. The mean residence time (tm) increased with increases in the quantities and lengths of the emergent vegetation installations (Table 5). The effective volume () increased with increases in the volumes of the emergent vegetation (Figure 5a). In the cases with low aspect ratios, the hydraulic efficiency (λ) increased with increases in the lengths of the emergent vegetation installations and with increases in the quantity of the emergent vegetation (Figure 5b). In cases 3-1, 3-2, and 3-3, λ increased to 0.75 or more, representing good hydraulic efficiency. In the cases with high aspect ratios, λ increased with increases in the lengths of the emergent vegetation installations on both sides. However, the improvement in efficiency was less significant than that associated with the low aspect ratios; λ reached a value of 0.5 or higher, representing satisfactory hydraulic efficiency.

Table 5.
Nominal retention time, mean residence time, peak time, effective volume, and hydraulic efficiency of cases with high-density emergent vegetation.
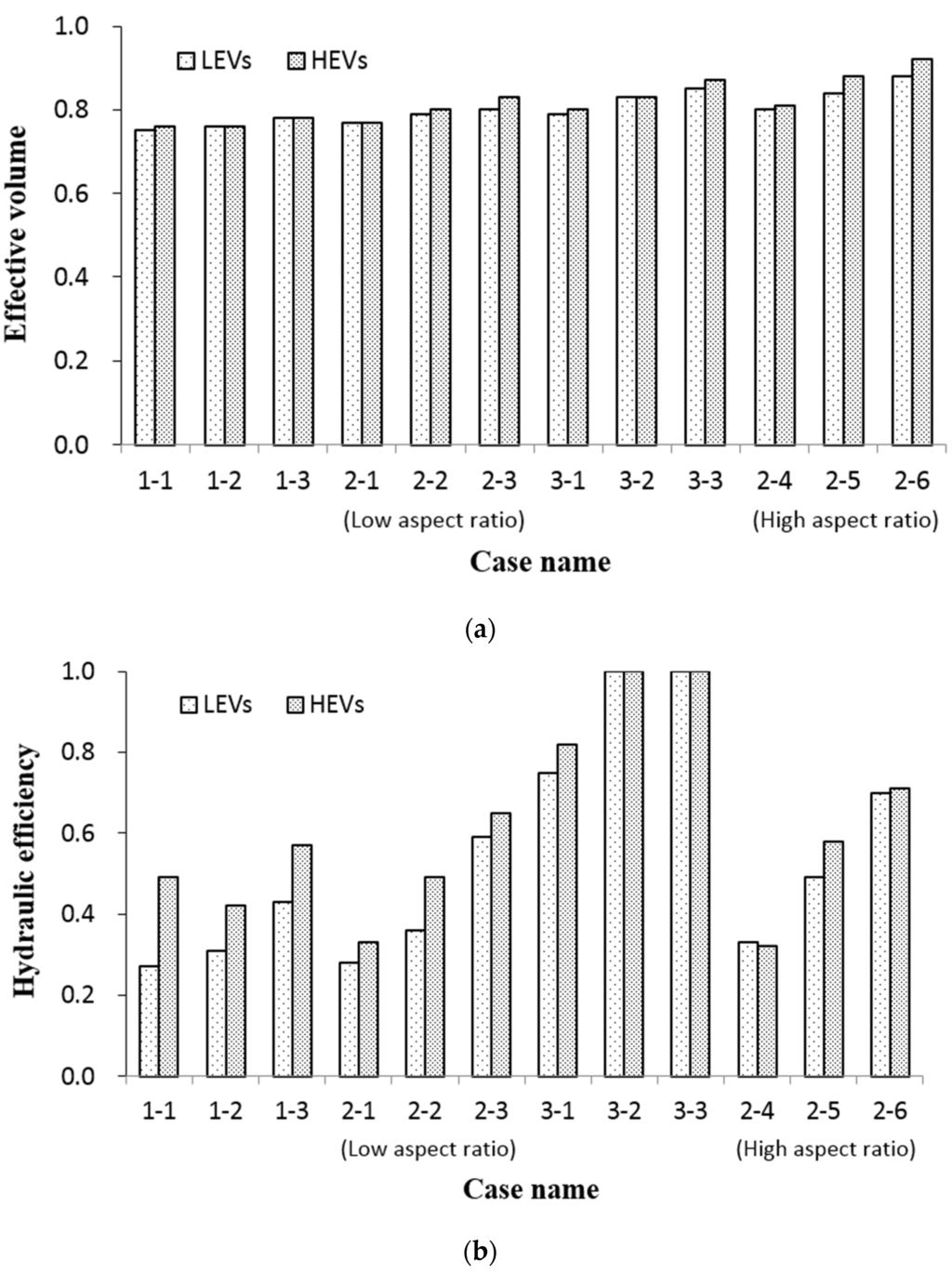
Figure 5.
(a) Effective volumes and (b) hydraulic efficiencies associated with low- and high-density emergent vegetation.
The nominal retention time (tn) associated with the LEV decreased linearly with increases in the volume of the emergent vegetation. The mean residence time (tm) increased with increases in the quantity and lengths of the emergent vegetation installations. The effective volume () increased with increases in the volume of the emergent vegetation (Table 6). In the cases with low aspect ratios, the hydraulic efficiency (λ) increased with increases in the lengths of the emergent vegetation installations. λ exhibited a clear increase with increases in the quantity of emergent vegetation. In cases 3-2 and 3-3, λ increased to 0.75 or greater, representing good hydraulic efficiency. The quantity of high-aspect-ratio emergent vegetation (cases 2-4, 2-5 and 2-6) was positively correlated with the hydraulic efficiency regardless of whether the vegetation consisted of HEV or LEV. In the cases with high aspect ratios, λ increased with increases in the lengths of the emergent vegetation installations on both sides. However, the improvement in efficiency was less significant than that associated with the low aspect ratios; λ reached 0.5 or more, representing satisfactory hydraulic efficiency. Furthermore, the HEV increased the hydraulic efficiency more than did the LEV. The differences between the increases in λ were larger when the quantity of simulated vegetation was low and were smaller when the quantity of simulated vegetation was high.

Table 6.
Nominal retention time, mean residence time, peak time, effective volume, and hydraulic efficiency of cases with low-density emergent vegetation.
3.4. Optimization of Hydraulic Performance
Figure 6 presents a comparison of the hydraulic efficiency (λ) associated with various placement configurations of the obstructions and emergent vegetation. In the cases with low aspect ratios with placements involving smaller surface areas and quantities (such as cases 1-1, 1-2, and 1-3), the λ values associated with the EOs were clearly superior to those associated with the other placements. In the placements involving larger surface areas and quantities (such as cases 2-1, 2-2, 2-3, 3-1, 3-2, and 3-3), the λ values associated with the emergent vegetation were higher than those associated with the obstructions. In the cases of high aspect ratios, the λ of the EOs was the lowest because the EOs altered the directions of flow. Since the placements differed, it was easier for short-circuited flow to occur. In the cases with high aspect ratios, the emergent vegetation was more effective in increasing the hydraulic efficiency. The λ values associated with the SOs were all less than those associated with the emergent vegetation. The differences between the λ values were larger in the placements involving larger surface areas and quantities. The improvements associated with the HEV were all better than those associated with the LEV. In the cases with high aspect ratios (cases 2-4, 2-5, and 2-6), increasing the lengths of the EOs on both sides did not improve the hydraulic efficiency.
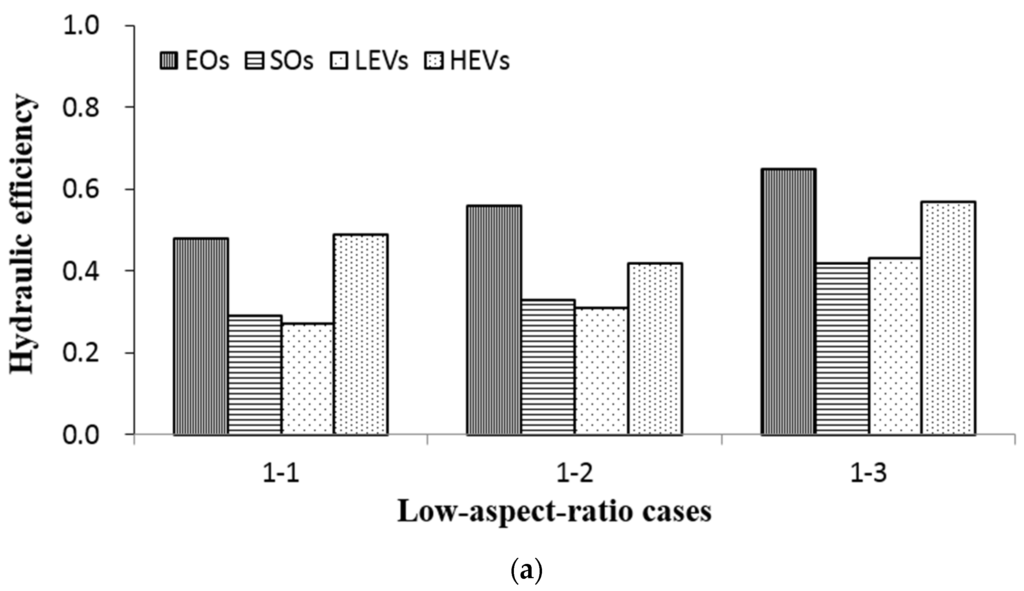
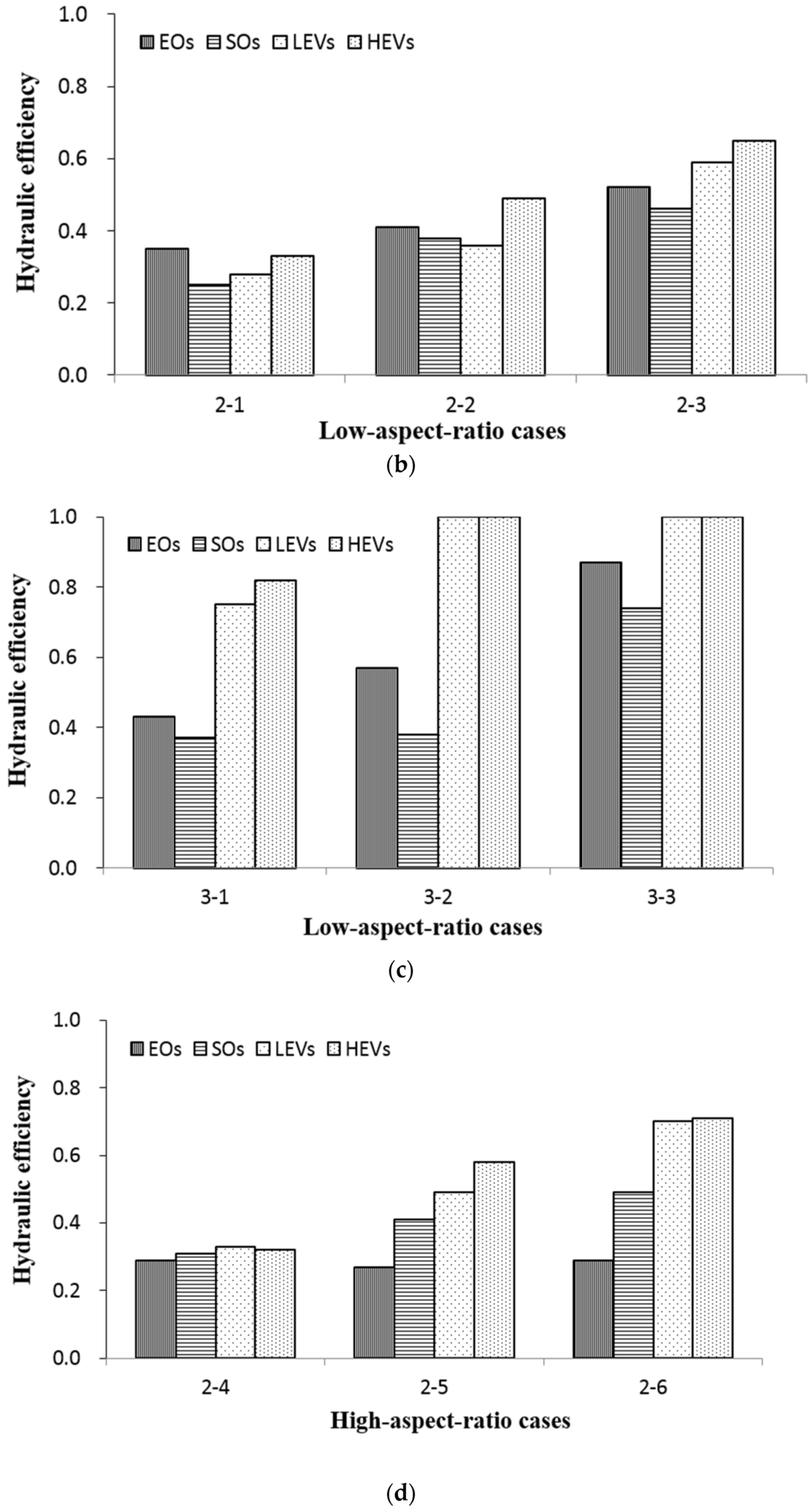
Figure 6.
Hydraulic performance of (a) low-aspect-ratio cases 1-1, 1-2, and 1-3; (b) low-aspect-ratio cases 2-1, 2-2, and 2-3; (c) low-aspect-ratio cases 3-1, 3-2, and 3-3; and (d) high-aspect-ratio cases 2-4, 2-5, and 2-6 with emergent obstructions, submerged obstructions, and high- and low-density emergent vegetation.
Cases 3-1, 3-2, and 3-3 involving HEV, cases 3-2, 3-3 involving LEV, and case 3-3 involving EOs achieved good hydraulic efficiency. As previously mentioned, emergent vegetation allows water to pass through, whereas the EOs block water and might constrain the water conveyance and induce short-circuited flow. Furthermore, planting of emergent vegetation was suggested to enhance the wastewater treatment efficiency and create lateral connectivity of wetland ecosystems [8]. At the start of the growing season, new growth of emergent vegetation enhanced the hydraulic performance. However, at the end of the growing season, senescing vegetation created short-circuiting [10]. The area of plant cultivation should be less than 10% of the area of open water to avoid overly dense growth. This restriction might improve the removal of organic substances [23]. Therefore, the placement used in case 3-1, which involved high-density emergent vegetation, achieved the optimum hydraulic efficiency.
4. Conclusions
In this study, we altered the density, spatial extent, aspect ratio, and configurations of obstructions and emergent vegetation to observe improvements in the hydraulic efficiency of a deep-water wetland, and we analyzed the differences in the improvements associated with emergent obstructions (EOs), submerged obstructions (SOs), and high- and low-density emergent vegetation placed on the SOs. In the cases with low aspect ratios, the improvements in hydraulic efficiency associated with the EOs were significantly greater than those associated with the SOs. However, in the cases with high aspect ratios, the improvements associated with the EOs were weaker than those associated with the SOs because the high-aspect-ratio EOs altered the flow direction and constrained the water conveyance area, which may have caused a short-circuited flow pattern. To increase the improvement in hydraulic efficiency associated with the SOs, emergent plants were placed on the SOs. The resulting λ values associated with the SOs were all lower than those associated with the emergent vegetation. The emergent vegetation installations involving the low aspect ratios yielded hydraulic efficiencies that were superior to those associated with the high aspect ratios with larger numbers of installations. In the cases with low aspect ratios, the placements involving smaller surface areas and fewer obstructions yielded λ values associated with the EOs exceeding those associated with the other placements. In contrast, among the placements involving larger surface areas and quantities, the λ values associated with the emergent vegetation exceeded those associated with the EOs. To achieve better contamination removal and lateral connectivity of the wetland ecosystems (i.e., material and energy cycling and biological dispersal), aquatic plant cultivation in constructed wetlands was suggested. In addition to considering a restriction of the planted area, case 3-1 involved the use of high-density emergent vegetation and was the optimum configuration for improving the hydraulic efficiency.
Acknowledgments
The study was supported by grant numbers NSC 102-2218-E-002-008- from the National Science Council and MOST 104-2625-M-002-020- from the Ministry of Science and Technology of Taiwan. W.S. Yu and G.W. Hwang provided helpful suggestions regarding the flume experiment setup. The useful suggestions from three anonymous reviewers were incorporated into the manuscript.
Author Contributions
Shang-Shu Shih and Tsang-Jung Chang contributed in the study design. Shang-Shu Shih and Shang-Shang Hong contributed in the data collection and analyses. Shang-Shu Shih performed the data analyses and wrote the manuscript. Tsang-Jung Chang and Shang-Shu Shih contributed in the discussion and interpretation of the results. All authors participated in reading and finalizing the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fogler, H.S. Elements of Chemical Reaction Engineering, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Kadlec, R.; Knight, R. Treatment Wetlands; CRC Press, Lewis Publishers: Boca Raton, FL, USA, 1996; p. 892. [Google Scholar]
- Arega, F. Hydrodynamic modeling and characterizing of Lagrangian flows in the West Scott Creek wetlands system, South Carolina. J. Hydro Environ. Res. 2013, 7, 50–60. [Google Scholar] [CrossRef]
- Wang, N.; Mitsch, W.J. A detailed ecosystem model of phosphorus dynamics in created riparian wetlands. Ecol. Model. 2000, 126, 101–130. [Google Scholar] [CrossRef]
- Wahl, M.D.; Brown, L.C.; Soboyejo, A.O.; Dong, B. Quantifying the hydraulic performance of treatment wetlands using the reliability functions. Ecol. Eng. 2012, 47, 120–125. [Google Scholar] [CrossRef]
- Holland, J.F.; Martin, J.F.; Granata, T.; Bouchard, V.; Quigley, M.; Brown, L. Effects of wetland depth and flow rate on residence time distribution characteristics. Ecol. Eng. 2004, 23, 189–203. [Google Scholar] [CrossRef]
- Min, J.; Wise, W.R. Simulating short-circuiting flow in a constructed wetland: The implications of bathymetry and vegetation effects. Hydrol. Process. 2009, 23, 830–841. [Google Scholar] [CrossRef]
- Chang, T.; Chang, Y.; Lee, W.; Shih, S. Flow uniformity and hydraulic efficiency improvement of Deep-Water constructed wetlands. Ecol. Eng. 2016, 92, 28–36. [Google Scholar] [CrossRef]
- Bastviken, S.K.; Weisner, S.E.B.; Thiere, G.; Svensson, J.M.; Ehde, P.M.; Tonderski, K.S. Effects of vegetation and hydraulic load on seasonal nitrate removal in treatment wetlands. Ecol. Eng. 2009, 35, 946–952. [Google Scholar] [CrossRef]
- Keefe, S.H.; Daniels, J.S.T.; Runkel, R.L.; Wass, R.D.; Stiles, E.A.; Barber, L.B. Influence of hummocks and emergent vegetation on hydraulic performance in a surface flow wastewater treatment wetland. Water Resour. Res. 2010, 46, 1–13. [Google Scholar] [CrossRef]
- Persson, J.; Somes, N.L.G.; Wong, T.H.F. Hydraulics efficiency of constructed wetlands and ponds. Water Sci. Technol. 1999, 40, 291–300. [Google Scholar] [CrossRef]
- Shih, S.; Kuo, P.; Fang, W.; LePage, B.A. A correction coefficient for pollutant removal in free water surfacewetlands using first-order modeling. Ecol. Eng. 2013, 61, 200–206. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of Open Channel Flow, 2nd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Chang, W.L. The Treatment Efficiency Applying Aquatic Vegetation in Constructed Wetlands; Manual of River Water Quality Improvement Workshop; Environmental Protection Administration: Taipei City, Taiwan, 2006. (In Chinese) [Google Scholar]
- Williams, M.D.; Reimus, P.W.; Vermeul, V.R.; Rose, P.E.; Dean, C.A.; Waston, T.B.; Newell, D.L.; Leecaster, K.B.; Brauser, E.M. Development of Models to Simulate Tracer Tests for Characterization of Enhanced Geothermal Systems; U.S. Department of Energy; Pacific Northwest National: Laboratory: Ridgeland, WA, USA, 2013.
- Su, T.; Yang, S.; Shih, S.; Lee, H.; Su, T.; Yang, S.; Shih, S.; Lee, H. Optimal design for hydraulic efficiency performance of free-water-surface constructed wetlands. Ecol. Eng. 2009, 35, 1200–1207. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Thackston, E.L.; Shields, F.D.; Schroeder, P.R. Residence time distributions of shallow basins. J. Environ. Eng. 1987, 113, 1319–1332. [Google Scholar] [CrossRef]
- Dierberg, F.E.; Juston, J.J.; Debusk, T.A.; Pietro, K.; Gu, B. Relationship between hydraulic efficiency and phosphorus removal in a submerged aquatic vegetation-dominated treatment wetland. Ecol. Eng. 2005, 25, 9–23. [Google Scholar] [CrossRef]
- Kadlec, R.H.; Roy, S.B.; Munson, R.K.; Charlton, S.; Brownlie, W. Water quality performance of treatment wetlands in the Imperial Valley, California. Ecol. Eng. 2010, 36, 1093–1107. [Google Scholar] [CrossRef]
- Jenkins, G.A.; Greenway, M. The hydraulic efficiency of fringing versus banded vegetation in constructed wetlands. Ecol. Eng. 2005, 25, 61–72. [Google Scholar] [CrossRef]
- Shih, S.S.; Fang, W.T. Tracer Experiments and Hydraulic Performance Improvements in a Farm Pond Wetland; National Scientific Council: Taipei City, Taiwan, 2013. [Google Scholar]
- USEPA. Manual of Constructed Wetlands Treatment of Municipal Wastewaters; USEPA: Cincinnati, OH, USA, 2000. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).