Multifractal Detrended Fluctuation Analysis of Streamflow in the Yellow River Basin, China

Abstract

Multifractal detrended fluctuation analysis (MFDFA) can provide information about inner regularity, randomness and long-range correlation of time series, promoting the knowledge of their evolution regularity. The MFDFA are applied to detect long-range correlations and multifractal behavior of streamflow series at four hydrological stations (Toudaoguai, Longmen, Huangfu and Ganguyi) in the main channel and tributaries of the Yellow River. The results showed that there was one crossover point in the log−log curve of the fluctuation function F_q(s) versus s. The location for the crossover point is approximately one year, implying an unchanged annual periodicity within the streamflow variations. The annual periodical feature of streamflow was removed by using seasonal trend decomposition based on locally weighted regression (STL). All the decomposed streamflow series were characterized by long-term persistence in the study areas. Strong dependence of the generalized Hurst exponent h(q) on q exhibited multifractal behavior in streamflow time series at four stations in the Yellow River basin. The reduction of dependence of h(q) on q for shuffled time series showed that the multifractality of streamflow series was responsible for the correlation properties, as well as the probability density function of the streamflow series.

1. Introduction

Streamflow is an important component of water circulation, which carries large amounts of information on this dynamic mechanism. Water circulation and hydrological processes are greatly affected by climate change and human activities such as agricultural irrigation, exploitation of water resources and construction of reservoirs, and these factors have caused evident changes in the last century. Some studies showed that climate change led to changes in streamflow. Labat et al. [1] showed that global streamflow increased with the rise of global temperature by approximately 4% from only a 1 °C global temperature rise. Zhao et al. [2] analyzed the annual and seasonal trends of streamflow and the correlations between streamflow and climatic variables in the Poyang Lake basin, indicating that both annual and seasonal streamflow showed increasing trends, and streamflow is more sensitive to changes in precipitation than potential evapotranspiration. Some studies paid close attention to the effects of human activities on streamflow changes. Mu et al. [3] showed that soil conservation measures had a great impact on the streamflow regime in the Loess Plateau. Baker and Miller [4] employed the soil and water assessment tool (SWAT) model to assess the relative impact of land cover changes on hydrological processes in Kenya’s Rift Valley, and the results showed that land use changes led to corresponding increases in surface runoff and decreases in groundwater recharge. These studies suggest that streamflow variation is complex as a result of the interaction of numerous related factors. Thus, the inherent law of streamflow series, which is important to water resources management and ecological conservation of river basins, is worth investigation.

Streamflow time series represent complex nonlinear and non-stationary characteristics. The long-range correlation in streamflow time series is helpful for prediction. The earliest research on long-range correlation can be found in Hurst [5]. Hurst’s finding is recognized as the first example of self-affine fractal behavior in empirical time series [6]. Since then, many researchers have shown great interest in detecting the long-range correlation of streamflow [7,8,9,10,11,12]. In these studies, detrended fluctuation analysis (DFA) was commonly applied to investigate the long-range correlation of streamflow. The DFA was introduced by Peng et al. [13], and the method is proven to be efficient for long-range correlation detection. DFA can decompose the changing trends of the time series at different timescales. Labat et al. [14] applied DFA to investigate streamflow series of two karstic watersheds in the south of France, suggesting that the correlation properties exist in small scales and anti-correlated properties exist in large scales. Hirpa et al. [15] analyzed and compared the long-range correlations of river flow fluctuations from 14 stations in the Flint River Basin in the state of Georgia in the southeastern United States. They found that the basin area is an important factor in long-range correlation studies of streamflow. To detect multifractal properties of the time series, Kantelhardt et al. [16] developed the multifractal detrended fluctuation analysis (MFDFA) by considering the qth-order statistical moment of the fluctuation to detect the scaling behavior of time series with a different density. The MFDFA is a development of DFA and can be applied to non-stationary streamflow time series. Kantelhardt et al. [17] found that daily streamflow records were long-range correlated, which is related to the spatial behavior of rainfall above a crossover timescale of several weeks. Zhang et al. [18] found that streamflow time series were characterized by short-term correlations on shorter time scale in the Pearl River basin, China, and the streamflow variations were mainly the result of climate changes, especially precipitation variations. Rego et al. [19] applied the MFDFA to detect the complex water fluctuations of 12 principal Brazilian rivers, and the result indicated the presence of multifractality and long-range correlations for all the stations after eliminating the climatic periodicity. Rybski et al. [20] investigated the scaling behavior of long daily river discharge at 42 hydrological stations around the world by using the MFDFA, suggesting that daily streamflow is characterized by a power-law decay of the autocorrelation function above some crossover time that is several weeks in most cases. Below the crossover time, pronounced short-term correlations occurred. The above analyses indicated that the hydrological system was a complex dynamic system that displays self-similar and exhibits self-fractal behaviors over a certain range of time scales. However, it should be noted that some period or quasi-period may lead to spurious appearance of crossovers when we detect the long-range correlations through the MFDFA method [21]. Better understanding of the scaling properties of streamflow removing periodicity will be important for prediction of the evolution of streamflow.

The Yellow River is the second longest river in China. The annual streamflow is only approximately 2% of China’s total, but it directly supports 12% of the national population (mostly farmers and rural people), feeds 15% of the irrigation area, and contributes to 9% of China’s GDP. The Yellow River suffered from serious water shortages and significant reduction (p < 0.05) in streamflow in the past decades [22,23,24,25]. It is important to understand the streamflow processes in terms of the streamflow time series reflecting the effects of the climate, topographical features, and human activities. Exploring the scaling behaviors and multifractal characteristics of streamflow series of the Yellow River is important to understand the future evolution trend of streamflow and to make decisions for water management.

Thus, the objectives of this study are: to analyze the statistical characteristics of streamflow series in the main channel and tributaries of the Yellow River; to remove the periodicity of streamflow for investigating the scaling behavior; and to detect multifractal characteristics in the streamflow series.

2. Study Area

The Yellow River basin covers an area of approximately 75.2 × 10⁴ km², located between 96° ~ 119° E and 32° ~ 42° N. The river originates from the Qinghai−Tibetan Plateau in western China and flows eastward through the Loess Plateau and the North China Plain before entering into the Bohai Sea, for a total length of 5464 km (Figure 1). From the river source to Toudaoguai, its upper reaches, it is 3472 km long with an area of 38.6 × 10⁴ km². The streamflow in the upper reaches accounts for approximately 61% of the whole basin. The upper reaches belongs to an arid climate with an annual average precipitation of 396 mm. Longmen station lies in the middle reaches of the Yellow River. The region between Toudaoguai and Longmen is suffering from severe soil erosion. The climate is semi-arid and arid with an annual average precipitation of 516 mm.

The Huangfuchuan watershed is located in a region crisscrossed by wind and water erosion at 110°18' ~ 111°12' E and 39°12' ~ 39°54' N, with a catchment area of 3246 km² (Figure 1). The Huangfuchuan River is a first-order tributary in midstream Yellow River with a river length of 137 km and average channel slope of 2.7%. The watershed is located in the transitional belt of warm temperate and mesothermal zones with an average precipitation of 350–450 mm, more than 80% of which occurs between June and September [26]. The Huangfuchuan watershed is one of the most severe soil erosion areas and brings approximately 0.15 billion t sediment into the Yellow River each year. The Yanhe watershed is located to the south of the Huangfuchuan River with a drainage area of 7687 km² (Figure 1). The Yanhe River is also a first-order tributary in the midstream of the Yellow River. The Yanhe watershed is dominated by a typical warm temperate continental monsoonal climate. Annual precipitation is approximately 500 mm and the average annual temperature ranges from 8.8 °C to 10.2 °C. The Yanhe watershed is covered by forests in the south and steppe grassland in the north, and arable land is mostly distributed in the alluvial plains and gentle slope hills. In the Yanhe watershed, the loess hilly-gully region accounts for 90% of the basin, and the slope in most areas is >15°, where soil erosion is very serious [3].

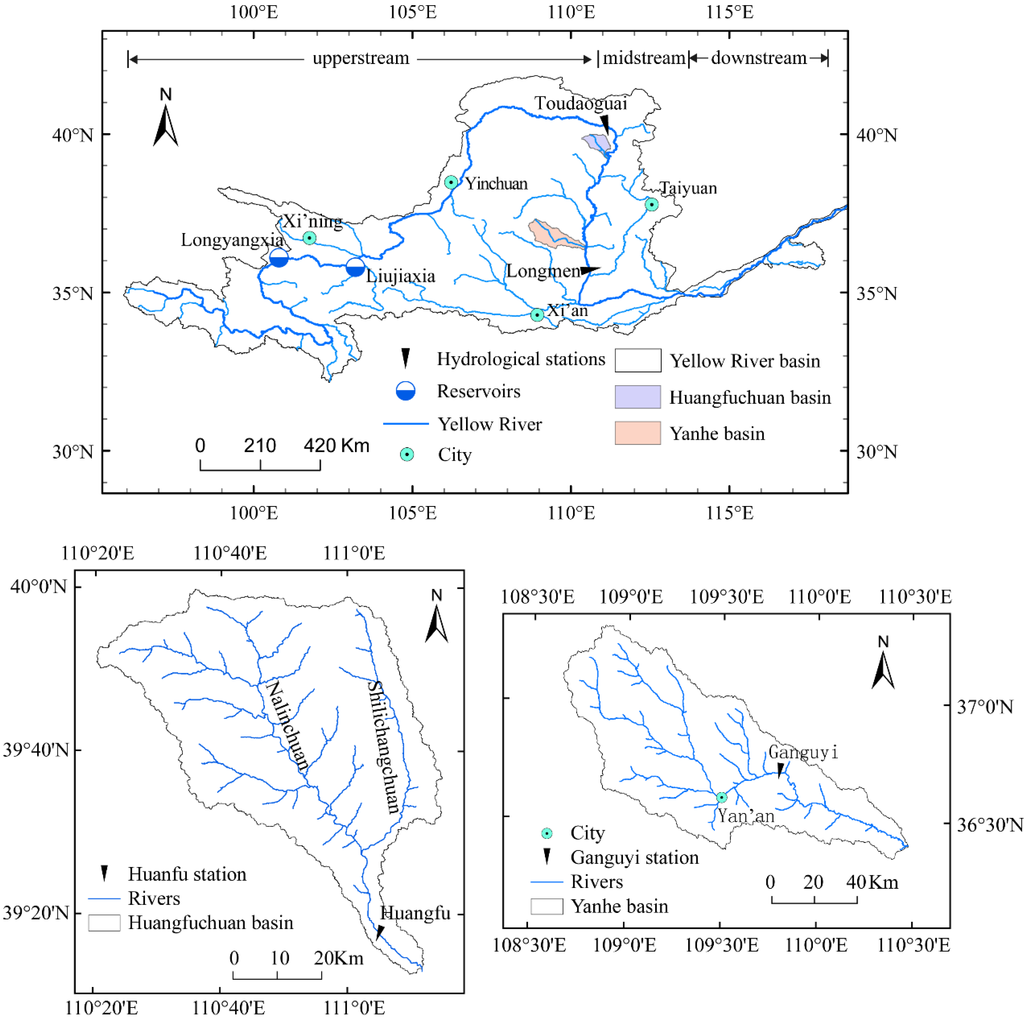
Figure 1. Study sites in the Yellow River basin.

Figure 1. Study sites in the Yellow River basin.

3. Data and Method

3.1. Data

Monthly streamflow at the Toudaoguai and Longmen stations and daily streamflow at the Huangfu and Ganguyi stations are available for this study (Figure 1). The detailed information of the streamflow series is listed in Table 1. All the streamflow data are collected from the Hydrological Yearbook and the Yellow River Conservancy Commission. The data in this study have been checked by corresponding agencies to guarantee their consistency.

Table 1. Data information at the four stations in the Yellow River.

River	Station	Area (km2)	Series Length	Time Interval	Annual Streamflow (108 m3)
Yellow River	Toudaoguai	367,898	January 1919–December 2009	Monthly	228.01
Yellow River	Longmen	497,552	January 1919–December 2009	Monthly	285.69
Huangfuchuan	Huangfu	3,175	1 January 1960–31 December 2009	Daily	1.20
Yanhe	Ganguyi	5,891	1 January 1960–31 December 2009	Daily	1.97

Table 1. Data information at the four stations in the Yellow River.

River	Station	Area (km2)	Series Length	Time Interval	Annual Streamflow (108 m3)
Yellow River	Toudaoguai	367,898	January 1919–December 2009	Monthly	228.01
Yellow River	Longmen	497,552	January 1919–December 2009	Monthly	285.69
Huangfuchuan	Huangfu	3,175	1 January 1960–31 December 2009	Daily	1.20
Yanhe	Ganguyi	5,891	1 January 1960–31 December 2009	Daily	1.97

3.2. Method

3.2.1. Seasonal Trend Decomposition Based on Locally Weighted Regression

The seasonal trend decomposition based on locally weighted regression (STL) method can be applied for detecting nonlinear trends and seasonal components in long-term time series. The STL method is a filtering procedure for decomposing a time series into three components: seasonality, trend, and remainder. A complete description and details about the model can be found in Cleveland et al. [27]. The STL method was applied to the streamflow time series with a view of analyzing trends and seasonal components over time, since some components of streamflow time series produce distortions impeding our understanding of their long-range correlations. The streamflow time series (Y_t) was regarded as an additive form of three components: Trend (T_t), Seasonality (S_t) and Remainder (R_t).

$$Y_t=T_t+S_t+R_t$$

(1)

In this study, streamflow time series were divided into the components of trend, seasonality and remainder by the STL. Seasonality was removed and the remaining components formed a new time series for MFDFA analysis.

3.2.2. Multifractal Detrended Fluctuation Analysis

The multifractal detrended fluctuation analysis (MFDFA) can be used to detect the scaling behaviors and multifractal properties of nonstationary time series such as hydrological series. For a streamflow time series X (x₁, x₂ … x_N), N is the length of the time series. The detailed computational procedure can be found as follows [28,29,30,31,32]:

Step 1. The accumulated deviation of the series can be calculated as:

$$Y(i)={\displaystyle \sum _{k=\mathrm{1}}^i[x_k-\overline{x}]} i=1,\dots ,N$$

(2)

where $\overline{x}$ is the mean of $x_k$.

Step 2. The accumulated deviation Y(i) can be divided into non-overlapping intervals by the equal length s. There are N_s = int(N/s) segments and N_s is the nearest integer part of N/s. Since the length N of the series may not be an integer multiple of the timescale s, some data may remain at the end of the series Y(i). In order not to ignore the rest of the series, the same computation procedure is repeated from the end to the start of the series. Thus, 2N_s segments can be obtained.

Step 3. A least squares fit method is applied to calculate the trend of each 2N_s segments, and the variance is determined by:

$$F^2(s,v)=\frac{1}{s}{\displaystyle \sum _{i=1}^s{\{Y[(v-1)s+i]-y_v(i)\}}^2}$$

(3)

for each segment v, v = 1,…,N_s, and

$$F^2(s,v)=\frac{1}{s}{\displaystyle \sum _{i=1}^s{\{Y[N-(v-N_s)s+i]-y_v(i)\}}^2}$$

(4)

for v = N_s + 1,…, 2N_s.

Here, y_v(i) is the fitted piecewise polynomial trend function in segment v, and any order polynomial can be calculated, such as linear, quadratic, or cubic.

Step 4. For the 2N_s segments, the qth-order fluctuation function is determined by:

$$F_q(s)={\left\{\frac{1}{2N_s}{\displaystyle \sum _{v=1}^{2N_s}{[F^2(s,v)]}^{q/2}}\right\}}^{1/q}$$

(5)

where $q\ne 0$ and $s\ge m+2$. In this study, we make m = 1 and s = N/4.

Step 5. There is a power−law relationship between the fluctuation function F_q(s) and s:

$$F_q(s)~s^{h(q)}$$

(6)

For each order of q, the scaling behavior of the fluctuation functions can be determined by the logarithmic chart of F_q(s) versus s. The slope of logF_q(s) and logs is the generalized Hurst exponent h(q). For stationary time series, the exponent h(2) is identical to the well-known Hurst exponent H, and h(2) varies between 0 and 1 [6]. The exponent h(2) can be used to analyze correlations in time series. The scaling exponent H = 0.5 means that the time series are uncorrelated; 0.5 < H < 1 implies long-term persistence and 0 < H < 0.5 implies short-term persistence [28].

In addition, when the time series is monofractal, h(q) will be a constant coefficient, independent of q. When the time series is multifractal, there is a significant dependence of h(q) on q, for q > 0, h(q) depicts the scaling behavior of the segments with large fluctuations and q < 0, h(q) depicts the scaling behavior of the segments with small fluctuations [33].

The relationship between the generalized Hurst exponent h(q) and the scaling exponent $\tau (q)$ is as follows:

$$\tau (q)=qh(q)-1$$

(7)

The singularity spectrum f(α) is another index used to describe a multifractal time series, which can be obtained from $\tau (q)$ via the first-order Legendre transformation:

$$\text{α}={\tau }^{\prime }(q), f(\text{α})=q\text{α}-\text{τ}(q)$$

(8)

where α is the Hölder exponent. Using Equation (6), we can obtain the relationship as follows:

$$\text{α}=h(q)+q{h}^{\prime }(q), f(\text{α})=q\left[\text{α}-h(q)\right]+1$$

(9)

The width of the spectrum f(α) reflects the strength of multifractality effects in the time series. For monofractal data, the spectrum f(α) will be a single point, and both functions $\text{τ}(q)$ and h(q) are linear.

4. Results

4.1. Statistical Characteristics

Temporal changes of streamflow at the four stations are shown in Figure 2. The streamflow shows fluctuating changes and starts to decrease in 1985 at the Toudaoguai and Longmen stations. This may be due to the construction of Longyangxia Reservoir upstream of the Yellow River. The variation of streamflow at the Ganguyi station is relatively stable, while the streamflow at the Huangfu station varies greatly with many flood peaks and low zero flow values.

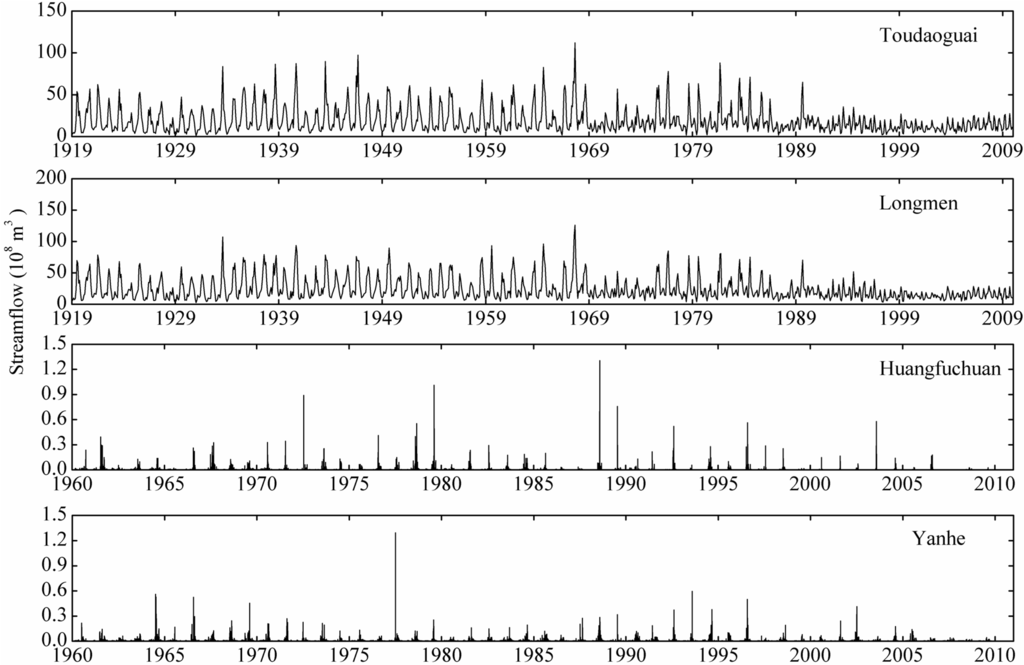
Figure 2. Temporal variation of streamflow at the Toudaoguai, Longmen, Huangfu and Ganguyi stations of the Yellow River.

Figure 2. Temporal variation of streamflow at the Toudaoguai, Longmen, Huangfu and Ganguyi stations of the Yellow River.

Table 2 shows basic statistical characteristic of streamflow in the main channel and tributary stations of the Yellow River. The average monthly streamflow at Toudaoguai and Longmen stations are 18.9 × 10⁸ m³ and 23.6 × 10⁸ m³, respectively. The standard deviation of streamflow at the Longmen station is higher than that at Toudaoguai, indicating that streamflow fluctuates greatly at the Longmen station. The skewness and kurtosis are greater than 0, suggesting that the streamflow distribution is not subject to the random normal distribution. The daily streamflow at Ganguyi, with more precipitation and extensive vegetation, is relatively higher than that in Huangfuchuan watershed, which has less precipitation and poor vegetation. The standard deviation of streamflow at Huangfu is greater than that at Ganguyi due to the different geomorphological types. The Huangfuchuan watershed is covered by bare weathered rocks, and low permeability and storage capacity improve runoff yield. In addition, the Huangfuchuan watershed is a rainstorm center, leading to changes of large magnitude in streamflow. The streamflow distributions at both Ganguyi and Huangfu stations are non-normal distribution due to skewness and kurtosis greater than 0.

Table 2. Characteristics of streamflow for the main river and tributaries of the Yellow River basin.

Hydrological Station	Mean (108 m3)	Max (108 m3)	Min (108 m3)	Standard Deviation	Skewness	Kurtosis
Toudaoguai	18.9	112.0	1.31	15.3	1.92	4.37
Longmen	23.6	126.1	2.81	17.7	1.76	3.33
Ganguyi	0.005	1.296	0	0.019	26.5	1246.7
Huangfu	0.003	1.305	0	0.024	26.9	1036.2

Table 2. Characteristics of streamflow for the main river and tributaries of the Yellow River basin.

Hydrological Station	Mean (108 m3)	Max (108 m3)	Min (108 m3)	Standard Deviation	Skewness	Kurtosis
Toudaoguai	18.9	112.0	1.31	15.3	1.92	4.37
Longmen	23.6	126.1	2.81	17.7	1.76	3.33
Ganguyi	0.005	1.296	0	0.019	26.5	1246.7
Huangfu	0.003	1.305	0	0.024	26.9	1036.2

4.2. Multifractal Detrended Fluctuation Analysis

Figure 3 shows the scaling behavior of streamflow at four hydrological stations. Clearly, one crossover point can be found for the four log−log plots of F_q(s) versus s of the streamflow series. The crossover points occur at approximately 12 months at the Toudaoguai and Longmen stations, and after approximately 372 days at Ganguyi and Huangfu stations. The location of the crossover point indicates annual periodicity of streamflow, implying a strong relationship between precipitation and streamflow.

The crossover points have been detected by the MFDFA method in many studies, suggesting that the scaling behavior of the time series is more complicated, and different parts have various scaling exponents [34]. The crossover point often comes from a change in the correlation properties of the series at different scales of time or space, or from seasonal component in the time series [28]. The STL method was employed to eliminate the effect of annual periodicity of streamflow.

Figure 4 illustrates different components decomposed by the STL method for the monthly streamflow at Toudaoguai station. The originally observed time series was decomposed into seasonality, trend and residue. The seasonal component shows regular variations in monthly time series, with high flows in flood season and low flows in dry season being a consistent pattern, as a result of annual climate patterns. The trend component shows fluctuations before 1985, but there exists an obvious decreasing trend after 1985 which is possibly caused by the construction of Longyangxia Reservoir.

Figure 3. The fluctuation function F₂(s) versus time scale s in double logarithmic plots for the streamflow time series at the Toudaoguai, Longmen, Ganguyi and Huangfu stations of the Yellow River.

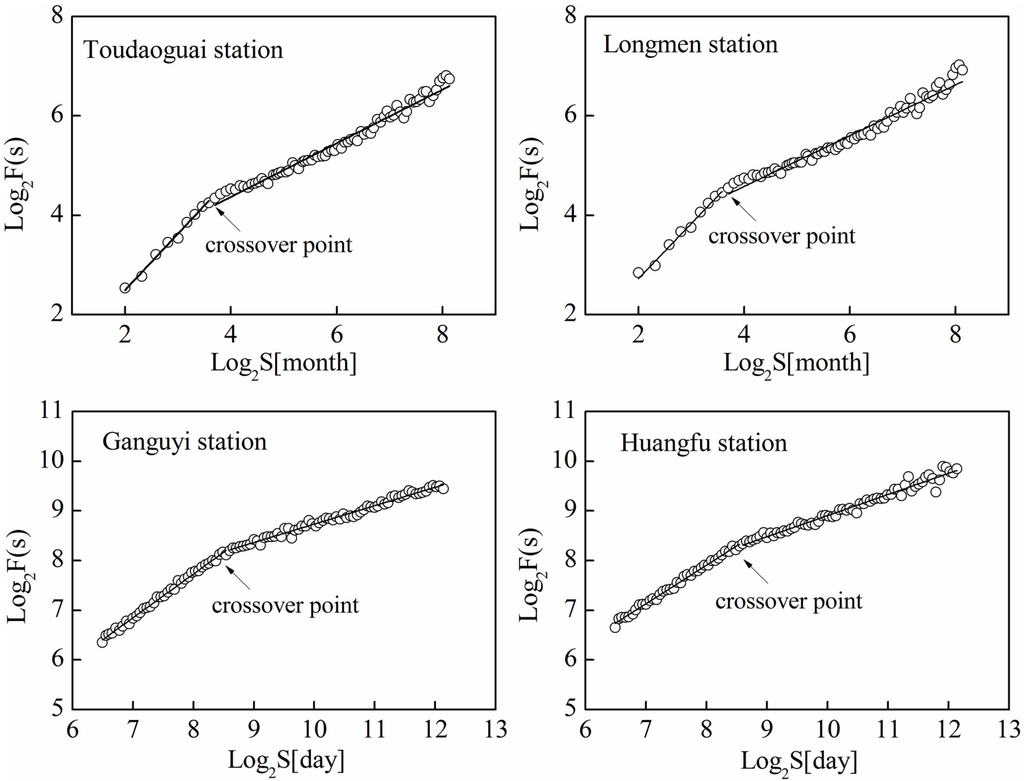
Figure 3. The fluctuation function F₂(s) versus time scale s in double logarithmic plots for the streamflow time series at the Toudaoguai, Longmen, Ganguyi and Huangfu stations of the Yellow River.

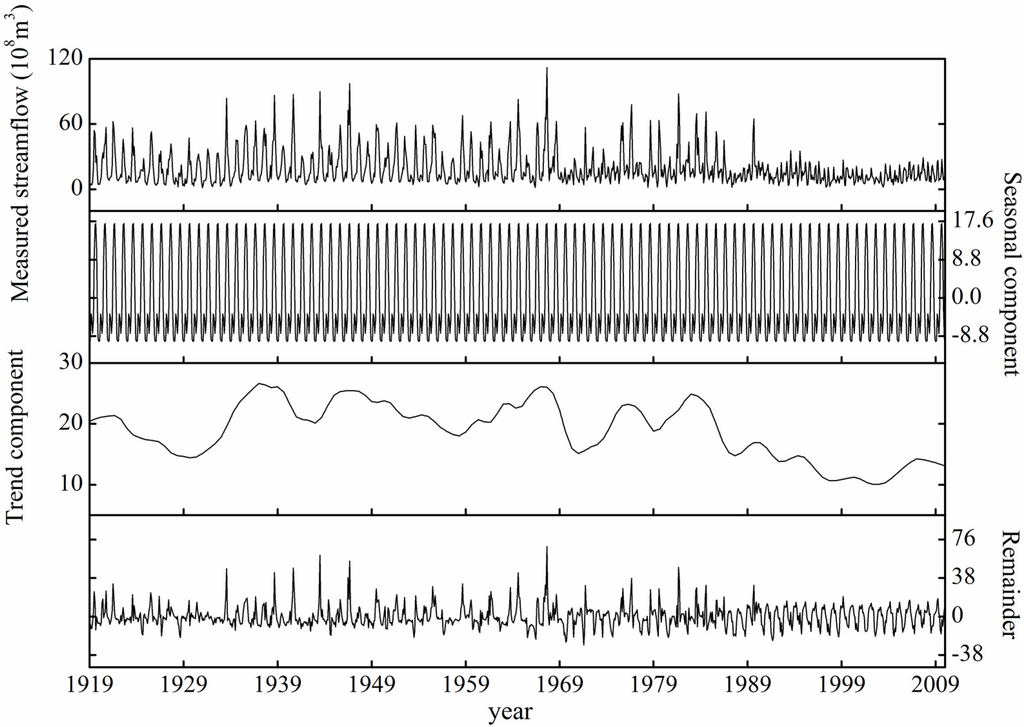
Figure 4. STL decomposition for streamflow at Toudaoguai station. The plots show the original measured streamflow, the seasonal component, trend component and the remainder from top to bottom, respectively.

Figure 4. STL decomposition for streamflow at Toudaoguai station. The plots show the original measured streamflow, the seasonal component, trend component and the remainder from top to bottom, respectively.

As mentioned above, the STL method can easily extract periodicity of streamflow time series. The periodicity of the streamflow at the four stations are therefore removed by the STL method. New streamflow time series including trend and remainder noise are constructed to detect the long-term correlations. Figure 5 shows the scaling behavior of streamflow time series removing the periodicity at the four stations by the MFDFA method. It can be clearly found that the crossover point disappears due to annual periodicity in the log−log plots of F_q(s) versus s. The h(2) values of streamflow are respectively 0.8257 and 0.8231 at Toudaoguai and Longmen stations, suggesting long-term persistence of the streamflow time series. It implies that scaling properties of the streamflow series in the upper and middle reaches of the Yellow River are similar. At the Ganguyi and Huangfu stations, streamflow fluctuations are also characterized by long-term persistence, as the values of h(2) are 0.5742 and 0.5882, respectively. This implies that the changing trends may remain stable for the next few years. The scaling properties of streamflow series at the four stations showed similar characteristics over a scale. This may imply universal scaling properties within the Yellow River basin because they have similar climate patterns.

Figure 5. The fluctuation function F₂(s) versus time scale s in double logarithmic plots for the streamflow time series removing the periodicity at the Toudaoguai, Longmen, Ganguyi and Huangfu stations of the Yellow River.

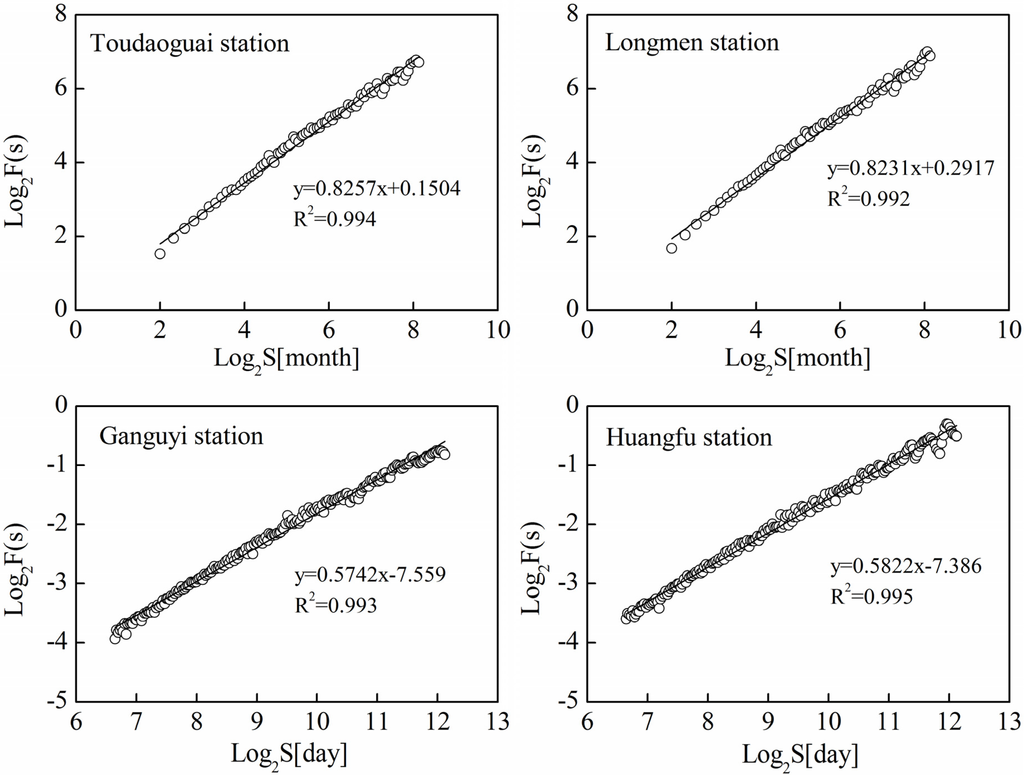
Figure 5. The fluctuation function F₂(s) versus time scale s in double logarithmic plots for the streamflow time series removing the periodicity at the Toudaoguai, Longmen, Ganguyi and Huangfu stations of the Yellow River.

Figure 6a–c show the dependence of h(q) and τ(q) on q, and the relationship between singularity spectrum f(α) and singularity exponent α. It shows that h(q) varies with the changes in q, which suggests that the streamflow series at the four stations in the Yellow River are characterized by multifractality. There are different behaviors for q < 0 and q > 0 between the scaling exponent τ(q) and q at the four stations. The slopes of τ(q) versus q are summarized in Table 3.

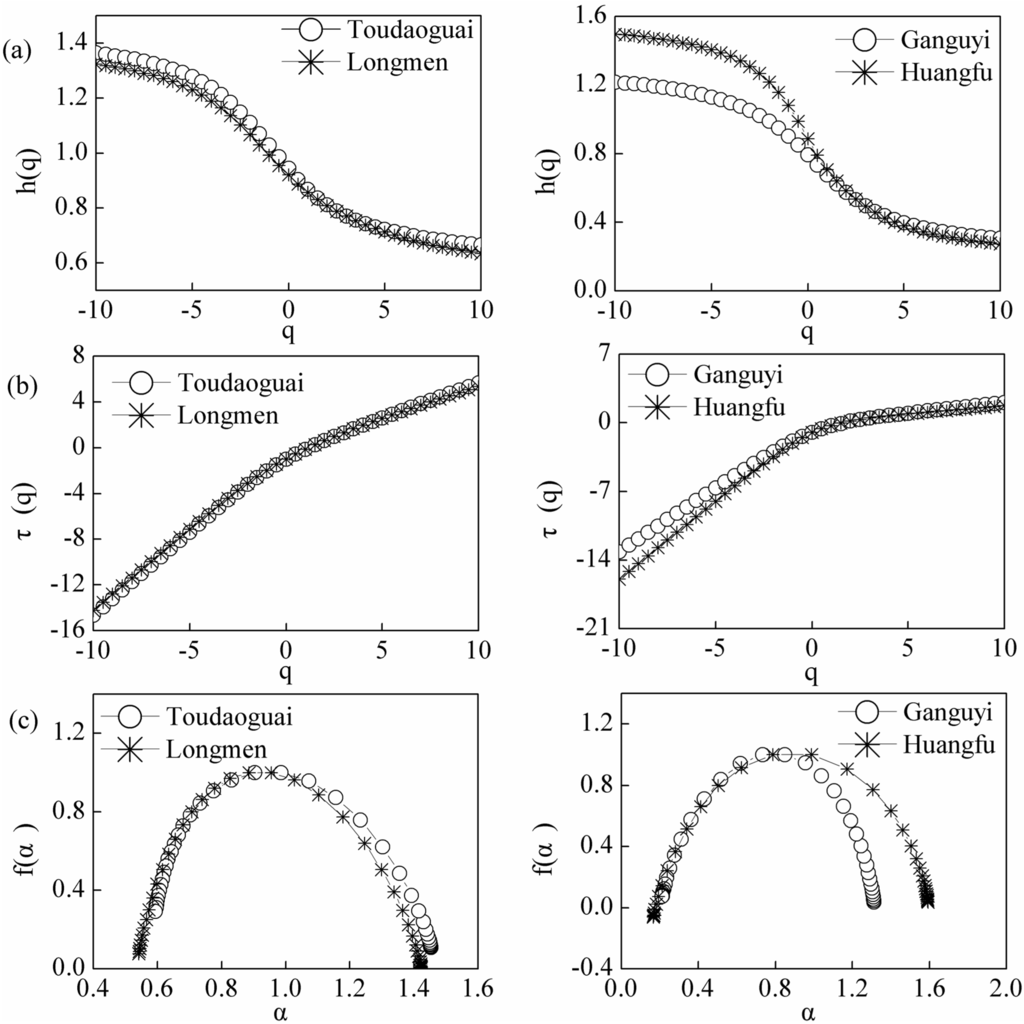
Figure 6. The relationships of (a) the generalized Hurst exponent h(q) and q; (b) the mass exponent function τ(q) and q; and (c) the singularity spectrum f(α) and singularity exponent α for the streamflow series at the Toudaoguai, Longmen, Ganguyi and Huangfu stations of the Yellow River.

Figure 6. The relationships of (a) the generalized Hurst exponent h(q) and q; (b) the mass exponent function τ(q) and q; and (c) the singularity spectrum f(α) and singularity exponent α for the streamflow series at the Toudaoguai, Longmen, Ganguyi and Huangfu stations of the Yellow River.

Table 3. Slopes of the mass exponent function τ(q) for the streamflow series at Toudaoguai, Longmen, Ganguyi and Huangfu stations of the Yellow River.

Study Area	Slopes
	−10 < q < 0	0 < q < 10
Toudaoguai	1.4070	0.6501
Longmen	1.3361	0.6191
Ganguyi	1.2538	0.2738
Huangfu	1.5456	0.2358

Table 3. Slopes of the mass exponent function τ(q) for the streamflow series at Toudaoguai, Longmen, Ganguyi and Huangfu stations of the Yellow River.

Study Area	Slopes
	−10 < q < 0	0 < q < 10
Toudaoguai	1.4070	0.6501
Longmen	1.3361	0.6191
Ganguyi	1.2538	0.2738
Huangfu	1.5456	0.2358

The nonlinear τ(q) means multiple scaling, and the degree of nonlinearity of the τ(q) function can reflect the degree of multifractality [35]. The slopes of τ(q) at the Toudaoguai and Longmen stations are similar, indicating a similar degree of multifractality. The distinct values of slopes between q < 0 and q > 0 of τ(q) are 0.7569, 0.7170, 0.980 and 1.3098, respectively, at Toudaoguai, Longmen, Ganguyi, and Huangfu stations. This may suggest that the streamflow time series at the Huangfu station have the highest degree of multifractality in scaling properties among these stations.

Figure 6c shows the multifractal spectra f(α) of four streamflow time series. All of them exhibit the shape of a parabolic curve, indicating the multifractal structure of the streamflow time series. The multifractal spectra at Toudaoguai, Longmen, and Ganguyi stations are not symmetrical and all have left truncation, whereas the multifractal spectrum has a right truncation at the Huangfu station. This is because streamflow time series at Huangfu station have a multifractal structure that is sensitive to large magnitudes of local fluctuations. Ihlen [36] concluded that the time series had a long left tail when it was insensitive to local fluctuations with small magnitudes, and would have a long right tail when it was insensitive to the larger magnitudes of local fluctuations. The widest range ($\mathrm{\Delta }\text{α}$) of the multifractal spectrum is similar between Toudaoguai and Longmen stations, and the values are 0.86 and 0.88, respectively, indicating similar multifractal characteristics. The widest range of the multifractal spectrum at Ganguyi and Huangfu stations are 1.10 and 1.43, respectively, suggesting that the strength and complexities of streamflow fluctuations at Huangfu are higher than those at the Ganguyi station.

5. Discussion

There are two causes that lead to the multifractality of the time series [16,28]. One is that a broadening of the probability density function (PDF) of the time series can result in multifractality. Another is different fluctuations of correlations in small and large scales. To distinguish the two types of multifractality, we can shuffle the streamflow time series at the Toudaoguai, Longmen, Huangfu and Ganguyi stations. The method generates two random integers, i and j, in the interval from 1 to N (N is the length of the streamflow time series) and then swaps the position of X(i) and X(j). The process is repeated 10N times in this study and the shuffled time series formed. The shuffled time series have the same distribution as the original time series, but they do not have the fluctuations of correlations and will exhibit a random behavior with h(q) = 0.5. If the shuffled series show weaker multifractality characteristics than the original one, it means that both of the two reasons mentioned above together lead to the multifractality in the streamflow time series.

Figure 7 shows that the h(q) is dependent on q and the curves of h(q) versus q are lower for the shuffled time series than the original one, behaving as a monotonically decreasing function of q for all hydrological stations, which indicates that the multifractality is due to the correlation properties and the PDF of the hydrological series.

The streamflow time series in the Yellow River present multifractal characteristics, which is related to precipitation, different topographical features, the size of the drainage area, land use/cover, the hydrodynamic system of self-organized behavior, and the exploitation of water resources. Koscielny-Bunde et al. [9] examined the temporal correlations and multifractal properties of long-term streamflow records from 41 hydrological stations throughout the world and showed that there were no universal scaling behaviors in the streamflow series, and the widest range of the multifractal spectrum was slightly decreasing with increasing basin area. Özger et al. [37] also showed that the larger the drainage area, the smaller the multifractality and the higher the persistency was. The widest ranges of the multifractal spectrum are 1.10 (at Ganguyi, 5891 km²) and 1.43 (at Huangfu, 3246 km²), respectively. The results in this study are consistent with Koscielny-Bunde et al. [9] and Özger et al. [37]. Kantelhardt et al. [17] found that the persistence of streamflow was related to storage processes occurring in the soil and the highly intermittent spatial behavior of rainfall. The h(2) values and multifractal spectra f(α) of the streamflow series at the Toudaoguai and Longmen stations are similar, but the values h(2) and multifractal spectra f(α) are different at the Ganguyi and Huangfu stations. For the mainstream of the Yellow River, most of the streamflow comes from the upper reaches of the Yellow River. Fluctuations in streamflow may be similar at Toudaoguai and Longmen stations, resulting in similar scaling behaviors, but the Ganguyi and Huangfu stations are located in different regions which have uneven spatial and temporal distribution of precipitation, various land covers and different soil types. The average annual precipitation are 364.3 mm and 504.1 mm in Huangfuchuan and Yanhe watershed, respectively [38]. There are many rainstorms in the Huangfuchuan basin, which has complex geomorphological types including a weathered sandstone hilly-gully region, a loess hilly-gully region and a sandy loess hilly-gully region. By contrast, the loess hilly-gully region is the dominant geomorphological type, accounting for 90% of the Yanhe basin. Human activities, such as exploitation, utilization of water resources, and the construction of check dams can heavily affect streamflow variation. The number of check dams had reached 567, and the dam-controlled area was 2216.47 km² in 2010, accounting for 68.3% of the Huangfuchuan basin area [26]. Yang et al. [39] illustrated that hydrological processes downstream of dams were closely associated with the regulating activities of reservoirs, and dam construction had significant influence on hydrological alterations. The interaction of all these complicated factors leads to the different multifractality of the streamflow series at the Huangfu and Ganguyi stations.

Figure 7. Generalized Hurst exponent h(q) as a function of q for original and shuffled streamflow series of the Toudaoguai, Longmen, Ganguyi, and Huangfu stations of the Yellow River.

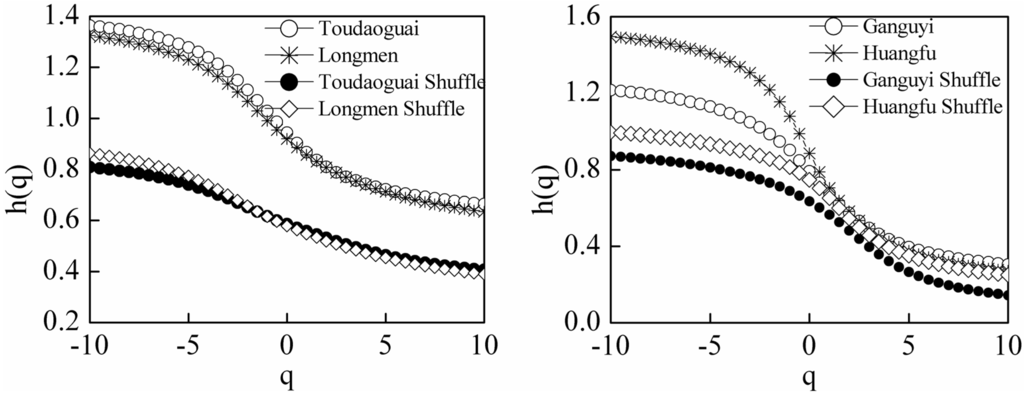
Figure 7. Generalized Hurst exponent h(q) as a function of q for original and shuffled streamflow series of the Toudaoguai, Longmen, Ganguyi, and Huangfu stations of the Yellow River.

The long-range correlations and multifractal behavior of streamflow time series are detected by MFDFA method. By contrast, the traditional methods such as rescaled range analysis and spectral analysis may produce spurious results of long-range correlation when the time series have changing trends. These trends are systematic deviations from the average streamflow that are caused by human activities, the seasonal cycle, or a changing climate [9]. The MFDFA has been employed to detect long-range correlation of time series with the superposition of a non-stationary trend. This method can deal with non-stationary time series and also avoid the spurious detection of long-range correlations [40]. The annual periodicity of streamflow time series resulted in the existence of a crossover point using MFDFA method (Figure 3). The STL method provides a graphical view for describing nonlinear trends with seasonal periodicity by using the generalized additive modeling approach [41,42]. This method can be applied to addressing the changes in timing, amplitude, and variance that occur in the seasonal cycle. The STL method decomposes the time series into three components: seasonal, trend, and remainder. Periodical components can be extracted and removed from the original time series [43]. Afterwards, the MFDFA method can be used to detect the long-range correlation and multifractal behavior of streamflow time series.

6. Conclusions

This study applied the MFDFA and STL methods to investigate long-term correlations and multifractal behaviors of the streamflow series at the Toudaoguai station and Longmen stations in the main river and at the Huangfu and Ganguyi stations in tributaries of the Yellow River. The results can be summarized as follows:

(1)

One crossover point can be found for the four log−log plots of F_q(s) versus s in the streamflow series. The crossover point occurred in approximately 12 months at the Toudaoguai and Longmen stations, and in approximately 372 days at Ganguyi and Huangfu station, which is attributed to a one-year periodicity of streamflow.

(2)

The scaling properties of the decomposed streamflow series at the four stations showed long-range correlations. This may imply universal scaling properties within Yellow River basin.

(3)

The q dependence of h(q) and τ(q) indicated that streamflow time series have multifractal behavior, which is due to the correlation properties, as well as to the PDF of the hydrological series. Comparing with Yanhe, streamflow time series at Huangfuchuan have a multifractal structure that is sensitive to large magnitudes of local fluctuations. Different precipitation−geomorphological types−runoff relationships at Yanhe and Huangfuchuan watershed may be the major effect factors inducing different multifractal behaviors.