A Physics-Guided Optimization Framework Using Deep Learning Surrogates for Multi-Objective Control of Combined Sewer Overflows
Abstract
1. Introduction
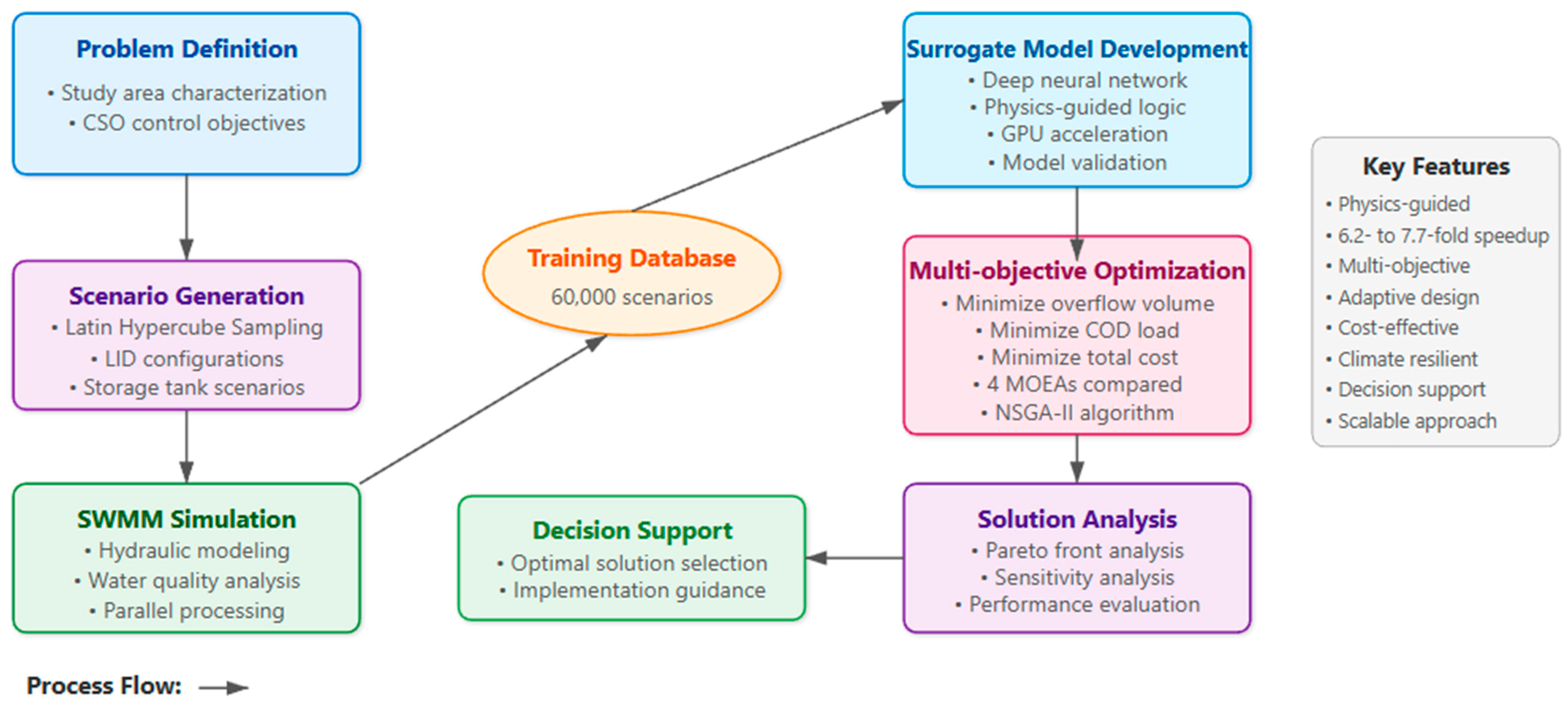
2. Materials and Methods
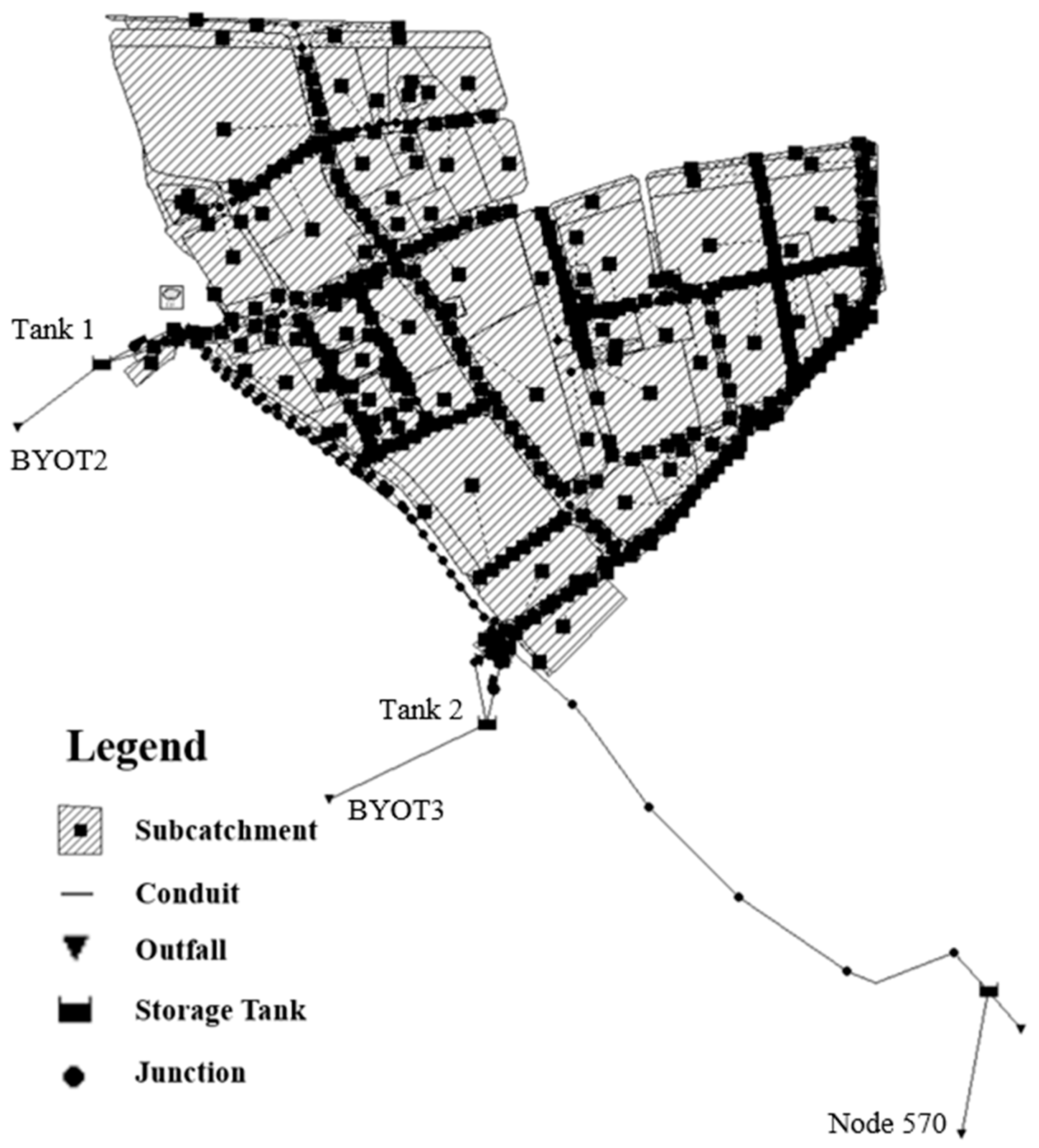
2.1. Study Area and SWMM Model Construction
2.2. Deep Learning Surrogate Model Development
2.2.1. Data Generation
2.2.2. Simulation and Data Collection
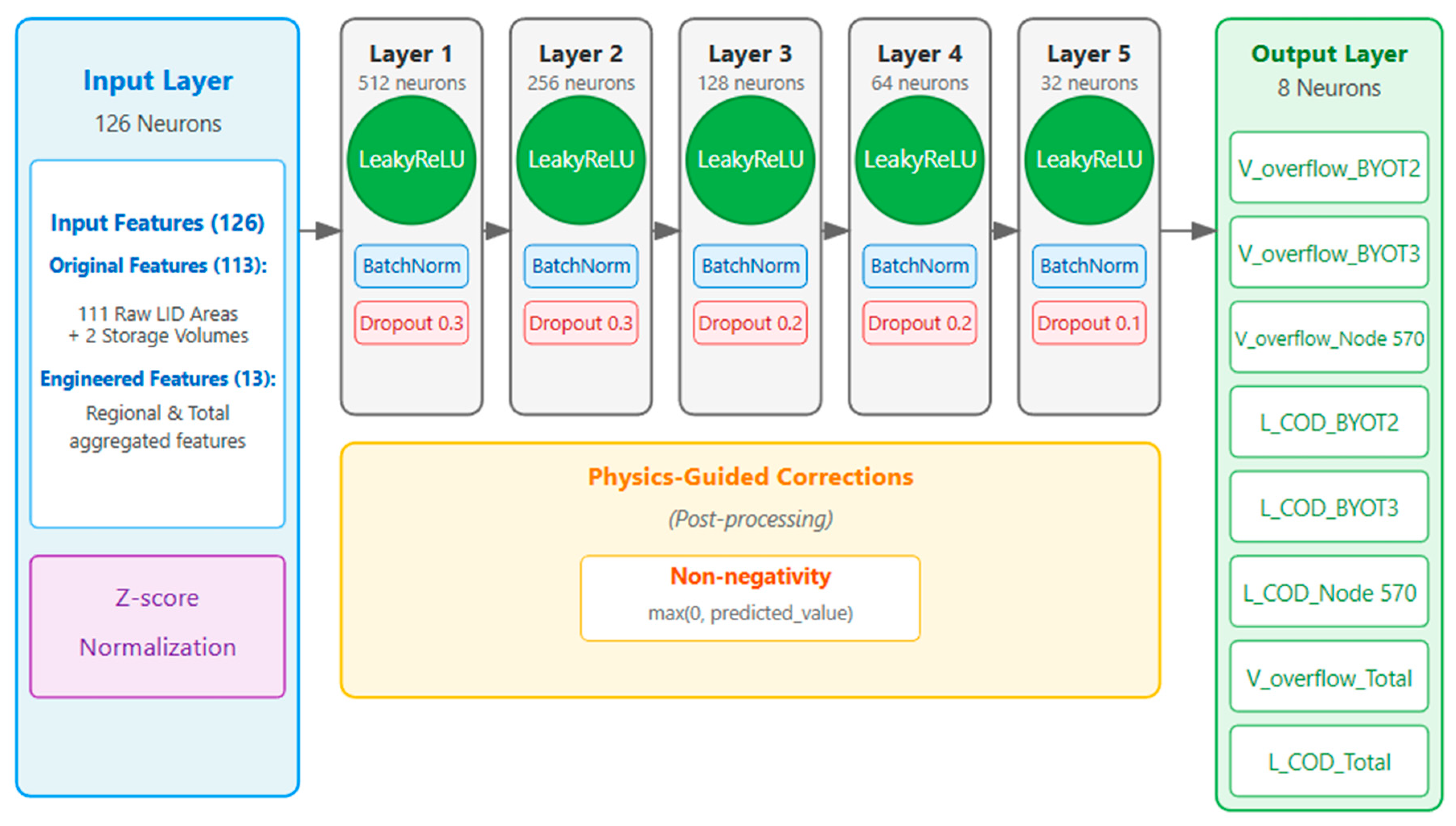
2.2.3. Neural Network Architecture
- (1)
- Input layer: The input layer consists of 126 neurons, corresponding to the 113 original features (111 raw LID areas and 2 storage volumes) and 13 aggregated features derived from our physics-guided feature engineering
- (2)
- Hidden layers: Five fully connected hidden layers with neurons progressively decreasing (512→256→128→64→32)
- (3)
- Output layer: 8 neurons, corresponding to the overflow volume and COD load for ‘BYOT2’, ‘BYOT3’, ‘Node 570’, and the total values (‘total volume’, ‘total cod’)
2.2.4. Training Process
2.2.5. Integration of Physical Principles
- (1)
- Physics-Guided Feature Engineering (Pre-processing)
- Regional LID Totals: Aggregated LID areas (by type: Bioretention Facilities, Permeable Pavement, Green Roofs) for each main outfall’s catchment area (e.g., BYOT2_ Bioretention Facilities _total, BYOT3_ Permeable Pavement _total).
- System-wide LID Totals: Total area for each LID type across the entire study area (e.g., Total_ Bioretention Facilities, Total_ Permeable Pavement, Total_ Green Roofs).
- Overall Aggregate Totals: Total combined LID area for each region (BYOT2_LID_Total, BYOT3_LID_Total) and the entire system (Total_LID), as well as total storage (Storage_total).
- (2)
- Non-negativity Constraints (Post-processing)
2.3. Multi-Objective Optimization Framework
2.3.1. Optimized Objective Functions for CSO Control
2.3.2. Decision Variables and Constraints
2.3.3. Algorithm Configuration
2.4. Performance Evaluation and Analysis
3. Results
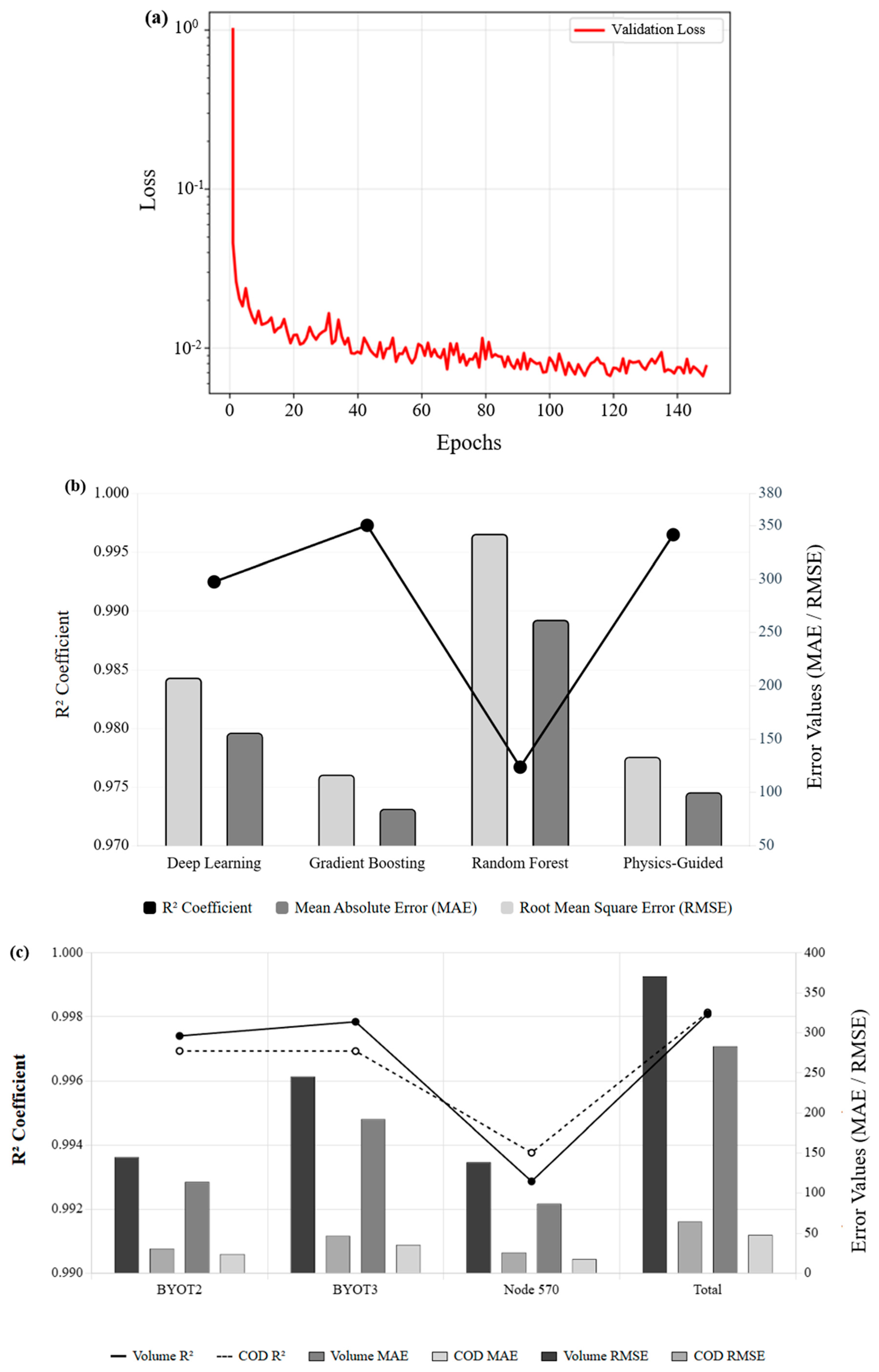
3.1. Surrogate Model Development and Validation
3.1.1. Surrogate Model Performance and Selection
3.1.2. Feature Importance Analysis
3.2. Multi-Objective Optimization Performance
3.2.1. Performance Metrics and Solution Quality
3.2.2. Pareto Front Characteristics and Trade-Off Analysis
3.2.3. Computational Efficiency and Validation
3.3. Optimized System Performance Analysis
3.3.1. Representative Solution Selection and Configuration
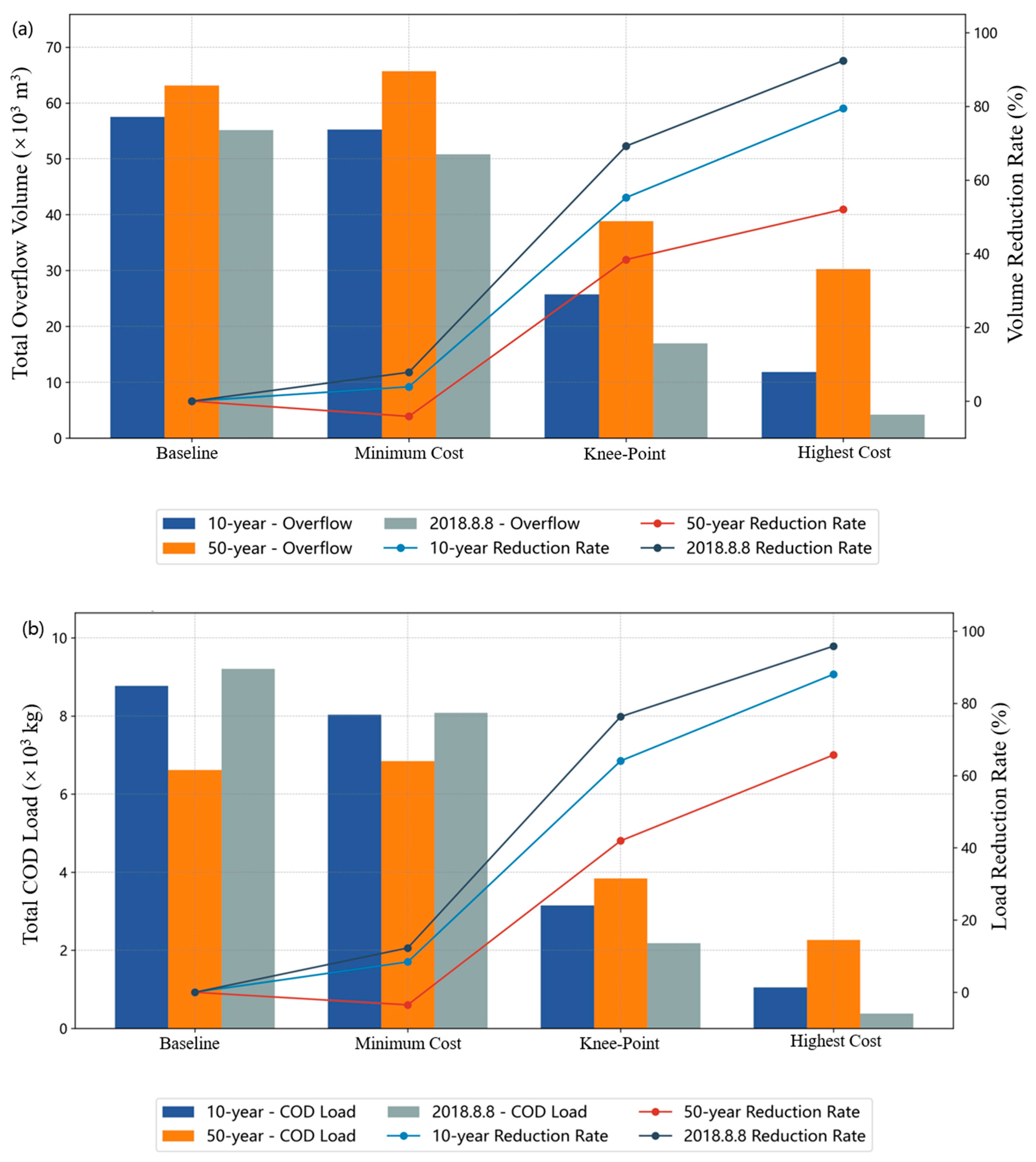
3.3.2. Performance Under Design Rainfall Conditions
3.3.3. System Resilience Under Variable Rainfall Conditions
3.3.4. Sensitivity Analysis and Component Contributions
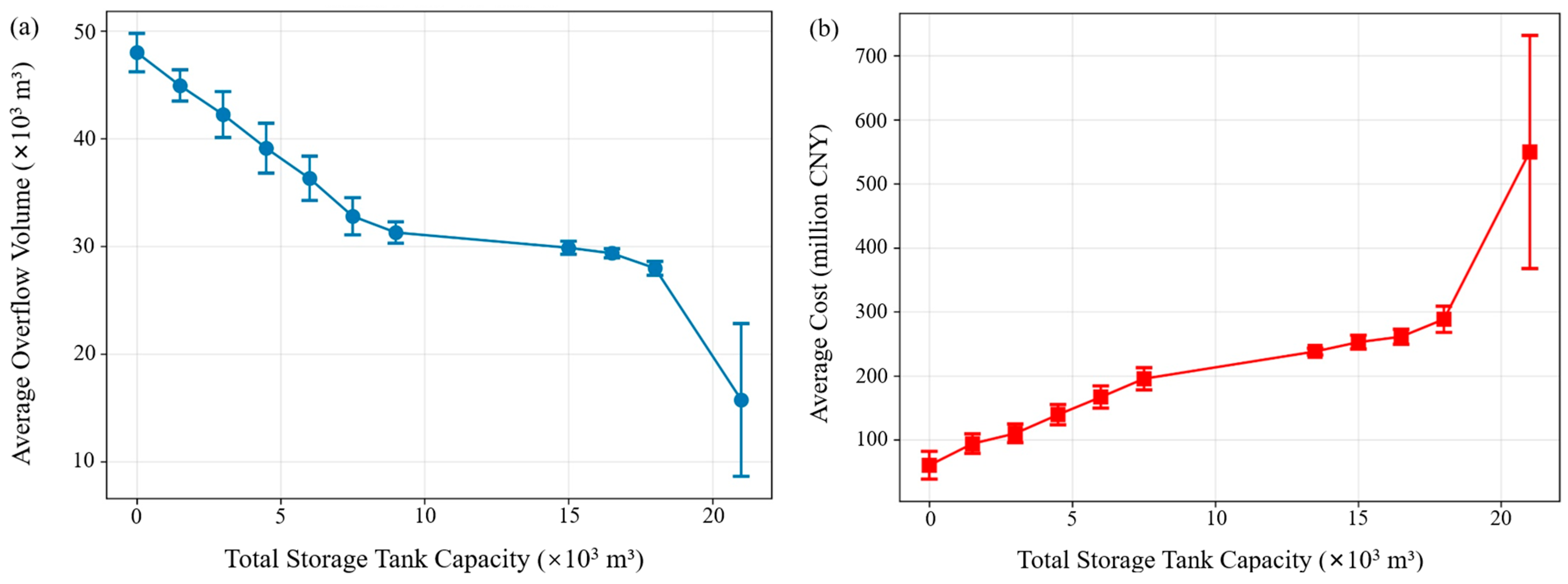
3.3.5. Storage Tanks Capacity Optimization Patterns
3.4. Economic Assessment and Implementation Benefits
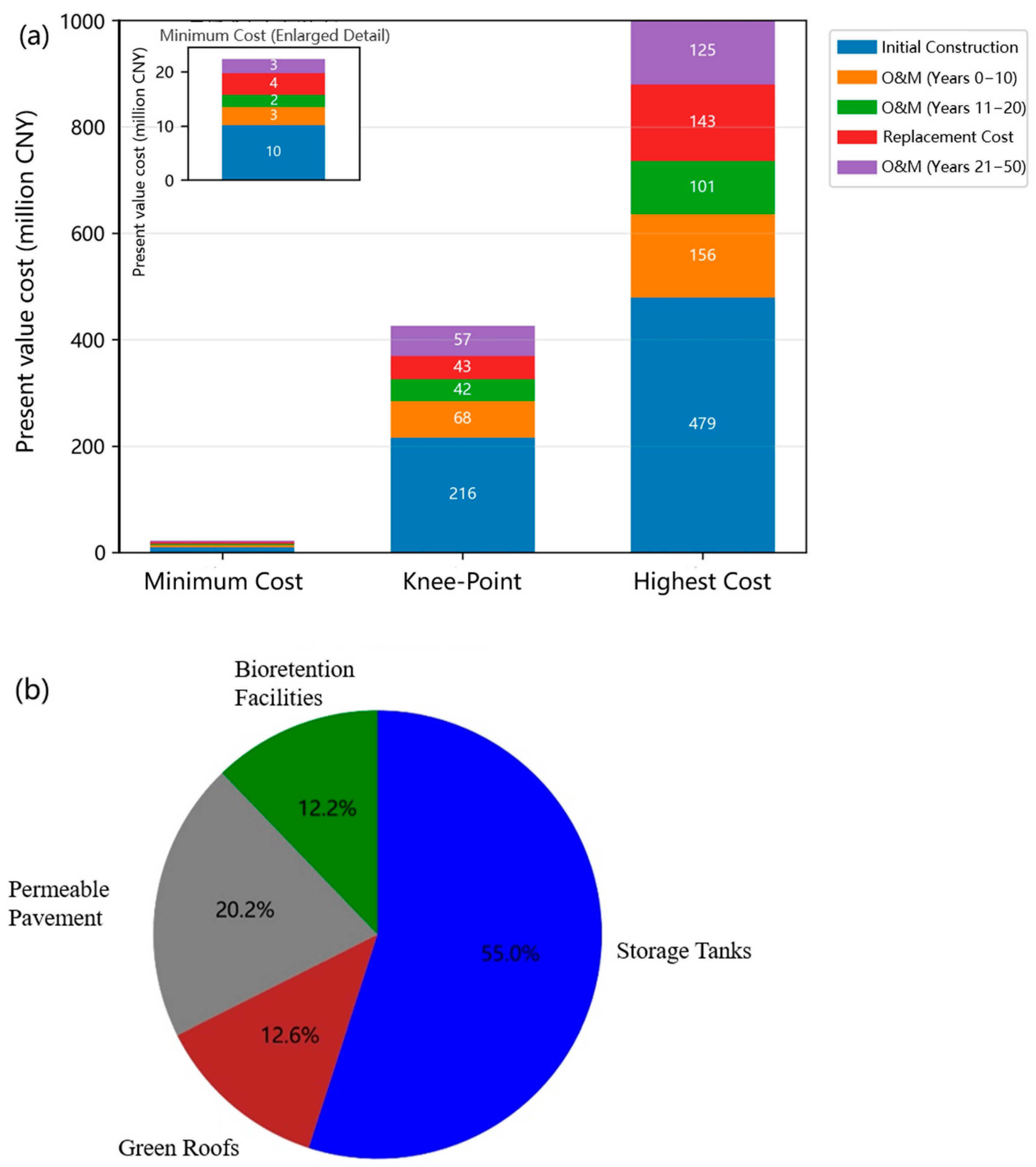
3.4.1. Life-Cycle Cost Analysis and Investment Structure
3.4.2. Component Economic Optimization and Configuration Rationale
4. Discussion
4.1. Methodological Innovations in CSO Control Optimization
4.2. Economic Optimality and the Principle of Diminishing Returns
4.3. System Performance and Climate Resilience
4.4. Implementation Considerations and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, X.; Liao, Z.; Zhang, G.; Xie, J.; Zhang, J. Modelling the Effects of Water Diversion and Combined Sewer Overflow on Urban Inland River Quality. Environ. Sci. Pollut. Res. 2017, 24, 21038–21049. [Google Scholar] [CrossRef]
- Reyes-Silva, J.D.; Bangura, E.; Helm, B.; Benisch, J.; Krebs, P. The Role of Sewer Network Structure on the Occurrence and Magnitude of Combined Sewer Overflows (CSOs). Water 2020, 12, 2675. [Google Scholar] [CrossRef]
- Gogien, F.; Dechesne, M.; Martinerie, R.; Kouyi, G.L. Assessing the Impact of Climate Change on Combined Sewer Overflows Based on Small Time Step Future Rainfall Timeseries and Long-Term Continuous Sewer Network Modelling. Water Res. 2023, 230, 119504. [Google Scholar] [CrossRef] [PubMed]
- Perry, W.B.; Ahmadian, R.; Munday, M.; Jones, O.; Ormerod, S.J.; Durance, I. Addressing the Challenges of Combined Sewer Overflows. Environ. Pollut. 2024, 343, 123225. [Google Scholar] [CrossRef] [PubMed]
- Rathnayake, U. Migrating Storms and Optimal Control of Urban Sewer Networks. Hydrology 2015, 2, 230–241. [Google Scholar] [CrossRef]
- Cuce, P.M.; Cuce, E.; Santamouris, M. Towards Sustainable and Climate-Resilient Cities: Mitigating Urban Heat Islands Through Green Infrastructure. Sustainability 2025, 17, 1303. [Google Scholar] [CrossRef]
- Dong, X.; Guo, H.; Zeng, S. Enhancing Future Resilience in Urban Drainage System: Green versus Grey Infrastructure. Water Res. 2017, 124, 280–289. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, D.; Adhityan, A.; Ng, W.J.; Dong, J.; Tan, S.K. Assessing Cost-Effectiveness of Bioretention on Stormwater in Response to Climate Change and Urbanization for Future Scenarios. J. Hydrol. 2016, 543, 423–432. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; TIK-Report 103; Computer Engineering and Networks Laboratory (TIK), ETH Zurich: Zurich, Switzerland, 2001; p. 21. [Google Scholar]
- Eckart, K.; McPhee, Z.; Bolisetti, T. Multiobjective Optimization of Low Impact Development Stormwater Controls. J. Hydrol. 2018, 562, 564–576. [Google Scholar] [CrossRef]
- Macro, K.; Matott, L.S.; Rabideau, A.; Ghodsi, S.H.; Zhu, Z. OSTRICH-SWMM: A New Multi-Objective Optimization Tool for Green Infrastructure Planning with SWMM. Environ. Model. Softw. 2019, 113, 42–47. [Google Scholar] [CrossRef]
- Wang, B.; Gong, Y.; Li, X.; Zhang, Y.; Li, Z. Multi-Objective Optimization of Urban Stormwater Systems. J. Environ. Manag. 2025, 386, 125671. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liu, J.; Mei, C.; Wang, H.; Lu, J. A Multi-Objective Optimization Model for Synergistic Effect Analysis of Integrated Green-Gray-Blue Drainage System in Urban Inundation Control. J. Hydrol. 2022, 609, 127725. [Google Scholar] [CrossRef]
- Feng, W.; Wang, C.; Lei, X.; Wang, H. A Simplified Modeling Approach for Optimization of Urban River Systems. J. Hydrol. 2023, 623, 129689. [Google Scholar] [CrossRef]
- Garzón, A.; Kapelan, Z.; Langeveld, J.; Taormina, R. Machine Learning-Based Surrogate Modeling for Urban Water Networks: Review and Future Research Directions. Water Resour. Res. 2022, 58, e2021WR031808. [Google Scholar] [CrossRef]
- Tripathy, K.P.; Mishra, A.K. Deep Learning in Hydrology and Water Resources Disciplines: Concepts, Methods, Applications, and Research Directions. J. Hydrol. 2024, 628, 130458. [Google Scholar] [CrossRef]
- Li, B.; Li, R.; Sun, T.; Gong, A.; Tian, F.; Khan, M.Y.A.; Ni, G. Improving LSTM Hydrological Modeling with Spatiotemporal Deep Learning and Multi-Task Learning: A Case Study of Three Mountainous Areas on the Tibetan Plateau. J. Hydrol. 2023, 620, 129401. [Google Scholar] [CrossRef]
- Wan, H.; Xu, R.; Zhang, M.; Cai, Y.; Li, J.; Shen, X. A Novel Model for Water Quality Prediction Caused by Non-Point Sources Pollution Based on Deep Learning and Feature Extraction Methods. J. Hydrol. 2022, 612, 128081. [Google Scholar] [CrossRef]
- Roy, A.M.; Guha, S. A Data-Driven Physics-Constrained Deep Learning Computational Framework for Solving von Mises Plasticity. Eng. Appl. Artif. Intell. 2023, 122, 106049. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, S.; Zheng, Y.; Han, F.; Kumar, R.; Rakovec, O.; Li, S. Distributed Hydrological Modeling With Physics-Encoded Deep Learning: A General Framework and Its Application in the Amazon. Water Resour. Res. 2024, 60, e2023WR036170. [Google Scholar] [CrossRef]
- Gong, Y.; Chen, Y.; Yu, L.; Li, J.; Pan, X.; Shen, Z.; Xu, X.; Qiu, Q. Effectiveness Analysis of Systematic Combined Sewer Overflow Control Schemes in the Sponge City Pilot Area of Beijing. Int. J. Environ. Res. Public Health 2019, 16, 1503. [Google Scholar] [CrossRef] [PubMed]
- GB/T 51345-2018; Assessment Standard for Sponge City Construction. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, China Architecture & Building Press: Beijing, China, 2018.
- Chan, A.L.S.; Chow, T.T. Energy and Economic Performance of Green Roof System Under Future Climatic Conditions in Hong Kong. Energy Build. 2013, 64, 182–198. [Google Scholar] [CrossRef]
- Houle, J.J.; Roseen, R.M.; Ballestero, T.P.; Puls, T.A.; Sherrard, J. Comparison of Maintenance Cost, Labor Demands, and System Performance for LID and Conventional Stormwater Management. J. Environ. Eng. 2013, 139, 932–938. [Google Scholar] [CrossRef]
- Hu, M.; Zhang, X.; Siu, Y.L.; Li, Y.; Tanaka, K.; Yang, H.; Xu, Y. Flood Mitigation by Permeable Pavements in Chinese Sponge City Construction. Water 2018, 10, 172. [Google Scholar] [CrossRef]
- Jia, H.; Yao, H.; Tang, Y.; Yu, S.L.; Field, R.; Tafuri, A.N. LID-BMPs Planning for Urban Runoff Control and the Case Study in China. J. Environ. Manag. 2015, 149, 65–76. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Li, H.; Zhang, C.; Chen, M.; Shen, D.; Niu, Y. Data-Driven Surrogate Modeling: Introducing Spatial Lag to Consider Spatial Autocorrelation of Flooding within Urban Drainage Systems. Environ. Model. Softw. 2023, 161, 105623. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, W.; Feng, Q.; Zeng, J. Multi-Objective Optimization of the Spatial Layout of Green Infrastructures with Cost-Effectiveness Analysis Under Climate Change Scenarios. Sci. Total Environ. 2024, 948, 174851. [Google Scholar] [CrossRef]
- Roseboro, A.; Torres, M.N.; Zhu, Z.; Rabideau, A.J. The Impacts of Climate Change and Porous Pavements on Combined Sewer Overflows: A Case Study of the City of Buffalo, New York, USA. Front. Water 2021, 3, 725174. [Google Scholar] [CrossRef]
- Sun, C.; Rao, Q.; Wang, M.; Liu, Y.; Xiong, Z.; Zhao, J.; Fan, C.; Rana, M.A.I.; Li, J.; Zhang, M. Multi-Stage Optimization of Drainage Systems for Integrated Grey–Green Infrastructure Under Backward Planning. Water 2024, 16, 1825. [Google Scholar] [CrossRef]
- Dandy, G.; Wu, W.; Simpson, A.; Leonard, M. A Review of Sources of Uncertainty in Optimization Objectives of Water Distribution Systems. Water 2023, 15, 136. [Google Scholar] [CrossRef]
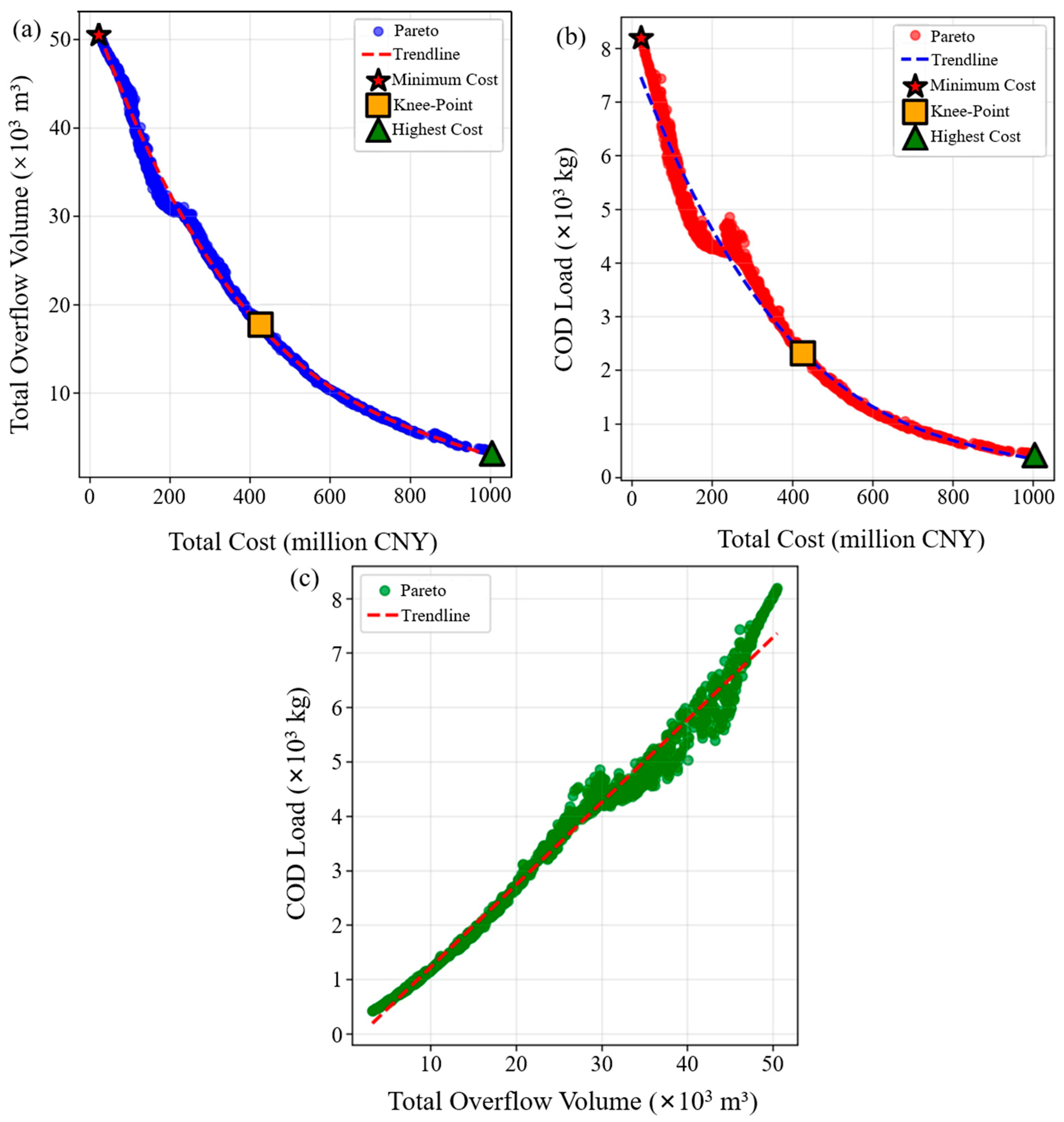
| Algorithm | Number of Solutions | Overflow Volume Standard Deviation (×103 m3) | COD Load Standard Deviation (×103 kg) | Cost Standard Deviation (Million CNY) | Spread | Spacing Indicator | Hypervolume Indicator |
|---|---|---|---|---|---|---|---|
| NSGA-II | 1255 | 13.30 | 2.03 | 24 | 1.732 | 0.0027 | 143,426,935 |
| OMOPSO | 950 | 14.97 | 2.29 | 29 | 1.728 | 0.0044 | 131,023,527 |
| NSGA-III | 853 | 12.04 | 1.88 | 22 | 1.732 | 0.0041 | 86,903,330 |
| SPEA2 | 943 | 9.76 | 1.49 | 17 | 1.731 | 0.0044 | 72,853,662 |
| Metric | Current Status | Minimum Cost | Knee-Point | Highest Cost |
|---|---|---|---|---|
| Bioretention Area (×103 m2) | 0 | 8.80 | 45.63 | 327.70 |
| Permeable Pavement Area (×103 m2) | 0 | 11.86 | 120.33 | 354.83 |
| Green Roof Area (×103 m2) | 0 | 5.47 | 77.91 | 206.63 |
| Storage Tanks (×103 m3) | 0 | 0 | 21 | 21 |
| Overflow Volume (×103 m3) | 53.79 | 50.49 | 17.74 | 3.19 |
| Overflow Volume Reduction rate (%) | 0 | 6.1 | 67.0 | 94.1 |
| Overflow COD Load (×103 kg) | 9.01 | 8.19 | 2.31 | 0.42 |
| Overflow COD Load Reduction rate (%) | 0 | 9.1 | 74.4 | 95.3 |
| Total Cost (million CNY) | 0 | 23 | 426 | 1005 |
| Overflow Reduction-to-Cost Ratio (%/10 M CNY) | 0 | 2.7 | 1.6 | 0.9 |
| COD Reduction-to-Cost Ratio (%/10 M CNY) | 0 | 4.0 | 1.8 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Gao, J.; Wang, M.; Gong, Y. A Physics-Guided Optimization Framework Using Deep Learning Surrogates for Multi-Objective Control of Combined Sewer Overflows. Water 2025, 17, 3255. https://doi.org/10.3390/w17223255
Li T, Gao J, Wang M, Gong Y. A Physics-Guided Optimization Framework Using Deep Learning Surrogates for Multi-Objective Control of Combined Sewer Overflows. Water. 2025; 17(22):3255. https://doi.org/10.3390/w17223255
Chicago/Turabian StyleLi, Tianyu, Jiabin Gao, Mengge Wang, and Yongwei Gong. 2025. "A Physics-Guided Optimization Framework Using Deep Learning Surrogates for Multi-Objective Control of Combined Sewer Overflows" Water 17, no. 22: 3255. https://doi.org/10.3390/w17223255
APA StyleLi, T., Gao, J., Wang, M., & Gong, Y. (2025). A Physics-Guided Optimization Framework Using Deep Learning Surrogates for Multi-Objective Control of Combined Sewer Overflows. Water, 17(22), 3255. https://doi.org/10.3390/w17223255







