Evaluation of Priority Queues in the Priority Flood Algorithm for Hydrological Modelling

Abstract

The Priority-Flood algorithm, widely recognized for its computational efficiency in hydrological analysis, serves as the fundamental method for depression identification in DEMs, and the efficiency of the Priority-Flood algorithm hinges largely on the core component—priority queue implementation. Existing studies have focused predominantly on reducing the amount of data processed by queues, with few systematic reports on concrete queue implementations and corresponding performance analyses. In this study, six priority queues in the Priority-Flood algorithm are compared: a mini-heap (Heap), an AVL tree, a red-black tree (RBTree), a pairing heap (PairingHeap), a skip list (SkipList), and the Hash Heap (HHeap) structure proposed herein. Using multiscale DEM datasets as benchmarks, the results show that HHeap consistently outperforms the other structures across all scales, with particular advantages in ultralarge queues and in scenarios with high data duplication, rendering it the most effective choice for priority queues. The pairing heap approach typically ranks second in terms of overall runtime, whereas the AVL tree exhibits stable performance across scales; min-heap shows pronounced weaknesses under large-scale data conditions. This study provides empirical evidence to guide efficient priority queue selection and implementation and offers a viable technical pathway for ultralarge-scale terrain analysis. Future work will explore integrating HHeap with learning-based sorting and parallelization to further enhance processing performance and robustness in massive DEM contexts.

1. Introduction

The preprocessing of digital element models (DEMs) to remove topographic depressions represents a critical challenge in physically based hydrological modelling [1,2,3,4,5,6]. Unresolved depressions induce artificial flow path distortions, erroneous confluence computations, and other hydrological artefacts, thereby significantly degrading the reliability of watershed-scale hydrological simulations [7].

The Priority-Flood algorithm is an efficient depression preprocessing algorithm. Owing to its well-defined physical mechanisms and computational efficiency, this algorithm has emerged as the prevailing approach for DEM depression preprocessing [8,9,10]. Despite ongoing debates regarding its modification of original DEM data and parallel river network artefacts, the algorithmic stability of Priority-Flood provides a robust foundation for further optimization of computational performance [11,12,13,14,15]. This reliability has enabled scholars to concentrate exclusively on algorithmic efficiency enhancements, yielding substantial academic advancements in the field [16,17].

Overall, current research on improving the efficiency of priority flood algorithms focuses primarily on developing high-performance parallel mechanisms. However, the performance of parallel algorithms is often constrained by the efficiency of their underlying serial counterparts; thus, the optimization of serial algorithms remains a critical research area [18,19,20,21]. Notably, existing studies on optimizing serial priority flood algorithms have mostly concentrated on reducing the data volume processed by the priority queue [22], while systematic research on optimizing the efficiency of the priority queue structure itself is lacking. Researchers such as Barnes et al. (2014) have pioneered a methodology utilizing a plain queue structure for storing depression region grids, which was the first empirical validation of the feasibility of raster classification processing [23]. Zhou et al. (2016) further refined this approach by significantly reducing the number of cells handled by the priority queue [24]. Wei et al. (2019) analyzed the depression cell queuing mechanism and achieved a 70% reduction in queue data volume [25]. Cordonnier et al. (2019) transformed the problem into a node-based graph search model, effectively eliminating the efficiency constraints inherent in priority queues [26,27]. However, this approach may be terrain dependent and has shown inferior performance compared with Barnes’ method in depression-dense regions [28].

Although the aforementioned refinements markedly reduce the data footprint of the priority queue, the refined algorithms consistently rely on conventional priority queues (min heap) for data processing, leaving room for further increases in sorting efficiency. As a fundamental data structure, priority queues demonstrate substantial performance advantages in various applications requiring dynamic sorting, including image recognition, traffic scheduling, data compression, and discrete event simulation [29,30]. While individual priority queue operations (push and pop) are typically completed within microsecond timescales, the cumulative access time becomes the dominant performance bottleneck when millions of such operations are executed [31]. Research on increasing the processing speed of the priority queue in the Priority-Flood algorithm is important for increasing the algorithm’s operational efficiency.

Noteworthy papers comparing priority queues occasionally appear, but dedicated studies for terrain-analysis applications remain relatively scarce. In related efforts, Bai et al. (2015) experimented with using balanced binary trees (AVL trees) to increase queue-sorting efficiency, achieving favourable results [32]. However, numerous structures and implementations have emerged that outperform AVL trees in practical computations, and systematic comparative studies focusing on specific terrain analysis tasks, such as DEM depression processing, remain inadequate.

Time complexity is a common indicator used to evaluate the efficiency of queues. However, under the influence of multilevel caches and pipeline cores in modern computing architecture, accurately reflecting the actual performance of queues is difficult, so balancing theory and practice [33] is necessary. For example, data structures such as red-black trees (RBTree), pairing heaps (PairingHeap), skip lists (SKipList), and min-heaps (Heap) exhibit similar theoretical time complexity; however, their practical performance is significantly influenced by cache behaviour and branch prediction [34]. Although the performance characteristics of these structures have been validated in graph algorithms, the effects of their applicability and efficiency in the specific context of DEM-based depression identification remain systematically understudied.

This study seeks to address this research gap by systematically investigating and evaluating the performance of multiple advanced data structures—including Heap, AVL Tree, RBTree, PairingHeap, SKipList, and the proposed hash-backed heap (HHeap)—through metrics such as memory consumption and execution time. This research aims to characterize their performance using the specific access patterns of the Priority-Flood algorithm, establish their relative merits, and identify suitable application scenarios. This work ultimately provides a technical pathway for enhancing the performance of Priority-Flood algorithms.

2. Materials and Methods

2.1. Data

2.1.1. Dataset

A typical depression-dense region in Minnesota, USA (commonly referred to as the “Land of 10,000 Lakes”), was selected as the research site. High-resolution LiDAR-derived DEM data (with resolutions ranging from 1 to 3 m; source: https://resources.gisdata.mn.gov/pub/data/elevation/, accessed on 10 October 2024.). Through this integration, 9 test datasets spanning grid scales from millions to tens of billions of cells were constructed (Table 1). The largest dataset contained 10.8 billion grid cells, effectively simulating ultralarge-scale terrain processing scenarios encountered in practical engineering applications.

Table 1. Datasets used in this study, including cell width, height, and number of cells.

NO.	Width	Height	Number
1	8236	22,030	181,439,080
2	17,252	11,673	201,382,596
3	13,938	15,116	210,686,808
4	16,897	16,427	277,567,019
5	21,925	13,967	306,226,475
6	21,037	15,412	324,222,244
7	19,409	17,116	332,204,444
8	27,160	18,307	497,218,120
9	20,311	33,681	684,094,791

All the algorithms listed in Section 2.2 are implemented and evaluated. The code used is publicly available online at https://github.com/riverbasin2021/Priority-HHeap, accessed on 10 October 2024.

The experimental platform was configured with an Intel Core i7-14700(Intel corporation, Santa Clara, CA, USA) processor (2.10 GHz) and 64 GB of DDR5 memory. The algorithm was implemented in Microsoft Visual C++ using the Visual Studio 2022 compiler (version 17.14.6).

2.1.2. Test Plan

The computational workflow of the Priority-Flood algorithm can be systematically decomposed into three core phases. In phase one, the boundary cells of the DEM are inserted into a priority queue, forming the algorithm’s initial working set. In phase two, the lowest-elevation cell is dynamically extracted from the priority queue and marked as processed. In phase three, the eight-neighbourhood of that cell is traversed, and the unprocessed neighbouring cells are reinserted in ascending order of elevation so that they propagate in subsequent iterations according to the global minima. Because the efficiency of each phase is directly influenced by the chosen priority queue implementation, the distribution of time across phases and the memory footprint prominently reflects the differences among various implementations.

To quantitatively assess the performance differentials among various priority-queue architectures across the stages, this study designs two targeted test suites. The first, described in Section 3.1, evaluates processing efficiency by recording enqueue and dequeue times. The second, described in Section 3.2, simulates dynamic variations in queue size to test stability and throughput in scenarios where extreme values are frequently extracted. Finally, by employing real terrain datasets, Section 3.3 compares the memory footprint and total runtime of the competing priority-queue schemes. An experimental workflow diagram illustrates the three stages and their performance evaluation trajectories across implementations, facilitating comparison with actual datasets (Figure 1).

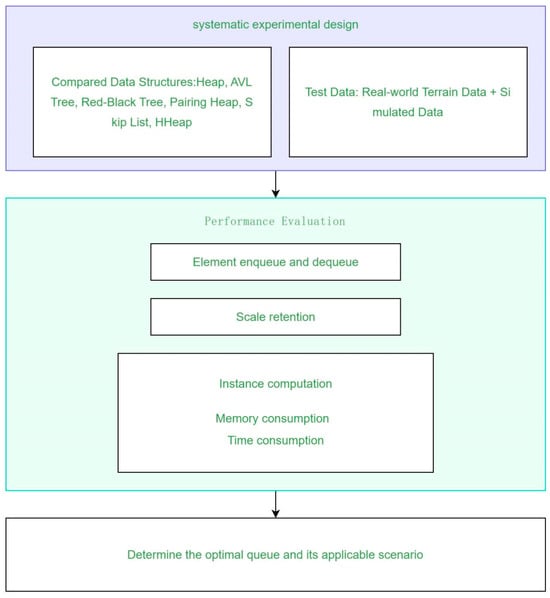
Figure 1. Experimental flowchart.

2.2. Algorithm

2.2.1. Heap

Heap (min-heap) is a conventional priority queue offering an O(log N) performance (where N denotes the number of items in the queue) [35]. The min-heap property requires that each element’s priority surpass its two children, preserving this invariant at all times. Consequently, the highest-priority element always resides at the root of the tree. This characteristic makes heaps a widely used data structure in the Priority-Flood algorithm because it guarantees that the highest-priority units are processed first. However, during the computation of the Priority-Flood algorithm, one must pop the highest-priority element and examine all adjacent cells to enqueue them. If the priority of a cell to be updated is lower than that of the root, a global reconfiguration from the root is triggered (Figure 2a). This dynamic adjustment mechanism of the heap collides fundamentally with the access pattern of the Priority-Flood algorithm, becoming a critical performance bottleneck. By contrast, when newly encrypted data do not induce frequent heap adjustments or when the priority distribution minimizes the need for upwards percolation, the algorithm’s throughput is markedly enhanced.

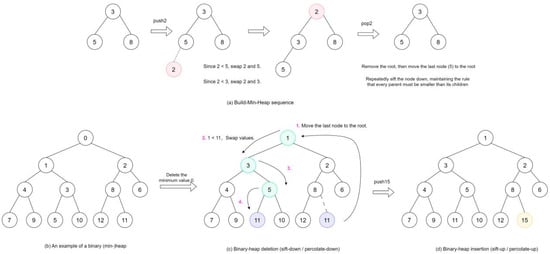
Figure 2. Concept of heap. (a) illustrates the insertion and heap adjustment processes of a binary heap (min-heap) for grid nodes. Insertion of an element requires the heap to percolate from bottom to top, and after the root is removed, the last element is moved to the root position and then percolated downwards; (b) an example of a deletion operation for heap; (c) an example of a insertion operation for heap.

An example of min-heap is shown in Figure 2b. After the minimum value of 0 is removed, the root is replaced by the last element, 11, followed by a top-down sift-down adjustment (Figure 2c): 11 is compared with its left and right children; if a child smaller than 11 exists, 11 is sunk and swapped with the smaller child; after the swap, it is compared with its new children, and this process is repeated until no child is smaller than 11, thereby restoring the heap property. When node 15 is inserted, it is placed at the end and percolated upwards (Figure 2d); since its parent, 8, is smaller than 15, no swap is needed, and the adjustment terminates.

2.2.2. AVL Tree

Compared with heaps implemented via arrays, a pointer-based binary search tree offers greater structural flexibility [32]. In a binary search tree, nodes are linked by pointers, and moving or reorganizing nodes typically involves simply reassigning or swapping pointers rather than copying the data stored in the nodes themselves. The AVL tree is a class of self-balancing BSTs that preserves the core property of ordinary BSTs: every node’s left subtree contains values less than the node’s value, and every node’s right subtree contains values greater than the node’s value. This property maintains the orderly arrangement of data within the tree. Moreover, a balanced BST maintains a balance indicator for each node to measure the local height difference, ensuring that the height disparity between the left and right subtrees of any node does not exceed 1, thereby resulting in the worst-case time complexity of the insert, delete, and search operations O(log n). This stringent balance endows AVL trees with notable advantages in query-intensive applications, particularly in scenarios where lookups far outnumber data updates (Figure 3).

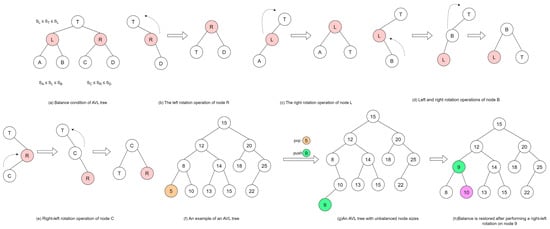
Figure 3. Concept of the AVL tree. SA, SL, and SB denote the values of nodes A, L, and B, respectively. (a) balance condition of AVL Tree; (b) an example of left rotation operation for node R; (c) an example of right rotation operation for node r; (d) an example of left–right rotation operation for node r; (e) an example of right–left rotation operation for node r; (f–h) illustrate a single operation on the AVL tree.

2.2.3. RBTree

AVL trees guarantee stable sorting performance through rigorous balancing, but this introduces additional computational overhead because of node rotations [36]. RBTree maintains an approximately balanced tree structure via node colour attributes (each node is either red or black) and supplementary constraints [37], trading these for fewer structural rotations (Figure 4). Consequently, the time complexity of red-black trees is on par with that of AVL trees, yet the number of rotations required during insertions and deletions is typically lower. Owing to the reduced rotation count, red-black trees often outperform AVL trees in general scenarios that demand efficient dynamic updates while also requiring high query performance.

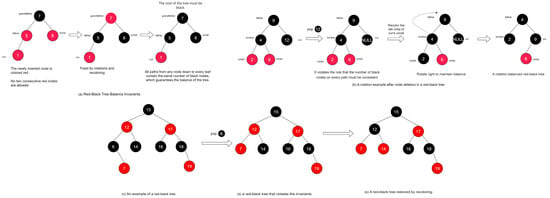
Figure 4. Concept of RBTree. (a) “brother” denotes the sibling node, whereas “lchild” and “rchild” denote the left and right child nodes, respectively. “Cur” represents the newly processed node. (b) shows the adjustment process that a red-black tree undertakes after a node is deleted to maintain the red-black properties. The adjustment process includes recolouring and, in certain cases, rotations (left rotation/right rotation) to ensure that no two consecutive red nodes appear and to preserve the same number of black nodes on every path from any node to its leaves. (c–e) illustrate an instance of a red-black tree.

2.2.4. Pairing Heap

Compared with a fully ordered and more complex red-black tree used as a priority queue, the pairing heap offers a simpler implementation with advantageous amortized performance characteristics (Figure 5). A pairing heap is built upon two basic operations—linking and pairing [38]—and regards the heap as a forest of root nodes, maintaining the heap-order property through successive pairwise merge operations [39]. Its insert, merge, and find-min operations are highly efficient in most implementations, typically outperforming binary heaps. In both theoretical analyses and empirical studies, the amortized times for insert, merge, and find-min operations are O(1); delete-min requires several rounds of pairing and merging among the root subtrees, with an amortized time of O(log n). Consequently, pairing heaps are particularly well suited for scenarios that demand frequent insertions and the extraction of the minimum (or maximum) element.

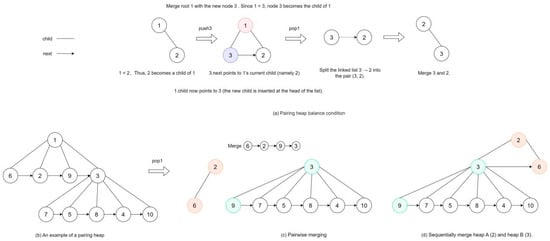
Figure 5. Concept of pairing heaps. (a) Illustration of the pairing heap process during the insertion and deletion of nodes. (b–d) demonstrate the structural changes in the pairing heap after the minimum value node has been removed. When the heap needs to delete node 1, all of node 1’s children are detached and then merged into pairs. Node 6 is merged with node 2, and node 9 is merged with node 3. Finally, a sequential merge operation is performed, merging node 2 with node 3. Since 3 < 2, node 3 attaches its children so that they all become children of node 2, and the next pointer points to the head of node 2’s child list.

2.2.5. Skip List

Skip lists (Figure 6) are probabilistic data structures designed for rapid searches within an ordered sequence that are capable of reliably extracting the minimum element (pop) and inserting adjacent elements (push) in the logarithm of the expected time without the need for global restructuring [40]. This property aligns closely with the needs of the priority flood algorithm, which frequently retrieves the lowest node and inserts adjacent nodes. Moreover, the multilevel index structure of skip lists naturally supports efficient range queries, avoiding the overhead associated with the min-heap repeatedly popping boundary points. In the flood-filling process, updates to neighbouring nodes after local depressions are filled typically require only adjustments to adjacent pointers, without rotations or rebalancing as in red–black trees, thereby reducing the constant factor. The time complexities for search, insertion, and deletion operations in a skip list are O(log n) on average, with the performance depending on the level-generation strategy and the maximum height setting. The skip list implemented in this work sets the maximum height to 20; height advancement employs a fixed-probability random-increment strategy, with each node promoted to the next level with a 30% probability until the maximum height is reached [41]. To increase generation efficiency, random-number generation is implemented via bitwise operations, using a 16-bit random mask and precomputed probability thresholds for comparison, maintaining distribution balance while speeding up the generation of random levels.

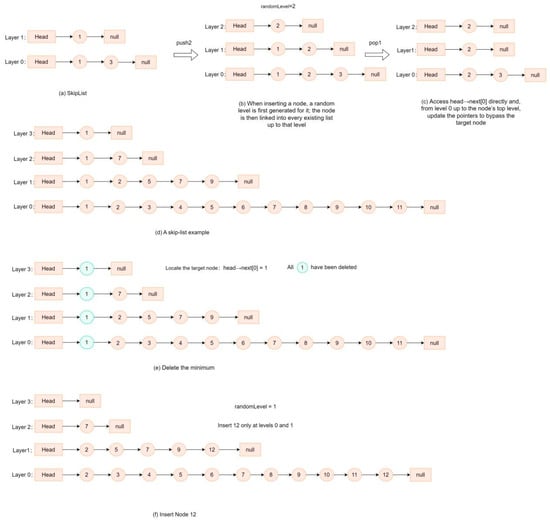
Figure 6. Concept of a skip list. (a) Illustration of the layered, multilevel linked-list structure of a skip list. (b) Insertion process: the new node’s level is determined by a random-generation mechanism, after which the node is inserted at the corresponding levels. (c) Deletion of the minimum-value node, in which the node pointed to by head→next [0] is accessed directly, and pointers are updated from the bottom layer up to its highest level to bypass the target node. (d–f) State changes in a skip list after the minimum value of 1 are deleted and the new value of 12 is inserted.

2.2.6. HHeap

By virtue of their multilevel indexing, skip lists theoretically achieve efficient insertions and deletions (amortized O(log n)) and demonstrate excellent performance on dynamic datasets. However, in specialized scenarios that require frequent handling of floating-point priorities and very large data volumes, the logarithmic time complexity of skip lists may still become a bottleneck for algorithmic efficiency. To address this issue, this paper proposes a HHeap structure to enhance the performance of priority queues. HHeap fully exploits data redundancy by distributing the N elements of the priority queue into k buckets using hash buckets, thereby reducing the average size of each heap by a factor of k and lowering the enqueue and dequeue costs to O(log(K)). The corresponding allocation function is relatively simple H(spill) = spill/1.00, where spill denotes the elevation value of a grid cell and serves as the priority in the Priority-Flood algorithm. Moreover, this work abstracts a bucket as a data node and maintains the ordering among data nodes with a heap structure.

The complete workflow for extracting data from DEMs and constructing a hash-heap based on hash buckets is shown in Figure 7. Elevation samples are mapped to k buckets by a hash function; samples sharing identical elevation values coalesce within the same bucket, and the data inside each bucket are organized as a linked list to support efficient insertion and deletion. Globally, the hash heap is maintained by an external min-heap: each bucket corresponds to an external heap node whose key records the bucket’s current minimum elevation (since all the elements within a bucket share the same elevation, the bucket’s minimum value equals that elevation). When the global minimum from the hash heap is popped, the corresponding bucket identifier is first retrieved from the external heap; then, the bucket is located, and one sample with that elevation is removed (typically from the bucket’s head or tail to preserve the O(1) update). If the bucket remains nonempty after removal, its minimum value remains unchanged, and no further adjustment to the external heap is needed; if the bucket becomes empty, the bucket node is removed from the external heap to maintain global ordering. Through this two-tier structure, HHeap ensures rapid extraction of the global minimum while reducing the scale of individual buckets, thereby increasing the efficiency for highly repetitive data and floating-point priority scenarios.

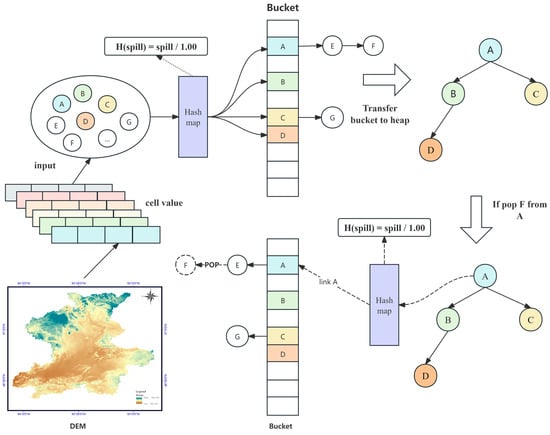
Figure 7. Concept of HHeap.

2.3. Algorithm Processing

The approach for implementing different data structures has a significant effect on the efficiency of priority queues. To maximize the priority queue performance, we adopt multiple key technical optimizations during implementation.

The efficiency of a priority queue is profoundly influenced by its implementation. To maximize priority-queue performance and ensure that all the data structures can be fairly compared, we employed multiple key optimization techniques across all the structures during implementation (Table 2). The handling approaches are detailed in the accompanying code.

Table 2. Four key techniques for optimizing the priority queue.

NO.	Width Optimization Strategies	Content	Benefits
1	Memory pool	Memory pool techniques further balance computational performance and memory efficiency through preallocation and mark-and-sweep reclamation.	Memory allocation and deallocation overhead are minimized, and cache locality is enhanced.
2	Memory cache	Access to heap nodes is optimized through a contiguous memory layout, leveraging cache locality to reduce cache misses and improve performance.	Cache misses are significantly reduced, thereby accelerating access to nodes.
3	Iteration replacing recursion	A while loop and explicit stacks or pointers are used to maintain the traversal path, thereby avoiding recursive calls.	The risk of stack overflow is eliminated; function-call overhead is minimized, making it suitable for handling massive data volumes.
4	Pointer to the minimum node	A pointer to the current global minimum element is dynamically maintained.	Achieve O(1) time complexity for the pop() operation, down from O(log N).

3. Results

3.1. Enqueuing and Dequeuing Times

The execution flow of the Priority-Flood algorithm begins with the initial enqueuing of boundary DEM data into a priority queue. In subsequent processing, queue elements are popped and processed one by one, with each element potentially triggering the enqueuing of its neighbouring cells. However, when a popped element at a given moment has all of its neighbouring cells already processed or already present in the queue, no new enqueuing events are triggered until the queue is completely drained. To quantify the difference in performance between the enqueuing and dequeuing stages, the time series curves of the queue’s filling and draining are plotted in Figure 8, which illustrates the temporal consumption characteristics of each stage.

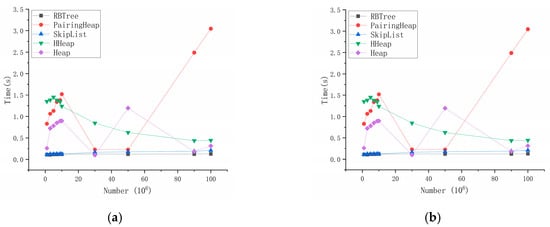
Figure 8. Average enqueue and dequeue speed per element. (a) Enqueue speed, which is the average time per enqueue, measured by dividing the time required to enqueue N elements into an initially empty queue by N. (b) Dequeue speed, which is the average time per dequeue, measured by dividing the time required to dequeue all N elements from a queue containing N elements by N.

To assess the performance of the priority queue during this phase, we construct a queue containing N elements, where each element is assigned a randomly generated priority value uniformly distributed within the range of [1000, 3000]. The time required to progressively populate the priority queue from an empty state to N elements is measured. Additionally, we record the total time taken to continuously execute dequeue operations until the queue is entirely emptied, starting from a state of N elements.

Notably, the execution time of priority queue operations increases linearly with data size, a phenomenon that is consistent with the empirical laws governing resource consumption in real-world applications. However, this trend reflects only changes in absolute time and does not directly convey the relative performance of priority queue operations across different data scales. To remove the confounding influence of absolute time units on performance evaluation, this study proposes using the operation time for processing one million data elements (1 × 10⁶) as a baseline. By plotting relative time curves across data scales (i.e., the ratio of the time at each scale to the baseline), we achieve cross-scale standardized performance comparisons. This normalization effectively decouples the data scale from absolute time, making per-operation time comparisons across scales more universal and comparable.

As shown in Figure 8, the enqueue time of the heap structures is weakly correlated with the data size N, with Heap, PairingHeap, and HHeap demonstrating excellent enqueue performance. PairingHeap records the shortest enqueue time, indicating the best performance; HHeap’s enqueue performance trails slightly behind that of Heap, but the performance gap narrows as the data size increases. The enqueue operation of HHeap requires additional maintenance of a bucket structure, which incurs an initial performance penalty. However, once the bucket size reaches a critical threshold, the newly encrypted data can directly reuse the existing buckets and heap nodes (Figure 8a), avoiding the repeated creation of structures and thereby achieving performance uplift.

As Hendriks (2010) demonstrated [33], compared with binary trees, heap extract-min operations are relatively expensive (Figure 8b). The extract-min performance of PairingHeap deteriorates as the data size increases, since PairingHeap is a leftist heap, and the merge operation traverses the heap’s left spine; as the size increases, the merge overhead increases, causing the extraction time to increase exponentially with scale. HHeap’s extract-min performance shows a marked improvement as the data scale increases, largely owing to its innovative K-bucket partition design. By distributing the priority-queue data across K independent buckets, the system effectively reduces the frequency of heap adjustments while also lowering the complexity of reallocation within buckets. Moreover, as explained by Doberkat [42], the performance results for red-black trees indicate that the time spent on insertions in binary trees is substantially greater than the time spent on deletions.

3.2. Hold Model

In the application of the Priority-Flood algorithm for depression identification, the computational process continuously repeats two operations: extracting the cell with the minimum value from the priority queue and importing its neighbouring grid cells. As the computation progresses, the data volume within the priority queue gradually increases. The performance characteristics of element extraction and insertion operations vary significantly at different priority queue scales. Evaluating the performance of this process is of paramount importance for elucidating the efficiency of priority queue data structures.

The Hold model, which serves as a conventional benchmark for performance evaluation [43,44], is intentionally simple and refrains from making excessive assumptions about the input dataset. Building on a dataset similar to that used in the previous section, this paper assumes a priority queue containing N elements and repeatedly performs a single operation 10⁶ times (a dequeue operation immediately followed by an enqueue operation) so that the timing function can record precise timing information [22]. Each time an element is dequeued, we increment it by a random value drawn from a uniform distribution in [0, 50] and re-enqueue this modified element; the results are shown in Figure 9.

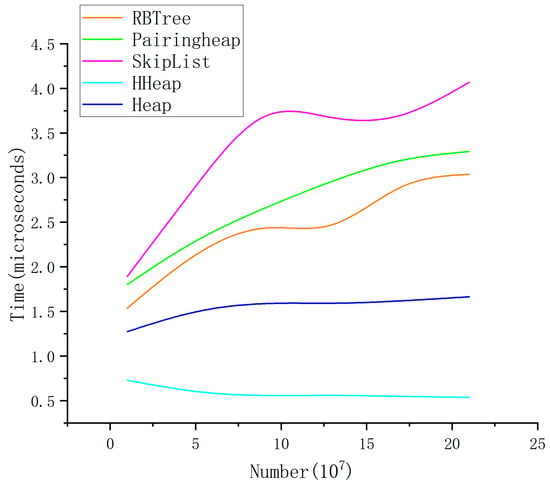
Figure 9. Speed of hold operation. The number denotes the number of elements in the queue, which ranges from 10⁶ to 10⁸. All except algorithms are O(log N) operations.

The results in Figure 8 demonstrate that the time per operation for all queues increases as the data scale increases, in line with the fundamental principle stating that data volume and processing time are positively correlated. However, several noteworthy features in the figure are analyzed in the remainder of this subsection.

SkipList exhibits the steepest growth curve, indicating that frequent insertions and deletions with large-scale data markedly impact its performance, rendering it unsuitable as the default choice for large-scale scenarios. PairingHeap theoretically offers favourable time complexity; however, in this experiment, its performance is comparable to that of RBTree, suggesting that the constants in its implementation with this access pattern do not significantly surpass those of a red-black tree. As a balanced binary search tree, RBTree maintains a well-balanced profile for the insert, delete, and search operations; hence, its curve rises more gradually with increasing data size. HHeap, as the data scale increases, increasingly demonstrates lower latency, becoming the most efficient structure in this study, which is attributable to implementation optimizations that reduce unnecessary comparisons or restructuring operations, thereby lowering the constant factor and increasing the actual runtime efficiency.

3.3. Practice

To demonstrate the importance of selecting an efficient priority queue in algorithm implementation, this study focuses on the Wang and Liu algorithm—a variant of the Priority-Flood algorithm—and replaces its default priority queue with the proposed implementation [10]. The goal is to quantitatively analyze how priority queue selection affects the algorithm’s overall performance.

3.3.1. Memory Requirements

In computer science, increasing memory usage to increase programme speed is a common optimization strategy. Its core principle lies in reducing CPU interactions with slower storage devices (e.g., disks), thereby minimizing I/O wait times. Below, we analyze the rationality of this strategy from both technical principles and experimental validation perspectives.

As shown in Figure 10, the memory consumption of all priority queues generally increases as the data scale increases, although notable variations exist among them.

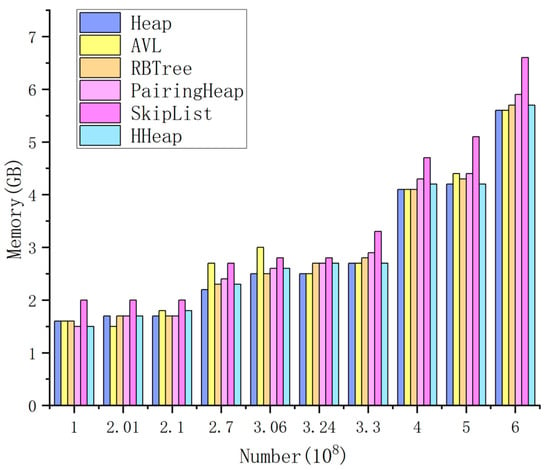
Figure 10. Memory requirements of the queues.

Skip lists exhibit higher memory usage for the same datasets, primarily because of their multilevel indexing design. The structure increases the query efficiency by building several levels of indexes atop the underlying linked list; however, each level requires additional storage. Each index node must not only store the data value but also maintain multilevel pointers—horizontal next pointers and vertical down pointers—causing the per-node memory footprint to be significantly larger than that of a standard linked-list node. Notably, the number of index levels in a skip list increases dynamically with the data size, and this adaptivity further exacerbates memory consumption.

As Hendriks (2010) demonstrated [33], the various versions of Heap, HHeap, AVL, RBTree, and PairingHeap all occupy roughly the same amount of memory, close to the theoretical minimum. As the data scale increases from 1 × 10⁸ to 6 × 10⁸, the increase in memory does not exceed 30%. Although the HHeap structure requires additional pointers, the reduced node count offsets the pointer overhead, resulting in robust memory performance at large data scales.

3.3.2. Computational Time

Computational time is a key metric for evaluating algorithm performance, and this paper analyses the actual performance of different data structures on datasets (Figure 11).

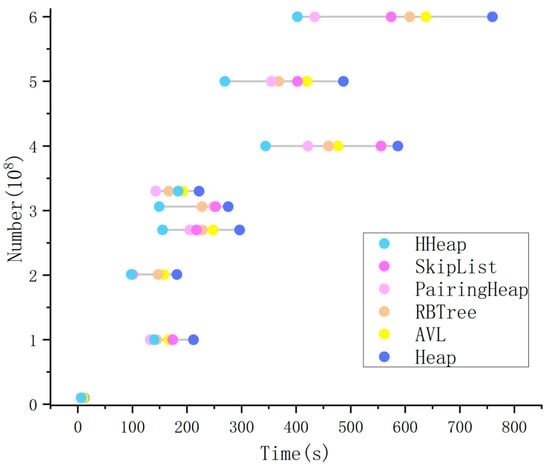
Figure 11. Computation times of different queues in the dataset.

As the data scale increases, the runtime of all priority queue structures tends to increase, with variations in execution time across different implementations. The min-heap structure has the highest latency across all the datasets, indicating the potential for further optimization of the computational efficiency of the Priority-Flood algorithm. In contrast, SkipList, Heap, HHeap, AVL, RBTree, and PairingHeap demonstrate better performance with different data volumes, although with distinguishable efficiency differences.

HHeap stands out, with significant performance advantages, achieving an approximately 45.37% improvement over min-heap on billion-scale datasets and ranking the top performer among the six structures. PairingHeap follows as the second best, demonstrating excellent theoretical amortized complexity but slightly trailing HHeap at experimental scales. RBTree, as a representative self-balancing BST, maintains stable performance but falls behind PairingHeap. AVL trees, owing to their strict balancing constraints, incur higher constant factors, resulting in marginally slower execution than RBTree achieves. SkipList benefits from efficient range queries, providing certain advantages in priority management scenarios. However, its performance instability stems from randomized layer assignments for new nodes.

4. Discussion

As a fundamental criterion for algorithmic assessment, computational performance significantly influences technological selection paradigms in engineering applications. This study presents a systematic performance evaluation of six distinct priority queue implementations within Priority-Flood algorithm frameworks.

As shown in Figure 10, in large-scale data scenarios, the time cost of min-heap is the most pronounced because although the insertion and deletion operations of a min-heap operation have time complexity O(log n), frequent dynamic priority adjustments trigger scale-up of heap operations (downwards or upwards heapifications), thereby increasing the constant factors and reducing throughput at large data scales. Moreover, binary heaps are typically implemented as arrays; while memory is contiguous, insertions and deletions require many element swaps, which can lead to cache misses.

In contrast, the pairing heap, in addition to HHeap, demonstrates a lower latency in this experiment. The reason lies in the near-constant-cost merge operation of the pairing heap, and during the flooding phase of the algorithm, many neighbouring nodes are enqueued after the minimum element is popped. The pairing heap excels in scenarios that entail rapid insertion and merging, and its multiway tree structure is amenable to cache prefetching on modern CPUs.

Among self-balancing trees, the AVL tree has been shown to offer superior performance [32]; however, red-black trees outperform AVL trees, further indicating that the choice of tree structure influences performance. However, for very small queues, employing a red-black tree may yield only marginal time gains. If the queue size exceeds the cache capacity, opting for a more sophisticated pairing heap is worthwhile. HHeap remains extremely effective across all queue sizes.

Essentially, HHeap’s novelty lies in optimizing duplicate data, and the degree of data repetition influences the performance of the priority queue. To validate this scenario’s performance, a dataset of one billion elements is constructed, and the speedup of the HHeap structure relative to that of the Heap structure for a single complete operation is analyzed across repetition rates from 10% to 90%—from filling an empty queue to size N and then popping back to empty (Figure 12). The results indicate that the higher the data repetition rate is, the more pronounced the performance advantage of the hash heap becomes.

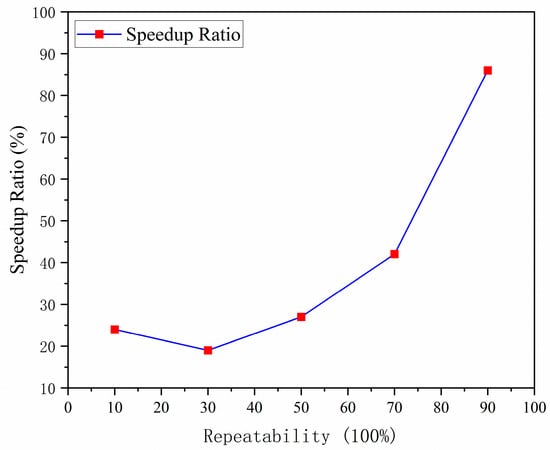
Figure 12. Influence of data repetition on HHeap performance. The horizontal axis denotes the data repetition rate, while the vertical axis indicates the corresponding computation speedup; the exact formula is given in Zhou et al. (2016) [25].

Another distinctive advantage of HHeap lies in its memory management capabilities. When pop operations generate empty hash buckets, the system automatically reclaims memory spaces occupied by deleted buckets, effectively mitigating memory fragmentation. This characteristic transcends the traditional time-space trade-off paradigm in computing, proving the feasibility of performance enhancement through innovative data structure reorganization. Notably, this optimization has significant application value in memory-constrained scenarios such as edge computing devices.

Although HHeap outperforms traditional heap structures in terms of dynamic updates, its implementation involves trade-offs. The approach relies on strict elevation-based classification of DEM cells, which, using low-resolution datasets, may introduce statistical redundancy, causing small elevation changes to be magnified into substantial computational costs. Nevertheless, in the processing of high-fidelity terrain data, the same mechanism can discern microtopographic features with greater precision, thereby increasing the accuracy and resolution advantages for downstream tasks such as hydrological analyses.

Notably, at very small data scales, the advantages of HHeap may not be particularly pronounced. Conversely, when the data volume reaches or exceeds the cache capacity and with the deployment of more sophisticated hashing and bucketing strategies, HHeap can still maintain its edge. Therefore, by considering data redundancy, caching behaviour, and the required granularity of the features, it is generally advisable to favour hash-related structures in large-scale scenarios with substantial data repetition. Moreover, the strength of HHeap lies in its ability to optimize for data repetition, which reduces heap adjustments and lowers the number of heap nodes from N to K. However, when the processed data are in a discrete state (K = N), HHeap degenerates into a conventional heap, and its performance advantage no longer exists.

5. Conclusions

Rapid advances in computer architecture compel us to continually reassess the performance of fundamental algorithms. In this study, multiscale digital elevation model (DEM) datasets are employed to systematically evaluate the efficiency of six priority-queue structures—Heap, RBTree, AVL Tree, SkipList, PairingHeap, and HHeap—in the Priority-Flood algorithm. The results show that the conventional min-heap structure is not the optimal choice under large-scale data conditions; red-black trees, balanced binary trees, and skip lists outperform min-heap in most scenarios, with PairingHeap generally delivering the best overall execution time. The most striking finding concerns HHeap: across all the data scales, it markedly outperforms the other queues and exhibits outstanding memory management capabilities. When the data scale reaches 10⁹, HHeap achieves an approximately 45% relative speedup over that of min-heap.

Despite achieving notable computational performance gains, the present study does not surpass the general lower bound of the sorting algorithm’s time complexity (O(n log n) in the comparison model). Future work will explore the integration of learned data structure approaches to increase the efficiency of queue sorting and deduplication. Furthermore, in future work, additional optimizations in parallel implementation will be studied to continuously enhance HHeap’s potential in large-scale, highly repetitive data scenarios.