Influence of the Semicircular Cycle in a Labyrinth Weir on the Discharge Coefficient
Abstract
1. Introduction
2. Materials and Methods
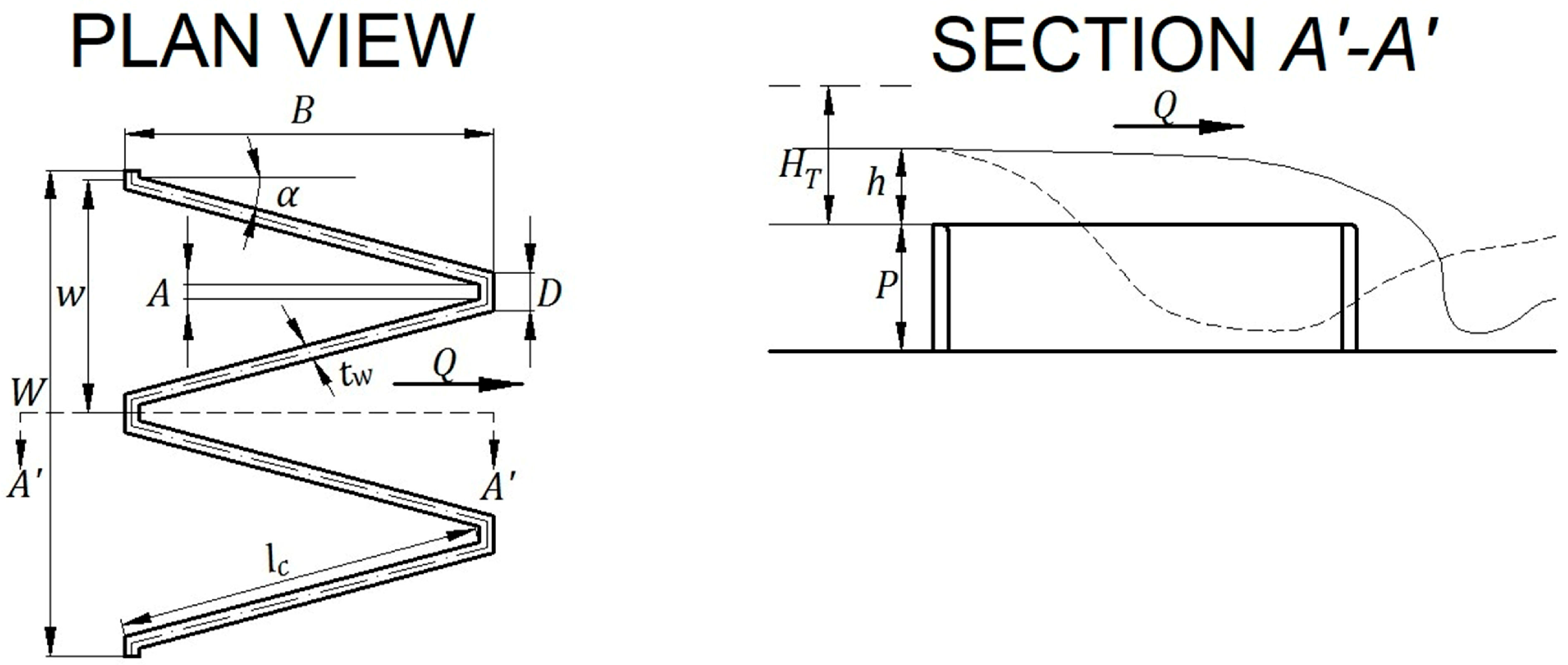
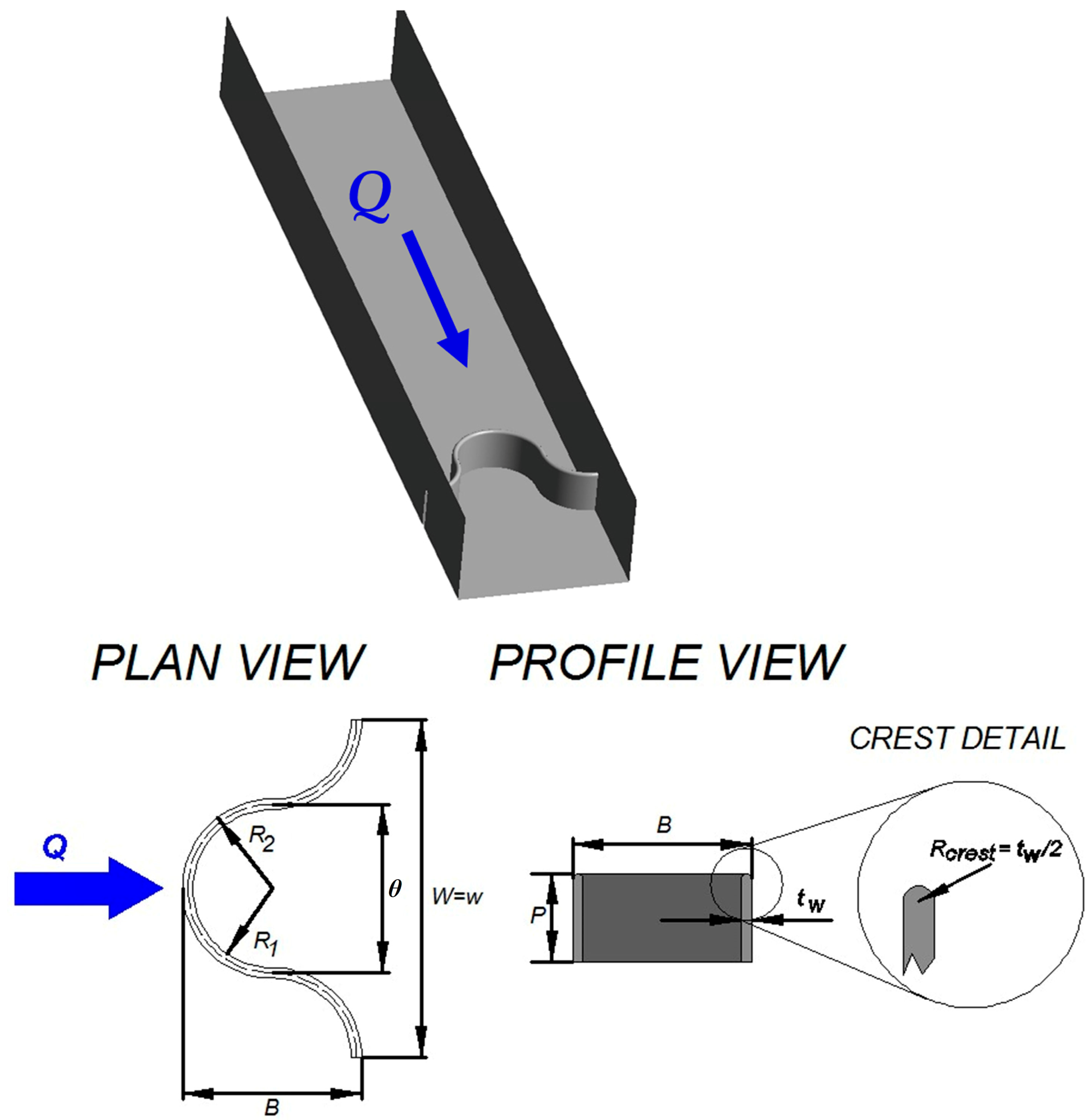
2.1. Physical Model
2.2. Numerical Study
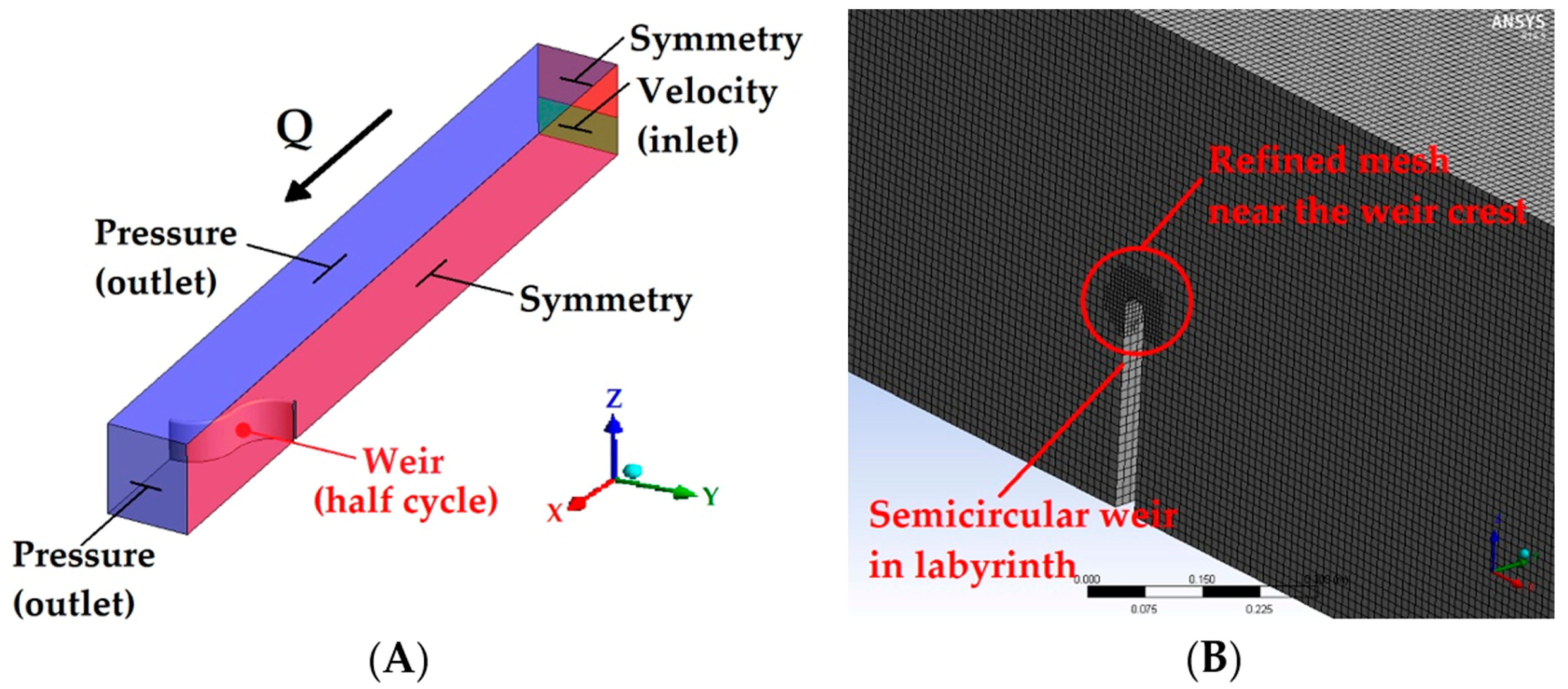
2.2.1. Computational Fluid Dynamics
2.2.2. Grid Convergence Index (GCI)
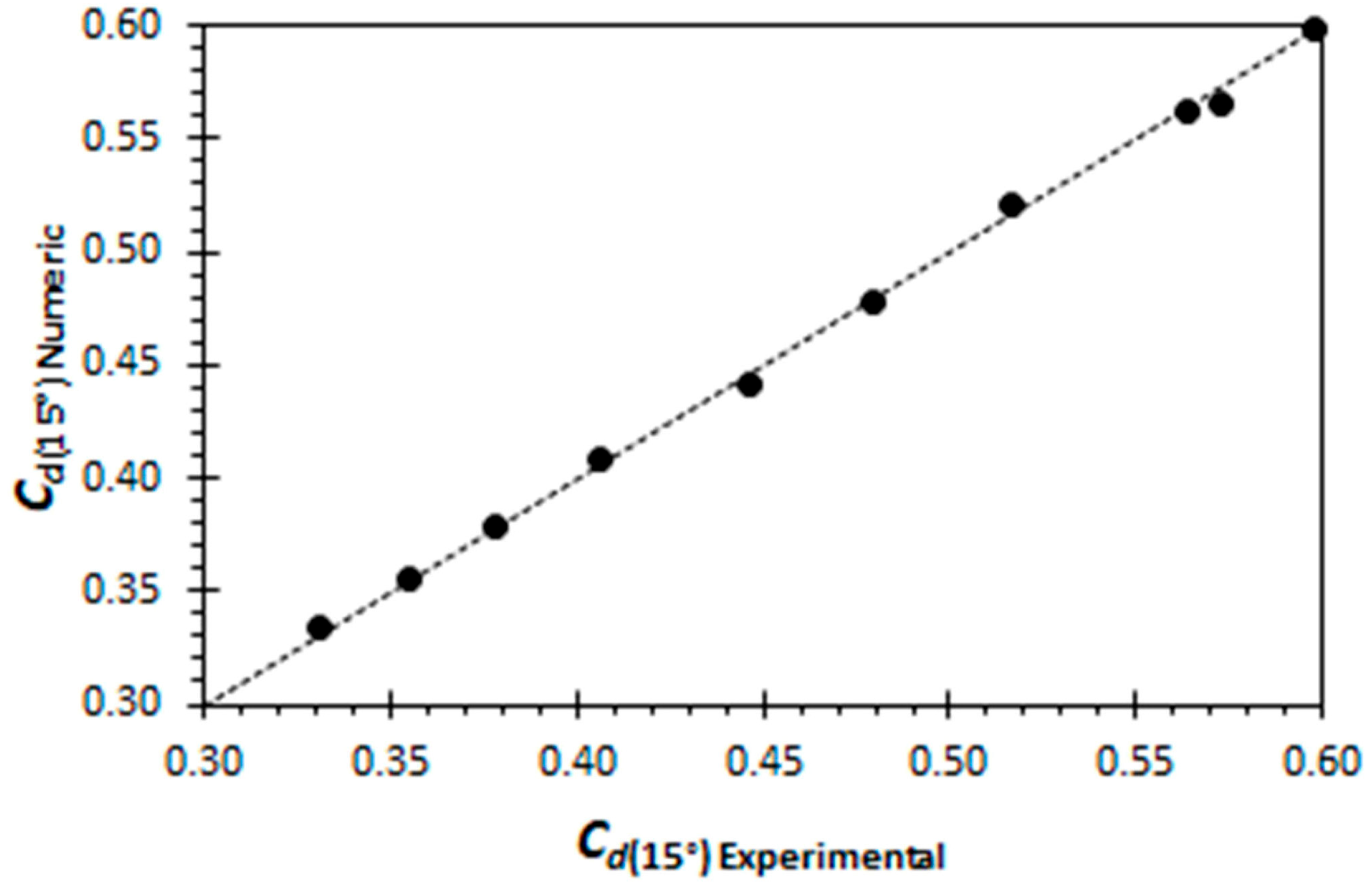
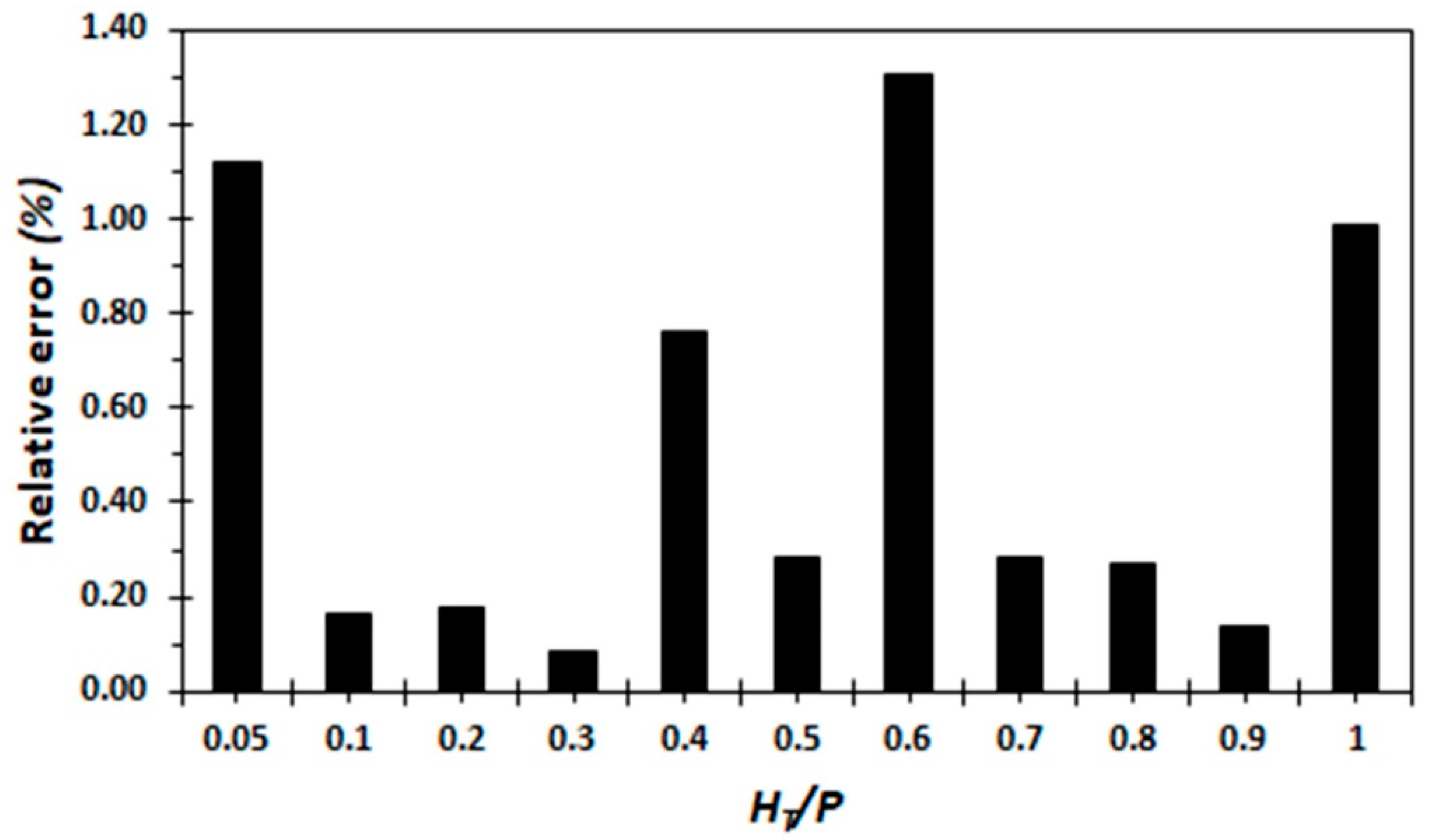
2.3. Numerical Model Evaluation
2.4. Description of the Computational Model
3. Results
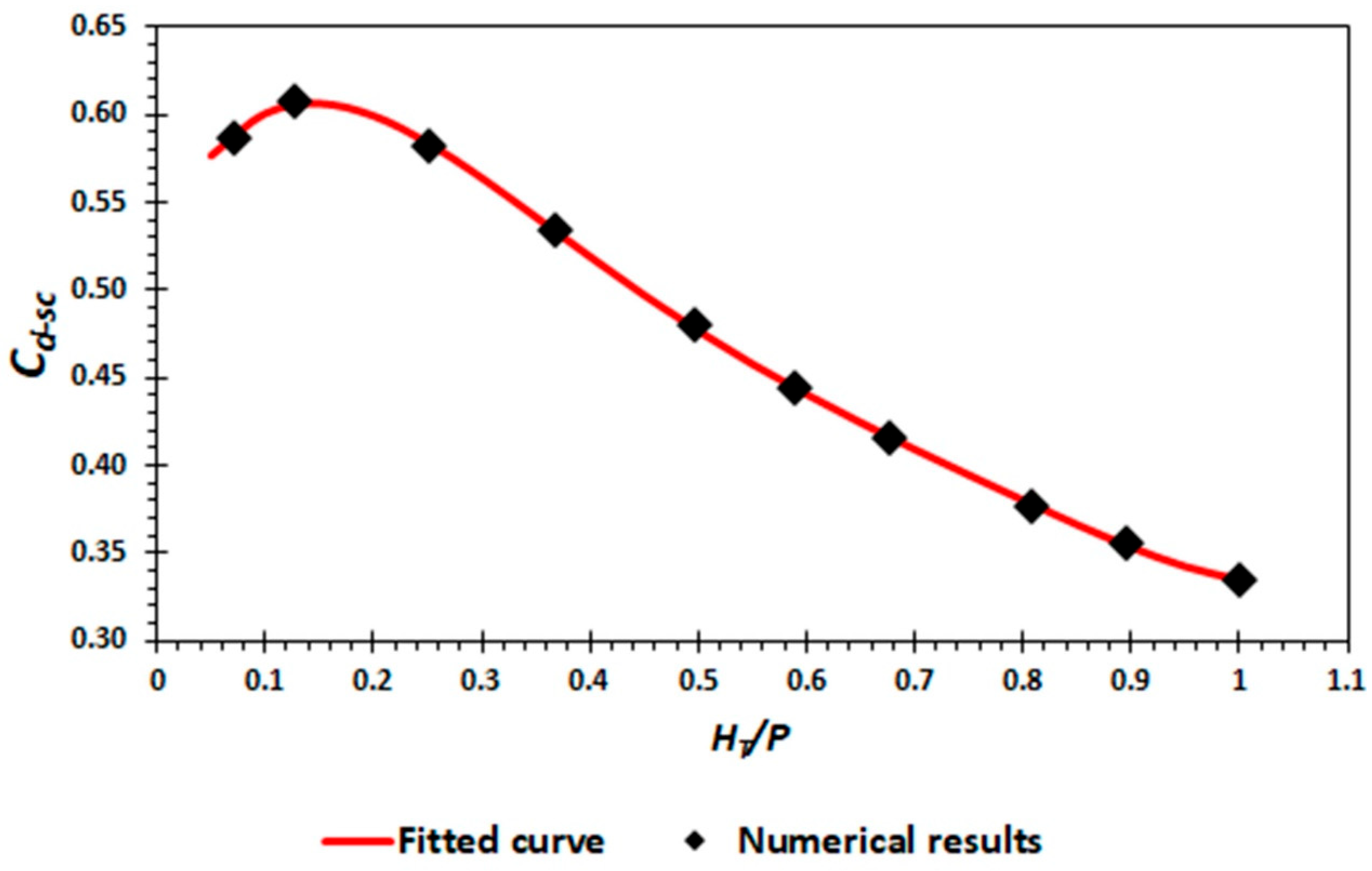
3.1. Discharge Coefficient, Weir and Cycle Efficiency
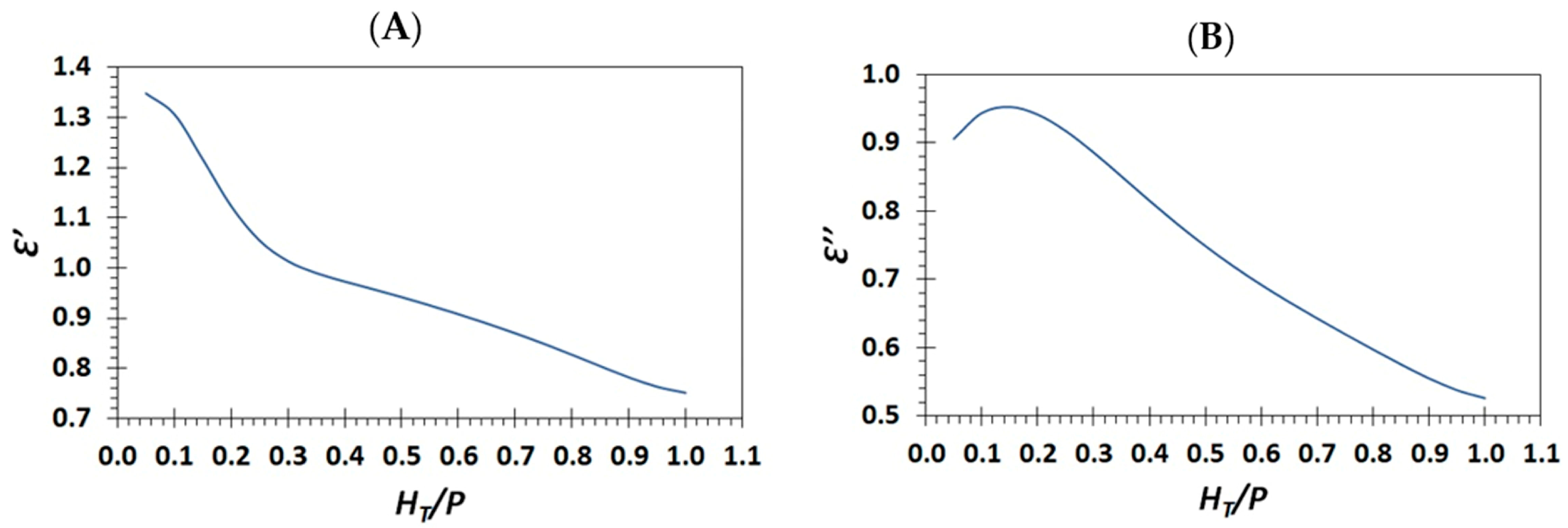
3.2. Weir and Cycle Efficiency
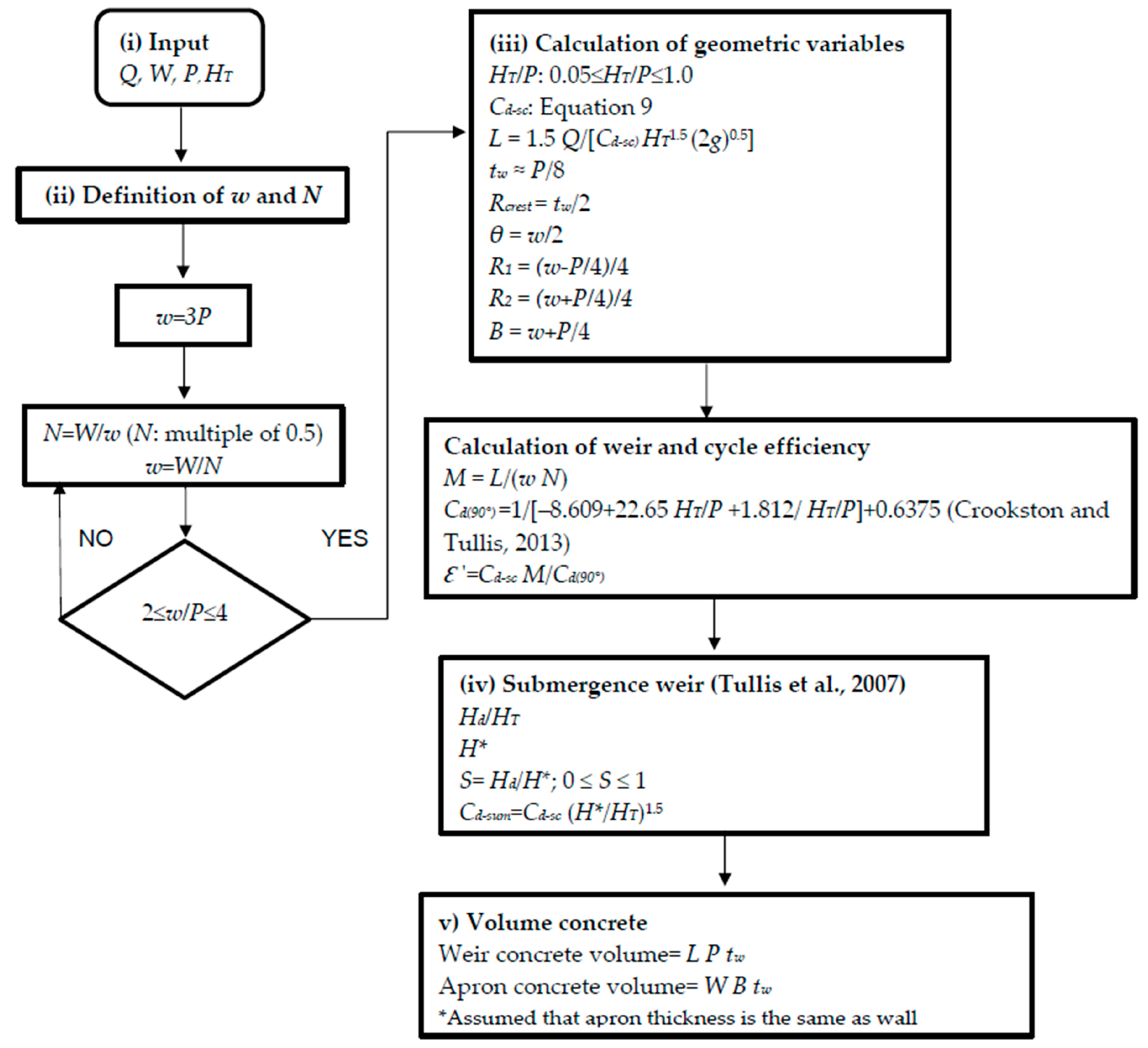
3.3. Design Sequence for the Semicircular Labyrinth Weir
4. Discussion
4.1. Discussion of Discharge Coefficient
4.2. Discussion of Weir and Cycle Efficiency
4.3. Discussion of the Design Sequence
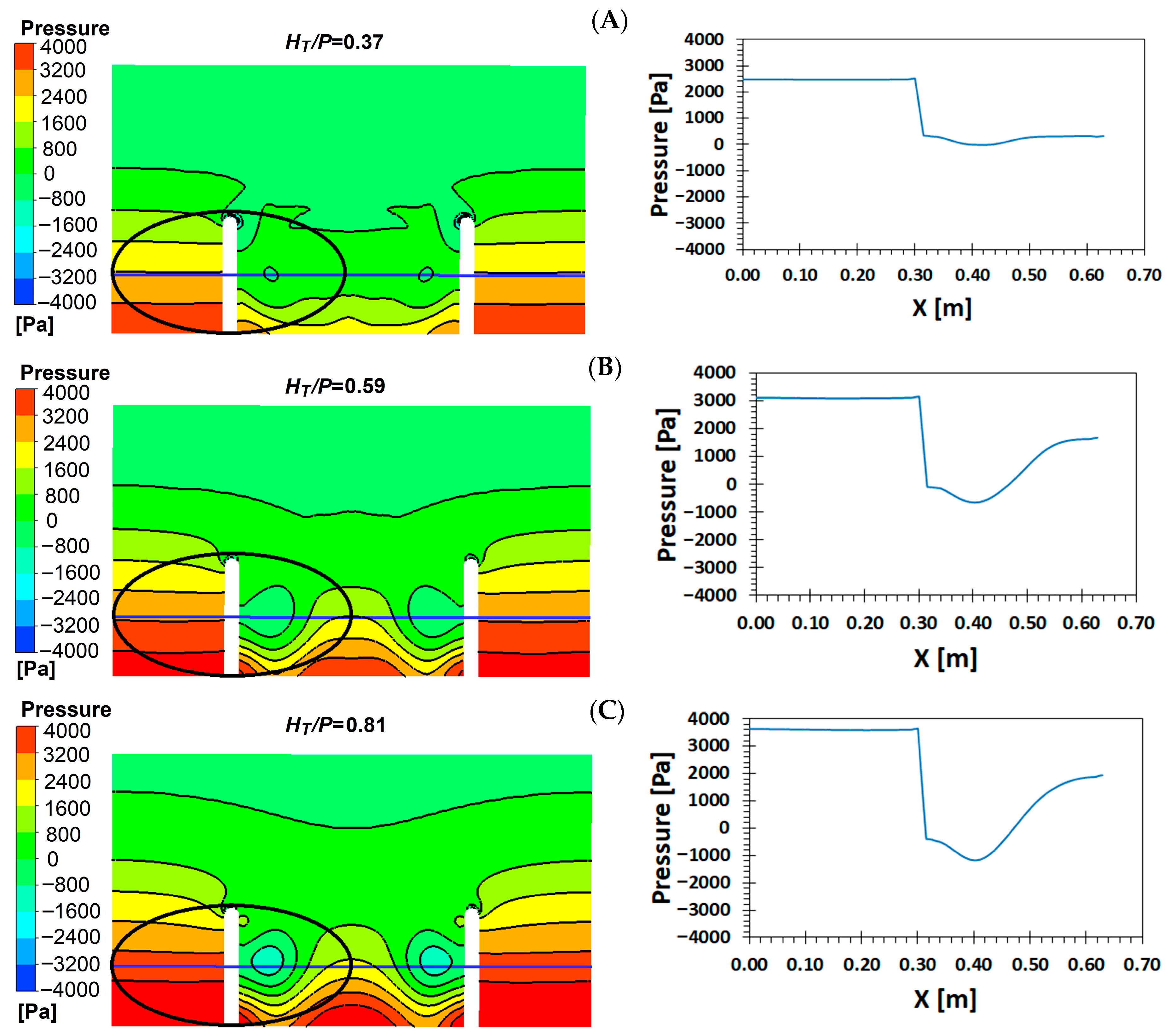
4.4. Pressure Between the Walls of the Weir
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | inside width at apex |
| a | adjustment factor to obtain the discharge coefficient |
| B | length of apron |
| b | adjustment factor to obtain the discharge coefficient |
| c | adjustment factor to obtain the discharge coefficient |
| Cd | discharge coefficient |
| Cd-circular | discharge coefficient of circular apex weir |
| Cd-sc | semicircular labyrinth weir discharge coefficient |
| Cd-sum | submerged weir discharge coefficient |
| Cd-tr | trapezoidal labyrinth weir discharge coefficient |
| Cd(α) | trapezoidal labyrinth weir discharge coefficient |
| Cd(90°) | linear weir discharge coefficient |
| Cov | covariance |
| D | outside width of apex |
| d | adjustment factor to obtain the discharge coefficient |
| e | adjustment factor to obtain the discharge coefficient |
| Fs | security factor |
| f | adjustment factor to obtain the discharge coefficient |
| fi | control variable |
| g | acceleration gravity |
| Hd | downstream total head |
| HT | upstream total head |
| H* | downstream total head of drowned weir |
| h | piezometric head |
| k | turbulent kinetic energy |
| L | characteristic length of the weir |
| Lcycle | cycle length |
| lC | centerline length of sidewall |
| N | number of cycles |
| NC | number of cells |
| P | weir height |
| p | order of convergence |
| Q | design flow |
| R2 | Pearson’s coefficient of determination |
| R1 | internal radius of the apex |
| R2 | external radius of the apex |
| Rcrest | crest radius |
| r | mesh refinement ratio |
| S | submergence level |
| tw | weir wall width |
| W | channel width |
| w | cycle width |
| x | coordinate axis in flow direction |
| Yexp | experimental results |
| Ynum | numerical results |
| y | coordinate axis in the direction of the channel width |
| z | coordinate axis in the direction of the channel height |
| α | angle of sidewall |
| ∆Vi | volume of the i-th cell |
| representative cell size | |
| ε | dissipation rate |
| Ꜫ | relative error |
| Ꜫ′ | weir efficiency |
| Ꜫ″ | cycle efficiency |
| θ | diameter of the cycle apex |
| σ2exp | variance of the experimental results |
| σ2num | variance of the numerical results |
References
- Ackers, P.; White, W.R.; Perkins, J.A.; Harrison, A.J. Weirs and Flumes for Flow Measurements; Wiley: Chichester, UK, 1978; p. 327. [Google Scholar]
- Mattos-Villarroel, E.; Flores-Velázquez, J.; Ojeda-Bustamante, W.; Díaz-Delgado, C.; Salinas-Tapia, H. Influence of crest geometric on discharge coefficient efficiency of labyrinth weirs. Flow Meas. Instrum. 2021, 81, 102031. [Google Scholar] [CrossRef]
- Crookston, B. Labyrinth Weirs. Ph.D. Thesis, Utah State University, Logan, UT, USA, December 2010. [Google Scholar]
- Samadi, A.; Salmasi, F.; Arvanaghi, H.; Mousaviraad, M. Effects of Geometrical Parameters on Labyrinth Weir Hydraulics. J. Irrig. Drain. Eng. 2022, 148, 06022006. [Google Scholar] [CrossRef]
- Emiroglu, M.E.; Kaya, N.; Agaccioglu, H. Discharge capacity of labyrinth side weir located on a straight channel. J. Irrigat. Drain. Eng. 2010, 136, 37–46. [Google Scholar] [CrossRef]
- Darvas, L.A. Discussion of performance and design of labyrinth weirs, by Hay and Taylor. J. Hydraul. Eng. 1971, 97, 1246–1251. [Google Scholar] [CrossRef]
- Bilhan, O.; Emiroglu, E.; Miller, C.J. Experimental investigation of discharge capacity of labyrinth weirs with and without nappe breakers. World J. Mech. 2016, 6, 207–221. [Google Scholar] [CrossRef]
- Willmore, C. Hydraulic Characteristics of Labyrinth Weirs. Master’s Thesis, Utah State University, Logan, UT, USA, April 2004. [Google Scholar]
- Tullis, B.P.; Young, J. Lake Brazos Dam Model Study of the Existing Spillway Structure and a New Labyrinth Weir Spillway Structure; Report No. 1575; Utah Water Research Laboratory: Logan, UT, USA, 2005. [Google Scholar]
- Bilhan, O.; Aydin, M.C.; Emiroglu, M.E.; Miller, C.J. Experimental and CFD analysis of circular labyrinth weirs. J. Irrig. Drain. Eng. 2018, 144, 04018007. [Google Scholar] [CrossRef]
- Dabling, M.R.; Tullis, B.P.; Crookston, B.M. Staged labyrinth weir hydraulics. J. Irrig. Drain. Eng. 2013, 139, 955–960. [Google Scholar] [CrossRef]
- Hay, N.; Taylor, G. Performance and design of labyrinth weirs. J. Hydraul. Div. 1970, 96, 2337–2357. [Google Scholar] [CrossRef]
- Hinchliff, D.; Houston, K. Hydraulic Design and Application of Labyrinth Spillways; Division of Research Engineering and Research Center, Bureau of Reclamation: Denver, CO, USA, 1984. [Google Scholar]
- Lux, F., III. Design and application of labyrinth weirs. In Design of Hydraulic Structures 89; Alberson, M.L., Kia, R.A., Eds.; Balkema/Rotterdam/Brookfield: Toronto, ON, Canada, 1989; pp. 205–215. [Google Scholar]
- Magalhães, A.; Lorena, M. Hydraulic Design of Labyrinth Weirs; Report No. 736; National Laboratory of Civil Engineering: Lisboa, Portugal, 1989. [Google Scholar]
- Tullis, B.P.; Amanian, N.; Waldron, D. Design of labyrinth spillways. J. Hydraul. Eng. 1995, 121, 247–255. [Google Scholar] [CrossRef]
- Falvey, H.T. Hydraulic Design of Labyrinth Weirs; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2003; pp. 31–108. [Google Scholar] [CrossRef]
- Tullis, B.P.; Young, J.C.; Chandler, M.A. Head-discharge relationships for submerged labyrinth weirs. J. Hydraul. Eng. 2007, 133, 248–254. [Google Scholar] [CrossRef]
- Crookston, B.M.; Tullis, B.P. Hydraulic design and analysis of labyrinth weirs. I: Discharge relationships. J. Irrig. Drain. Eng. 2013, 139, 363–370. [Google Scholar] [CrossRef]
- Mattos-Villarroel, E.D.; Ojeda-Bustamante, W.; Díaz-Delgado, C.; Salinas-Tapia, H.; Flores-Velázquez, J.; Bautista-Capetillo, C. Methodological proposal for the hydraulic design of Labyrinth Weirs. Water 2023, 15, 722. [Google Scholar] [CrossRef]
- Aydin, M.C.; Emiroglu, M.E. Determination of capacity of labyrinth side weir by CFD. Flow Meas. Instrum. 2013, 29, 1–8. [Google Scholar] [CrossRef]
- Shaghaghian, M.R.; Sharifi, M.T. Numerical modeling of sharp-crested triangular plan form weirs using FLUENT. Ind. J. Sci. Technol. 2015, 8, 1–7. [Google Scholar] [CrossRef]
- Savage, B.M.; Crookston, B.M.; Paxson, G.S. Physical and numerical modeling of large headwater ratios for a 15 labyrinth spillway. J. Hydraul. Eng. 2016, 142, 04016046. [Google Scholar] [CrossRef]
- Ben Said, M.; Hafnaoui, M.A.; Madi, M. Numerical analysis of the influence of approach flow conditions on the efficienc y of labyrinth weir. Model. Earth Syst. Environ. 2022, 9, 41–51. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, L.; Ansar, M.; Damisse, E.; González-Castro, J.A. Applications of computational fluid dynamics to flow ratings at prototype spillways and weirs. I: Data generation and validation. J. Irrig. Drain. Eng. 2017, 143, 04016072. [Google Scholar] [CrossRef]
- Idrees, A.K.; Al-Ameri, R.; Das, S. Using CFD modelling to study hydraulic flow over labyrinth weirs. Water Supply 2022, 22, 3125–3142. [Google Scholar] [CrossRef]
- Yildiz, A.; Marti, A.I.; Gogus, M. Determination of hydraulic characteristics of flow over a triangular sectioned weir by using experimental and numerical modeling. J. Comput. Appl. Mech. 2021, 52, 215–232. [Google Scholar] [CrossRef]
- Carrillo, J.M.; Matos, J.; Lopes, R. Numerical modeling of free and submerged labyrinth weir flow for a large sidewall angle. Environ. Fluid. Mech. 2020, 20, 357–374. [Google Scholar] [CrossRef]
- Torres, C.; Borman, D.; Sleigh, A.; Neeve, D. Application of three-dimensional CFD VOF to characterize free-surface flow over trapezoidal labyrinth weir and spillway. J. Hydraul. Eng. 2021, 147, 04021002. [Google Scholar] [CrossRef]
- Rezazadeh, S.; Manafpour, M.; Ebrahimnejadian, H. Three-Dimensional Simulation of Flow Over Sharp-Crested Weirs Using Volume of Fluid Method. Appl. Eng. Sci. 2020, 10, 75–82. [Google Scholar] [CrossRef]
- Hargreaves, D.M.; Morvan, H.P.; Wright, N.G. Validation of the volume of fluid method for free surface calculation: The broad-crested weir. Eng. Appl. Comput. Fluid Mech. 2007, 1, 136–146. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries: La Canada, CA, USA, 1998; Volume 2, pp. 103–217. [Google Scholar]
- Driver, D.M.; Seegmiller, H.L. Features of a reattaching turbulent shear layer in divergent channel flow. AIAA J. 1985, 23, 163–171. [Google Scholar] [CrossRef]
- Koldewyn, S.J. Using Computational Fluid Dynamics for Predicting Hydraulic Performance of Arced Labyrinth Weirs. Master’s. Thesis, Utah State University, Logan, UT, USA, 2023. [Google Scholar]
- San Mauro, J.; Salazar, F.; Toledo, M.A.; Caballero, F.J.; Ponce-Farfán, C.; Ramos, T. Physical and numerical modeling of labyrinth weirs with polyhedral bottom. Ing. Agua 2016, 20, 127–138. [Google Scholar] [CrossRef]
- Jiang, L.; Diao, M.; Sun, H.; Ren, Y. Numerical Modeling of Flow Over a Rectangular Broad-Crested Weir with a Sloped Upstream Face. Water 2018, 10, 1663. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Ansell, A. Evaluation of pool-type fish passage with labyrinth weirs. Sustainability 2022, 14, 1098. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Xuan, G.; Liang, D. Effect of parameters of pool geometry on flow characteristics in low slope vertical slot fishways. J. Hydraul. Res. 2020, 58, 395–407. [Google Scholar] [CrossRef]
- Fernández, J.M. Técnicas Numéricas en Ingeniería de Fluidos: Introducción a la Dinámica de Fluidos Computacional (CFD) por el Método de Volumen Finito, 1st ed.; Reverté: Barcelona, Spain, 2012; pp. 98–294. [Google Scholar]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Carrillo, J.M.; Castillo, L.G. Consideraciones del mallado aplicadas al cálculo de flujos bifásicos con las técnicas de dinámica de fluidos computacional. Jorn. Introd. Investig. UPCT 2011, 4, 33–35. [Google Scholar]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluid. Eng. 2008, 130, 7. [Google Scholar] [CrossRef]
- Liu, H.L.; Liu, M.M.; Bai, Y.; Dong, L. Effects of mesh style and grid convergence on numerical simulation accuracy of centrifugal pump. J. Cent. South Univ. 2015, 22, 368–376. [Google Scholar] [CrossRef]
- Baker, N.; Kelly, G.; O’Sullivan, P.D. A grid convergence index study of mesh style effect on the accuracy of the numerical results for an indoor airflow profile. Int. J. Vent. 2020, 19, 300–314. [Google Scholar] [CrossRef]
- Slater, J. Examining Spatial (Grid) Convergence. NASA Glenn Research Center. 2008. Available online: https://www.grc.nasa.gov/www/wind/valid/tutorial/spatconv.html (accessed on 8 May 2025).
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid. Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Tullis, B.P. Standley Lake Service Spillway Model Study; Report No. 341; Utah Water Research Laboratory: Logan, UT, USA, 1993. [Google Scholar]




| Authors | Cycle Geometry | Apex Geometry | Crest Profile |
|---|---|---|---|
| Present study | Semicircular | Semicircular | HR |
| Mattos-Villarroel et al. [20] | Trapezoidal | Semicircular | HR |
| Idrees et al. [26] | Trapezoidal | Straight | Flat |
| Samadi et al. [4] | Trapezoidal, rectangular, triangular | Straight | QR |
| Yildiz et al. [27] | Triangular | ─ | Flat |
| Carrillo et al. [28] | Trapezoidal | Straight | QR |
| Bilhan et al. [10] | Semicircular | Semicircular (upstream)-straight (downstream) | Sharp |
| Shaghaghian et al. [22] | Triangular | ─ | Sharp |
| Dabling et al. [11] | Trapezoidal | Straight | QR |
| Crookston and Tullis [19] | Trapezoidal | Straight | QR-HR |
| Tullis and Young [9] | Trapezoidal | Semicircular | QR |
| α (°) | N | L (m) | A (m) | w (m) | P (m) | W (m) | Crest Profile |
|---|---|---|---|---|---|---|---|
| 15 | 2 | 4 | 0.038 | 0.617 | 0.305 | 1.235 | Quarter-round |
| Boundary and Initial Conditions | Solution Method |
|---|---|
| Inlet | Velocity |
| Outlet | Atmospheric pressure |
| Weir and channel | Solid, stationary, and non-slip. |
| Time | Steady-state |
| Viscosity model | k-ε standard |
| Multiphasic model | Volume of fluid (VOF) |
| Model fluid | Two-phase |
| Pressure–velocity coupling | SIMPLE |
| Spatial discretization scheme | Second-order Upwind |
| Grid | r | p | h1 (m) | h2 (m) | h3 (m) | Richardson Extrapolate (m) | Ꜫ21 | Ꜫ32 | GCI21 (%) | GCI32 (%) | Asymptotic Range of Convergence |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 1.66 | 1.56 | 0.1247 | 0.1282 | 0.1359 | 0.1218 | 0.004 | 0.008 | 2.92 | 6.25 | 0.97 |
| II | 1.70 | 1.02 | 0.1514 | 0.1563 | 0.1647 | 0.1445 | 0.005 | 0.008 | 5.65 | 9.40 | 0.97 |
| Scenario | α (°) | Diameter θ (m) | P (m) | Lcycle (m) | w/P | N | Flow Rate (m3 s−1) | Crest Profile | Cycle Geometry |
|---|---|---|---|---|---|---|---|---|---|
| 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 | 15 | ─ | 0.305 | 2.00 | 2.024 | 2 | 0.0126, 0.0379, 0.1065, 0.1839, 0.2616, 0.3362, 0.4071, 0.4746, 0.5394, 0.6026, 0.6651 | QR | Trapezoidal |
| 12, 13, 14, 15, 16,17, 18, 19, 20, 21 | ─ | 0.617 | 0.305 | 1.00 | 4.048 | 1 | 0.0126, 0.0379, 0.1065, 0.1839, 0.2616, 0.3362, 0.4071, 0.4746, 0.5394, 0.6026 | HR | Circular |
| θ (m) | N | L (m) | w (m) | P (m) | W (m) | Rcrest (m) | R1 (m) | R2 (m) | Crest Profile |
|---|---|---|---|---|---|---|---|---|---|
| 0.617 | 1 | 1.938 | 1.235 | 0.305 | 1.235 | 0.038 | 0.289 | 0.328 | Half-round |
| Concept | Symbol | Value-Unit | Observations |
|---|---|---|---|
| (i) Initial data | |||
| Flow rate | Q | 1538 m3/s | Input |
| Reservoir elevation | ─ | 1680.91 m.a.s.l. | Input |
| Approach channel elevation | ─ | 1675.75 m.a.s.l. | Input |
| Crest elevation | ─ | 1678.80 m.a.s.l. | Input |
| Total head | HT | 1.975 m.a.s.l. | ─ |
| (ii) Assumed data | |||
| Estimated inlet loss at Q | ─ | 0.13 m | Estimated |
| Number of cycles | N | 13 | 3 ≤ w/P ≤ 4 |
| Crest height | P | 3.05 | P ≈ 1.4 HT |
| Angle of side legs | α | 8° | 8°≤ α ≤ 16° |
| (iii) Calculated data | |||
| Thickness of wall | tw | 0.51 m | tw ≈ P/6 |
| Inside width at apex | A | 0.95 m | tw ≤ A ≤ 2tw |
| Outside width of apex | D | 1.83 m | ─ |
| Head water ratio | HT/P | 0.65 | ─ |
| Discharge coefficient | Cd | 0.3255 | ─ |
| Effective crest length | L | 576.6 m | ─ |
| Length of apron | B | 22.72 m | ─ |
| Actual length of side leg | lc | 22.45 m | ─ |
| Total length of walls | L1 | 620 m | ─ |
| Cycle width | w | 9.42 m | ─ |
| Weir width | W | 123 m | ─ |
| Length of linear weir for same flow | ─ | 249 m | ─ |
| Vertical aspect ratio | w/P | 3.09 | 3 ≤ w/P ≤ 4 |
| (iv) Concrete volume | |||
| Wall concrete volume | ─ | 964.41 m3 | ─ |
| Apron concrete volume | ─ | 1425.22 m3 | ─ |
| Total | ─ | 2389.63 m3 | ─ |
| Concept | Symbol | Value-Unit | Equations and Limits |
|---|---|---|---|
| (i) Input data | |||
| Desing flow | Q | 1538.00 m3/s | |
| Weir width | W | 123.00 m | |
| Weir height | P | 3.05 m | |
| Upstream total head | HT | 1.98 m | |
| (ii) Definition of cycle width (w) and number of cycles | |||
| Cycle width | w | 9.15 m | w = 3 P |
| Number of cycles | N | 13.00 | N = W/w |
| New cycle width | w | 9.46 m | w = W/N |
| Vertical aspect ratio | w/P | 3.10 | 2 ≤ w/P ≤ 4 |
| (iii) Calculation of geometric variables, weir and cycle efficiencies | |||
| Geometric variables | |||
| Head water ratio | HT/P | 0.65 | 0.05 ≤ HT/P ≤ 1.0 |
| Labyrinth weir discharge coefficient | Cd-sc | 0.425 | Cd-sc = f (HT/P). Equation (9) |
| Total centerline length of weir | L | 441.14 m | L = 1.5 Q/[Cd HT1.5 (2 g)0.5] |
| Wall width | tw | 0.38 m | tw = P/8 |
| Crest radius | Rcrest | 0.19 m | Rcrest = tw/2 |
| Diameter of the cycle apex | θ | 4.73 m | θ = w/2 |
| Internal radius of the apex | R1 | 2.17 m | R1 = (w − P/4)/4 |
| External radius of the apex | R2 | 2.56 m | R2 = (w + P/4)/4 |
| Length of apron | B | 5.11 m | B = w + P/4 |
| Weir and cycle efficiencies | |||
| Magnification ratio | M | 3.59 | M = L/W |
| Linear weir coefficient discharge | Cd(90°) | 0.75 | Cd(90°) = 1/[−8.609 + 22.65 × (HT/P) + 1.812/(HT/P)] + 0.6375 [19] |
| Weir efficiency | Ꜫ′ | 2.03 | Ꜫ′ = Cd-sc M/Cd(90°) |
| Cycle efficiency | Ꜫ″ | 1.53 | Ꜫ″ = Cd-sc M |
| (iv) Submergence [18] | |||
| Downstream total head | Hd | 0.98 m | |
| Head ratio | Hd/HT | 0.50 m | |
| Submergence upstream total head | H* | 2.11 m | |
| Submergence level | S | 0.46 | S = Hd/H*; 0 ≤ S ≤ 1 |
| Submerged weir discharge coefficient | Cd-sum | 0.385 | Cd-sum = Cd-sc (HT/H)1.5 |
| (v) Volume concrete | |||
| Weir concrete volume | ─ | 512.96 m3 | Volume = L P tw |
| Apron concrete volume * | ─ | 239.72 m3 | Volume = W B tw |
| Total | ─ | 752.68 m3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mattos-Villarroel, E.D.; Ojeda-Bustamante, W.; Díaz-Delgado, C.; Salinas-Tapia, H.; Bautista-Capetillo, C.F.; Flores-Velázquez, J.; Aguilar-Rodríguez, C.E. Influence of the Semicircular Cycle in a Labyrinth Weir on the Discharge Coefficient. Water 2025, 17, 3151. https://doi.org/10.3390/w17213151
Mattos-Villarroel ED, Ojeda-Bustamante W, Díaz-Delgado C, Salinas-Tapia H, Bautista-Capetillo CF, Flores-Velázquez J, Aguilar-Rodríguez CE. Influence of the Semicircular Cycle in a Labyrinth Weir on the Discharge Coefficient. Water. 2025; 17(21):3151. https://doi.org/10.3390/w17213151
Chicago/Turabian StyleMattos-Villarroel, Erick Dante, Waldo Ojeda-Bustamante, Carlos Díaz-Delgado, Humberto Salinas-Tapia, Carlos Francisco Bautista-Capetillo, Jorge Flores-Velázquez, and Cruz Ernesto Aguilar-Rodríguez. 2025. "Influence of the Semicircular Cycle in a Labyrinth Weir on the Discharge Coefficient" Water 17, no. 21: 3151. https://doi.org/10.3390/w17213151
APA StyleMattos-Villarroel, E. D., Ojeda-Bustamante, W., Díaz-Delgado, C., Salinas-Tapia, H., Bautista-Capetillo, C. F., Flores-Velázquez, J., & Aguilar-Rodríguez, C. E. (2025). Influence of the Semicircular Cycle in a Labyrinth Weir on the Discharge Coefficient. Water, 17(21), 3151. https://doi.org/10.3390/w17213151