Abstract
Global warming has made water resources more uneven in space and time, making water management harder. This study used the HBV-XGBoost model to see how climate change affects runoff in the Xiangxi River Basin. The HBV model simulated water processes, and XGBoost improved predictions by handling complex relationships. This study used the SDSM to create climate data for 2025–2100 and looked at runoff trends under different emission scenarios. The HBV-XGBoost model performed better than the HBV model in simulating runoff. Future predictions showed big differences in runoff trends under various SSP scenarios in the 2040s and 2080s. For example, under SSP585, the ACCESS-CM2 model projected a May runoff increase from 1527.52 m3/s to 2344.42 m3/s by the 2080s, and ACCESS-ESM1-5 projected an increase from 1462.11 m3/s to 2889.58 m3/s. All GCMs predicted a large rise in annual runoff under SSP585 by the 2080s, with FGOALS-g3 showing the highest growth rate of 76.54%. The model accurately simulated runoff changes and provided useful insights for adapting water management to climate change. However, this study has limitations, including uncertainties in machine learning models, potential input data biases, and varying applicability under different conditions. Future work should explore more climate models and downscaling methods to improve accuracy and consider local policies to better address climate impacts on water resources.
1. Introduction
In recent years, global warming has become the dominant trend in climate change [1]. Climate change directly or indirectly affects various hydrological elements, such as precipitation, evaporation, runoff, and soil moisture, thereby inevitably causing changes in the global hydrological cycle [2]. The IPCC’s Special Report on Climate Change and Land, released in 2019, pointed out that the continuous development of climate change has amplified human impacts and pressures on land, leading to changes in the spatiotemporal distribution of hydrological processes and water resources at different spatial scales of river basins [3,4,5,6,7]. As an important component of water resources, the changing trend in runoff is of great significance for water resource management, flood control, and disaster reduction, as well as ecosystem protection. Since the mid-20th century, the World Meteorological Organization (WMO) has recognized the importance of hydrological forecasting in reducing disaster risks and water resource management and has taken many measures to promote the development of runoff forecasting systems [8,9]. Runoff forecasting plays a crucial role in water resource planning and management activities, such as water conservancy project scheduling, flood control, dam planning, reservoir scheduling, drinking water allocation, and navigation planning [10].
Runoff forecasting has attracted widespread attention in recent decades [11] and is an important component of hydrological system prediction. Long-term runoff forecast results are influenced by a variety of factors, including climate conditions, human inputs, soil properties, soil texture, vegetation cover, and topography [12]. Currently, commonly used runoff forecasting methods include physical causality analysis, mathematical statistics, intelligent algorithms, and integrated forecasting based on numerical weather prediction [13,14]. However, due to the impacts of climate change and human activities, runoff in river basins has exhibited increased variability and inconsistency, which has introduced significant uncertainty into runoff forecasting [15]. Different runoff forecasting methods are applicable to different scenarios, and these methods are continuously evolving and improving [16]. Traditional hydrological forecasting methods rely on mathematical models and physical laws to capture the objective patterns of hydrological phenomena. However, due to geographical constraints, traditional hydrological models often fail to ensure applicability across different regions, resulting in larger forecasting errors. To address this issue, linear-based models such as autoregressive models [17,18] and trend-based moving average models [19] have been proposed. However, these models are unable to accurately capture the complex nonlinear relationships involved in hydrological changes [20]. In contrast, many nonlinear data-driven models, such as artificial neural networks (ANNs) [21,22,23,24], adaptive neuro-fuzzy inference systems (ANFISs) [25,26], genetic programming (GP) [27,28,29], and support vector machines (SVMs) [30,31], have demonstrated strong nonlinear mapping capabilities in medium- and long-term runoff forecasting. However, these models also face challenges such as slow learning speed, overfitting, and the curse of dimensionality [11].
In recent years, with the rapid development of computer technology, machine learning (ML) methods have been widely used in many fields [32,33]. ML primarily identifies patterns and relationships by iterating through large amounts of data and excels at handling highly nonlinear and complex influencing factors [34,35]. For example, the Long Short-Term Memory (LSTM) model can address the issues of gradient vanishing and explosion that occur in recurrent neural networks during long-term training. Machine learning models, such as Extreme Gradient Boosting (XGBoost) [36], provide feature importance and nonlinear relationships. XGBoost is one of the most popular algorithms in machine learning. Its fundamental idea is to aggregate weak learners to form a powerful model with higher prediction accuracy, that is, to enhance the generalization ability and robustness of a single model by integrating multiple learners [37]. However, the limitations of machine learning methods lie in the requirement of a large amount of in situ training data and their inability to describe the true physical processes [38]. Compared to process-driven models, data-driven models typically do not consider the physical mechanisms involved in runoff formation [39,40,41]. In recent years, artificial intelligence has made significant progress. To improve the accuracy of runoff forecasting, Reichstein et al. [38] developed a coupled model that integrates physical models and data-driven models. Data-driven models can be pre-trained based on the simulation results of physical models and then used to construct a coupled model. Wang and Peng [42] proposed a machine learning hydrological simulation model combining K-means and XGBoost (KXGBoost) and developed an interpretable machine learning-based hydrological model using SHAP (SHapley Additive exPlanations) to enhance the prediction capability of machine learning models in hydrological simulation and address the ambiguity in explaining runoff generation mechanisms. The results showed that the K-means clustering method based on SHAP interpretation could effectively capture the spatiotemporal heterogeneity of runoff and accurately predict its spatiotemporal variations. The Nash–Sutcliffe efficiency of the KXGBoost model during training and testing was 0.803 and 0.596, respectively, which represents an improvement of 0.089 and 0.029 in prediction accuracy compared with the XGBoost model. These results demonstrate the effectiveness of the coupling method of machine learning and physical models in enhancing the performance and interpretability of data-driven hydrological models, providing a new perspective for understanding hydrological processes and improving runoff simulation and highlighting the potential of machine learning-based hydrological models in water resource management.
The Xiangxi River Basin, located in the western part of Hubei Province, China, is a vital component of the Three Gorges Reservoir. Characterized by a subtropical monsoon climate, the basin experiences a highly uneven spatiotemporal distribution of precipitation, leading to frequent floods and droughts. These hydrological extremes pose significant challenges for water resource management and ecological conservation within the basin. Runoff variations in the Xiangxi River Basin not only affect agricultural irrigation and hydropower station operations locally but also have critical implications for the regulation of the Three Gorges Reservoir and water supply to the middle and lower reaches. Therefore, the accurate prediction of runoff changes in the Xiangxi River Basin is of paramount importance for ensuring water resource security and maintaining ecological balance in the region. Previous studies have extensively examined the hydrological characteristics and runoff predictions of the Xiangxi River Basin. For instance, Wang et al. [43] used the Soil and Water Assessment Tool (SWAT) model to simulate runoff in the Xiangxi River Basin, emphasizing the importance of accurate meteorological data in enhancing model performance. They found that the SWAT model could effectively simulate runoff dynamics under historical conditions but suggested further improvements for future climate scenarios. Another study conducted by Dams et al. [44] applied a multi-model approach to assess the impact of climate change on runoff, highlighting the necessity of high-resolution climate data for improving prediction accuracy. These studies collectively underscore the complexity of runoff prediction due to the unique climatic and topographic features of the Xiangxi River Basin. Future climate change poses significant risks to hydrological conditions in the Xiangxi River Basin. The Sixth Assessment Report (AR6) of the Intergovernmental Panel on Climate Change (IPCC) indicates that global surface temperatures are rising, and precipitation patterns are becoming more uncertain [45]. These changes are expected to intensify the frequency and severity of hydrological extremes such as floods and droughts in the region. For example, under a high-emission scenario (SSP585), predictions show significant temperature increases and marked variability in precipitation patterns [46]. This could lead to more frequent and severe flood events during the wet season and prolonged droughts during the dry season, further complicating water resource management efforts. Moreover, increased evaporation rates due to higher temperatures may reduce overall water availability, affecting agricultural productivity and hydropower generation.
The objective of this study is to develop a hybrid streamflow forecasting system though integrating XGBoost into the HBV model. The HBV model is employed in this study. The HBV model is one popular hydrological model, praised for its availability, speed, and accuracy in simulating hydrological processes [47,48]. This model has a simple structure and a limited number of parameters, making it easy to understand and calibrate. Moreover, the HBV model can effectively prevent overparameterization issues. In many comparative tests of models, the HBV model has shown excellent performance, especially in simulating streamflow aggregation. Although there are more complex models on the market, the HBV model often performs better in practical applications due to its simplicity and efficiency [49]. The HBV model has also proven its excellent adaptability in studying the impact of climate change and land use changes on runoff [50]. In addition, the XGBoost method is integrated into the HBV model system. Because XGBoost is a widely used supervised learning algorithm, it has excellent performance, robustness, and efficient operation, especially in the field of hydrology [51,52,53]. As an excellent ensemble learning algorithm, XGBoost optimizes the algorithm structure and uses CPU multithreading for parallel calculations, significantly improving the model’s training speed and prediction accuracy. It can effectively overcome limitations in computational speed and accuracy, reduce training and prediction time, and support various objective functions, including classification and regression. XGBoost is good at handling complex relationships and can clearly identify important features, making it significantly advantageous in feature selection and model interpretation [54]. These features collectively make the model more accurate and better at dealing with climate change. This combination also makes the model more reliable and gives us a better way to manage water and protect the environment in the Xiangxi River Basin. In this study, a coupled HBV-HGBoost model based on the HBV model was developed to predict future runoff. The objective was to construct and compare the performance of the HBV and HBV-XGBoost coupled models in order to enhance the runoff prediction accuracy of the Xiangxi River Basin under climate change. This study utilized high-resolution climate data from the Statistical Downscaling Model (SDSM) and leveraged the strengths of both the HBV and XGBoost models to evaluate runoff variation trends under different emission scenarios. The HBV-XGBoost model outperformed the HBV model in predicting runoff. This validation provides a scientific basis for water resource management and flood control in the Xiangxi River Basin.
2. Materials and Methods
2.1. Study Area
The Xiangxi River (110°47′–111°13′ E, 30°59′–31°07′ N) is located in the western part of Hubei Province and is the largest tributary of the Chuanjiang River on the north bank of the Xiling Gorge section of the Three Gorges. It originates from Xinhua in the Shennongjia Forestry District, with a drainage area of about 3100 square kilometers and a main stream length of approximately 97.3 km, as shown in Figure 1. The average annual runoff of the basin is 1.159 billion cubic meters per year. The basin’s terrain is primarily composed of high mountains and sub-high mountains. Forests are the predominant land use type in the basin, covering 87.36% of its total area. The climate of the basin is characterized by significant spatiotemporal variations in precipitation. The annual precipitation decreases from the northwest to the southeast, ranging from 900 to 1200 mm [55]. Meteorological data for the basin come from the Xingshan meteorological station, including daily precipitation, temperature, and evaporation. According to research, both the maximum temperature (Tmax) and minimum temperature (Tmin) in the basin are projected to increase under future climate change scenarios, especially under the high-emission scenario (SSP585), where the temperature rise is more significant. The changes in precipitation are more complex, with significant differences in precipitation changes under different General Circulation Models (GCMs) and Shared Socioeconomic Pathway (SSP) scenarios, showing both increases and decreases. The Shared Socioeconomic Pathways (SSPs) include three representative scenarios, SSP126, SSP245, and SSP585, corresponding to low-, medium-, and high-emission trajectories, respectively. The SSP126 scenario envisions a future where global efforts are focused on sustainable development, leading to effectively controlled and low levels of greenhouse gas emissions. In contrast, the SSP245 scenario represents a medium-emission future, where greenhouse gas emissions remain at a stable, moderate level. The SSP585 scenario, however, depicts a high-emission future that is heavily reliant on fossil fuels, with a significant increase in greenhouse gas emissions anticipated. This study employs the SSP scenarios to assess the combined impacts of climate change and human activities. This approach is chosen because the SSPs integrate both physical climate factors and socioeconomic dimensions, making them suitable for complex climate regions like the Xiangxi River Basin [56]. The SSP scenarios provide a more accurate prediction of runoff changes, which is crucial for water resource and ecological management. When combined with high-resolution climate data, the SSPs are particularly well-suited for basin-scale simulations. Compared to the Representative Concentration Pathways (RCPs), which lack socioeconomic considerations, and Integrated Assessment Models (IAMs), which focus on macro-scale interactions between climate and human systems, the SSPs offer detailed insights at the basin level. This makes them more appropriate for predicting future runoff in the Xiangxi River Basin.
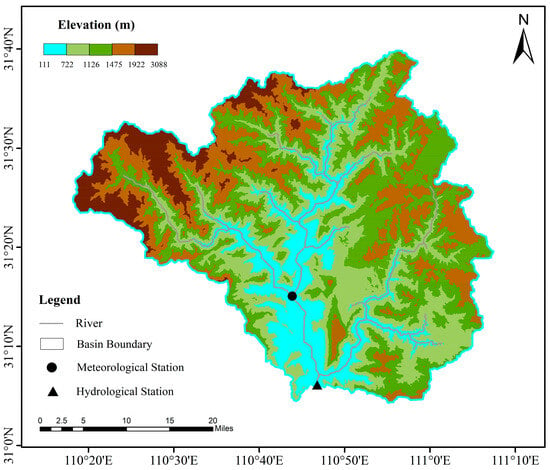
Figure 1.
Research area and locations of hydrological and meteorological stations.
The geographical spatial data involved in this study mainly include the Digital Elevation Model (DEM), land use types, and soil types. The DEM data were obtained from the Geospatial Data Cloud Platform of the Computer Network Information Center, Chinese Academy of Sciences (www.gscloud.cn). The resolution of the data is 30 m × 30 m. The land use data are based on the 2000 land use remote sensing monitoring data released by the Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences (www.resdc.cn), with a resolution of 30 m. The secondary land use types were reclassified into primary land use types using ArcGIS 10.4 software. Meteorological data were collected from the Xingshan Meteorological Station in Hubei Province. The data include daily precipitation, temperature, evaporation, and humidity from 1991 to 2008. The hydrological model was calibrated and validated using daily runoff data from the Xingshan Hydrological Station for the same period [55]. During the data preprocessing stage, the various data were sorted. The data were also analyzed in detail. The specific steps are shown in Table 1. In the process of constructing the hydrological model, the period from 1993 to 2004 (12 years) was used as the calibration period. The period from 2005 to 2008 (4 years) was used as the validation period. Moreover, a 2-year pre-run period (1991–1992) was employed for model initialization [55].

Table 1.
Sources of data and associated processing [44].
2.2. HBV
The (Hydrologiska Byråns Vattenbalansavdelning) HBV model is a process-driven, semi-distributed conceptual hydrological model that was initially developed by the Swedish Meteorological and Hydrological Institute (SMHI) in the 1970s. It is primarily used to simulate hydrological processes in a basin, especially the formation of and variation in runoff. The model integrates physical processes and empirical formulas to predict the hydrological response of a basin by simulating processes such as precipitation, evapotranspiration, and runoff. The rapid response capability of the HBV model gives it a significant advantage in flood forecasting and water resource management [55].
In this study, we used HBV-light 4.0.24 software to construct the model framework and optimize the parameters. The input data for the software included key meteorological variables such as daily precipitation, temperature, and evaporation recorded at meteorological observation stations in the Xingshan Basin. To fulfill the operational requirements of the HBV model, the Xiangxi Jiang River Basin was classified into five altitude zones and three vegetation belts using land use and DEM data. For parameter calibration, the Monte Carlo method was utilized to generate a suite of parameter values within the predefined range. Following 5000 iterations, the optimal set of model parameters was identified under the specified conditions. The underlying principle of the HBV model is based on the water balance concept, which is described as follows [57]:
where represents the total runoff; n represents the number of time steps; and represents the precipitation amount at the i-th time step, including both rainfall and snowfall. represents evaporation, and represent the water in the runoff storage reservoirs, and U represents the baseflow.
2.3. XGBoost
XGBoost is a machine learning algorithm based on gradient boosting, specifically designed to efficiently handle large-scale datasets and deliver superior predictive performance [58]. XGBoost optimizes the prediction results step by step by constructing a series of decision trees, and this is an ensemble learning method. The model has many significant advantages, among which its ability to accurately capture complex nonlinear relationships is particularly prominent [59]. During the optimization process, XGBoost aims to minimize a regularized objective function that includes both a loss term and a regularization term:
In the model, represents the objective function of the model and is the sum of the loss function and the regularization term, n represents the number of samples and refers to the number of observations in the dataset, and K refers to the number of decision trees utilized in the model. quantifies the error between the prediction and the observation, while the regularization term penalizes the complexity of each tree . represents the minimum weight for the leaves of the tree, which is used to control the minimum reduction in loss for the leaf nodes; T represents the number of leaf nodes in the tree; represents the L2 regularization term coefficient for the weights, which is used to control the model’s complexity and prevent overfitting; and represents the square of the L2 norm of the weights in the tree, which is the sum of the squares of the weights.
The model optimizes the prediction by iteratively constructing trees using gradient descent. Hyperparameter tuning is performed through grid search to optimize key parameters such as the learning rate, maximum tree depth, and the number of trees.
2.4. HBV-XGBoost Framework
The development and application of the HBV-XGBoost model mainly involve four essential steps: (1) Data Collection and Preprocessing. (2) The HBV-XGBoost Model: We integrated the strengths of both the HBV hydrological model and the XGBoost machine learning algorithm to enhance simulation accuracy. (III) Climate Variable Prediction Using the SDSM: Precipitation and temperature data were generated using the SDSM to produce high-resolution climate variable outputs. (IV) Future Runoff Prediction with the HBV-XGBoost Model. This coupling of models allows for more accurate and reliable runoff forecasts by combining the physical basis of the HBV model with the predictive power of XGBoost.
In the HBV-XGBoost coupled model, the output results of the HBV model are used as input features. Specifically, the model selects actual evapotranspiration (AET), upper zone storage (SUZ), and the fast and slow runoff components (Q1 and Q2) as input variables [55]. These variables are key indicators of hydrological processes and ensure that the model can accurately capture both large-scale and local hydrological dynamic changes. In addition to these hydrological model output variables, meteorological variables such as precipitation and temperature are also included. This helps to further enhance the model’s predictive accuracy. Finally, the measured runoff data from the Xingshan Hydrological Station are used as the target variable for the systematic training and validation of the model.
2.5. SDSM and Future Meteorological Data
In the field of climate simulation, the Statistical Downscaling Model (SDSM) is an important tool. It can downscale the large-scale output data from Global Climate Models (GCMs) or Regional Climate Models (RCMs) to local or regional levels. This process provides more detailed predictions for local climate variables such as precipitation and temperature. The SDSM establishes the relationship between large-scale and local climate variables through statistical methods. It converts large-scale data into small-scale data [60]. This downscaling process is crucial for understanding the potential impacts of climate change on fields such as water resources, agriculture, and ecosystems. These fields typically require high-resolution climate data to develop effective response strategies [55]. In this study, we used version 6.2.9 of the SDSM to generate high-resolution climate data for the period from 2025 to 2100. To assess the model’s performance, three statistical indicators, namely R2, NSE, and RMSE, were employed for quantitative analysis. The specific statistical results and related data can be found in Table 2.

Table 2.
The optimal values of sensitive parameters for the HBV model in the Xiangxi River Basin [44].
3. Results
3.1. Assessment of Hydrological Model Efficiency
Figure 2 illustrates a comparison of the runoff simulation accuracy between the standard HBV model and the enhanced HBV-XGBoost model. During the model calibration phase, the runoff simulation results of the HBV model showed an R2 value of 0.79, an NSE value of 0.77, and an RMSE value of 19.31 m3/s. In contrast, the corresponding indicators for the HBV-XGBoost model were an R2 of 0.854, an NSE of 0.85, and an RMSE of 14.24 m3/s. These results indicate that the HBV-XGBoost model has a slight edge in simulation accuracy, being able to more accurately reflect the actual trends in runoff changes, with better data fitting and smaller errors. During the model validation phase, the performance indicators of the HBV model were an R2 of 0.74, an NSE of 0.71, and an RMSE of 23.21 m3/s. The performance indicators of the HBV-XGBoost model were an R2 of 0.79, an NSE of 0.79, and an RMSE of 19.81 m3/s, once again showing superior performance. These results demonstrate that during the calibration and validation stages, the HBV-XGBoost model maintains high fitting accuracy, can more accurately predict future runoff data, and better adapts to the complexity of hydrological processes, thereby improving the accuracy and reliability of runoff simulation.
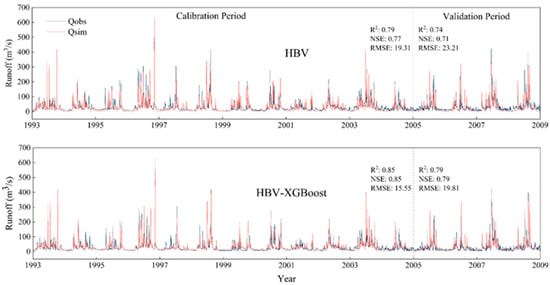
Figure 2.
Daily runoff: simulated vs. observed data in calibration and validation phases.
3.2. Projections of Future Climate Change via SDSM
Figure 3 shows the trends in temperature and precipitation changes in the 2040s and 2080s of the 21st century under different Shared Socioeconomic Pathway (SSP) scenarios. The figure involves three SSP scenarios: SSP126, SSP245, and SSP585. First, as seen from Figure 3a, the daily maximum temperature (Tmax) is on the rise under all SSP scenarios. In the 2040s, the change in maximum temperature (Tmax) is the highest under the SSP585 scenario, with an average increase of 4.5 °C. Under the SSP126 and SSP245 scenarios, the increases are 2.5 °C and 3.5 °C, respectively. By the 2080s, Tmax increases by 6.5 °C under the SSP585 scenario, 3.5 °C under the SSP126 scenario, and 5.5 °C under the SSP245 scenario. This indicates that under the high-emission scenario (SSP585), the rise in Tmax is more pronounced. Figure 3b shows the trend in the daily minimum temperature (Tmin), which is similar to that of Tmax. In the 2040s, Tmin increases by 3.5 °C under the SSP585 scenario, 2.0 °C under the SSP126 scenario, and 3.0 °C under the SSP245 scenario. By the 2080s, Tmin rises by 5.5 °C under the SSP585 scenario, 3.0 °C under the SSP126 scenario, and 4.5 °C under the SSP245 scenario. This further confirms that under the high-emission scenario, the rise in Tmin is also more significant. Figure 3c reflects the rate of change in precipitation. In the 2040s, the changes in precipitation under different SSP scenarios are more complex, with both increases and decreases. For example, the rate of change in precipitation under the SSP585 scenario is approximately −10%, while the changes under the SSP126 and SSP245 scenarios are about −5% and 0%, respectively. By the 2080s, the rate of change in precipitation under the SSP585 scenario improves, with an average of about 5%, while the changes under the SSP126 and SSP245 scenarios are approximately 0% and −5%, respectively. Under the high-emission scenario (SSP585), precipitation might decrease in the short term but improve in the long term. In all scenarios, both the maximum and minimum temperatures are on the rise, with the most significant increases observed under the SSP585 scenario. Precipitation changes are more complex, with a potential decline in the short term, though this trend is anticipated to be offset by the 2080s.
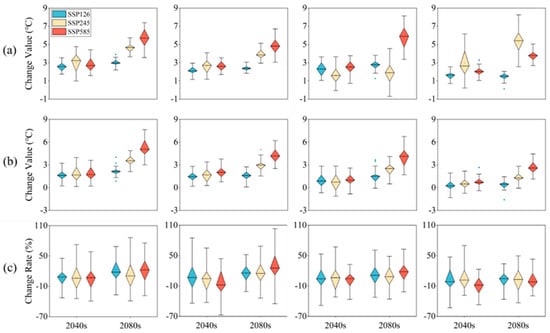
Figure 3.
Changes in (a) Tmax, (b) Tmin, and (c) precipitation in comparison to the baseline period (1991-2008) across various climate projections.
3.3. Utilizing SDSM for Simulated Future Climate Downscaling
Figure 4 shows the monthly runoff predictions of the Xiangxi River under different GCMs and SSP scenarios. With the analysis using the HBV-XGBoost model, the trends in runoff changes under different scenarios can be clearly seen. On a seasonal scale, all models consistently show a significant increase in runoff from May to August, with the lowest runoff occurring from December to February. In contrast to the historical period, future projections for the 2040s and 2080s indicate a shift in peak runoff from June to May. This change may be attributed to increased spring precipitation leading to earlier soil saturation, as well as rising temperatures accelerating the hydrological cycle and increasing evaporation rates, especially under the high-emission scenario (SSP585) in the 2080s, where runoff increases from about 1527.52 cubic meters per second to 2344.42 cubic meters per second and from 1462.11 cubic meters per second to 2889.58 cubic meters per second, respectively. This may be due to the significant increase in temperature and precipitation under the SSP585 scenario, leading to increased runoff during high-precipitation months, while high temperatures in low-precipitation months reduce soil moisture by increasing evaporation and transpiration rates, potentially worsening drought conditions. In contrast, the EC-Earth3-Veg-LR model and the FGOALS-g3 model predict more moderate fluctuations in runoff in the future periods under the SSP585 scenario. Both the ACCESS-CM2 and ACCESS-ESM1-5 models anticipate an escalation in runoff during May under the SSP126 and SSP245 scenarios. In summary, different emission pathways show different results, but there is a clear enhancement in peak summer runoff. These results highlight the urgency of developing robust and highly adaptive water resource management strategies. To effectively manage anticipated seasonal extreme events and address uncertainties in future runoff patterns due to climate change, it is crucial to implement strategies. Additionally, establishing a comprehensive monitoring and early warning system for extreme weather events is of great significance. This system aids in reducing the impacts of floods and droughts, safeguarding water resources, and ensuring the safety of local communities.
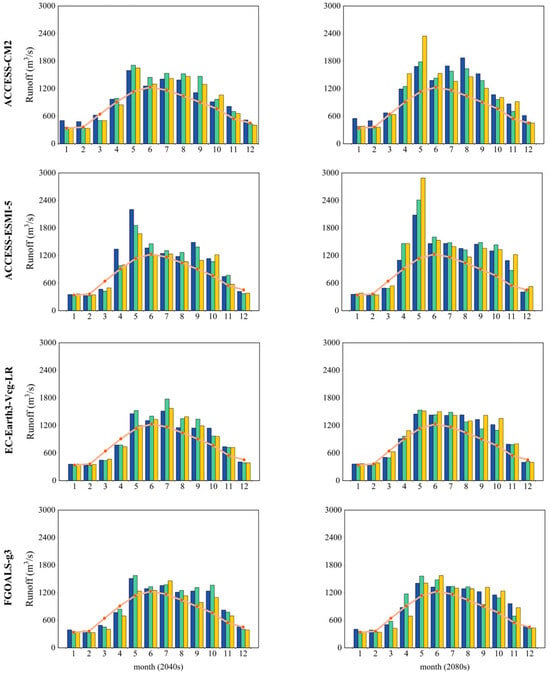
Figure 4.
A comparative analysis of monthly runoff patterns across climate scenarios for the 2040s and 2080s relative to the baseline period (1993–2008).
Table 3 highlights notable variances in how various Global Climate Models (GCMs) and climate scenarios influence the projected runoff for the decades of the 2040s and 2080s. The Sen slope measures the extent of the trend, and the M-K test determines whether the trend is statistically significant [61,62]. A positive Sen’s slope signifies an upward trend in runoff, whereas a negative slope implies a downward trend. The Z-value determines the significance of the trend, with a larger absolute value indicating a more pronounced significance. In the 2040s, the ACCESS-CM2 model under the SSP585 scenario shows a significant increasing trend with a Sen’s slope of 0.0025 m3/s and a Z-value of 1.33. In contrast, during the same period, the EC-Earth3-Vcg-LR model under the SSP245 scenario exhibits a non-significant decrease with a Sen’s slope of −0.0030 m3/s and a Z-value of −0.65. In the 2080s, the increase in runoff under the SSP585 scenario for the ACCESS-CM2 model is even more pronounced, with a Sen’s slope of 0.0047 m3/s and a Z-value of 2.15, indicating a trend towards increased runoff under high-emission scenarios. Conversely, under the low-emission scenario SSP126, the FGOALS-g3 model in the 2080s shows a significant decreasing trend, with a Sen’s slope of −0.0050 m3/s and a Z-value of −2.19. These results suggest that the impact of climate change on runoff is complex and variable, with considerable differences in predictions under different models and scenarios, highlighting the need to consider this uncertainty and complexity when formulating water resource management strategies. Moreover, these findings underscore the necessity for adjustments in runoff prediction and management strategies under different climate scenarios, particularly under high-emission scenarios.

Table 3.
Analysis of Sen slope and M-K trend tests for future runoff projections.
Figure 5 illustrates the predicted annual runoff using violin and radar plots. The violin plot on the left depicts the distribution of annual runoff across four GCMs under three scenarios, while the radar plot on the right offers a visual comparison of percentage changes relative to the historical period (1993–2008). The findings reveal substantial changes in the projected annual runoff under different scenarios. It is evident that all Global Climate Models (GCMs) forecast a notable increase in annual runoff under the high-emission scenario SSP585, particularly in the 2080s, suggesting a more severe impact of high-emission scenarios on water resources. For instance, the FGOALS-g3 model predicts the highest growth rate in runoff for the 2080s compared to historical data, at 76.54%, under the SSP585 scenario. The ACCESS-ESM1-5 model exhibits greater variability under the SSP585 scenario, with a more dispersed distribution of predicted runoff values, and a growth rate of 53% for the 2080s compared to historical data, indicating higher sensitivity to emission scenarios. The ACCESS-CM2 model and the EC-Earth3-Veg-LR model also show increases under the SSP585 scenario, but the magnitude of growth is relatively small. In contrast, apart from the FGOALS-g3 model, the other three models show smaller increases under the lower-emission scenarios (SSP126 and SSP245), indicating a lower impact of climate change. The FGOALS-g3 model predicts the highest growth rate in runoff for the 2080s under the SSP126 scenario, at 77.38%, compared to historical data. The ACCESS-CM2 model and the ACCESS-ESM1-5 model predict growth rates of 47.92% and 40.07%, respectively, for the 2080s under the SSP126 scenario. Under all scenarios, the runoff is anticipated to rise progressively from the historical period to the 2040s and then to the 2080s, suggesting that the influence of climate change on water resources will become more severe over time.
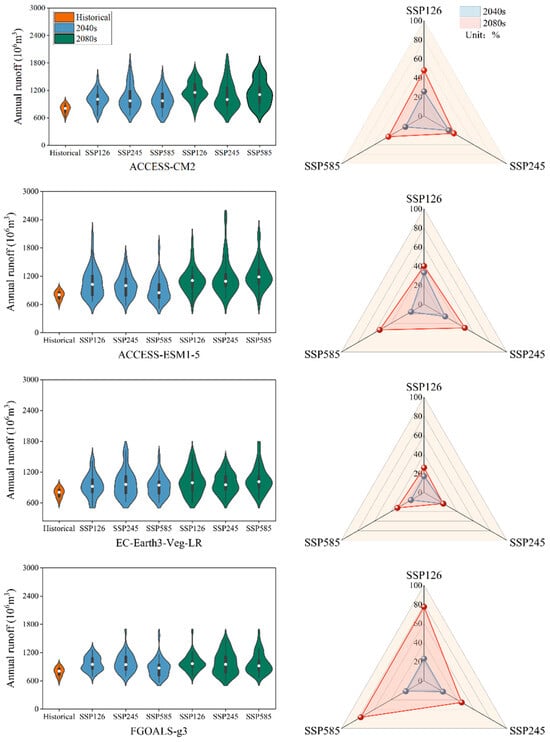
Figure 5.
The projected annual runoff in the 2040s and 2080s under different climate scenarios compared to the historical period (1993–2008).
Figure 6 depicts the monthly mean runoff for the years 2040 and 2080, considering various Global Climate Models (GCMs) and three distinct climate scenarios: SSP126, SSP245, and SSP585. It is evident that the monthly runoff increases for all GCMs from 2040 to 2080, with the largest increase occurring under the high-emission scenario (SSP585). The ACCESS-CM2 and FGOALS-g3 models show the greatest changes in monthly average runoff. For example, under the SSP585 scenario, the ACCESS-CM2 model predicts that the average runoff in May will increase dramatically from 12.81 and 39.72 in 2040 to 88.05 and 84.34 in 2080. The FGOALS-g3 model predicts that the average runoff in May will increase from 21.93 in 2040 to 50.9 in 2080 under the SSP585 scenario. In contrast, the ACCESS-ESM1-5 and EC-Earth3-Veg-LR models show more significant changes in the monthly average runoff predictions for 2080. The ACCESS-ESM1-5 model forecasts that in 2080, there will be an increase in the number of months experiencing a substantial rise in monthly average runoff under both the SSP245 and SSP585 scenarios. Meanwhile, the EC-Earth3-Veg-LR model projects a notable increase in monthly average runoff in 2080 under the SSP126 and SSP245 scenarios. In terms of seasonal variation, the peak monthly average runoff typically occurs from April to July, which may be related to the seasonal precipitation pattern. This reflects the profound impact of climate change on the water cycle, which may lead to significant changes in the spatial and temporal distribution of water resources and thus exacerbate the challenges of water resource management.
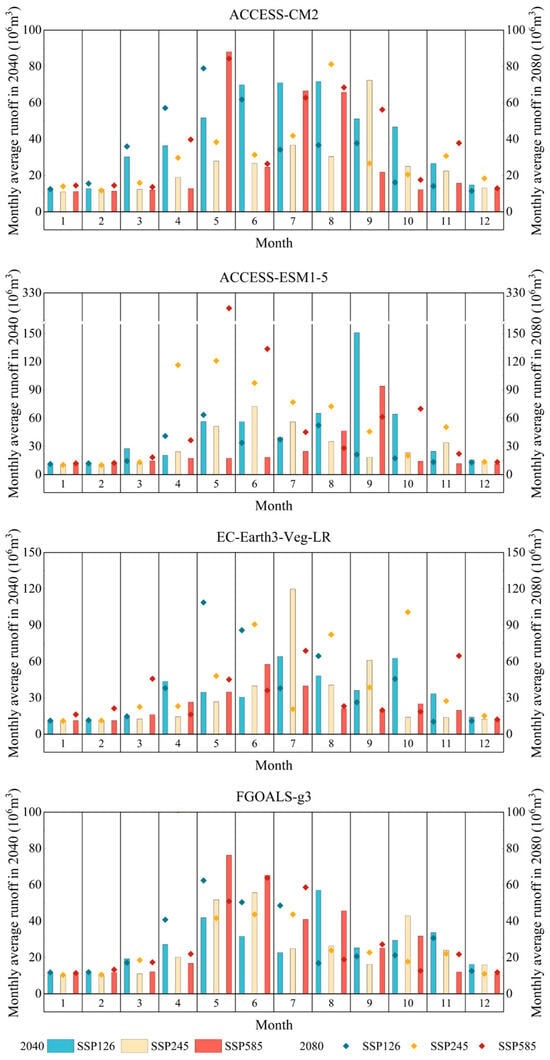
Figure 6.
Monthly runoff averages in 2040 and 2080 across different climate scenarios.
4. Conclusions
In this study, we employed the HBV-XGBoost hybrid model to predict the impact of climate change on runoff in the Xiangxi River Basin. We integrated high-resolution climate data provided by the SDSM with the physical basis of the HBV model. This allowed us to assess future runoff changes under different emission scenarios. Additionally, we leveraged the strong predictive capabilities of the XGBoost model. By comparing the prediction results of the HBV model and the HBV-XGBoost model, we verified the superiority of the coupled model in runoff prediction. Our model evaluation utilized statistical metrics such as R2, NSE, and RMSE to ensure the accuracy and reliability of the prediction results. Compared with previous studies in similar arid regions, such as the study by Su et al. [7] in the Weigan River Basin, which used the SWAT model to predict future runoff changes under climate change scenarios, our HBV-XGBoost model demonstrated higher prediction accuracy and better adaptability to different emission scenarios. This suggests that the hybrid model approach can provide more robust and reliable runoff predictions in the context of climate change, especially in regions with complex hydrological processes and significant climate variability.
The research findings indicate that the HBV-XGBoost model has a relatively high level of accuracy in simulating runoff changes. It can accurately reflect the actual dynamics of runoff. Under different Shared Socioeconomic Pathway (SSP) scenarios, we forecast that the peak runoff could shift from June to May in the future periods of the 2040s and 2080s. For instance, both the ACCESS-CM2 and ACCESS-ESM1-5 models predict a surge in May runoff under various emission scenarios, particularly under the high-emission scenario (SSP585) in the 2080s, where runoff increases from approximately 1527.52 cubic meters per second to 2344.42 cubic meters per second and from 1462.11 cubic meters per second to 2889.58 cubic meters per second, respectively. This may be due to the significant rise in temperature and precipitation under the SSP585 scenario, leading to increased runoff in months with high precipitation, while high temperatures in months with low precipitation reduce soil moisture by enhancing evaporation and transpiration rates, potentially exacerbating drought conditions. Predicted annual runoff also shows significant changes under different scenarios. All four Global Climate Models (GCMs) forecast a notable increase in annual runoff under the high-emission scenario SSP585, mainly in the 2080s, indicating a more severe impact on water resources under high-emission scenarios. For example, the FGOALS-g3 model predicts the highest growth rate in runoff for the 2080s under the SSP585 scenario compared to historical data, at 76.54%. The ACCESS-ESM1-5 model exhibits considerable variability under the SSP585 scenario, with a more dispersed distribution of predicted annual runoff, and a growth rate of 53% compared to historical data for the 2080s, indicating higher sensitivity to emission scenarios. These findings highlight the necessity for developing robust and adaptive water resource management strategies. These strategies are crucial for addressing potential seasonal extreme events and are essential for effectively managing the uncertainties brought by climate change.
This study provides valuable insights and predictions. However, there are some limitations. The uncertainty of model predictions may be influenced by the selected climate models and downscaling methods. The model’s generalizability under different climate scenarios and basin conditions may vary. Future research could explore combinations of more climate models and downscaling methods. This could improve the accuracy and robustness of predictions. Further investigation into the effectiveness of different management strategies and technologies is also needed. This would help in adapting to climate change and water resource management. It will also help in developing more effective water resource management measures. These measures are necessary to address the challenges posed by climate change.
Author Contributions
J.G.: Conceptualization, Project administration, Methodology, Investigation, Data curation, Software, Formal analysis, Writing—original draft, Writing—review and editing, and Visualization. W.L. and F.Z.: Writing—review and editing, Validation, Software, Resources, Visualization, Project administration, and Data curation. A.Y. and Y.F.: Resources, Data curation, Formal analysis, Writing—review and editing, Visualization, Software, and Writing—original draft. J.L.: Writing—review and editing, Visualization, and Validation. All authors have read and agreed to the published version of the manuscript.
Funding
International Cooperation Projects of Fujian Provincial Department of Science and Technology, China (2025I0052), the Royal Society International Exchanges Programme (IES\R1\251575).
Data Availability Statement
The data sources are detailed on the websites listed in Table 1.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sun, A.Y.; Scanlon, B.R. How can Big Data and machine learning benefit environment and water management: A survey of methods, applications, and future directions. Environ. Res. Lett. 2019, 14, 073001. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, H.; Reggiani, P. Climate Variability and Climate Change Impacts on Land Surface, Hydrological Processes and Water Management. Water 2019, 11, 1492. [Google Scholar] [CrossRef]
- Ma, K.; Huang, X.; Liang, C.; Zhao, H.; Zhou, X.; Wei, X. Effect of land use/cover changes on runoff in the Min River watershed. River Res. Appl. 2020, 36, 749–759. [Google Scholar] [CrossRef]
- Nanda, A.; Sen, S. A complex network theory based approach to better understand the infiltration-excess runoff generation thresholds. J. Hydrol. 2021, 603, 127038. [Google Scholar] [CrossRef]
- Li, B.; Zheng, J.; Shi, X.; Chen, Y. Quantifying the impact of mountain precipitation on runoff in Hotan River, northwestern China. Front. Earth Sci. 2020, 14, 568–577. [Google Scholar] [CrossRef]
- Li, Z.; Murshed, M.; Yan, P. Driving force analysis and prediction of ecological footprint in urban agglomeration based on extended STIRPAT model and shared socioeconomic pathways (SSPs). J. Clean. Prod. 2023, 383, 135424. [Google Scholar] [CrossRef]
- Su, J.; Zhang, P.; Deng, X.; Ren, C.; Zhang, J.; Chen, F.; Long, A. Predicting Runoff from the Weigan River under Climate Change. Appl. Sci. 2024, 14, 541. [Google Scholar] [CrossRef]
- Hundecha, Y.; Bárdossy, A. Modeling of the effect of land use changes on the runoff generation of a river basin through parameter regionalization of a watershed model. J. Hydrol. 2004, 292, 281–295. [Google Scholar] [CrossRef]
- Napoli, M.; Massetti, L.; Orlandini, S. Hydrological response to land use and climate changes in a rural hilly basin in Italy. CATENA 2017, 157, 1–11. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Adnan, R.M. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Ji, Y.; Dong, H.T.; Xing, Z.X.; Sun, M.X.; Fu, Q.; Liu, D. Application of the decomposition-prediction-reconstruction framework to medium- and long-term runoff forecasting. Water Supply 2021, 21, 696–709. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Q.; Li, G.; Li, J. Data-driven runoff forecasting for Minjiang River: A case study. Water Supply 2020, 20, 2284–2295. [Google Scholar] [CrossRef]
- Pan, T.; Wang, R. State space neural networks for short term rainfall-runoff forecasting. J. Hydrol. 2004, 297, 34–50. [Google Scholar] [CrossRef]
- Badrzadeh, H.; Sarukkalige, R.; Jayawardena, A.W. Hourly runoff forecasting for flood risk management: Application of various computational intelligence models. J. Hydrol. 2015, 529, 1633–1643. [Google Scholar] [CrossRef]
- Moosavi, V.; Talebi, A.; Hadian, M.R. Development of a Hybrid Wavelet Packet- Group Method of Data Handling (WPGMDH) Model for Runoff Forecasting. Water Resour. Manag. 2017, 31, 43–59. [Google Scholar] [CrossRef]
- Löwe, R.; Mikkelsen, P.S.; Madsen, H. Stochastic rainfall-runoff forecasting: Parameter estimation, multi-step prediction, and evaluation of overflow risk. Stoch. Environ. Res. Risk Assess. 2014, 28, 505–516. [Google Scholar] [CrossRef]
- Guo, T.; Song, S.; Yan, Y. A time-varying autoregressive model for groundwater depth prediction. J. Hydrol. 2022, 613, 128394. [Google Scholar] [CrossRef]
- Pérez-Alarcón, A.; Garcia-Cortes, D.; Fernández-Alvarez, J.C.; Martínez-González, Y. Improving Monthly Rainfall Forecast in a Watershed by Combining Neural Networks and Autoregressive Models. Environ. Process. 2022, 9, 53. [Google Scholar] [CrossRef]
- Mohammadi, K.; Eslami, H.R.; Kahawita, R. Parameter estimation of an ARMA model for river flow forecasting using goal programming. J. Hydrol. 2006, 331, 293–299. [Google Scholar] [CrossRef]
- Liu, S.; Qin, H.; Liu, G.; Xu, Y.; Zhu, X.; Qi, X. Runoff Forecasting of Machine Learning Model Based on Selective Ensemble. Water Resour. Manag. 2023, 37, 4459–4473. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Gosain, A.K.; Ramasastri, K.S. A data-driven algorithm for constructing artificial neural network rainfall-runoff models. Hydrol. Process. 2002, 16, 1325–1330. [Google Scholar] [CrossRef]
- Sivapragasam, C.; Vincent, P.; Vasudevan, G. Genetic programming model for forecast of short and noisy data. Hydrol. Process. 2007, 21, 266–272. [Google Scholar] [CrossRef]
- Shiri, J.; Kisi, O. Short-term and long-term streamflow forecasting using a wavelet and neuro-fuzzy conjunction model. J. Hydrol. 2010, 394, 486–493. [Google Scholar] [CrossRef]
- Humphrey, G.B.; Gibbs, M.S.; Dandy, G.C.; Maier, H.R. A hybrid approach to monthly streamflow forecasting: Integrating hydrological model outputs into a Bayesian artificial neural network. J. Hydrol. 2016, 540, 623–640. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.P.; Rangan, D.M.; Ramasastri, K.S. A neuro-fuzzy computing technique for modeling hydrological time series. J. Hydrol. 2004, 291, 52–66. [Google Scholar] [CrossRef]
- Ashrafi, M.; Chua, L.H.C.; Quek, C.; Qin, X. A fully-online Neuro-Fuzzy model for flow forecasting in basins with limited data. J. Hydrol. 2017, 545, 424–435. [Google Scholar] [CrossRef]
- Kisi, O.; Cimen, M. A wavelet-support vector machine conjunction model for monthly streamflow forecasting. J. Hydrol. 2011, 399, 132–140. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Kahya, E.; Olyaie, E. Streamflow prediction using linear genetic programming in comparison with a neuro-wavelet technique. J. Hydrol. 2013, 505, 240–249. [Google Scholar] [CrossRef]
- Ravansalar, M.; Rajaee, T.; Kisi, O. Wavelet-linear genetic programming: A new approach for modeling monthly streamflow. J. Hydrol. 2017, 549, 461–475. [Google Scholar] [CrossRef]
- Asefa, T.; Kemblowski, M.; McKee, M.; Khalil, A. Multi - time scale stream flow predictions: The support vector machines approach. J. Hydrol. 2006, 318, 7–16. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Monthly streamflow prediction using modified EMD-based support vector machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Jin, Z.; Yang, Y.; Liu, Y. Stock closing price prediction based on sentiment analysis and LSTM. Neural Comput. Appl. 2020, 32, 9713–9729. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Luo, H.; He, J.; Cheung, R.W.M. AI-powered landslide susceptibility assessment in Hong Kong. Eng. Geol. 2021, 288, 106103. [Google Scholar] [CrossRef]
- Okkan, U.; Serbes, Z.A. Rainfall–runoff modeling using least squares support vector machines. Environmetrics 2012, 23, 549–564. [Google Scholar] [CrossRef]
- Khosravi, K.; Shahabi, H.; Pham, B.T.; Adamowski, J.; Shirzadi, A.; Pradhan, B.; Dou, J.; Ly, H.B.; Gróf, G.; Ho, H.L.; et al. A comparative assessment of flood susceptibility modeling using Multi-Criteria Decision-Making Analysis and Machine Learning Methods. J. Hydrol. 2019, 573, 311–323. [Google Scholar] [CrossRef]
- Fei, K.; Du, H.; Gao, L. Accurate water level predictions in a tidal reach: Integration of Physics-based and Machine learning approaches. J. Hydrol. 2023, 622, 129705. [Google Scholar] [CrossRef]
- Leng, Z.; Chen, L.; Yang, B.; Li, S.; Yi, B. An extreme forecast index-driven runoff prediction approach using stacking ensemble learning. Geomat. Nat. Hazards Risk 2024, 15, 2353144. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Cheng, G.; Huang, G.; Dong, C.; Zhu, J.; Zhou, X.; Yao, Y. High-resolution projections of 21st century climate over the Athabasca River Basin through an integrated evaluation-classification-downscaling-based climate projection framework. J. Geophys. Res. Atmos. 2017, 122, 2595–2615. [Google Scholar] [CrossRef]
- Li, K.; Huang, G.; Wang, S.; Baetz, B.; Xu, W. A stepwise clustered hydrological model for addressing the temporal autocorrelation of daily streamflows in irrigated watersheds. Water Resour. Res. 2022, 58, e2021WR031065. [Google Scholar] [CrossRef]
- Wang, W.C.; Du, Y.J.; Chau, K.W.; Xu, D.M.; Liu, C.J.; Ma, Q. An ensemble hybrid forecasting model for annual runoff based on sample entropy, secondary decomposition, and long short-term memory neural network. Water Resour. Manag. 2021, 35, 4695–4726. [Google Scholar] [CrossRef]
- Wang, S.; Peng, H. Multiple spatio-temporal scale runoff forecasting and driving mechanism exploration by K-means optimized XGBoost and SHAP. J. Hydrol. 2024, 630, 130650. [Google Scholar] [CrossRef]
- Wang, H.; Qin, H.; Liu, G.; Liu, S.; Qu, Y.; Wang, K.; Zhou, J. A novel feature attention mechanism for improving the accuracy and robustness of runoff forecasting. J. Hydrol. 2023, 618, 129200. [Google Scholar] [CrossRef]
- Dams, J.; Nossent, J.; Senbeta, T.B.; Willems, P.; Batelaan, O. Multi-model approach to assess the impact of climate change on runoff. J. Hydrol. 2015, 529, 1601–1616. [Google Scholar] [CrossRef]
- IPCC. AR6 Synthesis Report: Climate Change 2023; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Li, G.; Liu, Z.; Zhang, J.; Han, H.; Shu, Z. Bayesian model averaging by combining deep learning models to improve lake water level prediction. Sci. Total Environ. 2024, 906, 167718. [Google Scholar] [CrossRef]
- Dash, S.S.; Sahoo, B.; Raghuwanshi, N.S. SWAT model calibration approaches in an integrated paddy-dominated catchment-command. Agric. Water Manag. 2023, 278, 108138. [Google Scholar] [CrossRef]
- Roy, A.; Kasiviswanathan, K.S.; Patidar, S.; Adeloye, A.J.; Soundharajan, B.S.; Ojha, C.S.P. A Physics-Aware Machine Learning-Based Framework for Minimizing Prediction Uncertainty of Hydrological Models. Water Resour. Res. 2023, 59, 034630. [Google Scholar] [CrossRef]
- Breuer, L.; Huisman, J.A.; Willems, P.; Bormann, H.; Bronstert, A.; Croke, B.F.W.; Frede, H.G.; Gräff, T.; Hubrechts, L.; Jakeman, A.J.; et al. Assessing the impact of land use change on hydrology by ensemble modeling (LUCHEM). I: Model intercomparison with current land use. Adv. Water Resour. 2008, 32, 129–146. [Google Scholar] [CrossRef]
- Seibert, J.; Vis, M.J.P.; Lewis, E.; Meerveld, H.J.V. Upper and lower benchmarks in hydrological modelling. Hydrol. Process. 2018, 32, 1120–1125. [Google Scholar] [CrossRef]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-based method for flash flood risk assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Wang, S.; Peng, H.; Hu, Q.; Jiang, M. Analysis of runoff generation driving factors based on hydrological model and interpretable machine learning method. J. Hydrol. Reg. Stud. 2022, 42, 101139. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, Z.; Wang, M.; Gan, W.; Zhao, Z.; Wu, Z. Impacts of building configurations on urban stormwater management at a block scale using XGBoost. Sustain. Cities Soc. 2022, 87, 104235. [Google Scholar] [CrossRef]
- Torlay, L.; Perrone-Bertolotti, M.; Thomas, E.; Baciu, M. Machine learning–XGBoost analysis of language networks to classify patients with epilepsy. Brain Inform. 2017, 4, 159–169. [Google Scholar] [CrossRef]
- Li, W.; Liu, H.; Gao, P.; Yang, A.; Fei, Y.; Wen, Y.; Su, Y.; Yuan, X. Development of an MPE-BMA Ensemble Model for Runoff Prediction Under Future Climate Change Scenarios: A Case Study of the Xiangxi River Basin. Sustainability 2025, 17, 4714. [Google Scholar] [CrossRef]
- Yang, S.; Cui, X. Building Regional Sustainable Development Scenarios with the SSP Framework. Sustainability 2019, 11, 5712. [Google Scholar] [CrossRef]
- Sadayappan, K.; Keen, R.; Jarecke, K.M.; Moreno, V.; Nippert, J.B.; Kirk, M.F.; Sullivan, P.L.; Li, L. Drier streams despite a wetter climate in woody-encroached grasslands. J. Hydrol. 2023, 627, 130388. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ding, B.; Yu, X.; Jia, G. Exploring the controlling factors of watershed streamflow variability using hydrological and machine learning models. Water Resour. Res. 2025, 61, e2024WR039734. [Google Scholar] [CrossRef]
- Karami, M.; Abedi Koupai, J.; Gohari, S.A. Integration of SWAT, SDSM, AHP, and TOPSIS to Detect Flood-Prone Areas. Nat. Hazards 2024, 120, 6307–6325. [Google Scholar] [CrossRef]
- Rahman, A.U.; Dawood, M. Spatio-statistical analysis of temperature fluctuation using Mann–Kendall and Sen’s slope approach. Clim. Dyn. 2017, 48, 783–797. [Google Scholar] [CrossRef]
- Khalil, A. Combined use of graphical and statistical approaches for rainfall trend analysis in the Mae Klong River Basin, Thailand. J. Water Clim. Change 2023, 14, 4642–4668. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).