A Systematic Literature Review of MODFLOW Combined with Artificial Neural Networks (ANNs) for Groundwater Flow Modelling
Abstract
1. Introduction
2. Systematic Review Methodology
2.1. Research Questions
- RQ1: What is the temporal and geographical distribution of research integrating MODFLOW models and ANNs for groundwater flow modeling?
- RQ2: What are the primary strategies for integrating MODFLOW models and ANNs, and what is their relative prevalence in the literature?
- RQ3: What are the reported advantages, limitations, and performance outcomes for each integration strategy?
2.2. Finding and Identifying Studies
2.3. Study Selection Criteria
2.4. Data Extraction and Synthesis
3. The Physical-Based Model: MODFLOW
MODFLOW Applications in Groundwater Modelling
4. Artificial Neural Networks (ANNs)
- We identified about 250 key terms by looking at the most frequently occurring words (at least ten times) in the titles and abstracts of research papers pertaining to groundwater. These terms were divided into four primary groups, each of which stood for a significant field of study in Figure 2.
- Many terms were included in the first cluster (dark purple), which focused on subjects pertaining to ML applications, specifically the use of artificial neural networks for environmental prediction. Artificial, neural, network, model, machine, support vector, learning, prediction, ANN, and forecasting were among the most prominent terms in this cluster.
- The second cluster (green–blue) concentrated on hydrological processes and the evaluation of groundwater quantity and quality. Groundwater, aquifer, level, fluctuation, depth, recharge, soil, quality, transport, and contamination were among the terms it included.
- Terms related to time-series analysis and forecasting, frequently in combination with neural networks, made up the third cluster (yellow). Forecasting, wavelet, trends, time series, uncertainty, performance, and optimization were among the terms that appeared frequently.
Application of ANNs in Groundwater Flow Simulation
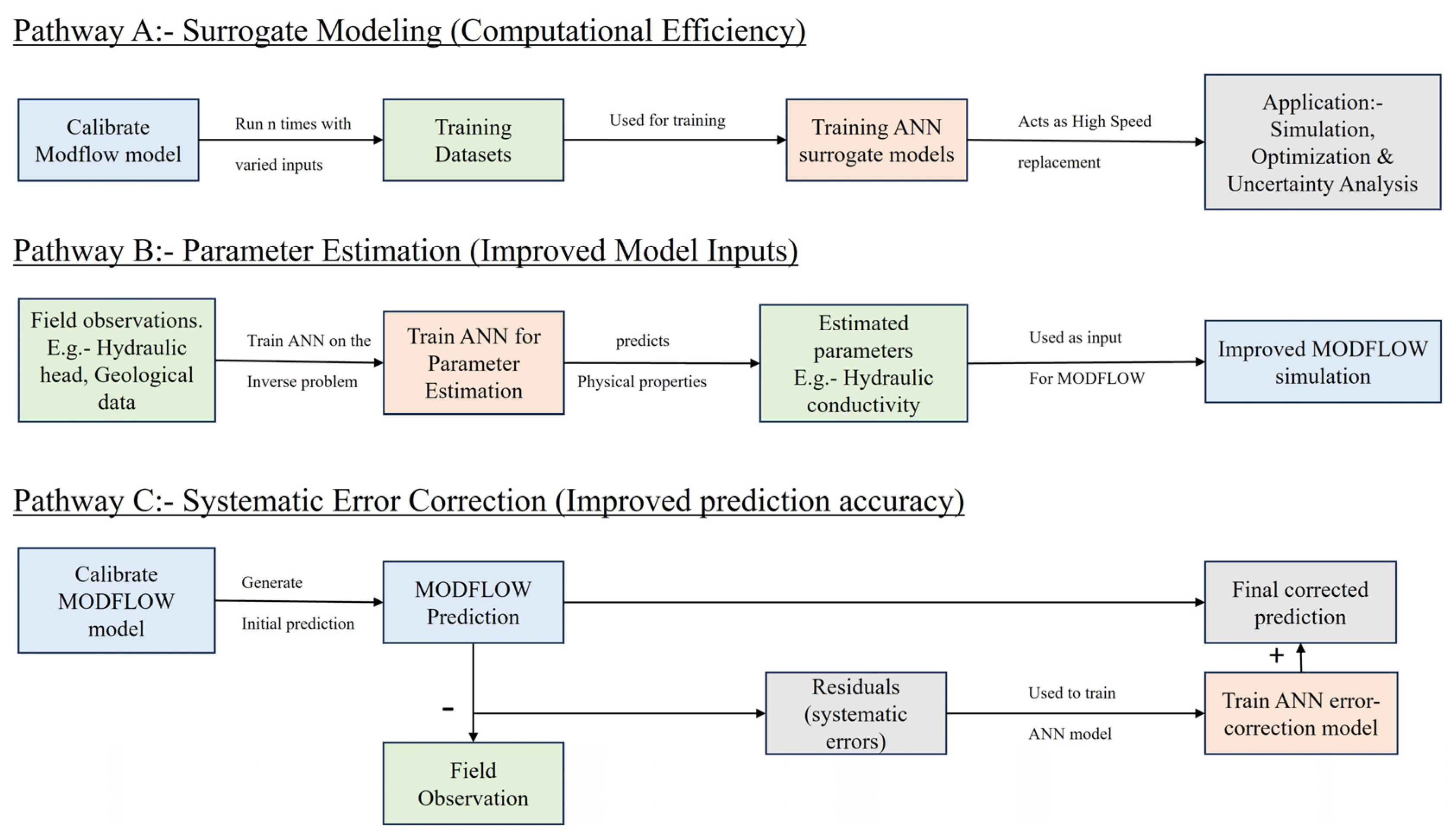
5. A Classification Framework of MODFLOW–ANN Integration
5.1. Strategy 1: An ANN as a Surrogate Model
5.2. Strategy 2: ANNs for Parameter Estimation (Inverse Modeling)
5.3. Strategy 3: An ANN as an Error-Correction Model
6. Synthesis and Discussion
7. Conclusions and Future Research Directions
- Explainable AI (XAI) and Physics-Informed Neural Networks (PINNs): The most significant barrier to broader adoption remains the black box problem. Future research must prioritize the development of techniques like PINNs, which bake physical laws directly into the network architecture, to make these models more transparent and trustworthy.
- Scalability and High-Performance Computing (HPC): A major challenge is scaling these hybrid approaches to large regional or national scales, which will require leveraging HPC resources to handle the massive datasets and complex training procedures involved.
- Real-Time Data Assimilation: Future work should focus on developing methods to dynamically assimilate real-time data streams from sources like remote-sensing satellites and IoT-enabled sensors into these hybrid models, enabling a shift from static to dynamic, adaptive forecasting systems.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Full Form |
| ANN | Artificial Neural Network |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| BCF | Block-Centered Flow package |
| DISV | Discretization by Vertices |
| DRN | Drain package |
| FNN | Feedforward Neural Network |
| GHB | General Head Boundary package |
| GIS | Geographic Information System |
| GMS | Groundwater Modeling System |
| HPC | High-Performance Computing |
| LSTM | Long Short-Term Memory |
| MAW1 | Multi-Aquifer Well package (MODFLOW 6) |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MODFLOW | Modular Finite Difference Flow model |
| MODFLOW-NWT | MODFLOW Newton Solver |
| MODFLOW-USG | MODFLOW Unstructured Grid |
| MT3DMS | Modular Three-Dimensional Transport Model |
| NSE | Nash-Sutcliffe Efficiency |
| PEST | Parameter ESTimation |
| PINN | Physics-Informed Neural Network |
| PSO | Particle Swarm Optimization |
| R2 | Coefficient of Determination |
| RCH | Recharge package |
| ReLU | Rectified Linear Unit |
| RIV | River package |
| RMSE | Root Mean Square Error |
| SEAWAT | SEA Water Transport model |
| SWAT | Soil and Water Assessment Tool |
| SVM | Support Vector Machine |
| WULUMOD | Water-Use and Land-Use Change Model |
References
- Angelakis, A.N.; Voudouris, K.S.; Mariolakos, I. Groundwater utilization through the centuries focusing οn the Hellenic civilizations. Hydrogeol. J. 2016, 24, 1311–1324. [Google Scholar] [CrossRef]
- Bobeck, P. Henry Darcy and the Public Fountains of the City of Dijon. In Henry P. G. Darcy and Other Pioneers in Hydraulics; American Society of Civil Engineers: Philadelphia, PA, USA, 2003; pp. 37–50. [Google Scholar] [CrossRef]
- Brown, G.O. Jules Dupuit’s Contributions in Water Resources. In Water Resources and Environmental History; American Society of Civil Engineers: Salt Lake City, UT, USA, 2004; pp. 104–110. [Google Scholar] [CrossRef]
- Okuyade, W.I.A.; Abbey, T.M.; Abbey, M.E. Application of the Dupuit–Forchheimer model to groundwater flow into a well. Model. Earth Syst. Environ. 2022, 8, 2359–2367. [Google Scholar] [CrossRef]
- Theis, C.V. The relation between the lowering of the Piezometric surface and the rate and duration of discharge of a well using ground-water storage. Eos Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Igboekwe, M.U.; Achi, N.J. Finite Difference Method of Modelling Groundwater Flow. J. Water Resour. Prot. 2011, 3, 192–198. [Google Scholar] [CrossRef]
- Sarkar, B.C. Geostatistics in Groundwater Modelling. In Groundwater Development and Management; Sikdar, P.K., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 147–169. [Google Scholar] [CrossRef]
- Ma, Q.; Abily, M.; Du, M.; Gourbesville, P.; Fouché, O. Integrated Groundwater Resources Management: Spatially-Nested Modelling Approach for Water Cycle Simulation. Water Resour. Manag. 2020, 34, 1319–1333. [Google Scholar] [CrossRef]
- McDonald, M.G. A Modular Three-Dimensional Finite-Difference Ground-Water Flow Model; US Geological Survey: Reston, VA, USA, 1988. [Google Scholar] [CrossRef]
- Pathak, R.; Awasthi, M.K.; Sharma, S.K.; Hardaha, M.K.; Nema, R.K. Ground Water Flow Modelling Using MODFLOW—A Review. Int. J. Curr. Microbiol. Appl. Sci. 2018, 7, 83–88. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, U.S. Geological Survey Modular Ground-Water Model—The Groundwater Flow Process. U.S. Geological Survey Techniques and Methods 6-A16. 2005. Available online: https://pubs.usgs.gov/tm/2005/tm6A16/PDF/TM6A16.pdf (accessed on 5 August 2025).
- Doherty, J.E.; Hunt, R.J. Approaches to Highly Parameterized Inversion—A Guide to Using PEST for Groundwater-Model Calibration; U.S. Geological Survey Scientific Investigations Report 2010–5169; U.S. Geological Survey: Reston, VA, USA, 2010; 59p. [Google Scholar]
- Zeydalinejad, N. Artificial neural networks vis-à-vis MODFLOW in the simulation of groundwater: A review. Model. Earth Syst. Environ. 2022, 8, 2911–2932. [Google Scholar] [CrossRef]
- Kohzadi, N.; Boyd, M.S.; Kaastra, I.; Kermanshahi, B.S.; Scuse, D. Neural Networks for Forecasting: An Introduction. Can. J. Agric. Econ. Can. Agroecon. 1995, 43, 463–474. [Google Scholar] [CrossRef]
- Sharma, Y.K.; Kim, S.; Tayerani Charmchi, A.S.; Kang, D.; Batelaan, O. Strategic Imputation of Groundwater Data Using Machine Learning: Insights from Diverse Aquifers in the Chao-Phraya River Basin. Groundw. Sustain. Dev. 2024, 18, 101394. [Google Scholar] [CrossRef]
- Sun, A.Y. Predicting groundwater level changes using GRACE data: Predicting Groundwater Level Changes Using Grace Data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef]
- Chen, C.; He, W.; Zhou, H.; Xue, Y.; Zhu, M. A comparative study among machine learning and numerical models for simulating groundwater dynamics in the Heihe River Basin, northwestern China. Sci. Rep. 2020, 10, 3904. [Google Scholar] [CrossRef]
- Nikolos, I.K.; Stergiadi, M.; Papadopoulou, M.P.; Karatzas, G.P. Artificial neural networks as an alternative approach to groundwater numerical modelling and environmental design. Hydrol. Process. 2008, 22, 3337–3348. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef] [PubMed]
- Zizaan, A.; Idri, A. Machine learning based Breast Cancer screening: Trends, challenges, and opportunities. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2023, 11, 976–996. [Google Scholar] [CrossRef]
- Silva, R.L.S.; Neiva, F.W. Systematic Literature Review in Computer Science—A Practical Guide; Federal University of Juiz de Fora: Juiz de Fora, Brazil, 2016. [Google Scholar] [CrossRef]
- Carrera-Rivera, A.; Ochoa, W.; Larrinaga, F.; Lasa, G. How-to conduct a systematic literature review: A quick guide for computer science research. MethodsX 2022, 9, 101895. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Huang, G.; Zhan, H.; Qu, Z.; Huang, Q. Integration of SWAP and MODFLOW-2000 for modeling groundwater dynamics in shallow water table areas. J. Hydrol. 2012, 412–413, 170–181. [Google Scholar] [CrossRef]
- Zaresefat, M.; Derakhshani, R. Revolutionizing Groundwater Management with Hybrid AI Models: A Practical Review. Water 2023, 15, 1750. [Google Scholar] [CrossRef]
- Langevin, C.D.; Hughes, J.D.; Banta, E.R.; Provost, A.; Niswonger, R.; Panday, S. MODFLOW 6, The U.S. Geological Survey Modular Hydrologic Model, U.S. Geological Survey: Reston, VA, USA, 2017. [CrossRef]
- Grodzka-Łukaszewska, M.; Sinicyn, G.; Grygoruk, M.; Mirosław-Świątek, D.; Kardel, I.; Okruszko, T. The role of the river in the functioning of marginal fen: A case study from the Biebrza Wetlands. PeerJ 2022, 10, e13418. [Google Scholar] [CrossRef]
- Langevin, C.D.; Hughes, J.D.; Provost, A.M.; Russcher, M.J.; Morway, E.D.; Reno, M.J.; Bonelli, W.P.; Panday; Sorab; Merrick; et al. MODFLOW Version 6.5.0, U.S. Geological Survey: Reston, VA, USA, 2024. [CrossRef]
- Panday, S.; Langevin, C.D.; Niswonger, R.G.; Ibaraki, M.; Hughes, J.D. MODFLOW–USG Version 1: An Unstructured Grid Version of MODFLOW for Simulating Groundwater Flow and Tightly Coupled Processes Using a Control Volume Finite-Difference Formulation; U.S. Geological Survey Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2013. [Google Scholar]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Sharma, Y.K.; Mohanasundaram, S.; Kim, S.; Shrestha, S.; Babel, M.S.; Loc, H.H. Enhancing Aquifer Reliability and Resilience Assessment in Data-Scarce Regions Using Satellite Data: Application to the Chao Phraya River Basin. Remote Sens. 2025, 17, 1731. [Google Scholar] [CrossRef]
- Neville, C.J. Modeling Multiaquifer Wells with MODFLOW. Groundwater 2004, 42, 910–919. [Google Scholar] [CrossRef]
- Gao, H. Groundwater Modeling for Flow Systems with Complex Geological and Hydrogeological Conditions. Procedia Earth Planet. Sci. 2011, 3, 23–28. [Google Scholar] [CrossRef]
- Brunner, P.; Simmons, C.T.; Cook, P.G.; Therrien, R. Modeling Surface Water-Groundwater Interaction with MODFLOW: Some Considerations. Groundwater 2010, 48, 174–180. [Google Scholar] [CrossRef]
- Wróbel, M.; Brandyk, A.; Tereba, A. Modflow model in the assessment of water conditions in forest areas. Int. J. Hydrol. Sci. Technol. 2023, 15, 207. [Google Scholar] [CrossRef]
- Sharma, Y.; Aggarwal, A.; Singh, J. Development of Flow Duration Curves and Eco-Flow Metrics for the Tawi River Basin—(Jammu, India). Int. J. Adv. Remote Sens. GIS 2019, 8, 3114–3125. [Google Scholar] [CrossRef]
- Rejani, R.; Jha, M.K.; Panda, S.N.; Mull, R. Simulation Modeling for Efficient Groundwater Management in Balasore Coastal Basin, India. Water Resour. Manag. 2008, 22, 23–50. [Google Scholar] [CrossRef]
- Khadri, S.F.R.; Pande, C. Ground water flow modeling for calibrating steady state using MODFLOW software: A case study of Mahesh River basin, India. Model. Earth Syst. Environ. 2016, 2, 39. [Google Scholar] [CrossRef]
- Varalakshmi, V.; Venkateswara Rao, B.; SuriNaidu, L.; Tejaswini, M. Groundwater Flow Modeling of a Hard Rock Aquifer: Case Study. J. Hydrol. Eng. 2014, 19, 877–886. [Google Scholar] [CrossRef]
- Kirubakaran, M.; Colins Johnny, J.; Samson, S. MODFLOW Based Groundwater Budgeting Using GIS: A Case Study from Tirunelveli Taluk, Tirunelveli District, Tamil Nadu, India. J. Indian Soc. Remote Sens. 2018, 46, 783–792. [Google Scholar] [CrossRef]
- Momejian, N.; Abou Najm, M.; Alameddine, I.; El-Fadel, M. Groundwater Vulnerability Modeling to Assess Seawater Intrusion: A Methodological Comparison with Geospatial Interpolation. Water Resour. Manag. 2019, 33, 1039–1052. [Google Scholar] [CrossRef]
- Rajamanickam, R.; Nagan, S. Groundwater Quality Modeling of Amaravathi River Basin of Karur District, Tamil Nadu, Using Visual Modflow. Int. J. Environ. Sci. 2010, 1, 91–108. [Google Scholar]
- Siva Prasad, Y.; Venkateswara Rao, B.; Surinaidu, L. Groundwater flow modeling and prognostics of Kandivalasa river sub-basin, Andhra Pradesh, India. Environ. Dev. Sustain. 2021, 23, 1823–1843. [Google Scholar] [CrossRef]
- Thomas, B.; Behrangi, A.; Famiglietti, J. Precipitation Intensity Effects on Groundwater Recharge in the Southwestern United States. Water 2016, 8, 90. [Google Scholar] [CrossRef]
- Martinez, M.B.; Widdowson, M.A. Evaluating Flow Distribution in a Multiaquifer Recharge Well Using an In Situ Flowmeter. Groundwater 2024, 62, 605–616. [Google Scholar] [CrossRef] [PubMed]
- Langevin, C.D.; Guo, W. MODFLOW/MT3DMS–Based Simulation of Variable-Density Ground Water Flow and Transport. Groundwater 2006, 44, 339–351. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT–MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Merchán-Rivera, P.; Wohlmuth, B.; Chiogna, G. Identifying stagnation zones and reverse flow caused by river-aquifer interaction: An approach based on polynomial chaos expansions. Water Resour. Res. 2021, 57, e2021WR029824. [Google Scholar] [CrossRef]
- Reeves, H.W.; Zellner, M.L. Linking MODFLOW with an Agent-Based Land-Use Model to Support Decision Making. Groundwater 2010, 48, 649–660. [Google Scholar] [CrossRef]
- Batelaan, O.; De Smedt, F. SEEPAGE, a New MODFLOW DRAIN Package. Groundwater 2004, 42, 576–588. [Google Scholar] [CrossRef]
- Bedekar, V.; Niswonger, R.G.; Kipp, K.; Panday, S.; Tonkin, M. Approaches to the Simulation of Unconfined Flow and Perched Groundwater Flow in MODFLOW. Groundwater 2012, 50, 187–198. [Google Scholar] [CrossRef]
- Rahnama, M.B.; Zamzam, A. Quantitative and qualitative simulation of groundwater by mathematical models in Rafsanjan aquifer using MODFLOW and MT3DMS. Arab. J. Geosci. 2013, 6, 901–912. [Google Scholar] [CrossRef]
- Wang, Q.; Zhan, H.; Tang, Z. A New Package in MODFLOW to Simulate Unconfined Groundwater Flow in Sloping Aquifers. Groundwater 2014, 52, 924–935. [Google Scholar] [CrossRef] [PubMed]
- Antoniou, M.; Theodossiou, N.; Karakatsanis, D. Coupling groundwater simulation and optimization models using MODFLOW and Harmony Search Algorithm. Desalination Water Treat. 2017, 86, 297–304. [Google Scholar] [CrossRef]
- AL-Hashmi, S. A numerical groundwater flow model of Wadi Samail Catchment using MODFLOW software. Int. J. GEOMATE 2020, 18, 30–36. [Google Scholar] [CrossRef]
- Bailey, R.T.; Park, S.; Bieger, K.; Arnold, J.G.; Allen, P.M. Enhancing SWAT+ simulation of groundwater flow and groundwater-surface water interactions using MODFLOW routines. Environ. Model. Softw. 2020, 126, 104660. [Google Scholar] [CrossRef]
- Boczoń, A.; Wróbel, M.; Kowalska, A. Long-Term Changes in Groundwater Levels in the Białowieża Forest, Poland, Under Climate Change. Water 2025, 17, 2027. [Google Scholar] [CrossRef]
- Senthilkumar, M.; Elango, L. Three-dimensional mathematical model to simulate groundwater flow in the lower Palar River basin, southern India. Hydrogeol. J. 2004, 12, 197–208. [Google Scholar] [CrossRef]
- Chatterjee, C.; Kumar, R.; Chakravorty, B.; Lohani, A.K.; Kumar, S. Integrating Remote Sensing and GIS Techniques with Groundwater Flow Modeling for Assessment of Waterlogged Areas. Water Resour. Manag. 2005, 19, 539–554. [Google Scholar] [CrossRef]
- Majumdar, P.K.; Kumar, S.; Singh, V.; Jose, M.K. Characterization of groundwater flow in the depleting water table areas in central Punjab. In Proceedings of the XII World Water Congress of IWRA, New Delhi, India, 22–25 November 2005. [Google Scholar]
- Kant, S.; Singh, S.; Nema, A.K.; Chandola, V.K. Modeling of Groundwater Levels in the Sonar sub-basin, Madhya Pradesh Using Visual MODFLOW. Indian J. Dryland Agric. Res. Dev. 2013, 28, 33–37. [Google Scholar]
- Surinaidu, L. Quantifying Stream Flows and Groundwater Response under the Climate and Land Use Change through Integrated Hydrological Modelling in a South Indian River Basin. Water Security 2022, 17, 100129. [Google Scholar] [CrossRef]
- Surinaidu, L. Application of MODFLOW for groundwater Seepage Problems in the Subsurface Tunnels. J. Indian Geophys. Union 2015, 19, 422–443. [Google Scholar]
- Sajeena, S.; Kurien, E.K. Studies on groundwater resources using visual MODFLOW—A case study of Kadalundi river basin, Malappuram, Kerala. Indian J. Soil Conserv. 2019, 47, 21–29. [Google Scholar]
- Behera, A.K.; Pradhan, R.M.; Kumar, S.; Chakrapani, G.J.; Kumar, P. Assessment of Groundwater Flow Dynamics Using MODFLOW in Shallow Aquifer System of Mahanadi Delta (East Coast), India. Water 2022, 14, 611. [Google Scholar] [CrossRef]
- Timaniya, A.; Soni, N. Modeling of Saline Water Intrusion using MODFLOW in Una Coastal Aquifer of Gujarat, India. Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 634–640. [Google Scholar] [CrossRef]
- Siddiqi, F.U.R.; Ahmad, S.; Akram, T.; Ali, M.U.; Zafar, A.; Lee, S.W. Artificial Neural Network-Based Data-Driven Parameter Estimation Approach: Applications in PMDC Motors. Mathematics 2024, 12, 3407. [Google Scholar] [CrossRef]
- Malakar, P.; Sarkar, S.; Mukherjee, A.; Bhanja, S.; Sun, A.Y. Use of machine learning and deep learning methods in groundwater. In Global Groundwater; Elsevier: Amsterdam, The Netherlands, 2021; pp. 545–557. [Google Scholar] [CrossRef]
- Sharma, Y.; Srivastava, M.; Sharma, P.; Kumar, D. Deterministic Seismic Hazard Assessment by Revisiting 1991 Uttarkashi and 1999 Chamoli Earthquake for Uttarakhand, India. Available online: https://meetingorganizer.copernicus.org/EGU23/EGU23-11563.html (accessed on 19 March 2025).
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’adi, Z.; Mehr, A.D.; et al. Groundwater level prediction using machine learning models: A comprehensive review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- D’Oria, M.; Fienen, M.N. MODFLOW-Style Parameters in Underdetermined Parameter Estimation. Groundwater 2012, 50, 149–153. [Google Scholar] [CrossRef]
- Fahimi, F.; Yaseen, Z.M.; El-shafie, A. Application of soft computing based hybrid models in hydrological variables modeling: A comprehensive review. Theor. Appl. Climatol. 2017, 128, 875–903. [Google Scholar] [CrossRef]
- Chu, H.; Bian, J.; Lang, Q.; Sun, X.; Wang, Z. Daily Groundwater Level Prediction and Uncertainty Using LSTM Coupled with PMI and Bootstrap Incorporating Teleconnection Patterns Information. Sustainability 2022, 14, 11598. [Google Scholar] [CrossRef]
- Solgi, R.; Loáiciga, H.A.; Kram, M. Long short-term memory neural network (LSTM-NN) for aquifer level time series forecasting using in-situ piezometric observations. J. Hydrol. 2021, 601, 126800. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, Y.; Hu, H.; Li, H.; Ma, Y.; Khan, M.Y.A. Combined Wavelet Transform With Long Short-Term Memory Neural Network for Water Table Depth Prediction in Baoding City, North China Plain. Front. Environ. Sci. 2021, 9, 780434. [Google Scholar] [CrossRef]
- Loudyi, D.; Falconer, R.; Lin, B. MODFLOW: An Insight into Thirty Years Development of a Standard Numerical Code for Groundwater Simulations; CUNY Academic Works; CUNY: New York, NY, USA, 2014. [Google Scholar]
- Noureldeen, A.S.; Ghaly, S.; Ali, K.; Abozaid, G. ANN-Based Approach to Predict Changes in Ground Water Levels as a Result of Constructing New Naga-Hammadi Barrage, Egypt. In Recent Advances in Environmental Science from the Euro-Mediterranean and Surrounding Regions; Kallel, A., Ksibi, M., Ben Dhia, H., Khélifi, N., Eds.; Advances in Science, Technology & Innovation; Springer International Publishing: Cham, Switzerland, 2018; pp. 853–856. ISBN 978-3-319-70547-7. [Google Scholar]
- Motawej, H. Integrating MODFLOW and LSTM models for enhanced groundwater management in the coastal plains of Lattakia Governorate. Water Pract. Technol. 2025, 20, 413–423. [Google Scholar] [CrossRef]
- Trichakis, I.C.; Nikolos, I.K.; Karatzas, G.P. Artificial Neural Network (ANN) Based Modeling for Karstic Groundwater Level Simulation. Water Resour. Manag. 2011, 25, 1143–1152. [Google Scholar] [CrossRef]
- Chidepudi, S.K.R.; Massei, N.; Jardani, A.; Henriot, A.; Allier, D.; Baulon, L. A wavelet-assisted deep learning approach for simulating groundwater levels affected by low-frequency variability. Sci. Total Environ. 2023, 865, 161035. [Google Scholar] [CrossRef]
- Sharma, Y.; Tyagi, A.; Sharma, M.L.; Sharma, P.; Aggarwal, A. Building Vulnerability Assessment Using Artificial Intelligence for Landslide Susceptibility Zone in Champawat District, India. Available online: https://meetingorganizer.copernicus.org/EGU23/EGU23-1957.html (accessed on 30 March 2025).
- Chowdhury, T.N.; Battamo, A.; Nag, R.; Zekker, I.; Salauddin, M. Impacts of climate change on groundwater quality: A systematic literature review of analytical models and machine learning techniques. Environ. Res. Lett. 2025, 20, 033003. [Google Scholar] [CrossRef]
- Khosravi, K.; Farooque, A.A.; Naghibi, A.; Heddam, S.; Sharafati, A.; Hatamiafkoueieh, J.; Abolfathi, S. Enhancing Pan evaporation predictions: Accuracy and uncertainty in hybrid machine learning models. Ecol. Inform. 2025, 85, 102933. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Toghraie, D. An optimal feed-forward artificial neural network model and a new empirical correlation for prediction of the relative viscosity of Al2O3-engine oil nanofluid. Sci. Rep. 2021, 11, 17072. [Google Scholar] [CrossRef]
- Li, J.; Yoder, R.E.; Odhiambo, L.O.; Zhang, J. Simulation of nitrate distribution under drip irrigation using artificial neural networks. Irrig. Sci. 2004, 23, 29–37. [Google Scholar] [CrossRef]
- Daliakopoulos, I.N.; Coulibaly, P.; Tsanis, I.K. Groundwater level forecasting using artificial neural networks. J. Hydrol. 2005, 309, 229–240. [Google Scholar] [CrossRef]
- Giustolisi, O.; Simeone, V. Optimal design of artificial neural networks by a multi-objective strategy: Groundwater level predictions. Hydrol. Sci. J. 2006, 51, 502–523. [Google Scholar] [CrossRef]
- Joorabchi, A.; Zhang, H.; Blumenstein, M. Application of Artificial Neural Networks to Groundwater Dynamics in Coastal Aquifers. J. Coast. Res. 2007, II, 966–970. [Google Scholar]
- Szidarovszky, F.; Coppola, E.A.; Long, J.; Hall, A.D.; Poulton, M.M. A Hybrid Artificial Neural Network-Numerical Model for Ground Water Problems. Groundwater 2007, 45, 590–600. [Google Scholar] [CrossRef] [PubMed]
- Nourani, V.; Mogaddam, A.A.; Nadiri, A.O. An ANN-based model for spatiotemporal groundwater level forecasting. Hydrol. Process. 2008, 22, 5054–5066. [Google Scholar] [CrossRef]
- Kim, K.-D.; Lee, S.; Oh, H.-J. Prediction of ground subsidence in Samcheok City, Korea using artificial neural networks and GIS. Environ. Geol. 2009, 58, 61–70. [Google Scholar] [CrossRef]
- Jalalkamali, A.; Sedghi, H.; Manshouri, M. Monthly groundwater level prediction using ANN and neuro-fuzzy models: A case study on Kerman plain, Iran. J. Hydroinformatics 2011, 13, 867–876. [Google Scholar] [CrossRef]
- Nakhaei, M.; Nasr, A.S. A combined Wavelet-Artificial Neural Network model and its application to the prediction of groundwater level fluctuations. Geopersia 2012, 2, 77–91. [Google Scholar] [CrossRef]
- Fallah-Mehdipour, E.; Bozorg Haddad, O.; Mariño, M.A. Prediction and simulation of monthly groundwater levels by genetic programming. J. Hydro-Environ. Res. 2013, 7, 253–260. [Google Scholar] [CrossRef]
- Demirci, M.; Üneş, F.; Körlü, S. Modeling of groundwater level using artificial intelligence techniques: A case study of Reyhanli region in Turkey. Appl. Ecol. Environ. Res. 2019, 17, 2651–2663. [Google Scholar] [CrossRef]
- Hanifian, S.; Khaleghi, M.R.; Najarchi, M.; Jafarnia, R.; Varvani, J. A comparative study of artificial neural networks and multivariate regression for predicting groundwater depths in the Arak aquifer. Acta Geophys. 2023, 72, 419–432. [Google Scholar] [CrossRef]
- Shahbazi, M.; Zarei, H.; Solgi, A. A new approach in using the GRACE satellite data and artificial intelligence models for modeling and predicting the groundwater level (case study: Aspas aquifer in Southern Iran). Environ. Earth Sci. 2024, 83, 240. [Google Scholar] [CrossRef]
- Singh, R.M.; Datta, B.; Jain, A. Identification of Unknown Groundwater Pollution Sources Using Artificial Neural Networks. J. Water Resour. Plan. Manag. 2004, 130, 506–514. [Google Scholar] [CrossRef]
- Agarwal, A.; Singh, R.; Mishra, S.; Bhunya, P. ANN-based sediment yield models for Vamsadhara river basin (India). Water SA 2005, 31, 85–100. [Google Scholar] [CrossRef]
- Nayak, P.C.; Rao, Y.R.S.; Sudheer, K.P. Groundwater Level Forecasting in a Shallow Aquifer Using Artificial Neural Network Approach. Water Resour. Manag. 2006, 20, 77–90. [Google Scholar] [CrossRef]
- Prasad, R.K.; Mathur, S. Groundwater Flow and Contaminant Transport Simulation with Imprecise Parameters. J. Irrig. Drain. Eng. 2007, 133, 61–70. [Google Scholar] [CrossRef]
- Sreekanth, P.D.; Geethanjali, N.; Sreedevi, P.D.; Ahmed, S.; Kumar, N.R.; Jayanthi, P.D.K. Forecasting groundwater level using artificial neural networks. Curr. Sci. 2009, 96, 933–939. [Google Scholar]
- Mohanty, S.; Jha, M.K.; Kumar, A.; Sudheer, K.P. Artificial Neural Network Modeling for Groundwater Level Forecasting in a River Island of Eastern India. Water Resour. Manag. 2010, 24, 1845–1865. [Google Scholar] [CrossRef]
- Banerjee, P.; Singh, V.S.; Chatttopadhyay, K.; Chandra, P.C.; Singh, B. Artificial neural network model as a potential alternative for groundwater salinity forecasting. J. Hydrol. 2011, 398, 212–220. [Google Scholar] [CrossRef]
- Sreekanth, P.D.; Sreedevi, P.D.; Ahmed, S.; Geethanjali, N. Comparison of FFNN and ANFIS models for estimating groundwater level. Environ. Earth Sci. 2011, 62, 1301–1310. [Google Scholar] [CrossRef]
- Charulatha, G.; Srinivasalu, S.; Uma Maheswari, O.; Venugopal, T.; Giridharan, L. Evaluation of ground water quality contaminants using linear regression and artificial neural network models. Arab. J. Geosci. 2017, 10, 128. [Google Scholar] [CrossRef]
- Balavalikar, S.; Nayak, P.; Shenoy, N.; Nayak, K. Particle swarm optimization based artificial neural network model for forecasting groundwater level in Udupi district. In Proceedings of the International Conference on Electrical, Electronics, Materials and Applied Science, Secunderabad, India, 22–23 December 2017; p. 020021. [Google Scholar] [CrossRef]
- Saran, S.; Chaudhary, P.; Uttam, A.; Gupta, S. Analysis and Optimization of Groundwater Distribution Using SVM and Neural Networks. SSRN Electron. J. 2021, 17, 17–36. [Google Scholar] [CrossRef]
- Malik, A.; Bhagwat, A. Modelling groundwater level fluctuations in urban areas using artificial neural network. Groundw. Sustain. Dev. 2021, 12, 100484. [Google Scholar] [CrossRef]
- Kochhar, A.; Singh, H.; Sahoo, S.; Litoria, P.K.; Pateriya, B. Prediction and forecast of pre-monsoon and post-monsoon groundwater level: Using deep learning and statistical modelling. Model. Earth Syst. Environ. 2022, 8, 2317–2329. [Google Scholar] [CrossRef]
- Navale, V.; Mhaske, S. Artificial Neural Network (ANN) and Adaptive Neuro-Fuzzy Inference System (ANFIS) model for Forecasting Groundwater Level in the Pravara River Basin, India. Model. Earth Syst. Environ. 2023, 9, 2663–2676. [Google Scholar] [CrossRef]
- Asher, M.J.; Croke, B.F.W.; Jakeman, A.J.; Peeters, L.J.M. A review of surrogate models and their application to groundwater modeling. Water Resour. Res. 2015, 51, 5957–5973. [Google Scholar] [CrossRef]
- Khan, J.; Lee, E.; Balobaid, A.S.; Kim, K. A Comprehensive Review of Conventional, Machine Leaning, and Deep Learning Models for Groundwater Level (GWL) Forecasting. Appl. Sci. 2023, 13, 2743. [Google Scholar] [CrossRef]
- Haggerty, R.; Sun, J.; Yu, H.; Li, Y. Application of machine learning in groundwater quality modeling—A comprehensive review. Water Res. 2023, 233, 119745. [Google Scholar] [CrossRef]
- Scheibe, T.D.; Murphy, E.M.; Chen, X.; Rice, A.K.; Carroll, K.C.; Palmer, B.J.; Tartakovsky, A.M.; Battiato, I.; Wood, B.D. An Analysis Platform for Multiscale Hydrogeologic Modeling with Emphasis on Hybrid Multiscale Methods. Groundwater 2015, 53, 38–56. [Google Scholar] [CrossRef]
- Deb, K.; Roy, P.; Hussein, R. Surrogate Modeling Approaches for Multiobjective Optimization: Methods, Taxonomy, and Results. Math. Comput. Appl. 2020, 26, 5. [Google Scholar] [CrossRef]
- Al-Maktoumi, A.; Rajabi, M.M.; Zekri, S.; Govindan, R.; Panjehfouladgaran, A.; Hajibagheri, Z. Accelerating regional-scale groundwater flow simulations with a hybrid deep neural network model incorporating mixed input types: A case study of the northeast Qatar aquifer. J. Hydroinformatics 2024, 26, 1333–1350. [Google Scholar] [CrossRef]
- Mohammadi, K. Groundwater Table Estimation Using MODFLOW and Artificial Neural Networks. In Practical Hydroinformatics; Abrahart, R.J., See, L.M., Solomatine, D.P., Eds.; Water Science and Technology Library; Springer: Berlin/Heidelberg, Germany, 2008; Volume 68, pp. 127–138. [Google Scholar] [CrossRef]
- Twumasi, F. Applying MODFLOW and Artificial Neural Networks to Model the Formation of MinePools in Underground Coal Mines. Master’s Thesis, Ohio University, Athens, OH, USA, 2018. [Google Scholar]
- Demissie, Y.; Valocchi, A.; Minsker, B.; Bailey, B. Bias-corrected groundwater model prediction uncertainty analysis. In Proceedings of the International Conference on Calibration and Reliability in Groundwater Modelling: Credibility of Modelling, Copenhagen, Denmark, 9–13 September 2007. [Google Scholar]
- Kantode, A.; Prashanth, T.; Ganguly, S. Development of a Precise Regional-Scale Groundwater Model by Coupling MODFLOW & Machine Learning Algorithms: A Case Study in Bist-Doab Region, Punjab, India. Available online: https://meetingorganizer.copernicus.org/EGU25/EGU25-1365.html (accessed on 30 July 2025).
- Coulibaly, P.; Anctil, F.; Aravena, R.; Bobée, B. Artificial neural network modeling of water table depth fluctuations. Water Resour. Res. 2001, 37, 885–896. [Google Scholar] [CrossRef]
- Verma, S.; Parthiban, P.; Ravikumar, K.; Das, I.C.; Das, A. Steady-state Assessment of Hydraulic Potential at Water Scarce regions of Agniyar River Basin, India using GMS-MODFLOW. Disaster Adv. 2023, 16, 38–43. [Google Scholar] [CrossRef]
- Demichele, F.; Micallef, F.; Portoghese, I.; Mamo, J.A.; Sapiano, M.; Schembri, M.; Schüth, C. Determining Aquifer Hydrogeological Parameters in Coastal Aquifers from Tidal Attenuation Analysis, Case Study: The Malta Mean Sea Level Aquifer System. Water 2023, 15, 177. [Google Scholar] [CrossRef]
- Ghaseminejad, A.; Uddameri, V. Physics-inspired integrated space-time Artificial Neural Networks for regional groundwater flow modeling. Hydrol. Earth Syst. Sci. 2020, 24, 5759–5779. [Google Scholar] [CrossRef]
- Payne, K.; Chami, P.; Odle, I.; Yawson, D.O.; Paul, J.; Maharaj-Jagdip, A.; Cashman, A. Machine Learning for Surrogate Groundwater Modelling of a Small Carbonate Island. Hydrology 2022, 10, 2. [Google Scholar] [CrossRef]
- Ruidas, D.; Pal, S.C.; Towfiqul Islam, A.R.M.; Saha, A. Hydrogeochemical Evaluation of Groundwater Aquifers and Associated Health Hazard Risk Mapping Using Ensemble Data Driven Model in a Water Scares Plateau Region of Eastern India. Expo Health 2023, 15, 113–131. [Google Scholar] [CrossRef]
- Alghafli, K.; Shi, X.; Sloan, W.; Ali, A.M. Investigating the Role of ENSO in Groundwater Temporal Variability across Abu Dhabi Emirate, United Arab Emirates Using Machine Learning Algorithms. Groundw. Sustain. Dev. 2025, 28, 101389. [Google Scholar] [CrossRef]
- Mohanty, S.; Jha, M.K.; Kumar, A.; Panda, D.K. Comparative evaluation of numerical model and artificial neural network for simulating groundwater flow in Kathajodi–Surua Inter-basin of Odisha, India. J. Hydrol. 2013, 495, 38–51. [Google Scholar] [CrossRef]
- Devarajan, K. Application of numerical and empirical models for groundwater level forecasting. Int. J. Res. Eng. Technol. 2015, 4, 127–133. [Google Scholar] [CrossRef]
- Moghaddam, H.K.; Moghaddam, H.K.; Kivi, Z.; Bahreinimotlagh, M.; Alizadeh, M.J. Developing comparative mathematic models, BN and ANN for forecasting of groundwater levels. Groundw. Sustain. Dev. 2019, 9, 100237. [Google Scholar] [CrossRef]
- Sanginabadi, H.; Saghafian, B.; Delavar, M. Coupled Groundwater Drought and Water Scarcity Index for Intensively Overdrafted Aquifers. J. Hydrol. Eng. 2019, 24, 04019003. [Google Scholar] [CrossRef]
- Malekzadeh, M.; Kardar, S.; Shabanlou, S. Simulation of groundwater level using MODFLOW, extreme learning machine and Wavelet-Extreme Learning Machine models. Groundw. Sustain. Dev. 2019, 9, 100279. [Google Scholar] [CrossRef]
- Nassery, H.R.; Zeydalinejad, N.; Alijani, F.; Shakiba, A. A proposed modelling towards the potential impacts of climate change on a semi-arid, small-scaled aquifer: A case study of Iran. Environ. Monit. Assess. 2021, 193, 182. [Google Scholar] [CrossRef]
- Mohammed, K.S.; Shabanlou, S.; Rajabi, A.; Yosefvand, F.; Izadbakhsh, M.A. Prediction of groundwater level fluctuations using artificial intelligence-based models and GMS. Appl. Water Sci. 2023, 13, 54. [Google Scholar] [CrossRef]
- Akbarifard, S.; Madadi, M.R.; Zounemat-Kermani, M. An artificial intelligence-based model for optimal conjunctive operation of surface and groundwater resources. Nat. Commun. 2024, 15, 553. [Google Scholar] [CrossRef]
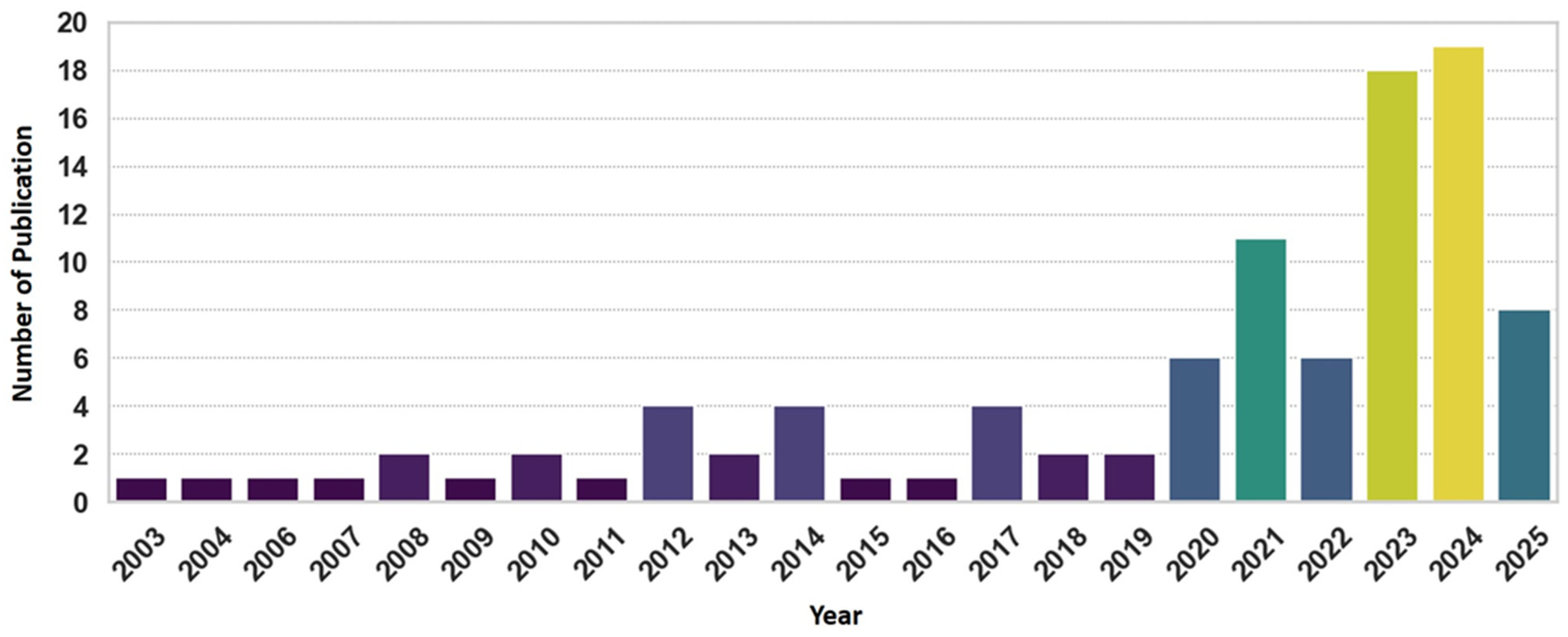

| Database | Search String |
|---|---|
| Scopus | TITLE-ABS-KEY(MODFLOW AND (“Artificial Neural Network” OR ANN) AND (groundwater OR aquifer)) AND (PUBYEAR > 2002 AND PUBYEAR < 2025) |
| Web of Science | TS = (MODFLOW AND (“Artificial Neural Network” OR ANN) AND (groundwater OR aquifer OR “ground water”)) AND PY = (2003–2025) |
| Google Scholar | MODFLOW “Artificial Neural Network” OR ANN OR “hybrid model” OR “coupled model” groundwater |
| Inclusion Criteria | Exclusion Criteria |
|---|---|
| Peer-reviewed journal articles or full conference reports. | Non-peer-reviewed publications, such as editorials, conference papers, abstracts, notes, case reports, and short commentaries. |
| Publications written exclusively in English, between 1 January 2003 and 30 March 2025. | Studies that only focus on surface water |
| Studies explicitly investigating groundwater flow modeling, MODFLOW models, ANNs, and hybrid models. | Studies only relevant to solute movement or water quality, without a clear connection to groundwater flow modelling. |
| Year | Advancement/Development | Significance | Ref. |
|---|---|---|---|
| 1984 | Initial release of MODFLOW by the USGS | Revolutionized groundwater modeling by providing a modular, finite-difference approach for simulating groundwater flow. | [9] |
| 1990 | Development of Visual MODFLOW | Simplified the modeling process with a user-friendly graphical interface, making MODFLOW accessible to a broader audience. | [25] |
| 2000 | Integration with MT3DMS for solute transport modeling | Enabled combined groundwater flow and contaminant transport simulations critical for water quality management. | [27] |
| 2010 | Coupling with GIS and remote-sensing tools | Enhanced model inputs and calibration using spatial datasets, improving the accuracy of hydrological assessments. | [26] |
| 2012 | Development of MODFLOW-USG (Unstructured Grid) | Allowed for irregular grids, enabling more precise representation of complex hydrogeological features. | [28] |
| 2015 | Integration with SWAT and other surface water models | Facilitated comprehensive watershed-scale hydrological simulations, linking groundwater and surface water dynamics. | [29] |
| 2020 | High-performance computing (HPC) and ML integration | Improved the efficiency of large-scale and real-time simulations while enhancing predictions in data-scarce regions through ML. | [30] |
| Ref. | Study Area | Model(s) Used | Key Input Data | Findings |
|---|---|---|---|---|
| [39] | Tirunelveli, Tamil Nadu | MODFLOW | Geology, soil, hydraulic heads, daily rainfall, well yield | The negative water budget in the study area indicates over-extraction and the need for better management. |
| [40] | Balasore, Orissa | Visual MODFLOW | Salinity, hydraulic conductivity, specific storage, recharge, river influence | The strategy advises reducing downstream pumping and increasing it at specific sites for sustainability. |
| [41] | Amaravathi River Basin, Tamil Nadu | Visual MODFLOW | Effluent discharge with TDS, lithology, hydrogeological parameters | Effluent from dyeing units severely harms groundwater quality; stopping discharge improves it over 15 years. |
| [42] | Mahesh River Basin, Maharashtra | MODFLOW | Hydrological, hydrogeological, rainfall, well data | Coupling surface and groundwater models improves accuracy and prediction of aquifer behavior. |
| [44] | Western United States | MODFLOW | Hydraulic heads, well radius, transmissivity, boundary heads | The MAW1 Package aligns well with analytical solutions and is not sensitive to grid refinement. |
| [45] | - | SEAWAT, MODFLOW, MT3DMS | Boundary conditions, initial fluid distribution | For the 3D saltpool problem, SEAWAT results were reasonable but had some discrepancies. |
| [46] | Musimcheon Basin, South Korea | MODFLOW | Land use, surface runoff, hydraulic conductivity, specific yield, recharge | The integrated SWAT-MODFLOW model improved simulation of drawdown and reduced streamflow from pumping. |
| [47] | - | MODFLOW, HydroGeoSphere (HGS) | Hydraulic conductivity, river geometry, van Genuchten parameters | Neglecting the unsaturated zone in MODFLOW underestimates infiltration flux, especially for disconnected systems. |
| [48] | Monroe County, Michigan | MODFLOW-2000 | GIS spatial data: road infrastructure, soil quality, distances | The model links groundwater flow and decision-making, highlighting policy impacts on water resources. |
| [49] | Canada | MODFLOW | Hydrogeological properties, boundary conditions, stresses (wells, recharge) | Multiple model layers enhance accuracy for complex sites. Diverse evidence for calibration is crucial. |
| [50] | - | MODFLOW | Conductivity, specific yield/storage, prescribed heads, recharge rates | A stable method uses upstream weighting, Newton–Raphson linearization, and an ORTHOMIN solver. |
| [51] | Iran | MODFLOW, MT3DMS | Topographical and bedrock surface, initial head conditions | Groundwater levels will drop by 15 m in 10 years. Rising chloride and EC levels threaten water quality. |
| [52] | Sloping aquifer | MODFLOW-SP | Aquifer geometry, specific yield, hydraulic conductivity, river levels | MODFLOW-SP accurately predicts hydraulic heads in unconfined aquifers with slopes under 26.6 degrees. |
| [53] | - | MODFLOW, Harmony Search Algorithm | Pumping well positions, total water demand | Coupling flow simulation with optimization models streamlines complex groundwater management. |
| [54] | Oman | MODFLOW | Borehole data, rainfall, initial hydraulic conductivity | Manual calibration with PEST is advised for complex geology. |
| [55] | Texas, USA | SWAT+, MODFLOW | Land use, soil, DEM, hydraulic properties, groundwater balance | SWAT+ effectively models groundwater flow and interactions, improving hydrological simulation accuracy. |
| [56] | Poland | MODFLOW | Filtration coefficient, layer drainage, conductivity of channel zone | Using 100 cm high dams in forest areas can boost water retention by 38% compared to no dams. |
| [57] | Lower Palar River Basin, Tamil Nadu | MODFLOW | Hydraulic conductivity, abstraction rates, recharge rates | Pumping an extra 2 MGD would cause the groundwater head to drop below sea level in the eastern area. |
| [58] | Vaishali Canal, Bihar | MODFLOW | Remote sensing data (IRS-1A/1C LISS sensors) | Integrating remote sensing and GIS with flow modeling helps identify waterlogged areas. |
| [59] | Punjab | Visual MODFLOW | Rainfall, evaporation, soil characteristics, agricultural data | The model highlighted the impact of the Wheat-Paddy cropping pattern on groundwater recharge and depletion. |
| [60] | Sonar Sub-basin, Madhya Pradesh | Visual MODFLOW | Hydraulic conductivity, storage coefficient, water levels, recharge rates | Groundwater levels were accurately simulated, with minimal impact from pumping rates. |
| [61] | Osmansagar and Himayathsagar, Telangana | Visual MODFLOW | Recharge, groundwater draft, withdrawal rates | Continuing current withdrawal rates could lower water levels by over 45 m by 2020. |
| [62] | Jammu and Kashmir | MODFLOW | Hydro-geomorphological features, borewell data, seepage estimates | Perforated pipes in the tunnel effectively drained groundwater seepage, matching observed rates. |
| [63] | Kadalundi River Basin, Kerala | Visual MODFLOW | Base map, calibration/validation data, pumping data | The basin may remain safe for five years, but the water table will eventually reach bedrock, requiring artificial recharge. |
| [64] | Mahanadi Delta, Odisha | Visual MODFLOW, PEST | Hydraulic head data, conductivities, specific yield, annual outflow | The model showed groundwater depletion from agriculture and net outflow into the Bay of Bengal. |
| [65] | Una Coastal Region, Gujarat | MODFLOW, SWI2 | Water samples, seawater infiltration, transmissivity data | Pumping increases seawater intrusion but reducing pumping rates can mitigate this. |
| Ref. | Study Area | Model(s) Used | Key Input Data | Findings |
|---|---|---|---|---|
| [84] | - | ANN | Soil water, nitrate concentration, discharge rate, fertilizer concentration | ANN model with a 6-10-6-1 architecture accurately estimated soil nitrate distribution (R2 = 0.83). |
| [85] | Messara, Greece | ANN (Levenberg–Marquardt) | Rainfall, temperature, well depth, groundwater level | Standard FNN accurately predicts groundwater levels up to 18 months in advance. |
| [86] | Brindisi, Italy | MO-IODNN | Rainfall, groundwater level time series | NARX suits long-term predictions, while ARX is ideal for short-term forecasts. |
| [87] | Australia | ANN, MATLAB | Water table, hydraulic conductivity, tide elevation, beach slope | ANN model successfully predicted groundwater fluctuations and tide variations accurately within 100 m from the coastline. |
| [88] | - | ANN | Transmissivity, hydraulic conductivity, constant head values, well extraction | The hybrid approach of combining ANNs with numerical models reduces predictive errors. |
| [89] | Tabriz, Azerbaijan | ANN (LM algorithm) | Temperature, rainfall, mean discharge, groundwater level | The Spatio-Temporal ANN (STANN) model shows higher efficiency compared to other hybrid models. |
| [90] | Samcheok, South Korea | MATLAB | DEM, slope gradient, groundwater level, permeability, geology, land use | The ANN model achieved 96.06% accuracy in predicting ground subsidence. |
| [91] | Kerman Plain, Iran | ANN, ANFIS | Monthly groundwater levels, air temperature, rainfall | Neuro-fuzzy methods show superior performance for groundwater level prediction. |
| [92] | Qorveh Plain, Iran | WANN, MLP, FF-ANN | Groundwater level data from 26 piezometers | The WANN model, using db2 and db4 wavelets, outperformed other wavelets in forecasting. |
| [93] | Karaj Plain, Iran | ANFIS, GP (MATLAB) | Groundwater level, precipitation, evaporation | Genetic Programming (GP) outperforms ANFIS, especially when using combined surface and groundwater data. |
| [94] | Turkey | ANFIS, RBNN, SVM | Monthly groundwater level, precipitation, average temperature | SVM-RBF and SVM-PK models showed the highest accuracy in predicting groundwater levels. |
| [95] | Arak Plain, Iran | ANN (Neurosolution) | Transmissivity, altitude, precipitation, evaporation, groundwater level | The ANN model surpassed the MLR method in predicting groundwater depth, demonstrating superior accuracy. |
| [96] | Aspas Aquifer, Iran | ANN, SVR, WT, CEEMD | Precipitation, temperature, evaporation, groundwater level | The CEEMD–ANN hybrid model outperformed other models and the GRACE satellite algorithm in prediction. |
| [97] | - | ANN | Rainfall, temperature, relative humidity | The ANN approach effectively estimates unknown groundwater pollution sources. |
| [98] | Vamsadhara River Basin | FF-BP ANN | Rainfall, runoff, suspended sediment yield | Generalized pattern-learned models demonstrated superior performance overall. |
| [99] | Godavari Delta, Andhra Pradesh | ANN | Rainfall, canal release | The ANN models proved statistically adequate, accurately predicting water levels. |
| [100] | - | ANN | Rainfall, recharge, transmissivity, pumping rate | The ANN approach measured uncertainty in simulations efficiently, reducing computational effort. |
| [101] | Maheshwaram Watershed, Telangana | FFNN, LMB | Rainfall, temperature, evaporation, relative humidity | The FFNN-LMB model demonstrated high accuracy (93%) in forecasting monthly groundwater level fluctuations. |
| [102] | Orissa | ANN (BR algorithm) | Weekly rainfall, evaporation, river stage, water level | The ANN accurately predicted groundwater levels one week ahead at 18 sites. |
| [103] | Kavaratti Islands, Lakshadweep | ANN | Rainfall, topology, runoff | The ANN model recommended pumping rates below 13,000 L/day to stabilize salinity. |
| [104] | Ranga Reddy, Telangana | FFNN-LM, ANFIS | Rainfall, temperatures, evaporation, relative humidity | Both models provided high accuracy for forecasting groundwater levels (R2 > 0.93). |
| [105] | Chennai | MLR, PCR, ANN, PC-ANN | Temperature, EC, pH, TDS, nitrate, sodium, chloride | The PC-ANN model outperformed all others in predicting nitrite concentration. |
| [106] | Udupi | PSO, ANN model | Groundwater level, rainfall data | The hybrid ANN-PSO algorithm predicts groundwater levels more accurately than the standard backpropagation algorithm. |
| [107] | New Delhi | ANN, Random Forest, ARIMA | Groundwater level, temperature, rainfall, humidity | The ANN model outperformed SVM and LR in predicting groundwater levels. |
| [108] | Delhi | ANN | Groundwater level, rainfall, population, temperature | The 3-15-1 ANN model architecture is the most effective for predicting groundwater fluctuations in urban areas. |
| [109] | Punjab | MLP, LSTM, SARIMA | Rainfall, groundwater level | Both MLP and LSTM models outperformed SARIMA, with MLP slightly better for pre-monsoon and LSTM excelling post-monsoon. |
| [110] | Pravara River Basin | ANN, ANFIS | Annual temperature, rainfall, groundwater level | The ANFIS model outperformed the ANN model in predicting groundwater levels (R2 of 0.817 vs. 0.763). |
| Framework Type | Classification Basis | Key Categories | Primary Utility | Ref. |
|---|---|---|---|---|
| Functional Framework | The functional role of the ANN within the physical modeling workflow. | (1) Surrogate Modeling (emulation), (2) Parameter Estimation (input improvement), (3) Error Correction (output refinement) | Provides a practical guide for hydrogeologists on how and why to integrate an ANN with MODFLOW to solve specific modeling challenges. | [111,112] |
| Algorithmic ML Framework | The type of machine learning algorithm and its learning style. | Supervised (e.g., ANN, SVM), unsupervised (e.g., Clustering, SOM), ensemble (e.g., Random Forest) | Catalogues the spectrum of ML techniques applied in a domain. Useful for data scientists selecting appropriate algorithms based on data structure and task. | [113] |
| Multiscale Modeling Framework (e.g., MAP) | The degree of spatial, temporal, and physical processes coupling between models at different scales. | Hierarchical vs. concurrent top-down vs. bottom-up loose vs. tight coupling | A platform for selecting appropriate multiscale simulation methods for complex systems where processes occur at disparate scales. | [114] |
| Integration Strategy | Core Objective | Role of MODFLOW | Role of ANN | Key Advantage | Ref. |
|---|---|---|---|---|---|
| Surrogate Modeling | Accelerate computation | Generates training data (input–output pairs) | Learns the input–output mapping to emulate MODFLOW | Computational efficiency for optimization/uncertainty analysis | [115,116,117] |
| Parameter Estimation | Improve model inputs and calibration | Simulates flow based on ANN-estimated parameters | Learns the inverse relationship (e.g., heads to conductivity) | Automates and improves estimation of heterogeneous parameters | [118] |
| Error Correction | Refine model predictions | Provides the primary physics-based prediction | Models the systematic error (residuals) of the MODFLOW prediction | Corrects for unmodeled physics and conceptual errors | [119,120] |
| Ref. | Study Area | Model(s) Used | Key Input Data | Findings |
|---|---|---|---|---|
| [30] | China | MLP, RBF, SVM | Pumping rates, recharge rates, streamflow rates, groundwater level | The RBF model excelled in accuracy and computation time during training, but the numerical model showed better generalization. |
| [119] | Synthetic aquifer (Argonne Lab) | MODFLOW, ANN | Hydraulic conductivity, infiltration, evapotranspiration | An error-mapping ANN is an efficient approach for estimating model uncertainty. |
| [127] | Poland | ANN, MODFLOW | Rainfall, river currents, irrigation, well discharge, evaporation | TLRNs (R2 = 0.958) showed higher accuracy than MLPs (R2 = 0.865) in simulating groundwater levels. |
| [128] | Kathajodi-Surua, Odisha | ANN, MODFLOW | Weekly groundwater level data | The ANN model provided better predictions for short-term forecasts compared to MODFLOW. |
| [129] | Trivandrum, India | MODFLOW, RBFNN | Recharge, evapotranspiration, pumping rate, groundwater level | The RBFNN model outperformed MODFLOW for weekly groundwater level forecasting. |
| [130] | Birjand Aquifer, Iran | MODFLOW, ANN, BN | Temperature, evaporation, recharge, discharge, water tables | BN models (R2 = 0.9) surpassed ANNs (R2 = 0.76) and mathematical models (R2 = 0.72). |
| [131] | Qazvin Plain, Iran | MODFLOW, ANN | Monthly weather, precipitation data | The DWS index indicated the aquifer’s safe yield is only 44% of the current abstraction volume. |
| [132] | Kabodarahang Plain, Iran | MODFLOW, ELM, WA-ELM | Hydraulic conductivity, storage coefficients, recharge coefficients | The WA-ELM model was superior for simulating groundwater levels (R2 = 0.959, NSC = 0.915). |
| [133] | Iran | MODFLOW, HACRES | - | Stream discharge rates are projected to decrease in the future, especially under the RCP8.5 scenario. |
| [134] | Iran | GMS, ANN | Monthly precipitation, groundwater level data | The ORELM AI model outperformed other AI models and the GMS numerical model (RMSE of 0.37 in training). |
| [135] | Iran | BF-ANN | River flow, precipitation, evaporation, groundwater level, demands | The SOS-MSA-ANN model achieved the highest sustainability index, supplying over 99% of total demands. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kishor, K.; Aggarwal, A.; Srivastava, P.K.; Sharma, Y.K.; Lee, J.; Ghobadi, F. A Systematic Literature Review of MODFLOW Combined with Artificial Neural Networks (ANNs) for Groundwater Flow Modelling. Water 2025, 17, 2375. https://doi.org/10.3390/w17162375
Kishor K, Aggarwal A, Srivastava PK, Sharma YK, Lee J, Ghobadi F. A Systematic Literature Review of MODFLOW Combined with Artificial Neural Networks (ANNs) for Groundwater Flow Modelling. Water. 2025; 17(16):2375. https://doi.org/10.3390/w17162375
Chicago/Turabian StyleKishor, Kunal, Ashish Aggarwal, Pankaj Kumar Srivastava, Yaggesh Kumar Sharma, Jungmin Lee, and Fatemeh Ghobadi. 2025. "A Systematic Literature Review of MODFLOW Combined with Artificial Neural Networks (ANNs) for Groundwater Flow Modelling" Water 17, no. 16: 2375. https://doi.org/10.3390/w17162375
APA StyleKishor, K., Aggarwal, A., Srivastava, P. K., Sharma, Y. K., Lee, J., & Ghobadi, F. (2025). A Systematic Literature Review of MODFLOW Combined with Artificial Neural Networks (ANNs) for Groundwater Flow Modelling. Water, 17(16), 2375. https://doi.org/10.3390/w17162375







