Deformation and Stress of a Runner in Large Francis Turbines Under Wide-Load Operating Conditions
Abstract
1. Introduction
2. Materials and Methods
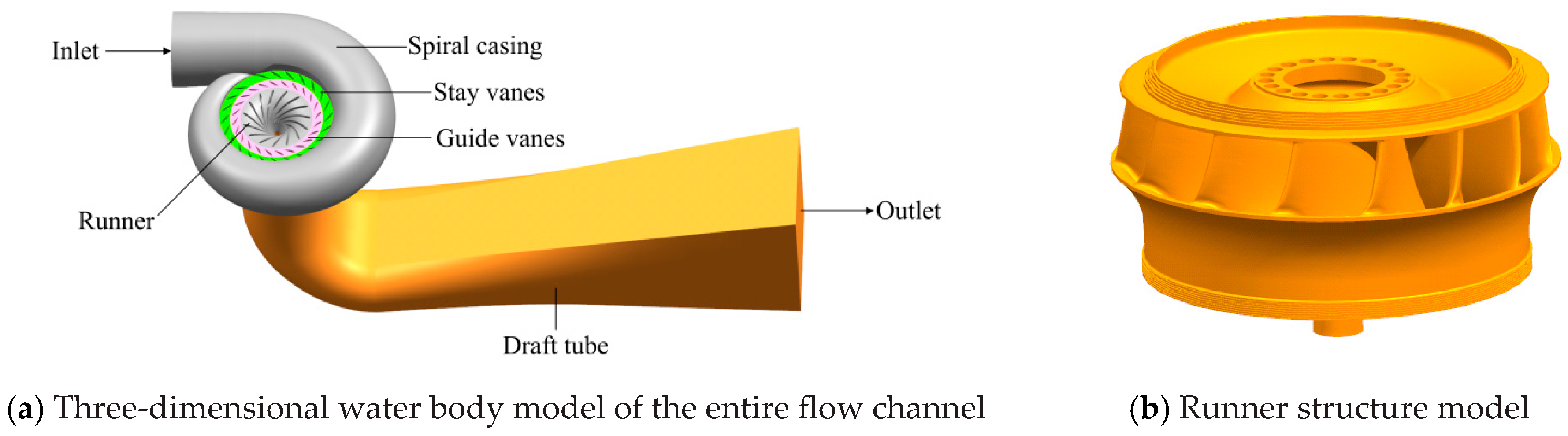
2.1. Three-Dimensional Geometric Model
2.2. Mathematical Model
- (1)
- Turbulence model
- (2)
- Fluid–structure coupling model
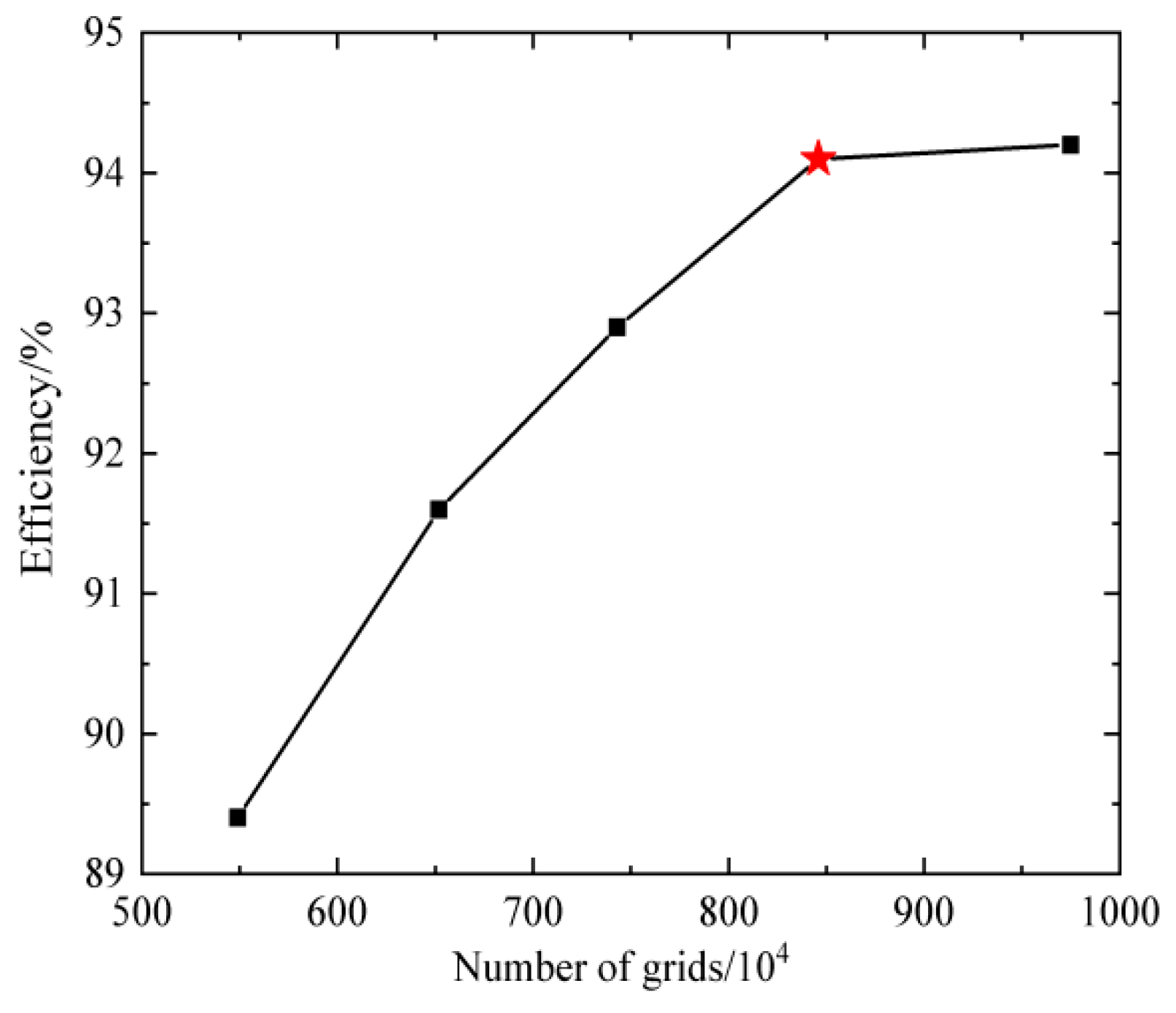
2.3. Grid Division
2.4. Boundary Condition Setting
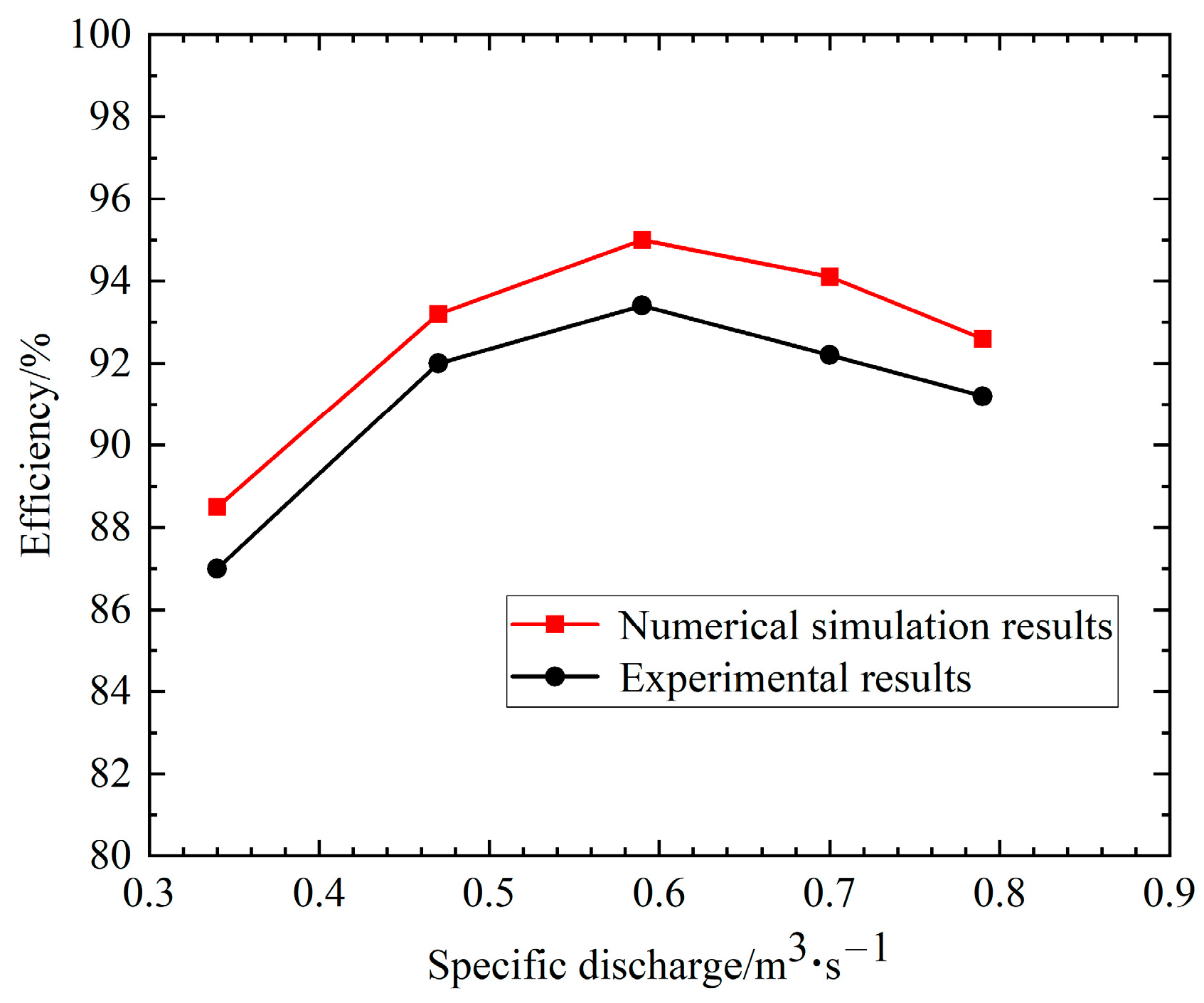
2.5. Verification of Numerical Computation Accuracy
3. Results and Analysis
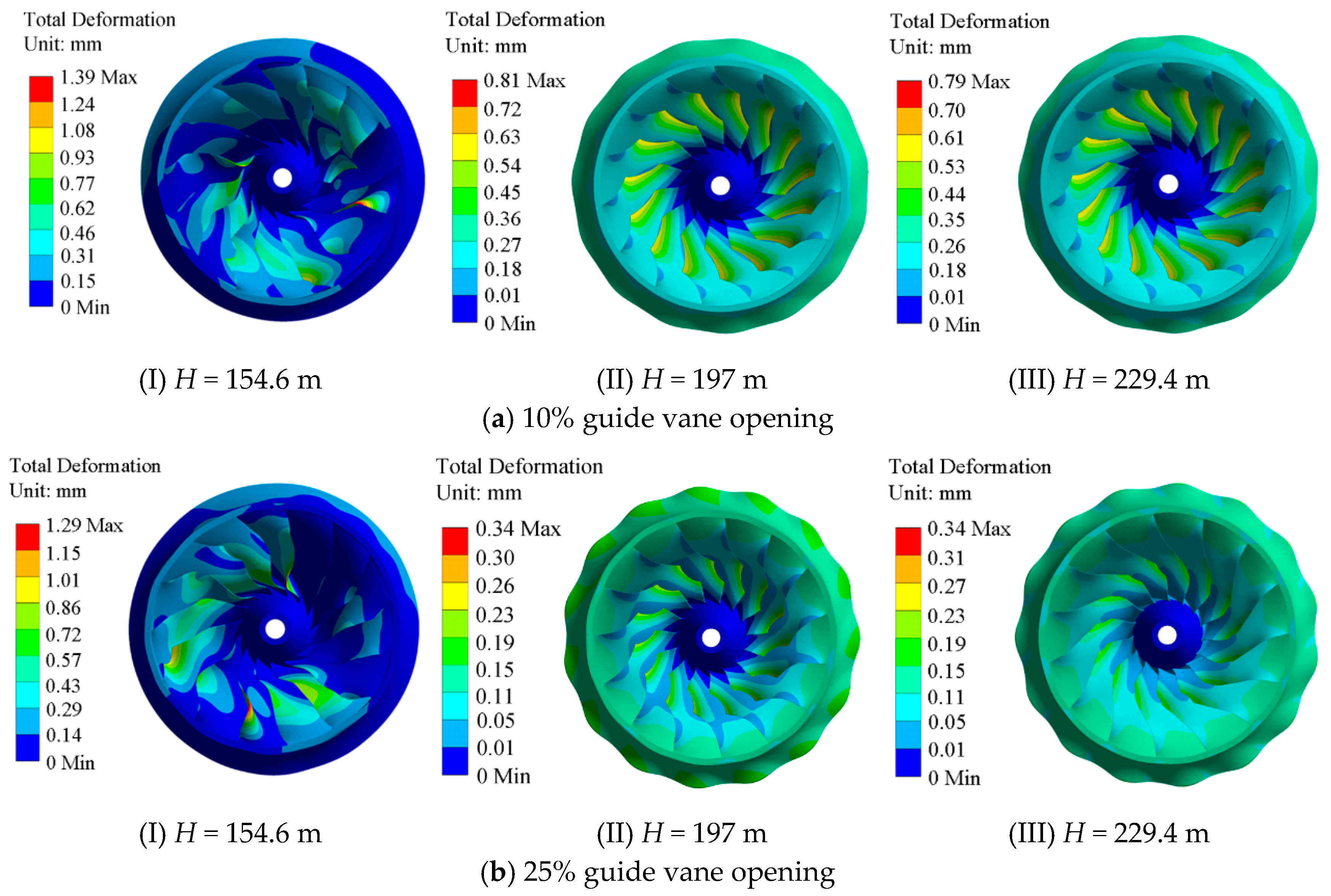
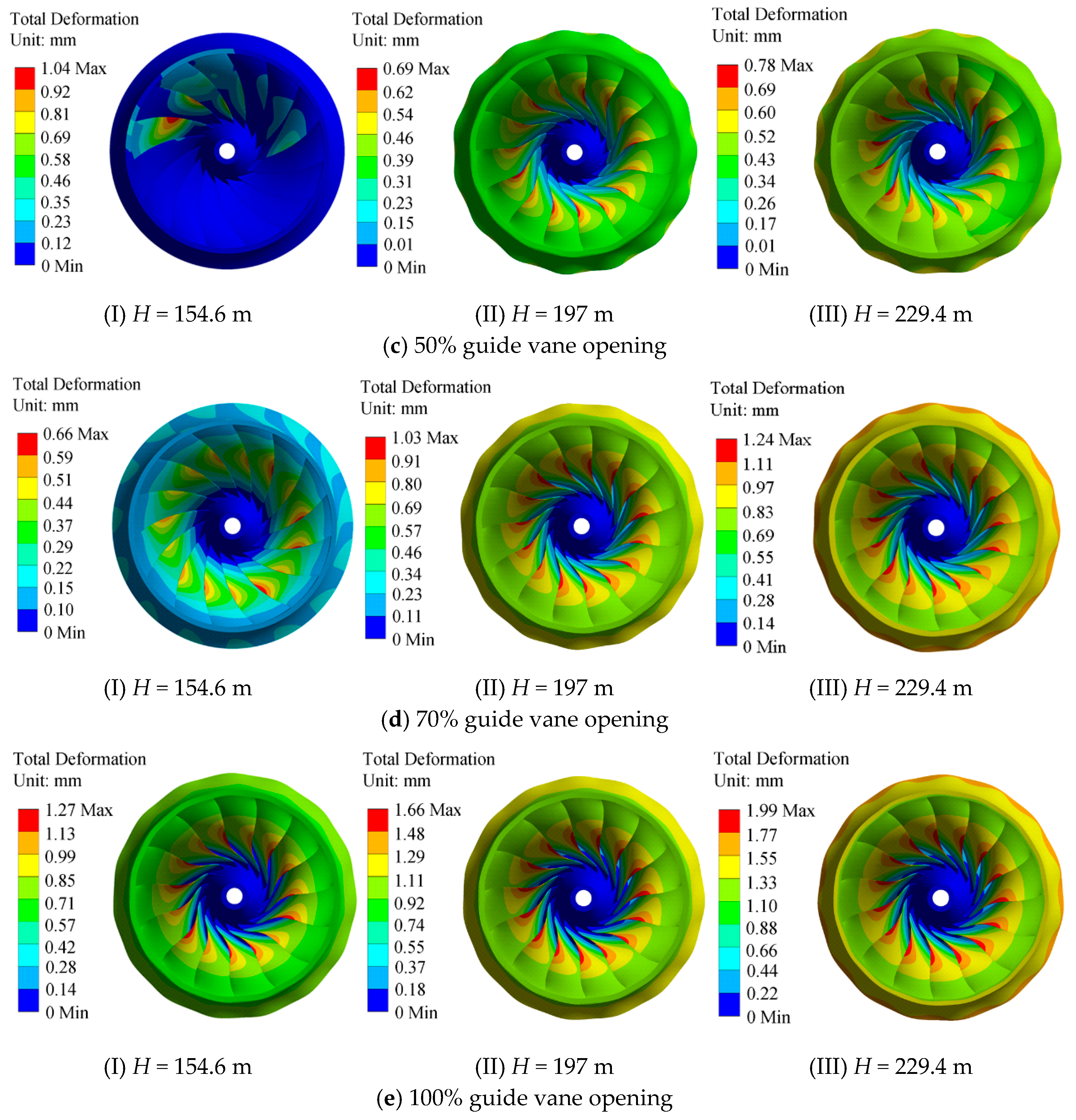
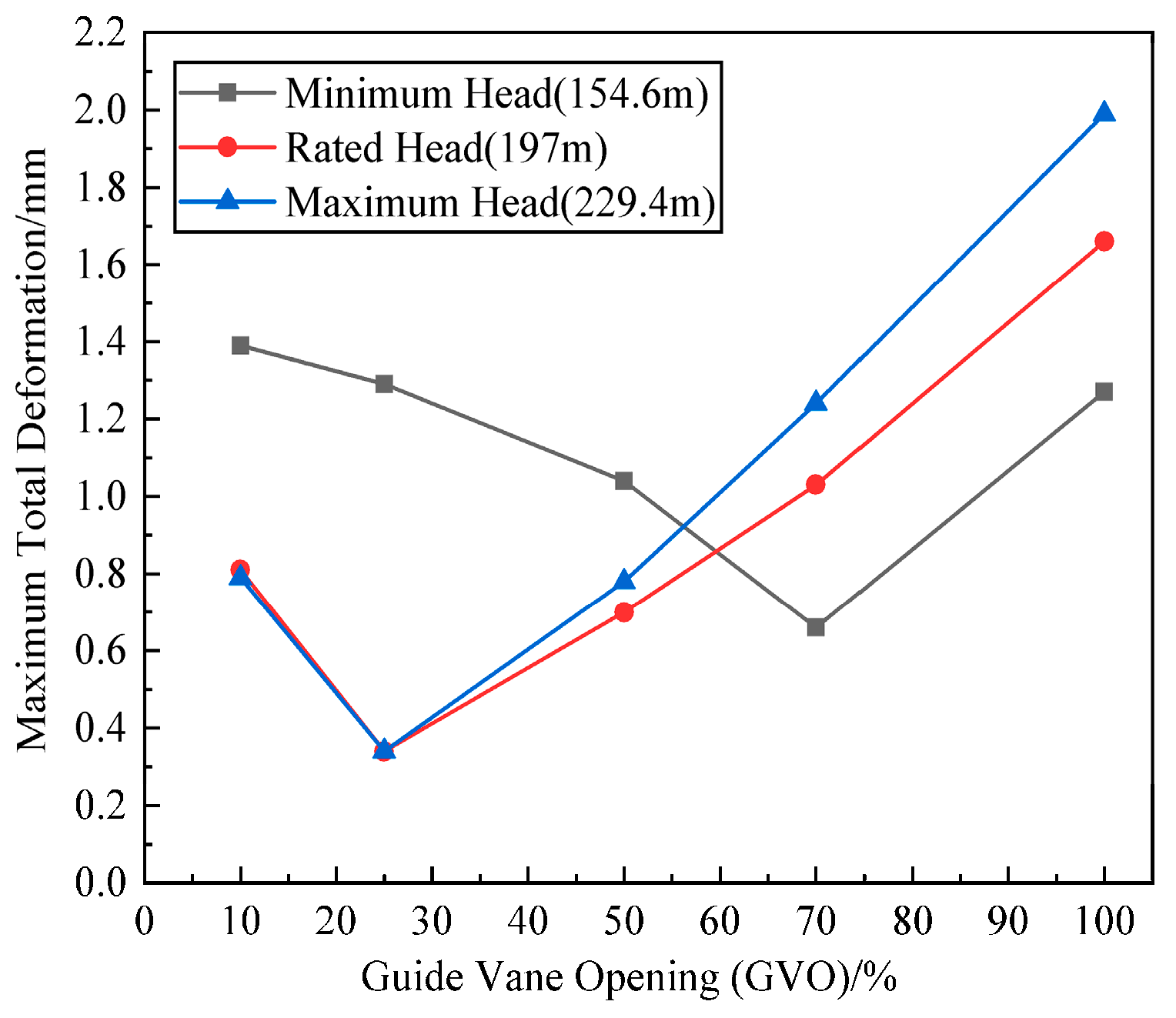
3.1. Deformation Law of the Runner
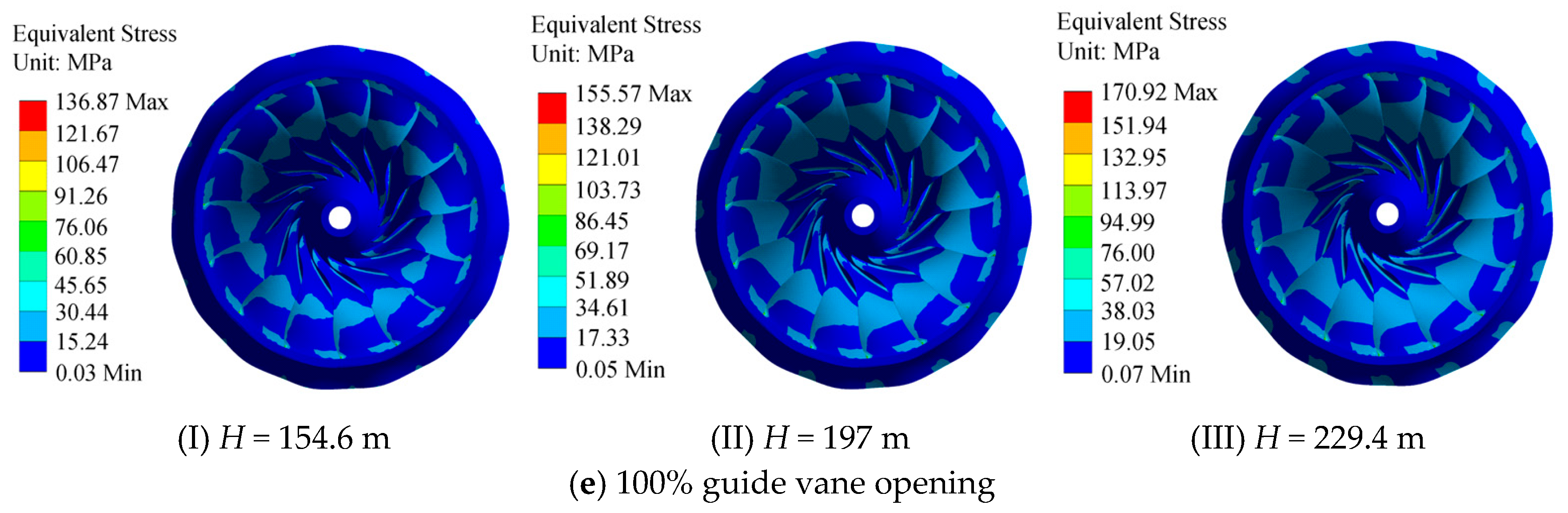
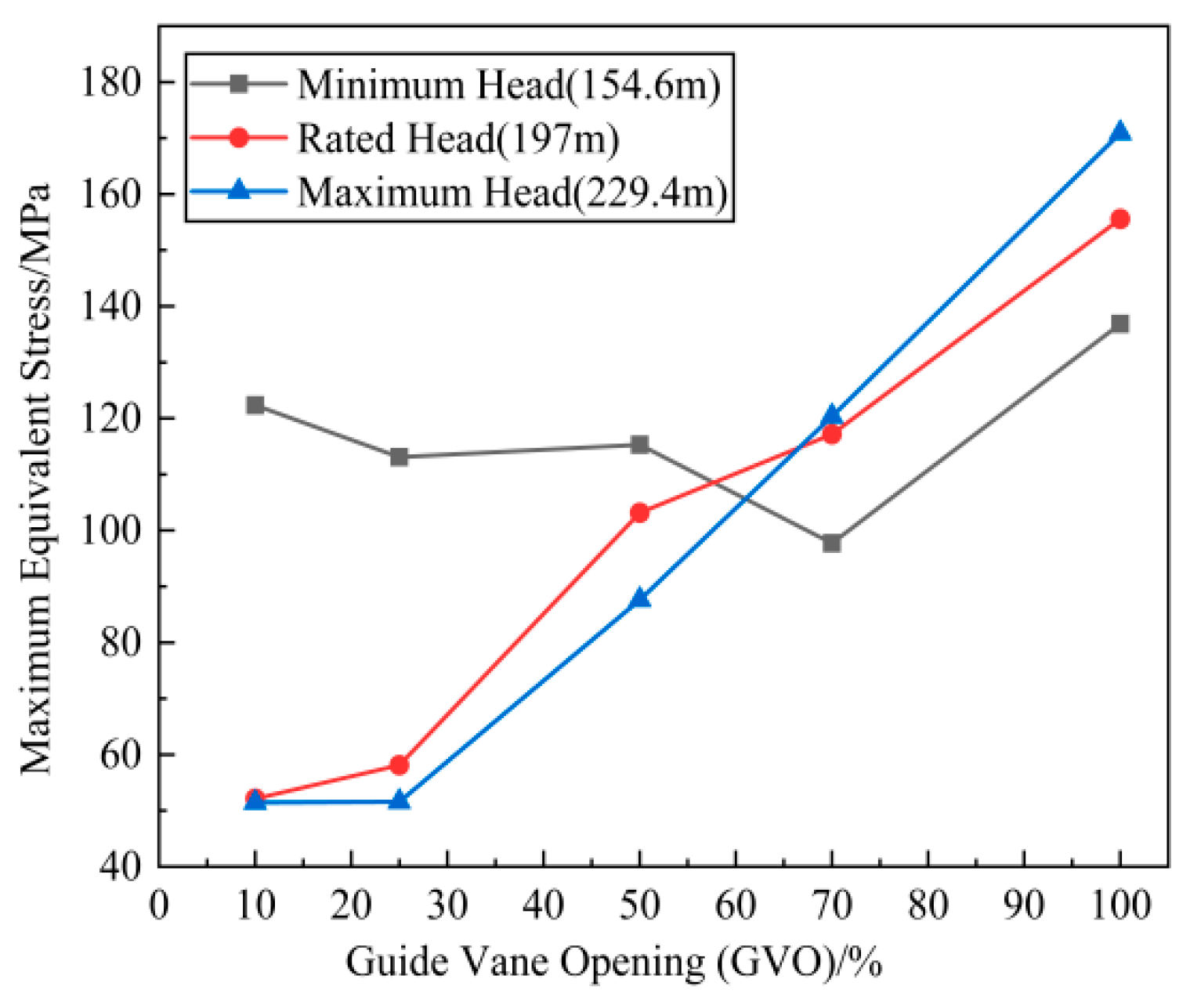
3.2. Equivalent Stress Distribution Law of the Runner
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iliescu, M.; Houde, S.; Deschenes, C.; Lemay, S. Investigations of the cavitational behavior of an axial hydraulic turbine operating at partial discharge by 3D-PIV. In Proceedings of the International Symposium on Particle Image Velocimetry-PIV, Kobe, Japan, 21–23 July 2011. [Google Scholar]
- Wang, F.; Liao, C.; Tang, X. Numerical simulation of pressure fluctuations in a large Francis turbine runner. Chin. J. Mech. Eng. 2012, 25, 1198–1204. [Google Scholar] [CrossRef]
- Chen, Z.; Singh, P.M.; Choi, Y.-D. The effect of runner blade loading on the performance and internal flow of a Francis hydro turbine model. J. Mech. Sci. Technol. 2016, 30, 1617–1623. [Google Scholar] [CrossRef]
- Liu, X. Simulation Research on Full Flow Channel of Mixed-Flow Turbine and Pressure Pulsation Analysis. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2017. [Google Scholar]
- Tian, C.; Yuan, S.; Wang, J.; Liu, X. Numerical Simulation of Internal Flow of Turbine Runner in Hydropower Station on Sediment River. Hydropower Energy Sci. 2020, 38, 163–166. [Google Scholar]
- Song, H. Numerical Simulation Study on the Internal Flow and Pressure Pulsation Characteristics of Medium-Head Mixed-Flow Turbines. Master’s Thesis, Xihua University, Chengdu, China, 2021. [Google Scholar]
- Tang, W.; Liu, X.; He, L.; Ma, T. The influence of guide vane opening on the internal flow state of the runner in a mixed-flow turbine. J. Eng. Therm. Energy Power/Reneng Dongli Gongcheng 2022, 37, 40–47+76. [Google Scholar]
- Xu, L.H.; Guo, T.; Wang, W.Q. Effects of vortex structure on hydraulic loss in a low head Francis turbine under overall operating conditions base on entropy production method. Renew. Energy 2022, 198, 367–379. [Google Scholar] [CrossRef]
- Xu, T.; Cheng, Q.; Lin, C.; Yu, Q.; Hu, X. Study on Flow Characteristics of Francis Turbine Based on Large-Eddy Simulation. Water 2023, 15, 3372. [Google Scholar] [CrossRef]
- Pang, J.; Yao, B.; Liu, X.; Li, J.; Xiao, M.; Jiang, D.; Tang, W.; Zhou, L.; Lai, Z. Influence of guide vane opening on channel vortex and pressure pulsation in Francis turbine runners. Phys. Fluids 2024, 36, 043325. [Google Scholar] [CrossRef]
- Ji, R.; Zheng, J.; Xue, M.-A.; Sun, K.; Ye, Y.; Zhu, R.; Fernandez-Rodriguez, E.; Zhang, Y. Investigations on the performance and wake dynamics of a tidal stream turbine under different yaw-offset conditions. Phys. Fluids 2025, 37, 015192. [Google Scholar] [CrossRef]
- Wang, H.; Pang, J.; Lai, Z.; Gan, L.; Huang, D.; Hua, H.; Yu, Z.; Liu, X. Internal flow stability of a Francis turbine under wide load operating range. Phys. Fluids 2025, 37, 023346. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, Y.; Xu, J.; Zhang, D.; Feng, C.; Zhang, Z.; Zheng, Y. Vortex and energy characteristics in the hump region of pump-turbines based on the rigid vorticity and local hydraulic loss method. Phys. Fluids 2025, 37, 35194. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, Y.; Xu, J.; Wang, Y.; Feng, C.; Yang, Y.; Liu, D.; Liu, X.; Zheng, Y. Towards the integration of new-type power systems: Hydraulic stability analysis of pumped storage units in the S-characteristic region based on experimental and CFD studies. Energy 2025, 329, 136755. [Google Scholar] [CrossRef]
- Feng, J.; Ling, Z.; Zhao, Z.; Li, M.; Chen, W. Research on the Stability of Runner Structure of Mixed-Flow Turbine under Eccentric Load Conditions. J. Hydropower 2021, 40, 107–114. [Google Scholar]
- Liao, W.; Xu, B.; Lu, P.; Zhang, H.; Wang, J. The influence of runner blade deformation of mixed-flow turbine under partial load on the flow field. J. Mech. Eng. 2006, 42, 55–59. [Google Scholar] [CrossRef]
- Xu, B. Dynamic Characteristics Analysis of Rotor Solid-State Coupling in Mixed-Flow Turbine. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2006. [Google Scholar]
- Xiao, R.F.; Wang, Z.W.; Luo, Y.Y. Static stress characteristics analysis of Francis turbine runner based on fluid-structure interaction. J. Hydroelectr. Eng. 2007, 26, 120–123. [Google Scholar]
- Wang, W.Q.; He, X.Q.; Zhang, L.X.; Liu, J.; Chen, Y. Strongly coupled simulation of fluid–structure interaction in a Francis hydroturbine. Int. J. Numer. Methods Fluids 2009, 60, 515–538. [Google Scholar] [CrossRef]
- Wang, Z.W.; Qin, L.; Zeng, J.D.; Li, H.; Zhang, Y. Hydroturbine operating region partitioning based on analyses of unsteady flow field and dynamic response. Sci. China Technol. Sci. 2010, 53, 519–528. [Google Scholar] [CrossRef]
- Thibault, D.; Gagnon, M.; Godin, S. The effect of materials properties on the reliability of hydraulic turbine runners. Int. J. Fluid Mach. Syst. 2015, 8, 254–263. [Google Scholar] [CrossRef]
- Presas, A.; Luo, Y.; Wang, Z.; Guo, B. Fatigue life estimation of Francis turbines based on experimental strain measurements: Review of the actual data and future trends. Renew. Sustain. Energy Rev. 2019, 102, 96–110. [Google Scholar] [CrossRef]
- Julian, U.; Markus, E.; Eduard, D. Fatigue analysis of Francis Turbines with different specific speeds using site measurements. WASSERWIRTSCHAFT 2019, 109, 48–53. [Google Scholar] [CrossRef]
- Zhu, D.; Tao, R.; Xiao, R.; Li, Y.; Wang, Q. Solving the runner blade crack problem for a Francis hydro-turbine operating under condition-complexity. Renew. Energy 2020, 149, 298–320. [Google Scholar] [CrossRef]
- Shi, G.; Zhu, Y.; Liu, Z.; Li, J. The influence of guide vane opening on the stress and strain of the runner in a mixed-flow turbine. J. Drain. Irrig. Mach. Eng. 2020, 38, 1. [Google Scholar]
- Liu, D.; Deng, X.; Zhao, Y.; Li, Y.; Zhang, J. Research on Dynamic Stress and Pressure Pulsation Test of Large Mixed-Flow Model Unit. J. Mech. Eng. 2020, 55, 9–18. [Google Scholar]
- Presas, A.; Valentin, D.; Zhao, W.; Egusquiza, M.; Valero, C.; Egusquiza, E. On the use of neural networks for dynamic stress prediction in Francis turbines by means of stationary sensors. Renew. Energy 2021, 170, 652–660. [Google Scholar] [CrossRef]
- Zhao, Y.; Dang, M.; Feng, J.; Luo, X.; Li, Z. The influence of free liquid surface and water body gravity on the stress and strain of tubular turbine blades. Chin. J. Agric. Eng. 2022, 38, 52–60. [Google Scholar]
- Hua, H.; Zhang, Y.; Qin, Z.; Yang, Y.; Fernandez-Rodriguez, E. Dynamic response of a semi-submersible floating wind turbine-point absorption wave energy hybrid energy system under rated and extreme conditions. Phys. Fluids 2025, 37, 017144. [Google Scholar] [CrossRef]
- Vantadori, S.; Carpinteri, A.; Scorza, D. Simplified analysis of fracture behaviour of a Francis hydraulic turbine runner blade. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 679–688. [Google Scholar] [CrossRef]
- Georgievskaia, E. Analytical system for predicting cracks in hydraulic turbines. Eng. Fail. Anal. 2021, 127, 105489. [Google Scholar] [CrossRef]
- Seydoux, M.; Vagnoni, E.; Nicolet, C.; Paolone, M. On the prediction of the induced damage by the start-up sequence of Francis turbines: On operational resilience framework. Renew. Energy 2024, 228, 120587. [Google Scholar] [CrossRef]



| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Rated head H/(m) | 197 | Number of guide vanes Zg | 24 |
| Rated flow rate Q/(m3/s) | 432.67 | Number of rotor blades Zr | 15 |
| Rated speed n/(r/min) | 125 | Rated output P/(MW) | 784 |
| Rotor diameter D1/(m) | 7.4 | Efficiency η/(%) | 96.61 |
| Guide Vane Opening (%) | 10 | 25 | 50 | 70 | 100 | |
|---|---|---|---|---|---|---|
| Head (m) | ||||||
| 154.6 | 1 | 2 | 3 | 4 | 5 | |
| 197 | 6 | 7 | 8 | 9 | 10 | |
| 229.4 | 11 | 12 | 13 | 14 | 15 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, X.; Hua, H.; Li, C.; Wei, S.; Yan, Z.; Deng, W.; Pang, J.; Xiong, Y.; Li, L.; Liu, X. Deformation and Stress of a Runner in Large Francis Turbines Under Wide-Load Operating Conditions. Water 2025, 17, 2374. https://doi.org/10.3390/w17162374
Deng X, Hua H, Li C, Wei S, Yan Z, Deng W, Pang J, Xiong Y, Li L, Liu X. Deformation and Stress of a Runner in Large Francis Turbines Under Wide-Load Operating Conditions. Water. 2025; 17(16):2374. https://doi.org/10.3390/w17162374
Chicago/Turabian StyleDeng, Xin, Hong Hua, Chaoshun Li, Shuman Wei, Zhu Yan, Wanquan Deng, Jiayang Pang, Yufan Xiong, Lihao Li, and Xiaobing Liu. 2025. "Deformation and Stress of a Runner in Large Francis Turbines Under Wide-Load Operating Conditions" Water 17, no. 16: 2374. https://doi.org/10.3390/w17162374
APA StyleDeng, X., Hua, H., Li, C., Wei, S., Yan, Z., Deng, W., Pang, J., Xiong, Y., Li, L., & Liu, X. (2025). Deformation and Stress of a Runner in Large Francis Turbines Under Wide-Load Operating Conditions. Water, 17(16), 2374. https://doi.org/10.3390/w17162374





