Groundwater Level Estimation Using Improved Transformer Model: A Case Study of the Yellow River Basin
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.2.1. The Gravity Recovery and Climate Experiment (GRACE)
2.2.2. Global Land Data Assimilation System (GLDAS)
2.2.3. Measured Groundwater Level
2.3. Methods
2.3.1. Calculation Method of Groundwater Level
2.3.2. Spatial Interpolation Methods
- 1.
- Inverse Distance Weighting
- 2.
- Ordinary Kriging
2.3.3. Machine Learning Methods
- 1.
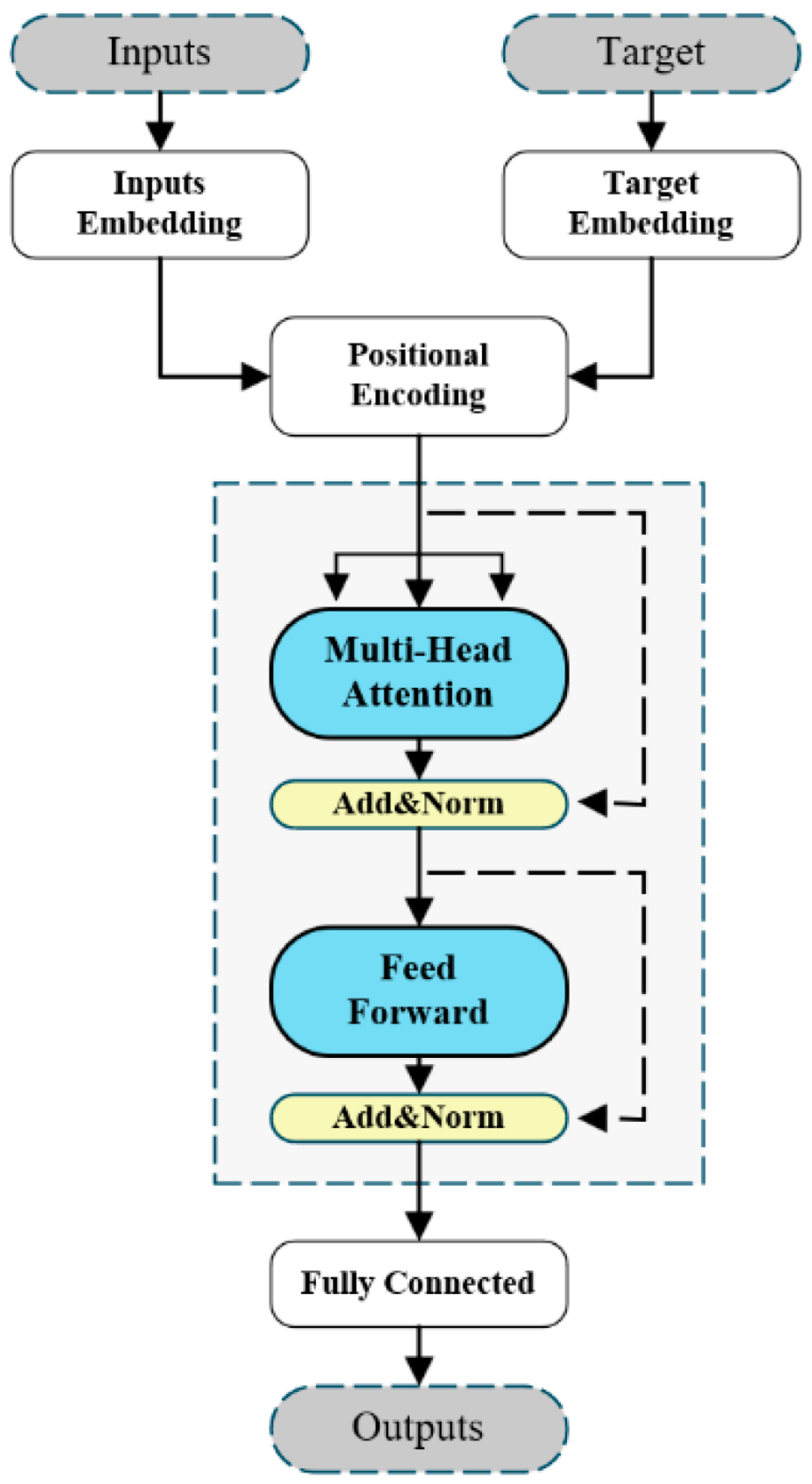
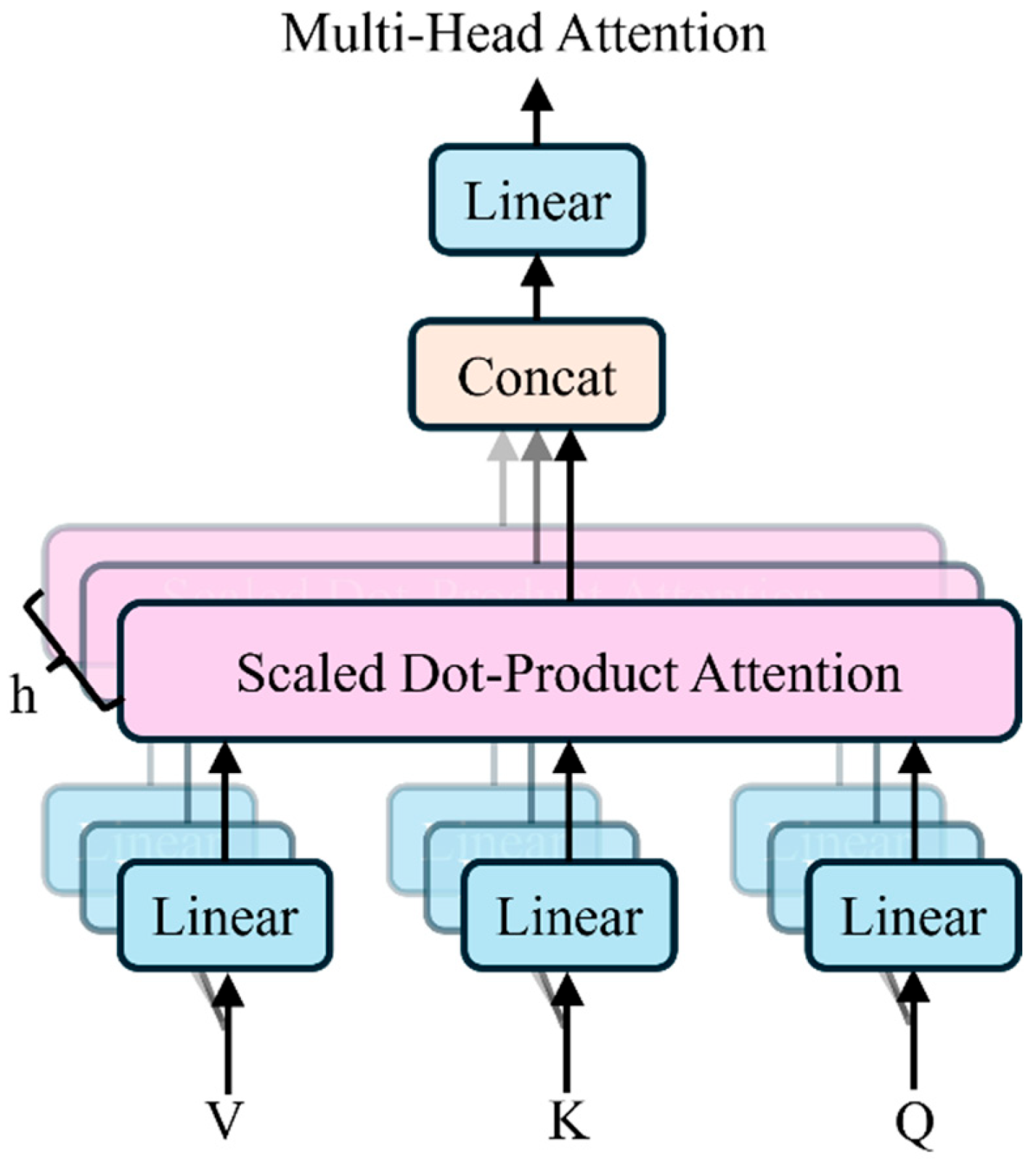
- Transformer model
- 2.
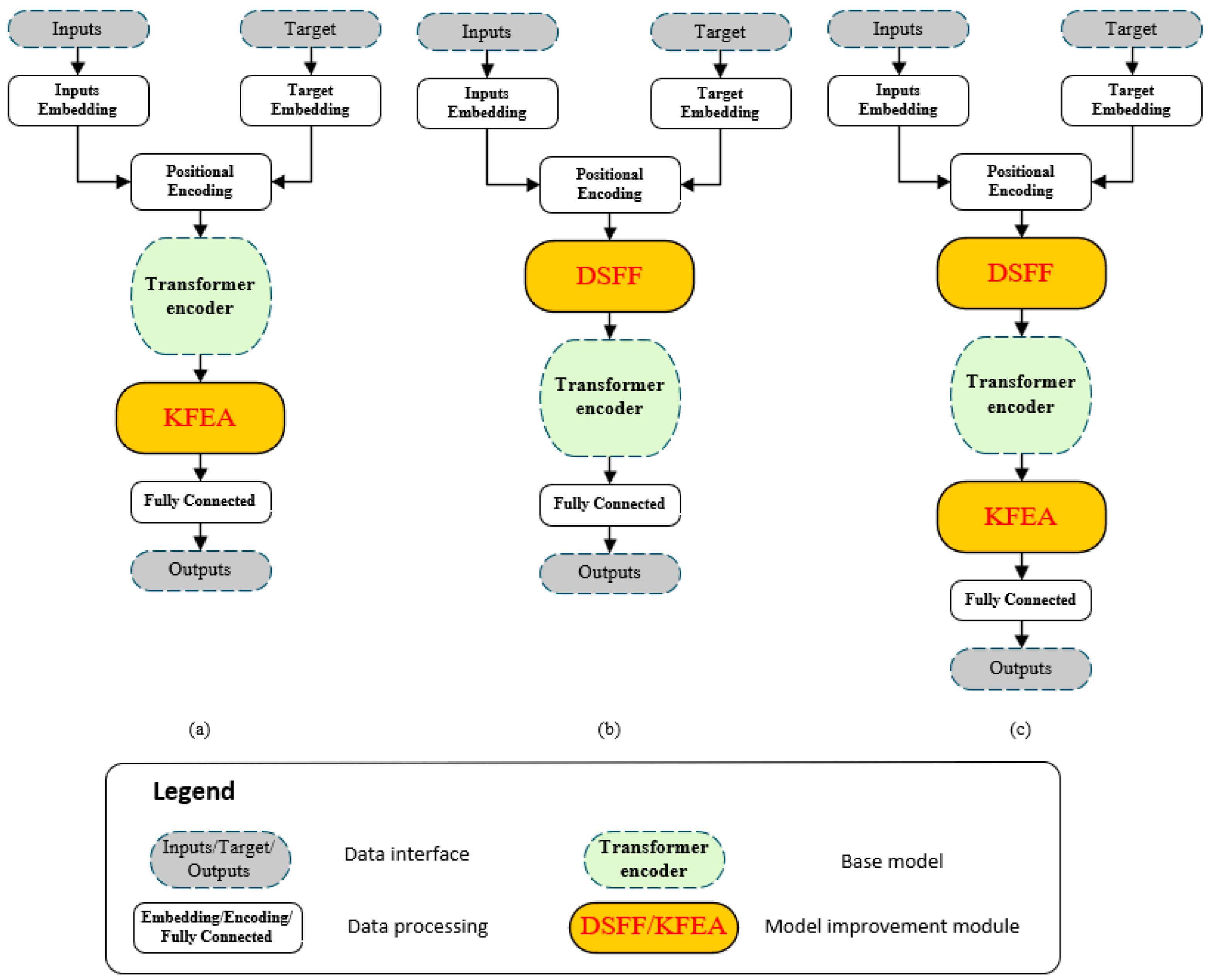
- Key Feature Enhancement Architecture
- 3.
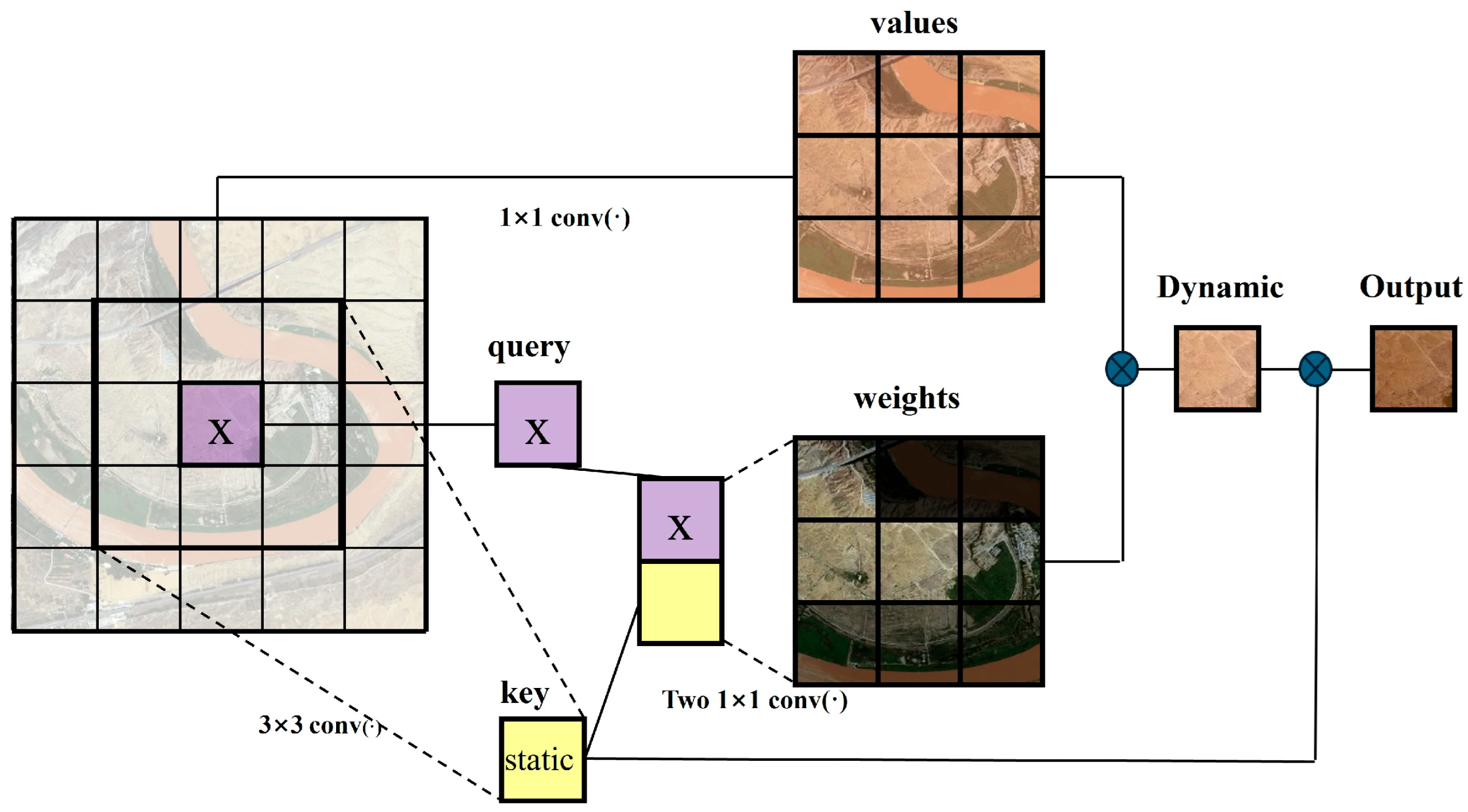
- Dynamic–Static Feature Fusion
- 4.
- Integrated Transformer model
- 5.
- LSTM
2.3.4. Core Metrics and Hyperparameter Configuration
3. Results
3.1. Comparison of Estimation Performance of Various Machine Learning Models
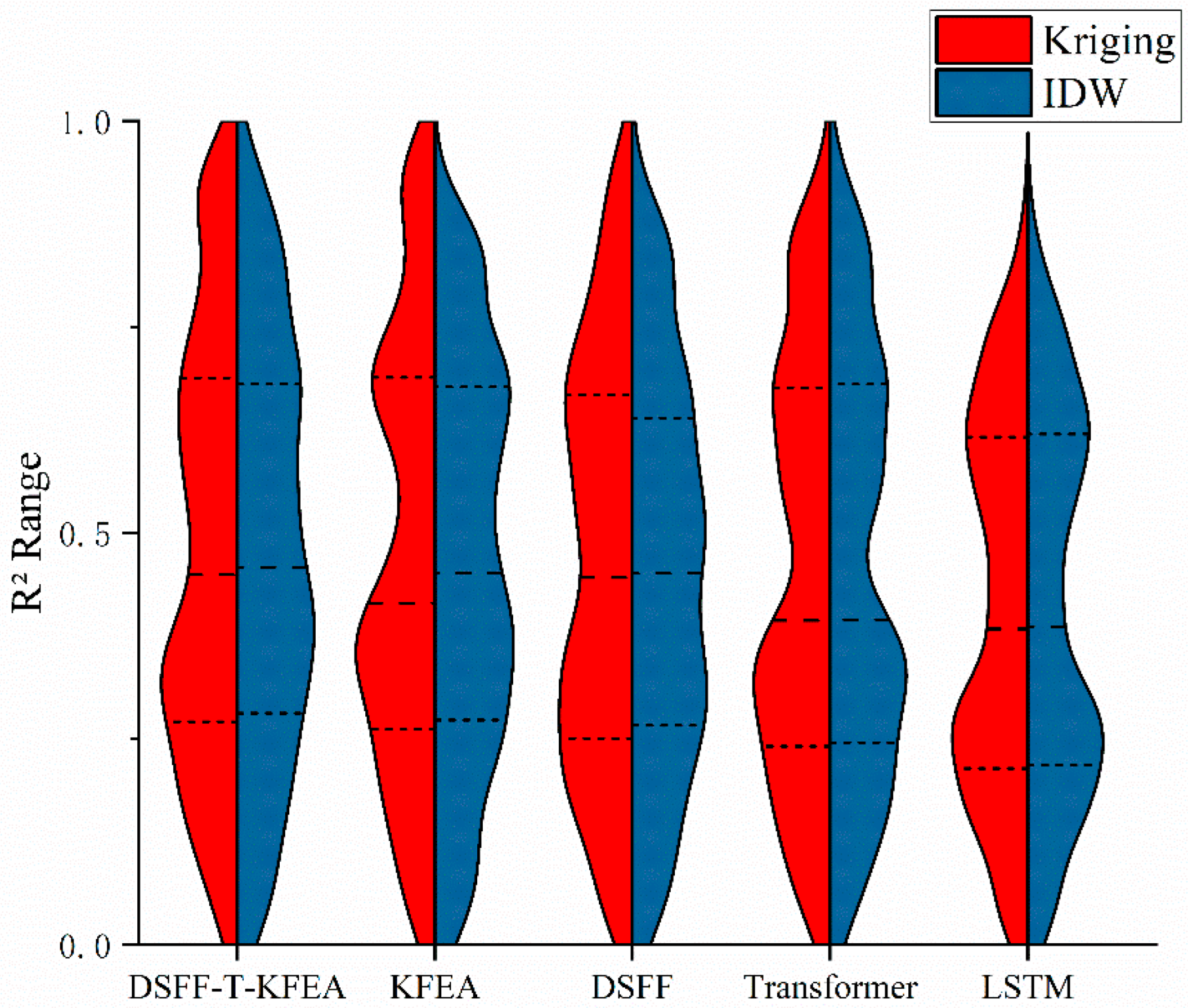
3.1.1. Influence of Spatial Interpolation Method on Model Estimation
3.1.2. Influence of Machine Learning Model on Estimation
3.2. Spatial Representation of Estimation Results
4. Discussion
4.1. Application of Self-Attention Mechanism in Estimation
4.2. Application of Spatial Information
4.3. Application of Feature Filtering
4.4. Application of Improved Model
4.5. Deficiencies and Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- van der Gun, J. Groundwater and Global Change; United Nations Educational, Scientific and Cultural Organization (UNESCO): Paris, France, 2012; pp. 1–42+44. [Google Scholar]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef]
- Vorosmarty, C.J.; Green, P.; Salisbury, J.E.; Lammers, R.B. Global Water Resources:Vulnerability from Climate Change and Population Growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef]
- Jasechko, S.; Perrone, D. Global groundwater wells at risk of running dry. Science 2021, 372, 418–421. [Google Scholar] [CrossRef]
- Shin, Y.S. On the “Groundwater”. Logging Landslides 1976, 13, 16–21. [Google Scholar] [CrossRef][Green Version]
- Ding, K.; Zhao, X.; Cheng, J.; Yu, Y.; Couchot, J.; Zheng, K.; Lin, Y.; Wang, Y. GRACE/ML-based analysis of the spatiotemporal variations of groundwater storage in Africa. J. Hydrol. 2025, 647, 132336. [Google Scholar] [CrossRef]
- Peng, M.; Lu, Z.; Zhao, C.; Motagh, M.; Bai, L.; Conway, B.D.; Chen, H. Mapping land subsidence and aquifer system properties of the Willcox Basin, Arizona, from InSAR observations and independent component analysis. Remote Sens. Environ. 2022, 271, 112894. [Google Scholar] [CrossRef]
- Ma, R.; Chen, K.; Andrews, C.B. Methods for Quantifying Interactions Between Groundwater and Surface Water. Annu. Rev. Environ. Resour. 2024, 49, 623–653. [Google Scholar] [CrossRef]
- Noorduijn, S.L.; Harrington, G.A.; Cook, P.G. The representative stream length for estimating surface water–groundwater exchange using Darcy’s Law. J. Hydrol. 2014, 513, 353–361. [Google Scholar] [CrossRef]
- Thanh, N.N.; Thunyawatcharakul, P.; Ngu, N.H.; Chotpantarat, S. Global review of groundwater potential models in the last decade: Parameters, model techniques, and validation. J. Hydrol. 2022, 614, 128501. [Google Scholar] [CrossRef]
- Yang, M.; Liu, H.; Meng, W. An analytical solution of the tide-induced groundwater table overheight under a three-dimensional kinematic boundary condition. J. Hydrol. 2021, 595, 125986. [Google Scholar] [CrossRef]
- Islam, Z.; Abdel-Aty, M.; Mahmoud, N. Using CNN-LSTM to predict signal phasing and timing aided by High-Resolution detector data. Transp. Res. Part C Emerg. Technol. 2022, 141, 103742. [Google Scholar] [CrossRef]
- Alabdulkreem, E.; Alruwais, N.; Mahgoub, H.; Dutta, A.K.; Khalid, M.; Marzouk, R.; Motwakel, A.; Drar, S. Sustainable groundwater management using stacked LSTM with deep neural network. Urban Clim. 2023, 49, 101469. [Google Scholar] [CrossRef]
- Turkoglu, M.O.; Stefano, A.; Wegner, J.D.; Schindler, K. Gating Revisited: Deep Multi-layer RNNs That Can Be Trained. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4081–4092. [Google Scholar] [CrossRef]
- Choudhary, A.; Arora, A. Assessment of bidirectional transformer encoder model and attention based bidirectional LSTM language models for fake news detection. J. Retail. Consum. Serv. 2024, 76, 103545. [Google Scholar] [CrossRef]
- Zhang, H.; Shafiq, M.O. Survey of transformers and towards ensemble learning using transformers for natural language processing. J. Big Data 2024, 11, 25. [Google Scholar] [CrossRef]
- Su, L.; Zuo, X.; Li, R.; Wang, X.; Zhao, H.; Huang, B. A systematic review for transformer-based long-term series forecasting. Artif. Intell. Rev. 2025, 58, 80. [Google Scholar] [CrossRef]
- Subhadarsini, S.; Kumar, D.N.; Govindaraju, R.S. Enhancing Hydro-climatic and land parameter forecasting using Transformer networks. J. Hydrol. 2025, 655, 132906. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, Z.; Gui, H. A Meteorology-Driven Transformer Network to Predict Soil Moisture for Agriculture Drought Forecasting. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4405818. [Google Scholar] [CrossRef]
- Zhang, D.; Madsen, H.; Ridler, M.E.; Kidmose, J.; Jensen, K.H.; Refsgaard, J.C. Multivariate hydrological data assimilation of soil moisture and groundwaterhead. Hydrol. Earth Syst. Sci. 2016, 20, 4341–4357. [Google Scholar] [CrossRef]
- Boo, K.B.W.; El-Shafie, A.; Othman, F.; Khan, M.H.; Birima, A.H.; Ahmed, A.N. Groundwater level forecasting with machine learning models: A review. Water Res. 2024, 252, 121249. [Google Scholar] [CrossRef]
- Kostić, S.; Stojković, M.; Guranov, I.; Vasović, N. Revealing the background of groundwater level dynamics: Contributing factors, complex modeling and engineering applications. Chaos Solitons Fractals 2019, 127, 408–421. [Google Scholar] [CrossRef]
- Sabzehee, F.; Amiri-Simkooei, A.; Iran-Pour, S.; Vishwakarma, B.; Kerachian, R. Enhancing spatial resolution of GRACE-derived groundwater storage anomalies in Urmia catchment using machine learning downscaling methods. J. Environ. Manag. 2023, 330, 117180. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, L.; Li, H. Monthly 8-km Gridded Meteorological Dataset for the Upper and Middle Reaches of the Yellow River Basin (1980–2015). J. Glob. Change Data Discov. 2022, 6, 25–36, 184–195. [Google Scholar]
- Akl, M.; Thomas, B.F. Challenges in applying water budget framework for estimating groundwater storage changes from GRACE observations. J. Hydrol. 2024, 639, 131600. [Google Scholar] [CrossRef]
- Shi, Z.; Zhu, X.; Tang, Y. Analysis of Terrestrial Water Storage Changes and Influencing Factors in China Based on GRACE Satellite Data. Arid. Land Geogr. 2023, 46, 1397–1406. [Google Scholar]
- Castellazzi, P.; Ransley, T.; McPherson, A.; Slatter, E.; Frost, A.; Shokri, A.; Wallace, L.; Crosbie, R.; Janardhanan, S.; Kilgour, P.; et al. Assessing Groundwater Storage Change in the Great Artesian Basin Using GRACE and Groundwater Budgets. Water Resour. Res. 2024, 60, e2024WR037334. [Google Scholar] [CrossRef]
- Zhang, L.; Ke, P.; Zhang, L. Study on Spatiotemporal Variation of Groundwater Storage in China Based on GRACE Data. J. Hydroecol. Ecol. 2024, 9–17. [Google Scholar]
- Gong, H.; Pan, Y.; Zheng, L.; Li, X.; Zhu, L.; Zhang, C.; Huang, Z.; Li, Z.; Wang, H.; Zhou, C. Long-term groundwater storage changes and land subsidence development in the North China Plain (1971–2015). Hydrogeol. J. 2018, 26, 1417–1427. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Rivera, A.; Huang, J.; Pavlic, G.; Calderhead, A.I.; Chaussard, E.; Garfias, J.; Salas, J. Groundwater depletion in Central Mexico: Use of GRACE and InSAR to support water resources management. Water Resour. Res. 2016, 52, 5985–6003. [Google Scholar] [CrossRef]
- Diego-Alejandro, S.-A.; Alexandra, S.; Luiz-Carlos, F. Characterization of groundwater storage changes in the Amazon River Basin based on downscaling of GRACE/GRACE-FO data with machine learning models. Sci. Total Environ. 2024, 912, 168958. [Google Scholar]
- Hellwig, J.; de Graaf, I.E.M.; Weiler, M.; Stahl, K. Large-scale assessment of delayed groundwater responses to drought. Water Resour. Res. 2020, 56, e2019WR025441. [Google Scholar] [CrossRef]
- Lu, F.; You, W.; Fan, D. Inversion of Water Storage and Ocean Mass Changes in Mainland China over the Last Decade from GRACE RL05 Data. Acta Geod. Cartogr. Sin. 2015, 44, 160–167. [Google Scholar]
- Frappart, F.; Ramillien, G. Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review. Remote Sens. 2018, 10, 829. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Yang, Z.L.; Niu, G.Y. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models. J. Geophys. Res. 2009, 114, B05404. [Google Scholar] [CrossRef]
- Long, D.; Yang, W.; Sun, Z. Satellite Gravimetry Inversion and Basin Water Balance for Groundwater Storage Changes in the Haihe Plain. J. Hydraul. Eng. 2023, 54, 255–267. [Google Scholar]
- Kang, X.; Li, L.; Sun, C. Sustainability Study of Groundwater in the Gansu Section of the Yellow River Basin Based on GRACE and GLDAS Data. J. Desert Res. 2024, 44, 196–206. [Google Scholar]
- UNESCO. The United Nations World Water Development Report 2022: Groundwater: Making the Invisible Visible. 2022. Available online: https://www.unwater.org/publications/un-world-water-development-report-2022 (accessed on 24 July 2024).
- Cao, J.; Xiao, Y.; Long, D. Monitoring Groundwater Storage Changes in the North China Plain by Combining Satellite Gravimetry and Well Data. Geomat. Inf. Sci. Wuhan Univ. 2024, 5, 805–818. [Google Scholar]
- Zhu, X.-H.; Li, K.-R.; Deng, Y.-J.; Long, C.-F.; Wang, W.-Y.; Tan, S.-Q. Center-Highlighted Multiscale CNN for Classifcation of Hyperspectral Images. Remote Sens. 2024, 16, 4055. [Google Scholar] [CrossRef]
- Huang, J.; Yan, H.; Chen, Q.; Liu, Y. Multi-Granularity Temporal Embedding Transformer Network for Traffc Flow Forecasting. Sensors 2024, 24, 8106. [Google Scholar] [CrossRef]
- Vasan, V.; Sridharan, N.V.; Vaithiyanathan, S.; Aghaei, M. Detection and classification of surface de-fects on hot-rolled steel using vision transformers. Heliyon 2024, 10, e38498. [Google Scholar] [CrossRef]
- Deihim, A.; Alonso, E.; Apostolopoulou, D. STTRE: A Spatio-Temporal Transformer with Relative Embeddings for multivariate time series forecasting. Neural Netw. 2023, 168, 549–559. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wu, X.; Zhang, J.; Wang, W.; Zheng, L.; Shang, J. Series clustering and dynamic periodic patching-based transformer for multivariate time series forecasting. Appl. Soft Comput. 2025, 174, 112980. [Google Scholar] [CrossRef]
- Min, L.; Fan, Z.; Lv, Q.; Reda, M.; Shen, L.; Wang, B. YOLO-DCTI: Small Object Detection in Remote Sensing Base on Contextual Transformer Enhancement. Remote Sens. 2023, 15, 3970. [Google Scholar] [CrossRef]
- Zhu, D.; Yang, P. Study on the Evolutionary Characteristics of Post-Fire Forest Recovery Using Unmanned Aerial Vehicle Imagery and Deep Learning: A Case Study of Jinyun Mountain in Chongqing, China. Sustainability 2024, 16, 9717. [Google Scholar] [CrossRef]
- Liu, C.; Wei, Z.; Zhou, L.; Shao, Y. Multidimensional time series classification with multiple attention mechanism. Complex Intell. Syst. 2025, 11, 14. [Google Scholar] [CrossRef]






| Model Name | Epochs/ Patience | Learning Rate (Adam) | Dim | Self-Attention Heads | Encoder Layers | COT Convolution Kernel | SEnet Channel Compression Ratio |
|---|---|---|---|---|---|---|---|
| Transformer | 200/75 | 0.0001 | 128 | 4 | 4 | - | - |
| Transformer-KFEA | 200/75 | 0.00005 | 128 | 4 | 4 | - | 16 |
| DSFF-Transformer | 200/75 | 0.0001 | 128 | 4 | 4 | 3 × 3 | - |
| DSFF-Transformer-KFEA | 200/75 | 0.0001 | 128 | 4 | 4 | 3 × 3 | 16 |
| LSTM | 200/75 | 0.002 | - | - | - | - | - |
| Model Name | Epochs/ Patience | Learning Rate (Adam) | Dim | Self-Attention Heads | Encoder Layers | Test Set R2 |
|---|---|---|---|---|---|---|
| Transformer | 200/75 | 0.0001 | 32 | 4 | 4 | 0.59 |
| Transformer | 200/75 | 0.00005 | 32 | 4 | 4 | 0.52 |
| Transformer | 200/75 | 0.00001 | 32 | 4 | 4 | 0.5 |
| Transformer | 200/75 | 0.0001 | 64 | 4 | 4 | 0.62 |
| Transformer | 200/75 | 0.00005 | 64 | 4 | 4 | 0.54 |
| Transformer | 200/75 | 0.00001 | 64 | 4 | 4 | 0.53 |
| Transformer | 200/75 | 0.0001 | 128 | 4 | 4 | 0.68 |
| … | … | … | … | … | … | … |
| Index | Interpolation Scheme | DSFF-Transformer-KFEA | Transformer-KFEA | DSFF- Transformer | Transformer | LSTM |
|---|---|---|---|---|---|---|
| R2 | Kriging | 0.478 | 0.468 | 0.461 | 0.450 | 0.404 |
| IDW | 0.476 | 0.464 | 0.451 | 0.453 | 0.408 | |
| RMSE | Kriging | 0.467 | 0.479 | 0.494 | 0.494 | 0.534 |
| IDW | 0.759 | 0.778 | 0.805 | 0.811 | 0.865 | |
| MAE | Kriging | 0.362 | 0.369 | 0.376 | 0.380 | 0.408 |
| IDW | 0.589 | 0.596 | 0.617 | 0.620 | 0.658 |
| Model | DSFF-Transformer-KFEA | Transformer-KFEA | DSFF-Transformer | Transformer | LSTM |
|---|---|---|---|---|---|
| Kriging | 9.08% | 5.40% | 12.37% | 8.61% | 9.40% |
| IDW | 8.07% | 5.87% | 11.12% | 8.93% | 10.18% |
| Basin | Interpolation Scheme | DSFF-Transformer -KFEA | Transformer -KFEA | DSFF- Transformer | Transformer | LSTM |
|---|---|---|---|---|---|---|
| Upstream | Kriging | 0.446 | 0.430 | 0.425 | 0.441 | 0.387 |
| IDW | 0.496 | 0.445 | 0.471 | 0.489 | 0.405 | |
| midstream | Kriging | 0.495 | 0.498 | 0.490 | 0.435 | 0.413 |
| IDW | 0.445 | 0.461 | 0.419 | 0.410 | 0.396 | |
| downstream | Kriging | 0.880 | 0.875 | 0.783 | 0.796 | 0.637 |
| IDW | 0.785 | 0.777 | 0.800 | 0.804 | 0.650 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Fu, C.; Liu, Y.; Xiang, L. Groundwater Level Estimation Using Improved Transformer Model: A Case Study of the Yellow River Basin. Water 2025, 17, 2318. https://doi.org/10.3390/w17152318
Zhou T, Fu C, Liu Y, Xiang L. Groundwater Level Estimation Using Improved Transformer Model: A Case Study of the Yellow River Basin. Water. 2025; 17(15):2318. https://doi.org/10.3390/w17152318
Chicago/Turabian StyleZhou, Tianming, Chun Fu, Yezhong Liu, and Libin Xiang. 2025. "Groundwater Level Estimation Using Improved Transformer Model: A Case Study of the Yellow River Basin" Water 17, no. 15: 2318. https://doi.org/10.3390/w17152318
APA StyleZhou, T., Fu, C., Liu, Y., & Xiang, L. (2025). Groundwater Level Estimation Using Improved Transformer Model: A Case Study of the Yellow River Basin. Water, 17(15), 2318. https://doi.org/10.3390/w17152318





