Abstract
Given the global rise in magnitude and frequency of extreme events due to climate change, accurately determining these values—typically through frequency analysis—is especially important. The article analyzes the particular aspects of three probability distributions of 4 and 5 parameters in flood frequency analysis (FFA) using the L-moments as a parameter estimation method. Aspects regarding the behavior of the five-parameter Wakeby, four-parameter generalized Pareto and four-parameter Burr distributions are highlighted in generating the maximum flow values in the area of low annual exceedance probabilities characteristic of rare and very rare events. After applying these distributions to four case studies, it was found that for the 10,000-year return period event, the relative error between multi-parameter distributions is under 20%—a more than acceptable margin given the extremely low exceedance probability. However, its importance depends on the use of the generated values, which in some cases can lead to excessive costs in establishing structural flood protection measures (urban planning), which can be avoided. It also highlights possible negative consequences (material and human lives) regarding the risk associated with these analyses that can lead to an under-dimensioning of this infrastructure.
Keywords:
flood; dam; statistical distribution; frequency analysis; L-moments; Burr; Wakeby; uncertainties; Pareto 1. Introduction
Probability distributions represent the main component in the frequency analysis of rare events. Taking into account the need to determine the maximum annual flows with certain return periods, frequency analysis is the main way of directly determining these values.
The design of various hydrotechnical retention works, a special case being the dams, requires the dimensioning and verification of the components of the hydrotechnical arrangement at different annual exceedance probabilities.
The FFA presented in this article is part of wider research on establishing the structural and non-structural flood control measures, including for the most economically affected urban areas, in which conventional flood control can give a false sense of security.
Urban areas and especially areas proposed for urban development and expansion are generally in flood zones in Romania. The rivers presented in the case study are in areas where some require flood defense measures, such as making non-permanent accumulations or making dams in urban areas. Another measure proposed for the expansion of urban areas is more space for the river.
The most restrictive are the conditions for the dams (Class I hydrotechnical works), which require the design using maximum flows with annual exceedance probabilities of 0.01% and 0.1%.
These conditions can be found both in international regulations and in regulations specific to Romania [1,2].
Thus, for example, Table 1 presents the provisions regarding the annual exceedance probabilities specific to these hydrotechnical works [3].

Table 1.
Annual exceedance probabilities of interest in FFA.
A special case also has the determination of the bankfull channel, which in Romania is established as the value of the maximum flow corresponding to the annual probability of exceeding 80% [4].
All these values corresponding to these probabilities must be determined directly, even if the data length is short. Unfortunately, the hydrographic network of Romania suffers from great deficiencies regarding these lengths of recorded data, generally being characterized by an average of only 30 values, and where more than 30 years are given, there are substantial land use changes, including important hydrotechnical works [1,3,4].
Thus, the choice of distributions and optimal methods for estimating their parameters is an essential element, the generated values needing to be characterized by statistical uncertainties as low as possible, because otherwise the costs would be much too expensive, and most importantly, with possible negative effects on the safety of the population.
In this manuscript, only the L-moments and distributions of at least four parameters are analyzed, these having special importance regarding this method. The L-moments are a method that, over time, has proven to be more stable and robust than other methods [5,6,7,8,9,10,11,12]. It is a method characterized by certain statistical indicators, such as the coefficient of L-variation, L-skewness, and L-kurtosis, which represent important tools in the processes of regionalization in hydrology. It also represents the main method used in regionalization analyses of maximum flows [13,14,15,16,17,18,19], maximum precipitation [20,21,22,23,24,25,26], and minimum flows [27,28,29,30,31,32].
The analyzed distributions, namely the five-parameter Wakeby distribution (WK5), the four-parameter generalized Pareto distribution (PG4) and the four-parameter Burr distribution (BR4), have varied applicability in frequency analysis. The Burr distribution was usually applied using the MOM and L-moments [33]. The Wakeby distribution represents one of the most used probability distributions, being usually applied for all frequency analyses [5,6,7,8,34,35,36,37,38,39,40]. This distribution presents certain particular aspects that have been presented in other materials [5,6,7,8], among which the most important is the observance of the so-called “separation effect”, respectively, the particular case of this distribution, namely the transformation into the generalized Pareto distribution Type 2. These aspects were also presented in previous materials [5,6,7,8], as well as new elements regarding the estimation of the parameters of this distribution using MOM and high-order linear moments method (LH-moments).
The individual superiority of each analyzed distribution, especially compared to distributions with a lower number of parameters, has been highlighted in other materials [5,6,7,8], but until now no comparative analysis has been carried out regarding their behavior and differences between the generated results, all respecting simultaneously the conditions imposed by the L-moments method, namely the calibration of the higher order statistical indicators L-skewness, respectively, L-kurtosis.
The general idea in FFA, using the L-moments, is that it is sufficient to predominantly use a certain statistical distribution, which is at least inaccurate considering that each statistical distribution has its own characteristics (soft tail, heavy tail, upper bound presence, algebraically decreased tail, exponentially decreased tail, etc.) generally dictated by the specific characteristics of the family to which it belongs. These observations also apply to distributions with a high number of parameters, an aspect that is highlighted in the present manuscript.
An important problem is the fact that it is often considered that the use of a distribution with a high number of parameters can be the answer for any analysis related to the analysis of maximum extreme events. They have a real advantage compared to the classical two- and three-parameter distributions, but the results obtained must be carefully analyzed, since the degree of confidence is greatly influenced by the method of parameter estimation and by the particular aspects and characteristics of the distributions and families to which they belong.
Thus, if we analyze the method of ordinary moments (MOM), the parameters of the distributions are calibrated according to the statistical indicators: the arithmetic mean (expected value), the coefficient of variation, the skewness, and the kurtosis. But in the case of short and medium lengths of data, the skewness and especially the kurtosis require important corrections. If for the skewness there are certain correction relationships [6,13,14], in the case of kurtosis, there is none, the errors being much too high. Thus, the “exact” calibration achieved by these distributions with a high number of parameters, using MOM, is not related to the real statistical situation, but only to the relative one highlighted by the analyzed data site, whose indicators require important corrections.
Other methods useful in complex statistical contexts are the Bayesian method [41,42,43] and the maximum entropy method [44], but each comes with its own disadvantages. In the case of the Bayesian method, the results are strongly influenced by the choice of the a priori distribution, which in most cases is subjective or difficult to justify, in order to have a robust estimate, more data or a very well-informed prior are needed, otherwise the uncertainty remains high [43]. It is also a method that requires a high level of theoretical and mathematical understanding, especially when combined with nonlinear or unusual models. In the case of the entropy method, the results depend essentially on the choice of constraints (e.g., known statistical moments, which require important corrections).
In the case of the L-moments, the four statistical indicators are much more stable and robust to variations in recorded data lengths [4,5,6,7,8,9,10,11], the degree of confidence being high. But, although the distributions with a high number of parameters calibrate all the linear moments appropriately, the results (the shape of the tail of the distributions) differ, the most obvious being for the area of small and very small annual probabilities of exceeding.
Thus, the need for this comparative analysis resulted from the holistic research carried out within the Faculty of Hydrotechnics regarding the frequency analysis of the maximum flows in which it was observed that although the distributions with a high number of parameters calibrate all the high-order statistical indicators (L-skewness and L-kurtosis), the distributions generate different values for rare and very rare events, (p < 0.1%). The analysis in the manuscript also consists of verifying the general concept that the predominant use of a statistical distribution of 4 or 5 parameters is the ideal solution, and the generated values have the highest degree of confidence.
Thus, the article analyzes all these distributions to forecast the values for these probabilities (stated in Table 1), having as case studies four rivers with different morphometric characteristics and hydrological aspects.
The main innovation of this study consists of the comparative approach, carried out for the first time, of the most widely used 4- and 5-parameter distributions in hydrology, analyzed under identical statistical and hydrological conditions. This approach allows highlighting the differences in behavior and uncertainty associated with each distribution, in a rigorous and fair framework. Unlike the usual practice, in which the selection of a complex distribution (usually with several parameters) is considered sufficient, this study demonstrates that the subjective choice of the distribution can introduce systematic errors already at the estimation stage. Thus, the research provides a solid basis for a statistically substantiated selection of frequency models, significantly contributing to the reduction of uncertainty in the estimation of extreme values used in hydrotechnical design.
It compares various distributions (belonging to different families) and shows to what extent a subjective choice can lead to a priori errors. To rigorously emphasize these differences, various frequency analyses of in-situ annual maximum discharges were conducted, since such analyses are required by international standards and legislation to determine extreme values with high return periods (for dam design, even discharges with a mean return period of 10,000 years are required), often considered as practically impossible events.
2. Methods
The analysis presented in the manuscript focuses on the results obtained with distributions with a high number of parameters. Three statistical distributions with a high number of parameters, belonging to families of distributions widely used in FFA, are analyzed: WK5, BR4, and PG4 [5,6,7,8,9,10,11,12,33].
Only distributions of at least four parameters are presented because they meet all the conditions imposed by the L-moments method, chosen as the reference method, namely the appropriate calibration of all higher-order indicators (L-skewness and L-kurtosis).
2.1. Checking Stationarity, Data Homogeneity, and Outliers
To verify the homogeneity and stationarity of the data, the von Neumann tests [45], respectively, the simple t-test [45], were used. The verification of this tool was conducted using the Grubbs and Pilon tests [13,14]. After processing and analyzing the data, they are homogeneous and stationary, and no outliers have been identified.
Considering that the analyzed data represent maximum values that characterize each year of analysis (maximum block), they are independent. For verification, the USWRC 1976 criterion was also used [46].
The analysis flow chart and the involved steps are highlighted in Figure 1.
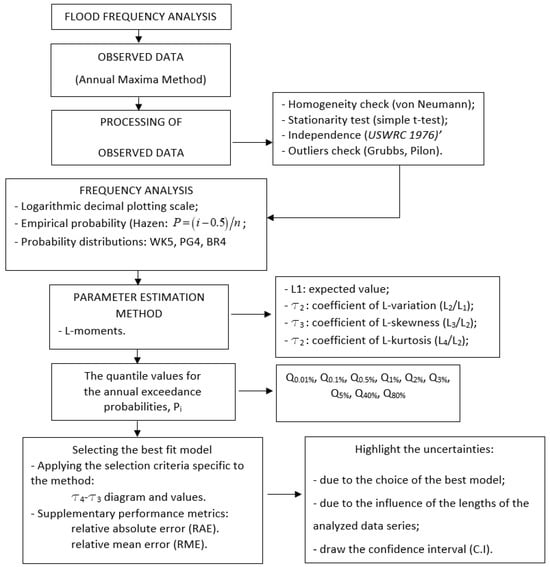
Figure 1.
Methodological flow chart.
2.2. Probability Distributions Functions
This section presents the three analyzed statistical distributions. Table 2 shows the density function, the complementary cumulative distribution function, and the inverse function.

Table 2.
The analyzed probability distributions.
As can be seen, the WK5 distribution does not have a defined shape in terms of the density function and the complementary cumulative distribution function. The meaning of the parameters is presented in Section 2.2.
2.3. Parameter Estimation (Using L-Moments)
2.3.1. The Five-Parameter Wakeby Distribution (WK5)
The WK5 distribution is classified as a quantile function. The four conditions that define the system of linear equations for determining the parameters are the following [6,7]:
where are scale parameters, are shape parameters, and is the position parameter. The location parameter characterizes the expected value (first linear moment), the scale parameter characterizes the coefficient of L-variation, and the shape parameter characterizes the L-skewness.
2.3.2. The Four-Parameter Generalized Pareto (PG4)
It is a generalized form of the beta_p or Singh–Maddala distribution [47]. The nonlinear equations for the PG4 distribution are the following:
where are the shape parameters, is the scale parameter, and is the position parameter.
2.3.3. The Four-Parameter Burr Distribution (BR4)
This BR4 is a generalized case of the Burr Type XII distribution by adding a position parameter. When we have the Burr Type XII distribution (Dagum, Beta k, inverse Burr III); when and we have the 2 parameter Burr Type XII distribution; when and we have the Lomax distribution; when we have the Log-logistic distrinution [47]. The four conditions imposed are the following:
where are shape parameters, is the scale parameter, and is the position parameter.
In order to estimate the parameters of the analyzed distributions, it is necessary to solve nonlinear systems of equations. For this purpose, the Levenberg–Marquardt algorithm was employed (using Mathcad). This method is well-suited for nonlinear least squares problems and provides a robust iterative approach that combines the advantages of both the Gauss–Newton method and the gradient descent technique. The estimation process involves minimizing the sum of squared differences between the theoretical and empirical values (e.g., moments, L-moments, or quantiles, depending on the distribution and the fitting method used). The algorithm adjusts the parameter values iteratively until convergence criteria are met, ensuring a reliable estimation even in cases of complex or highly parameterized distributions. Establishing initial values (“initial guesses”) is an essential step in solving systems of nonlinear equations, especially when using iterative methods such as Levenberg–Marquardt. This initial stage involves trying several starting combinations to see which one leads to convergence, approximate analytical solutions (such as the Wakeby distribution), and user experience.
3. Case Studies and Data
The case study consists of performing a frequency analysis to determine the maximum annual flows corresponding to the usual return periods in hydrology, in the monitoring sections on the rivers Siret, Jijia, Sitna, and Bahlui, located in the North-Eastern area of Romania. (Figure 2) [48].
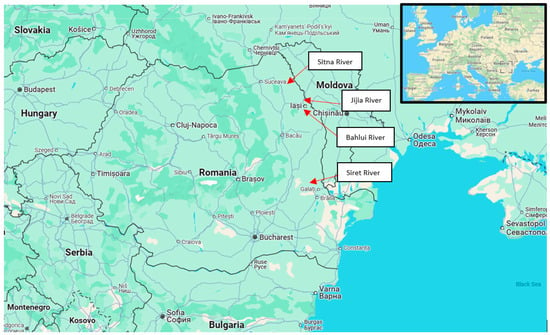
Figure 2.
Positioning of the Siret, Bahlui, Jijia, and Sitna Rivers, in Romania.
The selection of the four locations was primarily based on hydrological and statistical criteria. The selection aimed to ensure relevant morphometric diversity, reflected by variations in catchment areas, mean altitudes, and other physical-geographical characteristics. At the same time, essential statistical aspects were considered, so that each location would highlight distinct hydrological features, such as differences in the length of the analyzed data series, varying degrees of torrentiality, and the amplitude of peak flow variability. This approach allowed for a more comprehensive and representative evaluation of the behavior of hydrological extremes across different morphological and climatic contexts.
The hydrographic basins of the Siret River and those of the Jijia, Sitna, and Bahlui Rivers (tributaries of the Prut River) are characterized by a temperate-continental climate, influenced by air masses from the west and northwest, as well as from the east, leading to significant seasonal variations in temperature and precipitation.
The average annual temperature ranges between 6 °C and 10 °C, depending on altitude. Annual precipitation varies between 500 and 800 mm, with higher values in mountainous areas and lower values in the plains. Winters are cold, with temperatures that can drop below −15 °C, while summers are warm, with maximum temperatures exceeding 30 °C. The predominant winds come from the northwest and west, but in the eastern part, more pronounced continental influences may occur.
Table 3 highlights the river’s morphometric indicators for the analyzed rivers, in the hydrometric stations section [49].

Table 3.
The morphometric indicators for the analyzed rivers (in hydrometric sections).
From the point of view of the origin of the maximum recorded flows, they mainly come from snowmelt in the case of the Siret river, respectively, a mixed origin (snowmelt and rain) in the case of the Bahlui, Sitna, and Jijia Rivers.
Figure 3 shows the time series of maximum annual flow rates recorded for the rivers Siret, Jijia, Bahlui, and Sitna, Romania.
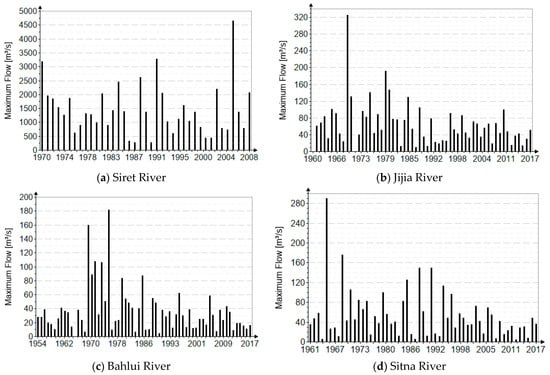
Figure 3.
The chronological series of peak discharges.
Regarding the statistical indicators, the L-skewness and L-kurtosis are the most important [6,7,8,9,10,11] because their values are the ones that most influence the shape of the tails of the distributions in the field of probabilities of rare events. In general, for these types of analyses, these two indicators are considered positive (the values are taken in the mode), varying between 0 and 1 (representing ratios of linear moments). The closer the values are to the value 1, the more pronounced the heavy-tail character is, highlighting a more pronounced torrentiality and asymmetric character. For the analyzed data, the values of these two indicators are presented in Table 4.

Table 4.
The statistical indicators of the observed data.
4. Results
As mentioned earlier, FFA aims to forecast the values of extreme events corresponding to the return periods of interest.
For the present case studies, the quantile values of the analyzed distributions are presented for exceedance probabilities between 0.01% and 80%, the latter value representing the bankfull discharge.
Thus, Table 5 presents the values obtained from applying the three statistical distributions to the four analyzed rivers.

Table 5.
Quantile results for Siret, Jijia, Bahlui, and Sitna Rivers.
Figure 4 shows the fitting distributions for the four rivers. Hazen’s empirical probability was used for plotting position [50]. The horizontal axis is on a logarithmic decimal scale.
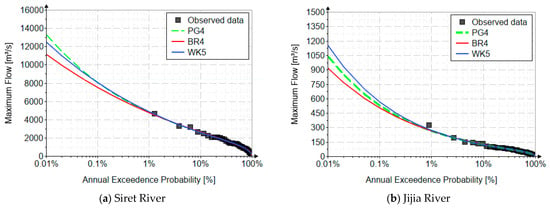
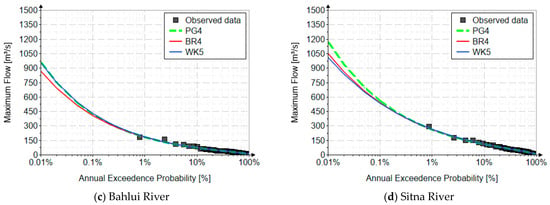
Figure 4.
The curves of the quantile functions for the analyzed distribution.
5. Discussions
Analyzing the results obtained after performing the frequency analysis on the 4 case studies, using the three proposed distributions, whose parameters were estimated using the L-moments, it can be noticed that, in general, the values generated by the curves of the inverse functions of the distributions are very close. This aspect is due to the fact that being distributions with a high number of parameters, all three statistical distributions properly calibrate all four high-order linear moments specific to the L-moments.
The values generated for Q0.01% vary between 11,128 m3/s and 13,279 m3/s in the case of the Siret river, between 916 m3/s and 1152 m3/s for the Jijia river, between 866 m3/s and 961 m3/s for the Bahlui river; respectively, and between 1009 m3/s and 1171 m3/s for the Sitna river. The extreme values, for the Siret and Bahlui rivers, are generated by the BR4 and PG4 distributions, for the Sitna river, the values correspond to the PG4 and WK5 distributions, and for the Jijia river, the values correspond to the BR4 and WK5 distributions.
It should be highlighted that although all distributions properly calibrate the linear moments, they generate, for events with a very long return period (especially for the discharge with a return period of 10,000 years, Q0.01%), different values having an imposed behavior of the structure of the distribution and the specific characteristics of the family it belongs to. However, in general, the relative errors between the values obtained for Q0.01% are below 20%, a more than acceptable error value.
Although there is a general concept that a distribution with a high number of parameters can calibrate any series, and the values obtained are characterized by a high degree of confidence, the results of this research highlight the fact that they must also be addressed with certain reservations.
Considering that all three distributions adequately fulfill the conditions imposed by the L-moments regarding the choice of the best distributions, their performances are additionally analyzed using two usual performance indicators in such analyses, namely relative absolute error (RAE) and relative mean error (RME) [51], both using the inverse functions of the distributions, an important aspect considering that for the WK5 distribution there is no defined forms of the density (PDF) and cumulative (CDF) functions.).
where, , represent data length, recorded data, and forecasted values.
The distribution’s performance values are presented in Table 6.

Table 6.
Distribution performance values.
According to Table 6, the best-fitted distribution with the smallest RME and RAE values for all the analyzed rivers is WK5. The RME and RAE for the Siret River have the lowest values, namely 0.0101 and 0.044, respectively. In the case of the Jijia River, the indicators have the values 0.0082 and 0.0446. For the Bahlui River, the values are 0.009 and 0.0569, and in the case of the Sitna River, the two indicators have the results of 0.0171 and 0.074, respectively.
However, it should be noted that, in general, performance indicators and tests are only relevant within the probability range corresponding to the recorded values; beyond this range (for rare and very rare events), their relevance diminishes.
Thus, taking into account that all three distributions generate close values with acceptable relative errors (approximately 20%), the general use of the Wakeby distribution is recommended because it presents certain important characteristics, among which the most significant being the possibility of this distribution to model different shapes regarding the heavy tail tails (generalized Pareto type II distribution has a special case), as well as the existence of an approximate solution for determining the parameters that can constitute initial values in the exact calculation that involves solving the system of nonlinear equations. In other words, it represents a distribution specially introduced in FFA, having another important particularity, namely the fulfillment of the so-called flow separation effect.
After establishing as rigorously as possible the distribution from which the analyzed data come, it is mandatory to highlight the uncertainties. In general, these must be highlighted on three levels, namely: (1) Uncertainties due to the choice of the best model, which in this case of the exclusive use of distributions of at least four parameters, the relative errors are between ±20%; (2) Uncertainties due to the influence of the lengths of the analyzed data series, which also have a variability depending on hydrological aspects (variability, torrentiality, etc.) transposed into statistical aspects (statistical indicators). (3) Highlighting the confidence interval of the best model, which includes all these uncertainties.
Thus, in Table 7, the uncertainties (theoretical, systematic biases) of the Wakeby distribution are highlighted for the most interesting event, for that value also registering the strongest influences. The degree of uncertainty increases with the decrease in the number of recorded values and high values of L-skewness and L-kurtosis.

Table 7.
The theoretical biases (%) of the Wakeby distribution.
The analysis uses the theoretical values of the statistical indicators of the data series for the Siret River (presented in Table 4). Considering that L-skewness and L-kurtosis depend on at least two parameters, the holistic analysis of the theoretical biases of these distributions implies a more complex analysis of the entire theoretical field of defining statistical indicators specific to the method of linear moments, which define surfaces.
Regarding the confidence interval, the most accessible approach to quantifying and representing these uncertainties is the determination of the confidence interval using Chow’s relation (Equation (15)) but using the frequency factor estimated with the L-moments (Equations (16)–(18)), for a 95% confidence level, based on a Gaussian assumption [13,14,50].
where is the first linear moment (arithmetic mean), is the second linear moment (it characterizes the coefficient of L-variation, ), is the frequency factor of the theoretical distribution estimated with L-moments, is the confidence level, and represents the number of recorded values.
The frequency factors specific to the analyzed distributions have the following expressions:
- -
- WK5 distribution:
- -
- PG4 distribution:
- -
- BR4 distribution:
Figure 5 presents the confidence interval for the WK5 distribution for the four analyzed case studies.
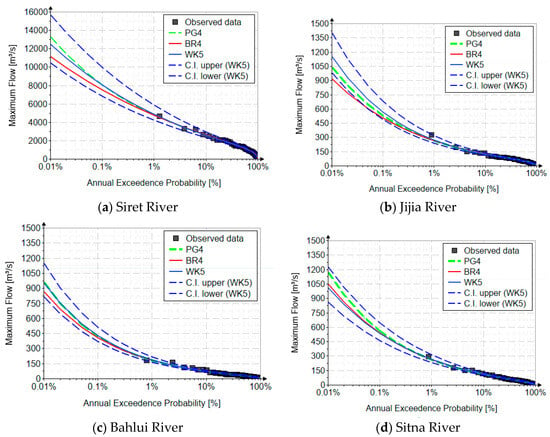
Figure 5.
The confidence interval for the WK5 distribution.
Considering that in Romania, the Pearson III distribution (PE3) is regarded as the “parent” distribution, it is mandatory to present a comparative analysis of the results obtained with WK5 (L-moments) and those forecasted with the PE3 distribution, using parameters estimated by the method of ordinary moments (MOM), as this is the standard method used in Romania. Additionally, the values of the PE3 distribution obtained using the L-moments method are also presented.
Table 8 shows the values obtained for the quantile with a return period of 1000 years (annual exceedance probability of 0.01%) using WK5 and PE3 for the four analyzed case studies.

Table 8.
(a) Forecasted values with WK5 and PE3 distributions–Siret and Jijia Rivers. (b) Forecasted values with WK5 and PE3 distributions–Bahlui and Sitna Rivers.
Analyzing the values obtained in the four case studies presented in Table 8a,b, significant differences can be observed, primarily due to the parameter estimation method and the use of distributions with a different number of parameters.
Regarding the method used in Romania for estimating the parameters of statistical distributions, the method of ordinary moments has a major disadvantage: the inability to adequately correct higher-order statistical indicators (skewness and kurtosis). In Romania, skewness correction is performed by multiplying the coefficient of variation by a factor (2, 3, or 4) that reflects the genesis of peak flows (snowmelt, rain and snow, or rainfall), often chosen without a rigorous scientific basis. This introduces a strong element of subjectivity, which, in general, should not be present in such analyses.
Moreover, the method of ordinary moments is highly influenced by the variability of available data lengths. In Romania, the hydrometric network is generally characterized by short to medium data series (n < 50 values), further impacting the accuracy of parameter estimation. For this reason, it is recommended to adopt the L-moments method (preferably with distributions having at least four parameters), as numerous scientific studies have demonstrated its greater stability and robustness against both the variability of available data lengths and the presence of outliers.
It should be noted that since PE3 is a three-parameter distribution, it fails to calibrate all four L-moments specific to the L-moments method, leading to either underestimation or overestimation of the predicted values. In general, if a two- or three-parameter distribution is to be used, a preselection and, ultimately, a selection of the best model should be performed based on the values of the higher-order statistical indicators specific to the L-moments method (L-skewness and L-kurtosis).
The L-moments method involves selecting the statistical distribution that best calibrates the values of these statistical indicators for the analyzed data.
For the analyzed case studies, the PE3 distribution succeeds in calibrating the L-skewness of the analyzed data (presented in Table 4) but fails to calibrate the L-kurtosis, which is particularly important as it influences the tail behavior of the distribution in the domain of these extremely rare events. The theoretical values of L-kurtosis () generated by the PE3 interdependence relationship are 0.14 (for the Siret River), 0.156 (for the Jijia River), 0.187 (for the Bahlui River), and 0.173 (for the Sitna River), which are significantly lower than the values of the analyzed data presented in Table 4 (0.185, 0.229, 0.271, 0.245).
It is therefore recommended to re-analyze/update the frequency of maximum flows, especially when combined with climate change projections, which can have a significant impact on engineering design decisions. For example, estimating higher maximum flows for given return periods implies the need to revise safety margins in the design and sizing of hydrotechnical works, especially dams, protective dikes, and spillways. In the context of a likely increase in the frequency and intensity of extreme events, future projects must incorporate these new hydrological hazard assessments to reduce the risk of flooding, structural damage, and economic or human losses. Thus, modern approaches and more complex frequency analysis models using more robust criteria and methods become essential for adapting infrastructure to changing climate conditions. The use of different statistical distributions in the analysis of peak flow frequency inevitably involves trade-offs between over-design—which can lead to unreasonably high costs—and under-design, which increases the risk of flooding and structural failure. The choice of distribution directly influences the values of design flows for various return periods, and the variations can be significant depending on the model used. Therefore, the analysis must be adapted to each case, but the general principle is to use models that are as stable and robust as possible, statistically and physically validated. In all situations, there will be a balance between the accepted risk and the resources invested, but this trade-off must be carefully calibrated so that the risks remain within acceptable limits, without leading to over- or under-dimensioning of the infrastructure.
6. Conclusions
Many rivers in Romania, located near urban areas, are increasingly impacted by riparian urbanization and extreme weather, trends expected to intensify with continued development. Agriculture, livestock, and industry are key sources of carbon emissions driving these events. [52,53,54,55]. A recently explored question is: Do floods attack cities, or do cities invade floodplains? [56].
The direct approach for forecasting extreme hydrological events is based on frequency analysis (FFA) using statistical probability distributions. A critical component in applying these distributions is the method of parameter estimation. The L-moments method, analyzed in this study, requires the use of statistical distributions with a sufficient number of parameters to properly calibrate all four specific linear moments.
In line with this requirement, the manuscript focused on analyzing three statistical distributions with four and five parameters commonly used in FFA, namely the WK5, PG4, and BR4 distributions. The analysis was conducted through four case studies, each representing rivers with distinct morphometric characteristics in terms of basin area, river length, torrential behavior, and flood genesis.
This comparative analysis was necessary because it was observed that although distributions with a high number of parameters theoretically satisfy the calibration requirements of the L-moments method, they can still produce significant differences, particularly at low probabilities of exceedance (p < 0.1%).
The results show that the WK5, BR4, and PG4 distributions are relatively stable, with the maximum relative error in estimating Q0.01% remaining within 20%. This finding highlights that even when using high-parameter distributions, uncertainties persist and must be carefully considered.
Considering the practical aspect of parameter estimation, where solving nonlinear equation systems is required, the WK5 distribution is recommended. This is because an accessible algorithm exists for approximating initial parameter values [6,7], which greatly facilitates the convergence of the nonlinear solution process.
Despite their advantages, high-parameter distributions remain sensitive to factors such as the type of distribution, the parameter estimation method, and the sample size. As the case studies illustrated, even under rigorous conditions, relative errors of up to ±20% can still occur when selecting the most suitable model.
Given that most historical data series in hydrology are of short to medium length, it is essential to evaluate not only the fit of the model but also its statistical behavior under these limitations, including an assessment of confidence intervals.
These considerations are particularly important because the predicted extreme values are often used beyond dam design—specifically, for establishing flood protection measures for local communities. Inaccurate quantile estimates can lead to over- or under-designing protective infrastructure, with serious economic and human safety consequences.
Finally, this study represents a part of a broader effort aimed at identifying the most appropriate statistical distributions and parameter estimation methods for the frequency analysis of maximum flows in Romania [33,57]. The findings will contribute to the development of new national guidelines, including the creation of open-source automated tools to support these analyses.
Although this study is based exclusively on Romanian rivers, the conclusions regarding the applicability and performance of different statistical distributions in estimating maximum discharges may also be relevant for other geographical regions, especially those with temperate climate regimes or similar continental influences. However, extrapolation should be performed with caution, taking into account local climatic, hydrological, and morphological characteristics. In regions with different rainfall regimes (such as tropical, arid, or mountainous areas), model validation might require specific adjustments or the selection of other distributions. In this regard, an important direction for future research will be the application of the methodologies tested here in river basins from other climatic regions, as well as in areas where hydrological data are limited or discontinuous, where robust and adaptive methods become essential for reliable risk estimation.
7. Future Research
Considering the impact of climate change on extreme hydrological events [54], future research will focus on non-stationary models in which distribution parameters evolve over time. The analysis will also be extended to additional river basins to validate the current findings and support the development of more broadly applicable recommendations. Another promising direction involves integrating statistical distributions with machine learning techniques and flow direction algorithms, in order to better capture the complex interactions between extreme events and their climatic drivers.
Author Contributions
Conceptualization, C.G.A. and D.I.; methodology, C.G.A. and D.I.; software, C.G.A. and D.I.; validation, C.G.A. and D.I.; formal analysis, C.G.A. and D.I.; investigation, C.G.A. and D.I.; resources, C.G.A. and D.I.; data curation, C.G.A. and D.I.; writing—original draft, C.G.A. and D.I.; writing—review and editing, C.G.A. and D.I.; visualization, C.G.A. and D.I.; supervision, C.G.A. and D.I.; project administration, C.G.A. and D.I.; funding acquisition, C.G.A. and D.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| FFA | flood frequency analysis |
| MOM | the method of ordinary moments |
| L-moments | the method of linear moments |
| expected value; arithmetic mean | |
| standard deviation | |
| coefficient of variation | |
| coefficient of skewness; skewness | |
| coefficient of kurtosis; kurtosis | |
| linear moments | |
| coefficient of variation based on the L-moments method | |
| coefficient of skewness based on the L-moments method | |
| coefficient of kurtosis based on the L-moments method |
References
- STAS 4273-83; Hydrotechnical Constructions, Classification in the Importance Class. The Romanian Standardization Institute: Bucharest, Romania, 1983.
- Popovici, A. Dams for Water Accumulations; Technical Publishing House: Bucharest, Romania, 2002; Volume 2. [Google Scholar]
- STAS 4068/2-87; Annual Probabilities of Maximum Flows and Volumes Under Normal and Special Operating Conditions. The Romanian Standardization Institute: Bucharest, Romania, 1987.
- ORDER no. 326; Methodology for the Delimitation of Minor Watercourses that Belong to the Public Domain of the State. Ministry of the Environment and Water Management: Bucharest, Romania, 2007.
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis; CRC Press LLC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability Weighted Moments: Definition and Relation to Parameters of Several Distributions Expressable in Inverse Form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Houghton, J.C. Birth of a parent: The Wakeby distribution for modeling flood flows. Water Resour. Res. 1978, 14, 1105–1109. [Google Scholar] [CrossRef]
- Sharwar, M.S.; Park, B.-J.; Jeong, B.-Y.; Park, J.-S. LH-Moments of Some Distributions Useful in Hydrology. Commun. Stat. Appl. Methods 2009, 16, 647–658. [Google Scholar]
- Hosking, J.R.M. L-moments: Analysis and Estimation of Distributions using Linear, Combinations of Order Statistics. J. R. Stat. Soc. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Wang, Q.J. LH moments for statistical analysis of extreme events. Water Resour. Res. 1997, 33, 2841–2848. [Google Scholar] [CrossRef]
- Gaume, E. Flood frequency analysis: The Bayesian choice. WIREs Water 2018, 5, e1290. [Google Scholar] [CrossRef]
- Bulletin 17B Guidelines for Determining Flood Flow Frequency; Hydrology Subcommittee; Interagency Advisory Committee on Water Data; U.S. Department of the Interior; U.S. Geological Survey; Office of Water Data Coordination: Reston, VA, USA, 1981. Available online: https://water.usgs.gov/osw/bulletin17b/dl_flow.pdf (accessed on 21 May 2025).
- Bulletin 17C Guidelines for Determining Flood Flow Frequency; U.S. Department of the Interior; U.S. Geological Survey: Reston, VA, USA, 2017.
- Meshgi, A.; Davar, K. Comprehensive evaluation of regional flood frequency analysis by L- and LH-moments. I. A re-visit to regional homogeneity. Stoch. Environ. Res. Risk Assess. 2009, 23, 119–135. [Google Scholar] [CrossRef]
- Nouri Gheidari, M.H. Comparisons of the L- and LH-moments in the selection of the best distribution for regional flood frequency analysis in Lake Urmia Basin. Civ. Eng. Environ. Syst. 2013, 30, 72–84. [Google Scholar] [CrossRef]
- Pearson, C.P. New Zealand Regional Flood Frequency Analysis Using L-Moments. J. Hydrol. 1991, 30, 53–64. Available online: https://www.jstor.org/stable/43944682 (accessed on 20 May 2025).
- Saf, B. Regional Flood Frequency Analysis Using L-Moments for the West Mediterranean Region of Turkey. Water Resour. Manag. 2009, 23, 531–551. [Google Scholar] [CrossRef]
- Noto, L.V.; La Loggia, G. Use of L-Moments Approach for Regional Flood Frequency Analysis in Sicily, Italy. Water Resour. Manag. 2009, 23, 2207–2229. [Google Scholar] [CrossRef]
- Kar, K.K.; Yang, S.K.; Lee, J.H.; Khadim, F.K. Regional frequency analysis for consecutive hour rainfall using L-moments approach in Jeju Island, Korea. Geoenviron. Disasters 2017, 4, 18. [Google Scholar] [CrossRef]
- Guttman, N.B. The Use of L-Moments in the Determination of Regional Precipitation Climates. J. Clim. 1993, 6, 2309–2325. [Google Scholar] [CrossRef]
- Guttman, N.B.; Hosking, J.R.M.; Wallis, J.R. Regional Precipitation Quantile Values for the Continental United States Computed from L-Moments. J. Clim. 1993, 6, 2326–2340. Available online: https://www.jstor.org/stable/26198616 (accessed on 20 May 2025). [CrossRef]
- Bora, D.J.; Borah, M.; Bhuyan, A. Regional analysis of maximum rainfall using L-moment and LH-moment: A comparative case study for the northeast India. Mausam 2017, 68, 451–462. [Google Scholar] [CrossRef]
- Khan, S.A.; Hussain, I.; Hussain, T.; Faisal, M.; Muhammad, Y.S.; Mohamd Shoukry, A. Regional Frequency Analysis of Extremes Precipitation Using L-Moments and Partial L-Moments. Adv. Meteorol. 2017, 6954902, 20. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Z.; Lai, C.; Lin, W.; Wu, X.; Chen, X. A regional frequency analysis of precipitation extremes in Mainland China with fuzzy c-means and L-moments approaches. Int. J. Climatol. 2017, 37, 429–444. [Google Scholar] [CrossRef]
- Lin, G.M.B.; Bonnin, D.L.; Martin, T.; Parzybok, M.; Yekta, D.R. Regional Frequency Studies of Annual Extreme Precipitation in the United States Based on Regional L-Moments Analysis. World Environ. Water Resour. Congr. 2006, 31, 1–11. [Google Scholar] [CrossRef]
- Chen, Y.D.; Huang, G.; Shao, Q.; Xu, C.Y. Regional analysis of low flow using L-moments for Dongjiang basin, South China. Hydrol. Sci. J. 2006, 51, 1051–1064. [Google Scholar] [CrossRef]
- Modarres, R. Regional Frequency Distribution Type of Low Flow in North of Iran by L-moments. Water Resour. Manag. 2008, 22, 823–841. [Google Scholar] [CrossRef]
- Dodangeh, E.; Soltani, S.; Sarhadi, A.; Shiau, J.-T. Application of L-moments and Bayesian inference for low-flow regionalization in Sefidroud basin, Iran. Hydrol. Process. 2014, 28, 1663–1676. [Google Scholar] [CrossRef]
- Shi, P.; Chen, X.; Qu, S.M.; Zhang, Z.C.; Ma, J.L. Regional Frequency Analysis of Low Flow Based on L Moments: Case Study in Karst Area, Southwest China. J. Hydrol. Eng. 2010, 15, 370–377. [Google Scholar] [CrossRef]
- Ahmad, I.; Yasin, M.; Fawad, M.; Saghir, A. Regional Frequency Analysis of Low Flows Using L. Moments for Indus Basin, in Pakistan. Pak. J. Sci. 2017, 69, 75–84. [Google Scholar]
- Sarhadi, A.; Soltani, S.; Modarres, R. Regional low flow frequency distribution in Jiroft area by L-moments. Iran. Water Res. J. 2008, 2, 45–54. [Google Scholar]
- Anghel, C.G. Revisiting the Use of the Gumbel Distribution: A Comprehensive Statistical Analysis Regarding Modeling Extremes and Rare Events. Mathematics 2024, 12, 2466. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy—Based Parameter Estimation in Hydrology; Springer Science & Business Media: Dordrecht, The Netherlands, 1998; ISBN 978-90-481-5089-2/978-94-017-1431-0 (eBook). [Google Scholar] [CrossRef]
- Rahman, A.; Zaman, M.A.; Haddad, K.; El Adlouni, S.; Zhang, C. Applicability of Wakeby distribution in flood frequency analysis: A case study for eastern Australia. Hydrol. Process. 2015, 29, 602–614. [Google Scholar] [CrossRef]
- Seckin, N.; Haktanir, T.; Yurtal, R. Flood frequency analysis of Turkey using L-moments method. Hydrol. Process. 2011, 25, 3499–3505. [Google Scholar] [CrossRef]
- Haktanir, T.; Horlacher, H.B. Evaluation of various distributions for flood frequency analysis. Hydrol. Sci. J. 1993, 38, 15–32. [Google Scholar] [CrossRef]
- Wiltshire, S.E. Regional flood frequency analysis I: Homogeneity statistics. Hydrol. Sci. J. 1986, 31, 321–333. [Google Scholar] [CrossRef]
- Griffiths, G.A. A theoretically based Wakeby distribution for annual flood series. Hydrol. Sci. J. 1989, 34, 231–248. [Google Scholar] [CrossRef]
- Neslihan, S.; Recep, Y.; Tefaruk, H.; Ahmet, D. Comparison of Probability Weighted Moments and Maximum Likelihood Methods Used in Flood Frequency Analysis for Ceyhan River Basin. Arab. J. Sci. Eng. 2010, 35, 49–69. [Google Scholar][Green Version]
- Wang, W.; Gui, W. Estimation and Bayesian Prediction for the Generalized Exponential Distribution Under Type-II Censoring. Symmetry 2025, 17, 222. [Google Scholar] [CrossRef]
- Alotaibi, N.; Al-Moisheer, A.S.; Elbatal, I.; Shrahili, M.; Elgarhy, M.; Almetwally, E.M. Bayesian and Non-Bayesian Estimation for a New Extension of Power Topp–Leone Distribution under Ranked Set Sampling with Applications. Axioms 2023, 12, 722. [Google Scholar] [CrossRef]
- Haddad, K. A Comprehensive Review and Application of Bayesian Methods in Hydrological Modelling: Past, Present, and Future Directions. Water 2025, 17, 1095. [Google Scholar] [CrossRef]
- Song, S.; Song, X.; Kang, Y. Entropy-Based Parameter Estimation for the Four-Parameter Exponential Gamma Distribution. Entropy 2017, 19, 189. [Google Scholar] [CrossRef]
- Machiwal, D.; Jha, M. Hydrologic Time Series Analysis: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lang, T.B.M.J.M.; Ouarda, B.B. Towards operational guidelines for over-threshold modeling. J. Hydrol. 1999, 225, 103–117. [Google Scholar] [CrossRef]
- Crooks, G.E. Field Guide to Continuous Probability Distributions; Berkeley Institute for Theoretical Science: Berkeley, CA, USA, 2019. [Google Scholar]
- Bîrsan, M.V. The Variability of the Natural Flow Regime of Rivers in Romania; Ars Docendi Publishing House: Bucharest, Romania, 2017. [Google Scholar]
- Ministry of the Environment. The Romanian Water Classification Atlas, Part I—Morpho−Hydrographic Data on the Surface Hydrographic Network; Ministry of the Environment: Bucharest, Romania, 1992. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill, Inc.: New York, NY, USA, 1988; ISBN 007-010810-2. [Google Scholar]
- Singh, K.; Singh, V.P. Parameter Estimation for Log-Pearson Type III Distribution by Pome. J. Hydraul. Eng. 1988, 114, 112–122. [Google Scholar] [CrossRef]
- Elahi, E.; Li, G.; Han, X.; Zhu, W.; Liu, Y.; Cheng, A.; Yang, Y. Decoupling livestock and poultry pollution emissions from industrial development: A step towards reducing environmental emissions. J. Environ. Manag. 2024, 350, 119654. [Google Scholar] [CrossRef]
- Elahi, E.; Khalid, Z.; Zhang, Z. Understanding farmers’ intention and willingness to install renewable energy technology: A solution to reduce the environmental emissions of agriculture. Appl. Energy 2022, 309, 118459. [Google Scholar] [CrossRef]
- Abbas, A.; Mushtaq, Z.; Ikram, A.; Yousaf, K.; Zhao, C. Assessing the factors of economic and environmental inefficiency of sunflower production in Pakistan: An epsilon-based measure model. Front. Environ. Sci. 2023, 11, 2023. [Google Scholar] [CrossRef]
- Abbas, A.; Zhao, C.; Ullah, W.; Ahmad, R.; Waseem, M.; Zhu, J. Towards Sustainable Farm Production System: A Case Study of Corn Farming. Sustainability 2021, 13, 9243. [Google Scholar] [CrossRef]
- Sargentis, F.G.; Ioannidis, R.; Kougia, M.; Benekos, I.; Iliopoulou, T.; Dimitriadis, P.; Koukouvinos, A.; Dimitrakopoulou, D.; Mamassis, N.; Tsouni, A.; et al. Do Floods Attack Cities or Cities Invade Flood Plains? Case Study: Athens, Greece. In Proceedings of the International Conferences on Digital Technology Driven Engineering 2024, OPT-ii 2024, Amman, Jordan, 1–4 October 2024; Lagaros, N.D., Alrousan, R.Z., Abdalla, K.M., Phocas, M.C., Marano, G.C., Eds.; Lecture Notes in Civil Engineering. Springer: Cham, The Netherlands, 2025; Volume 647. [Google Scholar] [CrossRef]
- Anghel, C.-G.; Ianculescu, D. An In-Depth Statistical Analysis of the Pearson Type III Distribution Behavior in Modeling Extreme and Rare Events. Water 2025, 17, 1539. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).