Abstract
The non-Darcy seepage characteristics of broken rock mass is important for analyzing the seepage and stability of rock and soil mass. At present, the research on non-Darcy seepage models considering hydraulic conditions and medium void structures has considerable room for improvement. In this study, non-Darcy seepage tests were conducted on broken rock mass under the influence of different hydraulic pressures, sample gradations, and porosities. The influence of sample gradation and porosity on the linear and nonlinear term coefficients of Forchheimer’s law, the critical criterion of non-Darcy seepage, and the seepage flow regime was clarified. The influence of hydraulic gradient on the value of traditional hydraulic conductivity was revealed. A non-Darcy equivalent hydraulic conductivity, which changed with pressure gradient, was defined, then Forchheimer’s law and Darcy’s law were modified. Results showed that the relationship between pressure gradient and flow rate highly obeyed Forchheimer’s law. The minimum value of Forchheimer number was 9.4 times the critical value. Owing to the influence of inertial force and variable seepage channels, the linear and nonlinear term coefficients of Forchheimer’s law decreased while the Forchheimer number increased with the increase of pressure gradient, sample gradation, and porosity. With high hydraulic gradient, the non-Darcy equivalent hydraulic conductivity decreased nonlinearly, causing Darcy’s law to overestimate the seepage flow in this study by 2.47–13.40 times. Finally, Forchheimer’s law and Darcy’s law were modified to consider the influence of hydraulic gradient, sample gradation, and porosity. The modified Darcy’s law does not require the determination of the seepage flow regime and can accommodate the mutual transformation and coexistence between Darcy and non-Darcy seepage.
1. Introduction
Broken rock mass with large particles, pore sizes, and permeability widely exists in geological structures such as fault zones, fracture zones, and dislocation zones, and can be regarded as a porous medium [1,2,3,4]. Compared with intact rock mass, broken rock mass possesses larger porosity and loose clastic sediments that dominate the seepage channels for fluid flow [5,6,7,8]. The pores and channels of broken rock mass provide substantial storage space to facilitate the disposal of hazardous wastes, including nuclear waste, carbon dioxide, and wastewater [9,10,11,12]. However, the pores and channels are prone to causing water inrush disasters and landslide accidents during the construction of underground engineering projects and exploitation of coal, oil, and natural gas [13,14,15,16,17,18]. Exploring and revealing the mechanisms of fault permeability characteristics are fundamental for the disposal of hazardous waste, the construction of underground engineering, and the exploitation of natural resources.
The behavior of laminar single-phase fluid flow under an isothermal condition and constant fluid viscosity transport in a porous medium without solid–fluid interaction can be governed by Darcy’s law [19]. Darcy’s law describes the behavior of one-dimensional fluid flow as follows [20]:
where Q is the flow rate, A is the area of flow section, K is the hydraulic conductivity, ΔH is the hydraulic head loss, L is the seepage path, and i = ΔH/L is the hydraulic gradient.
For a porous medium, hydraulic conductivity is used to evaluate the flow efficiency of a fluid when passing through the pore framework and can be expressed as [21]:
where K is the permeability of porous medium, ρw is the water density, g is the gravitational acceleration, and μ is the fluid dynamic viscosity coefficient.
In Equation (2), k is only affected by the porous structure of particles and a porous medium, whereas μ is only determined by fluid temperature. Thus, the hydraulic conductivity of a porous medium at a constant altitude remains constant without changes in fluid density, temperature, and the porous structure of the medium. The flow rate of fluid transport in porous medium increases linearly with the increase in hydraulic gradient according to Darcy’s law.
However, abundant evidence shows that for the porous medium with large permeability, Darcy’s law has a very limited range of applicability [19], especially with high hydraulic pressure conditions, where the flow rate increases less than proportionally with unit hydraulic gradient, and the flow regime can be described as the post-Darcy flow. Darcy’s law is no longer applicable for the post-Darcy flow [22,23,24,25,26]. The Reynolds number is usually used to distinguish Darcy flow from non-Darcy flow, and when it is greater than a critical value, the flow state can be considered as a non-Darcy flow. This critical value ranges from 0.001 to 25 or 0.002 to 2.79 [27,28]. However, there is no universally accepted value for the critical Reynolds number [29].
After tests and numerical investigations, the possible reasons for post-Darcy flow in a porous medium can be summarized as the complex particle and porous structure of the medium and high hydraulic pressure [23,24,30,31]. The linear Darcy’s law is simplified from the Navier–Stokes equations and neglects the only nonlinear term, which is the inertia force. When fluid flow is driven by high hydraulic pressure or when the particle and porous structure of a porous medium is complex, the effect of the inertia force of turbulent fluid flow is worthy of attention [23,26,31]. With the consideration of inertia force, some nonlinear seepage models, including the famous Forchheimer’s law and Izbash’s law, are widely applied in porous and fractured media, which can describe the nonlinear relationship between flow rate and pressure gradient and determine whether fluid flow is in a nonlinear state [8,10,31,32]. Both Forchheimer’s law and Izbash’s law are established from a macro perspective. The non-Darcy coefficient β of Forchheimer’s law and regression coefficients m, λ of Izbash’s law are empirical coefficients, which are usually confirmed by laboratory or field tests [1,2,25,26,33]. Furthermore, the Kozeny–Carman (K-C) equation is a classical semi-empirical formula for describing the permeability of porous media, which is widely used for predicting the fluid permeability of soils, rocks, and engineering materials [34]. Its core idea is based on hydraulic radius theory, which relates permeability to pore structure parameters [35]. Some comprehensive seepage models for pre-Darcy, Darcy, and post-Darcy flow are available [36,37,38]. The core of these models is switching the internal algorithm according to the flow regime and porous structure with a transition point [24,36,37].
In addition, after theoretical analysis or tests, Darcy’s law can be modified to a nonlinear form. In a single fracture, cubic law (another form of Darcy’s law) is usually modified with morphology characteristics of fracture (including roughness, contact area, tortuosity, spatial correlation, anisotropy, etc.) and hydraulic pressure (or hydraulic gradient, Reynolds number) by establishing the relationship between hydraulic and mechanical aperture. According to cubic law, the hydraulic conductivity of fracture is the proportion square of aperture; thus, after modifying the value of fracture, hydraulic conductivity is affected by hydraulic pressure [10,39,40,41,42]. This phenomenon also occurs on fault water injection tests [8]. For a porous medium, the form of Darcy’s law is simple and clearly shows the relationship among flow rate, area of flow section, hydraulic conductivity, and hydraulic gradient with a strict theoretical basis. Darcy’s law is convenient to apply and serves as the theoretical basis for most seepage analysis. A feasible basis exists for modifying the hydraulic conductivity value to avoid the errors caused by applying Darcy’s law to post-Darcy flow.
In this study, non-Darcy seepage tests of broken rock mass were carried out with different hydraulic pressures, sample gradations, and porosities. The relationship between flow rate and pressure gradient was analyzed using Forchheimer’s law. The changes in the linear and nonlinear term coefficients of Forchheimer’s law, Forchheimer number, and flow regime were revealed. The influence of hydraulic gradient on the value of traditional hydraulic conductivity was clarified and the non-Darcy equivalent hydraulic conductivity, which changed with the pressure gradient, was defined. Lastly, Forchheimer’s law and Darcy’s law were modified.
2. Tests
2.1. Test Equipment
The test equipment in this study was composed of a WAW-1000 microcomputer controlled electro-hydraulic servo universal testing machine and a self-developed seepage test system. The test equipment is shown in Figure 1. The main body of the seepage system consisted of the cylindrical sample container, catchment funnel, and pedestal from top to bottom. The American Society for Testing and Materials (ASTM) considered that the maximum particle size should not exceed one third of the cylinder diameter of the specimen [43]; in order to weaken the influence of size effect, the previous studies suggested that the cylinder diameter should be set to the maximum particle size five times [44,45]. In this study, the maximum particle size of the broken rock mass was 20 mm, so the inner diameter of the cylindrical sample container was 100 mm. The cylindrical sample container from top to bottom was the loading bucket (Figure 1b h7 section), water injection plate (Figure 1b h4 section), permeable plate (Figure 1b h3, h2 section), and broken rock mass (Figure 1b hs section). The outer diameter of the loading bucket was 100 mm (Figure 1c, same as the red part of Figure 1b), which directly contacted with the loading shaft in the normal pressure system to transfer the normal force to the broken rock mass. The diameter of the water injection plate was 100 mm (Figure 1d, same as the blue part of Figure 1b). Six plum-shaped water injection holes with a diameter of 6 mm were connected to the water inlet pipe so that the water flow evenly passed through the broken rock mass. An O-shaped rubber ring existed between the water injection plate and the cylindrical sample container, and a rubber gasket was arranged between the filler bucket and the water collecting funnel to ensure sealing. The diameter of the permeable plate was 100 mm (Figure 1e, same as the green part of Figure 1b), and the small hole filter stone with a diameter of 2 mm was evenly arranged to pass water. The permeable plate was placed at the top and bottom of the broken rock mass. The seepage flow was measured by an electronic flow meter.
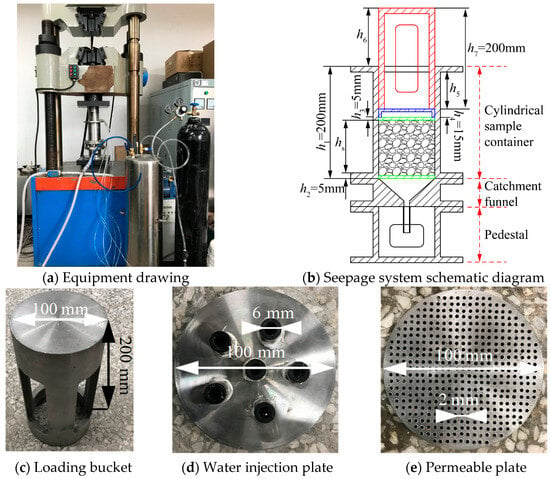
Figure 1.
Seepage test equipment for broken rock mass.
2.2. Sample Preparations
The sandstone sample in this study was taken from the fault of the Sanhekou underground tunnel in Hanzhong, China, whose natural density is 2511 kg/m3. The sandstone was broken into particles less than 25 mm. Using a sieve, the particles were screened to specified sizes: 2.5–5 mm, 5–8 mm, 8–10 mm, 10–12 mm, 12–15 mm, and 15–20 mm. The sandstone particles with different sizes were distributed by a continuous grading method. Talbot [46] proposed the widely used continuous grading method as follows:
where d is the identified rock particle size, D is the largest rock particle size, M is the rock particle mass with size less than or equal to d, Mt is the rock particle total mass, and η is the Talbot index.
In this study, the total mass of the sandstone particles was 1200 g. In order to obtain a comprehensive gradation distribution and extend the application of the results of this study. Based on the results of field investigation and the setting of similar test conditions by Ma et al. [18], the sandstone particles were configured with η = 0.2, 0.4, 0.6, 0.8, and 1. According to Equation (3), Table 1 lists the sandstone particle mass for different size intervals. The particle size distribution curve with different η is shown in Figure 2, and the sandstone particles with different η are shown in Figure 3.

Table 1.
Sandstone particle masses of different size intervals with different η values.
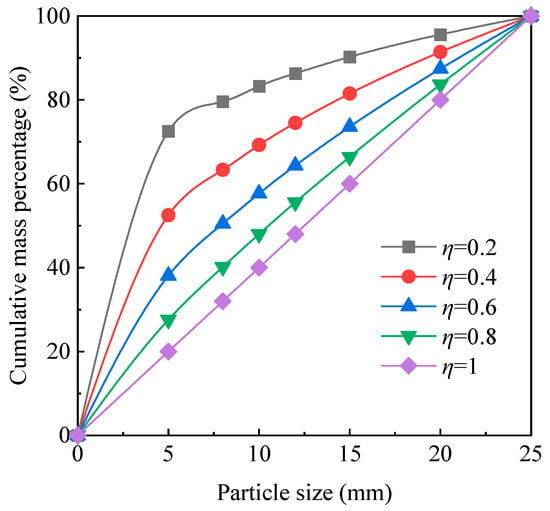
Figure 2.
Particle size distribution curves with different η values.

Figure 3.
Sandstone particles with different η values: (a) η = 0.2; (b) η = 0.4; (c) η = 0.6; (d) η = 0.8; (e) η = 1.
In this study, the confined compression of the sample was carried out by applying the normal force. The height and volume of the sample were adjusted and the porosity of the sample was controlled based on the following equation:
where φ is the porosity of the broken rock mass sample, dimensionless; Vo is the volume of the sample in the barrel in the natural state; vs. is the original rock volume of the same mass sample; ms is the sample mass; ρs is the original rock density of the sample; and r is the radius of the barrel.
For the test equipment in this study, as shown in Figure 1b, the hs calculation equation in Equation (4) is as follows:
The h6 value of the sample used in this study was 133.5 mm in the uncompacted state and 119.5 mm in the ultimate compression state, this means that for the fault broken rock mass selected in this study, the limit range of sample height was 119.5 mm to 133.5 mm. In order to obtain a comprehensive porosity value and extend the application of the results of this study, the h6 values were controlled to 132.0 mm, 129.0 mm, 126.0 mm, 123.0 mm, and 120 mm. The corresponding sample heights were 107 mm, 104 mm, 101 mm, 98 mm, and 95 mm, and the values of φ were 0.431, 0.415, 0.397, 0.379, and 0.359, respectively.
2.3. Test Procedures
The average water depth in front of the dam of Sanhekou reservoir is about 130 m. Considering the effect of different water levels, the inlet water pressures were 0.25 MPa, 0.5 MPa, 0.75 MPa, 1 MPa, and 1.25 MPa, and the outlet pressures were atmospheric pressure. Considering the influence of porosity, gradation, and hydraulic pressure, 125 groups of comparative tests were carried out. During the test, the configured sample was first immersed in water for 12 h to reach a saturation state; the sample was then stirred evenly and poured into the cylindrical sample container. After the equipment was assembled, the sample was compressed to the set height. Water was subsequently supplied until the effluent flow became stable. During the test, when the design height of the sample changed, additional filler was added. To reduce the test error, the average value of the test results was taken after triplicate runs tests in each group. There was no mass loss during the tests, and the flow rate was recorded when the outflow flow was stable for more than 10 min.
3. Results
3.1. Forchheimer’s Law
Forchheimer’s law holds that a nonlinear relationship exists between seepage flow and pressure gradient in seepage process. Its mathematical form is as follows:
where − is the pressure gradient, Q is the seepage flow, A is the coefficient of linear term, B is the coefficient of nonlinear term, μ is the coefficient of dynamic viscosity, k is the medium permeability, As is the flow area, and β is the non-Darcy seepage coefficient.
Forchheimer’s law is simplified from the Navier–Stokes equation and consists of a linear term AQ and a nonlinear term BQ2, where the nonlinear term takes into account the inertial force of water flow. When the BQ2 term is neglected, Equation (6) degenerates to Darcy’s law. In Forchheimer’s law, β represents the degree of deviation of non-Darcy flow from Darcy’s law, which is related to the porous structure of the medium. It is usually determined by test and inverse calculation of Equation (6).
Before applying Forchheimer’s law, the flow regime must be determined. The Reynolds number (Re) is often used to determine the fluid flow regime, which is expressed as the ratio of the inertial force to the viscous force of the water flow. When the Re value is greater than a critical value, non-Darcy flow occurs. However, for media such as broken rock mass, the characteristic length of the seepage channels is difficult to obtain when calculating the Re. In this regard, Ma and Ruth [47] defined the Forchheimer number to determine the seepage flow regime. Its physical meaning is consistent with Re, and its form of expression is as follows:
where Fo is the Forchheimer number.
Non-Darcy flow occurs when Fo is greater than the critical Forchheimer number (Foc). Foc can be calculated with the following equation:
where E is the non-Darcy influence coefficient, when E = 10%, it is the critical point of Darcy and non-Darcy seepage, and the corresponding Foc value is 0.11.
3.2. Relationship Between Flow Rate and Hydraulic Gradient
The relationship between the pressure gradient and seepage flow under different schemes is shown in Figure 4. In this study, the top-down seepage mode is adopted. The data in Figure 4 eliminate the influence of gravity on seepage flow, so the starting point of the curve is the origin of the coordinates and conforms to the mathematical form of Forchheimer’s law. The R2 range of the fitting results in Figure 4 is 0.9965–0.9994. The test results are highly consistent with Forchheimer’s law and conform to non-Darcy seepage. With the increase of pressure gradient, the increase of seepage flow decreases continuously. This result proves that the larger the pressure gradient, the more significant the non-Darcy seepage effect of broken rock mass. In addition, Figure 4 shows that the larger the values of η and φ, the stronger the flow capacity of the sample, and the greater the flow rate.
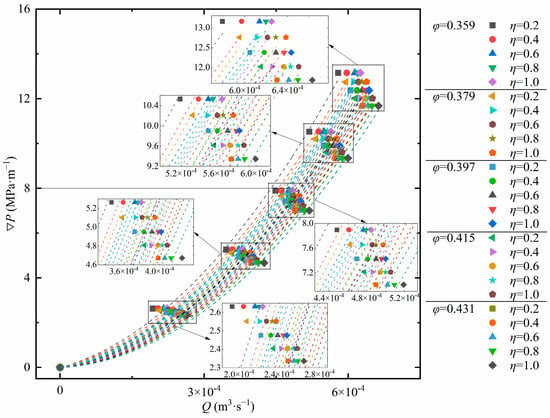
Figure 4.
Relationship between pressure gradient and flow rate with the influence of φ and η.
3.3. Results of Coefficients A and B of Forchheimer’s Law
Based on Figure 4, the numerical results of Forchheimer’s law A and B are shown in Figure 5. The larger values of η and φ mean that the porosity of the sample is larger and the flow capacity is stronger. From the mathematical form of Equation (6), when − is fixed, the larger the Q value, the smaller the A and B values. Therefore, the test results show that the coefficients A and B of Forchheimer’s law decrease nonlinearly with the increase of η and φ. This finding is consistent with the results of Moutsopoulos [48] and Mohammad and Salehi [49]. At the same time, the independent changes in η and φ have a significant effect on the values of coefficients A and B. The results show that for broken rock mass, the influence of particle size distribution and porosity should be considered when determining the A and B coefficients of Forchheimer’s law.
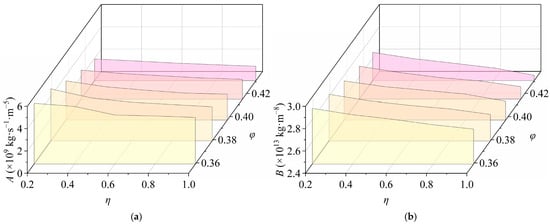
Figure 5.
Results of the coefficients of Forchheimer’s law with the influence of φ and η: (a) coefficient A; (b) coefficient B.
3.4. Nonlinear Seepage Regime Determination with Fo
Based on Equations (7) and (8), the Fo calculation results when sample gradation and porosity change are shown in Figure 6. The minimum value of Fo in the 125 groups of tests conducted in this study is 1.03, which is greater than Foc. This outcome is consistent with the conclusion of Figure 4 and the seepage process is non-Darcy seepage. In addition, the Fo values show a significant positive correlation with −, η, and φ. From the previous analysis, −, η, and φ are the key factors leading to the increase of seepage flow and seepage velocity. The inertial force is proportional to the square of the velocity and the viscous force is proportional to the first square of the velocity. When the flow velocity increases, the increase of inertia force is greater than the increase of viscous force and the Fo increases. According to Forchheimer’s law, the increase in seepage flow has a more significant impact on the BQ2 term, causing the seepage process to deviate further from Darcy seepage. In addition to the influence of flow velocity, the larger η and φ values mean that the size of broken rock mass pores is larger, and more dominant leakage channels are formed. Owing to the influence of different pores sizes, the leakage channels exhibit multiple sections with varying diameters. In areas where the diameter decreases, backflow vortexes easily form, leading to flow irregularities. Moreover, the local water head loss is obvious when the water flows through the sudden expansion and contraction sections. Consequently, the critical point for non-Darcy seepage decreases.
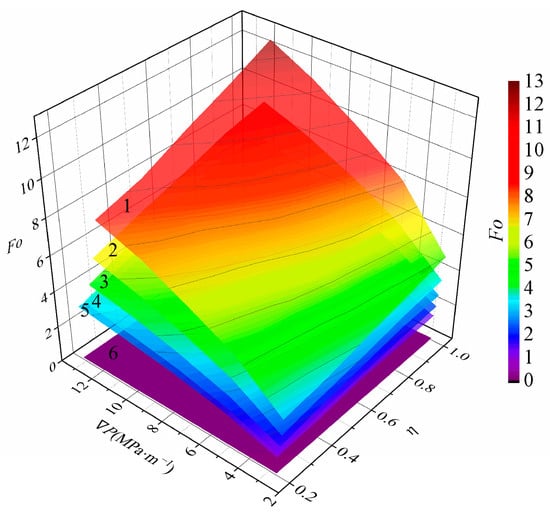
Figure 6.
Distribution of Fo with different , η, and φ.
3.5. Results of Non-Darcy Equivalent Hydraulic Conductivity
From Equation (2) and the assumptions of Darcy’s law, the hydraulic conductivity for Darcy seepage is a constant value. However, for incompressible single laminar flow, its value is only related to the properties of the permeating medium itself. For non-Darcy seepage in this study, the relationship curve between K and i is shown in Figure 7. When η and φ are larger, the conveyance capacity of broken rock mass pores is stronger and the hydraulic conductivity is larger. This finding is consistent with the above results and Equation (2). When η and φ are fixed, the hydraulic conductivity decreases nonlinearly when i increases and tends to stabilize when i increases indefinitely. This phenomenon violates the traditional definition of hydraulic conductivity. For non-Darcy seepage, the combined effect of the characteristics of the medium and the seepage characteristics should be considered when determining the hydraulic conductivity. The traditional hydraulic conductivity overestimates the flow capacity of the medium when non-Darcy seepage occurs. By contrast, the hydraulic conductivity, which varies with i in Figure 7, is defined in this study as the non-Darcy equivalent hydraulic conductivity (Kn-d).
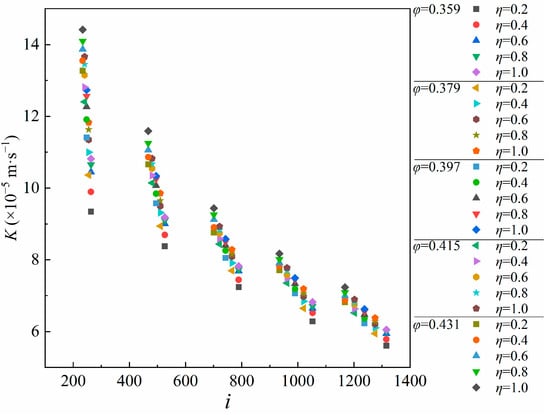
Figure 7.
Relationship between hydraulic conductivity and hydraulic gradient with the influence of φ and η.
4. Modified Non-Darcy Seepage Model
4.1. Modified Forchheimer’s Law
Equation (6) indicates that the values of A and B coefficients in Forchheimer’s law are related to k and β. Based on Kozeny–Carman (K-C) equation [34] and the relation between k and K, the following relationship can be obtained:
where τ is the tortuosity of porous structure and Ao is the specific surface area of solid particles.
In practical engineering, parameters τ and Ao are difficult to obtain. In this study, the relationship between k and φ3/(1 − φ)2 and the relationship between 1/(2τAo) and η are shown in Figure 8. The changes in β with η and φ are shown in Figure 9. Through the nonlinear fitting of the relationship curves in Figure 8 and Figure 9, combined with multivariate nonlinear regression analysis, the calculation model of k and β is obtained as follows, which has been validated in the relevant literature [44]:
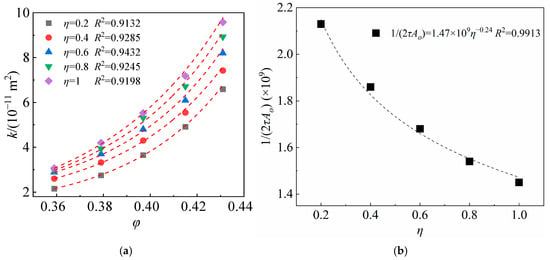
Figure 8.
Results of k with changed η and φ: (a) relationship between k and η; (b) relationship between k and φ.
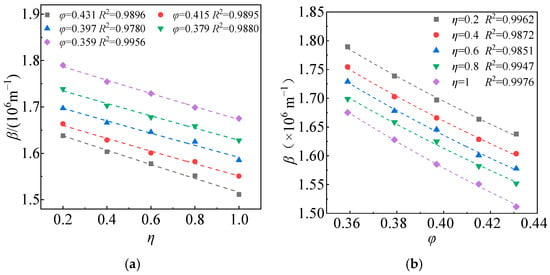
Figure 9.
Results of β with changed η and φ: (a) relationship between β and η; (b) relationship between β and φ.
By substituting Equations (10) and (11) into Equation (6), the calculation model of A and B coefficients can be obtained.
The modified Forchheimer’s law can be obtained by combining Equations (12) and (6). The modified model in this study takes into account the effects of grading and porosity of broken rock mass pores.
4.2. Modified Darcy’s Law
Although Darcy’s law cannot be adapted to non-Darcy seepage, its mathematical form is simple. The physical meaning of each parameter is clear and it serves as an important basis for most seepage analysis theories. Taking the test results η = 0.2 and φ = 0.431 as an example, as shown in Figure 10, the curve is divided into an infinite number of straight line segments on the basis of differentiation. Segmentation regression analysis is then carried out. The relationship between the pressure gradient and the flow rate of each straight line segment is considered to satisfy Darcy’s law, where the slope of the straight line segment represents the correlation function of the hydraulic conductivity. To ensure accuracy, the length of the line segment is assumed to be infinitely small and the slope of the line segment is the tangent slope on each point of the curve in Figure 10. At this time, the values of Kn-d under different seepage pressures can be obtained so that the segmented Darcy’s law can satisfy the non-Darcy seepage analysis [50].
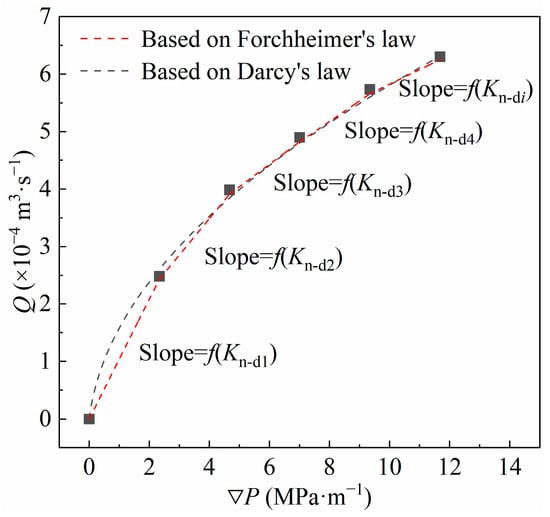
Figure 10.
Comparison between Forchheimer’s law and segmented Darcy’s law.
When Darcy seepage occurs, K can be calculated by Equations (2) and (9) for the test in this study. The relationship curve between K/Kn-d and J is shown in Figure 11. The value of K/Kn-d ranges from 2.47 to 13.40 and increases linearly with the increase of i. The larger the K/Kn-d, the greater the error of Darcy’s law.
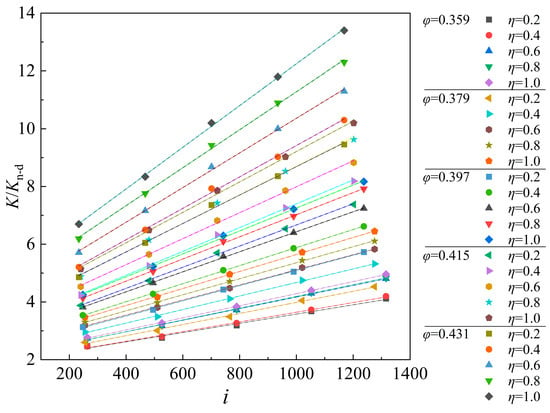
Figure 11.
Relationship between K/Kn-d and i.
Through the linear regression analysis of the relationship curve in Figure 11, the following relationship can be obtained, where R2 ranges from 0.9904 to 0.9997:
where a and b are regression coefficients.
The values of a and b in Equation (14) are related to samples η and φ and their relationships are shown in Figure 12. After the multiple regression analysis of the data in Figure 12, the calculation model of a and
b in Equation (14) can be obtained as follows:
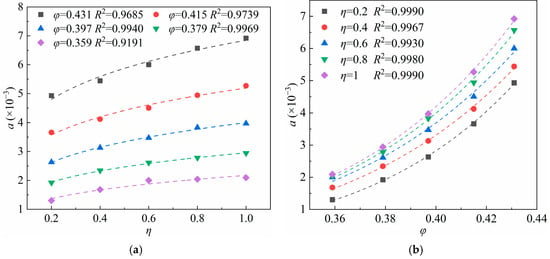
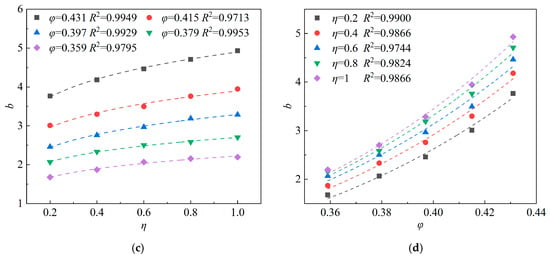
Figure 12.
Variation of a and b of Equation (12) with changed φ and η; (a) relationship between a and η; (b) relationship between a and φ; (c) relationship between b and η; (d) relationship between b and φ.
On the basis of Equations (13), (14), and (1), the modified Darcy’s law model can be obtained as follows:
Equation (14) indicates that the corrected mathematical form of Darcy’s law remains unchanged and the relationship between Q and i is no longer linear. When the value of i is small in the study area, that of K/Kn-d will approach 1 when Darcy seepage occurs, eliminating the need to judge the convection state. Equation (14) can automatically convert the value of Kn-d according to hydraulic conditions and medium characteristics, enabling it to handle the coexistence or conversion of Darcy and non-Darcy seepage in the study area.
4.3. Verification and Limitations Remarks
In order to validate the proposed non-Darcy and modified Forchheimer’s laws, independent test was conducted with η = 0.5, φ = 0.391 (ls = 125 mm), inlet water pressure was 0.8 MPa. The measured flow rate was 5.03 × 10−4 m3∙s−1. According to Equations (11) and (14), the flow rate calculated by the proposed non-Darcy and modified Forchheimer’s laws were 5.19 × 10−4 m3∙s−1 and 5.23 × 10−4 m3∙s−1 and the relative errors were 3.2% and 3.8%.
Despite the meticulous care we have taken, the following limitations were unavoidable in our study. In this study, the porous structure was reflected by macroscopic parameters such as η and φ and the seepage process was unobservable. The effect of pore throat morphology, pores size, and seepage channels morphology on seepage regime cannot be studied. For example, for multiple sets of specimens with the same η and φ, the meso-pore parameters may vary greatly. Therefore, transparent rock-soil mass, CT scanning technology, CFD-DEM coupling model, and other visual test methods are encouraged. The microscopic parameter measurement equipment for pore structure needs to be developed and improved. In addition, the seepage-stress coupling, long-term seepage, factors coupling and dynamically changing, and mass-loss are common in rock-soil mass, which is means it is easy to make dynamic changes in pore structure and lead to more complicated seepage process. Thus, seepage-stress coupling and mass-loss tests under different conditions are encouraged.
5. Conclusions
In this study, non-Darcy seepage tests are carried out with broken rock mass pores as the research object, revealing the influence of water pressure, sample grading, and porosity on its non-Darcy seepage characteristics and the critical criterion of the flow regime. Forchheimer’s law and Darcy’s law are modified and the main conclusions are as follows:
(1) The test results in this study are highly consistent with Forchheimer’s law. Considering the influence of η and φ, the equations for calculating A and B coefficients are established, and Forchheimer’s law is modified. Owing to the influence of hydrodynamic inertia force and variable diameter seepage channels, the values of A and B coefficients of Forchheimer’s law decrease with the increase of η and φ. The non-Darcy seepage phenomena of water pressure, η, and φ become more significant. For η = 0.2–1, φ = 0.359–0.431 broken rock mass pores, the minimum Fo value is 1.03, which is much higher than the critical value. When Darcy’s law is used to evaluate the flow capacity of the sample in this study, the seepage quantity is overestimated by 2.47–13.40 times.
(2) Only when i changes, the traditional hydraulic conductivity in the non-Darcy seepage process varies. The Kn-d proposed in this study can reflect the influence of hydraulic gradient on the flow capacity of broken rock mass pores. It decreases in a nonlinear trend with the increase of i. In addition, considering the influence of i, η, and φ, the calculation equation for the value of K/Kn-d is established and Darcy’s law is modified. The modified Darcy’s law can adapt to the coexistence or conversion of Darcy and non-Darcy seepage in the study area without judging the flow regime.
(3) The loss of filling fine particles is not considered in this test, and η and φ of the sample are fixed. When the infiltration fails, the void structure inside the broken rock mass pores will undergo a dynamic change, which complicates the seepage flow regime. The non-Darcy seepage model without considering the change of time will not be applicable. The construction of a non-Darcy seepage model considering the process and timing of filling particle loss is the focus of future research.
Author Contributions
C.C.: conceptualization, methodology, validation, writing—original draft, writing—review and editing, project administration, funding acquisition. Z.Z.: methodology, validation, writing—original draft, writing—review and editing, project administration. Z.X.: formal analysis, investigation, software, supervision. J.C.: data curation, project administration, visualization. Y.S.: data curation, investigation. N.L.: data curation, methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This study received financial support from the National Natural Science Foundation of China (52209167), Scientific Research Program Funded by Shaanxi Provincial Education Department (24JP124), and China Postdoctoral Science Foundation (2023MD744254).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xiao-Lei, L.; Xin-Lei, L.; Yue, W.; Wei-Hang, P.; Xuan, F.; Zheng-Zheng, C.; Rui-Fu, L.; Xin, L. The Seepage Evolution Mechanism of Variable Mass of Broken Rock in Karst Collapse Column under the Influence of Mining Stress. Geofluids 2023, 2023, 7256937. [Google Scholar] [CrossRef]
- Xian, M.; Xu, Z.; Chen, B. Numerical investigation of variable-mass seepage mechanism of broken rock mass in faults. Comput. Geotech. 2023, 160, 105527. [Google Scholar] [CrossRef]
- Kan, Z.; Zhang, L.; Li, M.; Yuan, X.; Huang, M.; Sracek, O. Investigation of Seepage Law in Broken Coal and Rock Mass under Different Loading and Unloading Cycles. Geofluids 2021, 2021, 8127250. [Google Scholar] [CrossRef]
- Hao, D.Y.; Tu, S.H.; Zhang, L.; Zhao, H.B.; Xu, S.K. Experimental study on characteristics of gas seepage in broken coal and rock. Energy Sci. Eng. 2024, 12, 4737–4752. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Y.; Zhu, X.; Li, P.; Cao, Z.; Yang, H.; Ma, D. Mechanical Constitutive and Seepage Theoretical Model of Water Storage Media Based on Fractional Derivative. Geofluids 2022, 2022, 8553646. [Google Scholar] [CrossRef]
- Cao, Z.; Xie, Q.; Xu, X.; Sun, W.; Fumagalli, A.; Fu, X. Mass-loss effects on the non-Darcy seepage characteristics of broken rock mass with different clay contents. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 32. [Google Scholar] [CrossRef]
- Li, Q.; Ma, D.; Zhang, Y.; Liu, Y.; Ma, Y.; Hu, D. Insights into Controlling Factors of Pore Structure and Hydraulic Properties of Broken Rock Mass in a Geothermal Reservoir. Lithosphere 2022, 2021, 3887832. [Google Scholar] [CrossRef]
- Meng, F.; Liu, W.; Pu, H.; Li, M.; Chen, Y. The Influence of Grain Size Gradation on Deformation and the Void Structure Evolution Mechanism of Broken Rock Mass in the Goaf. Appl. Sci. 2024, 14, 6764. [Google Scholar] [CrossRef]
- Zhang, B.; He, Q.; Lin, Z.; Li, Z. Experimental study on the flow behaviour of water-sand mixtures in fractured rock specimens. Int. J. Min. Sci. Technol. 2021, 31, 377–385. [Google Scholar] [CrossRef]
- Cao, C.; Xu, Z.G.; Chai, J.R.; Li, Y.Q. Radial fluid flow regime in a single fracture under high hydraulic pressure during shear process. J. Hydrol. 2019, 579, 124142. [Google Scholar] [CrossRef]
- Feng, S.X.; Chai, J.R.; Xu, Z.G.; Qin, Y.; Li, Y.L. Test Study on the Suffusion Process of Sand-Rock Mixtures by NMR Systems. Geotech. Test. J. 2020, 43, 1286–1299. [Google Scholar] [CrossRef]
- Romano, V.; Bigi, S.; Carnevale, F.; Hyman, J.D.; Karra, S.; Valocchi, A.J.; Tartarello, M.C.; Battaglia, M. Hydraulic characterization of a fault zone from fracture distribution. J. Struct. Geol. 2020, 135, 104036. [Google Scholar] [CrossRef]
- Wang, M.; Yang, W.; Zhou, Z.; Yang, J.; Yang, F.; Sheng, S. Experimental study on fractal characteristics of fault filling medium in the tunnel and relationship between fractal dimension and permeability coefficient. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 8, 6. [Google Scholar] [CrossRef]
- Rutqvist, J.; Rinaldi, A.P.; Cappa, F.; Moridis, G.J. Modeling of fault activation and seismicity by injection directly into a fault zone associated with hydraulic fracturing of shale-gas reservoirs. J. Pet. Sci. Eng. 2015, 127, 377–386. [Google Scholar] [CrossRef]
- Banks, E.W.; Hatch, M.; Smith, S.; Underschultz, J.; Lamontagne, S.; Suckow, A.; Mallants, D. Multi-tracer and hydrogeophysical investigation of the hydraulic connectivity between coal seam gas formations, shallow groundwater and stream network in a faulted sedimentary basin. J. Hydrol. 2019, 578, 124132. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, D.; Fang, Q.; Xiong, L.; Yu, L.; Zhou, M. Analytical solutions of non-Darcy seepage of grouted subsea tunnels. Tunn. Undergr. Space Technol. 2020, 96, 103182. [Google Scholar] [CrossRef]
- Cao, C.; Xu, Z.G.; Chai, J.R.; Qin, Y.; Cao, J. Determination method for influence zone of pumped storage underground cavern and drainage system. J. Hydrol. 2021, 595, 126018. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.Y.; Zhang, J.X.; Liu, X.W.; Li, Z.H. Numerical Simulation of Water-Silt Inrush Hazard of Fault Rock: A Three-Phase Flow Model. Rock Mech. Rock Eng. 2022, 55, 5163–5182. [Google Scholar] [CrossRef]
- Dejam, M.; Hassanzadeh, H.; Chen, Z. Pre-Darcy flow in porous media. Water Resour. Res. 2017, 53, 8187–8210. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon; Victor Dalmont: Paris, France, 1856; pp. 304–311. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publishing Company: New York, NY, USA, 1972. [Google Scholar]
- Kececioglu, I.; Jiang, Y. Flow through porous media of packed spheres saturated with water. J. Fluids Eng. 1994, 116, 164–170. [Google Scholar] [CrossRef]
- Dejam, M.; Hassanzadeh, H.; Chen, Z. Shear dispersion in a fracture with porous walls. Adv. Water Resour. 2014, 74, 14–25. [Google Scholar] [CrossRef]
- Kundu, P.; Kumar, V.; Mishra, I.M. Experimental and numerical investigation of fluid flow hydrodynamics in porous media: Characterization of pre-Darcy, Darcy and non-Darcy flow regimes. Powder Technol. 2016, 303, 278–291. [Google Scholar] [CrossRef]
- Arshadi, M.; Khishvand, M.; Aghaei, A.; Piri, M.; Al-Muntasheri, G.A. Pore-scale experimental investigation of two-phase flow through fractured porous media. Water Resour. Res. 2018, 54, 3602–3631. [Google Scholar] [CrossRef]
- Huang, T.; Du, P.; Peng, X.; Wang, P.; Zou, G. Pressure drop and fractal non-Darcy coefficient model for fluid flow through porous media. J. Pet. Sci. Eng. 2020, 184, 106579. [Google Scholar] [CrossRef]
- Muljadi, B.P.; Blunt, M.J.; Raeini, A.Q.; Bijeljic, B. The impact of porous media heterogeneity on non-Darcy flow behaviour from pore-scale simulation. Adv. Water Resour. 2016, 95, 329–340. [Google Scholar] [CrossRef]
- Javadi, M.; Sharifzadeh, M.; Shahriar, K.; Mitani, Y. Critical Reynolds number for nonlinear flow through rough-walled fractures: The role of shear processes. Water Resour. Res. 2014, 50, 1789–1804. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, X.L.; Wang, E.Z. Quantitative Evaluation of the Onset and Evolution for the Non-Darcy Behavior of the Partially Filled Rough Fracture. Water Resour. Res. 2024, 60, 25. [Google Scholar] [CrossRef]
- Macini, P.; Mesini, E.; Viola, R. Laboratory measurements of non-Darcy flow coefficients in natural and artificial unconsolidated porous media. J. Pet. Sci. Eng. 2011, 77, 365–374. [Google Scholar] [CrossRef]
- Sukop, M.C.; Huang, H.; Alvarez, P.; Variano, E.A.; Cunningham, K.J. Evaluation of permeability and non-Darcy flow in vuggy macroporous limestone aquifer samples with lattice Boltzmann methods. Water Resour. Res. 2013, 49, 216–230. [Google Scholar] [CrossRef]
- Zhou, J.Q.; Chen, Y.F.; Wang, L.; Cardenas, M.B. Universal relationship between viscous and inertial permeability of geologic porous media. Geophys. Res. Lett. 2019, 46, 1441–1448. [Google Scholar] [CrossRef]
- Chen, Y.F.; Hu, S.H.; Hu, R.; Zhou, C.B. Estimating hydraulic conductivity of fractured rocks from high-pressure packer tests with an Izbash’s law-based empirical model. Water Resour. Res. 2015, 51, 2096–2118. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Indraratna, B. The role of particle shape on hydraulic conductivity of granular soils captured through Kozeny-Carman approach. Géotech. Lett. 2020, 10, 398–403. [Google Scholar] [CrossRef]
- Rehman, M.; Hafeez, M.B.; Krawczuk, M. A Comprehensive Review: Applications of the Kozeny–Carman Model in Engineering with Permeability Dynamics. Arch. Comput. Methods Eng. 2024, 31, 3843–3855. [Google Scholar] [CrossRef]
- Skjetne, E.; Auriault, J.L. New insights on steady, non-linear flow in porous media. Eur. J. Mech. B-Fluids. 1999, 18, 131–145. [Google Scholar] [CrossRef]
- Liu, M.M.; Chen, Y.F.; Hong, J.M.; Zhou, C.B. A generalized non-Darcian radial flow model for constant rate test. Water Resour. Res. 2016, 52, 9325–9343. [Google Scholar] [CrossRef]
- Zhou, H.W.; Yang, S. Fractional derivative approach to non-Darcian flow in porous media. J. Hydrol. 2018, 566, 910–918. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; AL-Yaarubi, A.; Pain, C.C.; Grattoni, C.A. Non-linear regimes of fluid flow in rock fractures. Int. J. Rock Mech. Min. Sci. 2004, 41, 163–169. [Google Scholar] [CrossRef]
- Xiong, X.; Li, B.; Jiang, Y.; Koyama, T.; Zhang, C. Experimental and numerical study of the geometrical and hydraulic characteristics of a single rock fracture during shear. Int. J. Rock Mech. Min. Sci. 2011, 48, 1292–1302. [Google Scholar] [CrossRef]
- Li, B.; Liu, R.; Jiang, Y. Influences of hydraulic gradient, surface roughness, intersecting angle, and scale effect on nonlinear flow behavior at single fracture intersections. J. Hydrol. 2016, 538, 440–453. [Google Scholar] [CrossRef]
- Zhang, Y.; Chai, J.R.; Cao, C.; Shang, T. Combined influences of shear displacement, roughness, and pressure gradient on nonlinear flow in self-affine fractures. J. Pet. Sci. Eng. 2021, 198, 108229. [Google Scholar] [CrossRef]
- ASTM Standard C192/C192M-13a; Standard Practice for Making and Curing Concrete Test Specimens in the Lab. ASTM International: West Conshohocken, PA, USA, 2013.
- Wu, J.; Feng, M.; Mao, X.; Xu, J.; Zhang, W.; Ni, X.; Han, G. Particle size distribution of aggregate effects on mechanical and structural properties of cemented rockfill: Experiments and modeling. Constr. Build. Mater. 2018, 193, 295–311. [Google Scholar] [CrossRef]
- Feng, M.; Wu, J.; Ma, D.; Ni, X.; Yu, B.; Chen, Z. Experimental investigation on seepage property of saturated broken red sandstone of continuous gradation. Bull. Eng. Geol. Environ. 2018, 77, 1167–1178. [Google Scholar] [CrossRef]
- Talbot, A.N.; Richart, F.E. The Strength of Concrete, Its Relation to the Cement Aggregates and Water. University of Illinois at Urbana Champaign, College of Engineering: Champaign, IL, USA, 1923; pp. 25–30. [Google Scholar]
- Ma, H.; Ruth, D. The microscopic analysis of high Forchheimer number flow in porous media. Transp. Porous Media 1993, 13, 139–160. [Google Scholar] [CrossRef]
- Moutsopoulos, K.N.; Papaspyros, J.; Tsihrintzis, V.A. Experimental investigation of inertial flow processes in porous media. J. Hydrol. 2009, 374, 242–254. [Google Scholar] [CrossRef]
- Mohammad, S.; Salehi, S. Non-darcy flow of water through a packed column test. Transp. Porous Media. 2014, 101, 215–227. [Google Scholar] [CrossRef]
- Xu, Z.; Cao, C.; Chai, J.; Li, Y.; Li, L. Study on non-Darcy seepage characteristic and model of the broken rock mass of fault zone. Chin. J. Rock Mech. Eng. 2023, 42, 4099–4108. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).